2019暑假五年级精英班讲义 第16讲-+期末考试(教师版)
2019暑假五年级精英班讲义 第15讲-+整理与复习(二)(教师版)

÷ ⨯10 。
JY(5)第十五讲 整理与复习(二)解答 姓名1、计算:120 1 10 47 387 693 77答案:11。
407 693 817 11⨯ 37 32 ⨯ 7 ⨯11 19 ⨯ 43解析:原式 = ⨯ ⨯ = ⨯ ⨯ =11 。
387 703 77 32⨯ 43 19 ⨯ 37 7 ⨯112、有 A 、B 、C 三支足球队,每两队比赛一场,比赛结果为A :两胜,共失 2 球;B :进 4 球,失 5 球;C :有一场踢平,进 2 球,失 8 球。
请问:A 与 B 两队间的比分是多少?答案:3:2。
解析:A 队胜了两场,说明它战胜了其他两支球队.C 队有一场平局,说明 它与 B 队打平。
所以比赛的胜负关系是:A 胜 B ,B 平 C ,A 胜 C 。
三场比赛只有一场平局,这场平局就是一个特殊条件,我们来分析它的比 分:由于是平局,只要知道 B 队和 C 队在这场比赛的总进球数,就能知道这 场比赛的比分 B 、C 两队一共进了 6 个球,A 队共失 2 球,说明这 6 个球中射 进 A 队大门的有 2 个,剩下的 4 个都是在 B 和 C 的比赛中打进的,于是这场 平局的比分是 2:2。
B 队共进 4 球失 5 球,可知它在同 A 队的比赛中进 2 球 失 3 球,因此 A 与 B 的比分是 3:2。
3、甲、乙两人星期天一起上街买东西,两人身上所带的钱共计是 86 元。
在人民市场,甲买一双运动鞋花去了所带钱的 4,乙买一件衬衫花去了人民币9 16 元。
这样两人身上所剩的钱正好一样多。
问甲、乙两人原先各带了多少钱?答案:甲 45;乙 41。
解析:把甲所带的钱视为单位“1”,由题意,乙花去16 元后所剩的钱与甲所带 钱的 5 一样多,那么86 -16 元钱正好是甲所带钱的 5+1 ,那么甲原来带了9 95(86 - 16) ÷ ( + 1) = 45 (元),乙原来带了86 - 45 = 41 (元)。
2019年新部编人教版五年级上册语文第16课《松鼠》优秀课件(65页)

在这部分中,从哪些地方可以 看出松鼠是一种漂亮的小动物呢?
食性
它们虽然有时也捕捉鸟雀,却不 是肉食动物,常吃的是杏仁、榛子、 榉实和橡栗。
举例子
杏仁
榛子
榉实
橡栗
外形特征
它们面容清秀,眼睛闪闪发
光,身体矫健,四肢轻快,非
常敏捷,非常机警。玲珑的小 从头到脚 面孔,衬上一条帽缨形的美丽
二、说说下列各句所用的说明方法。
(1)松鼠的叫声很响亮,比黄鼠狼的叫声还要尖些。
(
) (2)松鼠通常一胎能生三四个。
)
作比较
( 列数字
三、选择合适的关联词语填在句子中。
既……又…… 虽然……但…… 只有……才…… 只要……就……
1. 松鼠( 虽然 )有时也捕捉鸟雀,( 但
)
不是肉食动物。
2. 它们在树上做窝,摘果实,喝露水,( 只有 )
三个动词“跑”“躲”“逃”来表示松鼠对 微小危险的快速应变能力,从而更显出它“十分 警觉”的灵性,由此强调它的“乖巧”。
储备粮食
松鼠在秋天拾榛子,塞到老树 空心的缝隙里,塞得满满的, 留到 冬天吃。
聪明
动作 行为
在冬天,他们也常用爪子把雪扒 开,在雪下面找榛子。松鼠轻快 极了,总是小跳着前进,有时也 连蹦带跑。它们的爪子是那样锐 利,动作是那样敏捷,一棵很光 滑的高树,一忽儿就爬上去了。
结构梳理
形体特征
松 两个方面 鼠 三个角度
讨 人 喜
其他习性
欢
主题概括
本文以生动形象的描写及准确而简练的说 明方法介绍了松鼠漂亮的外貌,驯良的习性与 乖巧的行为,表达了作者对松鼠的喜爱之情。
拓展延伸
点击欣赏·松鼠与啄木 鸟
2019年部编人教版五年级语文上册第16课《太阳》精品课件(46页)

太阳的作用
促进动植物的生长
影响煤炭、雨、雪、风的形成 能杀菌、预防和治疗疾病
能带来光明和温暖
一句话,没有太阳,就没有我们这个美 丽可爱的世界。
结尾的一几句话有什么作用? 总结句:
这既是对前两句的总结,也是对全文的总结, 再次强调了太阳的重要性。
我们吃的粮食、蔬菜、水果、肉类, 穿的棉、麻、毛、丝,都和太阳有密切 的关系。
举例子: 以人们的生活实际为例,说明太阳和
人类的关系密切。
埋在地下的煤炭,看起来好像跟太阳没有关系, 其实离开太阳也不能形成,因为煤炭是由远古时代的 植物埋在地层底下变成的。
举例子: 煤的形成离不开太阳,而
人类生活又离不开煤,进一步 说明太阳与人类关系密切。
同学们,你们对太阳有哪些了解?今 天我们来学习一篇课文——《太阳》,看 看通过今天的学习,你会有哪些新的收获。
16 太 阳
普照万物 温暖人间
1.认识5个生字,会写12个生字。正确读写“繁殖、蔬 菜”等词语。(重点) 2.有感情地朗读课文,理解课文内容,了解太阳的有关 知识,初步认识太阳与人类的密切关系,激发对自然科 学的兴趣。(重点) 3.初步学习阅读说明文,学习说明事物的一些方法。 (难点)
地面上的水被太阳晒着的时候,吸收了热,变成了
水蒸气。空气上升时,温度下降,其中的水蒸气凝成了
无数的小水滴,飘浮在空中,变成云。云层里的小水滴
越聚越多,就变成雨或雪落下来。
小水滴
云
水蒸气 水
雨雪
举例子: 水蒸气、云、雨(雪)三者环环相扣,都离不开太阳,
说明太阳在自然界中有很大的作用。
如果没有太阳,地球上将到处是黑暗,到处是 寒冷,没有风、雪、雨、露,没有草、木、鸟、兽, 自然也不会有人。
五年级升六年级暑假课程讲义第16讲——因数与倍数提升拓展专题 人教版

2021五年级升六年级暑假课程讲义第16讲——因数与倍数提升拓展专题一、用推理法解决一个数的因数问题:1.渗透两种数学思想:推理思想、化归思想。
2.学习两类思维方法:推理法、排除法。
[例]向阳小学的舞蹈队有42人,编舞时需要把他们平均分成若干个小队,每小队要求多于2人且少于8人,可以分成几个小队?有几种分法?[分析]每小队的人数应该是42的因数,由此推断每小队的人数可能是1,2, 3,6, 7,14, 21,42,其中1,2, 14, 21,42,不符合每小队要求多于2人且少于8人的要求,所以每小队只能是3人,6人, 7人。
[解答]42÷3=14(个) 42÷6=7(个) 42÷7=6(个)答:可以分成14、7个或6个小队。
有3种分法。
[技巧]解决此类问题的关键是准确找出这个数的所有因数,再根据已知条件判断得出答案。
举一反三:1.五一班有48人,把他们平均分成若干小组,每小组要求多于2人且少于8人,一共可以分成几组?2.妈妈买来30个苹果,让琪琪把它们放在盘子里。
不许一个一个的拿,也不许一次拿完,要每次拿的个数相同,拿到最后一个也不剩。
琪琪共有几种拿法?每种拿法每次各拿几个?3.把36个乒乓球装在盒子里,如果每个盒子装球的个数同样多,且数量比2个多,比20个少,那么共有多少种装法?每种装法各需要几个盒子?二、列方程解答连续偶数的问题:1.渗透三种数学思想:化归思想、符号化思想、方程思想。
2.学习一类思维方法:推理法。
[例]五个连续偶数的和是60,你知道这五个连续的偶数分别是多少吗?[分析]因为这五个偶数是连续的,所以这五个连续偶数的关系就是后一个数比前一个数多2。
我们可以设最小的偶数是x,其他的四个偶数可以表示为x+2,x +4,x+6,x+8,根据它们的和是60列方程解答。
[解答]设:这五个连续偶数分别是x,x+2,x+4,x+6,x+8,则x+x+2+x+4+x+6+x+8 = 605x+20 = 605x = 40x= 8x+2=10,x+4=12,x+6=14,x+8=16答:这五个连续的偶数分别是8,10,12,14,16。
第16讲 圆的方程7种常见考法归类(原卷版)高二数学暑假自学讲义人教A版2019)

第16讲圆的方程7种常见考法归类回顾确定圆的几何要素,在平面直角坐标系中,探索并掌握圆的标准方程与一般方程.知识点1圆的标准方程1.圆的定义:平面上到定点的距离等于定长的点的集合叫做圆,定点称为圆心,定长称为圆的半径.2.圆的要素:是圆心和半径,圆心确定圆的位置,半径确定圆的大小.如图所示.3.圆的标准方程:圆心为A(a,b),半径长为r的圆的标准方程是(x-a)2+(y-b)2=r2.当a=b=0时,方程为x2+y2=r2,表示以原点为圆心、半径为r的圆.注:(1)圆的方程的推导:设圆上任一点M(x,y),则|MA|=r,由两点间的距离公式,得(x-a)2+(y-b)2=r,化简可得:(x-a)2+(y-b)2=r2.(2)当圆心在原点即A(0,0),半径长r=1时,方程为x2+y2=1,称为单位圆.(3)相同的圆,建立坐标系不同时,圆心坐标不同,导致圆的方程不同,但是半径是不变的.(4)圆上的点都满足方程,满足方程的点都在圆上.知识点2点与圆的位置关系(1)根据点到圆心的距离d与圆的半径r的大小判断:d>r⇔点在圆外;d=r⇔点在圆上;d<r⇔点在圆内.(2)根据点M(x0,y0)的坐标与圆的方程(x-a)2+(y-b)2=r2的关系判断:(x 0-a )2+(y 0-b )2>r 2⇔点在圆外;(x 0-a )2+(y 0-b )2=r 2⇔点在圆上;(x 0-a )2+(y 0-b )2<r 2⇔点在圆内.知识点3圆的一般方程1.圆的一般方程的概念当D 2+E 2-4F >0时,二元二次方程x 2+y 2+Dx +Ey +F =0叫做圆的一般方程.注:将方程x 2+y 2+Dx +Ey +F =0,配方可得=D 2+E 2-4F 4,当D 2+E 2-4F >0时,方程x 2+y 2+Dx +Ey +F =0表示圆.当D 2+E 2-4F =0时,方程x 2+y 2+Dx +Ey +F =0,表示一个点-D 2,-2.圆的一般方程对应的圆心和半径圆的一般方程x 2+y 2+Dx +Ey +F =0(D 2+E 2-4F >0)-D 2,-12D 2+E 2-4F .注:圆的一般方程表现出明显的代数结构形式,其方程是一种特殊的二元二次方程,圆心和半径长需要代数运算才能得出,且圆的一般方程x 2+y 2+Dx +Ey +F =0(其中D ,E ,F 为常数)具有以下特点:(1)x 2,y 2项的系数均为1;(2)没有xy 项;(3)D 2+E 2-4F >0.3.常见圆的方程的设法标准方程的设法一般方程的设法圆心在原点x 2+y 2=r 2x 2+y 2-r 2=0过原点(x -a )2+(y -b )2=a 2+b 2x 2+y 2+Dx +Ey =0圆心在x 轴上(x -a )2+y 2=r 2x 2+y 2+Dx +F =0圆心在y 轴上x 2+(y -b )2=r 2x 2+y 2+Ey +F =0与x 轴相切(x -a )2+(y -b )2=b 2x 2+y 2+Dx +Ey +14D 2=0与y 轴相切(x -a )2+(y -b )2=a 2x 2+y 2+Dx +Ey +14E 2=04.二元二次方程Ax 2+Bxy +Cy 2+Dx +Ey +F =0A =C ≠0,=0,2+E 2-4AF >0.5.以A (x 1,y 1),B (x 2,y 2)为直径端点的圆的方程为(x -x 1)(x -x 2)+(y -y 1)(y -y 2)=0.知识点4圆的轨迹问题轨迹和轨迹方程区别:轨迹是指点在运动变化中形成的图形,比如直线、圆等.轨迹方程是点的坐标满足的关系式.1、求圆的标准方程的方法确定圆的标准方程就是设法确定圆心C(a,b)及半径r,其求解的方法:一是待定系数法,建立关于a,b,r的方程组,进而求得圆的方程;二是借助圆的几何性质直接求得圆心坐标和半径.常用到中点坐标公式、两点间距离公式,有时还用到平面几何知识,如“弦的中垂线必过圆心”“两条弦的中垂线的交点必为圆心”等.一般地,在解决有关圆的问题时,有时利用圆的几何性质作转化较为简捷.2、判断点与圆的位置关系的方法(1)确定圆的方程:化为(x-a)2+(y-b)2=r2.(2)将点的坐标代入代数式(x-a)2+(y-b)2,比较代数式的值与r2的大小关系.(3)下结论:若(x-a)2+(y-b)2=r2,表示点在圆上;若(x-a)2+(y-b)2>r2,表示点在圆外;若(x-a)2+(y-b)2<r2,表示点在圆内.此外,也可以利用点与圆心的距离d与半径r的大小关系来判断.当d>r时,点在圆外;当d=r时,点在圆上;当d<r时,点在圆内.3、圆的一般方程辨析判断二元二次方程与圆的关系时,一般先看这个方程是否具备圆的一般方程的特征,当它具备圆的一般方程的特征时,再看它能否表示圆.此时有两种途径:一是看D2+E2-4F是否大于零;二是直接配方变形,看方程等号右端是否为大于零的常数.4、方程x2+y2+Dx+Ey+F=0表示的图形5、利用待定系数法求圆的方程的解题策略(1)如果由已知条件容易求得圆心坐标、半径或需利用圆心的坐标或半径列方程,一般采用圆的标准方程,再用待定系数法求出a ,b ,r .(2)如果已知条件与圆心和半径都无直接关系,一般采用圆的一般方程,再用待定系数法求出常数D ,E ,F .6、求与圆有关的轨迹问题的方程(1)直接法:直接根据题目提供的条件列出方程.(2)定义法:根据圆、直线等定义列方程.(3)代入法:找到要求点与已知点的关系,代入已知点满足的关系式等.7、用代入法求轨迹方程的一般方法8、圆上的点到定点的最大、最小距离设A 的方程222()()x a y b r -+-=,圆心(,)A a b ,点M 是A 上的动点,点P 为平面内一点;记||d PA =;①若点P 在A 外,则max ||PM d r =+;min ||PM d r =-②若点P 在A 上,则max ||2PM r =;min ||0PM =③若点P 在A 内,则max ||PM d r =+;min ||PM r d =-9、与圆有关的最值问题常见的几种类型(1)形如u =y -bx -a形式的最值问题,可转化为过点(x ,y )和(a ,b )的动直线斜率的最值问题.(2)形如l =ax +by 形式的最值问题,可转化为动直线y =-a b x +lb截距的最值问题.(3)形如(x -a )2+(y -b )2形式的最值问题,可转化为动点(x ,y )到定点(a ,b )的距离的平方的最值问题.考点一:求圆的标准方程(一)由圆的标准方程求圆心、半径例1.(2023秋·高二课时练习)已知圆C 的标准方程为()22113x y -+=,则此圆的圆心及半径长分别为()A .()1013r =,,B .()10r =,,C .()1013r -=,,D .()10r -=,,变式1.(2023秋·高二单元测试)圆()()22437x y ++-=的圆心和半径分别是()A .()4,3,7-B .()4,3-C .()4,3,7-D .()4,3-变式2.(2023·江苏·高二假期作业)已知圆C 的标准方程为()()22112x y -+-=,则圆心C 的坐标为________,圆的面积为________.(二)求圆的标准方程例2.(2023春·河北邯郸·高二统考期末)已知圆C 的圆心为点()2,1C ,且经过原点,则圆C 的标准方程为__________.变式1.(广东省广州市培正中学2022-2023学年高二上学期期中数学试题)求圆心在y 轴上,半径为1,且过点(1,2)的圆的标准方程.变式2.(福建省泉州外国语中学2022-2023学年高二上学期期中质量监测数学试题)与x 轴相切,且圆心坐标为()1,2--的圆的标准方程为_______________变式3.(2023春·重庆沙坪坝·高一重庆八中校考期末)在平面直角坐标系xOy 中,已知()10,2P 、()24,4P 两点,若圆M 以12PP 为直径,则圆M 的标准方程为()A .()()22235x y -+-=B .()()2223x y -+-=C .()()22145x y -+-=D .()()2214x y -+-=变式4.(2023·江苏·高二假期作业)求经过点()1,1P 和坐标原点,并且圆心在直线2310x y ++=上的圆的方程.变式5.(广东省肇庆市百花中学2022-2023学年高二上学期期中数学试题)直线1:25120l x y +-=与直线2:310l x y -++=相交于点A ,直线l 过点A 且与直线210x y -+=平行.(1)求直线l 的方程;(2)求圆心在直线l 上且过点()()0,0,2,0O B 的圆的方程.考点二:圆的一般方程(一)圆的一般方程辨析例3.(2023秋·江苏盐城·高二盐城市伍佑中学校考期末)方程2220x y y m +++=表示一个圆,则m的取值范围是()A .()1,+∞B .(),1-∞C .[)1,+∞D .(],1-∞变式1.(2023秋·河南许昌·高二禹州市高级中学校考阶段练习)方程222210x y ax ay a +-+++=表示圆,则实数a 的可能取值为()A .1B .2C .0D .2-(二)由圆的一般方程求圆心、半径例4.(上海市第三女子中学2022-2023学年高二下学期期中数学试题)圆22240x y x y ++-=的圆心坐标是________.变式1.(2023春·湖北武汉·高二武汉市新洲区第一中学校考开学考试)已知圆C :22430x y y +-+=,则圆C 的圆心和半径为()A .圆心(0,2),半径1r =B .圆心(2,0),半径1r =C .圆心(0,2),半径2r =D .圆心(2,0),半径2r =变式2.(2023秋·高二课时练习)圆C :224230x y x y ++-+=的圆心是_____,半径是_____.(三)求圆的一般方程例5.(2023秋·新疆克拉玛依·高二克拉玛依市高级中学校考期中)求适合下列条件的圆的方程:(1)圆心在直线230x y --=上,且过点()()2,3,2,5A B ---的圆;(2)过三点()()()1,0,1,2,3,2A B C ---的圆.变式1.(2023·河南·校联考模拟预测)已知圆C 经过抛物线248y x x =--与x 轴的交点,且过点(0,2),则圆C 的方程为______.变式2.(2023·河南郑州·模拟预测)已知点(2,1),(1,0),(2,3),(,2)A B C D a --四点共圆,则点D 到坐标原点O 的距离为______.变式3.(2023·江苏·高二假期作业)过坐标原点,且在x 轴和y 轴上的截距分别为2和3的圆的方程为()A .22230x y x y +--=B .22230x y x y ++-=C .22230x y x y +-+=D .22230x y x y +++=变式4.(2023秋·高二校考课时练习)已知圆经过点(2,1)和(1,0)-,该圆与两坐标轴的四个截距之和为2-,求圆的方程.考点三:根据对称性求圆的方程例6.(2023秋·重庆荣昌·高二重庆市荣昌永荣中学校校考期中)圆()()22124x y ++-=关于直线0y =对称的圆的标准方程为______.变式1.(2023秋·高二单元测试)圆()()22141x y ++-=关于直线y x =对称的圆是()A .()()22141x y ++-=B .()()22141x y -+-=C .()()22411x y ++-=D .()()22411x y -++=变式2.(2023·全国·高三专题练习)与圆22:20C x y x y +-+=关于直线:0l x y +=对称的圆的标准方程是______.变式3.(2023秋·高二课时练习)已知圆2212210:C x y x y -=+++,圆2C 与圆1C 关于直线10x y --=对称,则圆2C 的方程为()A .224470x y x y +-++=B .224470x y x y +--+=C .224470x y x y ++++=D .224470x y x y ++-+=变式4.(2023春·河南开封·高二统考期末)已知圆221:4C x y +=与圆2C 关于直线250x y ++=对称,则圆2C 的标准方程为()A .()()22424x y +++=B .()()22424x y -+-=C .()()22244x y +++=D .()()22244x y -+-=变式5.(2023秋·高二课时练习)求圆22412390x y x y ++-+=关于直线3450x y --=的对称圆方程.考点四:点与圆的位置关系例7.【多选】(2023秋·高二课时练习)(多选)下列各点中,不在圆22(1)(2)25x y -++=的外部的是()A .(0,2)B .(3,3)C .(2,2)-D .(4,1)变式1.(2023·江苏·高二假期作业)写出圆心为3(2,)A -,半径为5的圆的标准方程,并判断点122())5,7,,1(M M ---是否在这个圆上.若该点不在圆上,说明该点在圆外还是在圆内?变式2.(2023秋·高二校考课时练习)若点()1,1a a +-在圆22240x y ay +--=的内部,则a 的取值范围是().A .1a >B .01a <<C .115a -<<D .1a <变式3.(2023秋·高二课时练习)点()5,P m 与圆2224x y +=的位置关系是()A .点在圆上B .点在圆内C .点在圆外D .不确定考点五:圆过定点问题例8.(2023秋·山西晋中·高二山西省平遥中学校校考期中)若圆()()22222320C x y m x m y m m +--+-+-+=:过坐标原点,则实数m 的值为()A .1B .2C .2或1D .-2或-1变式1.(2023·高二课时练习)点(),P x y 是直线250x y +-=上任意一点,O 是坐标原点,则以OP 为直径的圆经过定点()A .()0,0和()1,1B .()0,0和()2,2C .()0,0和()1,2D .()0,0和()2,1变式2.(2023·全国·高三专题练习)若抛物线2y x ax b =++与坐标轴分别交于三个不同的点A 、B 、C ,则ABC 的外接圆恒过的定点坐标为_______变式3.(2023春·上海徐汇·高二上海中学校考期中)对任意实数m ,圆2236920x y mx my m +--+-=恒过定点,则定点坐标为__.变式4.(2023秋·四川内江·高二四川省内江市第六中学校考阶段练习)已知曲线C :()()2211480a x a y x ay +++-+=.(1)当a 取何值时,方程表示圆?(2)求证:不论a 为何值,曲线C 必过两定点.(3)当曲线C 表示圆时,求圆面积最小时a 的值.考点六:与圆有关的轨迹问题例9.(上海市上海中学2022-2023学年高二下学期期中数学试题)点M 与两个定点()0,0O ,()2,0P 的距离的比为3:1,则点M 的轨迹方程为______.变式1.(2023秋·高二课时练习)已知圆C :2286160x y x y +--+=,过点(4,1)P 的直线与圆C 交于点M ,N ,线段MN 的中点为Q ,则点Q 的轨迹方程为___________.变式2.(2023秋·安徽阜阳·高二校联考阶段练习)已知圆E 经过点()()0,0,1,1A B ,且被直线()0R mx y m m --=∈平分.(1)求圆E 的一般方程;(2)设P 是圆E 上的动点,求线段AP 的中点M 的轨迹方程.变式3.(2023秋·山东日照·高二校考阶段练习)已知圆C 经过点()()3,11,3A B -,且圆心C 在直线320x y --=上.(1)求圆C 方程;(2)若E 点为圆C 上任意一点,且点()4,0F ,求线段EF 的中点M 的轨迹方程.变式4.(2023秋·高二课时练习)正方形ABCD 与点P 在同一平面内,已知该正方形的边长为1,且222PA PB PC +=,则PD 的取值范围为___________.变式5.【多选】(2023秋·高一单元测试)已知点()1,0A ,()2,0B -动点P 满足2PA PB=,则下面结论正确的为()A .点P 的轨迹方程为22(3)4x y ++=B .点P 到原点O 的距离的最大值为5C .PAB 面积的最大值为4D .PA PB ⋅的最大值为18考点七:与圆有关的最值问题例10.(2023秋·四川巴中·高二统考期末)已知圆C 过点()()2,024A B ,,-,当圆C 到原点O 的距离最小时,圆C 的标准方程为______.变式1.(2023秋·高二课时练习)已知圆C 经过点()1,0A ,且圆心在直线21y x =-上运动,求当半径最小时的圆的标准方程为_______________变式2.(2023秋·高二课时练习)圆过点(1,2),(1,4)A B --,求面积最小的圆的方程为_________变式3.(2023秋·高二课时练习)如果圆的方程为22220x y kx y k ++++=,那么当圆面积最大时,该圆的方程为________,最大面积为________.变式4.(2023春·山东青岛·高二校联考期中)圆2244100x y x y +---=上的点到直线60x y ++=的最大距离是()A .22B .42C .82D .1621.(2020·山东·统考高考真题)已知圆心为()2,1-的圆与y 轴相切,则该圆的标准方程是()A .()()22211x y ++-=B .()()22214x y ++-=C .()()22211x y -++=D .()()22214x y -++=2.(2022·全国·统考高考真题)设点M 在直线210x y +-=上,点(3,0)和(0,1)均在M 上,则M 的方程为______________.3.(2022·全国·统考高考真题)过四点(0,0),(4,0),(1,1),(4,2)-中的三点的一个圆的方程为____________.4.(2022·北京·统考高考真题)若直线210x y +-=是圆22()1x a y -+=的一条对称轴,则=a ()A .12B .12-C .1D .1-一、单选题1.(2023·江苏·高二假期作业)将圆222440x y x y +--+=平分的直线是()A .10x y +-=B .30x y ++=C .10x y -+=D .30x y -+=2.(2022秋·高二课时练习)若点()12P -,是圆()()22:4325C x y ++-=的弦MN 的中点,则弦MN 所在的直线方程为()A .350x y --=B .350x y +-=C .350x y -+=D .350x y ++=3.(2022秋·高二课时练习)过三点()()()4,2,1,1,14A B C --,的圆的一般方程为()A .227320x y x y ++-+=B .227320x y x y ++++=C .227320x y x y +-++=D .227320x y x y +--+=4.(2021秋·高二课时练习)已知圆C 与圆2220x y y +-=关于直线20x y --=对称,则圆C 的方程是()A .()2211x y ++=B .()()22321x y -++=C .()()22321x y ++-=D .()()22231x y ++-=5.(2023·重庆·高二统考学业考试)已知圆C 的一条直径的两个端点是分别是(1,1)O 和(3,3)A ,则圆的标准方程是()A .()222(2)1x y -+-=B .()222(2)2x y -++=C .()222(2)2x y -+-=D .()222(2)2x y +++=6.(2023·广东佛山·统考模拟预测)已知圆C :()2214x y -+=,过点()0,1A 的两条直线1l ,2l 互相垂直,圆心C 到直线1l ,2l 的距离分别为1d ,2d ,则12d d 的最大值为()A .2B .1C D .47.(2021秋·广东深圳·高二深圳中学校考期中)过定点A 的动直线0x ky +=和过定点B 的动直线210kx y k --+=交于点M ,则MA MB +的最大值是()A .B .3C D8.(2023春·辽宁·高一辽宁实验中学校考期中)已知A ,B ,P 是直径为4的圆上的三个动点,且AB = 则PA PB ⋅ 最小值为()A .4-B .3-C .2-D .1-二、多选题9.(2023·江苏·高二假期作业)若直线240mx ny +-=始终平分圆224240x y x y +---=的周长,则mn 的取值可能是()A .12B .-12C .13D .210.(2023·辽宁葫芦岛·统考二模)过四点()()()()0,0,4,0,1,1,4,2-中的三点的圆的方程为()A .22(2)(1)5x y -+-=B .22(2)(3)13x y -+-=C .2247()()2233x y -+-=D .2289()(1)55x y -+-=11.(2022·高二课时练习)设有一组圆k C :22()()4x k y k -+-=(R)k ∈,下列命题正确的是()A .不论k 如何变化,圆心C 始终在一条直线上B .所有圆kC 均不经过点(30),C .经过点(22),的圆k C 有且只有一个D .所有圆的面积均为412.(2023·江苏·高二假期作业)已知曲线22:0C Ax By Dx Ey F ++++=()A .若1AB ==,则C 是圆B .若0A B =≠,2240D E AF +->,则C 是圆C .若0A B ==,220DE +>,则C 是直线D .若0A ≠,0B =,则C 是直线13.(2023秋·高二课时练习)已知圆222410x y x y ++-+=关于直线220ax by -+=(),a b ∈R 对称,则下列结论正确的是()A .圆222410x y x y ++-+=的圆心是(1,2)-B .圆222410x y x y ++-+=的半径是2C .1a b +=D .ab 的取值范围是1,4⎛⎤-∞ ⎥⎝⎦三、填空题14.(2023秋·高二课时练习)圆222()()x a y b r -+-=过原点,则a ,b ,r 应满足的条件是__________.15.(2023春·上海宝山·高二统考期末)若()222220x m m y mx m ++++=表示圆,则实数m 的值为______.16.(2023秋·高二课时练习)过点()8,0A 的直线与圆224x y +=交于点B ,则线段AB 中点P 的轨迹方程为___________.17.(2023秋·高二课时练习)已知实数x y ,满足22430x y x +-+=,则()()2223x y ++-的最大值为_________.18.(2023秋·高二课时练习)已知()2,0A -,()2,0B ,动点M 满足2MA MB =,则点M 的轨迹方程是______.四、解答题19.(2023秋·四川南充·高二四川省南充高级中学校考期末)已知方程222440x y x y m +-++=.(1)若此方程表示圆,求实数m 的取值范围;(2)若m 的值为(1)中能取到的最大整数,则得到的圆设为圆E ,若圆E 与圆F 关于y 轴对称,设(),P x y 为圆F 上任意一点,求(),P x y 到直线10x y +-=的距离的最大值和最小值.20.(2023·全国·高三专题练习)在直角坐标系xOy 中,线段4MN =,且两个端点M 、N 分别在x 轴和y 轴上滑动.求线段MN 的中点C 的轨迹方程;21.(2023秋·高二课时练习)求经过三点()0,0,()3,2,()4,0-的圆的方程.22.(2023秋·高二课时练习)已知圆C ,圆心在直线20x y --=上,且过点()2,1-,求圆C 的标准方程.23.(2023·江苏·高二假期作业)赵州桥位于我国河北省,是我国现存最早、保存最好的巨大石拱桥.如图所示,赵州桥是一座空腹式的圆弧形石拱桥,利用解析几何的方法,用赵州桥的跨度a 和圆拱高b 表示出赵州桥圆弧所在圆的半径.24.(2023秋·高二课时练习)已知点()12A -,和()3,4B ,求:(1)线段AB的垂直平分线l的方程;(2)以线段AB为直径的圆的标准方程.。
五年级数学暑期培训班总复习资料

第一讲.因数与倍数(自然数)一.知识点1.因数、倍数概念:如果a×b=c(a、b、c都是不为0的整数)我们就说a和b都是c的因数c是a的倍数也是b的倍数。
倍数和因数是相互依存的。
2.一个数的因数个数是有限的,最小因数是1,最大因数是它本身。
一个数的倍数个数是无限的,最小倍数是它本身,没有最大倍数。
3.2、3、5倍数的特征(1)2的倍数的特征:个位上是0、2、4、6、8(双数)。
是2的倍数的数叫做偶数(个位是双数);不是2的倍数的数叫做奇数(个位是单数)。
(2)5的倍数特征:个位上是0、5。
(3)3的倍数的特征:一个数各位数上的和是3的倍数这个数是3的倍数。
4.质数和合数。
(1)一个数,如果只有1和它本身两个因数,这样的数叫做质数(素数)。
最小的质数是2。
(2)一个数,除了1和它本身还有别的因数,这样的因数叫做合数。
最小的合数是4,合数至少有三个因数。
(3)0、1既不是质数,也不是合数。
(4)20以内质数:合数:5.质因数和分解质因数。
(1)每个合数都可以写成几个质数相乘的形式。
其中每个质数都是这个合数的因数,叫做这个合数的质因数。
(2)把一个合数用质因数相乘的形式表示出来,叫做分解质因数。
例:30=2×3×56.最大公因数和最小公倍数。
(1)几个数公有的因数,叫做这几个数的公因数,其中最大的一个,叫做这几个数的最大公因数。
(2)几个数公有的倍数,叫做这几个数的公倍数,其中最小的一个,叫做这几个数的最小公倍数。
7.互质数:公因数只有1的两个数,叫做互质数。
8.两数能整除时:最大公因数是:最小公倍数是:两数互质时::最大公因数是:最小公倍数是:二.新授例题15的倍数:10的倍数:15的倍数:18的因数:24的因数36的因数:28的因数:巩固练习1.一个数最小的因数是(),最大的因数是(),因数的个数是(),一个数的最小倍数是(),倍数的个数是()。
2.56的因数有哪些?100的因数有哪些?3.a×b=c, 所以()和()是()的因数;()是()和()的倍数;q÷c=x,所以()是()和()的倍数。
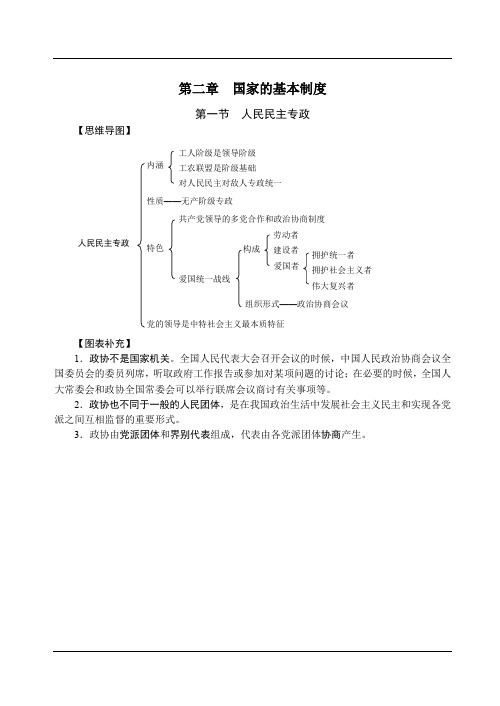
独角兽2019基础讲义-第16节宪法-国家的基本制度(1)-杨帆
制
政党或人民团体可以单独或联合推荐;选民或代表 10 人以上联合推荐
度
直接选举:多于应选名额 1/3 至 1 倍;间接多于 1/5-1/2 候选人提名
代表候选人不得接受境外提供的与选举有关的任何形式的资助
初步的候选人名单选举日 15 日前公布,正式候选人名单 7 日前公布
赞成、反对、弃权、另选其他选民
【思维导图】
第三节 文化、社会制度
以意识形态为核心,《魏玛宪法》首次全面系统规定
文化制度
发展教育事业
发展科学事业
文
内容
化
发展文学艺术和其他文化事业
社
倡导核心价值观,开展道德教育
会
制
特征
平等、公平、法治
度
社会保障制度
同经济发展水平适应
社会制度
医疗卫生事业
内容
劳动保障制度
人才培养
计划生育
同经济和社会发展计划适应
【思维导图】
第四节 人民代表大会制度
人民代表大会制度
内容
人民主权 人大是人民行使权力的机关 代表由人民选举,受人民监督 人大产生其他机关,受其监督,对其负责
性质
根本政治制度 实现民主的基本形式
【图表补充】
1.人民代表大会制度是我国的政权组织形式。 2.资本主义国家的政权组织形式有:
定义、特征
举例
以君主为核心,由君主在国家体系中发挥主导作用的政权组织形式。其主要特
日本
国家设有总统,总统既是国家元首,又是政府首脑;总统由选民选举产生,不
总统制
美国
对议会负责,议会不能通过不信任案迫使总统辞职,总统也无权解散议会。
议员由选民选举产生,政府由获得议会下院多数席位的政党或构成多数席位的 议会共和
2019暑假五年级精英班讲义 第10讲-+应用题综合(教师版)

四季教育-2018 年-夏季-精英班-五年级-第 10 讲+ ) - JY(5)第十讲 应用题综合解答一、例题选讲1、由于天气逐渐变冷,牧场上的草每天以均匀的速度减少。
经计算,牧 场上的草可供20头牛吃5天,或可供16头牛吃6天。
那么,可供11头牛吃几天?答案:8。
解析:设 1 头牛 1 天的吃草量为 1,6-5=1 天自然减少的草量为 20×5-16×6=4,原有草量为:(20+4)×5=120。
若有 11 头牛来吃草,每天草减少 11+4=15;所以可供 11 头牛吃 120÷15=8(天)。
2、有一批书,小明 9 天可装订 3 ,小丽 20 天可装订 5 ,小明和小丽两个 4 6人合做几天可以装订完?答案:8。
解析:小明装订完一批书所需的天数:9÷ 3 =12(天);小丽装订完一批书 4 所需的天数:20÷ 5 =24(天);所以,小明和小丽两个人合做装订完一批书所6 需的天数:1÷( 1 1 =8(天)。
12 243、五(一)班原计划抽 1的人参加大扫除,临时又有 2 个同学主动参加,实5 际参加扫除的人数是其余人数的 1 。
原计划抽多少个同学参加大扫除?3答案:8。
解析:又有 2 个同学参加扫除后,实际参加扫除的人数与其余人数的比是 1: 3 ,实际参加人数比原计划多 1 1 = 1 。
即全班共有 2 ÷ 1 = 40 (人)。
原计 划抽 40 ⨯ 1 = 8 (人)参加大扫除。
51 + 3 5 20 204、同学们可能知道,歌星、影星一般都不愿意公开自己的年龄。
这个小 故事说的就是一个记者千方百计要从一个女影星嘴里打听出她的年龄。
影星不 想说谎,却又不愿意把自己的年龄讲出来,于是就对记者说:“我 5 年后岁数 的 5 倍,减去我 5 年前岁数的 5 倍,正好是我现在的年龄。
”记者想了半天,还 是没有想出来影星的年龄。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
JY(5)第十六讲期末测试卷解答姓名
(共20 题,每题5 分,满分100 分,60 分钟完成。
★当堂讲评)
一、基础篇
1、计算:0.125×7.37+ 1
×2.63= 。
8
答案:1.25。
解析:原式= 0.125⨯(7.37 + 2.63) = 1.25 。
知识点:计算—小数巧
算
2、小明的妈妈比小明大24 岁,那么妈妈岁时,她的年龄是小明的9 倍。
答案:27。
解析:设小明的年龄是“1”,妈妈的年龄是“9”,两人年龄相差“8”=
24 岁,所以“1”=3岁,所以妈妈3×9=27岁。
知识点:应用题—年
龄问题
3、四年级一班有6 名女学生,她们的平均身高是140 厘米。
如果她们当
中有1 人离开,剩下5 人的平均身高就变成135 厘米,请问:离开的那个女生身高是厘米。
答案:165。
解析:6 个女生的平均身高是140 厘米,那么她们的总身高就是140×
6=840 厘米。
一个女生离开之后,余下5个人的平均身高是135 厘米,那么总身高就是135×5=675厘米。
又知两次总身高相差的就是离开的女生的身高,因此离开的女生的身高是840-675=165 厘米。
知识点:应用题—平均数问题
4、象棋兴趣小组一共有5 名同学,如果从中选3 名同学去参加一次全市
比赛,一共有种选法。
答案:10。
解析:从5名同学中,任意选取3名去参加比赛,选取的顺序是无所谓的,则共有5×4×3÷(3×2×1)=10 种不同的选择。
知识点:组合数学—组合
+ 5、一项工程,甲单独做需要 28 天时间,乙单独做需要 21 天时间,如果 甲、乙合作需要 天。
答案:12 解析:将整个工程的工作量看作“1”个单位,那么甲每天完成总量的 1
28 ,乙每天完成总量的 1 ,两人合作每天能完成总量的 1 1 = 1 ,所以两人合 21 作的话,需要1 ÷ 1
= 12 天能够完成。
12 知识点:应用题—工程问题
28 21 12
6、某餐馆有 27 道招牌菜。
兰兰吃过其中的 13 道,英英吃过其中的 7 道,而且有 2 道菜是两人都吃过的。
那么有 道招牌菜是两人都没有吃过 的。
答案:9。
解析:至少被一人吃过的有 13+7-2=18 道。
两人都没吃过的有 27-18=9 道。
知识点:组合数学—重叠原理
7、7 个连续质数从大到小排列是 a , b , c , d , e , f , g ,已知它们的和是偶数, 那么 d 是 。
答案:7。
解析:因为 7 个质数的和是偶数,所以这 7 个质数不可能都是奇数。
我们 知道是偶数的质数只有 2,因此这 7 个质数中必有一个是 2。
又因为 2 是最小 的质数,并且这 7 个连续质数是从大到小排列的,所以 g = 2 ,其他 6 个数从大 到小依次是 17、13、11、7、5、3。
这样 d = 7 。
知识点:数论—质数合数分解质因数
8、如下图, DE 平行于 BC ,且 AD =3, AB =9, AE = 4 ,则 AC 的长为。
答案:12。
四季教育-2018 年-夏季-精英班-五年级-第16 讲
解析:由D E 平行于B C 得△ADE∽△ABC,则AD = AE = DE = 3 = 1 ,所以
AB AC BC 9 3
四季教育-2018 年-夏季-精英班-五年级-第16 讲
AC =4÷
1 =12。
3
知识点:图形问题—相似应用题
9、四个人进行象棋单循环赛,规定胜者得2 分,负者得0 分,和棋双方各得1 分,比赛结束后统计发现,四个人的得分加起来一定是分。
答案:12。
解析:四个人循环比赛总共比赛4⨯ 3 ÷ 2 = 6 (场),每场无论分出胜负还是打平,两人的得分和一定是2分,因此最终四个人的得分加起来一定是
2 ⨯ 6 = 12 (分)。
知识点:组合数学—体育比赛问题
10、牧场上长满牧草,每天牧草都匀速生长。
这片牧场可供10 头牛吃20 天,可供15 头牛吃10 天。
供25 头牛可吃天。
答案:5。
解析:设1头牛1天的吃草量为“1”,10 头牛吃20 天共吃了10 ⨯ 20 = 200 份;15 头牛吃10 天共吃了15 ⨯10 = 150 份。
第一种吃法比第二种吃法多吃了200 - 150 = 50 份草,这50 份草是牧场的草20 - 10 = 10 天生长出来的,所以每天
生长的草量为50 ÷10 = 5 ,那么原有草量为:200 - 5 ⨯ 20 = 100 。
供 25 头牛吃,若有 5 头牛去吃每天生长的草,剩下 20 头牛需要100 ÷ 20 = 5 (天)可将原有牧草吃完,即它可供25 头牛吃5天。
知识点:应用题—牛吃草
二、拓展篇
••••
11、计算:0.91+ 0.82+ 0.73+ 0.6 4
答案:31 。
9
解析:原式= 82 + 74 + 66 + 58 = 28 =3 1 。
90 90 90 90 9 9
知识点:计算—循环小数
1 1
12、一根木杆,第一次截去了全长的2 ,第二次截去全长的3 ,第三次截
1。
