2010年湖北十堰中考数学试题(word版)(有答案)
2010湖北武汉市中考数学试卷及答案 全word

2010湖北武汉市中考数学试卷亲爱的同学,在你答题前,请认真阅读下面以及“答卷”上的注意事项:1. 本试卷由第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分组成。
全卷共6页,三大题,满分120 分。
考试用时120分钟。
2. 答题前,请将你的姓名、准考证号填写在“答卷”相应位置,并在“答卷”背面左上角填写姓 名和准考证号后两位。
3. 答第Ⅰ卷(选择题)时,选出每小题答案后,用2B 铅笔把“答卷”上对应题目的答案标号涂 黑。
如需改动,用橡皮擦干净后。
再选涂其它答案,不得答在“试卷”上。
4. 第Ⅱ卷(非选择题)用0.5毫米黑色笔迹签字笔书写在“答卷”上。
答在“试卷”上无效。
预祝你取得优异成绩! 第Ⅰ卷 (选择题,共36分)一、选择题 (共12小题,每小题3分,共36分) 下列各题中均有四个备选答案,其中有且只有一个正确,请在答卷上将正确答案的代号涂黑。
1. 有理数-2的相反数是 (A) 2 (B) -2 (C)21 (D) -21。
2. 函数y =1-x 中自变量x 的取值范围是 (A) x ≥1 (B) x ≥ -1 (C) x ≤1 (D) x ≤ -1 。
3. 如图,数轴上表示的是某不等式组的解集,则这个不等式组可能是(A) x > -1,x >2 (B) x > -1,x <2 (C) x < -1,x <2 (D) x <-1,x >2 。
4. 下列说法: “掷一枚质地均匀的硬币一定是正面朝上”; “从一副普通扑克牌中任意抽取 一张,点数一定是6”;(A) 都正确 (B) 只有 正确 (C) 只有 正确 (D) 都错误 。
5. 2010年上海世博会开园第一个月共售出门票664万张,664万用科学计数法表示为(A) 664⨯104 (B) 66.4⨯105 (C) 6.64⨯106 (D) 0.664⨯107 。
6. 如图,△ABC 内有一点D ,且DA =DB =DC ,若∠DAB =20︒,∠DAC =30︒,则∠BDC 的大小是 (A) 100︒ (B) 80︒ (C) 70︒ (D) 50︒ 。
湖北十堰中考数学试题版有答案.doc

绝密*启用前:湖北省十堰市2010年初中毕业生学业考试数学试题卷注意事项:本试卷分为试题卷和答题卡两部分,考试时间为120分钟,满分120分.一、仔细选一选(本题有10个小题,每小题3分,共30分)下面每小题给出的四个选项中,只有一个是正确的,请把正确选项的字母填在答题卷中相应的格子内.注意可以用多种不同的方法选取正确答案. 1.(2010.十堰)-3的绝对值是( C )A .13B .-13C .3D .-32.(2010.十堰)下列运算中正确的是( D )A .a 3a 2=a 6B .(a 3)4= a 7C .a 6 ÷ a 3 = a 2D .a 5 + a 5 =2 a 5 3.(2010.十堰))据人民网5月20日电报道:中国森林生态系统年涵养水源量4947.66亿立方米,相当于12个三峡水库2009年蓄水至175米水位后库容量,将4947.66亿用科学记数法表示为( C ) A .4.94766×1013 B .4.94766×1012 C .4.94766×1011 D .4.94766×1010 4.(2010.十堰)若一个几何体的三视图如图所示,则这个几何体是( A ) A .三棱柱 B .四棱柱 C .五棱柱 D .长方体错误!未指定书签。
5.要了解哪种品牌最畅销,公司经理最关心的是上述数据找( B ) A .平均数 B .众数 C .中位数 D .方差 6.(2010.十堰)如图,将△ABC 绕点C 顺时针方向旋转40°得△A ’CB ’,若AC ⊥A’B’,则∠BAC 等于( A )A .50°B .60°C .70°D .80° 错误!未指定书签。
7.(2010.十堰)如图,已知梯形ABCD 的中位线为EF ,且△AEF 的面积为6cm 2,则梯形ABCD 的面积为( C ) 错误!未指定书签。
最新整理湖北省十堰市中考数试卷及答案.doc

湖北省十堰市 初中毕业生学业考试数 学 试 题友情提示:Hi ,展示自己的时候到啦,你可要冷静思考、沉着答卷啊!即使遇到困难也不要放弃,要相信自己,能行!祝你取得好成绩!⒈本试卷共8页,25个小题,满分120分,考试时间120分钟.⒉在密封区内写明县(市、区)名、校名、姓名和考号,不要在密封区内答题. ⒊答题时允许使用规定的科学计算器.一、选择题(本题共10个小题,每小题3分,共30分)下面每题给出的四个选项中,只有一个是正确的,请 把你认为正确选项的代号填在下表内题号 1 2 3 4 5 6 7 8 9 10 答案1.5的倒数是A .51B .51- C .-5 D .52.下列长度的三条线段,能组成三角形的是A .1cm ,2 cm ,3cmB .2cm ,3 cm ,6 cmC .4cm ,6 cm ,8cmD .5cm ,6 cm ,12cm3.如图,C 、D 是线段AB 上两点,若CB =4cm ,DB =7cm ,且D 是AC 的中点,则AC 的长等于A .3cmB .6cmC .11cmD .14cm4.如图,在ΔABC 中,AC =DC =DB ,∠ACD =100°,则∠B 等于 A .50° B .40° C .25° D .20°5.把方程2133123+-=-+x x x 去分母正确的是 A.)1(318)12(218+-=-+x x x B .)1(3)12(3+-=-+x x xC .)1(18)12(18+-=-+x x xD .)1(33)12(23+-=-+x x x6.经过某十字路口的汽车,它可以继续直行,也可以向左转或向右转.如果这三种可能性大小相同,则两辆汽车经过这个十字路口全部继续直行的概率是题 号 一 二 三 四 五 六 总分 得 分 评卷人得分 评卷人C B 第4题图DA 第3题图D C BAA .91B .61C .31D .217.如图,桌上放着一摞书和一个茶杯,从左边看到的图形是8.如图,点E 在AD 的延长线上,下列条件中能判断BC ∥AD 的是 A .∠3=∠4 B .∠A +∠ADC =180° C .∠1=∠2 D .∠A =∠59.如图,将ΔPQR 向右平移2个单位长度,再向下平移3个单位长度,则顶点P 平移后的坐标是A . (-2,-4)B . (-2,4)C .(2,-3)D .(-1,-3)10.如果函数x y 2=的图象与双曲线)0(≠=k xky 相交,则当0x < 时,该交点位于A .第一象限B .第二象限C .第三象限D .第四象限二、填空题(本题共6小题,每小题3分,共18分.请将答案直接填写在该题目中的横线上)11. 5月18日晚,中央电视台举办了“爱的奉献”大型募捐活动.据了解,本次活动社会各界共向四川灾区捐款大约1514000000元人民币,这个数字用科学记数法可表示为 元人民币.12.已知,|x |=5,y =3,则=-y x . 13.计算:=---31922a a a .14.如图,直线AB 、CD 相交于点O ,AB OE ⊥,垂足为O , 如果︒=∠42EOD ,则=∠AOC .得分 评卷人第9题图AC 第8题图E E 54321D B 第14题图┌OE A BCD第15题图PRFEA BCDBCA15.如图,已知矩形ABCD ,P 、R 分别是BC 和DC 上的点,E 、F 分别是P A 、PR 的中点.如果DR =3,AD =4,则EF 的长为 . 16.观察下面两行数:根据你发现的规律,取每行数的第10个数,求得它们的和是(要求写出最后的计算结果) .三、解答题(本题共3小题,每小题7分,共21分)17.(7分)计算:022)21(45sin 2)1(--︒+-- 解:022)21(45sin 2)1(--︒+--= =18.(7分)解方程组: ⎩⎨⎧=-=+. ②y x , ① y x 54219.(7分)在同一条件下,对同一型号的汽车进行耗油1升所行驶路程的实验,将收集到的数据作为一个样本进行分析,绘制出部分频数分布直方图和部分扇形统计图.如下图所示(路程单位:km)得分 评卷人2, 4, 8, 16, 32, 64, … ①5, 7, 11, 19, 35, 67, … ②12.5≤x <1312≤x <12.513.5≤x <1413≤x <13.530%30%14≤x <14.513.3%6.7%结合统计图完成下列问题:⑴扇形统计图中,表示135.12x <≤部分的百分数是 ;⑵请把频数分布直方图补充完整,这个样本数据的中位数落在第 组; ⑶哪一个图能更好地说明一半以上的汽车行驶的路程在1413x <≤之间?哪一个图能更好地说明行驶路程在135.12x <≤的汽车多于在5.1414x <≤的汽车?四、应用题(本大题2小题,共15分)20.(7分)海中有一个小岛P ,它的周围18海里内有暗礁,渔船跟踪鱼群由西向东航行,在点A 测得小岛P 在北偏东60°方向上,航行12海里到达B 点,这时测得小岛P 在北偏东45°方向上.如果渔船不改变航线继续向东航行,有没有触礁危险?请说明理由.21.(8分)如图,利用一面墙(墙的长度不超过45m ),用80m 长的篱笆围一个矩形场地.⑴怎样围才能使矩形场地的面积为750m 2?⑵能否使所围矩形场地的面积为810m 2,为什么?得分 评卷人西 东第20题图第21题图五、推理与计算(本大题2小题,共15分)22.(7分)如图,把一张矩形的纸ABCD 沿对角线BD 折叠,使点C 落在点E 处,BE 与AD 交于点F .⑴求证:ΔABF ≌ΔEDF ;⑵若将折叠的图形恢复原状,点F 与BC 边上的点M 正好重合,连接DM ,试判断四边形BMDF 的形状,并说明理由.23.(8分)如图,AB 、BC 、CD 分别与⊙O 切于E 、F 、G ,且AB ∥CD .连接OB 、OC ,延长CO 交⊙O 于点M ,过点M 作MN ∥OB 交CD 于N . ⑴求证:MN 是⊙O 的切线;⑵当0B =6cm ,OC =8cm 时,求⊙O 的半径及MN 的长.第23题图O GCABDN MFE得分 评卷人得分 评卷人C D B A M第22题图F E六、综合应用与探究(本大题2小题,共21分)24.(9分)5月12日,我国四川省汶川县等地发生强烈地震,在抗震救灾中得知,甲、乙两个重灾区急需一种大型挖掘机,甲地需要25台,乙地需要23台;A、B两省获知情况后慷慨相助,分别捐赠该型号挖掘机26台和22台并将其全部调往灾区.如果从A省调运一台挖掘机到甲地要耗资0.4万元,到乙地要耗资0.3万元;从B省调运一台挖掘机到甲地要耗资0.5万元,到乙地要耗资0.2万元.设从A省调往甲地x台挖掘机,A、B两省将捐赠的挖掘机全部调往灾区共耗资y万元.⑴请直接写出y与x之间的函数关系式及自变量x的取值范围;⑵若要使总耗资不超过15万元,有哪几种调运方案?⑶怎样设计调运方案能使总耗资最少?最少耗资是多少万元?2与x轴的一个交点为A(-1,0),与y轴的25.(12分)已知抛物线b=2-ax+y+ax正半轴交于点C.⑴直接写出抛物线的对称轴,及抛物线与x轴的另一个交点B的坐标;⑵当点C在以AB为直径的⊙P上时,求抛物线的解析式;⑶坐标平面内是否存在点M,使得以点M和⑵中抛物线上的三点A、B、C为顶点的四边形是平行四边形?若存在,请求出点M的坐标;若不存在,请说明理由.湖北省十堰市 初中毕业生学业考试数学试题参考答案及评分说明一、选择题(每题3分,共30分)第1~10题:A C B D A A D C A C二、填空题(每空3分,共18分)11.910514.1⨯ 12.2或-8(错一个扣1分,错两个不得分)13.31+a 14.48° 15.2.5 16.2051 三、解答题(第17~19题,每题7分,共21分)17.解:原式=12121-⨯+ ……………………………6分=1 …………………………………7分说明:第一步三项中,每对一项给2分. 18.解:①+②,得,x 93= ∴.x 3= ………………3分把3=x 代入②,得,y 53=- ∴.y 2-= …6分∴原方程组的解是 ⎩⎨⎧-==.y ,x 23 ………………………7分 说明:其它解法请参照给分.19.解:⑴20%; …………………………………………2分⑵补图略;3; …………………5分说明:频数为6,补对直方图给2分;组数填对给1分.⑶扇形统计图能很好地说明一半以上的汽车行驶的路程在1413x <≤之间; 条形统计图(或直方统计图)能更好地说明行驶路程在135.12x <≤的汽 车多于在5.1414x <≤的汽车. ……………7分说明:只回答“扇形统计图”;“条形统计图(或直方统计图)”也给满分.四、应用题(第20题7分,第21题8分,共15分)20.解:有触礁危险.………………………………1分理由: 过点P 作PD ⊥AC 于D .…………………2分设PD 为x ,在Rt △PBD 中,∠PBD=90°-45°=45°. ∴BD =PD =x . ………………………………3分 在Rt △PAD 中,∵∠PAD =90°-60°=30°,∴x .xAD 330tan =︒=………………………………4分 ∵BD ,AB AD +=∴x .x +=123 ∴)13(61312+=-=x .………6分∵,<18)13(6+∴渔船不改变航线继续向东航行,有触礁危险. ………………7分 说明:开头“有触礁危险”没写,但最后解答正确不扣分.21.解:⑴设所围矩形ABCD 的长AB 为x 米,则宽AD 为)80(21x -米. ………1分说明:AD 的表达式不写不扣分依题意,得 ,x x 750)80(21=-∙ …………………2分即,.x x 01500802=+-解此方程,得 ,x 301= .x 502= ………3分∵墙的长度不超过45m ,∴502=x 不合题意,应舍去. …4分当30=x 时,.x 25)3080(21)80(21=-⨯=-所以,当所围矩形的长为30m 、宽为25m 时,能使矩形的面积为750m 2. ……5分⑵不能.因为由,x x 810)80(21=-∙得.x x 01620802=+- ………………………………6分 又∵ac b 42-=(-80)2-4×1×1620=-80<0,∴上述方程没有实数根.…………………………7分因此,不能使所围矩形场地的面积为810m 2……………8分 说明:如果未知数的设法不同,或用二次函数的知识解答,只要过程及结果正确,请参照给分.五、推理与计算(第22题7分,第23题8分,共15分) 22.解:⑴证明:由折叠可知,C .E ED ,CD ∠=∠= ……1分在矩形ABCD 中,C ,A CD ,AB ∠=∠=∴E .A ED AB ∠=∠=, ∵∠AFB =∠EFD ,∴△AFB ≌△EFD . ……………………4分⑵四边形BMDF 是菱形. ………………………5分 理由:由折叠可知:BF =BM ,DF =DM . …………6分 由⑴知△AFB ≌△EFD ,∴BF =DF .∴BM =BF =DF =DM . ∴四边形BMDF 是菱形. …………………7分23.解:⑴证明:∵AB 、BC 、CD 分别与⊙O 切于点E 、F 、G ,∴DCB .OCB ABC ,OBC ∠=∠∠=∠2121 …………………1分 ∵AB ∥CD ,∴∠ABC +∠DCB =180°.∴.DCB ABC OCB OBC ︒=︒⨯=∠+∠=∠+∠9018021)(21∴.OCB OBC -BOC ︒=︒-︒=∠+∠︒=∠9090180)(180 ……2分 ∵MN ∥OB ,∴∠NMC =∠BOC =90°.∴MN 是⊙O 的切线.……4分⑵连接OF ,则OF ⊥BC .…………………………………5分由⑴知,△BOC 是Rt △,∴.OC DB BC 10862222=+=+= ∵OF ,BC OC OB S BOC ∙∙=∙∙=∆2121∴6×8=10×OF .∴0F =4.8.即⊙O 的半径为4.8cm . …………………………………6分 由⑴知,∠NCM =∠BCO ,∠NMC =∠BOC =90°, ∴△NMC ∽△BOC . …………………7分 ∴.MN .CO CM OB MN 88.486+==即 ∴MN =9.6(cm). …………………………………8分 说明:不带单位不扣分.六、综合应用与探究(第24题9分,第25题12分,共21分)24.解:⑴.x x x x y )2623(2.0)25(5.0)26(3.04.0+-+-+-+=或:.x x x x y )2522(2.0)25(5.0)26(3.04.0+-+-+-+=即:.x y 7.192.0+-= (253≤≤x ) ………3分说明:函数式正确给2分,x 的取值范围正确给1分,函数式不化简不扣分. ⑵依题意,得.x 157.192.0≤+- 解之,得.x 247≥又∵253≤≤x ,且x 为整数, ∴.x 2524或=……5分说明:用建立不等式组的方法求解也可,请参照给分.即,要使总耗资不超过15万元,有如下两种调运方案:方案一:从A 省往甲地调运24台,往乙地调运2台;从B 省往甲地调运1台,往乙地调运21台.方案二:从A 省往甲地调运25台,往乙地调运1台;从B 省往甲地调运0台,往乙地调运22台. …………6分⑶由⑴知:.x y 7.192.0+-= (253≤≤x )∵-0.2<0, ∴y 随x 的增大而减小.∴当25=x 时,∴.y 7.147.19252.0=+⨯-=最小值 ……8分答:设计如下调运方案:从A 省往甲地调运25台,往乙地调运1台;从B 省往甲地调运0台,往乙地调运22台,能使总耗资最少, 最少耗资为14.7万元. ……………9分25.解:⑴对称轴是直线:1=x ,点B 的坐标是(3,0). ……2分说明:每写对1个给1分,“直线”两字没写不扣分.⑵如图,连接PC ,∵点A 、B 的坐标分别是A (-1,0)、B (3,0),∴AB =4.∴.AB PC 242121=⨯==在Rt △POC 中,∵O P =PA -OA =2-1=1, ∴.PO PC OC 3122222=-=-=∴b =.3 ………………………………3分 当01=-=,y x 时,,a a 032=+--∴.a 33=………………………………4分 ∴.x x y 3332332++-= ………………5分 ⑶存在.……………………………6分理由:如图,连接AC 、BC .设点M 的坐标为),(y x M .①当以AC 或BC 为对角线时,点M 在x 轴上方,此时CM ∥AB ,且CM =AB . 由⑵知,AB =4,∴|x |=4,3==OC y .∴x =±4.∴点M 的坐标为)3,4()3,4(-或M .…9分说明:少求一个点的坐标扣1分.②当以AB 为对角线时,点M 在x 轴下方.过M 作MN ⊥AB 于N ,则∠MNB =∠AOC =90°.∵四边形AMBC 是平行四边形,∴AC =MB ,且AC ∥MB .∴∠CAO =∠MBN .∴△AOC ≌△BNM .∴BN =AO =1,MN =CO .∵OB =3,∴0N =3-1=2.∴点M 的坐标为(2,M . ……………………………12分说明:求点M 的坐标时,用解直角三角形的方法或用先求直线解析式,然后求交点M 的坐标的方法均可,请参照给分.综上所述,坐标平面内存在点M ,使得以点A 、B 、C 、M 为顶点的四边形是平行四边形.其坐标为123((2,M M M -.说明:①综上所述不写不扣分;②如果开头“存在”二字没写,但最后解答全部正确,不扣分。
分式的化简求值经典练习题(带答案)

精心整理精心整理分式的化简乘方:()n n n nn a a aa a aa ab b bb b bb b ⋅=⋅=⋅个个n 个=(n 为正整数)整数指数幂运算性质: ⑴m n m n a a a +⋅=(m 、n 为整数) ⑵()m n mn a a =(m 、n 为整数) ⑶()n n n ab a b =(n 为整数)⑷m n m n a a a -÷=(0a ≠,m 、n 为整数)中考要求精心整理精心整理负整指数幂:一般地,当n 是正整数时,1n na a -=(0a ≠),即n a -(0a ≠)是n a 的倒数分式的加减法法则:同分母分式相加减,分母不变,把分子相加减,a b a b ccc+±=异分母分式相加减,先通分,变为同分母的分式再加减,a c ad bc ad bc bdbdbdbd±±=±=分式的混合运算的运算顺序:先算乘方,再算乘除,后算加减,如有括号,括号内先算.【例1【例2【题型】解答 【关键词】【解析】222221(1)()4111(1)a a a a a a a a a ---+÷⋅=-=--++-【答案】4-【例3】 先化简,再求值:22144(1)1a a a a a-+-÷--,其中1a =-..【考点】分式的化简求值 【难度】2星 【题型】解答【关键词】2010年,安徽省中考【解析】()()2221144211122a a a a a a a a a a a a --+-⎛⎫-÷=⋅= ⎪----⎝⎭-当1a =-时,原式112123a a -===---【答案】13【例4】 先化简,再求值:2291333x x x x x⎛⎫-⋅ ⎪--+⎝⎭其中13x =.【考点】分式的化简求值 【难度】2星 【题型】解答【关键词】2010年,湖南省长沙市中考试题 【解析】原式()()()33133x x x x x +-=⋅-+ 当13x =时,原式3=【答案】3【例5】 先化简,再求值:211(1)(2)11x x x -÷+-+-,其中x =. 【考点】分式的化简求值 【难度】2星 【题型】解答【关键词】2010年,湖北省十堰市中考试题 【解析】原式()()()111121x x x x x +-=⋅+-+-+当x时,原式224=-=.【答案】4精心整理精心整理【例6】 先化简,后求值:22121(1)24x x x x -++÷--,其中5x =-. 【考点】分式的化简求值 【难度】2星 【题型】解答【关键词】2010年,广东省肇庆市中考试题【解析】22121(1)24x x x x -++÷--=221(1)2(2)(2)x x x x x -+-÷-+-【例7。
DA湖北省十堰市中考真题

十堰市2010年初中毕业生学业考试数学参考答案及评分标准二、认真填一填(本题有6个小题,每小题3分,共18分)11.()()22a b a b+-12.2x≥且3x≠13.55︒14.()m n--,15. 37770 1214n+·三、全面答一答(本大题共9小题,满分72分)17.(本小题满分7分)解:原式1851232=-+-+⨯=- ················································································(7分)18. (本小题满分7分)解:原式=()()()11211x xxxx+-+-+········································································(3分)=2(1)(2)2x x x x-+-=- ···························································································(2分)当x=224-= ·································································(2分)19. (本小题满分7分)证明:90BD AC CE AB ADB AEC⊥⊥∴∠=∠=︒,,········································(2分)在ABD△和ACE△中,A AADB AECAB AC∠=∠⎧⎪∠=∠⎨⎪=⎩ABD ACE∴△≌△ ······································································································(3分)BD CE∴=····················································································································(2分)20. (本小题满分8分)解:过D作DE AB⊥于E,则DE BC∥设AB h=米,在Rt ABC△中,60tan30BC h h=︒=︒·cot ································(2分)在Rt AED△中,tan45tan45AE DE BC=︒=︒=又12AB AE BE CD-===123h h∴-= ·············································································································(2分)18186 1.73h∴====+=+⨯1810.3828.4=+≈(米)····························································································(2分)答:山高AB是28.4米··································································································(1分)21.(本小题满分8分)解:(1)张明、王艳各摸一球可能出现的结果有6530⨯=个,它们出现的可能性相等,张明到中国馆做义工的概率()151302P==中国馆·································································(4分)(2)张明、王艳各自在世博轴、演艺中心的结果共4个,其概率为423015P== ··(4分)22.(本小题满分8分)解:(1)设反比例函数解析式为kyx=,点()14A,在反比例函数的图象上441kk∴=∴=∴,,反比例函数的解析式为4yx=······················································(4分)(2)设直线AB的解析式为()00y ax b a b=+>>,联立2440yax bxxy ax b⎧=⎪⇒+-=⎨⎪=+⎩(★)·································································(1分)y ax b=+过点()1A,44a b ∴+=4b a ∴=-代入(★)得:()2440ax a x +--= ··································································································· (1分) 方法1.由114a -⨯可得1x =或4x a =-显然1x =是A 点的横坐标,4x a=-是B 点的横坐标.设直线AB 交y 轴于点C ,则()0C b ,,即()04C a -, 由()112AOB AOC BOC S S S a =+=⨯+△△△·4-()141522a a ⎛⎫=⎪⎝⎭·4-,整理得 215160a a +-=1a ∴=或16a =-(舍去)413b ∴=-=∴直线AB 的解析式为3y x =+ ··················································································· (2分) 方法2.同方法1.得()2440ax a x +--=由求根公式也可得1x =或4x a=- 方法3.同方法1.得()2440ax a x +--=由2111522AOB S OC x x =-=△·()21440a a x x a a a ++-===> 4OC b a ==-可得()1415422a a a +⎛⎫-= ⎪⎝⎭解得1a =或16=-(舍去) 23.(本小题满分8分) 解:(1)由题可得1270238y x y x =+⎧⎨=-⎩当12y y =时,即70238x x -+=-3108x ∴= 36x ∴=当36x =时,1234y y ==,所以该药品的稳定价格为36(元/件)稳定需求量为34(万件) ········································································································································· (4分) (2)令10y =,得70x =,由图象可知,当药品每件价格大于36元小于70元时,该药品的需求量低于供应量.(3)设政府对该药品每件介格补贴a 元,则有346703462()38x x a +=-+⎧⎨+=+-⎩解得309x a =⎧⎨=⎩所以政府部门对该药品每件应补贴9元. ······································································· (4分) 24.(本小题满分9分)解:(1)1AO 是2O ⊙的切线,122190O A AO O AB BAO ∴⊥∴∠+∠=︒, 又221122211O A O C O A O B O CB O AB O BC ABO BAO ==∴∠=∠∠=∠=∠,,,22212290O CB O BC O AB BAO O C O B ∴∠=∠=∠+∠=︒∴⊥,,即212O C O O ⊥ ·· (3分) (2)延长21O O 交1O ⊙于点D 连结AD .BD 是1O ⊙的直径,90BAD ∴∠=︒又由(1)可知290BO C ∠=︒2BAD BO C ∴∠=∠,又2ABD O BC ∠=∠ 2O BC ABD ∴△∽△2O B BCAB BD∴= 2·AB BC O B BD ∴=·又12BD BO =212AB BC O B BO ∴=·· ································································································· (3分) (3)由(2)证可知2D C O AB ∠=∠=∠,即2D O AB ∠=∠,又22AO B DO A ∠=∠22AO B DO A ∴△∽△2222222222AO O BDO O AAO O B O D O C O A∴=∴== · 2222O C O B O D ∴=·①又由(2)2ABBC O B BD =··② 由①-②得2222O C AB BC O B -=·即221412O B -=22O B ∴= 又212O B BD AB BC ==··6BD ∴= 126AO BD ∴== 13AO ∴= ······························································ (3分)25.(本小题满分10分) 解:(1)分两种情况讨论.1︒当0m =时,方程为x 20-= 2∴= 方程有实数根2︒当0m ≠,则一元二次方程的根的判别式()()2222314229618821m m m m m m m m m ∆=----=-+-+=++⎡⎤⎣⎦=()21m +≥0不论m 为何实数,∆≥0成立,∴方程恒有实数根综合1︒、2︒,可知m 取任何实数,方程()231220mx m x m --+-=恒有实数根 ········································································································································· (3分) (2)设12x x ,为抛物线()43122y mx m x m =--+-与x 轴交点的横坐标. 则有12123122m m x x x x m m --+==,由12x x -=1m m==+=由122x x -=,得1122m m m m++=∴=,或12m m +=- 1m ∴=或13m =-,∴所求抛物线的解析式为2212182233y x x y x x =-=-+-,,即121(2)(2)(4)3y x x y x x =-=---,其图象为右图所示:方法2.由2(31)220mx m x m --+-=得[](2)(1)0x mx m ---=可知抛物线2(31)22y mx m x m =--+-不论m 为任何不为0的实数时恒过定点12(20)2x x -= ,可得22220x x -=∴=或24x =,对应的m 的值为1m =或13m =- 即所求抛物线解析式为212(2)y x x x x =-=-,221812(2)(4)333y x x x x =-+-=--- ····································································· (3分)m1 ()1m -2-(3)在(2)条件下,直线y x b =+与抛物线12y y ,组成的图象只有两个交点,结合图象,求b 的取值范围.212y x x y x b⎧=-⎨=+⎩当1y y =时,得230x x b --= 由940b ∆=+= 得94b =- 同理2218294(83)033y x x b y x b⎧=-+-⎪⇒∆=-+=⎨⎪=+⎩得2312b =-观察函数图象可知当94b <-或2312b >-时,直线y x b =+与(2)中的图象只有两个交点.由21221(2)(4)3y x xy x x ⎧=-⎪⎨=---⎪⎩当12y y =时,有2x =或1x = 当1x =时,1y =-所以过两抛物线交点(11)20,-,(,)的直线为2y x =-,综上所述可知:当94b <-或2312b >-或2b =-时,直线y x b =+与(2)中的图象只有两个交点. ····················· (4分)。
湖北省十堰市2010年中考数学试题及详解答案

湖北省十堰市2010年中考数学试题及详解答案注意事项:⒈本试卷共8页,25个小题,满分120分,考试时间120分钟.⒉在密封区内写明县(市、区)名、校名、姓名和考号,不要在密封区内答题.⒊请用蓝色或黑色钢笔、中性笔(圆珠笔)答题,作图可用铅笔.不允许使用计算器. 一、选择题(本题共10个小题,每小题3分,共30分)下面每题给出的四个选项中,只有一个是正确的,请 把你认为正确选项的字母代号填在下表内1.-7的相反数是A .7B .-7C .71D .71- 2.函数9-=x y 中自变量x 的取值范围是A .x> 0B .x≥0C .x>9D .x≥9 3.一次函数y=2x -2的图象不经过...的象限是 A .第一象限 B .第二象限 C .第三象限 D .第四象限 4.下列方程中,有两个不相等实数根的是A .0122=--x xB .0322=+-x xC .3322-=x x D .0442=+-x x5.下列运算正确的是 A .523=+B .623=⨯C .13)13(2-=- D .353522-=-6.下列命题中,错误的是A .三角形两边之和大于第三边B .三角形的外角和等于360°C .三角形的一条中线能将三角形面积分成相等的两部分D .等边三角形既是轴对称图形,又是中心对称图形 7.如图,△ABC 内接于⊙O ,连结OA 、OB , 若∠ABO=25°,则∠C 的度数为 A .55° B .60° C .65° D .70°8.如图是四棱锥(底面是矩形,四条侧棱等长) ,则它的俯视图是9.同时掷两个质地均匀的正方体骰子,骰子的六个面上分别刻有1到6的点数,则两个骰子向上的一面的点数和为8的概率为 A .91 B .365 C .61 D .367 10.如图,已知Rt ΔABC 中,∠ACB=90°,AC= 4,BC=3,以AB 边所在的直线为轴,将ΔABC 旋转一周,则所得几何体的表面积是A .π5168B .π24C .π584D .π12二、填空题(本题共6个小题,每小题3分,共18分.)请将答案直接填写在该题目中的横线上11.据统计,今年我市参加初中毕业学业考试的学生约为38000人,这个数据用科学记数法表示为 .12.方程(x +2)(x -1)=0的解为 . 13.如图,直线a 与直线b 被直线c 所截, a ∥b ,若∠1=62°,则∠3= 度. 14. 的平行四边形是 是菱形(只填一个条件).15.如图,在平面直角坐标系中,点A 的坐标 为(1,4),将线段OA 绕点O 顺时针旋转90°得到 线段OA′,则点A′的坐标是 . 16.已知函数1+-=x y 的图象与x 轴、y 轴分 别交于点C 、B ,与双曲线xky =交于点A 、D, 若AB+CD= BC ,则k 的值为 . 三、解答题(本题共4个小题,共27分)17.(6分)计算:02)45cos 1(3)3(︒---+-18.(6分)已知:a+b=3,ab=2,求下列各式的值: (1)a 2b+ab 2 (2)a 2+b 219.(7分)“一方有难,八方支援”,在四川汶川大地震后,某市文华中学全体师生踊跃捐款,向灾区人民献爱心. 为了了解该校学生捐款情况,对其中60个学生捐款数x (元)分五组进行统计,第一组:1≤x ≤5,第二组:6≤x ≤10,第三组:11≤x ≤15,第四组:16≤x ≤20;,第五组:x ≥21,并绘制如下频数分布直方图(假定每名学生捐款数均为整数),解答下列问题:(1) 补全频数分布直方图;(2) 这60个学生捐款数的中位数落在第____组; (3)已知文华中学共有学生1800人,请估算该校捐款数 不少于16元的学生人数.20.(8分)如图,直线l 切⊙O 于点A ,点P 为直线l 上一点,直线PO 交⊙O 于点C 、B ,点D 在线段AP 上,连结DB ,且AD=DB . (1)求证:DB 为⊙O 的切线.(2)若AD=1,PB=BO ,求弦AC 的长. 四、应用题(本题共3个小题,共23分)21.(7分)如图,在一次数学课外活动中,小明同学在点P 处测得教学楼A 位于北偏东60°方向,办公楼B 位于南偏东45°方向.小明沿正东方向前进60米到达C 处,此时测得教学楼A 恰好位于正北方向,办公楼B 正好位于正南方向.求教学楼A 与办公楼B 之间的距离(结果精确到0.1米). (供选用的数据:2≈1.414,3≈1.732)22.(8分)某工厂准备加工600个零件,在加工了100个零件后,采取了新技术,使每天的工作效率是原来的2倍,结果共用7天完成了任务,求该厂原来每天加工多少个零件? 23.(8分)为执行中央“节能减排,美化环境,建设美丽新农村”的国策,我市某村计划建造A 、B 两种型号的沼气池共20个,以解决该村所有农户的燃料问题.两种型号沼气池的占地面积、使用农户数及造价见下表:已知可供建造沼气池的占地面积不超过365m ,该村农户共 有492户.(1)满足条件的方案共有几种?写出解答过程. (2)通过计算判断,哪种建造方案最省钱. 五、综合与探究题(本题共2小题,共22分)24.(10分)如图①,四边形ABCD 是正方形, 点G 是BC 上任意一点,DE ⊥AG 于点E ,BF ⊥AG 于点F .(1) 求证:DE -BF = EF .(2) 当点G 为BC 边中点时, 试探究线段EF 与GF 之间的数量关系, 并说明理由.(3) 若点G 为CB 延长线上一点,其余条件不变.请你在图②中画出图形,写出此时DE 、BF 、EF 之间的数量关系(不需要证明).25.(12分)如图①, 已知抛物线32++=bx ax y (a ≠0)与x 轴交于点A(1,0)和点B (-3,0),与y 轴交于点C . (1) 求抛物线的解析式;(2) 设抛物线的对称轴与x 轴交于点M ,问在对称轴上是否存在点P ,使△CMP 为等腰三角形?若存在,请直接写出所有符合条件的点P 的坐标;若不存在,请说明理由.(3) 如图②,若点E 为第二象限抛物线上一动点,连接BE 、CE ,求四边形BOCE 面积的最大值,并求此时E 点的坐标.湖北省十堰市2009年初中毕业生学业考试数学试题参考答案及评分说明一、选择题(每题3分,共30分)第1~5题:A D B A B 第6~10题:D C C B C 二、填空题(每空3分,共18分)11.4108.3⨯ 12.-2,1;-2或1(x=-2,x=1或1,221=-=x x )13.62 14.对角线互相垂直(或有一组邻边相等,或一条对角线平分一组对角) 15.(4,-1) 16.43-三、解答题(6分+6分+7分+8分=27分)17.解:原式=9+3-1……………………………5分 =8+3……………………………… 6分 说明:第一步计算中,只对一项给2分,只对两项给4分. 18.解法①:(1)632)(22=⨯=+=+b a ab ab b a ………………………3分 (2) ∵2222)(b ab a b a ++=+∴52232)(2222=⨯-=-+=+ab b a b a …………… 6分 解法②:由题意得 ⎩⎨⎧==+23ab b a 解得:⎩⎨⎧==1211b a ⎩⎨⎧==2122b a ……………………2分当1,2==b a 时,514,6242222=+=+=+=+b a ab b a ……………4分 当2,1==b a 时,541,6422222=+=+=+=+b a ab b a ……………6分 说明:(1)第二种解法只求出一种情形的给4分;(2)其它解法请参照上述评分说明给分. 19.解:(1)如图(频数为15)…2分 (2)三 ………………4分(3)600180060155=⨯+……6分∴ 捐款数不少于16元的学生数大约为600人. ……7分 说明:(1)未说明“频数是15”不扣分;(2)未写“大约”不扣分.20.(1)证明: 连结OD ………………………………………………………1 分 ∵ PA 为⊙O 切线 ∴ ∠OAD = 90°………………………………………2 分 ∵ OA=OB ,DA=DB ,DO=DO , ∴ΔOAD ≌ΔOBD …………………3分 ∴ ∠OBD=∠OAD = 90°, ∴PA 为⊙O 的切线…………………4 分 (2)解:在RtΔOAP 中, ∵ PB=OB=OA ∴ ∠OPA=30°………………5 分 ∴ ∠POA=60°=2∠C , ∴PD=2BD=2DA=2……………………………6 分 ∴ ∠OPA=∠C=30°…………………………………7 分∴ AC=AP=3…………………………………………8 分 说明:其它解法请参照上述评分说明给分. 四、应用题(7分+8分+8分=23分)21.解:由题意可知 ∠ACP= ∠BCP= 90°,∠APC=30°,∠BPC=45°…2分 在Rt △BPC 中,∵∠BCP=90°,∠BPC =45°,∴60==PC BC ……3分 在Rt △ACP 中,∵∠ACP=90°,∠APC =30°,∴320=AC …… 5分 ∴32060+=+=BC AC AB ………………………………………6分 ≈60+20×1.732 =94.64≈94.6(米)答:教学楼A 与办公楼B 之间的距离大约为94.6米.………………7分 说明:(1)其它解法请参照上述评分说明给分;(2)不作答不扣分. 22.解:设该厂原来每天加工x 个零件,………………………………1分由题意得:72500100=+xx ………………………………………5分解得 x=50 ………………………………………………………6分 经检验:x=50是原分式方程的解………………………………………7分 答:该厂原来每天加工50个零件.……………………………………8分 说明:其它解法请参照上述评分说明给分.23.解: (1) 设建造A 型沼气池 x 个,则建造B 型沼气池(20-x )个………1分依题意得: ()()⎩⎨⎧≥-+≤-+492203018365202015x x x x …………………………………………3分解得:7≤ x ≤ 9 ………………………………………………………………4分 ∵ x 为整数 ∴ x = 7,8 ,9 ,∴满足条件的方案有三种.. ……………5分 (2)设建造A 型沼气池 x 个时,总费用为y 万元,则:y = 2x + 3( 20-x) = -x+ 60 ………………………………………………6分 ∵-1< 0,∴y 随x 增大而减小,当x=9 时,y 的值最小,此时y= 51( 万元 ) …………………………………7分 ∴此时方案为:建造A 型沼气池9个,建造B 型沼气池11个. ……………8分解法②:由(1)知共有三种方案,其费用分别为:方案一: 建造A 型沼气池7个, 建造B 型沼气池13个, 总费用为:7×2 + 13×3 = 53( 万元 ) ……………………………6分 方案二: 建造A 型沼气池8个, 建造B 型沼气池12个, 总费用为:8×2 + 12×3 = 52( 万元 ) ……………………………7分 方案三: 建造A 型沼气池9个, 建造B 型沼气池11个, 总费用为:9×2 + 11×3 = 51( 万元 )∴方案三最省钱. …………………………………………… 8分 说明:(1)若只有正确结论,给1分;(2)不带单位不扣分;(3)其它解法请参照上述评分说明给分;五、综合与探究题(10分+12=22分)24.(1) 证明:∵ 四边形ABCD 是正方形, BF ⊥AG , DE ⊥AG∴ DA=AB , ∠BAF + ∠DAE = ∠DAE + ∠ADE = 90° ∴ ∠BAF = ∠ADE ………………………2 分 ∴ △ABF ≌ △DAE ………………………3 分 ∴ BF = AE , AF = DE∴ DE -BF = AF -AE = EF ……………………4 分(2)EF = 2FG 理由如下: ∵ AB ⊥BC , BF ⊥AG , AB =2 BG∴ △AFB ∽△BFG ∽△ABG ………………5 分 ∴2===FGBFBF AF BF AB ………………………6分 ∴ AF = 2BF , BF = 2 FG …………………7分 由(1)知, AE = BF ,∴ EF = BF = 2 FG ……8分 (3) 如图 …………………………………………9分 DE + BF = EF ……………………………10分说明:第(2)问不先下结论,只要解答正确,给满分.若只有正确结论,给1分. 25.解: (1)由题知: ⎩⎨⎧=+-=++033903b a b a ……………………………………1 分解得: ⎩⎨⎧-=-=21b a ……………………………………………………………2分∴ 所求抛物线解析式为: 322+=x --x y ……………………………3分(2) 存在符合条件的点P, 其坐标为P (-1, 10)或P(-1,- 10)或P (-1, 6) 或P (-1, 35)………………………………………………………7分 (3)解法①:过点E 作EF ⊥x 轴于点F , 设E ( a ,-2a -2a +3 )( -3< a < 0 )∴EF=-2a -2a +3,BF=a +3,OF=-a ………………………………………………8 分∴S 四边形BOCE =21BF·EF + 21(OC +EF)·OF =21( a +3 )·(-2a -2a +3) + 21(-2a -2a +6)·(-a )……………………………9 分 =2929232+--a a ………………………………………………………………………10 分=-232)23(+a +863∴ 当a =-23时,S 四边形BOCE 最大, 且最大值为 863.……………………………11 分此时,点E 坐标为 (-23,415)……………………………………………………12分解法②:过点E 作EF ⊥x 轴于点F , 设E ( x , y ) ( -3< x < 0 ) …………………………8分则S 四边形BOCE =21(3 + y )·(-x) + 21( 3 + x )·y ………………………………………9分 = 23( y -x)= 23(332+x --x ) …………………………………10 分= -232)23(+x + 863∴ 当x =-23时,S 四边形BOCE 最大,且最大值为 863. …………………………11分此时,点E 坐标为 (-23,415) ……………………………………………………12分说明:(1)抛物线解析式用其它形式表示,只要正确不扣分.(2)直接应用公式法求抛物线顶点坐标或最大值不扣分. (3)其它解法请参照评分说明给分.。
2010年湖北各地中考数学试卷及答案集锦(12套)(WORD版)
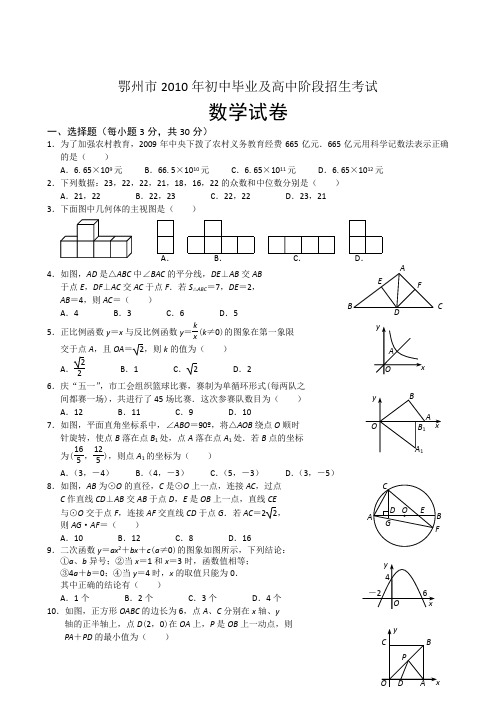
ABCF EAB C GFEDO鄂州市2010年初中毕业及高中阶段招生考试数学试卷一、选择题(每小题3分,共30分)1.为了加强农村教育,2009年中央下拨了农村义务教育经费665亿元.665亿元用科学记数法表示正确的是( )A .6.65×109元B .66.5×1010元C .6.65×1011元D .6.65×1012元 2.下列数据:23,22,22,21,18,16,22的众数和中位数分别是( ) A .21,22 B .22,23 C .22,22 D .23,21 3.下面图中几何体的主视图是( )4.如图,AD 是△ABC 中∠BAC 的平分线,DE ⊥AB 交AB 于点E ,DF ⊥AC 交AC 于点F .若S △ABC =7,DE =2, AB =4,则AC =( )A .4B .3C .6D .55.正比例函数y =x 与反比例函数y = kx (k ≠0)的图象在第一象限交于点A ,且OA =2,则k 的值为( )A .22 B .1 C . 2 D .2 6.庆“五一”,市工会组织篮球比赛,赛制为单循环形式(每两队之 间都赛一场),共进行了45场比赛.这次参赛队数目为( ) A .12 B .11 C .9 D .107.如图,平面直角坐标系中,∠ABO =90º,将△AOB 绕点O 顺时 针旋转,使点B 落在点B 1处,点A 落在点A 1处.若B 点的坐标 为( 16 5, 125),则点A 1的坐标为( ) A .(3,-4) B .(4,-3) C .(5,-3) D .(3,-5) 8.如图,AB 为⊙O 的直径,C 是⊙O 上一点,连接AC ,过点 C 作直线CD ⊥AB 交AB 于点D ,E 是OB 上一点,直线CE 与⊙O 交于点F ,连接AF 交直线CD 于点G .若AC =22, 则AG ·AF =( )A .10B .12C .8D .169.二次函数y =ax 2+bx +c (a ≠0)的图象如图所示,下列结论: ①a 、b 异号;②当x =1和x =3时,函数值相等; ③4a +b =0;④当y =4时,x 的取值只能为0. 其中正确的结论有( )A .1个B .2个C .3个D .4个 10.如图,正方形OABC 的边长为6,点A 、C 分别在x 轴、y轴的正半轴上,点D (2,0)在OA 上,P 是OB 上一动点,则A .B .C .D .A BCDDA .210B .10C .4D .6二、填空题(每小题3分,共18分)11.5的算术平方根是 .12.圆锥的底面直径是2m ,母线长4m ,则圆锥的侧面积是 m 2.13.已知α、β是方程x 2―4x ―3=0的两个实数根,则(α―3)(β―3)= .14.在一个黑色的袋子中装有除颜色外其他均相同的3个红球和6个白球,从中任意摸出1个球,摸出的球是白球的概率是 . 15.已知⊙O 的半径为10,弦AB =103,⊙O 上的点C 到弦AB 所在直线的距离为5,则以O 、A 、B 、C为顶点的四边形的面积是 .16.如图,四边形ABCD 中,AB =AC =AD ,E 是BC 的中点,AE =CE ,∠BAC =3∠CBD ,BD =62+66,则AB = .三、解答题(共72分)17.(8分)解不等式组⎪⎩⎪⎨⎧-<--≥--,,13524)2(3x x x x 并写出该不等式组的整数解.18.(8分)先化简2211112-÷⎪⎭⎫ ⎝⎛+--x x x x ,然后从-1、1、2中选取一个数作为x 的值代入求值.19.(8分)我市第四高级中学与第六高级中学之间进行一场足球比赛,邀请某校两位体育老师及两位九年级足球迷当裁判,九年级的一位足球迷设计了开球方式.(1)两位体育老师各抛掷一枚硬币,两枚硬币落地后正面朝上,则第四高级中学开球;否则,第六高级中学开球.请用树状图或列表的方法,求第四高级中学开球的概率.(2)九年级的另一位足球迷发现前面设计的开球方式不合理,他修改规则:如果两枚硬币都朝上时,第四高级中学得8分;否则,第六高级中学得4分.根据概率计算,谁的得分高,谁开球.你认为修改后的规则公平吗?若公平,请说明理由;若不公平,请你设计对双方公平的开球方式.20.(8分)春节期间,某客运站旅客流量不断增大,旅客往往需要长时间排队等候购票.经过调查发现,每天开始售票时,约有400人排队购票,同时又有新的旅客不断进入售票厅排队等候购票.售票时售A B C D EG H M A B C D E 60º30º与售票时间x (分钟)的关系如图所示,已知售票的前a 分钟只开放了两个售票窗口(规定每人只能购票一张).(1)求a 的值.(2)求售票到第60分钟时,售票厅排队等候购票的旅客人数.(3)若要在开始售票后半小时内让所有的排队旅客都能够购到票,以便后来到站的旅客随到随购,至少需要同时开放几个售票窗口?21.(8分)如图,一艘潜艇在海面下500m A 点处测得俯角为30º前下方的海底C 处有黑匣子信号发出,继续在同一深度直线航行4000m 后再次在B 点处测得俯角为60º前下方的海底C 处有黑匣子信号发出,求海底黑匣子C 点距离海面的深度(结果保留根号).22.(10分)工程师有一块长AD =12分米,宽AB =8分米的铁板,截去长AE =2分米、AF =4分米的直角三角形,在余下的五边形中,截得矩形MGCH ,其中点M 在线段EF 上. (1)若截得矩形MGCH 的面积为70平方分米,求矩形MGCH 的长与宽. (2)当EM 为多少时,矩形MGCH 的面积最大?并求此时矩形的周长.23.(10分)如图,一面利用墙,用篱笆围成的矩形花圃ABCD 的面积为S m 2,平行于墙的BC 边长为x m .(1)若墙可利用的最大长度为10m ,篱笆长为24m ,花圃中间用一道篱笆隔成两个小矩形,求S 与x 之间的函数关系式.(2)在(1)的条件下,围成的花圃的面积为45m 2时,求AB 的长.能否围成面积比45m 2更大的花圃?如果能,应该怎样围?如果不能,请说明理由.(3)若墙可利用最大长度为40m ,篱笆长77m ,中间用n 道篱笆隔成小矩形,且当这些小矩形为正方形和x 为正整数时,请直接写出一组满足条件的x 、n 的值.24.(12分)如图,在直角坐标系中,已知点A (-1,0)、B (0,2),动点P 沿过B 点且垂直于AB 的射线BM 运动,其运动的速度为每秒1个单位长度,射线BM 与x 轴交于点C . (1)求点C 的坐标.(2)求过A 、B 、C 三点的抛物线的解析式. (3)若点P 开始运动时,点Q 也同时从C 点出发,以点P 相同的速度沿x 轴负方向向点A 运动,t 秒后,以P 、Q 、C 为顶点的三角形为等腰三角形(点P 到点C 时停止运动,点Q 也同时停止运动),求t 的值.(4)在(2)(3)的条件下,当CQ =CP 时,求直线OP 与抛物线的交点坐标.A D BCA BD C…图1图22010年恩施自治州初中毕业及高中招生考试数 学 试 题注意事项:1.本试卷分试题卷和答题卡两部分,考试时间为120分钟,满分为120分.2.考生在答题前请阅读答题卡中的“注意事项”,然后按要求答题. 3.所有答案均须做在答题卡相应区域,做在其它区域无效.一、填空题:(本大题共8个小题,每小题3分,共24分) 1.9的相反数是 .2.据有关部门预测,恩施州煤炭总储量为2.91亿吨,用科学记数法表示这个数是 吨(保留两个有效数字). 3. 分解因式:=+-b ab b a 22 .4.在一个不透明的盒子里装有5个黑球,3个红球和2个白球,它们除颜色外其余都相同,从中随机摸出一个球,摸到红球的概率是 . 5.在同一直角坐标系中,正比例函数x k y 1=的图象与反比例函数xk y 2=的图象有公共点,则21k k 0(填“>”、“=”或“<”).6.如图1,在ABCD 中,已知AB=9㎝,AD=6㎝,BE 平分∠ABC 交DC 边于点E ,则DE 等 于 ㎝.7.如图2,在矩形ABCD 中,AD =4,DC =3,将△ADC 按逆时针方向绕点A 旋转到△AEF (点A 、B 、E 在同一直线上),连结CF ,则CF = .8.如图3,有一个形如六边形的点阵,它的中心是一个点,作为第一层,第二层每边有两个点,第三层每边有三个点,依次类推,如果n 层六边形点阵的总点数为331, 则n 等于 .二、选择题:(下列各小题都给出四个选项,其中只有一项是符合题目要求的.本大题共8个小题,每小题3分,共24分) 9.()24-的算术平方根是:A. 4B. 4±C. 2D. 2± 10.下列计算正确的是:()223()3图3图2图111.用4个棱长为1的正方体搭成一个几何体模型,其主视图与左视图如图4所示,则该立方体的俯视图不可..能.是:12.不等式组⎩⎨⎧≤-<+5148x x x 的解集是:A. 5≤xB. 53≤<-xC.53≤<xD. 3-<x13.某品牌商品,按标价九折出售,仍可获得20%的利润.若该商品标价为28元,则商品的进价为:A. 21元B. 19.8元C. 22.4元D. 25.2元 14.如图5,EF 是△ABC 的中位线,将△AEF 沿中线AD 方向平移到△A 1E 1F 1的位置,使E 1F 1与BC 边重合,已知△AEF 的面积为7,则图中阴影部分的面积为: A. 7 B. 14 C. 21 D. 2815.某班随机抽取6名同学的一次地生测试成绩如下:82,95,82,76,76,82.数据中的众数和中位数分别是:A. 82,76B. 76,82C. 82,79D. 82,82 16.如图6, 已知圆锥的高为8,底面圆的直径为12,则此圆锥的侧面积是A .24πB .30πC .48πD .60π 三、解答题(本大题共8个小题,满分72分) 17.(6分) 计算:2+()()()121212010-++--313⨯-18.(8分)解方程:14143=-+--xx x19.(8分)如图7,已知,在ABCD 中,AE=CF ,M 、N 分别是DE 、BF 的中点.求证:四边形MFNE 是平行四边形 .20.(8分)2010年4月14日青海玉树发生7.1级地震,地震灾情牵动全国人民的心.某社区响应恩施州政府的号召,积极组织社区居民为灾区人民献爱心活动.为了解该社区居民捐款情况,对社区部分捐款户数进行分组统计(统计表如下),数据整理成如图8所示的不完整统计图.已知A、B两组捐款户数直图7 图4图6图5⑴ A 组的频数是多少?本次调查样本的容量是多少? ⑵ 求出C 组的频数并补全直方图.⑶ 若该社区有500户住户,请估计捐款不少于300元的户数是多少?21.(10分) 如图9,已知,在△ABC 中,∠ABC=090,BC 为⊙O 的直径, AC 与⊙O 交于点D,点E 为AB 的中点,PF ⊥BC 交BC 于点G,交AC 于点F. (1)求证:ED 是⊙O 的切线. (2)如果CF =1,CP =2,sinA =54,求⊙O 的直径BC.22.(10分) 恩施州绿色、富硒产品和特色农产品在国际市场上颇具竞争力,其中香菇远销日本和韩国等地.上市时,外商李经理按市场价格10元/千克在我州收购了2000千克香菇存放入冷库中.据预测,香菇的市场价格每天每千克将上涨0.5元,但冷库存放这批香菇时每天需要支出各种费用合计340元,而且香菇在冷库中最多保存110天,同时,平均每天有6千克的香菇损坏不能出售.(1)若存放x 天后,将这批香菇一次性出售,设这批香菇的销售总金额为y 元,试写出y 与x 之间的函数关系式.(2)李经理想获得利润22500元,需将这批香菇存放多少天后出售?(利润=销售总金额-收购成本-各种费用)(3)李经理将这批香菇存放多少天后出售可获得最大利润?最大利润是多少? 图8 图923.(10分)(1)计算:如图10①,直径为a 的三等圆⊙O 1、⊙O 2、⊙O 3两两外切,切点分别为A 、B 、C ,求O 1A 的长(用含a 的代数式表示).(2)探索:若干个直径为a 的圆圈分别按如图10②所示的方案一和如图10③所示的方案二的方式排放,探索并求出这两种方案中n 层圆圈的高度n h和(用含n 、a 的代数式表示). (3)应用:现有长方体集装箱,其内空长为5米,宽为3.1米,高为3.1米.用这样的集装箱装运长为5米,底面直径(横截面的外圆直径)为0.1米的圆柱形钢管,你认为采用(2)中的哪种方案在该集装箱中装运钢管数最多?并求出一个这样的集装箱最多能装运多少根钢管?(3≈1.73)24.(12分) 如图11,在平面直角坐标系中,二次函数c bx x y ++=2的图象与x 轴交于A 、B 两点, A 点在原点的左侧,B 点的坐标为(3,0),与y 轴交于C (0,-3)点,点P 是直线BC 下方的抛物线上一动点.(1)求这个二次函数的表达式.(2)连结PO 、PC ,并把△POC 沿CO 翻折,得到四边形POP /C , 那么是否存在点P ,使四边形POP /C 为菱形?若存在,请求出此时点P 的坐标;若不存在,请说明理由.(3)当点P 运动到什么位置时,四边形 ABPC 的面积最大并求出此时P 点的坐标和四边形ABPC 的最大面积.②③①图11图10数学试题卷注意事项:1. 本试卷分为试题卷和答题卷两部分。
2010-2023历年初中毕业升学考试(湖北十堰卷)数学(带解析)

2010-2023历年初中毕业升学考试(湖北十堰卷)数学(带解析)第1卷一.参考题库(共12题)1.如图,直线BD∥EF,AE与BD交于点C,若∠ABC=30°,∠BAC=75°,则∠CEF 的大小为()A.60°B.75°C.90°D.105°2.如图,O是正△ABC内一点,OA=3,OB=4,OC=5,将线段BO以点B为旋转中心逆时针旋转60°得到线段BO′,下列结论:①△BO′A可以由△BOC绕点B逆时针旋转60°得到;②点O与O′的距离为4;③∠AOB=150°;④S四边形AOBO ;⑤S△AOC+S△AOB=.其中正确的结论是()A.①②③⑤B.①②③④C.①②③④⑤D.①②③3.如图,正三角形ABC的边长是2,分别以点B,C为圆心,以r为半径作两条弧,设两弧与边BC围成的阴影部分面积为S,当≤r<2时,S的取值范围是.4.先化简,再求值:,其中a=2.5.某中学九(1)班为了了解全班学生喜欢球类活动的情况,采取全面调查的方法,从足球、乒乓球、篮球、排球等四个方面调查了全班学生的兴趣爱好,根据调查的结果组建了4个兴趣小组,并绘制成如图所示的两幅不完整的统计图(如图①,②,要求每位学生只能选择一种自己喜欢的球类),请你根据图中提供的信息解答下列问题:(1)九(1)班的学生人数为,并把条形统计图补充完整;(2)扇形统计图中m= ,n= ,表示“足球”的扇形的圆心角是度;(3)排球兴趣小组4名学生中有3男1女,现在打算从中随机选出2名学生参加学校的排球队,请用列表或画树状图的方法求选出的2名学生恰好是1男1女的概率.6.如图,AB∥CD,CE平分∠BCD,∠DCE=18°,则∠B等于A.18°B.36°C.45°D.54°7.如图是某体育馆内的颁奖台,其主视图是()A.B.C.D.8.一个不透明的布袋里装有3个大小、质地均相同的乒乓球,分别标有数字1,2,3,小华先从布袋中随即取出一个乒乓球,记下数字后放回,再从袋中随机取出一个乒乓球,记下数字.求两次取出的乒乓球上数字相同的概率.9.计算:.10.一列快车从甲地开往乙地,一列慢车从乙地开往甲地,两车同时出发,两车离乙地的路程S(千米)与行驶时间t(小时)的函数关系如图所示,则下列结论中错误的是【】A.甲、乙两地的路程是400千米B.慢车行驶速度为60千米/小时C.相遇时快车行驶了150千米D.快车出发后4小时到达乙地11.如图,二次函数y=ax2+bx+c(a≠0)的图象的顶点在第一象限,且过点(0,1)和(﹣1,0).下列结论:①ab<0,②b2>4a,③0<a+b+c<2,④0<b <1,⑤当x>﹣1时,y>0,其中正确结论的个数是A.5个B.4个C.3个D.2个12.如图,矩形ABCD中,AB=2,AD=4,AC的垂直平分线EF交AD于点E、交B C于点F,则EF= 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
绝密*启用前:湖北省十堰市2010年初中毕业生学业考试数学试题卷注意事项:本试卷分为试题卷和答题卡两部分,考试时间为120分钟,满分120分.一、仔细选一选(本题有10个小题,每小题3分,共30分)下面每小题给出的四个选项中,只有一个是正确的,请把正确选项的字母填在答题卷中相应的格子内.注意可以用多种不同的方法选取正确答案. 1.(2010.十堰)-3的绝对值是( C )A .13B .-13C .3D .-32.(2010.十堰)下列运算中正确的是( D )A .a 3a 2=a 6B .(a 3)4= a 7C .a 6 ÷ a 3 = a 2D .a 5 + a 5 =2 a 53.(2010.十堰))据人民网5月20日电报道:中国森林生态系统年涵养水源量4947.66亿立方米,相当于12个三峡水库2009年蓄水至175米水位后库容量,将4947.66亿用科学记数法表示为( C )A .4.94766×1013B .4.94766×1012C .4.94766×1011D .4.94766×10104.(2010.十堰)若一个几何体的三视图如图所示,则这个几何体是( A ) A .三棱柱 B .四棱柱 C .五棱柱 D .长方体5.要了解哪种品牌最畅销,公司经理最关心的是上述数据找( B ) A .平均数 B .众数 C .中位数 D .方差6.(2010.十堰)如图,将△ABC 绕点C 顺时针方向旋转40°得△A ’CB ’,若AC ⊥A ’B ’,则∠BAC 等于( A )A .50°B .60°C .70°D .80°主视图 俯视图 左视图(第4题)(第6题)AA ′CBB ′7.(2010.十堰)如图,已知梯形ABCD 的中位线为EF ,且△AEF 的面积为6cm 2,则梯形ABCD的面积为( C )A .12 cm2B .18 cm 2C .24 cm 2D .30 cm 28.(2010.十堰)下列命题中,正确命题的序号是( D )①一组对边平行且相等的四边形是平行四边形 ②一组邻边相等的平行四边形是正方形 ③对角线相等的四边形是矩形 ④对角互补的四边形内接于圆A .①②B .②③C .③④D .①④ 9.(2010.十堰)方程x 2+2x -1=0的根可看成函数y =x +2与函数1y x=的图象交点的横坐标,用此方法可推断方程x 3+x -1=0的实根x 所在范围为( C ) A . 102x -<< B .102x << C .112x << D .312x << 10.(2010.十堰)如图,点C 、D 是以线段AB 为公共弦的两条圆弧的中点,AB =4,点E 、F 分别是线段CD ,AB 上的动点,设AF =x ,AE 2-FE 2=y ,则能表示y 与x 的函数关系的图象是( C )二、认真填一填(本题有6个小题,每小题3分,共18分)11.(2010.十堰)分解因式:a 2-4b 2= (a +2b )(a -2b ) .(第10题) C DE BA D BC E F (第7题)12.(2010.十堰)函数3y x =-的自变量x 的取值范围是 x ≥2且x ≠3 . 13.(2010湖北十堰,13,3分)如图,直线l 1∥l 2被直线l 3所截,∠1=∠2=35°,∠P =90°,则∠3= 55° .14.(2010.十堰)在平面直角坐标系中,若点P 的坐标(m ,n ),则点P 关于原点O 对称的点P ’的坐标为 (-m ,-n ) .15.(2010.十堰) 下图是根据某中学为地震灾区玉树捐款的情况而制作的统计图,已知该校在校学生3000人,请根据统计图计算该校共捐款 37770 元.16.(2010.十堰)如图,n +1个上底、两腰长皆为1,下底长为2的等腰梯形的下底均在同一直线上,设四边形P 1M 1N 1N 2面积为S 1,四边形P 2M 2N 2N 3的面积为S 2,……,四边形P n M n N n N n+1的面积记为S n ,通过逐一计算S 1,S 2,…,可得S n =14214n -⋅+ .三、全面答一答(本题有9个小题,满分72分)本大题解答应写出文字说明,证明过程或推理步骤,如果觉得有的题目有点困难,那么把自己能写的解答写出一部分也可以. 17.(2010.十堰)(本小题满分7分)l 1l 2 l 3 3 12P(第13题)初一 32% 初二 33%初三35%(图1) 人数统计(图2)(第15题) (第16题)N 1N 2N 3N 4N 5计算:30(2)|5|2)2sin30-+--+︒解:原式=-8 + 5-1+ 2×12 =-3.18.(2010.十堰)(本小题满分7分)先化间,再求值:211(1)(2)11x x x -÷+-+-,其中x =解:原式=111x x +-⋅+(x +1)(x -1)+(x -2) =x (x -1)+(x -2) =x 2-2当x = 6 时,原式=( 6 )2-2=4.19.(2010.十堰)(本小题满分7分)如图,△ABC 中,AB =AC ,BD ⊥AC ,CE ⊥AB . 求证:BD =CE .证明:∵BD ⊥AC ,CE ⊥AB ∴∠ADB =∠AEC =90°在△ABD 和△AEC 中,∠ADB =∠AEC =90°,∠A =∠A ,AB =AC ∴△ABD ≌△AEC ∴BD =CE .20.(2010.十堰)(本小题满分8分)某乡镇中学数学活动小组,为测量数学楼后面的山高AB ,用了如下的方法.如图所示,在教学楼底C 处测得山顶A 的仰角为60°,在教学楼顶D 处,测得山顶A 的仰角为45°.已知教学楼高CD =12米,求山高AB .(参考数据 3 =1.73, 2 =1.41,精确到0.1米,化简后再代入参考数据运算)解:过D 作DE ⊥AB 于E ,而AB ⊥BC ,DC ⊥BC ,故四边形DEBC 为矩形,ABC D E(第19题)A则CD =BE ,∠ADE =45°,∠ACB =60°.设AB =h 米,在Rt △A BC 中,BC =h ·cot 60°=h ·tan 30°=3h在Rt △AED 中,AE =DE ·tan 45°=BC ·tan 45° 又AB -AE =BE =CD =12∴h =12∴h18=+=18+6×1.73=18+10.38≈28.4(米)答:山高AB 是28.4米.21.(2010.十堰)(本小题满分8分)暑假快到了,老家在十堰的大学生张明与王艳打算留在上海,为世博会做义工.学校争取到6个义工名额,分别安排在中国馆园区3个名额,世博轴园区2个名额,演义中心园区1个名额. 学校把分别标号为1、2、3、4、5、6的六个质地大小均相同的小球,放在不透明的袋子里,并规定标号1、2、3的到中国馆,标号4、5到世博轴,标号6的到演艺中心,让张明、王艳各摸1个. (1)求张明到中国馆做义工的概率;(2)求张明、王艳各自在世博轴、演艺中心做义工的概率(两人不同在一个园区内).解:(1)如表所示,张明、王艳各摸一球可能出现的结果有6×5=30个,它们出现的可能性相等,张明到中国馆的结果有15个,∴P (张明到中国馆做义务)=151=.(2)张明、王艳各自在世博轴、演艺中心的结果共4个,其概率P=23015=. 22.(2010.十堰)(本小题满分8分)如图所示,直线AB 与反比例函数图像相交于A ,B 两点,已知A (1,4).(1)求反比例函数的解析式;(2)连结OA ,OB ,当△AOB 的面积为152 时,求直线AB 的解析式.解:(1)设反比例函数解析式为y= kx ,∵点A (1,4)在反比例函数的图象上 ∴4=1k ,∴k =4,∴反比例函数的解析式为y =4x. (2)设直线AB 的解析式为y =ax +b (a >0,b >0),则当x =1时,a +b =4即b =4-a .联立4y x y ax b⎧=⎪⎨⎪=+⎩,得ax 2 +bx -4=0,即ax 2+(4-a方法1:(x -1)(ax +4)= 0,解得x 1=1或x =-4a设直线AB 交y 轴于点C ,则C (0,b ),即C (0,由S △AOB =S △AOC +S △BOC =114(4)1(4)222a a a -⨯+-⨯=a 2+15a -16=0,∴a =1或a =-16(舍去) ∴b =4-∴ 直线AB 的解析式为y =x +3方法2:由S △AOB = 12 |OC |·|x 2-x 1|=152而|x 2-x 14()a=4||a a +=4a a +(a >0), |OC |=b =4-a ,可得1415(4)()22a a a +-=,解得a =1或a =-16(舍去). 23.(2010.十堰)(本小题满分8分)如图所示,某地区对某种药品的需求量y 1(万件),供应量y 2(万件)与价格x (元/件)分别近似满足下列函数关系式:y 1=-x + 70,y 2=2x -38,需求量为0时,即停止供应.当y 1=y 2时,该药品的价格称为稳定价格,需求量称为稳定需求量. (1)求该药品的稳定价格与稳定需求量.(2)价格在什么范围内,该药品的需求量低于供应量?(3)由于该地区突发疫情,政府部门决定对药品供应方提供价格补贴来提高供货价格,以利提高供应量.根据调查统计,需将稳定需求量增加6万件,政府应对每件药品提供多少元补贴,才能使供应量等于需求量.解:(1)由题可得1270238y x y x =-+⎧⎨=-⎩,当y 1=y 2时,即-x +70=2x -38 ∴3x =108,∴x =36当x =36时,y 1=y 2=34,所以该药品的稳定价格为36元/件,稳定需求量为34万件.(2)令y 1=0,得x =70,由图象可知,当药品每件价格在大于36元小于70元时,该药品的需求量低于供应量.(3)设政府对该药品每件价格补贴a 元,则有346703462()38x x a +=-+⎧⎨+=+-⎩,解得309x a =⎧⎨=⎩ 所以政府部门对该药品每件应补贴9元.24.(2010.十堰)(本小题满分9分)如图,已知⊙O 1与⊙O 2都过点A ,AO 1是⊙O 2的切线,⊙O 1交O 1O 2于点B ,连结AB 并延长交⊙O 2于点C ,连结O 2C . (1)求证:O 2C ⊥O 1O 2;(2)证明:AB ·BC =2O 2B ·BO 1;(3)如果AB ·BC =12,O 2C =4,求AO 1的长.元/件)解:(1)∵AO 1是⊙O 2的切线,∴O 1A ⊥AO 2 ∴∠O 2AB +∠BAO 1=90° 又O 2A =O 2C ,O 1A =O 1B ,∴∠O 2CB =∠O 2AB ,∠O 2BC =∠ABO 1=∠BAO 1 ∴∠O 2CB +∠O 2BC =∠O 2AB +∠BAO 1=90°,∴O 2C ⊥O 2B ,即O 2C ⊥O 1O 2 (2)延长O 2O 1交⊙O 1于点D ,连结AD . ∵BD 是⊙O 1直径,∴∠BAD =90° 又由(1)可知∠BO 2C =90°∴∠BAD =∠BO 2C ,又∠ABD =∠O 2BC ∴△O 2BC ∽△ABD ∴2O B BCAB BD= ∴AB ·BC =O 2B ·BD 又BD =2BO 1 ∴AB ·BC =2O 2B ·BO 1(3)由(2)证可知∠D =∠C =∠O 2AB ,即∠D =∠O 2AB ,又∠AO 2B =∠DO 2A ∴△AO 2B ∽△DO 2A ∴2222AO O BDO O A=∴AO 22=O 2B ·O 2D ∵O 2C =O 2A∴O 2C 2=O 2B ·O 2D ① 又由(2)AB ·BC =O 2B ·BD ②由①-②得,O 2C 2-AB ·BC = O 2B 2 即42-12=O 1B 2 ∴O 2B =2,又O 2B ·BD =AB ·BC =12 ∴BD =6,∴2AO 1=BD =6 ∴AO 1=325.(2010.十堰)(本小题满分10分)已知关于x 的方程mx 2-(3m -1)x +2m -2=0(1)求证:无论m 取任何实数时,方程恒有实数根.(2)若关于x 的二次函数y= mx 2-(3m -1)x +2m -2的图象与x 轴两交点间的距离为2时,求抛物线的解析式.(3)在直角坐标系xoy 中,画出(2)中的函数图象,结合图象回答问题:当直线y =x +b 与(2)中的函数图象只有两个交点时,求b 的取值范围. 【答案】解:(1)分两种情况讨论:①当m =0 时,方程为x -2=0,∴x =2 方程有实数根 ②当m ≠0时,则一元二次方程的根的判别式△=[-(3m -1)]2-4m (2m -2)=m 2+2m +1=(m +1)2≥0 不论m 为何实数,△≥0成立,∴方程恒有实数根综合①②,可知m 取任何实数,方程mx 2-(3m -1)x +2m -2=0恒有实数根.(2)设x 1,x 2为抛物线y= mx 2-(3m -1)x +2m -2与x 轴交点的横坐标. 则有x 1+x 2=31m m -,x 1·x 2=22m m- 由| x 1-x 21||m m +, 由| x 1-x 2|=2得1||m m +=2,∴1m m +=2或1m m+=-2 ∴m =1或m =13-∴所求抛物线的解析式为:y 1=x 2-2x 或y 2=13-x 2+2x -83即y 1= x (x -2)或y 2=13-(x -2)(x -4)其图象如右图所示.(3)在(2)的条件下,直线y =x +b 与抛物线y 1,y 2组成的图象只有两个交点,结合图象,求b 的取值范围.212y x x y x b ⎧=-⎨=+⎩,当y 1=y 时,得x 2-3x -b =0,△=9+4b =0,解得b =-94; 同理2218233y x x y x b ⎧=-+-⎪⎨⎪=+⎩,可得△=9-4(8+3b )=0,得b =-2312. 观察函数图象可知当b <-94 或b >-2312时,直线y =x +b 与(2)中的图象只有两个交点.由2122218233y x x y x x ⎧=-⎪⎨=-+-⎪⎩当y 1=y 2时,有x =2或x =1 当x =1时,y =-1所以过两抛物线交点(1,-1),(2,0)的直线y =x -2,综上所述可知:当b <-94 或b >-2312 或b =-2时,直线y =x +b 与(2)中的图象只有两个交点.。
