2015-2016学年高中数学 2.1.2第1课时 离散型随机变量的分布列课时作业 新人教A版选修2-3
2.1.2《离散型随机变量的分布列》

解:X的取值有1、2、3、4、5、6 则P(X=1)=1/6, P(X=2)=1/6,
P(X=3)=1/6, P(X=4)=1/6, P(X=5)=1/6, P(X=6)=1/6 列成表格形式为 表2 1
X
1
2
3
4
5
6
1
1
1
1
1
1
P
6
6
6
6
6
6
4、求离散型随机变量的分布列的步骤:
(1)找出随机变量ξ的所有可能的取值(明确随机变量的具体取
bability distriution),简称为X的分 布 列 (distributio
nseries).有时为了表达简单,也用等式PX xi
pi,i 1,2, ,n 表 示X的 分布 列.
P
离 散 型 随 机 变 量 分 布 列的 变 0.2
化 情 况 可 以 用 图 象 表 示.如 在
2 根 据 随 机 变 量 X的 分 布 列, 可 得 只 少 取 到 1
件次品的概率
PX 1 PX 1 PX 2 PX 3
0.138 06 0.005 88 0.000 06
0.144 00.
也可以用P(X≥1)=1-P(X=0)来做
一 般 地, 在 含 有M件 次 品 的N件 产 品 中, 任 取n件,
2.1.2离散型随机变量 的分布列
莱西市实验学校 吕淑丽
一、复习回顾,巩固旧知 1、随机变量 2、离散型随机变量 3、概率的性质
二、创设情境,引入新课 【引例】抛掷一枚质地均匀的骰子,所得的点数X有 哪些值?是否是离散型随机变量?取每个值的概率是 多少?以试验结果设计奖项,可有哪些设计方案?
2[1].1.2离散型随机变量的分布列(1).ppt1
![2[1].1.2离散型随机变量的分布列(1).ppt1](https://img.taocdn.com/s3/m/901789f004a1b0717ed5dd0f.png)
1 2 3 4 5 6 5 4 3 2 1 p 36 36 36 36 36 36 36 36 36 36 36
例1:某一射手射击所得环数ξ
ξ P 4
0.02
的分布列如下:
5
0.04
6
0.06
7
0.09
8
0.28
9
0.29
10
0.22
求此射手”射击一次命中环数≥7”的概率. 分析: ”射击一次命中环数≥7”是指互斥事 件”ξ=7”, ”ξ=8”, ”ξ=9”, ”ξ=10” 的和.
0.88
例2.随机变量ξ的分布列为
ξ -1 0 1 2 3
p
0.16
a/10
a2
a/5
0.3
解:(1)由离散型随机变量的分布列的性质有 a a 9 2 3 0.16 a 0.3 1 解得: a (舍)或 a 10 10 5 5
(1)求常数a;(2)求P(1<ξ<4)
1 1 5 C3 C10 P( 2) 2 26 A13
2 1 5 A C P( 3) 3 10 3 143 A13
分布列为:
1
10 13
2
5 26
3
5 143
4
1 286
P
例5 从一批有10个合格品与3个次品的产品中,一件一件 地抽取产品,设各个产品被抽到的可能性相同,在下列两 种情况下,分别求出直到取出合格品为止时所需抽取的次 数 的分布列. (2)每次取出的产品都放回此批产品中; 解:
… …
P
小结: 1、理解离散型随机变量的分布列的意义,会 求某些简单的离散型随机变量的分布列; 2、掌握离散型随机变量的分布列的两个基本 性质,并会用它来解决一些简单问题; 会求离散型随机变量的概率分布列:
2[1].1.2离散型随机变量的分布列导学案(选修2-3)1
![2[1].1.2离散型随机变量的分布列导学案(选修2-3)1](https://img.taocdn.com/s3/m/1fea6bc2d5bbfd0a7956732b.png)
§2.1.2离散型随机变量的分布列预习案一、教学目标1、理解离散型随机变量的分布列的意义,会求某些简单的离散型随机变量的分布列;2、掌握离散型随机变量的分布列的两个基本性质,并会用它来解决一些简单的问题.3. 理解二点分布的意义.二、预习自测:问题一:(1)抛掷一枚骰子,可能出现的点数有几种情况?(2)姚明罚球2次有可能得到的分数有几种情况?(3)抛掷一枚硬币,可能出现的结果有几种情况?思考:在上述试验开始之前,你能确定结果是哪一种情况吗?随机变量是如何定义的?问题二:按照我们的定义,所谓的随机变量,就是随机试验的试验结果与实数之间的一个对应关系。
那么,随机变量与函数有类似的地方吗?问题三:下列试验的结果能否用离散型随机变量表示?为什么?(1)已知在从汕头到广州的铁道线上,每隔50米有一个电线铁站,这些电线铁站的编号;(2)任意抽取一瓶某种标有2500ml的饮料,其实际量与规定量之差;(3)某城市1天之内的温度;(4)某车站1小时内旅客流动的人数;(5)连续不断地投篮,第一次投中需要的投篮次数.(6)在优、良、中、及格、不及格5个等级的测试中,某同学可能取得的等级。
导学案重点:离散型随机变量的分布列的意义及基本性质. 难点:分布列的求法和性质的应用.1.离散型随机变量 随着试验结果的变化而变化的变量称为随机变量,通常用字母X 、Y 表示。
如果对于随机变量可能取到的值,可以按 一一列出,这样的变量就叫离散型随机变量。
2.离散型随机变量的分布列(1)设离散型随机变量X 可能取的值为12,,,,i x x x ,X 取每一个值(1,2,)i x i = 的概率()i i P X x p ==,则表称为随机变量X 的概率分布,简称X 的分布列。
离散型随机变量的概率分布还可以用条形图表示, 如图所示。
离散型随机变量的分布列具有以下两个性质:① ;②一般地,离散型随机变量在某一范围内取值的概率等于它取这个范围内各个值的 。
离散型随机变量的分布列教案

2. 1.2离散型随机变量的分布列授课人:周受萍 授课时间2015.5.22 指导老师: 曾英义 教学目标:1、 知识与技能:会求出某些简单的离散型随机变量的概率分布;理解超几何概率分布类型。
2、过程与方法:认识概率分布列对于刻画随机现象的重要性。
3、情感、态度与价值观:感悟数学与生活的和谐之美 ,体现数学的文化功能与人文价值。
教学重点:明确离散型随机变量的分布列的求法,理解超几何概率分布类型。
教学难点:掌握超几何概率分布类型的求法,会求一些离散型随机变量的分布列 授课类型:新授课教 具:多媒体、实物投影仪 教学过程: 一、情景引入:思考:掷一枚骰子,向上一面的点数ξ有哪些值?ξ取每个值的概率是多少?请同学们阅读课本P46-48的内容,说明什么是随机变量的分布列? 二、讲解新课:1. 分布列:设离散型随机变量ξ可能取得值为 x 1,x 2,…,x 3,…,x nξ取每一个值x i (i =1,2,…,n )的概率为()i i P x p ξ==,则称表为随机变量的概率分布,简称的分布列分布列的两个性质:任何随机事件发生的概率都满足:1)(0≤≤A P ,并且不可能事件的概率为0,必然事件的概率为1.由此你可以得出离散型随机变量的分布列都具有下面两个性质:(1)P i ≥0,i =1,2,…,n ;⑵P 1+P 2+…+P n =1.问题1:给出离散型随机变量 X 的分布列为:试说明他的计算结果是否正确。
问题2:现要发行1000张彩票,其中中奖金额为2元的彩票有300张,10元的100张,100元的1张,求买1张彩票可能中奖金额X 的分布列 归纳: 求离散型随机变量ξ的概率分布的步骤: (1)确定随机变量的所有可能的值x i (2)求出各取值的概率p(ξ=x i )=p i (3)列成表格例题分析:例1. 在掷一枚图钉的随机试验中,令 ⎧⎨⎩1,针尖向上;X=0,针尖向下.如果针尖向上的概率为p ,试写出随机变量 X 的分布列.解:根据分布列的性质,针尖向下的概率是(1p -) .于是,随机变量 X 的分布列是. 2.两点分布列:两点分布列的应用非常广泛.如抽取的彩券是否中奖;买回的一件产品是否为正品;新生婴儿的性别;投篮是否命中等,都可以用两点分布列来研究.如果随机变量X 的分布列为两点分布列,就称X 服从两点分布 ( two 一point distribution),而称p =P (X = 1)为成功概率.两点分布又称0一1分布.由于只有两个可能结果的随机试验叫伯努利( Bernoulli ) 试验,所以还称这种分布为伯努利分布.()q P ==0ξ, ()p P ==1ξ,10<<p ,1=+q p .变式:在射击的随机试验中,令X= 如果射中的概率为0.8,求随机变量X 的分布列。
2.1.2离散型随机变量的分布列
5
0.3
解:由离散型随机变量的分布列的性质有
0.16 + a + a2 + a + 0.3 = 1
10
5
解得:a = - 9 (舍)或 a = 3
10
5
(3)设随机变量 的分布列为:P(ξ k) k ,k 1,2,3,4,5,
15
求 ① P( 1或 2) ;
② P( 1 ξ 5 ) ;
思考
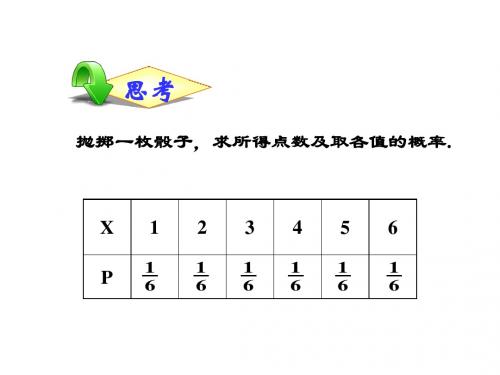
抛掷一枚骰子,求所得点数及取各值的概率.
X1 2 3 4 5 6
P
1 6
1111 6666
1 6
2.1.2离散型随机 变量的分布列
知识要点
1.分布列
设离散型随机变量ξ可能取得值为
x1,x2,x3,…,
新疆 王新敞
奎屯
ξ取每一个值xi(i=1,2,…)的概率为
P(ξ= xi)=pi,则称表
ξ
x1
ξ
-1
0
1
P
0.3
Hale Waihona Puke 0.40.3ξ
1
2
3
P
0.3
0.4
0.4
3.解答题
(1)某厂生产电子元件,其产品的次品率 为5%,现从一批产品中的任意连续取出2件, 求次品数的概率分布.
解: ξ的取值分别为0、1、2
ξ =0表示抽取两件均为正品 ; ∴p(ξ=0)=C20(1-0.05)2=0.9025 .
继续解答
0.5
0.25
3. 设抽出的5张牌中包含A牌的张数为X,则X
服从超几何分布,其分布列为 P(X=i)=C4iC485-i/C525,i=0,1,2,3,4 .
因此抽出的5张牌中至少有3张A的概率为
2.1.2 离散型随机变量的分布列

C35C09 5 C130 0
五、超几何分布列
一般地,在含有M件次品的N件产品中,任取n件, 其中恰有X件次品数,则事件{X=k}发生的概率为
P其(中Xm=mkin){M,nC},且M k CCnNnNNn,MkMN, k,n,M,N0,1N,*2., , m,
称分布列
X
0
1
…
m
P
CM0
C n0 N M
CM1
C n1 N M
…
CMm
C nm N M
CNn
CNn
CNn
为超几何分布列.
如果随机变量X的分布列为超几何分布列,则称 随机变量X服从超几何分布.
例3、某年级的联欢会上设计了一个摸奖游戏,在 一个口袋中有10个红球和20个白球,这些球除颜色 外完全相同.一次从中摸出5个球,至少摸到3个红球 就中奖.求中奖的概率.
练习: 5.将一枚质地均匀的骰子抛掷10次,试写出1点向上的 次数ξ的分布列.
答案:
ξ 0 1 2 … k … 10
P
510 C110 59 C120 58 … C1k0 510k …
610 610 610
610
1 610
二.分布列的表示法: (1) 表格法: 优点: 能直观得到随机变量取各个不同值的概率. 缺点: 当随机变量的取值个数较多时,不容易制作. (2) 解析式法:
3. 随机变量与函数的类比: 随机变量和函数都是映射. 随机变量把随机试验的结果映为实数, 函数把实数映 为实数. 试验结果的范围相当于函数的定义域, 随机变 量的取值范围相当于函数的值域. 随机变量的取值范围叫做随机变量的值域.
4. 离散型随机变量: 所有取值可以一一列出的随机变量 称为离散型随机变量.
数学:2.1.2《离散型随机变量的分布列》课件(新人教A版选修2-3)

P
的变 0.2 离散型随机变量分布列 .如在 化情况可以用图象表示 ,掷出的点数 0.1 X 掷骰子试验中 的分布列在直角坐标系 中的 O 2 . 图象如图 .1− 2所示
1
2 3
4 5
6
X
在图 2.1 − 2 中, 横坐标是随 机变量的取值, 纵坐标为概 率 .从中可以看出, X 的取值 范围是 { ,2,3,4,5, 6},它取每 1 1 个值的概率都是 . 6
表2 −1
X P
1 1 6
2 1 6
3 1 6
4 1 6
5 1 6
6 1 6
利用表2 − 1可以求出能由X表示的事件的概率.例如, 在这个随机试验中事件{X < 3} = {X = 1} ∪ {X = 2}, 由概率的可加性得 1 1 1 P(X < 3 ) = P(X = 1) + P(X = 2) = + = . 6 6 3
3 3 4 4 5 5 C10C5−−10 C10C5−−10 C10C5−−10 30 30 30 = + + ≈ 0.191. 5 5 5 C30 C30 C30 55 左右 , 思考 如果要将这个游戏的中 奖控制在 % 那么应该如何设计中奖 ? 规则
Байду номын сангаас 作业:P49A组(4—6)和B组 P49A 4—6 B
X
P
0
0 n CMCN−0 −M n CN
1
n C1 CN−1 M −M n CN
⋅⋅⋅ ⋅⋅⋅
3
m n CMCN−m −M n CN
.如果随机变量 的分布列为 X 为 超几何分布列 , 超几何分布列 则称随机变量X服从超几何分 布(hypergeome tric distributi on).
第二章 2.1.2 离散型随机变量的分布列(一)

2.1.2 离散型随机变量的分布列(一)学习目标 1.在对具体问题的分析中,理解取有限个值的离散型随机变量及其分布列的概念;认识分布列对于刻画随机现象的重要性.2.掌握离散型随机变量分布列的表示方法和性质.知识点 离散型随机变量的分布列思考 掷一枚骰子,所得点数为x ,则x 可取哪些数字?x 取不同的值时,其概率分别是多少?你能用表格表示x 与p 的对应关系吗? 答案 (1)x =1,2,3,4,5,6,概率均为16.(2)1.离散型随机变量的分布列的概念一般地,若离散型随机变量X 可能取的不同值为x 1,x 2,…,x i ,…,x n ,X 取每一个值x i (i =1,2,…,n )的概率P (X =x i )=p i ,以表格的形式表示如下:的分布列. 2.离散型随机变量的分布列的性质 (1)p i ≥0,i =1,2,3,…,n ; (2)∑i =1np i =1.类型一 离散型随机变量的分布列的性质的应用例1 设随机变量X 的分布列为P (X =i )=ai (i =1,2,3,4),求: (1)P ({X =1}∪{X =3}); (2)P ⎝⎛⎭⎫12<X <52.解 题中所给的分布列为由离散型随机变量分布列的性质得a +2a +3a +4a =1,解得a =110.(1)P ({X =1}∪{X =3})=P (X =1)+P (X =3) =110+310=25. (2)P ⎝⎛⎭⎫12<X <52=P (X =1)+P (X =2) =110+210=310. 反思与感悟 1.本例利用方程的思想求出常数a 的值. 2.利用分布列及其性质解题时要注意以下两个问题: (1)X 的各个取值表示的事件是互斥的.(2)不仅要注意∑i =1np i =1,而且要注意p i ≥0,i =1,2,…,n .跟踪训练1(1)下面是某同学求得的离散型随机变量X 的分布列.试说明该同学的计算结果是否正确.(2)设ξ是一个离散型随机变量,其分布列为①求q 的值; ②求P (ξ<0),P (ξ≤0).解 (1)因为P (X =-1)+P (X =0)+P (X =1)=12+14+16=1112,不满足概率之和为1的性质,因而该同学的计算结果不正确.(2)①由分布列的性质得,1-2q ≥0,q 2≥0,12+(1-2q )+q 2=1, ∴q =1-22. ②P (ξ<0)=P (ξ=-1)=12,P (ξ≤0)=P (ξ=-1)+P (ξ=0) =12+1-2⎝⎛⎭⎫1-22=2-12. 类型二 求离散型随机变量的分布列例2 一袋中装有6个同样大小的黑球,编号分别为1,2,3,4,5,6,现从中随机取出3个球,以X 表示取出球的最大号码,求X 的分布列.解 随机变量X 的可能取值为3,4,5,6.从袋中随机地取出3个球,包含的基本事件总数为C 36,事件“X =3”包含的基本事件总数为C 11C 22,事件“X =4”包含的基本事件总数为C 11C 23,事件“X =5”包含的基本事件总数为C 11C 24,事件“X =6”包含的基本事件总数为C 11C 25, 从而有P (X =3)=C 11C 22C 36=120,P (X =4)=C 11C 23C 36=320,P (X =5)=C 11C 24C 36=310,P (X =6)=C 11C 25C 36=12,所以随机变量X 的分布列为:反思与感悟 求离散型随机变量的分布列的步骤(1)明确随机变量的所有可能取值以及取每个值所表示的意义. (2)利用概率的有关知识,求出随机变量取每个值的概率. (3)按规范形式写出分布列,并用分布列的性质验证.跟踪训练2 袋中有1个白球和4个黑球,每次从中任取一个球,每次取出的黑球不再放回,直到取出白球为止,求取球次数X 的分布列. 解 X 的可能取值为1,2,3,4,5,则第1次取到白球的概率为P (X =1)=15,第2次取到白球的概率为P (X =2)=4×15×4=15,第3次取到白球的概率为P (X =3)=4×3×15×4×3=15,第4次取到白球的概率为P (X =4)=4×3×2×15×4×3×2=15,第5次取到白球的概率为P (X =5)=4×3×2×1×15×4×3×2×1=15,所以X 的分布列为类型三 离散型随机变量的分布列的综合应用例3 袋中装有黑球和白球共7个,从中任取2个球都是白球的概率为17,现有甲、乙两人从袋中轮流摸取1球,甲先取,乙后取,然后甲再取……取后不放回,直到两人中有一人取到白球时终止,每个球在每一次被取出的机会是等可能的,用ξ表示取球终止所需要的取球次数.(1)求袋中原有的白球的个数. (2)求随机变量ξ的分布列. (3)求甲取到白球的概率.解 (1)设袋中原有n 个白球,由题意知17=C 2nC 27=n (n -1)27×62=n (n -1)7×6.可得n =3或n =-2(舍去),即袋中原有3个白球. (2)由题意,ξ的可能取值为1,2,3,4,5. P (ξ=1)=37;P (ξ=2)=4×37×6=27;P (ξ=3)=4×3×37×6×5=635;P (ξ=4)=4×3×2×37×6×5×4=335;P (ξ=5)=4×3×2×1×37×6×5×4×3=135.所以ξ的分布列为:(3)因为甲先取,所以甲只有可能在第一次、第三次和第五次取到白球,记“甲取到白球”为事件A ,则P (A )=P (ξ=1)+P (ξ=3)+P (ξ=5)=2235.反思与感悟 求离散型随机变量的分布列,首先要根据具体情况确定ξ的取值情况,然后利用排列、组合与概率知识求出ξ取各个值的概率,即必须解决好两个问题,一是求出ξ的所有取值,二是求出ξ取每一个值时的概率.跟踪训练3 北京奥运会吉祥物由5个“中国福娃”组成,分别叫贝贝、晶晶、欢欢、迎迎、妮妮.现有8个相同的盒子,每个盒子中放一只福娃,每种福娃的数量如下表:从中随机地选取5只.(1)求选取的5只恰好组成完整“奥运会吉祥物”的概率.(2)若完整地选取奥运会吉祥物记100分;若选出的5只中仅差一种记80分;差两种记60分;以此类推,设X 表示所得的分数,求X 的分布列.解 (1)选取的5只恰好组成完整“奥运会吉祥物”的概率P =C 12·C 13C 58=656=328.(2)X 的取值为100,80,60,40.P (X =100)=C 12·C 13C 58=328,P (X =80)=C 23(C 22·C 13+C 12·C 23)+C 33(C 22+C 23)C 58=3156, P (X =60)=C 13(C 22·C 23+C 12·C 33)+C 23·C 33C 58=1856=928, P (X =40)=C 22·C 33C 58=156.X 的分布列为1.已知随机变量X 的分布列如下:则P (X =10)等于( ) A.239 B.2310 C.139 D.1310 答案 C解析 P (X =10)=1-23-…-239=139.2.设随机变量ξ的分布列为P (ξ=k )=k15(k =1,2,3,4,5),则P ⎝⎛⎭⎫12<ξ<52等于( ) A.12 B.19 C.16 D.15 答案 D解析 由12<ξ<52知ξ=1,2.P (ξ=1)=115,P (ξ=2)=215,∴P ⎝⎛⎭⎫12<ξ<52=P (ξ=1)+P (ξ=2)=15. 3.将一枚硬币扔三次,设X 为正面向上的次数,则P (0<X <3)=________. 答案 0.75解析 P (0<X <3)=1-P (X =0)-P (X =3) =1-123-123=0.75.4.将一颗骰子掷两次,求两次掷出的最大点数ξ的分布列. 解 由题意知ξ=i (i =1,2,3,4,5,6), 则P (ξ=1)=1C 16C 16=136;P (ξ=2)=3C 16C 16=336=112;P (ξ=3)=5C 16C 16=536;P (ξ=4)=7C 16C 16=736;P (ξ=5)=9C 16C 16=936=14;P (ξ=6)=11C 16C 16=1136.所以抛掷两次掷出的最大点数构成的分布列为1.离散型随机变量的分布列,不仅能清楚地反映其所取的一切可能的值,而且能清楚地看到取每一个值时的概率的大小,从而反映了随机变量在随机试验中取值的分布情况.2.一般地,离散型随机变量在某一范围内取值的概率等于它取这个范围内各个值的概率之和.一、选择题1.随机变量ξ的所有可能的取值为1,2,3,…,10,且P (ξ=k )=ak (k =1,2,…,10),则a 的值为( )A.1110B.155 C.110 D.55 答案 B解析 ∵随机变量ξ的所有可能的取值为1,2,3,…,10, 且P (ξ=k )=ak (k =1,2,…,10), ∴a +2a +3a +…+10a =1, ∴55a =1,∴a =155.2.若随机变量X 的概率分布列为:P (X =n )=an (n +1)(n =1,2,3,4),其中a 是常数,则P ⎝⎛⎭⎫12<X <52的值为( ) A.23 B.34 C.45 D.56 答案 D解析 ∵P (X =1)+P (X =2)+P (X =3)+P (X =4) =a ⎝⎛⎭⎫1-15=1, ∴a =54.∴P ⎝⎛⎭⎫12<X <52=P (X =1)+P (X =2)=a 1×2+a 2×3=a ⎝⎛⎭⎫1-13=54×23=56. 3.若随机变量η的分布列如下:则当P (η<x )=0.8时,实数x 的取值范围是( ) A.x ≤1 B.1≤x ≤2 C.1<x ≤2 D.1≤x <2答案 C解析 由分布列知,P (η=-2)+P (η=-1)+P (η=0)+P (η=1) =0.1+0.2+0.2+0.3=0.8, ∴P (η<2)=0.8,故1<x ≤2. 4.随机变量ξ的分布列如下:其中a ,b ,c 成等差数列,则函数f (x )=x 2+2x +ξ有且只有一个零点的概率为( ) A.16 B.13 C.12 D.56 答案 B解析 由题意知⎩⎪⎨⎪⎧2b =a +c ,a +b +c =1,解得b =13.∵f (x )=x 2+2x +ξ有且只有一个零点, ∴Δ=4-4ξ=0,解得:ξ=1, ∴P (ξ=1)=13.5.已知随机变量ξ只能取三个值x 1,x 2,x 3,其概率依次成等差数列,则该等差数列公差的取值范围是( ) A.⎣⎡⎦⎤0,13 B.⎣⎡⎦⎤-13,13 C.[-3,3] D.[0,1]答案 B解析 设随机变量ξ取x 1,x 2,x 3的概率分别为a -d ,a ,a +d ,则由分布列的性质得(a -d )+a +(a +d )=1,故a =13,由⎩⎨⎧13-d ≥013+d ≥0,解得-13≤d ≤13.6.抛掷2颗骰子,所得点数之和X 是一个随机变量,则P (X ≤4)等于( )A.16B.13C.12D.23 答案 A解析 根据题意,有P (X ≤4)=P (X =2)+P (X =3)+P (X =4).抛掷两颗骰子,按所得的点数共36个基本事件,而X =2对应(1,1),X =3对应(1,2),(2,1),X =4对应(1,3),(3,1),(2,2), 故P (X =2)=136,P (X =3)=236=118,P (X =4)=336=112,所以P (X ≤4)=136+118+112=16.二、填空题7.一批产品分为一、二、三级,其中一级品是二级品的两倍,三级品为二级品的一半,从这批产品中随机抽取一个检验,其级别为随机变量ξ,则P ⎝⎛⎭⎫13≤ξ≤53=________. 答案 47解析 设二级品有k 个,∴一级品有2k 个,三级品有k 2个,总数为72k 个.∴分布列为P ⎝⎛⎭⎫13≤ξ≤53=P (ξ=1)=47. 8.由于电脑故障,使得随机变量X 的分布列中部分数据丢失,以□代替,其表如下:根据该表可知X 取奇数值时的概率是________. 答案 0.6解析 由离散型随机变量的分布列的性质可求得P (X =3)=0.25,P (X =5)=0.15,故X 取奇数值时的概率为P (X =1)+P (X =3)+P (X =5)=0.20+0.25+0.15=0.6.9.甲、乙两队在一次对抗赛的某一轮中有3道题,比赛规则:对于每道题,没有抢到题的队伍得0分,抢到题,并回答正确的得1分,抢到题目但回答错误的扣1分(即-1分),若X 是甲队在该轮比赛获胜时的得分(分数高者胜),则X 的所有可能值为________. 答案 -1,0,1,2,3解析 X =-1表示甲抢到1题但答错了, 若乙两题都答错,则甲获胜; 甲获胜还有以下可能:X =0,甲没抢到题,或甲抢到2题,但答时1对1错. X =1时,甲抢到1题,且答对或甲抢到3题,且1错2对. X =2时,甲抢到2题均答对. X =3时,甲抢到3题均答对.10.将3个小球任意地放入4个大玻璃杯中,一个杯子中球的最多个数记为X ,则X 的分布列是________. 答案解析 由题意知X =1,2,3. P (X =1)=A 3443=38;P (X =2)=C 23A 2443=916;P (X =3)=A 1443=116.∴X 的分布列为三、解答题11.某篮球运动员在一次投篮训练中的得分ξ的分布列如下表,其中a ,b ,c 成等差数列,且c =ab .求这名运动员投中3分的概率.解 由题中条件知,2b =a +c ,c =ab ,再由分布列的性质,知a +b +c =1,且a ,b ,c 都是非负数,由三个方程联立成方程组,可解得a =12,b =13,c =16,所以投中3分的概率是16.12.设S 是不等式x 2-x -6≤0的解集,整数m ,n ∈S .(1)设“使得m +n =0成立的有序数组(m ,n )”为事件A ,试列举事件A 包含的基本事件; (2)设ξ=m 2,求ξ的分布列.解 (1)由x 2-x -6≤0,得-2≤x ≤3, 即S ={x |-2≤x ≤3}.由于m ,n ∈Z ,m ,n ∈S 且m +n =0,所以事件A 包含的基本事件为:(-2,2),(2,-2),(-1,1),(1,-1),(0,0). (2)由于m 的所有不同取值为-2,-1,0,1,2,3, 所以ξ=m 2的所有不同取值为0,1,4,9,且有 P (ξ=0)=16,P (ξ=1)=26=13,P (ξ=4)=26=13,P (ξ=9)=16.故ξ的分布列为:13.某商店试销某种商品20天,获得如下数据:试销结束后(假设该商品的日销售量的分布规律不变),设某天开始营业时有该商品3件,当天营业结束后检查存货,若发现存量少于2件,则当天进货补充至3件,否则不进货,将频率视为概率.(1)求当天商店不进货的概率;(2)记X为第二天开始营业时该商品的件数,求X的分布列.解(1)P(“当天商店不进货”)=P(“当天商品销售量为0件”)+P(“当天商品销售量为1件”)=120+520=310.(2)由题意知,X的可能取值为2,3.P(X=2) =P(当天商品销售量为1件)=520=1 4;P(X=3)=P(当天商品销售量为0件)+P(当天商品销售量为2件)+P(当天商品销售量为3件)=120+920+520=34.故X的分布列为。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
【成才之路】2015-2016学年高中数学 2.1.2第1课时 离散型随机
变量的分布列课时作业 新人教A 版选修2-3
一、选择题
1.(2014~2015·杭州高二检测)设某项试验的成功率是失败率的2倍,用随机变量ξ描述一次试验的成功次数,则P (ξ=1)=( )
A .0
B .1
2 C .1
3 D .23
[答案] D
[解析] 由题意,“ξ=0”表示试验失败,“ξ=1”表示试验成功,设失败率为p ,则成功率为2p ,则ξ的分布列为
∵p +2p =1,∴p =13,∴P (ξ=1)=3
.
2.设随机变量ξ的分布列为P (ξ=i )=a ⎝ ⎛⎭
⎪⎫13i
,i =1、2、3,则a 的值为( )
A .1
B .913
C .1113
D .2713
[答案] D
[解析] 设P (ξ=i )=p i ,则p 1+p 2+p 3=13a +19a +127a =1,∴a =27
13.
3.已知随机变量ξ的概率分布如下:
则P (ξ=10)=(
A .239
B .2310
C .139
D .13
10 [答案] C
[解析] P (ξ=10)=m =1-⎝ ⎛⎭⎪⎫23+2
32+…+239
=1-23⎣⎢⎡⎦⎥⎤1-⎝ ⎛
⎭⎪⎫1391-13
=139.
4.一批产品共50件,其中5件次品,45件正品,从这批产品中任抽两件,则出现次品的概率为( )
A .2245
B .949
C .47245
D .以上都不对
[答案] C
[解析] P =1-C 2
45C 50=1-45×4450×49=47
245
,故选C .
5.甲、乙两人进行乒乓球比赛,比赛规则为“3局2胜”,即以先赢2局者为胜,根据经验,每局比赛中甲获胜的概率为0.6,则本次比赛甲获胜的概率是( )
A .0.216
B .0.36
C .0.432
D .0.648
[答案] D
[解析] 甲获胜的概率为P =0.6×0.6+0.6×0.4×0.6+0.4×0.6×0.6=0.648. 6.设袋中有80个红球,20个白球,若从袋中任取10个球,则其中恰有6个红球的概率为( )
A .C 4
80C 6
10
C 10100
B .
C 680C 4
10C 10100
C .C 4
80C 620C 10100
D .C 6
80C 4
20C 10100
[答案] D
[解析] P (ξ=6)=C 6
80C 4
20
C 10100.
二、填空题
7.设随机变量ξ的概率分布为P (ξ=k )=
c
k +1
,k =0、1、2、3,则c =________.
[答案]
1225
[解析] c +c 2+c 3+c 4=1,∴c =12
25
.
8.从装有3个红球、2个白球的袋中随机取出2个球,设其中有ξ个红球,则随机变量ξ的概率分布列为
[答案] 0.1 0.6 0.3 [解析] P (ξ=0)=C 2
2
C 25
=0.1,
P (ξ=1)=C 13C 12C 25=0.6,P (ξ=2)=C 2
3
C 25
=0.3.
9.设随机变量ξ的可能取值为5、6、7、…、16这12个值,且取每个值的概率均相同,则P (ξ>8)=________,P (6<ξ≤14)=________.
[答案] 23 2
3
[解析] P (ξ>8)=112×8=2
3
,
P (6<ξ≤14)=112×8=23
.
三、解答题
10.(2014·宝鸡市质检)为了参加广州亚运会,从四支较强的排球队中选出18人组成女子排球国家队,队员来源人数如下表:
(1)从这18
(2)中国女排奋力拼搏,战胜了韩国队获得冠军,若要求选出两位队员代表发言,设其中来自北京队的人数为ξ,求随机变量ξ的分布列.
[解析] (1)“从这18名队员中选出两名,两人来自于同一队”记作事件A , 则P (A )=C 2
4+C 2
6+C 2
3+C 2
5C 2
18=2
9. (2)ξ的所有可能取值为0,1,2.
∵P (ξ=0)=C 2
14C 218=91153,P (ξ=1)=C 14C 1
14C 218=56
153,
P (ξ=2)=C 2
4C 218=6
153
,
∴ξ的分布列为:
一、选择题
11.(2014~2015·九江市高二检测)某12人的兴趣小组中,有5名“三好生”,现从中任意选6人参加竞赛,用X 表示这6人中“三好生”的人数,则下列概率中等于C 35C 3
7
C 612的是
( )
A .P (X =2)
B .P (X =3)
C .P (X ≤2)
D .P (X ≤3)
[答案] B
[解析] C 3
5表示从5名“三好生”中选择3名,C 3
7表示从其余7名学生中选3名,从而P (X =3)=C 35C 3
7
C 612
.
12.随机变量ξ的分布列如下:
,其中a 、b 、c ) A .13 B .14 C .12 D .23
[答案] D
[解析] ∵a 、b 、c 成等差数列,∴2b =a +c . 又a +b +c =1,∴b =13,∴P (|ξ|=1)=a +c =2
3
.
13.一盒中有12个乒乓球,其中9个新的,3个旧的,从盒中任取3个球来用,用完后装回盒中,此时盒中旧球个数X 是一个随机变量,则P (X =4)的值是( )
A .1
220 B .2755 C .27220 D .2155
[答案] C
[解析] 由题意知取出的3个球必为2个旧球1个新球,故P (X =4)=C 19C 2
3C 312=27
220.
14.设ξ是一个离散型随机变量,其分布列为
则a =( ) A .1 B .1±22 C .1+
22
D .1-
22
[答案] D
[解析] 由分布列的性质,得 ⎩⎪⎨⎪⎧
1-2a ≥0,12
+-2a +a 2
=1,
解得a =1-2
2
. 二、填空题
15.随机变量η的分布列如下
则x =[答案] 0.1 0.55
[解析] ∵0.2+x +0.25+0.1+0.15+0.2=1, ∴x =0.1.
P (η≤3)=P (η=1)+P (η=2)+P (η=3)
=0.2+0.1+0.25=0.55.
三、解答题
16.(2014·保定市八校联考改)某班同学利用寒假在三个小区进行了一次生活习惯是否符合低碳观念的调查,若生活习惯符合低碳观念的称为“低碳族”,否则称为“非低碳族”,这两族人数占各自小区总人数的比例如下:
(1)从A ,B ,C
(2)在B 小区中随机选择20户,从中抽取的3户中“非低碳族”数量为X ,求X 的分布列.
[解析] (1)记这3人中恰好有2人是低碳族为事件A ,
P (A )=12×45×13+12×15×23+12×45×23=715
.
(2)在B 小区中随机选择20户中,“非低碳族”有4户, P (X =k )=C k 4C 3-k
16
C 320,(k =0,1,2,3),
∴X 的分布列为
动小组有6名男生,4名女生,从中选出4人参加数学竞赛考试,用X 表示其中男生的人数.
(1)请列出X 的分布列;
(2)根据你所列的分布列求选出的4人中至少有3名男生的概率. [解析] (1)依题意得,随机变量X 服从超几何分布, ∵随机变量X 表示其中男生的人数, ∴X 可能取的值为0,1,2,3,4. ∴P (X =k )=C k
6·C 4-k
4
C 4
10,k =0,1,2,3,4. ∴X 的分布列为:
(2)由分布列可知选出的4人中至少有3名男生的概率为:
即P(X≥3)=P(X=3)+P(x=4)=8
21
+
1
14
=
19
42
.。
