第3.3节 minimax估计
(整理)计量经济学 第三章 多元线性回归与最小二乘估计

第三章 多元线性回归与最小二乘估计3.1 假定条件、最小二乘估计量和高斯—马尔可夫定理1、多元线性回归模型:y t = β0 +β1x t 1 + β2x t 2 +…+ βk - 1x t k -1 + u t (3.1) 其中y t 是被解释变量(因变量),x t j 是解释变量(自变量),u t 是随机误差项,βi , i = 0, 1, … , k - 1是回归参数(通常未知)。
对经济问题的实际意义:y t 与x t j 存在线性关系,x t j , j = 0, 1, … , k - 1, 是y t 的重要解释变量。
u t 代表众多影响y t 变化的微小因素。
使y t 的变化偏离了E( y t ) = β0 +β1x t 1 + β2x t 2 +…+ βk - 1x t k -1 决定的k 维空间平面。
当给定一个样本(y t , x t 1, x t 2 ,…, x t k -1), t = 1, 2, …, T 时, 上述模型表示为 y 1 = β0 +β1x 11 + β2x 12 +…+ βk - 1x 1 k -1 + u 1,y 2 = β0 +β1x 21 + β2x 22 +…+ βk - 1x 2 k -1 + u 2, (3.2) ………..y T = β0 +β1x T 1 + β2x T 2 +…+ βk - 1x T k -1 + u T经济意义:x t j 是y t 的重要解释变量。
代数意义:y t 与x t j 存在线性关系。
几何意义:y t 表示一个多维平面。
此时y t 与x t i 已知,βj 与 u t 未知。
)1(21)1(110)(111222111111)1(21111⨯⨯-⨯---⨯⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡T T k k k T k T TjT k j k jT T u u u x x x x x x x x x y y yβββ (3.3) Y = X β + u (3.4)2假定条件为保证得到最优估计量,回归模型(3.4)应满足如下假定条件。
3.3 minimax估计

B
) = max R(θ , d B ) = C .
θ ∈Θ
于是 d ( x 1 ," , x n ) ,的风险函数
R(θ , d ) ≤
R
M
( d ) < C , ∀θ ∈ Θ .
对上式两边在给定的先验分布下求期望,得到
R
B
(d ) = E[ R(θ , d )] < C =
R (d
B
B
).
这表明 d B ( x1 ,", xn) 不可能是这个先验分布下的贝 叶斯决策函数,从而产生了矛盾。因此,d B ( x1 ,", xn) 必 定是一个 minimax 决策函数。 对于上述矛盾,若给定的统计决策问题为参数的点 估计,且定理的条件满足,则相应的决策函数
表 3.2
地层结构分布规律表 0 1
θ
x
θ
0
(无油) (有油)
0.6 0.3
0.4 0.7
θ
1
它表示如果该地区蕴藏石油,那么地层结构呈现状态 0 的概率为 0.3,呈现状态 1 的概率为 0.7,如果该地区不 蕴藏石油, 那么地层结构呈现状态 0 的概率为 0.6, 呈现 状态 1 的概率为 0.4, 土地所有者希望根据地质学家对地 层结构的分析来决定自己投资钻探石油,还是出卖土地 所有权或者在该地区开辟旅游点,分别记这三种决策为
a , a , a , 于是决策空间 Α = {a , a , a }。土地所有者权衡
1 2 3
1
2
3
利弊之后取损失函数 L(θ,a)为表 3.3 所示。
表 3.3
L( θ ,a)
损失函数 L(θ,a)取值表
a
a
有约束的多元模型的Minimax估计及多元正态分布熵的估计的开题报告

有约束的多元模型的Minimax估计及多元正态分布熵的估计的开题报告一、课题背景多元统计分析中,多元模型的参数估计是重要的研究内容之一。
在多元模型中,有时需要对参数进行估计,在这种情况下,最小二乘估计可能不是最优的选择,因为它可能受到数据中的异常值影响。
因此,Minimax估计就被提出,它是一种对参数进行估计的方法,可以抵抗异常值的影响,从而提高了估计的准确性。
另外,多元正态分布的熵也是多元统计分析中非常重要的内容之一。
正如单变量分布的熵可以衡量随机变量的不确定性一样,多元正态分布的熵可以衡量多元随机变量的不确定性。
在一些实际问题中,我们需要估计多元正态分布的熵以了解它的基本特征或计算其他与熵相关的统计量。
因此,本文将重点探讨有约束的多元模型的Minimax估计和多元正态分布熵的估计。
二、研究目的与意义在实际研究中,数据中常常存在异常值等噪声因素,这些因素会对估计参数的精度造成负面影响,因此如何提高参数估计的鲁棒性是很有意义的研究方向。
Minimax 估计是一种抵抗异常值影响的估计方法,能够准确地估计参数,因此具有很高的应用价值。
另一方面,多元正态分布的熵是描述多元随机变量不确定性的重要指标,它不仅可以用于统计分析,还可以应用于工程、经济学、计算机科学等多个领域。
因此,研究多元正态分布熵的估计方法有助于更好地理解多元随机变量的统计特性,为相关应用提供更可靠的基础数据。
三、研究内容本文拟就有约束的多元模型的Minimax估计和多元正态分布熵的估计展开研究,具体内容如下:1. 有约束的多元模型的Minimax估计(1) 介绍Minimax估计的基本概念和原理,并分析Minimax估计的优缺点;(2) 探讨有约束的多元模型中的Minimax估计,包括有限制条件下的Minimax 估计和先验信息下的Minimax估计;(3) 针对具体问题,利用实例进行实证分析,验证Minimax估计的优越性。
2. 多元正态分布熵的估计(1) 简述多元正态分布的概念和特性,重点介绍其熵的计算方法和性质;(2) 探究多元正态分布熵的估计方法,包括直接估计和间接估计两种方法,比较其优缺点;(3) 针对具体问题,利用实例进行实证分析,评估各种多元正态分布熵的估计方法的表现。
Minimax算法及实例分析

Minimax算法及实例分析发表于2015/5/11 15:20:32 2419人阅读分类: AI算法计算机科学中最有趣的事情之一就是编写一个人机博弈的程序。
有大量的例子,最出名的是编写一个国际象棋的博弈机器。
但不管是什么游戏,程序趋向于遵循一个被称为Minimax算法,伴随着各种各样的子算法在一块。
Minimax算法又名极小化极大算法,是一种找出失败的最大可能性中的最小值的算法。
Minimax算法常用于棋类等由两方较量的游戏和程序,这类程序由两个游戏者轮流,每次执行一个步骤。
我们众所周知的五子棋、象棋等都属于这类程序,所以说Minimax算法是基于搜索的博弈算法的基础。
该算法是一种零总和算法,即一方要在可选的选项中选择将其优势最大化的选择,而另一方则选择令对手优势最小化的方法。
1. Minimax是一种悲观算法,即假设对手每一步都会将我方引入从当前看理论上价值最小的格局方向,即对手具有完美决策能力。
因此我方的策略应该是选择那些对方所能达到的让我方最差情况中最好的,也就是让对方在完美决策下所对我造成的损失最小。
1. Minimax不找理论最优解,因为理论最优解往往依赖于对手是否足够愚蠢,Minimax中我方完全掌握主动,如果对方每一步决策都是完美的,则我方可以达到预计的最小损失格局,如果对方没有走出完美决策,则我方可能达到比预计的最悲观情况更好的结局。
总之我方就是要在最坏情况中选择最好的。
实例分析:现在考虑这样一个游戏:有三个盘子A、B和C,每个盘子分别放有三张纸币。
A放的是1、20、50;B放的是5、10、100;C放的是1、5、20。
单位均为“元”。
有甲、乙两人,两人均对三个盘子和上面放置的纸币有可以任意查看。
游戏分三步:1. 甲从三个盘子中选取一个。
2. 乙从甲选取的盘子中拿出两张纸币交给甲。
3. 甲从乙所给的两张纸币中选取一张,拿走。
其中甲的目标是最后拿到的纸币面值尽量大,乙的目标是让甲最后拿到的纸币面值尽量小。
Minimax极大极小算法、Alpha-BetaPruning剪枝算法
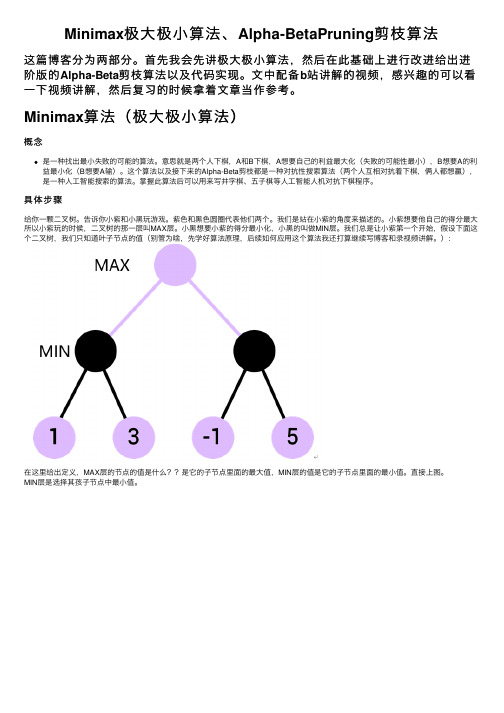
Minimax极⼤极⼩算法、Alpha-BetaPruning剪枝算法这篇博客分为两部分。
⾸先我会先讲极⼤极⼩算法,然后在此基础上进⾏改进给出进阶版的Alpha-Beta剪枝算法以及代码实现。
⽂中配备b站讲解的视频,感兴趣的可以看⼀下视频讲解,然后复习的时候拿着⽂章当作参考。
Minimax算法(极⼤极⼩算法)概念是⼀种找出最⼩失败的可能的算法。
意思就是两个⼈下棋,A和B下棋,A想要⾃⼰的利益最⼤化(失败的可能性最⼩),B想要A的利益最⼩化(B想要A输)。
这个算法以及接下来的Alpha-Beta剪枝都是⼀种对抗性搜索算法(两个⼈互相对抗着下棋,俩⼈都想赢),是⼀种⼈⼯智能搜索的算法。
掌握此算法后可以⽤来写井字棋、五⼦棋等⼈⼯智能⼈机对抗下棋程序。
具体步骤给你⼀颗⼆叉树。
告诉你⼩紫和⼩⿊玩游戏。
紫⾊和⿊⾊圆圈代表他们两个。
我们是站在⼩紫的⾓度来描述的。
⼩紫想要他⾃⼰的得分最⼤所以⼩紫玩的时候,⼆叉树的那⼀层叫MAX层。
⼩⿊想要⼩紫的得分最⼩化,⼩⿊的叫做MIN层。
我们总是让⼩紫第⼀个开始,假设下⾯这个⼆叉树,我们只知道叶⼦节点的值(别管为啥,先学好算法原理,后续如何应⽤这个算法我还打算继续写博客和录视频讲解。
):在这⾥给出定义,MAX层的节点的值是什么??是它的⼦节点⾥⾯的最⼤值,MIN层的值是它的⼦节点⾥⾯的最⼩值。
直接上图。
MIN层是选择其孩⼦节点中最⼩值。
MAX层选择其孩⼦节点中的最⼤值。
算法概念就是这个样⼦。
算法的输⼊是构造的这⼀棵满⼆叉树,输出是最上层MAX节点的值。
代码实现class Node{ //结点类public:const int value;Node *left;Node *right;Node(int v,Node* l,Node* r):value(v),left(l),right(r) {};};为了遍历这棵树,⾸先我们得创建出来这棵树对吧?但是你的代码⾥没有创建⼆叉树这⼀部分啊。
高级计量经济学

第3章 最小二乘法和最小二乘估计Chapter 3 Least Squares线性模型中的参数估计有多种方法,其中最小二乘法是最为著名的。
即使已经发现其他方法比较优越,但是最小二乘法仍然是线性模型估计的基础方法,最小二乘估计的性质已经得到了广泛应用。
§3.1 最小二乘回归(least squares regression)随机线性关系i i i y ε+'=βx 中的未知系数是我们考虑的重点,也是我们进行估计的主要目标。
这时我们有必要区分母体变量(例如β和i ε)和它们的样本估计,对应地表示为b 和i e 。
母体回归方程可以表示为:βx x i i i y E '=]|[它的估计表示为:b x i i y '=ˆ (3.1) 与第i 个数据点相关的扰动项可以表示为:βx i i i y '-=ε (3.2) 如果获得了回归系数的估计,则可以利用回归方程的残差来估计随机扰动项,即b x i i i y e '-= (3.3) 根据这些定义和表示,可以得到:i i i i i e y +'=+'=b x βx ε (3.4)母体量β是每个i y 的概率分布中的未知系数,我们希望利用样本数据),(i i y x 来估计这些参数。
虽然这是一个统计推断问题,但是我们仍然可以直观地认为应该选取向量b ,使得拟合直线b x i '尽量地靠近数据点。
如果描述这种靠近性,需要一定的拟合准则,其中最为广泛使用的是最小二乘法。
§3.1.1 最小二乘系数向量可以通过极小化下述残差平方和来获得最小二乘系数向量。
∑∑=='-=n i i n i i y e120120)(b x (3.5) 其中0b 表示系数向量的选择。
利用矩阵形式表示上述残差平方和:)()()(Minminze 000000Xb y Xb y e e b b -'-='=S (3.6) 将上述目标函数展开得到(注意利用标量的转置不变的性质):0000002)(Xb X b Xb y y y e e b ''+'-'='=S (3.7)极小化的一阶条件为(相当于对向量求导数,要么利用向量展开,要么利用向量求导公式):022)(000='+'-=∂∂Xb X y X b b S (3.8) 假设b 是最小二乘的解,则它必须满足最小二乘正规方程(least square normal equations): y X Xb X '=' (3.9) 如果解释变量矩阵的满秩条件满足,则有:K rank rank K n K K =='⨯⨯)()(X X X这说明矩阵K K ⨯')(X X 是可逆矩阵,因此正规方程的唯一解为:y X X X b ''=-1)( (3.10) 注意到上述条件只是极小化问题的必要条件,为了判断充分性,我们需要求出目标函数的Hessian 矩阵:X X bb b '='∂∂∂2)(2S (3.11) 如果这个Hessian 矩阵是正定的,则可以判断所得到的解是唯一的最小二乘解。
基于遗传算法的不确定对象pid优化

parameters of uncertain objects. Finally it gets satisfactory optimization results.Keywords: Proportion-Integral – Derivative Controller,Genetic Algorithm,Uncertainty System,MINIMAX Optimization,Hybrid Genetic Algorithm; Robustness目录摘要 (I)Abstract (II)目录 (IV)第一章绪论 (1)1.1 引言 (1)1.2 PID 控制器简介 (2)1.2.1 PID 控制器的结构和原理 (2)1.2.2 控制参数对 PID 控制的影响 (3)1.3 遗传算法简介 (4)1.3.1 遗传算法的特点 (4)1.3.2 遗传算法在控制工程中的应用 (5)1.4 国内外研究现状 (5)1.5 本文的研究内容及结构 (6)1.5.1 论文的研究内容 (6)1.5.2 论文的组织结构 (7)第二章不确定性优化问题的描述 (8)2.1 不确定优化命题的表达 (8)2.2 不确定优化命题的研究现状 (8)2.3 不确定优化问题的讨论 (10)2.3.1 不确定优化问题的提出与讨论 (10)2.3.2 参数不确定系统的优化命题 (11)2.4 参数不确定系统的优化解 (12)2.4.1 区间数运算 (12)2.4.2 优化解 (14)2.5 本章小结 (15)第三章基于全局 MINIMAX 优化问题的改进混合遗传算法 (16)3.1 全局 MINIMAX 优化问题 (16)3.1.1 全局 MINIMAX 优化问题的描述 (16)3.1.2 MINIMAX 优化命题研究的意义 (18)3.1.3 MINIMAX 的理论基础 (19)3.2 用 SGA 求解 MINIMAX 优化问题的算法 (20)3.2.1 简单遗传算法基础操作 (20)3.2.2 运用 SGA 解 MINIMAX 优化问题的算法描述 (21)3.2.3 运用 SGA 求解出现的困难 (22)3.3 改进的混合遗传算法求解 MINIMAX 优化问题 (23)3.3.1 改进遗传算法 (23)3.3.2 单纯形法的引入 (25)3.3.3 算法描述 (26)1.5.3 matlab 仿真实例计算 (27)1.5.4 本章小结 (28)第四章基于 HGA-I 的不确定对象 PID 优化 (30)2.6 PID 控制器参数的传统整定方法简介 (30)4.1.1 Ziegler-Nichols 整定方法 (30)4.1.2 遗传算法 PID 参数整定方法 (31)4.2 PID 控制性能指标 (33)4.2.1 动态指标 (33)4.2.2 综合指标 (34)4.3 HGA-I 整定不确定对象的 PID 参数的思想 (35)4.3.1 PID 控制器的选取 (35)4.3.2 不确定对象的描述 (36)4.3.3 参数的编码方案 (38)4.3.4 最优指标的选取 (38)4.3.5 适应度函数的选取 (40)4.3.6 参数整定的思想 (41)4.4 不确定对像的 PID 优化的参数整定算法 (42)4.5 matlab 实例仿真及结果分析 (44)4.6 本章小结 (47)第五章结论及展望 (48)参考文献 (49)致谢 (54)第一章绪论1.6引言常规比例积分微分(PID)控制是到现在为止最早发展起来的最通用最基本的控制器之一。
经典参数估计方法(3种方法)

经典参数估计方法:普通最小二乘(OLS)、最大似然(ML)和矩估计(MM)普通最小二乘估计(Ordinary least squares,OLS)1801年,意大利天文学家朱赛普.皮亚齐发现了第一颗小行星谷神星。
经过40天的跟踪观测后,由于谷神星运行至太阳背后,使得皮亚齐失去了谷神星的位置。
随后全世界的科学家利用皮亚齐的观测数据开始寻找谷神星,但是根据大多数人计算的结果来寻找谷神星都没有结果。
时年24岁的高斯也计算了谷神星的轨道。
奥地利天文学家海因里希.奥尔伯斯根据高斯计算出来的轨道重新发现了谷神星。
高斯使用的最小二乘法的方法发表于1809年他的著作《天体运动论》中。
法国科学家勒让德于1806年独立发现“最小二乘法”,但因不为世人所知而默默无闻。
勒让德曾与高斯为谁最早创立最小二乘法原理发生争执。
1829年,高斯提供了最小二乘法的优化效果强于其他方法的证明,因此被称为高斯-莫卡夫定理。
最大似然估计(Maximum likelihood,ML)最大似然法,也称最大或然法、极大似然法,最早由高斯提出,后由英国遗传及统计学家费歇于1912年重新提出,并证明了该方法的一些性质,名称“最大似然估计”也是费歇给出的。
该方法是不同于最小二乘法的另一种参数估计方法,是从最大似然原理出发发展起来的其他估计方法的基础。
虽然其应用没有最小二乘法普遍,但在计量经济学理论上占据很重要的地位,因为最大似然原理比最小二乘原理更本质地揭示了通过样本估计总体的内在机理。
计量经济学的发展,更多地是以最大似然原理为基础的,对于一些特殊的计量经济学模型,最大似然法才是成功的估计方法。
对于最小二乘法,当从模型总体随机抽取n组样本观测值后,最合理的参数估计量应该使得模型能最好地拟合样本数据;而对于最大似然法,当从模型总体随机抽取n组样本观测值后,最合理的参数估计量应该是使得从模型中抽取该n组样本观测值的概率最大。
从总体中经过n次随机抽取得到的样本容量为n的样本观测值,在任一次随机抽取中,样本观测值都以一定的概率出现。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
x
0 0.6
1 0.4
0 1
0.3
0.7
设土地所有者有三种决策
a1 { 自己投资钻探石油} a2 {出卖土地所有权} a3 {该地区开辟旅游景点}
这些决策对应的损失函数为
L( , a ) a
a1
a2
a3
0
1
12 0
1 10
6 5
现在选用9个决策函数
x1
d1 ( x1 ) d 2 ( x1 ) d3 ( x1 ) d 4 ( x1 ) d5 ( x1 )
例3(p106例3.19) 设X ( X1,X 2 , ,X n )T 为来自正态
总体N ( ,1)的一个样本,取参数的先验分布为正态
分布N (0, 2 ), 其中已知,损失函数取为
1, L( , d ) 0,
| d | , 0 | d | , 0
7.9 9.6 5.4 7 3.5 3 7.9 9.6 5.4
1 10 10
3 8.4 6.5 1.5 6.5 8.4
4 8.5 8.5
6 5 6
由最小最大决策函数的定义可知,d 4为统计决策 问题的minimax决策函数 .即样本为0时,选择a2 , 样本为1时,选择a1 .
三、利用贝叶斯估计计算 最小最大决策函数
ˆ的风险函数为 p
ˆ ) E( R( p, p
2 nX 1 2( n 1)
- p)
2
2 nX 1 2 2 nX 1 D( ) E ( p) 2( n 1) 2( n 1) 4n p(1 p) 2 n p 1 2 ( p) 2 n 4( n 1) 2( n 1) 1 (为常数) 2 4( n 1)
先验分布列{ k ( ) : k 1}选取为{ N (0, ) : 1
2 i
n
i 1
iபைடு நூலகம்
},
相应的贝叶斯估计列为{d i ( X ), i 1,2, }. 1 1 1 1 2 又由于d i ( X ) N ( (1 2 ) , (1 2 ) ) n n n 则d 的风险函数为
解
平方损失下的贝叶斯估计为:
d * ( x ) E ( p | X x ) ph( p | x )dp
而
q( x | p)π( p) h( p | x ) m( x )
p i 1 (1 p ) xi
n n
q( x | p)π( p)
n
xi
i 1 n i 1
由此可以得到
R(d k ) max R( , d 0 ),
k 1
则
lim R( d k ) max R( , d 0 )
k
显然这与假设的条件矛盾,因此
d0是的最小最大估计.
定理3.10 给定一个贝叶斯决策问题, 若的一个
估计d0的风险函数R( , d0 )在上为常数,且存在一个先
于是,d ( x1 , x2 , , xn )的风险函数满足 R( , d ) RM (d ) C , ,
对R( , d ) RM (d ) C在给定的先验分布下求期望, 得
RB (d ) E( R( , d )) C RB (d B ),
这表明d B ( x1 , x2 ,
注 函数达不到最大值时,可以理解为上确界. 如果我们讨论的统计决策问题是一个估计问题, 则由定义3.10得到的决策函数为最小最大估计量. 下面介绍寻求最小最大决策函数的一般步骤
二、计算minimax决策函数的步骤
计算minimax决策函数的步骤:
1、对D 中每个决策函数d ( x1 , x2 ,
, xn )
的风险函数为
R( , d B ) C ,
因而它的贝叶斯风险为
,
RB (d B ) C .
假设d B ( x1 , x2 ,
, xn )不是最小最大决策函数, , xn ),使得
那么必定有一个决策函数d ( x1 , x2 ,
RM (d ) RM (d B ) C
验分布列{ k ( ) : k 1},使得相应的贝叶斯估计dk的贝叶
斯风险满足
lim R( d k )
n
则d0为的minimax估计.
证
对任意的 ,有
max R( , d 0 ) R( , d 0 ) lim R(d k )
n
显然满足了定理4.9,因而d0是的最小最大估计.
n
显然 p | x
* ˆ p d ( x)
n n n ( xi ,n xi ) 2 2 i 1 i 1 ph( p | x )dp
(1 p )
n
n
d p n 0 n n n ( xi ,n xi ) 2 2 i 1 i 1
, xn )不可能是这个先验分布下的
贝叶斯决策函数,从而产生矛盾,因此d B ( x1 , x2 , , xn )必定是一个minimax决策函数.
例2(p104例3.18) 设总体X服从两点分布B(1,p), 其中参数p未知,而p在[0,1]上服从分布 (
n n , ), 2 2
( X1 , X 2 , , X n )来自总体X,损失函数为平方损失, 则参数p的贝叶斯估计为p的minimax估计量。
d6 ( x1 ) d7 ( x1 ) d8 ( x1 ) d9 ( x1 )
0
1
a1 a1
a1 a2
a1 a3
a2 a1
a2 a2
a2 a3
a3 a1
a3 a2
a3 a3
计算决策函数对应的风险函数,以第四个决策函 数为例
R(0 , d4 ) L(0 , a1 )P 0 ( X1 1) L(0 , a2 ) P 0 ( X1 0)
第3.3节
minimax估计
一、 minimax决策函数 二、 计算minimax决策函数步骤 三、利用贝叶斯估计计算最小最大决策函数
一、minimax决策函数
在贝叶斯决策中,通常以风险函数最小为衡量标 准。但有的时候人们处于保守考虑,决策时考虑最坏 情形,即风险最大时寻找最佳策略-最小最大决策. 定义3.10 给定一个统计决策问题,设D*是由
n
1
0
q( x | p)π( p)dp
( p) ( p)dp
i 1 n
1
0
p i 1 (1 p )
xi
n
n
xi
n
p
n xi 1 2 i 1
(1 p )
xi
n 1 2
n n n ( xi ,n xi ) 2 2 i 1 i 1
*
, xn ), 求
出其风险函在上的最大风险值 max R( , d )。
2、在所有最大风险值中选取相对最小值,此 值对应的决策函数便是最小最大决策函数。
例1(p102例3.17)地质学家要根据某地区的底层结构 来判断该地是否蕴藏有石油,地层结构总是0,1两种状 之一,记该地层无油为 0 ,记该地层有油为 1, 已知 它们的分布规律如下表所示
全体决策函数组成的类,如果存在一个决策函数
d * d * ( x1 , x2 , , xn ), d * D* , 使得对任意一个决策
d d ( x1 , x2 ,
, xn ),总有
max R( , d ) max R( , d ),
*
d D
*
则称d *为统计决策问题的最小最大决策函数。
n
1
p
n xi 2 i 1
n
i 1
n
xi
n 1 2
n n n ( xi 1, n xi ) 2 nX 1 2 2 i 1 i 1 n n n n 2( n 1) ( xi ,n xi ) 2 2 i 1 i 1
因而其为minimax估计.
定理3.9
给定一个贝叶斯决策问题,设 { k ( ) : k 1}
{dk : k 1},{ R(d k ) : k 1} 为参数空间上的一个先验分布列,
分别为相应的贝叶斯估计列和贝叶斯风险列,若d0 是的一个估计,且它的风险函数R( , d0 )满足决策
定理3.8 给定一个统计决策问题,如果存在某个先 验分布,使得在这个先验分布下的贝叶斯决策函数
d B ( x1 , x2 , x2 ,
决策函数.
, xn )的风险函数为一个常数,那么d B ( x1 ,
, xn )必定是这个统计决策问题的一个最小最大
证 记RM (d ) max R( , d ),且设d B ( x1 , x2 ,
其对应的参数的贝叶斯估计为 1 n 1 1 d ( X ) ( X i )(1 2 ) n i 1 n 1 n 试用定理3.10证明X n X i 是的最小最大估计. n i 1
证
在对应损失函数下,参数的贝叶斯估计为
d ( X ) ( X i )(n 2 )1
函数.
max R( , d 0 ) lim R(d k )
n
则d0为的minimax估计.
证 设d0不是的最小最大估计,则存在这样的一个
估计d,使得
max R( , d ) max R( , d 0 )
dk是贝叶斯估计,因而
R(d k ) R(d ) R( , d )πk( )d max R( , d )
