弹簧曲线图
笛卡尔曲线方程和图

圓柱坐标方程:r = 5theta = t*3600z =(sin(3.5*theta-90))+24*t2。
葉形线.笛卡儿坐標标方程:a=10x=3*a*t/(1+(t^3))y=3*a*(t^2)/(1+(t^3))3。
螺旋线(Helical curve)圆柱坐标(cylindrical)方程:r=ttheta=10+t*(20*360)z=t*3球坐标方程:rho = 8 *t theta = 360 *t * 4 phi = —360 * t *85。
渐开线采用笛卡尔坐标系方程:r=1ang=360*ts=2*pi*r*tx0=s*cos(ang)y0=s*sin(ang)x=x0+s*sin(ang)y=y0-s*cos(ang)z=0笛卡儿坐标方程:x = 4 *cos (t *(5*360)) y = 4 *sin (t *(5*360))z = 10*t7.对数曲线笛卡尔坐标系方程:z=0x = 10*ty = log(10*t+0.0001)8。
球面螺旋线采用球坐标系方程:rho=4theta=t*180phi=t*360*20卡迪尔坐标方程:l=2.5b=2.5x=3*b*cos(t*360)+l*cos(3*t*360)Y=3*b*sin(t*360)+l*sin(3*t*360)10。
星行线卡迪尔坐标方程:a=5x=a*(cos(t*360))^3y=a*(sin(t*360))^311。
心脏线圓柱坐标方程:a=10r=a*(1+cos(theta))theta=t*360采用柱座标系方程:theta=t*360r=10+10*sin(6*theta)z=2*sin(6*theta)13。
正弦曲线笛卡尔坐标系方程:x=50*ty=10*sin(t*360)z=015。
费马曲线(有点像螺纹线)数学方程:r*r = a*a*theta圓柱坐标方程1: theta=360*t*5a=4r=a*sqrt(theta*180/pi)方程2: theta=360*t*5a=4r=-a*sqrt(theta*180/pi)由于Pro/e只能做连续的曲线,所以只能分两次做16.Talbot 曲线卡笛尔坐标方程:theta=t*360a=1。
弹簧设计
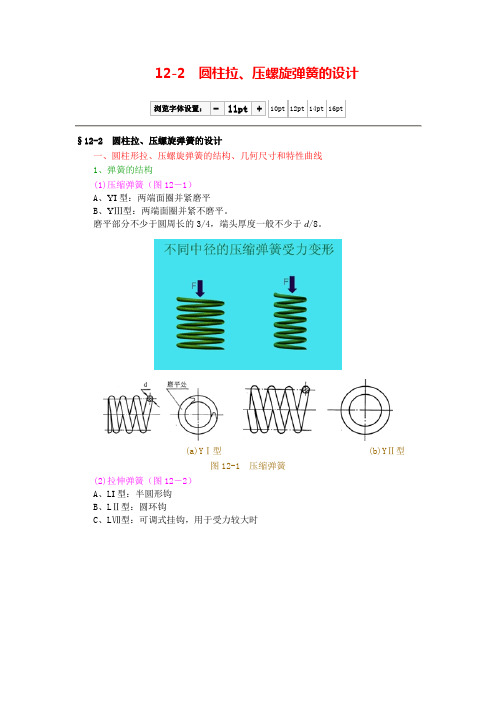
12-2 圆柱拉、压螺旋弹簧的设计浏览字体设置:- 11pt + 10pt 12pt 14pt 16pt§12-2 圆柱拉、压螺旋弹簧的设计一、圆柱形拉、压螺旋弹簧的结构、几何尺寸和特性曲线1、弹簧的结构(1)压缩弹簧(图12-1)A、YI型:两端面圈并紧磨平B、YⅢ型:两端面圈并紧不磨平。
磨平部分不少于圆周长的3/4,端头厚度一般不少于d/8。
(a)YⅠ型(b)YⅡ型图12-1 压缩弹簧(2)拉伸弹簧(图12-2)A、L I型:半圆形钩B、LⅡ型:圆环钩C、LⅦ型:可调式挂钩,用于受力较大时图12-2 拉伸弹簧2、主要几何尺寸弹簧丝直径d、外径D、内径、中径、节距p、螺旋升角 、自由高度(压缩弹簧)或长度(拉伸弹簧),如图12-3。
此外还有有限圈数n,总圈数,几何尺寸计算公式见表12-1。
(a) (b)图12-3 圆柱形拉、压螺旋弹簧的参数弹簧指数C:弹簧中径D2和簧丝直径d的比值即:C=D2/d。
弹簧丝直径d相同时,C值小则弹簧中径D2也小,其刚度较大。
反之则刚度较小。
通常C值在4~16范围内,可按表12-2选取。
表12-2 圆柱螺旋弹簧常用弹簧指数C弹簧直径d/mm0.2~0.40.5~1 1.1~2.2 2.5~67~1618~42C7~145~125~104~104~84~63、特性曲线弹簧所受载荷与其变形之间的关系曲线称为弹簧的特性曲线。
(1)压缩弹簧其特性曲线如图12-4所示。
图中H0为弹簧未受载时的自由高度。
F min为最小工作载荷,它是使弹簧处于安装位置的初始载荷。
在F min的作用下,弹簧从自由高度H0被压缩到H1,相应的弹簧压缩变形量为λmin。
在弹簧的最大工作载荷F max作用下,弹簧的压缩变形量增至λmax。
图中F lim为弹簧的极限载荷,在其作用下,弹簧高度为H lim,变形量为λlim,弹簧丝应力达到了材料的弹性极限。
此外,图中的h=λmax-λmin,称为弹簧的工作行程。
workbench圆柱弹簧 载荷 变形 曲线

workbench圆柱弹簧载荷变形曲线workbench圆柱弹簧是一种常见的弹簧设计,广泛应用于工程领域。
它的主要功能是承受和调节载荷,并通过变形产生力的反作用。
在本文中,我将深入探讨workbench圆柱弹簧的载荷和变形特性,并分析其相关的曲线表示。
1. 弹簧的载荷:workbench圆柱弹簧通常用于承受并分配载荷。
弹簧的载荷可以分为静载荷和动载荷两种。
1.1 静载荷:静载荷是指弹簧在无动力作用下所受的恒定的力。
例如在机械装置中,工具或设备的自重会施加静载荷在弹簧上。
圆柱弹簧的静载荷可以通过弹簧试验或计算来测量或估算。
1.2 动载荷:动载荷是指弹簧在运动或振动过程中所受的变化的力。
例如在汽车悬挂系统中,弹簧会承受车辆行驶中的颠簸和震动。
动载荷会引起弹簧的周期性变形。
2. 弹簧的变形:弹簧的变形是指弹簧在受力作用下发生的尺寸或形状的改变。
弹簧的变形可以分为线性变形和非线性变形两种。
2.1 线性变形:线性变形是指弹簧在小范围内受力时,其变形与载荷成正比。
当载荷增加时,圆柱弹簧的长度或直径会发生线性的变化。
2.2 非线性变形:非线性变形是指弹簧在大范围内受力时,其变形与载荷不成正比。
在工程中,当载荷超过一定的阈值时,圆柱弹簧的变形会呈现出曲线的形状。
3. 弹簧的曲线表示:弹簧的载荷和变形可以通过曲线图来表示。
这些曲线图可以帮助我们了解弹簧的性能和行为。
3.1 载荷-变形曲线:载荷-变形曲线是一种常见的表示弹簧行为的图表形式。
该曲线以载荷作为x 轴,以变形作为y 轴。
它显示了弹簧在不同载荷下的变形情况。
在workbench圆柱弹簧中,载荷-变形曲线通常呈现出非线性的特征。
随着载荷的增加,曲线的斜率也会发生变化,从而导致弹簧的变形量逐渐增加。
3.2 弹簧刚度曲线:弹簧刚度曲线是描述弹簧刚度与变形之间关系的图表。
刚度是指弹簧对单位变形所产生的力的大小。
弹簧刚度通常以弹簧的刚度系数表示,其单位为牛顿/米或千克/秒^2。
氮气弹簧压力曲线

氮气弹簧压力曲线
摘要:
一、氮气弹簧压力曲线的定义和特点
二、氮气弹簧压力曲线的测量和计算方法
三、氮气弹簧压力曲线在实际应用中的意义和作用
四、如何根据氮气弹簧压力曲线选择合适的弹簧
正文:
氮气弹簧压力曲线,是指在一定范围内,氮气弹簧的弹性变形与所受压力之间的关系曲线。
它反映了氮气弹簧在受到压力时的形变特性和弹性恢复能力,是氮气弹簧性能的重要参数。
氮气弹簧压力曲线的测量和计算方法主要依赖于弹簧的弹性模量、截面积、长度等几何参数以及所使用的气体种类和压力。
其中,弹性模量是弹簧材料的一个重要特性,决定了弹簧的弹性变形能力;截面积和长度则影响了弹簧的承载能力和变形程度。
氮气弹簧压力曲线在实际应用中的意义和作用主要体现在以下几个方面:首先,它可以用来评估氮气弹簧的性能,如弹性恢复能力、承载能力等;其次,可以根据压力曲线选择合适的弹簧,以满足特定的应用需求;最后,压力曲线还可以用来预测弹簧在实际使用过程中的行为,如疲劳寿命、故障模式等。
在选择氮气弹簧时,需要根据具体的应用场景和使用要求,参考氮气弹簧的压力曲线,选择合适的弹簧。
一般来说,对于需要较高承载能力的应用,应
选择压力曲线较陡峭的弹簧;而对于需要较高弹性恢复能力的应用,则应选择压力曲线较平缓的弹簧。
气弹簧介绍

3、曲线图 4、参数表 随意停气弹簧 1、结构图 2、特点: 随意停气弹簧又称平衡气弹簧或摩擦式气弹簧,产品在负载时不需要 外部控制机构,行程就可以停止在任意位置,多用于医疗和橱柜,视 频设备等
3、曲线图 lan 4、参数表 阻尼气弹簧 1、结构图 2、特点 阻尼气弹簧俗称阻尼器,起到阻尼,减震,消噪的作用,多用于 机床,医院护理床床栏,屋门等。按内部结构不同可分为普通阻尼器 和双向阻尼器,普通阻尼器与双向阻尼器相比,缺点是当活塞杆将要 完全伸展时会有一定的无阻尼段,双向阻尼器是全程阻尼,普通阻尼 器优点是结构紧凑,尺寸短小。两种阻尼器的阻尼大小均可通过对阻 尼油的流量和阻尼油的粘稠度来调节。
气弹簧介绍
普通气弹簧 1、结构图
2、特点: 普通气弹簧俗称支撑杆,压缩气弹簧,原始状态为伸展状态,应
用在各个行业,起到支撑,助力的作用。
3、曲线图 4、可选择列表 见附件弹簧 1.JPG 拉伸气弹簧 1、结构图
2、特点: 拉伸气弹簧俗称拉簧,也被称为牵引式气弹簧,原始状态为压缩 状态,医疗行业应用最多,起到牵引和拉伸的作用。拉伸气弹簧由于 内部结构不同,有长,短之分。根据客户安装的尺寸来定,长的相对 短的而言,拉伸,收缩曲线较平缓,F1 变化率较小。
弹簧比普通弹簧有着很显著的优点:速度相对缓慢、动态力变化不大 (一般在 1:1.2 以内)、容易控制;缺点是相对体积没有螺旋弹簧 小,成本高、寿命相对短。 一、自由型气弹簧(支撑杆)是应用最为广泛的气弹簧。它主要起支 撑作用,只有最短、最长两个位置,在行程中无法自行停止。在汽车、 纺织机械、印刷设备、办公设备、工程机械等行业应用最广。 二、自锁型气弹簧(调角器)在医疗器械上应用的最多。该种气弹簧 借助一些释放机构可以在行程中的任意位置停止,并且停止以后有很 大的锁紧力(可以达到 10000N 以上)。 三、随意停气弹簧(摩擦式气弹簧、平衡式气弹簧)主要应用在厨房 家具、医疗器械等领域。它的特点介于自由型气弹簧和自锁型气弹簧 之间:不需要任何的外部结构而能停在行程中的任意位置,但没有额 外的锁紧力。 四、转椅气弹簧(气压棒)主要应用在转椅上,起调节位置的作用。 其特点是可控,需求量比较大。 五、牵引式气弹簧是一种特殊的气弹簧:别的气弹簧在自由状态的时 候都处在最长的位置,即在受到外力后是从最长的位置向最短的位置 运动,而牵引式气弹簧的自由状态在最短的位置,受到牵引时从最短 处向最长处运行。牵引式气弹簧中也有相应的自由型、自锁型等。 六、阻尼器在汽车和医疗设备上都用得比较多,其特点是阻力随着运 行的速度而改变。可以明显的对相连的机构的速度起缓冲作用。 另外,从材质上分还有普通钢气弹簧和不锈钢气弹簧。普通钢气弹簧
第十四章 弹簧

F D2/2
压缩弹簧最大切应力
max
8CF K d 2
F D2 2
T'' N
M A
Q F B
T=F D2 2 m d F n
剖面B-B
K——曲度系数
4C 1 0.615 K 4C 4 C
A
F
max=K =F+T T F
BB
m
n
三、弹簧的刚度计算
有关因素
许用应力
弹簧类型、材料、钢丝直径、载荷性质
注: 弹簧材料的许用扭转切应力 [] 和许用弯曲应力 [b] 的大 小和载荷性质有关,静载荷时的 [] 和 [b] 较变载荷时的大。
二、弹簧制造
弹簧是由板材、棒材、线材或者管材经过各种塑性加工而形 成所需要的形状。 螺旋弹簧是用弹簧丝卷绕制成的,由于制造简便,所以应用 最广。在一般机械中,最常用的是圆柱螺旋弹簧。 螺旋弹簧的制造过程主要包括:
解: (1) 选材料,确定许用应力 [τ]。根据弹簧所受的载荷特性在表14-5中选用
C级碳素弹簧钢丝,则由表14-5可知[τ]=0.5σb 。弹簧钢丝的抗拉强度σb与弹簧钢丝 直径d有关 。先假设d=6mm,查表14-6,则对应的σb=1420MPa。
[τ] = 0.5σb = 0.5×1420MPa = 710MPa
F F1 O 1 d p
D1 D2 D
H0 H1 H2 F3 F max U 2 max 3 H3
等节距圆柱螺旋弹簧的特性曲线
第五节
圆柱螺旋压缩、拉伸弹簧的设计
一、基本参数及其选择
圆柱螺旋弹簧的主要参数有: 弹簧丝直径d、弹簧圈外径D、内径D1、中径D2、弹簧节距p和 螺旋升角α、弹簧指数C(旋绕比) C D2 d 簧工作 圈数 n和自由高度H0、 弹
弹簧设计参考

弹簧参考资料§12-1 概述弹簧是常用的弹性零件,它在受载后产生较大的弹性变形,吸收并储存能量。
弹簧有以下的主要功能:(1)减振和缓冲。
如缓冲器,车辆的缓冲弹簧等。
(2)控制运动。
如制动器、离合器以及内燃机气门控制弹簧。
(3)储存或释放能量。
如钟表发条,定位控制机构中的弹簧。
(4)测量力和力矩。
用于测力器、弹簧秤等。
按弹簧的受力性质不同,弹簧主要分为:拉伸弹簧,压缩弹簧,扭转弹簧和弯曲弹簧。
按弹簧的形状不同又可分为螺旋弹簧、板弹簧、环形弹簧、碟形弹簧等。
此外还有空气弹簧、橡胶弹簧等。
§12-2 圆柱拉、压螺旋弹簧的设计一、圆柱形拉、压螺旋弹簧的结构、几何尺寸和特性曲线1、弹簧的结构(1)压缩弹簧(图12-1)A、YI型:两端面圈并紧磨平B、YⅢ型:两端面圈并紧不磨平。
磨平部分不少于圆周长的3/4,端头厚度一般不少于d/8。
(a)YⅠ型(b)YⅡ型图12-1 压缩弹簧(2)拉伸弹簧(图12-2)A、LI型:半圆形钩B、LⅡ型:圆环钩C、LⅦ型:可调式挂钩,用于受力较大时图12-2 拉伸弹簧2、主要几何尺寸弹簧丝直径d、外径D、内径、中径、节距p、螺旋升角、自由高度(压缩弹簧)或长度(拉伸弹簧),如图12-3。
此外还有有限圈数n,总圈数,几何尺寸计算公式见表12-1。
(a) (b)图12-3 圆柱形拉、压螺旋弹簧的参数表12-1 圆柱形压缩、拉伸螺旋弹簧的几何尺寸计算公式螺旋升角对压缩弹簧,推荐=5°~9°间距 /mm=p-d=0L=D2n1/cos L=D2n+钩部展开长度弹簧指数C:弹簧中径D2和簧丝直径d的比值即:C=D2/d。
弹簧丝直径d相同时,C值小则弹簧中径D2也小,其刚度较大。
反之则刚度较小。
通常C值在4~16范围内,可按表12-2选取。
表12-2 圆柱螺旋弹簧常用弹簧指数C3、特性曲线弹簧所受载荷与其变形之间的关系曲线称为弹簧的特性曲线。
(1)压缩弹簧其特性曲线如图12-4所示。
第一章 弹簧受力分析.

压缩弹簧
取标准值
b在1~5.3的范围选取
两端并紧,磨平; H0≈pn+(1.5~2)d 自由高度或长度H0 两端并紧,不磨平; H0≈pn+(3~3.5)d 工作高度或长度 H1 H1 …….H1 Hn = H0 +λn
H0 =nd+Hh
Lh为钩环展开长度
Hn = H 0 + λn
λn ---工作变形量
FFF
D2 /2 D2 /2
8FD2 4 F 8 FD2 合成应力: T F 2 3 3 d d d
令
新疆大学专用
d 1 2 D 2
D2 C d
8FC 0.5 1 2 d C
作者: 潘存云教授
C----旋绕比,或弹簧指数。
最大工作载荷--- Fmax 在Fmax的作用下,τ
弹簧在安装位置所受压 力,它能使弹簧可靠地 稳定在安装位置上。
F Fmin
Fmax
Ek arctg
Flim
压缩弹簧的 特性曲线
λmin λ0
λ
max<[τ
]
Fmin
λmax λlim
保证不并紧
对应的变形---λmax <0.8nδ
极限载荷--- Flim
极限变形--- λlim 一般取: Fmax ≤ 0.8Flim
Fmax Flim
潘存云教授研制
Hlim H2 H1
Fmin Fmax 常数 弹簧刚度:k min min
H0
弹簧势能 E
新疆大学专用
自由高度
作者: 潘存云教授
2、拉伸弹簧的特性曲线 a)没有预应力
