r语言与统计分析第五章课后答案
《统计分析与SPSS的应用(第五版)》课后练习答案(第5章)
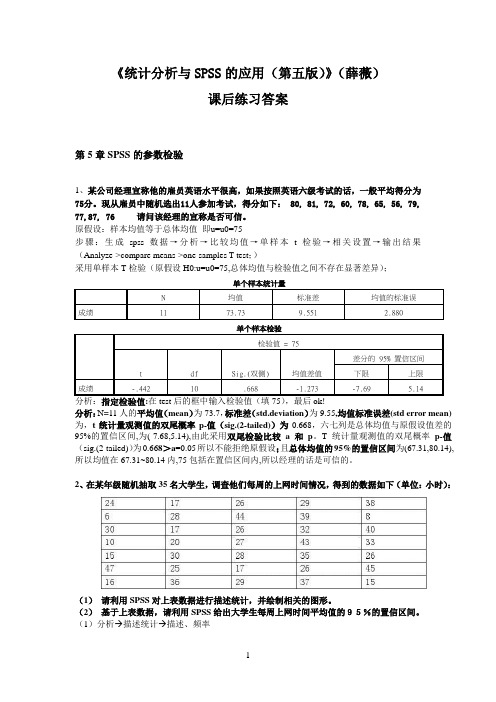
《统计分析与SPSS的应用(第五版)》(薛薇)课后练习答案第5章SPSS的参数检验1、某公司经理宣称他的雇员英语水平很高,如果按照英语六级考试的话,一般平均得分为75分。
现从雇员中随机选出11人参加考试,得分如下: 80, 81, 72, 60, 78, 65, 56, 79, 77,87, 76 请问该经理的宣称是否可信。
原假设:样本均值等于总体均值即u=u0=75步骤:生成spss数据→分析→比较均值→单样本t检验→相关设置→输出结果(Analyze->compare means->one-samples T test;)采用单样本T检验(原假设H0:u=u0=75,总体均值与检验值之间不存在显著差异);单个样本统计量N 均值标准差均值的标准误成绩11 73.73 9.551 2.880单个样本检验检验值 = 75t df Sig.(双侧) 均值差值差分的 95% 置信区间下限上限成绩-.442 10 .668 -1.273 -7.69 5.14分析:指定检验值:在test后的框中输入检验值(填75),最后ok!分析:N=11人的平均值(mean)为73.7,标准差(std.deviation)为9.55,均值标准误差(std error mean)为,t统计量观测值的双尾概率p-值(sig.(2-tailed))为0.668,六七列是总体均值与原假设值差的95%的置信区间,为(-7.68,5.14),由此采用双尾检验比较a和p。
T统计量观测值的双尾概率p-值(sig.(2-tailed))为0.668>a=0.05所以不能拒绝原假设;且总体均值的95%的置信区间为(67.31,80.14),所以均值在67.31~80.14内,75包括在置信区间内,所以经理的话是可信的。
2、在某年级随机抽取35名大学生,调查他们每周的上网时间情况,得到的数据如下(单位:小时):(1)请利用SPSS对上表数据进行描述统计,并绘制相关的图形。
学习使用R编程语言进行统计分析和数据建模

学习使用R编程语言进行统计分析和数据建模导论在现代数据分析和统计学中,R编程语言已经成为了一种非常受欢迎的工具。
它是一种免费开源的软件,具有强大的统计分析和数据建模功能。
本文将介绍如何学习使用R编程语言进行统计分析和数据建模,并探讨一些实际应用案例。
第一章:R语言的基础知识在开始学习R编程语言之前,我们首先要了解一些基础知识。
R语言是一种具有面向对象特性的编程语言,它可以用于数据处理、统计分析、数据可视化等领域。
在这一章节中,我们将介绍R语言的安装方法,基本语法,常用函数和数据结构等内容。
第二章:常用数据处理技巧数据处理是数据分析的第一步,它包括数据清洗、数据转换、数据合并等过程。
在R语言中,有许多常用的数据处理函数和技巧可以帮助我们完成这些任务。
在这一章节中,我们将介绍如何使用R语言对数据进行清洗和转换,以及如何使用函数和包来处理缺失值、异常值等常见问题。
第三章:统计分析方法R语言提供了众多的统计分析函数和方法,可以帮助我们进行描述统计、假设检验、方差分析等各种分析。
在这一章节中,我们将介绍如何使用R语言进行常见统计分析,如线性回归、逻辑回归、聚类分析等,并演示如何从结果中提取有用的信息。
第四章:数据可视化方法数据可视化是将数据转化为图形和图表的过程,有助于我们更好地理解和分析数据。
R语言提供了许多功能强大的数据可视化包,如ggplot2、lattice等。
在这一章节中,我们将介绍如何使用R语言进行数据可视化,并演示如何创建散点图、柱状图、折线图等图形。
第五章:高级数据建模技术除了基本的统计分析外,R语言还可以用于更高级的数据建模任务,如机器学习、深度学习等。
在这一章节中,我们将介绍一些常用的数据建模方法,如决策树、随机森林、神经网络等,并演示如何使用R语言构建和评估这些模型。
第六章:实际应用案例最后,我们将通过一些实际应用案例来展示R语言在统计分析和数据建模中的应用。
这些案例包括金融风险评估、医疗数据分析、市场营销策略等。
多元统计分析及R语言建模

y:分类变量(去年是否出过事故,1表示出过事故,0表示没有)。
5广义与一般线性模型及R使用
5.2 广义线性模型
(1)建立全变量logistic回归模型:
d5.1=read.table("clipboard",header=T) #读取例5.1数据 logit.glm<-glm(y~x1+x2+x3,family=binomial,data=d5.1) #Logistic回归模型 summary(logit.glm) #Logistic回归模型结果
与 要
基本要求:
求
要求学生针对因变量和解释变量的取值性质,了解统计模型的类型。
掌握数据的分类与模型选择方法,并对广义线性模型和一般线性模型
有初步的了解。
5广义与一般线性模型及R使用
5.1 数据的分类与模型选择
5广义与一般线性模型及R使用
5.1 数据的分类与模型选择
2.模型选择方式:基本公式
Y X e E(e) 0, cov(e) 2I
程 序 与 结 果
由此得到新的logistic回归模型:
5广义与一般线性模型及R使用
5.2 广义线性模型
(3):预测发生交通事故的概率
pre1<-predict(logit.step,data.frame(x1=1)) #预测视力正常司机Logistic回归结果
程
p1<-exp(pre1)/(1+exp(pre1)) #预测视力正常司机发生事故概率
序
pre2<-predict(logit.step,data.frame(x1=0)) #预测视力有问题的司机Logistic回归结果
R统计分析教程

R统计分析教程第一章:介绍R统计分析工具R是一种免费且开源的统计分析工具,广泛应用于数据科学、机器学习和统计学等领域。
它具有强大的数据处理和可视化能力,以及丰富的统计函数库,可以处理各种复杂的统计分析任务。
本教程将详细介绍R的基本用法和常用统计分析技巧。
第二章:R语言基础在开始R统计分析之前,我们首先需要了解一些基础的R语言知识。
R语言是一种面向数据分析的编程语言,具有数据结构、条件判断、循环和函数等基本语法。
本章将介绍R语言的基本数据类型、变量赋值、运算符和逻辑控制等内容。
第三章:数据导入和处理在进行统计分析之前,我们通常需要将数据导入到R中并进行预处理。
本章将介绍如何使用R中的函数来读取和导入常见的数据文件,如CSV、Excel和数据库等。
同时,还将介绍数据清洗、缺失值处理和异常值检测等常用数据处理技巧。
第四章:数据可视化数据可视化是数据分析过程中非常重要的一步,它可以帮助我们更好地理解数据的特征和趋势。
R提供了多种绘图函数,可以生成各种类型的图表,如散点图、折线图、柱状图和箱线图等。
本章将详细介绍如何使用R进行数据可视化,以及如何调整图形的样式和布局。
第五章:描述统计分析描述统计分析是对数据进行总结和描绘的一种方法,它包括均值、中位数、标准差、百分位数等统计指标的计算,以及频数分布表和直方图的绘制等内容。
本章将介绍R中常用的描述统计分析函数和技巧,并通过实例演示其应用。
第六章:推断统计分析推断统计分析是用于从样本数据中推断总体特征的一种方法。
它包括假设检验、置信区间估计和相关性分析等内容。
本章将介绍R中常用的推断统计分析函数和技巧,并通过实例演示如何对样本数据进行推断。
第七章:线性回归和方差分析线性回归和方差分析是常用的统计建模方法,用于研究变量之间的关系和差异。
本章将介绍如何使用R进行线性回归分析和方差分析,并解释如何解释模型结果和进行假设检验。
第八章:其他常用统计方法除了以上介绍的统计分析方法外,R还提供了许多其他常用的统计方法,如非参数检验、逻辑回归和时间序列分析等。
《R语言数据分析》课程教案(全)

《R语言数据分析》课程教案(全)第一章:R语言概述1.1 R语言简介介绍R语言的发展历程、特点和应用领域讲解R语言的安装和配置1.2 R语言基本操作熟悉R语言的工作环境学习如何创建、保存和关闭R剧本掌握R语言的基本数据类型(数值型、字符串、逻辑型、复数、数据框等)1.3 R语言的帮助系统学习如何使用帮助文档(help()、?、man()函数)掌握如何搜索和安装R包第二章:R语言数据管理2.1 数据导入与导出学习如何导入CSV、Excel、txt等格式的数据掌握如何将R数据导出为CSV、Excel等格式2.2 数据筛选与排序掌握如何根据条件筛选数据学习如何对数据进行排序2.3 数据合并与分割讲解数据合并(merge、join等函数)的方法和应用场景讲解数据分割(split、apply等函数)的方法和应用场景第三章:R语言统计分析3.1 描述性统计分析掌握R语言中的统计量计算(均值、中位数、标准差等)学习如何绘制统计图表(如直方图、箱线图、饼图等)3.2 假设检验讲解常用的假设检验方法(t检验、卡方检验、ANOVA等)掌握如何使用R语言进行假设检验3.3 回归分析介绍线性回归、逻辑回归等回归分析方法讲解如何使用R语言进行回归分析第四章:R语言绘图4.1 ggplot2绘图系统介绍ggplot2的基本概念和语法学习如何使用ggplot2绘制柱状图、线图、散点图等4.2 基础绘图函数讲解R语言内置的绘图函数(plot、barplot、boxplot等)掌握如何自定义图形和调整图形参数4.3 地图绘制学习如何使用R语言绘制地图讲解如何使用ggplot2绘制地理数据可视化图第五章:R语言编程5.1 R语言编程基础讲解R语言的变量、循环、条件语句等基本语法掌握如何编写R函数和模块化代码5.2 数据框操作学习如何使用数据框进行编程讲解如何使用dplyr等工具包进行数据框操作5.3 面向对象编程介绍R语言的面向对象编程方法掌握如何使用R6和S3编程范式第六章:R语言时间序列分析6.1 时间序列基础介绍时间序列数据的类型和结构学习时间序列数据的导入和预处理6.2 时间序列分解讲解时间序列的分解方法,包括趋势、季节性和随机成分使用R语言进行时间序列分解6.3 时间序列模型介绍自回归模型(AR)、移动平均模型(MA)、自回归移动平均模型(ARMA)和自回归积分滑动平均模型(ARIMA)学习如何使用R语言建立和预测时间序列模型第七章:R语言机器学习7.1 机器学习概述介绍机器学习的基本概念、类型和应用学习机器学习算法选择的标准和评估方法7.2 监督学习算法讲解回归、分类等监督学习算法使用R语言实现监督学习算法7.3 无监督学习算法介绍聚类、降维等无监督学习算法使用R语言实现无监督学习算法第八章:R语言网络分析8.1 网络分析基础介绍网络分析的概念和应用领域学习网络数据的导入和预处理8.2 网络图绘制讲解如何使用R语言绘制网络图学习使用igraph包进行网络分析8.3 网络分析应用介绍网络中心性、网络结构等分析方法使用R语言进行网络分析案例实践第九章:R语言生物信息学应用9.1 生物信息学概述介绍生物信息学的概念和发展趋势学习生物信息学数据类型和常用格式9.2 生物序列分析讲解生物序列数据的导入和处理使用R语言进行生物序列分析9.3 基因表达数据分析介绍基因表达数据的特点和分析方法使用R语言进行基因表达数据分析第十章:R语言项目实战10.1 数据分析项目流程介绍数据分析项目的流程和注意事项10.2 R语言项目实战案例一分析一个真实的统计数据集,实践R语言数据分析方法10.3 R语言项目实战案例二使用R语言解决实际问题,如商业分析、社会研究等10.4 R语言项目实战案例三结合数据库和API接口,进行大规模数据分析和处理重点和难点解析重点环节1:R语言的安装和配置解析:R语言的安装和配置是学习R语言的第一步,对于初学者来说,可能会遇到操作系统兼容性、安装包选择等问题。
统计建模与R软件课后答案

第二章2.1> x<-c(1,2,3);y<-c(4,5,6)> e<-c(1,1,1)> z<-2*x+y+e;z[1] 7 10 13> z1<-crossprod(x,y);z1[,1][1,] 32> z2<-outer(x,y);z2[,1] [,2] [,3][1,] 4 5 6[2,] 8 10 12[3,] 12 15 182.2(1) > A<-matrix(1:20,nrow=4);B<-matrix(1:20,nrow=4,byrow=T) > C<-A+B;C(2)> D<-A%*%B;D(3)> E<-A*B;E(4)> F<-A[1:3,1:3](5)> G<-B[,-3]2.3> x<-c(rep(1,5),rep(2,3),rep(3,4),rep(4,2));x2.4> H<-matrix(nrow=5,ncol=5)> for (i in 1:5)+ for(j in 1:5)+ H[i,j]<-1/(i+j-1)(1)> det(H)(2)> solve(H)(3)> eigen(H)2.5> studentdata<-data.frame(姓名=c('张三','李四','王五','赵六','丁一') + ,性别=c('女','男','女','男','女'),年龄=c('14','15','16','14','15'),+ 身高=c('156','165','157','162','159'),体重=c('42','49','41.5','52','45.5')) 2.6> write.table(studentdata,file='student.txt')> write.csv(studentdata,file='student.csv')2.7count<-function(n){if (n<=0)print('要求输入一个正整数')else{repeat{if (n%%2==0)n<-n/2elsen<-(3*n+1)if(n==1)break}print('运算成功')}}第三章3.1首先将数据录入为x。
统计建模与R软件第五章课后习题答案

统计建模与R软件第五章习题答案(假设检验)Ex5.1> x<-c(220, 188, 162, 230, 145, 160, 238, 188, 247, 113, 126, 245, 164, 231, 256, 183, 190, 158, 224, 175)> t.test(x,mu=225)One Sample t-testdata: xt = -3.4783, df = 19, p-value = 0.002516alternative hypothesis: true mean is not equal to 22595 percent confidence interval:172.3827 211.9173sample estimates:mean of x192.15原假设:油漆工人的血小板计数与正常成年男子无差异。
备择假设:油漆工人的血小板计数与正常成年男子有差异。
p值小于0.05,拒绝原假设,认为油漆工人的血小板计数与正常成年男子有差异。
上述检验是双边检验。
也可采用单边检验。
备择假设:油漆工人的血小板计数小于正常成年男子。
> t.test(x,mu=225,alternative="less")One Sample t-testdata: xt = -3.4783, df = 19, p-value = 0.001258alternative hypothesis: true mean is less than 22595 percent confidence interval:-Inf 208.4806sample estimates:mean of x192.15同样可得出油漆工人的血小板计数小于正常成年男子的结论。
Ex5.2> pnorm(1000,mean(x),sd(x))[1] 0.5087941> x[1] 1067 919 1196 785 1126 936 918 1156 920 948> pnorm(1000,mean(x),sd(x))[1] 0.5087941x<=1000的概率为0.509,故x大于1000的概率为0.491.要点:pnorm计算正态分布的分布函数。
r语言与统计分析第五章课后答案

r语言与统计分析第五章课后答案第五章5.1设总体某是用无线电测距仪测量距离的误差,它服从(α,β)上的均匀分布,在200次测量中,误差为某i的次数有ni次:某i:3579111315171921Ni:21161526221421221825求α,β的矩法估计值α=u-β=u+程序代码:某=eq(3,21,by=2)y=c(21,16,15,26,22,14,21,22,18,25)u=rep(某,y)u1=mean(u)=var(u)1=qrt()a=u1-qrt(3)某1b=u1+qrt(3)某1b=u1+qrt(3)某1得出结果:a=2.217379b=22.402625.2为检验某自来水消毒设备的效果,现从消毒后的水中随机抽取50L,化验每升水中大肠杆菌的个数(假设1L水中大肠杆菌的个数服从泊松分布),其化验结果如下表所示:试问平均每升水中大肠杆菌个数为多少时,才能使上述情况的概率达到最大大肠杆菌数/L:0123456水的升数:1720222100γ=u是最大似然估计程序代码:a=eq(0,6,by=1)b=c(17,20,10,2,1,0,0)c=a某bd=mean(c)得出结果:d=7.1428575.3已知某种木材的横纹抗压力服从正态分布,现对十个试件做横纹抗压力试验,得数据如下:482493457471510446435418394469(1)求u的置信水平为0.95的置信区间程序代码:某=c(482493457471510446435418394469)t.tet(某)得出结果:data:某t=6.2668,df=9,p-value=0.0001467alternativehypothei:truemeaninotequalto095percentconfidenceinterval:7.66829916.331701ampleetimate:meanof某12由答案可得:u的置信水平为0.95的置信区间[7.66829916.331701](2)求σ的置信水平为0.90的置信区间程序代码:chiq.var.tet<-function(某,var,alpha,alternative="two.ided"){ option(digit=4)reult<-lit()n<-length(某)v<-var(某)reult$var<-vchi2<-(n-1)某v/varreult$chi2<-chi2p<-pchiq(chi2,n-1)reult$p.value<-pif(alternative=="le")reult$p.value<-pchaiq(chi2,n-1,loer.tail=F)eleif(alternative=="two.ider")reult$p.value<-2某min(pchaiq(chi2,n-1),pchaiq(chi2,n-1,lower.tail=F))reult$conf.int<-c((n-1)某v/qchiq(alpha/2,df=n-1,lower.tail=F),(n-1)某v/qchiq(alpha/2,df=n-1,lower.tail=T))reult}某<-c(482,493,457,471,510,446,435,418,394,469)y=var(某)chiq.var.tet(某,0.048^2,0.10,alternative="two.ide")得出结果:$conf.int:659.83357.0由答案可得:σ的置信水平为0.90的置信区间[659.83357.0]5.4某卷烟厂生产两种卷烟A和B现分别对两种香烟的尼古丁含量进行6次试验,结果如下:A:252823262922B:282330352127若香烟的尼古丁含量服从正态分布(1)问两种卷烟中尼古丁含量的方差是否相等(通过区间估计考察)(2)试求两种香烟的尼古丁平均含量差的95%置信区间程序代码:某=c(25,28,23,26,29,22)Y=c(28,23,30,35,21,27)Var.tet(某,y)data:某andyF=0.2992,numdf=5,denomdf=5,p-value=0.2115alternativehypothei:trueratioofvarianceinotequalto195percentconfidenceinterval:0.041872.13821ampleetimate:ratioofvariance0.2992由答案可得:其方差不相等,方差区间为[0.041872.13821](2)5.5比较两个小麦品种的产量,选择24块条件相似地实验条,采用相同的耕作方法做实验,结果播种甲品种的12块实验田的单位面积产量和播种乙品种的12块试验田的单位面积产量分别为:A:628583510554612523530615573603334564B:535433398470567480498560503426338547假定每个品种的单位面积产量服从正态分布,甲品种产量的方差为2140,乙品种产量的方差为3250,试求这两个品种平均面积产量差的置信水平为0.95的置信上限和置信水平为0.90的置信下限。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第五章5.1 设总体x 是用无线电测距仪测量距离的误差,它服从( α,β)上的均匀分布,在200次测量中,误差为xi 的次数有ni次:Xi:3 5 7 9 11 13 15 17 19 21Ni:21 16 15 26 22 14 21 22 18 25求α,β的矩法估计值α=u- 3sβ=u+ 3s程序代码:x=seq(3,21,by=2)y=c(21,16,15,26,22,14,21,22,18,25)u=rep(x,y)u1=mean(u)s=var(u)s1=sqrt(s)a=u1-sqrt(3)*s1b=u1+sqrt(3)*s1b=u1+sqrt(3)*s1得出结果:a= 2.217379b= 22.402625.2 为检验某自来水消毒设备的效果,现从消毒后的水中随机抽取50L,化验每升水中大肠杆菌的个数(假设1L 水中大肠杆菌的个数服从泊松分布),其化验结果如下表所示:试问平均每升水中大肠杆菌个数为多少时,才能使上述情况的概率达到最大大肠杆菌数/L:0 1 2 3 4 5 6水的升数:17 20 10 2 1 0 0γ=u 是最大似然估计程序代码:a=seq(0,6,by=1)b=c(17,20,10,2,1,0,0)c=a*bd=mean(c)得出结果:d= 7.1428575.3 已知某种木材的横纹抗压力服从正态分布,现对十个试件做横纹抗压力试验,得数据如下:482 493 457 471 510 446 435 418 394 469 ( 1)求u 的置信水平为0.95 的置信区间程序代码:x=c(482 493 457 471 510 446 435 418 394 469 )t.test(x)得出结果:data: xt = 6.2668, df = 9, p-value = 0.0001467 alternative hypothesis: truemean is not equal to 0 95 percent confidence interval:7.668299 16.331701 sample estimates: mean of x12由答案可得:u的置信水平为0.95 的置信区间[7.668299 16.331701] ( 2)求σ的置信水平为0.90 的置信区间程序代码:chisq.var.test<-function(x,var,alpha,alternative="two.sided "){ options(digits=4) result<-list() n<-length(x) v<-var(x) result$var<-vchi2<-(n-1)*v/var result$chi2<-chi2 p<-pchisq(chi2,n-1) result$p.value<-p if(alternative=="less")result$p.value<-pchaisq(chi2,n-1,loer.tail=F) elseif(alternative=="two.sider") result$p.value<-2*min(pchaisq(chi2,n-1), pchaisq(chi2,n-1,lower.tail=F))result$conf.int<-c((n-1)*v/qchisq(alpha/2,df=n-1,lower.tail=F), (n-1)*v/qchisq(alpha/2,df=n-1,lower.tail=T)) result}x<-c(482,493,457,471,510,446,435,418,394,469)y=var(x)chisq.var.test(x,0.048^2,0.10,alternative="two.side")得出结果:$conf.int :659.8 3357.0由答案可得:σ的置信水平为0.90 的置信区间[659.8 3357.0]5.4 某卷烟厂生产两种卷烟A和B 现分别对两种香烟的尼古丁含量进行6 次试验,结果如下:A:25 28 23 26 29 22B:28 23 30 35 21 27若香烟的尼古丁含量服从正态分布( 1)问两种卷烟中尼古丁含量的方差是否相等 (通过区间估计考察) ( 2)试求两种香烟的尼古丁平均含量差的95%置信区间(1)程序代码:X=c(25,28,23,26,29,22)Y=c(28,23,30,35,21,27)Var.test(x,y) 得出结果:F test to compare two variances data: x and yF = 0.2992, num df = 5, denom df = 5, p-value = 0.2115 alternative hypothesis: true ratio of variances is not equa l to 195 percent confidence interval:0.04187 2.13821 sample estimates: ratio of variances0.2992 由答案可得:其方差不相等,方差区间为[0.041872.13821](2)5.5 比较两个小麦品种的产量,选择24 块条件相似地实验条,采用相同的耕作方法做实验,结果播种甲品种的12 块实验田的单位面积产量和播种乙品种的12 块试验田的单位面积产量分别为:A:628 583 510 554 612 523 530 615 573 603 334 564B:535 433 398 470 567 480 498 560 503 426 338 547 假定每个品种的单位面积产量服从正态分布,甲品种产量的方差为2140,乙品种产量的方差为3250,试求这两个品种平均面积产量差的置信水平为0.95 的置信上限和置信水平为0.90 的置信下限程序代码:two.sample.ci=function(x,y,conf.level=0.95,sigma1.sigma2){options(digits=4)m=length(x); n=length(y) xbar=mean(x)-mean(y) alpha=1-conf.level zstar=qnorm(1-alpha/2)*(sigma1/m+sigma2/n)^(1/2) xbar+c(-zstar,+zstar)} x=c(628,583,510,554,612,523,530,615,573,603,334,564)y=c(535,433,398,470,567,480,498,560,503,426,338,547) sigma1=2140 sigma2=3250 two.sample.ci(x,y,conf.level=0.95,sigma1.sigma2) 得到结果:31.29 114.37程序代码:two.sample.ci=function(x,y,conf.level=0.95,sigma1.sigma2) {options(digits=4)m=length(x); n=length(y)xbar=mean(x)-mean(y) alpha=1-conf.level zstar=qnorm(1-alpha/2)*(sigma1/m+sigma2/n)^(1/2) xbar+c(-zstar, +zstar)} x=c(628,583,510,554,612,523,530,615,573,603,334,564)y=c(535,433,398,470,567,480,498,560,503,426,338,547) sigma1=2140 sigma2=3250two.sample.ci(x,y,conf.level=0.90,sigma1.sigma2) 得到结果:37.97 107.695.6 有两台机床生产同一型号的滚珠,根据以往经验知,这两台机床生产的滚珠直径都服从正态分布,现分别从这两台机床生产的滚珠中随机地抽取7 个和9 个,测得它们的直径如下:机床甲:15.2 14.5 15.5 14.8 15.1 15.6 14.7机床乙:15.2 15.0 14.8 15.2 15 14.9 15.1 14.8 15.3 试问机床乙生产的滚珠的方差是否比机床甲生产的滚珠直径的方差小?程序代码:x=c(5.2,14.5,15.5,14.8,15.1,15.6,14.7)y=c(15.2,15.0,14.8,15.2,15,14.9,15.1,14.8,15.3) var.test(x,y) 得出结果:F test to compare two variances data: x and yF = 430.1, num df = 6, denom df = 8, p-value = 2.723e-09alternative hypothesis: true ratio of variances is not equal to 195 percent confidence interval:92.47 2408.54sample estimates:ratio of variances430.1 由结果可得:其甲机床的滚珠半径远超出乙机床的滚珠半径5.7 某公司对本公司生产的两种自行车型号A,B 的销售情况进行了了解,随机选取了400 人询问他们对A B的选择,其中有224 人喜欢A,试求顾客中喜欢A的人数比例p 的置信水平为0.99 的区间估计。
方程代码:Binom.test(224,400,conf.level=0.99)得出结果:Exact binomial testdata: 224 and 400number of successes = 224, number of trials = 400, p-value= 0.01866alternative hypothesis: true probability of success is notequal to 0.599 percent confidence interval:0.4944077 0.6241356sample estimates:probability of success0.56由结果可得:顾客中喜欢a的人数比例p的置信水平为0.99 的区间估计:[0.4944077 0.6241356]5.8 某公司生产了一批新产品,产品总体服从正态分布,现估计这批产品的平均重量,最大允许误差为1,样本标准差s=10,试问在0.95 的置信水平下至少要抽取多少个产品程序代码:Size,norm2=function(s,alpha,d,m){t0=qt(alpha/2,m,lower.tail = FALSE)n0=(t0*s/d)^2t1=qt(alpha/2,n0,lower.tail = FALSE) n1=(t1*s/d)^2while(abs(n1-n0)>0.5){n0=(qt(alpha/2,n1,lower.tail = FALSE)*s/d)^2n1=(qt(alpha/2,n0,lower.tail = FALSE)*s/d)^2n1}Size.norm2(10,0.01,2,100)得出结果:98.44268由结果可得,在0.95 的置信水平下至少要抽取99 个产品5.9 根据以往的经验,船运大量玻璃器皿,损坏率不超过5%,现要估计某船中玻璃器皿的损坏率,要求估计与真值间不超过1%,且置信水平为0.90 ,那么要抽取多少样本验收可满足上诉要求程序代码:size.bin=function(d,p,conf.level){alpha=1-conf.level((qnorm(1-alpha/2))/d)^2*p*(1-p)}size.bin(0.01,0.05,0.90)得出结果:1285.133由结果可得:要抽取1285 个样本验收可满足上诉要求}。
