初三下数学周末卷(二)
初三下学期数学周末提优卷4答案.docx

初三数学答案及评分标准一.填空题(每空2分,共32分)9. 10 10. 40°11. —7T12. 6憑30°8二•选择题(每题3分,共24分)19. B 20. B三解答题(共8题,共76分)24. (1)由题意有△二(2加一1)2-4〃心0, 解得mW?即实数加的取值范围是加W丄. ---------- (4分)4(2)由彳一球=0得(兀]+兀2)(西一兀2)= 0 •若兀]+兀2=°,即一(2血一1) = 0,解得m =~ ■*•* — > — » m ——不合题意,舍去.2 4 2若Xj - x2 = 0 ,即 %, = x2/. A = 0 ,由(1)知加=占.故当—x^= 0 时,m = —.----------------- (8 分)- 425. (1)证明:连OC,因为点C在OO上,OA=OC,所以ZOCA = ZOAC.因为CD丄PA ,所以ZCDA =90“, 有ACAD + ZDCA = 90°.因为AC 平分ZPAE,所以ZDAC = ZCAO.所以ZDCO = ZDCA + ZACO = ZDCA + ZCAO = ZDCA + ZDAC = 901又因为点C在0O±, OC为(DO的半径,所以CQ为(DO的切线. .......... (4分)(2)解:过O作OF丄AB,垂足为F,所以ZOCD = ZCDA = ZOFD = 90°,所以四边形OCDF为矩形,所以OC = FD,OF = CD.因为DC+DA=6,设AD = x,则0F = CD = 6-x.因为OO的直径为10,所以DF = OC = 5,所以AF = 5-x.即(5-X)2+(6-X)2=25.化简得X2-11X+18=0,解得x = 2或x=9.由AD< DF ,知0 vxv5,故x = 2.从而/10=2, AF = 5 — 2 = 3.因为OF丄AB,由垂径定理知F为4B的中点,所以AB = 2AF = 6. .......................... (8分)27.解:(1)假设四边形PQCM是平行四边形,则PM//QC. ・・・AP二AM.10 - t=2t,解得t=—.3---------- (3 分)・・.当t二〒吋,四边形PQCM是平行四边形.(2)过P作PE丄AC,交AC于E.•・・PQ〃AC,•••△PBQs/\ABC,・・・APBQ是等腰三角形,PQ二PB=t.解得BF=-r.54AFD=BD - BF=8 - -t.5又VMC=AC-AM=10-2t,1 1 / 4 \ °y= -(^2 + MCyJFD = -(/ +10-2/) 8 ——t =-t2-& + 40.2 2 5 /52答;歹=土尸一& + 40 ................ (6分)5(3)S AABC= -ACEBD = -x 10X8 = 40.2 2比_ 16。
北师大版数学九年级下册:第二章《二次函数》测试卷

新北师大版第二章《二次函数》测试卷一、选择题(每小题3分,满分24分)1.下列函数:y =x (8-x ),y =1-221x ,y =42-x ,y =x x 62-,其中以x 为自变量的二次函数有( )A .1个B .2个C .3个D .4个 2.在函数2y x=,5y x =+,2y x =的图象中,关于y 轴对称的图形有( ) A .0个 B .1个 C .2个 D .3个3.点A (2,3)在函数21y ax x =-+的图象上,则a 等于( )A .1B .-1C .2D .-24.若抛物线228y x x h =++的顶点在x 轴上,则 ( )A .0h =B .16h =±C .4h =±D .4h =5.在同一坐标系中,图象与22x y =的图象关于x 轴对称的函数为( )A .221x y =B .221x y -= C .22x y -= D .2x y -= 6.二次函数y=ax 2+bx +c 的图象如图所示,则下列结论正确是( )A .a >0,b >0,c >0B .a <0,b <0,c <0C .a <0,b >0,c <0D .a >0,b <0,c >0 7.将抛物线22x y =经过平移得到抛物线2=y (4-x )21-是( )A .向左平移4个单位,再向下平移1个单位B .向左平移4个单位,再向上平移1个单位C .向右平移4个单位,再向下平移1个单位D .向右平移4个单位,再向上平移1个单位二、填空题(每小题3分,满分21分)1.抛物线2241y x x =--的开口向 ;顶点坐标是 ;对称轴方程为 .2.抛物线232y x x =-+不经过第 象限.3.若点),1(1y P 、Q 2(1,)y -都在抛物线21y x =+上,则线段P Q 的长为 .4.如图所示,二次函数26y x x =--的图象交x 轴于A 、B 两点,交y 轴于C 点,则ABC ∆的面积ABC S ∆= .5.一条抛物线,顶点坐标为(4,2)-,且形状与抛物线22y x =+相同,则它的函数表达式是 .6.函数2412x x y -+=的图象与x 轴有 个交点;当 时,y 值随x 值增大而增大;当=x 时, y 有最 值.7.函数c bx ax y ++=2的图象如图所示,则c b a ++ 0,c b a ++24 0.(用“=”、“>”或“<”填空)三、解答题:1.(12分)如图所示,二次函数2y ax bx c =++(0)a ≠的图象与x 轴交于A 、B 两点,与y 轴交于(0,2)C ,若90ACB ∠=︒,5BC =,试求:(1)A 、B 两点的坐标;(2)二次函数的表达式.2.(10分)已知一抛物线经过点()2,6-,它与x 轴的两交点间的距离为4,对称轴为直线1x =-,求此抛物线的解析式.解:3.(12分)抛物线2y x bx c =++(0)a ≠与x 轴交于(1,0)A -,(3,0)B 两点.(1)求该抛物线的解析式.(2)一动点P 在(1)中抛物线上滑动且满足10ABP S ∆=,求此时P 点的坐标.。
二次函数课后检测(二)

二次函数课后检测(二)一、单选题1.已知抛物线y=-x 2+1,下列结论:①抛物线开口向上; ②抛物线与x 轴交于点(-1,0)和点(1,0);③抛物线的对称轴是y 轴; ④抛物线的顶点坐标是(0,1);⑤抛物线y=-x 2+1是由抛物线y=-x 2向上平移1个单位得到的.其中正确的个数有( )A .5个B .4个C .3个D .2个2.对于函数y =-2(x -3)2,下列说法不正确的是( )A .开口向下B .对称轴是3x =C .最大值为0D .与y 轴不相交 3.关于二次函数y =12(x+1)2的图象,下列说法正确的是( )A .开口向下B .经过原点C .对称轴右侧的部分是下降的D .顶点坐标是(﹣1,0) 4.若函数y=(1﹣m )x m 2−2+2是关于x 的二次函数,且抛物线的开口向上,则m 的值为( )A.﹣2B.1C.2D.﹣15.下列抛物线中,开口最大的是( )A .y=√3x 2B .y =−√2x 2C .y =- x 2D .y=-12x 26.在同一坐标系中,抛物线22y x =, 212y x =, 212y x =-的共同特点是( )A .关于y 轴对称,开口向上B .关于y 轴对称,y 随x 增大而减小C .关于y 轴对称,y 随x 增大而增大D .关于y 轴对称,顶点在原点7.若对任意实数x ,二次函数y=(a+1)x 2的值总是非负数,则a 的取值范围是()A .a≥-1B .a≤-1C .a>-1D .a<-18.已知a<-1,点(a -1,y 1),(a ,y 2),(a+1,y 3)都在函数y=x 2的图象上,则( ) A .y 1<y 2<y 3 B .y 1<y 3<y 2 C .y 3<y 2<y 1 D .y 2<y 1<y 39.直线y=x 与抛物线y=-2x 2的交点是()A .(12,0)B .(12-, 12-) C .(12-, 12-),(0,0) D .(0,0)10.抛物线y =2x 2-3的顶点在( )A .第一象限B .第二象限C .x 轴上D .y 轴11.在二次函数①y =3x 2;②2224;33y x y x ==③中,图象在同一水平线上的开口大小顺序用题号表示应该为() A .①>②>③ B .①>③>② C .②>③>① D .②>①>③12.在下列二次函数中,其图象对称轴为x =2的是A .y =2x 2﹣4B .y =2(x -2)2C .y =2x 2+2D .y =2(x +2)213.给出下列函数:①y=2x﹣3;②y=1x;③y=2x2;④y=﹣3x+1.上述函数中符合条件“当x>0时,函数值y随自变量x增大而减小”的是()A.①③B.③④C.②④D.②③14.已知点(x1,y1),(x2,y2)均在抛物线y=x2﹣1上,下列说法中正确的是()A.若y1=y2,则x1=x2B.若x1=﹣x2,则y1=﹣y2C.若0<x1<x2,则y1>y2D.若x1<x2<0,则y1>y2二、解答题15.把y=−12x2的图象向上平移2个单位.(1)求新图象的解析式、顶点坐标和对称轴;(2)画出平移后的函数图象;(3)求平移后的函数的最大值或最小值,并求对应的x的值.参考答案1.B【解析】【分析】根据a 确定抛物线的开口方向;令y=0解方程得到与x 轴的交点坐标;根据抛物线的对称轴、顶点坐标以及平移的性质,对各小题分析判断后即可得解.【详解】①∵a=-1<0,∴抛物线开口向下,故本小题错误;②令y=0,则-x 2+1=0,解得x 1=1,x 2=-1,所以,抛物线与x 轴交于点(-1,0)和点(1,0),故本小题正确;③抛物线的对称轴2b x a=-=0,是y 轴,故本小题正确; ④抛物线的顶点坐标是(0,1),故本小题正确;⑤抛物线y=-x 2+1是由抛物线y=-x 2向上平移1个单位得到,故本小题正确;综上所述,正确的有②③④⑤共4个.故选B .【点睛】本题考查了二次函数的性质,理解二次函数图象与系数关系是关键.2.D【解析】【分析】根据二次函数的性质即可一一判断.【详解】对于函数y=-2(x-3)2的图象,∵a=-2<0,∴开口向下,对称轴x=3,顶点坐标为(3,0),函数有最大值0,故选项A 、B 、C 正确, 选项D 错误,故选D .【点睛】本题考查二次函数的性质,解题的关键是熟练掌握二次函数的性质,属于基础题,中考常考题型.3.D 【解析】【分析】根据抛物线的性质由a=12得到图象开口向上,将x=0代入求出相应的y值即可判断是否经过原点,由抛物线的性质可判断对称轴右侧图象的变化情况,根据顶点式即可得到顶点坐标,由此即可得答案.【详解】二次函数y=12(x+1)2中a=12>0,所以抛物线开口向上,当x=0时,y=12,所以图象不经过原点,因为抛物线开口向上,所以在对称轴右侧的部分是上升的,由解析式可知顶点坐标为(-1,0),所以选项A、B、C是错误的,D是正确的,故选D.【点睛】本题考查了二次函数的性质,牢记其y=a(x-h)2+k的顶点坐标、对称轴及开口方向是解答本题的关键.当a>0时,抛物线的开口向上,当a<0时,抛物线(a≠0)的开口向下.4.A【解析】【分析】先依据二次函数的定义知,系数1-m一定不为0,1-m>0,再得出m 2-2=2,求出m的值即可.【详解】∵y=(1-m)x m2−2+2是关于x的二次函数,∴m2-2=2且1-m≠0,解得m=2或-2,∵抛物线的开口向上,∴1-m>0,解得m<1,∴m=-2,故选:A.【点睛】考查二次函数的定义和性质,利用二次函数的定义得到关于m 的方程是解题的关键. 5.D【解析】抛物线y =ax 2 ,| a |越小,抛物线的开口越大.∵|√3|=√3,|−√2|=√2,|−1|=1,|−12|=12,∴12<1<√2<√3,∴y=-12x 2开口最大. 故选:D.6.D【解析】解:∵函数y =2x 2,y =12x 2,y =12-x 2中,a 取值范围分别为:a >0,a >0,a <0,∴抛物线的开口方向分别为:向上、向上、向下,即开口方向不同;由函数y =2x 2,y =12x 2,y =12-x 2的解析式可知:顶点坐标都为(0,0); ∴他们共同的特点是都关于y 轴对称,抛物线的顶点都是原点.故选D .7.C【解析】∵若对任意实数x ,二次函数y=(a+1)x 2的值总是非负数,∴其图象开口应该向上,∴a+1>0,解得a>-1.故选C.8.C【解析】由a <-1可得a -1<a <a +1<0,又因点(a -1,y 1),(a ,y 2),(a +1,y 3)都在函数y =x 2的图象上,在对称轴的左侧,y 随x 的增大而减小,所以 y 3<y 2<y 1,故选C. 9.C【解析】由题意可得: 2{ 2y x y x ==- ,解得: 110{ 0x y == , 2212{ 12x y =-=- , ∴直线y=x 与抛物线y=-2x 2的交点是()00,和1122⎛⎫-- ⎪⎝⎭,. 故选C.点睛:求一次函数图象和二次函数图象的交点坐标就是把两个函数的解析式组合在一起构成一个方程组,再求方程组的解,方程组的解就是这两个函数图象的交点坐标(自变量的值作横坐标,对应的函数值作纵坐标).10.D【解析】试题分析:b=0,抛物线的对称轴是y 轴,所以顶点在y 轴上,故选D.11.C【解析】根据二次函数的性质,可知系数a 决定开口方向和开口大小,且a 的值越大开口越小,因此可知②>③>①.故选:C.12.B【解析】【分析】根据二次函数顶点式y=a(x-h)+k 的对称轴为直线x=h 对各选项逐一判断即可.【详解】A 、y=2x 2-4的对称轴为x=0,故该选项不符合题意,B 、y=2(x-2)2的对称轴为x=2,故该选项符合题意,C 、y=2x 2+2的对称轴为x=0,故该选项不符合题意,D 、y=2(x+2)2对称轴为x=-2,故该选项不符合题意,故选B .【点睛】本题考查了二次函数的对称轴,形如y=a (x-h )2+k 的顶点为(h ,k );也可以把抛物线解析式化为一般形式,再根据对称轴公式x=-2b a 求出对称轴. 13.C【解析】【分析】分别利用一次函数、正比例函数、反比例函数、二次函数的增减性分析得出答案.【详解】①y =2x ﹣2,当x >0时,函数值y 随自变量x 增大而增大,故此选项错误;②y =1x,当x >0时,函数值y 随自变量x 增大而减小,故此选项正确;③y =2x 2,当x >0时,函数值y 随自变量x 增大而增大,故此选项错误;④y =﹣3x ,当x >0时,函数值y 随自变量x 增大而减小,故此选项正确;故选C .【点睛】本题考查了三种函数的性质,了解它们的性质是解答本题的关键,难度不大.14.D【解析】试题分析:A 、若y 1=y 2,则x 1=﹣x 2;B 、若x 1=﹣x 2,则y 1=y 2;C 、若0<x 1<x 2,则在对称轴的右侧,y 随x 的增大而增大,则y 1<y 2;D 、正确.故选D .考点:二次函数图象上点的坐标特征.15.(1)y=−12x 2+2,顶点坐标是(0,2),对称轴是y 轴;(2)画图见解析;(3)x=0时,y 有最大值,为2.【解析】试题分析:(1)根据平移规律“上加下减”写出平移后的抛物线的解析式;(2)根据抛物线解析式列函数对应值表,并作函数图象;(3)结合函数图象回答问题.试题解析:(1)把y=-12x 2的图象向上平移2个单位后得到抛物线的解析式为:y=-12x 2+2, 所以它的顶点坐标是(0,2),对称轴是x=0,即y 轴;(2)由y=-12x 2+2,得其函数图象如图所示:;(3)如图所示:当x=0时,y最大=2.。
荔湾区2019学年第二学期阶段训练(二)初三年级数学学科答案(A卷)

③如图 2-3 中,作 GH AP 于 H ,设 GH x .
由△ PHG ∽△ PBA ,可得 PH 2x , P'G 3x,GB P' B P'G 2 2 3x ,
GAH 30 , GHA 90 ,则 AG=2x,
在△ABG 中,由勾股定理,解得: x 6 2 6
∴ GH 6 2 6
12
21
即所抽的两人恰好都是女生的概率是 2 1 . 20 10
………………(10 分)
21. (12 分) 解:(1)设 A 种口罩每件的进价为 x 元,根据题意得:
……………………(1 分)
7200 2 5000 ,解得 x=1.8,
x
x 0.7
经检验 x=1.8 是原方程的解,
……………………(5 分) ……………………(6 分)
x+0.7=2.5(元),
……………………(7 分)
答:A 种口罩每件的进价为 1.8 元,B 种口罩每件的进价为 2.5 元;……………………(8 分)
(2)设购进 B 品牌的口罩 m 个,根据题意得:
(2.1-1.8)(8000-m)+(3-2.5)m≥3000
解得 m≥3000,
∵m 为整数, ∴m 的最小值为 3000.
∵直线 y=kx+b 经过点 A(﹣ 1 ,2),B(1,﹣1), 2
∴
1 2
k
b=2
k b= 1
,解得
k b
2 1
∴直线的表达式为 y=﹣2x+1;
…………(6 分)
(2)当 y=﹣2x+1=0 时,x= 1 ,∴点 C( 1 ,0).
2
2
设点 P 的坐标为(x,0),
2023北京海淀区初三二模数学试卷(含答案)

2023北京海淀初三二模数 学2023.05学校 姓名 准考证号一、选择题(共16分,每题2分)第1-8题均有四个选项,符合题意的选项只有一个.1. 一个正五棱柱如右图摆放,光线由上到下照射此正五棱柱时的正投影是(A ) (B ) (C ) (D )2. 下列运算正确的是 (A )23a a +=25a(B )a a a ⋅⋅=3a(C )32()a =5a(D )()a m n +=am an +3. 实数a 在数轴上对应点的位置如图所示.若实数b 满足a +b <0,则b 的值可以是(A )2−(B)1−(C )0(D )14. 如图,由正六边形和正三角形组成的图形为轴对称图形,该图形的对称轴的条数为 (A )1 (B )2 (C )3(D )45. 投掷两枚质地均匀的骰子,两枚骰子向上一面的点数相同的概率是 (A )112(B )16(C )13(D )126. 如果2a b −=,那么代数式221b a b a b ⎛⎫⋅+ ⎪+−⎝⎭的值是 (A )12(B )1(C(D )27. 如图,在正方形网格中,以点O 为位似中心,△ABC 的位似图形可以是 (A )△DEF (B )△DHF(C )△GEH(D )△GDH8.小明近期计划阅读一本总页数不低于300页的名著,他制定的阅读计划如下:(A ) (B )(C ) (D )第二部分 非选择题二、填空题(共16题,每题2分) 9. 若代数式12x−有意义,则实数x 的取值范围是.10.分解因式:24ax a −= .11. 用一个x x =”是错误..的,则x 的值可以是 . 12. 如图,正方形ABCD ,点A 在直线l 上,点B 到直线l 的距离为3,点D 到直线l 的距离为2,则正方形的边长为 .13. 在平面直角坐标系xOy 中,点1(1)A y ,和点2(3)B y ,在反比例函数k y x=的图象上.若12y y <,写出一个满足条件的k 的值 .14. 咖啡树种子的发芽能力会随着保存时间的增长而减弱.咖啡树种子保存到三个月时,发芽率约为lDCBA95%;从三个月到五个月,发芽率会逐渐降到75%;从五个月到九个月,发芽率会逐渐降到25%.农科院记录了某批咖啡树种子的发芽情况,结果如下表所示:据此推测,下面三个时间段中,这批咖啡树种子的保存时间是 (填“三个月内”或“五至九个月”).15.如图,AB 为☉O 的弦,C 为☉O 上一点,OC ⊥AB 于点D . 若OA =AB =6,则tan AOD ∠= .16.四个互不相等的实数a ,b ,c ,m 在数轴上的对应点分别为A ,B ,C ,M ,其中a =4,b =7,c 为整数,m =0.2(a +b +c ).(1)若c =10,则A ,B ,C 中与M 距离最小的点为 ;(2)若在A ,B ,C 中,点C 与点M 的距离最小,则符合条件的点C 有 个.三、解答题(共 68 分,第 17 - 20 题,每题 5 分,第 21 题 6 分,第 22 题 5 分,第 23 - 24 题,每 题 6 分,第 25 题 5 分,第 26 题 6 分,第 27 - 28 题,每题 7 分) 解答应写出文字说明、演算步骤或证明过程.17.计算:011t 1an 60(π20223−−++−⎛⎫ ⎪⎝⎭).18.解不等式12123x x −−≥,并把它的解集在数轴上表示出来.19.如图,在△ABC 中,AB =AC .(1)使用直尺和圆规,作AD⊥BC 交BC 于点D (保留作图痕迹); (2)以D 为圆心,DC 的长为半径作弧,交AC 于点E ,连接BE ,DE .①∠BEC = °;②写出图中一个..与∠CBE 相等的角 .20.已知关于x 的一元二次方程220x x m −+=(0m <).(1)判断方程根的情况,并说明理由;(2)若方程一个根为1−,求m 的值和方程的另一个根.21.在平面直角坐标系xOy 中,直线1y kx =−与12y x =交于点A (2,m ) .(1)求k ,m 的值;CCB A(2)已知点P (n ,0) ,过点P 作垂直于x 轴的直线交直线1y kx =−于点M ,交直线12y x =于点N .若MN=2,直接写出n 的值.22.如图,平行四边形ABCD 的对角线AC ,BD 交于点O ,E 为OA 中点.连接DE 并延长至点F ,使得EF=DE .连接AF ,BF .(1)求证:四边形AFBO 为平行四边形;(2)若∠BDA =∠BDC ,求证:四边形AFBO 为矩形.23.某企业生产甲、乙两款红茶,为了解两款红茶的质量,请消费者和专业机构分别测评.随机抽取25名消费者对两款红茶评分,并对数据进行整理、描述和分析,下面给出了部分信息. a .甲款红茶分数(百分制)的频数分布表如下:b .甲款红茶分数在85≤x <90这一组的是:86 86 86 86 86 87 87 88 88 89c .甲、乙两款红茶分数的平均数、众数、中位数如下表所示:根据以上信息,回答下列问题:(1)补全甲款红茶分数的频数分布直方图; (2)表格中m 的值为_______,n 的值为_______;(3)专业机构对两款红茶的条索、色泽、整碎、净度、内质、香气、滋味醇厚度、汤色、叶底来进行综合评分如下:甲款红茶93分,乙款红茶87分.若以这25名消费者评分的平均数和专业机构的评分按照6:4的比例确定最终成绩,可以认定_______款红茶最终成绩更高(填“甲”或“乙”).FE ODCBA24.如图,P 为☉O 外一点,P A ,PB 是☉O 的切线,A ,B 为切点,点C 在☉O 上,连接OA ,OC ,AC . (1)求证:∠AOC =2∠P AC ;(2)连接OB ,若AC ∥OB ,☉O 的半径为5,AC =6,求AP 的长. 25.小明发现某乒乓球发球器有“直发式”与“间发式”两种模式.在“直发式”模式下,球从发球器出口到第一次接触台面的运动轨迹近似为一条抛物线;在“间发式”模式下,球从发球器出口到第一次接触台面的运动轨迹近似为一条直线,球第一次接触台面到第二次接触台面的运动轨迹近似为一条抛物线.如图1和图2分别建立平面直角坐标系xOy .图1 直发式 图2 间发式通过测量得到球距离台面高度y (单位:dm )与球距离发球器出口的水平距离x (单位:dm )的相关数据,如下表所示:表1 直发式表2 间发式根据以上信息,回答问题:(1)表格中m =_________,n =_________;(2)求“直发式”模式下,球第一次接触台面前的运动轨迹的解析式;(3)若“直发式”模式下球第一次接触台面时距离出球点的水平距离为1d ,“间发式”模式下球第二次接触台面时距离出球点的水平距离为2d ,则1d ______2d (填“>”“ =” 或“<”) .26.在平面直角坐标系xOy 中,已知抛物线220y ax bx a a =+++>()过点(1,4a +2).(1)求该抛物线的顶点坐标;(2)过抛物线与y 轴的交点作y 轴的垂线l ,将抛物线在y 轴右侧的部分沿直线l 翻折,其余部分保持不变,得到图形G ,()11M a y −−,,()21N a y −+,是图形G 上的点,设12t y y =+. ①当1a =时,求t 的值;P②若69t≤≤,求a的取值范围.27.如图,在△ABC中,AB=AC,∠BAC=2α(45°<α<90°),D是BC的中点,E是BD的中点,连接AE.将射线AE绕点A逆时针旋转α得到射线AM,过点E作EF⊥AE交射线AM于点F .(1)①依题意补全图形;②求证:∠B=∠AFE;(2)连接CF,DF,用等式表示线段CF,DF之间的数量关系,并证明.28.在平面直角坐标系xOy中,对于△OAB和点P(不与点O重合)给出如下定义:若边OA,OB上分别存在点M,点N,使得点O与点P关于直线MN对称,则称点P为△OAB的“翻折点”.(1)已知A(3,0),B(0,).①若点M与点A重合,点N与点B重合,直接写出△OAB的“翻折点”的坐标;②P是线段AB上一动点,当P是△OAB的“翻折点”时,求AP长的取值范围;(2)直线34y x b=−+(b>0)与x轴,y轴分别交于A,B两点,若存在以直线AB为对称轴,且斜边长为2的等腰直角三角形,使得该三角形边上任意一点都为△OAB的“翻折点”,直接写出b的取值范围.参考答案第一部分 选择题一、选择题 (共16分,每题2分)二、填空题(共16分,每题2分) 9.2x ≠10.()()22a x x +− 11.1−(答案不唯一)12 13.1−(答案不唯一) 14.三至五个月 15.3 16.A ,3三、解答题(共68分,第17-20题,每题5分,第21题6分,第22题5分,第23-24题,每题6分,第25题5分,第26题6分,第27-28题,每题7分)解答应写出文字说明、演算步骤或证明过程. 17.(本题满分5分)解:原式211= ………………………………………………………………4分0=. ……………………………………………………………5分18.(本题满分5分)解:去分母,得3(1)46x x −≥−.…………………………………………………………1分去括号,得3346x x −≥− ………………………………………………………2分 移项,得3463x x −≥−+.合并同类项,得3x −≥−.……………………………………………………………3分 系数化为1,得3x ≤.………………………………………………………………4分 解集在数轴上表示如图所示:…………………………………5分19.(本题满分5分)解:(1)DCBA∴AD 即为所求. ………………………………………………………2分 (2)①90; ……………………………………………………………………4分②DEB ∠(答案不唯一). ………………………………………………5分20.(本题满分5分)解:(1)方程有两个不相等的实数根. …………………………………………………1分理由如下:∵1a =,2b =−,c m =, ∴2(2)444m m ∆=−−=−. ∵0m <, ∴0∆>.∴方程有两个不相等的实数根. ………………………………………………2分 (2)∵方程的一个根为1−,∴120m ++=.∴3m =−.………………………………………………………………………3分 ∴2230x x −−=. ∴13x =,21x =−.∴方程的另一个根为3x =.……………………………………………………5分21. (本题满分6分)解:(1)∵点(2)A m ,在直线12x 上, ∴1212m =⨯=. …………………………………………………………………2分 ∴点(21)A ,在直线1y kx =−上. ∴211k −=.∴1k =. …………………………………………………………………………4分 (2)2−或6.……………………………………………………………………………6分22.(本题满分5分)(1)证明:∵四边形ABCD 为平行四边形,∴OB OD =.…………………………………………………………………1分 ∵EF DE =, ∴OE BF ∥,12OE BF =. ∵E 为OA 中点,∴12OE OA =.FEODCBA∴OA BF =.∴四边形AFBO 为平行四边形. …………………………………………3分(2)证明:∵四边形ABCD 为平行四边形,∴AD BC ∥. ∴CBD BDA ∠=∠. ∵BDA BDC ∠=∠, ∴CBD BDC ∠=∠. ∴CB CD =.∴平行四边形ABCD 为菱形. ∴AC BD ⊥. ∴90AOB ∠=°.∵四边形AFBO 为平行四边形,∴四边形AFBO 为矩形. ……………………………………………5分23.(本题满分6分)(1)补全甲款红茶分数的频数分布直方图………………………………2分(2)86,87;……………………………………………………………………………4分 (3)甲.…………………………………………………………………………………6分 24.(本题满分6分)(1) 证明:∵P A 是O 的切线,切点为A , ∴OA ⊥P A . ∴∠OAP =90°. ∴∠OAC =90°-∠P AC . ∵OA =OC ,∴∠OAC =∠OCA .∴∠AOC =180°-2∠OAC .∴∠AOC =2∠P AC . ………………………………………3分P(2)解:延长AC 交PB 于点D ,过点O 作OE ⊥AC 于E . ∴∠OEC =90°. ∵OA =OC ,∴AE =EC ,∠AOE =∠COE. ∵∠AOC =2∠P AC , ∴∠AOE =12∠AOC =∠P AC . ∵AC =6,O 的半径为5,∴AE =12AC =3.∴4OE ==. ∴cos ∠AOE =45OE OA =. ∴cos ∠P AC =cos ∠AOE =45. ∵ PB 是O 的切线,切点为B ,∴ OB ⊥PB .∴∠OBP =90°. ∵AC ∥OB ,∴∠ADB =180°-∠OBP =90°. ∵∠OEC =90°, ∴四边形OEDB 是矩形. ∴ED =OB =5.∴AD =AE +ED =8.在△APD 中,∠APD =90°, ∴AP =10cos ADPAC=∠. …………………………………………………6分25.(本题满分5分)(1)3.84,2.52; ………………………………………………………………………2分 (2)由题意可知,抛物线的顶点为(4,4),∴设抛物线的解析式为2(4)4y a x =−+. ∵当x =6时,y =3.96,∴23.96(64)4a =−+,解得 0.01a =−.∴抛物线的解析式为20.01(4)4y x =−−+. ………………………………………4分 (3)= . ……………………………………………………………………………………5分 26.(本题满分6分)(1)∵抛物线22y ax bx a =+++ 过点()142a +,, ∴422a a b a +=+++.∴2b a =.………………………………………………………………………1分 ∴()222212y ax ax a a x =+++=++.∴抛物线的顶点坐标为()12−,.……………………………………………………2分 (2)①∵1a =,∴点()()1220M y N y −,,,,()212y x =++.∴12 3.y y ==∴12 6.t y y =+=…………………………………………………………………3分 ②∵222y ax ax a =+++, ∴直线l 的解析式为2y a =+. 当01a <<时,110a a −−+<-<,∴点M N ,在原抛物线上. ∴点M N ,关于1x =−对称. ∴12y y =.当0x =时,02y a =+. ∵0a >,∴抛物线开口向上.∴1x ≥−时,y 随x 的增大而增大. ∴20y y <.∴122(2)6t y y a =+<+<,不符合题意.当1a =时,由①可知6t =,符合题意. 当1a >时,101a a −−<<+-.∴点M 在原抛物线上,点N 在原抛物线沿直线l 翻折后的抛物线上.∴点N 关于直线l 的对称点N '在原抛物线上.∴点()11M a y −−,与点N '2124a a y −++−(,)关于1x =−对称.∴1224y a y =+−. ∴1224t y y a =+=+. ∵69t ≤≤, ∴512a ≤≤.∴512a <≤. 综上所述, a 的取值范围是512a ≤≤.…………………………………………6分27.(本题满分7分)(1)①依题意补全图形.………………………………………1分②∵AB AC =,2BAC α∠=, ∴1802902B C αα︒−∠=∠==︒−.∵EF AE ⊥, ∴90AEF ∠=︒. ∵EAF α∠=, ∴90AFE α∠=︒−.∴B AFE ∠=∠. ………………………………3分(2) 线段CF 与DF 的数量关系为CF =DF . ………………………………4分证明:延长FE 至点G ,使EG =EF ,连接AG ,BG . ∵AE ⊥EF , ∴AE 垂直平分GF . ∴AG =AF .∴∠GAE =∠EAF =α.∴∠GAF =∠GAE +∠EAF =2α. ∵∠BAC =2α, ∴∠GAF =∠BAC . ∴∠GAB =∠F AC . ∵AB =AC ,AG =AF , ∴△AGB ≌△AFC (SAS ).BC∠°∠°C∴GB=FC.∵E为BD中点,∴BE=DE.∵∠GEB=∠DEF,∴△GBE≌△FDE(SAS).∴GB=DF.∴DF=CF. ………………………………………………………………………7分28.(本题满分7分)(1)①9(2;…………………………………………………………………………2分②∵如图,点O与点P关于直线MN对称,∴MN垂直平分OP.∴OM=PM,ON=PN.∴点P为分别以点M,N为圆心,MO,NO为半径的圆的交点(其中一个交点为O,另一个交点为P).………………………………………………………3分∵点M,N分别在OB,OA上,∴如图,点P所在的区域为分别以点A,B为圆心,OA,OB(含边界,不含点O),设两圆与线段AB分别交于C,D两点,则点P在线段CD上运动.∵A(3,0),B(0,),∴OA=AC=3,OB=BD=∵∠AOB=90°,∴AB=6.∴AP的最大值为3,AP的最小值为6−∴63AP−≤≤.………………………………………………………………5分(2)12b+≥…………………………………………………………………………7分。
2023年嘉兴市中考数学名师原创试卷(2)

2023年嘉兴市中考数学名师原创试卷(2) 学校:__________ 姓名:__________ 班级:__________ 考号:__________注意事项:1.答题前填写好自己的姓名、班级、考号等信息2.请将答案正确填写在答题卡上第I 卷(选择题)请点击修改第I 卷的文字说明一、选择题1.下列四幅图形中,表示两颗小树在同一时刻阳光下的影子的图形可能是( )A .B .C .D . 2.如图,在菱形ABCD 中,∠ADC=120°,则BD :AC 等于( )A .3:2B .3:1C .1:2D .1:33.一个多边形的内角和与外角和相等,则这个多边形是( )A .三角形B .四边形C .五边形D .六边形 4.下列方程一定是一元二次方程的是( ) A .0ax bx c ++=B .22321x x mx -+=C .11x x +=D .22(1)230a x x +--=5.一次函数34y x =-的图象不经过( )A .第一象限B .第二象限C .第三象限D .第四象限6.下列语句中,不是命题的是 ( )A .两点之间线段最短B .不平行的两条直线有一个交点C .x 与y 的和等于0吗D .对顶角不相等7. 若a 的值使得224(2)1x x a x ++=+-成立,则a 值为( )A . 5B .4C . 3D . 28. 若216x mx ++是完全平方式,则m 的值等于( ) A .-8 B .8 C .4 D .8或一89.已知235x x ++的值为 3,则代数式2391x x +-的值为( ) A .-9 B .-7 C .0D .3 10.用代数式表示“2a 与 3 的差”为( )A.23a-B.32a-C.2(3)a-D.2(3)a-二、填空题11.如图所示,在把易拉罐中的水倒入一个圆水杯的过程中,若水杯中的水在点 P与易拉罐刚好接触,则此时水杯中的水深为㎝.12.若α是锐角,则α的余弦记作,α正切记作.13.用计算器求:(1)sin12036/= ;(2)cos53018/40//= ;(3)tan39040/53//= . (保留4个有效数字).14.已知A、B、C、D点的坐标如图所示,E是图中两条虚线的交点,若△ABC∽△ADE,则点 E的坐标是.解答题15.圆上各点到圆心的距离都等于;到圆心的距离等于半径的点都在上.16.如图,一张矩形纸片沿BC折叠;顶点A落在A′处,第二次过A′再折叠,使折痕 DE ∥BC,若AB=2,AC=3,则梯形BDEC的面积为 .17.关于x的方程一元二次方程的2(1)30k x kx-+-=.(1)当k时,是一元一次方程;(2)当k时,一元二次方程.18.如图,l1反映了某公司的销售收入与销量的关系,l2 反映了该公司产品的销售成本与销量的关系,当该公司赢利(收入大于成本)时,销售量必须____________.19.在长方形ABCD 中,AB = 2cm,BC = 3cm,则AD与BC之间的距离为 cm,AB与DC之间的的距离为 cm.20.已知某种植物花粉的直径约为 0.00035 m,用科学记数法表示该种花粉的直径是 .21.已知方程组23a bb c-=⎧⎨-=⎩,则a c-= .22.福顺路交通拥堵现象十分严重.上周末,陈新同学在福顺人行天桥处对3 000名过往行人作了问卷调查,问题是:从这里横过福顺路时,你是否自觉走人行天桥?供选择的答案有:A.是;(B)否;(C)无所谓.他将得到的数据处理后,画出了扇形统计图(如图).根据这个扇形统计图,可知被调查者中自觉走人行天桥的有 人.23.如图,∠E =∠F =90°,∠B =∠C ,AE =AF ,给出下列结论:①∠1=∠2;②BE =CF ;③△ACN ≌△ABM ;④CD =DN .其中正确的结论是____________________________(将你认为正确的结论序号填上).三、解答题24.如图,已知,EF ⊥AB ,CD ⊥AB ,G 在AC 边上,DG ∥BC .求证:∠1=∠2.25.某中学开展“八荣八耻”演讲比赛活动,九(1)、九(2)班根据初赛成绩各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩(满分为100分)如下图所示.(1)根据左图填写下表(2)结合两班复赛成绩的平均数和中位数,分析哪个班级的复赛成绩较好?(3)如果在每班参加复赛的选手中分别选出2人参加决赛,你认为哪个班的实力更强一些,说明理由.平均分(分) 中位数(分) 众数(分) 九(1)班85 85 九(2班 85 80 21G F E D CB A26.你画一个等腰三角形,使它的腰长为 3cm.27.如图,AB ∥CD ,∠2:∠3=1:2,求∠1的度数.28.(1)观察下列各式:544622⨯=- ,10491122⨯=- ,164151722⨯=-…… 试用你发现的规律填空:___4495122⨯=-,___4646622⨯=-;(2)请你用含一个字母的等式将上面各式呈现的规律表示出来,并用所学数学知识说明你所写式子的正确性.29.用简便方法计算:(1) 8825⨯;(2) 200820081()22-⨯;(3) 202180.125⨯;(4)14300.252-⨯30.A 地海拔是-40 m ,B 地比A 地高 20 m ,C 地又比B 地高 30m ,试用正数或负数表示B 、C 两地的海拔.【参考答案】学校:__________ 姓名:__________ 班级:__________ 考号:__________注意事项:1.答题前填写好自己的姓名、班级、考号等信息2.请将答案正确填写在答题卡上第I卷(选择题)请点击修改第I卷的文字说明一、选择题1.D2.D3.B4.D5.B6.C7.C8.D9.B10.A第II卷(非选择题)请点击修改第II卷的文字说明二、填空题11.12.13.14.15.16.17.18.19.20.21.22.23.三、解答题24.25.26.27.28.29.30.【参考答案及解析】学校:__________ 姓名:__________ 班级:__________ 考号:__________注意事项:1.答题前填写好自己的姓名、班级、考号等信息2.请将答案正确填写在答题卡上第I卷(选择题)请点击修改第I卷的文字说明一、选择题1.D解析:D2.D解析:D3.B解析:B4.D解析:D5.B解析:B6.C解析:C7.C解析:C8.D解析:D9.B解析:B10.A第II卷(非选择题)请点击修改第II卷的文字说明二、填空题11.612.cosα,tanα13.(1)0.2181;(2)0.5975;(3)0.829714.(4,-3)15.半径,圆16.917.(1)=1;(2)≠118.大于419.2,320.43.510-⨯21.522.165923.①②③24.略25.(1)85;100.(2)解:∵两班的平均数相同,初三(1)班的中位数高,初三(1)班的复赛成绩好些.(3)解:∵初三(1)班、初三(2)班前两名选手的平均分分别为92.5,100分, ∴在每班参加复赛的选手中分别选出2人参加决赛,初三(2)班的实力更强一些. 26.略27.60°28.(1)50, 65;(2))1(4)2)(2()2(22+=-+++=-+n n n n n n n .29.(1)810;(2)1;(3)18;(4)-4 30.B :-20 mC :+10 m【题目及参考答案、解析】学校:__________ 姓名:__________ 班级:__________ 考号:__________注意事项:1.答题前填写好自己的姓名、班级、考号等信息2.请将答案正确填写在答题卡上第I卷(选择题)请点击修改第I卷的文字说明一、选择题1.下列四幅图形中,表示两颗小树在同一时刻阳光下的影子的图形可能是()A.B.C.D.答案:D解析:D2.如图,在菱形ABCD中,∠ADC=120°,则BD:AC等于()A.3:2B.3:1C.1:2D.1:3答案:D解析:D3.一个多边形的内角和与外角和相等,则这个多边形是()A.三角形B.四边形C.五边形D.六边形答案:B解析:B4.下列方程一定是一元二次方程的是()A.0ax bx c++=B.22321x x mx-+=C.11xx+=D.22(1)230a x x+--=答案:D 解析:D5.一次函数34y x =-的图象不经过( )A .第一象限B .第二象限C .第三象限D .第四象限 答案:B解析:B6.下列语句中,不是命题的是 ( )A .两点之间线段最短B .不平行的两条直线有一个交点C .x 与y 的和等于0吗D .对顶角不相等答案:C解析:C7. 若a 的值使得224(2)1x x a x ++=+-成立,则a 值为( )A . 5B .4C . 3D . 2答案:C解析:C8. 若216x mx ++是完全平方式,则m 的值等于( )A .-8B .8C .4D .8或一8 答案:D解析:D9.已知235x x ++的值为 3,则代数式2391x x +-的值为( )A .-9B .-7C .0D .3 答案:B解析:B10.用代数式表示“2a 与 3 的差”为( )A .23a -B .32a -C .2(3)a -D .2(3)a -答案:A解析:A二、填空题11.如图所示,在把易拉罐中的水倒入一个圆水杯的过程中,若水杯中的水在点 P 与易拉罐刚好接触,则此时水杯中的水深为 ㎝.解析:612.若α是锐角,则α的余弦记作,α正切记作.解析:cosα,tanα13.用计算器求:(1)sin12036/= ;(2)cos53018/40//= ;(3)tan39040/53//= . (保留4个有效数字).解析:(1)0.2181;(2)0.5975;(3)0.829714.已知A、B、C、D点的坐标如图所示,E是图中两条虚线的交点,若△ABC∽△ADE,则点 E的坐标是.解答题解析:(4,-3)15.圆上各点到圆心的距离都等于;到圆心的距离等于半径的点都在上.解析:半径,圆16.如图,一张矩形纸片沿BC折叠;顶点A落在A′处,第二次过A′再折叠,使折痕DE∥BC,若AB=2,AC=3,则梯形BDEC的面积为 .解析:917.关于x的方程一元二次方程的2-+-=.k x kx(1)30(1)当k时,是一元一次方程;(2)当k时,一元二次方程.解析:(1)=1;(2)≠118.如图,l1反映了某公司的销售收入与销量的关系,l2 反映了该公司产品的销售成本与销量的关系,当该公司赢利(收入大于成本)时,销售量必须____________.解析:大于419.在长方形ABCD 中,AB = 2cm,BC = 3cm,则AD与BC之间的距离为 cm,AB与 DC之间的的距离为 cm.解析:2,320.已知某种植物花粉的直径约为 0.00035 m,用科学记数法表示该种花粉的直径是 .解析:43.510-⨯21.已知方程组23a b b c -=⎧⎨-=⎩,则a c -= . 解析:522.福顺路交通拥堵现象十分严重.上周末,陈新同学在福顺人行天桥处对3 000名过往行人作了问卷调查,问题是:从这里横过福顺路时,你是否自觉走人行天桥?供选择的答案有:A .是;(B)否;(C)无所谓.他将得到的数据处理后,画出了扇形统计图(如图).根据这个扇形统计图,可知被调查者中自觉走人行天桥的有 人.解析:165923.如图,∠E =∠F =90°,∠B =∠C ,AE =AF ,给出下列结论:①∠1=∠2;②BE =CF ;③△ACN ≌△ABM ;④CD =DN .其中正确的结论是____________________________(将你认为正确的结论序号填上).解析:①②③三、解答题24.如图,已知,EF ⊥AB ,CD ⊥AB ,G 在AC 边上,DG ∥BC .求证:∠1=∠2.解析:略 25.某中学开展“八荣八耻”演讲比赛活动,九(1)、九(2)班根据初赛成绩各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩(满分为100分)如下图所示.21G F E D CB A(1)根据左图填写下表平均分(分)中位数(分)众数(分)九(1)班8585九(2班8580(2)结合两班复赛成绩的平均数和中位数,分析哪个班级的复赛成绩较好?(3)如果在每班参加复赛的选手中分别选出2人参加决赛,你认为哪个班的实力更强一些,说明理由.解析:(1)85;100.(2)解:∵两班的平均数相同,初三(1)班的中位数高,初三(1)班的复赛成绩好些.(3)解:∵初三(1)班、初三(2)班前两名选手的平均分分别为92.5,100分,∴在每班参加复赛的选手中分别选出2人参加决赛,初三(2)班的实力更强一些.26.你画一个等腰三角形,使它的腰长为 3cm.解析:略27.如图,AB∥CD,∠2:∠3=1:2,求∠1的度数.解析:60°28.(1)观察下列各式:544622⨯=- ,10491122⨯=- ,164151722⨯=-…… 试用你发现的规律填空:___4495122⨯=-,___4646622⨯=-;(2)请你用含一个字母的等式将上面各式呈现的规律表示出来,并用所学数学知识说明你所写式子的正确性.解析:(1)50, 65;(2))1(4)2)(2()2(22+=-+++=-+n n n n n n n .29.用简便方法计算:(1) 8825⨯;(2) 200820081()22-⨯;(3) 202180.125⨯;(4)14300.252-⨯解析: (1)810;(2)1;(3)18;(4)-430.A 地海拔是-40 m ,B 地比A 地高 20 m ,C 地又比B 地高 30m ,试用正数或负数表示B 、C 两地的海拔.解析:B :-20 m C :+10 m。
顺德一中外国语学校初三年级2024学年第一学期第3周数学测试卷1

初三年级2024学年第一学期数学测试卷一.选择题(每小题3分,10小题,共30分)1.下列给出的四组线段中,是成比例线段的是()A.a=1,b=,c=,d=2B.a=,b=,c=2,d=3C.a=2,b=4,c=6,d=9D.a=1,b=2,c=3,d=42.菱形和矩形都具有的性质是()A.对角线互相垂直B.对角线长度相等C.对角线平分一组对角D.对角线互相平分3.如果方程(m﹣3)x m2−7−x+3=0,是关于x的一元二次方程,那么m的值为()A.±3B.3C.﹣3 D.04.校园里一片小小的树叶(图1),也蕴含着“黄金分割”,如图,P为AB的黄金分割点(AP >PB),如果AB的长度为10cm,那么AP的长度为()cm.A.﹣1B.2﹣2C.5﹣5D.10﹣105.在估算一元二次方程x2+2x﹣4=0的根时,小晗列表如表:x1 1.1 1.2 1.3 1.4 x2+2x﹣4﹣1﹣0.59﹣0.160.290.76由此可估算方程x2+2x﹣4=0的一个根x的范围是()A.1<x<1.1B.1.1<x<1.2C.1.2<x<1.3D.1.3<x<1.46.如图2,一块矩形ABCD绸布的长AB=a,宽AD=3,按照图中的方式将它裁成相同的三面矩形彩旗,如果裁出的每面彩旗与矩形ABCD绸布相似,则a的值等于()A.3B.2C.3D.27.如图3,从一个大正方形中截去面积为3cm2和12cm2的两个小正方形,若随机向大正方形内投一粒米,则米粒落在图中阴影部分的概率为()A.B.C.D.图1 图2 图38.如图4,AC、BD是四边形ABCD的两条对角线,顺次连接四边形ABCD各边中点得到四边形EFGH,要使四边形EFGH为矩形,应添加的条件是()A.AC⊥BD B.AB=CD C.AB∥CD D.AC=BD9.某市从2018年开始大力发展旅游产业.据统计,该市2018年旅游收入约为2亿元.预计2020年旅游收入约达到2.88亿元,设该市旅游收入的年平均增长率为x,下面所列方程正确的是()A.2(1+x)2=2.88B.2x2=2.88C.2(1+x%)2=2.88D.2(1+x)+2(1+x)2=2.8810.如图5,已知正方形ABCD的边长为12,BE=EC,将正方形边CD沿DE折叠到DF,延长EF交AB于G,连接DG,现在有如下4个结论:①△ADG≌△FDG;②GB=2AG;③∠GDE=45°;④S=.在以上4个结论中,正确的有()个.△BEFA.1B.2C.3D.4图4 图5 图6二.填空题(每小题3分,5小题,共15分)11.方程4x2+x=0的根为.12.若,且b+d+f=3,则a+c+e=.13.不透明的口袋中装有8个红球和若干个白球,它们除颜色外其他完全相同,通过多次摸球试验后发现,摸到白球的频率稳定在0.6附近,估计口袋中白球大约有个.14.已知m是一元二次方程x2+x﹣6=0的一个根,则代数式m2+m的值等于.15.如图6,在矩形ABCD中,E、F分别是BC和CD的中点,连接AE交对角线BD于点G,连接BF交AE于点H.则=.三.解答题(8小题,共75分)16.(8分)解方程:(1)(x+2)2=3(x+2)(2)2x2﹣7x﹣2=0.17.(10分)小明正在参加全国“数学竞赛”,只要他再答对最后两道单选题就能顺利过关,其中第一道题有3个选项,第二道题有4个选项,而这两道题小明都不会,不过小明还有一次“求助”没有使用(使用“求助”可让主持人去掉其中一题的一个错误选项).(1)如果小明第一题不使用“求助”,随机选择一个选项,那么小明答对第一道题的概率是多少?(2)如果小明将“求助”留在第二题使用,请用画树状图或列表法求小明能顺利过关的概率.(3)请你从概率的角度分析,建议小明在第几题使用“求助”,才能使他过关的概率较大.18.(6分)已知如图,正方形ABCD中,等边△AEF的顶点E,F分别在边BC和CD上,求证:∠CEF=∠CFE.19.(8分)已知关于x的一元二次方程x2+2mx+m2+m=0有实数根.(1)求m的取值范围;(2)若该方程的两个实数根分别为x1、x2,且+=12,求m的值.20.(8分)如图,点B为线段AC上一点,满足∠A=∠EBD=∠C=90°,AE=1,AB=BC=2.(1)求CD长度;(2)求证:△ABE∽△BDE.21.(10分)2023年杭州亚运会吉祥物一开售,就深受大家的喜爱.某商店以每件35元的价格购进某款亚运会吉祥物,以每件58元的价格出售.经统计,4月份的销售量为256件,6月份的销售量为400件.(1)求该款吉祥物4月份到6月份销售量的月平均增长率;(2)从7月份起,商场决定采用降价促销的方式回馈顾客,经试验,发现该吉祥物每降价1元,月销售量就会增加20件.当该吉祥物售价为多少元时,月销售利润达8400元?22.(11分)在正方形ABCD 外侧作直线AP ,点B 关于直线AP 的对称点为E ,连接BE ,DE ,其中DE 交直线AP 于点F .(1)依题意补全图1;(2)若∠P AB =20°,求∠ADF 的度数;(3)如图2,若45°<∠P AB <90°,用等式表示线段AB ,FE ,FD 之间的数量关系,并证明.23.(14分)在△ABC 中,∠ACB =45°.点D (与点B 、C 不重合)为射线BC 上一动点,连接AD ,以AD 为一边且在AD 的右侧作正方形ADEF .(1)如果AB =AC .如图①,且点D 在线段BC 上运动.试判断线段CF 与BD 之间的位置关系,并证明你的结论.(2)如果AB >AC ,如图②,且点D 在线段BC 上运动.(1)中结论是否成立,为什么?(3)若正方形ADEF 的边DE 所在直线与线段CF 所在直线相交于点P ,设AC =,BC =3,CD =x ,求线段CP 的长.(用含x 的式子表示)A B C D P 图2。
九下数学周末作业试卷(第2周)
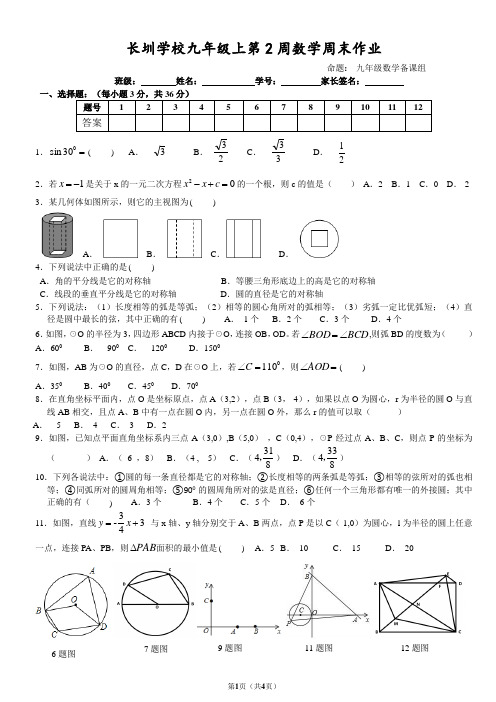
长圳学校九年级上第2周数学周末作业命题: 九年级数学备课组班级: 姓名: 学号: 家长签名:一、选择题:(每小题3分,共36分)题号123456789101112答案1.=030sin ( ) A . 3 B .23 C . 33 D . 21 2.若1-=x 是关于x 的一元二次方程02=+-c x x 的一个根,则c 的值是( ) A .2 B .1 C .0 D .-2 3.某几何体如图所示,则它的主视图为( )A .B .C .D .4.下列说法中正确的是( )A .角的平分线是它的对称轴B .等腰三角形底边上的高是它的对称轴C .线段的垂直平分线是它的对称轴D .圆的直径是它的对称轴5.下列说法:(1)长度相等的弧是等弧;(2)相等的圆心角所对的弧相等;(3)劣弧一定比优弧短;(4)直径是圆中最长的弦,其中正确的有( ) A . 1个 B .2个 C .3个 D .4个 6.如图,☉O 的半径为3,四边形ABCD 内接于☉O ,连接OB ,OD 。
若BCD BOD ∠=∠,则弧BD 的度数为( ) A .600 B . 900 C . 1200 D .15007.如图,AB 为☉O 的直径,点C ,D 在☉O 上,若0110=∠C ,则=∠AOD ( )A .350B .400C .450D .7008.在直角坐标平面内,点O 是坐标原点,点A (3,2),点B (3,-4),如果以点O 为圆心,r 为半径的圆O 与直线AB 相交,且点A 、B 中有一点在圆O 内,另一点在圆O 外,那么r 的值可以取( ) A . 5 B . 4 C . 3 D .29.如图,已知点平面直角坐标系内三点A (3,0),B (5,0) ,C (0,4),☉P 经过点A 、B 、C ,则点P 的坐标为( ) A .( 6 ,8) B .(4 , 5) C .(8314,) D .(8334,)10.下列各说法中:①圆的每一条直径都是它的对称轴;②长度相等的两条弧是等弧;③相等的弦所对的弧也相等;④同弧所对的圆周角相等;⑤900的圆周角所对的弦是直径;⑥任何一个三角形都有唯一的外接圆;其中正确的有( ) A .3个 B .4个 C .5个 D . 6个 11.如图,直线343-+=x y 与x 轴、y 轴分别交于A 、B 两点,点P 是以C (-1,0)为圆心,l 为半径的圆上任意一点,连接PA 、PB ,则PAB ∆面积的最小值是( ) A .5 B . 10C . 15D . 206题图7题图9题图11题图12题图12. 如图,以矩形ABCD 对角线AC 为底边作等腰直角ACE ∆,连接BE ,分别交AD ,AC 于点F ,N ,CD=AF ,AM 平分BAN ∠,下列结论:①ED EF ⊥; ②NCM BCM ∠=∠ ; ③EM AC 2=; ④222EN EF BN=+; ⑤FM NE AM AE ⋅=⋅,其中正确结论的个数是( ) A . 2 B . 3 C . 4 D . 5二.填空题(每题3分,共12分)13.若多项式5322+-x x 的值是8,则多项式5962+-x x 的值是 ___14.若3=n m ,则分式()m n nmn m n m -•+-+2222的值是 ______. 15.如图,反比例函数()0>=k xky 的图像与以原点(0,0)为圆心的圆交于A 、B 两点,且A (1,3),图中阴影部分的面积等于 ______16.如图,已知正方形ABCD 的边长为6,O 是对角线AC 与BD 的交点,E 为CD 上一点,且CE DE 2=,过点C 作BE CF ⊥,垂足为F ,连接OF ,则OF 的长为 ______.三.解答题(共52分)17.解下列方程:(每题4分,共8分)(1)()0433130sin 31-π---++ (2)0232=--x x18.(5分)先化简,再求值:,⎪⎭⎫⎝⎛-⋅+x x x x 422,其中0422=--x x19.(8分)深圳市实施行人闯红灯违法处罚,处罚方式分为四类:“罚款20元”、“罚款50元”、“罚款100元”、“穿绿马甲维护交通”。
