勾股定理、平方根专题复习
勾股定理与平方根复习

勾股定理与平方根班级 姓名 学号 学习目标:1回顾勾股定理及其逆定理,利用勾股定理解决生活中的实际问题2平方根及立方根,能说出一个近似数的精确度或有几个有效数字,能按照要求用四舍五入的方法取一个数的近似数,会进行实数的有关计算学习难点:勾股定理及其应用,平方根及立方根教学过程:一、知识要点1、勾股定理:在一个直角三角形中,两直角边的平方和等于斜边的平方。
2、勾股定理的应用:在一个直角三角形中,知道其中的任意两边都可以求第三边。
①c2=a2+b2;②a2=c2-b2;③b2=c2-a2。
3、直角三角形的识别(勾股定理的逆定理):如果三角形的三边长a 、b 、c 满足a2+b2 =c2,那么这个三角形是直角三角形。
(这是判定一个三角形是直角三角形的又一种方法)4、平方根的定义:一般地,如果一个数的平方等于a ,那么这个数叫做a 的平方根。
也称二次方根,也就是说,如果x2=a ,那么x 就叫做a 的平方根。
5、平方根的性质:①一个正数有两个平方根,它们互为相反数;②0的平方根是0,记作0 ;③负数没有平方根。
6、开平方的定义:求一个数a 的平方根的运算,叫做开平方。
7、算术平方根的定义:正数a 有2个平方根,其中正数a 的正的平方根,也叫做a 的算术平方根。
公式:( a )2=a (a ≥0),a2 =a (a ≥0) , a2 =-a(a ≤0)。
8、立方根的定义:一般地,如果一个数的立方等于a ,这个数就叫做a 的立方根,也称为三次方根;也就是说,如果x3=a ,那么x 叫做a 的立方根,数a 的立方根记作3a 读作“三次根号a ”。
9、开立方的定义:求一个数的立方根的运算,叫做开立方。
开立方和立方互为逆算。
10、立方根的性质:正数有一个正的立方根,负数有一个负的立方根,0的立方根0。
二、课堂小练习 1、16 的平方根________,64 的立方根_______。
2、若一正数的平方根是2a -1与-a +2,则_____ a 。
勾股定理、方根专题知识点整理
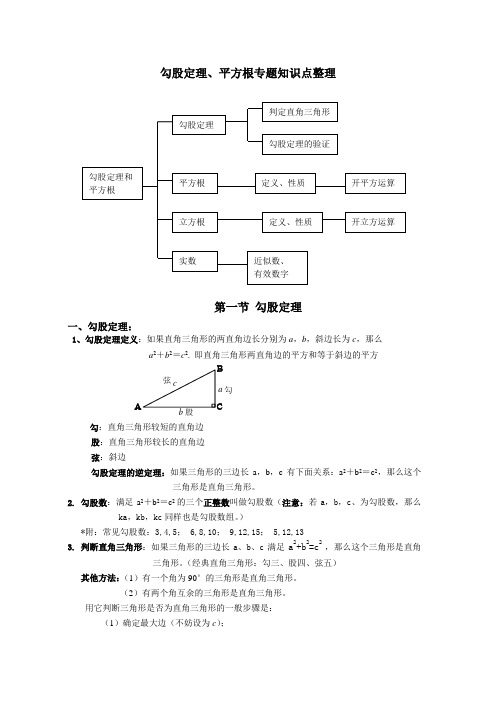
勾股定理、平方根专题知识点整理第一节勾股定理一、勾股定理:1、勾股定理定义:如果直角三角形的两直角边长分别为a,b,斜边长为c,那么a2+b2=c2. 即直角三角形两直角边的平方和等于斜边的平方ABCabc弦股勾勾:直角三角形较短的直角边股:直角三角形较长的直角边弦:斜边勾股定理的逆定理:如果三角形的三边长a,b,c有下面关系:a2+b2=c2,那么这个三角形是直角三角形。
2. 勾股数:满足a2+b2=c2的三个正整数叫做勾股数(注意:若a,b,c、为勾股数,那么ka,kb,kc同样也是勾股数组。
)*附:常见勾股数:3,4,5; 6,8,10; 9,12,15; 5,12,133. 判断直角三角形:如果三角形的三边长a、b、c满足a2+b2=c2 ,那么这个三角形是直角三角形。
(经典直角三角形:勾三、股四、弦五)其他方法:(1)有一个角为90°的三角形是直角三角形。
(2)有两个角互余的三角形是直角三角形。
用它判断三角形是否为直角三角形的一般步骤是:(1)确定最大边(不妨设为c);(2)若c 2=a 2+b 2,则△ABC 是以∠C 为直角的三角形; 若a 2+b 2<c 2,则此三角形为钝角三角形(其中c 为最大边); 若a 2+b 2>c 2,则此三角形为锐角三角形(其中c 为最大边)4.注意:(1)直角三角形斜边上的中线等于斜边的一半(2)在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半。
(3)在直角三角形中,如果一条直角边等于斜边的一半,那么这条直角边所对的角等于30°。
5. 勾股定理的作用:(1)已知直角三角形的两边求第三边。
(2)已知直角三角形的一边,求另两边的关系。
(3)用于证明线段平方关系的问题。
(4)利用勾股定理,作出长为n 的线段二、平方根:(11——19的平方)1、平方根定义:如果一个数的平方等于a ,那么这个数就叫做a 的平方根。
勾股定理与平方根复习

DCB A-2-14321第二章 勾股定理和平方根期末复习【学习目标】1. 理解平方根、算术平方根、立方根的概念,会用勾股定理解决简单问题,会用勾股定理的逆定理判定直角三形2、了解无理数和实数的概念;了解近似数与有效数字的概念。
【重点难点】勾股定理的应用及勾股定理的逆定理判定及其应用。
【基础训练】 一、知识点 (一)勾股定理:1、如图,△ABC 中∠ACB=90°,(1)若∠A=70°,则∠B=(2)若AC=5,AB=12,则AB= ,S △ABC = ,AB 边上的高为 (3)若∠B=30°,AC=4,则AB= ,BC=(4)若点D 为AB 的中点,若AB=10,则CD=2、已知Rt ABC ∆两边为3,4,则第三边长________.3、在△ABC 中,∠A 、∠B 、∠C 的对边分别是a 、b 、c ,下列条件中,能判断△ABC 为直角三角形的是 ( )A.a +b =cB. a :b :c =3:4:5C.a =b =2cD.∠A =∠B =∠C (二)平方根与立方根:1、16 =________ ________ 38-= = 2、 12+x 的算术平方根是2,x =___. 3、 64 的平方根是 ,立方根是____。
4、若4)4(33-=-k k ,则k 的值是 。
5、 一个数的平方根等于它本身,那么这个数是________。
某数的立方根等于它本身,则这个数是 。
某数的立方根等于它的算术平方根,那么这个数是 。
(三)实数:1、 和 统称为实数。
2、在实数257, 38-,3.1415926,π,- 20.121121112…中有理数有 ;无理数的有3、点M 在数轴上与原点相距 5 个单位,则点M 表示的实数为 ,在数轴上表示出来4、比较下列各组数的大小:-л -3.14159 23__________32 (四)近似数与有效数字:1、近似数0.4062精确到 ,有 个有效数字。
勾股定理与平方根回顾与复习(1)

2
9、如图,一圆柱高8cm,底面半径2cm,一只 蚂蚁从点A爬到点B处吃食,要爬行的最短 路程(圆周率取3)是 ( B) A.20cm; B.10cm; C.14cm; D.无法确定.
B ·
A·
10、用四舍五入法对下列各数按要求取 近似数: (1)26 074 000 (精确到万位) (2)7049(保留2个有效数字) (3)0.0249(保留2个有效数字) (4)35.6(精确到十位)
第二章
勾股定理与平方根
小结与思考(1)
勾股定理概念回顾
1、勾股定理 直角三角形两条直角边的平方和等于 斜边的平方 2、勾股定理逆定理
如果三角形的三边长a、b、c满足 a2+b2=c2,那么这个三角形是直角三角形.
3、满足a2+b2=c2的三个正整数a、b、c, 称为勾股数
4、平方根与立方根的比较:
⑴在图1中画出长度为 10 的线段AB; ⑵在图2中画出边长都是无理数的△ DEC; ⑶在图3中画出以格点为顶点面积为5的正方 形. B
E
D
A
C
课堂小结
你有什么收获?
6、有效数字
对一个近似数,从左边第一个不是0的数 字起,到末位数字止,所有的数字称为这 个近似数的有效数字 对科学计数法的有效数字例如:a×10n, 则以a的有效数字为整个数据的有效数字.
对近似数的认识
一个近似数四舍五入到哪一位,那么这 个近似数就精确到哪一位 .
题型有两类: Leabharlann 型一:对某个数按要求取近似数;7、有下列四个说法:①1的算术平方根
是1,②64的立方根是±4,③-27没有
立方根,④互为相反数的两数的立方根 互为相反数,其中正确的是(
数学第一章第二章知识点

1 / 10第一章勾股定理复习专题一、知识要点回顾:1、勾股定理:直角三角形两直角边的 等于斜边的 ;如果直角三角形两直角边分2、勾股定理的逆定理:如果三角形的三边长a,b,c 满足 ,那么这个三角形是___________.3、勾股数:满足a 2+b 2=c 2的三个 a,b,c,成为勾股数;写出常用的几组勾股数 , , 4.直角三角形斜边上的高为------------------。
二、典型例题解析与练习专题一:勾股定理例题1、在Rt △ABC ,∠C=90°则:⑴已知a=b=5,求c 2。
⑵已知a=1,c=2, 求b 2。
⑶已知c=17,b=8, 求a 。
⑷已知a :b=3:4,c=25, 求 b 。
例题2、已知直角三角形的两边长分别为5和12,求第三边。
练习:1、已知直角三角形的两边长分别为3cm 和5cm ,,则第三边长为 。
例题3、已知:如图,等边△ABC 的边长是6cm。
⑴求等边△ABC 的高。
⑵求S △ABC 。
例题4、 如图,有一个直角三角形纸片,两直角边AC=18cm ,BC=24cm ,现将直角边AC 沿直线AD 折叠,使它落在斜边AB 上,且与AE 重合,你能求出BD 的长吗?DBA2 / 10练习。
如图,在矩形ABCD 中,AB =5cm ,在边CD 上适当选定一点E ,沿直线AE 把△ADE 折叠,使点D 恰好落在边BC 上一点F 处,且△ABF 的面积是30cm 2.(1)求此时AD 的长. (2)求DE 的长。
2.如图,将一个边长分别为4、8的长方形纸片ABCD 折叠,使C 点与A 点重合,则EB 的长是( ).A .3B .4 CD .5例题5、一个直角三角形的周长为9,斜边为4,求这个三角形的面积。
练习:1.直角三角形两直角边长分别为5和12,则它斜边上的高为_______. 2.直角三角形的三边长为连续偶数,则这三个数分别为__________.3、图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形.若正方形A 、B 、C 、D 的边长分别是3、5、2、3,则最大正方形E 的面积是_________(3题图) (第4题图) (第5题图) (第6题图)4、如图,在△ABC 中,CE 是AB 边上的中线,CD ⊥AB 于D,且AB=5,BC=4,AC=6,则DE 的长为_______.5、如图,已知△ABC 中,∠ABC =90°,AB =BC ,三角形的顶点在相互平行的三条直线l 1,l 2,l 3上,且l 1,l 2之间的距离为2 , l 2,l 3之间的距离为3 ,则AC 的长是__________6、如图,等腰ABC △中,AB AC =,AD 是底边上的高,若5cm 6cm AB BC ==,,则AD = cm .7.一辆装满货物的卡车,高2.5米,宽1.6米,要开进厂门形状如图所示的某工厂,问这辆卡能否通过厂门(厂门上方为半圆形拱门)?说明你的理由.AC DBll 2 l 3ACBABCFEDCBA专题二:勾股定理的逆定理例题1、判断由线段abc组成的三角形是不是直角直角三角形:(1)a=15,b=8,c=17 (2)a=13,b=14,c=15 (3)三边长之比为 3∶4∶5;练习: 1、试判断下列三角形是否是直角三角形:⑴a=9,b=41,c=40;⑵a=15,b=16,c=6;(3)a=5k,b=12k,c=13k(k>0)。
勾股定理与平方根的数学知识点

勾股定理与平方根的数学知识点一、勾股定理勾股定理:直角三角形两直角边的平方和等于斜边的平方。
我国古代把直角三角形中,较短的直角边叫做勾,较长的直角边叫做股,斜边叫做弦。
结论为:勾三股四弦五a2+b2=c21、如果三角形的三边长a、b、c满足a+b=c,那么这个三角形是直角三角形。
2、满足a+b=c的3个正整数a、b、c称为勾股数。
(例如,3、4、5是一组勾股数)。
利用勾股数可以构造直角三角形。
二、平方根1、定义一般地,如果一个数的平方等于a,那么这个数叫做a的平方根,也称为二次方根。
也就是说,如果x2=a,那么x就叫做a的平方根。
2、一个正数有2个平方根,它们互为相反数;0只有一个平方根,它是0本身;负数没有平方根。
3、求一个数a的平方根的运算,叫做开平方。
4、正数a有两个平方根,其中正的平方根,也叫做a的算术平方根。
例如:4的平方根是2,其中2叫做4的算术平方根,记作=2;2的平方根是其中2的算术平方根。
0只有一个平方根,0的平方根也叫做0的算术平方根,即三、立方根1、定义一般地,如果一个数的立方等于a,那么这个数叫做a的立方根,也称为三次方根。
也就是说,如果x=a,那么x就叫做a的立方根,数a的立方根记作,读作三次根号a。
2、求一个数a的立方根的运算,叫做开立方。
3、正数的立方根是正数,负数的立方根是负数,0的立方根是0。
四、实数1、无限不循环小数称为无理数。
2、有理数和无理数统称为实数。
3、每一个实数都可以用数轴上的一个点来表示,反之,数轴上的每一个点都表示一个实数,实数与数轴上的点是一一对应的。
五、近似数与有效数字1、例如,本册数学课本约有100千字,这里100是一个近似似数。
2、对一个近似数,从左边第一个不是0的数字起,到末位数字止,所有的数字都称为这个近似数的有效数字。
初二数学勾股定理知识点勾股定理在任何一个直角三角形(Rt△)中(等腰直角三角形也算在内),两条直角边的长度的平方和等于斜边长度的平方,这就叫做勾股定理。
勾股定理与平方根的数学知识点

勾股定理与平方根的数学知识点一、勾股定理勾股定理是描述直角三角形边的关系的定理,它由公式a²+b²=c²表示,其中a、b、c分别代表直角三角形的两个直角边和斜边。
这一定理源自古希腊的数学家毕达哥拉斯提出的观察和实验结果。
应用:勾股定理在几何学中的应用非常广泛,可以用于求解直角三角形的边长、计算三角形的面积等。
同时,它还有重要的应用于导出三角函数的定义和性质。
例如,我们可以通过勾股定理计算一个直角三角形的斜边长度。
如果已知两个直角边的长度分别是a=3和b=4,那么根据勾股定理,可以计算出斜边c的长度:c²=a²+b²c²=3²+4²c²=9+16c²=25c=√25c=5所以,直角三角形的斜边长度为5二、平方根平方根是一种运算,表示一个数的平方根。
对于非负实数x,它的平方根是一个非负实数y,满足y²=x。
平方根的正号由计算的上下文决定。
平方根的运算方法可以通过求解方程x²=y来实现。
实质上,平方根是指数运算的逆运算。
应用:平方根在代数学中的应用广泛,可用于求解方程、计算数值等。
它还在几何学中有重要的应用,例如计算直角三角形的斜边长度、计算圆的半径等。
在实际应用中,平方根的计算可以通过手算、计算器、计算机等方式进行。
一些常见的平方根的近似值也被广泛使用,例如√2≈1.414,√3≈1.732三、勾股定理与平方根的关系勾股定理和平方根的关系可以通过勾股定理的应用来理解。
当我们需要求解直角三角形的斜边长度时,可以使用平方根运算。
在勾股定理中,由于a²+b²=c²,所以有c=√(a²+b²)。
这个式子告诉我们,当已知两个直角边的长度时,我们可以通过平方根运算来计算斜边的长度。
例如,当已知两个直角边的长度分别为a=3和b=4时,根据勾股定理,我们可以计算出斜边c的长度为c=√(3²+4²)=√(9+16)=√25=5这个例子展示了勾股定理和平方根的关系,它们在求解直角三角形边长时密切相关。
勾股定理与平方根要点回顾

勾股定理与平方根要点回顾勾股定理及逆定理揭示了形和数之间的紧密联系,在现实生活中也有着广泛的应用,体现了数学的价值。
而且,在数学发展史上有着重要的地位,对人类的发展也起着重要的作用。
平方根、算术平方根、立方根概念的引入,体现了引入新数的必要性。
从而把对数的认识上升到“实数”上。
一.重点、难点1.勾股定理及逆定理的理解与应用。
2.无理数和实数的概念,实数与数轴上的点一一对应。
3.近似数字与有效数字的概念。
二.知识要点1.勾股定理:直角三角形两直角边的平方和等于斜边的平方2.勾股定理逆定理:如果一个三角形的三边c b a 、、满足222c b a =+,那么这个三角形是直角三角形。
(判定三角形是直角三角形的一种方法)满足222c b a =+的三个正整数c b a 、、称为勾股数。
如:3、4、5;5、12、13等3. 平方根与算术平方根(1)平方根 如果一个数的平方等于a ,那么这个数叫做a 的平方根,也称二次方根。
即:若a x 2=,那么x 就叫做a 的平方根。
用a ±表示,读作:“正、负根号a ”如:的平方根。
都是、所以933,9)3(,9322-+=-=[注意]一个正数有两个平方根,它们互为相反数;如:2的平方根为2±0只有一个平方根,它是0本身;即00=负数没有平方根。
(2)算术平方根正数a 有两个平方根,其中正的平方根,也叫做a 的算术平方根。
如:15的平方根是15±;算术平方根是15(3)平方与开平方求一个数的平方根的运算,叫做开平方。
平方的结果是唯一的。
在开平方的运算中,被开方数必须是非负数,开平方的结果不一定是唯一的。
4.立方根 如果一个数的立方等于a ,那么这个数叫做a 的立方根,也称三次方根。
即:若a x 3=,那么x 就叫做a 的立方根。
用3a 表示,读作:“三次根号a ”。
如:的立方根。
是,所以)的立方根;(是所以828282,8233---=-= [注意]正数的立方根是正数;0的立方根是0;即003=负数的立方根是负数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第一节 勾股定理
一、勾股定理:
二、平方根:(11——19的平方)Leabharlann 三、立方根:(1——9的立方)
2、实数的分类:
正有理数 有理数 零 有限小数或无限循环小数 实数 负有理数 正无理数 无限不循环小数 无理数 负无理数
2、实数的分类:
勾股定理:
(一)结合三角形:
(二)、实际应用:
勾股定理:
(二)、实际应用:
勾股定理:
(三)求边长:
(五)方向问题:
(六)利用三角形面积相等:
(七)旋转问题:
(七)旋转问题:
(七)旋转问题:
(七)旋转问题:
(八)折叠问题:
(八)折叠问题:
(八)折叠问题:
平方根:
(一)文字类题目:
(二). 定义:
(二). 定义:
(二). 定义:
(二). 定义:
(二). 定义:
