Delta并联机构工作空间解析及尺度综合
Tsai氏并联机构工作空间解析及尺度综合

Tsai氏并联机构工作空间解析及尺度综合陈桂兰;曹毅;王强【摘要】以Tsai氏异型DELTA并联机构为研究对象,利用螺旋理论进行自由度分析,简化机构并以无量纲参数对其进行运动学分析、空间解析及尺度综合。
利用曲面包络理论求得机构可达工作空间,导出最大内切球优化空间位置与无量纲参数的约束关系。
以雅可比矩阵各列单位化所构成新矩阵乘其转置的行列式作为机构操作性能的衡量指标进行尺度综合,最后得到使机构操作性能最优的无量纲尺度参数。
%The spiral theory is used to do the DOF analysis, simplifying organization, dimensionless parameter kinematic analysis, workspace resolution and dimensional synthesis of Tsai al otype DELTA paral el mechanism. The reachable workspace is obtained based on the curve envelope theory. The constraint relationship between the maximal spherical workspace and the dimensionless pa-rameter is obtained. This paper takes the spheroid as the design space and the determinant of the normalized Jacobian matrix post-multiplied and transposed as the mechanism performance index for the dimensional synthesis, and then the optimal dimensions for the Tsai al otype paral el mechanism are obtained.【期刊名称】《机械制造与自动化》【年(卷),期】2016(000)005【总页数】5页(P8-12)【关键词】并联机构;无量纲参数;工作空间;尺度综合【作者】陈桂兰;曹毅;王强【作者单位】江南大学机械工程学院江苏无锡214122;江南大学机械工程学院江苏无锡214122; 上海交通大学机械系统与振动国家重点实验室上海200240;江南大学机械工程学院江苏无锡214122【正文语种】中文【中图分类】TH112相对于传统的串联机构,并联机构在承载能力、刚度、精度和响应速度等方面具有一定的优势[1-2],但并联机构受到运动副约束、支链干涉、奇异位形、位姿耦合等因素的影响,存在工作空间小的缺点。
Delta并联机器人的机构设计1
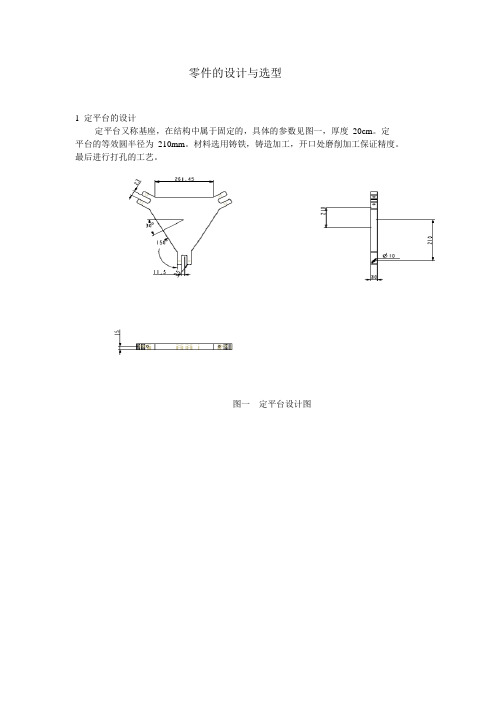
零件的设计与选型1 定平台的设计定平台又称基座,在结构中属于固定的,具体的参数见图一,厚度20cm。
定平台的等效圆半径为210mm。
材料选用铸铁,铸造加工,开口处磨削加工保证精度。
最后进行打孔的工艺。
图一定平台设计图具体参数为长* 厚* 宽:880mm*10mm*20mm。
孔的参数为φ10*10mm。
材料用铝合金,设计为杆式,质量小,经济,同时也满足载荷条件。
图二驱动杆的设计图3 从动杆的设计具体参数为长* 宽* 高:620*20*10mm。
孔参数为φ10*10mm。
材料选用铝合金。
图三从动杆的设计图参数如下图,考虑到重量因素,采用铝合金,切削加工。
动平台的等效圆半径为50mm,分布角为21.5°。
图四动平台的设计图5 链接销的设计45号钢,为主动杆和定平台的连接销:φ9*66mm。
6 球铰链的选型目前,大多数的Delta机构的主动杆与从动杆的链接方式为球铰链的链接。
球型连接铰链是用于自动控制中的执行器与调节机构的连接附件。
它采用了球型轴承结构具有控制灵活、准确、扭转角度大的优点,由于该铰链安装、调整方便、安全可靠。
所以,它广泛地应用在电力、石油化工、冶金、矿山、轻纺等工业的自动控制系统中。
球铰链由于选用了球型轴承结构,能灵活的承受来自各异面的压力。
本文选用球铰链设计,是主要因为球铰链的可控性,以及结构简单,易于装配。
且有很好的可维护性。
本文选用了伯纳德的SD 系列球铰链,相对运动角为60°。
7 垫圈的选型此处我们选用标准件。
GB/T 97.1 10‐140HV ,10.5*1.6mm。
8 电机的选型本设计的Delta 机器人,主要面向工业中轻载的场合,比如封装饼干等。
因此,以下做电动机的选型处理。
由于需要对角度的精确控制,因此决定选用伺服电机。
交流伺服电机有以下特点:启动转矩大,运行范围广,无自转现象,正常运转的伺服电动机,只要失去控制电压,电机立即停止运转,这也是Delta 机构需要的。
一种Delta型并联机器人的机构设计与分析

LI Ya -b U n o
(eat et f cai S anintue f eh o g X ’ hnx; 132 D p r n h n m o Me c,h nx istt o T cn l y, i nS ani700)  ̄ ' , [ o a
【 s atOfr gadl ido aa e rb t sdfr akn 。1 i mahn t cuecndl e t na dp w r 1,hc eil Ab t c] f i et kn f rl l oo e cig s c ies u tr a ei r i n o e e w ihi f xbe r en a p l u op r v mo o 1 sl
在 自由度 的分析 中。 一般 涉及闲置 自由度 、 冗余 自由度 、 过约束 、 公 共 约 束 等 问 题 。 对 较 复 杂 的 并 联 机 构 自由度 分 析 . 般 用 螺 旋 理 论 一 进行分析 。d l et a型并联器人 , 在运 动过程 中 , 四个支臂始终保 持空间 平 行 四边 形 。 根 据 螺 旋 理论 分析 末 端 执 行 器 运 动 , 知 螺旋 系 约 束 了 可 绕 三 个 轴 的转 动 . 明 此 机 构 只有 三 个 方 向 的平 动 自 由度 . 有 转 动 说 没
联 机 器人 工 作范 围 , 可根 据 情 况 不 使 用 。 也 此 机 构 在 运 动 过 程 中 , 端 执 行 器 只 有 平 动 自由 度 , 有 转 动 自 末 没
自 由度 分 析
具有高度非线性 、 强耦合 的特点 , 使其控制较为复杂 。总体来讲 , 并联 机 器 人 与 串 联 机 器 人 构 成 互 补 的关 系 ,扩 大 了整 个 机 器 人 的应 用 领 域 。 联 机器 人 机构 多种 多 样 , l e 提 出 了一 种 称 为 D l 并 Ca l v et 三 维 移 a的 动 机 构 。 et 构 是 最 典 型 的空 间 三、 度 移 动 的并 联 机构 , 多数 Dl a机 自由 大 空间三 自由度并联机构都是从 b i et a机构衍生 的 De a 。 l 机器人是一种 t
Delta型并联运动激光切割机床的工作空间分析

2007年1月农业机械学报第38卷第1期Delta 型并联运动激光切割机床的工作空间分析王 霄 韩亚锋 林跃强 刘会霞 高传玉 【摘要】 提出了一种基于Delt a 并联机构的新型激光切割机床。
建立了三自由度D elta 并联机构的反解方程和工作空间求解模型,分析了各支链子工作空间的几何形状及其内部出现空洞的条件,从而将工作空间解析归结为可达工作空间外部边界与内部空洞边界求解。
采用几何分析与数值迭代相结合的方法,探索了工作空间每一区域的边界,得到了机构工作空间的完整描述。
整个求解过程直观、简明,计算速度快。
关键词:激光切割机床 Delt a 并联机构 工作空间中图分类号:T G 485;T P242文献标识码:AWorkspace Analysis of a Laser Cutting Machine ToolBased on Delta Parallel StructureWang Xiao Han Yafeng Lin Yueqiang Liu Huix ia Gao Chuanyu(J iangsu University )AbstractA new laser cutting m anipulator based o n Delta parallel robot is proposed.Inv erse equations and even the inverse kinematics model of the three -deg ree -o f -freedom Delta parallel structure areestablished .T he geom etric shape of each subchain's w orkspace is analyzed and how the interior hole is fo rmed are discussed in the test,so the pr oblem of wo rkspace depends o n the solution of outside boundary and interior hole boundary of w ing the com bined m ethod betw een geom etric algo rithm and numerical iter ative algorithm ,the geom etric contour of each subchain's w orkspace is taken into account and the boundar y co nditions o f all the w or kspace r eg io n are discussed thoroughly.T hr oug h abo ve analy sis,the whole solution pr ocess is intuitio nistic and co ncise ,and the calculatio n speed is ev en faster .Key words Laser cutting m anipulator ,Delta parallel structure ,Workspace收稿日期:2005-09-02王 霄 江苏大学机械工程学院 副教授,212013 镇江市韩亚锋 江苏大学机械工程学院 硕士生林跃强 江苏大学机械工程学院 硕士生刘会霞 江苏大学机械工程学院 教授高传玉 江苏大学机械工程学院 教授 引言并联机床又称为虚拟轴机床,是一种基于并联机构原理并结合现代机器人技术和机床技术而产生的一种新型数控机床。
并联机构工作空间方法的分析

并联机构工作空间方法的分析引入并联机构的定义以及其具有的优点。
相对串联机构,并联机构刚性好,具有高的稳定性;惯性较小、动态响应好、累积误差小等特点成为学者的研究热点。
并联机构的工作空间是机构性能的重要指标。
文中总结并联机构工作空间求解的方法以及各种方法的特点及区别,为并联机构的应用和研究提供理论意义和实用价值。
标签:并联机构;工作空间;求解方法并联机构是机械、电子及计算机控制相结合的产物,是机器人学的一个重要分支。
并联机构的定义:由2个或2个以上的独立运动链连接动平台和静平台,通过并联方式驱动的闭环系统。
与串联机构相比,并联机构具有的优点:闭环支链结构刚度大,稳定性较好;运动惯性小、动态响应快、累积误差小、精度较高等;其中对于完全对称的并联机构具有较好的各向同性,可以避开机构的奇异点等,使得并联机构得到广泛的应用及发展[1]。
最早并联机构由学者Stewart提出的6自由度Stewart平台机构,该机构具有输出精度高,承载能力强以及易于控制,将其应用在飞行三维空间模拟器中。
由学者Fichter和Sugimoto将此平台用于操作器和力矩传感器。
并联机构中包含一类自由度小于6称少自由度并联机构,为并联机构中的重要分支[2]。
相对于6自由度并联机构,少自由度并联机构具有结构简单、造价低,易于控制优点。
Hunt提出一种3自由度并联平台机构,该并联机构动平台末端输出为2个转动自由度和1个移动自由度。
Gosselin提出了平面和球面3自由度机器人。
黄真和赵铁石综合出一种4-URU对称4自由度并联机构,可以实现3个移动自由度和1个转动自由度。
少自由度并联机构适合应用在模块化可重组制造系统中。
可用来构造串、并联机构、微动机构特殊用途机器人,从而进一步促进并联机构的实用性。
1 并联机构工作空间的定义及分类并联机构的工作空间定义[3]为:当给并联机构的驱动构件输入驱动时,动平台输出末端的参考点的所有运动区域,也即为此并联机构的工作空间。
并联机构工作空间方法的分析

并联机构工作空间方法的分析并联机构是指由若干个运动副构成的平行结构,其中多个副同时对同一运动变量进行控制。
不同于串联机构,其运动自由度数目可以大于其中每个运动副的自由度数目之和。
并联机构不仅具有高刚度、高精度、高载荷能力等优势,还能够提供更大的工作空间并实现高精度运动和控制。
工作空间是指机构能够执行运动的位置和方向的组合。
在分析并联机构的工作空间时,应先确定其基本运动副及其限制条件,然后对每个基本运动副进行建模,最后求解并联机构的整体工作空间。
在基本运动副建模方面,目前主要有基于Minkowski(闵可夫斯基)和基于代数运算等两种方法。
基于Minkowski方法是将运动副看做一些联立的凸多面体,通过求解这些多面体的Minkowski和来得到机构的工作空间边界。
该方法的优势在于其高精度且应用范围广泛;缺点则是其计算复杂度较高,对于大型机构而言时间较长。
基于代数运算的方法则是基于运动副的运动学关系以及代数方程求解的原理,其优势是可以有效解决复杂机构的计算问题,但其缺点是对于数学求解能力要求较高。
在整体工作空间求解方面,可使用约束优化方法、遗传算法、神经网络等较为常见的算法。
其中,约束优化方法是一种以优化函数为目标,通过求解约束条件的方法得到最优解的算法。
而遗传算法和神经网络则是通过模拟自然界进化和人类神经网络的工作原理来求解并联机构的工作空间。
需要注意的是,由于并联机构存在多个运动副同时控制同一运动变量的情况,因此运动副之间的干涉问题需要得到充分的考虑。
在机构设计过程中,需要进行多次优化以及演示分析,以保证机构的工作稳定性和灵活性。
综上所述,分析并联机构的工作空间是一个十分重要而复杂的问题。
该问题需要考虑机构的设计、运动干涉等复杂因素,需要运用数学、计算机技术等多种专业知识和技能来解决。
近年来,随着机器人等高精度机电一体化系统的不断发展和应用,对并联机构工作空间分析的研究也将越来越深入和广泛。
并联机构工作空间方法的分析

并联机构工作空间方法的分析
并联机构是一种常见的工程机械结构,它通过多个并联的连杆或轴来实现机械传动和工作空间的控制。
在工程设计和机械运动控制领域,对并联机构工作空间的方法分析是非常重要的,因为它能够帮助工程师和设计师了解并联机构的运动特性,优化机构结构和控制系统。
一般来说,对并联机构工作空间的方法分析主要包括以下几个方面:工作空间的定义和表示方法、工作空间的几何特性分析、工作空间的优化设计和控制策略的研究。
以下将对这几个方面进行详细分析。
工作空间的定义和表示方法是对并联机构工作空间方法分析的基础。
工作空间通常可用数学方法来描述,它是机构在给定位置和姿态下能够达到的所有可能的位姿和方向的集合。
常用的方法有基于欧拉角、四元数和转动矩阵的表示方法,这些方法能够有效地描述机构的位姿和方向,并为后续的工作空间分析提供基础。
工作空间的几何特性分析是对并联机构工作空间方法分析的重要内容。
在这一方面,通常需要进行机构运动学分析和几何建模,通过求解机构的运动学方程和几何限制条件,得到机构的工作空间和其几何特性,如面积、体积、最大位移等。
这些几何特性能够为机构设计和控制提供重要的参考依据,使工程师和设计师能够更好地理解并联机构的工作特性。
工作空间的控制策略的研究是对并联机构工作空间方法分析的重要内容之一。
在实际应用中,机构的工作空间通常需要通过控制系统来实现,因此需要研究机构的控制策略和方法。
这包括对机构运动学和动力学的建模和仿真,对机构运动轨迹和工作空间的路径规划和控制,以及对机构的传感器和执行器的集成和控制算法的设计等内容。
这些研究能够帮助工程师和设计师更好地实现对并联机构工作空间的控制和优化。
DELTA并联机器人工作空间求解

有空间三个平移 自由度。 机器人工作空间定义为 , 在 结构限制下末端操作器 能够 达到的所有位置 的集 合。 求解工作空间是 D E L T A机器人数学建模和控制 等必须解决的关键问题。 计算 D E L T A工作空间的传 统方法有搜索法 、 作图法等。 文献 [ 1 ] 利用 D E L T A机 器人的运动学反解方程 ,提 出了一种工作空间的求 法。 文献 [ 2 ] 通过 C A D作为工具对 D E L T A的工作空
机 电控 制 。
2 0 1 7年第 1 1 期
陈统 书: D E L T A并联机器人工作空间求解
如上页图 2 所示 , 三个平移矢量 P , O ’ 、 P 2 O 。 、 P 3 D ’
坐标 为 : 式中:
F O I 册’ I ・ n . I F O ’ l = 、 /
平台组成 , 静平台的三条边通过三条相同的运动支 链分别连接到动平台的三个边上。每条运动链 中均
有 一个 由 四个 球 铰 与 杆 件 构 成 的平 行 四边形 闭环 。
三个平行四边形闭环的应用保证了动平台与静平 台 始终保持平行 , 消除了动平台的转动 自由度 , 保 留了
动平 台三个 平移 自由度 。
一
( 1 1 ) ,
1 一 r c 0 s 1
.
D f _ r s i n =
l 0 J
式 中: r 为 动平 台外 接 圆半 径 。 G 三 点矢 量 为
_ 1 , 2 , 3 . ( 1 )
耵 一
G ×C 3 C 1
’
这样 , 求取 了 O F和 F O ’ , 由式( 5 ) 可求解得三棱
出D E L T A工作空间中离散点求解过程 , 而没有很直 观地将 D E L T A的工作空间表达 出来 。 本文介绍一种 能直观表达 D E L T A工作空间大小的方法 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2008年5月农业机械学报第39卷第5期Delta 并联机构工作空间解析及尺度综合*高秀兰 鲁开讲 王娟平摘要 提出了Delta 并联机构工作空间解析及尺度综合的方法。
利用曲面包络理论得到Delta 并联机构单开链子空间边界曲面的解析表达式,求得机构可达工作空间,进而导出工作空间包容的最大内切球体及其位置与尺度参数的关系。
最后将上述球体作为设计空间,以雅可比矩阵条件数在设计空间的全域平均值作为机构操作性能衡量指标进行尺度综合,得到使机构操作性能最优的尺度参数。
关键词:并联机构 工作空间 尺度综合中图分类号:T P24文献标识码:AWorkspace Resolution and Dimensional Synthesis onDelta Parallel MechanismGao Xiulan Lu Kaijiang Wang Juanping(Baoj i Univer sity of A rts and Sciences,Bao j i,721007,China)AbstractA method of workspace resolution and dimensional synthesis on Delta parallel mechanisms was presented.T he resolution ex pression of the single open chain sub space boundary surface and the reachable workspace of the Delta parallel mechanism were obtained based on curve envelope theory.T hen the max imal inscribed spheroid contained in workspace was educed,and the relationship between its position and the dimensions was established.T aking the spheroid as the design space and using the universal average value of Jacobian m atrices condition number in desig n space as mechanism performance index for dimensional synthesis,the optimal dimensions for the Delta parallel mechanism w ere obtained lastly.Key words Parallel mechanism,Workspace,Dimensional sy nthesis 收稿日期:2007 01 08*陕西省教育厅科学研究项目(项目编号:05JK 138)高秀兰 宝鸡文理学院机电工程系 副教授,721007 陕西省宝鸡市鲁开讲 宝鸡文理学院机电工程系 副教授王娟平 宝鸡文理学院机电工程系 讲师引言并联机构受到运动副约束、支链干涉、奇异位形、位姿耦合等因素的影响,存在工作空间小的缺点,6自由度并联机构的问题更为突出。
3自由度并联机构如果选型合理,则可以改善以上不足。
Delta 并联机构只有3个移动自由度,具有工作空间大、正解运动学简单、定位精度高等优点。
工作空间解析与尺度综合是并联机构运动学原理设计的核心问题[1]。
工作空间解析的方法有几何法和代数法[2~4],尺度综合是在保证并联机构实现预定工作空间的前提下,以操作性能最优为目标确定机构的尺度参数[5~6]。
针对Delta 并联机构的结构特点,在几何分析的基础上,得到工作空间边界曲面解析表达式及其内切球体与机构尺度参数的关系,然后以此球体为设计空间进行尺度综合,得到机构最优尺度参数。
1 机构的约束方程Delta 并联机构由上、下2个等边三角形平台及3条完全相同的支链组成,如图1所示,每条支链都由1个定长杆和1个平行四边形机构组成,定长杆图1 Delta 型并联机构运动简图Fig.1 K inematic diagr am of Delta parallel mechanism与下面的静平台用转动副连接,平行四边形机构与动平台及定长杆均以转动副连接,这3处转动副轴线相互平行,机构具有3个移动自由度。
在静平台上固连参考坐标系Ox yz ,坐标原点位于静平台中心,x 轴过点A 1,y 轴平行于A 3A 2。
设OA i 到A i B i 的转角为 i ,动静平台外接圆半径分别为r 0和r ,则B i 、C i 在参考坐标系的位置矢量为b i =r cos i sin i 0+l 1cos i cos icosi sin i sin i(i =1,2,3)c i =r 0cos isin i 0+xy z(i =1,2,3)式中 l 1!!!定长杆长度x 、y 、z !!!动平台中心P 的坐标 i !!!转动副中心A i 、C i 的方向角按B i C i =l 2建立机构约束方程f i =(x -x i )2+(y -y i )2+(z -z i )2-l 22=0(i =1,2,3)(1)其中x i =l 1cos i cos i +(r -r 0)cos iy i =l 1sin i cos i +(r -r 0)sin i z i =l 1sin i(2)2 工作空间解析2 1 单开链子空间边界曲面方程对每一支链,式(2)是关于输入角 i 的单参数方程,表示一圆弧,记作 i ,圆心N i ((r -r 0)cos i ,(r -r 0)sin i ,0),半径为l 1。
式(1)则表示球心位于S i (x i ,y i ,z i ),半径为l 2的球面,记作!i 。
当 i 变化时,动平台中心P 的变化范围是球面!i 的球心S i 沿圆弧 i 连续移动所形成的包络体,其外边界为圆环面,轴线过N i ,轴线方向的单位向量为n i ,i 即为各子空间边界圆环面的中心线,这3条中心线相交于点G (0,0,l 21-(r -r 0)2),如图2所示。
下面推导各子空间边界圆环面方程。
图2 单开链子空间边界圆环面中心线示意图Fig.2 Graphic of single open chain sub spaceboundar y torus ∀center line图3 单开链子空间边界圆环面形成原理图Fig.3 Forming theory of single open chainsub space boundary torus各支链子空间边界圆环面可以看作圆母线∀绕其轴线n i 旋转形成的,如图3所示,设M 1(x 1,y 1,z 1)是母线上任意一点,其坐标满足母线方程[x 1-(l 1+r -r 0)cos i ]2+[y 1-(l 1+r -r 0)sin i ]2+z 21=l 22z 1=0(3)过M 1的纬线圆可以看成是过M 1且垂直于轴线n i 的平面与以N i 为球心、半径为M 1N i 球面的交线,所以该纬线圆方程为n x (x -x 1)+n y (y -y 1)+n z (z -z 1)=0(x -x 0)2+(y -y 0)2+(z -z 0)2= (x 1-x 0)2+(y 1-y 0)2+(z 1-z 0)2(4)从式(3)、(4)中消去x 1、y 1、z 1得到的关于x 、y 、z 的三元方程即为单开链子空间边界圆环面方程,具体为[x 2+y 2+z 2-2(r -r 0)(x cos i +y sin i )+l 21-l 22+(r -r 0)2]2=4l 21[x 2cos 2i +y 2sin 2i +z 2+2xy cos i sin i -2(r -r 0)(x cos i +y sin i )+(r -r 0)2](5)147第5期 高秀兰等:Delta 并联机构工作空间解析及尺度综合2 2 实例并联机构的工作空间是动平台中心点可以到达的工作区域,它是各支链子空间的交集,其边界也由各支链边界曲面围成,各支链边界曲面的交线形成了工作空间不规则的凸起,在这些位形时机构的运动性能都会变差,为了避开这些位形,通常以可达空间的最大内切规则几何体作为并联机构的设计空间。
各支链子空间边界环面中心线相交于点G ,则以G 为球心、l 2为半径的球体必内切于各子空间,该球体包容于工作空间中。
下面用数值方法求出机构工作空间,并验证该球体为工作空间的最大内切球体。
给定机构尺度参数:l 1=7 2cm ,l 2=4 2cm ,r =3cm ,r 0=2cm ,求解工作空间边界的步骤如下:(1)确定工作空间最高点和最低点z max =l 21-(r -r 0)2+l 2z min =l 21-(r -r 0)2-l 2(2)用一系列平行于Ox y 坐标面的平面将并联机构可达工作空间分割成厚度为#z 的微分子空间。
(3)在每一截面,将z j =z max -(j -1)#z 依次代入各支链边界圆环面方程(5),用极坐标法即能求得截面z j 与各支链i 边界圆环面的交线,如图4a 所示。
对每一方向,取m in {∃i |i =1,2,3},可得截面z j 上工作空间等高线图,如图4b 所示。
(4)循环j ,即可求得全部工作空间的边界,如图5所示。
(5)对每个截面z j ,在计算工作空间边界等高线时,同时计算该截面与球体G 的截交线圆,如图6所示。
该圆内切于工作空间边界等高线。
图4 工作空间截面等高线图F ig.4 Diag rams o f w orkspace ∀s cross section contour(a)截平面与单开链子工作空间边界交线(b)工作空间截面等高线图由图5、6可见:(1)Delta 并联机构的工作空间在每个截面上均为外凸的曲线六边形,这些曲线多边形的顶点是其中两个支链边界圆环面与截面z j的三面共有点,最终形成工作空间局部的凸起。
(2)球体G 为工作空间的最大内切球体,可以将它作为机构的设计空间进行尺度综合。
图5 Delta 型并联机构工作空间边界曲面Fig.5 Workspace boundary curve of Delta parallel mechani sms图6 设计空间与可达空间F ig.6 Reachable wor kspace and design(a)z =10 5cm (b)z =7 13cm (c)z =3 77cm3 并联机构尺度综合尺度综合是并联机构运动学设计的最终目标,它以在设计空间内机构的操作性能最优为目标,确定机构的尺度参数。
