【名师一号】2014-2015学年高中数学 第一章 立体几何初步双基限时练1(含解析)北师大版必修2
【名师一号】2014-2015学年高中数学 第一章 三角函数双基限时练2(含解析)新人教A版必修4

双基限时练(二)1.终边在y 轴的非负半轴上的角的集合是( ) A .{α|α=k π,k ∈Z }B.⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫α⎪⎪⎪α=k π+π2,k ∈Z C .{α|α=2k π,k ∈Z }D.⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫α⎪⎪⎪α=2k π+π2,k ∈Z 解析 A 选项表示的角的终边在x 轴上;B 选项表示的角的终边在y 轴上;C 选项表示的角的终边在x 轴非负半轴上;D 选项表示的角的终边在y 轴非负半轴上,故选D.答案 D2.在半径为5 cm 的圆中,圆心角为周角的23的角所对的圆弧长为( )A.4π3cm B.20π3cm C.10π3cm D.50π3cm 解析 记r =5,圆心角α=23×2π=4π3,∴l =|α|r =203π.答案 B3.将-1485°化成α+2k π(0≤α<2π,k ∈Z )的形式是( ) A .-π4-8πB.74π-8π C.π4-10π D.7π4-10π 解析 ∵-1485°=-5×360°+315°, 又2π=360°,315°=74π,∴-1485°=-5×2π+74π=7π4-10π.答案 D4.把-114π表示成θ+2k π(k ∈Z )的形式,使|θ|最小的θ为( )A .-34πB.π4C.34π D .-π4解析 ∵-11π4=-2π-3π4,∴θ=-34π.又-11π4=-4π+5π4,∴θ=5π4.∴使|θ|最小的θ=-3π4.答案 A5.若一圆弧长等于其所在圆的内接正三角形的边长,则其圆心角的弧度数的绝对值为( )A.π3B.2π3C. 3 D .2解析 设所在圆的半径为r ,圆内接正三角形的边长为2r sin60°=3r ,所以弧长3r 的圆心角的弧度数为3rr= 3.答案 C6.用集合表示终边在阴影部分的角α的集合为( )A.⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫α⎪⎪⎪π4≤α≤π3 B.⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫α⎪⎪⎪π4≤α≤5π3 C.⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫α⎪⎪⎪2k π+π4≤α≤2k π+π3,k ∈ZD.⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫α⎪⎪⎪2k π+π4≤α≤2k π+5π3,k ∈Z解析 由图可知在[0,2π)内角的终边落在阴影部分时π4≤α≤5π3, ∴满足条件的集合为⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫α⎪⎪⎪2k π+π4≤α≤2k π+5π3,k ∈Z. 答案 D7.圆的半径变为原来的12,而弧长不变,则该弧所对的圆心角变为原来的________倍.解析 由公式θ=l r 知,半径r 变为原来的12,而弧长不变,则该弧所对的圆心角变为原来的2倍.答案 28.将下列弧度转化为角度: (1)π12=________; (2)-7π8=________;(3)13π6=________;(4)-512π=________.答案 (1)15° (2)-157°30′ (3)390° (4)-75°9.将下列角度化为弧度: (1)36°=________rad ; (2)-105°=________rad ; (3)37°30′=________rad ; (4)-75°=________rad. 解析 利用1°=π180rad 计算.答案 (1)π5(2)-7π12(3)5π24(4)-5π1210.在直径为20 cm 的圆中,圆心角为150°时所对的弧长为________. 解析 150°=150×π180=5π6,∴l =5π6×10=25π3(cm).答案 25π3cm11.如图所示,分别写出适合下列条件的角的集合: (1)终边落在射线OM 上; (2)终边落在直线OM 上;(3)终边落在阴影区域内(含边界).用弧度制表示终边在图中阴影区域内角的集合(包括边界)并判断2 012°是不是这个集合的元素.解 ∵150°=5π6.∴终边在阴影区域内角的集合为S ={β|5π6+2k π≤β≤3π2+2k π,k ∈Z }.∵2012°=212°+5×360°=⎝ ⎛⎭⎪⎫53π45+10πrad ,又5π6<53π45<3π2. ∴2012°=503π45∈S .12.如图所示,动点P 、Q 从点A (4,0)出发沿圆周运动,点P 按逆时针方向每秒钟转π3弧度,点Q 按顺时针方向每秒钟转π6弧度,求P 、Q 第一次相遇所用的时间及P 、Q 各自走过的弧长. 解 设P 、Q 第一次相遇时所用的时间为t 秒,则:t ·π3+t ·⎪⎪⎪⎪⎪⎪-π6=2π,解得t =4,即第一次相遇时所用的时间为4秒.P 点走过的弧长为:43π×4=163π, Q 点走过的弧长为:8π-16π3=8π3. 13.扇形AOB 的周长为8 cm.(1)若这个扇形的面积为3 cm 2,求圆心角的大小;(2)求这个扇形的面积取得最大值时圆心角的大小和弦长AB .解 (1)设扇形的圆心角为θ,扇形所在圆的半径为R ,依题意有⎩⎪⎨⎪⎧2R +R θ=8,12θ·R 2=3,解得θ=23或6.即圆心角的大小为23弧度或6弧度.(2)设扇形所在圆的半径为 x cm ,则扇形的圆心角θ=8-2xx,于是扇形的面积是S =12x 2·8-2x x=4x -x 2=-(x -2)2+4.故当x =2 cm 时,S 取到最大值.此时圆心角θ=8-42=2弧度,弦长AB =2 ·2sin 1=4sin1 (cm).即扇形的面积取得最大值时圆心角等于2弧度,弦长AB 等于4sin1 cm.。
【名师一号】2014-2015学年高中数学 第一章 数列双基限时练10(含解析)北师大版必修5

双基限时练(十)一、选择题1.各项都是正数的等比数列{a n }中,a 2,12a 3,a 1成等差数列,则a 4+a 5a 3+a 4的值为( )A.5-12 B.5+12 C.1-52D.5±12解析 由题意得,a 3=a 1+a 2, ∴q 2=1+q ,得q =1±52,又a n >0,∴q >0,故q =1+52.即a 4+a 5a 3+a 4=q =1+52. 答案 B2.公差不为0的等差数列{a n }中,2a 3-a 27+2a 11=0,数列{b n }是等比数列,且b 7=a 7,则b 6b 8=( )A .2B .4C .8D .16解析 2a 3-a 27+2a 11=0得4a 7-a 27=0,∴a 7=4,或a 7=0(舍).∵b 7=a 7,∴b 6b 8=b 27=16.答案 D3.公差不为零的等差数列{a n }的前n 项和为S n ,若a 4是a 3与a 7的等比中项,S 8=32,则S 10等于( )A .18B .24C .60D .90解析 设公差为d ,则a 4=a 1+3d ,a 3=a 1+2d ,a 7=a 1+6d ,由已知得(a 1+3d )2=(a 1+2d )(a 1+6d ),得2a 1=-3d ,又S 8= a 1+a 8 ×82=32,得d =2.∴S 10= a 1+a 10 ×102=5(2a 1+9d )=5×6d =60.答案 C4.数列{a n }是公差不为零的等差数列,且a 5,a 8,a 13是等比数列{b n }的相邻三项,若b 2=5,则b n =( )A .5·⎝ ⎛⎭⎪⎫53n -1B .5·⎝ ⎛⎭⎪⎫35n -1C .3·⎝ ⎛⎭⎪⎫35n -1D .3·⎝ ⎛⎭⎪⎫53n -1解析 由题意得a 28=a 5·a 13.即(a 1+7d )2=(a 1+4d )(a 1+12d ),得d =2a 1. ∴a 8=15a 1,a 5=a 1+4d =9a 1,q =15a 19a 1=53.∴b n =b 2·q n -2=5×⎝ ⎛⎭⎪⎫53n -2=3×⎝ ⎛⎭⎪⎫53n -1.答案 D5.数列9,99,999,9999,…的前n 项和等于( ) A .10n-1 B.109(10n-1)-n C.109(10n-1) D.109(10n-1)+n 解析 a n =10n-1,∴S n =10 1-10n1-10-n =10 10n-1 9-n .答案 B6.已知{a n }为等比数列,a 4+a 7=2,a 5a 6=-8,则a 1+a 10=( ) A .7 B .5 C .-5D .-7解析 由已知得⎩⎪⎨⎪⎧a 4+a 7=2,a 5a 6=a 4a 7=-8,解得⎩⎪⎨⎪⎧a 4=4,a 7=-2,或⎩⎪⎨⎪⎧a 4=-2,a 7=4.当a 4=4,a 7=-2时,易得a 1=-8,a 10=1,从而a 1+a 10=-7;当a 4=-2,a 7=4时,易得a 10=-8,a 1=1,从而a 1+a 10=-7.答案 D 二、填空题7.一个等比数列,它与一个首项为0,公差不为零的等差数列相应项相加后得到新的数列1,1,2,…,则相加以后新数列的前10项和为________.解析 设{a n }为等比数列,公比为q ,数列{b n }为等差数列,公差为d ,则⎩⎪⎨⎪⎧ b 1+a 1=1,q +d =1,q 2+2d =2,a 1=0,得⎩⎪⎨⎪⎧b 1=1,a 1=0,q =2,d =-1.∴新数列的前10项的和S 10=1-2101-2+10×92×(-1)=978.答案 9788.1,12,2,14,4,18,…的前2n 项的和是________.解析 S 2n =(1+2+4+…+2n -1)+⎝ ⎛⎭⎪⎫12+14+ (12)=1-2n1-2+12⎣⎢⎡⎦⎥⎤1-⎝ ⎛⎭⎪⎫12n 1-12=2n-⎝ ⎛⎭⎪⎫12n .答案 2n-⎝ ⎛⎭⎪⎫12n9.首项为2,公差为2的等差数列的前n 项和为S n ,则1S 1+1S 2+…+1S n=________.解析 由已知可知S n =2n +n n -12×2=n 2+n∴1S 1+1S 2+…+1S n=1-12+12-13+…+1n -1n +1=1-1n +1=nn +1. 答案nn +1三、解答题10.在等差数列{a n }中,公差d ≠0,且a 1,a 3,a 9成等比数列. 求a 1+a 3+a 9a 2+a 4+a 10的值.解 ∵{a n }为等差数列,且a 1,a 3,a 9成等比数列,∴a 23=a 1a 9,∴(a 1+2d )2=a 1(a 1+8d ),得a 1d =d 2,又d ≠0,∴a 1=d ,∴a 1+a 3+a 9a 2+a 4+a 10=13d 16d =1316.11.在等比数列{a n }中,a n >0(n ∈N +),公比q ∈(0,1),且a 1a 5+2a 3a 5+a 2a 8=25,又a 3与a 5的等比中项为2.(1)求数列{a n }的通项公式;(2)设b n =log 2a n ,数列{b n }的前n 项和为S n .求数列{S n }的通项公式. 解 (1)∵{a n }为等比数列,a 1a 5+2a 3a 5+a 2a 8=25, ∴a 23+2a 3a 5+a 25=25.又a n >0,∴a 3+a 5=5,又a 3与a 5的等比中项为2, ∴a 3a 5=4.而q ∈(0,1),∴a 3>a 5,∴a 3=4,a 5=1. ∴q =12,a 1=16.∴a n =16×⎝ ⎛⎭⎪⎫12n -1=25-n.(2)b n =log 2a n =5-n ,∴{b n }的前n 项和S n = 4+5-n n 2=n 9-n2.12.已知{a n }是一个公差大于0的等差数列,并且满足a 3·a 6=55,a 2+a 7=16. (1)求数列{a n }的通项公式;(2)如果数列{a n }和数列{b n }都满足等式:a n =b 12+b 222+…+b n2n (n 为正整数),求数列{b n }的前n 项和S n .解 (1)由{a n }为等差数列,知a 2+a 7=a 3+a 6=16,由⎩⎪⎨⎪⎧a 3·a 6=55,a 3+a 6=16,得⎩⎪⎨⎪⎧a 3=11,a 6=5,或⎩⎪⎨⎪⎧a 3=5,a 6=11.又公差d >0,∴a 3=5,a 6=11. 由a 6=a 3+3d ,得d =2. ∴a n =a 3+(n -3)d =2n -1. (2)当n =1时,a 1=b 12,得b 1=2.当n ≥2时,由a n =b 12+b 222+…+b n -12n -1+b n2n ,得a n -1=b 12+b 222+…+b n -12n -1.∴a n -a n -1=b n2n . ∴b n =2n +1.又n =1时,2n +1=4≠2,∴b n =⎩⎪⎨⎪⎧2 n =1 ,2n +1n ≥2 .当n =1时,S 1=b 1=2,当n ≥2时,S n =b 1+b 2+b 3+…+b n =2+b 2 1-2n -11-2=2n +2-6,又n =1时,上式也成立, ∴S n =2n +2-6.思 维 探 究13.已知数列{a n }为等差数列且公差d ≠0,{a n }的部分项组成下列数列:ak 1,ak 2,…,ak n 恰为等比数列,其中k 1=1,k 2=5,k 3=17,求k n .解 由题设有a 2k 2=ak 1ak 3,即a 25=a 1a 17,∴(a 1+4d )2=a 1(a 1+16d ),∴a 1=2d 或d =0(舍去),∴a 5=a 1+4d =6d ,∴等比数列的公比q =ak 2ak 1=a 5a 1=3. 由于ak n 是等差数列的第k n 项,又是等比数列的第n 项, 故ak n =a 1+(k n -1)d =ak 1q n -1,∴k n =2·3n -1-1.。
【名师一号】2014-2015学年高中数学 第一章 三角函数双基限时练13(含解析)北师大版必修4

双基限时练(十三) 三角函数的简单应用一、选择题1.已知函数y =2sin ωx (ω>0)的图像与直线y +2=0相邻的两个公共点之间的距离为2π3,则ω的值为( ) A .3 B.32 C.23D.13解析 由题可知T =23π,又ω>0,T =2πω,∴ω=3.答案 A2.一弹簧振子做简谐振动,离开平衡位置的位移s 与时间t 的函数关系式为s =3cos ⎝ ⎛⎭⎪⎫g a t +π3,t ∈[0,+∞),则弹簧振子振动的周期为( ) A. 2πagB. 2π a gC.2πagD. 2πg a解析 T =2πg a=2πa g.答案 B3.某人的血压满足函数关系式f (t )=24sin160πt +110,其中f (t )为血压,t 为时间,则此人每分钟心跳的次数为( )A .60B .70C .80D .90解析 ∵T =2π160π=180,∴f =1T=80.答案 C4.如图,设点A 是单位圆上的一定点,动点P 从点A 出发在圆上按逆时针方向旋转一周,点P 所旋转过的弧AP 的长为l ,弦AP 的长为d ,则函数d =f (l )的图像大致是图中的( )解析 令AP ︵所对圆心角为θ,由|OA |=1,则l =θ,sin θ2=d2,∴d =2sin θ2=2sin l 2,即d =f (l )=2sin l2(0≤l ≤2π),它的图像为C.答案 C5.动点A (x ,y )在以坐标原点为圆心,以1为半径的圆上沿逆时针方向匀速旋转,12秒旋转一周,已知时间t =0时,A ⎝ ⎛⎭⎪⎫12,32,则当0≤t ≤12时,动点A 的纵坐标y 关于t (时间:s)的函数的单调增区间为( )A. [0,1]B. [1,7]C. [7,12]D. [0,1]和[7,12]解析 动点A 的纵坐标y 关于时间t 的函数关系式为y =sin ⎝ ⎛⎭⎪⎫t12×2π+π3=sin ⎝ ⎛⎭⎪⎫π6t +π3由2k π-π2≤π6t +π3≤2k π+π2(k ∈Z ),又0≤t ≤12,可知t ∈[0,1]和[7,12].答案 D6.设函数y =f (t )是某港口水的深度y (米)关于时间t (时)的函数,其中0≤t ≤24.下表所示的是该港口某一天从0时至24时记录的时间t 与水深y 的关系:下面的函数中,最能近似地表示表中数据间对应关系的函数是( )A .y =12+3sin π6t ,t ∈[0,24]B .y =12+3sin ⎝⎛⎭⎪⎫π6t +π,t ∈[0,24]C .y =12+3sin π12t ,t ∈[0,24]D .y =12+3sin ⎝⎛⎭⎪⎫π12t +π2,t ∈[0,24]解析 易知k =12,A =3,由周期T =12知,ω=π6,由t =3时,y ≈15,得φ=0,故选A.答案 A7.一根长为l cm 的线,一端固定,另一端悬挂一个小球,小球摆动时离开平衡位置的位移s (cm)与时间t (s)的函数关系式是s =3cos ⎝ ⎛⎭⎪⎫g l t +π3,其中g 是重力加速度,当小球摆动的周期是1 s 时,线长l 等于( )A. gπ B. g2π C. g π2 D. g4π2 解 1=2πg l,∴l =g4π2.答案 D 二、填空题8.某城市一年中12个月的平均气温与月份的关系可近似地用三角函数y =a +A cos ⎣⎢⎡⎦⎥⎤π6x -6 (x =1,2,3,…,12)来表示,已知6月份的月平均气温最高,为28℃,12月份的月平均气温最低,为18℃,则10月份的平均气温值为________℃.解析 由题意得⎩⎪⎨⎪⎧a +A cos0=28,a +A cos ⎣⎢⎡⎦⎥⎤π6 12-6 =18,得⎩⎪⎨⎪⎧a =23,A =5,∴y =23+5cos ⎣⎢⎡⎦⎥⎤π6 x -6 ,当x =10时,y =23+5cos ⎝ ⎛⎭⎪⎫π6×4=23-52=20.5.答案 20.59.某时钟的秒针端点A 到中心点O 的距离为5 cm ,秒针均匀地绕点O 旋转,当时间t =0时,点A 与钟面上标12的点B 重合,将A ,B 两点的距离d (cm)表示成t (s)的函数,则d =__________,其中t ∈[0,60].解析 如图所示:经历t 秒钟,秒针转过的角度为∠AOB =πt30,取AB 的中点C ,则∠AOC =πt 60, d =|AB |=2|OA |sin ∠AOC =10sinπt 60.答案 10sin πt6010.某种商品一年内每件出厂价在7千元的基础上,按月呈f (x )=A sin(ωx +φ)+b (A >0,ω>0,|φ|<π2)的模型波动(x 为月份),已知3月份达到最高价9千元,7月份价格最低为5千元,根据以上条件可确定f (x )的解析式为________.解析 3月份最高,7月份最低,所以T =8,则ω=π4,A =2,b =7.令x =3,得9=2sin ⎝⎛⎭⎪⎫π4×3+φ+7⇒sin ⎝ ⎛⎭⎪⎫3π4+φ=1.又∵|φ|<π2,∴φ=-π4,∴f (x )=2sin ⎝ ⎛⎭⎪⎫π4x -π4+7.答案 f (x )=2sin ⎝ ⎛⎭⎪⎫π4x -π4+7三、解答题11.已知某游乐园内摩天轮的中心O 点距地面的高度为50 m ,摩天轮做匀速运动,摩天轮上的一点P 自最低点A 点起,经过t min 后,点P 的高度h =40sin ⎝ ⎛⎭⎪⎫π6t -π2+50(单位:m).那么在摩天轮转动一圈的过程中,点P 的高度在距地面70 m 以上的时间将持续多少分钟?解 依题意,得40sin ⎝ ⎛⎭⎪⎫π6t -π2+50≥70,即sin ⎝⎛⎭⎪⎫π6t -π2≥12,所以在一个周期内持续的时间为56π≥π6t -π2≥π6,解得4≤t ≤8,即持续时间为4分钟.12.在图中,点O 为做简谐运动的物体的平衡位置,取向右的方向为物体位移的正方向,若已知振幅为3 cm ,周期为3 s ,且物体向右运动到距平衡位置最远处时开始计时.(1)求物体对平衡位置的位移x (cm)和时间t (s)之间的函数关系式; (2)求该物体在t =5 s 时的位置.解 (1)设x 和t 之间的函数关系为x =3sin(ωt +φ)(ω>0,0≤φ<2π). 则由T =2πω=3,可得ω=2π3.当t =0时,有x =3sin φ=3, 即sin φ=1.又0≤φ<2π,故可得φ=π2.所以,所求函数关系为x =3sin ⎝ ⎛⎭⎪⎫2π3t +π2,即为x =3cos 2π3t .(2)令t =5,得x =3cos 10π3=-1.5,故该物体在t =5 s 时的位置是在O 点左侧且距O 点1.5 cm 处.13.在自然条件下,对某种细菌在一天内存活的时间进行了一年的统计,得到10次测量结果(时间近似到0.1小时),结果如下表所示:(1)以日期在365天中的位置序号x 为横坐标,一天内存活时间y 为纵坐标,作出这些数据的散点图;(2)试选用一个形如y =A sin(ωx +φ)+t 的函数来近似描述一年中该细菌一天内存活的时间y 与日期位置序号x 之间的函数关系;(3)用(2)中的结果估计该种细菌一年中有多少天存活时间大于15.9小时? 解 (1)散点图如下图所示:(2)由散点图知细菌存活时间与日期位置序号之间的函数关系式满足y =A sin(ωx +φ)+t ,由图形可认为函数的最大值为19.4,最小值为5.4,所以19.4-5.4=14,故A =7,由19.4+5.4=24.8,故t =12.4,又因为T =365,所以ω=2π365.当x =172时,2πx 365+φ=π2,所以φ=-323π730.故y =7sin ⎝⎛⎭⎪⎫2π365x -323π730+12.4(1≤x ≤365,x ∈N +).(3)由y >15.9,得sin ⎝ ⎛⎭⎪⎫2π365x -323730π>12,所以π6<2π365x -323730π<5π6,解得36512+3234<x <365×512+3234,112≤x ≤232.即这种细菌一年中大约有121天的存活时间大于15.9小时.。
【名师一号】2014-2015学年高中数学 第一章 三角函数双基限时练1(含解析)北师大版必修4
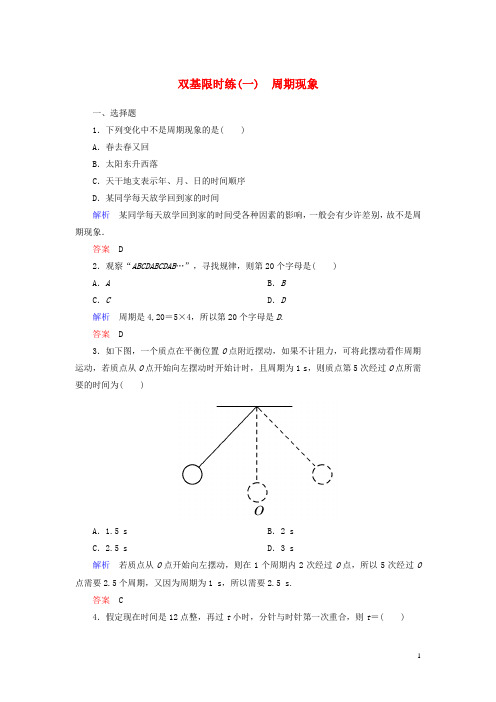
双基限时练(一) 周期现象一、选择题1.下列变化中不是周期现象的是( )A.春去春又回B.太阳东升西落C.天干地支表示年、月、日的时间顺序D.某同学每天放学回到家的时间解析某同学每天放学回到家的时间受各种因素的影响,一般会有少许差别,故不是周期现象.答案 D2.观察“ABCDABCDAB…”,寻找规律,则第20个字母是( )A.A B.BC.C D.D解析周期是4,20=5×4,所以第20个字母是D.答案 D3.如下图,一个质点在平衡位置O点附近摆动,如果不计阻力,可将此摆动看作周期运动,若质点从O点开始向左摆动时开始计时,且周期为1 s,则质点第5次经过O点所需要的时间为( )A.1.5 s B.2 sC.2.5 s D.3 s解析若质点从O点开始向左摆动,则在1个周期内2次经过O点,所以5次经过O 点需要2.5个周期,又因为周期为1 s,所以需要2.5 s.答案 C4.假定现在时间是12点整,再过t小时,分针与时针第一次重合,则t=( )A.1211B.1312C.2524D.2724解析 时针1小时转过30°,t 小时转过30t °;分针每分钟转过6°,t 小时转过(60t ×6)°,所以30t =60t ×6-360,解得t =1211.答案 A5.某市绿化委员会为了庆祝国庆节,要在道路的两侧摆放花卉,其中一侧需摆放红、黄、紫、白四种颜色的花,并且按红、黄、紫、白、红、黄、紫、白……的顺序摆放,那么第2014盆花的颜色是( )A .红B .黄C .紫D .白解析 因为按红、黄、紫、白、红、黄、紫、白……的顺序摆放,所以以4为一个周期,而2014÷4=503……2,为503个周期余2盆,所以第2014盆花为黄花.答案 B6.下图是汽油机的汽缸结构示意图,活塞在燃料的推动下往复运动的过程中,通过连杆带动曲轴做圆周运动.如果活塞每分钟往复运动2400次,则曲轴的运动周期是( )A .1分钟B .40秒C .0.05秒D .0.025秒解析 活塞往复一次,曲轴转动一圈,则曲轴的运动周期为60秒/2 400=0.025秒. 答案 D7.2011年是兔年,那么1949年是( ) A .牛年B .虎年C.兔年D.龙年解析∵1949+60+2=2011,∴1949年为牛年.答案 A二、填空题8.“春雨惊春清谷天,夏满芒夏暑相连,秋处露秋寒霜降,冬雪雪冬小大寒”,24节气________周期现象(填“是”或“不是”).答案是9.下列函数图像中具有周期性的序号是________.解析抓住周期现象的特点:重复性.对于(3),图像不重复出现,故不合题意.答案(1)(2)(4)10.水车上装有16个盛水槽,每个盛水槽最多盛水10升,假设水车5分钟转一圈,计算1小时内最多盛水________升.解析水车盛水是一个周期现象,由题意知,周期为5分钟,每一周期最多盛水10升×16=160升,1小时内有12个周期,因此在1小时内有12个周期,因此在1小时内最多盛水160升×12=1920升.答案1920三、解答题11.自行车的前轮胎上有一个标记P,则在自行车前进过程中,P点着地是否具有周期性?解当自行车匀速行驶时,就有周期性;若不是匀速行驶,就没有周期性.12.我们的心跳都是有节奏、有规律的,心脏跳动时,血压在增加或减少.下表是某人在1分钟内血压P(mmHg)与时间t(s)的对应关系表,通过表中数据来研究血压变化的规律.点图;(2)血压的变化是周期性的吗?解(1)作出血压P(mmHg)与时间t(s)的散点图.如下图:(2)由散点图可以看出,每经过15 s,血压就重复出现相同的数值,因此血压是周期性变化的.13.古希腊著名的哲学家、数学家、天文学家毕达哥拉斯有一次处罚学生,要他来回数戴安娜神庙的七根柱子(这七根柱子分别标有A,B,C,…,G),一直到指出第1999个数的柱子的标号是哪一个才能停止.你能否帮助他尽快结束这个处罚?A B C D E F G1 2 3 4 5 6 713 12 11 10 9 814 15 16 17 18 1925 24 23 22 21 20… … … … … …… … … … … …解“2,3,4…1997,1998,1999”按“B,C,D,E,F,G,F,E,D,C,B,A”12个数字循环出现,周期是12.解法一:先去掉第一行的7个数字,由(1999-7)÷12=166知:刚好是166个周期,所以数到1999的那根柱子的标号是G.解法二:先把1去掉,(1999-1)÷12=166……6,第1999个数的柱子的标号与第167个周期的第6个数的标号相同,是G.。
【名师一号】2014-2015学年新课标A版高中数学必修1双基限时练20

双基限时练(二十)1.若函数f (x )=x 3(x ∈R ),则函数y =f (-x )在其定义域上( ) A .单调递减的偶函数 B .单调递减的奇函数 C .单调递增的偶函数 D .单调递增的奇函数解析 ∵f (x )=x 3为奇函数. ∴y =f (-x )=-f (x )=-x 3.∴y =f (-x )在其定义域上单调递减且为奇函数,故选B. 答案 B2.设α∈⎩⎨⎧⎭⎬⎫-2,-1,-12,13,12,1,2,3,则使f (x )=x α为奇函数,且在(0,+∞)上单调递减的α的值的个数是( )A .1B .2C .3D .4解析 仅有α=-1时,f (x )=x -1满足题意,因此选A. 答案 A3.已知幂函数y =x m 在第一象限内的图象,如图所示.已知m 取2,-2,12,-12四个值,则相应于曲线C 1,C 2,C 3,C 4的m 依次是( )A .-2,-12,12,2 B .2,12,-12,-2 C .-12,-2,2,12D .2,12,-2,-12解析 由图象知,相应于曲线C 1,C 2,C 3,C 4的幂依次从大到小排列,∴选B.答案 B4.函数y =x 53的图象大致是( )解析 由于53>1,故可排除选项A ,D.根据幂函数的性质可知,当a >1时,幂函数的图象在第一象限内下凸,故排除选项C ,只有选项B 正确.答案 B5.函数y =log a (2x -3)+22的图象恒过定点P ,P 在幂函数f (x )的图象上,则f (9)=( )A.13B. 3 C .3D .9解析 由log a 1=0,对任意a >0且a ≠1都成立知,函数y =log a (2x-3)+22的图象恒过定点⎝⎛⎭⎪⎫2,22,设f (x )=x α,则22=2α,故α=-12,所以f (x )=x -12,所以f (9)=9-12=3-1=13.答案 A6.设a =⎝ ⎛⎭⎪⎫1234,b =⎝ ⎛⎭⎪⎫1534,c =⎝ ⎛⎭⎪⎫1212,则( )A .a <b <cB .c <a <bC .b <c <aD .b <a <c解析 构造幂函数y =x 34(x ∈R ),则该函数在定义域内单调递增,知a >b ;构造指数函数y =⎝ ⎛⎭⎪⎫12x,由该函数在定义域内单调递减,所以a <c ,故c >a >b .答案 D7.函数y =(m -1)xm 2-m为幂函数,则该函数为________(填序号).①奇函数;②偶函数;③增函数;④减函数. 解析 由y =(m -1)xm 2-m为幂函数,得m -1=1,即m =2,则该函数为y =x 2,故该函数为偶函数,在(-∞,0)上是减函数,在(0,+∞)上是增函数.答案 ②8.给出以下列结论:①当α=0时,函数y =x α的图象是一条直线;②幂函数的图象都经过(0,0),(1,1)两点;③若幂函数y =a α的图象关于原点对称,则y =x α在定义域内y 随x 的增大而增大;④幂函数的图象不可能在第四象限,但可能在第二象限.则正确结论的序号为________.解析 当α=0时,函数y =x α的定义域为{x |x ≠0,x ∈R },故①不正确;当α<0时,函数y =x α的图象不过(0,0)点,故②不正确;幂函数y =x -1的图象关于原点对称,但其在定义域内不是增函数,故③不正确.④正确.答案 ④9.已知n ∈{-2,-1,0,1,2,3},若⎝ ⎛⎭⎪⎫-12n >⎝ ⎛⎭⎪⎫-13n,则n =________.解析 ∵-12<-13,且⎝ ⎛⎭⎪⎫-12n >⎝ ⎛⎭⎪⎫-13n ,∴y =x n 在(-∞,0)上为减函数. 又n ∈{-2,-1,0,1,2,3}, ∴n =-1,或n =2. 答案 -1或2已知函数f (x )=(m 2-m -1)x -5m -3,m 为何值时,f (x ) (1)是幂函数; (2)是正比例函数; (3)是反比例函数; (4)是二次函数. 解 (1)∵f (x )是幂函数,故m 2-m -1=1,即m 2-m -2=0, 解得m =2或m =-1. (2)若f (x )是正比例函数, 则-5m -3=1,解得m =-45. 此时m 2-m -1≠0,故m =-45.(3)若f (x )是反比例函数,则-5m -3=-1,则m =-25,此时m 2-m -1≠0,故m =-25. (4)若f (x )是二次函数,则-5m -3=2, 即m =-1,此时m 2-m -1≠0,故m =-1.11.点(2,2)与点⎝ ⎛⎭⎪⎫-2,-12分别在幂函数f (x ),g (x )的图象上,问当x 为何值时,有:①f (x )>g (x );②f (x )=g (x );③f (x )<g (x ).解 设f (x )=x α,g (x )=x β. ∵(2)α=2,(-2)β=-12, ∴α=2,β=-1. ∴f (x )=x 2,g (x )=x -1.分别作出它们的图象,如图所示.由图象知,当x ∈(-∞,0)∪(1,+∞)时,f (x )>g (x ); 当x =1时,f (x )=g (x ); 当x ∈(0,1)时,f (x )<g (x ).12.已知幂函数y =x 3-p (p ∈N *)的图象关于y 轴对称,且在(0,+∞)上为增函数,求满足条件(a +1) p 2 <(3-2a ) p 2的实数a 的取值范围.解 ∵幂函数y =x 3-p (p ∈N *)的图象关于y 轴对称,∴函数y =x 3-p是偶函数.又y =x 3-p 在(0,+∞)上为增函数, ∴3-p 是偶数且3-p >0, ∵p ∈N *,∴p =1,∴不等式(a +1) p 2 <(3-2a ) p2化为:(a +1) 12<(3-2a ) 12.∵函数y =x 是[0,+∞)上的增函数, ∴⎩⎪⎨⎪⎧a +1<3-2a ,a +1≥0,3-2a ≥0⇒⎩⎪⎨⎪⎧a <23,a ≥-1,a ≤32⇒-1≤a <23,故实数a 的取值范围为⎣⎢⎡⎭⎪⎫-1,23.。
高中数学 第一章 立体几何初步阶段检测卷(含解析)新人

【名师一号】2014-2015学年高中数学 第一章 立体几何初步阶段检测卷(含解析)新人教B 版必修2一、选择题(本大题共10小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求)1.在长方体ABCD -A 1B 1C 1D 1中,与面ABCD 的对角线AC 异面的棱有( ) A .4条 B .6条 C .8条 D .10条解析 与AC 相交的直线有AB 、AD 、AA 1、CB 、CD 、CC 1,其他6条均与AC 异面. 答案 B2.两个球的体积之和为12π,且这两个球的大圆周长之和为6π,那么这两个球的半径之差为( )A.12B .1C .2D .3 解析 设两个球的半径分别为R 与r (R >r ) 则⎩⎪⎨⎪⎧43πR 3+43πr 3=12π,2πR +2πr =6π,∴⎩⎪⎨⎪⎧R 3+r 3=9,R +r =3,∴R -r =1. 答案 B 3.如图,将装有水的长方体水槽固定底面一边后倾斜一个小角度,则倾斜后水槽中的水形成的几何体是( )A .棱柱B .棱台C .棱柱与棱锥的组合体D .不能确定答案 A4.已知a、b、c、d是空间四条直线,如果a⊥c,b⊥c,a⊥d,b⊥d,那么( ) A.a∥b,c∥dB.a、b、c、d中至少有一对直线互相平行C.a、b、c、d中至多有一对直线互相平行D.a、b、c、d中任何两条直线都不平行解析当a与b相交或a与b异面时,c∥d;当a∥b时,c∥d或c与d异面.答案 B5.一个平行于圆锥底面的平面将圆锥的高分成相等的两段,那么圆锥被分成的两部分的侧面积的比为( )A.1 1 B.1 2 C.1 3 D.1 4解析设圆锥的母线长为l,底面半径为r,由于截面过圆锥高的中点,截得小圆锥的母线长为l2,底面半径为r2,∴圆锥被分成的两部分的侧面积之比为π×r2×l2π×r×l-π×r2×l2=13.答案 C6.若一个圆台的主视图如图所示,则其侧面积等于( )A.6 B.6π C.35π D.65π解析圆台的侧面积S=π(r1+r2)l,其中r1、r2是上、下底面半径,l是母线长,∴该圆台的侧面积为35π.答案 C7.如图所示,则这个几何体的体积等于( )A .4B .6C .8D .12 解析由三视图得几何体为四棱锥,如图记作S -ABCD ,其中SA ⊥面ABCD ,SA =2,AB =2,AD =2,CD =4,且ABCD 为直角梯形.∠DAB =90°,∴V =13SA ×12(AB +CD )×AD =13×2×12×(2+4)×2=4,故选A.答案 A8.如图 ,ABCD -A 1B 1C 1D 1为正方体,下面结论错误的是( ) A .BD ∥平面CB 1D 1 B .AC 1⊥BD C .AC 1⊥平面CB 1D 1D .异面直线AD 与CB 1所成的角为60°解析 由于BD ∥B 1D 1,易知BD ∥平面CB 1D 1;连接AC ,易证BD ⊥面ACC 1,所以AC 1⊥BD ;同理可证AC 1⊥B 1C ,因BD ∥B 1D 1,所以AC 1⊥B 1D 1,所以AC 1⊥平面CB 1D 1;对于选项D ,∵BC ∥AD ,∴∠B 1CB 即为AD 与CB 1所成的角,此角为45°,故D 错.答案 D 9.如图所示,梯形A 1B 1C 1D 1是平面图形ABCD 的直观图(斜二测),若A 1D 1∥y ′轴,A 1B 1∥C 1D 1,A 1B 1=23C 1D 1=2,A 1D 1=1,则四边形ABCD 的面积是( )A .10B .5C .5 2D .10 2 解析 平面图形还原如图所示.CD =C 1D 1=3,AD =2A 1D 1=2,AB =A 1B 1=2,∠ADC =90°.∴S ABCD =12×(2+3)×2=5.答案 B 10.用若干个体积为1的正方体搭成一个几何体,其主视图、左视图都是如图所示的图形,则这个几何体的最大体积与最小体积的差是( )A .3B .4C .5D .6解析 如图①所示,这个几何体体积最大时共有11个小正方体构成,如图②所示,这个几何体最小时有5个小正方体构成,因此,这个几何体的最大体积与最小体积的差是6.答案 D二、填空题(本大题共4小题,每小题5分)11.设m ,n 是不同的直线,α、β、γ是不同的平面,有以下四个命题 ①⎭⎪⎬⎪⎫α∥βα∥γ⇒β∥γ;②⎭⎪⎬⎪⎫α⊥βm ∥α⇒m ⊥β;③⎭⎪⎬⎪⎫m ⊥αm ∥β⇒α⊥β;④⎭⎪⎬⎪⎫m ∥n n ⊂α⇒m ∥α其中,真命题是________.解析 平行于同一个平面的两个平面平行,①是真命题;若一个平面平行于另一个平面的垂线,则两个平面垂直,③是真命题.答案 ①③12.在一个半径为13 cm 的球内有一个截面,此截面面积是25π cm 2,则球心到这个截面的距离为________.答案 12 cm 13.如图,在直三棱柱ABC -A 1B 1C 1中,AB =BC =2,BB 1=2,∠ABC =90°,E 、F 分别为AA 1、C 1B 1的中点,沿棱柱的表面从E 到F 两点的最短路径的长度是________.解析 将三棱柱侧面、底面展开有三种情形,如下图.在(1)中,EF =A 1E 2+A 1F 2=12+⎝ ⎛⎭⎪⎫3222=222;在(2)中,EF =EG 2+FG 2=22+⎝ ⎛⎭⎪⎫1+222=14+422; 在(3)中,EF =EG 2+FG 2=⎝ ⎛⎭⎪⎫322+⎝ ⎛⎭⎪⎫322=32 2.比较知(3)最小. 答案 322 14.将一副斜边长相等的直角三角板拼接成如图所示的空间图形,其中AD =BD =2,∠BAC =30°,若它们的斜边AB 重合,让三角板ABD 以AB 为轴转动,则下列说法正确的是________.①当平面ABD ⊥平面ABC 时,C 、D 两点间的距离为2;②在三角板ABD 转动过程中,总有AB ⊥CD ;③在三角板ABD 转动过程中,三棱锥D -ABC 的体积最大可达到36. 解析 取AB 中点O ,当三角板ABD 转动的过程中,AB 不垂直平面COD ,故AB 不垂直CD ,故②错,①③正确.答案 ①③三、解答题(本大题共4小题,共50分,解答应写出文字说明,证明过程或演算步骤) 15.(12分)如图所示的几何体中,四边形ABCD 是正方形,MA ⊥平面ABCD ,PD ∥MA ,E 、F 、G 分别为MB 、PC 、PB 的中点,且AD =PD =2MA .(1)求证:平面EFG∥平面ADPM;(2)求三棱锥P-MAB与四棱锥P-ABCD的体积之比.解析(1)证明:∵F、G为PC、PB中点,∴FG∥BC,又BC∥AD,∴FG∥AD,∵E、G为BM、PB中点,∴EG∥PM,又EG∩FG=G,∴平面EFG∥平面ADPM.(2)不妨设AB=2a,V P-MAB=23a3,V P-ABCD=83a3,所以V P-MABV P-ABCD=14.16.(12分)如图,已知平面α⊥平面β,α∩β=PQ,A∈PQ,B∈α,C∈β,CA=CB,∠BAP=45°.证明:BC⊥PQ.证明如图,过C做CO⊥PQ交PQ于O,连接OB.∵α⊥β,∴CO ⊥α. ∵BO ⊂α,∴CO ⊥BO ; 在Rt △COA 与Rt △COB 中,CA =CB ,CO =CO ,∴Rt △COA ≌Rt △COB .∴OA =OB .又∵∠BAP =45°,∴∠BOA =90°,即OB ⊥PQ . ∵PQ ⊥OC ,PQ ⊥OB ,OC ∩OB =O , ∴PQ ⊥面OBC .∵BC ⊂面OBC ,∴PQ ⊥BC . 17.(12分)某甜品店制作一种蛋筒冰淇淋,其上半部分呈半球形、下半部分呈圆锥形(如图).现把半径为10 cm 的圆形蛋皮等分成5个扇形,用一个扇形蛋皮围成圆锥的侧面(蛋皮厚度忽略不计),求该蛋筒冰淇淋的表面积和体积(精确到0.01).解 设圆锥底面半径为r ,高为h ,∵2πr =25π·10,∴r =2,h =102-22=46,∴该蛋筒冰淇淋的表面积S =π×1025+2π·22=28π≈87.96 cm 2.体积V =13×π·22×46+23π×23=163(6+1)π≈57.80 cm 3.故该蛋筒冰淇淋的表面积约为87.96 cm 2,体积约为 57.80 cm 3. 18.(14分)如图,在四棱锥S -ABCD 中,SA ⊥平面ABCD ,底面ABCD 为直角梯形,AD ∥BC ,∠BAD =90°,且BC =2AD ,AB =4,SA =3.(1)求证:平面SBC ⊥平面SAB ;(2)若E 、F 分别为线段BC 、SB 上的一点(端点除外),满足SF FB =CEEB=λ.①求证:不论λ为何值,都有SC ∥平面AEF ;②是否存在λ,使得△AEF 为直角三角形,若存在,求出所有符合条件的λ值;若不存在,说明理由.解 (1)证明:∵SA ⊥底面ABCD ,∴SA ⊥AD . ∵∠BAD =90°,∴AD ⊥AB . ∵SA ∩AB =A ,SA 、AB ⊂平面SAB ,∴AD ⊥平面SAB ,∵AD ∥BC ,∴BC ⊥平面SAB . ∵BC ⊂平面SBC ,∴平面SBC ⊥平面SAB . (2)①证明:∵在△SBC 中,SF FB =CE EB, ∴EF ∥SC .∵EF ⊂平面AEF ,SC ⊄平面AEF ,∴SC ∥平面AEF .11 ②当AF ⊥SB 时,由(1)知平面SAB ⊥平面SBC ,且平面SAB ∩平面SBC =SB ,∴AF ⊥平面SBC .∵EF ⊂平面SBC ,∴AF ⊥EF ,∴此时△AEF 为直角三角形.在Rt △SAB 中,AB =4,SA =3,∴AF =125.∴SF =95,FB =165,∴λ=SF FB =916.∴存在λ=916时,△AEF 为直角三角形.。
高中数学 第一章 立体几何初步单元同步测试(含解析)北师大版必修2

【名师一号】2014-2015学年高中数学 第一章 立体几何初步单元同步测试(含解析)北师大版必修2时间120分钟 满分150分一、选择题(本大题共10小题,每小题5分,共50分.在下列四个选项中,只有一项是符合题意的)1.下列说法正确的是( ) A .三点确定一个平面 B .四边形一定是平面图形 C .梯形一定是平面图形D .平面α与平面β有不同在一条直线上的三个交点解析 梯形有两条边平行,过两条平行直线有且只有一个平面. 答案 C2.室内有直尺,无论怎样放置,在地面上总有这样的直线,它与直尺所在的直线( ) A .异面 B .相交 C .平行 D .垂直答案 D3.若直线a ⊥b ,且直线a ∥平面α,则直线b 与平面α的位置关系是( ) A .b α B .b ∥αC .b α或b ∥αD .b 与α相交或b α或b ∥α答案 D4.若三球的半径之比是1:2:3,则半径最大的球的体积是其余两球的体积和的( ) A .4倍 B .3倍 C .2倍D .1倍解析 设三个球的半径依次为a,2a,3a ,V 最大=43π(3a )3=36πa 3,V 1+V 2=43πa 3+43π(2a )3=363πa 3=12πa 3,V 最大V 1+V 2=3.答案 B5.一个长方体去掉一个小长方体,所得几何体的主视图与左视图分别如图所示,则该几何体的俯视图为( )答案 C6.用a,b,c表示三条不同的直线,γ表示平面,给出下列命题:①若a∥b,b∥c,则a∥c;②若a⊥b,b⊥c,则a⊥c;③若a∥γ,b∥γ,则a∥b;④若a⊥γ,b⊥γ,则a∥b.其中真命题的序号是( )A.①②B.②③C.①④D.③④解析根据公理4,知①正确;根据垂直于同一平面的两直线平行可知④正确.答案 C7.在空间四边形ABCD中,若AD⊥BC,BD⊥AD,则有( )A.面ABC⊥面DBC B.面ABC⊥面ADCC.面ABC⊥面ADB D.面ADC⊥面DBC解析如图,在四面体ABCD中,∵AD⊥BC,AD⊥BD,BD∩BC=B,∴AD⊥面BCD.又AD面ADC,∴面ADC⊥面BCD.答案 D8.在直三棱柱ABC-A1B1C1中,AC=BC,D为AB的中点,下列说法中正确的个数有( )①CD⊥面ABB1A1;②BC1∥面A1DC;③面ADC⊥面ABB1A1.A.0个B.1个C.2个D.3个解析∵ABC-A1B1C1为直三棱柱,AC=BC,D为AB的中点,∴CD⊥AB,由两平面垂直的性质定理,可知CD⊥面ABB1A1,又CD面ADC,故面ADC⊥面ABB1A,故①、③正确,对于②连接AC 1,BC 1,设A 1C ∩AC 1=O ,则O 为AC 1的中点,又D 为AB 的中点,∴OD ∥BC 1. 又OD 面A 1DC ,BC 1面A 1DC ,∴BC 1∥面A 1DC ,故②正确. 答案 D9.一个几何体按比例绘制的三视图如图所示(单位:m),则该几何体的体积为( )A.73 m 3B.92 m 3C.72m 3D.94m 3 解析 由三视图可知,原几何体如图所示,故V =3×13+12×13=3+12=72m 3.答案 C10.如图,平行四边形ABCD中,AB⊥BD,沿BD将△ABD折起到A′BD,使面A′BD⊥面BCD,连接A′C,则在四面体A′BCD的四个面中,互相垂直的平面有( )①面ABD⊥面BCD;②面A′CD⊥面ABD;③面A′BC⊥面BCD;④面ACD⊥面ABC.A.1个B.2个C.3个D.4个解析由于面ABD⊥面BCD,故①正确.又AB⊥BD则A′B⊥BD,则A′B⊥BD,∴A′B ⊥面BCD,故面A′BC⊥面BCD,又CD⊥BD,∴面A′CD⊥面ABD,故②③正确,④显然不正确.答案 C二、填空题(本大题共5小题,每小题5分,共25分.把答案填在题中横线上)11.某几何体的三视图如图所示,则该几何体的体积是________.解析由三视图知,该几何体是由圆柱中间除去正四棱柱得到的,所以体积是4π×4-2×2×4=16π-16.答案16π-1612.若正三棱台的上、下底面的边长分别为2和8,侧棱长为5,则这个棱台的高为________.解析 由题可知,上底面三角形的高为2sin60°=3,下底面三角形的高为8sin60°=43,故棱台的高h =52-⎣⎢⎡⎦⎥⎤43-3×232=13.答案1313.已知圆锥的表面积为a m 2,且它的侧面展开图是一个半圆,则这个圆锥的底面半径为________.解析 设圆锥的底面半径为r ,母线长为l ,则πl =2πr ,即l =2r ,S 圆锥表=πr 2+πrl =3πr 2=a ,则r =3πa3π. 答案3πa3πm 14.如图四棱锥S -ABCD 中,底面ABCD 为平行四边形,E 为SA 上的点,当E 满足条件:________时,SC ∥面EBD .解析当E为SA的中点时,设AC∩BD=O,连接EO,EB,ED,∵ABCD为平行四边形,∴O为AC的中点.∴EO∥SC,又SC面EBD,OE面EBD,∴SC∥面EBD.答案E为SA的中点15.如图所示,平面α⊥平面β,在α与β的交线l上,取线段AB=4,AC、BD分别在平面α和平面β内,AC⊥l,BD⊥l,AC=3,BD=12,则线段CD的长为________.解析 连接BC ,∵AC ⊥l ,∴∠CAB =90°,CB =AC 2+AB 2=32+42=5.又BD ⊥l ,α⊥β, ∴BD ⊥平面α. 又BC α,∴BD ⊥BC . ∴CD =BD 2+BC 2=122+52=13. 答案 13三、解答题(本大题共6小题,共75分.解答时应写出必要的文字说明,证明过程或演算步骤)16.(12分)已知圆台的上、下底面半径分别是2,5,且侧面积等于两底面面积之和,求该圆台的母线长.解 设圆台的母线长为l ,则圆台的上、下底面面积为S 上=π·22=4π,S 下=π·52=25π,∴圆台的两底面面积之和S =S 上+S 下=29π, 又圆台的侧面积S 侧=π(2+5)·l =7πl , 由7πl =29π,得l =297,即母线长为297.17.(12分)如图所示,已知E ,F ,G ,H 分别为空间四边形ABCD 的边AB ,BC ,CD ,DA 上的点,且EH ∥FG .求证:EH∥BD.证明∵EH∥FG,E H⃘面BDC,FG面BDC,∴EH∥面BDC,又EH面ABD,面ABD∩面BDC=BD,∴EH∥BD.18.(12分)如图,三棱柱ABC-A1B1C1中,CA=CB,AB=AA1,∠BAA1=60°.(1)证明:AB⊥A1C;(2)若AB=CB=2,A1C=6,求三棱柱ABC-A1B1C1的体积.解(1)取AB的中点O,连接OC,OA1,A1B.因为CA=CB,所以OC⊥AB.由于AB=AA1,∠BAA1=60°,故△AA1B为等边三角形,所以OA1⊥AB.因为OC∩OA1=O,所以AB⊥平面OA1C.又A1C平面OA1C,故AB⊥A1C.(2)由题设知△ABC与△AA1B都是边长为2的等边三角形,所以OC=OA1= 3.又A1C=6,则A1C2=OC2+OA21,故OA1⊥OC.因为OC∩AB=O,所以OA1⊥平面ABC,OA1为三棱柱ABC-A1B1C1的高.又△ABC的面积S△ABC=3,故三棱柱ABC-A1B1C1的体积V=S△ABC×OA1=3.19.(13分)如图,已知PA垂直于正方形ABCD所在平面,E,F分别是AB,PC的中点,∠PDA=45°.(1)求证:EF∥面PAD;(2)求证:面PCE⊥面PCD.证明 (1)设PD 中点为G ,连接FG ,AG ,∵F ,G 分别为PC ,PD 的中点,∴FG 綊12CD .又E 为AB 的中点, ∴AE 綊FG .即四边形EFGA 为平行四边形.∴EF ∥AG .又EF 面PAD ,AG 面PAD ,∴EF ∥面PAD .(2)PA ⊥面ABCD ,∴PA ⊥AD ,PA ⊥CD .又∵在Rt △PAD 中,∠PDA =45°,∴PA =AD ,∴AG ⊥PD .又CD ⊥AD ,CD ⊥PA ,且PA ∩AD =A ,∴CD ⊥面PAD ,CD ⊥AG ,又PD ∩CD =D ,∴AG ⊥面PCD .由(1)知EF ∥AG ,∴EF ⊥面PCD ,又EF 面PCE ,∴面PCE ⊥面PCD .20.(13分)如图①,△ABC 是等腰直角三角形,AC =BC =4,E ,F 分别为AC ,AB 的中点,将△AEF 沿EF 折起,使A ′在平面BCEF 上的射影O 恰为EC 的中点,得到图②.(1)求证:EF ⊥A ′C ;(2)求三棱锥F —A ′BC 的体积.解 (1)证法1:在△ABC 中,EF 是等腰直角△ABC 的中位线,在四棱锥A ′—BCEF 中,EF ⊥A ′E ,EF ⊥EC ,∴EF ⊥平面A ′EC ,又A ′C 平面A ′EC ,∴EF ⊥A ′C .证法2:同证法1 EF ⊥EC ,∴A ′O ⊥EF ,∴EF ⊥平面A ′EC .又A ′C 平面A ′EC ,∴EF ⊥A ′C .(2)在直角梯形EFBC 中,EC =2,BC =4,∴S △FBC =12BC ·EC =4. 又∵A ′O 垂直平分EC ,∴A ′O =A ′E 2-EO 2=3,∴三棱锥F —A ′BC 的体积V F —A ′BC =V A ′—FBC =13S △FBC ·A ′O =13×4×3=433. 21.(13分)如图所示,已知正方体ABCD —A 1B 1C 1D 1,O 是底面ABCD 对角线的交点.(1)求证:C1O∥平面AB1D1;(2)求证:A1C⊥平面AB1D1;(3)若AA1=2,求三棱锥A1—AB1D1的体积.解(1)证明:设B1D1的中点为O1,∵ABCD—A1B1C1D1为正方体,∴C1O1綊AO.故AOC1O1为平行四边形.∴AO1∥C1O,又AO1面AB1D1,C1O面AB1D1,∴C1O∥面AB1D1.(2)证明:∵B1D1⊥A1C1,B1D1⊥CC1,A1C1∩C1C=C1. ∴B1D1⊥面ACC1A1,A1C面ACC1A1.∴B1D1⊥A1C.同理可证A1C⊥AB1.又AB1∩B1D1=B1,∴A1C⊥面AB1D1.(3)VA1—AB1D1=VA—A1B1D1=13×12×2×2×2=43.。
【名师一号】2014-2015学年高中数学 第一章 数列双基限时练2(含解析)北师大版必修5

双基限时练(二)一、选择题1.若数列{a n }的通项公式a n =3n +2,则数列{a n }的图像是( ) A .一条直线 B .一条抛物线 C .一群孤立的点D .一个圆解析 ∵n ∈N +,∴数列{a n }的图像是一群孤立的点,且这些点都在直线y =3x +2上. 答案 C2.在数列{a n }中,a n =3-2n ,则数列{a n }是( ) A .递增数列 B .递减数列 C .常数列D .摆动数列解析 ∵a n +1-a n =3-2(n +1)-3+2n =-2<0,∴数列{a n }为递减数列. 答案 B3.已知数列{a n }为递减数列,且a n =(3-2a )n +1,则实数a 的取值范围是( ) A .a <32B .a >32C .a ≤32D .a ≥32解析 由{a n }为递减数列,知3-2a <0,即a >32.答案 B4.数列{3n 2-28n }中,各项中最小的项是( ) A .第4项 B .第5项 C .第6项 D .第7项解析 对称轴n =286=143=423,∴当n =5时,a n 取得最小值.答案 B5.数列{a n }的通项公式是a n =anbn +1,其中a 、b 都为正实数,则a n 与a n +1的大小关系是( )A .a n >a n +1B .a n <a n +1C .a n =a n +1D .与n 有关解析 a n +1-a n =a n +1b n +1 +1-anbn +1=abn 2+abn +an +a -abn 2-abn -an bn +1 [b n +1 +1]=abn +1 [b n +1 +1].∵a ,b ∈R +,n ∈N +,∴a n +1-a n >0. 答案 B6.已知数列{-2n 2+4an +3}中的数值最大的项为第6项,则实数a 的取值范围是( ) A.⎝ ⎛⎭⎪⎫112,6B.⎣⎢⎡⎭⎪⎫6,132C.⎣⎢⎡⎦⎥⎤112,132D .{6}解析 由题意得,对称轴a ∈[5.5,6.5]. 答案 C 二、填空题7.已知数列{a n }满足a 1=1,a n +1=a n1+a n,则a 5=________. 解析 由a 1=1,a n +1=a n1+a n,得a 2=12,a 3=121+12=13,a 4=1343=14,a 5=1454=15.答案 158.数列{a n }满足a 1=1,a n +1=a n +2,则a n =_______________. 解析 由a n +1=a n +2,a 1=1,知a 2=3,a 3=5,a 4=7,…,a n =2n -1. 答案 2n -1 9.设f (n )=1n +1+1n +2+ (12)(n ∈N +),则f (n +1)-f (n )=________. 解析 由f (n )=1n +1+1n +2+…+12n ,得f (n +1)=1n +1+1+1n +1+2+…+12n +12n +1+12 n +1, ∴f (n +1)-f (n )=12n +1+12n +2-1n +1=12n +1-12n +2. 答案12n +1-12n +2三、解答题10.已知a n =a ·⎝ ⎛⎭⎪⎫12n(a ≠0且为常数),试判断{a n }的单调性.解 ∵a n -a n -1=-a ·⎝ ⎛⎭⎪⎫12n(n ≥2,且n ∈N +),∴当a >0时,a n -a n -1<0.即a n <a n -1,数列{a n }为递减数列. 当a <0时,a n -a n -1>0,即a n >a n -1,数列{a n }是递增数列. 11.已知数列{a n }的通项公式为a n =n 2-5n +4. (1)数列中有多少项是负数?(2)n 为何值时,a n 有最小值?求出最小值. 解 (1)由a n =n 2-5n +4=(n -52)2-94当n =2时,a n =-2, 当n =3时,a 3=-2, 当n =1时,a 1=0, 同理,当n =4时,a 4=0, 由函数的单调性可知, 当n ≥5时,a n >0,∴数列中只有a 2,a 3这两项为负数. (2)由a n =n 2-5n +4=(n -52)2-94,知对称轴为n =52=2.5,又n ∈N +,∴当n =2,或n =3时,a n 有最小值,其最小值为22-5×2+4=-2.12.已知数列{a n }满足a n ≤a n +1,a n =n 2+λn ,n ∈N +,求实数λ的取值范围. 解 ∵a n ≤a n +1,∴n 2+λn -(n +1)2-λ(n +1)≤0,即λ≥-(2n +1),n ∈N +.∴λ≥-3.∴实数λ的取值范围是[-3,+∞).思 维 探 究13.已知数列{a n }的通项公式是a n =1n 2+5n +4.(1)你能判断该数列是递增的,还是递减的吗? (2)该数列中有负数项吗? 解 (1)对任意n ∈N +, ∵a n+1-a n =1n +1 2+5 n +1 +4-1n 2+5n +4=-2 n +3[ n +1 2+5 n +1 +4] n 2+5n +4<0,∴数列{a n}是递减数列.(2)令a n<0,即1n+5n+4<0,∴n2+5n+4<0得(n+4)(n+1)<0,∴-4<n<-1. 而n∈N+,故数列{a n}没有负数项.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
答案63 cm2
8.用一张4 cm×8 cm的矩形硬纸卷成圆柱的侧面,接头忽略不计,则轴截面面积是________.
解析若圆柱的高为8 cm,则2πr=4(cm),
2r=,轴截面面积S=8·=(cm2),
若圆柱的高为4 cm,则2πr=8(cm),
2r=,轴截面面积S=4·=(cm2),
解如图所示,旋转所得的几何体是一个圆柱挖去两个圆锥后剩余部分而成的组合体.
11.如果一个圆锥的侧面展开图是半圆,求这个圆锥的轴截面的顶角.
解设圆锥的底面半径为r,母线长为l,
由题意,可得πl=2πr,∴r=.
∴轴截面的顶角α满足
sin==,∴=30°.
∴α=60°,即圆锥轴截面的顶角为60°.
12.已知一个圆台的母线长是5 cm,上、下底面的面积分别是9πcm2和16πcm2,求:
(1)圆台的高;
(2)截得此圆台的圆锥的母线长.
解(1)设圆台的上、下底面半径为r、R,高为h,
则r=3,R=4,h===
2(cm);
(2)设圆锥母线长为l′,则=,即=,l′=20(cm).
解析由旋转的过程,可知圆柱的任意两条母线所在直线互相平行.
答案C
3.如图所示,观察下面四个几何体,其中判断正确的是()
A.①是圆台B.②是圆台
C.③是圆锥D.④是圆台
答案C
4.如图①是由下面哪个平面旋转得到的()
解析由旋转的知识,可知答案为C.
答案C
5.一个圆锥的母线长为20 cm,母线与轴的夹角为30°,则圆锥的高为()
A.10cmB.20cm
C.20 cmD.10 cm
解析由图可知,h=20cos30°=10(cm),答案为A.
答案A
6.有下列四个命题:
①圆柱是将矩形旋转一周所得的几何体;②以直角三角形的一边为旋转轴,旋转所得几何体是圆锥;③圆台的任意两条母线的延长线可能相交也可Βιβλιοθήκη 不相交;④圆锥的轴截面是等腰三角形.
双基限时练(一)
一、选择题
1.下面几何体的截面一定是圆面的是()
A.圆柱B.圆锥
C.球D.圆台
答案C
2.下列说法正确的是()
A.圆锥是直角三角形绕其一边旋转而成
B.在圆台上、下底面圆周上各取一点,则这两点的连线是圆台的母线
C.圆柱的任意两条母线所在直线互相平行
D.用一平面截圆锥,截面与底面之间的部分为圆台
故答案为cm2.
答案cm2
9.一直角梯形上底长为1,下底长为3,高为2,现绕着直角梯形的下底旋转一周,所围成的几何体的轴截面的面积为________.
解析其轴截面由两部分组成其中一个为矩形,一个为三角形,S=4×1+×4×2=8.
答案8
三、解答题
10.
如图所示,已知梯形ABCD中,AD∥BC,且AD<BC,当梯形ABCD绕AD所在直线旋转一周时,其他各边旋转围成一个几何体,试描述该几何体的结构特征.
其中错误命题的个数是()
A.1B.2
C.3D.4
解析①错,以矩形某一边为轴旋转才是圆柱,以对角线为轴旋转则不是圆柱;②错,以其直角边为轴旋转才是圆锥;③错,一定相交;④正确.
答案C
二、填空题
7.圆台的两底面半径分别为2 cm和5 cm,母线长为3cm,则它的轴截面面积为________.
解析圆台的高h==9(cm),
