2.1指数函数
2.1 指数函数的概念 课时一等奖创新教学设计

2.1 指数函数的概念课时一等奖创新教学设计第3课时指数函数概念课时教学设计(一)教学内容指数函数的概念.(二)教学目标通过具体实例,了解指数函数的实际意义,理解指数函数的概念,发展数学抽象素养.(三)教学重点与难点教学重点:指数函数的概念.教学难点:指数函数的概念.(四)教学过程设计引导语:对于幂( >0),我们已经把指数的范围拓展到了实数.上一章学习了函数的概念和基本性质,通过对幂函数的研究,进一步了解了研究一类函数的过程和方法.下面继续研究其他类型的基本初等函数.问题1:随着中国经济高速增长,人民生活水平不断提高,旅游成了越来越多家庭的重要生活方式.由于旅游人数不断增加,A,B两地景区自2001年起采取了不同的对应措施,A地提高了景区门票价格,而B地则取消了景区门票.表4.2-1给出了A,B两地景区2001年至2015年的游客人次以及逐年增加量.表4.2-1时间/年A地景区B地景区人次/万次年增加量/万次人次/万次年增加量/万次2001 600 2782002 609 9 309 312003 620 11 344 352004 631 11 383 392005 641 10 427 442006 650 9 475 482007 661 11 528 532008 671 10 588 602009 681 10 655 672010 691 10 729 742011 702 11 811 822012 711 9 903 922013 721 10 1005 1022014 732 11 1118 1132015 743 11 1244 126比较两地景区游客人次的变化情况,你发现了怎样的变化规律?师生活动:(1)追问①:能否作出A,B两地景区游客人次变化的图象,根据图象并结合年增长量,说明两地景区游客人次的变化情况?学生独立思考、讨论交流. 教师利用Excel作出A,B两地景区游客人次变化的图象,直观感受A,B两地景区游客增长的情况.(2)追问②:用“增加量”刻画B地景区人次的变化规律不直观. 能不能换一个量来刻画?教师指出,可以用“增长率”,即从2002年起,将B地景区每年的游客人次除以上一年的游客人次,看看能否发现什么规律?学生动手计算,教师利用Excel算出B地景区游客人次年增长率为常数.(3)追问③:能否求出两地景区游客人次随时间(经过的年数)变化的函数解析式,并根据解析式说明两地景区游客人次的变化情况.如果设经过x年后的游客人次为2001年的y倍,那么.设计意图:通过寻求A,B两地景区游客人次增加的规律,引出用函数刻画指数增长的问题,为抽象出指数函数作准备.问题2:当生物死亡后,其机体内原有的碳14含量会按确定的衰减比率(称为衰减率),大约每经过5730年衰减为原来的一半,这个时间称为“半衰期”.按照上述变化规律,生物体内碳14含量与死亡年数之间有怎样的关系?师生活动:追问①:生物死亡后体内碳14含量每年衰减的比例是多少?追问②:能否求出生物体内碳14含量随死亡年数变化的函数解析式?教师提出问题,并让学生类比问题1对提出的问题进行思考.通过对问题的分析,引导学生用函数刻画碳14衰减的规律.设计意图:通过描述碳14衰减的规律,引出用函数刻画指数衰减的问题,为抽象得到指数函数作准备.问题3:比较问题1,2中的两个实例:B地景区游客人次增长的函数解析式与碳14衰减的函数解析式有什么共同特征?师生活动:从解析式上来看,如果用字母代替底数1.11和,那么上述函数和就都可以表示为=的形式,其中指数是自变量,底数是一个大于0且不等于1的常数.从而引出指数函数的概念:一般地,函数=叫做指数函数,其中指数是自变量,定义域是R.设计意图:通过分析、比较两个实例,概括它们的共同本质特征,从而得到指数函数概念的本质属性,抽象出指数函数的概念,发展学生数学抽象的核心素养.例1:已知指数函数,且,求,,的值.师生活动:教师引导学生,要求出,,的值,应先求出的解析式,即先求出的值.而已知,可由此求出的值.设计意图:通过求函数解析式,并根据解析式求出不同的函数值,从指数函数的对应关系和变化规律的角度理解指数函数的概念.例2:(1)在问题1中,如果平均每位游客出游一次可给当地带来1000元门票之外的收入,A地景区的门票价格为150元,比较这15年间A,B两地旅游收入变化情况.(2)在问题2中,某生物死亡10000年后,它体内碳14的含量衰减为原来的百分之几?师生活动:(1)教师引导学生得出A、B两地旅游收入的函数,教师利用geogebra画出图象,得出交点坐标,进而得出两地收入的变化情况.(2)利用geogebra进行计算第(2)小问.(3)教师指出:在实际问题中,经常会遇到类似于例2(1)的指数增长模型:设原有量为N,每次的增长率为,经过x次增长,该量增长到y,则=,其中表示增长率;还可以表示为=,其中表示衰减率.形如的函数是刻画指数增长或指数衰减变化规律的函数模型.设计意图:在引入概念的两个实例基础上,利用指数函数概念进一步解决与两个实例有关的问题,从而巩固对概念的理解.问题6:回顾本节课的学习内容,并回答以下问题:(1)我们是怎样通过实例问题1,问题2得出指数函数的?(2)指数函数的定义是什么?设计意图:回顾本节课的主要知识和研究过程,巩固指数函数概念的理解.(五)目标检测设计1、课堂检测教科书第115页练习1,2,3设计意图:1 ,2题利用函数的三种表示形式,从不同角度推动学生对指数函数概念的理解,进一步明确概念,学会表示指数函数,体会指数增长或衰减;3题考查学生对指数函数概念的理解;三题均属于水平一题目.2. 课后作业教科书第118页习题4.2第1,2,4,7,8题设计意图:考查学生对指数函数概念的理解,1,2,4题属于水平一题目,7,8题属于水平二题目.(六)课后反思。
2019A新高中数学必修第一册:2.1.1 指数与指数幂的运算

1 3
);
x-
1 2
y
2 3
)(-4
x
1 4
y
2 3
);
(7)
(2
x
1 2
+
3
y-
1 6
)(2
x
1 2
-
3
y
- 16
);
(8)
4
x
1 4
(-3
x
1 4
y-
1 3
)
(-6
x
- 12
y-
2 3
).
解:
(1)
13 7
a 3a4a12
=
a
13+
3 4
+172
=
a
5 3
.
(2)
23
a3a4
5
a6
=
a
32+
43-
3. 分数指数幂
我们将下面根式变形:
10
a>0 时, 5 a10 = 5 ( a2 )5 = a2 = a 5 .
12
a>0 时, 4 a12 = 4 ( a3 )4 = a3 = a 4 .
m
规定: a n = n am (a 0, m, nN *. 且n1).
a-
m n
=
1
m
(a 0,
m,
解:
(1)
原式
=
x3
y2(-
27
1 x3
y31)
=
-
1 27 y
.
(2) 原式 = 4(- 32)a2-(-1)b-1-(-1)= -6a3.
(3)
原式
2.1指数函数的图象与性质

2.1指数函数的图象与性质一、【知识解读】1.指数幂的有关概念:(1)正整数指数幂)(*∈⋅⋅⋅⋅=N n a a a a a n n个;(2)零指数幂)0(10≠=a a ;(3)负整数指数幂()1/0,n n a a a n N -*=≠∈;(4)正分数指数幂)/0,,,1m n a a m n N n *=>∈>;(5)负分数指数幂)//1/0,,,1m n m n a a a m n N n -*==>∈>;(6)0的正分数指数幂等于0,0的负分数指数幂没有意义。
2.指数幂的运算性质(1)(0)rsr sa a a a +=>;(2) ()()(0)r s s r rs a a a a ==> ;(3)()(0,0)rr rab a b a b =>> 3.根式的内容(1)根式的定义:一般地,如果a x n =,那么x 叫做a 的n 次方根,其中()*∈>N n n ,1,n a 叫做根式,n 叫做根指数,a 叫被开方数。
(2)根式的性质: ①当n 是奇数,则a a nn =;当n 是偶数,则⎩⎨⎧<-≥==00a aa a a a n n ;②na =;③负数没有偶次方根;④零的任何次方根都是零。
4y =a x (a >0,且a ≠1)的图象与性质(1)指数函数:①定义:函数)1,0(≠>=a a a y x且称指数函数,1)函数的定义域为R ;2)函数的值域为),0(+∞;3)当10<<a 时为减函数,当1>a 时为增函数。
②函数图像:1)指数函数的图象都经过点(0,1),且图象都在第一、二象限;2)图象都以x 轴为渐近线(当10<<a 时,向右无限接近x 轴,当1>a 时,图象向左无限接近x 轴);3)对于相同的)1,0(≠>a a a 且,函数xx a y a y -==与的图象关于y 轴对称。
高一数学必修一第二章基本初等函数知识点总结
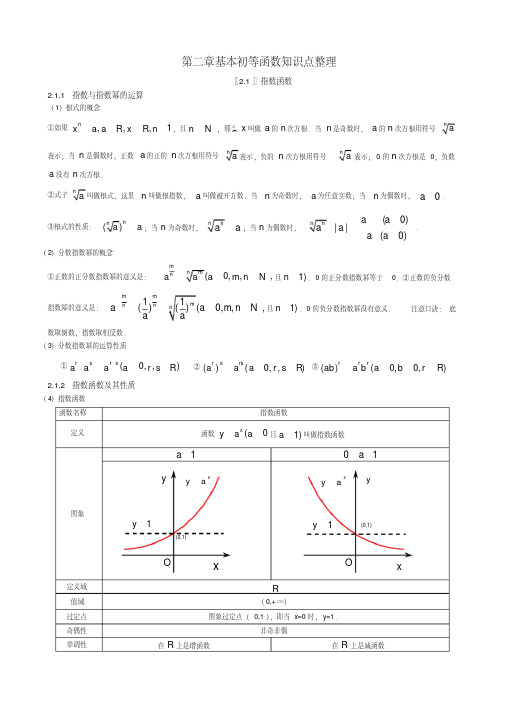
在 R 上是减函数
函数值的 变化情况
a 变化对
图象的影 响
y>1(x > 0), y=1(x=0), 0 < y<1(x < 0)
y> 1(x < 0), y=1(x=0), 0 < y< 1(x > 0)
在第一象限内, a 越大图象越高,越靠近 y 轴; 在第一象限内, a 越小图象越高,越靠近 y 轴; 在第二象限内, a 越大图象越低,越靠近 x 轴. 在第二象限内, a 越小图象越低,越靠近 x 轴.
y
f ( x) 中反解出 x
1
f ( y) ;
③将 x f 1( y ) 改写成 y f 1 ( x) ,并注明反函数的定义域.
( 8)反函数的性质
①原函数 y
f (x) 与反函数 y
1
f ( x) 的图象关于直线 y
x 对称.
②函数 y f ( x) 的定义域、值域分别是其反函数 y f 1 (x ) 的值域、定义域. ③若 P(a,b) 在原函数 y f (x ) 的图象上,则 P' (b, a) 在反函数 y f 1(x ) 的图象上.
③根式的性质: (n a )n a ;当 n 为奇数时, n an
a ;当 n 为偶数时, n an | a |
a (a 0)
.
a (a 0)
( 2)分数指数幂的概念
m
①正数的正分数指数幂的意义是: a n n a m (a 0, m, n N , 且 n 1) . 0 的正分数指数幂等于 0.②正数的负分数
设一元二次方程 ax 2 bx c 0( a 0) 的两实根为 x1, x2 ,且 x1 x2 .令 f ( x) ax 2 bx c ,从以下四个方
面来分析此类问题:①开口方向: a ②对称轴位置: x
2.1 指数函数

2.1 指数函数【2.1.1】指数与指数幂的运算(1)根式的概念①如果,,,1n x a a R x R n =∈∈>,且n N +∈,那么x 叫做a 的n 次方根.当n 是奇数时,a 的n 当n 是偶数时,正数a 的正的n 示,负的n 次方根用符号0的n 次方根是0;负数a 没有n 次方根.n 叫做根指数,a 叫做被开方数.当n 为奇数时,a 为任意实数;当n 为偶数时,0a ≥.③根式的性质:n a =;当n 为奇数时,a =;当n 为偶数时,(0)|| (0)a a a a a ≥⎧==⎨-<⎩. (2)分数指数幂的概念①正数的正分数指数幂的意义是:0,,,m na a m n N +=>∈且1)n >.0的正分数指数幂等于0.②正数的负分数指数幂的意义是: 1()0,,,m m nn aa m n N a -+==>∈且1)n >.0的负分数指数幂没有意义. 注意口诀:底数取倒数,指数取相反数.(3)分数指数幂的运算性质①(0,,)rsr sa a aa r s R +⋅=>∈ ②()(0,,)r s rs a a a r s R =>∈③()(0,0,)r r rab a b a b r R =>>∈【2.1.2】指数函数及其性质(4)指数函数当堂训练[基础训练A组]一、选择题1.计算122[(]-的结果是().A. D.-2.对任意实数x,下列等式恒成立的是().A.211332()x x= B.211332()x x= C.311535()x x= D.131355()x x--= 3.化简(21)(21)2222k k k-+----+等于().A.22k- B.(21)2k-- C.(21)2k-+- D.24.下列函数中指数函数的个数是().①23xy=⋅②13xy+=③3xy=④3y x=A.0 B.1 C.2 D.35.方程135108x x x-⋅=的解集是().A.{}1,4 B.14⎧⎫⎨⎬⎩⎭C.11,4⎧⎫⎨⎬⎩⎭D144⎧⎫⎨⎬⎩⎭,6.函数()(0,1)xf x a a a=>≠且对任意正实数,x y都有().A.()()()f xy f x f y= B.()()()f xy f x f y=+C .()()()f x y f x f y +=D .()()()f x y f x f y +=+ 二、填空题1.化简:1114424111244()a b ba ab --=- . 2.计算:120.750311(0.064)(16()23---÷÷-= .3.若239x=,3x-= .4.985316,8,4,2,2从小到大的排列顺序是 . 5.若函数()11x mf x a =+-是奇函数,则m 为 . 三、解答题1.化简下列各式: (1)11122()()x x x x x --++-;(2)222222223333x y x y xyxy--------+--+-;(3)3333441()()[(1)()]a a a a a a a a ----+-÷++-.2.计算下列各式:(1)1020.5231(2)2(2)(0.01)54--+⋅-;(2)20.520371037(2)0.1(2)392748π--++-+.3.已知2212213333334,3,3a b x a a b y b a b +==+=+,求2233()()x y x y ++-的值.4. 比较下列各组数的大小:(1)0.1()4-和 0.2-; (2)163()4和154()3-; (3)2(0.8)-和125()3- .5.家用电器(如冰箱等)使用的氟化物的释放破坏了大气上层的臭氧层,臭氧含量Q 呈指数函数型变化,满足关系式0.00250t Q Q e -=,其中0Q 是臭氧的初始量. (1)随时间的增加,臭氧的含量是增加还是减少? (2)多少年以后将会有一半的臭氧消失?[基础训练B 组] 一、选择题1.设全集为R ,且22{|0},{|1010}x x A x B x -=≤==,则()R A B ð为( ). A .{2} B .{1}- C .{|2}x x ≤ D .∅2.函数y x =3与y x =--3的图像关于下列那种图形对称( ). A .x 轴 B .y 轴 C .直线y x = D .原点中心对称3.函数11x x e y e -=+的值域是( ).A .(1,1)-B .[1,1]-C .(0,1)D .(,)e e - 4.已知集合{}11M =-,,11242x N x x +⎧⎫=<<∈⎨⎬⎩⎭Z ,,则M N = ( ). A .{}11-,B .{}1-C .{}0D .{}10,1-,5.函数11()()3x f x -=在区间[2,1]--上的最大值是( )A .1B .3C .9D .276.设1x ,2x 是函数()(1)x f x a a =>定义域内的两个变量,且12x x <,设121()2m x x =+.那么下列不等式恒成立的是( ). A .12|()()||()()|f m f x f x f m ->-B .12|()()||()()|f m f x f x f m -<-C .12|()()||()()|f m f x f x f m -=-D .212()()()f x f x f m > 二、填空题1.若集合{11|,|x A y y B x y -⎧⎫====⎨⎬⎩⎭,则集合A B = _________.2.方程33131=++-xx的解是_____________. 3.若1122a a-+=1114421124___________1111aaaa+++=+-++. 4.化简11410104848++的值等于__________. 5.若关于x 的方程12220x x a -++=有两个实数解,则实数 的取值范围是_______. 6.对于函数f (x )定义域中任意的x 1,x 2(x 1≠x 2),有如下结论:①)()()(2121x f x f x x f ⋅=+; ②)()()(2121x f x f x x f +=⋅;③0)]()([)(2121<-⋅-x f x f x x ; ④2)()()2(2121x f x f x x f +<+ 当xx f -=2)(时,上述结论正确结论的序号是 .(写出全部正确结论的序号) 三、解答题1.求函数11()()142xxy =-+在[]3,2x ∈-上的值域.2.求函数241(),[0,5)3x xy x -=∈的值域.3.解方程:(1)192327xx ---⋅= (2)649x x x +=.4.已知11()(),(0)212x f x x x =+≠-, (1)判断()f x 的奇偶性; (2)证明()0f x >.5.在工程技术中经常用到一类所谓的双曲函数,定义如下:双曲正弦,2x xe e shx --=;双曲余弦,2x x e e chx -+=;双曲正切,x xx xe e thx e e---=+,请证明: (1)()sh x y shxchy chxshy +=+;(2)()1thx thyth x y thxthy++=+.同步提升一、选择题(12*5分) 1.(369a )4(639a )4等于( )(A )a 16 (B )a 8(C )a 4(D )a 22.函数f (x )=(a 2-1)x在R 上是减函数,则a 的取值范围是( ) (A )1>a (B )2<a (C )a<2 (D )1<2<a3.下列函数式中,满足f(x+1)=21f(x)的是( ) (A)21(x+1) (B)x+41 (C)2x (D)2-x4.已知a>b,ab 0≠下列不等式(1)a 2>b 2,(2)2a>2b,(3)ba 11<,(4)a 31>b 31,(5)(31)a <(31)b 中恒成立的有( )(A )1个 (B )2个 (C )3个 (D )4个5.函数y=121-x 的值域是( ) (A )(-1,∞) (B )(-,∞0)⋃(0,+∞) (C )(-1,+∞) (D )(-∞,-1)⋃(0,+∞) 6.下列函数中,定义域为R 的是( ) (A )y=5x-21 (B )y=(31)1-x(C )y=1)21(-x(D )y=x 21- 7.下列关系中正确的是( )(A )(21)32<(51)32<(21)31 (B )(21)31<(21)32<(51)32(C )(51)32<(21)31<(21)32 (D )(51)32<(21)32<(21)318.若函数y=3·2x-1的反函数的图像经过P 点,则P 点坐标是( )(A )(2,5) (B )(1,3) (C )(5,2) (D )(3,1)9.函数f(x)=3x +5,则f -1(x)的定义域是( ) (A )(0,+∞) (B )(5,+∞) (C )(6,+∞) (D )(-∞,+∞)10.已知函数f(x)=a x+k,它的图像经过点(1,7),又知其反函数的图像经过点(4,0),则函数f(x)的表达式是( )(A)f(x)=2x +5 (B)f(x)=5x +3 (C)f(x)=3x +4 (D)f(x)=4x+311.已知0<a<1,b<-1,则函数y=a x+b 的图像必定不经过( ) (A)第一象限 (B)第二象限 (C)第三象限 (D)第四象限12.一批设备价值a 万元,由于使用磨损,每年比上一年价值降低b%,则n 年后这批设备的价值为( )(A )na(1-b%) (B )a(1-nb%) (C )a(1-(b%)n ) (D )a(1-b%)n二、填空题(4*4分) 13.若a 23<a2,则a 的取值范围是 。
4.2.2.1 指数函数的图象和性质

课堂检测·素养达标
1.函数y=10x-1的图象大致是 ( )
【解析】选C.函数y=10x-1的图象可以看作函数y=10x的图象向下平移1个单位 长度得到的,结合指数函数的图象与性质,即可得出函数的大致图象是C选项.
2.函数f(x)=3-ax+1(a>0,且a≠1)的图象恒过定点
第1课时 指数函数的图象和性质
必备知识·自主学习
导 思
1.怎样作出指数函数的图象?不同底数的 指数函数有何特征? 2.指数函数有哪些性质?
指数函数的图象和性质 (1)图象和性质
图象 定义域 值域 性质
0<a<1
a>1
R _(_0_,__+_∞__)_ 过定点_(_0_,__1_)_
在R上是减函数
【解题策略】
与指数函数相关的图象问题
(1)定点问题:令函数解析式中的指数为0,即可求出横坐标,再求纵坐标即可.
(2)平移问题:对于横坐标x满足“加左减右”.
(3)底数大小:对于y=
a1x
,y=
a
x 2
,y=
a
x 3
,y=
a
x 4
,如图,0<a4<a3<1<a2<a1.
【跟踪训练】(2020·榆林高一检测)函数y= xax(a>1)的图象的大致形状是 ( )
关键能力·合作学习
类型一 与指数函数相关的定义域问题(数学抽象)
【题组训练】
求下列函数的定义域
(1)y= (3)y=
1 .(2)y=
2 . x2-x-6
2x1 8. .
(1) . x22x-8 3
【解析】(1)函数有意义当且仅当x2-x-6≠0,解得x≠-2且x≠3,所以函数的 定义域为{x|x∈R,x≠-2且x≠3}. (2)函数有意义当且仅当x2+2x-8≥0,解得x≤-4或x≥2,所以函数的定义域为 {x|x≤-4或x≥2}. (3)函数有意义当且仅当2x-1-8≥0,即2x-1≥8,解得x≥4,所以函数的定义域 为[4,+∞).
第二章 2.1 2.1.2(一)指数函数

2.1.2指数函数及其性质(一)学习目标 1.理解指数函数的概念,了解对底数的限制条件的合理性.2.掌握指数函数图象的性质.3.会应用指数函数的性质求复合函数的定义域、值域.知识点一指数函数思考细胞分裂时,第一次由1个分裂成2个,第2次由2个分裂成4个,第3次由4个分裂成8个,如此下去,如果第x次分裂得到y个细胞,那么细胞个数y与次数x的函数关系式是什么?这个函数式与y=x2有什么不同?梳理一般地,叫做指数函数,其中x是自变量,函数的定义域是. 特别提醒:(1)规定y=a x中a>0,且a≠1的理由:①当a<0时,;②当a=0时,;③当a>0时,x可以取;④当a=1时,a x=1 (x∈R),无研究价值.因此规定y=a x中a>0,且a≠1.(2)要注意指数函数的解析式:①底数.②指数函数的自变量必须位于的位置上.③a x的系数必须为.④指数函数等号右边不能是多项式,如y=2x+1不是指数函数.知识点二指数函数的图象和性质指数函数y=a x(a>0,且a≠1)的图象和性质如下表:1.y =x x (x >0)是指数函数.( × )2.y =a x +2(a >0且a ≠1)是指数函数.( × )3.因为a 0=1(a >0且a ≠1),所以y =a x 恒过点(0,1).( √ ) 4.y =a x (a >0且a ≠1)的最小值为0.( × )类型一 求指数函数的解析式例1 已知指数函数f (x )的图象过点(3,π),求函数f (x )的解析式.跟踪训练1 已知指数函数y =(2b -3)a x 经过点(1,2),求a ,b 的值.类型二 求指数函数与其他函数复合所得函数的定义域、值域 命题角度1 f (a x )型例2 求下列函数的定义域、值域. (1)y =3x 1+3x ;(2)y =4x -2x+1. 跟踪训练2 求下列函数的定义域与值域. (1)y =1-⎝⎛⎭⎫12x;(2)y =a x -1a x +1(a >0,且a ≠1).命题角度2 a f (x )型 例3 求函数y =32x -1-19的定义域、值域.反思与感悟 y =a f (x )的定义域即 的定义域,求y =a f (x )的值域可先求 的值域,再利用y =a t 的单调性结合t =f (x )的范围求y =a t 的范围. 跟踪训练3 求下列函数的定义域、值域:11(1)0.3;x y -=(2)y =类型三 指数函数图象的应用 命题角度1 指数函数整体图象例4 在如图所示的图象中,二次函数y =ax 2+bx +c 与函数y =⎝⎛⎭⎫b a x的图象可能是( )反思与感悟 函数y =a x 的图象主要取决于 .但前提是a >0且a ≠1. 跟踪训练4 已知函数f (x )=4+a x+1的图象经过定点P ,则点P 的坐标是( )A .(-1,5)B .(-1,4)C .(0,4)D .(4,0) 命题角度2 指数函数局部图象例5 若直线y =2a 与函数y =|2x -1|的图象有两个公共点,求实数a 的取值范围. 反思与感悟 指数函数是一种基本函数,与其他函数一道可以衍生出很多函数,本例就体现了指数函数图象的“原料”作用.跟踪训练5 函数y =a |x |(a >1)的图象是( )1.下列各函数中,是指数函数的是( ) A .y =(-3)x B .y =-3x C .y =3x -1D .y =⎝⎛⎭⎫13x2.若函数y =(2a -1)x (x 是自变量)是指数函数,则a 的取值范围是( )A .a >0且a ≠1B .a ≥0且a ≠1C .a >12且a ≠1D .a ≥123.函数f (x )=a x-b的图象如图所示,其中a ,b 均为常数,则下列结论正确的是( )A .a >1,b <0B .a >1,b >0C .0<a <1,b >0D .0<a <1,b <04.函数23x y -=的值域是________. 5.函数f (x )=1-2x +1x +3的定义域为________.1.判断一个函数是不是指数函数,关键是看解析式是否符合y =a x (a >0,且a ≠1)这一结构形式,即a x 的系数是1,指数是x 且系数为1.2.指数函数y =a x (a >0,且a ≠1)的性质分底数a >1,0<a <1两种情况,但不论哪种情况,指数函数都是单调的.3.由于指数函数y =a x (a >0,且a ≠1)的定义域为R ,即x ∈R ,所以函数y =a f (x )(a >0,且a ≠1)与函数f (x )的定义域相同.4.求函数y =a f (x )(a >0,且a ≠1)的值域的方法如下: (1)换元,令t =f (x ),并求出函数t =f (x )的定义域; (2)求t =f (x )的值域t ∈M ;(3)利用y =a t 的单调性求y =a t 在t ∈M 上的值域.一、选择题1.若函数f (x )=(a 2-3a +3)a x 是指数函数,则( ) A .a =1或a =2 B .a =1 C .a =2D .a >0且a ≠12.函数y =a x -a (a >0且a ≠1)的大致图象可能是( )3.设指数函数f (x )=a x (a >0且a ≠1),则下列等式中不正确的是( ) A .f (x +y )=f (x )f (y ) B .f (x -y )=f (x )f (y )C .f (nx )=[f (x )]n (n ∈Q )D .[f (xy )]n =[f (x )]n [f (y )]n (n ∈N *)4.设f (x )=⎩⎪⎨⎪⎧x 2,x <0,2x ,x ≥0,若方程f (x )=a (a 为实常数)有2个根,则a 的取值范围是( )A .(0,1)B .(0,1]C .(1,+∞)D .[1,+∞)5.函数y =3x 与y =3-x 的图象关于下列哪条直线对称( ) A .x 轴 B .y 轴 C .直线y =xD .直线y =-x6.已知函数f (x )=(a 2-1)x ,若x >0时总有f (x )>1,则实数a 的取值范围是( ) A .1<|a |<2 B .|a |<2 C .|a |>1D .|a |> 27.若函数f (x )=12x +1,则此函数在(-∞,+∞)上( )A .单调递减且无最小值B .单调递减且有最小值C .单调递增且无最大值D .单调递增且有最大值8.如图所示,面积为8的平行四边形OABC 的对角线AC ⊥CO ,AC 与BO 交于点E .若指数函数y =a x (a >0,且a ≠1)的图象经过点E ,B ,则a 等于( )A. 2B.3 C .2 D .3 二、填空题9.函数y =32-2x 的定义域是________.10.已知5a =0.3,0.7b =0.8,则ab 与0的大小关系是________.11.给出函数f (x )=⎩⎪⎨⎪⎧2x ,x ≥3,f (x +1),x <3,则f (x )的值域为________.三、解答题12.求下列函数的定义域和值域.(1)y =(2)y =5-x -1.13.已知x ∈[-3,2],求f (x )=14x -12x +1的最小值与最大值.四、探究与拓展14.若函数f (x )=a x +b -1(a >0,且a ≠1)的图象经过第一、三、四象限,则一定有(a -1) b ____0.(填“>”“<”“=”) 15.已知函数y =131-⎪⎭⎫ ⎝⎛x(1)画出函数的图象(简图); (2)由图象指出函数的单调区间;(3)由图象指出当x 取何值时函数有最值,并求出最值.。
2.1指数函数

设x年后我国的GDP为2000年的y倍,那么
y (1 7.3%) 1.073 ( x N , x 20)
x x *
即从2000年起,x年后我国的GDP为2000年的1.073x倍。
想一想,正整数指数幂1.073x的含义是什么?它 具有哪些运算性质?
问题2 当生物死亡后,它机体内原有的碳14会 按确定的规律衰减,大约每经过5730年衰减为原来 的一半,这个时间称为“半衰期”. 根据此规律,人们获得了生物体内碳14含量P 与死亡年数t之间的关系
5
的近似值 9.518269694 9.672669973
2
9.735171039 9.738305174 9.738461907 9.738508928 9.738516765 9.738517705 9.738517736 …
然后通过计算器完成下表:
5
的近似值 11.18033989 9.829635328
2.1.1
指数与指数幂的运算 ——无理指数幂
课堂练习
1. 计算下列各式:
36 (1) ; 49
1 2 1 4 1 8
3 2
(2)2 3 1.5 12;
3 6
1 3 1 3 2 3
1 ( 3)a a a ; (4)2 x ( x 2 x ). 2
课本第54页练习第3题,解题过程可见参考书.
25=32,那么2是32的5次方根,记作 5 32 2 ; 35=243,那么3是243的5次方根,记作 5 243 3 ; 24=16,那么2是16的4次方根,记作 4 16 2 ;
4 4 3 =81,那么3是81的4次方根,记作
81 3 ;
(-2)5=-32,那么2是-32的5次方根,记作 5 32 2 ; (-2)2=16,那么2也是16的4次方根,记作 4 16 2 .源自0的任何次方根都是0,记作
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
例3 比较下列各题中两个值的大小 (1)1.7 2.5 <
1.7
2.5
3
解: ∵函数 y 1.7 x在R上是增函数, 而指数2.5<3. ∴
1.7 < 1.7
3
5 4.5
4
3.5
fx = 1.7x
2.5 2 1.5 1
3
0.5
-2
-1
1
2
3
4
5
6
-0.5
例3 比较下列各题中两个值的大小
0.1 0.2 ( 2) 0.8 < 0.8
C. y 2
x
)
D. y 3 2
x
2. 比较下列各题中两个值的大小: (1)3 0.8 与 3 0.7 ; ( 2 ) 0.75 -0.1 与 0.75 0.1
点滴收获: 1. 本节课学习了那些知识? 指数函数的定义 指数函数的图象及性质
2.如何记忆函数的性质?
数形结合的方法记忆
y
y 2x
0.4
0.2
0.2
-2
-1.5
-1
-0.5 -0.2
0.5
1
1.5
2
2.5
-0.5 -0.2
0.5
1
1.5
2
2.5
3
3.5
4
-0.4
-0.4
比较两个指数幂大小的方法:
1.同底:构造1个指数函数,借助单调性
2.不同底:借助中间值1
练习2
1.下列函数中一定是指数函数的是( A. y 2 x 1 B. y x 3
x
2
x
…
…
1 8
1 4
1 2
1 1
2
1 2
4
1 4
8
1 8
…
1 x ( ) 2
…
8
4
2
1 y ( )x 2
y 2x
探求图象
y 2x
1 x y ( ) 2
1 y 5
x
y
y 5
x
y 3x
1 x y ( ) 3
1
0
1
x
探求图象
1 y 3
2
3.记住两个基本图形:
1 x y( ) 2
1
Байду номын сангаас
y=1
2
-2
-1
o1
x
课后作业
习题2.1 A组 (写在练习本上)
引例2:《庄子·天下篇》中写道:“一尺之棰, 日取其半,万世不竭。”请你写出截取x次后,木 棰剩余量 y 关于 x 的函数关系式?
截取 次数 1次 2次 3次 4次 x次
1 x * y ( ) , xN 2
木棰 剩余
1 2
1 2
2
1 2
3
1 2
四. 典例分析、巩固训练
x f ( x ) a (a 0且a 1) 例1、已知指数函数 的图像经过
点(3,π)求 f(0), f(1), f(-3)的值。
解:因为 f ( x) a x 的图像过点 (3, ), 所以
f (3) ,
即 a , 解得 a , 于是
解: ∵函数 y 0.8 x在R上是减函数, 而-0.1>-0.2
0.1 0.2 0 . 8 0 . 8 ∴
1.8
fx = 0.8x
1.6
1.4
1.2
1
0.8
0.6
0.4
0.2
-1.5
-1
-0.5
0.5
1
例3 比较下列各题中两个值的大小
(3)1.7 0.3
0.9
3.1
解:根据指数函数的性质,得:
x
y
y 0.2 x
y 5x
y 3x
y 2x
1 y 2
x
1
0
1
x
二.指数函数的图象与性质
y=ax(a>1)
图
象
y
y=ax (0<a<1)
y
(0,1)
y=ax
(0,1)
o x (1)定义域: R (2)值域:(0,+∞)
o
x
性 (3)图象过定点:(0,1) ,即x=0 时,y=1.
4
1 2
x
两个关系式的共同特征是什么?
y2
x x
它们都是函数
1 y 2
a
x
x
形如 y a 的函数叫做指数函数.其 中x是自变量,函数的定义域是R
形成概念
一般地:形如y = ax(a>0且a≠1) 的函数叫做指数函数.其中x是自变量, 函数的定义域是R
观察指数函数的特点:
y 1 a
系数为1
x
指数只有x
底数为正数且不为1
练习1:判断下列函数是否是指数函数?
(1) y x
3 x
(2) y 3 (4) y 3
x
(3) y (3)
x
1 x ( ) 3
1 x y ( ) x R 的图象. 用描点法来作出函数 y 2 和 2 … … -3 -2 -1 x 0 1 2 3
3
1 3
f ( x) .
所以,f (0) 1, f (1) , f (3) .
0 3 1 1 3
x 3
1
例 2 求下列函数的定义域: (1) y 3
x2
1 x ; (2) y ( ) 2
1
解: (1)要使函数有意义,则 x 2 0 ,解得 x 2 , 原函数的定义域是{x x 2} . (2)要使函数有意义,则 x 0 , 原函数的定义域是{x x 0} .
给我一个支点, 我就可以撬动地球.
阿基米德
引例1: 给我一张纸,我就可以使它的厚度超过珠穆朗 玛峰! 若纸的厚度为1mm,对折x次后厚度y为多少?
折纸次数
1次 2次 3次
纸张厚(mm)
2 2
1
42 3 8 2
2
……
x次
……
y2
x
一张1毫米的纸,对折23次后可以达到 珠穆朗玛峰的8848米的高度。 这个答案违变了实验事实,有人做过 实验,纸折到7次以上就很难再折动了,与 纸张大小无关。
在R上是减函数 (4)在R上是增函数 (5)非奇非偶函数 x的图象关于y轴对称 (6)函数y=ax与y=( 1 ) a (7)当x>0时,y>1. 当x<0时,0<y<1. 当x>0时,0<y<1, 当x<0时,y>1.
质
三. 深化理解
左右无限上冲天,
永与横轴不沾边.
大一增,小一减,
图象恒过(0,1)点.
1.70.3 1.70 1, 0.93.1 0.90 1
从而有
3.2
3.2
1.7
0.3
0.9
3.1
3
3
2.8
2.8
2.6
2.6
2.4
2.4
2.2
2.2
2
2
1.8
fx = 1.7x
1.8
fx = 0.9x
1.6
1.6
1.4
1.4
1.2
1.2
1
1
0.8
0.8
0.6
0.6
0.4
