南开试题
天津市南开区2023-2024学年高三上学期质量检测(二)语文试题及参考答案

天津市南开区2023-2024学年高三上学期质量检测(二)语文试题及参考答案语文试卷分为第Ⅰ卷(选择题)和第Ⅱ卷两部分,共150分,考试用时150分钟。
第Ⅰ卷本试卷共11小题,每小题3分,共33分。
在每小题给出的四个选项中,只有一项是最符合题目要求的。
一、(9分)阅读下面一段文字,完成1~3题。
春秋笔法作为中国历史叙述的一个传统,a来源于据传为孔子所撰的《春秋》。
它从当时的伦理道德出发,b以定名分、明等级作为评判人物和事件的标准,“褒贬劝惩,各有义例”,有时一字暗含褒贬,由此就形成了所谓的“春秋笔法”“()”。
c《左传》继承和发扬了这一精神,在叙事中敢于(),往往以“礼也”“非礼也”来评判人物或其行为,表现了鲜明的政治与道德倾向。
它的观念较接近于儒家,强调等级秩序与宗法伦理,重视长幼尊卑之别,同时也表现出“民本”思想。
书中不少地方揭示了权势者暴虐淫侈的行为,也()了许多忠于职守、正直和具有远见的政治家,反映出儒家的政治理想。
d《左传》中人物众多,写来无一不形象鲜明。
这部书甚至通过连续记载人物的事迹,描述了人物性格发展的过程。
比如,对晋公子重耳的描写,他颠沛流离在外十九年。
______在战争中,老谋深算,决胜于帷幄,显示了卓越的才略,这不是很可以看到其性格发展的脉络吗?1.依次填入文中括号内的词语,最恰当的一组是()A.微言大义直言不讳表彰B.微言大义和盘托出彰显C.言近旨远直言不讳彰显D.言近旨远和盘托出表彰2.对文中画波浪线句子的解说正确的一项是()A.a处“来源于据传为孔子所撰的《春秋》”与“据传来源于为孔子所撰的《春秋》”语义一致。
B.b处标点使用完全正确。
C.c处“这一精神”指“一字暗含褒贬”。
D.d处使用双重否定句,起到舒缓语气的作用。
3.为使文段语意连贯,逻辑严密,第二段画横线处填入7句话,排序最恰当的一项是()①到了秦国,秦人妻以怀嬴,奉画沃盥以后,他曾情不自禁地“挥之”,引起怀嬴愤怒。
2023-2024学年天津市南开中学高三上学期第一次月考数学试题及答案

南开中学2024届高三第一次月检测数学学科试卷考试时间:120分钟本试卷分第Ⅰ卷(选择题)和第Ⅱ卷两部分,共150分.考试结束后,请交回答题卡.第I卷一、选择题(在每小题给出的四个选项中,只有一项是符合题目要求的.)1. 已知集合{}2|230A x x x =-->,{}1,2,3,4B =,则()A B ⋂=Rð()A. {}1,2 B. {}1,2,3 C. {}3,4 D. {}42. “sin 0x =”是“cos 1x =”的( )A 充要条件B. 充分不必要条件C. 必要不充分条件D. 既不充分也不必要条件3. 函数()||sin 2f x x x =的部分图象可能是( )AB. C. D.4. 下列函数中,是奇函数且在()0,∞+上单调递减的是( )A. 2y = B. sin xy x=C. )lg2y x=- D. e e 2x xy --=5. 计算:0ln 228241.1e log 1lg10ln e log +-+++的值( )A. 0B.152C. 2D. 36. 已知1sin 3a =,0.913b ⎛⎫= ⎪⎝⎭,271log 92c =,则( )A. a c b<< B. a b c << C. b a c << D. c a b<<7.π2cos 63αα⎛⎫--= ⎪⎝⎭,则πsin 26α⎛⎫-= ⎪⎝⎭( )..A. 19-B.19C.13D.898. 将函数()π3sin 26f x x ⎛⎫=+ ⎪⎝⎭的图象向右平移π6个单位长度后,所得图象对应的函数为()y g x =,有下列命题:①函数()g x 的图象关于直线πx =对称 ②函数()g x 图象关于点π,012⎛⎫⎪⎝⎭对称③函数()g x 在π5π,2424⎡⎤-⎢⎥⎣⎦上单调递增 ④函数()g x 在[]0,2π上恰有5个极值点其中正确命题个数为( )A. 1B. 2C. 3D. 49. 设函数ln 2,0()π1sin ,π042x x x f x x x ω⎧+->⎪=⎨⎛⎫+--≤≤ ⎪⎪⎝⎭⎩有7个不同的零点,则正实数ω的取值范围为( )A. 131744⎡⎫⎪⎢⎣⎭,B. 174⎡⎢⎣C. 49121652⎡⎫⎪⎢⎣⎭, D. 65121732⎡⎫⎪⎢⎣⎭,第II 卷二、填空题(本大题共6小题,每小题5分,共30分.)10. 已知i 是虚数单位,化简32i12i-+的结果为____________.11.在代数式521x ⎫-⎪⎭的展开式中,常数项为_____________.12. 函数()()ππ2sin 0,22f x x ωϕωϕ⎛⎫=+>-<< ⎪⎝⎭的部分图象如图所示,则π=3f ⎛⎫⎪⎝⎭__________.的的13. 在亚运会女子十米跳台决赛颁奖礼上,五星红旗冉冉升起,在坡度15 的看台上,同一列上的第一排和最后一排测得旗杆顶部的仰角分别为60 和30 ,第一排A 点和最后一排E 点的距离为(如图所示),则旗杆的高度为____________米.14. 已知定义在[)0+∞,上的函数()f x ,当[0,2)x ∈时,()()1611f x x =--,且对任意的实数1[2222)n n x +∈--,(*2N n n ∈,≥),都有()1122x f x f ⎛⎫=- ⎪⎝⎭,若函数()()log a g x f x x =-有且仅有五个零点,则a 的取值范围__________.15. 记()ln f x x ax b =++(0a >)在区间[],2t t +(t 为正数)上的最大值为(),t M a b ,若{|(,)ln 3}R t b M a b a ≥+=,则实数t 的最大值为__________.三、解答题(本大题共5小题,共75分.解答应写出文字说明,证明过程或演算步骤.)16. 已知函数()()2π2sin πcos 2f x x x x ⎛⎫=+-+-⎪⎝⎭(1)求()f x 的最小正周期及对称轴方程;(2)当ππ,42x ⎡⎤∈⎢⎥⎣⎦时,求()f x 的最大值和最小值.17. 在ABC 中,角,,A B C 所对的边分别为,,a b c ,其中2C π≠,已知cos 2cos cos b c A a B C -=.(1)求角B 的大小;(2)若223125b c ac +=-,求ABC 面积的最大值.18. 如图,在四棱锥P ABCD -中,PA ⊥底面ABCD ,AD AB ⊥,//AB DC ,2AD DC AP ===,1AB =,E 为棱PC 的中点.(1)证明://BE 平面PAD ;(2)求直线BE 与平面PBD 所成角的正弦值;(3)求点D 到平面PBC 的距离.19. 已知椭圆()2222:10x y C a b a b +=>>,短轴长为.(1)求C 的方程;(2)如图,经过椭圆左顶点A 且斜率为()0k k ≠的直线l 与C 交于A ,B 两点,交y 轴于点E ,点P 为线段AB 的中点,若点E 关于x 轴的对称点为H ,过点E 作OP (O 为坐标原点)垂直的直线交直线AH 于点M ,且APM △,求k 的值.20. 已知函数()11lnx aF x x x =--+.(Ⅰ)设函数()()()1h x x F x =-,当2a =时,证明:当1x >时,()0h x >;(Ⅱ)若()0F x >恒成立,求实数a 取值范围;(Ⅲ)若a 使()F x 有两个不同的零点12,x x,证明:21a a x x e e -<-<-.的南开中学2024届高三第一次月检测数学学科试卷考试时间:120分钟本试卷分第Ⅰ卷(选择题)和第Ⅱ卷两部分,共150分.考试结束后,请交回答题卡.第I卷一、选择题(在每小题给出的四个选项中,只有一项是符合题目要求的.)1. 已知集合{}2|230A x x x =-->,{}1,2,3,4B =,则()A B ⋂=Rð()A. {}1,2 B. {}1,2,3 C. {}3,4 D. {}4【答案】B 【解析】【分析】首先解一元二次不等式求出集合A ,再根据补集、交集的定义计算可得.【详解】由2230x x -->,即()()130x x +->,解得3x >或1x <-,所以{}2|230{|1A x x x x x =-->=<-或3}x >,所以{}|13A x x =-≤≤R ð,又{}1,2,3,4B =,所以(){}1,2,3A B ⋂=R ð.故选:B2. “sin 0x =”是“cos 1x =”的( )A. 充要条件B. 充分不必要条件C. 必要不充分条件D. 既不充分也不必要条件【答案】C 【解析】【分析】根据充分性和必要性的定义结合同角三角函数的关系即可得出结论.【详解】解:因为sin 0x =,根据三角函数的基本关系式,可得cos 1x ==±,反之:若cos 1x =,根据三角函数的基本关系式,可得sin 0x ==,所以“sin 0x =”是“cos 1x =”的必要不充分条件.故选:C.3. 函数()||sin 2f x x x =的部分图象可能是( )A. B. C. D.【答案】C 【解析】【分析】根据()f x 是奇函数,排除B ,再取特殊值验证.【详解】因为()()||sin 2||sin 2()f x x x x x f x -=--=-=-所以()f x 是奇函数,排除B ,由02f ⎛⎫= ⎪⎝⎭π,排除A ,由44f ππ⎛⎫= ⎪⎝⎭,排除D .故选:C .【点睛】本题主要考查函数的图象和性质,还考查了数形结合的思想和理解辨析的能力,属于基础题.4. 下列函数中,是奇函数且在()0,∞+上单调递减的是( )A. 2y = B. sin x y x=C. )lg2y x=- D. e e 2x xy --=【答案】C 【解析】【分析】根据奇偶性定义、对数函数、指数函数单调性,结合复合函数的单调性依次判断各个选项即可.【详解】A 选项:()()2f x f x -==,不是奇函数,故A 选项错误;B 选项:()()()sin sin sin x x xf x f x x x x---====--,不是奇函数,故B 选项错误;C 选项:因为()f x 的定义域为R ,且()()))()22lg 2lg2lg 414lg10f x f x x x x x -+=++=+-==,∴()f x 是奇函数.设2t x ==因为t =()0,∞+上单调递减,lg y t =在()0,∞+上单调递增,由复合函数单调性知,()f x 在()0,∞+上单调递减,故C 选项正确;D 选项:()11e 2e x xf x ⎛⎫=- ⎪⎝⎭,因为1e e ,xxy y ==-在()0,∞+上都单调递增,所以()f x 在()0,∞+上单调递增,故D 选项错误,故选:C .5. 计算:0ln 228241.1e log 1lg10ln e log +-+++的值( )A. 0B.152C. 2D. 3【答案】B 【解析】【分析】根据指数及对数的运算法则计算可得;【详解】0ln 222423151.1e log 1lg10ln e log 812012log 222+-+++=+-+++=.故选:B6. 已知1sin 3a =,0.913b ⎛⎫= ⎪⎝⎭,271log 92c =,则( )A. a c b <<B. a b c <<C. b a c <<D. c a b<<【答案】A 【解析】【分析】化简得13c =,构造函数()sin ,0,2πf x x x x ⎛⎫=-∈ ⎪⎝⎭,通过导数可证得sin ,0,2πx x x ⎛⎫<∈ ⎪⎝⎭,可得a c <,而0.91133b c ⎛⎫=>= ⎪⎝⎭,从而可得答案.【详解】2711lg 912lg 31log 922lg 2723lg 33c ==⨯=⨯=.设()sin ,0,2πf x x x x ⎛⎫=-∈ ⎪⎝⎭,则有()cos 10f x x '=-<,()f x 单调递减,从而()(0)0f x f <=,所以sin ,0,2πx x x ⎛⎫<∈ ⎪⎝⎭,故11sin 33<,即a c <,而0.91133b c ⎛⎫=>= ⎪⎝⎭,故有a c b <<.故选:A .7.π2cos63αα⎛⎫--=⎪⎝⎭,则πsin26α⎛⎫-=⎪⎝⎭()A.19- B.19C.13D.89【答案】A【解析】【分析】利用三角恒等变换化简已知条件,结合诱导公式、二倍角公式求得正确答案.π2cos63αα⎛⎫--=⎪⎝⎭,12sin cos23ααα⎫+-=⎪⎪⎭,1π2cos sin263ααα⎛⎫+=+=⎪⎝⎭.πππsin2cos2626αα⎡⎤⎛⎫⎛⎫-=--⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦2ππcos2cosπ233αα⎡⎤⎛⎫⎛⎫=-=-+⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦2ππcos22sin136αα⎛⎫⎛⎫=-+=+-⎪ ⎪⎝⎭⎝⎭2212139⎛⎫=⨯-=-⎪⎝⎭.故选:A8. 将函数()π3sin26f x x⎛⎫=+⎪⎝⎭的图象向右平移π6个单位长度后,所得图象对应的函数为()y g x=,有下列命题:①函数()g x的图象关于直线πx=对称②函数()g x的图象关于点π,012⎛⎫⎪⎝⎭对称③函数()g x在π5π,2424⎡⎤-⎢⎥⎣⎦上单调递增④函数()g x 在[]0,2π上恰有5个极值点其中正确的命题个数为( )A. 1 B. 2C. 3D. 4【答案】B 【解析】【分析】根据函数图象平移变换的特点,利用正弦弦函数的对称性、单调性、最值,结合函数的极值点定义逐项判断即可求解.【详解】函数()π3sin 26f x x ⎛⎫=+⎪⎝⎭的图象向右平移π6个单位长度后,所得图象对应的函数为()πππ3sin 23sin 2666y g x x x ⎡⎤⎛⎫⎛⎫==-+=- ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦,对于①,当πx =时,()π3π3sin 2π62g ⎛⎫=-=- ⎪⎝⎭,不是函数()y g x =的最值,故①错误;对于②,当π12x =时,πππ3sin 2012126g ⎛⎫⎛⎫=⨯-= ⎪ ⎪⎝⎭⎝⎭,故②正确;对于③,当π5π,2424x ⎡⎤∈-⎢⎥⎣⎦时,πππ2,644x ⎡⎤-∈-⎢⎥⎣⎦,故函数在该区间上单调递增,故③正确;对于④,令(ππ2πZ 62x k k -=+∈,解得()ππZ 23k x k =+∈,当0,1,2,3k =时,π5π4π11π,,,3636x =,在[]0,2π上有4个极值点,故④错误.故选:B.9. 设函数ln 2,0()π1sin ,π042x x x f x x x ω⎧+->⎪=⎨⎛⎫+--≤≤ ⎪⎪⎝⎭⎩有7个不同的零点,则正实数ω的取值范围为( )A. 131744⎡⎫⎪⎢⎣⎭, B. 172144⎡⎫⎪⎢⎣⎭, C. 49121652⎡⎫⎪⎢⎣⎭, D. 65121732⎡⎫⎪⎢⎣⎭,【答案】C 【解析】【分析】分段函数分段处理,在1x >,01x <<各有1个零点,所以π0x -≤≤有5个零点,利用三角函数求出所有的零点,保证π0x -≤≤之间有5个零点即可.【详解】由题,当1x ≥时,()ln 2f x x x =+-,显然()f x 在()1,+∞上单调递增,且()110f =-<,()22ln 220f =+->,此时()f x 在()1,+∞在有一个零点;当01x <<时,()ln 2f x x x =--,1()10f x x'=-<,所以()f x 在()0,1上单调递减,2211()220e ef =+->,此时()f x 在()0,1上只有一个零点;所有当π0x -≤≤时,()π1sin 42f x x ω⎛⎫+- ⎪⎝⎭=有5个零点,令()0f x =,则π1sin 42x ω⎛⎫+= ⎪⎝⎭,即ππ2π46x k ω+=+,或π5π2π46x k ω+=+,k ∈Z ,解得π2π12k x ω-+=,或7π2π12k x ω-+=,k ∈Z ,当0k =时,12π7π1212,x x ωω--==;当1k =时,34π7π2π2π1212,x x ωω----==;当2k =时,56π7π4π4π1212,x x ωω----==;由题可得π0x -≤≤区间内的5个零点,即π4π12π7π4π12πωω⎧--⎪≥-⎪⎪⎨⎪--⎪<-⎪⎩,解得54912126ω≤<,即49651212ω⎡⎫∈⎪⎢⎣⎭,.故选:C.【点睛】分段函数的零点问题点睛:根据函数的特点分别考虑函数在每段区间上的单调性,结合零点存在性定理,得到每一段区间上的零点的个数,从而得出函数在定义域内的零点个数.第II 卷二、填空题(本大题共6小题,每小题5分,共30分.)10. 已知i 是虚数单位,化简32i12i-+的结果为____________.【答案】18i 55--【解析】分析】运用复数运算法则计算即可.【【详解】2232i (32i)(12i)36i 2i 4i 38i 418i 12i (12i)(12i)14i 1455-----+--====--++--+.故答案为:18i 55--.11.在代数式521x ⎫-⎪⎭的展开式中,常数项为_____________.【答案】-5【解析】【分析】写出二项式定理的通项,化简后,使得x 的指数幂为0,即可求得k 的值.【详解】521x ⎫-⎪⎭的展开式的通项为:()51552215521C C 1rrrr r r r T x x x --+⎛⎫⎛⎫=-=- ⎪ ⎪⎝⎭⎝⎭令5502r -=,解得1r =,所以()11215C 15T +=-=-,521x ⎫⎪⎭的展开式中的常数项为5-.故答案为:-512. 函数()()ππ2sin 0,22f x x ωϕωϕ⎛⎫=+>-<< ⎪⎝⎭的部分图象如图所示,则π=3f ⎛⎫⎪⎝⎭__________.【解析】【分析】根据函数()f x 的图象结合正弦函数的图象及性质,求得函数的解析式,再代入求值即可.【详解】由函数()f x 的图象可知,35ππ3π41234T ⎛⎫=--= ⎪⎝⎭,则2π=πT ω=,2ω=.把5π12x =代入()f x ,则5ππ22π122k ϕ⨯+=+,而ππ22ϕ-<<,所以π3ϕ=-,所以()π2sin 23f x x ⎛⎫=- ⎪⎝⎭,所以ππππ=2sin 22sin 3333f ⎛⎫⎛⎫⨯-==⎪ ⎪⎝⎭⎝⎭.13. 在亚运会女子十米跳台决赛颁奖礼上,五星红旗冉冉升起,在坡度15 的看台上,同一列上的第一排和最后一排测得旗杆顶部的仰角分别为60 和30 ,第一排A 点和最后一排E 点的距离为(如图所示),则旗杆的高度为____________米.【答案】27【解析】【分析】根据已知可得30ECA ∠= ,在EAC 中由正弦定理可得AC ,再利用t ABC R 中计算可得答案.【详解】由图可得3609012012030∠=---= ECA ,在EAC sin 30= EA,即sin 452sin 30===EA AC ,在t ABC R 中,60CAB ∠= ,可得sin 6027=⨯== BC AC 米.故答案为:27.14. 已知定义在[)0+∞,上的函数()f x ,当[0,2)x ∈时,()()1611f x x =--,且对任意的实数1[2222)n n x +∈--,(*2N n n ∈,≥),都有()1122x f x f ⎛⎫=- ⎪⎝⎭,若函数()()log a g x f x x =-有且仅有五个零点,则a 的取值范围__________.【答案】1410⎛ ⎝【解析】【分析】写出()f x 的解析式并画出()f x 的图象,结合已知条件将问题转化为()y f x =图象与log a y x =图象在(0,)+∞上有且仅有5个交点,结合图象分析即可求得结果.【详解】当[0,2)x ∈,()16(1|1|)f x x =--,当2n =时,[2,6)x ∈,此时1[0,2)2x -∈,则11()(1)16(1|2|)8(1|2|)22222x x xf x f =-=⨯--=--,当3n =时,[6,14)x ∈,此时1[2,6)2x -∈,则1155()(1)8(1||)4(1||)2224242x x x f x f =-=⨯--=--,当4n =时,[14,30)x ∈,此时1[6,14)2x-∈,则111111()(1)4(1||)2(1||)2228484x x x f x f =-=⨯--=--,……因为()()log a g x f x x =-有且仅有5个零点,所以()y f x =图象与log a y x =图象在(0,)+∞上有且仅有5个交点,如图所示,由图可知,当log a y x =经过点(10,4)A 时,两函数图象有4个交点,经过点(22,2)B 时,两函数图象有6个交点,所以当()y f x =图象与log a y x =图象在(0,)+∞上有且仅有5个交点时,则1log 104log 222a aa >⎧⎪<⎨⎪>⎩,解得1410a <<.故答案为:1410(.15. 记()ln f x x ax b =++(0a >)在区间[],2t t +(t 为正数)上的最大值为(),t M a b ,若{|(,)ln 3}R t b M a b a ≥+=,则实数t 的最大值为__________.【答案】14##0.25【解析】【分析】由函数单调性性质及图象变换可画出()f x 的图象,进而可得(,)()t M a b f t ≥,结合已知条件可知只需()ln 3f t a ≥+,即(ln )ln 3t at b a -++≥+,由()(2)f t f t =+可得ln(2)ln 2(1)2t t a t b ++++=-,联立两者进而可求得结果.【详解】设()ln g x x ax b =++,(0a >),定义域为(0,)+∞,由单调性性质可知,()g x 在(0,)+∞上单调递增,当x 趋近于0时,()g x 趋近于-∞;当x 趋近于+∞时,()g x 趋近于+∞,设0()0g x =,则()g x 的图象如图所示,所以()f x 的图象如图所示,则由图象可知,{}max (),()(2)()(,)max (),(2)(2),()(2)t f t f t f t f x M a b f t f t f t f t f t ≥+⎧==+=⎨+<+⎩,所以(,)()t M a b f t ≥,如图所示,当()(2)f t f t =+时,有(ln )ln(2)(2)t at b t a t b -++=++++,则ln(2)ln 2(1)2t t a t b ++++=-,①又因为{|(,)ln 3}R t b M a b a ≥+=,所以()ln 3f t a ≥+,即(ln )ln 3t at b a -++≥+,所以ln ln 3b t at a ≤----,②由①②得ln(2)ln 2(1)ln ln 32t t a t t at a ++++≤-----,整理得ln(2)ln 2ln 3ln 9t t t +≥+=,即29t t +≥,所以14t ≤.故t 的最大值为14.故答案为:14【点睛】恒成立问题解题方法指导:方法1:分离参数法求最值.(1)分离变量.构造函数,直接把问题转化为函数的最值问题.(2)()a f x ≥恒成立⇔max ()a f x ≥;()a f x ≤恒成立⇔min ()a f x ≤;()a f x ≥能成立⇔min ()a f x ≥;()a f x ≤能成立⇔max ()a f x ≤.方法2:根据不等式恒成立构造函数转化成求函数的最值问题,一般需讨论参数范围,借助函数单调性求解.三、解答题(本大题共5小题,共75分.解答应写出文字说明,证明过程或演算步骤.)16. 已知函数()()2π2sin πcos 2f x x x x ⎛⎫=+-+-⎪⎝⎭(1)求()f x 的最小正周期及对称轴方程;(2)当ππ,42x ⎡⎤∈⎢⎥⎣⎦时,求()f x 的最大值和最小值.【答案】(1)πT =,()5ππ122k x k =+∈Z (2)min 1y =,max 2y =.【解析】【分析】(1)根据诱导公式以及二倍角公式化简,再根据周期公式、对称轴公式进行求解;(2)由x 的取值范围求出整体角的取值范围,再结合正弦型函数图像及性质得出结果.【小问1详解】()()2πcos 2sin πcos 2f x x x x ⎤⎛⎫=+-+⋅ ⎪⎥⎝⎭⎦)22sin cos 1cos2sin2x x x x x =+⋅=-+sin22sin 23x x x π⎛⎫=-=- ⎪⎝⎭,故周期为2ππ2T ==,令2π,32x k k ππ-=+∈Z ,解得()5ππ122k x k =+∈Z ,对称轴方程()5ππ122k x k =+∈Z ,【小问2详解】()2sin 23f x x π⎛⎫=- ⎪⎝⎭∵ππ42x ≤≤,∴ππ2π2,363t x ⎡⎤=-∈⎢⎥⎣⎦,当π6t =时,即π4x =时,()min π1sin sin 62t ==,此时min 1y =,当π2t =时,即5π12x =时,()max πsin sin 12t ==,此时max 2y =.17. 在ABC 中,角,,A B C 所对的边分别为,,a b c ,其中2C π≠,已知cos 2cos cos b c A a B C -=.(1)求角B 的大小;(2)若223125b c ac +=-,求ABC 面积的最大值.【答案】(1)3π(2【解析】【分析】(1)根据正弦定理边化角或余弦定理化简原式,根据2C π≠,所以cos 0C ≠或2222a b c b+-≠,化简即可得出1cos 2B =,即可得出答案;(1)根据余弦定理结合第一问得出的角B 的大小得出222a c b ac +-=,结合已知223125b c ac +=-,得出224412a ac c ++=,根据基本不等式得出22412422a c ac a c +=-≥⋅⋅即32ac ≤,即可由三角形面积公式得出答案;或将224412a ac c ++=化简为2(2)12a c +=,由三角形面积公式结合基本不等式得出ABC 的面积212sin 222a c S ac B c +⎫===⋅≤=⎪⎭,即可得出答案.【小问1详解】方法一:由cos 2cos cos b c A a B C -=根据正弦定理边化角得:sin sin cos 2sin cos cos B C A A B C -=,即()sin sin cos 2sin cos cos A C C A A B C +-=,所以sin cos 2sin cos cos A C A B C =,因为2C π≠,所以cos 0C ≠,又sin 0A >,所以1cos 2B =,又0πB <<,所以3B π=.方法二:由cos 2cos cos b c A a B C -=根据余弦定理:得2222222cos 22b c a a b c b c a B bc ab+-+--=⋅,即2222222cos 22b c a a b c B b b -++-=⋅,因为2C π≠,所以22202a b c b+-≠,所以1cos 2B =,又0πB <<,得3B π=.小问2详解】方法一:由(1)及余弦定理知2221cos 22a cb B ac +-==,所以222a c b ac +-=,因为223125b c ac +=-,所以()2221235a c c ac ac +---=,化简得224412a ac c ++=,因为0,0a c >>,所以22412422a c ac a c +=-≥⋅⋅,所以32ac ≤,当且仅当2a c ==a c ==时取等号,所以ABC的面积1sin 2S ac B ==≤,所以ABC方法二:由(1)及余弦定理知2221cos 22a cb B ac +-==,所以222a c b ac +-=.因为223125b c ac +=-,所以()2221235a c c ac ac +---=,化简得224412a ac c ++=,即2(2)12a c +=,所以ABC的面积212sin 222a c S ac B c +⎫===⋅≤=⎪⎭,【当且仅当2a c ==a c ==时取等号,所以ABC 18. 如图,在四棱锥P ABCD -中,PA ⊥底面ABCD ,AD AB ⊥,//AB DC ,2AD DC AP ===,1AB =,E 为棱PC 的中点.(1)证明://BE 平面PAD ;(2)求直线BE 与平面PBD 所成角的正弦值;(3)求点D 到平面PBC 的距离.【答案】(1)证明见解析(2(3【解析】【分析】(1)以A 为原点建立空间直角坐标系,利用向量法证明线面平行;(2)求出平面PBD 的一个法向量,再由向量法求解;(3)求出平面PBC 的法向量()2111,,n x y z =,再由向量法求解.【小问1详解】解:以点A 为原点,AB ,AD ,AP 分别为x 轴,y 轴,z 轴,建立空间直角坐标系.可得()1,0,0B ,()2,2,0C ,()0,2,0D ,()002P ,,,由E 为棱PC 的中点,得()1,1,1E ,向量()0,1,1BE = ,()1,0,0AB =,故0BE AB ⋅= ,又AB为平面PAD 的一个法向量,又BE ⊄面PAD ,所以//BE 平面PAD .【小问2详解】向量()1,2,0BD =-,()1,0,2PB =- ,()0,1,1BE = 设(),,n x y z = 为平面PBD 的法向量,则0n BD n PB ⎧⋅=⎪⎨⋅=⎪⎩,即2020x y x z -+=⎧⎨-=⎩,令1y =,得()2,1,1n =为平面PBD 的一个法向量,所以cos ,n BE n BE n BE⋅===⋅所以直线BE 与平面PBD【小问3详解】向量()1,2,0BC = ,设平面PBC 的法向量()2111,,n x y z =,220n BC n PB ⎧⋅=⎪⎨⋅=⎪⎩,即11112020x y x z +=⎧⎨-=⎩,令11y =-,得()22,1,1n =- 为平面PBC 的一个法向量,则22BD n d n ⋅===.19. 已知椭圆()2222:10x y C a b a b +=>>,短轴长为..(1)求C 的方程;(2)如图,经过椭圆左顶点A 且斜率为()0k k ≠的直线l 与C 交于A ,B 两点,交y 轴于点E ,点P 为线段AB 的中点,若点E 关于x 轴的对称点为H ,过点E 作OP (O 为坐标原点)垂直的直线交直线AH 于点M ,且APM △,求k 的值.【答案】(1)22142x y += (2)【解析】【分析】(1)根据题意得出,a b 的值,进而可得结果;(2)设直线l 的方程为()2y k x =+,将其与椭圆方程联立,得出EM 斜率,联立方程组得出M 点的坐标,利用点到直线距离公式式,结合韦达定理以及三角形面积公式将面积表示为关于k 的方程,解出即可得结果.小问1详解】由题意可得2222c e a b a b c ⎧==⎪⎪⎪=⎨⎪=+⎪⎪⎩,解得2a =,b =,c =∴椭圆C 的方程为22142x y +=.【小问2详解】易知椭圆左顶点()2,0A -,设直线l 的方程为()2y k x =+,则()0,2E k ,()0,2H k -,由()222142y k x x y ⎧=+⎪⎨+=⎪⎩,消y 可得()2222128840k x k x k +++-=,设()11,A x y ,()22,B x y ,()00,P x y ,∴()()422644841216k k k ∆=--+=,【则有2122812k x x k +=-+,21228412k x x k-=+,∴()2012214212k x x x k =+=-+,()0022212=+=+k y k x k ,∴0012OP y k x k ==-,∴直线EM 的斜率2EM k k =,∴直线EM 的方程为22y kx k =+,直线AH 的方程为()2y k x =-+,∴点42,33M k ⎛⎫-- ⎪⎝⎭,∴点M 到直线:20l kx y k -+=的距离d =,∴AB ==∴1||2AP AB ==∴241132212APM k S AP d k =⋅=⨯==+△,解得k =.20. 已知函数()11lnx a F x x x =--+.(Ⅰ)设函数()()()1h x x F x =-,当2a =时,证明:当1x >时,()0h x >;(Ⅱ)若()0F x >恒成立,求实数a 的取值范围;(Ⅲ)若a 使()F x 有两个不同的零点12,x x ,证明:21a a x x e e -<-<-.【答案】(Ⅰ)证明见解析;(Ⅱ)2a ≤;(Ⅲ)证明见解析.【解析】分析】(Ⅰ)当2a =时对()h x 求导,证明1x >时,()0h x '>即可.(Ⅱ)设函数()()1ln 1a x f x x x -=-+,根据函数的单调性判断ln x 与()11a x x -+的关系,根据()0F x >恒成立,确定a 的取值范围;(Ⅲ)根据函数的单调性求出2121a a t t x x e e --<-<-,得到【21t t -==,证明结论成立即可.【详解】(Ⅰ)()()ln 111x a h x x x x ⎛⎫=--⎪-+⎝⎭当2a =时,()()()21ln 21ln 111x x h x x x x x x -⎛⎫=--=- ⎪-++⎝⎭()()()()()()()()2222221211111114x x x x h x x x x x x x x +---+-'=-==+++,当1x >时,()0h x '>,所以()h x 在()1,+∞上为单调递增函数,因为()10h =,所以()()10h x h >=,(Ⅱ)设函数()()1ln 1a x f x x x -=-+,则()()()222111x a x f x x x +-+'=+,令()()2211g x x a x =+-+,当1a ≤时,当0x >时,()0g x >,当12a <≤时,2480a a ∆=-≤,得()0g x ≥,所以当2a ≤时,()f x 在()0,∞+上为单调递增函数,且()10f =,所以有()101f x x >-,可得()0F x >.当2a >时,有2480a a ∆=->,此时()g x 有两个零点,设为12,t t ,且12t t <.又因为()12210t t a +=->,121t t =,所以1201t t <<<,在()21,t 上,()f x 为单调递减函数,所以此时有()0f x <,即()1ln 1a x x x -<+,得ln 011x a x x -<-+,此时()0F x >不恒成立,综上2a ≤.(Ⅲ)若()F x 有两个不同的零点12, x x ,不妨设12x x <,则12, x x 为()()1ln 1a x f x x x -=-+的两个零点,且11x ≠,21x ≠,由(Ⅱ)知此时2a >,并且()f x 在()10,t ,()2,t +∞为单调递增函数,在()12,t t 上为单调递减函数,且()10f =,所以()10f t >,()20f t <,因为()201a a a f e e -=-<+,()201aa a f e e =>+,1a a e e -<<,且()f x 图象连续不断,所以()11,a x e t -∈,()22,a x t e∈,所以2121a a t t x x e e--<-<-,因为21t t -==综上得:21||a a x x e e -<-<-.【点睛】方法点睛:求不等式恒成立问题的方法(1)分离参数法若不等式(),0f x λ≥()x D ∈(λ是实参数)恒成立,将(),0f x λ≥转化为()g x λ≥或()()g x x D λ≤∈恒成立,进而转化为()max g x λ≥或()()min g x x D λ≤∈,求()g x 的最值即可.(2)数形结合法结合函数图象将问题转化为函数图象的对称轴、区间端点的函数值或函数图象的位置关系(相对于x 轴)求解.此外,若涉及的不等式转化为一元二次不等式,可结合相应一元二次方程根的分布解决问题.(3)主参换位法把变元与参数变换位置,构造以参数为变量的函数,根据原变量的取值范围列式求解,一般情况下条件给出谁的范围,就看成关于谁的函数,利用函数的单调性求解.。
2023-2024学年天津市南开区九年级上学期期末数学试题
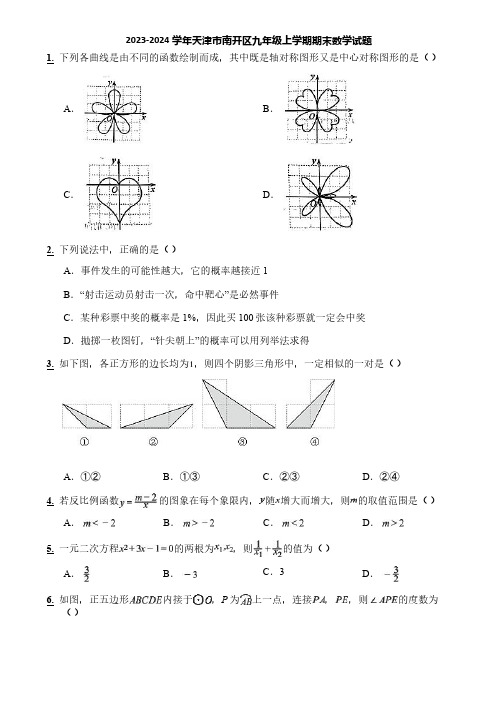
2023-2024学年天津市南开区九年级上学期期末数学试题1.下列各曲线是由不同的函数绘制而成,其中既是轴对称图形又是中心对称图形的是()A.B.C.D.2.下列说法中,正确的是()A.事件发生的可能性越大,它的概率越接近1B.“射击运动员射击一次,命中靶心”是必然事件C.某种彩票中奖的概率是1%,因此买100张该种彩票就一定会中奖D.拋掷一枚图钉,“针尖朝上”的概率可以用列举法求得3.如下图,各正方形的边长均为,则四个阴影三角形中,一定相似的一对是()A.①②B.①③C.②③D.②④4.若反比例函数的图象在每个象限内,随增大而增大,则的取值范围是()A.B.C.D.5.一元二次方程的两根为,则的值为()A.B.C.3D.6.如图,正五边形内接于,P为上一点,连接,,则的度数为()A.18°B.36°C.54°D.72°7.已知,二次函数的图象如图所示,则点所在的象限是()A.第一象限B.第二象限C.第三象限D.第四象限8.如图,的内切圆分别与,,相切于点D,E,F,且,,则的周长为()A.16B.14C.12D.109.为了宣传环保,某学生写了一份倡议书在微博传播,规则为:将倡议书发表在自己的微博,再邀请n个好友转发倡议书,每个好友转发倡议书,又邀请n个互不相同的好友转发倡议书,以此类推,已知经过两轮传播后,共有1641人参与了传播活动,则方程列为()A.B.C.D.10.如图,在等腰直角中,,点为斜边AB上一点,将绕点逆时针旋转得到,则下列说法错误的是()A.B.是等腰直角三角形C.D.11.如图,点P是外一定点,连接线段,与交于点A.按照如下尺规作图的步骤进行操作:①分别以P,O为圆心,以大于长为半径画弧,两弧交于点M,N,作直线,交于点B;②以点为圆心,以为半径作,与交于点Q,R两点;③连接,,,,,线段与相交于点C.则下列说法中不一定正确的是()A.,均为的切线B.C.D.12.从地面竖直向上抛出一小球,小球的高度h(单位,m)与小球运动时间t(单位:s)之间的函数关系为,其中.有下列结论:①当时,小球运动到最大高度;②当小球的运动高度为时,运动时间为或;③小球运动中的最大高度为;④小球从抛出到落地需要;其中正确的结论有()A.1个B.2个C.3个D.4个13.如图是一个可以自由转动的质地均匀的转盘,被分成12个相同的小扇形.若把某些小扇形涂上红色,使转动的转盘停止时,指针指向红色的概率是,则涂上红色的小扇形有______个.14.如图,在中,D、E分别是边AB、AC的中点,若的面积是1,则的面积是______;15.在平面直角坐标系中,直线与双曲线交于A,B两点.若点A,B的纵坐标分别为,则的值为_______.16.如图,点A,B,C在上,.若点D为上一点(不与点A,C重合),则的度数为___________.17.如图,是正方形的外接圆,,点是上任意一点,于.当点从点出发按顺时针方向运动到点时,则的最小值为_____.18.如图,在每个小正方形的边长为1的网格中,点A,B,均在格点上.(1)的长为______;(2)若以为边的矩形,其面积为11.请用无刻度的直尺,在如图所示的网格中,画出矩形,并简要说明点C,D的位置是如何找到的(不要求证明)______.19.现有四张完全相同的不透明卡片,其正面分别写有数,0,1,2,把这四张卡片背面朝上洗匀后放在桌面上.(1)随机的取一张卡片,直接写出抽取的卡片上的数为非负数的概率.(2)先随机抽取一张卡片,其上的数作为点A的横坐标;然后放回并洗匀,再随机抽取一张卡片,其上的数作为点A的纵坐标,试用画树状图或列表的方法求出点A在双曲线上的概率.20.已知一次函数的图象与反比例函数的图象相交于点,.(1)求一次函数和反比例函数的解析式;(2)填空:①直接写出不等式的解集______;②点,,都在反比例函数的图象上,若,比较,,的大小(用号连接),其结果是______.21.如图1,中,,,(1)求证;(2)如图2,若,,,求a的值.22.如图1,在中,,,以为直径的与相交于点D.过点D的切线与相交于点E.(1)求和的度数;(2)如图2,过点O作于点F,过点F作于点H,交于点M和N.若,求的长.23.如图1,有长为的篱笆,一面利用墙(墙的最大可用长度a为10m),围成中间隔有一道篱笆的矩形花圃.设花圃的宽为(宽不大于长),面积为.(1)求S与x之间的函数关系式,并写出自变量x的取值范围;(2)请求出花圃能围成的最大面积,并写出此时x的值;(3)如图2,为了方便出入,在建造篱笆花圃时,在上用其他材料做了宽均为1m的两扇小门,能否使围成的花圃面积为?如果能,请直接写出花圃宽和长的值;如果不能,请说明理由.24.如图1,在平面直角坐标系中,为坐标原点,正方形的顶点A坐标为:将正方形绕点O逆时针旋转,旋转角为.的延长线交x轴于点D,与y轴交于点E.(1)如图2,当时,求点E的坐标;(2)如图3,在旋转过程中,连接,,交于点F,与轴交于点G,连接.设,的面积为.①求的度数;②求关于m的函数表达式,并直接写出m的取值范围;(3)在(2)的情况下,设,的面积为,.请直接写出S关于n的函数表达式(无需写出n的取值范围).25.在平面直角坐标系中,拋物线与y轴交于点,与x轴交于点和点C,拋物线的顶点为P.(1)求此抛物线的解析式和顶点P的坐标;(2)若点D,E均在此拋物线上,其横坐标分别为,.且D,E两点的纵坐标的差为3.①求m的值.②将点C向上平移个单位得到点,将拋物线沿x轴向右平移n个单位得到新拋物线,点D的对应点为点,点E的对应点为点,顶点P的对应点为点.在抛物线平移过程中,当的值最小时,请填空:______,新抛物线的顶点的坐标为______,的最小值为______.。
2023-2024学年天津市南开中学高三上学期第一次月考语文试题及答案

南开中学2024届高三第一次月检测语文学科试卷考试时间:150分钟第Ⅰ卷(共33分)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷两部分,共150分。
考试结束后,将答题卡、答题纸与作文纸一并交回。
一、 (9分,每小题3分)阅读下面一段文字,完成1~3题。
2023年9月23日,钱塘江畔。
杭州用一场以“潮起亚细亚”为总主题的盛大开幕式,为第19届亚洲运动会( )。
这是一场( ) 的文化盛宴。
采集于良渚古城遗址的火种,历经一路传递,最终点燃主火炬,恰似中华五千年文明( )、生生不息;文艺演出上篇《国风雅韵》尽展钱塘繁华、江南风韵,又巧妙地与“亚运”谐音,透出中国语言文字的精妙;开幕式上播放的短片《相约杭州》诗情画意,纵贯古今,勾勒出古都杭州的隽美、活力与现代。
,这是杭州人的浪漫,是今日中国的自信与从容。
以体育促和平,以体育促团结,以体育促包容,杭州亚运会必将成为推动构建亚洲命运共同体的生动实践。
(取材于新华社官方账号,“新华社体育”相关报道)1.依次填入文中括号内的词语,最恰当的一组是 ( )A.启航意味深长薪火相传B.启航意蕴悠长薪火相传C.起航意蕴悠长一脉相承D.起航意味深长一脉相承2.下列填入文中横线处的句子,最恰当的一组是( )A. 开幕式用“活力浙江”之新向亚洲发出邀约,又以“诗画江南”之秀展现中国式现代化的万千气象。
B. 开幕式用“诗画江南”之新展现中国式现代化的万千气象,又以“活力浙江”之秀向亚洲发出邀约。
C. 开幕式用“活力浙江”之秀展现中国式现代化的万千气象,又以“诗画江南”之新向亚洲发出邀约。
D. 开幕式用“诗画江南”之秀向亚洲发出邀约,又以“活力浙江”之新展现中国式现代化的万千气象。
3.下列文学文化常识,解说不正确的一项是( )A.杭州,古称临安、钱塘,是三吴地区的大都会,自古繁华。
柳永的词作《望海潮》主要表现的就是杭州的富庶与美丽。
B. 六艺经传,指《诗》《书》《礼》《乐》《易》《春秋》六种经书,其中《乐》久已失传。
2024届天津市南开中学高三上学期12月月考数学试题及答案

2024南开中学高三数学第二次月考一.选择题:在每小题给出的四个选项中,只有一项是符合题目要求的.1. 设集合{}ln A x y x ==,{}21B y y x ==+,则()R A B ⋂=ð( )A. ()0,1 B. (]0,1 C. [)0,1 D. []0,12. 设数列{}n a 的公比为q ,则“10a >且01q <<”是“{}n a 是递减数列”的( )A. 充分不必要条件B. 必要不充分条件C. 充要条件D. 既不充分也不必要条件3. 函数()2cos e ex x x x f x -+=-的大致图像为( )A. B.C. D.4. 设5log 2a =,ln 2b =,0.20.5c -=,则a ,b ,c 的大小关系为( )A. a c b <<B. a b c <<C. b<c<aD. c a b <<5. 设n S 为正项等比数列{}n a 的前n 项和,5a ,33a ,4a 成等差数列,则84S S 的值为( )A. 116 B. 117 C. 16D. 176. 已知35a b =且211a b +=,则a 的值为( )A. 3log 15 B. 5log 15 C. 3log 45 D. 5log 457. 我国古代数学名著《九章算术》中记载“今有羡除,下广六尺,上广一丈,深三尺,末广八尺,无深,袤七尺.问积几何?”这里的“羡除”,是指由三个等腰梯形和两个全等的三角形围成的五面体.在图1所示羡除中,////AB CD EF ,10AB =,8CD =,6EF =,等腰梯形ABCD 和等腰梯形ABFE 的高分别为7和3,且这两个等腰梯形所在的平面互相垂直.按如图2的分割方式进行体积计算,得该“羡除”的体积为( )A. 84B. 66C. 126D. 1058. 记()n a τ表示区间[],n n a 上的偶数的个数.在等比数列{}n a n -中,14a =,211a =,则()4a τ=( )A. 39B. 40C. 41D. 429. 将函数πsin 24y x ⎛⎫=+ ⎪⎝⎭图象上所有点向右平移π4个单位长度,得到函数()y g x =的图象,则( )A. ()g x 为奇函数 B. ()3πcos 24g x x ⎛⎫=- ⎪⎝⎭C. ()g x 最小正周期为2πD. ()g x 的单调递增区间为5πππ,π88k k ⎡⎤-+-+⎢⎥⎣⎦,Zk ∈二.填空题:本大题共6小题,每小题5分,共30分.试题中包含两个空的,答对1个的给3分,全部答对的给5分.10. 设i 是虚数单位,()12a i i bi +=+(,a b ∈R ),则b a -=_____.11. 在5223x x ⎛⎫- ⎪⎝⎭的展开式中,x 的系数是______.12. 已知直线():20l y kx k =->与圆221x y +=相切,且被圆()()2240x y a a ++=>截得的弦长为k =______;=a ______.13. 锐角α,β满足2π23αβ+=,tan tan 22αβ=-α和β中的较小角等于______.14. D 为ABC 的边AB 一点,满足2AD DB = .记CA a = ,CB b = ,用a ,b 表示CD = ______;若的的1CD = ,且ABC 的面积为98,则ACB ∠的最小值为______.15. 若二次函数()()2121f x ax b x a =+---在区间[]2,3上存在零点,则22a b +的最小值为______.三.解答题:本大题共5小题,共60分.解答应写出文字说明,证明过程或演算步骤.16. 在ABC 中,,,A B C 对应的边为,,a b c .已知1cos 2a C cb +=.(Ⅰ)求A ;(Ⅱ)若4,6b c ==,求cos B 和()cos 2A B +的值.17. 如图,在直三棱柱111ABC A B C -中,AB BC ⊥,12AB BC BB ===,D 为棱AB 中点.M 为线段1BC 的中点.(1)求证:1//BC 平面1ACD ;(2)求平面1ACD 与平面1C DC 的夹角的余弦值;(3)求点M 到平面1ACD 的距离.18. 椭圆22221x y a b+=的左、右顶点分别为A ,B ,上顶点为()0,2C ,左、右焦点分别为1F ,2F ,且1AF ,12F F ,1F B 成等比数列.(1)求椭圆的方程;(2)过1F 的直线l 与椭圆交于M ,N 两点,直线CM ,CN 分别与x 轴交于P ,Q 两点.若CMN CPQ S S =△△,求直线l 的斜率.19. 已知数列{}n a 是首项为1的等差数列,数列{}n b 是公比不为1的等比数列,满足122a a b +=,233a a b +=,454a a b +=.(1)求{}n a 和{}n b 的通项公式;的(2)求数列{}n n a b 的前n 项和n S ;(3)若数列{}n d 满足11d =,1n n n d d b ++=,记12nk n i k d T b ==∑.是否存在整数m ,使得对任意*n ∈N 都有212n n nd mT b ≤-<成立?若存在,求出m 的值;若不存在,说明理由.20. 已知函数()2e xf x a x =-,0a >且1a ≠.(1)当e a =时,求曲线()y f x =在1x =处的切线方程;(2)若1a >,且()f x 存在三个零点1x ,2x ,3x .(i )求实数a 的取值范围;(ii )设123x x x <<,求证:1233x x x ++>.的2024南开中学高三数学第二次月考一.选择题:在每小题给出的四个选项中,只有一项是符合题目要求的.【1题答案】【答案】A【2题答案】【答案】A【3题答案】【答案】A【4题答案】【答案】B【5题答案】【答案】D【6题答案】【答案】C【7题答案】【答案】A【8题答案】【答案】C【9题答案】【答案】B二.填空题:本大题共6小题,每小题5分,共30分.试题中包含两个空的,答对1个的给3分,全部答对的给5分.【10题答案】【答案】3.【11题答案】【答案】720【12题答案】【答案】①. ②. 4【13题答案】【答案】π6##30︒【14题答案】【答案】 ① 1233a b + ②. π2【15题答案】【答案】125三.解答题:本大题共5小题,共60分.解答应写出文字说明,证明过程或演算步骤.【16题答案】【答案】(Ⅰ)π3A =(Ⅱ)1114-【17题答案】【答案】(1)证明见解析;(2; (3.【18题答案】【答案】(1)22154x y += (2)12-或0【19题答案】【答案】(1)21n a n =-,2n n b =(2)()12326n n S n +=-⋅+(3)存在5m =,理由见解析【20题答案】【答案】(1)e e 0x y -+=(2)(i)1a <<,(ii )证明见解析.。
南开期末试题及答案

南开期末试题及答案一、选择题1.下列哪个选项是正确的?A. 太阳是绕地球旋转的B. 北京是中国的首都C. 水的沸点是0摄氏度D. 马是反刍动物答案:B. 北京是中国的首都2.以下哪个不是水的三态?A. 气态B. 固态C. 液态D. 等态答案:D. 等态3.下列哪个是中国四大发明之一?A. 蒸汽机B. 印刷术C. 电视D. 电话答案:B. 印刷术二、填空题1.中国的首都是__北京__。
2.地球的自转周期是__24__小时。
3.中国的国花是__牡丹__。
三、简答题1.请简要解释什么是供需关系?答:供需关系是指市场上商品供给量与需求量之间的相互关系。
当供给量大于需求量时,商品供应过剩,价格下降;当需求量大于供给量时,商品供应不足,价格上涨。
2.请简单介绍古希腊文明的特点。
答:古希腊文明是欧洲历史上重要的文明之一。
其特点包括:注重政治、哲学和艺术;发展了直接民主制度,居民参与政治决策;强调个人的自由和个性发展;建立了奥运会等重要的体育赛事。
四、论述题请论述中国改革开放政策的影响。
中国改革开放政策自1978年实施以来,对中国的经济社会发展产生了巨大影响。
首先,改革开放政策打破了过去的封闭局面,引入了外资和先进技术,为中国的经济发展提供了新动力。
其次,改革开放使得中国加入了国际贸易体系,促进了经济的全球化发展。
第三,改革开放政策激发了国内创新和企业家精神,推动了中国科技的发展和产业的升级。
最后,改革开放带来了人民生活水平的提高,提供了更多的就业机会,减轻了贫困问题。
总之,中国改革开放政策的影响是深远而积极的,推动了中国的现代化进程,提高了人民的生活水平,使中国在国际舞台上崭露头角。
以上是南开期末试题及答案的内容。
希望对你有所帮助。
天津市南开区2023-2024学年八年级下学期期末数学试题

天津市南开区2023-2024学年八年级下学期期末数学试题一、单选题1.下列x)A.13 B.10 C.7 D.42.下列长度的线段中,能构成直角三角形的一组是()A.5,12,13 B.6,8,12 C.3,4,6 D.8,15,163.直线y=-x-2不经过()A.第一象限B.第二象限C.第三象限D.第四象限4.)AB.C.D5.一个四边形的四边长依次为a,b,c,d,且()20a cb d-+-=,则这个四边形一定为()A.平行四边形B.矩形C.菱形D.正方形6.某共享单车前a公里1元,超过a公里的,每公里2元,若要使用该共享单车50%的人只花1元钱,a应该要取什么数()A.平均数B.中位数C.众数D.方差7.将直线123y x=-向上平移3个单位长度,得到新的直线解析式为()A.133y x=+B.113y x=+C.113y x=-D.153y x=-8.甲、乙两名同学本学期五次引体向上的测试成绩(单位:个)如图所示,则下列判断正确的是()A.乙的最好成绩比甲高B.甲的成绩的平均数比乙大C .乙的成绩比甲稳定D .甲的成绩的中位数比乙大9.如图,在Rt ABC △中,分别以这个三角形的三边为边长向外侧作正方形,面积分别记为1S ,2S ,3S .若110S =,324S =.则图中阴影部分的面积为( )A .14BC .7D 10.如图,将矩形ABCD 沿对角线BD 所在直线折叠,点C 落在同一平面内,落点记为C ',BC '与AD 交于点E ,若AB =2BC =,则DE 的长为( )A .12B .1C .32D .2 11.如图,直线483y x =+与x 轴、y 轴分别交于点A ,B .按照如下尺规作图的步骤进行操作:①以点A 为圆心,以AB 为半径画弧,交x 轴负半轴于点C .连接BC ;②分别以点B ,C 为圆心,以大于12BC 长为半径画弧,两弧交于点D ; ③连接DA 并延长,交y 轴于点E .则下列结论中错误的是( )A .点A 的坐标为()6,0-B .点B 的坐标为()0,8C .点C 的坐标为()16,0-D .点E 的坐标为()0,8-12.如图,在平面直角坐标系中,点()0,4A ,点B 在x 轴正半轴上,点C 在y 轴负半轴上,直线AB ,BC 的解析式分别为12y x a =-+和2y kx b =+(其中a ,k ,b 均为常数),有下列结论:①点B 的坐标为()2,0;②方程组2x y a kx y b +=⎧⎨-+=⎩的解为24x y =⎧⎨=⎩; ③不等式2x a kx b -+≥+的解集为2x ≥;④若点()4,P m ,点()4,Q n 分别在直线12y x a =-+和2y kx b =+上.则4n m b -+=. 其中,正确的结论个数是( )A .1B .2C .3D .4二、填空题13.直线()0y kx k =≠过点()4,2-,则k 的值为.14.计算的结果为.15.在ABCD Y 中,若200B D ∠+∠=︒,则B ∠为(度).16.如图,边长为1的正方形OABC 的边OC 落在数轴上,点C 表示的数为1,点P 表示的数为1-,以P 点为圆心,PB 长为半径画弧与数轴交于点D ,则点D 表示的数为.17.如图,正方形ABCD 的边长为4,点E 在边AB 上,点F 在边AD 的延长线上,且BE DF ==M ,N 分别在边AD ,BC 上,MN 与EF 交于点P ,且45MPF ∠=︒,则MN 的长为.18.如图,在每个小正方形的边长为1的网格中,每个小正方形的顶点叫做格点.平行四边形ABCD 的顶点A ,D 均在格点上,B ,C 的在网格线上.(1)线段AD 的长为;(2)在直线CD 上找一点P ,连接BP ,使得BP 平分ABC ∠.请用无刻度的直尺在如图所示的网格中,画出点P ,并简要说明点P 的位置是如何找到的(不要求证明).三、解答题19.计算(1)+;(2)2. 20.某部门为了解工人的生产能力情况,进行了抽样调查,随机抽取了a 名工人每天每人加工零件的个数(单位:个),绘制出如下的统计图①和图②,请根据相关信息,解答下列问题:(1)填空:a 的值为______,图①中的m 值为______;(2)求统计的a 名工人每天每人加工零件数据的平均数、众数和中位数.21.如图,正方形ABCD 中,点F 为CD 的中点,点E 为BC 上一点,且14CE BC =,设CE 的长为()0a a >.(1)用含有a 的式子表示AF 和EF ;(2)求AFE ∠的大小.22.菱形ABCD 的对角线AC ,BD 相交于点O ,取OC 中点F ,连接BF 并延长,使得BF FE =,连接CE ,DE .(1)如图1,求证:四边形OCED 为矩形;(2)如图2,若15EBD ∠=︒,16BE =,连接DF .求:BED V 的面积和菱形ABCD 的面积.23.已知甲、乙、丙三地依次在一条直线上,丙地距离甲地480km ,乙地距离甲地300km .张师傅驾车从甲地出发匀速行驶了5h 到达乙地,在乙地休整了1h ,然后继续以原来的速度匀速行驶到达丙地.当张师傅从甲地出发时,王师傅驾车从丙地出发匀速行驶到达甲地后,立即以原速返回丙地,结果他比张师傅提前1h 到达丙地.给出的图象反映了这个过程中两位师傅离甲地的距离y (单位:km )与他们行驶的时间x (单位:h )之间的对应关系.请结合相关信息,解答下列问题:(1)填表:(2)请直接写出王师傅离甲地的距离y (单位:km )与他行驶的时间x (单位:h )之间的函数解析式;(3)填空:①在王师傅返回丙地的过程中,他与张师傅相遇时距离乙地______km ;②两位师傅从出发到张师傅到达丙地的整个过程中,他们相距100km 时,x 为______(h ). 24.在平面直角坐标系中,O 为原点,平行四边形ABCD 的顶点()6,0A ,()10,0B ,()0,6D ,矩形OBEF 的顶点(F .(1)如图1,EF 与AD ,BC 交于点G ,H .①直接写出直线BC 的解析式和点H 的坐标;②求证:四边形ABHG 为菱形;(2)如图2,将矩形OBEF 沿水平方向向右平移,得到矩形O B E F ''''.点O ,B ,E ,F 的对应点分别为O ',B ',E ',F '.设()0OO t t '=>,矩形O B E F ''''与平行四边形ABCD 重合部分图形的周长为L .①在平移过程中,当矩形O B E F ''''与平行四边形ABCD 重合部分为四边形时,直接用含有t 的式子表示L ,并直接写出t 的取值范围;②如图3,若F O ''的中点为M ,矩形O B E F ''''对角线的交点为N ,连接MA ,NB .在平移过程中,当MA NB +最小时,直接写出此时L 的值.。
天津市南开区2023-2024学年七年级上学期期末语文试题(含答案)

2023—2024学年度第一学期阶段性质量监测(二)七年级语文学科本试卷分第Ⅰ卷(选择题)和第II卷两部分。
试卷满分100分,考试用时120分钟。
第Ⅰ卷(选择题共27分)一、(本大题共11小题,共27分。
1~6小题,每题2分;7~11小题,每题3分。
以下每小题给出的四个选项中,只有一个最符合题意。
)1.下面各组词语中加点字的注音,完全正确的一项是()A.派遣.(qiǎn)抽噎.(yè)勋.章(xūn)拈.轻拍重(niān)B.慷.慨(kāng)纯粹.(cuì)怅.然(cháng)神采奕.奕(yì)C.莅.临(wèi)静谧.(mì)恍.惚(huǎng)骇.人听闻(hài)D.殉.职(xùn)热忱.(chén)坍.塌(tān)淅.淅沥沥(xī)2.下面词语书写完全正确的一项是()A.气概篷勃炫耀参差不齐B.惭愧云霄安详沉墨寡言C.徘徊狭隘突兀漠不关心D.渊博消耗废虚不毛之地阅读《济南的冬天》一文,回答3~5题。
济南的冬天老舍①对于一个在北平住惯的人,像我,冬天要是不刮大风,便觉得是奇迹;济南的冬天是没有风声的。
对于一个刚由伦敦回来的人,像我,冬天要能看得见日光,便觉得是怪事;济南的冬天是响晴的。
自然,在热带的地方,日光是永远那么毒,响亮的天气反有点儿叫人害怕。
可是,在北中国的冬天,而能有温晴的天气,济南真得算个宝地。
②设若单单是有阳光,那也算不了出奇。
请闭上眼想:一个老城,有山有水,全在蓝天下很暖和安适地睡着,只等春风来把他们唤醒,这是不是个理想的境界?,③小山整把济南围了个圈儿,只有北边缺着点儿口儿。
这一圈小山在冬天特别可爱,好像是把济南放在一个小摇篮里,他们全安静不动地低声地说:“你们放心吧,这儿准保暖和。
”真的,济南的人们在冬天是面上含笑的。
他们一看那些小山,心中便觉得有了着落,有了依靠。
他们由天上看到山上,便不觉地想起:“明天也许就是春天了吧□这样的温暖,今天夜里山草也许就绿起来了吧□就是这点儿幻想不能一时实现,他们也并不着急,因为有这样慈善的冬天,干啥还希望别的呢!④最妙的是下点儿小雪呀。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
南开大学08—09年真题
08年现当代文学
一,填空
1、1806年严复将()的原著翻译为《天演论》出版。
另一位用文言文翻译外国小说的古文家是()。
2、1902年,梁启超在题为()的文章中提到了“欲新一国之民,不可不先新一国之小说”,1909年,周树人,周作人合译的小说集()出版。
3、蒋纯植、王利发分别是小说()和话剧()中的人物。
4、1926年1月,全部由中国共产党员组成的作家社团()成立,倡导“革命文学”,同年3月,徐志摩,梁实秋创办刊物月,徐志摩,梁实秋船板刊物()月刊,两种相互对立的文学思想由此形成。
5、1950年整理出版的《阿诗玛》是云南()族人民的民间叙事诗。
阿来小说《尘埃落定》展现的是()族的历史生活和文化背景。
6、1961年对电影()的批判成为新中国成立后第一次大规模的文艺批判活动。
7、小说《受戒》的作者是()《受活》的作者是()
8、诗歌《帕斯捷沃尔纳克》的作者是()《饿死诗人》的作者是()
二、词语解释
1、中国新文学大系(1917—1927)
2、爱美剧
3、未名社
4、“双百方针”
5、底层写作
三、简答
1、作为新文学开山之作的《狂人日记》不同于传统小说的叙事特征
2、冯至《十四行集》的生命意义
3、沈从文小说的语言特征
4、戏剧《茶馆》的结构优长
5、革命样板戏的叙事模式
6、余华《十八岁出门远行》的先锋性特征
四、论述
1、比较分析曹禺话剧《原野》与梁斌小说《红旗谱》农民复仇主题机器复杂性
2、《子夜》所表现出的作家的“社会科学家气质”及这部作品在20世纪中国文学史中的地位
3、距离说明现代中国随笔所受西方文学和中国古典文学的影响
4、与朦胧诗比较,“第三代诗”有何艺术创新
5、结合代表作家作品,概述1990年代的女性文学创作与1980年代相比所发生的变化
2009年现代中国文学
一、填空
1、曹禺在中学时代参加的喜剧社团(),是有南开学校创始人,张伯苓严范孙于1909不把所以创建的我过较早的喜剧社团
2、“梁刚夫”和“强猛”是矛盾小说()和()中的男性人物
3、《喀尔美萝姑娘》和《猫城记》分别是()()的小说。
4、1934年1月10日,沈从文在《大公报》文艺副刊发表了()一文,引起了一场“京派”和“海派”的文学论争,鲁迅与1934年2月3日在《申报·自由谈》发表()一文,把京派和海派分别称为“官的闲帮”和“商的闲帮”。
5、1943年,张爱玲在周庚娟主编的刊物()发表小说《沉香屑·第一香炉》,由此登上文坛,翻译家傅雷以笔名()发表评论文章《张爱玲的小说》
6、()的散文随笔集《负暄琐话》也被称之为“现代的《世说新语》”。
7、“文革”期间,张扬的()和()的《波功》是比较著名的“手抄本小说”
8、1930年,丁玲发表的小说《韦护》以现实中的作家()为原型
9、被胡风称为“吹芦笛的诗人”是指()
10、1985年,翟永明在组诗()的序言《黑夜的意识》中第一次把女性诗学和“黑夜意识”联系在一起,称为女性诗歌的宣言和理论概要。
二,词语解释
1、《小河》
2、太阳社
3、陈白露
4、中国新诗派
5、《文艺报》
6、典型共名
7、文艺黑线
三,简答
1、创造社,太阳社倡导的革命文学功过
2、早期独幕剧的创作成绩
3、初期象征诗派关于“纯诗”概念的内涵和意义
4、王小波小说中的“文革”书写的独特性
5、网络文学的基本特征
6、“新世纪文学”称谓的由来以及其基本内涵
四,论述
1、鲁迅的文学地位
2、新文学第一个十年的散文
3、1990年代小说创作“现实主义冲击波”的形成原因及创作得失。
4、以穆旦和冯至为例,论述当代文学在1950年代的创作转型及其历史动因。
5、结合创作实际,阐述海外华文女性文学的特点和成就
2008年文学基础真题
名词解释
1、新感觉派
2、《负暄琐话》
3、永明体
4、桐城派
5、陌生化
6、意识流小说
7、狂飙突进
简答
1、简述晚明小品文的主要特点
2、简述欧美现代主义文学的基本特点
3、结合具体作品,谈谈“期待视野”在文学接受中的作用
4、以《憩园》为例,简析巴金创作风格和转变
论述
1、比较分析“新写实小说”与传统“现实主义”小说的异同
2、有学者认为,《水浒传》中的李逵和宋江是一对互补的形象,谈谈你对这一问题的理解?
3、从聂赫笛朵夫的形象塑造看列夫·托尔斯泰的“心灵辩证法”
2009年文学基础真题
名词解释
1、创作动机
2、文学风格
3、潘陆
4、唐传奇
5、《财主的女儿们》
6、辛笛
7、古典主义
8、严肃喜剧
简答
1、诗歌的基本特征是什么?
2、以李玉“一笠庵四种曲”及《清忠》为例,简要谈谈苏州派戏剧的创作特点
3、为什么说《梅雨之夕》是一部“心里分析”小说
4、启蒙文学的主要特征是什么?代表作家和代表作品有哪些?(3—4个)
文本分析
1、细读下面温庭筠和韦庄的《菩萨蛮》词。
比较分析它们各自的表现特点
水晶帘里玻璃枕,暖香惹梦鸳鸯锦,江上柳如烟,雁飞残月天。
藕丝秋色浅,人胜参差剪,双鬓隔香红,玉钗头上凤。
人人尽说江南好,游人只合江南老。
春水碧于天,画船听眠。
炉边人似月,皓腕凝霜雪,未老莫还乡,还乡须断肠。
2、分析《面朝大海,春暖花开》
论述
1、简述文学的审美意识形态性质
2、以“行行重行行”、“迢迢牵牛星”、“西北有高楼”等诗歌(或你熟悉的《古诗十九首》的其他诗歌)为例,谈谈《古诗十九首》的艺术表现特征。
3、结合《老人与海》谈谈海明威创作的主题和特征。
