河南省郑州市2019-2020学年下学期阶段性学业检测题八年级数学(PDF版)
2019学年八年级数学下学期学业质量测试(期末)试题(无答案) 苏科版

2019学年八年级数学下学期学业质量测试(期末)试题本试卷由选择题、填空题和解答题三大题组成.共28小题,满分100分,考试时间100分钟.注意事项:1.答题前,考生务必将自己的姓名、考点名称、考场号、座位号、考试号填涂在答题卡相应的位置上;2.答选择题必须用2B 铅笔把答题卡上对应题目的答案标号涂黑,如需改动,请用橡皮擦干净后,再选涂其他答案;答非选择题必须用0.5毫米黑色墨水签字笔写在答题卡指定的位置上, 不在答题区域内的答案一律无效,不得用其他笔答题;3.考生答题必须答在答题卡上,保持卡面清洁,不要折叠,不要弄破,答在试卷和草稿纸上一律无效.一、选择题:本大题共10小题,每小题2分,共20分,在每小题给出的四个选项中,只有一项是符合题目要求的,请将选择题的答案用2B 铅笔填涂在答题卡相应的位置上.1.某汽车制造厂为了使顾客了解一种新车的耗油量,公布了调查20辆该车每辆行驶100千米的 耗油量,在这个问题中总体是A.所有该种新车的100千米耗油量B. 20辆该种新车的100千米耗油量C.所有该种新车D. 20辆汽车 2.下列标志图中,既是轴对称图形,又是中心对称图形的是3.下列说法正确的是A.若你在上一个路口遇到绿灯,则在下一路口必遇到红灯B.某篮球运动员2次罚球,投中一个,则可断定他罚球命中的概率一定为50%C.“明天我市会下雨”是随机事件D.若某种彩票中奖的概率是1%,则买100张该种彩票一定会中奖4.一种药品经过两次降价,药价从每盒60元下调至每盒48.6元,则平均每次降价的百分率是 A. 1 % B. 10% C. 1.9% D. 19%5.如图,ABC ∆中,//,//DE BC EF AB ,要判定四边形DBFE是菱形,还需要添加的条件是A.BE 平分ABC ∠B.AD BD =C. BE AC ⊥D. AB AC = 6.己知四边形ABCD 是平行四边形,下列结论中不正确的是A.当AB BC =时,它是菱形B.当AC BD ⊥时,它是菱形C.当90ABC ∠=︒时,它是矩形D.当AC BD =时,它是正方形 7.若关于x 的一元二次方程2210kx x +-=有实数根,则k 的取值范围是A. 1k ≥-且0k ≠B. 1k ≥-C. 1k >-D. 1k >-且0k ≠ 8.己知反比例函数12my x-=的图像上两点1122(,),(,)A x y B x y ,当120x x <<时,有12y y <,则m 的取值范围是A. 0m >B. 12m >C. 0m <D. 12m < 9.如图,王华晚上由路灯A 下的B 处走到C 处时,测得影子CD 的长为1米,继续往前走3米到达E 处时,测得影子EF 的长为2米,已知王华的身高是1.5米,那么路灯A 的高度AB 等于A. 4.5米B. 6米 C . 7.2米 D. 8米10.如图,四边形AOBC 和四边形CDEF 都是正方形,边AO 在x 轴上,边OB 在y 轴上,点D 在边BC 上,反比例函数8y x=-在第二象限的图像经过点E ,则正方形AOBC 和正方形CDEF 的面积之差为 A. 12 B. 10 C. 8 D. 6二、填空题:本大题共8小题,每小题2分,共16分,把答案直接填写在答题卡相应位置上,11.某校对1200名女生的身高进行了测量,身高在 1.58m-1.63m 这一小组的频率为0.25,则该组共有 人.12.在一个不透明的口袋中,装有4个红球和1个白球,这些球除颜色之外其余都相同,那么摸出1个球是红球的概率为 . 11.如果反比例函数ky x=的图像经过点(1,3),则k = . 14.己知关于x 的方程230x x m -+=的一个根是2,则它的另一个根是 .15.如图,平行四边形ABCD 中,E 为AD 的中点,连接CE ,若平行四边形ABCD 的面积为24cm 2,则C D E∆的面积为 cm 2.16.如图,在四边形A B C D 中,P 是对角线BD 的中点,,E F 分别是,A B C D 的中点,A DB C=,100FPE ∠=︒,则PFE ∠的度数是 .17.如图,在平面直角坐标系中,点(,)A a b 为第一象限内一点,且a b <.连接OA ,并以点A 为旋转中心把OA逆时针转90°后得线段BA .若点,A B 恰好都在同一反比例函数的图像上,则ba的值等于 . 18.如图,在ABC ∆中,90ABC ∠=︒, BD 为AC 的中线,过点C 作CE BD ⊥于点E ,过点A 作BD 的平行线,交CE 的延长线于点F ,在AF 的延长线上截取FG BD =,连接,BG DF .若13,6AG CF ==,则BG = .三、解答题:本大题共10小题,共64分,把解答过程写在答题卡相应的位置上,解答时应写出必要的计算过程、推演步骤或文字说明.作图时用2B 铅笔或黑色墨水签字笔. 19.(本题满分6分,每小题3分)解方程:(1) 22510x x -+= ; (2) 3(2)2(2)x x x -=-.20. (本题满分4分)先化简,再求值: 222444(1)42x x x x x x -++-÷--+,其中22150x x +-=. 21.(本题满分5分)如图,在平面直角坐标系中,ABC ∆的 顶点坐标分别(1,3),(2,1),(4,2)A B C ,以坐标原点为位 似中心,在第三象限画出与ABC ∆位似的三角形,使相似比为2:1,并写出所画三角形的顶点坐标.22.(本题满分5分)随着移动终端设备的升级换代,手机己经成 为我们生活中不可缺少的一部分,为了解中学生在假期使用 手机的情况(选项:A.和同学亲友聊天;B.学习;C.购物;D.游戏;E. 其它),端午节后某中学在全校范围内随机抽取了若干名学生 进行调查,得到如右表格(部分信息未给出): 根据以上信息解答下列问题: (1)这次被调查的学生有多少人? (2)求表中,m n 的值:(3)若该中学有800名学生,估计全校学生中利用手机购物或玩游戏的共有多少人?23.(本题满分6分)一个容器盛满纯药液63L ,第一次倒出一部分纯药液后,用水加满;第二次 又倒出同样多的药液,若此时容器内剩下的纯药液是28L ,则每次倒出的液体是多少?24.(本题满分6分)在矩形纸片ABCD 中,6,8AB BC ==.将矩形 纸片折叠,使点B 与点D 重合,求折痕GH 的长.25.(本题满分6分)如图,反比例函数1k y x =的图像与一次函数214y x =的图像交于点,A B ,点 B 的横坐标是4,点(1,)P m 在反比例函数1ky x=的图像上.(1)求反比例函数的表达式;·(2)观察图像回答:当x 为何值时,12y y >.26.(本题满分8分)如图,Rt ABC ∆中90C ∠=︒且,AC CD E D ==为CB 的三等分点.(1)求证: ADE BDA ∆∆;(2)证明: ADC AEC B ∠=∠+∠;(3)若点P 为线段AB 上一动点,连接PE 则使线段PE的长度为 整数的点的个数有 个.(直接写答案无需说明理由)27.(本题满分8分)如图,AM 是ABC ∆的中线,D 是线段AM 上一点(不与点A 重合). //DE AB 交AC 于点F , //CE AM 连结AE .(1)如图1,当点D 与D 重合时,求证:四边形ABDE 是平行四边形; (2)如图2,当点D 不与D 重合时,(1)中的结论还成立吗?请说明理由;(3)如图3,延长BD 交AC 于点H ,若BH AC ⊥,且BH AM =,求CAM ∠的度数.28.(本题满分10分)如图,在平面直角坐标系中,直线210y x =-+与x 轴、x 轴分别交于,A B 两点. (1)反比例函数1k y x=的图像与直线AB 交于第一象限内的,C D 两点(BD BC <),当 4AD DB =时,求1k 的值;·(2)设线段AB 的中点为P ,过P 作x 轴的垂线,垂足为点M ,交反比例函数2k y x的图像于点Q ,连接,OP OQ ,当以,,P O Q 为顶点的三角形与以,,O B P 为顶点的三角形相似时,求2k 的值.。
河南省郑州市2019-2020学年高二下学期期末考试数学(理)试题Word版含解析

河南省郑州市2019-2020学年高二下学期期末考试数学(理)试题注意事项:本试卷分第I卷(选择题)和第II卷(非选择题)两部分。
考试时间120分钟,满分150分。
考生应首先阅读答题卡上的文字信息,然后在答题卡上作答,在试题卷上作答无效。
交卷时只交答题卡。
第I卷〖选择题,共60分)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题所给出的四个选项中,只有一项是符合题目要求的1.已知i是虚数单位,则复数的共轭复数在复平面内对应的点所在的象限为()A. 第一象限B. 第二象限C. 第三象限D. 第四象限2.在某项测量中,测量结果,若在内取值的概率为0.3,则在(0,+∞)内取值的概率为()A. 0.2B. 0.4C. 0.8D. 0.93.有一段“三段论”,推理是这样的:对于可导函数,如果,那么是函数的极值点,因为在处的导数值,所以是函数的极值点.以上推理中()A. 大前提错误B. 小前提错误C. 推理形式错误D. 结论正确4.函数y=x2- lnx的单调递减区间为()A. (-1,1)B. (0,1)C. (1,+∞);D. (0,+∞)5.已知具有线性相关关系的五个样本点A1(0,0),A2(2,2),A3(3,2),A4(4,2)A5(6,4),用最小二乘法得到回归直线方程l1:y=bx+a,过点A1,A2的直线方程l2:y=mx+n那么下列4个命题中(1) ;(2)直线过点; (3) ; (4) .(参考公式,)正确命题的个数有()A. 1个B. 2个C. 3个D. 4个6.由曲线,直线及轴所围成的平面图形的面积为( ).A. B. 4 C. D. 67.已知直线y=x+1与曲线相切,则α的值为A. 1B. 2C. -1D. -28.从中任取个不同的数,事件为“取到的个数之和为偶数”,事件为“取到的个数均为偶数”,则等于A. B. C. D.9.已知函数f(x)=4x2+sin(+x),f ' (x)为f(x)的导函数,则f ' (x)的图象是()A. B. C. D.10.现有4种不同品牌的小车各2辆(同一品牌的小车完全相同),计划将其放在4个车库中(每个车库放2辆则恰有2个车库放的是同一品牌的小车的不同放法共有()A. 144种B. 108种C. 72种D. 36种11.设a=sin1,b=2sin,c=3sin,则()A. c<a<bB. a<c<bC. a<b<cD. c<b<a12.已知函数f(x)是定义在R上的增函数,f(x)+2>f ' (x),f(0)=1,则不等式ln[f(x)+2]>ln3+x的解集为()A. (一∞,0)B. (0,+∞)C. (一∞,1)D. (1,+∞)第Ⅱ卷(非选择题,共90分)二、填空题(每题5分,满分20)13.若将函数f(x)=x5表示为f(x)=a o+a1(1+x)+a2(1+x)2+…+a5(1+x)5,其中a(i=0,1, …,5)为实数,则a3=__________14.一次英语测验由50道选择题构成,每道题有4个选项,其中有且仅有一个是正确的,每个选对得3分,选错或不选均不得分,满分150.某学生选对每一道题的概率均为0.7,则该生在这次测验中的成绩的期望是__________15.已知函数f(x)=kx3+3(k-1)x2-k2+1(k>0)在(0,4)上是减函数,则实数k的取值范围是____________16.如图所示,由直线x=a , x=a+1(a>0),y=x2及x轴围成的曲边梯形的面积介于小矩形和大矩形的面积之间,即,类比之,恒成立,则实数A=___________三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.〉17.设实部为正数的复数z,满足|z|=,且复数(1+3i)z在复平面内对应的点在第一、三象限的角平分线上.(I)求复数z(II)若复数+ m2(1 +i)-2i十2m -5为纯虚数,求实数m的值.18.已知(1+m)n(m是正实数)的展开式的二项式系数之和为128,展开式中含x项的系数为84,(I)求m,n的值(II)求(1+m)n (1-x)的展开式中有理项的系数和.19.已知某公司为郑州园博园生产某特许商品,该公司年固定成本为10万元,每生产千件需另投入2 .7万元,设该公司年内共生产该特许商品工x千件并全部销售完;每千件的销售收入为R(x)万元,且,(I)写出年利润W(万元〉关于该特许商品x(千件)的函数解析式;〔II〕年产量为多少千件时,该公司在该特许商品的生产中所获年利润最大?20.为了响应党的十九大所提出的教育教学改革,某校启动了数学教学方法的探索,学校将髙一年级部分生源情况基本相同的学生分成甲、乙两个班,每班40人,甲班按原有传统模式教学,乙班实施自主学习模式.经过一年的教学实验,将甲、乙两个班学生一年来的数学成绩取平均数,两个班学生的平均成绩均在[50,100],按照区间[50,60),[60,70),[70,80),[80,90),[90,100]进行分组,绘制成如下频率分布直方图,规定不低于80分(百分制)为优秀,,(I)完成表格,并判断是否有90%以上的把握认为“数学成绩优秀与教学改革有关”〔Ⅱ)从乙班[70,80),[80,90),[90,100]分数段中,按分层抽样随机抽取7名学生座谈,从中选三位同学发言,记来自[80,90)发言的人数为随机变量x,求x的分布列和期望.21.已知数列{a n}的前n项和S n满足,且,(I)求a1,a2,a3;(II)猜想数列{a n}的通项公式,并用数学归纳法证明.22.已知函数f(x)= ln(a x)+bx在点(1,f(1))处的切线是y=0;(I)求函数f(x)的极值;(II)当恒成立时,求实数m的取值范围(e为自然对数的底数)河南省郑州市2019-2020学年高二下学期期末考试数学(理)试题参考答案注意事项:本试卷分第I卷(选择题)和第II卷(非选择题)两部分。
2019-2020年八年级数学下学期单元练习试题(二) 浙教版

2019-2020年八年级数学下学期单元练习试题(二) 浙教版【考生须知】全卷共5页,有三大题, 24小题.满分120分,考试时间90分钟.【温馨提示】请仔细审题, 细心答题, 相信你一定会有出色的表现.一、仔细选一选(每小题3分,共30分).1x 不能取的是( ▲ )A . 1B .C . 2D . 42.下列语句中,属于命题的是 ( ▲ )A .任何一元二次方程都有实数解;B .作直线AB 的平行线;C .∠1与∠2相等吗?D .若2a 2= 9,求a 的值. 3.用配方法解方程,变形结果正确的是( ▲ )A .B .C .D .4.一幅美丽的图案,在某个顶点处由四个边长相等的正多边形镶嵌而成,其中三个分别是正三角形、正四边形、正六边形,则另一个是 ( ▲ ) A .正三角形 B .正四边形 C .正五边形 D .正六边形 5、下面这几个车标,是中心对称图形而不是轴对称图形的共有( ▲ ) A .0个B .1个C .2个D .3个6、近年来,温州市区增加了多个绿化广场和公园.如图是某广场上的一个形状是平行四边形的花坛,分别种有红,黄,蓝,绿,橙,紫6种颜色的花.如果有AB ∥EF ∥DC ,BC ∥GH ∥AD ,那么下列说法中错误的是( ▲ )A .红花,绿花种植面积一定相等B .紫花,橙花种植面积一定相等C .红花,蓝花种植面积一定相等D .蓝花,黄花种植面积一定相等7、某超市一月份的营业额为300万元,第一季度的营业额共为1500万元,如果平均每月增长率为x ,则由题意可列方程为 ( ▲ )A . 2300(1)1500x += B . 30030021500x +⨯=C . 30030031500x +⨯=D . 23001(1)(1)1500x x ⎡⎤++++=⎣⎦8、下列四个命题中:① 对角线相等的四边形是矩形;② 对角线互相平分的四边形是平行四边形;③ 对角线互相垂直的四边形是菱形;④ 对角线互相垂直且相等的四边形是正方形.其中正确的命题有 ( ▲ ) A .1个 B .2个 C .3个 D .4个9.在平面直角坐标系内,A 、B 、C 三点的坐标为(0,0)、(4,0)、(3,2),以A 、B 、C 三点为顶点画平行四边形,则第四个顶点不可能在( ▲ ) A .第一象限B .第二象限C .第三象限D .第四象限10.意大利著名数学家斐波那契在研究兔子繁殖问题时,发现有这样一组数:1,1,2,3,5,8,13,……,其中从第三个数起,每一个数都等于它前面两个数的和.现以这组数中的各个数作为正方形的长度构造一组正方形(如下图),再分别依次从左到右取2个,3个,4个,5个正方形拼成如下矩形并记为①、②、③、④,相应矩形的周长如下表所示:若按此规律继续作矩形,则序号为⑧的矩形周长是( ▲ ) A .288 B .178 C .128 D .110 二、细心填一填(本题有6小题,每小题4分,共24分)11、在一组数据中,最大值为99,最小值是28,则这组数据的极差为 . 12、点(5,9)与点(,)x y 关于原点对称,则x +y = .13、任写一个一根为1-,另一根大于0小于1的一元二次方程 . 14、将50个数据分成5组列出频数分布表,其中第一组的频数是6,第二组与第五组的频数和为20,第三组的频率为0.2,则第四组的频数为 .15.如图,点O 是AC 的中点,将周长为4㎝的菱形AB CD 沿对角线AC 方向平移AO 长度得到菱形OB 'C 'D ',则四边形OECF 的周长是 ㎝.16.把图一的矩形纸片ABCD 折叠,B 、C 两点恰好重合落在AD 边上的点P 处(如图二), 已知∠MPN = 90°,PM = 3,PN = 4,(1)BC 的长为 ;(2)矩形纸片ABCD 的面积为 .三、解答题(本题有8小题,共66分,各小题都必须写出解答过程)图一D CB A (第16题) (第15题)17、化简(本题5分):218、(本题6分)解一元二次方程:22620 x x-=19、(本小题8分)为了开展阳光体育运动,坚持让中小学生“每天锻炼一小时”,某体育组搞了一个随机调查,调查的内容是:“每天锻炼是否超过1小时,及锻炼未超过1小时的原因”。
2019-2020学年第一学期期末调研考试八年级数学试题及答案(含解析与评分标准)

2019—2020学年度第一学期期末调研考试八年级数学试题注意:本份试卷共8页,三道大题,26个小题;总分120分,时间120分钟。
一、选择题(本大题共16个小题,共42分.1~10小题各3分,11~16小题各2分,共42分.在每小题给出的四个选项中,只有一项是符合题目要求的.请将正确的选项填在下表中)1.如图一个五边形木架,要保证它不变形,至少要再钉上几根木条 A .1 B .2 C .3 D .42.要使分式242x x -+有意义,则x 的取值范围是A .x ≠﹣2B .x =2C .x =﹣2D .x ≠±2 3.如图,在△ABC 和△DEF 中,AB =DE ,∠A =∠D ,添加一个条件不能判定这两个三角形全等的是A .AC =DFB .∠B=∠EC .∠C =∠FD .BC =EF 4.下列计算正确的是A .(a 2)3=a 5B .(﹣ab )2=a 2b 2C .2a (a ﹣b )=2a 2﹣bD .(2a 2b ﹣ab 2)÷2ab =a ﹣b 5.将1022变形正确的是A .1022 =1002 +22B .1022 =(100+2)(100﹣2)C .1022 =1002 +2×100×2+22D .1022 =1002 +100×2+22 6.如图,在△ABC 中,点D 是∠ABC 和∠ACB 的角平分线的交点,∠A =80°,∠ABD =30°, 则∠DCB 为A .25°B .20°C .15°D .10° 7.若n 边形的内角和等于外角和的3倍,则边数n 为 A .n =6 B .n =7 C .n =8 D .n =98.若点P (2a ﹣1,3)关于y 轴对称的点为Q (3,b ),则点M (a ,b )关于x 轴对称的点的坐标为A .(﹣1,﹣3)B .(﹣1,3)C .(1,﹣3)D .(1,3) 9.等腰三角形的周长为18cm ,其中一边长为4cm ,则该等腰三角形的腰长为 A .6cm B .7cm 或4cm C .7cm D .4cm 10.下列各选项中,所求的最简公分母错误的是A .13x 与16x的最简公分母是6x B .2313a b 与2313a b c 的最简公分母是3a 2b 3cC .1m n +与1m n-的最简公分母是m 2﹣n 2D .()1a x y -与()1b y x -的最简公分母是ab (x ﹣y )(y ﹣x )11.若20.2a =-,22b -=-,212c -⎛⎫=- ⎪⎝⎭,012d ⎛⎫=- ⎪⎝⎭,则它们的大小关系是A .b <a <d <cB .a <b <d <cC .a <d <c <bD .c <d <a <b12.若分式21x x +□1xx +的运算结果为x (x ≠0),则在“口”中添加的运算符号为A .+B .﹣C .+或÷D .﹣或× 13.如果关于x 的分式方程2122m xx x-=--无解,那么m的值为A .4B .﹣4C .2D .﹣214.如图所示,将矩形纸片ABCD 折叠,使点D 与点B 重合,点C 落在点C ′处,折痕为EF ,若∠EFC ′=122°,那么∠ABE 的度数为A.24°B.32°C.30°D.26°15.同学们都玩过跷跷板的游戏,如图是一个跷跷板的示意图,立柱OC与地面垂直,OA=OB.当跷跷板的一头A着地时,∠AOA′=50°,则当跷跷板的另一头B着地时,∠COB′等于A.25°B.50°C.65°D.130°16.如图,在第一个△ABA1中,∠B=20°,AB=A1B,在A1B上取一点C,延长AA1到A2,使得A1A2=A1C,得到第二个△A1A2C;在A2C上取一点D,延长A1A2到A3,使得A2A3=A2D;…,按此做法进行下去,则第5个三角形中,以点A4为顶点的等腰三角形的顶角的度数为A.170°B.175°C.10°D.5°二、填空题(本大题共3小题,共11分.17小题3分,18、19小题各有2个空,每空2分.把答案写在题中横线上)17.分解因式:2a3﹣2a=.18.已知a m=8,a n=2.则a m﹣n=,m与n的数量关系为.19.如图,长方形台球桌面ABCD上有两个球P、Q.PQ∥AB,球P连续撞击台球桌边AB,BC反射后,撞到球Q.已知点M、N是球在AB、BC边的撞击点,PQ=4,∠MPQ=30°,且点P到AB边的距离为3,则MP的长为,四边形PMNQ的周长为.三、解答题(本大题共7小题,共67分.解答应写出文字说明、证明过程或演算步骤)20.(本题满分8分)计算:(1)(x﹣y)2﹣x(y﹣2x)(2)2344111x xxx x++⎛⎫-+÷⎪++⎝⎭21.(本题满分9分)如图,在所给正方形网格(小正方形的边长为1)的图中完成下列各问:(用直尺画图)(1)求格点△ABC(顶点均在格点上)的面积;(2)画出△ABC关于直线l对称的△A1B1C1;(3)在直线l上画出点D,使△ABD的周长最小.22.(本题满分9分)如图,已知点D和点B在线段AE上,且AD=BE,点C和点F在AE的同侧,∠A=∠E,AC=EF,DF和BC相交于点H.(1)求证:△ABC≌△EDF;(2)当∠CHD=120°,猜想△HDB的形状,并说明理由.23.(本题满分9分)阅读与思考分组分解法分组分解法指通过分组分解的方式来分解用提公因式法和公式法无法直接分解的多项式,比如,四项的多项式一般按照“两两”分组或“三一”分组进行分组分解.分析多项式的特点,恰当的分组是分组分解法的关键.例1:“两两”分组:ax+ay+bx+by=(ax+ay)+(bx+by)=a(x+y)+b(x+y)=(a+b)(x+y)我们把ax和ay两项分为一组,bx和by两项分为一组,分别提公因式,立即解除了困难.同样,这道题也可以这样做:ax+ay+bx+by=(ax+bx)+(ay+by)=x(a+b)+y(a+b)=(a+b)(x+y)例2:“三一”分组:2xy+x2﹣1+y2=(x2+2xy+y2)﹣1=(x+y)2﹣1=(x+y+1)(x+y﹣1)我们把x2,2xy,y2三项分为一组,运用完全平方公式得到(x+y)2,再与﹣1用平方差公式分解,问题迎刃而解.归纳总结:用分组分解法分解因式的方法是先恰当分组,然后用提公因式法或运用公式法继续分解.请同学们在阅读材料的启发下,解答下列问题:(1)分解因式:①a2﹣ab+3a﹣3b;②x2﹣2xy﹣9+y2.(2)若多项式ax2﹣9y2+bx+3y利用分组分解法可分解为(2x+3y)(2x﹣3y+1),请直接写出a,b的值.24.(本题满分10分)如图所示,在△ABC中:(1)下列操作中,作∠ABC的平分线的正确顺序是(将序号按正确的顺序写在横线上).①分别以点M、N为圆心,大于12MN的长为半径作圆弧,在∠ABC内,两弧交于点P;②以点B为圆心,适当长为半径作圆弧,交AB于点M,交BC于N点;③画射线BP,交AC于点D.(2)能说明∠ABD=∠CBD的依据是(填序号).①SSS.②ASA.③AAS.④角平分线上的点到角两边的距离相等.(3)若AB=18,BC=12,S△ABC=120,过点D作DE⊥AB于点E,求DE的长.25.(本题满分10分)亚洲未来最大火车站雄安站是京雄城际铁路的终点站,于2018年12月1日正式开工建设,预计2020年底投入使用.该车站建成后,可实现雄安新区与北京、天津半小时交通圈,与石家庄1小时交通圈,将进一步完善京津冀区域高速铁路网结构,便利沿线群众出行,对提高新区全国辐射能力,促进京津冀协同发展,均具有十分重要的意义.某工厂承包了雄安站建设中某一零件的生产任务,需要在规定时间内生产24000个零件,若每天比原计划多生产30个零件,则在规定时间内可以多生产300个零件.(1)求原计划每天生产的零件个数和规定的天数.(2)为了提前完成生产任务,工厂在安排原有工人按原计划正常生产的同时,引进5组机器人生产流水线共同参与零件生产,已知每组机器人生产流水线每天生产零件的个数比20个工人原计划每天生产的零件总数还多20%,按此测算,恰好提前两天完成24000个零件的生产任务,求原计划安排的工人人数.26.(本题满分12分)如图1,△ABC是直角三角形,∠C=90°,∠CAB的角平分线AE与AB的垂直平分线DE相交于点E.(1)如图2,若点E正好落在边BC上.①求∠B的度数;②证明:BC=3DE.(2)如图3,若点E满足C、E、D共线.线段AD、DE、BC之间是否满足AD+DE =BC,若满足请给出证明;若不满足,请说明理由.2019—2020 (一) 八年级数学参考答案及评分标准说明:1.在阅卷过程中,如果考生还有其它正确解法,可参照评分参考酌情给分;2.填空题缺少必有的单位或答案不完整不得分;3.坚持每题评阅到底的原则,当考生的解答在某一步出现错误,影响了后继部分时,如果该步以后的解答未改变这一题的内容和难度,可视影响的程度决定后面部分的给分,但不得超过后继部分应给分数的一半;如果这一步后面的解答有较严重的错误,就不给分;4.解答右端所注分数,一般表示正确做到这一步应得的累积分数.一、选择题(本大题有16小题,共42分.1~10小题各3分,11~16小题各2分)二、填空题(本大题有3个小题,共11分.17小题各3分;18、19小题各有2个空,每空2分)17. 2a(a+1)(a﹣1);18. 4;m=3n;19. 6;16.三、解答题(本大题有7小题,共67分)20. 解:(1)原式=x2﹣2xy+y2﹣xy+2x2……………………………………………3分=3x2﹣3xy+y2;…………………………………………………4分(2)原式()()211344=111x x x xx x x-+⎡⎤++-÷⎢⎥+++⎣⎦……………………………1分22444=11x x x x x -+++÷++………………………………………………2分()()()2221=12x x x x x -+-+++…………………………………………3分 22x x -=-+.……………………………………………………………4分 21. (1)解:S △ABC =3×3﹣×2×1﹣×1×3﹣×2×3 ………………2分=9﹣1﹣1.5﹣3=3.5 ………………………………………………………3分(2)△A 1B 1C 1如图所示; ………………………………………………………6分(3)图中点D 即为所求.……………………………………………………9分 22.(1)证明:∵AD =BE ,∴AD +DB =BE +DB ,即AB =ED ,…………………………………………1分 在△ABC 和△EDF 中,AB ED A E AC EF =⎧⎪∠=∠⎨⎪=⎩………………………………………………………………………3分 ∴△ABC ≌△EDF (SAS ); …………………………………………………4分 (2)解:△HDB 是等边三角形,理由如下: ……………………………5分 ∵△ABC ≌△EDF ,∴∠HDB =∠HBD ,…………………………………………………………6分 ∵∠CHD =∠HDB +∠HBD =120°,。
洪山区2019-2020学年度第二学期期末考试八年级数学试卷(word版)

八年级数学试卷 第1页(共6页)2019-2020学年度第二学期洪山区复学质量检测八年级数学试卷洪山区教育科学研究院命制 2020.8.13第Ⅰ卷(选择题 共30分)一、选择题(本大题共10小题,每小题3分,共30分)下列各题中均有四个备选答案,其中有且只有一个正确,请在答题卡上将正确答案的选项涂黑.1.二次根式√x +9在实数范围内有意义,则x 的取值范围是A .9x ≥-B .9x ≤-C .9x >-D .9x <-2.下列二次根式是最简二次根式的是( )A .√14B .√5C .√24D .√323.2020年的新冠病毒疫情,武汉从高风险的红色,到中风险的黄色,再到低风险的绿色;从全国疫情“风暴眼”到院士、专家眼中的“目前全国最安全城市”,背后是英雄的武汉和武汉人民历经千辛万苦的英勇奋斗、咬牙坚守.若用横轴表示时间,纵轴表示人数,下面函数图像能够大致反应武汉在疫情期间确诊人数的是A B C D4.以下列长度的线段为边,不能..组成直角三角形的是 A .6、8、10B .√3、√4、√5C .1、1、√2D .8、15、17 5.网课期间,某同学对全班40名同学日常在家锻炼的时间统计如下:则关于这40名同学锻炼时间的说法不正确...的是 A. 平均数是0.6 B .中位数是0.5 C .众数是15 D .极差是1.56.下列性质中,矩形具有、正方形也具有、但是菱形却不具有...的性质是 A .对角线互相垂直B .对角线互相平分C .对角线长度相等D .一组对角线平分一组对角八年级数学试卷 第2页(共6页)第10题图第9题图 7.若直线3y x b =-+不经过...第三象限,则b 的值可以为 A .1 B .2- C .1- D .3- 8.将2020个形状、大小均相同的菱形按照如图所示的方式排成一列,使得右侧菱形的顶点与左侧菱形的对角线交点重合,若这些菱形的边长均为a ,则阴影部分的周长总和等于A .2020aB .4038aC .4040aD .4042a9.如图,将长为2,宽为1的四个矩形如图所示摆放在坐标系中,若正比例函数y kx =的图像恰好将所组成的图形分为面积相等的两部分,则k 的值等于A .1B .32C .23D .4310.如图,直线4y x =-分别交x 轴、y 轴于A 、B 两点,C 为OB 中点(O 为坐标原点),D 点在第四象限,且满足∠ADO =45°,则线段CD 长度的最大值等于A .√2+4B .2√2+2C .4D .√2+2第Ⅱ卷(非选择题,共90分)二、填空题(本大题共6小题,每小题3分,共18分)下列各题不需要写出解答过程,请将结果直接写在答题卡指定位置.11.化简√18 = ______. 12.若y 关于x 的函数y =-7x +2+m 是正比例函数,则m =___________.13.已知一组数据-1、2、x 、3、1的平均数等于1.4,则这组数据的中位数等于________.14.两边之比为黄金分割比(√5−12)的矩形称为“黄金矩形”,许多经典的艺术作品如希腊雅典的巴特农神庙、蒙娜丽莎或断臂维纳斯等都包含有黄金分割比,它能给人们带来视觉上的美感.如图,矩形ABCD就是一个“黄金矩形”,其对角线AC与边AD的夹角近似为32°,F为边BC上的一点,DF与AC的交点为O.现将矩形一边DC沿直线DF 折叠,使点C落在点E上,且满足DE与AC垂直,则∠DOC= °.15.直线y=2x上有一点C,与A(3,0)、B(0,2)组成的三角形满足S△ABC=6,则C点的坐标为 .16.如图,M为钝角△ABC中BC边的中点,经过M的直线MN将△ABC分成了周长相等的两部分.已知AB=6,∠A=120°,则MN= .三、解答题(本大题共8小题,共72分)下列各题需要在答题卡指定位置写出文字说明、证明过程、演算步骤或画出图形. 17.(本小题满分8分)计算:(1)12188-+(2)(232)(31)-+18.(本小题满分8分)如图,矩形ABCD中AE=CF,连接DE、BF.(1)求证:四边形BEDF是平行四边形;(2)取DE、BF的中点M、N并连接,若AB=8,BC=4,CF=3,试求线段MN的长度.八年级数学试卷第3页(共6页)19.(本小题满分8分)在这个信息瞬息万变的时代,电商行业每年都在发生变化,随着客户和企业适应了网上零售的流行,他们的购物偏好和方式变得合理.电商趋势处于不断变化的状态,相比以往,2020年将会成为一个更辉煌的年份.下面是艾媒咨询(iiMedia Research)统计的过去一年里电商用户的人数及年龄分布情况:组别A B C D E年龄分布25岁以下25~30岁31~35岁36~40岁40岁以上试根据以上统计,回答下列问题:(1)本次调查共涉及电商用户____________亿人,其中年龄25岁以下占_________%,电商用户年龄中位数在____________组;(2)E组共有____________亿人,扇形统计图中其所对应的扇形圆心角为______°;(3)截止2019年年底,湖北人在天猫上消费85.88亿元,同比增长29%,排全国第九,其中武汉人“剁手力”最强,以46.45亿元列全国城市第八.据统计,武汉市电商用户约有300万人,那么其中年龄在25岁以下的用户大约有多少人?20.(本小题满分8分)在如图所示的方格纸中,每个小正方形的边长为1个单位长度,我们称每个小正方形的顶点为“格点”.(1)若格点C在线段AB右侧,且满足AC=BC,则当△ABC的周长最小时,△ABC的面积等于____________;(2)若格点D在线段AB左侧,且满足AD⊥BD,则△ABD的面积等于____________.(以上两问均直接写出结果即可)八年级数学试卷第4页(共6页)21.(本小题满分8分)如图,在平面直角坐标系中,折线y=-|x-2|+1与直线y=kx+2k(k>0)如图所示.(1)直线y=kx+2k(k>0)与x轴交点的坐标为____________;(2)请用分段函数的形式表示折线y=-|x-2|+1;(3)若直线y=kx+2k(k>0)与折线y=-|x-2|+1有且仅有一个交点,直接写出k的取值范围____________.22.(本小题满分10分)今年两会,李克强总理点赞“地摊经济”称,地摊经济、小店经济是就业岗位的重要来源,鼓励通过线上线下一体销售.据统计,武汉王家湾夜市和虎泉夜市等多家夜市自五一假期以来,人流量、经济流通收入同比增长142.9%,服装行业的增长最为迅速.记者了解到,两家夜市主要服装进货来源是佛山和广州两家服装批发厂,其中某种服装的进货价格如下:虎泉夜市现需服装5000件,王家湾夜市需8000件,最多可从佛山服装批发厂调进10000件,剩余的则从广州服装批发厂进货,若虎泉夜市从佛山进货x件,两家夜市的进货总费用为W元.(1)W=__________________________()(括号内写出x的取值范围);(2)请你设计一种进货方案使两家夜市的进货总费用最少,并计算此时的最少费用;(3)六月份开始,广州服装厂与两家夜市签订长期协议,对虎泉夜市进货单价统一降低a元,对王家湾夜市进货单价统一降低2a元,其中0<a≤10,试求此时两家夜市最少进货总费用y关于a的函数关系式.八年级数学试卷第5页(共6页)八年级数学试卷 第6页(共6页)23.(本小题满分10分)如图,M 为正方形ABCD 的对角线BD 上一点.过M 作BD 的垂线交AD 于E ,连BE ,取BE 中点O .(1)如图1,连AO 、MO ,试证明∠AOM =90°;(2)如图2,连接AM 、AO ,并延长AO 交对角线BD 于点N ,试探究线段DM 、MN 、NB 之间的数量关系并证明;(3)如图3,延长对角线BD 至Q 、延长DB 至P ,连CP 、CQ ,若PB =2,PQ =9,且∠PCQ =135°,则PC =________.(直接写出结果)图1 图2 图324.(本小题满分12分)在平面直角坐标系中,经过点A (0,2)且与33y x=-平行的直线,交x 轴于点B ,如图1所示.(1)试求B 点坐标,并直接写出∠ABO 的度数;(2)过M (1,0)的直线与AB 成45°夹角,试求该直线与AB 交点的横坐标;(3)如图2,现有点C (m ,n )在线段AB 上运动,点D (-3m+2,0)在x 轴上,N 为线段CD 的中点.①试求点N 的纵坐标y 关于横坐标x 的函数关系式;②直接写出N 点的运动轨迹长度为 .图1 图2。
江苏省2019-2020学年八年级数学下学期期中测试卷二(含答案)

江苏省2019-2020学年八年级下学期期中测试卷数 学一.选择题(本大题共6小题,每小题2分,共12分,每小题只有一个选项符合题意) 1.下列图形中,既是中心对称图形,又是轴对称图形的是( )A ..B ..C .D ..2.以下调查方式比较合理的是( )A .为了解一沓钞票中有没有假钞,采用抽样调查的方式B .为了解全区七年级学生节约用水的情况,采用抽样调查的方式C .为了解某省中学生爱好足球的情况,采用普查的方式D .为了解某市市民每天丢弃塑料袋数量的情况,采用普查的方式3.如图,在两个同心圆中,四条直径把大圆分成八等份,若往圆面投掷飞镖,则飞镖落在黑色区域的概率是( ) A .12B .13C .14D .16(第3题)(第4题)4.如图,在四边形ABCD 中,对角线AC ,BD 相交于点O ,添加下列条件后仍不能判定四边形ABCD 是平行四边形的是( ) A .//AD BC ,AO CO = B .AD BC =,AO OC = C .AD BC =,CD AB =D .AOD COD BOC S S S ∆∆∆==5.如图,已知菱形ABCD 的对角线交于点O ,6DB =,5AD =,则菱形ABCD 的面积为()A.20 B.24 C.30 D.36(第5题)(第6题)6.如图是由三个边长分别是2,3和x的正方形所组成的图形,若直线AB将它分成面积相等的两部分,则x的值是()A.1或4 B.2或3 C.3或4 D.1或2二.填空题(本大题共10小题,每小题2分,共12分,请将答案填写到答题卡对应的位置上)7.某校七年级为调查该年级400名学生一分钟跳绳次数成绩,打算从中随机抽取50人进行测试,则该问题中的样本容量为.8.3月12日是中国的植树节,如图是某种幼树在移植过程中成活率的统计图,估计该种幼树在此条件下移植成活的概率为(结果精确到0.01).9.李老师组织本班学生进行跳绳测试,根据学生测试的成绩,列出了如下表格,则成绩为“良”的频率为.成绩优良及格不及格频数10 22 15 310.在一次捐款活动中,某班50名同学都拿出自己的零花钱,有捐5元、10元、20元的,还有捐50元和100元的,如图所示的统计图反映了不同捐款数的人数比例,那么根据图中信息,该班同学平均每人捐款元.11.为了了解全区近3600名初三学生数学学习状况,随机抽取600名学生的测试成绩作为样本,将他们的成绩整理后分组情况如下:(每组数据含最低值,不含最高值) 分组(分) 40~5050~6060~7070~8080~9090~100频数 12 18 180 频率0.160.04根据上表信息,由此样本请你估计全区此次成绩在70~80分的人数大约是 .12.如图,平行四边形ABCD 中,60B ∠=︒,12BC =,10AB =,点E 在AD 上,且4AE =,点F 是AB 上一点,连接EF ,将线段EF 绕点E 逆时针旋转120︒得到EG ,连接GD ,则线段GD 长度的最小值为 .(第12题)(第13题) (第14题)13.如图,为估计池塘岸边A ,B ,两点间的距离,在池塘的一侧选取点O ,分别取OA ,OB 的中点M ,N ,测得40MN m =,则A ,B 两点间的距离是m .14.如图,在矩形ABCD 中,对角线AC 、BD 相交于点O ,60AOB ∠=︒,点E 、F 分别是BO 、BC 的中点,若6AB cm =,则BEF ∆的周长为 cm .15.如图,在平行四边形ABCD 中,8AD cm =,4AB cm =,AE 平分BAD ∠交BC 边于点E ,交DC 的延长线于点F ,则下列结论:①4CE cm =; ②线段AF 、BC 互相平分; ③AC DF ⊥.④DE AF ⊥;其中正确的结论是: (填序号).(第15题)(第16题)16.如图,矩形纸片ABCD ,4AD =,3AB =,如果点E 在边BC 上,将纸片沿AE 折叠,使点B 落在点F 处,联结FC ,当EFC ∆是直角三角形时,那么BE 的长为 . 三.解答题(本大题共11小题,共计88分)17.如图所示,已知ABC ∆的三个顶点的坐标分别为(2,3)A -,(6,0)B -,(1,0)C -. (1)请直接写出点A 关于x 轴、y 轴、原点对称的点的坐标分别是什么;(2)将ABC ∆绕坐标原点O 顺时针旋转90︒,不画出图形,直接写出点A 、B 、C 的对应点的坐标;(3)请直接写出:以A ,B ,C 为顶点的平行四边形 的第四个顶点D 的坐标.18.如图,E,F是四边形ABCD对角线AC上的两点,//=.AD BC,//DF BE,AE CF求证:(1)AFD CEB∆≅∆;(2)四边形ABCD是平行四边形.19.我区对七年级学生体育测试情况进行调查,从全区3600名学生中抽取了部分学生的成绩(成绩分为A,B,C三个层次)进行分析,绘制了频数分布表与频数分布直方图,请根据图表信息解答下列问题:分组频数频率C10 0.1B a0.5A40 b合计100 1(1)表中的a=,b=;(2)补全频数分布直方图;(3)如果成绩为A等级的同学属于优秀,请你估计全区七年级的有多少人达到优秀水平?20.在一个不透明的盒子里装有黑、白两种颜色的球共40只,这些球除颜色外其余完全相同.小颖做摸球实验,搅匀后,她从盒子里随机摸出一只球记下颜色后,再把球放回盒子中,不断重复上述过程,如表是实验中的一组统计数据:(1)请估计:当n很大时,摸到白球的频率将会接近(精确到0.01);(2)若从盒子里随机摸岀一只球,则摸到白球的概率的估计值为;(3)试估算盒子里白球有只;(4)某小组在“用频率估计概率”的试验中,符合这一结果的试验最有可能的是.A.从一副扑克牌中任意抽取一张,这张牌是“红色的”B.掷一枚质地均匀的硬币,落地时结果是“正面朝上”C.掷一个质地均匀的正六面体骰子(面的点数标记分别为1到6),落地时面朝上的点数小于521.某校开设武术、舞蹈、剪纸三项活动课程,为了了解学生对这三项活动课程的兴趣情况,随机抽取了部分学生进行调查(每人从中只能选一顶),并将调查结果绘制成下面两幅统计图,请你结合图中信息解答问题.(1)将条形统计图补充完整;(2)本次抽样调查的样本容量是;(3)在扇形统计图中,计算女生喜欢剪纸活动课程人数对应的圆心角度数;(4)已知该校有1200名学生,请结合数据简要分析该校学生对三项活动课程的兴趣情况.22.已知:如图,平行四边形ABCD各角的平分线分别相交于点E,F,G,H.求证:四边形EFGH是矩形.23.定义:一条对角线垂直平分另一条对角线的四边形叫做筝形,如图,筝形ABCD的对角线AC、BD相交于点O.且AC垂直平分BD.(1)请结合图形,写出筝形两种不同类型的性质:性质1:;性质2:.(2)若//AB CD,求证:四边形ABCD为菱形.24.已知如图平行四边形ABCD中,EF垂直平分对角线BD,交点为O,求证:四边形BFDE 是菱形.25.如图,ABC∆中,D是BC边上一点,E是AD的中点,过点A作BC的平行线交CE的延长线于F,且AF BD=,连接BF.(1)求证:D是BC的中点.(2)当ABC∆满足什么条件时,四边形AFBD是正方形,并说明理由.26.如图,在平行四边形ABCD中,以点A为圆心AB长为半径画弧交AD于点F,再分别以点B,F为圆心,大于12BF的长度为半径画弧,两弧交于点P;连接AP并延长交BC于点E,连接EF.(1)求证:四边形ABEF是菱形;(2)若60C∠=︒,43AE=,求菱形ABEF的面积.27.已知:正方形ABCD,45∠=︒.EAF(1)如图1,当点E、F分别在边BC、CD上,连接EF,求证:EF BE DF=+;童威同学是这样思考的,请你和他一起完成如下解答:证明:将ADF∆绕点A顺时针旋转∆≅∆.∆,所以ADF ABG90︒,得ABG(2)如图2,点M、N分别在边AB、CD上,且BN DM=.当点E、F分别在BM、DN 上,连接EF,探究三条线段EF、BE、DF之间满足的数量关系,并证明你的结论.(3)如图3,当点E、F分别在对角线BD、边CD上.若2FC=,则BE的长为.期中测试卷(解析版)一.选择题(本大题共6小题,每小题2分,共12分,每小题只有一个选项符合题意)1.下列图形中,既是中心对称图形,又是轴对称图形的是()A..B..C.D..【解答】A、不是轴对称图形,也不是中心对称图形.故不合题意.B、不是轴对称图形,是中心对称图形.故不合题意;C、既是轴对称图形,也是中心对称图形.故符合题意;D、是轴对称图形,不是中心对称图形.故不合题意.故选:C.2.以下调查方式比较合理的是()A.为了解一沓钞票中有没有假钞,采用抽样调查的方式B.为了解全区七年级学生节约用水的情况,采用抽样调查的方式C.为了解某省中学生爱好足球的情况,采用普查的方式D.为了解某市市民每天丢弃塑料袋数量的情况,采用普查的方式【解答】A .为了解一沓钞票中有没有假钞,采用全面调查的方式,故不符合题意;B .为了解全区七年级学生节约用水的情况,采用抽样调查的方式,故符合题意;C .为了解某省中学生爱好足球的情况,采用抽样调查的方式,故不符合题意;D .为了解某市市民每天丢弃塑料袋数量的情况,采用抽样调查的方式,故不符合题意;故选:B .3.如图,在两个同心圆中,四条直径把大圆分成八等份,若往圆面投掷飞镖,则飞镖落在黑色区域的概率是( )A .12B .13C .14D .16【解答】因为两个同心圆等分成八等份,飞镖落在每一个区域的机会是均等的,其中黑色区域的面积占了其中的四等份, 所以P (飞镖落在黑色区域)4182==. 故选:A .4.如图,在四边形ABCD 中,对角线AC ,BD 相交于点O ,添加下列条件后仍不能判定四边形ABCD 是平行四边形的是( )A .//AD BC ,AO CO =B .AD BC =,AO OC = C .AD BC =,CD AB = D .AOD COD BOC S S S ∆∆∆==【解答】若//AD BC Q ,ADO CBO ∴∠=∠,且AO CO =,AOD BOC ∠=∠,()AOD COB AAS ∴∆≅∆ AD BC ∴=,∴四边形ABCD 是平行四边形,故A 选项不合题意;若AD BC =,CD AB =,∴四边形ABCD 是平行四边形,故C 选项不合题意;若AOD COD BOC S S S ∆∆∆==, AO CO ∴=,BO DO =,∴四边形ABCD 是平行四边形,故D 选项不合题意;故选:B .5.如图,已知菱形ABCD 的对角线交于点O ,6DB =,5AD =,则菱形ABCD 的面积为( )A .20B .24C .30D .36【解答】Q 四边形ABCD 是菱形, 12AO CO AC ∴==,132BO DO BD ===,AC BD ⊥, 222594AO AD DO ∴=-=-=, 8AC ∴=,∴菱形ABCD 的面积1242AC BD =⨯⨯=, 故选:B .6.如图是由三个边长分别是2,3和x 的正方形所组成的图形,若直线AB 将它分成面积相等的两部分,则x 的值是( )A .1或4B .2或3C .3或4D .1或2【解答】如图,Q若直线AB将它分成面积相等的两部分,∴11(23)3(3)(23)321 22x x x x++⨯--=⨯++⨯-⨯g,解得1x=或2x=,故选:D.二.填空题(本大题共10小题,每小题2分,共12分,请将答案填写到答题卡对应的位置上)7.某校七年级为调查该年级400名学生一分钟跳绳次数成绩,打算从中随机抽取50人进行测试,则该问题中的样本容量为50 .【解答】从中随机抽取50人进行测试,则该问题中的样本容量为,在这个问题中,样本容量是50,故答案为:50.8.3月12日是中国的植树节,如图是某种幼树在移植过程中成活率的统计图,估计该种幼树在此条件下移植成活的概率为0.88 (结果精确到0.01).【解答】概率是大量重复实验的情况下,频率的稳定值可以作为概率的估计值,即次数越多的频率越接近于概率∴这种幼树移植成活率的概率约为0.88.故答案为:0.88.9.李老师组织本班学生进行跳绳测试,根据学生测试的成绩,列出了如下表格,则成绩为“良”的频率为0.44 .成绩优良及格不及格频数10 22 15 3【解答】成绩为“良”的频率为220.44 1022153=+++;故答案为:0.44.10.在一次捐款活动中,某班50名同学都拿出自己的零花钱,有捐5元、10元、20元的,还有捐50元和100元的,如图所示的统计图反映了不同捐款数的人数比例,那么根据图中信息,该班同学平均每人捐款33 元.【解答】由统计图可得,捐款100元的学生有:5012%6⨯=(人),捐款10元的学生有:5041911610----=(人),该班同学平均每人捐款:5410102019501110063350⨯+⨯+⨯+⨯+⨯=(元),故答案为:33.11.为了了解全区近3600名初三学生数学学习状况,随机抽取600名学生的测试成绩作为样本,将他们的成绩整理后分组情况如下:(每组数据含最低值,不含最高值)分组(分)40~5050~6060~7070~8080~9090~100频数12 18 180频率0.16 0.04根据上表信息,由此样本请你估计全区此次成绩在70~80分的人数大约是1620 .【解答】由题意可得,样本中成绩在70~80分的人数为:60012181806000.166000.04270----⨯-⨯=,27036001620600⨯=,故答案为:1620.12.如图,平行四边形ABCD中,60B∠=︒,12BC=,10AB=,点E在AD上,且4AE=,点F是AB上一点,连接EF,将线段EF绕点E逆时针旋转120︒得到EG,连接GD,则线段GD 长度的最小值为 23 .【解答】将线段AE 绕点E 逆时针旋转120︒得到EH ,连接HG ,过点H 作HM AD ⊥, Q 四边形ABCD 是平行四边形,180A B ∴∠+∠=︒, 120A ∴∠=︒,Q 将线段AE 绕点E 逆时针旋转120︒得到EH ,将线段EF 绕点E 逆时针旋转120︒得到EG ,4EF EG ∴==,AE EH =,120AEH FEG ∠=∠=︒, 60DEH ∴∠=︒,AEF HEG ∠=∠,且EF EG =,AE EH =,()AEF HEG SAS ∴∆≅∆120A EHG AEH ∴∠=∠=︒=∠, //AD HG ∴,∴点G 的轨迹是过点H 且平行于AD 的直线, ∴当DG HG ⊥时,线段GD 长度有最小值,60HEM ∠=︒Q ,4EH =,HM AD ⊥,2EM ∴=,323MH EM ==,∴线段GD 长度的最小值为23,故答案为:23.13.如图,为估计池塘岸边A ,B ,两点间的距离,在池塘的一侧选取点O ,分别取OA ,OB 的中点M ,N ,测得40MN m =,则A ,B 两点间的距离是 80m .【解答】Q 点M 、N 是OA 、OB 的中点,MN ∴是OAB ∆的中位线,224080()AB MN m ∴==⨯=,故答案为:80.14.如图,在矩形ABCD 中,对角线AC 、BD 相交于点O ,60AOB ∠=︒,点E 、F 分别是BO 、BC 的中点,若6AB cm =,则BEF ∆的周长为 633+ cm .【解答】Q 矩形ABCD ,OA OB = 又60AOB ∠=︒Q AOB ∴∆是等边三角形. 6OA AB cm ∴==,6OC OB cm ∴==,12AC cm =, 2212663()BC cm ∴=-=,Q 点E 、F 分别是BO 、BC 的中点,12EF CO ∴=,12BE BO =,12BF BC =,BEF ∴∆的周长为BOC ∆周长的一半为:1(6663)6332++=+.故答案是:633+.15.如图,在平行四边形ABCD 中,8AD cm =,4AB cm =,AE 平分BAD ∠交BC 边于点E ,交DC 的延长线于点F ,则下列结论:①4CE cm =; ②线段AF 、BC 互相平分; ③AC DF ⊥.④DE AF ⊥;其中正确的结论是: ①②④ (填序号).【解答】Q 四边形ABCD 是平行四边形,AB CD ∴=,8BC AD cm ==,//AB DF ,//AD BC ,BEA EAD ∴∠=∠, AE Q 平分BAD ∠,BAE EAD ∴∠=∠, BEA BAE ∴∠=∠,4AB BE cm ∴==,844CE BC BE cm cm cm ∴=-=-=,①正确; 4BE CE cm ∴==, //AB DF Q , ABE FCE ∴∠=∠,在BAE ∆和CFE ∆中,ABE FCE BE CE BEA CEF ∠=∠⎧⎪=⎨⎪∠=∠⎩,()BAE CFE ASA ∴∆≅∆,EFC BAE ∴∠=∠,AB CF =,AE EF =,∴线段AF 、BC 互相平分,②正确;AB CF =Q ,AB CD =, 4CF CD ∴==, CE CF ∴=,只有60B ∠=︒时,60F ADF ∠=∠=︒,才能AC DF ⊥,而B ∠没有给出60︒的条件, AC ∴不一定垂直DF ,③错误; EFC BAE ∠=∠Q ,BAE EAD ∠=∠, EFC EAD ∴∠=∠,AE EF =Q ,DE AF ∴⊥,④正确;故答案为:①②④.16.如图,矩形纸片ABCD ,4AD =,3AB =,如果点E 在边BC 上,将纸片沿AE 折叠,使点B 落在点F 处,联结FC ,当EFC ∆是直角三角形时,那么BE 的长为 1.5或3 .【解答】分两种情况: ①当90EFC ∠=︒时,如图1, 90AFE B ∠=∠=︒Q ,90EFC ∠=︒,∴点A 、F 、C 共线,Q 矩形ABCD 的边4AD =,4BC AD ∴==,在Rt ABC ∆中,2222345AC AB BC =+=+=, 设BE x =,则4CE BC BE x =-=-,由翻折的性质得,3AF AB ==,EF BE x ==, 532CF AC AF ∴=-=-=,在Rt CEF ∆中,222EF CF CE +=, 即2222(4)x x +=-, 解得 1.5x =, 即 1.5BE =;②当90CEF ∠=︒时,如图2,由翻折的性质得,190452AEB AEF ∠=∠=⨯︒=︒,∴四边形ABEF 是正方形,3BE AB ∴==,综上所述,BE 的长为1.5或3. 故答案为:1.5或3.三.解答题(本大题共11小题,共计88分)17.如图所示,已知ABC ∆的三个顶点的坐标分别为(2,3)A -,(6,0)B -,(1,0)C -. (1)请直接写出点A 关于x 轴、y 轴、原点对称的点的坐标分别是什么;(2)将ABC ∆绕坐标原点O 顺时针旋转90︒,不画出图形,直接写出点A 、B 、C 的对应点的坐标;(3)请直接写出:以A,B,C为顶点的平行四边形的第四个顶点D的坐标.【解答】(1)点(2,3)--,A-关于x轴的对称点坐标为(2,3)点(2,3)A-关于y轴的对称点坐标为(2,3),点(2,3)-;A-关于原点的对称点坐标为(2,3)(2)点(2,3)-,A-的对应点的坐标为(3,2)点(6,0)B-的对应点坐标为(0,6),点(1,0)C-的对应点坐标为(0,1);(3)如图,点D的坐标为(7,3)--.-或(3,3)或(5,3)18.如图,E,F是四边形ABCD对角线AC上的两点,//=.DF BE,AE CFAD BC,//求证:(1)AFD CEB∆≅∆;(2)四边形ABCD是平行四边形.【解答】证明:(1)如图,//AD BC Q ,//DF BE ,12∴∠=∠,34∠=∠.又AE CF =,AE EF CF EF ∴+=+,即AF CE =.在AFD ∆与CEB ∆中, 1234AF CE ∠=∠⎧⎪=⎨⎪∠=∠⎩, ()AFD CEB ASA ∴∆≅∆;(2)由(1)知,AFD CEB ∆≅∆,则AD CB =. 又//AD BC Q ,∴四边形ABCD 是平行四边形.19.我区对七年级学生体育测试情况进行调查,从全区3600名学生中抽取了部分学生的成绩(成绩分为A ,B ,C 三个层次)进行分析,绘制了频数分布表与频数分布直方图,请根据图表信息解答下列问题: 分组 频数 频率 C100.1 B a0.5 A40 b合计1001(1)表中的a = 50 ,b = ; (2)补全频数分布直方图;(3)如果成绩为A等级的同学属于优秀,请你估计全区七年级的有多少人达到优秀水平?【解答】(1)本次调查的人数是:100.1100÷=,1000.550a=⨯=,401000.4b=÷=,故答案为:50,0.4;(2)由(1)知,B组人数为50,补全的频数分布直方图如右图所示;(3)36000.41440⨯=(人),答:全区七年级的有1440人达到优秀水平.20.在一个不透明的盒子里装有黑、白两种颜色的球共40只,这些球除颜色外其余完全相同.小颖做摸球实验,搅匀后,她从盒子里随机摸出一只球记下颜色后,再把球放回盒子中,不断重复上述过程,如表是实验中的一组统计数据:摸球的次数n100 200 300 500 800 1000 3000摸到白球的次数m70 124 190 325 538 660 2004摸到白球的频率mn0.70 0.62 0.633 0.65 0.6725 0.660 0.668(1)请估计:当n很大时,摸到白球的频率将会接近0.67 (精确到0.01);(2)若从盒子里随机摸岀一只球,则摸到白球的概率的估计值为;(3)试估算盒子里白球有只;(4)某小组在“用频率估计概率”的试验中,符合这一结果的试验最有可能的是.A.从一副扑克牌中任意抽取一张,这张牌是“红色的”B.掷一枚质地均匀的硬币,落地时结果是“正面朝上”C.掷一个质地均匀的正六面体骰子(面的点数标记分别为1到6),落地时面朝上的点数小于5【解答】(1)由表可知,当n很大时,摸到白球的频率将会接近0.67,故答案为:0.67;(2)若从盒子里随机摸岀一只球,则摸到白球的概率的估计值为0.67,故答案为:0.67;(3)试估算盒子里白球约有400.6726.827⨯=≈(只),故答案为:27;(4)A.从一副扑克牌中任意抽取一张,这张牌是“红色的”的概率为270.50.16 54==>,故此选项不符合题意;B.掷一枚质地均匀的硬币,落地时结果是“正面朝上”的概率为10.52=,不符合题意;C.掷一个质地均匀的正六面体骰子(面的点数标记分别为1到6),落地时面朝上的点数小于5的概率为40.676≈,符合题意;所以某小组在“用频率估计概率”的试验中,符合这一结果的试验最有可能的是C,故答案为:C.21.某校开设武术、舞蹈、剪纸三项活动课程,为了了解学生对这三项活动课程的兴趣情况,随机抽取了部分学生进行调查(每人从中只能选一顶),并将调查结果绘制成下面两幅统计图,请你结合图中信息解答问题.(1)将条形统计图补充完整;(2)本次抽样调查的样本容量是100 ;(3)在扇形统计图中,计算女生喜欢剪纸活动课程人数对应的圆心角度数;(4)已知该校有1200名学生,请结合数据简要分析该校学生对三项活动课程的兴趣情况.【解答】(1)被调查的女生人数为1020%50÷=人,则女生舞蹈类人数为50(1016)24-+=人,补全图形如下:(2)样本容量为5030614100+++=,故答案为:100;(3)扇形图中舞蹈类所占的圆心角度数为16360115.250︒⨯=︒, 故答案为:115.2;(4)估计全校学生中喜欢剪纸的人数是14161200360100+⨯=,全校学生中喜欢武术的有401200480100⨯=,故全校喜欢武术的有的学生多. 22.已知:如图,平行四边形ABCD 各角的平分线分别相交于点E ,F ,G ,H .求证:四边形EFGH 是矩形.【解答】证明:Q 四边形ABCD 是平行四边形,//AD BC ∴,180DAB ABC ∴∠+∠=︒,AH Q ,BH 分别平分DAB ∠与ABC ∠,12HAB DAB ∴∠=∠,12HBA ABC ∠=∠,11()1809022HAB HBA DAB ABC ∴∠+∠=∠+∠=⨯︒=︒,90H ∴∠=︒,同理90HEF F ∠=∠=︒,∴四边形EFGH 是矩形.23.定义:一条对角线垂直平分另一条对角线的四边形叫做筝形,如图,筝形ABCD 的对角线AC 、BD 相交于点O .且AC 垂直平分BD . (1)请结合图形,写出筝形两种不同类型的性质: 性质1: 对角线互相垂直 ;性质2: . (2)若//AB CD ,求证:四边形ABCD 为菱形.【解答】(1)由筝形的定义得:对角线互相垂直,即AC BD⊥;是轴对称图形,对称轴为AC;故答案为:对角线互相垂直,是轴对称图形;(2)证明:ACQ垂直平分BD,AB AD∴=,BO DO=,同理:BC DC=,//AB CDQ,ABO ODC∴∠=∠,在ABO∆和CDO∆中,ABO ODCBO DOAOB DOC∠=∠⎧⎪=⎨⎪∠=∠⎩,()AOB CDO ASA∴∆≅∆,AB CD∴=,AB CD BC AD∴===,∴四边形ABCD为菱形.24.已知如图平行四边形ABCD中,EF垂直平分对角线BD,交点为O,求证:四边形BFDE 是菱形.【解答】证明:Q在平行四边形ABCD中,O为对角线BD的中点,BO DO∴=,EDB FBO∠=∠,在DOE∆和BOF∆中,EDO FBO OD OBEOD FOB ∠=∠⎧⎪=⎨⎪∠=∠⎩, ()DOE BOF ASA ∴∆≅∆; OE OF ∴=,又OB OD =Q ,∴四边形EBFD 是平行四边形,EF BD ⊥Q ,∴四边形BFDE 为菱形.25.如图,ABC ∆中,D 是BC 边上一点,E 是AD 的中点,过点A 作BC 的平行线交CE 的延长线于F ,且AF BD =,连接BF . (1)求证:D 是BC 的中点.(2)当ABC ∆满足什么条件时,四边形AFBD 是正方形,并说明理由.【解答】(1)证明://AF BC Q , AFE DCE ∴∠=∠, Q 点E 为AD 的中点,AE DE ∴=,在AEF ∆和DEC ∆中,AFE DCEAEF DEC AE DE ∠=∠⎧⎪∠=∠⎨⎪=⎩,()AEF DEC AAS ∴∆≅∆, AF CD ∴=,AF BD =Q ,CD BD ∴=,D ∴是BC 的中点;(2)若ABC ∆是等腰直角三角形时,四边形AFBD 是正方形,理由如下:AEF DEC ∆≅∆Q , AF CD ∴=,AF BD =Q ,CD BD ∴=;//AF BD Q ,AF BD =,∴四边形AFBD 是平行四边形,AB AC =Q ,BD CD =, 90ADB ∴∠=︒,AD BD =,∴平行四边形AFBD 是正方形.26.如图,在ABCD Y 中,以点A 为圆心AB 长为半径画弧交AD 于点F ,再分别以点B ,F 为圆心,大于12BF 的长度为半径画弧,两弧交于点P ;连接AP 并延长交BC 于点E ,连接EF .(1)求证:四边形ABEF 是菱形;(2)若60C ∠=︒,43AE =,求菱形ABEF 的面积.【解答】(1)EAB EAF ∠=∠Q , //AD BC Q ,EAF AEB EAB ∴∠=∠=∠, BE AB AF ∴==.//AF BE Q ,∴四边形ABEF 是平行四边形,AB BE =Q ,∴四边形ABEF 是菱形;(2)如图,连结BF ,交AE 于G . Q 四边形ABCD 是平行四边形,60BAD C ∴∠=∠=︒, Q 四边形ABEF 菱形,BF AE ∴⊥,23AG EG ==,30BAG FAG ∠=∠=︒,32BG FG AG ∴===, 4BF ∴=,∴菱形ABEF 的面积114348322AE BF =••=⨯⨯=. 27.已知:正方形ABCD ,45EAF ∠=︒.(1)如图1,当点E 、F 分别在边BC 、CD 上,连接EF ,求证:EF BE DF =+; 童威同学是这样思考的,请你和他一起完成如下解答:证明:将ADF ∆绕点A 顺时针旋转90︒,得ABG ∆,所以ADF ABG ∆≅∆.(2)如图2,点M 、N 分别在边AB 、CD 上,且BN DM =.当点E 、F 分别在BM 、DN 上,连接EF ,探究三条线段EF 、BE 、DF 之间满足的数量关系,并证明你的结论. (3)如图3,当点E 、F 分别在对角线BD 、边CD 上.若2FC =,则BE 的长为2 .【解答】(1)证明:将ADF ∆绕点A 顺时针旋转90︒,得ABG ∆, ADF ABG ∴∆≅∆AF AG ∴=,DF BG =,DAF BAG ∠=∠ Q 正方形ABCD90D BAD ABE ∴∠=∠=∠=︒,AB AD =90ABG D ∴∠=∠=︒,即G 、B 、C 在同一直线上 45EAF ∠=︒Q904545DAF BAE ∴∠+∠=︒-︒=︒45EAG BAG BAE DAF BAE ∴∠=∠+∠=∠+∠=︒即EAG EAF ∠=∠ 在EAG ∆与EAF ∆中,EA EA EAG EAF AG AF =⎧⎪∠=∠⎨⎪=⎩()EAG EAF SAS ∴∆≅∆ EG EF ∴=BE DF BE BG EG +=+=QEF BE DF ∴=+(2)222EF BE DF =+,证明如下:将ADF ∆绕点A 顺时针旋转90︒,得ABH ∆,(如图2)ADF ABH ∴∆≅∆AF AH ∴=,DF BH =,DAF BAH ∠=∠,ADF ABH ∠=∠45EAF ∠=︒Q904545DAF BAE ∴∠+∠=︒-︒=︒45EAH BAH BAE DAF BAE ∴∠=∠+∠=∠+∠=︒即EAH EAF ∠=∠ 在EAH ∆与EAF ∆中, EA EA EAH EAF AH AF =⎧⎪∠=∠⎨⎪=⎩()EAH EAF SAS ∴∆≅∆EH EF ∴=BN DM =Q ,//BN DM∴四边形BMDN 是平行四边形ABE MDN ∴∠=∠90EBH ABH ABE ADF MDN ADM ∴∠=∠+∠=∠+∠=∠=︒222EH BE BH ∴=+ 222EF BE DF ∴=+(3)作ADF ∆的外接圆⊙ O ,连接EF 、EC ,过点E 分别作EM CD ⊥于M ,EN BC ⊥于N (如图3) 90ADF ∠=︒QAF ∴为⊙O 直径BD Q 为正方形ABCD 对角线45EDF EAF ∴∠=∠=︒∴点E 在⊙ O 上90AEF ∴∠=︒AEF ∴∆为等腰直角三角形 AE EF ∴=在ABE ∆与CBE ∆中 AB CB ABE CBE BE BE =⎧⎪∠=∠⎨⎪=⎩()ABE CBE SAS ∴∆≅∆ AE CE ∴= CE EF ∴=EM CF ⊥Q ,2CF = 112CM CF ∴==EN BC ⊥Q ,90NCM ∠=︒∴四边形CMEN 是矩形1EN CM ∴== 45EBN ∠=︒Q 22BE EN ∴==。
河南省郑州市2019-2020学年高二下学期阶段性学业检测题(5月)高二年级英语学科检测题 参考答案

2019-2020学年下期阶段性学业检测题高二年级英语参考答案一、客观题(1-60):1.C2.C3.B4.A5.B6.A7.C8.A9.B 10.B 11.C 12.B 13.B 14.C 15.B 16.A 17.B 18.C 19.A 20.B 21.D 22.A 23.B 24.A 25.D 26.C 27.D 28.C 29.B 30.A 31.C 32.A 33.D 34.A 35.B 36.D 37.E 38.G 39.A 40.B 41.C 42.A 43.B 44.A 45.C 46.D 47.C 48.A 49.A 50.B 51.B 52.D 53.C 54.B 55.A 56.D57.A 58.C 59.B 60.D二、语言知识运用第二节(61-70):61. patients 62. to see 63. would / could 64. leaves / will leave / is leaving 65. fishing 66. which 67. treatment / treating / to be treated 68. as 69. warned 70. thankful三、短文改错:The Small Friends Pet Shelter was started with a group of high school students and their71. byparents when they saw many pets abandoned after their families move away. Today, there’re about72. moved70 cats, 50 dogs and a few rabbits lived at the shelter. The young people who run the shelter work73. livinghardly in many ways. They keep the place clean, take care of and advertise the animal so that they 74. hard 75. animalscan be adopted. They have already helped finding homes for nearly 200 animals. While it is76. find或finding前加inhard work, but the young people working there think it is highly benefit and worthwhile. So if you77 78. beneficialmeet with a pet that ∧lost, call the young people at the Small Friends Pet Shelter. And if you79. iswant to help out, go and join them. The very thing what the animals need is love and care.80. that或删除what四、书面表达:Possible Version IDear Mason,Glad to hear from you. We’ve been suffering a hard time since the COVID-19 outbreak. The whole nation is still fighting against the virus and we won’t have the epidemic stop us learning.Every day I attended classes online instead of in the classroom. Our teachers gave us lessons using Ding Talk as scheduled. Besides, I often surfed the Internet for various learning resources. When I had problems, I usually discussed them with my classmates or teachers on WeChat or cellphone. Although it was inconvenient, I was determined to overcome difficulties to go on with my studies.I hope the epidemic will soon disappear, and everything can go back to normal. By the way, how are you learning now?Yours,Li HuaPossible Version IIDear Mason,How are you? Knowing you’re interested in my learning at home after the COVID-19 outbreak, now I’ll tell you about it.Every day, I got up early to do some reading and then watched the live lessons online given by my teachers as scheduled. Whenever having a problem, I tried to solve it myself by referring to textbooks or dictionaries. Sometimes, I discussed with my classmates, surfed the Internet for help or turned to teachers for advice. I felt a little sad because learning at home brought some inconvenience. I hope the epidemic will soon come to an end so that I can return to normal life as usual.Are you learning at home now? Looking forward to your reply.Yours,Li Hua评卷细则一、客观题部分(共100分)听力:1-20题,共20小题,每小题1.5分,共计30分。
2019-2020年八年级数学下册专题讲解+课后训练:梯形的辅助线 课后练习及详解
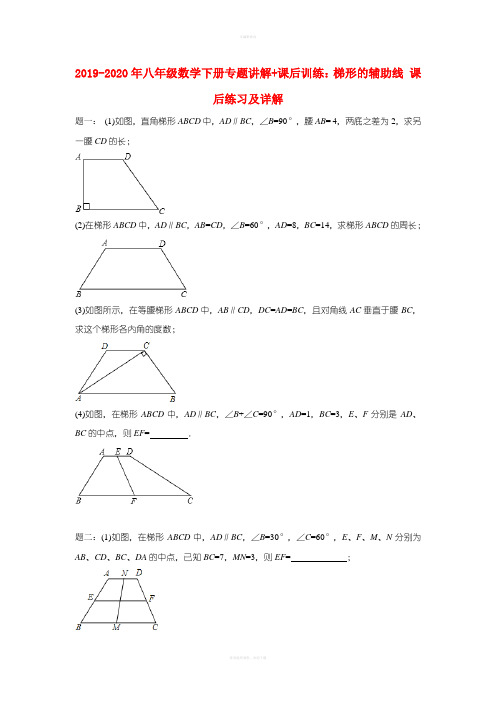
2019-2020年八年级数学下册专题讲解+课后训练:梯形的辅助线课后练习及详解题一:(1)如图,直角梯形ABCD中,AD∥BC,∠B=90°,腰AB= 4,两底之差为2,求另一腰CD的长;(2)在梯形ABCD中,AD∥BC,AB=CD,∠B=60°,AD=8,BC=14,求梯形ABCD的周长;(3)如图所示,在等腰梯形ABCD中,AB∥CD,DC=AD=BC,且对角线AC垂直于腰BC,求这个梯形各内角的度数;(4)如图,在梯形ABCD中,AD∥BC,∠B+∠C=90°,AD=1,BC=3,E、F分别是AD、BC的中点,则EF= .题二:(1)如图,在梯形ABCD中,AD∥BC,∠B=30°,∠C=60°,E、F、M、N分别为AB、CD、BC、DA的中点,已知BC=7,MN=3,则EF= ;(2)如图,在梯形ABCD中,AD=DC,AB=DC,∠D=120°,对角线CA平分∠BCD,且梯形的周长为20,则梯形ABCD的面积为;(3)如图,等腰梯形ABCD中,AD∥BC,AD=3,AB= 4,BC=7,求∠B的度数;(4)如图,梯形ABCD中,AD∥BC,AC⊥BD,AD=3,BC=7,E在BC上,CE=2,则DE= .题三:已知:等腰梯形的上底是2cm,腰长是4cm,一个底角是60°,则等腰梯形的下底是cm.题四:已知:等腰梯形的一个底角等于60°,它的两底分别为4cm和7cm,则它的周长为cm.题五:如图所示,在梯形ABCD中,AD∥BC,AB=CD,AC⊥BD,且AD= 4,BC=8,求AC的长.题六:如图,在梯形ABCD中,AD∥BC,对角线AC⊥BD,若AD=3,BC=7,求梯形ABCD 面积的最大值.题七:如图,梯形ABCD中,AD∥BC,点E在BC上,AE=BE,点F是CD的中点,且AF ⊥AB,若AD=2.7,AF=4,AB=6,求CE的长.题八:如图,在梯形ABCD中,AB∥CD,∠A+∠B=90°,CD=5,AB=11,点M、N分别为AB、CD的中点,求线段MN的长.题九:如图,在梯形ABCD中,AD∥BC,∠ABC=90°,AB= 4,AD=3,BC=5,点M是边CD的中点,连接AM、BM.求△ABM的面积.题十:如图,已知直角梯形ABCD中,AD∥BC(AD<BC),∠B=90°,AB=AD+BC.点E 是CD的中点,点F是AB上的点,∠ADF= 45°,FE=a,梯形ABCD的面积为m.(1)求证:BF=BC;(2)求△DEF的面积(用含a、m的代数式表示).题十一:以线段a=16,b=13为梯形的两底,c=10,d=6为腰画梯形,这样的梯形() A.只能画出一个B.能画出2个C.能画出无数个D.不能画出题十二:以线段a=5,b=10,c=15,d=20做梯形四边形,这样的梯形(不全等的)() A.至少能做3个B.恰好能做2个C.仅仅只能做1个D.一个也不能做梯形的辅助线课后练习参考答案题一:(1)2;(2)34;(3)60°,60°,120°,120°;(4)1.详解:(1)过D作DE⊥BC于E,∵AB⊥BC,DE⊥BC,AD∥BC,∴四边形ADEB是个矩形,∴AB=DE= 4,CE=BC AD=2,Rt△DEC中,CD===2;;(2)过A、D点作AE⊥BC于E,DF⊥BC于F,∵AB=CD,∠B=∠C,AE=DF,∴△ABE≌△DCF,∴BE=CF,∵AD=8,BC=14,BE=CF=3,又∵在Rt△ABE中,∠B=60°,∴AB=2BE=6,∴梯形ABCD的周长为8+14+6+6=34;(3)如图所示,过点C作CE∥AD,又DC∥AE,∴四边形AECD为平行四边形,又DC=AD=BC,∴四边形AECD为菱形,∴AE=CE=BC,∴∠EAC=∠ECA,∠CEB=∠B,∵∠B+∠CAB=90°,即3∠CAE=90°,∴∠CAE=30°,∴∠B=60°=∠DAB,∠D=∠DCB=120°;(4)过点E作AB、CD的平行线,与BC分别交于G,H,∵∠B+∠C=90°,∴∠EGH=∠B,∠EHG=∠C,∴∠EGH+∠EHG=90°,∴四边形ABGE和四边形CDEH都是平行四边形,△EGH为直角三角形,∵E、F分别是AD、BC的中点,∴BG=CH=0.5,GH=2,根据直角三角形中斜边上的中线是斜边的一半知,EF=GH=1,∴EF=1.题二:(1)4;(2)12;(3)60°;(4)5.详解:(1)过点N分别作NG∥AB,NH∥CD,得平行四边形ABGN和平行四边形DCHN,∴∠NGM+∠NHM=∠B+∠C=90°,GH=BC AD,MG=MH,∴GH=2MN=6,∴AD=76=1,∴EF= 4;(2)∵在梯形ABCD中,AB=DC,∴梯形ABCD是等腰梯形,∴∠D+∠DCB=180°,∵∠D=120°,∴∠B=∠DCB=60°,∵对角线CA平分∠BCD,∴∠ACB=30°,∵AD=DC,∴∠DAC=∠ACD=30°,∴∠BAC=90°,∴BC=2AB,∵梯形的周长为AD+DC+BC+AB=5AB=20,∴AB= 4,∴AC=4,BC=8,过点A作AE⊥BC于点E,∵AB= 4,AC=4,BC=8,∴AE=2,∴梯形ABCD的面积为(4+8)×2×=12;(3)过点A作AE∥DC交BC于E,∵AD∥BC,∴四边形AECD是平行四边形,∴EC=AD=3,DC=AE,∴BE=BC CE=73= 4,∴CD=AB= 4,∴AE=AB=BE= 4,∴△ABE是等边三角形,∴∠B=60°;(4)过D作DF∥AC交BC的延长线于F,∵AD∥BC,∴四边形ACFD是平行四边形,∴CF=AD=3,∵BC=7,∴BF=BC+CF=7+3=10,∵CE=2,∴BE=72=5,EF=2+3=5,∴BE=EF,又∵AC⊥BD,DF∥AC,∴∠BDF=90°,∴DE=BF=5.题三:6cm.详解:过D作DE∥AB交BC于E,∵DE∥AB,AD∥BC,∴四边形ABED是平行四边形,∴AD=BE=2cm,DE=AB=4cm,∠DEC=∠B=60°,AB=DE=DC,∴△DEC是等边三角形,∴EC=CD= 4cm,∴BC= 4cm+2cm=6cm.题四:17cm.详解:过上底顶点D作DE∥AB交BC于E,则四边形ABED是平行四边形,∴DE=AB,AD=BE,∵梯形的一个底角是60°,∴∠C=60°,又∵腰长AB=CD=DE,∴△CDE是等边三角形,∴CD=CE=BC BE=74=3cm,∴它的周长为3+7+3+4=17cm.题五:.详解:过D作DE∥AC交BC的延长线于E,∵AD∥BC,AB=CD,∴四边形ABCD是等腰梯形,∴ADEC是平行四边形,∴AD=CE,AC=DE,即可得出BE=BC+CE=BC+AD=12,又∵AC=BD,∴BD=ED,∴△BDE为等腰直角三角形,∴AC=BD=.题六:25.详解:过D作DE∥AC交BC延长线于E,∵AD∥BC,DE∥AC,∴四边形ACED是平行四边形,∴AD=CE,∴根据等底等高的三角形面积相等得出△ADC的面积等于△DCE的面积,即梯形ABCD的面积等于△BDE的面积,∵AC⊥BD,DE∥AC,∴∠BDE=90°,BE=3+7=10,∴此时△BDE的边BE边上的高越大,它的面积就越大,即当高是BE时最大,即梯形的最大面积是×10××10=25.题七:2.3.详解:延长AF、BC交于点G,∵AD∥BC,∴∠D=∠FCG,∠DAF=∠G,又DF=CF,∴△AFD≌△GFC,∴AG=2AF=8,CG=AD=2.7,∵AF⊥AB,AB=6,∴BG=10,∴BC=BG CG=7.3,∵AE=BE,∴∠BAE=∠B,∴∠EAG=∠AGE,∴AE=GE,∴BE=BG=5,∴CE=BC BE=2.3.题八:3.详解:如图,过D作DE∥BC,DF∥MN,∵在梯形ABCD中,AB∥CD,DE∥BC,∴CD=BE=5,AE=AB BE=115=6,∵M为AB的中点,∴MB=AM=AB=×11=5.5,ME=MB BE=5.55=0.5,∵N为DC的中点,∴DN=DC=×5=2.5,在四边形DFMN中,DC∥AB,DF∥MN,∴FM=DN=2.5,∴FE=FM+ME=2.5+0.5=3=AE,∴F为AE的中点,又∵DE∥BC,∴∠B=∠AED,∵∠A+∠B=90°,∴∠A+∠AED=90°,∴∠ADE=90°,即△ADE是直角三角形,∴DF=MN=AE=×6=3.题九:8.详解:延长AM交BC的延长线于点N,∵AD∥BC,∴∠DAM=∠N,∠D=∠MCN,∵点M是边CD的中点,∴DM=CM,∴△ADM≌△NCM(AAS),∴CN=AD=3,AM=MN=AN,∴BN=BC+CN=5+3=8,∵∠ABC=90°,∴S△ABN=×AB•BN=×4×8=16,∴S△ABM=S△ABN=8,即△ABM的面积为8.题十:见详解.详解:(1)∵四边形ABCD是直角梯形,∴∠A=90°,∵∠ADF=45°,∴∠AFD= 45°,∴AD=AF,∵AB=AF+BF,AB=AD+BC,∴BF=BC;(2)连接FC,设AD=AF=x,BC=BF=y,连接CF,作DH⊥BC于H,易证四边形ABHD为矩形、△CDF为直角三角形,又∵E是CD中点,∴CD=2EF=2a,由勾股定理得x2+y2=2a2…①,由直角梯形的面积公式可得:(x+y)2=2m…②,由②①,得xy=m a2,∵S△DFC=S梯形ABCD S△AFD S△BFC=(x+y)2 x2 y2 = xy,∴S△DEF=S△DFC=m a2.题十一:D.详解:如图,过点B作BE∥AD,则出现平行四边形ABED和一个△BEC,∵AB=13,CD=16,AD=10,BC=6∴CE=3,BE=10,∵3+6<10,∴BE,CE,BC不能构成三角形∴这样的梯形一个也不能作.故选D.题十二:C.详解:作DE∥AB,则DE=AB,①当a=5为上底,b=10为下底,c、d为腰时,105=5,与15,20不能构成三角形,故不满足题意;②当a=5为上底,b=15为下底,b、d为腰时,155=10,与10,20不能构成三角形,故不满足题意;③当a=5为上底,d=20为下底,b、c为腰时,205=15,与10,15可以构成三角形,故满足题意;④当b=10为上底,c=15为下底,a、d为腰时,1510=5,与5,20不能构成三角形,故不满足题意;⑤当b=10为上底,d=20为下底,a、c为腰时,2010=10,与5,15不能构成三角形,故不满足题意;⑥当c=15为上底,d=20 为下底,a、b为腰时,2015=5,与5,10不能构成三角形,故不满足题意;综上可得只有当a=5为上底,d=20为下底,b、c为腰时,满足题意,即以线段a=5,b=10,c=15,d=20做梯形四边形,这样的梯形(不全等的)只能做一个.故选C..。
