(完整word版)基本建模法建立理想Buck电路的小信号模型
Buck-Boost电路建模及分析
题目：Buck-Boost电路建模及分析摘要：作为研究开关电源的基础，DC-DC开关变换器的建模分析对优化开关电源的性能和提高设计效率具有重要意义。
而Buck-Boost电路作为DC-DC开关变换器的其中一种电路拓扑形式，因其输出电压极性与输入电压相反，而幅度既可比输入电压高，也可比输入电压低，且电路结构简单而流行。
为了达到全面而深入的研究效果，本文对Buck-Boost电路进行了稳态分析和小信号分析。
稳态分析中，首先介绍了电路工作原理，得出了两种工作模式下的电压转换关系式，并同时可知基于占空比怎样计算其输出电压以及最小最大电感电流和输出纹波电压计算公式；接着推导了状态空间模型，以在MATLAB中进行仿真；而最后仿真得到的电感电流、输出电压的变化规律符合理论分析。
小信号分析中，首先推导了输出与输入间的传递函数表达式，以了解低频交流小信号分量在电路中的传递过程；接着分析其零极点，且仿真绘制波特图进行了验证。
经过推导与研究，稳态分析和小信号分析下仿真得到的变化规律均与理论上的推导一致。
关键词：Buck-Boost；稳态分析；小信号分析；MATLAB仿真1.概论现代开关电源有两种：直流开关电源、交流开关电源。
本课题主要介绍直流开关电源，其功能是将电能质量较差的原生态电源，如市电电源或蓄电池电源，转换为满足设备要求的质量较高的直流电源，即将“粗电”转换为“精电”。
直流开关电源的核心是DC-DC变换器。
作为研究开关电源的基础，DC-DC开关变换器的建模分析对开关电源的分析和设计具有重要意义。
DC-DC开关变换器最常见的三种电路拓扑形式为：降压(Buck)、升压(Boost)和降压-升压(Buck-Boost) [1]，如图1-1所示。
其中Buck-Boost变换器因其输出电压极性与输入电压相反，而幅度既可比输入电压高，也可比输入电压低，且电路结构简单而流行。
(a) Buck型电路结构(b) Boost型电路结构(c) Buck-Boost型电路结构图1-1 DC-DC变换器的三种电路结构本课题针对Buck-Boost变换器的建模分析进行深入研究，以优化开关电源的性能和提高设计效率。
16、buck-boost变换器DCM小信号建模
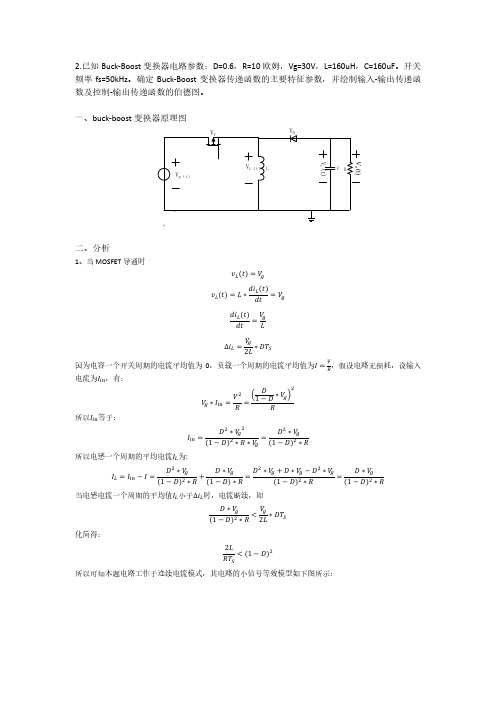
一、buck-boost 变换器原理图
VT
VD
Vo(t) Vc(t)
VL（t） L
CR
Vg（t）
+
二、分析
1、当 MOSFET 导通时
������ (������) = ������
������������ (������)
������ (������) = ������ ∗
= ������
������������
������������ (������) ������ =
7.2 ∗ 10 ������ + 300 ������ (������) = −
2.56 ∗ 10 ������ + 1.6 ∗ 10 ������ + 1.6 MATLAB 程序如下： >>num=-[7.2*10^(-3),-300]; >>den=[2.56*10^(-7),1.6*10^(-4),1.6]; >>figure(2);bode(num,den);grid; Bode 图如下：
������ ������������������
∗ ������ +1
+
������������
=
������
������ ∗ ������
������ ∗ ������
=
∗ ������ + ������������ ∗ (������������������ + 1) ������ ������������������ + ������������ + ������
Buck变换器建模和仿真
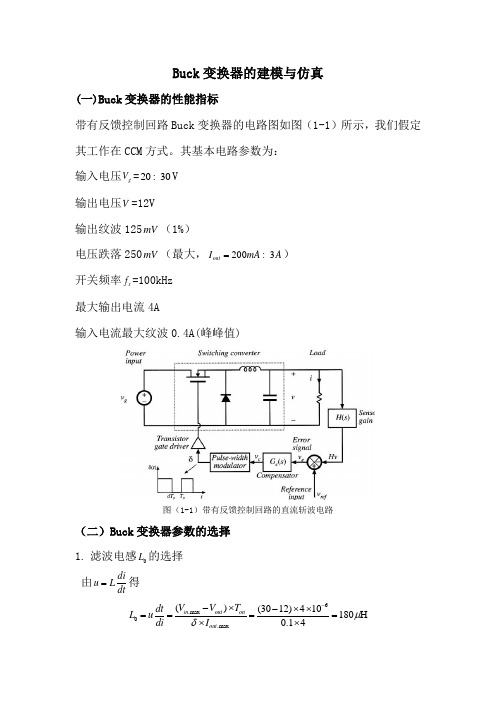
Buck 变换器的建模与仿真(一)Buck 变换器的性能指标带有反馈控制回路Buck 变换器的电路图如图（1-1）所示，我们假定其工作在CCM 方式。
其基本电路参数为： 输入电压g V =2030V 输出电压V =12V 输出纹波125mV （1%）电压跌落250mV （最大，2003out I mA A =） 开关频率s f =100kHz 最大输出电流4A输入电流最大纹波0.4A(峰峰值)图（1-1）带有反馈控制回路的直流斩波电路（二）Buck 变换器参数的选择 1. 滤波电感0L 的选择 由diu Ldt=得 6.max 0.max ()(3012)410180H 0.14in out on out V V T dt L u di I μδ--⨯-⨯⨯====⨯⨯这里我们取0L 为180H μ 最大负载时的峰值电流为.max .max 40.054 4.22peak out out I I I A δ=+=+⨯=2. 滤波电容0C 的选择 由dui cdt=得 其向量形式为I j cU ω=I jcUω=所以需要穿越频率的带宽为2outc out outI f C V π∆=∆如果假定穿越频率为10kHz250892.8out c out V mZ m I ∆===Ω∆ 原则上为了留有设计裕量，电阻的阻抗按13计算阻抗选取 根据上面计算结果，我们可以在Rubycon 公司的ZL 系列，16V 中选取以下规格：C=330F μ,760C rms I mA =@105A C =︒ ,72ESR low R m =Ω@20A T C =︒ ,220ESR low R m =Ω@10A T C =-︒电容ESR 的阻抗应小于输出电容在穿越频率处的阻抗11482 6.2810330c out m f C k π==Ω⨯⨯86c Z m ≤==Ω设计余量不足，我们重新选ZL 系列中C=1000F μ，同样的过程，我们可以得出满足条件。
15、buck变换器DCM小信号建模
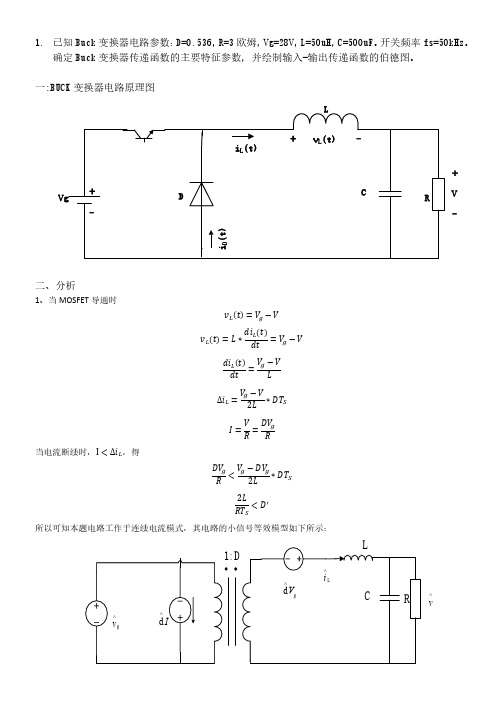
一:BUCK 变换器电路原理图 L
+ Vg
-
iL(t)
+ vL(t) -
D
C
+
带入参数得：
0.536 ∗ 3 ������ (������) =
7.5 ∗ 10 ∗ ������ + 5 ∗ 10 ∗ ������ + 3
② 、控制扰动与输出扰动的传递函数： 忽略输入扰动的作用，其小信号模型等效电路图为：
L
iL
d Vg
C
R
v
������
∗
1 ������������
������(������) ������ ������(������)
MATLAB 程序如下： >>num=[0.536*3]; >>den=[7.5*10^(-8),5*10^(-5),3]; >>figure(1);bode(num,den);grid; Bode 图如下：
RV -
iD(t)
二、分析
1、当 MOSFET 导通时
������ (������) = ������ − ������
������������ (������)
������ (������) = ������ ∗
= ������ − ������
������������
������������ (������) ������ − ������
基本建模法建立理想Buck电路的小信号模型
利用基本建模法建立理想Buck 电路的小信号模型：一 求平均变量模态1：电感电压和电容电流的表达式L g d ()()=()()d i t v t Lv t v t t=- d ()()()=()d C v t v t i t Ci t t R=- 当变换器满足低频假设和小纹波假设时，s s L g d ()()=()()d T T i t v t Lv t v t t≈〈〉-〈〉 s s ()d ()()=()d T C T v t v t i t C i t t R〈〉≈〈〉-模态2：电感电压和电容电流的表达式L d ()()=()d i t v t Lv t t=- d ()()()=()d C v t v t i t Ci t t R=- 当变换器满足低频假设和小纹波假设时，s L d ()()=()d T i t v t Lv t t≈-〈〉 s s ()d ()()=()d T C T v t v t i t C i t t R〈〉≈〈〉-进一步得到电感电压与电容电流在一个开关周期内的平均值：s s s s L g ()=(t)(()())(1())(())T T T T v t d v t v t d t v t 〈〉〈〉-〈〉+--〈〉sss s s ()()()=()(())(1())(())T T C T T T v t v t i t d t i t d t i t RR〈〉〈〉〈〉〈〉-+-〈〉-整理后，得ss s g d ()()()()d T T T i t L d t v t v t t 〈〉=〈〉-〈〉sss d ()()()d T T T v t v t Ci t tR〈〉〈〉=〈〉-二 分离扰动g ˆd[+()]ˆˆˆ(())[()][()]d g I i t L D d t V v t V v t t=++-+ ˆˆd[()]()ˆ()d V v t V v t CI i t t R++=+- 合并同类项后，g ˆ()ˆˆˆ()()d()-()d g g dI di t L DV V Dvt V t v t dt t+=-++ ˆˆd d ()()ˆ()()d d V v t V vt C I i t t t R R+=-+- 分离直流项和交流项，g =ˆ()ˆˆˆ()d()-()d g g dILDV V dtdi t L Dv t V t v t t -=+d d ˆˆd ()()ˆ()d V VCI t R v t v t C i t t R =-=-三 线性化g ˆ()ˆˆˆ()d()-()d g di t L Dvt V t v t t=+ ˆˆd ()()ˆ()d v t v t Ci t t R=- 又in ˆˆˆ()=()+()it Di t Id t 则可以得到理想Buck 电路模式下交流小信号等效电路模型：R CL.DV g d (t )^V (t )^⑴vg 2ˆ(s)ˆ(s)=|(s)=0=ˆ()1g vDG d L vs s LC s R++⑵gvg 2ˆ(s)(s)==ˆ()1V vG Ld s s LC s R++⑶开环输入阻抗22s +s+1(s)=1L LC R R Z D RCs + ⑷开环输出阻抗2s(s)=s+1L Z LLCs R+（注：文档可能无法思考全面，请浏览后下载，供参考。
Buck电路建模实验指导
Buck电路建模实验指导一、实验目的1.掌握Buck电路的基本建模方法2.掌握利用波特图设计Buck电路控制器的基本方法3.通过实验观察不同控制器参数对电路静态和动态性能的影响二、实验设备1.示波器2.Intersil ZL6100VAL1Z 评估板3.12V直流电源4.20A空开，0.1Ω/15W负载5.电脑三、实验原理1.图1所示为本次实验所采用的Buck电路原理图。
表1列出了电路的主要参数。
图1. Buck电路原理图表1. 主要参数输入电压 V in 12V 负载 R o 0.1Ω输出电压 V o 1.2V 开关频率 f s 400kHz滤波电感 L 360nH MOSFET S1 30V/12A滤波电容 C 2.54mF MOSFET S2 30V/23A电容ESR R C 0.4mΩ 额定功率 P o 18W2.图2所示为实际电路连接图。
图2 实际电路连接示意图3. 电路的控制框图如图3所示。
其中虚线框内为数字控制器。
图3 电路控制框图已知采样增益H =64000，数字PWM 增益1812DPWM G =。
从控制量到电路输出的传递函数G vd 需要根据通过建模得到。
之后，根据求得的电路模型合理的设计数字控制器中的补偿环节G comp 。
4. 数字补偿器说明实验所采用的评估板提供了一种指定类型的数字补偿器，其增益‐频率特性如图4所示。
允许同学们通过配置两个零点和一个极点设计补偿器，补偿器的传递函数可以写为()22122211111z z z n n comp p p s s s s Q G s G G s s s s ωωωωωω⎛⎞⎛⎞++++⎜⎟⎜⎟⎝⎠⎝⎠==⎛⎞⎛⎞++⎜⎟⎜⎟⎜⎟⎜⎟⎝⎠⎝⎠其中12z z z Q =n ω=。
图4 数字补偿器增益‐频率特性5. CompZL TM Simulation Tool 辅助设计软件界面介绍这款配套的软件提供了辅助设计数字控制器的一种方法，可以对设计好的补偿器参数进行核对和校正。
10、buck变换器小信号建模
一:BUCK 变换器电路原理图二：线性化若BUCK 变换器工作在某一静态工作点 稳态占空比 dt D ，稳态输入电压sg g v t =T V ，电感电流，电容电压，和输入电流si t v t ssgT T T i t 的稳态值分别为I ，V ，g I 。
当电路达到稳态时，由电感电压的伏秒平衡原理0ssTL T d i t L v t d t，并代入占空比和各电量的稳态值，有g V DV ；根据电荷平衡原理，0ssT C T d v t Ct dt，有0VDI R ，对于输入电流有g I DI 。
如果对输入电压和输入电流在其工作点附近做微小扰动，即ˆsg g g T v t V v ，引起buck 变换器各状态变量和输入电流量的微小扰动，即 ˆd t D dt ，ˆsT i t I it ，ˆsT v t V vt ，ˆsg g g T i t I it ，则 ˆˆˆˆg g d I i t L D d t V v t V v t dt，即ˆˆˆˆˆˆg g g g di t dI L DV V Dv t V d t v t d t v t dt dt ，其中包含直流项，一阶交流项，二阶交流项，忽略二阶交流项，则有 ˆˆˆˆg g di t L Dvt V d t v t dt，同理，对于电容 ˆˆˆd V v t V v CI i t dt R，可以简化为 ˆˆˆdv t v t C i t dt R，输入电流方程为 ˆˆˆg g I i D d t I i t 。
汇总得到buck 变换器线性化交流小信号交流模型为：ˆˆˆˆˆˆˆˆˆg g g dv t v t Ci t dt R I i D d t I i t it Di t Id t三：小信号等效电路ˆg v t t四：MATLAB 仿真。
完整word版,boost小信号建模
3 （30分）Project: Control Loop Design and Simulation of a Boost Converter Fig.1 shows a circuit diagram of a boost converter and the parameters for circuit elements.Fig.1. Boost converter circuit diagram and system parameters1）Derive the large-signal average model of the boost converter and draw the corresponding circuit diagram.2）Derive the small-signal model of the boost converter and draw the corresponding circuit diagram.3）From the small-signal model, derive the control to output transfer function (G vd) and plot its frequency-domain response (Bode plot) with MATLAB ‘bode’ command. 4）Design a controller to compensate the open-loop Bode plot with MATLAB‘sisotool’ toolbox. Clearly mark the poles and zeros of the designed controller and the phase margin of the compensated system. Write down the controller transfer function.5）Simulate the performance of the compensated converter system inMATLAB/Simulink with the converter average model and the designed controller. Add disturbances to the input voltage and load power and record the output voltage waveforms.A report containing the above five aspects is required.准备工作：小信号模型是一种平均模型，它是假设在稳态情况下，对系统加一低频的交流扰动信号，然后可以得到扰动信号之间的传递函数。
Buck变换器小信号模型
Buck 变换器小信号模型
本文为大家介绍Buck 电路电感电流连续时的小信号模型。
Buck 电路电感电流连续时的小信号模型
图1 为典型的Buck 电路，为了简化分析，假定功率开关管S 和D 为理想开关，滤波电感L 为理想电感（电阻为0），电路工作在连续电流模式（CCM）下。
Re 为滤波电容C 的等效串联电阻，R0 为负栽电阻。
各状态变量的正方向定义如下图中所示。
图1 典型buck 电路
s 导通时，对电感列状态方程
s 断开时，D1 续流导通时，状态方程变成
占空比为D 时，一个开关周期过程中，式（1）及式（2）分别持续了DTs 和（1-D）Ts 的时间（Ts 为开关周期），因此，一个周期内电感的平均状态方程为。
BUCK电路的建模
系统建模作业——BUCK电路的建模一．BUCK 电路简介BUCK 电路是一种降压式变换电路，降压变换器输出电压平均值U 0总是小于输出电压U D 通常电感中的电流是否连续，取决于开关频率、滤波电感L 和电容C 的数值。
二．BUCK 电路建模1. BUCK 电路基本结构Va)VVb) c)图1. BUCK 电路基本结构a) Buck 变换器 b)开关处于通态[t ，t+DTs] c)开关处于断态[t+DTs ，t+Ts]2．符号说明1、 输入直流电压(Vg)：2、 输出电压(Vo)：3、 输入电流(Ig)：4、 输出电流(Io)：5、 电感电压(VL)：6、 电感电流(IL)：7、 电容电流(IC)：3. Buck 变换器达到稳态时的电压电流关系当Buck 变换器达到稳态时，电感电压为()()()ss L s0L L T I t T I t V t LT +-==（1）并且()()()()sss ss L L L L ss 11d d d t T t DT t T g o T tt t DT v t V t t V t t V t t V D V T T ++++⎡⎤==+=-⎢⎥⎣⎦⎰⎰⎰ （2） 则结合（1）和（2），其稳态电压传输比为：goV D V = （3）若略去开关损耗，则Buck 变换器的输入输出功率平衡有：g g o o V I V I =，得o g DI I =。
4.大信号模型在开关管处于通态时，即时间在[t ，t+DT s ]区间时，电感两段电压为:()()()()L g d d L o I t V t LV t V t t==- （4）通过电容的电流为：()()()()C d d o og V t V t I t CI t t R==- （5）当开关管处于断态时，即时间[t+DT s ，t+T s ]区间时，电感两端电压为：()()()L d d L o I t V t LV t t==- （6）通过电容的电流为：。
开关电源小信号模型
开关电源小信号模型1Buck电路电感电流连续时的小信号模型图1为典型的Buck电路，为了简化分析，假定功率开关管S和D1为理想开关，滤波电感L为理想电感（电阻为0），电路工作在连续电流模式（CCM）下。
Re为滤波电容C的等效串联电阻，Ro为负载电阻。
各状态变量的正方向定义如图1中所示。
S导通时，对电感列状态方程有L(dil/dt)=Uin－Uo（1）S断开，D1续流导通时，状态方程变为L(dil/dt)=－Uo（2）占空比为D时，一个开关周期过程中，式（1）及式（2）分别持续了DTs和（1－D）Ts的时间（Ts为开关周期），因此，一个周期内电感的平均状态方程为 L(dil/dt)=D(Uin－Uo)＋(1－D)(－Uo)=DUin－Uo（3）稳态时，=0，则DUin=Uo。
这说明稳态时输出电压是一个常数，其大小与占空比D和输入电压Uin成正比。
由于电路各状态变量总是围绕稳态值波动，因此，由式（3）得L[d(il+il’’’’)/dt]=(D＋d)(Uin＋Uin’’’’)－(Uo＋Uo’’’’)（4）式（4）由式（3）的稳态值加小信号波动值形成。
上标为波浪符的量为波动量，d为D的波动量。
式（4）减式（3）并略去了两个波动量的乘积项得L(dil’’’’/dt)=DUin’’’’＋dUin－Uo’’’’（5）由图1，又有iL=C(duc/dt)＋Uo/R0（6）Uo=Uc＋ReC(duc/dt)（7）式（6）及式（7）不论电路工作在哪种状态均成立。
由式（6）及式（7）可得iL＋ReC(dil/dt)=1/Ro(Uo＋CRo(duo/dt))（8）式（8）的推导中假设Re 式（9）减式（8）得iL+ReC(dil/dt)=1/Ro(Uo＋CRo(dUo/dt))（10）将式（10）进行拉氏变换得iL(s)=(Uo(s)/Ro)·[(1+sCRo)/(1+sCRe)](11)(s)=（11）一般认为在开关频率的频带范围内输入电压是恒定的，即可假设=0并将其代入式（5），将式（5）进行拉氏变换得sLiL’’’’(s)=d(s)Uin－Uo’’’’(s)（12）由式（11），式（12）得Uo’’’’(s)/d(s)=Uin[(1+sCRe)/(s2LC+s(ReC+L/Ro)+1]（13）iL’’’’(s)/d(s)=[(1+sCRo)/s2LC+s(ReC+L/Ro)+1]·Uin/Ro（14）式(13)，式(14)便为Buck电路在电感电流连续时的控制－输出小信号传递函数。
BUCK电路仿真报告_小信号分析
主电路的零极点图，我们要做的就是拿 PID 的零点补偿掉它 备注：如果增大控制频率即 减小 T 到 1E-6 时，不稳定极点会向 1,0 点靠拢..这样匹配起来更简单。 但是会引入一个问题就是 处理速度实在达不到，而且频率越高，高频下的各种电路现象会涌现出来。
Aaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa 小信号分析：aaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa
Aaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa 系统框图：aaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa
Aaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa 主电路：aaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa 当 MOS 管导通时：
但是发散了，所以需要减小 Kp ：不影响系统的动态性能，但是会改变响应速度。
AaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaPID1 与主电路级联：aaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa 所取： Kp = -2.5227*0.01; Ti = -50112.97;%2123188.4; Td = -2.745758513e-4;%1.245e-3;
1 / L Il 0 Uin 1 / RC Uo 0
设系统导通占空比为 D 由状态空间平均法得：
d Il 0 dt Uo 1 / C
最新Buck电路的系统建模资料
在开关管处于通态时，即 ［t ，t+DT s ］时，电感两段电压uck 变换器的建模1、Buck 变换器及其工作状态分析/YYYXLVg^------------------------------------------------ ----------------------- ---------------------- ------------ b)c)图1 Buck 变换器及其工作状态分析 a) Buck 变换器b)开关处理通态［t , t+DT s ］ c)开关处于断态［t+DT s , t+Tj21 t 嚨1 _ t -DT st代"I又〈VL (t j T =lj VL (tdt =l|[VL (tdt +J* VL (tdt =VgD —V,则其稳态sT s 1T sI 1t4DT s」电压传输比为：］DBUck 变换器的输入输出功率平衡有：V g l g "I °，得 l g =DI °。
2、大信号模型FRn当Buck 变换器达到稳态时,% t T si t T s -it T s若略去开关损耗，则为:V L t二V g t -vt ,通过电容的电流i CC-dv ^二i t 一吐;当开关 dt gdt R管处于断态时，即［t+DT s , t+T s ］时，电感两端电压为V L t ，通过dt电容的电流为i Ct 二i t - U 。
R1 t <s1 一 t -dT s1V Lt.T S =- TV Ld.〒七VLd .t如果输入电压V g t 连续，而且在一个开关周期内变化很小，于是 V g t 在［t ，t+dT s ］区间的值可以近似用开关周期的平均值 V g t : T表示，这样t T s dT sVLdt -T s\ 1 t -^dT St -'T s_v d _td Tv dtV g d. _ tv d由于输出电压vt 连续，另外vt 在一个周期中变化很小，于是vt 在［t, t+T s ］ 区间的值可以近似的表示为［vt T。
Buck电路的小信号频域模型
在已知环路其他部分的传递函数表达式后，即可设计电压误差放大器了。
由于KLC提供了一个零点和两个谐振极点，因此，一般将E/A设计成PI调节器即可，KEA=KP(1＋ωz/s)。
其中ωz用于消除稳态误差，一般取为KLC零极点的1/10以下；KP用于使剪切频率处的开环增益以－20dB/十倍频穿越0dB线，相角裕量略小于90°。
2 电压模式控制（VMC）电压模式控制方法仅采用单电压环进行校正，比较简单，容易实现，可以满足大多数情况下的性能要求，如图2所示。
图2中，当电压误差放大器（E/A）增益较低、带宽很窄时，Vc波形近似直流电平，并有D=Vc/Vs （15）d=Vc'/Vs （16）式（16）为式（15）的小信号波动方程。
整个电路的环路结构如图3所示。
图3没有考虑输入电压的变化，即假设Uin=0。
图3中，（一般为0）及分别为电压给定与电压输出的小信号波动；KFB=UREF/Uo，为反馈系数；误差e为输出采样值偏离稳态点的波动值，经电压误差放大器KEA放大后，得；KMOD为脉冲宽度调制器增益，KMOD=d/=1/Vs；KPWR为主电路增益，KPWR=/d=Uin；KLC为输出滤波器传递函数，KLC=(1+sCRe)/[S2LC+s(ReC+L/Ro)+1]。
在已知环路其他部分的传递函数表达式后，即可设计电压误差放大器了。
由于KLC提供了一个零点和两个谐振极点，因此，一般将E/A设计成PI调节器即可，KEA=KP(1＋ωz/s)。
其中ωz用于消除稳态误差，一般取为KLC零极点的1/10以下；KP用于使剪切频率处的开环增益以－20dB/十倍频穿越0dB线，相角裕量略小于90°。
VMC方法有以下缺点：1）没有可预测输入电压影响的电压前馈机制，对瞬变的输入电压响应较慢，需要很高的环路增益；2）对由L和C产生的二阶极点（产生180°的相移）没有构成补偿，动态响应较慢。
VMC的缺点可用下面将要介绍的CMC方法克服。
Buck-Boost电路建模及分析
题目：Buck-Boost电路建模及分析摘要：作为研究开关电源的基础，DC-DC开关变换器的建模分析对优化开关电源的性能和提高设计效率具有重要意义。
而Buck-Boost电路作为DC-DC开关变换器的其中一种电路拓扑形式，因其输出电压极性与输入电压相反，而幅度既可比输入电压高，也可比输入电压低，且电路结构简单而流行。
为了达到全面而深入的研究效果，本文对Buck-Boost电路进行了稳态分析和小信号分析。
稳态分析中，首先介绍了电路工作原理，得出了两种工作模式下的电压转换关系式，并同时可知基于占空比怎样计算其输出电压以及最小最大电感电流和输出纹波电压计算公式；接着推导了状态空间模型，以在MATLAB中进行仿真；而最后仿真得到的电感电流、输出电压的变化规律符合理论分析。
小信号分析中，首先推导了输出与输入间的传递函数表达式，以了解低频交流小信号分量在电路中的传递过程；接着分析其零极点，且仿真绘制波特图进行了验证。
经过推导与研究，稳态分析和小信号分析下仿真得到的变化规律均与理论上的推导一致。
关键词：Buck-Boost；稳态分析；小信号分析；MATLAB仿真1.概论现代开关电源有两种：直流开关电源、交流开关电源。
本课题主要介绍直流开关电源，其功能是将电能质量较差的原生态电源，如市电电源或蓄电池电源，转换为满足设备要求的质量较高的直流电源，即将“粗电”转换为“精电”。
直流开关电源的核心是DC-DC变换器。
作为研究开关电源的基础，DC-DC开关变换器的建模分析对开关电源的分析和设计具有重要意义。
DC-DC开关变换器最常见的三种电路拓扑形式为：降压(Buck)、升压(Boost)和降压-升压(Buck-Boost) [1]，如图1-1所示。
其中Buck-Boost变换器因其输出电压极性与输入电压相反，而幅度既可比输入电压高，也可比输入电压低，且电路结构简单而流行。
(a) Buck型电路结构(b) Boost型电路结构(c) Buck-Boost型电路结构图1-1 DC-DC变换器的三种电路结构本课题针对Buck-Boost变换器的建模分析进行深入研究，以优化开关电源的性能和提高设计效率。
(完整版)Buck-Boost电路设计
500W Buck/Boost电路设计与仿真验证一、主电路拓扑与控制方式Buck/Boost变换器是输出电压可低于或高于输入电压的一种单管直流变换器，其主电路与Buck或Boost 变换器所用元器件相同，也有开关管、二极管、电感和电容构成，如图1—1所示。
与Buck和Boost电路不同的是，电感L f在中间，不在输出端也不在输入端，且输出电压极性与输入电压相反。
开关管也采用PWM控制方式。
Buck/Boost变换器也有电感电流连续喝断续两种工作方式，本文只讨论电感电流在连续状态下的工作模式。
图1-2是电感电流连续时的主要波形。
图1-3是Buck/Boost变换器在不同工作模态下的等效电路图。
电感电流连续工作时，有两种工作模态，图1-3(a)的开关管Q导通时的工作模态，图1-3（b）是开关管Q关断、D续流时的工作模态。
V o图1—1 主电路Vi LFi Qi DV图1-2 电感电流连续工作波形V oV o(a） Q导通 (b） Q关断,D续流图1—3 Buck/Boost不同开关模态下等效电路二、电感电流连续工作原理和基本关系电感电流连续工作时，Buck/Boost变换器有开关管Q导通和开关管Q关断两种工作模态.在开关模态1[0～t on]：t=0时,Q导通，电源电压V in加载电感L f上,电感电流线性增长,二极管D戒指，负载电流由电容C f提供:f L f in di L V dt=(2-1）oo LDV I R =(2—2） ofo dV C I dt=（2-3）t=t on 时,电感电流增加到最大值max L i ，Q 关断。
在Q 导通期间电感电流增加量f L i ∆f inL y fV i D T L ∆=⋅ (2-4)在开关模态2［t on ~ T]：t=t on 时，Q 关断，D 续流，电感L f 贮能转为负载功率并给电容C f 充电，f L i 在输出电压Vo 作用下下降：f L fo di L V dt=（2-5）f o o oL fo f LDdV dV V i C I C dt dt R =+=+（2—6)t=T 时，f L i 见到最小值min L i ，在t on ~ T 期间f L i 减小量f L i ∆为：(1)f o o L off y f fV Vi t D T L L ∆=⋅=- （2-7）此后,Q 又导通，转入下一工作周期.由此可见，Buck/Boost 变换器的能量转换有两个过程：第一个过程是Q 开通电感L f 贮能的过程,第二个是电感能量向负载和电容C f 转移的过程。
(完整word版)BUCK电路
题目：BUCK电路闭环PID控制系统的MATLAB仿真目录一、课题简介 (2)二、BUCK变换器主电路参数设计 (2)2.1设计及内容及要求 (2)2.2主电路设计 (2)1、滤波电容的设计 (3)2、滤波电感设计 (3)3、占空比计算 (3)三、BUCK变换器PID控制的参数设计 (3)3.1主电路传递函数分析 (4)四、BUCK变换器系统的仿真 (7)4.1仿真参数及过程描述 (7)4.2仿真模型图及仿真结果 (8)五、总结 (10)六、参考文献 (10)七、附录 (10)一、课题简介BUCK 电路是一种降压斩波器，降压变换器输出电压平均值Uo 总是小于输出电压U D 通常电感中的电流是否连续，取决于开关频率、滤波电感L 和电容C 的数值。
简单的BUCK 电路输出的电压不稳定，会受到负载和外部的干扰，当加入PID 控制器，实现闭环控制。
可通过采样环节得到PWM 调制波，再与基准电压进行比较，通过PID 控制器得到反馈信号，与三角波进行比较，得到调制后的开关波形，将其作为开关信号，从而实现BUCK 电路闭环PID 控制系统。
二、BUCK 变换器主电路参数设计2.1设计及内容及要求1、 输入直流电压(VIN)：15V2、 输出电压(VO)：5V3、 输出电流(IN)：10A4、 输出电压纹波峰-峰值 Vpp ≤50mV5、 锯齿波幅值Um=1.5V6、开关频率(fs)：100kHz7、采样网络传函H(s)=0.38、BUCK 主电路二极管的通态压降VD=0.5V ，电感中的电阻压降VL=0.1V，开关管导通压降 VON=0.5V,滤波电容C 与电解电容RC 的乘积为2.2主电路设计根据以上的对课题的分析设计主电路如下：图2-1 主电路图F *Ωμ751、滤波电容的设计因为输出纹波电压只与电容的容量以及ESR 有关，rr rrC L N0.2V V R i I ==∆ （1）电解电容生产厂商很少给出ESR ，但C 与R C 的乘积趋于常数，约为50~80μ*ΩF [3]。
平均电流模式控制Buck电路小信号分析
平均电流模式控制Buck 电路小信号分析平均电流模式控制在电池充电电路以及PFC 中有着广泛的应用。
因其电流环和电压环均需补偿，故分析其小信号特性相当必要。
本文将采用参考[1]的建模方法来分析平均电流模式下buck 电路的特性，给出了其简化等式，并利用K 因子方法设计了补偿电路。
一 电流环补偿设计图一所示为电路的方框图及其小信号模型。
占空比到输出以及到电感电流的传递函数为[2]图一 电路方框图及小信号模型其中图二 Gvd 和Gid 传递函数输入和输出的反馈为从Vcl 到Ri V 的传递函数为其中 因Go<<1，故上式简化形式为其高频近似为此处采用Type II 来补偿，参考[3][4]给出了避免电路不稳定的补偿中频增益的限制，其中选定中频增益后，电流环的交越频率也随之确定利用K 因子法，确定补偿的零点为则有补偿的极点为进而有补偿的传函为电流环传递函数为图3 电流环bode 图 交越频率和相位裕量计算如下二 电压环补偿设计控制Vc 到输出的传递函数为 其近似为其低频近似为为了减少电流环对电压环的影响，后者交越频率要小于前者。
设定电压环交越频率 fc利用K 因子法，确定补偿的零点为补偿的极点为补偿的传函为则电压环传函为图4 Gvc Bode 图图5电压环bode 图交越频率和相位裕量计算如下参考：[1]. Philip Cooke." Modeling Average Current Control". Unitrode Integrated Circuits Corporation(TI).2005.[2].Doaer"buck".[3].Lloyd Dixon."Average Current Mode Control of Switching Power Supplies"Unitrode(TI) Application Note .[4].Jian Sun. Richard M.Bass."Modeling and Practical Design Issues for Average Current Control".1999 IEEE。
开关电源Buck电路的小信号模型及环路设计word资料6页
0 引言设计一个具有良好动态和静态性能的开关电源时，控制环路的设计是很重要的一个部分。
而环路的设计与主电路的拓扑和参数有极大关系。
为了进行稳定性分析，有必要建立开关电源完整的小信号数学模型。
在频域模型下，波特图提供了一种简单方便的工程分析方法，可用来进行环路增益的计算和稳定性分析。
由于开关电源本质上是一个非线性的控制对象，因此，用解析的办法建模只能近似建立其在稳态时的小信号扰动模型，而用该模型来解释大范围的扰动（例如启动过程和负载剧烈变化过程）并不完全准确。
好在开关电源一般工作在稳态，实践表明，依据小信号扰动模型设计出的控制电路，配合软启动电路、限流电路、钳位电路和其他辅助部分后，完全能使开关电源的性能满足要求。
开关电源一般采用Buck电路，工作在定频PWM控制方式，本文以此为基础进行分析。
采用其他拓扑的开关电源分析方法类似。
1 Buck电路电感电流连续时的小信号模型为理图1为典型的Buck电路，为了简化分析，假定功率开关管S和D1想开关，滤波电感L为理想电感（电阻为0），电路工作在连续电流模式（CCM）下。
R e为滤波电容C的等效串联电阻，R o为负载电阻。
各状态变量的正方向定义如图1中所示。
图1 典型Buck电路S导通时，对电感列状态方程有L=U－ U o （1）inS断开，D续流导通时，状态方程变为1L=－U（2）o占空比为D时，一个开关周期过程中，式（1）及式（2）分别持续了DT s 和（1－D）T s的时间（T s为开关周期），因此，一个周期内电感的平均状态方程为L=D(U－U o)＋(1－D)(－U o)=DU in－U o（3）in稳态时，=0，则DU in=U o。
这说明稳态时输出电压是一个常数，其大小与占空比D和输入电压U in成正比。
由于电路各状态变量总是围绕稳态值波动，因此，由式（3）得L=(D＋d)(Uin＋)－(U o＋) （4）式（4）由式（3）的稳态值加小信号波动值形成。