渗流力学课后习题答案第三章演示教学
《流体力学》徐正坦主编课后答案第三章解析
第三章习题简答3-1 已知流体流动的速度分布为22y x u x -= ，xy u y 2-=，求通过1,1==y x 的一条流线。
解：由流线微分方程yx u dyu dx =得dy u dx u x y =则有 dy y x xydx )(222-=-两边积分可得C y y x yx +-=-3322即0623=+-C y x y将x=1,y=1代入上式，可得C=5，则 流线方程为05623=+-y x y3-3 已知流体的速度分布为⎭⎬⎫==-=-=tx x u ty y u y x 00εωεω（ω>0，0ε>0）试求流线方程，并画流线图。
解：由流线微分方程yx u dyu dx =得dy u dx u x y =则有 tydy txdx 00εε-=两边积分可得C y x +-=22流线方程为C y x =+223-5 以平均速度s m v /5.1=流入直径为D=2cm 的排孔管中的液体，全部经8个直径d=1mm 的排孔流出，假定每孔出流速度依次降低2%，试求第一孔与第八孔的出流速度各为多少？题3-5图解：由题意得：v 2=v 1(1-2%)，v 3=v 1(1-2%)2，…，v 8=v 1(1-2%)7 根据质量守恒定律可得282322212832144444dv d v d v d v D v Q Q Q Q Q πππππ⋅+⋅⋅⋅+⋅+⋅+⋅=⋅+⋅⋅⋅+++=sm d vD v v d v v v v d D v /4.80)98.01(001.002.002.05.1)98.01()98.01(98.01)98.01(4)(448228221812832122=-⨯⨯⨯=--⋅=∴--⋅=+⋅⋅⋅+++⋅=⋅πππ则 v 8=v 1(1-2%)7=80.4×(1-2%)7=69.8m/s3-6 油从铅直圆管向下流出。
管直径cm d 101=，管口处的速度为s m v /4.11=，试求管口处下方H=1.5m 处的速度和油柱直径。
《土力学》第三章练习题及答案
《土力学》第三章练习题及答案《土力学》第三章练习题及答案第3章土的渗透性和渗流一、填空题1.当渗流方向，且水头梯度大于水头梯度时，会发生流砂现象。
2.渗透系数的数值等于水力梯度为1时，地下水的渗透，颗粒越粗的土，渗透系数数值越。
二、名词解释1.渗流力2.流砂3.水力梯度4.临界水力梯度三、简答题1.影响渗透系数大小的主要因素有哪些？2.流砂现象防治的方法有哪些？3.管涌发生的条件是什么？防治措施有哪些？四、单项选择题1.流砂产生的条件为：（A）渗流由上而下，动水力小于土的有效重度（B）渗流由上而下，动水力大于土的有效重度（C）渗流由下而上，动水力小于土的有效重度（D）渗流由下而上，动水力大于土的有效重度您的选项（）2.流砂发生的土层为：（A）颗粒级配均匀的饱和砂土（B）颗粒级配不均匀的饱和砂土（C）颗粒级配均匀的不饱和砂土（D）颗粒级配不均匀的不饱和砂土您的选项（）3.饱和重度为20kN/m3的砂土，在临界水头梯度ICr时，动水力GD大小为：（A）1 kN/m3（B）2 kN/m3（C）10 kN/m3（D）20 kN/m3您的选项（）第3章土的渗透性和渗流一、填空题1.向上、临界2.速度、大二、名词解释1.渗流力：水在土中流动时，单位体积土颗粒受到的渗流作用力。
2.流砂：土体在向上动水力作用下，有效应力为零时，颗粒发生悬浮、移动的现象。
3.水力梯度：土中两点的水头差与水流过的距离之比。
为单位长度上的水头损失。
4.临界水力梯度：使土开始发生流砂现象的水力梯度。
三、简答题1.影响渗透系数大小的主要因素有哪些？(1)土的粒度成分和矿物成分(2)土的密实度(3)土的饱和度(4)土的结构(5)水的温度(6)土的构造2.流砂现象防治的方法有哪些？（1）减小或消除水头差：采用坑外降低地下水位或采用水下挖掘。
（2）增长渗流路径：打板桩。
（3）在向上渗流出口处地表压重。
（4）加固土层：冻结法、注浆法。
3.管涌发生的条件是什么？防治措施有哪些？发生条件:（1）必要条件：土中粗颗粒所构成的孔隙直径必须大于细颗粒的直径。
高等渗流力学习题集答案
作业1—程林松写出下列问题的运动方程：（1）多相渗流（油、气、水）（2）多重介质渗流（孔隙-裂缝-溶洞介质）（3）各向异性介质（4）非线性渗流（低渗）（5）非牛顿渗流作业2—程林松如下图所示，水平、均质、等厚、长度为a2，宽度为b2的长方形地层（两条断层和两条供给边界），地层厚度为h ，渗透率为K ，流体粘度为μ，综合压缩系数为t C ，在地层中间有一口生产井，弹性不稳定渗流，油井半径为w R ,原始地层压力为e p （供给边界压力也为e p ），导压系数：tC K μη=。
要求： （1） 在0=t 时刻以定产量Q 生产时，建立描述该流动的数学模型；（2） 在0=t 时刻以定压Pw 生产时，建立描述该流动的数学模型；（3） 在0=t 时刻以定产量Q 生产时，简述两种求解任一时刻地层任一点压力的思路和方法。
作业3—程林松要求：（1）推导该流场的等势线和流线方程，并画出渗流场示意图；（2）以此为例说明复势叠加原理；（3）定量分析在x轴和y轴上等势线、流线、渗流速度的特点和变化规律；（4）说明这是一个什么流动过程？作业4—程林松推导底水油藏水平井产量计算公式，油井见水时间计算公式。
作业5—程林松利用保角变换方法求解三分支裂缝井渗流问题：（1）写出等势线和流线方程；（2）绘制相应的渗流场图，分析三分支裂缝井渗流场的特点；（3）推导相应的产量计算公式。
作业6—程林松对比说明常规黑油模型和多相多组分模型流体物性参数的计算方法的差别。
作业7—程林松与常规油藏相比，低渗、特低渗油藏渗流特征的差别，建立渗流数学模型时如何考虑？作业8—程林松写出你理解的N-R迭代求解方法及过程（举例说明）？作业9—程林松如图所示有一边水油藏，已知地层厚度h，孔隙度Φ，流体粘度µ，刚性稳定渗流，已知Pe，Pw，Rw，a，B。
要求：（1）简述用势的迭加原理求油井产量Q的方法和步骤？（2）用保角变换方法推导油井产量Q的计算公式？作业10—程林松如图所示，距直线供给边a处有一产量为Q的生产井，已知Pe，Pw，Q，h，K，µ，a，Rw，刚性稳定渗流，试利用复势函数理论，定量分析该流场的特点（等势线分布及特点、流线分布及特点、渗流速度）作业11—程林松写出黑油与多组份渗流数学模型，说明物性参数计算方法的差别？作业12—程林松写出完成一流体混合物完整PT相图的求解过程和方法？黄世军老师作业绪论1、水平、均质、等厚三角形油藏（如图所示，两侧具有封闭边界、一侧具有恒定定压边界，压力为Pi，渗透率K，流体粘度为μ，厚度为h，弹性压缩系数为Ct，在油藏中部（位置如图所示）有一口井初始时刻（t=0）恒定产量 Q 生产，井筒半径为 Rw，地层原始压力为 Pi，弹性不稳定渗流；请写出该渗流问题的渗流数学模型。
渗流力学课件第三章2
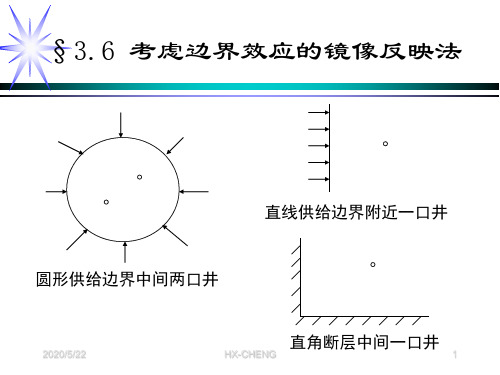
实际边缘
Pwf
re
⊙说明：①同样情况下，中心井的产量大于直线
供给边界附近一口井的产量，实际情况下的产量
一般介于两者之间； ②由于定错边界形状而引起的产量误差 一般不超过10﹪，可见边缘形状对井产量影响不 大。 实际供给边缘简化 示意图
●油井所处位置对井产量的影响 其它条件相同时，井距直线边界越近产量越大；对圆形供 给边界，偏心距对产量有影响： 2 re re l 2 q偏心 / q中心 ln / ln rw rw re
连续性方程：
divv 0
2 P 0
divJ 0
2U 0
基本微分方程：
流体渗流 与 电流流动
＊物理量一一对应； ＊满足相同的 数学方程； ＊若具有相似的 几何条件和 边界条件。
将有完全 相似的解
即：电场中电位的分布 与渗流场中压力的分布相同； 电流线的分布与渗流线的分布相同。
水电相似原理的应用 ＊电模拟实验。在实验室中，用电场中电流的流动来模 拟各种边界条件下地下流体的渗流。 铜棒 生产井
低电位
环形铜片
高电位
re
平面径向渗流模型
h
供给边界
打开程度不完善电模拟 实验装置
＊用电场中电流的流动定律来研究地下流体的渗流问题 。
§3.7 等值渗流阻力法
二、等值渗流阻力法（应用方法）
q圆 / q直线
re (m)
取 rw 0.1m ，计算如下表：
2re re re ln / ln 1 0.301 / lg rw rw rw
lg( re / rw )
3 4 5
1.1 1.075 1.0605
误差 10﹪ 7.5 ﹪ 6.05﹪
渗流力学第三章1
K Pe Pwf 1 渗流速度： v re r dr ln rw K dP
平面径向流 产量公式 （裘比公式）
q 2Kh( Pe Pwf )
产量公式： q Av 2rh v
Pe Pwf ln re rw q
ln
re rw
又由产量公式变形：
2Kh
代入压力分布公式得：
dr 2rh rw r r1 区间内压力分布规律为：
v K dP q
分离变量积分得：
K1 K2
r
re
Pwf r 1
Pe
积分：
P
dp
Pwf
2h
q
q
1
rw
Kr
r rw
dr
r
P 1
渗透率突变的圆形地层 r1 r re 区间内压力分布规律为： re q Pe q re 1 dp dr 积分： P Pe 2K h ln r P 2 2h r Kr Pe re q r1 1 1 产量为： Pwf dp 2h [rw K r dr r1 K r dr ] 1 2
★提高地层压力 P （通常难于做到）或降低井底压力 Pwf e ，放大压差； ★改善地层渗透率可提高产量，如油井压裂、酸化等； ★降低原油粘度 可提高产量，如热力采油等； ★供给半径 re 和油井半径 rw 均在对数内，其变化对产量 q 影响较小。
②实际应用时，产量公式中各物理量可如下确定： ★ Pwf 可以实测；
，习惯称为“压降漏斗
”。
o
re r 平面径向流压力分布曲线
r
●
dP
dr r 速度大，压力梯度大，能量损耗也越大；
等压线
渗流力学课件第三章(复势)
Ψ = ∫ v y dx vx dy
L
为常数时表示流线方程, 则Ψ称为流函数, Ψ为常数时表示流线方程,给 称为流函数, 定不同的常数可得不同的流线. 定不同的常数可得不同的流线. 由(6)式知渗流速度与流函数关系: )式知渗流速度与流函数关系:
Ψ y Ψ vy = x vx =
(7)
因渗流场为有势场, 因渗流场为有势场,其旋度
C1为一常数,表示一条等势线. 为一常数,表示一条等势线.
设在渗流场中有流线S, 设在渗流场中有流线 ,其中 一点M处的切线方向 处的切线方向, 一点 处的切线方向,为该点 流体质点运动方向. 流体质点运动方向. 点渗流速度为v,则在x, 设M点渗流速度为 ,则在 , 点渗流速度为 y方向的分速度为 x,vy. 方向的分速度为v 方向的分速度为 点沿流线S取一微小增量 在M点沿流线 取一微小增量 点沿流线 dS,则在 ,y方向的增量为 , 方向的增量为dx, ,则在x, 方向的增量为 dy,由相似关系有: ,由相似关系有:
q q W ( z) = ln( z a ) ln( z + a ) + C 2π 2π q za = ln +C 2π z + a r1e iθ1 q = ln iθ 2 + C 2π r2 e
(1) )
则势函数为: 则势函数为: 流函数为: 流函数为:
r1 q Φ= ln + C1 2π r2
∴Ψ =
又
Φ Ψ = x y
即
q y q y = + C ' ( x) 2π x 2 + y 2 2π x 2 + y 2
∴ C ' ( x) = 0
则
C ( x) = C2
渗流力学课件第三章
2kh( p e p w ) Q Re ln Rwr
井的不完善性引起的 附加压降等于：
Q p c .C 2kh
△ PC
C－表皮系数，为一反映井壁污染和不完善井结构的附加 渗流阻力的无量刚值。
井产量公式为：
2kh( p e p w ) Q Re (ln C) Rw
已知：k、Φ、h、Re、Rw、pe、pw、μ
Q
1、平面径向稳定渗 流的压力分布公式
pe
pw
r
Rw
Re
数学模型：
d 2 p 1 dp 0 2 r dr dr
（1）
r=Rw，p=pw r=Re，p=pe （2）
dp 令 dr
则（1）式变为：
d dr r
分离变量积分得：
ln ln r ln C1
如代入
pe p w r p pw ln Re Rw ln Rw
有
pe p w Re 1 p pw (ln ) Re Rw 2 ln Rw
5、液体质点的运移规律
因
dr v dt
dt dr 2rhdr v Q
则液体质点从r0移到r需时间t为
则
r C1
dp r C1 dr
即
分离变量积分：
p C1 ln r C2
（3）
代入边界条件得：
Pe Pw C1 Re ln Rw
pe p w pe p w C 2 pe ln Re p w ln Rw Re Re ln ln Rw Rw
代回（3）得：
压力分布：
在0<x<L1期间：
渗流力学习题答案1-7章
一、 公式推导1、均质水平圆形地层中心一口生产井，油井以定产量q 生产，已知井折算半径r we ，边界压力p e ，地层厚度h ，若在r e 到r 1（地层中某点）之间服从线性渗流规律，r 1到r we 之间服从二项式非线性渗流规律（2dp v v dr Kμβρ=+，v —渗流速度），求井底压力p wf 的表达式。
2αρννμ+=Kdr dp 2[()]22e ewfwe p rp r q q dp dr K rh rhμαρππ=+⎰⎰11221211111ln 2222e we r r e wf r r we e r q q q q p p dr dr Kh r h r Kh r h r r μαρμαρππππ⎛⎫-=+=+-⎰⎰ ⎪⎝⎭2、均质水平等厚圆形地层中有一口完善生产油井以定井底压力p wf 生产，地层流体向井的流动服从达西定律且呈稳定渗流，已知油井半径r w ，供给边界半径r e ，供给边界压力p e ，地层厚度h ，地层流体粘度为K ，地层流体粘度为μ。
请导出油井产量的表达式。
渗流0122=+drdpr r d p d 转换0)(1=dr dpr dr dp r 积分 1C drdpr = 分离变量 dr rC dp 11=21ln C r C p += 带入初始条件 21ln C r C p e e += 21ln C r C p w w += 联立求得 r r r r p p p p ewe w e e ln ln --= 求导r r r p p drdp we w e 1ln -=带入达西表达式 r r r p p K v wew e 1ln -=μ 产量表达式 rhv Av q π2==wew e r r p p Kh q ln)(2μπ-=P191-1、H g pe p ∆+=ρ(1)p=9+850*9.8*（-940+950）*106-=9.0833MPa (2)p=8.5164MPa (3)p=9.633MPa (4)p=9.4831MPa 1号井是低压的1-2、9+850*9.8*（-1000-x ）*106-+1000*9.8*（x+1300）*106-=11.7 1-3、都折算到B 平面MPa gh p p A za 43.9=+=ρ<B p 所以由B 流向A P342-1、计算雷诺数dv l q π= s cm ld qv /018.0==π2.0103.35.17Re 35.1〈*==-μφρkv 所以服从达西定律2-2、3600*241002v r q π= v=58.9 cm/s Re=10.66>0.3 所以不服从达西定律。
油气渗流力学习题答案
油气渗流力学习题答案油气渗流力学习题答案油气渗流力学是石油工程中的重要学科，它研究的是油气在地下储层中的流动规律和特性。
在学习过程中，我们常常会遇到一些练习题，下面我将为大家提供一些典型的油气渗流力学习题的答案，希望对大家的学习有所帮助。
题目一：已知油藏的有效厚度为20m，孔隙度为0.25，渗透率为1000md，油层压力为30MPa，地层温度为80℃，求油藏的孔隙流量。
解答：首先，我们需要计算油藏的有效孔隙度。
有效孔隙度等于总孔隙度乘以有效饱和度，而有效饱和度等于原油饱和度乘以孔隙度。
假设原油饱和度为0.8，则有效饱和度为0.8 * 0.25 = 0.2。
油藏的有效孔隙度为0.25 * 0.2 = 0.05。
接下来，我们可以使用达西定律计算孔隙流量。
达西定律可以表示为：Q = (k * A * ΔP) / (μ * L)其中，Q表示孔隙流量，k表示渗透率，A表示流动截面积，ΔP表示压力差，μ表示黏度，L表示流动长度。
假设流动截面积为1平方米，压力差为30MPa，黏度为0.1Pa·s，流动长度为20m。
代入上述数值，我们可以计算出孔隙流量为：Q = (1000md * 1m^2 * 30MPa) / (0.1Pa·s * 20m) = 1500000m^3/d所以，油藏的孔隙流量为1500000立方米/天。
题目二：已知油藏的有效厚度为30m，孔隙度为0.3，渗透率为800md，地层温度为70℃，油层压力为25MPa，求油藏的渗流能力系数。
解答：渗流能力系数可以通过渗透率和孔隙度的乘积来计算。
即：C = k * φ其中，C表示渗流能力系数，k表示渗透率，φ表示孔隙度。
代入上述数值，我们可以计算出渗流能力系数为：C = 800md * 0.3 = 240md所以，油藏的渗流能力系数为240md。
题目三：已知油藏的有效厚度为40m，孔隙度为0.35，渗透率为1200md，地层温度为60℃，油层压力为20MPa，求油藏的有效渗透率。
（完整版）流体力学第三章课后习题答案
（完整版）流体⼒学第三章课后习题答案⼀元流体动⼒学基础1.直径为150mm 的给⽔管道，输⽔量为h kN /7.980，试求断⾯平均流速。
解：由流量公式vA Q ρ= 注意：()vA Q s kg h kN ρ=?→//A Qv ρ=得：s m v /57.1=2.断⾯为300mm ×400mm 的矩形风道,风量为2700m 3/h,求平均流速.如风道出⼝处断⾯收缩为150mm ×400mm,求该断⾯的平均流速解：由流量公式vA Q = 得：A Q v =由连续性⽅程知2211A v A v = 得：s m v /5.122=3.⽔从⽔箱流经直径d 1=10cm,d 2=5cm,d 3=2.5cm 的管道流⼊⼤⽓中. 当出⼝流速10m/ 时,求(1)容积流量及质量流量;(2)1d 及2d 管段的流速解：(1)由s m A v Q /0049.0333==质量流量s kg Q /9.4=ρ (2)由连续性⽅程：33223311,A v A v A v A v ==得：s m v s m v /5.2,/625.021==4.设计输⽔量为h kg /294210的给⽔管道，流速限制在9.0∽s m /4.1之间。
试确定管道直径，根据所选直径求流速。
直径应是mm 50的倍数。
解：vA Q ρ= 将9.0=v ∽s m /4.1代⼊得343.0=d ∽m 275.0 ∵直径是mm 50的倍数，所以取m d 3.0= 代⼊vA Q ρ= 得m v 18.1=5.圆形风道，流量是10000m 3/h,，流速不超过20 m/s 。
试设计直径，根据所定直径求流速。
直径规定为50 mm 的倍数。
解：vA Q = 将s m v /20≤代⼊得：mm d 5.420≥ 取mm d 450= 代⼊vA Q = 得：s m v /5.17=6.在直径为d 圆形风道断⾯上，⽤下法选定五个点，以测局部风速。
渗流力学课件第三章2
●复杂直线边界镜像反映的适用条件
＊成 2 / n（n为整数）夹角
的两直线断层，能进行反映的条 件是： ①n为偶数时，井可在所研究 区域中的任意位置；
120°
虚拟井
A
②n为奇数时，井只有在所研
究区域角的平分线上才能反映；
＊成 2 / n（n为整数）夹角
的两混合边界，能进行反映的条 件是：n应为4的倍数。
对称 等强度 异号反映
e
A w
源一汇来求解，所得解的一部分即为所求。
◆汇源反映法：以等产量的异号像代替供给边缘作用的方
法，称为汇源反映法。
2013-8-9 HX-CHENG 6
●势的分布、产量公式 地层中任一点 M 的势为：
q r1 M ln C 2h r2
供给边缘上，r1 r2 , M e 则：
直线供给边缘 圆形供给边缘 单一直线断层
等势边界（如： 供给边缘） 边界类型
不渗透边界（如 ：断层）
复杂直线边界
4
2013-8-9
HX-CHENG
§3.6 考虑边界效应的镜像反映法
一、供给边缘的镜像反映法
1.直线供给边缘附近一口生产井的反映 ●条件分析 ＊供给边界是等势线，势值为 e ； ＊井壁也是一条等势线，势值为 w ；
成120°(2 / 3) 夹角 两断层中一口井
●复杂直线边界镜像反映的检验方法 反映完取消边界后，原渗流场不变，即供给边界所在位置 为等势线，断层所在位置为流线，可分别用势的叠加和速度的 M 合成方法来验证。 r3 r1 供给边界
q r1r2 M ln C 2h r3r4
A
r4
r2
A
A
直线断层附近 两口生产井
土力学习题集答案__第三章
第3章土的渗透性及渗流一、简答题1.试解释起始水力梯度产生的原因。
2.简述影响土的渗透性的因素主要有哪些。
3.为什么室内渗透试验与现场测试得出的渗透系数有较大差别？4.拉普拉斯方程适应于什么条件的渗流场？5.为什么流线与等势线总是正交的？6.流砂与管涌现象有什么区别和联系？7.渗透力都会引起哪些破坏？二、填空题1.土体具有被液体透过的性质称为土的。
2.影响渗透系数的主要因素有：、、、、、。
3.一般来讲，室内渗透试验有两种，即和。
4.渗流破坏主要有和两种基本形式。
5.达西定律只适用于的情况，而反映土的透水性的比例系数，称之为土的。
三、选择题1.反应土透水性质的指标是（）。
A.不均匀系数B.相对密实度C.压缩系数D.渗透系数2.下列有关流土与管涌的概念，正确的说法是（）。
A．发生流土时，水流向上渗流；发生管涌时，水流向下渗流B.流土多发生在黏性土中，而管涌多发生在无黏性土中C.流土属突发性破坏，管涌属渐进式破坏D.流土属渗流破坏，管涌不属渗流破坏3.土透水性的强弱可用土的哪一项指标来反映？（）A.压缩系数B.固结系数C.压缩模量D.渗透系数4.发生在地基中的下列现象，哪一种不属于渗透变形？（）A.坑底隆起B.流土C.砂沸D.流砂5.下属关于渗流力的描述不正确的是（）。
A.其数值与水力梯度成正比，其方向与渗流方向一致B.是一种体积力，其量纲与重度的量纲相同C.流网中等势线越密集的区域，其渗流力也越大D.渗流力的存在对土体稳定总是不利的6.下列哪一种土样更容易发生流砂？（）A.砂砾或粗砂B.细砂或粉砂C.粉质黏土D.黏土7.成层土水平方向的等效渗透系数与垂直方向的等效渗透系数的关系是（）。
A.>B.=C.<8. 在渗流场中某点的渗流力（）。
A.随水力梯度增加而增加B.随水利力梯度增加而减少C.与水力梯度无关9.评价下列说法的正误。
（）①土的渗透系数越大，土的透水性也越大，土的水力梯度也越大；②任何一种土，只要水力梯度足够大，就有可能发生流土和管涌；③土中任一点渗流力的大小取决于该点孔隙水总水头的大小；④渗流力的大小不仅取决于水力梯度，还与其方向有关。
渗流力学课件第三章(复势)解读
y
v M ds vy dx vx dy S
x
（4）
dx dy vx vv
（4）为流线方程。
即
vy dx vx dy 0
因无源渗流场中，
即
vx v y 0 x y
div v 0
v y vx x y
（5）
（5）式表示（4）式是某一函数的全微分，并用 dΨ 表示：
r为任意点M到原点的距离， q 2z M点取在原点时，r为0，渗流 2 ( z a )(z a ) 速度为零，为死油点。 q r r1 r2
补充习题：
已知平面渗流场的复势
求势函数和流函数。
w( z) q0 ze
i
第九节 平面渗流问题的保角变换求解法
一、保角变换的概念
一、势函数、流函数及复势
1、势函数和流函数
单相液体平面径向稳定渗流时，渗流速度为：
k p vx x k p vy y
x vy y vx
有
（1）
在无源区域内，因
即
div v 0
（2）
vx v y 0 x y
将（1）代入有：
w( z) ( x, y) i( x, y)
dw d id (
（14）
dx dy) i ( dx dy) x y x y 由（14）式： (dx dy) (dy idx) x y ( i )(dx idy) x y
令 上式化简为：
2 xy 1 2 2 2 c0 x y a
x 2 y 2 2c0 xy a 2 0
（4）
流线方程为双曲线方程，C0为无穷时，有x=0或y=0， 即x轴和y轴都是流线，其中y轴为分流线。 地层中任意点的渗流速度为：
渗流力学课后答案解析
第一章1．有四口油井测压资料间表1。
已知原油的相对密度0.8，原始油水界面的海拔为－950m ，试分析在哪个井附近形成低压区。
解：将4口井的压力折算成折算压力进行比较111m m zm H g p p ∆+=ρ=9.0×106+0.8×103×9.8×(950－940)=9.08MPa222m m zm H g p p ∆+=ρ=9.0×106+0.8×103×9.8×(950－870)=9.48MPa333m m zm H g p p ∆+=ρ=9.0×106+0.8×103×9.8×(950－850)=9.58MPa444m m zm H g p p ∆+=ρ=9.0×106+0.8×103×9.8×(950－880)=9.45MPa由数值上可以看出在第一口井处容易形成低压区。
2．某油田有一口位于含油区的探井，实测油层中部的原始地层压力为8.822×106Pa ，油层中部海拔为－1000m 。
位于含水区有一口探井，实测地层中部原始地层压力为11.47×106 Pa ，地层中部海拔－1300m 。
已知原油的相对密度为0.85，地层水的相对密度为1。
求该油田油水界面的海拔高度。
解：由于未开采之前，油层中的油没有流动，所以两口探井的折算压力应相等，设h 为油水界面的海拔高度，则：()10008.91085.010822.8361111-⨯⨯⨯+⨯=∆+=h H g p p m m zm ρ()13008.91011047.11362222-⨯⨯⨯+⨯=∆+=h H g p p m m zm ρ由21zm zm p p =可得：=h -1198.64m 该油田油水界面的海拔高度为-1198.64 m3．某油田在开发初期钻了五口探井，实测油层中部原始地层压力资料见表2。
渗流力学课后习题答案 第三章
第三章 刚性水压驱动下的油井干扰理论【3-1】平面无穷地层上有一源一汇，相距2σ，强度为q ，试用分析法证明地层任一点处的渗流速度的绝对值为12/()v q r r σπ=。
【证】由势的叠加原理，储层中任一点M 的势为22111222()ln ln ln ln 2224()M r q q q q x y r r C C C r x yσΦππππσ-+=-+=+=+++ 222222122()2()4()()2M Mx q x x q x x v x x y x y r r Φσσσσπσσπ⎡⎤⎡⎤∂-+-+=-=--=--⎢⎥⎢⎥∂-+++⎣⎦⎣⎦ 同理 22122My q y y v r r π⎡⎤=--⎢⎥⎣⎦又 ∵ Mx My v v i v j =+∴12/()v q r r σπ=== 【3-2】求液体质点沿上题的源汇连线的运动规律，即时间与距离的关系。
【解】x 轴上流体质点的运动速度为112M q v x a x a π⎡⎤=-⎢⎥+-⎣⎦∵ 真实渗流速度Mt v dxv dtφ==∴22112dx q q a dt x a x a x a πφπφ⎛⎫=-=-⋅ ⎪+--⎝⎭ 分离变量220()xtaqax a dx dt πφ--=-⎰⎰积分后 323233x qaa x a t πφ--=- 则时间与距离的关系为 323(2)3a a x x t qaπφ+-=【3-3】在2A 井投产前，1A 井已经投产，两口井间距离2100m σ=，1A 井的14MPa w p =，两井之半径127.5cm w w r r ==，15Km e r =，6MPa e p =，求2A 的2w p 为多少时1A 井停止生产？【解】根据井间干扰现象可知，当2A 井单独工作时，2A 井在1A 井处的压力为1A 井的井底压力，则1A 井停止生产，由于e w r r ，可将2A 视为在地层中心，2A 井在1A 井处的压降为21ln 22e e w r Q p p p Kh μ∆πσ==- 2A 的产量为 222()lne w ew Kh p p Q r r πμ-=将2Q 带入上式有 2()ln 2ln e w e e wp p rp r r ∆σ-=解得21ln ()ln 2e w w e e w e r r p p p p r σ=--331510ln0.0756(64) 1.13MPa 1510ln 100⨯=--=⨯ 【3-4】某产油层有10Km e r =的圆形供给边线，距地层中心2Km d =处钻了一口生产井，10cm w r =，5m h =，20.5m K μ=，25MPa e p =，23MPa w p =，2mPa s μ=⋅，求油井产量；假设油井位于地层中心，其余参数不变，产量为多少？【解】本题可看作为求一口偏心井的产量 偏心井的产量公式126322332()20.5105(2523)10118.3m /d 10102210ln 1ln 10.110e w e w e Kh p p Q r d r r ππμ---⨯⨯⨯⨯-⨯===⎡⎤⎡⎤⨯⎛⎫⎛⎫⨯⨯-⎢⎥⎢⎥- ⎪ ⎪⎝⎭⎢⎥⎢⎥⎣⎦⎝⎭⎣⎦由丘比（Dupuit ）公式知32()117.5m /d ln e w ewKh p p Q r r πμ-== 【3-5】某井距直线供给边线的距离1Km a =，8m h =，20.3m k μ=，4mPa s μ=⋅，0.1m w r =，2MPa p ∆=，求：(1)油井产量；(2)若井位于1Km e r =的圆形供给边线中心，其余参数不变，油井产量等于多少？【解】(1)该题是属于距直线供给边界为a 的地方有一口生产井的生产问题图3.27 30°交角井位图由公式 1263332()20.310821065.78m /d 2210ln 410ln 0.1e w w Kh p p Q qh a r ππμ---⨯⨯⨯⨯⨯====⨯⨯ (2) 由丘比（Dupuit ）公式126332()20.310821070.69m /d 1000410ln ln 0.1e w ewKh p p Q r r ππμ---⨯⨯⨯⨯⨯===⨯【3-6】两不渗透断层，交角为30，在它们的分角线上有一口生产井距离顶点为r ，假设离断层交点为e r 处，有一圆形供给边界，且e r r >>，如何求这口井的产量？【解】根据镜像反应原理，该问题可以看作是无穷大地层中等强度的12口生产井和12口注水井同时工作的问题，因此由势的叠加原理有1212131424...ln 2...M r r r qC r r r Φπ=+ ① 由于e r r >>，可将12口注水井忽略，则有1212ln ...2M qr r r C Φπ=+ ② 将M 点放到生产井的井壁上1212ln ''...'2w Kqp r r r C μπ=+ ()()()22ln 2sin152sin 30...2sin 902w q r r r r C π⎡⎤=︒︒︒+⎣⎦11ln(12)2w q r r C π=+ ③ 将M 点放到供给边界上1212ln ''''...''2e Kqp r r r C μπ=+ 由于e r r >>，每一口井到供给边界上一点的距离都可看为e r ，上式可化简为12ln()2e e K qp r C μπ=+ ④ ④-③有 1211()ln 212e e w w r Kqp p r rμπ-= er rep12112()2()ln 12ln ln 1212e w e w e e w w Kh p p Kh p p Q qh r r r r r r r ππμμ--===⎡⎤+⎢⎥⎣⎦ 【3-7】设半圆形供给边线的直径为不渗透边界，在通过供给边线的中心且与不渗透边线垂直的垂线上有一口井半径为w r 、井底压力为w p 的生产井，该井到不渗透边界的距离为d ，供给半径为e r ，供给压力为e p ，地层渗透率为K ，有效厚度为h ，流体粘度μ，求油井的产量公式。
渗流力学课件第三章(势)
因
r22 (x a)2 y 2
代入（2）式配方得：
(x2
y 2 )2
2( y 2
x2 )a2
a4
C
2 0
0（3）
（3）式为四次曲线族方程，给C0不同的值，得到不同 的等势线。
Y轴为分流线
等产量两汇时的渗流场
同样由流线与等势线的正交关系，可得一双曲线型 流线族方程：
x2 y 2 2C1xy a 2 0
三、渗流速度的合成原则
1、利用等势线和等压线确定渗流速度
求出渗流场的等势线分布或流线分布后，用渗
流速度与等势线的正交关系确定渗流速度方向。 大小可由下式计算：
v 1 2 k p1 p2
L
L
v1
vn
2、用矢量合成法
q1
各井单独生产时的渗流速度：
qn
n井同时生产：
vi
qi 2ri
vM v1 v2 v3 ... vn
这是注水开发采收率低的重要原因。
3、以知生产井和注入井势时的产量公式
由（1）式，把任意点取在注水井和生产井井壁：
i
q
2
ln
2a Rw
C
p
q
2
ln
Rw 2a
C
上两式相减有：
i
p
q
2
ln( 2a )2 Rw
q
ln
2a Rw
q (i p )
ln 2a Rw
Q kh( pi p p ) ln 2a
Rw
二、等产量两汇
在无限大地层中存在等产量的两汇，相距2a。
1、势及流场
由叠加原理地层中任意点的 势为；
v2 M
r2
v
渗流力学课后题
第一章 渗流的基本规律【1-1】一圆柱岩样6cm D =，10cm L =，22m K μ=，0.2φ=，油样沿轴向流过岩样，04mPa s μ=⋅，密度为800kg/m 3，入口端压力为0.3MPa e p =，出口端压力为0.2MPa w p =。
求：(1) 每分钟渗过的液量？ (2) 求雷诺数e R 。
(3) 求粘度162mPa s w μ=⋅、密度3=1000kg/m ρ的水通过岩样是的雷诺数(其余条件不变)。
【解】(1) 由达西定律知2212633(610)210(0.30.2)106084.82cm /min 44100.1∆πμ---⨯⨯⨯⨯-⨯==⨯=⨯⨯=⨯⨯AK p Q qt t L (2) 4284.82/60510m/s 6/4π-===⨯⋅q v A334e 3/23/210108005100.0090.24R ρφμ---⨯⨯⨯===⨯(3) 356e 3/2101000 1.210 6.8100.2162R ---⨯⨯⨯==⨯⨯ 【1-2】设液体通过直径10cm D =，长30cm L =的砂管，已知0.2φ=，00.65mPa s μ=⋅，0.7MPa p ∆=，0.3wc S =，200.2m μ=K ，求产量Q 、渗流速度v 和真实渗流速度t v 。
【解】由达西定律知产量 212663330.10.2100.710 5.610m /s 5.6cm /s 40.65100.3∆πμ---⨯⨯⨯⨯==⨯=⨯=⨯⨯AK p Q L 渗流速度 126430.2100.7107.1910m /s 0.65100.3K p v L ∆μ---⨯⨯⨯===⨯⨯⨯ 真实渗流速度 43t 7.1910= 3.6010m /s 0.2φ--⨯==⨯vv 【1-3】砂层500m L =，宽100m B =，厚4m h =，20.3m μ=K ，孔隙度0.32φ=，0 3.2mPa s μ=⋅，315m /d Q =，0.17wc S =，求：(1)压差p ∆，渗流速度V 和真实渗流速度t V 。
渗流力学课后题答案(1)
ln
2a Rw
9
*
ln
2
*
250 *102 10
是圆形供给边缘时
Q
2 khP
2*3.14*300*103 *8*102 * 20
428.08
cm3 / s
ln
a Rw
9 * ln
250 *102 10
圆形供给边缘比直线供给边缘多
428.08 393.24 *100% 8.86% 393.24
1200 1000
800 600 400 200
0 0
10
20
30
得Q（cm3/s)为：980.4, 826.8, 658.5, 580.06
绘图（△P，Q）曲线，得采油指数 K 47.6
k k
Q
ln
Re Rw
ln
Re Rw
47.6
*9*
ln
30910 10
0.36
m2
2 hP
P
Q
ln
Re Rw
2 kh
626.3617
*
9
*
ln
3.091*104 1
2*3.14*400*103 *103
23.2(0.1MPa)
2.32
MPa
P Pe P 10.5 2.32 8.18MPa
第三章 单相稳定流 习题3-8
利用 Q Qo *106 * Bo
o *86400
任意点M取在生产井井壁
q
q
b
q
aq
q
w 2 ln
Rw *2b*2a*
4a2 4b2
q
C 2 ln 8abRw
a2 b2
C
石油工程渗流力学习题答案
石油工程渗流力学习题答案本页仅作为文档页封面，使用时可以删除This document is for reference only-rar21year.March1、由题意知ΔL=10cm 时：3260/60(/)*1.5()*10()p 0.5()1.5()*20()q L cm s cp cm atm KA D cm μ∆∆===a 05.0MP P =∆1（2旧版）：设有一均质无限大地层中有一生产井，油井产量q =100m 3/d ，孔隙度=，h =10m ，求r =10m ，100m ，1000m ，10000m 时渗流速度和液流速度，通过计算，能看出什么 解：2h A r π=，渗流速度qv A=，液流速度w v φ＝当r=10m 时，34q 100/864001000(/)0.00184/22 3.1410()10()0.00184100/10000.000184/ 1.8410/q m ks v m ksA rh m m cm s cm sπ-⨯====⨯⨯⨯=⨯==⨯ s /cm 1037.7w 4-⨯＝当r=100m 时，51.8410cm /s v -=⨯，s /cm 1037.7w 5-⨯＝ 当r=1000m 时，61.8410cm /s v -=⨯，s /cm 1037.7w 6-⨯＝ 当r=10000m 时，71.8410cm /s v -=⨯，s /cm 1037.7w 7-⨯＝ 由此可以看出，离井眼越远，渗流速度以及液流速度也越小2（4旧版）：设油层p e =12MPa ，p w =，r e =10000m ，r w =，r =100m ，求r ~r e 及r w ~r 两区内的平均压力。
解：e w e e e w r ln r r ln r P P P P =－－；e w e wr 2ln r e P PP P －＝－ 当r ＝100m 时，1210.51000012ln 11.410000100ln0.1P MPa ==－－在r ～re ：，e 1211.4e 11.931211.94r 100002ln 2ln100re P P P P MPa --=-=-=＝MPa在r w ～r ：w w 11.33r 2ln r P PP P MPa -=-11.4-10.5＝11.4-=1002ln0.15（7旧版）：已知液体服从达西定律成平面径向流入井，r e =10km ，r w =10cm ，试确定离井多远处地层压力为静压力与井底流动压力的算术平均值解：由题意得：e w e e we e wr ln r r 2ln r P P P P P P +==－－→e w r r r =解得r ＝6（8旧版）：地层渗透率与井距离r 成线性规律变化，在井底r =r w 处，K =K w ，在供给边缘r =r e 处，K =K e ，计算流体服从达西定律平面径向流的产量，并将此产量与同等情况下，各自渗透率都为K w 的均质地层平面径向流产量相比较。