椭圆的五种画法及各种弦的制作(很不错的几何画板教程)
数学中常用几何画板绘制椭圆
数学中常⽤⼏何画板绘制椭圆圆锥曲线是⾼中数学的重点和难点，也是历来⾼考的必考内容，所以对于⾼中⽣来说，弄懂圆锥曲线这块难啃的⾻头，是很有必要的。
其中要熟练掌握的圆锥曲线之⼀就是椭圆，它是圆锥与平⾯的截线，其实要想画出椭圆，其⽅法不⽌⼀种，下⾯就⼀起来通过学学椭圆的五种画法。
⽅法⼀、利⽤椭圆第⼀定义构造椭圆椭圆第⼀定义：平⾯内到两个定点的距离之和等于定长2a（a>0）的点的轨迹就是椭圆，按照此定义可画出椭圆，具体步骤如下：1.单击“圆⼯具”，在画板的适当位置任意画⼀个圆，将圆⼼的标签改为F1。
单击“点⼯具”，在圆上任意画⼀点C，同时选中点F1和点C，执⾏“构造”-“线段”命令，构造出线段F1C。
单击“点⼯具”，在线段F1C任意画⼀点F2。
2.在圆上任意画⼀点E，并构造线段EF1和线段EF2。
选中线段EF2，执⾏“构造”-“中点”命令，构造线段EF2的中点F。
3.选中线段EF2和点F，执⾏“构造”-“垂线”命令，构造出线段EF2的垂直平分线j。
同时选中线段EF1和直线j，选择“构造”-“交点”命令，构造线段EF1和直线j的交点G。
4.选中点G和点E（把点E称做是点G的相关点，改变G点的位置，点E的位置也跟着改变），选择“构造”-“轨迹”命令，可画出椭圆。
拖动点B 和点F2可改变椭圆的形状。
⽅法⼆、利⽤椭圆第⼆定义画椭圆椭圆的第⼆定义：设动点M（x， y）与定点F(c, 0)的距离和它到定直线l： x＝a2/c的距离的⽐是常数（a>c>0），则点M的轨迹是椭圆。
点F 是椭圆的⼀个焦点，直线l是椭圆中对应于焦点F的准线，常数e＝c/a（0<e<1）。
具体的操作步骤如下：步骤⼀打开⼏何画板，使⽤“点⼯具”画任意⼀点F，使⽤“线⼯具”画直线L（点F不在L上）。
过点F作⼀条直线，在直线上取⼀点P；步骤⼆选中点F、P执⾏“度量”--“距离”命令，度量FP的长度；选中点F和度量的FP的长度，执⾏“构造”--“以圆⼼和半径绘圆”构造以点F为圆⼼，FP为半径的圆。
机械制图椭圆的画法
四心圆弧法作近似椭圆
M O4 C
M1
A O1
O
O3
B
D O2
E
H
F
G
第六节 斜度和锥度
一、斜度
1 斜度的概念 斜度是指一直线(或平面)相对于另一直线(或平面)的
倾斜程度，其大小用该两直线(或两平面)间夹角的正 切值来表示(图2-15a)，即
斜度=tan α=CA/AB=H/L 在图2-15b中，斜度=（H-h）/L 通常在图样中把比值化成1∶n的形式。
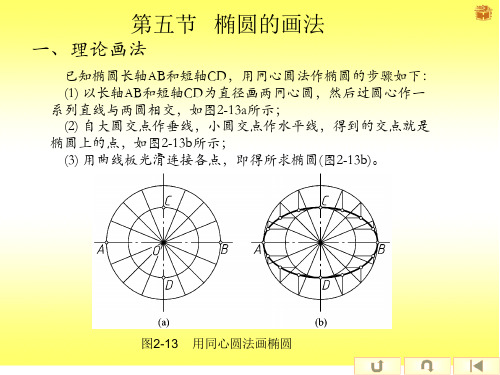
图2-13 用同心圆法画椭圆
同心圆法作椭圆
CAOB来自D第五节 椭圆的画法
二、近似画法
已知椭圆长轴AB和短轴CD，用四心圆法作椭圆的步骤如下： (1) 画出相互垂直且平分的长轴AB与短轴CD； (2) 连接AC，并在AC上取CE=OA-OC,如图2-14a所示； (3) 作AE的中垂线，与长、短轴分别交于O1、O2，再作对称点O3、 O4，如图2-14b所示； (4) 以O1、O2、O3、O4各点为圆心，O1A、O2C、O3B、O4D为 半径，分别画弧，即得近似椭圆，如图2-14c所示。
第五节 椭圆的画法
一、理论画法
已知椭圆长轴AB和短轴CD，用同心圆法作椭圆的步骤如下： (1) 以长轴AB和短轴CD为直径画两同心圆，然后过圆心作一 系列直线与两圆相交，如图2-13a所示； (2) 自大圆交点作垂线，小圆交点作水平线，得到的交点就是 椭圆上的点，如图2-13b所示； (3) 用曲线板光滑连接各点，即得所求椭圆(图2-13b)。
2. 斜度的画法和标注
15 1:4
1个单位 7 17
4个单位
33
第六节 斜度和锥度
二、锥度
几何画板生成椭圆曲线八种方法
选择“文件”→“新绘图”，选择“图表”→“建立坐标轴”，用“圆”工具作两圆心为原点的同心圆（外圆半径长就是最终椭圆的长半轴长a，内圆半径长就是最终椭圆的短半轴长b），选中点B和圆周上的点C和D，按Ctrl+H键隐藏。
选择“显示”→“线型”→“虚线”，在外圆圆周上任取一点E，按住shift键，同时选中点A和点E，按Ctrl+L作出线段AE，同时选中线段AE和内圆圆周，按Ctrl+I键作出交点F。
2.按住shift键，先后选中点F，选择“显示”→“追踪点”，同样选中点G和点C，选择“显示”→“追踪点”。
按住shift键，先后选中点C和线段AB，选择“编辑”→“操作类按钮”→“动画”，弹出“匹配路径”对话框，选择“双向”、“沿着线段j”、“慢慢地”，按“动画”按钮完成设置。这时，绘图板上会出现一个“动画”按钮，双击“动画”按钮，就会自动画出椭圆。完成，存盘退出。
同时选中点A和点D，按Ctrl+L键作线段AD。再同时选中垂线k和线段AD定值。
选中点F，按Ctrl+T键追踪点F。选中点D和圆周，选择“编辑”→“操作类按钮”→“动画”，弹出“匹配路径”对话框，选择“单向”、“绕圆c1”、“正常地”，按“动画”按钮完成设置。这时，绘图板上会出现一个“动画”按钮，双击“动画”按钮，就会自动画出椭圆（如图4）。另外您也可以同时选中点F和点D，选择“作图”→“轨迹”也可以作出该椭圆。完成，存盘退出
二、准线法（到定点的距离与到定直线的距离之比为常数e）
打开一个新的绘图板，选择“图表”→“建立坐标轴”。
用“线段”工具作线段CD，在线段CD上任取一点E。同时选中点C和点E，选择“度量”→“距离”，量出CE的长。同样量出CD的长。
按住shift键，选中量出的CE和CD的距离，按鼠标右键弹出对话框，选择“度量”→“计算”。在打开的计算器中选择“数值”→“距离（C到E）”。选择“/”→“距离（C到D）”→“确定”。在绘图板上就会出现CE和CD的比值。用“文本工具”双击该值，弹出“度量值格式”对话框，选择“T文本格式”。 将“距离（C到E）/距离（C到D）”改成“e”，确定，完成改变。选中点B，按Ctrl+H键隐藏，在X轴上取点F（F为椭圆的一个焦点）。作线段GH，在其上取点I。用上面的方法量出GI的距离，并将其距离名称改为c。选中c和e的值，打开计算器，将c除以e的值求出，并将其名改为a。
椭圆的画法
椭圆的画法
方法一：
1、画长轴AB、短轴CD，轴心O；
2、取与长轴等长的线绳两端固定在图钉上；
3、对折线绳，一端于C点，另一端落在AO上为F1 点、OB上为F2点；
4、将线绳两端的图钉分别钉在F1、F2上；
5、用画笔尖绷紧线绳画一周，即得所需椭圆。
方法二：
椭圆的画法很多，机械制图中常用的是用四心圆法作近似椭圆。
椭圆的长轴为AB，短轴为CD。
作图步骤如下：
1、连接A、C，以O为圆心、OA为半径画弧，与CD的延长线交于点E，以C为圆心、CE为半径画弧，与AC交于点E1；
2、作AE1的垂直平分线，与长短轴分别交于点O1、O2，再作对称点O
3、O4；O1、O2、O3、O4即为四段圆弧的圆心；
3、分别作圆心连线O1O
4、O2O3、O3O4并延长；
4、分别以O1、O3为圆心，O1A或O3B为半径画小圆弧K1AK和NBN1，分别以O2、O4为圆心，O2C或O4D为半径画大圆弧KCN和N1DK1（切点K、K1、N1、N分别位于相应的圆心连线上），即完成近似椭圆的作图。
运用几何画板绘制椭圆的有效方法
运用几何画板绘制椭圆的有效方法作者：于翠玲来源：《黑龙江教育·中学》2019年第06期在圆锥曲线中，曲线上的点到定点的距离与到定直线的距离的商是常数e，且0<e<1时为椭圆。
椭圆教学是中学数学教学中的重点和难点，椭圆的知识和图像都极为抽象，学生很难理解。
不仅如此，有些教师在绘制椭圆图形时也会感到困难，并且准确性不够。
而运用几何画板软件画出的椭圆既准确又美观，还能增加教学的趣味性，引发学生的学习兴趣，可以让学生轻松、直观地观察并理解椭圆的定义及其性质，从而收到很好的教学效果。
几何画板以点、线、圆作为基础图形，对这些基础图形进行拼接、平移、变换、度量、构造、轨迹追踪以及对基本图形的性质进行运用。
学生可以在此过程中探究图形的内在关系并发现数学的本质，探究数学的奥妙和趣味性，激发学习数学的兴趣。
笔者结合自身教学经验，在总结、归纳、提炼和创新的基础上整理出七种常用的运用几何画板绘制椭圆的方法，分享如下：一、定义法定义法的原理是圆锥曲线的统一定义，即焦点距离与到准线距离的商是定值的点的轨迹。
椭圆的定义，即平面内一个动点到两个定点的距离之和等于常数，这个动点的轨迹叫椭圆，这两个定点叫椭圆的焦点，两焦点的距离叫作椭圆的焦距。
绘制的具体步骤为：打开软件，新建文件，在绘画板内画线段AB的同时在AB上绘制出C点，然后在AB外选取D、E两点，满足DE>AB;选中A、C两点进行标记向量，然后通过标记向量将D平移，得到D';选中D和D'点，绘制出一个以D为圆心，以D和D'间距离为半径的圆并且隐藏;同理，标记B、C两个点为标记向量，并且作出E的平移点到E'点，构造出圆，隐藏E'点;运用点工具做出两个圆周交点为F、G两点。
接下来分两种方法研究。
分别选中F、C和G、C两组点进行构造轨迹绘制出椭圆曲线，如图1所示。
点击F点，点击显示、追踪交点，同理操作G点;点击C点，选择操作类按钮、动画、确定，完成设置;点击绘画板上的动画键，绘画板就绘制出一个椭圆，如图2所示。
几何画板画椭圆的几种方法介绍.
<<几何画板>>画椭圆的几种方法介绍随着课改的发展，数学问题“视觉化”显得越来越重要（“视觉化”直观，学生更容易接受，课程改革也是朝这个发展方向），《几何画板》以其学习入门容易和操作简单的优点及其强大的图形和图象功能、方便的动画功能被许多数学教师看好，并已成为制作中学数学课件的主要创作平台之一。
下面介绍几种椭圆画法：一、到两定点的距离和等于定长具，在绘图板中作一线段AB（线段AB的长度为椭圆的长轴长2a）。
用“点”工具在线段上任取一点C，先后选中A，C点，选择“变换”->“标记向量"A->C"”（下图）。
再用“线段”工具作线段DE（线段DE的长为2c），选中点D，选择“变换”->“平移”，显示按标记的向量“从A到C”，点击“平移”，会得到点D'。
先后选中点D和D'，选择“作图”->“以圆心和圆周上的点画圆”，选中点D'，先后选中B，C点，选择“变换”->“标记向量"B->C"”。
同样的把点E，按向量BC平移，得到点E'。
以E为圆心过E'作圆选中两个圆的圆周，选择“作图”->“交点”，作出交点F和G。
让点C在线段AB上移动（选中点C，点击“编辑”下的“操作类按钮”中的“动画”可以生成动画），交点F、G的轨迹就是我们要作的椭圆（最后可以把无用的点、线隐藏）。
二、同心圆法（教材例5）选择“图表”->“定义坐标系”，用“圆”工具作两圆心为原点的同心圆（外圆半径长就是最终椭圆的长半轴长a，内圆半径长就是最终椭圆的短半轴长b），光标放原点处，击左键拖动光标，松开左键就得到所需圆。
在外圆圆周上任取一点E（可以选中圆，点击“作图”下的“对象上的点”；或者选取“点”工具，然后把光（选中点A（原点）和点E，点击“作图”下的“线段、射线或直线”），再作AE与小圆的交点（选中线段AE和内圆圆周，可用快捷键Ctrl+I作出交点）F。
怎么画椭圆简单方法
怎么画椭圆简单方法
画椭圆的简单方法有很多，这里我将介绍其中两种常见的方法：使用两根针和使用短绳及两根钉。
方法一：使用两根针
这种方法需要使用两根针和一根绳子。
1. 取一根绳子，将其两端绑在两根针的各自末端，形成一个三角形。
2. 将两根针分别固定在纸上，使之成为一条直线，并保持一定距离。
3. 拉紧绳子，并沿着直线移动，使绳子在两根针之间循环。
4. 沿着绳子的轨迹慢慢移动，绳子的末端将会画出一个椭圆形状的轨迹。
这种方法的原理是，当绳子被拉紧并以一定角度移动时，绳子的两端会形成一个不断变化的角度，从而在纸上画出一个椭圆。
方法二：使用短绳及两根钉
这种方法只需要使用一根短绳、两根钉和一支铅笔。
1. 在纸上选择一个你想要画椭圆的位置，插入两根钉并固定。
2. 将铅笔固定在短绳的一端，并在纸上选择一个焦点。
3. 将另一端的绳子固定在另一个焦点，并拉紧绳子。
4. 保持绳子的张力，用另一只手将铅笔围绕焦点画圆，并慢慢移动绳子，画出整个椭圆形状。
这种方法的原理也是利用焦点的特性来画椭圆。
当绳子保持拉紧且长度不变时，铅笔的移动会受到焦点吸引，因此可以画出一个完美的椭圆。
无论使用哪种方法，画椭圆需要一定的实践和耐心。
随着不断的尝试和练习，你会越来越熟练，并能够画出更加精确的椭圆。
椭圆的五种画法及各种弦的制作(很不错的几何画板教程).
椭圆的画法和性质一．椭圆的定义： 1．在平面内，到两个定点F 1、F 2的距离的和等于常数(大于|F 1F 2|)的点的轨迹叫做椭圆。
这两个定点叫做椭圆的焦点，两焦点间的距离叫做焦距。
2．椭圆的标准方程：设M (x , y )是椭圆是上任意一点，椭圆的焦距为2c (c >0)，则如图建立直角坐标系，又F 1、F 2的坐标分别是F 1(－c , 0), F 2(c , 0)，若M 点与F 1、F 2两点的距离的和等于2a (a >c >0)，则 |MF 1|＋|MF 2|＝2a ,∴a y c x y c x 2)()(2222=+-+++, 图9－1整理化简，并且设b 2＝a 2－c 2得椭圆的标准方程12222=+b y a x . 3．椭圆的第二定义：设动点M (x , y )与定点F (c , 0)的距离和它到定直线l : x ＝ca2的距离的比是常数ac(a >c >0)，则点M 的轨迹是椭圆。
点F 是椭圆的一个焦点，直线l 是椭圆中对应于焦点F 的准线。
常数e ＝ac(0<e <1)是椭圆的离心率。
图9－24．椭圆的参数方程：以原点为圆心，分别以a 、b (a >b >0)为半径作两个圆，点A 是大圆上的一个点，点B 是OA 与小圆的交点，过点A 作AN ⊥Ox ，垂足为N ，过点B 作BM ⊥AN ，垂足为M ，当点A 在大圆上运动时，M 点的轨迹是椭圆。
设点M 的坐标是(x , y )，φ是以Ox 为始边，OA 为终边的正角，取φ为参数，那么x ＝|ON |＝|OA |cos φ＝a cos φ,y ＝|NM |＝|OB |sin φ＝b sin φ,∴ 椭圆的参数方程是⎩⎨⎧φ=φ=sin cos b y a x (φ是参数).二．椭圆的画法：画法1：1．在x 轴上取两点F 1、F 2，使|OF 1|＝|OF 2|，用它们作为两个焦点； 2．在图形外作一条线段CD ，使|CD |＝2a ，(|CD |>|F 1F 2|)； 3．以O 为中心，在x 轴上取两点A 1、A 2，使|A 1A 2|＝|CD |；4．在CD 上分别取C '、D '，使|CC '|＝|A 1F 1|＝|DD '|；作线段C 'D '，并用“作图”菜单中的“对象上的点”功能在C 'D '上作点M ；5．分别以F 1、F 2为圆心，用|CM |、|MD |为半径作圆，两圆相交于P 1、P 2两点；同样方法分别以F 1、F 2为圆心，用|DM |、|CD |为半径作圆，两圆相交于P 3、P 4两点；并将这四个点定义为“追踪点”；6．依次选中点M 、点P 1 (或点M 、点P 2)，用“作图”菜单中的“轨迹”功能，作出椭圆。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
椭圆的画法和性质一．椭圆的定义： 1．在平面内，到两个定点F 1、F 2的距离的和等于常数(大于|F 1F 2|)的点的轨迹叫做椭圆。
这两个定点叫做椭圆的焦点，两焦点间的距离叫做焦距。
2．椭圆的标准方程：设M (x , y )是椭圆是上任意一点，椭圆的焦距为2c (c >0)，则如图建立直角坐标系，又F 1、F 2的坐标分别是F 1(－c , 0), F 2(c , 0)，若M 点与F 1、F 2两点的距离的和等于2a (a >c >0)，则 |MF 1|＋|MF 2|＝2a ,∴a y c x y c x 2)()(2222=+-+++, 图9－1整理化简，并且设b 2＝a 2－c 2得椭圆的标准方程 12222=+by a x.3．椭圆的第二定义：设动点M (x , y )与定点F (c , 0)的距离和它到定直线l : x ＝c a 2的距离的比是常数ac(a >c >0)，则点M 的轨迹是椭圆。
点F 是椭圆的一个焦点，直线l 是椭圆中对应于焦点F 的准线。
常数e ＝ac(0<e <1)是椭圆的离心率。
图9－24．椭圆的参数方程：以原点为圆心，分别以a 、b (a >b >0)为半径作两个圆，点A 是大圆上的一个点，点B 是OA 与小圆的交点，过点A 作AN ⊥Ox ，垂足为N ，过点B 作BM ⊥AN ，垂足为M ，当点A 在大圆上运动时，M 点的轨迹是椭圆。
设点M 的坐标是(x , y )，φ是以Ox 为始边，OA 为终边的正角，取φ为参数，那么x ＝|ON |＝|OA |cos φ＝a cos φ,y ＝|NM |＝|OB |sin φ＝b sin φ,∴ 椭圆的参数方程是⎩⎨⎧φ=φ=sin cos b y a x (φ是参数).二．椭圆的画法：画法1：1．在x 轴上取两点F 1、F 2，使|OF 1|＝|OF 2|，用它们作为两个焦点； 2．在图形外作一条线段CD ，使|CD |＝2a ，(|CD |>|F 1F 2|)； 3．以O 为中心，在x 轴上取两点A 1、A 2，使|A 1A 2|＝|CD |；4．在CD 上分别取C '、D '，使|CC '|＝|A 1F 1|＝|DD '|；作线段C 'D '，并用“作图”菜单中的“对象上的点”功能在C 'D '上作点M ；5．分别以F 1、F 2为圆心，用|CM |、|MD |为半径作圆，两圆相交于P 1、P 2两点；同样方法分别以F 1、F 2为圆心，用|DM |、|CD |为半径作圆，两圆相交于P 3、P 4两点；并将这四个点定义为“追踪点”；6．依次选中点M 、点P 1 (或点M 、点P 2)，用“作图”菜单中的“轨迹”功能，作出椭圆。
理论根据： 点P 1是两圆的交点，∴ 点P 1到F 1与F 2的距离的和等于两圆的半径和, 即 |PF 1|＋|PF 2|＝|CM |＋|MD |＝|CD |＝2a . 说明：M 点不要直接在CD 上取，那样画出来的椭圆将在x 轴附近断开一段，因为计算机画的曲线实际上是由若干条小线段形成的，这些线段的端点是由符合条件的若干个点中随机选取的，当我们使点M 在CD 上运动时，一般情况点C '、D '都取不到，于是画出来的图形就不好看了。
画法2：1．在x 轴上取两点F 1、F 2，使|OF 1|＝|OF 2|，用它们作为两个焦点； 2．在图形外作一条线段，使它的长度为2a ，(2a >|F 1F 2|)； 3．以F 1为圆心，2a 为半径作圆，在圆上任取一点P ；4．连接PF 1、PF 2，作PF 2的中垂线与PF 1交于点M ，连接MF 2；5．将点M 定义为“追踪点”，分别选中点M 、点P ，用“作图”菜单中的“轨迹”功能画出椭圆。
理论根据：点M 在PF 2的中垂线上，∴ |MP |＝|MF 2|, ∴ |MF 1|＋|MF 2|＝|MF 1|＋|MP |＝|F 1P |＝2a . 即点M 到两个定点F 1和F 2的距离的和等于定长。
点M 的轨迹是一个椭圆。
画法3：图9－61．在平面中作两条直线，使直线l 为准线，另一条直线AB 与直线l 垂直；两条直线的交点为C ； 2．在图形外取两条线段a 和c ，使a >c ；3．计算c c a -2，在直线AB 上取一点F ，使|CF |＝c ca -2,点F 作为椭圆的焦点；4．在线段FC 上，取点A ，使|AF |＝a －c , 在CF 的延长线上，取点B ，使|FB |＝a ＋c ，作线段AB ，用“作图”菜单中的“对象上的点”功能，取动点P ；5．计算e ＝a c ，度量|CP |的长，计算|CP |×ac；6．以点F 为圆心，|CP |×ac为半径作圆，此圆与过点P 且垂直于AB的直线相交于M 1，M 2两点；7．分别选中点M 1和点P (或点M 2和点)，用“作图”菜单中的“轨迹”功能，画出椭圆。
理论根据：点M 1到点F 的距离是|CP |×ac，点M 1到准线l 的距离|M 1D |＝|CP |,∴ 的距离到直线点的距离到点l M F M 11＝ac＝e . ∴ 点M 1在椭圆上。
画法4：1．以坐标原点O 为圆心，分别以a 、b (a >b >0)为半径画两个圆; 2．在大圆上取一点A ，连接OA 与小圆交于点B ；3．过点A 作AN 垂直于Ox 轴，垂足为N ；作BM 垂直于AN ，垂足为M ；4．分别选中点M 和点A ，用“作图”菜单中的“轨迹”功能，画出椭圆。
理论根据：|ON |＝a cos φ, |NM |＝b sin φ, 根据椭圆的参数方程知，点M 的轨迹是一个椭圆。
画法5：1．以坐标原点O 为圆心，分别以a 、b (a >b >0)为半径画两个圆;2．在大圆上取一点P ，过点P 作PN ⊥Ox 轴，垂足为N ；3．计算两圆半径的比k ＝ab ，定义为“标记比”，选中点N ，定义为“缩放中心”； 4．选中点P ，用“变换”菜单图9－8中的“缩放”功能，将点P 用标记比缩放得到点M ；5．分别选中点M 和点P ，用“作图”菜单中的“轨迹”功能，画出椭圆。
理论根据：设点M 的坐标是(x , y )，则点P 的横坐标为x ，纵坐标y 0＝bay,∵ 点P 在圆x 2＋y 2＝a 2上，∴ 2222b y a x +＝a 2, 整理得 12222=+by a x . 结论：只要动点P 在一个圆上运动，那么在一个方向上按一定比例压缩或延长PD ，所得到的点M 的轨迹都是椭圆。
三．椭圆中动弦的画法(一)．椭圆焦点弦的画法：图9－91．用参数方程的画法画出一个椭圆，计算它的a , b , c 的值，在长轴上画出两个焦点F 1、F 2(使|OF 1|＝c )；2．在大圆上任取一点P ，相应作出它在椭圆上的对应点M ； 3．连接PF 1延长与大圆交于点Q ； 4．作出点Q 在椭圆上的对应点N ；5．连接MN ，则线段MN 一定过焦点F 1，且点M 、N 都在椭圆上；6．保留坐标系、椭圆、焦点和焦点弦MN ，隐藏其它的内容，这时选中点M ，在椭圆上拖动它，则点N 相应在椭圆上移动，且MN 始终经过点F 1.理论根据：椭圆上的点M 、N 是由大圆上的点P 、Q 得到的，线段PQ 在大圆上经过定点F 1，则相应的线段MN 在椭圆上也经过定点F 1.(二) 椭圆中过定点M 的弦的画法： 1．用参数方程的画法画出一个椭圆，标出定点M ；计算两圆半径的比k ＝ba，定义为“标记比”； 2．作MD ⊥Ox 轴，垂足是D ，以D 为缩放中心，把点M 用标记比缩放，得到点M '；3．在大圆上取一点P '，作出它在椭圆上的相应点P ；4．连接P 'M '，延长与大圆交于Q '，作出点Q '在椭圆上的对应点Q ； 图9－105．连接PQ ，则PQ 始终经过点M ，且P 、Q 都在椭圆上；6．保留坐标系、椭圆、定点M 和过定点M 的弦PQ ，隐藏其它的内容，这时选中点P ，在椭圆上拖a=3.116 cmb=2.592 cmc=1.729 cm动它，则点Q 相应在椭圆上移动，且PQ 始终经过点M .理论根据：椭圆上的点P 、Q 是由大圆上的点P '、Q '得到的，线段P 'Q '在大圆上经过定点M '，则相应的线段PQ 在椭圆上也经过定点M .。
问题的关键是怎样由点M 得到点M '，我们看到，只要在纵坐标是以定比ba缩放点M ，就得到了对应点M '.(三) 椭圆中平行弦的画法的画法：图9－111．用参数方程的画法画出一个椭圆，计算两圆半径的比k ＝ba，定义为“标记比”； 2．在图形外画一条线段AC ，过点A 作水平线AD ，过C 作CD ⊥AD ；3．选中点D 作为“缩放中心”，再选中点C ，用“标记比”缩放，得到点B ，连接AB ； 4．在大圆上任取一点P '，过P '作AB 的平行线角大圆于Q '；5．用参数方程的作法，分别作出P '、Q '在椭圆上的对应点P 、Q ； 6．连接PQ ，则PQ 就是与AC 平行的椭圆中的弦；7．保留坐标系、椭圆、AC 和PQ ，隐藏其它的内容；选中点P 在椭圆上拖动点P ，则弦PQ 始终与AC 平行，且点P 、Q 在椭圆上；8．作PQ 的中点，标记为“追踪点”，则点P 运动时，可以看到中点的轨迹是一条线段。
理论根据：在大圆上，P 'Q '//AB ，这个关系保持不变，相应的点P 、Q 是点P '、Q '在椭圆上的对应点，∴ 线段PQ 的斜率保持不变。
那么我们只要找到线段AC 与AB 的关系就可以了。
在这个作法中，改变已知条件AC 的倾斜角，那么相应的PQ 的斜率也发生同样的变化。
四．椭圆切线的画法(一) 过椭圆上一个定点M 的切线：1．在直角坐标系中画一个椭圆，同时标出它的两个焦点F 1、F 2； 2．在椭圆上标出定点M ；3．以F 1为圆心，椭圆的长轴2a 为半径作圆；4．连接F 1M 延长交大圆于点N ；5．连接F 2N ，作F 2N 的中垂线，这条中垂线过点M ，并且是椭圆的切线。
理论根据：∵ 点M 在椭圆上， ∴ |MF 1|＋|MF 2|＝2a ,又|F 1N |＝2a ，∴ |MF 2|＝|MN |,点M 在F 2N 的中垂线上，直线MD 经过点M 且与椭圆有且仅有一个交点，所以直线MD 是椭圆过点M 的切线。