光学——球面反射和折射
合集下载
第三章几何光学球面反射折射物像公式
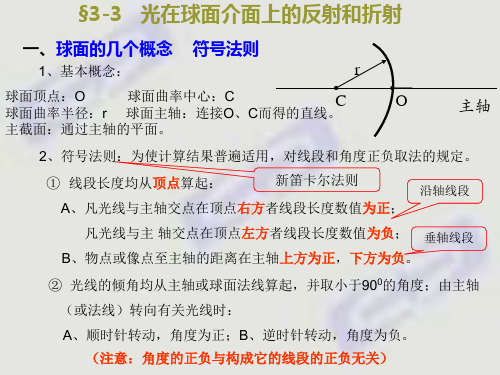
例3.4:
一个折射率为1.6的玻璃哑铃,长20cm,两端的曲率半径为 2cm。若在 离哑铃左端5cm处的轴上有一物点,试求像的位置和性质。
[解]:两次折射成像问题。
n
P
O1
n
P’1 n` O 2
1、P为物, 对球面O1折射成像P1’
已知 : s1 5cm , r1 2cm , n 1, n ' 1.6 n n n n 由折射成像公式 ' r1 s1 s1
沿轴线段
A、凡光线与主轴交点在顶点右方者线段长度数值为正; 凡光线与主 轴交点在顶点左方者线段长度数值为负; B、物点或像点至主轴的距离在主轴上方为正,下方为负。 ② 光线的倾角均从主轴或球面法线算起,并取小于900的角度;由主轴 (或法线)转向有关光线时: A、顺时针转动,角度为正;B、逆时针转动,角度为负。 (注意:角度的正负与构成它的线段的正负无关)
2
r
2
s r
'
2
2 r s ' r cos
光程 PAP ' nl nl ' n
r 2 r s 2 2 r r s cos r
2
n
s r
'
2
2 r s r cos
1、高斯公式:
球面反射 : f ' f 1 1 2 ' s s r
六、理想成象的两个普适公式
n' n n' n 将物像公式 ' 变形为 : s s r n' n r r ' ' ' f f n n n n 1 1 ' ' s s s s
单球面反射和折射

5. 特例
(1)球面反射
n n'
1 1 2 p p' r
平行光线入射,p ,代入物像公式 1 1 2 得 pf'' 2r 2r,f ' 此时对应的像点叫焦点(fpocusp)' r 焦点到顶点的距离— 焦距(focal length)
物像公式为
11 1 p p' f '
(Gauss公式)
1.5 1.0
(8) (1)
1.2
,即成正立、放大的实像。
总的横向放大率
1
2
3
0.5 (
1) 1.2 3
为20cm和15cm,薄透镜折射率为1.5,在凸面 镀银。在球面前方40处的主轴上置一高为1cm 的物,求像的位置和成像的性质。
[解](1)P经凹球面折射成像:
p1=-40cm,n=1.0,n’=1.5,r1=-20cm,代入
n' n n'n p1' p1 r1
1
np1 ' n' p1
1 2
,
1.5 1.0 0.5 p1' 40 20
三、傍轴球面折射的物象关系式
nn'n (u(' u in)) unn('(n'('niu'))') n
p
u
i o
n' h i' c u '
p'
u h p'
r
p
p'
u h p
h
n n nn
p' p r
物像关系式
r
定义 光焦度
Φ n'n r
光在单球面上的折射和反射-四川大学

β =−
x′ f′
y′ f =− y x
从 Q 作 O 点的入射线 QO ,其折射线是 OQ′ 。由图可知,得
ny n′y′ =− −s s′
或 讨论:
β=
y′ ns′ = y n′s
(1) β > 0 时, y′ 与 y 同号。物正立时像也是正立的。即物是实物时,像必定是虚像,反之, 当物是虚物时,像必定是实像。 (2) 当 β < 0 时,物和像在主光轴的异侧,而且当物是实物时,生成的像也是实像,当物是虚 物时,生成的像也是虚像。 总之,当 β > 0 时,物和像一定是一实一虚; 当 β < 0 时,物和像的虚实相同。
n n’ P n n’
P’
P’ P
虚物成实像
虚物成虚像
n′ n n′ − n − = s′ s r f′ f + =1 s′ s xx′ = ff ′
1 1 2 + = s′ s r 1 1 1 + = s′ s f xx′ = f 2
φ=
f′=
n′ r n′ − n n f =− r n′ − n
n′ − n r
φ=
f′ n′ =− f n
β=
ns′ n′s
N
P
F
(e) 轴上物点成像作图法
图 作图法的几个例子
四川大学精品课程《光学》
六.球面反射镜 1.方法:将反射看作是折射的特殊情况 2.球面反射的物像距公式:
1 1 2 + = s′ s r
i = −i′ ; n′ = −n
3. 单球面折射饿球面反射镜公式对比
球面折射和球面反射公式对照表 球面折射成像 球面反射成像 公式 公式 物 像 距 焦距和光焦度 横向放 大率
x′ f′
y′ f =− y x
从 Q 作 O 点的入射线 QO ,其折射线是 OQ′ 。由图可知,得
ny n′y′ =− −s s′
或 讨论:
β=
y′ ns′ = y n′s
(1) β > 0 时, y′ 与 y 同号。物正立时像也是正立的。即物是实物时,像必定是虚像,反之, 当物是虚物时,像必定是实像。 (2) 当 β < 0 时,物和像在主光轴的异侧,而且当物是实物时,生成的像也是实像,当物是虚 物时,生成的像也是虚像。 总之,当 β > 0 时,物和像一定是一实一虚; 当 β < 0 时,物和像的虚实相同。
n n’ P n n’
P’
P’ P
虚物成实像
虚物成虚像
n′ n n′ − n − = s′ s r f′ f + =1 s′ s xx′ = ff ′
1 1 2 + = s′ s r 1 1 1 + = s′ s f xx′ = f 2
φ=
f′=
n′ r n′ − n n f =− r n′ − n
n′ − n r
φ=
f′ n′ =− f n
β=
ns′ n′s
N
P
F
(e) 轴上物点成像作图法
图 作图法的几个例子
四川大学精品课程《光学》
六.球面反射镜 1.方法:将反射看作是折射的特殊情况 2.球面反射的物像距公式:
1 1 2 + = s′ s r
i = −i′ ; n′ = −n
3. 单球面折射饿球面反射镜公式对比
球面折射和球面反射公式对照表 球面折射成像 球面反射成像 公式 公式 物 像 距 焦距和光焦度 横向放 大率
几何光学 第二章 球面和球面系统

1 反射面只是折射面在 n ' n 的特殊情况 2 平面是半径为无穷大的球面
因此首先讨论球面系统是最有意义的 本章我们首先讨论光线经单个折射球面时的计算方法, 有了这个方法就可以方便的解决光线经过整个球面系统的 计算问题
图2-1
如图所示是一条在纸平面上的光经球面折射的光路。对于单个球面,凡经过 球心的直线就是其光轴,光轴与球面的交点成为顶点,球面的半径用r表示。 物方截距:从顶点O到入射光线与光轴交点A的距离L 物方倾斜角:入射光线与光轴的夹角U 相应的L‘、U’称为像方截距和像方倾斜角
图2-3
n ' n n ' n 对于公式 l' l r
分别另l 和l ' 可得
n' f ' r n ' n n f r n ' n
根据光焦度定义式和以上两式,可得出光焦度和焦 距之间有如下关系:
n' n f' f f' f n' n f ' f r
C
F’
O
O
F’
C
-f ’
f’
-r
r
2.5 共轴球面系统
B1 n1 n’1=n2 u’1 r1 C1 A’1 A2 u 2 -y’1 -y2 B’ B2
1
n’2=n3
O2 r2 C2 -u’2 B’2 B3 A’2 A3 O3 h3
y1
A1 -u1
O1 h1
-l1
l’1 d1
-l2
l’2 d2
-l3
在公式中
lr i u r n i' i n' u' u i i' i' l' rr u'
因此首先讨论球面系统是最有意义的 本章我们首先讨论光线经单个折射球面时的计算方法, 有了这个方法就可以方便的解决光线经过整个球面系统的 计算问题
图2-1
如图所示是一条在纸平面上的光经球面折射的光路。对于单个球面,凡经过 球心的直线就是其光轴,光轴与球面的交点成为顶点,球面的半径用r表示。 物方截距:从顶点O到入射光线与光轴交点A的距离L 物方倾斜角:入射光线与光轴的夹角U 相应的L‘、U’称为像方截距和像方倾斜角
图2-3
n ' n n ' n 对于公式 l' l r
分别另l 和l ' 可得
n' f ' r n ' n n f r n ' n
根据光焦度定义式和以上两式,可得出光焦度和焦 距之间有如下关系:
n' n f' f f' f n' n f ' f r
C
F’
O
O
F’
C
-f ’
f’
-r
r
2.5 共轴球面系统
B1 n1 n’1=n2 u’1 r1 C1 A’1 A2 u 2 -y’1 -y2 B’ B2
1
n’2=n3
O2 r2 C2 -u’2 B’2 B3 A’2 A3 O3 h3
y1
A1 -u1
O1 h1
-l1
l’1 d1
-l2
l’2 d2
-l3
在公式中
lr i u r n i' i n' u' u i i' i' l' rr u'
3.5光在球面上的反射和折射符号法则

Chap.3 Basic Principles of Geometrical Optics
主讲人:尹国盛 教授 河南大学物理与信息光电子学院
1
主要内容
3.1 光线的概念 3.2 费马原理 3.3 单心光束 实像和虚像 3.4 光在平面界面上的反射和折射
光学纤维 3.5 光在球面上的反射和折射 3.6 光连续在几个球面界面上的折射
如果:n1 > n2,那么 y < y ,即像点P 位于 物点 P 的上方,视深度减小。
(渔民叉鱼) 如果:n1 < n2, 那么 y > y ,即像点P 位于
物点 P 的下方,视深度增大。
20
三. 全反射 光学纤维
1.全反射:
对光线只有反射而无折射的现像。
当光从光密介质n1射向光疏介质
n2(<n1)时,i1 i2 i1 =ic
18
∵ 单心光束的波面是球面, ∴ 在平面界面上折射后,波面的形状发生 变化,不再是球面了。这样形成的互相垂直 的两小段像且不那么清晰的现像称为像散。
② 当i1=0,即当P所发出的光束几乎垂直于 界面时,有 x =0 , y = y1 = y2 = y n2 n1 。
19
这表明 y 近似地与入射角 i1 无关,则折 射光束是近似单心的,y 称为像视深度,y 为 物的实际深度。
25
例题3.1 人眼前一小物体,距人眼25cm,今 在人眼和小物体之间放置一块平行平面玻璃 板,玻璃板的折射率为1.5 ,厚度为5mm。 试问此时看小物体相对它原来的位置移动多 远?
解:利用 P162 L 3.1 的结果,
PPˊ= d ( 1-1/n )
可得:
s = 5×(1-1/1.5)= 5/3≈1.67(mm)
主讲人:尹国盛 教授 河南大学物理与信息光电子学院
1
主要内容
3.1 光线的概念 3.2 费马原理 3.3 单心光束 实像和虚像 3.4 光在平面界面上的反射和折射
光学纤维 3.5 光在球面上的反射和折射 3.6 光连续在几个球面界面上的折射
如果:n1 > n2,那么 y < y ,即像点P 位于 物点 P 的上方,视深度减小。
(渔民叉鱼) 如果:n1 < n2, 那么 y > y ,即像点P 位于
物点 P 的下方,视深度增大。
20
三. 全反射 光学纤维
1.全反射:
对光线只有反射而无折射的现像。
当光从光密介质n1射向光疏介质
n2(<n1)时,i1 i2 i1 =ic
18
∵ 单心光束的波面是球面, ∴ 在平面界面上折射后,波面的形状发生 变化,不再是球面了。这样形成的互相垂直 的两小段像且不那么清晰的现像称为像散。
② 当i1=0,即当P所发出的光束几乎垂直于 界面时,有 x =0 , y = y1 = y2 = y n2 n1 。
19
这表明 y 近似地与入射角 i1 无关,则折 射光束是近似单心的,y 称为像视深度,y 为 物的实际深度。
25
例题3.1 人眼前一小物体,距人眼25cm,今 在人眼和小物体之间放置一块平行平面玻璃 板,玻璃板的折射率为1.5 ,厚度为5mm。 试问此时看小物体相对它原来的位置移动多 远?
解:利用 P162 L 3.1 的结果,
PPˊ= d ( 1-1/n )
可得:
s = 5×(1-1/1.5)= 5/3≈1.67(mm)
光在球面上的反射和折射参考幻灯片

s'0.10m
顶点O的右边,虚像。
如右图,光线从右向
左传播,此时
A 物空间
巳知:S=0.05m, r=0.20m
Байду номын сангаас
P’
O PC
像空间
由球面镜物像公式,
11 2 s s' r
10/8/2020
1 1 2 0.05 s' 0.20
s'0.1m 0
顶点O的左边,虚像。
3.3.4 球面折射对 光束单心性的破坏
-s
考虑光线P-A-P’的光程 PA' P nln'l
n[ (r)2(rs)22(r)(rs)cos]12
n[ (r)2(s'r)22(r)(s'r)cos]12
当A点在镜面上移动时,是位置的变量。由费马原理
可得
dPA ' P 0 rss'r0
d
l
l'
由此可见,若s已知,则反射线与主轴的交点P’到O 点的距离s’随入射线的倾角u(亦即角)而变。也
由费马原理可得
d PAP' 0
d
n(rs)n'(s'r)0
l
l'
折射线与主轴的交点P’到O点的距离s’随入射线的倾角 u(亦即角)而变。
物点发出的单心光束经球面折射后,单心性也被破坏。
10/8/2020
3.3.5 近轴光线条件下球面折射的物像公式
近轴光线条件下,
角很小,在一级近似下,cos≈1,则有:l≈-s ,l’≈s’
10/8/2020 返回第3 章
3.3.1 符号法则
几何光学中的“符号”是人为规定的具有任意 性,需统一;
光在球面上的反射和折射.ppt
2 s' r
n {s r 2 1 1 } n'{s' r 2 1 1 }
2 s r
2 s' r
Fermat原理
M
等
r
P
O
P’
光 程
n n’ r C
-s
s’
n PM n'MP' n PO n'OP'
n {s r 2 1 1 } n'{s' r 2 1 1 } n (s) n's'
f
'
(nL
1)
1 r1
1 r2
C2
O
证明: I1面: s1, s1’, r1 I2面: s2, s2’, r2
-r2
nL
I1 I2
r1 C1
薄透镜
s = s1, s’ = s2’, s2 = s1’
I 面:nL 1 nL 1
s1' s1
r1
II 面:1 nL 1 nL
s2 ' s2
r2
透镜制造者公式
s1’
解:
-s1
n' n n'n s' s r
n=1.5
O1 R
O2 P’ P1’ s2’ s2
s1’
(1). O1面:s1=-, r1=+R, n1=1, n1’=1.5 O2面:s2=R, r2= -R, n2=1.5, n2’=1
s1’ = 3R O1
C
n n’ r
-s s’
单个折射面成像系统的笛卡尔符号规则
线段
笛卡尔坐标规则补充
纵向线段 以球面顶点O为原点,以入射光线进行 的方向为正方向,建立物空间坐标 s 和像空间坐标 ,
n {s r 2 1 1 } n'{s' r 2 1 1 }
2 s r
2 s' r
Fermat原理
M
等
r
P
O
P’
光 程
n n’ r C
-s
s’
n PM n'MP' n PO n'OP'
n {s r 2 1 1 } n'{s' r 2 1 1 } n (s) n's'
f
'
(nL
1)
1 r1
1 r2
C2
O
证明: I1面: s1, s1’, r1 I2面: s2, s2’, r2
-r2
nL
I1 I2
r1 C1
薄透镜
s = s1, s’ = s2’, s2 = s1’
I 面:nL 1 nL 1
s1' s1
r1
II 面:1 nL 1 nL
s2 ' s2
r2
透镜制造者公式
s1’
解:
-s1
n' n n'n s' s r
n=1.5
O1 R
O2 P’ P1’ s2’ s2
s1’
(1). O1面:s1=-, r1=+R, n1=1, n1’=1.5 O2面:s2=R, r2= -R, n2=1.5, n2’=1
s1’ = 3R O1
C
n n’ r
-s s’
单个折射面成像系统的笛卡尔符号规则
线段
笛卡尔坐标规则补充
纵向线段 以球面顶点O为原点,以入射光线进行 的方向为正方向,建立物空间坐标 s 和像空间坐标 ,
1.5 光在单球面上的反射和折射
(1) 横向放大率
B y A
n
i
n
A
o
i
C
s
B
y
s
y i . s
在上图的折射系统中, 由几何关系,得
AB 是 AB 的像.
y i , s
近轴条件下,在入射点 O 处,由折射定律:
ni ni
物理科学与信息工程学院 21
将
y y i , i s s
(1) 物和像的虚实
< 0 物像互为倒立实物实像或虚物虚像,
> 0物像互为正立, 实物虚像或虚物实像.
(2) 像的放大和缩小
> 1,像放大; <1,像缩小;
= 1,物象等大.
物理科学与信息工程学院 25
(2)角放大率
B
u
A
h
C
u s
A' B'
s
和
在上图折射系统中, A和A是一对共轭物像点,
物理科学与信息工程学院 14
2、近轴光线条件下,球面折射的物象公式
在近轴光线条件下, 很小,在一级近似下, cos1,
• P
n u
s
i
A
i
C
n
n
O
u
P'
•
r
B
因此
s
l [r (r s )]2 s
l ' [r ( s ' r )]2 s '
u 是一对共轭角. 我们定义角放大率为 u , u
u
物理科学与信息工程学院 26
由上图可得
u s , u s
B y A
n
i
n
A
o
i
C
s
B
y
s
y i . s
在上图的折射系统中, 由几何关系,得
AB 是 AB 的像.
y i , s
近轴条件下,在入射点 O 处,由折射定律:
ni ni
物理科学与信息工程学院 21
将
y y i , i s s
(1) 物和像的虚实
< 0 物像互为倒立实物实像或虚物虚像,
> 0物像互为正立, 实物虚像或虚物实像.
(2) 像的放大和缩小
> 1,像放大; <1,像缩小;
= 1,物象等大.
物理科学与信息工程学院 25
(2)角放大率
B
u
A
h
C
u s
A' B'
s
和
在上图折射系统中, A和A是一对共轭物像点,
物理科学与信息工程学院 14
2、近轴光线条件下,球面折射的物象公式
在近轴光线条件下, 很小,在一级近似下, cos1,
• P
n u
s
i
A
i
C
n
n
O
u
P'
•
r
B
因此
s
l [r (r s )]2 s
l ' [r ( s ' r )]2 s '
u 是一对共轭角. 我们定义角放大率为 u , u
u
物理科学与信息工程学院 26
由上图可得
u s , u s
光学——球面反射和折射
PC AC
sin i2 sin u
A
n
-i1
n`
-i2
-u
u`
P
O
r
C
P`
-s
s`
PC s r r s PC s r
nsini1 nsini2
AC r
15
PC sin u PC sin u n r ssin u s r sin u n
n
n
s r n sin u r s
f n n n f f
f
n
“-”号表示 f 和 f 永远异号,
物、像方焦点一定位于球面两侧.
23
四、理想成象的两个普适公式
1.高斯公式
将f、f’的表达式分别代入反射、折射理想成象 公式中,经整理后可得到同一表达式
f f 1 ——高斯公式 s s
对于任何形式的成象过程,只要确定相应的f、
率就取物方折射率.(与虚像类似;如上图中P4---物方折 射率为n4)
④ 虚物仍遵从符号法则.(如上图中S4>0)
33
§1.6 薄透镜
透镜 近轴条件下薄透镜的物像公式 横向放大率 薄透镜作图求像法
34
一、透镜
1.定义
用玻璃或其它透明介质研磨抛光为两个 球面或一个球面一个平面所形成的薄片. 通常做成园形.
P1
P2 P1
P3
P4
29
二、逐个球面成像法
1.定义:依球面的顺序,应用成像公式逐个对球面
求像,最后得到整个共轴光具组的像.
P1
n n1
P3
2P2
n3
n4
P2' P1'
S1' S2 d12
n5
sin i2 sin u
A
n
-i1
n`
-i2
-u
u`
P
O
r
C
P`
-s
s`
PC s r r s PC s r
nsini1 nsini2
AC r
15
PC sin u PC sin u n r ssin u s r sin u n
n
n
s r n sin u r s
f n n n f f
f
n
“-”号表示 f 和 f 永远异号,
物、像方焦点一定位于球面两侧.
23
四、理想成象的两个普适公式
1.高斯公式
将f、f’的表达式分别代入反射、折射理想成象 公式中,经整理后可得到同一表达式
f f 1 ——高斯公式 s s
对于任何形式的成象过程,只要确定相应的f、
率就取物方折射率.(与虚像类似;如上图中P4---物方折 射率为n4)
④ 虚物仍遵从符号法则.(如上图中S4>0)
33
§1.6 薄透镜
透镜 近轴条件下薄透镜的物像公式 横向放大率 薄透镜作图求像法
34
一、透镜
1.定义
用玻璃或其它透明介质研磨抛光为两个 球面或一个球面一个平面所形成的薄片. 通常做成园形.
P1
P2 P1
P3
P4
29
二、逐个球面成像法
1.定义:依球面的顺序,应用成像公式逐个对球面
求像,最后得到整个共轴光具组的像.
P1
n n1
P3
2P2
n3
n4
P2' P1'
S1' S2 d12
n5
光在球面上的反射折射
13 – 3 光在球面上的反射、折射成像 一 . 球面镜的反射成像 1. 凹面镜的反射成像 近轴光线 : 靠近 球面对称轴( 主光 轴 ),且与对称轴具 有微小夹角的光线 . 焦距
1 2 3 4 5
物理学教程 (第二版)
凹面镜的焦点
F
f r 2
曲率半径
主 光 轴
f
* 第十三章 几何光学
13 – 3 光在球面上的反射、折射成像 利用作图法 确定像的位置和 大小 成像公式 A 2 1 2 1
物理学教程 (第二版)
2 . 凸面镜的反射成像
1
虚焦点
1 2 3 4 5
O
F
h0
1 2 2
O
f
p0
p
h1
f
F
f 0
凸面镜焦距
* 第十三章 几何光学
p0 0, p 0
凸面镜成像
13 – 3 光在球面上的反射、折射成像 二 . 球面上的折射成像 1. 成像公式(近轴光线)
物理学教程 (第二版)
O
物理学教程 (第二版)
h0 F
h1
p
1 1 1 p p f
凹面镜 f 0 (A) p 0, p 0 B
p
f
p
h0
1 F
O
h1
1 2
2
(B)
p 0, p 0
* 第十三章 几何光学
p
f
13 – 3 光在球面上的反射、折射成像 成像公式
物理学教程 (ቤተ መጻሕፍቲ ባይዱ二版)
n n n n p p r
M
f f 1 p p
Q
i
o
i
c
1 2 3 4 5
物理学教程 (第二版)
凹面镜的焦点
F
f r 2
曲率半径
主 光 轴
f
* 第十三章 几何光学
13 – 3 光在球面上的反射、折射成像 利用作图法 确定像的位置和 大小 成像公式 A 2 1 2 1
物理学教程 (第二版)
2 . 凸面镜的反射成像
1
虚焦点
1 2 3 4 5
O
F
h0
1 2 2
O
f
p0
p
h1
f
F
f 0
凸面镜焦距
* 第十三章 几何光学
p0 0, p 0
凸面镜成像
13 – 3 光在球面上的反射、折射成像 二 . 球面上的折射成像 1. 成像公式(近轴光线)
物理学教程 (第二版)
O
物理学教程 (第二版)
h0 F
h1
p
1 1 1 p p f
凹面镜 f 0 (A) p 0, p 0 B
p
f
p
h0
1 F
O
h1
1 2
2
(B)
p 0, p 0
* 第十三章 几何光学
p
f
13 – 3 光在球面上的反射、折射成像 成像公式
物理学教程 (ቤተ መጻሕፍቲ ባይዱ二版)
n n n n p p r
M
f f 1 p p
Q
i
o
i
c
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
可见,由P点发出不同u角 的单心光束,经球面反射 后,s’不同,即反射光不再 交于一点,不是单心光束.
球面反射破坏光束的单心性—不理想成像.
7
A i
i’
2.近轴光线下球面反射的物像公式
-u P
φ C
-u’ P’ (-s')
O
很小的区域为近轴(或傍轴)区域, 光学上称:
(-r)
此区域内的光线为近轴光线.
结合
i i
6
A
r s s in i s in ( u ) s r s in u s in ( i )
i
i’
-u P
C
φ
-u’ P’ (-s') (-r)
O
(-s)
s i n ( u ) s r ( r s ) s i n ( u ')
19
像空间
物空间 物空间 像空间 S’>0:实像
n
P P` -s` O -s 虚像在物空间,但实
际存在的是像空间 的发散光束,故像方 折射率仍为n’.
n P -s O
n` s` P`
n`
S’<0:虚像
物空间 像空间
像空间 物空间
P
-s
P` -s` O
P -s
s’
P’ S’>0:虚像
S’<0:实像
20
O
P C (s ) r r s
(-s)
利用正弦定理:
P C A C r s 在 P A C 中 , s i n i s i n ( u ) s i n i
C P A C s r 在 P A C 中 , s i n ( i ) s i n ( u ) i n ( i ) s
②当介质和球面一定时(n、n’、r 一定),
n n 不变量 r
计算时r 取米 为单位
n n 定义:光焦度 表征球面的光学特性 r
18
③ 物像公式对凹球面折射同样适用。 ④ 物像共轭:P’为P的像点,即:当物点为P’时,像
⑤ 点必在P点;这种物像可易性称为物像共轭.
⑥ 它是光路可逆原理的必然结果. ⑤ 物空间与像空间: 规定:入射线在其中进行的空间——物空间; 折射线在其中进行的空间——像空间.
(-s)
• 若 u (u’)极小,即入射光仅在傍轴的狭窄范围内 传播,则
s i n u gu u , t
s i n u t g u u
8
A
由图又可知:
sin u AO ( s)
-u P
C φ
i
i’
-u’ P’ (-s') (-r)
§1.4 球面反射和折射
• 符号法则
• 球面反射
• 球面折射 • 理想成象的两个普适公式
1
E
(1)线段
y A
-s
O
r
C
s’
沿轴线段
-y’
以单球面折射系统为例, 从顶点算起:
A、光线与主轴交于顶点右方者,线段长度为正; 光线与主轴交于顶点左方者,线段长度为负; B、物点或像点至主轴的距离在主轴上方为正, 下方为负.
[解]:设光线从左至右 已知:s=-0.`
1 1 2 s s r
C
P
-r
-s O
s’
0 . 2 0 . 0 5 r s 得: s 0 . 1 m 2 s r 20 . 0 5 0 . 2
OA OA sin( u) sin u ' s s'
代入s’表达式并整理,
得
n' n n'n s' s r
n— 物方介质折射率; n`— 象方介质折射率
17
讨
② 一对应,即:
论
n' n n'n s' s r
①当介质和球面一定时(n、n’、r 一定),S’与S一
③ 在近轴光线条件下光束单心性得到保持.
i n u ns s r r s s n i n u
可见,s’也是随u(u’)而变的,不同的光线将有不 同的s’值,故球面折射时光束亦不能保持单心性.
球面折射破坏光束的单心性
16
2.近轴光线下球面折射的物像公式
• 同理,当u(u’)很小时,光仅在近轴范围内传播
f’ — 象方焦距 f — 物方焦距
反射球面特点: f ’ = f , 物方焦点F 和象方焦点F’重合.
10
焦点:沿主轴方向的平行光束经球面反射后会聚
于主轴上一点,该点称为反射球面的焦点(F’).
焦距:焦点到球面顶点的距离( f’= r/2 ).
它同样遵守符号法则.
11
所以,球面反射的成象公式又可以写成
得
n f s r n n
F
n`
O
-s -f
s’
物方焦距
22
C、由前两点,可知两焦距之间满足:
f n f n
nn f f
f 和 f 永远异号,
“-”号表示
物、像方焦点一定位于球面两侧.
23
四、理想成象的两个普适公式
1.高斯公式
将f、f’的表达式分别代入反射、折射理想成象 公式中,经整理后可得到同一表达式
11 1 s f s 球 面 反 射 物 像 公 式
说明:1、它是球面反射成像的基本公式,只在近轴条件 下成立;
2、式中各量必须严格遵从符号法则;
3、对凸球面反射同样适用; 4、当光线从右至左时同样适用.
12
[例] 一个点状物放在凹面镜前0.05m处,凹面镜的 曲率半径为0.20m,试确定像的位置和性质.
⑥ 焦点、焦距
A、像方焦点F’、像方焦距 f
当s=-∞时,由物象公式
n n n n s s r
n
-s
O
n` s’ f’
F’
得
n f s r n n
像方焦距
21
B、物方焦点F、物方焦距 f 当s’= +∞时,由物象公式
n
n n n n s s r
由折射成像公式,代入数据,即可求得结果. 26
§1.5 光连续在几个球面上的折射 虚物
共轴光具组
逐个球面成像法
虚物的概念
27
一、共轴光具组
实际的光学系统大多由两个或两个以上的球面所
构成.研究多个球面上的折射成像更具实际意义. 1.定义: 由两个或两个以上的球面构成的,其曲率中心
处在同一条直线上的光学系统,称为共轴光具组. 该直线为共轴光具组的光轴. 反之,称为非共轴光具组.
成像就只能以它的顶点为取值原点,不能混淆.
③ 必须针对每一个球面使用符号法则;对哪个球面 ④ ④ 计算次一个球面物距时要考虑两个球面间的距离.
31
三、虚物
P1
n1
P3
n2
P 2'
P2
n3
n4
n5
P4
P1 '
P 4'
P 3'
1.定义: 会聚的入射光束的顶点,称为虚物.如P3;
发散的入射光束的顶点,称为实物.如P1、P2和P4.
33
§1.6 薄透镜
透镜 近轴条件下薄透镜的物像公式 横向放大率 薄透镜作图求像法
34
一、透镜
1.定义
用玻璃或其它透明介质研磨抛光为两个 球面或一个球面一个平面所形成的薄片.
通常做成园形.
35
2.分类:按表面形状分
① 凸透镜:中间部分比边缘厚的透镜.
o1
c2
r2
o2
c1
r1
双凸
r2
c2
求像,最后得到整个共轴光具组的像.
P1
n1
P3
n2
P 2'
P2
n3
n4
n5
P4
P1 '
S2
S 1'
P 4'
P 3'
d 12
30
2.方法特点及注意事项
① 必须在近轴光线条件下使用,才能得到最后像. ② 前一球面面的像是后一球面的物;
③ ④
前一球面的像空间是次一球面的物空间;
前一球面的折射线是后一球面的入射线.
像是处于镜后0.1米处的虚像.
13
三、球面折射
n
p
Q
i
O
d
A
n
u
r r
i
C
p
u
1
Q
s
s
14
1.球面折射对光束单心性的破坏
与反射一样, 对△PAC和△P’AC应用正弦定理:
P C A C s i n i s i n u 1
n -u -i1 O -s A -i2 P r C s` u` P` n`
化简可得: xx ff ——牛顿公式 也可以用于任何成象过程.
25
[例] 一个折射率为1.6的玻璃哑铃,长20cm,两端的曲率 半径为2cm.若在离哑铃左端5cm处的轴上有一物点,试 求像的位置和性质.
[解]:两次折射成像问题.
1、P为物对球面O1折射成像P1’ 已知:s1=-5cm,r1=2cm n=1,n’=1.6 由折射成像公式: P
平凸
o1
o2
c1
c2
r2
r1
o1
o2
弯凸
r 1
② 凹透镜:中间部分比边缘薄的透镜.
f f 1 s s
f’,均可由高斯公式求出像.
