第四章 电介质
第四章 近代电介质击穿理论
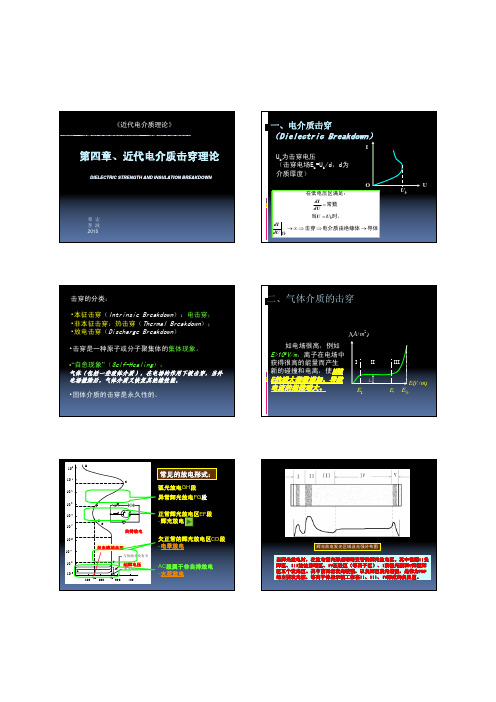
邓宏李波2015《近代电介质理论》DIELECTRIC STRENGTH AND INSULATION BREAKDOWN一、电介质击穿(Dielectric Breakdown )UIOU bU b 为击穿电压(击穿电场E b =U b /d,d为介质厚度)导体电介质由绝缘体击穿时,当常数在低电压区满足:→⇒⇒∞→==Ubb dUdI U U dUdI击穿的分类:•本征击穿(Intrinsic Breakdown ):电击穿;•非本征击穿:热击穿(Thermal Breakdown );•放电击穿(Discharge Breakdown )•击穿是一种原子或分子聚集体的集体现象。
•“自愈现象”(Self-Healing ):气体(包括一些液体介质),在电场的作用下被击穿,当外电场撤除后,气体介质又恢复其绝缘性能。
•固体介质的击穿是永久性的。
二、气体介质的击穿)/(2m A j )/(m V E IIIIII1E iE Sj bE 如电场很高,例如E>108V/m ,离子在电场中获得很高的能量而产生新的碰撞和电离,使N 随E 的增大指数增加,导致电流的指数增大。
1002003004001010 1010 10 10 10 1010100 HGFEV Vs与初始引发有关着火电压VDCA常见的放电形式:AC 段属于非自持放电-火花放电自持放电正常辉光放电区EF 段-辉光放电欠正常的辉光放电区CD 段-电晕放电起辉电压异常辉光放电FG 段弧光放电GH 段放电维持电压辉光放电发光区域及光强分布图当辉光放电时,在放电管内形成明暗交替的辉光放电区。
其中包括II 负辉区、III 法拉弟暗区、IV 正柱区(等离子区)、I 阴极光膜和V 阳极辉区五个发光区。
其中前两者发光较强,以负辉区发光最强,是作为PDP 的主要发光源,等离子体显示板工作在II 、III 、IV 形成的负阻区。
汤申特(Townsend) 碰撞游离理论1. 碰撞游离的必要条件:EVE q W L L L E q W E W W ii i =⋅≥∴⋅⋅=≥ 电荷的运动距离—为:的作用下所积累的能量一个电荷在电场(分子的游离能量)(电子的积累能量),且满足:金属电极表面逸出电子∵•多级碰撞,如果碰撞能量较小但之间间隔周期很短,可能使分子游离;•电子与受激的中性分子碰撞,中性分子回到零位状态,而电子被加速能量增大,可使下一个中性分子游离;•两个受激的分子碰撞,一个交出能量,而另一个获得能量而游离。
高电压技术第四章

3、介质的体积电导和表面电导
三电极法测量介质的体积电阻率ρV为 单位Ω.cm
S v Rv d
式中S 为测量电极的面积,d 为介质厚度 RV 由测量的漏导电流ig及电压值u决定,RV=U/ig
介质的体积电导率γv 为
v
1
v
������
介质的表面电阻率和电导率
b s Rs l
电介质电气性能的划分
极化特性:介电常数ε 损耗特性:介损tgδ 电气传导特性:载流子移动、高场强下的电气传
导机理等,电导G 或电阻R 电气击穿特性:包括击穿机理、劣化、电压--时 间特性曲线(V–t )等,击穿电压UC 或击穿场强EC
第1 节电介质的极化及介电常数
������ ������ ������ ������ ������
2、电介质中传导电流的测量
三电极法
测量介质中电流的电路图
介质中的电流与时间的关系
ic:快速极化造成的充电电流 ia:空间电荷极化等缓慢极化 形成的,又称吸收电流
ig:趋向稳定值的漏导电流,
又称泄漏电流
例:聚乙烯的电流-时间特性
在温度高于室温附近, 要达到稳定的泄漏电 流需要几个小时的时 间,在更低的温度下 (20℃),电流很难趋向 稳定的漏导电流 通常的1min绝缘电阻 测量仅仅是为了工程 上的方便,实际上并 没有物理意义,关于 这一点必须注意。
用极化强度P来表征极化的强度,定义为单位
体积的电极矩,与外加电场强度有关 极化强度P与介电常数 ε 的关系:
3、电介质极化基本类型
电介质的极化有五种基本形式: 电子位移极化 离子位移极化 转向极化 空间电荷极化
夹层介质界面极化(归到空间电荷极化)
第四章4交变电场中电介质的损耗德拜方程ppt课件

求出:
4-76
式中 ωm 为出现 εr’’ 最大值时的角频率。
图 4-10
和
与ωτ 的关系
4-72
4-73
4-74
4-75
经营者提供商品或者服务有欺诈行为 的,应 当按照 消费者 的要求 增加赔 偿其受 到的损 失,增 加赔偿 的金额 为消费 者购买 商品的 价款或 接受服 务的费 用
前面已经指出: 松弛时间τ 是一个与时间无关但与温度有关的常数。 因此,讨论德拜方程时,须注意到 εr’ 与 εr’’ 大小既与频率 ω 有关,也与温度 T 有关;前者可从方程式中直接看出,而后 者隐含于介电常数和松弛时间与温度有关的特性中。 根据德拜弛豫理论模型,将松弛时间τ 表示为: 1nτ = 常数 + Uτ/kT 即 τ 随温度 T 的变化呈指教规律变化。
(1)εr’ ~ ω ,考虑两个极端情形:
频率很高时, ω→ ∞ ,由式 ( 4-73 ) 可知,εr’ ≌ εr∞ 。 此时,相对介电常数可用光频下相对介电常数来表示。 频率很低时, ( ω→0 ) ,εr’ ≌ εrs,静态相对介电常数。 此时,可用静态相对介电常数来表示。 对一般情况: εr’ 随频率 ω 增高而降低。 εr’ 从低频到高频可作成图分析,如图 4-9 ( a ) 所示曲线。
εr’ = (εrs+εr∞)/2;
tgδ=(εrs-εr∞)/(εrs+εr∞) εr’’= εr’ tgδ= (εrs-εr∞)/2
电介质物理课件(2005-4)
1
2. 电子崩的形成:
粒子从电场中获得的动能: T=mv2/2=q2E2τ2/2m 从公式中看出:在电场作用下,带电粒子的动能正比于电 场强度的平方,反比于粒子的质量。而气体粒子中电子的 质量最小,所以在一定的电场下,自由电子所获得的动能 最大。因此,在气体所有粒子的相互碰撞中,与自由电子 的碰撞最容易引起碰撞电离。 发生碰撞电离的条件是: q Eλ≥Wi (原子、分子电离能) 随着 x的增加,电子数按指数增加。
3. 自持放电条件:
正离子沿电场方向运动 会与中性分子碰撞产生 游离,设
自持放电: 气体介质在阴极电子逸出(游离 剂)的作用下产生放电,当游离剂去除 后,气体介质的放电仍能够维持下去, 这种现象叫做“自持放电”。
游离碰撞系数为 (第二游离系数)。 但,这种游离碰撞的几 率很小, 0。
阴极上出现正离子堆积区 堆积区的厚度=10-10m;电压=10-2V; 堆积区的电场可达:E= 10-2V/ 10-10m=108V/m
气体介质本身,由于原子激励还原及离子复合时所 放出的光子产生了新的游离,以促使游离沿着通道发 展,构成流柱,最后导致击穿。
5. 不均匀电场中的气体放电(击穿) 不均匀电场中气体放电的特点:
• • • • • 在高电场区先产生电晕; U增大,电晕边缘出现树枝状放电:辉光放电或火花放电; U进一步增大,树枝状放电连通第二极 ——最终击穿。 从游离场强开始到击穿,随E增加,电流增大,但较慢。 击穿电场强度与电极的形状、距离有关。
j( A / m
2
)
IEII源自jS1IIIE (V / m )
E
i
E
b
常见的放电形式: •火花放电 瞬时,间断产生 常压附近 •辉光放电 出现均匀的明暗相间的辉光区 •电晕放电 电极的曲率小,电场不均匀,在电场尖端出现 暗蓝色微光 •电弧放电 功率大,连续弧光,温度极高
2014-第四章-5-交变电场中电介质的损耗-弛豫机制与松弛时间资料PPT课件

复介电常数 介质损耗 弛豫现象 德拜方程 弛豫机制 介质损耗与温度的关系 考虑漏电导时的介质损耗
2020年9月28日
1
1. 电介质的弛豫机制与松弛时间 热转向极化与热离子极化是常见的两种松弛极化。 它们有着不同的弛豫机制。
介绍弛豫机制; 不同模型假设下所引出的松弛时间; 为下节讨论 εr’ 、εr’’ 与温度关系打下基础。
2020年9月28日
16
将式 (4-111) 代入式 (4-112), 即得到随时间变化的热离子极化强度:
4-113
式中松弛时间:
4-114
此式表明: 1)温度 T 一定时,固体介质中弱离子活化能 U 越大,
松弛时间τ亦越大,即极化建立时间越长。 2)对一定结构的介质,U 不变时,
则松弛时间τ 随温度 T 升高而呈指数关系减小,反之亦然。
4-111
式中,由电场引起的位能变化 △U= qδE/2
加电场
2020年9月28日
15
式 ( 4-111) 说明,加上电场后,存在过剩跃迁离子,位置 2 与 1 相比离子 比较集中,这破坏了原先电荷均匀分布状态,出现了偶极矩。 其极化强度为:
4-112
式中 ( n2 - n1 ) 除 2 说明过剩跃迁离子数为 ( n2 - n1 ) 的一半,其含义是: 当从 “1” 迁移到 “2” 的离子数比从 “2” 迁移到 “1” 的离子数净多一个 时 ( 即过剩迁移离子为一个 ),“2” 处虽多了一个,而 “l” 处却少了一个, 其差 ( n2 - n1 ) 便为 2,因此,计算极化强度时,应取其一半计算。
2020年9月28日
10
因此,平均来说,处在 “1” 位置与处在 “2” 位置的离子 数保持相等。
【精选】电子材料物理第四章.幻灯片

电介质材料的特点:
➢ 不存在载流子,是绝缘体,绝缘电阻率>109Ω.cm ➢ 具有介电常数 ➢ 部分介质具有特殊功能(压电性、铁电性、热释电性)
❖ ε是反映电介质极化行为的宏观物理量;极化能力越强,介电 常数越大。
❖ 用介质电容器可以作为储能元件,储能密度大小可以表示为
ω=1/2ε0εrE2
5
(2)电偶极矩
➢偶极子的产生:
在电场的作用下,正负电荷重心的分离
➢电偶极矩的定义
ql
l
-q
+q
E
方向为从负电荷指向正电荷
介质中的极性分子可看作偶极子(在电场的作用下极性 分子发生转向)
设想一个质量为m,带电为-e的粒子,为一带正电 +e的中心所束缚,弹性恢复力为-kx。这里k是弹性回 复系数,x表示粒子的位移。我们考虑它在交变电场下运
动,电场用复数表示: Eloc E0eit
电荷的运动方程
2x m
t2
kxeE0eit
e
m
e2
02 2
静态极化率
e
e2
m
2 0
(ω0趋于0)
6
(3)极化率():
单位电场强度下,质点的电偶极矩的大小。
E loc
其中:Eloc为作用在微观质点上的局部电场。 (它与宏观外电场并不一定相同)
极化率表征材料极化能力的微观物理量,只与材
料的性质有关,其单位为F·m2(法拉·米2)
7
(4)极化强度(矢量):单位体积内电偶极矩的矢量和
第四章 电介质

2 1
即 1E1R1 2 E2 R2
r
R max max dr dr2 r 21 0 r1 2 2 0 r2
2
r
R1
2 2 rEmax 2 r R Emax 2 r R2 ln rEmax 2 ln ln 1 R1 r 2 rR1
4-24、设一同轴电缆里边导体的半径为R1,外边导体
的半径为R3 ,两导体间充满了两层均匀介质,它们的分界
面的半径是R2,设内外两层电介质常量分别为 和
1
2
(如图所示), 它们的介电强度分别为E1 和 E2 , 证明:当两极间的电压逐渐升高时,在1E1R1 2 E2 R2 的 条件下,首先被击穿的是外层电介质
解:(1)设沿轴线单位长度上的电量为内筒+ ,外筒-
由 D E
E2 2 2 0 r 1 0 r
r 2 R2 2 R1
对于同一种介质,半径r小的地方场强大,故内层介质最容 易在R1处被击穿,外层介质最容易在分界面r处被击穿.
Emax1 R2 知Emax1 Emax 2 Emax 2 2 R1
因两介质的介电强度都是Emax ,即外层介质先被击穿
U max
2 Emax r R2 ln 2 rR1
E1 R2 D 思路; 由 D E 知E1 E2 r 0 E2 2R1
两层均匀介质中的场强分布规律分别为
解:(1)设沿轴线单位长度上的电量为内筒 + ,外筒
E1 21 0 r
两层均匀介质中 的场强分布规律 分别为 在每层介质中场 强最大的地方在其 内侧,在给定 的 条件下那里的场强 分别为
第4章 电介质

§ 2 电介质中的静电场
E E´
介质中的合场强 极化电荷的场强
+ +
+
σ + ++
E0
+
Hale Waihona Puke σ´0E´
+ +
0
E0
自由电荷的场强
E = E0 + E ´ E = E0 E ´ σ0 σ´ =
ε
0
ε
E = E0
ε
P = E0 ce E
0
0
σ E =ε σ ´= Pn = P P = e ce E
0 0 0
ε D = E + P = E + e 0 ce E ε
0 0
ε =
0
(1 + ce ) E = ε r E = E ε ε
0
D = E ε
[ 练习 ] 一平行板电容器,其中填充了一 层介质,尺寸如图,介质的相对介电常数为 εr。 1. 用高斯定理求: 1, D2 , E1 , E 2 ; D U 2. 求: A U B ; 3. 求此电容器之电容。 σ + + + + + + A d1 ε 0 E1 D1 C d2 ε r E 2 D2 B
A + + + + + ++ σ
ε
r
σ
设真空时电容为C0,充满介质时的电容为C
则:
称ε
r
C =ε
r
C0
为相对介电常数,或相对电容率
在平行板电容器情况下
C =ε
r
C0
ε S =ε r d
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第四章 电磁介质第一节 电介质一、电介质—绝缘介质1.电介质内没有可以自由移动的电荷 在电场作用下,电介质中的电荷只能在 分子范围内移动。
2.分子电矩·分子—电偶极子(模型)分子的正负电中心相对错开。
·分子电矩二、电介质的极化1.极性电介质的极化p 分+- 电介质分子(1) 极性分子·正常情况下,内部电荷分布不对称, 正负电中心已错开,有固有电矩p 分, ·极性分子:如HCl 、H 2O 、CO 等。
(2)无外电场时·每个分子p 分 ≠ 0·由于热运动,各p 分取向混乱·小体积∆V (宏观小、微观大,内有大量 分子)内 ∑ p 分= 0(3)有外电场时·各 p 分向电场方向取向(由于热运动,取向 并非完全一致)外有外电场 无外电场分 ·且外电场越强 ⇒ | ∑ p 分| 越大·这种极化称取向极化2.非极性电介质的极化(1)非极性分子·正常情况下电荷分布对称,正负电中心重 合,无固有电矩。
·非极性分子:如He 、 H 2、 N 2、 O 2、 CO 2等。
(2)无外电场时·每个分子 p 分 = 0·∆V 内∑ p 分 = 0 (3)有外电场时·正负电中心产生相对位移,p 分(称感应电矩) ≠ 0E 外分 ·且外电场越强 ⇒ | ∑ p 分| 越大·这种极化称位移极化三、电极化强度1.电极化强度·为描写电介质极化的强弱,引入电极化强度矢量。
·定义:单位体积内分子电矩的矢量和或·P 是位置的函数·单位: C/m 2·对非极性电介质,因各p 分相同,有 P = n p 分n ---单位体积内的分子数·综上,对极性、非极性电介质都有 无外电场时, P = 0 有外电场时,P ≠ 0且电场越强 ⇒ | P | 越大2.电极化强度和场强的关系·由实验,对各向同性电介质,当电介质中 电场E 不太强时,有·χe :电极化率(χe ≥ 0),决定于电介质性质。
·E :是电介质中某点的场强(包括该点的外 电场以及电介质上所有电荷在该点产生的电场)。
·对各向同性介质: P ∝ EP ↑↑ E四、束缚电荷电介质极化后,在电介质体内及表面上可以出现束缚电荷(又称极化电荷)。
1.体束缚电荷(1)体束缚电荷·考虑电介质体内面元d S处的极化·以位移极化为例,设负电中心不动,·在电场作用下,d V= l分d S cosθ内所有分子的正电荷中心将越过d S面。
·越过d S面元的总电荷d q'= q分n(l分d S cosθ)= np分cosθ d S= P cosθ d Sd q ' = P ⋅ d S·在电介质体内取任一封闭曲面S ,则净穿 出整个封闭面的电荷为q '出= ⎰ S P ⋅dSq '内 = - q '出 电介质体内任一封闭面内的束缚电荷 为(2)可以证明:对均匀电介质,若电介质体内 无自由电荷,则不管电场是否均匀,电介 质体内都无束缚电荷。
(我们只讨论均匀电介质,即以后只考虑下面所说的表面上的束缚电荷)2.面束缚电荷·若前述d S面元刚好在电介质表面上,n 即电介质的外法线方向,则d q' = P⋅ d S即为电介质表面d S面积上的束缚电荷。
·单位面积上的束缚电荷σ' = d q' /d S束缚电荷面密度n—电介质表面外法线方向的单位矢量(方向:由电介质体内指向体外)·如图电介质五电位移矢量D D的高斯定理'-n·由于电介质极化后会出现束缚电荷,空间某点的电场应是由自由电荷与束缚电荷共同产生的。
E = E f + E '·怎样求E?E = E f + E 'Pσ'本想求E E才能求出E ”,情况复杂。
·引入一辅助矢量(一)、电位移矢量D,D的高斯定理·由真空中的高斯定理⎰S E⋅d S = ∑q内/ε0∑q内应包括高斯面所包围的自由电荷与束缚电荷。
∑q内= ∑q f内+∑q'内·由前,高斯面包围的束缚电荷为 ∑q '内 = - ⎰ S P ⋅dS·于是⎰S ε0E ⋅dS =∑q f 内 - ⎰ S P ⋅d S⎰S ( ε0E + P )⋅d S =∑q f 内·引入电位移矢量单位: C/m 2·D 的高斯定理通过任意封闭曲面的电位移通量等于该封闭面所包围的自由电荷的代数和。
(二)、关于D 的讨论1.对D的理解(1) D只和自由电荷有关吗?·D的高斯定理说明D在闭合面上的通量只和自由电荷有关,这不等于说D只和自由电荷有关。
·由D = 0E + P,也说明D既和自由电荷又和束缚电荷有关( E是空间所有电荷共同产生的)。
(2)电位移线·类似于电场线(E线),在电场中也可以画出电位移线(D线);·由于闭合面的电位移通量等于被包围的自由电荷,所以D线发自正自由电荷;止于负自由电荷。
2. D、E、P的关系(1)一般关系D = ε0E + P(2)对各向同性电介质(且场强不太大时) ·因P = ε0χe E 代入上式,D = ε0E + ε0χe E = ε0(1+ χe ) E·引入:相对介电常数εr = (1+ χe ), (εr ≥ 1) 介电常数 ε = ε0 εr·P 可写作P = ε0(εr -1)E·对各向同性电介质(且场强不太大时) D ∝ E ,且二矢量同向。
第2节磁介质(一)分子电流观点一、磁介质及其分类1.磁介质:能够影响磁场的物质。
2.分类(1)弱磁性物质·顺磁质·抗磁质(2)强磁性物质铁磁质二、分子电流分子磁矩1.分子电流·分子中电子有轨道运动自旋运动·分子中所有电子的运动形成分子电流(可看成是一通电小圆线圈)。
2.分子磁矩(1) 电子的轨道磁矩 ·轨道半径—r (圆轨道) 电子速率—υ ·轨道电流·电子轨道磁矩对氢原子基态, p m = 0.93⨯10-23 A ⋅m 2 ·电子轨道角动量(圆轨道) L = m υ r m —电子质量·电子轨道磁矩与轨道角动量的关系(2)电子自旋磁矩p m= IS = ( ) π r 2=e υ 2πr e υ r 2 p m = - ( )Le2mI = e ( )υ 2πrp·实验证明:电子有自旋磁矩p s = 0.927⨯10-23 A ⋅m 2·自旋磁矩和自旋角动量S 的关系(3)分子磁矩p 分 =[ ∑所有电子(p m + p s )] +∑ p 核p 核 — 核(自旋)磁矩分子磁矩是分子中所有电子的轨道磁矩和自旋磁矩与所有核磁矩的矢量和。
三、顺磁质的磁化在外磁场作用下磁介质出现磁性或磁性发生变化的现象称磁化。
1.顺磁质(如铝、铂、氧)·无外磁场时, p 分 ≠ 0 (固有磁矩) 由于热运动,其取向混乱ep S = - ( ) Sm·∆V (宏观小微观大)内 ∑p 分= 02.顺磁质的顺磁性·有外磁场时,p 分沿外磁场取向, ∆V 内 ∑p 分 ≠ 0 ·p 分取向后,产生附加磁场B ' B = B 0 + B 'B ' ↑↑B 0 , (B '<<B 0) 此即顺磁质的顺磁性,p 分取向则是顺磁性的来源。
3.顺磁质的抗磁性无外磁场 有外磁场 B 0(1)外磁场对电子轨道运动的作用·当分子处于外磁场中时,电子的轨道运动 会受一力矩 M = p m ⨯ B 0·在力矩作用下,L 绕B 0进动。
根据是角动量定理(2)附加磁矩·由于进动,电子产生了附加磁矩∆p m 。
·不管电子轨道运动方向如何, 附加磁矩总与外磁场方向相反。
d Ld tM = B⊗MB 0 ⊙·对自旋磁矩,外磁场也有同样作用。
(3)感应磁矩·感应磁矩:分子中所有附加磁矩的矢量和。
·∆p感总与外磁场方向相反,此即抗磁性的来源。
(4)顺磁质的抗磁性可以忽略·对顺磁质| p分| >> |∆p感|·顺磁质主要表现为顺磁性。
四.抗磁质的磁化·抗磁质:如铋、汞、铜、氢。
·抗磁质分子没有固有磁矩(p分= 0),只有感应磁矩∆p感·抗磁质表现为抗磁性。
·对抗磁质B = B0 + B'B'↑↓B0,(B'<<B0)五、磁化强度矢量1.定义:单位体积内分子磁矩的矢量和·对抗磁质,M则为分子感应磁矩的矢量和。
·单位:A/m2.磁化强度随磁场增强而增大·对顺磁质、抗磁质均如此·具体定量关系见后六、磁化电流磁介质磁化后,在磁介质体内和表面上可出现磁化电流。
1.磁化体电流(1) 磁化体电流·在磁介质体内取面元∆S ,现在求通过它的 磁化电流I '。
·穿过∆S 两次的i 分对I '无贡献,和∆S 的 边界相套住的i 分(只穿过∆S 一次) 对I '有贡献。
·与边界上d l 段套住的分子电流: (凡中心在d V 内的i 分将套住d l ) d I '= i 分 n d V = i 分n (S 分⋅d l ) = n (p 分⋅d l ) = M ⋅d l·与∆S 的整个边界L 相套住的分子电流ni 分—穿过∆S 的磁化电流 I '= ⎰L d I '= ⎰L M ⋅ d l 磁化体电流(2)可以证明,在均匀磁介质内部,不管磁场是否均匀,在没有传导电流的地方,也没 有体磁化电流。
2.磁化面电流·若d l 正好在磁介质边界上,则d I '表现为 磁化面电流。
磁化面电流密度:磁介质表面垂直于电流 方向的单位宽度上的电流。
大小:j '= d I '/ d l = M ⋅d l / d l =M l(当M 和表面平行时, j '= M )方向:⊥ M可综合写作n —磁介质表面的外法线方向的单位矢量(方向:由磁介质体内→体外)·均匀磁化 介质棒表 面的磁化 电流j '式亦可由I '式用环路a-b-c-d 得出(请自 己做)。
