相似三角形证明题精选
全等三角形相似三角形证明(中难度题型)
43.如图,已知∠A=∠D,AB=DE,AF=CD,BC=EF.求证:BC∥EF
44.如图,已知AC∥BD,EA、EB分别平分∠CAB和∠DBA,CD过点E,则AB与AC+BD相等吗请说明理由
45、(10分)如图,已知: AD是BC上的中线 ,且DF=DE.求证:BE∥CF.
全等三角形证明经典50题.doc
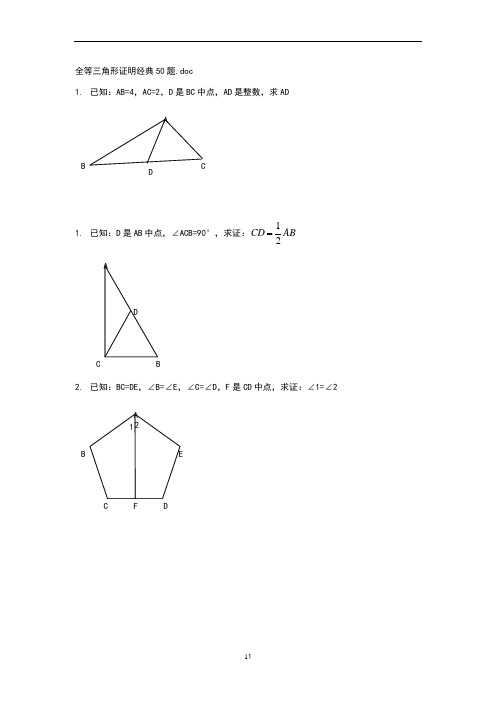
1.已知:AB=4,AC=2,D是BC中点,AD是整数,求AD
1.已知:D是AB中点,∠ACB=90°,求证:
2.已知:BC=DE,∠B=∠E,∠C=∠D,F是CD中点,求证:∠1=∠2
已知:∠1=∠2,CD=DE,EF 如图,四边形ABCD中,AB∥DC,BE、CE分别平分∠ABC、∠BCD,且点E在AD上。求证:BC=AB+DC。
50.如图9所示,△ABC是等腰直角三角形,∠ACB=90°,AD是BC边上的中线,过C作AD的垂线,交AB于点E,交AD于点F,求证:∠ADC=∠BDE.
相似三角形的判定练习
相似三角形的判定练习.doc
【知能点分类训练】
知能点1 角角识别法
1.如图1,(1)若 =_____,则△OAC∽△OBD,∠A=________.
12.如图,等腰直角三角形ABC中,顶点为C,∠MCN=45°,试说明△BCM∽△ANC.
13.在 ABCD中,M,N为对角线BD的三等分点,连接AM交BC于E,连接EN并延长交AD于F.(1)试说明△AMD∽△EMB;(2)求 的值.
14.在△ABC中,M是AB上一点,若过M的直线所截得的三角形与原三角形相似, 试说明满足条件的直线有几条,画出相应的图形加以说明.
相似三角形证明题

相似三角形证明题1.如图,在ABC ∆中,C ABC ∠=∠2,BD 平分ABC ∠,试说明:AB·B C = AC·CD2.已知:ΔACB 为等腰直角三角形,∠ACB=900延长BA 至E ,延长AB 至F ,∠ECF=135求证:ΔEAC ∽ΔCBF3.如图,点C 、D 在线段AB 上,且ΔPCD 是等边三角形. (1)当AC ,CD ,DB 满足怎样的关系时,ΔACP ∽ΔPDB ; (2)当ΔPDB ∽ΔACP 时,试求∠APB 的度数.4.如图,4531===∠=∠∠=∠BC DE AB D B ,,, (1)ABC ∆∽ADE ∆吗?说明理由。
(2)求AD 的长。
5.已知:如图,CE 是Rt ΔABC 的斜边AB 上的高,BG ⊥AP. 求证:CE 2=ED ·EP.6.如图,四边形ABCD 是平行四边形,AE ⊥BC 于E ,AF ⊥CD 于F. (1)ΔABE 与ΔADF 相似吗?说明理由. (2)ΔAEF 与ΔABC 相似吗?说说你的理由.7.如图,D 为ΔABC 内一点,E 为ΔABC 外一点,且∠1=∠2,∠3=∠4. (1)ΔABD 与ΔCBE 相似吗?请说明理由. (2)ΔABC 与ΔDBE 相似吗?请说明理由.8.如图:⊿ABC 中,D 是AB 上一点,AD = AC ,BC 边上的中线AE 交CD 于F ,求证: DF CF AC AB ::AB C EDF9.四边形ABCD 中,AC 为AB 、AD 的比例中项,且AC 平分∠DAB ,求证:22CD BC DE BE =10.矩形ABCD 中,a AB =,b BC =,M 是BC 的中点,DE ⊥AM ,E 是垂足, 求证:2242ba ab DE +=11.如图,过平行四边形ABCD 的顶点A 的直线交BD 于P ,交CD 于Q ,并交BC 的延长线于R ,求证:22PBPD PR PQ =A BCR12.如图所示,在平行四边形ABCD 中,过点B 作BE ⊥CD ,垂足为E ,连结AE ,F 为AE 上一点,且∠BFE =∠C(1)求证:△ABF ∽△EAD ;(2)若AB =4,∠BAE =30°, 求AE 的长;(3)在(1)(2)的条件下,若AD =3,求BF 长.(计算结果含根号).13.如图,P 在线段MN 上,如果PM 2= MN ·PN ,,那么,P 是线段MN 的一个黄金分割点。
完整版)相似三角形题型归纳

完整版)相似三角形题型归纳1、在平行四边形ABCD中,点E为对角线AC上的一点,且AE∶EC=1∶3.将BE延长至与CD的延长线交于点G,与AD交于点F。
证明BF∶FG=1∶2.2、在直角三角形ABC中,∠BAC=90°,AB=AC,D为BC的中点,E为AC上的一点。
点G在BE上,连接DG并延长至交AE于点F,且∠FGE=45°。
证明:(1)BD·BC=BG·BE;(2)AG⊥BE;(3)若E为AC的中点,则EF∶FD=1∶2.3、在直角三角形ABC中,∠BAC=90°,AD⊥BC于点D,点O是AC边上的一点,连接BO交AD于点F,OE⊥OB交BC边于点E。
证明:(1)△ABF∽△COE;(2)当O为AC的中点时,求△ABC的面积;(3)当O为AC边中点时,求△ABC的面积。
4、在平行四边形ABCD和平行四边形ACED中,点R为DE的中点,BR分别交AC、CD于点P、Q。
写出各对相似三角形(相似比为1除外),并求出BP∶PQ∶QR的值。
5、在△ABC中,AD平分∠BAC,EM为AD的中垂线,交BC延长线于点E。
证明DE=BE·CE。
6、过△ABC的顶点C任作一直线,与边AB及中线AD分别交于点F和E。
证明AE∶ED=2AF∶FB。
7、在Rt△ABC中,CD为斜边AB上的高,点M在CD 上,DH⊥BM且与AC的延长线交于点E。
证明:(1)△AED∽△CBM;(2)DE=DM。
8、在△ABC中,BD、CE分别是两边上的高,过D作DG⊥BC于点G,分别交CE及BA的延长线于点F、H。
证明:(1)DG=BG·CG;(2)BG·CG=GF·GH。
9、在平行四边形ABCD中,点P为对角线AC上的一点。
过P的直线与AD、BC、CD的延长线、AB的延长线分别相交于点E、F、G、H。
证明:AG∶GB=CP∶PD。
1、求证:如图,已知平行四边形ABCD中,点P在AC上,点Q在BC上,且AP=CQ。
相似三角形的判定(证明题)

相似三角形的判定1 •如图,锐角A4BC的髙CD和BE相交于点0,图中与△OD3相似的三角形有(A4个 B3个 C2个 D1个3•已知:AACB为等腰直角三角形,ZACB=90°延长BA至E,延长AB至F, ZECF二135°求证:CBF5・、如图,点C、D在线段AB上,且APCD是等边三角形.(1)当AC, CD, DB满足怎样的关系时,AACP S APDB:⑵当A PDBs A ACP时,试求ZAPB的度数.6•如图,Z1 = Z3, ZB = Z£>, AB = DE = 5, EC = 4(1)AABC- AADE吗?说明理由。
(2)求AD的长。
7.已知:如图,CE是RtAABC的斜边AB上的髙,BG丄AP・求证:CE:=ED €P.9 •如图,D为A ABC内一点,E为AABC外一点,且Z1=Z2, Z3:⑴AABD与4CBE相似吗?请说明理由.(2) A ABC与ADBE相似吗?请说明理由.AA EACs AB C判断题:⑴两个顶角相等的等浸三角形是相似的三角形。
((2)两个等腰直角三角形是相似三角形。
((3)底角相等的两个等艮三角形是相似三角形,((4)两个直角三角形一定是相似三角形。
((5)—个钝角三角形和一个锐角三角形有可能相似n ((6)有一个角相等的两个宜角三角形是相似三角形n ((7)有一个锐角相等的两个直角三角形是相似三角形。
( (3)三角形的三条中位线围成的三角形与原三角形相似.((9)所有的正三角形都相似n ( )(10)两个等艮三角形只要有一个角对应相等就相似. ( ) 2・如圍,AD/J BC, AE平分ZDAB, BE平分ZABC・ EF丄AB•证明:AAEF^AABE.3 •如尿,AABC是等边三角形,点D、E分别在BC、AC上,且BD^CE, AD与BE相交于点F・<1)试说明△ ABD坐ZkBCEj<2)AEAF与相似吗?说说你的理也.4.如釦在AABC中’ ZBAC=90\ D为BC的中点,AE丄AD, AE交CB的延长纟壬于点E・(1)求证:AEAB^AECA.:(2)4ABE和AADC是否一定相似?妇果相似,加以说明5如杲不相似,那么增加一个怎徉的条件,A.4BE和4ADC-定相似.5・如囲在AABC中,ZC=905, D. E衽BC上,BD=DE=EC=AC,指出團中哪两个三角形棉似,并证明你的结论.A6・如團,ZkABC 申,ZBAC=90% AB=AC, D 在BC 匕 E 在AC 匕 且上ADETS 廈 (1) 求证:△ABD S /XDCE ・ (2) 台D 莊什么位贵时,AABD^ADCE ・7. 如图,在AABC 中,AB ・8cm, BC-16c 叫 点P 从点A 开始沿AB 向B 以2cE 啲速度移动‘点 Q 从点B 幵弟沿BC 向C 点^4cm,s 的速虔移动.加果P, Q 分别从、B 同时出拓 经过几秒绅ZkPB Q与△ ABC 相似?8. 如囹,已知AABC 中CE 丄AB 干E, BF 丄AC 于F,求证;△AEF S ^ACB.9 •如图、UAABC 中,ZACB=PO% AC=4, BO3,点P 在线段AB 上臥每秽1个单位的速度从点B 问点A 运动,同时点Q 曲圭段A C 上以同样的速虎从点A 向点C 运动,运动的时间用1 (单位:秒)表示.(1)求线股AB 的长;<2)求当t 为何值时,AAPQ 与AABC 相似?10・如虱在MBCD 中’ E 豹BC 边上一点'连接AE 、DE, F 为线段DE 上一点,且ZAFE=ZB .试 说明△ADF S ADEC ・11 ・如釦 已知MBC 中’ AB=2& AC=4js, BC=6? AMN 与AABC 相似,求MN 的长.3A312・如團,点E 是匹边形ABCD 的对角线BD 上一点,SZBAC-Z3DC-ZDAE ・求证:AABE^AAC D.14.已知,如團:在AABC 中,AD=CD, /ADE=ZDCB, 求还;△ABCsACDE.16・已知:D 、ElAABC^j±AB^ AC±^].^, AB=9, AD=4, AC=7.2, AE=5,求证:AABCooAAE D ・18 ・已知:如园.在△ ABC 和△ ADE 中,ZBAC=ZDAE, ZABC=ZADE. 求证:AABIX^AACE・D17 ・ 4±AABC 中,ZBAC=90c , E,求证:AABIX O ADCE ・19・如园.在正万形网格上有6个斜三角形:①②△CDB,③ADEB, @AFBG, ©AHGF,⑥△ERF 请在三角形②〜⑥中,找出与①相佩的三鱼形的序号是_〈把 前序号埴上〉并证明你的结论.20.如冒所示,在A ABC 中,AB=8cm ? BC=16cm ?点P 从点A 开始沿边AB 向点B 以lens 的速庶移 动,点Q 从点B 幵始沿边BC 向点C 以2cm/啲速庚移动,如果点.P 、Q 同时出紀 经过多长时间后,厶PB ABC 相似?试说明理由■21・将两个全等的等腰宜角三角形摆成如團所示的祥子(團中所有的点、线都在同一平面内〉・ CD 请在图中找出两対相似而不全手的三角形〉话从其中一对说明埋宙.C2)你还能再找一对相似而不全等的三角形吗?请说明遅由.22・如园:己知△ABgZkADE 的边BC 、AD 相交于点0,旦Z1=Z2-Z3.求证:AABCsAADE.23.如园,APQR 罡尊边三角形,ZAPBJ20J I 乩每两个三角形沏一组写出园中所有的相 似三角形,并迭择耳中的一爼加以证明.2S.如图’已知:厶ABC 中〉ZABC-90% AB-BC,延长BC 到E,使得CE-2BC,馭CE 的中点D,连接AE 、 AD ・求iib AACD<7>AECA ・26.如阂.D 是Z\ABC 的边BC 上的一点,AB=2, BD=1, DC=3,求证:AABD^ACBA.5 I D327・已知:AABC为手瑕直角三角形,ZACB=90%延长BA至E,延长AB至F, ZECF=135S求证:AEAC^ACBF.28・如因所示'R仏ABC中’已^DZBAC=O0\ AB=AC=2,点D在BC上运动(不能到达点B, C),过点D作ZADE=45% DE交AC于点E.(1)求证:△AEIX^XDCE;(2)当AADE是等腰三角形时,求AE的长.29・如團已知AB丄BD, CD丄BD・若・4B=9, CD=4, BD-10,话问在BD上是否存在P点,使以P、4、B三点为页点的三角形与以P、C、D三点为顶点的三角形相似・?若存在,求BP的长:若不存在'请说明理由.30・如臥AABCx ADEPf两个全竽的等腰直毎三角形,ZBAC=ZPDE=90\(1)若将ADEP的顶点.P放在BC上(如图1) , PD、PE分别与AC、AB相交于点F. G.求证:△PBGs^FCP;(2)肴使ADEP的顶点P与顶点A重台〔如图2) , PD-. PE与BC相交干点几G・试问APBG与AFCP还相似吗勺为什么?1・如国,在4ABC和ADEF中ZA=ZD=90\ AB=DE=3, AC=2DF=4 ・(1)判断这两个三角形杲否殆似并说明为什么?(2)能否分别过A, D在这两个三角形中各作一条湘助纵使△ ABC分黑成的两个三角形与ADEFB-割成的两个三角形分别对应相似?证明惋的结论.2 •如團,在A ABC中,AB=AC,若4 ABC^ADEF,且点A往DE上,点E在BC上,EF与AC交于点M・求证:AABE^AECM・5.己知:如图'AABC中'AD=DB, Zl=/2.求证:AABCxoAEAD.S・如图'在厶ABC中,AB=AC, ZADB=90°, ZCBE=ZCAD;求证:△BECsAADC ・10・?0g.. ZABC=ZBCD,且BC^=AB・CD・ ^15: AABC^ABCD.O11・已务Ih如图,AD是△ ABC的高,BE丄AB, AE交BC于点、F> AB・AC-AD・AE・求证:ABEFcoAACF ・13.妇團所不‘在铁角AABC中,高CD: BE相交于点、F・ <1)拷出图中所有的相似三角形,并证明一对三角形柜似3 (2)连结DE,试说明:AADEccAACB.4・如凰,集一时別一根2米长的竹竿EF嶷长GE为I球'此时,小红测得一棵被凤吹斜的杨树与地面成30。
相似三角形判定证明题

相似三角形的判定(证明题)1.如图,∠1=∠2=∠3,写出图中的相似三角形,并说明理由。
2.AF 如图,∥,CD ∠1=∠2,∠B =∠D ,写出图中四对相似三角形,并说明相似的理由。
3.如图,D 为ΔABC 内一点,E 为ΔABC 外一点,且∠1=∠2,∠3=∠4. (1)ΔABD 与ΔCBE 相似吗?请说明理由. (2)ΔABC 与ΔDBE 相似吗?请说明理由.4. AD 为ΔABC 的中线,E 为AD 的中点,若∠DAC =∠B ,CD =CE求证;(1)ΔACE ∽ΔBAD (2)CD 2=AE ·AD5.如图,AB BC ACAD DE AE==.求证:(1)∠BAD=∠CAE. (2)ΔABD∽ΔACE. 6.已知:如图,AD ·AB=AE ·AC ,求证:△EOC ∽△DOB 。
321F EDCBA 21F EDC BABA EABCED7.已知:如图,AE 2=AD ·AB ,且12∠=∠,求证: BCE ∆∽EBD ∆8.如图,等腰直角三角形ABC 中,顶点为C ,∠MCN=45°,试说明△BCM ∽△ANC9.如图,点C 、D 在线段AB 上,且ΔPCD 是等边三角形.∠APB=1200求证:(1)ΔACP ∽ΔPDB ;(2)CD 2=AC ·BD10.如图,ABCD 中,M 是AB 上的一点,连结CM 并延长交DA 的延长线于P ,交对角线BD 于N ,求证:NP MN CN ⋅=211.如图,CD 是Rt △ABC 的斜边上的高线,∠BAC 的平分线交BC ,CD 于E ,F . 求证:(1)△ACF ∽△ABE ;(2)AC ·AE= AF ·AB .12.如图,⊿ABC 是等边三角形,点D,E 分别在BC,AC 上,且BD=CE,AD 与BE 相交于点F. (1)试说明⊿ABD ≌⊿BCE.(2)⊿AEF 与⊿ABE 相似吗?说说你的理由.(3)BD 2=AD ·DF 吗?请说明理由.13、如图,在平行四边形ABCD 中,过点A 作AE ⊥BC ,垂足为E ,连接DE ,F 为线段DE 上一点,且∠AFE =∠B. (1) 求证:△ADF ∽△DEC(2) 若AB=8,AD=6,AF=4,求AE 的长。
相似三角形精选好题-证明题25题

相似三角形精选好题解答题学校:___________姓名:___________班级:___________考号:___________一、解答题(本大题共25小题,共200.0分)1.如图,在△AAA中,AA=AA=20AA,AA=30AA,点P从A点出发,沿着AB以每秒4cm的速度向B点运动;同时点Q从C点出发,沿着CA以每秒3cm的速度向A点运动,设运动时间为x秒.2.(1)A为何值时,AA//AA;3.(2)是否存在某一时刻,使△AAA∽△AAA?若存在,求出此时AP的长;若不存在,请说明理由;4.(3)当A△AAAA△AAA =13时,求A△AAAA△AAA的值.5.6.7.8.9.10.11.12.如图,△AAA中,AA=AA,AA⊥AA于A,A是BC中点,连接AD与BE交于点F,求证:△AAA∽△AAA.13.14.15.16.…17.如图,已知四边形ABCD中,∠AAA=90°,∠AAA=90°,AA=6,AA=4,AA的延长线与AD的延长线交于点E.18.(1)若∠A=60°,求BC的长;19.(2)若sin A=45,求AD的长.20.(注意:本题中的计算过程和结果均保留根号)21.22.23.24.25.26.27.28. 如图,在△AAA 中,点D 在BC 边上,∠AAA =∠A .点E 在AD 边上,AA =AA .29. (1)求证:△AAA ∽△AAA ;30. (2)若AA =6,AA =92,AA =2,求AE 的长.31.32.33. 如图,在四边形ABCD 中,AA //AA,AA =2AA,AA=2,AA =5,AA //AA ,交BC 于点F ,连接AF .34. (1)求CF 的长;35. (2)若∠AAA =∠AAA ,求AB 的长.36. 如图,在锐角三角形ABC 中,点A,A 分别在边AA,AA上,AA ⊥AA 于点A,AA ⊥AA 于点A,∠AAA =∠AAA .37. (1)求证:△AAA ∽△AAA ;38. (2)若AA =3,AA =5,求AAAA 的值.~39.如图,在AA△AAA中,∠A=90°,点D是BC.边的中点,AA=2,tan A=3440.(1)求AD和AB的长;41.(2)求sin∠AAA的值.42.43.44.45.46.从三角形(不是等腰三角形)一个顶点引出一条射线与对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原三角形相似,我们把这条线段叫做这个三角形的完美分割线.47.(1)如图1,在△AAA中,CD为角平分线,∠A=40°,∠A=60°,求证:CD为△AAA的完美分割线.48.(2)在△AAA中,∠A=48°,AA是△AAA的完美分割线,且△AAA为等腰三角形,求∠AAA的度数.49.(3)如图2,△AAA中,AA=2,AA=√2,AA是△AAA的完美分割线,且△AAA是以CD为底边的等腰三角形,求完美分割线CD的长.50.51.如图,大楼AB右侧有一障碍物,在障碍物的旁边有一幢小楼DE,在小楼的顶端D处测得障碍物边缘点C的俯角为30°,测得大楼顶端A的仰角为45°(点A,A,A在同一水平直线上),已知AA=80A,AA=10A,求障碍物A,A两点间的距离(结果精确到0.1A)(参考数据:√2≈1.414,√3≈1.732)52.53.54.`55.如图是将一正方体货物沿坡面AB装进汽车货厢的平面示意图.已知长方体货厢的高,现把图中的货物继续往前平移,当货物顶点D与C重合度BC为√5米,tan A=13时,仍可把货物放平装进货厢,求BD的长.(结果保留根号)56.如图,某大楼的顶部树有一块广告牌CD,小李在山坡的坡脚A处测得广告牌底部D的仰角为60°.沿坡面AB向上走到B处测得广告牌顶部C的仰角为45°,已知山坡AB的坡度i=1:√3,AB=10米,AE=15米.(i=1:√3是指坡面的铅直高度BH与水平宽度AH的比)57.(1)求点B距水平面AE的高度BH;58.(2)求广告牌CD的高度.59.(测角器的高度忽略不计,结果精确到0.1米.参考数据:√2≈1.414,√3≈1.732)60.61.62.63.64.65.66.67.如图,在Rt△ACB中,∠C=90°,AC=16cm,BC=8cm,动点P从点C出发,沿CA方向运动;动点Q同时从点B出发,沿BC方向运动,如果点P的运动速度为4cm/s,Q点的运动速度为2cm/s,那么运动几秒时,△ABC和△PCQ相似?68.69.70.71.72.73.74.75.如图所示,∠C=90°,BC=8cm,AC=6cm,点P从点B出发,沿BC向点C以2cm/s的速度移动,点Q从点C出发沿CA向点A以1cm/s的速度移动,如果P、Q分别从B、C同时出发,过多少时,以C、P、Q为顶点的三角形恰与△ABC相似?76.77.78.79.80.81.82.83.如图,小明在教学楼A处分别观测对面实验楼CD底部的俯角为45°,顶部的仰角为37°,已知教学楼和实验楼在同一平面上,观测点距地面的垂直高度AB为15m,求实验楼的垂直高度即CD长(精确到1m)84.参考值:sin37°=0.60,cos37°=0.80,tan37°=0.75.85.}86.如图,某校数学兴趣小组为测量校园主教学楼AB的高度,由于教学楼底部不能直接到达,故兴趣小组在平地上选择一点C,用测角器测得主教学楼顶端A的仰角为30°,再向主教学楼的方向前进24米,到达点E处(C,E,B三点在同一直线上),又测得主教学楼顶端A的仰角为60°,已知测角器CD的高度为1.6米,请计算主教学楼AB的高度.(√3≈1.73,结果精确到0.1米)87.已知:如图,△ABC是等边三角形,点D、E分别在边BC、AC上,∠ADE=60°.88.(1)求证:△ABD∽△DCE;,求DC的长.89.(2)如果AB=3,EC=2390.91.92.93.如图,CD是一高为4米的平台,AB是与CD底部相平的一棵树,在平台顶C点测得树顶A点的仰角α=30°,从平台底部向树的方向水平前进3米到达点E,在点E处测得树顶A点的仰角β= 60°,求树高AB(结果保留根号)94.95.96.#97.钓鱼岛自古就是中国的领土,中国有关部门已对钓鱼岛及其附属岛屿开展常态化监视监测.一日,中国一艘海监船从A点沿正北方向巡航,其航线距钓鱼岛(设N、M为该岛的东西两端点)最近距离为15海里(即MC=15海里),在A点测得岛屿的西端点M在点A的东北方向,航行4海里后到达B点,测得岛屿的东端点N在点B的北偏东57°方向(其中N、M、C在同一条直线上),求钓鱼岛东西两端点MN之间的距离.(精确到0.1海里)参考数据:sin57°=0.84,cos57°=0.54,tan57°=1.54.98.99.100.101.102.103.104.105.探究证明:106.(1)如图1,矩形ABCD中,点M、N分别在边BC,CD上,AM⊥BN,求证:BNAM =BCAB.107.(2)如图2,矩形ABCD中,点M在边BC上,EF⊥AM,EF分别交AB,CD于点E、点F,试猜想EFAM 与BCAB有什么数量关系?并证明你的猜想.108.拓展应用:综合(1)、(2)的结论解决以下问题:109.(3)如图3,四边形ABCD中,∠ABC=90°,AB=AD=10,BC=CD=5,AM⊥DN,点M,N分别在边BC,AB上,求DNAM的值.110.111.如图,在某次数学活动课中,小明为了测量校园内旗杆AB的高度,站在教学楼CD上的E处测得旗杆底端B的仰角∠BEF的度数为45°,测得旗杆顶端A的仰角∠AEF的度数为17°,旗杆底部B处与教学楼底部C处的水平距离BC为9m,求旗杆的高度(结果精确到0.1m).112.【参考数据:sin17°=0.29,cos17°=0.96,tan17°=0.31】113.114.115.已知,如图,在四边形ABCD中,∠ADB=∠ACB,延长AD、BC相交于点E.求证:116.(1)△ACE∽△BDE;117.(2)BE?DC=AB?DE.118.119.120.…121.如图,在△ABC中,点D为BC边的任意一点,以点D为顶点的∠EDF的两边分别与边AB,AC交于点E、F,且∠EDF与∠A互补.122.(1)如图1,若AB=AC,D为BC的中点时,则线段DE与DF有何数量关系?请直接写出结论;123.(2)如图2,若AB=kAC,D为BC的中点时,那么(1)中的结论是否还成立?若成立,请给出证明;若不成立,请写出DE与DF的关系并说明理由;124.(3)如图3,若ABAC =a,且BDCD=b,直接写出DEDF=______ .125.126.放风筝是大家喜爱的一种运动,星期天的上午小明在市政府广场上放风筝.如图,他在A处不小心让风筝挂在了一棵树梢上,风筝固定在了D处,此时风筝AD与水平线的夹角为30°,为了便于观察,小明迅速向前边移动,收线到达了离A处10米的B处,此时风筝线BD与水平线的夹角为45°.已知点A,B,C在同一条水平直线上,请你求出小明此时所收回的风筝线的长度是多少米?(风筝线AD,BD均为线段,√2≈1.414,√3≈1.732,最后结果精确到1米).127.禁渔期间,我渔政船在A处发现正北方向B处有一艘可以船只,测得A、B两处距离为200海里,可疑船只正沿南偏东45°方向航行,我渔政船迅速沿北偏东30°方向前去拦截,经历4小时刚好在C处将可疑船只拦截.求该可疑船只航行的平均速度(结果保留根号).128.129.130.131.132.133.(134.某市开展一项自行车旅游活动,线路需经A、B、C、D四地,如图,其中A、B、C三地在同一直线上,D地在A地北偏东30°方向,在C地北偏西45°方向,C地在A地北偏东75°方向.且BC=CD=20km,问沿上述线路从A地到D地的路程大约是多少?(最后结果保留整数,参考数据:sin15°≈0.25,cos15°≈0.97,tan15°≈0.27,√2≈1.4,√3≈1.7)135.136.137.138.139.140.答案和解析【答案】1. 解:(1)由题意知?AP=4x,CQ=3x若PQ//BC?? 则△APQ∽△ABC,AP AB =AQAC,∵AB=BC=20,AC=30,∴AQ=30?3x,∴4x20=30?3x30,∴x=103,∴当x=103时,PQ//BC.(2)存在∵△APQ∽△CQB?则APCQ =AQCB,∴4x3x =30?3x20,∴9x2?10x=0,∴x1=0(舍去).x2=109.∴当AP的长为109时,△APQ∽△CQB,(3)∵S△BCQS△ABC =13,∴CQAC =13,又∵AC=30,∴CQ=10,即3x=10x=103,此时,AP=4x=403,∴APAB =40320=23.∴S△APQS△ABQ =APAB=23.??2. 证明:∵AB=AC,D是BC中点,∴AD⊥BC,∴∠ADC=90°,∴∠FAE+∠AFE=90°,∵BE⊥AC,∴∠BEC=90°,∴∠CBE+∠BFD=90°,∵∠AFE=∠BFD,∴∠FAE=∠CBE,∴△AFE∽△BCE.??3. 解:(1)∵∠A=60°,∠ABE=90°,AB=6,tanA=BEAB,∴∠E=30°,BE=tan60°?6=6√3,又∵∠CDE=90°,CD=4,sinE=CDCE,∠E=30°,∴CE=412=8,∴BC=BE?CE=6√3?8;(2))∵∠ABE=90°,AB=6,sinA=45=BEAE,∴设BE=4x,则AE=5x,得AB=3x,∴3x=6,得x=2,∴BE=8,AE=10,∴tanE=ABBE =68=CDDE=4DE,解得,DE=163,∴AD=AE?DE=10?163=143,即AD的长是143.??4. (1)证明:∵CE=CD,∴∠CDE=∠CED.∴∠ADB=∠CEA.∵∠DAC=∠B,∴△ABD∽△CAE.(2)解:由(1)△ABD∽△CAE,∴ABAC =BDAE.∵AB=6,AC=92,BD=2,∴AE=32.??5. 解:(1)作AG//CD交BC于点G,∵AD//BC,∴四边形AGCD是平行四边形,∴GC=AD,∵AD=2,∴GC=2,∵BC=5,∴BG=BC?GC=5?2=3,∵EF//DC,AG//CD,∴EF//AG,∴FGBF =AEEB,∴FGBG =AEAB,∵AE=2EB,∴AEAB =23,∴FGBG =23,∵BG=3,∴FG=2,∴CF=FG+GC=2+2=4;(2)∵∠BFE=∠FAB,∠B=∠B,∴△BFE∽△BAF,∴BEBF =BFAB,∴AB?BE=BF2,∴AB?13AB=BF2,∵BF=BC?FG=5?4=1,∴AB=√3.??(6. 解:(1)∵AG⊥BC,AF⊥DE,∴∠AFE=∠AGC=90°,∵∠EAF=∠GAC,∴∠AED=∠ACB,∵∠EAD=∠BAC,∴△ADE∽△ABC,(2)由(1)可知:△ADE∽△ABC,∴ADAB =AEAC=35由(1)可知:∠AFE=∠AGC=90°,∴∠EAF=∠GAC,∴△EAF∽△CAG,∴AFAG =AEAC,∴AFAG =35??7. 解:(1)∵D是BC的中点,CD=2,∴BD=DC=2,BC=4,在Rt△ACB中,由?tanB=ACCB =34,∴AC4=34,∴AC=3,由勾股定理得:AD=√AC2+CD2=√32+22=√13,AB=√AC2+BC2=√32+42=5;(2)过点D作DE⊥AB于E,∴∠C=∠DEB=90°,又∠B=∠B,∴△DEB∽△ACB,∴DEAC =DBAB,∴DE3=25,∴DE=65,∴sin∠BAD=DEAD =65√13=6√1365.??8. 解:(1)如图1中,∵∠A=40°,∠B=60°,∴∠ACB=80°,∴△ABC不是等腰三角形,∵CD平分∠ACB,∴∠ACD=∠BCD=12∠ACB=40°,∴∠ACD=∠A=40°,∴△ACD为等腰三角形,∵∠DCB=∠A=40°,∠CBD=∠ABC,∴△BCD∽△BAC,∴CD是△ABC的完美分割线.(2)①当AD=CD时,如图2,∠ACD=∠A=48°,∵△BDC∽△BCA,∴∠BCD=∠A=48°,∴∠ACB=∠ACD+∠BCD=96°.②当AD=AC时,如图3中,∠ACD=∠ADC=180°?48°2= 66°,∵△BDC∽△BCA,∴∠BCD=∠A=48°,∴∠ACB=∠ACD+∠BCD=114°.③当AC=CD时,如图4中,∠ADC=∠A=48°,∵△BDC∽△BCA,∴∠BCD=∠A=48°,∵∠ADC>∠BCD,矛盾,舍弃.∴∠ACB=96°或114°.(3)由已知AC=AD=2,∵△BCD∽△BAC,∴BCBA =BDBC,设BD=x,∴(√2)2=x(x+2),∵x>0,∴x=√3?1,∵△BCD∽△BAC,∴CDAC =BDBC=√3?1√2,∴CD=√3?1√2×2=√6?√2.??9. 解:如图,过点D作DF⊥AB于点F,过点C作CH⊥DF 于点H.则DE=BF=CH=10m,在直角△ADF中,∵AF=80m?10m=70m,∠ADF= 45°,∴DF=AF=70m.在直角△CDE中,∵DE=10m,∠DCE=30°,∴CE=DEtan30°=10√33=10√3(m),∴BC=BE?CE=70?10√3≈70?17.32≈52.7(m).答:障碍物B,C两点间的距离约为52.7m.??10. 解:如图,点D与点C重合时,B′C=BD,∠B′CB=∠CBD=∠A,∵tanA=13,,∴设B′B=x,则B′C=3x,在Rt△B′CB中,B′B2+B′C2=BC2,即:x2+(3x)2=(√5)2,x=√22(负值舍去),∴BD=B′C=3√22,??11. 解:(1)过B作BG⊥DE于G,Rt△ABH中,i=tan∠BAH=√3=√33,∴∠BAH=30°,∴BH=12AB=5;(2)∵BH⊥HE,GE⊥HE,BG⊥DE,∴四边形BHEG是矩形.∵由(1)得:BH=5,AH=5√3,∴BG=AH+AE=5√3+15,Rt△BGC中,∠CBG=45°,∴CG=BG=5√3+15.Rt△ADE中,∠DAE=60°,AE=15,∴DE=√3AE=15√3.∴CD=CG+GE?DE=5√3+15+5?15√3=20?10√3≈2.7m.答:宣传牌CD高约2.7米.??12. 解:设同时运动ts时两个三角形相似,当△PCQ∽△BCA,则PCBC =CQAC,4t8=8?2t16,t=0.8;当△PCQ∽△ACB,则CQBC =PCAC,8?2t8=4t16,t=2.答:同时运动0.8s或者2s时两个三角形相似.??13. 解:设经过y秒后,△CPQ∽△CBA,此时BP=2y,CQ=y.∵CP=BC?BP=8?2y,CB=8,CQ=y,CA=6.∵△CPQ∽△CBA,∴CPCB =CQCA,∴8?2y8=y6∴y=2.4设经过y秒后,△CPQ∽△CAB,此时BP=2y,CQ=y.∴CP=BC?BP=8?2y.∵△CPQ∽△CAB,∴CPCA=CQCB∴8?2y6=y8∴y=3211所以,经过2.4秒或者经过3211后两个三角形都相似??、14. 解:作AE⊥CD于E,∵AB=15m,∴DE=AB=15m,∵∠DAE=45°,∴AE=DE=15m,在Rt△ACE中,tan∠CAE=CEAE,则CE=AE?tan37°=15×0.75≈11cm,∴AB=CE+DE=11+15=26m.答:实验楼的垂直高度即CD长为26m.??15. 解:在Rt△AFG中,tan∠AFG=AGFG,∴FG=AGtan∠AFG =AG√3,在Rt△ACG中,tan∠ACG=AGCG,∴CG=AGtan∠ACG=√3AG.又∵CG?FG=24m,即√3AG?AG√3=24m,∴AG=12√3m,∴AB=12√3+1.6≈22.4m.??16. (1)证明:∵△ABC是等边三角形,∴∠B=∠C=60°,AB=AC,∵∠B+∠BAD=∠ADE+∠CDE,∠B=∠ADE=60°,∴∠BAD=∠CDE ∴△ABD∽△DCE;(2)解:由(1)证得△ABD∽△DCE,∴BDAB =CEDC,设CD=x,则BD=3?x,∴3?x3=23x,∴x=1或x=2,∴DC=1或DC=2.??17. 解:作CF⊥AB于点F,设AF=x米,在Rt△ACF中,tan∠ACF=AFCF,则CF=AFtan∠ACF =xtanα=xtan30°=√3x,在直角△ABE中,AB=x+BF=4+x(米),在直角△ABF中,tan∠AEB=ABBE ,则BE=ABtan∠AEB=x+4tan60°=√33(x+4)米.∵CF?BE=DE,即√3x?√33(x+4)=3.解得:x=3√3+42,则AB=3√3+42+4=3√3+122(米).答:树高AB是3√3+122米.??18. 解:在Rt△ACM中,tan∠CAM=tan45°=CMAC=1,∴AC=CM=15,∴BC=AC?AB=15?4=11.在Rt△BCN中,tan∠CBN=tan57°=CNBC=1.54.∴CN=1.54B?C=16.94.∴MN=16.94?15=1.94≈1.9海里.答:钓鱼岛东西两端点MN之间的距离约为1.9海里.??19. 解:(1)如图1中,∵四边形ABCD是矩形,∴∠ABC=∠C=90°∴∠NBA+∠NBC=90°,∵AM⊥BN,∴∠MAB+∠NBA=90°,∴∠NBC=∠MAB,∴△BCN∽△ABM,∴BNAM =BCAB.(2)结论:EFAM =BCAB.理由:如图2中,过点B作BG//EF交CD于G,∵四边形ABCD是矩形,∴AB//CD,∴四边形BEFG是平行四边形,∴BG=EF,∵EF⊥AM,∴BG⊥AM,∴∠GBA+∠MAB=90°,∵∠ABC=∠C=90°,∴∠GBC+∠GBA=90°,∴∠MAB=∠GBC,∴△GBC∽△MAB,∴BGAM =BCAB,∴EFAM =BCAB.(3)如图3中,过点D作平行于AB的直线交过点A平行于BC的直线于R,交BC的延长线于S,连接AC,则四边形ABSR是平行四边形.∵∠ABC=90°,∴四边形ABSR是矩形,∴∠R=∠S=90°,RS=AB=10,AR=BS,∵AM⊥DN,∴由(2)中结论可得:DNAM =BSAB,∵AB=AD,CB=CD,AC=AC,∴△ACD≌△ACB,∠ADC=∠ABC=90°,∴∠SDC+∠RDA=90°,∵∠RAD+∠RDA=90°,∴∠RAD=∠SDC,∴△RAD∽△SDC,∴∴CDAD =SCRD,设SC=x,∴510=xRD,∴RD=2x,DS=10?2x,在Rt△CSD中,∵CD2=DS2+SC2,∴52=(10?2x)2+x2,∴x=3或5(舍弃),∴BS=5+x=8,∴DNAM =BSAB=810=45.??20. 解:如图,由题意得EF=BC=9m,∠AEF=17°,∠BEF=45°,在Rt△BEF中,∵tan∠BEF=tan45°=BFEF,∴BF=EF=9m.???????????????????????????????????????????????????????????? 在Rt△AEF中,∵tan17°=AFEF,∴AF=9×0.31=2.79m.∴AB=AF+BF=11.79≈11.8m.答:旗杆AB的高度约为11.8m.??21. 证明:(1)∵∠ADB=∠ACB,∴∠BDE=∠ACE,∴△ACE∽△BDE;(2)∵△ACE∽△BDE,∴BEAE =EDEC,∵∠E=∠E,∴△ECD∽△EAB,∴AEEC =ABCD,∴BEED =ABCD,∴BE?DC=AB?DE.??:22. ba??23. 解:作DH⊥BC于H,设DH=x米.∵∠ACD=90°,∴在直角△ADH中,∠DAH=30°,AD=2DH=2x,AH=DH÷tan30°=√3x,在直角△BDH中,∠DBH=45°,BH=DH=x,BD=√2x,∵AH?BH=AB=10米,∴√3x?x=10,∴x=5(√3+1),∴小明此时所收回的风筝的长度为:AD?BD=2x?√2x=(2?√2)×5(√3+1)≈(2?1.414)×5×(1.732+1)≈8米.答:小明此时所收回的风筝线的长度约是8米.??24. 解:过点C作CD⊥AB,垂足为点D,设BD=x海里,则AD=(200?x)海里,∵∠ABC=45°,∴BD=CD=x,∵∠BAC=30°,∴tan30°=CDAD,在Rt△ACD中,则CD=AD?tan30°=√33(200?x),则x=√33(200?x),解得,x=100√3?100,即BD=100√3?100,在Rt△BCD中,cos45°=BDBC,解得:BC=100√6?100√2,则(100√6?100√2)÷4=25(√6?√2)(海里/时),则该可疑船只的航行速度约为25(√6?√2)海里/时.??25. 解:由题意可知∠DCA=180°?75°?45°=60°,∵BC=CD,∴△BCD是等边三角形.过点B作BE⊥AD,垂足为E,如图所示:由题意可知∠DAC=75°?30°=45°,∵△BCD是等边三角形,∴∠DBC=60°?BD=BC=CD=20km,∴∠ADB=∠DBC?∠DAC=15°,∴BE=sin15°BD≈0.25×20≈5m,∴AB=BEsin45°=5√22≈7m,∴AB+BC+CD≈7+20+20≈47m.答:从A地跑到D地的路程约为47m.??【解析】1. (1)当PQ//BC时,根据平行线分线段成比例定理,可得出关于AP,PQ,AB,AC的比例关系式,我们可根据P,Q的速度,用时间x表示出AP,AQ,然后根据得出的关系式求出x的值.(2)由△APQ∽△CQB?得出APCQ =AQCB,进一步代入求x的值;(3)当S△BCQS△ABC =13时得出CQ:AC=1:3,那么CQ=10cm,此时时间x正好是(1)的结果,那么此时PQ//BC,由此可根据平行这个特殊条件,得出三角形APQ和ABC的面积比,然后再根据三角形PBQ的面积=三角形ABC的面积?三角形APQ的面积?三角形BQC 的面积来得出答案即可.本题主要考查了相似三角形的判定和性质,根据三角形相似得出线段比或面积比是解题的关键.2. 根据等腰三角形的性质,由AB=AC,D是BC中点得到AD⊥BC,易得∠ADC=∠BEC=90°,再证明∠FAE=∠CBE,于是根据有两组角对应相等的两个三角形相似即可得到结论.本题考查了相似三角形的判定:有两组角对应相等的两个三角形相似.也考查了等腰三角形的性质,证题的关键是挖掘题目的隐藏条件:对顶角相等.3. (1)要求BC的长,只要求出BE和CE的长即可,由题意可以得到BE和CE的长,本题得以解决;(2)要求AD的长,只要求出AE和DE的长即可,根据题意可以得到AE、DE的长,本题得以解决.本题考查解直角三角形,解题的关键是明确题意,找出所求问题需要的条件,利用锐角三角函数进行解答.|4. (1)由CE=CD,推出∠CDE=∠CED,推出∠ADB=∠CEA,由∠DAC=∠B,即可证明.(2)由(1)△ABD∽△CAE,得到ABAC =BDAE,把AB=6,AC=92,BD=2,代入计算即可解决问题.本题考查相似三角形的判定和性质、等腰三角形的性质,三角形的外角的性质等知识,就提到过房间数灵活运用所学知识解决问题,属于中考常考题型.5. (1)作AG//CD交BC于点G,根据平行四边形的性质可知CG=AD=2,由EF//AG,AE=2EB,利用平行线分线段成比例定理可求出FG=2,CF=FG+GC即可求出结果;(2)先证明△BFE∽△BAF,得到BEBF =BFAB,由BE=13AB和BF=1可求出AB.本题主要考查了梯形的性质、平行四边形的判定与性质、平行线分线段成比例定理以及相似三角形的判定与性质,作AG//CD交BC于点G,构造平行四边形和相似三角形是解决问题的关键.6. (1)由于AG⊥BC,AF⊥DE,所以∠AFE=∠AGC=90°,从而可证明∠AED=∠ACB,进而可证明△ADE∽△ABC;(2)△ADE∽△ABC,ADAB =AEAC,又易证△EAF∽△CAG,所以AFAG=AEAC,从而可知AFAG=ADAB.本题考查相似三角形的判定,解题的关键是熟练运用相似三角形的判定,本题属于中等题型.7. (1)由中点定义求BC=4,根据tanB=34得:AC=3,由勾股定理得:AB=5,AD=√13;(2)作高线DE,证明△DEB∽△ACB,求DE的长,再利用三角函数定义求结果.本题考查了解直角三角形,熟练掌握直角三角形的边角关系是解题的关键.8. (1)根据完美分割线的定义只要证明①△ABC不是等腰三角形,②△ACD是等腰三角形,③△BDC∽△BCA即可.(2)分三种情形讨论即可①如图2,当AD=CD时,②如图3中,当AD=AC时,③如图4中,当AC=CD时,分别求出∠ACB即可.(3)设BD=x,利用△BCD∽△BAC,得BCBA =BDBC,列出方程即可解决问题.本题考查相似三角形的判定和性质、等腰三角形的性质等知识,解题的关键是理解题意,学会分类讨论思想,属于中考常考题型.9. 如图,过点D作DF⊥AB于点F,过点C作CH⊥DF于点H.通过解直角△AFD得到DF的长度;通过解直角△DCE得到CE的长度,则BC=BE?CE.本题考查了解直角三角形?仰角俯角问题.要求学生能借助仰角构造直角三角形并解直角三角形.10. 点D与点C重合时,B′C=BD,∠B′CB=∠CBD=∠A,利用tanA=13得到,然后设B′B=x,则B′C=3x,在Rt△B′CB中,利用勾股定理求得答案即可.本题考查了解直角三角形的应用,解题的关键是能够从实际问题中整理出直角三角形,难度不大.11. (1)过B作DE的垂线,设垂足为G.分别在Rt△ABH中,通过解直角三角形求出BH、AH;(2)在△ADE解直角三角形求出DE的长,进而可求出EH即BG的长,在Rt△CBG中,∠CBG=45°,则CG=BG,由此可求出CG的长然后根据CD=CG+GE?DE即可求出宣传牌的高度.此题综合考查了仰角、坡度的定义,能够正确地构建出直角三角形,将实际问题化归为解直角三角形的问题是解答此类题的关键.$12. 设同时运动ts时两个三角形相似,再分△PCQ∽△BCA或△PCQ∽△ACB两种情况进行讨论即可.本题考查的是相似三角形的判定,熟知相似三角形的判定定理是解答此题的关键.13. 设经过y秒后相似,由于没有说明对应角的关系,所以共有两种情况:△CPQ∽△CBA 与△CPQ∽△CAB本题考查相似三角形的判定,解题的关键是分两种情况进行讨论,本题属于中等题型.14. 作AE⊥CD于E,根据正切的定义求出CE和AE,计算即可.本题考查的是解直角三角形的应用?仰角俯角问题,解决此类问题要了解角之间的关系,找到与已知和未知相关联的直角三角形,当图形中没有直角三角形时,要通过作高或垂线构造直角三角形,另当问题以一个实际问题的形式给出时,要善于读懂题意,把实际问题划归为直角三角形中边角关系问题加以解决.15. 利用60°的正切值可表示出FG长,进而利用∠ACG的正切函数求AG长,加上1.6m即为主教学楼的高度AB.本题考查了解直角三角形的应用?仰角俯角问题,构造仰角所在的直角三角形,利用两个直角三角形的公共边求解是常用的解直角三角形的方法.16. (1)△ABC是等边三角形,得到∠B=∠C=60°,AB=AC,推出∠BAD=∠CDE,得到△ABD∽△DCE;(2)由△ABD∽△DCE,得到BDAB =CEDC,然后代入数值求得结果.本题考查了等边三角形的性质,相似三角形的判定和性质,注意数形结合和方程思想的应用.17. 作CF⊥AB于点F,设AF=x米,在直角△ACF中利用三角函数用x表示出CF的长,在直角△ABE中表示出BE的长,然后根据CF?BE=DE即可列方程求得x的值,进而求得AB的长.本题考查了解直角三角形的应用,解答本题关键是构造直角三角形,利用三角函数的知识表示出相关线段的长度.18. 在直角△ACM,∠CAM=45度,则△ACM是等腰直角三角形,即可求得AC的长,则BC可以求得,然后在直角△BCN中,利用三角函数求得AN,根据MN=CN?CM即可求解.本题考查了三角函数,从图形中抽象出直角三角形并正确求得BC的长度是关键.19. (1)根据两角对应相等两三角形相似即可证明.(2)结论:EFAM =BCAB.如图2中,过点B作BG//EF交CD于G,首先证明四边形BEFG是平行四边形,推出BG=EF,由△GBC∽△MAB,得BGAM =BCAB,由此即可证明.(3)如图3中,过点D作平行于AB的直线交过点A平行于BC的直线于R,交BC的延长线于S,连接AC,则四边形ABSR是平行四边形.由(2)中结论可得:DNAM =BSAB,想办法求出BS即可解决问题.本题考查相似三角形综合题、矩形的判定和性质、平行四边形的判定和性质、勾股定理等知识,解题的关键是正确寻找相似三角形,学会添加常用辅助线,构造相似三角形解决问题,属于中考压轴题.20. 先根据锐角三角函数的定义求出BF及AF的长,再由AB=AF+BF即可得出结论.本题考查的是解直角三角形的应用?仰角俯角问题,熟记锐角三角函数的定义是解答此题的关键.21. (1)根据邻补角的定义得到∠BDE=∠ACE,即可得到结论;(2)根据相似三角形的性质得到BEAE =EDEC,由于∠E=∠E,得到△ECD∽△EAB,由相似三角形的性质得到AEEC =ABCD,等量代换得到BEED=ABCD,即可得到结论.本题考查了相似三角形的判定和性质,邻补角的定义,熟练掌握相似三角形的判定和性质是解题的关键.22. 解:(1)结论:DF=DE,理由:如图1,连接AD,作DM⊥AB于M,DN⊥AC于N,则∠EMD=∠FND=90°,∵AB=AC,点D为BC中点,∴AD平分∠BAC,∴DM=DN,∵在四边形AMDN中.,∠DMA=∠DNA=90°,∴∠MAN+∠MDN=180°,又∵∠EDF与∠MAN互补,∴∠MDN=∠EDF,∴∠EDM=∠FDN,在△DEM与△DFN中,{∠DME=∠DNF ∠EDM=∠FDN DM=DN,∴△DEM≌△DFN,∴DE=DF.(2)结论DE:DF=1:k.理由:如图2,过点D作DM⊥AB于M,作DN⊥AC于N,连接AD,则∠EMD=∠FND= 90°,∵BD=DC,∴S△ABD=S△ADC,∴12?AB?DM=12?AC?DN,∵AB=kAC,∴DN=kDM,由(2)可知,∠EDM=∠FDN,∠DEM=∠DFN=90°,∴△DME∽△DNF,∴DEDF =DMDN=1k.(3)结论:DEDF =ba.理由:如图3,过点D作DM⊥AB于M,作DN⊥AC于N,连接AD,同(2)可证∠EDM=∠FDN,又∵∠EMD=∠FND=90°,∴△DEM∽△DFN,∴DEDF =DMDN,∵BDCD=b,∴S△ABD:S△ADC=b,∴12?AB?DM:12?AC?DN=b,∵AB:AC=a,∴DM:DN=ba,∴DEDF =DMDN=ba.故答案为ba.(1)如图1,连接AD,作DM⊥AB于M,DN⊥AC于N,则∠EMD=∠FND=90°,只要证明△DEM≌△DFN即可.(2)结论DE:DF=1:k.如图2,过点D作DM⊥AB于M,作DN⊥AC于N,连接AD,则∠EMD=∠FND=90°,由12?AB?DM=12?AC?DN,AB=kAC,推出DN=kDM,再证明△DME∽△DNF,即可.(3)结论DE:DF=1:k.如图3,过点D作DM⊥AB于M,作DN⊥AC于N,连接AD,同(2)可证∠EDM=∠FDN,由12?AB?DM:12?AC?DN=b,AB:AC=a,推出DM:DN=ba,再证明△DEM∽△DFN即可.本题考查相似三角形的判定和性质、三角形的面积、奇偶分析的性质定理等知识解题的关键是学会添加常用辅助线,学会理由面积法证明线段之间的关系,属于中考常考题型.23. 作DH⊥BC于H,设DH=x米,根据三角函数表示出AH于BH的长,根据AH?BH= AB得到一个关于x的方程,解方程求得x的值,进而求得AD?BD的长,即可解题.本题考查了直角三角形的运用,考查了30°角所对直角边是斜边一半的性质,本题中求得DH的长是解题的关键.24. 先过点C作CD⊥AB,垂足为点D,设BD=x海里,得出AD=(200?x)海里,在Rt△BCD中,根据tan45°=CDBD,求出CD,再根据BD=CD求出BD,在Rt△BCD中,根据cos45°=BDBC,求出BC,从而得出答案.此题考查了解直角三角形的应用,用到的知识点是方向角含义、三角函数的定义,关键是根据题意画出图形,构造直角三角形.25. 求出∠DCA的度数,再判断出BC=CD,据此即可判断出△BCD是等边三角形.过点B作BE⊥AD,垂足为E,求出∠DAC的度数,利用三角函数求出AB的长,从而得到AB+ BC+CD的长.本题考查了解直角三角形的应用--方向角问题;通过解直角三角形求出AB是解决问题的关键.。
(相似三角形)证明题

1、如图,△ABC中,三条内角平分线交于D,过D作AD垂线,分别交AB、AC于M、N,请写出图中相似的三角形,并说明其中两对相似的正确性。
2、如图,AD为△ABC的高,DE⊥AB,DF⊥AC,垂足分别为E、F,试判断∠ADF与∠AEF的大小,并说明明理由,…3、如图,在△ABC中,点D、E分别在BC、AB上,且∠CAD=∠ADE=∠B,AC:BC=1:2,设△EBD、△ADC、△ABC的周长分别为m1 、m2、m3,求的值,*4、如图,已知△ABC中,D为BC中点,AD=AC,DE⊥BC,DE与AB交于E,EC与AD相交于点F,(1)△ABC与△FCD相似吗请说明理由;(2)若S =5,BD=10,求DE的长。
:5、AD是△ABC的高,E是BC的中点,EF⊥BC交AC于F,若BD=15,DC=27,AC=45.求AF的长。
\6、已知:如图,在△PAB中,∠APB=120O,M、N是AB上两点,且△PMN是等边三角形。
求证: BM·PA=PN·BP7、已知:如图,D是△ABC的边AC上一点,且CD=2AD,AE⊥BC于E, 若BC=13, △BDC的面积是39, 求AE的长。
?????*8、已知:如图,在△ABC中,AB=15,AC=12,AD是∠BAC的外角平分线且AD交BC的延长线于点D,DE ∥AB交AC的延长线于点E。
《9、已知: 如图,四边形ABCD中,CB⊥BA于B,DA⊥BA于A,BC=2AD,DE⊥CD交AB于E,连结CE,求证:DE2=AE?CE】10、如图,矩形ABCD中,E为BC上一点,DF⊥AE于F.(1)ΔABE与ΔADF相似吗请说明理由.(2)若AB=6,AD=12,BE=8,求DF的长./11、如图:三角形ABC是一快锐角三角形余料,边BC=120mm,高AD =80mm,要把它加工成正方形零件,是正方形的一边在BC上,其余两个顶点分别在AB、AC上,这个正方形零件的边长是多少ANP12、已知:如图:FGHI 为矩形,AD ⊥BC 于D ,95GH FG ,BC =36cm,AD =12cm 。
相似三角形典型例题30道

相似三角形典型例题30道1: 在△ABC中,DE是平行于BC的线段,且AD/DB = 2/3。
求DE/BC的比值。
2: 已知△PQR与△XYZ相似,PQ = 6,XY = 9,求QR 与YZ的比值。
3: 在△ABC中,D、E分别是AB、AC上的点,且DE平行于BC,已知AD = 3,DB = 6,求AE与EC的比值。
4: 已知两个相似三角形的面积比为4:9,求它们对应边的比。
5: 在△XYZ中,MN是平行于XY的线段,且XM = 4,MY = 6,求MN/XY的比值。
6: 在△ABC中,AD是BC的中线,且AE是AB的延长线,若AE与BC相交于点F,求AF与FB的比值。
7: 在△DEF中,GH平行于EF,已知DE = 8,DF = 10,求GH/EF的比值。
8: 在一个相似三角形中,若大三角形的周长是36,小三角形的周长是24,求它们的面积比。
9: 在△JKL中,MN平行于JK,若JM = 3,MK = 5,求MN/JK的比值。
10: 如果两个相似三角形的对应边长分别为5和15,求它们的面积比。
11: 在△ABC中,AD是BC的中线,且DE平行于BC,已知AD = 4,BC = 8,求DE的长度。
12: 已知相似三角形的对应边长比为1:4,求它们的周长比。
13: 在△PQR中,S是PQ的中点,若ST平行于QR,求PS与PQ的比值。
14: 在相似三角形中,若小三角形的每条边长为5,大三角形的对应边长为15,求它们的面积比。
15: 在一个三角形中,若一条边的延长线与另一边的平行线相交,则形成的两小三角形与原三角形相似,求相似比。
16: 在△XYZ中,若XY = 10,XZ = 15,YZ = 12,求△XYZ的周长。
17: 已知△ABC与△DEF相似,若AB = 4,DE = 8,求AC与DF的比值。
18: 在△GHI中,JK平行于GH,若GJ = 5,GH = 20,求JK的长度。
19: 在相似三角形中,若一个三角形的面积是36,另一个三角形的面积是144,求其对应边的比。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1文档收集于互联网,已整理,word 版本可编辑.E A A B P DC 相似三角形证明专题训练1、已知:如图,DE ∥BC,AF ∶FB=AG ∶GE 。
求证:ΔAFG ∽ΔAED 。
2、已知:如图,ΔABC 中,CE ⊥AB,BF ⊥AC.求证:ΔAEF ∽ΔACB.3、如图,∠ADC=∠ACB=900,∠1=∠B,AC=5,AB=6,求AD 的长4、已知,如图,在正方形ABCD 中,P 是BC 上的点,且BP=3PC ,Q 是CD 的中点,△ADQ 与△QCP 是否相似?为什么?5、如图,CD 是Rt △ABC 的斜边AB 上的高,∠BAC 的平分线分别交BC 、CD 于点E 、F ,AC ·AE=AF ·AB 吗?说明理由。
6、如图,AD 是Rt △ABC 斜边BC 上的高,DE ⊥DF ,且DE 和DF 分别交AB 、AC E F AF AD BEBD于、。
则吗?说说你的理由。
=7、如图,在⊿ABC (AB >AC )的边AB 上取一点,在边AC 上取一点E ,使AD=AE ,直线DE 和BC 的延长线交于点P ,求证:BP :CP=BD :CE8、已知:如图,在△ABC 中,AB =AC ,AD ⊥AB ,AD 交于点E ,DC ⊥BC ,与AD 交于点D . 求证:AC 2=AE ·AD .9、已知:如图,在△ABC 中,∠CAB =90°,AD ⊥BC 于点D ,点E 是AC 边的中点,ED 的延长线与AB 的延长线交于点F .求证:△AFD ∽△DFB . 10、已知:如图,矩形ABCD 的对角线AC 、BD 相交于O ,OF ⊥AC 于点O ,交AB 于点E ,交CB 的延长线于点F ,求证:AO 2=OE · OF . 11、己知:如图,AB ∥CD,AF=FB,CE=EB. 求证:GC 2=GF ·GD.12、已知:如图,ΔABC 中,∠ACB=900,F 为AB 的中点,EF ⊥AB.求证:ΔCDF ∽ΔECF. 13、已知:如图,DE ∥BC,AD 2=AF ·AB 。
求证:ΔAEF ∽ΔACD 。
14、已知:如图,ΔABC 中,∠ABC=2∠C,BD 平分∠ABC.求证:AB ·BC=AC ·CD. 15、已知:如图,ΔABC 中,AD=DB,∠1=∠2.求证:ΔABC ∽ΔEAD. 16、已知:如图,∠1=∠2,∠3=∠4. 求证:ΔDBE ∽ΔABC. 17、已知,如图,在平行四边形ABCD 中,E 为AC 三分之一处,即AE =31AC ,DE 的延长线交AB 于F ,求证:AF = FB18、如图,∠B=900,AB=BE=EF=FC=1。
求证:ΔAEF ∽ΔCEA.19、如图,在梯形ABCD 中,AB ⊥BC ,∠BAD=90°,对角线BD ⊥DC 。
(1)△ABD 与△DCB 相似吗?请说明理由。
(2)如果AD=4,BC=9,求BD 的长。
20、已知:如图,在△PAB 中,∠APB=120O ,M 、N 是AB 上两点,且△PMN 是等边三角形。
求证: BM ·PA=PN ·BP21、如图,矩形ABCD 中,E 为BC 上一点,DF ⊥AE 于F.(1)ΔABE 与ΔADF 相似吗?请说明理由.(2)若AB=6,AD=12,BE=8,求DF 的长. 22、已知:如图,ΔABC 中,∠ACB=900,F 为AB 的中点,EF ⊥AB.求证:ΔCDF ∽ΔECF.23、如图:三角形ABC 是一快锐角三角形余料,边BC =120mm,高AD =80mm,要把它加工成正方形零件,是正方形的一边在BC 上,其余两个顶点分别在AB 、AC 上,这个正方形零件的边长是多少?24、已知:如图:FGHI 为矩形,AD ⊥BC 于D ,95=GH FG ,BC =36cm,AD =12cm 。
求:矩形FGNI 的周长。
25、如图ABC ∆中,边BC=60,高AD=40,EFGH 是内接矩形,HG 交AD 于P ,设HE=x, ⑴求矩形EFGH 的周长y 与x 的函数关系式; ⑵求矩形EFGH 的面积S 与x 的函数关系式。
26、已知:如图18—98,在△ABC 中,点D 、E 、F 分别在AC 、AB 、BC 边上,且四边形CDEF 是正方形,AC =3,BC =2,求△ADE、△EFB、△ACB 的周长之比和面积之比.(8分) 27、如图,正方形ABCD 中,E 是AD 的中点,DM ⊥CE,AB=6,求DM 的长。
28、已知:如图,在△PAB 中,∠APB=120O ,M 、N 是AB 上两点,且△PMN 是等边三角形。
求证: BM ·PA=PN ·BP29、己知:如图,AD 是ΔABC 的角平分线,EF 垂直平分AD 交BC 的延长线于F.求证:FD 2=FB ·FC. [提示:连结AF]30、已知:如图,ΔABC 中,∠ACB=900,CD ⊥AB,DE ⊥BC,AC=6,DE=4,求CD 和AB 的长31、如图,已知△ABC 中,D 为BC 中点,AD=AC ,DE ⊥BC ,DE 与AB 交于E ,EC 与AD 相交于点F ,△ABC 与△FCD 相似吗?请说明理由;32、已知:如图所示,D 是AC 上一点,BE//AC ,BE=AD ,AE 分别交BD 、BC 于点F 、G ,∠1=∠2。
则BF 是FG 、EF 的比例中项吗?请说明理由33、如图,已知△ABC 中,∠ACB=90°,AC=BC,点E 、F 在AB 上,∠ECF=45°.(1)求证:△ACF ∽BEC ;(2)设△ABC 的面积为S ,求证:AF ·BE=2S.34、如图,在中,过点B 作BE ⊥CD,垂足为E,连结AE,F 为AE 上一点,且∠BFE=∠C.(1)求证:△ABF ∽△EAD ;(2)若AB=4,∠BAE=30°,求AE 的长;(3)在(1)(2)的条件下,若AD=3,求BF 的长.35、如图,已知点E 是四边形ABCD 的对角线BD 上一点,且∠BAC=∠BDC=∠DAE.(1)求证:BE ·AD=CD ·AE ;(2)根据图形特点,猜想BCDE可能等于哪两条线段的比(只需写出图A DEBB C D A ECDA FE OB C DA E F45A EFB C A CEFDB2文档收集于互联网,已整理,word 版本可编辑.形中已有线段的一组比即可),并证明你的结论. 36、如图,在Rt△ABC 中,∠ACB=90°,CD ⊥AB,M 是CD 上的点,DH ⊥BM 于H,DH 的延长线交AC 的延长线于E.求证:(1)△AED ∽△CBM ;(2)AE ·CM=AC ·CD. 37、已知,如图,在△ABC 中,D 是BC 的中点,且AD=AC,DE ⊥BC 交AB 于点E,EC 与AD 相交于点F.(1)求证:△ABC ∽△FCD ;(2)若S △FCD =5,BC=10,求DE 的长. 38、已知:如图,D 是△ABC 的边AC 上一点,且CD=2AD ,AE ⊥BC 于E, 若BC=13,△BDC 的面积是39, 求AE 的长。
39、如图,正方形ABCD 的边长为2,AE=EB,MN=1,线段MN 的两端在BC 、CD 上,若△AED 与以M 、N 、C 为顶点的三角形相似,求CM 的长. 40、如图,等腰三角形ABC 中,AB=AC,D 为CB 延长线上一点,E 为BC 延长线上点,且满足AB 2=DB ·CE.(1)求证:△ADB ∽△EAC ;(2)若∠BAC=40°,求∠DAE 的度数 41、如图,在△ABC 中,∠BAC=90°D 为BC 的中点,AE ⊥AD,AE 交CB 的延长线于点E.(1)求证:△EAB ∽△ECA ;(2)△ABE 和△ADC 是否一定相似?如果相似,加以说明,如果不相似,那么增加一个怎样的条件, △ABE 和△ADC 一定相似. 42、如图,已知:DEBCAE AC AD AB ==,求证:BD AC CE AB ⋅=⋅ 43、如图,△ABC 中,三条内角平分线交于D ,过D 作AD 垂线,分别交AB 、AC 于M 、N ,请写出图中相似的三角形,并说明其中两对相似的正确性。
44、如图18—97,已知∠ACB=∠CBD=90°,AC =b ,CB =a ,当BD 与a 、b 之间满足怎样的关系式时,△ACB 与△CBD 相似?(6分) 45、如图18—102,已知:AB⊥DB 于B 点,CD⊥DB 于D 点,AB=6,CD =4,BD =14,问:在DB 上是否存在P 点,使以C 、D 、P 为顶点的三角形与以P 、B 、A 为顶点的三角形相似?如果存在,求DP 的长;如果不存在,说明理由.(10分)46、如图ΔABC 中,∠C=900, BC = 8cm, AC = 6cm,点P 从B 出发,沿BC 方向以2cm/s 的速度移动,点Q 从C 出发,沿CA 方向以1cm/s 的速度移动.若P 、Q 分别同时从B 、C 出发,经过多少时间以C 、P 、Q 为顶点的三角形与以C 、B 、A 为顶点的三角形相似..? 9分 47、如图,AD 为△ABC 的高,DE ⊥AB ,DF ⊥AC ,垂足分别为E 、F ,试判断∠ADF与∠AEF 的大小,并说明理由,48、已知:如图,CE 是Rt ΔABC 的斜边AB 上的高,BG ⊥AP. 求证:CE 2=ED ·EP. 49、如图,在正方形ABCD 中,E 是CD 的中点,EF ⊥AE. 求证:AE 2=AD ×AF. [提示:延长AE 、BC 交于G ,先证ΔADE ≌ΔGCE ,ΔGCE ∽ΔAEF] 50、已知: 如图,四边形ABCD 中,CB ⊥BA 于B ,DA ⊥BA 于A ,BC=2AD ,DE ⊥CD 交AB 于E ,连结CE ,求证:DE 2=AE •CE A B CE DM H K AB D ECF B CDM N E A AB CE D AB D E CE D CA。
