模型组合讲解——爆炸反冲模型
动量守恒之爆炸与反冲(火箭)模型高三物理一轮复习专题

一.必备知识精讲 1.反冲〔1〕定义:当物体的一局部以一定的速度离开物体时,剩余局部将获得一个反向冲量,这种现象叫反冲运动.〔2〕特点:系统内各物体间的相互作用的内力远大于系统受到的外力.实例:发射炮弹、发射火箭等.(3)规律:遵从动量守恒定律.(1)火箭加速的原理设火箭飞行时在极短的时间Δt 内喷射燃气的质量是Δm ,喷出的燃气相对喷气前火箭的速度是u ,喷出燃气后火箭的质量是m ,火箭在这样一次喷气后增加的速度为Δv 。
以喷气前的火箭为参考系。
喷气前火箭的动量是0,喷气后火箭的动量是m Δv ,燃气的动量是Δmu 。
根据动量守恒定律,喷气后火箭和燃气的总动量仍然为0,所以m Δv +Δmu =0, 解出Δv =-Δmmu 。
上式说明,火箭喷出的燃气的速度u 越大、火箭喷出物质的质量与火箭本身质量之比Δmm越大,火箭获得的速度Δv 越大。
(2)现代火箭的发射原理由于现代火箭喷气的速度在~4000 m/s ,近期内难以大幅度提高;火箭的质量比(火箭起飞时的质量与火箭除燃料外的箭体质量之比)一般要小于10,故为使火箭到达发射人造地球卫星的7.9 km/s 的速度,采用多级火箭,即把火箭一级一级地接在一起,第一级燃料用完之后就把箭体抛弃,减轻负担,然后第二级开始工作,这样一级一级地连起来,不过实际应用中一般不会超过四级。
〔3〕火箭获得的最终速度设火箭发射前的总质量为M 、燃料燃尽后的质量为m ,以地面为参考系,火箭燃气的喷射速度大小为v 1,燃料燃尽后火箭的飞行速度大小为v ,在火箭发射过程中,由于内力远大于外力,所以动量守恒。
发射前的总动量为0,发射后的总动量为(M -m )v 1-mv (以火箭的速度方向为正方向),那么:(M -m )v 1-mv =0,所以v =⎝⎛⎭⎪⎫Mm-1v 1,燃料燃尽时火箭获得的最终速度由喷气速度及质量比M m决定。
3.爆炸问题 动量守恒爆炸物体间的相互作用力远远大于受到的外力,所以在爆炸过程中,系二.典型例题精讲:题型一:爆炸类例1:(·全国卷Ⅰ)一质量为m 的烟花弹获得动能E 后,从地面竖直升空。
专题三 碰撞 爆炸和反冲
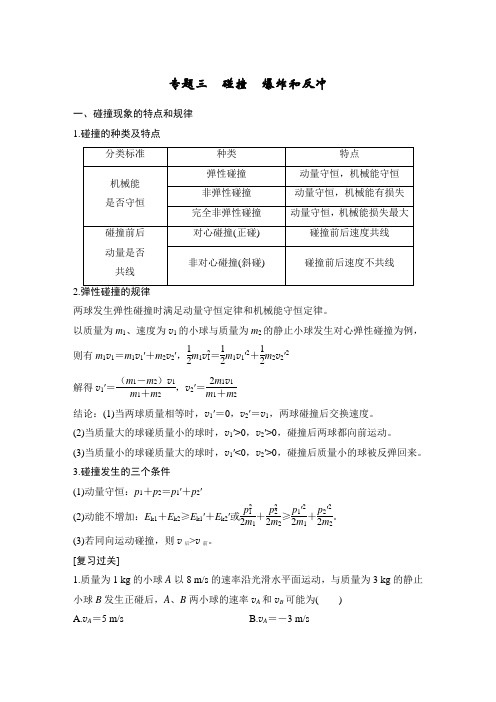
专题三碰撞爆炸和反冲一、碰撞现象的特点和规律1.碰撞的种类及特点2.两球发生弹性碰撞时满足动量守恒定律和机械能守恒定律。
以质量为m1、速度为v1的小球与质量为m2的静止小球发生对心弹性碰撞为例,则有m1v1=m1v1′+m2v2′,12m1v21=12m1v1′2+12m2v2′2解得v1′=(m1-m2)v1m1+m2,v2′=2m1v1m1+m2结论:(1)当两球质量相等时,v1′=0,v2′=v1,两球碰撞后交换速度。
(2)当质量大的球碰质量小的球时,v1′>0,v2′>0,碰撞后两球都向前运动。
(3)当质量小的球碰质量大的球时,v1′<0,v2′>0,碰撞后质量小的球被反弹回来。
3.碰撞发生的三个条件(1)动量守恒:p1+p2=p1′+p2′(2)动能不增加:E k1+E k2≥E k1′+E k2′或p212m1+p222m2≥p1′22m1+p2′22m2。
(3)若同向运动碰撞,则v后>v前。
[复习过关]1.质量为1 kg的小球A以8 m/s的速率沿光滑水平面运动,与质量为3 kg的静止小球B发生正碰后,A、B两小球的速率v A和v B可能为()A.v A=5 m/sB.v A=-3 m/sC.v B =1 m/sD.v B =6 m/s解析 若A 、B 发生弹性碰撞,则动量和机械能均守恒,m A v 0=m A v A +m B v B 及12m A v 20=12m A v 2A +12m B v 2B , 解得v A =m A -m B m A +m Bv 0=-4 m/s ,v B =2m A m A +m Bv 0=4 m/s 。
若A 、B 发生完全非弹性碰撞,则仅动量守恒,m A v 0=(m A +m B )v ,解得v =m Am A +m Bv 0=2 m/s 。
故A 的速度范围-4 m/s ≤v A ≤2 m/s ,小球B 的速度范围2 m/s ≤v B ≤4 m/s ,B 正确。
动量爆炸反冲模型32页PPT课件

D.两根导体棒和弹簧构成的系统动量 守恒、机械能不守恒
▲以初速度v0与水平方向成60°角斜向上抛出的手 榴弹,到达最高点时炸成质量分别为m和2m的两 块.其中质量大的一块沿着原来的方向以2v0 的速 度飞行.求
(1)喷出多少O2,宇航员才能安全返回飞船? (2)为了使总耗氧量最低,应该一次喷出多少氧气 ?返回时间是多少?
▲两位同学在公园里划船.租船时间将到,她们把小船 划向码头.当小船离码头大约2m左右时,有一位同学 心想:自己在体育课上立定跳远的成绩从未低于2m, 跳到岸上绝对没有问题.于是她纵身一跳,结果却掉到 了水里(如图).她为什么不能如她所想的那样跳到岸上 呢?(假设起跳时船已静止)
▲小车上装有一桶水,静止在光滑水平地面上,如图所 示,桶的前、后、底及侧面各装有一个阀门,分别为S1、 S2、S3、S4(图中未画出),要使小车向前运动,可采用的 方法是( ) A.打开阀门S1 B.打开阀门S2 C.打开阀门S3 D.打开阀门S4
▲运送人造地球卫星的火箭开始工作后,火箭做加速运 动的原因是( ) A.燃料燃烧推动空气,空气反作用力推动火箭 B.火箭发动机将燃料燃烧产生的气体向后推出,气体 的反作用力推动火箭
船s=45m处与飞船处于相对静止状态,他准备对太空中
的哈勃望远镜进行维修,宇航员背着装有质量为m0= 0.5kg的O2贮气筒,筒内有一个可以使O2以v=50m/s的速 度喷出的喷嘴.宇航员在维修完毕哈勃望远镜后,必须
向着返回飞船方向的反方向释放O2,才能回到飞船,同 时又必须保留一部分O2供途中宇航员呼吸之用,宇航员 的耗氧率为Q=2.5×10-4kg/s,如果不考虑喷出O2对设 备与宇航员总质量的影响,则:
动量守恒的条件 爆炸、反冲运动 人船模型(附精品解析)

动量守恒的条件爆炸、反冲运动人船模型考点一动量守恒的条件考点二爆炸、反冲运动考点三人船模型考点四连续射击问题1.动量守恒定律内容:如果一个系统不受外力,或者所受外力的矢量和为0,这个系统的总动量保持不变。
2.动量守恒定律常用表达式:m1v1+m2v2=m1v1′+m2v2′.1)p=p′:相互作用前系统的总动量p等于相互作用后的总动量p′.2)m1v1+m2v2=m1v1′+m2v2′:相互作用的两个物体组成的系统,作用前动量的矢量和等于作用后动量的矢量和.3)Δp1=-Δp2:相互作用的两个物体组成的系统,一个物体的动量变化量与另一个物体的动量变化量大小相等、方向相反.4)Δp=0:系统总动量增量为零.考点一动量守恒的条件⑴系统不受外力或者所受外力之和为零;⑵系统受外力,但外力远小于内力,可以忽略不计;⑶系统在某一个方向上所受的合外力为零,则该方向上动量守恒。
⑷全过程的某一阶段系统受的合外力为零,则该阶段系统动量守恒。
附:机械能守恒的条件:只有重力、系统内弹力做功.1.下列四幅图所反映的物理过程中,说法正确的是()A.甲图中子弹射入木块过程中,子弹和木块组成系统动量守恒,能量不守恒B.乙图中M、N两木块放在光滑水平面上,剪断束缚M、N的细线,在弹簧从压缩状态恢复原长过程中,M、N与弹簧组成的系统动量不守恒,机械能守恒C.丙图中细线断裂后,木球和铁球在水中运动的过程,两球组成的系统动量不守恒,机械能守恒D.丁图中木块沿光滑固定斜面下滑,木块和斜面组成的系统动量守恒,机械能守恒2.如图所反映的物理过程中,以物体A和物体B为一个系统符合系统机械能守恒且水平方向动量守恒的是()A.甲图中,在光滑水平面上,物块B以初速度v0滑上上表面粗糙的静止长木板AB.乙图中,在光滑水平面上,物块B以初速度v0滑下靠在墙边的表面光滑的斜面AC.丙图中,在光滑水平上面有两个带正电的小球A、B相距一定的距离,从静止开始释放D.丁图中,在光滑水平面上物体A以初速度v0滑上表面光滑的圆弧轨道B3.(多选)如图所示,A、B两物体质量之比为m A∶m B=3∶2,原来静止在足够长的平板小车C上,A、B间有一根被压缩的弹簧,地面光滑.当两物体被同时释放后,则( )A.若A、B与平板车上表面间的动摩擦因数相同,则A、B组成系统的动量守恒B.若A、B与平板车上表面间的动摩擦因数相同,则A、B、C组成系统的动量守恒C.若A、B所受的摩擦力大小相等,则A、B组成系统的动量守恒D.若A、B所受的摩擦力大小相等,则A、B、C组成系统的动量守恒4. (2021·全国乙卷·T14)如图,光滑水平地面上有一小车,一轻弹簧的一端与车厢的挡板相连,另一端与滑块相连,滑块与车厢的水平底板间有摩擦。
2022年高考物理模型专题突破-动量守恒中的“碰撞模型”和“反冲模型

真题模型——动量守恒中的“碰撞模型”和“反冲模型”来源图例考向模型核心归纳2015·新课标全国卷Ⅰ物体A、B、C位于同一直线上动量守恒、机械能守恒、“多物体作用模型”1.常考的模型(1)碰撞中的“两物体作用模型”(2)碰撞中的“多物体作用模型”(3)碰撞中的“图象类问题模型”(4)“反冲模型”(5)“爆炸模型”2.模型解法(1)牢记一个定律:动量守恒定律m1v1+m2v2=m1v1′+m2v2′。
(2)熟记两种碰撞①弹性碰撞:动量守恒和机械能守恒。
②非弹性碰撞:动量守恒、机械能不守恒。
(3)会用两个结论①“一动一静”两物体发生弹性正碰后的速度满足v1=m1-m2m1+m2v0,v2=2015·新课标全国卷Ⅱ滑块a、b沿水平面上同一条直线运动动量守恒、能量守恒(功能关系)2016·新课标全国卷Ⅱ光滑冰面上静止放置一表面光滑的斜面体,一蹲在滑板上的小孩和冰块均静止于冰面上动量守恒、机械能守恒2016·新课标全国卷Ⅲ静止的a和b相距l;b与墙也相距l 动量守恒、机械能守恒、功能关系2017·全国卷Ⅰ模型火箭点火升空动量守恒2m1m1+m2v0。
②质量相等的两物体发生弹性碰撞后交换速度;发生完全非弹性碰撞后两物体共速。
【预测1】如图14所示,在光滑的水平面上,有A、B、C三个物体,开始B、C皆静止且C在B上,A物体以v0=10 m/s的速度撞向B物体,已知碰撞时间极短,撞完后A物体静止不动,而B、C最终的共同速度为4 m/s。
已知B、C 两物体的质量分别为m B=4 kg、m C=1 kg。
图14(1)求A物体的质量;(2)A、B间的碰撞是否造成了机械能损失?如果造成了机械能损失,则损失了多少?解析(1)设B、C最终的共同速度为v,则由整个过程动量守恒可得:m A v0=(m B+m C)v代入数据解得m A=2 kg。
(2)设A与B碰撞后B的速度变为v′,在B与C相互作用的时间里,B与C组成的系统动量守恒,即m B v′=(m B+m C)v,解得v′=5 m/sA与B碰撞的过程中,碰前系统的动能为E k1=12m A v2,代入数据解得E k1=100 J碰后系统的动能为E k2=12m B v′2,代入数据解得E k2=50 J所以碰撞过程中损失了机械能,损失了50 J 。
爆炸、反冲及人船模型(解析版)
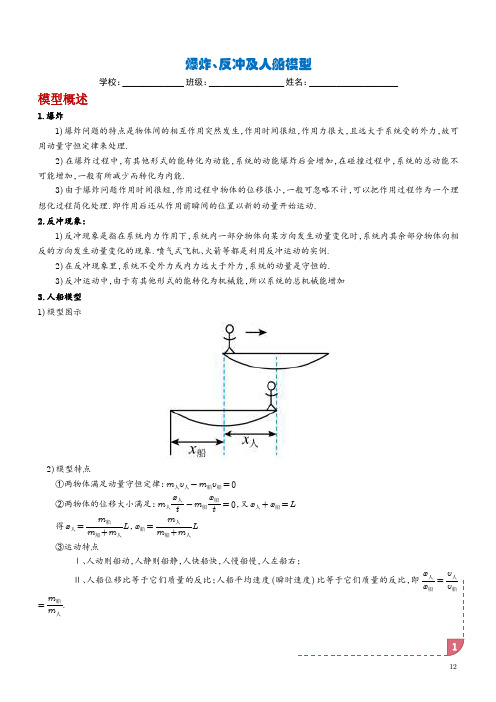
爆炸、反冲及人船模型学校:_________班级:___________姓名:_____________模型概述1.爆炸1)爆炸问题的特点是物体间的相互作用突然发生,作用时间很短,作用力很大,且远大于系统受的外力,故可用动量守恒定律来处理.2)在爆炸过程中,有其他形式的能转化为动能,系统的动能爆炸后会增加,在碰撞过程中,系统的总动能不可能增加,一般有所减少而转化为内能.3)由于爆炸问题作用时间很短,作用过程中物体的位移很小,一般可忽略不计,可以把作用过程作为一个理想化过程简化处理.即作用后还从作用前瞬间的位置以新的动量开始运动.2.反冲现象:1)反冲现象是指在系统内力作用下,系统内一部分物体向某方向发生动量变化时,系统内其余部分物体向相反的方向发生动量变化的现象.喷气式飞机、火箭等都是利用反冲运动的实例.2)在反冲现象里,系统不受外力或内力远大于外力,系统的动量是守恒的.3)反冲运动中,由于有其他形式的能转化为机械能,所以系统的总机械能增加3.人船模型1)模型图示2)模型特点①两物体满足动量守恒定律:m人v人-m船v船=0②两物体的位移大小满足:m人x人t-m船x船t=0,又x人+x船=L得x人=m船m船+m人L,x船=m人m船+m人L③运动特点Ⅰ、人动则船动,人静则船静,人快船快,人慢船慢,人左船右;Ⅱ、人船位移比等于它们质量的反比;人船平均速度(瞬时速度)比等于它们质量的反比,即x人x船=v人v船=m船m人.典题攻破1.爆炸1.(2024·青海海南·二模)斜向上发射的炮弹在最高点爆炸(爆炸时间极短)成质量均为m 的两块碎片,其中一块碎片沿原路返回。
已知炮弹爆炸时距地面的高度为H ,炮弹爆炸前的动能为E ,重力加速度大小为g ,不计空气阻力和火药的质量,则两块碎片落地点间的距离为()A.2EHmgB.22EH mgC.23EH mgD.42EH mg【答案】D【详解】火箭炸裂的过程水平方向动量守恒,设火箭炸裂前的速度大小为v ,则E =122mv 2得v =Em设炸裂后瞬间另一块碎片的速度大小为v 1,有2mv =-mv +mv 1解得v 1=3Em根据平抛运动规律有H =12gt 2得t =2H g两块碎片落地点之间的距离x =(v +v 1)t =42EH mg故D 。
高中物理模型—爆炸反冲模型

高中物理模型——爆炸反冲模型[模型概述]“爆炸反冲”模型是动量守恒的典型应用,其变迁形式也多种多样,如炮发炮弹中的化学能转化为机械能;弹簧两端将物块弹射将弹性势能转化为机械能;核衰变时将核能转化为动能等。
[模型讲解]例. 如图所示海岸炮将炮弹水平射出,炮身质量(不含炮弹)为M ,每颗炮弹质量为m ,当炮身固定时,炮弹水平射程为s ,那么当炮身不固定时,发射同样的炮弹,水平射程将是多少?解析:两次发射转化为动能的化学能E 是相同的。
第一次化学能全部转化为炮弹的动能;第二次化学能转化为炮弹和炮身的动能,而炮弹和炮身水平动量守恒,由动能和动量的关系式mp E k 22=知,在动量大小相同的情况下,物体的动能和质量成反比,炮弹的动能E mM M mv E E mv E +====2222112121,,由于平抛的射高相等,两次射程的比等于抛出时初速度之比,即:mM M v v s s +==122,所以m M M s s 2+=。
思考:有一辆炮车总质量为M ,静止在水平光滑地面上,当把质量为m 的炮弹沿着与水平面成θ角发射出去,炮弹对地速度为0v ,求炮车后退的速度。
提示:系统在水平面上不受外力,故水平方向动量守恒,炮弹对地的水平速度大小为θcos 0v ,设炮车后退方向为正方向,则mM mv v mv v m M -==--θθcos 0cos )(00, 评点:有时应用整体动量守恒,有时只应用某部分物体动量守恒,有时分过程多次应用动量守恒,有时抓住初、末状态动量即可,要善于选择系统,善于选择过程来研究。
[模型要点]内力远大于外力,故系统动量守恒21p p =,有其他形式的能单向转化为动能。
所以“爆炸”时,机械能增加,增加的机械能由化学能(其他形式的能)转化而来。
[误区点拨]忽视动量守恒定律的系统性、忽视动量守恒定律的相对性、同时性。
[模型演练](2005年物理高考科研测试)在光滑地面上,有一辆装有平射炮的炮车,平射炮固定在炮车上,已知炮车及炮身的质量为M ,炮弹的质量为m ;发射炮弹时,炸药提供给炮身和炮弹的总机械能E 0是不变的。
高考物理一轮复习课件第3讲第1课时动量守恒的常见模型反冲爆炸人船子弹打木块滑块与弹簧板块模型

知识回顾
三、人船模型
如图所示,两个原来静止的物体发生相互作用时,若所受外力的矢量和为零,则动量 守恒,在相互作用的过程中,任一时刻两物体的速度大小之比等于质量的反比。这样 的问题归为“人船”模型问题 模型构建
两物体满足动量守恒定律:m1v1-m2v2=0 模型特点
七、板块模型
谢 谢 大
家
(1)B、C第一次碰撞后,C的速度大小vC; (2)弹簧具有的最大弹性势能Ep; (3)整个运动过程中,B的动量变化量的大小Δp。
知识回顾
六、物块-斜面模型
模型图示
物块m从光滑的水平地面上滑到光滑的斜面体M(或曲面体)上,上升到最高点,又 模型特点
滑离斜面体。 (1)物块m和斜面体M组成的系统满足:①水平方向上动量守恒,②机械能守恒 模型规律 (2)物块滑到斜面体最高点:物块和斜面体有共同速度。(原因:物块参与了两 个分运动)
四、子弹打木块模型
【典例4】质量为m的子弹以某一初速度v0击中静止在光滑水平地面上质量为M的木块, 并陷入木块一定深度后与木块相对静止。甲、乙两图表示了这一过程开始和结束时子 弹和木块可能的相对位置,设木块对子弹的阻力大小恒定,下列说法正确的是( C )
A.M越大,子弹射入木块的时间越短 B.M越大,子弹射入木块的深度越浅
当弹簧恢复原长时,m1和m2两物体组成的系统没有机械能损失,系统机械能 守恒。此时,可看成m1和m2两物体发生弹性碰撞。 (2)对m1、弹簧和m2三者组成的系统,全过程系统动量守恒,系统机械能守恒。
五、弹簧-滑块模型
【典例5】如图所示,足够长的光滑水平直轨道上有物块A、B、C,质量分别为2m、m、m,B 的左侧固定一轻弹簧(不与A固定),A、B共同以速度v0向C运动,弹簧处于原长,C静止,B、C 间发生弹性碰撞。求:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
模型组合讲解——爆炸反冲模型
[模型概述]
“爆炸反冲”模型是动量守恒的典型应用,其变迁形式也多种多样,如炮发炮弹中的化学能转化为机械能;弹簧两端将物块弹射将弹性势能转化为机械能;核衰变时将核能转化为动能等。
[模型讲解]
例. 如图所示海岸炮将炮弹水平射出,炮身质量(不含炮弹)为M ,每颗炮弹质量为m ,当炮身固定时,炮弹水平射程为s ,那么当炮身不固定时,发射同样的炮弹,水平射程将是多少?
解析:两次发射转化为动能的化学能E 是相同的。
第一次化学能全部转化为炮弹的动能;第二次化学能转化为炮弹和炮身的动能,而炮弹和炮身水平动量守恒,由动能和动量的关系式m
p E k 22
=知,在动量大小相同的情况下,物体的动能和质量成反比,炮弹的动能E m
M M mv E E mv E +====2222112121,,由于平抛的射高相等,两次射程的比等于抛出时初速度之比,即:m M M v v s s +==122,所以m
M M s s 2+=。
思考:有一辆炮车总质量为M ,静止在水平光滑地面上,当把质量为m 的炮弹沿着与水平面成θ角发射出去,炮弹对地速度为0v ,求炮车后退的速度。
提示:系统在水平面上不受外力,故水平方向动量守恒,炮弹对地的水平速度大小为θcos 0v ,设炮车后退方向为正方向,则m
M mv v mv v m M -==--θθcos 0cos )(00, 评点:有时应用整体动量守恒,有时只应用某部分物体动量守恒,有时分过程多次应用动量守恒,有时抓住初、末状态动量即可,要善于选择系统,善于选择过程来研究。
[模型要点]
内力远大于外力,故系统动量守恒21p p =,有其他形式的能单向转化为动能。
所以“爆炸”时,机械能增加,增加的机械能由化学能(其他形式的能)转化而来。
[误区点拨]
忽视动量守恒定律的系统性、忽视动量守恒定律的相对性、同时性。
[模型演练]
(2005年物理高考科研测试)在光滑地面上,有一辆装有平射炮的炮车,平射炮固定在炮车上,已知炮车及炮身的质量为M ,炮弹的质量为m ;发射炮弹时,炸药提供给炮身和炮弹的总机械能E 0是不变的。
若要使刚发射后炮弹的动能等于E 0,即炸药提供的能量全部变为炮弹的动能,则在发射前炮车应怎样运动?
答案:若在发射前给炮车一适当的初速度v 0,就可实现题述的要求。
在这种情况下,用v 表示发射后炮弹的速度,V 表示发射后炮车的速度,由动量守恒可知:
><+=+1)(0MV mv v M m 由能量关系可知: ><+=++221
21)(21
22020MV mv E v M m 按题述的要求应有><=321
02E mv
由以上各式得:
><++++=+-+=4)
()
)((2)()(2000m M m m M M m M mE M m M M m mE v 作者:高志勇。
