模型组合讲解——弹簧模型(动力学问题)
弹簧问题模型PPT优秀课件
2021/6/3
A v0
B
6
4.两物块A、B用轻弹簧相连， A、C质量均 为2m，B质量4m,初始时A、B用一根轻绳压 缩并以V0运动，某时刻绳断开，A、B被弹 开，B与C碰撞后二者会粘在一起运动，最 终三则速度相同。求在以后的运动中：
(1)、碰后BC的速度 (2)、原系统中弹性势能的是多少?
2021/6/3
x0
自由落下，则物块与钢板回到O点
时，还具有向上的速度。求物块向
上运动到达的最高点与O点的距离。
图3
2021/6/3
9
部分资料从网络收集整 理而来，供大家参考，
感谢您的关注！
8
6：质量为m的钢板与直立轻弹簧的上端连接，
弹簧下端固定在地上。平衡时，弹簧的压缩量
为x0，如图3所示。一物块从钢板正上方距离为 3x0的A处自由落下，打在钢板上并立刻与
钢板一起向下运动，但不粘连。它
们到达最低点后又向上运动。已知
A
物块质量也为m时，它们恰能回到 3x0 O
O点。若物块质量为2m，仍从A处
弹簧问题中的能量与动量
2021/6/3
1
在如图1所示的装置中，木块B与水平桌面间的接 触是光滑的，子弹A沿水平方向射入木块后，留在 木块内，将弹簧压缩到最短。若木块的质量为M， 子弹的质量为m，弹簧为轻质弹簧，子弹以速度 v0射入木块B后能在极短时间内达到共同速度。求 弹簧的最大弹性势能。
2021/6/3
B 图1
A
2
例2：如图2所示，轻弹簧的一端固定，另一端与
滑块B相连，B静止在水平导轨上，弹簧处在原长
状态。另一质量与B相同的滑块A，从导轨上的P点
以某一初速度向B滑行，当A滑过距离L1时，与B相 碰，碰撞时间极短，碰后B紧贴在一起运动，但互
弹簧问题（动力学）
弹簧问题（动力学）知识升华一、弹簧的弹力1、弹簧弹力的大小弹簧弹力的大小由胡克定律给出，胡克定律的内容是：在弹性限度内，弹力的大小与弹簧的形变量成正比。
数学表达形式是：F=kx 其中k是一个比例系数，叫弹簧的劲度系数。
说明：①弹力是一个变力，其大小随着弹性形变的大小而变化，还与弹簧的劲度系数有关；②弹簧具有测量功能，利用在弹性限度内，弹簧的伸长（或压缩）跟外力成正比这一性质可制成弹簧秤。
2、弹簧劲度系数弹簧的力学性质用劲度系数描写，劲度系数的定义因弹簧形式的不同而不同，以下主要讨论螺旋式弹簧的劲度系数。
（1）定义：在弹性限度内，弹簧产生的弹力F（也可认为大小等于弹簧受到的外力）和弹簧的形变量（伸长量或者压缩量）x的比值，也就是胡克定律中的比例系数k。
（2）劲度系数的决定因素：劲度系数的大小由弹簧的尺寸和绕制弹簧的材料决定。
弹簧的直径越大、弹簧越长越密、绕制弹簧的金属丝越软越细时，劲度系数就越小，反之则越大。
如两根完全相同的弹簧串联起来，其劲度系数只是一根弹簧劲度系数的一半，这是因为弹簧的长度变大的缘故；若两根完全相同的弹簧并联起来，其劲度系数是一根弹簧劲度系数的两倍，这是相当于弹簧丝变粗所导致；二、轻质弹簧的一些特性轻质弹簧：所谓轻质弹簧就是不考虑弹簧本身的质量和重力的弹簧，是一个理想化的模型。
由于它不需要考虑自身的质量和重力对于运动的影响，因此运用这个模型能为分析解决问题提供很大的方便。
性质1、轻弹簧在力的作用下无论是平衡状态还是加速运动状态，各个部分受到的力大小是相同的。
其伸长量等于弹簧任意位置受到的力和劲度系数的比值。
如图1和2中相同的轻弹簧，其端点受到相同大小的力时，无论弹簧是处于静止、匀速还是加速运动状态，各个弹簧的伸长量都是相同的。
性质2、两端与物体相连的轻质弹簧上的弹力不能在瞬间变化——弹簧缓变特性；有一端不与物体相连的轻弹簧上的弹力能够在瞬间变化为零。
如在图1、2、3、4、中撤出任何一个力的瞬间，弹簧的长度不会变化，弹力的大小也不会变化；但是在图5中撤出力F的瞬时，弹簧恢复原长，弹力变为零。
高中物理二轮专题——弹簧模型(解析版)
高中物理第二轮专题——弹簧模型高考分析：轻弹簧就就是一种理想化得物理模型，以轻质弹簧为载体,设置复杂得物理情景,考查力得概念,物体得平衡,牛顿定律得应用及能得转化与守恒,就就是高考命题得重点,此类命题几乎每年高考卷面均有所见、由于弹簧弹力就就是变力,学生往往对弹力大小与方向得变化过程缺乏清晰得认识,不能建立与之相关得物理模型并进行分类,导致解题思路不清、效率低下、错误率较高、在具体实际问题中,由于弹簧特性使得与其相连物体所组成系统得运动状态具有很强得综合性与隐蔽性，加之弹簧在伸缩过程中涉及力与加速度、功与能等多个物理概念与规律,所以弹簧类问题也就成为高考中得重、难、热点、我们应引起足够重视、弹簧类命题突破要点:１、弹簧得弹力就就是一种由形变而决定大小与方向得力、当题目中出现弹簧时，要注意弹力得大小与方向时刻要与当时得形变相对应、在题目中一般应从弹簧得形变分析入手,先确定弹簧原长位置，现长位置,找出形变量ｘ与物体空间位置变化得几何关系,分析形变所对应得弹力大小、方向,以此来分析计算物体运动状态得可能变化、2、因弹簧(尤其就就是软质弹簧)其形变发生改变过程需要一段时间，在瞬间内形变量可以认为不变、因此,在分析瞬时变化时，可以认为弹力大小不变,即弹簧得弹力不突变、３、在求弹簧得弹力做功时,因该变力为线性变化，可以先求平均力，再用功得定义进行计算,也可据动能定理与功能关系:能量转化与守恒定律求解、同时要注意弹力做功得特点:Ｗ=-(kx2２－kｘ12）,弹力得功等于弹性势能增量得负值或弹力得功等于弹性势能得减少、弹性势k能得公式Eｐ=ｋx２,高考不作定量要求,该公式通常不能直接用来求弹簧得弹性势能,只可作定性讨论、因此,在求弹力得功或弹性势能得改变时，一般以能量得转化与守恒得角度来求解、一、“轻弹簧”类问题在中学阶段,凡涉及得弹簧都不考虑其质量,称之为“轻弹簧”，就就是一种常见得理想化物理模型、由于“轻弹簧”质量不计,选取任意小段弹簧,其两端所受张力一定平衡,否则，这小段弹簧得加速度会无限大、故簧轻弹簧中各部分间得张力处处相等,均等于弹簧两端得受力、弹一端受力为,另一端受力一定也为。
专题16 动力学动态分析、动力学图像问题(解析版)
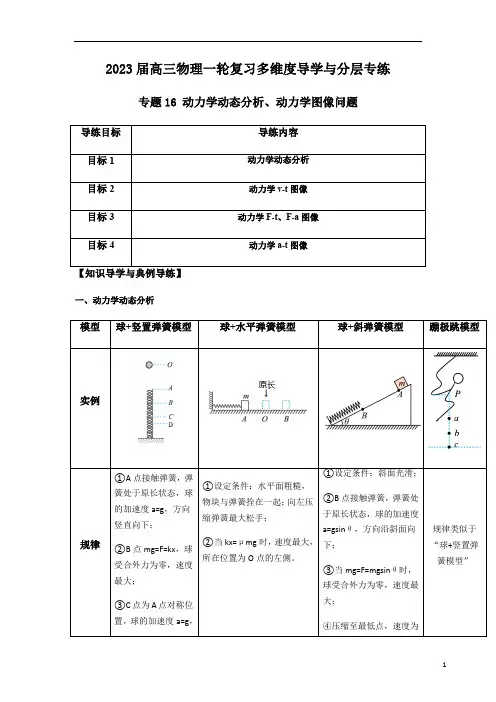
2023届高三物理一轮复习多维度导学与分层专练专题16 动力学动态分析、动力学图像问题 导练目标导练内容 目标1动力学动态分析 目标2动力学v -t 图像 目标3动力学F -t 、F -a 图像 目标4动力学a -t 图像一、动力学动态分析 模型球+竖置弹簧模型球+水平弹簧模型 球+斜弹簧模型 蹦极跳模型 实例规律 ①A 点接触弹簧，弹簧处于原长状态，球的加速度a=g ，方向竖直向下； ②B 点mg=F=kx ，球受合外力为零，速度最大； ③C 点为A 点对称位置，球的加速度a=g ，①设定条件：水平面粗糙，物块与弹簧拴在一起；向左压缩弹簧最大松手； ②当kx=μmg 时，速度最大，所在位置为O 点的左侧。
①设定条件：斜面光滑；②B 点接触弹簧，弹簧处于原长状态，球的加速度a=gsin θ，方向沿斜面向下；③当mg=F=mgsin θ时，球受合外力为零，速度最大；④压缩至最低点，速度为规律类似于“球+竖置弹簧模型”方向竖直向上； ④D 点为最低点，速度为零，加速度a>g ，方向竖直向上。
零，加速度a>gsin θ，方向斜面向上。
【例1】如图，小球自a 点由静止自由下落，到b 点时与弹簧接触，到c 点时弹簧被压缩到最短，若不计弹簧质量和空气阻力，在小球由c →b 的运动过程中，下列说法正确的是（ ）A ．小球的机械能守恒B ．小球的动能一直增加C ．小球的加速度随时间减少D ．小球动能的增加量小于弹簧弹性势能的减少量【答案】D【详解】A ．在弹簧、小球和地球组成的系统中，重力势能、动能、弹性势能相互转化，机械能总量守恒，A 错误；B ．小球由c →b 的运动过程中，小球先向上加速，当重力等于弹力时，加速度减小到零，速度达到最大，此后向上减速运动，则小球的动能先增大后减小，故B 错误；C ．小球由c→b 的运动过程为先加速后减速，加速度先向上减小到零，后变为向下逐渐增大，故C 错误；D ．小球由c →b 的运动过程，重力势能和动能增加，弹簧的弹性势能减小，由能量守恒定律可知pk k pG ΔΔΔE E E =+则有pk pG ΔΔE E >，pk k ΔΔE E >小球动能的增加量小于弹簧弹性势能的减少量，故D 正确；【例2】如图所示，弹簧左端固定，右端自由伸长到O点并系住物体m，现将弹簧压缩到A 点，然后释放，物体一直可以运动到B点，如果物体受到的摩擦力恒定，则（）A．物体从A到O加速，从O到B减速B．物体从A到O速度越来越小，从O到B加速度不变C．物体从A到O间先加速后减速，从O到B一直减速运动D．物体运动到O点时所受合力为零【答案】C【详解】D．物体在运动过程中，一直受到摩擦力的作用，在O点时，弹簧弹力为零，但仍受摩擦力作用，合力不为零，D错误；ABC．物体从A到O过程中，存在某个位置弹簧弹力等于摩擦力。
弹簧模型中的静力学与动力学问题
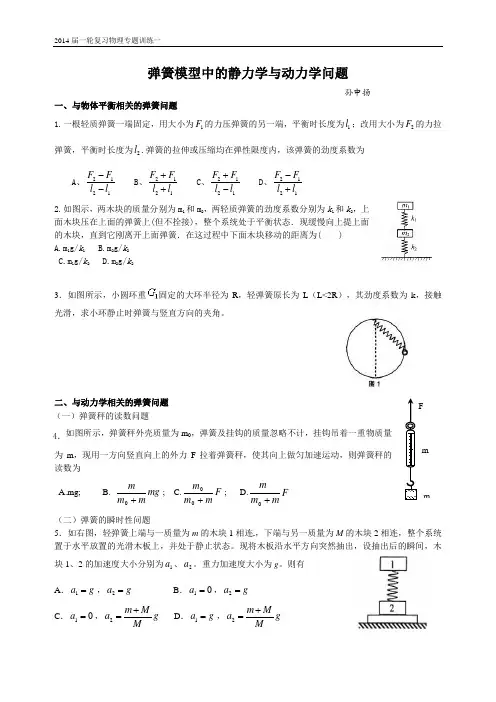
弹簧模型中的静力学与动力学问题孙中扬一、与物体平衡相关的弹簧问题1.一根轻质弹簧一端固定，用大小为1F 的力压弹簧的另一端，平衡时长度为1l ；改用大小为2F 的力拉弹簧，平衡时长度为2l .弹簧的拉伸或压缩均在弹性限度内，该弹簧的劲度系数为A 、2121F F l l --B 、2121F F l l ++C 、2121F F l l +-D 、2121F F l l -+2.如图示，两木块的质量分别为m 1和m 2，两轻质弹簧的劲度系数分别为k 1和k 2，上面木块压在上面的弹簧上(但不拴接)，整个系统处于平衡状态．现缓慢向上提上面的木块，直到它刚离开上面弹簧．在这过程中下面木块移动的距离为( )A.m 1g/k 1B.m 2g/k 2C.m 1g/k 2D.m 2g/k 23．如图所示，小圆环重固定的大环半径为R ，轻弹簧原长为L （L<2R ），其劲度系数为k ，接触光滑，求小环静止时弹簧与竖直方向的夹角。
二、与动力学相关的弹簧问题（一）弹簧秤的读数问题4．如图所示，弹簧秤外壳质量为m 0，弹簧及挂钩的质量忽略不计，挂钩吊着一重物质量为m ，现用一方向竖直向上的外力F 拉着弹簧秤，使其向上做匀加速运动，则弹簧秤的读数为 A.mg; B. mg mm m +0; C.F m m m +00; D.F m m m +0 （二）弹簧的瞬时性问题5．如右图，轻弹簧上端与一质量为m 的木块1相连，下端与另一质量为M 的木块2相连，整个系统置于水平放置的光滑木板上，并处于静止状态。
现将木板沿水平方向突然抽出，设抽出后的瞬间，木块1、2的加速度大小分别为1a 、2a 。
重力加速度大小为g 。
则有A ．1a g =，2a g =B ．10a =，2a g =C ．10a =，2m M a g M +=D ．1a g =，2m M a g M+=m m（三）弹簧的动态问题6.如图所示，轻质弹簧上面固定一块质量不计的薄板，在薄板上放重物，用手将重物向下压缩到一定程度后，突然将手撤去，则重物将被弹簧弹射出去，则在弹射过程中(重物与弹簧脱离之前)重物的运动情况是 ( )A.一直加速运动 B ．匀加速运动C.先加速运动后减速运动 D ．先减速运动后加速运动7.如图所示，一轻质弹簧一端系在墙上的O 点，自由伸长到B 点．今用一小物体m 把弹簧压缩到A 点，然后释放，小物体能运动到C 点静止，物体与水平地面间的动摩擦因数恒定，试判断下列说法正确的是( )A.物体从A 到B 速度越来越大，从B 到C速度越来越小B.物体从A 到B 速度越来越小，从B 到C加速度不变C.物体从A 到B 先加速后减速，从B 一直减速运动D.物体在B 点受到的合外力为零（四）.弹簧的对称性问题（弹簧振子）8.如图所示，在重力场中，将一只轻质弹簧的上端悬挂在天花板上，下端连接一个质量为M 的木板，木板下面再挂一个质量为m 的物体．当剪掉m 后发现：当木板的速率再次为零时，弹簧恰好能恢复到原长，(不考虑剪断后m 、M 间的相互作用)则M 与m 之间的关系必定为 ( )A.M>mB.M=mC.M<mD.不能确定9．如图所示，轻弹簧的一端固定在地面上，另一端与木块B 相连，木块A 放在木块B 上，两木块质量均为m ，在木块A 上施有竖直向下的力F ，整个装置处于静止状态．（1）突然将力F 撤去，若运动中A 、B 不分离，则A 、B 共同运动到最高点时，B 对A 的弹力有多大？（2）要使A 、B 不分离，力F 应满足什么条件？10．如图所示，一劲度系数为k =800N/m 的轻弹簧两端各焊接着两个质量均为m =12kg 的物体A 、B 。
2020高三物理模型组合讲解——水平方向上的碰撞+弹簧模型
2020高三物理模型组合讲解——水平方向上的碰撞+弹簧模型车晓红［模型概述］在应用动量守恒、机械能守恒、功能关系和能量转化等规律考查学生的综合应用能力时，常有一类模型，确实是有弹簧参与，因弹力做功的过程中弹力是个变力，并与动量、能量联系，因此分析解决这类咨询题时，要细致分析弹簧的动态过程，利用动能定理和功能关系等知识解题。
［模型讲解］一、光滑水平面上的碰撞咨询题例1. 在光滑水平地面上有两个相同的弹性小球A 、B ，质量都为m ，现B 球静止，A 球向B 球运动，发生正碰。
碰撞过程中总机械能守恒，两球压缩最紧时的弹性势能为E P ，那么碰前A 球的速度等于〔 〕A.mE PB.mE P2 C. mE P2D. mE P22解析：设碰前A 球的速度为v 0，两球压缩最紧时的速度为v ，依照动量守恒定律得出mv mv 20=，由能量守恒定律得220)2(2121v m E mv P +=，联立解得m E v P 20=，因此正确选项为C 。
二、光滑水平面上有阻挡板参与的碰撞咨询题例2. 在原子核物理中，研究核子与核子关联的最有效途径是〝双电荷交换反应〞。
这类反应的前半部分过程和下述力学模型类似，两个小球A 和B 用轻质弹簧相连，在光滑的水平直轨道上处于静止状态，在它们左边有一垂直于轨道的固定挡板P ，右边有一小球C 沿轨道以速度v 0射向B 球，如图1所示，C 与B 发生碰撞并赶忙结成一个整体D ，在它们连续向左运动的过程中，当弹簧长度变到最短时，长度突然被锁定，不再改变，然后，A 球与挡板P 发生碰撞，碰后A 、D 都静止不动，A 与P 接触而不粘连，过一段时刻，突然解除锁定〔锁定及解除锁定均无机械能缺失〕，A 、B 、C 三球的质量均为m 。
图1〔1〕求弹簧长度刚被锁定后A 球的速度。
〔2〕求在A 球离开挡板P 之后的运动过程中，弹簧的最大弹性势能。
解析：〔1〕设C 球与B 球粘结成D 时，D 的速度为v 1，由动量守恒得10)(v m m mv +=当弹簧压至最短时，D 与A 的速度相等，设此速度为v 2，由动量守恒得2132mv mv =，由以上两式求得A 的速度0231v v =。
高中物理二轮专题——弹簧模型(解析版)
资料范本本资料为word版本，可以直接编辑和打印，感谢您的下载高中物理二轮专题——弹簧模型(解析版)地点：__________________时间：__________________说明：本资料适用于约定双方经过谈判，协商而共同承认，共同遵守的责任与义务，仅供参考，文档可直接下载或修改，不需要的部分可直接删除，使用时请详细阅读内容高中物理第二轮专题——弹簧模型高考分析：轻弹簧是一种理想化的物理模型，以轻质弹簧为载体，设置复杂的物理情景，考查力的概念，物体的平衡，牛顿定律的应用及能的转化与守恒，是高考命题的重点，此类命题几乎每年高考卷面均有所见.由于弹簧弹力是变力，学生往往对弹力大小和方向的变化过程缺乏清晰的认识，不能建立与之相关的物理模型并进行分类，导致解题思路不清、效率低下、错误率较高.在具体实际问题中，由于弹簧特性使得与其相连物体所组成系统的运动状态具有很强的综合性和隐蔽性，加之弹簧在伸缩过程中涉及力和加速度、功和能等多个物理概念和规律，所以弹簧类问题也就成为高考中的重、难、热点.我们应引起足够重视.弹簧类命题突破要点：1.弹簧的弹力是一种由形变而决定大小和方向的力.当题目中出现弹簧时，要注意弹力的大小与方向时刻要与当时的形变相对应.在题目中一般应从弹簧的形变分析入手，先确定弹簧原长位置，现长位置，找出形变量x与物体空间位置变化的几何关系，分析形变所对应的弹力大小、方向，以此来分析计算物体运动状态的可能变化.2.因弹簧（尤其是软质弹簧）其形变发生改变过程需要一段时间，在瞬间内形变量可以认为不变.因此，在分析瞬时变化时，可以认为弹力大小不变，即弹簧的弹力不突变.3.在求弹簧的弹力做功时，因该变力为线性变化，可以先求平均力，再用功的定义进行计算，也可据动能定理和功能关系：能量转化和守恒定律求解.同时要注意弹力做功的特点：Wk=-（kx22-kx12），弹力的功等于弹性势能增量的负值或弹力的功等于弹性势能的减少.弹性势能的公式Ep=kx2，高考不作定量要求，该公式通常不能直接用来求弹簧的弹性势能，只可作定性讨论.因此，在求弹力的功或弹性势能的改变时，一般以能量的转化与守恒的角度来求解.一、“轻弹簧”类问题在中学阶段，凡涉及的弹簧都不考虑其质量，称之为“轻弹簧”，是一种常见的理想化物理模型.由于“轻弹簧”质量不计，选取任意小段弹簧，其两端所受张力一定平衡，否则，这小段弹簧的加速度会无限大.故簧轻弹簧中各部分间的张力处处相等，均等于弹簧两端的受力.弹一端受力为，另一端受力一定也为。
数学模型之弹簧模型
一个弹簧质量系统
问题
一个弹性系数为k的弹簧左端固定，右端连接一个质量为m的滑块，放在一个光滑的水平面上，给出一定的初始位移后让其运动，求该弹簧质量系统的运动规律。
问题的数学模型为：2
2d x m kx dt
=−22020d x x dt ω+= = ()x t + 62()
cos t
1个弹簧连接1个物体水平运动的动画演示
1个弹簧连接1个物体竖直运动的动画演示
3个弹簧连接2个物体的运动
这里建立一个这样的模型，两个物体之间连有弹簧，两个物体两端又分别连接1个弹簧，两个弹簧的另一端又分别固定在墙上。
将两个物体分别拉伸一段距离后放开物体，弹簧-质量系统就会做往复运动，观察它们的运动情况，列出它们的运动方程。
= ∂∂2
t
2()x1t − + 2()x1t ()
x2t = ∂∂
2t 2()x2t − + 2()x2t ()
x1t 求解系统的微分方程得
= ()x2t + 52()cos t 1
2
()cos 3t = ()x1t − 52()cos t 12()cos 3t
系统的动态演示图
2个弹簧连接2个物体竖直运动
个物体竖直运动动态演示图
6个弹簧连接5个物体水平运动的动画演示
= + + ⎛⎝⎜⎜⎞⎠⎟⎟∂∂2t 2()x t 15⎛⎝⎜⎜⎞⎠⎟⎟∂∂t ()x t ()x t
0欠阻尼状态
受到重击的弹簧质量系统示意图
5()t δπ−
3cos(2/5)cos(/8)t e t t ππ−+++周期外力。
高三物理复习教案模型组合讲解——绳件、弹簧、杆件模型(动力学问题)
模型组合讲解——绳件、弹簧、杆件模型（动力学问题）［模型概述］挂件问题是力学中极为常见的模型，其中绳件、弹簧件更是这一模型中的主要模具，相关试题在高考中一直连续不断。
它们间的共同之处是均不计重力，但是它们在许多方面有较大的差别。
［模型回顾］［模型讲解］例1.如图1中a所示，一质量为m的物体系于长度分别为l1、l2的两根细线上，l1的一端悬挂在天花板上，与竖直方向夹角为，l2水平拉直，物体处于平衡状态。
现将l2线剪断，求剪断瞬时物体的加速度。
图1（1）下面是某同学对题的一种解法：解：设l1线上拉力为，l2线上拉力为，重力为mg，物体在三力作用下保持平衡，，剪断线的瞬间，突然消失，物体即在反方向获得加速度。
因为，所以加速度，方向沿反方向。
你认为这个结果正确吗？请对该解法作出评价并说明理由。
（2）若将图a中的细线l1改为长度相同、质量不计的轻弹簧，如图b所示，其他条件不变，求解的步骤和结果与（1）完全相同，即，你认为这个结果正确吗？请说明理由。
解析：因为l2被剪断的瞬间，l1上的张力发生突变，故物体获得的瞬间加速度由重力的分力提供，大小为，方向垂直l1斜向下，所以（1）错。
因为l2被剪断的瞬间，弹簧的长度不能发生突变而导致弹力不能突变，所以（2）对。
拓展：在（1）中若l1、l2皆为弹性绳，剪断l2的瞬间，小球的加速度为多少？（参考答案）若l1、l2皆为弹性绳，剪断l1的瞬间，小球的加速度为多少？（参考答案）在（2）中剪断l1的瞬间，小球的加速度为多少？（参考答案）例2. 如图2所示，斜面与水平面间的夹角，物体A和B的质量分别为、。
两者之间用质量可以不计的细绳相连。
求：（1）如A和B对斜面的动摩擦因数分别为，时，两物体的加速度各为多大？绳的张力为多少？（2）如果把A和B位置互换，两个物体的加速度及绳的张力各是多少？（3）如果斜面为光滑时，则两个物体的加速度及绳的张力又各是多少？图2解析：（1）设绳子的张力为，物体A和B沿斜面下滑的加速度分别为和，根据牛顿第二定律：对A有对B有设，即假设绳子没有张力，联立求解得，因，故说明物体B运动比物体A的运动快，绳松弛，所以的假设成立。
模型组合讲解——弹簧模型(动力学问题)
模型组合讲解——弹簧模型（动力学问题）［模型概述］弹簧模型是高考中出现最多的模型之一，在填空、实验、计算包括压轴题中都经常出现，考查范围很广，变化较多，是考查学生推理、分析综合能力的热点模型。
［模型讲解］一. 正确理解弹簧的弹力例1. 如图1所示，四个完全相同的弹簧都处于水平位置，它们的右端受到大小皆为F 的拉力作用，而左端的情况各不相同：①中弹簧的左端固定在墙上。
②中弹簧的左端受大小也为F 的拉力作用。
③中弹簧的左端拴一小物块，物块在光滑的桌面上滑动。
④中弹簧的左端拴一小物块，物块在有摩擦的桌面上滑动。
若认为弹簧的质量都为零，以l 1、l 2、l 3、l 4依次表示四个弹簧的伸长量，则有（ ）①②③④图1A. l l 21>B. l l 43>C. l l 13>D. l l 24=解析：当弹簧处于静止（或匀速运动）时，弹簧两端受力大小相等，产生的弹力也相等，用其中任意一端产生的弹力代入胡克定律即可求形变。
当弹簧处于加速运动状态时，以弹簧为研究对象，由于其质量为零，无论加速度a 为多少，仍然可以得到弹簧两端受力大小相等。
由于弹簧弹力F 弹与施加在弹簧上的外力F 是作用力与反作用的关系，因此，弹簧的弹力也处处相等，与静止情况没有区别。
在题目所述四种情况中，由于弹簧的右端受到大小皆为F 的拉力作用，且弹簧质量都为零，根据作用力与反作用力关系，弹簧产生的弹力大小皆为F ，又由四个弹簧完全相同，根据胡克定律，它们的伸长量皆相等，所以正确选项为D 。
二. 双弹簧系统例2. （2004年苏州调研）用如图2所示的装置可以测量汽车在水平路面上做匀加速直线运动的加速度。
该装置是在矩形箱子的前、后壁上各安装一个由力敏电阻组成的压力传感器。
用两根相同的轻弹簧夹着一个质量为2.0kg 的滑块，滑块可无摩擦的滑动，两弹簧的另一端分别压在传感器a 、b 上，其压力大小可直接从传感器的液晶显示屏上读出。
现将装置沿运动方向固定在汽车上，传感器b 在前，传感器a 在后，汽车静止时，传感器a 、b 的示数均为10N （取g m s =102/）图2（1）若传感器a 的示数为14N 、b 的示数为6.0N ，求此时汽车的加速度大小和方向。
高中物理弹簧模型详解
高中物理弹簧模型详解弹簧模型是物理中常用的简化实验模型，可以应用于弹性力学、动力学、波浪等多种领域。
在高中物理课程中，弹簧模型常常用来分析物体在不同条件下的弹性变形及恢复力等问题。
下面详细介绍一下高中物理中弹簧模型的相关内容。
I. 弹簧模型的基本概念弹簧模型是用弹簧代替物体之间的接触面，以研究物体之间的弹性变形和弹性力的模型。
它可以用来模拟各种物体的弹性特性，具有简化实验和便于分析的优势。
在弹簧模型中，物体可以被看作是由若干个质点组成的系统。
质点与质点之间通过一根弹簧连接，弹簧的特性可以用弹性系数k来描述。
当弹簧被压缩或拉长时，会产生恢复力（弹力），大小与弹簧形变的大小成正比，与弹簧形变的方向成反比。
II. 弹簧模型的应用1. 弹性变形当外力作用于物体上后，物体发生形变，但形变量又不足以改变物体的结构，这种形变称为弹性变形。
在弹簧模型中，外力就是作用于质点上的力，当外力大小不超过弹簧的弹性限度时，质点会发生弹性变形，而当外力大小超过弹性限度时，弹簧会进入塑性变形区，质点将发生塑性变形。
2. 弹性力弹性力是被压缩或拉长的弹簧恢复到原状时产生的力。
根据胡克定律，弹簧恢复力的大小与弹簧形变的大小成正比，与形变的方向成反比。
因此，在弹簧模型中，弹性力也可以用弹簧的弹性系数k来计算。
3. 振动弹簧模型还可以用来研究物体的振动。
例如，可以用一根手摇弹簧将质点与质点之间的耦合作用建立起来，通过摇动弹簧可以激发质点的振动。
这种振动可以用弹簧的弹性系数和质点的质量等参数来描述。
III. 弹簧模型的计算方法在使用弹簧模型时，需要根据具体情况建立起质点与质点之间的耦合关系。
通常，假设所有质点间连接的弹簧都相等，弹性系数为k，每个质点的质量均为m，这样就可以通过牛顿第二定律推导出弹簧模型的运动方程：F = mam(d^2)x/dt^2 = -kx其中，F表示合力，a表示加速度，x表示形变，t表示时间。
这个动力学方程描述了弹簧模型中物体的运动规律，可以用来计算物体的位移、速度和加速度等参数。
专题4.1 弹簧模型(解析版)
第四部分 重点模型与核心问题深究专题4.1 弹簧模型目录模型一 静力学中的弹簧模型 (1)模型二 动力学中的弹簧模型 (3)模型三 与动量、能量有关的弹簧模型 (5)专题跟踪检测 (9)模型一 静力学中的弹簧模型静力学中的弹簧模型一般指与弹簧相连的物体在弹簧弹力和其他力的共同作用下处于平衡状态的问题，涉及的知识主要有胡克定律、物体的平衡条件等，难度中等偏下。
【例1】如图所示，一质量为m 的木块与劲度系数为k 的轻质弹簧相连，弹簧的另一端固定在斜面顶端。
木块放在斜面上能处于静止状态。
已知斜面倾角θ＝37°，木块与斜面间的动摩擦因数μ＝0.5。
弹簧在弹性限度内，最大静摩擦力等于滑动摩擦力，重力加速度为g ，sin37°＝0.6，cos 37°＝0.8。
则( )A ．弹簧可能处于压缩状态B ．弹簧的最大形变量为3mg 5kC ．木块受到的摩擦力可能为零D ．木块受到的摩擦力方向一定沿斜面向上【答案】C【解析】木块与斜面间的最大静摩擦力f max ＝μmg cos θ＝0.4mg ，木块重力沿斜面方向的分力为G 1＝mg sin θ＝0.6mg ，由G 1>f max 可知，弹簧弹力的方向不可能向下，即弹簧不可能处于压缩状态，故A 错误；弹簧有最大形变量时满足G 1＋f max ＝k Δx m ，解得Δx m ＝mg k，故B 错误；当G 1＝F 弹时，木块受到的摩擦力为零，故C 正确；当G 1>F 弹时，木块受到的摩擦力沿斜面向上，当G 1<F 弹时，木块受到的摩擦力沿斜面向下，故D 错误。
【规律方法】(1)弹簧的最大形变量对应弹簧弹力的最大值。
(2)当木块刚好不上滑时所受静摩擦力达到最大值，此时弹簧弹力最大。
【分类训练】类型1 形变情况已知的弹簧模型1.木块A、B分别重50 N和70 N，它们与水平地面之间的动摩擦因数均为0.2，与A、B相连接的轻弹簧被压缩了5 cm，系统置于水平地面上静止不动，已知弹簧的劲度系数为100 N/m。
弹簧模型的动力学分析方法文件.doc
弹簧模型的动力学分析方法【例二】如图所示，劲度系数为k1,k的轻质弹簧竖直悬挂，两弹簧之间有一质2量为m的重物，最下端挂一质量为m2的重物，用一力竖直向上缓慢托起m2，当1力为多少时，两弹簧的总长等于弹簧原长之和？解析：两弹簧的总长等于弹簧原长之和，必定是弹簧k伸长，k11弹簧k压缩，且形变量x1x2m12对m1物体有k1x1k2x2m1g k2对m物体有F m2g k2x2m22x 1x2m g1k1k2F m2gk m g21k1k2【变式3】如图所示，竖直放置的箱子内，用轻质弹簧支撑着一个重G的物块，静止时物块对箱顶P的压力为G2，若将箱子倒转，使箱顶向下，静止时物块对箱顶P的压力是多少？（物块和箱顶间始终没有发生相对滑动）P【变式4】如图所示，在倾角为的光滑斜面上有两个轻质弹簧相连的物块A,B，它们的质量分别为m A,m B，弹簧的劲度系数为k，C为一固定挡板，现开始用一恒力F沿斜面方向拉物块A使之向上运动，求物块B刚要离开C时物块A的加速度a和从开始到此时物块A的位置d（重力加速度为g）（变式3图）C AB（变式4图）【变式5】如图所示，水平面上质量均为m的两木块A,B用劲度系数为k的轻质弹簧连接，整个系统处于平衡状态，现用一竖直向上的力F拉动木块A，使木块A向上做加速度为a的匀加速直线运动，取木块A的起始位置为坐标原点，图乙中实线部分表示从力 F 作用在木块A到木块B 刚离开地面这个过程中， F 和木块A的位移x之间的关系，则（）A. x0 ma/ k F FB. x0 m(a g) /k A F0C. F ma0 BD. F ( ) x0 O x0 m a g甲乙【2】如图所示，A, B 两个物快的重力分别是G N G NA 3 , 4 ，弹簧的重力不B计，系统沿着竖直方向处于静止状态，此时弹簧的弹力 F 2N ，则天花板受到的拉力和地板受到的有压力有可能是（）A.1N ,6N AB. 5N ,6NC.1N ,2N BD. 5N,2N【5】如图所示，一辆有力驱动力驱动的小车上有一水平放置的弹簧，其左端固定在小车上，右端与一小球相连，设在某一段时间内小球与小车相对静止且弹簧处于压缩状态，若忽略小球与小车间的摩擦力，则在此段时间内小车可能是（）A.向右做加速运动B. 向右做减速运动C.向左做加速运动D. 向左做减速运动左右【6】如图所示，质量均为m的物体A,B 通过一劲度系数为k 的轻质弹簧相连，开始时B 放在地面上，A, B 都处于静止状态，现通过细绳缓慢地将A向上提升距离L时，B 刚要离开地面，若将A加速向上拉起， B 刚要离开地面时，A上升的1距离为L2 ，假设弹簧一直都在弹性限度范围内，则（）A.mgLB.L 2k2mgL1 L A2kmg 2 m gC. L1 , L2 L1 C. L1 , L2 1 BL k k【10】一个弹簧秤放在水平地面上，Q为与轻质弹簧上端连在一起的弹簧秤，P 为一重物，已知P的质量M10.5kg，Q的质量m 1.5kg，弹簧的质量不计，劲度系数k800N/m，系统处于静止状态，如图所示，现给P施加一个方向竖直向上的力F，使其从静止开始向上做匀加速运动，已知在前0.2s内F为变力，0.2s后F变为恒力，求力F的最大值与最小值（g取10m/2s）FPQ【8】一根劲度系数为k、质量不计的轻质弹簧上端固定，下端系一质量为m的物体，有一水平板将物体托住，并使弹簧处于自然长度，如图所示，现让木板由静止开始以加速度a(a g)匀加速向下运动，求经过多长时间木板开始与物体分离a。
专题16 动力学动态分析、动力学图像问题(解析版)-2024年高考物理一轮综合复习导学练
2024年高考物理一轮大单元综合复习导学练专题16动力学动态分析、动力学图像问题导练目标导练内容目标1动力学动态分析目标2动力学v-t图像目标3动力学F-t、a-F图像目标4动力学a-t、a-x图像【知识导学与典例导练】一、动力学动态分析【例1】如图所示，木板B 固定在弹簧上，木块A 叠放在B 上，A 、B 相对静止，待系统平衡后用竖直向上的变力F 作用于A ，使A 、B 一起缓慢上升，AB 不分离，在A 、B 一起运动过程中，下面说法正确的是（）A ．一起缓慢上升过程中A 对B 的摩擦力不变B ．在某时刻撤去F ，此后运动中A 可能相对B 滑动C ．在某时刻撤去F ，此后运动中AB 的加速度可能大于gD ．在某时刻撤去F ，在A 、B 下降的过程中，B 对A 的作用力一直增大【答案】D【详解】A ．一起缓慢上升过程中，以A 、B 为整体，根据受力平衡可得A B ()F F m m g +=+弹由于弹簧弹力逐渐减小，可知拉力F 逐渐增大；以A 为对象，设木板B 斜面倾角为θ，根据受力平衡可得A sin sin f F m g θθ+=可知B 对A 摩擦力不断变小，则A 对B 的摩擦力不断变小，故A 错误；B ．设A 、B 间的动摩擦因数为μ，根据题意有tan μθ>在某时刻撤去F ，设A 、B 向下加速的加速度大小为a ，以A 为对象，则有A A cos cos m g N m a θθ-=；A A sin sin m g f m a θθ-=可得A ()cos N m g a θ=-；A ()sin tan f m g a N N θθμ=-=<故此后运动中A 、B 相对静止，故B 错误；C ．在某时刻撤去F ，此后运动中A 、B 相对静止，则最高点时的加速度最大，且撤去力F 前，整体重力和弹簧弹力的合力小于整体重力，则最高点加速度小于g ，此后运动中AB 的加速度不可能大于g ，故C 错误；D ．在某时刻撤去F ，在A 、B 下降的过程中，A 的加速度先向下逐渐减小，后向上逐渐增大，则B 对A 的作用力一直增大，故D 正确。
高考研究(三) 动力学四大模型之三——弹簧
教 材 回 顾
高 考 研 究
课时跟踪检测
动力学四大模型之三——弹簧
结
束
[跟进训练]
2.(2017· 山西忻州一中等四校联考 )如图所示，质量均 为 m 完全相同的物块 A、B 用轻弹簧相连，置于带有挡板 C 的固定斜面上。斜面的倾角为 θ，弹簧的劲度系数为 k。 初始时弹簧处于原长，A 恰好静止。现用一沿斜面向上的 力拉 A，直到 B 刚要离开挡板 C，则此过程中物块 A 的位 移为(弹簧始终处于弹性限度内)( )
教 材 回 顾 高 考 研 究
课时跟踪检测
动力学四大模型之三——弹簧
结
束
| 利用弹簧的“迟滞性”考查瞬时性问题
牛顿第二定律是力的瞬时作用规律：力和 题型 简述 加速度同时产生，同时变化，同时消失。 分析物体的瞬时问题，关键是先分析瞬时 前后物体的受力情况和运动状态，再由牛 顿第二定律求出瞬时加速度。
结
束
教 材 回 顾
高 考 研 究
课时跟踪检测
动力学四大模型之三——弹簧
结
束
[例 4](多选)如图所示，小车板面上的物体质量为 m＝ 8 kg，它被一根水平方向上拉伸了的弹簧拉住而静止在小车 上， 这时弹簧的弹力为 6 N。 现沿水平向右的方向对小车施加 作用力，使小车由静止开始运动起来，运动中加速度由零逐 渐增大到 1 m/s2，随即以 1 m/s2 的加速度做匀加速直线运动。 以下说法中正确的是( )
教 材 回 顾
高 考 研 究
课时跟踪检测
动力学四大模型之三——弹簧
结
束
[例 2]如图所示，倾角为 θ 的固定光滑斜面底部有一垂直 斜面的固定挡板 C。劲度系数为 k1 的轻弹簧两端分别与质量 均为 m 的物体 A 和 B 连接，劲度系数为 k2 的轻弹簧一端与 A 连接，另一端通过细线与一轻质小桶相连，细线跨过斜面顶端 的光滑的定滑轮，B 靠在挡板 C 处，A 和 B 均静止。现缓慢 地向小桶内加入细砂，当 B 与挡板 C 恰要分离时，小桶下降 的距离是多少？
小球落弹簧模型——动力学篇
027小球落弹簧模型——动力学篇027/112小球落弹簧模型通解——动力学篇金题试做 经典题目 你来挑战例如图所示，小球自由下落，从它接触竖直放置的弹簧开始到弹簧压缩到最短的过程中，小球的加速度和速度的变化情况是（）A.加速度变小，速度变小B.加速度变大，速度变小C.加速度先变小后变大，速度先变大后变小D.加速度先变大后变小，速度先变大后变小技巧点拨问题识别小球自由下落（忽略空气阻力）至竖直弹簧，从刚接触弹簧到将弹簧压缩至最短（或从将弹簧压缩至最短到刚离开弹簧）的过程中，分析小球的速度大小、加速度大小分别如何变化。
方法提炼阶段：小球只受重力，做自由落体运动； 阶段：小球受重力和弹簧弹力，且，加速度向下，做加速运动，（ 表示不变、 表示变大、 表示变小），加速度逐渐减小，即小球在此阶段做加速度不断减小的加速运动；弹弹点：小球受重力和弹簧弹力，且，加速度为零，速度达到最大值；弹阶段：小球受重力和弹簧弹力，且，加速度向上，做减速运动，弹，加速度逐渐增大，即小球在此阶段做加速度不断增大的减速运动。
弹补充说明小球从点（刚接触弹簧）到 点（将弹簧压缩至最短）的过程中速度先增大后减小、加速度先减小后增大，在 点（受力平衡）时速度最大、加速度为零；小球从 到 的过程中也是如此。
1.除上图所示的情景外，常见的橡皮筋弹弓、弹性绳蹦极等问题均属于此模型。
2.随堂讲义大招笔记系列027金题点睛 课堂思维 妙解点睛例．如图所示，小球自由下落，从它接触竖直放置的弹簧开始到弹簧压缩到最短的过程中，小球的加速度和速度的变化情况是．加速度变小，速度变小．加速度变大，速度变小．加速度先变小后变大，速度先变大后变小．加速度先变大后变小，速度先变大后变小信息解读：小球自由下落，研究从刚接触弹簧到将弹簧压缩至最短的过程，符合小球落弹簧模型的情景思路分析：题目研究加速度和速度的变化情况，可直接套用结论大招解析小球从刚接触弹簧到将弹簧压缩至最短的过程中，重力不变、弹簧弹力随着形变量的增大而增大，时加速度变小、速度变大；时加速度变大、速度变小。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
模型组合讲解——弹簧模型（动力学问题）
［模型概述］
弹簧模型是高考中出现最多的模型之一，在填空、实验、计算包括压轴题中都经常出现，考查范围很广，变化较多，是考查学生推理、分析综合能力的热点模型。
［模型讲解］
一. 正确理解弹簧的弹力
例1. 如图1所示，四个完全相同的弹簧都处于水平位置，它们的右端受到大小皆为F 的拉力作用，而左端的情况各不相同：①中弹簧的左端固定在墙上。
②中弹簧的左端受大小也为F 的拉力作用。
③中弹簧的左端拴一小物块，物块在光滑的桌面上滑动。
④中弹簧的左端拴一小物块，物块在有摩擦的桌面上滑动。
若认为弹簧的质量都为零，以l 1、l 2、l 3、l 4依次表示四个弹簧的伸长量，则有（ ）
①
②
③
④
图1
A. l l 21>
B. l l 43>
C. l l 13>
D. l l 24=
解析：当弹簧处于静止（或匀速运动）时，弹簧两端受力大小相等，产生的弹力也相等，用其中任意一端产生的弹力代入胡克定律即可求形变。
当弹簧处于加速运动状态时，以弹簧为研究对象，由于其质量为零，无论加速度a 为多少，仍然可以得到弹簧两端受力大小相等。
由于弹簧弹力F 弹与施加在弹簧上的外力F 是作用力与反作用的关系，因此，弹簧的弹力也处处相等，与静止情况没有区别。
在题目所述四种情况中，由于弹簧的右端受到大小皆为F 的拉力作用，且弹簧质量都为零，根据作用力与反作用力关系，弹簧产生的弹力大小皆为F ，又由四个弹簧完全相同，根据胡克定律，它们的伸长量皆相等，所以正确选项为D 。
二. 双弹簧系统
例2. （2004年苏州调研）用如图2所示的装置可以测量汽车在水平路面上做匀加速直线运动的加速度。
该装置是在矩形箱子的前、后壁上各安装一个由力敏电阻组成的压力传感器。
用两根相同的轻弹簧夹着一个质量为2.0kg 的滑块，滑块可无摩擦的滑动，两弹簧的另一端分别压在传感器a 、b 上，其压力大小可直接从传感器的液晶显示屏上读出。
现将装置沿运动方向固定在汽车上，传感器b 在前，传感器a 在后，汽车静止时，传感器a 、b 的示数均为10N （取g m s =102
/）
图2
（1）若传感器a 的示数为14N 、b 的示数为6.0N ，求此时汽车的加速度大小和方向。
（2）当汽车以怎样的加速度运动时，传感器a 的示数为零。
解析：（1）F F ma 121-=，a F F m
m s 112
240=-=./ a 1的方向向右或向前。
（2）根据题意可知，当左侧弹簧弹力F 10'=时，右侧弹簧的弹力F N 220'=
F ma 22'=
代入数据得a F m
m s 22210=='
/，方向向左或向后
［模型要点］
弹簧中的力学问题主要是围绕胡克定律F kx =进行的，弹力的大小为变力，因此它引起的物体的加速度、速度、动量、动能等变化不是简单的单调关系，往往有临界值，我们在处理变速问题时要注意分析物体的动态过程，为了快捷分析，我们可以采用极限方法，但要注意“弹簧可拉可压”的特点而忽略中间突变过程，我们也可以利用弹簧模型的对称性。
［模型演练］
（2005年成都考题）如图3所示，一根轻弹簧上端固定在O 点，下端系一个钢球P ，球处于静止状态。
现对球施加一个方向向右的外力F ，吏球缓慢偏移。
若外力F 方向始终水平，移动中弹簧与竖直方向的夹角θ<90
且弹簧的伸长量不超过弹性限度，则下面给出弹簧伸长量x 与cos θ的函数关系图象中，最接近的是（ ）
图3 答案：D
3、真真的心，想你；美美的意，恋你；暖暖的怀，抱你；甜甜的笑，给你；痴痴的眼，看你；深深的夜，梦你；满满的情，宠你；久久的我，爱你！
4、不管从什么时候开始，重要的是开始以后不要停止；不管在什么时候结束，重要的是结束以后不要后悔。
爱情来了，你还在犹豫么？
5、美女，我注意你好久啦，就是不知道怎么表白。
我翻来覆去，思来想去，最终想到一个大胆的办法，我要俘虏你的心，让你爱上我。
爱上了吗？
6、对你的爱意，早已飞过万水千山，飞到你眼前，请你睁开眼，仔细看认真听，我的眼睛为你明亮，我的嗓音为你歌唱，来吧，让我们一起舞动爱情之歌！
7、爱你没商量，你的眼睛眨一下，我就死去，你的眼睛再眨一下，我就活过来，你的眼睛不停地眨来眨去，于是我便死去活来！
8、因为深爱，找不到词汇诠释，因为深爱，找不到言语概括，因为深爱，只能发条短信，轻声说一声“我爱你”,这不是三个字，而是一辈子！
9、我对你的心是鲜啤酒，清澈甘冽；我对你的情是葡萄酒，味美甘甜；我对你的爱是刀烧酒，热情浓烈；醉倒在怀，无限爱恋。
10、人生短短几十年，不要给自己留下了什么遗憾，想笑就笑，想哭就哭，该爱的时候就去爱，无谓压抑自己。
人生的苦闷有二，一是欲望没有被满足，二是它得到了满足。
11、一片琼花天庭落，万里江山披银河，冰凌也有相思苦，写意窗花含泪说，昙花一现夜梦短，早有晨光盼春歌。
想你，我的心会和你一起启程，祈祷每一个黎明。
12、戒指好比爱情，戴在手上，也是戴在心上；伤在心上，便也伤在手上。
不敢碰的，是那心里的伤；不愿摘的，是那难舍的爱。
13、在追求爱情的列车上，透过车窗，可以欣赏到许多优美的景色，但是，请不要留恋，因为终点站才是真正的目的地。
但愿我能够成为你永远的终点站！
14、爱一个人真的好难，让我欢喜让我忧！如果不让我去爱你的话，我会更难受，更彷徨。
所以为了我自己，我还是爱着你吧！
15、诚挚的微笑，每一次心跳，或许寂然无声，却胜过虚幻的海誓山盟；真情的碰撞，灵魂的契合，或许不够浪漫，却胜过无数的真情告白。
16、此时此刻我又想起了你，想你的感觉是一种酸酸的痛！不能打电话告诉你，只想用文字亲亲你！记住爱你的人始终是我！
17、爱你一万年，夸张！爱你五千年，无望！爱你一千年，荒唐！爱你一百年，太长！接连爱你七十年，只要我身体健康，就是我的强项！
18、如果不爱你，不会为你守着誓言，如果不爱你，不会承受一切的罪恶感，如果不爱你，不会因你而绽放幸福的光彩。
19、一个犀利并朦胧眼神，传递心中纠结情感，我们的距离愈近或愈远。
发条简朴并低调的信息，尽享真情互动，指尖点点，送你的却是心中真情满满。
20、上帝给了我这份缘，所以我每天都在天堂。
生活里因为有了爱，所以我身边幸福弥漫。
日子里面有了你，所以天天我都很美。