系统动力学模型案例分析
系统动力学课件与案例分析可编辑全文

能改善公司的成长,使得
以指数方式增长。
1企业成长与投资不足案例
❖ 系统边界的确定:划定系统边界应根据建模目的,把那些 与所研究的问题关系密切的重要变量划入系统边界内。在 此案例中,我们主要关注企业成长问题,研究影响企业营 业收入的因素。根据案例介绍因此我们将仅仅研究企业的 生产、市场、销售部门。不涉及其他部门,竞争对手等等。
(16)供应商生产率=DELAY3(供应商生产需求率,生产延迟) 单位:箱/周
2供应链中牛鞭效应
计算机仿真:
使用Vensim软件建立系统流图和填入方程式, 就可以对系统进行仿真。建立仿真模型可以与现 实对照,可以寻求削弱牛鞭效应的策略,可以预 测系统未来的行为趋势。
仿真结果
2供应链中牛鞭效应
2供应链中牛鞭效应
2供应链中牛鞭效应
问题识别:本案例主要研究供应链中牛鞭效应,各个供应链 节点库存积压,库存波动幅度比较大,不够稳定,导致供 应链的成本居高不下,失去了竞争优势。因此急需采取措 施来削弱牛鞭效应,从而能够降低整条供应链的成本,建 立稳定的竞争优势。因此本案例通过啤酒游戏来对供应链 进行仿真,从而为寻找较优的供应链结构来削弱牛鞭效应, 降低成本。
2供应链中牛鞭效应
2供应链中牛鞭效应
❖ 建立仿真方程式: (1)市场销售率=1000+IF THEN ELSE(TIME>4,RANDOM
NORMAL(-200,200,0,100,4),0) 单位:箱/周 (2)零售商销售预测=SMOOTH(市场销售率,移动平均时间)
单位:箱/周 (3)零售商期望库存=期望库存持续时间×零售商销售预测
1企业成长与投资不足案例
1企业成长与投资不足案例
❖ 3.那么从上图可以看出正反馈回路使得营业收入增长,但
系统动力学及vensim建模与模拟技术

系统行为分析
预测系统行为
在构建系统动力学模型时,需要对系统的行为进行预测和分析,了 解系统在不同条件下的响应和变化规律。
分析行为特征
通过对系统行为的深入分析,可以了解系统的动态特性和变化趋势, 为模型建立提供依据。
确定行为目标
在分析系统行为的基础上,需要确定系统的行为目标,即希望系统 达到的状态或结果,以便对模型进行有效的优化和控制。
定义模型规则
根据系统行为的特点,定义模型规则,如时 间延迟、逻辑规则等。
参数化模型
根据已知数据和经验,为模型中的参数赋值。
模型验证与测试
01
模型验证
通过对比历史数据和模拟结果,验 证模型的准确性和可靠性。
模型测试
通过多种情景模拟,测试模型的预 测能力和适用范围。
03
02
敏感性分析
分析模型对参数变化的敏感性,了 解参数对系统行为的影响。
详细描述
城市交通系统是一个复杂的网络,包括道路、交通信号、车辆、行人等。通过 建立城市交通系统模型,可以模拟不同交通政策或基础设施改进方案的效果, 为城市交通规划提供决策支持。
案例三:企业运营系统模拟
总结词
企业运营系统模拟是应用系统动力学和Vensim建模与模拟技术的实际应用案例 ,用于优化企业资源配置和提高运营效率。
03 系统动力学模型构建
系统边界设定
1 2
确定研究范围
在构建系统动力学模型时,首先需要明确系统的 研究范围,即确定系统的边界,以避免不必要的 复杂性和不确定性。
排除外部因素
在设定系统边界时,应将注意力集中在系统内部 的相互关系上,暂时忽略外部因素的影响。
3
确定主要变量
在确定系统边界后,应确定对系统行为有重要影 响的主要变量,这些变量将成为模型中的状态变 量。
多自由度振动系统的动力学模型构建

多自由度振动系统的动力学模型构建引言:多自由度振动系统是指由多个自由度的质点组成的系统,在这样的系统中,每个自由度都可以独立地进行运动。
动力学模型的构建是研究和理解振动系统行为的基础。
本文将介绍多自由度振动系统动力学模型的构建方法及应用。
一、质点模型多自由度振动系统的最基本组成单位是质点。
质点的运动可以用坐标形式以及质点的质量、刚性等参数来描述。
对于一个有n个自由度的振动系统,可以通过将每个自由度的质点模型相连接构成整个系统。
二、约束关系与广义坐标在多自由度振动系统中,质点之间相互约束,其运动不再是自由的,而是受到约束的影响。
为了描述约束关系,引入广义坐标来表示系统各个自由度的相对运动。
广义坐标是将实际坐标通过约束条件变换得到的坐标表示。
三、拉格朗日方程与振动方程拉格朗日方程是多自由度振动系统的基本动力学方程。
通过对系统的动能和势能进行推导和求导,可以得到描述系统运动的拉格朗日方程。
对于振动系统而言,通过求解拉格朗日方程,可以得到系统的振动方程,进一步描述系统的运动行为。
四、模态分析与特征频率模态分析是研究振动系统固有特性的方法。
对于多自由度振动系统,可以通过模态分析得到系统的固有模态和特征频率。
固有模态是指系统在自由振动时,各个自由度的振动模式。
特征频率是指系统在不同固有模态下的振动频率。
五、系统的耦合与动态响应多自由度振动系统中的各个质点之间存在耦合关系,一个自由度的振动会对其他自由度的振动产生影响。
通过研究系统的耦合关系,可以得到系统的动态响应。
动态响应是指系统对外界激励的响应行为,可以通过求解振动方程得到。
六、应用案例:建筑结构振动多自由度振动系统的应用广泛,尤其在建筑结构的振动研究中起到了重要作用。
通过对建筑结构的多自由度振动系统进行建模和分析,可以评估结构的稳定性、抗震性能等。
振动模型的构建和分析可以提供设计和改进建筑结构的依据。
结论:多自由度振动系统的动力学模型构建是研究振动系统行为的关键步骤。
《OSH、应急管理要素整合及系统动力学建模解析》

《OSH、应急管理要素整合及系统动力学建模解析》篇一一、引言随着工业化的快速发展,生产过程中的安全问题日益突出,职业安全健康(OSH)及应急管理成为企业管理的重中之重。
为了更好地进行安全管理及应对突发事件,将OSH、应急管理要素进行有效整合,并采用系统动力学建模技术进行分析与优化显得尤为重要。
本文将首先对OSH和应急管理的相关概念及重要性进行概述,然后对整合的要素进行详细分析,最后通过系统动力学建模解析整合后的效果。
二、OSH与应急管理概述1. 职业安全健康(OSH):指在生产过程中,通过科学的管理和技术手段,保障劳动者的人身安全和身体健康,预防职业病和工伤事故的发生。
2. 应急管理:指在突发事件发生时,采取科学、有效的方法和手段,保障人员生命安全,减少财产损失,尽快恢复正常的生产生活秩序。
三、OSH与应急管理要素整合1. 人员管理:包括员工的安全培训、健康检查、应急救援队伍的建设等。
2. 设备管理:包括设备的维护、检查、更新,以及应急设备的配备等。
3. 环境管理:包括作业环境的改善、危险源的识别与控制、应急避险设施的建设等。
4. 制度管理:包括安全管理制度的制定、执行与监督,以及应急预案的编制与演练等。
四、系统动力学建模解析系统动力学建模是一种以计算机仿真技术为基础的管理方法,通过构建系统动力学模型,对系统的结构、功能和行为进行深入分析。
在OSH与应急管理要素整合中,可以采用系统动力学建模技术,对整合后的效果进行定量分析和优化。
1. 模型构建:根据OSH与应急管理的要素,构建系统动力学模型。
模型包括人员、设备、环境、制度等子系统,以及各子系统之间的相互关系和影响。
2. 数据分析:通过收集历史数据和实时数据,对模型进行参数设置和校准。
利用模型进行模拟实验,分析各要素对OSH和应急管理的影响。
3. 策略制定:根据模拟实验结果,制定优化策略。
策略包括改进人员管理、设备管理、环境管理和制度管理等方面,以提高OSH和应急管理的效果。
系统动力学与案例分析

系统动力学与案例分析一、系统动力学发展历程(一)产生背景第二次世界大战以后,随着工业化的进程,某些国家的社会问题日趋严重,例如城市人口剧增、失业、环境污染、资源枯竭。
这些问题范围广泛,关系复杂,因素众多,具有如下三个特点:各问题之间有密切的关联,而且往往存在矛盾的关系,例如经济增长与环境保护等。
许多问题如投资效果、环境污染、信息传递等有较长的延迟,因此处理问题必须从动态而不是静态的角度出发。
许多问题中既存在如经济量那样的定量的东西,又存在如价值观念等偏于定性的东西。
这就给问题的处理带来很大的困难。
新的问题迫切需要有新的方法来处理;另一方面,在技术上由于电子计算机技术的突破使得新的方法有了产生的可能。
于是系统动力学便应运而生。
(二)J.W.Forrester等教授在系统动力学的主要成果:1958年发表著名论文《工业动力学——决策的一个重要突破口》,首次介绍工业动力学的概念与方法。
1961年出版《工业动力学》(Industrial Dynamics)一书,该书代表了系统动力学的早期成果。
1968年出版《系统原理》(Principles of Systems)一书,论述了系统动力学的基本原理和方法。
1969年出版《城市动力学》(Urban Dynamics),研究波士顿市的各种问题。
1971年进一步把研究对象扩大到世界范围,出版《世界动力学》(World Dynamics)一书,提出了“世界模型II”。
1972年他的学生梅多斯教授等出版了《增长的极限》(The Limits to Growth)一书,提出了更为细致的“世界模型III”。
这个由罗马俱乐部主持的世界模型的研究报告已被翻译成34种语言,在世界上发行了600多万册。
两个世界模型在国际上引起强烈的反响。
1972年Forrester领导MIT小组,在政府与企业的资助下花费10年的时间完成国家模型的研究,该模型揭示了美国与西方国家的经济长波的内在机制,成功解释了美国70年代以来的通货膨胀、失业率和实际利率同时增长的经济问题。
(完整版)系统动力学模型案例分析
系统动力学模型介绍1.系统动力学的思想、方法系统动力学对实际系统的构模和模拟是从系统的结构和功能两方面同时进行的。
系统的结构是指系统所包含的各单元以及各单元之间的相互作用与相互关系。
而系统的功能是指系统中各单元本身及各单元之间相互作用的秩序、结构和功能,分别表征了系统的组织和系统的行为,它们是相对独立的,又可以在—定条件下互相转化。
所以在系统模拟时既要考虑到系统结构方面的要素又要考虑到系统功能方面的因素,才能比较准确地反映出实际系统的基本规律。
系统动力学方法从构造系统最基本的微观结构入手构造系统模型。
其中不仅要从功能方面考察模型的行为特性与实际系统中测量到的系统变量的各数据、图表的吻合程度,而且还要从结构方面考察模型中各单元相互联系和相互作用关系与实际系统结构的一致程度。
模拟过程中所需的系统功能方面的信息,可以通过收集,分析系统的历史数据资料来获得,是属定量方面的信息,而所需的系统结构方面的信息则依赖于模型构造者对实际系统运动机制的认识和理解程度,其中也包含着大量的实际工作经验,是属定性方面的信息。
因此,系统动力学对系统的结构和功能同时模拟的方法,实质上就是充分利用了实际系统定性和定量两方面的信息,并将它们有机地融合在一起,合理有效地构造出能较好地反映实际系统的模型。
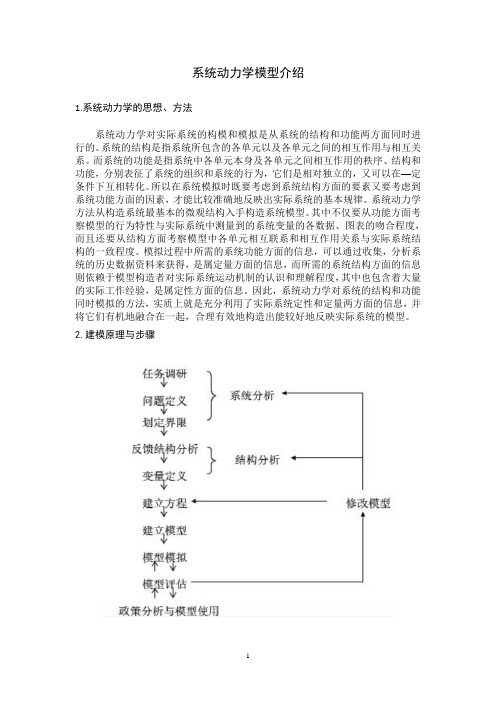
2.建模原理与步骤(1)建模原理用系统动力学方法进行建模最根本的指导思想就是系统动力学的系统观和方法论。
系统动力学认为系统具有整体性、相关性、等级性和相似性。
系统内部的反馈结构和机制决定了系统的行为特性,任何复杂的大系统都可以由多个系统最基本的信息反馈回路按某种方式联结而成。
系统动力学模型的系统目标就是针对实际应用情况,从变化和发展的角度去解决系统问题。
系统动力学构模和模拟的一个最主要的特点,就是实现结构和功能的双模拟,因此系统分解与系统综合原则的正确贯彻必须贯穿于系统构模、模拟与测试的整个过程中。
与其它模型一样,系统动力学模型也只是实际系统某些本质特征的简化和代表,而不是原原本本地翻译或复制。
案例研究——牛鞭效应的系统动力学分析
案例研究——牛鞭效应的系统动力学分析作者:赵军刘飞来源:《物流科技》2009年第04期摘要:利用系统动力学的方法和仿真软件Vensim,对Y公司K产品的供应链上的牛鞭效应进行了建模与仿真。
针对该供应链上牛鞭效应显著的实际情况,提出了缩短订单延迟时间,延长库存调节时间,采用供应商管理库存的综合解决方案,仿真结果表明该解决方案能在一定程度上减轻牛鞭效应的影响,研究结果可为Y公司的实际生产组织提供决策依据。
关键词:系统动力学;供应链;牛鞭效应;仿真;供应商管理库存中图分类号:F273.7文献标识码:AAbstract: This paper adopts the system dynamics and its simulation software Vensim to modeling and simulating the bullwhip effect in the supply chain of the Y company's k product. Based on the reality situation of the bullwhip effect in this supply chain, it brought forward shortening delay time of order, prolonging adjust time of inventory, adopting vendor managed inventory to solve this problem, the simulation results proved that these method could alleviate the effect of the bullwhip effect in some extend, the research results could enrich the decision about the reality product organization for company Y.Key words: system dynamics; supply chain; bullwhip effect; simulation; vendor managed inventory牛鞭效应指供应链中需求信息从下游企业向上游企业传递时,信息被扭曲并逐级放大的现象[1]。
应用于共同配送模式的系统动力学研究及其案例分析
w、 该 运 行 条 件 下 汽 车 的 载 质 量 i 一
户 要求 , 分别 将货 物运 送 到各 个 商铺 或 是 接 货点 的 物 流 配送 模
式 。系 统动 力学 ( y t y a c , 称 S ) 一 种 以 反 馈 控 S se D n mi 简 m s D是 制 理论 为基 础 , 以定性 分析 和 定 量研 究 相 结合 的研 究社 会 经 济 管理 系 统的 系统分 析方 法 。
州
2 年 月 旬) I1 5 C16 0 9( 刊 S0 0 N—1 1 下 S0 7 4I 1 N9 1 14 — /
应 用 于 共 同 配 送 模 式 的 系 统 动 力 学 研 究 及 其 案 例 分 析
郑 考 ( 济 大 学 交 通 运 输 工 程 学 院 上 海 2 1 0 ) 同 0 8 4
的共 同 配送模 型 , 态分 析 影 响 南 京路 共 同配 送 的各 种 因素 , 成 了满 载率 的下 降 。 动 相应 地 , 由于 满载 率的 提高 和车辆 内混载 的货 物增加 , 因此 并加 以方 案评价 。
南京路 坐落于上 海市 中心商业 区 , 受制 于地理条 件 以及 交通 车 辆在 配送过 程 中停 车次 数和 配送距 离也 发生 了增 长 。同样 配 条 件的 限制 , 配送 的需求 与配送 能力之 间的矛盾 已经变得 相 当尖 送 频 率 的 波 动 也 影 响 到 了 配 送 时 间 。 锐 。 以 下 三方 面 的 不 利 :
一
.
粗 犷的 配送模 式使 得物 流配 送成 本居 高不 下 。
每成员 每周配送成本节约
l O _ 伽
二 .产生 一系列 社会 问题 。诸 如 因车辆 有 效利 用 率低 而 加 重 城 区交通 负担 、 配送 车 辆 车 况 差 而 造 成 安 全 事 故 、 卸 设 备 装
系统动力学课件与案例分析
1
延迟现象在系统内无处不在。如货物需要运输,决策需要时间。延迟会对系统的行为有很大的影响,因此必须要刻画延迟机制。延迟包括物质延迟与信息延迟。系统动力学通过延迟函数来刻画延迟现象。如物质延迟中DELAY1,DELAY3函数;信息延迟的DLINF3函数。
延迟:
2
平滑是指从信息中排除随机因素,找出事物的真实的趋势,如一般决策者不会直接根据销售信息制定决策,而是对销售信息求出一段时间内的平均值。系统动力学提供SMOOTH函数来表示平滑。
1972年Forrester领导MIT小组,在政府与企业的资助下花费10年的时间完成国家模型的研究,该模型揭示了美国与西方国家的经济长波的内在机制,成功解释了美国70年代以来的通货膨胀、失业率和实际利率同时增长的经济问题。(经济长波通常是指经济发展过程中存在的持续时间为50年左右的周期波动 )
1.系统动力学发展历程
主要研究供应链中牛鞭效应(重点)
5.系统动力学实际案例
5.1 企业成长与投资不足案例
案例背景: S公司是一家高科技公司,因为有一项能产业化的科技创新成果而创业,且一开始便以流星般的速度成长。因为销售业绩太好,以致积欠交货的订单在第2年就开始越积越多,于是管理层决定扩大产量,但是这需要时间;与此同时使原先对顾客允诺的交货期一再拖延,但领导层认为,企业的产品功能是无法替代,顾客能够接受交货期的延长。同时为了继续能使公司发展增长,他们将收入的大部分直接投入营销,到第3年公司销售人员增加了一倍。但是,到了第3年年末开始出现困境,而第4年销售业绩出现危机。虽然企业雇用了更多的销售人员和新装置,但是销售速度反而下滑。于是企业的注意力又是集中营销:提高销售奖额、增加特别折扣和新的促销广告,跟着情况一时好转,但是很快困境再度出现;于是再进一步加强营销,如此循环如图的变化形态,虽然有小幅度而间歇性的成长,但是企业从来没发挥它真正的潜力。
系统动力学模型案例分析
糸统动力学模型介绍1.糸统动力学的思想.方法糸统动力学对实际糸统的构栈和栈拟是从糸统的结构和功能两方面同肘进行的。
糸统的结构是指糸统所包含的各单元以及各单元之间的和互作用与和互关糸。
而糸统的功能是指糸统中各单元本身及各单元之间相互作用的秩序、结构和功能,分别表征了糸统的纽织和糸统的行%,它们是相对独立的,又可以定条件下互和转化。
所以A糸统栈拟肘阮要考虑到糸统结构方面的要素又要考虑到糸统功能方面的因素,才能比较准确地反映出卖际糸统的基本规律。
糸统动力学方去从构凌糸统最基本的微观结构入手构凌糸统栈型。
其中不仅要从功能方面考疼栈型的行为特性与实际糸统中测量到的糸统变量的各数据、图表的吻合程度,而且还要从结构方面考案棋型中各单元相互联糸和相互作用关糸与实际糸统结构的一致程度。
槻拟过程中所需的糸统功能方面的信息,可以通过收集,分析糸统的0史数据资料来荻得,是属定量方面的信息,而所需的糸统结构方面的信息则依赖于栈型构凌者对实际糸统运动机制的认识和理解程度,其中也包含着丸量的实际工作经脸,是厲走性方面的信息。
因此,糸统动力学对糸统的结构和功能同肘栈拟的方比,实质上就是充分利用了卖际糸统定性和定量两方面的信息,并将•£们有机地融合衣一起.,合理有效地构凌岀能较好地反映实际糸统的栈空。
2.建核原理与步骤任务调研问平义划定界限反馈气伴分析变誓义修改模型建%模型政策分析与模型便用⑴建棋原理用糸统动力学方出进行建棋最根本的指导脛想就是糸统动力学的糸统观和方法怡。
糸统动力学认为糸统具有整体性、和关性、等级性和和彼性。
糸统部的反馈结构和机制决定了糸统的行为特性,任何复杂的丸糸统都可以由多个糸统最基本的信息反馈回路按芷种方无联结而成。
糸统动力学栈型的糸统目标就是针对实际应用情况,从支化和发畏的角盛去解决糸统问題。
糸统动力学构栈和栈拟的一个最主要的特点,就是卖现结构和功能的双栈拟,因此糸统分解与糸统综合原则的正确贯彻必须贯穿于糸统构栈、棋拟与测试的整个过程中。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
系统动力学模型介绍
1.系统动力学的思想、方法
系统动力学对实际系统的构模和模拟是从系统的结构和功能两方面同时进行的。
系统的结构是指系统所包含的各单元以及各单元之间的相互作用与相互关系。
而系统的功能是指系统中各单元本身及各单元之间相互作用的秩序、结构和功能,分别表征了系统的组织和系统的行为,它们是相对独立的,又可以在—定条件下互相转化。
所以在系统模拟时既要考虑到系统结构方面的要素又要考虑到系统功能方面的因素,才能比较准确地反映出实际系统的基本规律。
系统动力学方法从构造系统最基本的微观结构入手构造系统模型。
其中不仅要从功能方面考察模型的行为特性与实际系统中测量到的系统变量的各数据、图表的吻合程度,而且还要从结构方面考察模型中各单元相互联系和相互作用关系与实际系统结构的一致程度。
模拟过程中所需的系统功能方面的信息,可以通过收集,分析系统的历史数据资料来获得,是属定量方面的信息,而所需的系统结构方面的信息则依赖于模型构造者对实际系统运动机制的认识和理解程度,其中也包含着大量的实际工作经验,是属定性方面的信息。
因此,系统动力学对系统的结构和功能同时模拟的方法,实质上就是充分利用了实际系统定性和定量两方面的信息,并将它们有机地融合在一起,合理有效地构造出能较好地反映实际系统的模型。
2.建模原理与步骤
(1)建模原理
用系统动力学方法进行建模最根本的指导思想就是系统动力学的系统观和方法论。
系统动力学认为系统具有整体性、相关性、等级性和相似性。
系统内部的反馈结构和机制决定了系统的行为特性,任何复杂的大系统都可以由多个系统最基本的信息反馈回路按某种方式联结而成。
系统动力学模型的系统目标就是针对实际应用情况,从变化和发展的角度去解决系统问题。
系统动力学构模和模拟的一个最主要的特点,就是实现结构和功能的双模拟,因此系统分解与系统综合原则的正确贯彻必须贯穿于系统构模、模拟与测试的整个过程中。
与其它模型一样,系统动力学模型也只是实际系统某些本质特征的简化和代表,而不是原原本本地翻译或复制。
因此,在构造系统动力学模型的过程中,必须注意把握大局,抓主要矛盾,合理地定义系统变量和确定系统边界。
系统动力学模型的一致性和有效性的检验,有一整套定性、定量的方法,如结构和参数的灵敏度分析,极端条件下的模拟试验和统计方法检验等等,但评价一个模型优劣程度的最终标准是客观实践,而实践的检验是长期的,不是一二次就可以完成的。
因此,一个即使是精心构造出来的模型也必须在以后的应用中不断修改、不断完善,以适应实际系统新的变化和新的目标。
(2)建模步骤
系统动力学构模过程是一个认识问题和解决问题的过程,根据人们对客观事物认识的规律,这是一个波浪式前进、螺旋式上升的过程,因此它必须是一个由粗到细,由表及里,多次循环,不断深化的过程。
系统动力学将整个构模过程归纳为系统分析、结构分析、模型建立、模型试验和模型使用五大步骤这五大步骤有一定的先后次序,但按照构模过程中的具体情况,它们又都是交叉、反复进行的。
第一步系统分析的主要任务是明确系统问题,广泛收集解决系统问题的有关数据、资料和信息,然后大致划定系统的边界。
第二步结构分析的注意力集中在系统的结构分解、确定系统变量和信息反馈机制。
第三步模型建立是系统结构的量化过程(建立模型方程进行量化)。
第四步模型试验是借助于计算机对模型进行模拟试验和调试,经过对模型各种性能指标的评估不断修改、完善模型。
第五步模型使用是在已经建立起来的模型上对系统问题进行定量的分析研究和做各种政策实验。
3.建模工具
系统动力学软件VENSIM PLE软件
4.建模方法
因果关系图法
在因果关系图中,各变量彼此之间的因果关系是用因果链来连接的。
因果链是一个带箭头的实线(直线或弧线),箭头方向表示因果关系的作用方向,箭头旁标有“+”或“-”号,分别表示两种极性的因果链。
a.正向因果链A→+B:表示原因A的变化(增或减)引起结果B在同一方向上发生变化(增或减)。
b.负向因果链A→-B:表示原因A的变化(增或减)引起结果B在相反方向上发生变化(减或增)。
如图
流图法
流图法又叫结构图法,它采用一套独特的符号体系来分别描述系统中不同类型的变量以及各变量之间的相互作用关系。
①状态变量
状态变量又称作位,它是表征系统状态的内部变量,可以表示系统中的物
质、人员等的稳定或增减的状况。
状态变量的流图符号是一个方框,方框内填写状态变量的名字。
显然,能够对状态变量的变化产生影响的只是速率变量。
状态方程可根据有关基本定律来建立,如连续性原理、能量质量守恒原理等。
状态方程有三种最基本的表达方式:微分方程表达、差分方程表达和积分方程表达。
在一定的条件下,这三种表达方式可以互相转化。
如图
5.建模方程类型
以财政补贴为例
PT.K=PT.J+PTL*PT.J*Time
式中
PT.K—第K年财政补贴(万元);
PT.J—第J年年财政补贴(万元);
PTL—年财政补贴率
程序模块如图
方程建立好后,设置变量和时间步长,检查模型,运行得到模拟图像和预测数据。
下面用人口的出生率为例
影响出生率的因素我们可以认为有人口性别比例,人口年龄分布,政策系数等一般来说人口性别比例应该是1:1,但是考虑到统计的实际的数据有可能不是1:1,这个可以通过历年的不同性别的人口数量得到,人口年龄分布即为:婴儿,小孩,青年,中年,老年等。
影响出生率的当然就是达到生育年龄的青年和中年(一般16~45岁)。
政策系数即为计划生育政策执行的严格程度(政府部门可以得到)。
如果严格执行“一对夫妇一个孩”的人口政策,政策系数=1,随着执行程度的放松,其值增加。
例如,如果实施“一对夫妇两个孩”的人口政策,政策系数=2。
迁入迁出的人口数量可以通过统计数据得到。
下面主要看下这几个因素对出生率的影响,建模方程
d(出生率)/d(时间)=“青年和中年(一般16~45岁)”*出生率*(性别比)/(100+性别比)*政策系数+(迁入-迁出)*系数(函数);
(也有可能符合一定的非线性方程之类的,要继续深入的研究)
模型参数估计常用方法:
应用统计资料、调查资料确定参数;
一些常用的数学方法,如经济计量学方法,算法等;
从模型中部分变量关系中确定参数值;
根据模型的参考行为特征估计参数值
专家评估。
此处借用别人的图像解释效果。
GRAPH
2,000
4,000
2,000
6,000
0 1,000
4
4
4
4
4
4
44
4
4 3
3
3
3
3
3
3
3
3
33 2
2
2
2
2
222
2
2
2 1
1
1
1
1
1
1
1111
20102014201820222026203020342038204220462050
Time (Year)
0-14岁11111111111 15-64岁22222222222 65岁及以上3333333333
总人口4444444444
5.模型里还可以加入数学函数,逻辑函数,取大取小函数,阶跃函数,开关函数,延迟函数等,进而模型将会更复杂。
其他的小系统模块(投资收益,缴费金额等)的建模类似。
6.把每个小的系统模块的微分方程或者差分方程,输入系统,运行模块即可得到模拟曲线和一些模拟预测数据,通过改变变量,反复试验可以得到主要影响变量,每个小的系统模块再进行集成,一层一层的就可以得到目标的要求,同时还可以根据每次的实验结果给出相关的政策与对策。
