多元线性回归分析的实例研究

合集下载

建模实例(多元线性回归模型)

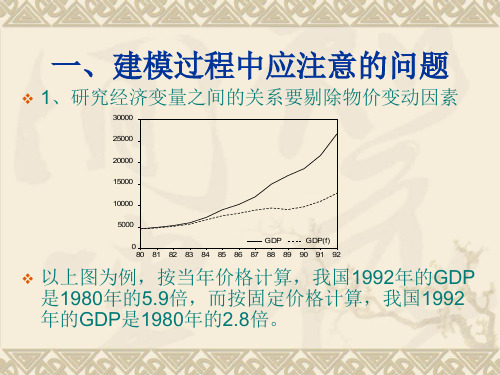
以上图为例，按当年价格计算，我国1992年的GDP 是1980年的5.9倍，而按固定价格计算，我国1992 年的GDP是80年的2.8倍。
2、依照经济理论以及对具体经济问题的深入
分析初步确定解释变量。例：关于某市的食用油消费量，文革前常驻人口肯定是重要解释变量。现在则不同，消费水平是重要解释变量，因为食用油供应方式已改变。 3、当引用现成数据时，要注意数据的定义是否与所选定的变量定义相符。例：“农业人口”要区别是“从事农业劳动的人口”还是相对于城市人口的“农业人口”。
t
案例2：《全国味精需求量的计量经济模型》
1．依据经济理论选择影响味精需求量变化的因素依据经济理论初设为：商品需求量 = f (商品价格，代用品价格，收入水平，消费者偏好) 根据分析，针对味精需求量只考虑两个重要解释变量，商品价格和消费者收入水平。味精需求量 = f (商品价格，收入水平)
一建模过程中应注意的问题?1研究经济变量之间的关系要剔除物价变动因素?以上图为例按当年价格计算我国1992年的gdp是1980年的59倍而按固定价格计算我国1992年的gdp是1980年的28倍
一、建模过程中应注意的问题

1、研究经济变量之间的关系要剔除物价变动因素
30000 25000 20000 15000 10000 5000 GD P GD P(f) 0 80 81 82 83 84 85 86 87 88 89 90 91 92
4、通过散点图，相关系数，确定解释变量与
被解释变量的具体函数关系。（线性、非线性、无关系）
5、谨慎对待离群值（outlier）。离群值可能是正常
值也可能是异常值。不能把建立模型简单化为一个纯数学过程，目的是寻找经济规律。（欧盟对华投资和中国从欧盟进口）

第三章多元线性回归模型案例

第三章多元线性回归模型案例第三章多元线性回归模型案例⼀、邹式检验（突变点检验、稳定性检验） 1.突变点检验1985—2002年中国家⽤汽车拥有量（t y ，万辆）与城镇居民家庭⼈均可⽀配收⼊（t x ，元），数据见表3.1。

表3.1 中国家⽤汽车拥有量（t y ）与城镇居民家庭⼈均可⽀配收⼊（t x ）数据年份 t y （万辆）t x （元）年份 t y （万辆）t x （元）1985 28.49 739.1 1994 205.42 3496.2 1986 34.71 899.6 1995 249.96 4283 1987 42.29 1002.2 1996 289.67 4838.9 1988 60.42 1181.4 1997 358.36 5160.3 1989 73.12 1375.7 1998 423.65 5425.1 1990 81.62 1510.2 1999 533.88 5854 1991 96.04 1700.6 2000 625.33 6280 1992 118.2 2026.6 2001 770.78 6859.6 1993155.772577.42002968.987702.8下图是关于t y 和t x 的散点图：从上图可以看出，1996年是⼀个突变点，当城镇居民家庭⼈均可⽀配收⼊突破4838.9元之后，城镇居民家庭购买家⽤汽车的能⼒⼤⼤提⾼。

现在⽤邹突变点检验法检验1996年是不是⼀个突变点。

H 0：两个⼦样本（1985—1995年，1996—2002年）相对应的模型回归参数相等 H 1：备择假设是两个⼦样本对应的回归参数不等。

在1985—2002年样本范围内做回归。

在回归结果中作如下步骤：输⼊突变点：得到如下验证结果：由相伴概率可以知道，拒绝原假设，即两个样本（1985—1995年，1996—2002年）的回归参数不相等。

所以，1996年是突变点。

2.稳定性检验以表3.1为例，在⽤1985—1999年数据建⽴的模型基础上，检验当把2000—2002年数据加⼊样本后，模型的回归参数时候出现显著性变化。

多元线性回归模型案例(DOC)

多元线性回归模型案例分析——中国人口自然增长分析一·研究目的要求中国从1971年开始全面开展了计划生育,使中国总和生育率很快从1970年的5.8降到1980年2.24,接近世代更替水平。

此后，人口自然增长率（即人口的生育率）很大程度上与经济的发展等各方面的因素相联系，与经济生活息息相关，为了研究此后影响中国人口自然增长的主要原因，分析全国人口增长规律，与猜测中国未来的增长趋势，需要建立计量经济学模型。

影响中国人口自然增长率的因素有很多，但据分析主要因素可能有：（1）从宏观经济上看，经济整体增长是人口自然增长的基本源泉；（2）居民消费水平，它的高低可能会间接影响人口增长率。

(3)文化程度，由于教育年限的高低，相应会转变人的传统观念，可能会间接影响人口自然增长率（4）人口分布，非农业与农业人口的比率也会对人口增长率有相应的影响。

二·模型设定为了全面反映中国“人口自然增长率”的全貌，选择人口增长率作为被解释变量，以反映中国人口的增长；选择“国名收入”及“人均GDP”作为经济整体增长的代表；选择“居民消费价格指数增长率”作为居民消费水平的代表。

暂不考虑文化程度及人口分布的影响。

从《中国统计年鉴》收集到以下数据（见表1）：表1 中国人口增长率及相关数据设定的线性回归模型为：1222334t t t t t Y X X X u ββββ=++++三、估计参数利用EViews 估计模型的参数，方法是：1、建立工作文件：启动EViews ，点击File\New\Workfile ，在对话框“Workfile Range ”。

在“Workfile frequency ”中选择“Annual ” (年度)，并在“Start date ”中输入开始时间“1988”，在“end date ”中输入最后时间“2005”，点击“ok ”，出现“Workfile UNTITLED ”工作框。

其中已有变量：“c ”—截距项 “resid ”—剩余项。

《2024年多元线性回归分析的实例研究》范文

《多元线性回归分析的实例研究》篇一一、引言多元线性回归分析是一种统计方法，用于研究多个变量之间的关系。

在社会科学、经济分析、医学等多个领域，这种分析方法的应用都十分重要。

本实例研究以一个具体的商业案例为例，展示了如何应用多元线性回归分析方法进行研究，以便深入理解和探索各个变量之间的潜在关系。

二、背景介绍以某电子商务公司的销售额预测为例。

电子商务公司销售量的影响因素很多，包括市场宣传、商品价格、消费者喜好等。

因此，本文通过收集多个因素的数据，使用多元线性回归分析，以期达到更准确的销售预测和因素分析。

三、数据收集与处理为了进行多元线性回归分析，我们首先需要收集相关数据。

在本例中，我们收集了以下几个关键变量的数据：销售额（因变量）、广告投入、商品价格、消费者年龄分布、消费者性别比例等。

这些数据来自电子商务公司的历史销售记录和调查问卷。

在收集到数据后，我们需要对数据进行清洗和处理。

这包括去除无效数据、处理缺失值、标准化处理等步骤。

经过处理后，我们可以得到一个干净且结构化的数据集，为后续的多元线性回归分析提供基础。

四、多元线性回归分析1. 模型建立根据所收集的数据和实际情况，我们建立了如下的多元线性回归模型：销售额= β0 + β1广告投入+ β2商品价格+ β3消费者年龄分布+ β4消费者性别比例+ ε其中，β0为常数项，β1、β2、β3和β4为回归系数，ε为误差项。

2. 模型参数估计通过使用统计软件进行多元线性回归分析，我们可以得到每个变量的回归系数和显著性水平等参数。

这些参数反映了各个变量对销售额的影响程度和方向。

3. 模型检验与优化为了检验模型的可靠性和准确性，我们需要对模型进行假设检验、R方检验和残差分析等步骤。

同时，我们还可以通过引入交互项、调整自变量等方式优化模型，提高预测精度。

五、结果分析与讨论1. 结果解读根据多元线性回归分析的结果，我们可以得到以下结论：广告投入、商品价格、消费者年龄分布和消费者性别比例均对销售额有显著影响。

多元线性回归模型案例

我国农民收入影响因素的回归分析本文力图应用适当的多元线性回归模型,对有关农民收入的历史数据和现状进行分析,探讨影响农民收入的主要因素,并在此基础上对如何增加农民收入提出相应的政策建议。

?农民收入水平的度量常采用人均纯收入指标。

影响农民收入增长的因素是多方面的，既有结构性矛盾因素，又有体制性障碍因素。

但可以归纳为以下几个方面：一是农产品收购价格水平。

二是农业剩余劳动力转移水平。

三是城市化、工业化水平。

四是农业产业结构状况。

五是农业投入水平。

考虑到复杂性和可行性，所以对农业投入与农民收入，本文暂不作讨论。

因此，以全国为例，把农民收入与各影响因素关系进行线性回归分析，并建立数学模型。

一、计量经济模型分析 (一)、数据搜集根据以上分析，我们在影响农民收入因素中引入7个解释变量。

即：2x -财政用于农业的支出的比重，3x -第二、三产业从业人数占全社会从业人数的比重，4x -非农村人口比重，5x -乡村从业人员占农村人口的比重，6x -农业总产值占农林牧总产值的比重，7x -农作物播种面积，8x —农村用电量。

资料来源《中国统计年鉴2006》。

(二)、计量经济学模型建立我们设定模型为下面所示的形式：利用Eviews 软件进行最小二乘估计，估计结果如下表所示：DependentVariable:Y Method:LeastSquares Sample:Includedobservations:19VariableCoefficientt-StatisticProb.C X1 X3 X4 X5 X6 X7 X8R-squaredMeandependentvarAdjustedR-squared 表1最小二乘估计结果回归分析报告为：()()()()()()()()()()()()()()()()23456782ˆ -1102.373-6.6354X +18.2294X +2.4300X -16.2374X -2.1552X +0.0100X +0.0634X 375.83 3.7813 2.066618.37034 5.8941 2.77080.002330.02128 -2.933 1.7558.820900.20316 2.7550.778 4.27881 2.97930.99582i Y SE t R ===---=230.99316519 1.99327374.66R Df DW F ====二、计量经济学检验(一)、多重共线性的检验及修正①、检验多重共线性 (a)、直观法从“表1最小二乘估计结果”中可以看出，虽然模型的整体拟合的很好，但是x4x6的t统计量并不显着，所以可能存在多重共线性。

多元线性回归实例分析

SPSS--回归—多元线性回归模型案例解析！（一）多元线性回归，主要是研究一个因变量与多个自变量之间的相关关系，跟一元回归原理差不多，区别在于影响因素（自变量）更多些而已，例如：一元线性回归方程为：毫无疑问，多元线性回归方程应该为：上图中的x1, x2, xp分别代表“自变量”Xp截止，代表有P个自变量，如果有“N组样本，那么这个多元线性回归，将会组成一个矩阵，如下图所示：那么，多元线性回归方程矩阵形式为:其中:代表随机误差，其中随机误差分为:可解释的误差和不可解释的误差，随机误差必须满足以下四个条件，多元线性方程才有意义（一元线性方程也一样）1：服成正太分布，即指：随机误差必须是服成正太分别的随机变量。

2:无偏性假设，即指:期望值为03:同共方差性假设，即指，所有的随机误差变量方差都相等4：独立性假设，即指：所有的随机误差变量都相互独立，可以用协方差解释.今天跟大家一起讨论一下，SPSS—-—多元线性回归的具体操作过程，下面以教程教程数据为例，分析汽车特征与汽车销售量之间的关系。

通过分析汽车特征跟汽车销售量的关系，建立拟合多元线性回归模型.数据如下图所示：点击“分析”——回归——线性——进入如下图所示的界面：将“销售量”作为“因变量"拖入因变量框内，将“车长，车宽，耗油率，车净重等10个自变量拖入自变量框内，如上图所示,在“方法”旁边,选择“逐步”，当然，你也可以选择其它的方式，如果你选择“进入”默认的方式，在分析结果中，将会得到如下图所示的结果：（所有的自变量，都会强行进入）如果你选择“逐步”这个方法，将会得到如下图所示的结果：(将会根据预先设定的“F统计量的概率值进行筛选，最先进入回归方程的“自变量”应该是跟“因变量”关系最为密切，贡献最大的,如下图可以看出，车的价格和车轴跟因变量关系最为密切,符合判断条件的概率值必须小于0.05，当概率值大于等于0.1时将会被剔除）“选择变量(E）" 框内,我并没有输入数据，如果你需要对某个“自变量”进行条件筛选，可以将那个自变量,移入“选择变量框”内，有一个前提就是：该变量从未在另一个目标列表中出现！，再点击“规则”设定相应的“筛选条件”即可，如下图所示：点击“统计量"弹出如下所示的框，如下所示：在“回归系数”下面勾选“估计，在右侧勾选”模型拟合度“ 和”共线性诊断“ 两个选项,再勾选“个案诊断”再点击“离群值”一般默认值为“3",（设定异常值的依据,只有当残差超过3倍标准差的观测才会被当做异常值）点击继续。

多元线性回归模型案例分析报告

多元线性回归模型案例分析——中国人口自然增长分析一·研究目的要求中国从1971年开始全面开展了计划生育,使中国总和生育率很快从1970年的5.8降到1980年2.24,接近世代更替水平.此后,人口自然增长率<即人口的生育率>很大程度上与经济的发展等各方面的因素相联系,与经济生活息息相关,为了研究此后影响中国人口自然增长的主要原因,分析全国人口增长规律,与猜测中国未来的增长趋势,需要建立计量经济学模型.影响中国人口自然增长率的因素有很多,但据分析主要因素可能有：<1>从宏观经济上看,经济整体增长是人口自然增长的基本源泉；<2>居民消费水平,它的高低可能会间接影响人口增长率.〕3〔文化程度,由于教育年限的高低,相应会转变人的传统观念,可能会间接影响人口自然增长率<4>人口分布,非农业与农业人口的比率也会对人口增长率有相应的影响.二·模型设定为了全面反映中国"人口自然增长率"的全貌,选择人口增长率作为被解释变量,以反映中国人口的增长；选择"国名收入"及"人均GDP"作为经济整体增长的代表；选择"居民消费价格指数增长率"作为居民消费水平的代表.暂不考虑文化程度及人口分布的影响.从《中国统计年鉴》收集到以下数据<见表1>：表1中国人口增长率及相关数据设定的线性回归模型为：三、估计参数利用EViews 估计模型的参数,方法是：1、建立工作文件：启动EViews,点击File\New\Workfile,在对话框"Workfile Range".在"Workfile frequency"中选择"Annual" 〕年度〔,并在"Start date"中输入开始时间"1988",在"end date"中输入最后时间"2005",点击"ok",出现"Workfile UNTITLED"工作框.其中已有变量："c"—截距项"resid"—剩余项.在"Objects"菜单中点击"New Objects",在"New Objects"对话框中选"Group",并在"Name for Objects"上定义文件名,点击"OK"出现数据编辑窗口.2、输入数据：点击"Quik"下拉菜单中的"Empty Group",出现"Group"窗口数据编辑框,点第一列与"obs"对应的格,在命令栏输入"Y",点下行键"↓",即将该序列命名为Y,并依此输入Y 的数据.用同年份人口自然增长率<%.> 国民总收入<亿元> 居民消费价格指数增长率<CPI>% 人均GDP<元> 1988 15.73 15037 18.8 1366 1989 15.04 17001 18 1519 1990 14.39 18718 3.1 1644 1991 12.98 21826 3.4 1893 1992 11.6 26937 6.4 2311 1993 11.45 35260 14.7 2998 1994 11.21 48108 24.1 4044 1995 10.55 59811 17.1 5046 1996 10.42 70142 8.3 5846 1997 10.06 78061 2.8 6420 1998 9.14 83024 -0.8 6796 1999 8.18 88479 -1.4 7159 2000 7.58 98000 0.4 7858 2001 6.95 108068 0.7 8622 2002 6.45 119096 -0.8 9398 2003 6.01 135174 1.2 10542 2004 5.87 159587 3.9 12336 2005 5.89 184089 1.8 14040 20065.38 213132 1.5 16024样方法在对应的列命名X 2、X 3、X 4,并输入相应的数据.或者在EViews 命令框直接键入"data Y 2X X 3 X 4… ",回车出现"Group"窗口数据编辑框,在对应的Y 、X 2、X 3、X 4下输入响应的数据.3、估计参数：点击"Procs"下拉菜单中的"Make Equation",在出现的对话框的"Equation Specification"栏中键入"Y C X 2 X 3 X 4",在"Estimation Settings"栏中选择"Least Sqares"〕最小二乘法〔,点"ok",即出现回归结果：表3.4根据表3.4中数据,模型估计的结果为：〕0.913842〔〕0.000134〔〕0.033919〔〕0.001771〔t= 〕17.08010〔〕2.482857〔〕1.412721〔〕-2.884953〔930526.02=R 915638.02=R F=62.50441四、模型检验1、经济意义检验模型估计结果说明,在假定其它变量不变的情况下,当年国民总收入每增长1亿元,人口增长率增长0.000332%；在假定其它变量不变的情况下,当年居民消费价格指数增长率每增长 1%,人口增长率增长0.047918%；在假定其它变量不变的情况下,当年人均GDP 没增加一元,人口增长率就会降低0.005109%.这与理论分析和经验判断相一致.2、统计检验<1>拟合优度：由表3.4中数据可以得到：930526.02=R ,修正的可决系数为915638.02=R,这说明模型对样本的拟合很好.<2>F 检验：针对0234:0H βββ===,给定显著性水平0.05α=,在F 分布表中查出自由度为k-1=3和n-k=14的临界值34.3)14,3(=αF .由表3.4中得到F=62.50441,由于F=62.50441 >(3,21) 3.075F α=,应拒绝原假设0234:0H βββ===,说明回归方程显著,即"国民总收入"、"居民消费价格指数增长率"、"人均GDP"等变量联合起来确实对"人口自然增长率"有显著影响.<3>t 检验：分别针对0H ：0(1,2,3,4)j j β==,给定显著性水平0.05α=,查t 分布表得自由度为n-k=14临界值145.2)(2/=-k n t α.由表3.4中数据可得,与^1β、^2β、^3β、^4β对应的t 统计量分别为17.08010、2.482857、1.412721、-2.884953除^3β,其绝对值均大于145.2)(2/=-k n t α,这说明分别都应当拒绝0H ：)4,2,1(0==j j β,也就是说,当在其它解释变量不变的情况下,解释变量"国民总收入"、"人均GDP"分别对被解释变量"人口自然增长率"Y 都有显著的影响.^3β的绝对值小于145.2)(2/=-k n t α,：这说明接受0H ：03=β,X3系数对t 检验不显著,这表明很可能存在多重共线性.所以计算各解释变量的相关系数,选择X2、X3、X4数据,点"view/correlations"得相关系数矩阵<如表4.4>：表4.4由相关系数矩阵可以看出：各解释变量相互之间的相关系数较高,证实确实存在严重多重共线性. 五、消除多重共线性采用逐步回归的办法,去检验和解决多重共线性问题.分别作Y 对X2、X3、X4的一元回归,结果如表4.5所示：表4.5按2R 的大小排序为：X4、X2、X3以X2为基础,顺次加入其他变量逐步回归.首先加入X2回归结果为：t=〕2.542529〔〕-2.970874〔 920622.02=R当取05.0=α时,131.2)318(025.0)(2/=-=-tt k n α,X2参数的t 检验显著,加入X3回归得t= 〕17.08010〔〕2.482857〔〕1.412721〔〕-2.884953〔930526.02=R 915638.02=R F=62.50441当取05.0=α时,145.2)418(2/=-αt ,X3参数的t 检验不显著,予以剔除即40005397.02000350.035540.16ˆX X Y -+=,这是最后消除多重共线性的结果.在假定其它变量不变的情况下,当年国民总收入每增长1亿元,人口增长率增长0.000332%；在假定其它变量不变的情况下,在假定其它变量不变的情况下,当年人均GDP 没增加一元,人口增长率就会降低0.005109%.金服131 王亚平13019122。

SPSS多元线性回归分析实例操作步骤-spss做多元线性回归

SPSS 统计分析多元线性回归分析方法操作与分析实验目的：引入1998~2008年上海市城市人口密度、城市居民人均可支配收入、五年以上平均年贷款利率和房屋空置率作为变量，来研究上海房价的变动因素。

实验变量：以年份、商品房平均售价（元/平方米）、上海市城市人口密度(人/平方公里)、城市居民人均可支配收入(元)、五年以上平均年贷款利率(%)和房屋空置率(%)作为变量。

实验方法：多元线性回归分析法软件：spss19.0操作过程：第一步：导入Excel数据文件1.open data document——open data——open；2.Opening excel data s ource——OK.第二步：1.在最上面菜单里面选中Analyze——Regression——Linear，Depende n（t因变量）选择商品房平均售价，Independents（自变量）选择城市人口密度、城市居民人均可支配收入、五年以上平均年贷款利率、房屋空置率；Method 选择Stepwise.进入如下界面：2.点击右侧Statistics，勾选Regression Coefficients（回归系数）选项组中的Estimates；勾选Residuals（残差）选项组中的Durbin-Watson、Casewise diagnostics 默认；接着选择Model fit、Collinearity diagnotics；点击Continue.3.点击右侧Plots，选择*ZPRED（标准化预测值）作为纵轴变量，选择DEPENDN T（因变量）作为横轴变量；勾选选项组中的Standardized Residual Plo t（s标准化残差图）中的Histogram、Normal probability plot；点击Continue.4.点击右侧Save，勾选Predicted Vaniues（预测值）和Residuals（残差）选项组中的Unstandardized；点击Continue.5.点击右侧Options，默认，点击Continue.a. Predictors: (Constant), 城市人口密度 (人/平方公里)b. Predictors: (Constant), 城市人口密度 (人/平方公里), 城市居民人均可支配收入(元)c. Dependent Variable: 商品房平均售价（元/平方米）Variables Entered/Removed aModel 1Variables Entered 城市人口密度 (人/平方公里)Variables Removed2城市居民人均可支配收入(元)Method. Stepwise (Criteria: Probability-of-F-to-enter <= .050,Probability-of-F-to-remove >= .100).. Stepwise (Criteria: Probability-of-F-to-enter <= .050,Probability-of-F-to-remove >= .100).a. Dependent Variable: 商品房平均售价（元/平方米）该表显示模型的拟合情况。

多元线性回归方法及其应用实例

多元线性回归方法及其应用实例多元线性回归方法（Multiple Linear Regression）是一种广泛应用于统计学和机器学习领域的回归分析方法，用于研究自变量与因变量之间的关系。

与简单线性回归不同，多元线性回归允许同时考虑多个自变量对因变量的影响。

多元线性回归建立了自变量与因变量之间的线性关系模型，通过最小二乘法估计回归系数，从而预测因变量的值。

其数学表达式为：Y=β0+β1X1+β2X2+...+βnXn+ε，其中Y是因变量，Xi是自变量，βi是回归系数，ε是误差项。

1.房价预测：使用多个自变量（如房屋面积、地理位置、房间数量等）来预测房价。

通过建立多元线性回归模型，可以估计出各个自变量对房价的影响权重，从而帮助房产中介或购房者进行房价预测和定价。

2.营销分析：通过分析多个自变量（如广告投入、促销活动、客户特征等）与销售额之间的关系，可以帮助企业制定更有效的营销策略。

多元线性回归可以用于估计各个自变量对销售额的影响程度，并进行优化。

3.股票分析：通过研究多个自变量（如市盈率、市净率、经济指标等）与股票收益率之间的关系，可以辅助投资者进行股票选择和投资决策。

多元线性回归可以用于构建股票收益率的预测模型，并评估不同自变量对收益率的贡献程度。

4.生理学研究：多元线性回归可应用于生理学领域，研究多个自变量（如年龄、性别、体重等）对生理指标（如心率、血压等）的影响。

通过建立回归模型，可以探索不同因素对生理指标的影响，并确定其重要性。

5.经济增长预测：通过多元线性回归，可以将多个自变量（如人均GDP、人口增长率、外商直接投资等）与经济增长率进行建模。

这有助于政府和决策者了解各个因素对经济发展的影响力，从而制定相关政策。

在实际应用中，多元线性回归方法有时也会面临一些挑战，例如共线性（多个自变量之间存在高度相关性）、异方差性（误差项方差不恒定）、自相关（误差项之间存在相关性）等问题。

为解决这些问题，研究人员提出了一些改进和扩展的方法，如岭回归、Lasso回归等。

多元线性回归实例分析报告

多元线性回归实例分析报告多元线性回归是一种用于预测目标变量和多个自变量之间关系的统计分析方法。

它可以帮助我们理解多个自变量对目标变量的影响，并通过建立回归模型进行预测。

本文将以一个实例为例，详细介绍多元线性回归的分析步骤和结果。

假设我们研究了一个电子产品公司的销售数据，并想通过多元线性回归来预测销售额。

我们收集了以下数据：目标变量（销售额）和三个自变量（广告费用、产品种类和市场规模）。

首先，我们需要对数据进行探索性分析，了解数据的分布、缺失值等情况。

我们可以使用散点图和相关系数矩阵来查看变量之间的关系。

通过绘制广告费用与销售额的散点图，我们可以观察到一定的正相关关系。

相关系数矩阵可以用来度量变量之间的线性关系的强度和方向。

接下来，我们需要构建多元线性回归模型。

假设目标变量（销售额）与三个自变量（广告费用、产品种类和市场规模）之间存在线性关系，模型可以表示为：销售额=β0+β1*广告费用+β2*产品种类+β3*市场规模+ε其中，β0是截距，β1、β2和β3是回归系数，ε是误差项。

我们可以使用最小二乘法估计回归系数。

最小二乘法可以最小化目标变量的预测值和实际值之间的差异的平方和。

通过计算最小二乘估计得到的回归系数，我们可以建立多元线性回归模型。

在实际应用中，我们通常使用统计软件来进行多元线性回归分析。

通过输入相应的数据和设置模型参数，软件会自动计算回归系数和其他统计指标。

例如，我们可以使用Python的statsmodels库或R语言的lm函数来进行多元线性回归分析。

最后，我们需要评估回归模型的拟合程度和预测能力。

常见的评估指标包括R方值和调整R方值。

R方值可以描述自变量对因变量的解释程度，值越接近1表示拟合程度越好。

调整R方值考虑了模型中自变量的个数，避免了过度拟合的问题。

在我们的实例中，假设我们得到了一个R方值为0.8的多元线性回归模型，说明模型可以解释目标变量80%的方差。

这个模型还可以用来进行销售额的预测。

基于SPSS多元线性回归分析的案例

农民收入影响因素的多元回归分析自改革开放以来,虽然中国经济平均增长速度为9.5 % ,但二元经济结构给经济发展带来的问题仍然很突出。

农村人口占了中国总人口的70 %多,农业产业结构不合理,经济不发达,以及农民收入增长缓慢等问题势必成为我国经济持续稳定增长的障碍。

正确有效地解决好“三农”问题是中国经济走出困境,实现长期稳定增长的关键。

其中,农民收入增长是核心,也是解决“三农”问题的关键。

本文力图应用适当的多元线性回归模型,对有关农民收入的历史数据和现状进行分析,寻找其根源,探讨影响农民收入的主要因素,并在此基础上对如何增加农民收入提出相应的政策建议。

一、回归模型的建立（1）数据的收集根据实际的调查分析，我们在影响农民收入因素中引入3个解释变量。

即：X2-财政用于农业的支出的比重，X3-乡村从业人员占农村人口的比重，X4 -农作物播种面积1991223.2510.2650.92149585.8 1992233.1910.0551.53149007.1 1993265.679.4951.86147740.7 1994335.169.252.12148240.6 1995411.298.4352.41149879.3 1996460.688.8253.23152380.6 1997477.968.354.93153969.2 1998474.0210.6955.84155705.7 1999466.88.2357.16156372.8 2000466.167.7559.33156299.9 2001469.87.7160.62155707.9 2002468.957.1762.02154635.5 2003476.247.1263.721524152004499.399.6765.64153552.6 2005521.27.2267.59155487.7（1）回归模型的构建Y i=1+2X2+3X3+4X4+u i二、回归模型的分析（1）多重共线性检验系数a(2)模型异方差的检验异方差产生的原因有：数据质量原因、模型设定原因。

多元线性回归模型的案例分析

多元线性回归模型的案例分析在实际生活中，多元线性回归模型可以广泛应用于各个领域。

以下是一个案例分析，以说明多元线性回归模型的应用。

案例：房价预测背景：城市的房地产公司想要推出一款房屋估价服务，帮助人们预测房屋的销售价格。

他们收集了一些相关数据，如房屋的面积、房间的数量、地理位置等因素，并希望通过建立一个多元线性回归模型来实现房价的预测。

步骤：1.数据收集：收集相关数据。

在本案例中，我们收集到了50个样本数据，每个样本包含了房屋的面积、房间的数量和房屋的销售价格。

2.数据预处理：对数据进行预处理，包括缺失值处理、异常值处理等。

在本案例中，我们假设数据已经经过清洗，没有缺失值和异常值。

3.特征选择：选择合适的特征变量。

在本案例中，我们选择房屋的面积和房间的数量作为特征变量，房屋的销售价格作为目标变量。

4.模型建立：建立多元线性回归模型。

根据特征变量和目标变量的关系，建立多元线性回归方程。

在本案例中，假设多元线性回归方程为：房价=β0+β1×面积+β2×房间数量+ε，其中β0、β1和β2分别为回归系数，ε为误差项。

5.模型训练：使用样本数据对模型进行训练。

通过最小二乘法等方法，估计出回归系数的取值。

6.模型评估：评估模型的性能。

通过计算模型的均方误差（MSE）、决定系数（R²）等指标，评估模型的拟合效果和预测能力。

7.模型应用：将模型用于房价的预测。

当有新的房屋数据输入时，通过模型的预测方程，可以得到该房屋的预测销售价格。

通过上述步骤，我们可以建立一个多元线性回归模型，并通过该模型对房价进行预测。

这个模型可以帮助房地产公司提供房价估价服务，也可以帮助购房者了解合理的房价范围。

多元线性回归spss案例

多元线性回归spss案例【篇一：多元线性回归spss案例】多元线性回归，主要是研究一个因变量与多个自变量之间的相关关系，跟一元回归原理差不多，区别在于影响因素（自变量）更多些而已，例如：一元线性回归方程为：毫无疑问，多元线性回归方程应该为：上图中的x1, x2, xp分别代表自变量xp截止，代表有p个自变量，如果有 n组样本，那么这个多元线性回归，将会组成一个矩阵，如下图所示：那么，多元线性回归方程矩阵形式为：其中：代表随机误差，其中随机误差分为：可解释的误差和不可解释的误差，随机误差必须满足以下四个条件，多元线性方程才有意义（一元线性方程也一样）1：服成正太分布，即指：随机误差必须是服成正太分别的随机变量。

2：无偏性假设，即指：期望值为03：同共方差性假设，即指，所有的随机误差变量方差都相等4：独立性假设，即指：所有的随机误差变量都相互独立，可以用协方差解释。

今天跟大家一起讨论一下，spss---多元线性回归的具体操作过程，下面以教程教程数据为例，分析汽车特征与汽车销售量之间的关系。

通过分析汽车特征跟汽车销售量的关系，建立拟合多元线性回归模型。

数据如下图所示：点击分析回归线性进入如下图所示的界面：将销售量作为因变量拖入因变量框内，将车长，车宽，耗油率，车净重等10个自变量拖入自变量框内，如上图所示，在方法旁边，选择逐步，当然，你也可以选择其它的方式，如果你选择进入默认的方式，在分析结果中，将会得到如下图所示的结果：（所有的自变量，都会强行进入）如果你选择逐步这个方法，将会得到如下图所示的结果：（将会根据预先设定的 f统计量的概率值进行筛选，最先进入回归方程的自变量应该是跟因变量关系最为密切，贡献最大的，如下图可以看出，车的价格和车轴跟因变量关系最为密切，符合判断条件的概率值必须小于0.05，当概率值大于等于0.1时将会被剔除）选择变量(e) 框内，我并没有输入数据，如果你需要对某个自变量进行条件筛选，可以将那个自变量，移入选择变量框内，有一个前提就是：该变量从未在另一个目标列表中出现！，再点击规则设定相应的筛选条件即可，如下图所示：点击统计量弹出如下所示的框，如下所示：在回归系数下面勾选估计，在右侧勾选模型拟合度和共线性诊断两个选项，再勾选个案诊断再点击离群值一般默认值为 3 ，（设定异常值的依据，只有当残差超过3倍标准差的观测才会被当做异常值）点击继续。

多元线性回归案例分析

多元线性回归案例分析案例背景:我们假设有一家制造业公司，想要研究员工的工作效率与其工作经验、教育水平和工作时间之间的关系。

公司收集了100名员工的数据，并希望通过多元线性回归模型来分析这些变量之间的关系。

数据收集:公司收集了每个员工的工作效率(因变量)、工作经验、教育水平和工作时间(自变量)的数据。

假设工作效率由工作经验、教育水平和工作时间这三个因素决定。

根据所收集的数据，我们可以建立如下的多元线性回归模型:工作效率=β0+β1*工作经验+β2*教育水平+β3*工作时间+ε在这个模型中，β0、β1、β2和β3分别是待估参数，代表截距和自变量的系数；ε是误差项，代表模型中未被解释的因素。

模型参数的估计:通过最小二乘法可以对模型中的参数进行估计。

最小二乘法的目标是让模型的预测值与观测值之间的残差平方和最小化。

模型诊断:在对模型进行参数估计后，我们需要对模型进行诊断，以评估模型的质量和稳定性。

常见的模型诊断方法包括：检查残差的正态分布、残差与自变量的无关性、残差的同方差性等。

模型解释和预测:根据参数估计结果，可以对模型进行解释和预测。

例如，我们可以解释每个自变量与因变量之间的关系，并分析它们的显著性。

我们还可以通过模型进行预测，比如预测一位具有一定工作经验、教育水平和工作时间的员工的工作效率。

结果分析:根据对模型的诊断和解释，我们可以对结果进行分析。

我们可以得出结论，一些自变量对因变量的影响显著，而其他自变量对因变量的影响不显著。

这些结论可以帮助公司更好地理解员工工作效率与工作经验、教育水平和工作时间之间的关系，并采取相应的管理措施来提高工作效率。

总结:通过以上的案例分析，我们可以看到多元线性回归在实际中的应用。

它可以帮助我们理解多个自变量与一个因变量之间的关系，并对因变量进行预测和解释。

通过多元线性回归分析，我们可以更好地了解因素对于结果的作用，并根据分析结果进行决策和管理。

然而，需要注意的是，多元线性回归的结果可能受到多种因素的影响，我们需要综合考虑所有的因素来做出准确的分析和决策。

多元线性回归分析案例

SPSS19.0实战之多元线性回归分析(2011-12-09 12:19:11)转载▼分类：软件介绍标签：文化线性回归数据（全国各地区能源消耗量与产量）来源，可点击协会博客数据挖掘栏：国泰安数据服务中心的经济研究数据库。

1.1 数据预处理数据预处理包括的内容非常广泛，包括数据清理和描述性数据汇总，数据集成和变换，数据归约，数据离散化等。

本次实习主要涉及的数据预处理只包括数据清理和描述性数据汇总。

一般意义的数据预处理包括缺失值填写和噪声数据的处理。

于此我们只对数据做缺失值填充，但是依然将其统称数据清理。

1.1.1 数据导入与定义单击“打开数据文档”，将xls格式的全国各地区能源消耗量与产量的数据导入SPSS中，如图1-1所示。

图1-1 导入数据导入过程中，各个字段的值都被转化为字符串型（String），我们需要手动将相应的字段转回数值型。

单击菜单栏的“ ”-->“ ”将所选的变量改为数值型。

如图1-2所示：图1-2 定义变量数据类型1.1.2 数据清理数据清理包括缺失值的填写和还需要使用SPSS分析工具来检查各个变量的数据完整性。

单击“ ”-->“ ”，将检查所输入的数据的缺失值个数以及百分比等。

如图1-3所示：图1-3缺失值分析能源数据缺失值分析结果如表1-1所示：单变量统计N均值标准差缺失极值数目a计数百分比低高能源消费总量309638.506175.9240.001煤炭消费量309728.997472.2590.002焦炭消费量30874.611053.0080.002原油消费量281177.511282.7442 6.701汽油消费量30230.05170.2700.001煤油消费量2845.4066.1892 6.704柴油消费量30392.34300.9790.002燃料油消费量30141.00313.4670.003天然气消费量3019.5622.0440.002电力消费量30949.64711.6640.003原煤产量269125.9712180.689413.302焦炭产量291026.491727.7351 3.302原油产量181026.481231.7241240.000燃料油产量2590.72134.150516.703汽油产量26215.18210.090413.302煤油产量2048.4462.1301033.300柴油产量26448.29420.675413.301天然气产量2029.2849.3911033.303电力产量30954.74675.2300.000表2-1 能源消耗量与产量数据缺失值分析表1-1 能源消耗量与产量数据缺失值分析SPSS提供了填充缺失值的工具，点击菜单栏“ ”-->“ ”，即可以使用软件提供的几种填充缺失值工具，包括序列均值，临近点中值，临近点中位数等。

多元回归分析原理及例子

多元回归分析原理回归分析是一种处理变量的统计相关关系的一种数理统计方法。

回归分析的基本思想是: 虽然自变量和因变量之间没有严格的、确定性的函数关系, 但可以设法找出最能代表它们之间关系的数学表达形式。

回归分析主要解决以下几个方面的问题:(1) 确定几个特定的变量之间是否存在相关关系, 如果存在的话, 找出它们之间合适的数学表达式;(2) 根据一个或几个变量的值, 预测或控制另一个变量的取值, 并且可以知道这种预测或控制能达到什么样的精确度;(3) 进行因素分析。

例如在对于共同影响一个变量的许多变量(因素)之间, 找出哪些是重要因素,哪些是次要因素, 这些因素之间又有什么关系等等。

回归分析有很广泛的应用, 例如实验数据的一般处理, 经验公式的求得, 因素分析, 产品质量的控制, 气象及地震预报, 自动控制中数学模型的制定等等。

多元回归分析是研究多个变量之间关系的回归分析方法, 按因变量和自变量的数量对应关系可划分为一个因变量对多个自变量的回归分析(简称为“一对多”回归分析)及多个因变量对多个自变量的回归分析(简称为“多对多”回归分析), 按回归模型类型可划分为线性回归分析和非线性回归分析。

本“多元回归分析原理”是针对均匀设计3.00软件的使用而编制的, 它不是多元回归分析的全面内容, 欲了解多元回归分析的其他内容请参阅回归分析方面的书籍。

本部分内容分七个部分, §1～§4介绍“一对多”线性回归分析, 包括数学模型、回归系数估计、回归方程及回归系数的显著性检验、逐步回归分析方法。

“一对多”线性回归分析是多元回归分析的基础, “多对多”回归分析的内容与“一对多”的相应内容类似, §5介绍“多对多”线性回归的数学模型, §6介绍“多对多”回归的双重筛选逐步回归法。

§7简要介绍非线性回归分析。

§1 一对多线性回归分析的数学模型§2 回归系数的最小二乘估计§3 回归方程及回归系数的显著性检验§4 逐步回归分析§5 多对多线性回归数学模型§6 双重筛选逐步回归§7 非线性回归模型1 一对多线性回归分析的数学模型§个自变量存在线性关系设随机变量与:, (1.1)式中为回归系数, 为随机误差。

多元回归分析SPSS案例

多元回归分析在大多数的实际问题中，影响因变量的因素不是一个而是多个，我们称这类回问题为多元回归分析。

可以建立因变量y与各自变量x j（j=1，2，3,…,n）之间的多元线性回归模型：其中：b0是回归常数；b k（k=1,2，3，…,n)是回归参数；e是随机误差。

多元回归在病虫预报中的应用实例：某地区病虫测报站用相关系数法选取了以下4个预报因子；x1为最多连续10天诱蛾量（头）;x2为4月上、中旬百束小谷草把累计落卵量(块);x3为4月中旬降水量(毫米)，x4为4月中旬雨日（天)；预报一代粘虫幼虫发生量y(头/m2）.分级别数值列成表2—1。

预报量y:每平方米幼虫0~10头为1级,11~20头为2级，21～40头为3级，40头以上为4级。

预报因子：x1诱蛾量0～300头为l级，301~600头为2级,601~1000头为3级,1000头以上为4级；x2卵量0～150块为1级，15l～300块为2级,301~550块为3级，550块以上为4级；x3降水量0～10.0毫米为1级,10。

1~13。

2毫米为2级，13.3～17。

0毫米为3级,17。

0毫米以上为4级；x4雨日0~2天为1级,3~4天为2级,5天为3级，6天或6天以上为4级.表2-1x1 x2 x3 x4 y年蛾量级别卵量级别降水量级别雨日级别幼虫密度级别1960 1022 4 112 1 4.3 1 2 1 10 1 1961 300 1 440 3 0。

1 1 1 1 4 1 1962 699 3 67 1 7.5 1 1 1 9 1 1963 1876 4 675 4 17.1 4 7 4 55 4 1965 43 1 80 1 1.9 1 2 1 1 1 1966 422 2 20 1 0 1 0 1 3 1 1967 806 3 510 3 11.8 2 3 2 28 3 1976 115 1 240 2 0.6 1 2 1 7 1 1971 718 3 1460 4 18.4 4 4 2 45 4 1972 803 3 630 4 13。