第六章风荷载内力计算
风荷载标准值
风荷载标准值关于风荷载计算风荷载是高层建筑的主要侧向荷载之一。
结构抗风分析（包括荷载、内力、位移、加速度等）是高层建筑设计计算中的重要因素。
脉动风和稳定风建筑表面的风荷载不均匀。
它具有静态作用（长周期部分）和动态作用（短周期部分）的双重特性。
静态作用变成稳定的风，而动态部分是我们经常接触的脉动风。
脉动风的作用是引起高层建筑的振动（简称风振）。
以顺风向这一单一角度来分析风载，我们又常常称静力稳定风为平均风，称动力脉动风为阵风。
平均风对结构的作用相当于静力，只要知道平均风的数值，就可以按结构力学的方法来计算构件内力。
阵风对结构的作用是动力的，结构在脉动风的作用下将产生风振。
注：无论风向如何，只要是在风荷载的结构计算理论中，脉动风一定是随机荷载。
因此，一般确定性结构动力分析方法不能用于分析脉动风对结构的动力影响，而应基于随机振动理论和概率统计方法。
从风振的性质看顺风向和横风向风力顺风风力分为平均风力和阵风。
平均风力相当于静力，不会引起振动。
阵风相当于功率并引起振动，但它会引起随机振动。
也就是说，除了静态风之外，沿着风向的风是脉动风。
不存在会导致周期性风振动的周期性风力。
绝对不是。
至少在风荷载的结构计算理论方面，沿着风向没有周期性风力。
横风向，既有周期性振动又有随机振动。
换句话说就是既有周期性风力又有脉动风。
反映在荷载上，它可能是周期性荷载，也可能是随机性荷载，随着雷诺数的大小而定。
一些计算方法根据现有的研究成果，风对结构作用的计算，分为以下三个不同的方面：（1）对于沿风向的平均风，采用静力计算方法（2）对于顺风向的脉动风，或横风向脉动风，则应按随机振动理论计算（3）对于横风向的周期性风力，或引起扭转振动的外部扭矩，通常将结构的动力计算作为稳定荷载进行风荷载标准值的表达可有两种形式，其一为平均风压加上由脉动风引起导致结构风振的等效风压；另一种为平均风压乘以风振系数。
由于在结构的风振计算中，一般往往是第1振型起主要作因此，与大多数国家一样，中国采用了后一种表达式，即风致振动系数βz。
钢结构的风荷载设计
钢结构的风荷载设计钢结构是一种广泛应用于建筑领域的结构形式，其设计过程是一个复杂而重要的环节。
在钢结构设计中，风荷载是必须考虑的关键因素之一。
本文将介绍钢结构的风荷载设计方法和相关的规范标准。
一、设计准则和规范在进行钢结构的风荷载设计时，需要参考相关的设计准则和规范，以确保结构的安全可靠。
目前国内常用的规范有《建筑结构荷载规范》(GB 50009-2012)和《钢结构设计规范》(GB 50017-2017)等。
这些规范对于风荷载的计算方法、风荷载分区、风荷载系数等都有详细的规定。
二、风荷载计算方法风荷载计算是钢结构设计过程中最关键的一步。
根据规范的要求，一般可以采用静力法或动力法进行计算。
静力法适用于简单结构和小型建筑，而动力法适用于高层建筑和大型桥梁等复杂结构。
1. 静力法静力法是一种简化的计算方法，其基本原理是将风荷载作为静力荷载来进行计算。
根据规范中的公式和风荷载分区图，可以确定各个部位的风荷载大小。
然后，根据结构的受力情况，进行内力计算和构件设计。
2. 动力法动力法是一种更加精确的计算方法，可以考虑结构的动力响应和风荷载的变化规律。
在动力法中，需要进行风洞试验或数值模拟，获取结构在风场中的响应数据，然后进行计算分析。
动力法适用于高层建筑、桥梁和塔吊等复杂结构，可以更好地反映实际情况。
三、风荷载分区根据规范的要求，建筑结构需要进行风荷载的分区计算。
通常将结构划分为不同的区域，根据风荷载的大小和分布特点，确定各个区域的风荷载系数。
常见的风荷载分区有正压区、负压区、顶部区域和支撑结构区域等。
四、风荷载系数钢结构的风荷载设计中，需要根据规范中的要求，确定相应的风荷载系数。
通常，风荷载系数分为平面方向系数、垂直方向系数和结构特殊性系数等。
1. 平面方向系数平面方向系数描述了风荷载对结构平面产生的影响。
根据规范的要求，根据结构的高度、宽度和长度等参数，确定相应的平面方向系数。
常见的平面方向系数有气候区系数、重要性系数、高度修正系数等。
(整理)风荷载作用下框架内力计算
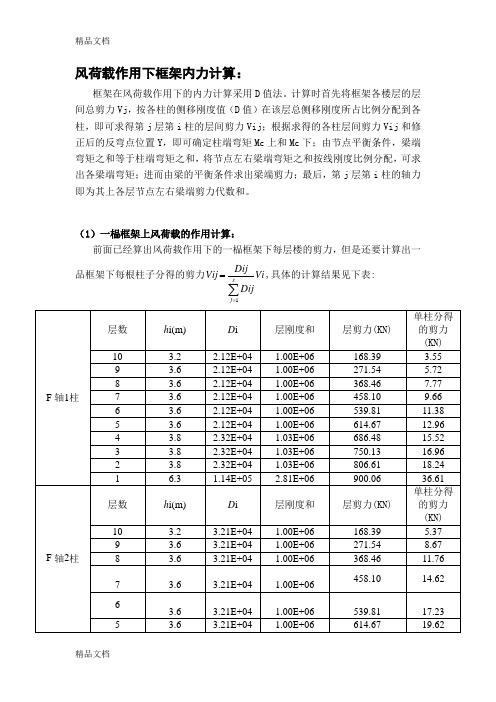
风荷载作用下框架内力计算：框架在风荷载作用下的内力计算采用D 值法。
计算时首先将框架各楼层的层间总剪力Vj ，按各柱的侧移刚度值（D 值）在该层总侧移刚度所占比例分配到各柱，即可求得第j 层第i 柱的层间剪力Vij ；根据求得的各柱层间剪力Vij 和修正后的反弯点位置Y ，即可确定柱端弯矩Mc 上和Mc 下；由节点平衡条件，梁端弯矩之和等于柱端弯矩之和，将节点左右梁端弯矩之和按线刚度比例分配，可求出各梁端弯矩；进而由梁的平衡条件求出梁端剪力；最后，第j 层第i 柱的轴力即为其上各层节点左右梁端剪力代数和。
（1）一榀框架上风荷载的作用计算：前面已经算出风荷载作用下的一榀框架下每层楼的剪力，但是还要计算出一品框架下每根柱子分得的剪力Vi DijDijVij sj ∑==1,具体的计算结果见下表:（2）风荷载作用下反弯点高度的计算:反弯点高度比即: V=V0+V1+V2+V3式中:V0 ——标准层反弯点高度比；注：本框架风荷载采用分段式均布荷载，故可查《高层建筑结构设计》表5.8a。
V1 ——因上、下层梁刚度比变化的修正值，查《高层建筑结构设计》表5.9；V2 ——因上层层高变化的修正值，查《高层建筑结构设计》表5.10；V3 ——因下层层高变化的修正值，查《高层建筑结构设计》表5.10。
具体计算结果见下表：（3）计算各柱端、梁端弯矩:①柱端弯矩计算：柱上下端弯矩按式：M u = V (1 - y)h，M d = Vyh计算；②梁端弯矩计算：梁端弯矩按式M = i b / ∑ i b ⨯ (M u + M d )具体结果如下：（4）计算各梁端剪力:计算方法：以梁为隔离体根据力矩平衡可得到梁端剪力。
具体计算结果如下表：注：单位为KN（5）计算各柱轴力:计算方法：已知梁的剪力，由上到下利用节点的竖向力平衡条件，即可得到柱的轴力，计算方法同恒。
（6）风荷载作用下的内力图绘制:风载作用下的梁端、柱端弯矩，梁端柱端剪力，柱的轴力计算完毕，恒载作用下的标准值如下几图所示：手算风荷载作用下柱端弯矩图手算风荷载作用下两端弯矩图与电算内力图的比较：电算风荷载作用下柱端弯矩图电算风荷载作用下两端弯矩图误差分析：风荷载作用下梁柱剪力图的绘制与误差分析：手算风荷载作用下的梁柱剪力图电算风荷载作用下的梁柱剪力图误差分析：风荷载作用下柱轴力图的绘制与误差分析：手算风荷载作用下的柱轴力图电算风荷载作用下的柱轴力图误差分析：水平地震作用下框架内力计算：框架在水平地震荷载作用下的内力计算采用D值法。
风荷载
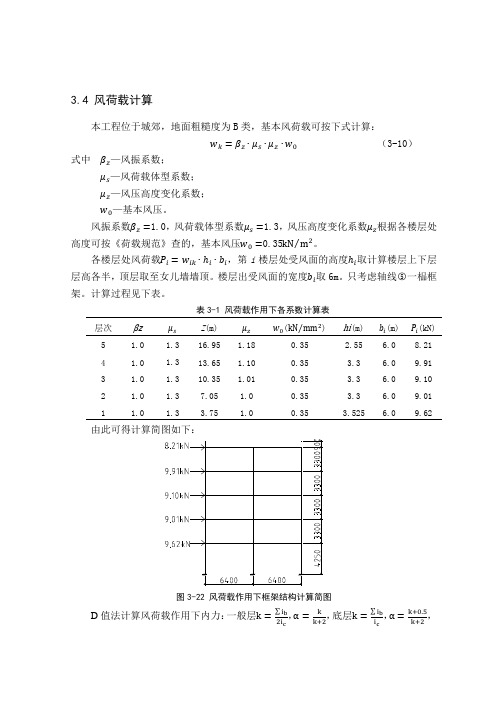
3.4 风荷载计算本工程位于城郊，地面粗糙度为B类，基本风荷载可按下式计算：w k=βz∙μs∙μz∙w0（3-10）式中βz—风振系数；μs—风荷载体型系数；μz—风压高度变化系数；w0—基本风压。
风振系数βz=1.0，风荷载体型系数μs=1.3，风压高度变化系数μz根据各楼层处高度可按《荷载规范》查的，基本风压w0=0.35kN m2⁄。
各楼层处风荷载P i=w ik∙ℎi∙b i，第i楼层处受风面的高度ℎi取计算楼层上下层层高各半，顶层取至女儿墙墙顶。
楼层出受风面的宽度b i取6m。
只考虑轴线○5一榀框架。
计算过程见下表。
表3-1 风荷载作用下各系数计算表层次βzμs Z(m) μz w0(kN mm2⁄) hi(m) b i(m) P i(kN)5 1.0 1.316.95 1.18 0.35 2.55 6.0 8.21图3-22 风荷载作用下框架结构计算简图D值法计算风荷载作用下内力：一般层k=∑i b2i c ，α=kk+2，底层k=∑i bi c，α=k+0.5k+2，柱子的抗侧移刚度D =α12i c h j2，计算结果如下表：表3-2 框架柱抗侧移刚度计算表层次 柱的类型 kα D （kN m ⁄）2~5层 中柱 (1根) 2.44 0.550 1.884×104 边柱（2根） 1.22 0.379 1.298×104 底层中柱（1根） 3.15 0.709 1.138×104 边柱（2根）1.570.5800.931×104注：∑i b 指框架梁线刚度之和，i c 指柱子的线刚度，k 指框架梁柱线刚度比，α指柱侧向线刚度降低系数。
3.4.1 各楼层风荷载剪力计算风荷载作用下各层剪力可按公式3-11计算： V jk =D jk∑D jk mk=1V j (3-11) 式中 V jk —第j 层第k 柱所分配到的剪力； D jk —第j 层第k 柱的侧向刚度D 值； m —第j 层框架柱数；V j —第j 层框架柱所承受的层间总剪力。
等效风荷载计算方法
等效静力风荷载的物理意义从风洞试验获取屋面风荷载气动力信息，到得到结构的风振响应整个过程来看，计算过程中涉及到风洞试验和随机振动分析等复杂过程，不易为工程设计人员所掌握，因此迫切需要研究简便的建筑结构抗风设计方法。
等效静力风荷载理论就是在这一背景下提出的。
其基本思想是将脉动风的动力效应以其等效的静力形式表达出来，从而将复杂的动力分析问题转化为易于被设计人员所接受的静力分析问题。
等效静力风荷载是联系风工程研究和结构设计的纽带[3]，是结构抗风设计理论的核心内容，近年来一直是结构风工程师研究的热点之一。
等效静力风荷载的物理意义可以用单自由度体系的简谐振动来说明[45, 108]。
图1.3 气动力作用下的单自由度体系对如图1.3的单自由度体系，在气动力()P t 作用下的振动方程为：()mx cx kx P t ++= (1.4.1)考虑粘滞阻尼系统，则振动方程可简化为：()()()200222P t x f x f x mξππ++=(1.4.2)式中0f =为该系统的自振频率，ξ=为振动系统的临界阻尼比。
假设气动力为频率为f 的简谐荷载，即()20i ft P t F e π=，那么其稳态响应为：()()()2020012i ft F kx t e f f i f f πξ=-+⋅ (1.4.3)进一步化简有：()()2i ft x t Ae πψ-= (1.4.4)其中A =，()0202arctan1f f f f ξψ=-，A 为振幅，ψ为气动力和位移响应之间的相位角。
现在假设该系统在某静力F 作用下产生幅值为A 的静力响应，那么该静力应该为：F kA ==(1.4.5)如果不考虑相位关系，静力F 与简谐气动力()P t 将产生一致的幅值响应，则这两种荷载之间存在一种“等效”的关系，那么F 可以称为()P t 的“等效静力风荷载”。
从上面这个简单的实例可以很清楚的体会到，所谓等效静力风荷载是指这样一种静力荷载，当把它作用于结构上时，其在结构上产生的静力响应（不仅指代位移响应，也包括内力响应等）与外加气动力荷载产生的动力响应最大幅值是完全相等的。
高层建筑结构设计 第06章 剪力墙结构内力计算
为简化计算，可将上述三式写成统一公式，并取G=0.4E 可得到整截面墙的等效刚度计算公式为
Ec Ieq Ec Iw
1
9Iw
AwH 2
引入等效刚度，可把剪切变形与弯曲变形 综合成弯曲变形的表达形式
11
V0
H
3
倒三角荷载
60 EIeq
1
V0
H
3
8 EIeq
• 内力 先将整体小开
口墙视为一个上 端自由、下端固 定的竖向悬臂构 件，如图所示， 计算出标高处 （第i楼层）截面 的总弯矩和总剪 力，再计算各墙 肢的内力。
• 墙肢的弯矩 将总弯矩Mi分为两部 分，其一为产生整体
弯曲的弯矩；另一为
产生局部弯曲的局部 弯矩，如图所示。
• 第j墙肢承受的全部弯矩可按下式计算
当剪力墙各墙段错开距离a不大于实体连接墙厚度的 8倍，并且不大于2.5m时，整片墙可以作为整体平 面剪力墙考虑；计算所得的内力应乘以增大系数1.2， 等效刚度应乘以折减系数0.8。当折线形剪力墙的各 墙段总转角不大于15°时，可按平面剪力墙考虑。
6.2 整体墙和小开口整体墙的计算
6.2.1 整体墙的内力和位移计算 1、墙体截面内力
Mi (x)
0.85M p (x)
Ii I
0.15M p (x)
Ii Ii
式中，Ii第i个墙肢的惯性矩，
I 对组合截面形心的组合截面惯性矩。
I I j Aj y2
• 墙肢的剪力 第j墙肢的剪力可近似按下式计算
Vi
1 2
Vp
A Ai
Ii Ii
输电线路风荷载的全方位计算
输电线路风荷载的全方位计算摘要：在高压架空送电线路设计中，最不利风向时的风荷载常决定着杆塔内力大小或基础作用力的大小。
本文将通过几个工程实例详细说明在高压架空送电线路设计中，如何确定几种特殊情况下最不利风向时的风荷载计算，以确保高压架空送电线路的安全运行。
关键词：全方位;基础作用力;运行情况;不平衡张力;风荷载Abstract: In the project design of overhead transmission lines, the most unfavorable wind direction, wind load often determines the internal force of tower or base force size. This article will through several engineering examples in detail in the overhead transmission line design, how to determine some special situations the most unfavorable wind direction wind load calculation, to ensure the high voltage overhead power transmission line safe operation.Key words: all-around; base forces; operation; unbalanced tension; wind load1 引言在高压架空送电线路设计中，杆塔荷载的计算应执行《110～750kV架空输电线路设计规范》（以下简称《规程》）中第10条“杆塔荷载及材料”。
其中正常运行情况下，应计算的荷载组合是：1 基本风速、无冰、未断线；2 设计覆冰、相应风速及气温、未断线3 最低气温、无冰、无风、未断线（适用于终端和转角杆塔）本文主要针对上述第一种情况，在正常运行大风情况下计算铁塔内力或基础作用力时可能出现的漏洞。
对风荷载计算的一点认识
目前规范[2]按主体结构和围护结构对风荷载的计 算进行了区分，基本公式如下： wk z s z w0 (2)
wk gz s1 z w0
(3)
上述两个公式分别用于主体结构计算和围护结 构计算，两个公式都是用静力等效的方法把复杂问题 简单化，在基本风压 w0 的基础上分别乘以相应系数。 其中，风压高度变化系数 μz、风荷载体型系数 μs 和局 部体型系数 μs1 主要与风的空间不均匀性有关；风振 系数 βz 和阵风系数 βgz 主要与风的时间脉动性和结构 阻尼特性有关。各参数的相关关系如图 2 所示（引自 中国建筑科学研究院陈凯博士的讲座演示文档）。
(a) 分区归并前体型系数极小值
（b） 分区归并前体型系数极大值
和分区归并等，分区归并是将相近测点的数据进行人 为归并以达到简化模型输入目的。图 4 给出了某体育 场屋盖结构风荷载体型系数分区归并前后的示意。需 要注意的是，当屋面高度变化较大时，归并的区块不
（上接第 32 页） 图 7 所示：9）套筒焊缝高出部分全部打磨平整，外观要求 光滑平整；10）Q100LY 和 Q345 芯材对接前要预热，预热 温度 150℃左右，层间温度不能大于 250℃，最终的预热工 艺与焊条选择需要焊接工艺评定后确定。 3 结论 （1）建立了巨型屈曲约束支撑的 ABAQUS 模型，对
图 3 新旧பைடு நூலகம்范风压高度变化系数对比
2.2.2 横风向、扭转风振等效风荷载的计算 《新荷规》对横风向和扭转风振进行了更明确的 规定。设计人员需了解什么情况下考虑横风向风振作 用，什么情况下考虑扭转风振作用。对体型简单规则 的建筑规范附录提供了简化计算公式，平面和立面体 型复杂的建筑宜通过风洞试验确定。 一般而言，以下两类建筑需要考虑横风向风振的 影响：1）建筑高度超过 150m 或高宽比大于 5 的高层
风荷载作用下框架内力计算
风荷载作用下框架内力计算：框架在风荷载作用下的内力计算采用D 值法。
计算时首先将框架各楼层的层间总剪力Vj ，按各柱的侧移刚度值（D 值）在该层总侧移刚度所占比例分配到各柱，即可求得第j 层第i 柱的层间剪力Vij ；根据求得的各柱层间剪力Vij和修正后的反弯点位置Y ，即可确定柱端弯矩Mc 上和Mc 下；由节点平衡条件，梁端弯矩之和等于柱端弯矩之和，将节点左右梁端弯矩之和按线刚度比例分配，可求出各梁端弯矩；进而由梁的平衡条件求出梁端剪力；最后，第j 层第i 柱的轴力即为其上各层节点左右梁端剪力代数和。
（1）一榀框架上风荷载的作用计算：前面已经算出风荷载作用下的一榀框架下每层楼的剪力，但是还要计算出一品框架下每根柱子分得的剪力,具体的计算结果见下表:Vi DijDijVij sj ∑==1层数h i(m)D i层刚度和层剪力(KN)单柱分得的剪力(KN)10 3.2 2.12E+04 1.00E+06168.39 3.55 9 3.6 2.12E+04 1.00E+06271.54 5.72 8 3.6 2.12E+04 1.00E+06368.46 7.77 7 3.6 2.12E+04 1.00E+06458.10 9.66 6 3.6 2.12E+04 1.00E+06539.81 11.38 5 3.6 2.12E+04 1.00E+06614.67 12.96 4 3.8 2.32E+04 1.03E+06686.48 15.52 3 3.8 2.32E+04 1.03E+06750.13 16.96 2 3.8 2.32E+04 1.03E+06806.61 18.24 F 轴1柱1 6.31.14E+052.81E+06900.06 36.61 层数h i(m)D i层刚度和层剪力(KN)单柱分得的剪力(KN)10 3.2 3.21E+04 1.00E+06168.39 5.37 9 3.6 3.21E+04 1.00E+06271.54 8.67 8 3.6 3.21E+04 1.00E+06368.46 11.76 7 3.6 3.21E+04 1.00E+06458.10 14.62 6 3.6 3.21E+04 1.00E+06539.81 17.23 5 3.6 3.21E+04 1.00E+06614.67 19.62 4 3.8 3.96E+04 1.03E+06686.48 26.51 F 轴2柱33.83.96E+041.03E+06750.1328.972 3.8 3.96E+04 1.03E+06806.61 31.15 1 6.3 1.31E+05 2.81E+06900.06 41.86层数h i(m)D i层刚度和层剪力(KN)单柱分得的剪力(KN)10 3.2 3.21E+04 1.00E+06168.39 5.379 3.6 3.21E+04 1.00E+06271.54 8.678 3.6 3.21E+04 1.00E+06368.46 11.767 3.6 3.21E+04 1.00E+06458.10 14.626 3.6 3.21E+04 1.00E+06539.81 17.235 3.6 3.21E+04 1.00E+06614.67 19.624 3.8 3.96E+04 1.03E+06686.48 26.513 3.8 3.96E+04 1.03E+06750.13 28.972 3.8 3.96E+04 1.03E+06806.61 31.15 F轴3柱1 6.3 1.31E+05 2.81E+06900.06 41.86层数h i(m)D i层刚度和层剪力(KN)单柱分得的剪力(KN)10 3.2 2.12E+04 1.00E+06168.39 3.559 3.6 2.12E+04 1.00E+06271.54 5.728 3.6 2.12E+04 1.00E+06368.46 7.777 3.6 2.12E+04 1.00E+06458.10 9.666 3.6 2.12E+04 1.00E+06539.81 11.385 3.6 2.12E+04 1.00E+06614.67 12.964 3.8 2.32E+04 1.03E+06686.48 15.523 3.8 2.32E+04 1.03E+06750.13 16.962 3.8 2.32E+04 1.03E+06806.61 18.24 F轴4柱1 6.3 1.14E+05 2.81E+06900.06 36.61（2）风荷载作用下反弯点高度的计算:反弯点高度比即: V=V0+V1+V2+V3式中:V0 ——标准层反弯点高度比；注：本框架风荷载采用分段式均布荷载，故可查《高层建筑结构设计》表5.8a。
建筑风荷载计算
风荷载标准值计算风荷载标准值计算公式为：0k z s z w w βμμ=，作用在屋面梁和楼面梁节点处的集中风荷载标准值计算公式为：0W z s z P w A βμμ= 式中：W P －作用于框架节点的集中风荷载标准值(KN) z β－风振系数s μ－风荷载体型系数 z μ－风压高度变化系数0w －基本风压（KN/㎡）A －一榀框架各层节点受风面积（㎡）本建筑基本风压为：200.3/w KN m =，由《荷载规范》得，地面粗糙为C 类。
s μ风荷载体系系数，根据建筑物体型查得 1.3s μ=。
z β风振系数，因结构总高度H=21.128m<30m ，故 1.0z β=。
风压高度变化系数z μ查《荷载规范》表7.2.1。
一榀框架各层节点受风面积A 计算，B 为3.3 3.9() 3.622m +=， h 取上层的一半和下层的一半之和，屋面层取到女儿墙顶，底层取底层的一半。
底层的计算高度从室外地面取()mm 45003004200=+。
一层： 24.5 3.9() 3.615.1222A m =+⨯= 二层： 23.9 3.9() 3.614.0422A m =+⨯=三层： 23.9 3.9() 3.614.0422A m =+⨯=四层： 23.9 3.9() 3.614.0422A m =+⨯=五层：23.9(1.50) 3.612.422A m =+⨯=计算过程见表所示：欠左风、右风荷载受荷简图框架梁柱线刚度计算框架梁柱线刚度计算见表表7-1 纵梁线刚度计算表表7-2 柱线刚度Ic 计算表7.2.2 侧移刚度D 值计算 考虑梁柱的线刚度比，用D 值法计算柱的侧位移刚度，表7-4 柱侧移刚度计算表2～5层柱D 值计算2～5层柱D 值合计：D ∑=1.572+1.572=3.144KN/m底层柱D 值计算低层柱D 值合计：D ∑=1.612+1.612=3.224KN/m 7.2.3 风荷载作用下框架位移的计算风荷载作用下框架的层间侧移可按下式计算，即jj ijV u D∆=∑式中：j V －第j 层的总剪力；ij D ∑－第j 层所有柱的抗侧刚度之和；j u ∆－第j 层的层间位移。
风荷载标准值
风荷载标准值关于风荷载计算风荷载是高层建筑主要侧向荷载之一，结构抗风分析（包括荷载，内力，位移，加速度等）是高层建筑设计计算的重要因素。
脉动风和稳定风风荷载在建筑物表面是不均匀的，它具有静力作用（长周期哦部分）和动力作用（短周期部分）的双重特点，静力作用成为稳定风，动力部分就是我们经常接触的脉动风。
脉动风的作用就是引起高层建筑的振动（简称风振）。
以顺风向这一单一角度来分析风载，我们又常常称静力稳定风为平均风，称动力脉动风为阵风。
平均风对结构的作用相当于静力，只要知道平均风的数值，就可以按结构力学的方法来计算构件内力。
阵风对结构的作用是动力的，结构在脉动风的作用下将产生风振。
注意：不管在何种风向下，只要是在结构计算风荷载的理论当中，脉动风一定是一种随机荷载，所以分析脉动风对结构的动力作用，不能采用一般确定性的结构动力分析方法，而应以随机振动理论和概率统计法为依据。
从风振的性质看顺风向和横风向风力顺风向风力分为平均风和阵风。
平均风相当于静力，不引起振动。
阵风相当于动力，引起振动但是引起的是一种随机振动。
也就是说顺风向风力除了静风就是脉动风，根本就没有周期性风力会引起周期性风振，绝对没有，起码从结构计算风载的理论上顺风向的风力不存在周期性风力。
横风向，既有周期性振动又有随机振动。
换句话说就是既有周期性风力又有脉动风。
反映在荷载上，它可能是周期性荷载，也可能是随机性荷载，随着雷诺数的大小而定。
有的计算方法根据现有的研究成果，风对结构作用的计算，分为以下三个不同的方面：（1）对于顺风向的平均风，采用静力计算方法（2）对于顺风向的脉动风，或横风向脉动风，则应按随机振动理论计算（3）对于横风向的周期性风力，或引起扭转振动的外扭矩，通常作为稳定性荷载，对结构进行动力计算风荷载标准值的表达可有两种形式，其一为平均风压加上由脉动风引起导致结构风振的等效风压；另一种为平均风压乘以风振系数。
由于在结构的风振计算中，一般往往是第1振型起主要作用，因而我国与大多数国家相同，采用后一种表达形式，即采用风振系数βz，它综合考虑了结构在风荷载作用下的动力响应，其中包括风速随时间、空间的变异性和结构的阻尼特性等因素。
风荷载标准值
风荷载标准值
风荷载标准值是将风力和风向按一定规定计算出来，用于对建筑物及其各种部件受风活动影响的程度进行参考的指标值。
一、计算标准
1. 计算参数：首先要确定计算的参数，包括计算的区域、风场及计算的强度均衡值之类的。
2. 计算方法：确定计算方法，根据计算所用的参数确定，一般可以采用大气环境的压力，蒸汽来源计算风压和风荷载的方法以及其他计算方法。
3. 风参数：还要确定不同区域不同时段的风参数，如最大风速，最大内力，均值风速等参数。
二、应用标准
1. 设计：确定构件在一定风速情况下，根据风荷载标准值，使用合理的设计方法防止受风活动的影响。
2. 检测：根据风荷载标准值，确定检测的点，进行受风影响的检测，确定预警阈值，保证建筑物安全使用。
3. 风环境：利用风荷载标准值，结合有限元分析，重点关注一些风环境，以确保设施及周围物体的安全。
三、风荷载标准值应用
1. 建筑物设计：根据风荷载标准值，对建筑物进行合理的设计，防止受风活动的影响，保证建筑物的安全使用。
2. 桥梁构件设计：根据风荷载标准值，对桥梁进行合理的设计，防止受风激励的影响，确保桥梁安全使用。
3. 钢结构确认：根据风荷载标准值，对钢梁等结构进行确认，确保钢梁等结构的安全使用。
4. 地面结构确认：根据风荷载标准值，确认地面结构，确保地面结构安全使用，
能够更好地抵御风荷载以及不利天气情况。
5. 抗震设计：根据风荷载标准值，对抗震设计进行确认，保证建筑物在发生地震情况下，不受外力影响，并能实现救援的目的。
风荷载标准值
风荷载标准值文件排版存档编号：[UYTR-OUPT28-KBNTL98-UYNN208]风荷载标准值关于风荷载计算风荷载是高层建筑主要侧向荷载之一，结构抗风分析（包括荷载，内力，位移，加速度等）是高层建筑设计计算的重要因素。
脉动风和稳定风风荷载在建筑物表面是不均匀的，它具有静力作用（长周期哦部分）和动力作用（短周期部分）的双重特点，静力作用成为稳定风，动力部分就是我们经常接触的脉动风。
脉动风的作用就是引起高层建筑的振动（简称风振）。
以顺风向这一单一角度来分析风载，我们又常常称静力稳定风为平均风，称动力脉动风为阵风。
平均风对结构的作用相当于静力，只要知道平均风的数值，就可以按结构力学的方法来计算构件内力。
阵风对结构的作用是动力的，结构在脉动风的作用下将产生风振。
注意：不管在何种风向下，只要是在结构计算风荷载的理论当中，脉动风一定是一种随机荷载，所以分析脉动风对结构的动力作用，不能采用一般确定性的结构动力分析方法，而应以随机振动理论和概率统计法为依据。
从风振的性质看顺风向和横风向风力顺风向风力分为平均风和阵风。
平均风相当于静力，不引起振动。
阵风相当于动力，引起振动但是引起的是一种随机振动。
也就是说顺风向风力除了静风就是脉动风，根本就没有周期性风力会引起周期性风振，绝对没有，起码从结构计算风载的理论上顺风向的风力不存在周期性风力。
横风向，既有周期性振动又有随机振动。
换句话说就是既有周期性风力又有脉动风。
反映在荷载上，它可能是周期性荷载，也可能是随机性荷载，随着雷诺数的大小而定。
有的计算方法根据现有的研究成果，风对结构作用的计算，分为以下三个不同的方面：（1）对于顺风向的平均风，采用静力计算方法（2）对于顺风向的脉动风，或横风向脉动风，则应按随机振动理论计算（3）对于横风向的周期性风力，或引起扭转振动的外扭矩，通常作为稳定性荷载，对结构进行动力计算风荷载标准值的表达可有两种形式，其一为平均风压加上由脉动风引起导致结构风振的等效风压；另一种为平均风压乘以风振系数。
风荷载作用下的内力和位移计算
风荷载作用下的内力和位移计算
风荷载作用下的内力和位移计算通常涉及以下步骤：
1.确定建筑物的风荷载标准以及建筑物的几何形状和尺寸参数；
2.计算建筑物的风荷载大小和方向，可采用建筑物结构设计规
范或专业软件进行计算；
3.将风荷载作用下的内力和位移分解为平面内力和垂直于平面
的剪力与弯矩，根据不同的加载条件，可以采用不同的计算方法进行计算；
4.通过应力-strain关系计算元件的应力和应变，然后对于剪切
应力和弯曲应力进行的评估。
对于抗弯性能较弱的构件，需要考虑稳定性及挠度分析；
5.通过数值算法，考虑各种边界条件下的结构位移情况，可以
计算出风荷载作用下的建筑物结构的整体变形情况，以评估结构的稳定性和安全性。
需要注意的是，针对不同的建筑物结构类型和工作条件，风荷载作用下的内力和位移计算方法可能会有所不同，需要设计师按照相关规范和标准进行具体的计算。
3.3.3 风荷载内力计算风荷载内力计算
三、在风荷载作用下内力计算对于作用在屋面的风荷载可以分解为水平方向的分力xq 和竖向分力yq 。
（1）在迎风面横梁上风荷载竖向分力2yqω作用下（见图）0206 3.333160.167610.04990.5973(3)30.5970.167(30.167) 4.125911=85=850.167=0.13381616 4.12591.8920kN 4.73kN 88( 1.8910 4.73)kN 14.17kN (4E A A E l H f h k h s k ql qlV V H H λμμλ===ψ=======++ψ+ψ=++⨯+=Φ+ψ⨯+⨯⨯-⨯===-=-⨯+=-==Φ=（）（）221.8920 3.3330.13384)kN 4.21kN 1.89200.1338kN=25.29kN 44BD ql MM-⨯⨯⨯=-⨯==Φ=⨯ 22[(1)]4C ql M α=-+ψΦ221.8920[0.5(10.167)0.1338]17.74kN =-⨯⨯-+=-17.74k N ·m在迎风面横梁上风荷载竖向分力作用的M 图(2) 在背风面横梁上风荷载竖向分力4yqω作用下（见图）4 1.23/q k N m ω=-0206 3.333160.167610.04990.5973(3)30.5970.167(30.167) 4.125911=85=850.167=0.13381616 4.12591.2320kN 3.08kN 88( 1.2310 3.08)kN 9.22kN 4A E A E l H f h k h s k ql qlV V H H λμμλ===ψ=======++ψ+ψ=++⨯+=Φ+ψ⨯+⨯⨯-⨯===-=-⨯+=-=-=-Φ=（）（）222222( 1.2320 3.3330.13384)kN 2.74kN 1.23200.1338kN=16.46kN 44[(1)] 1.2320[0.5(10.167)0.1338]411.54kN 4BDC ql ql MMM α--⨯⨯⨯=⨯==Φ=⨯=-+ψΦ=-⨯⨯-+=--11.54kN ·m在背风面横梁上风荷载竖向分力作用下M 图(3) 在迎风面柱上风荷载1q ω作用下（见图）A E020 3.333160.167610.04990.5973(3)30.5970.167(30.167) 4.12591l H f h k h s k λμα===ψ=======++ψ+ψ=++⨯+==222222211=[65]=[620.16750.597]=0.968744 4.12590.476kN 0.42kN22200.476(2)(20.9687)kN=4.36kN m4411(0.47 4.36)kN 2.1kN 62(0.476 2.1)kN 0.7kN[1(14A E B D A E C k qh l qh qh V V M M H H M μααΦ+ψ+++⨯⨯⨯=-==-=-⨯⨯==-Φ=-=⨯-==⨯-==-+ （2）（）220.4761)][1(10.167)0.9687]0.55kN m 4⨯⨯ψΦ=-+⨯=-(4) 在背风面柱上风荷载竖向分力3q ω作用下（见图）A E0206 3.333160.167610.04990.5973(3)30.5970.167(30.167) 4.12591l H f h k h s k λμα===ψ=======++ψ+ψ=++⨯+==22211=[65]=[620.16750.597]=0.968744 4.12591.046kN 0.94kN22201.04611(2)(20.9687)kN 4.73kN 2222(1.046 4.73) 1.51kN(4.736 1.0462)kN=9.66kN 1.516kN=9A E EA D Bk qh l qh V V H H M MμααΦ+ψ+++⨯⨯⨯=-==-=-⨯⨯⨯=--Φ=-⨯==⨯-==⨯-⨯=⨯（2）（）2222.06kN1.0461[1(1)][1(10.167)0.9687] 1.22kN 44C qh M α⨯⨯=-+ψΦ=-+⨯=-(5) 在迎风面横梁上风荷载水平分力2xq ω作用下（见图）160.167610.04990.5973(3)30.5970.167(30.167) 4.12591f h k h s k μαψ=======++ψ+ψ=++⨯+== 0.167=3=430.167=0.045588 4.12591.89161kN 0.61kN 22201.89110.0455kN 0.98kN 22(1.8910.98)0.91kN[0.5(1)]21.8916[0.50.167(10.167)2A E A E C qf h f l qf qfhV V H H M μψΦ+ψ+⨯⨯⨯=-=-+=-⨯+=⨯⨯=+Φ=+==⨯-==ψ-+ψΦ⨯⨯=⨯-+（4）（）（2）（2）（）（1）0.0455]0.17kN m0.986 5.88kN m0.916 5.46kN mB DM M⨯==⨯==⨯=C·m（6） 在背风面横梁上风荷载水平分力4xq ω作用下（见图）1.89k N/mA E160.167610.04990.5973(3)30.5970.167(30.167) 4.12591f h k h s k μαψ=======++ψ+ψ=++⨯+== 0.167=3=430.167=0.045588 4.12591.23161kN 0.40kN 22201.23110.0455kN 0.64kN 22(1.2310.64)0.59kN[0.5(1)]21.2316[0.50.167(10.167)2A E E A C qf h f l qf qfhV V H H M μψΦ+ψ+⨯⨯⨯=-=-+=-⨯+=⨯⨯=+Φ=+==⨯-==ψ-+ψΦ⨯⨯=⨯-+（4）（）（2）（2）（）（1）0.0455]0.11kN m0.596 3.54kN m0.646 3.84kN mB DM M⨯==⨯==⨯=A(7) 用叠加法绘制在风荷载作用下刚加的组合内力。
风荷载传力路径
风荷载传力路径风荷载传力路径是指风荷载从作用点开始，经过建筑物各构件和结构体系，最终传递到基础或地基上的整个过程。
在建筑工程中，对风荷载传力路径的准确分析和合理设计，对于确保建筑物的结构安全和稳定性具有重要意义。
一、风荷载的基本概念风荷载是指风对建筑物的作用力，主要包括风压力和风吸力。
风压力是指风吹向建筑物表面时产生的压力，而风吸力则是指风在建筑物背风面形成的负压。
风荷载的大小与风速、风压系数、建筑物形状、尺寸和位置等因素有关。
二、风荷载传力路径的组成风荷载传力路径主要由以下几个部分组成：1. 外围护结构：外围护结构是建筑物与外部环境直接接触的界面，包括外墙、屋顶和门窗等。
风荷载首先作用在外围护结构上，使其产生变形和内力。
2. 主体结构：主体结构是建筑物的承重骨架，包括梁、柱、楼板等。
外围护结构通过连接件与主体结构相连，将风荷载传递给主体结构。
3. 基础与地基：基础是建筑物与地基之间的连接部分，地基则是承受建筑物荷载的土体或岩体。
风荷载通过主体结构最终传递给基础和地基，由地基承担风荷载的作用。
三、风荷载传力路径的分析风荷载传力路径的分析主要包括以下几个方面：1. 确定风荷载作用点和方向：根据建筑物的形状、尺寸和位置等因素，确定风荷载的作用点和方向。
对于高层建筑，应考虑风荷载沿高度的变化。
2. 计算风荷载大小：根据风速、风压系数和建筑物形状等因素，计算风荷载的大小。
在计算过程中，应考虑建筑物的动态响应和风荷载的时程效应。
3. 分析外围护结构的传力机制：外围护结构在风荷载作用下会产生变形和内力，需要分析其传力机制。
对于柔性外围护结构，应考虑其变形对主体结构的影响；对于刚性外围护结构，应分析其与主体结构的相互作用。
4. 研究主体结构的传力路径：主体结构是风荷载传力路径的核心部分，需要研究其传力路径。
在分析过程中，应考虑主体结构的刚度、强度和稳定性等因素，以及各构件之间的相互作用。
5. 评估基础与地基的承载能力：基础与地基是风荷载传力路径的终点，需要评估其承载能力。
风荷载的计算
风荷载的计算垂直于建筑物外表上的风荷载标准值，应按以下公式计算：1、当计算主要承重构造时：Wk＝βz·μs·μz·W0 ……………………〔7.1.1-1〕式中：Wk----风荷载标准值〔KN/mm〕βz---高度Z处的风振系数；μs---风荷载体型系数；μz---风压高度变化系数；W0----根本风压〔KN/mm〕2、当计算维护构造时：Wk＝βgz·μs·μz·W0 ……………………〔7.1.1-2〕式中：βgz---高度Z处的阵风系数；根本风压应按本标准附录 D.4中附表 D.4给出的50年一遇的风压采用，但不得小于0.3KN/mm。
对于高层建筑、高耸构造以及风荷载比拟敏感的其它构造，根本风压应适当进步，并应由有关的构造设计标准详细规定。
一、风荷载计算1、标高为33.600处风荷载计算(1). 风荷载标准值计算:Wk: 作用在幕墙上的风荷载标准值(kN/m2)βgz: 33.600m高处阵风系数(按B类区计算):μf=0.5×(Z/10)-0.16＝0.412βgz=0.89×(1+2μf)=1.623μz: 33.600m高处风压高度变化系数(按B类区计算): (GB50009-2001)μz=(Z/10)0.32=1.474风荷载体型系数μs=1.50Wk=βgz×μz×μs×W0 (GB50009-2001)=1.623×1.474×1.5×0.600=2.153 kN/m2(2). 风荷载设计值:W: 风荷载设计值: kN/m2rw: 风荷载作用效应的分项系数：1.4按?建筑构造荷载标准?GB50009-2001随着现代高尚住宅的开展对铝合金门窗的要求越来越高，铝合金门窗不仅仅是框、扇的简单组合，而且要具备良好的物理性能〔风压强度、空气浸透、雨水渗漏等性能〕。
风荷载作用下的内力计算
计算如图所示的框架-剪力墙结构的风荷载及合力作用位置。
18层房屋总高度为58m ，地区的标准风压20w =0.64m KN ，
解：每个表面沿建筑物高度每米的风荷载是
z z 0iz si i i w =u u w cos B βα
其中w 0=1.1×0.64=0.7KN /m 2（《规范》中的基本风压是普通建筑，对于高层建筑而言，应乘以1.1的增大系数）
首先计算0si i i u w cos B α，按照8块表面积分别计算风力（压力或者吸力）在y 方向的投影值，投影后与y 坐标正向相同取正号，反之取负号，表面序号在O 中注明，计算如表1-1所示，
风力合力作用点距离原点 x 0=466.80/29.16=16m 框架剪力墙的基本周期的近似取值为0.07N,N 为结构层数
T=0.07×18=1.26s W 0T 2=0.7×1.262=1.11KN ·s 2/m 2 查表的ξ=1.45 B 类地区，v=0.35
i i z z z i z i z w =u w =u +=u +0.7629.16/m H H W KN H H βξν⎛⎫⎛
⎫⨯ ⎪ ⎪⎝⎭⎝⎭∑∑
计算结构如表1-2所示。
风荷载标准值
风荷载标准值关于风荷载计算风荷载是高层建筑主要侧向荷载之一;结构抗风分析包括荷载;内力;位移;加速度等是高层建筑设计计算的重要因素..脉动风和稳定风风荷载在建筑物表面是不均匀的;它具有静力作用长周期哦部分和动力作用短周期部分的双重特点;静力作用成为稳定风;动力部分就是我们经常接触的脉动风..脉动风的作用就是引起高层建筑的振动简称风振..以顺风向这一单一角度来分析风载;我们又常常称静力稳定风为平均风;称动力脉动风为阵风..平均风对结构的作用相当于静力;只要知道平均风的数值;就可以按结构力学的方法来计算构件内力..阵风对结构的作用是动力的;结构在脉动风的作用下将产生风振..注意：不管在何种风向下;只要是在结构计算风荷载的理论当中;脉动风一定是一种随机荷载;所以分析脉动风对结构的动力作用;不能采用一般确定性的结构动力分析方法;而应以随机振动理论和概率统计法为依据..从风振的性质看顺风向和横风向风力顺风向风力分为平均风和阵风..平均风相当于静力;不引起振动..阵风相当于动力;引起振动但是引起的是一种随机振动..也就是说顺风向风力除了静风就是脉动风;根本就没有周期性风力会引起周期性风振;绝对没有;起码从结构计算风载的理论上顺风向的风力不存在周期性风力..横风向;既有周期性振动又有随机振动..换句话说就是既有周期性风力又有脉动风..反映在荷载上;它可能是周期性荷载;也可能是随机性荷载;随着雷诺数的大小而定..有的计算方法根据现有的研究成果;风对结构作用的计算;分为以下三个不同的方面：1对于顺风向的平均风;采用静力计算方法2对于顺风向的脉动风;或横风向脉动风;则应按随机振动理论计算3对于横风向的周期性风力;或引起扭转振动的外扭矩;通常作为稳定性荷载;对结构进行动力计算风荷载标准值的表达可有两种形式;其一为平均风压加上由脉动风引起导致结构风振的等效风压；另一种为平均风压乘以风振系数..由于在结构的风振计算中;一般往往是第1振型起主要作用;因而我国与大多数国家相同;采用后一种表达形式;即采用风振系数βz;它综合考虑了结构在风荷载作用下的动力响应;其中包括风速随时间、空间的变异性和结构的阻尼特性等因素..W K=βzμsμZ W0W0基本风压WK 风荷载标准值βz z高度处的风振系数μs 风荷载体型系数μZ 风压高度变化系数基本风压值与风速大小有关..基本风压W0确定的标准条件务必记牢：空旷平坦平面;离地10m高;统计所得重现期为50年一遇和10min的平均最大风速V 为标准;并以W0=V2/1600来确定的..新的荷载规范将风荷载基本值的重现期由原来的30年一遇改为50年一遇且不得小于0.3kN/m2;新高规 3.2.2条规定:对于B级高度的高层建筑或特别重要的高层建筑;应按100年一遇的风压值采用..μZ 风压高度变化系数很明显在μZ表中可以看出高度10米以下的μZ基本小于一;10米以上的基本大于一..这是因为基本风压是按十米高度给出的;所以不同高度上的风压应将W0乘以高度系数得出..谈到μZ个人认为只要记住其和结构高度以及地面粗糙程度有关并弄明白为什么有关即可..A类：近海湖以及沙漠地区B类：田野乡村及中小城镇和大城市郊区C类：有密集建筑群的城市市区D类：有密集建筑群且房屋较高的城市市区一般的建筑都选B类;道理简单的很：这样μZ取值偏高;风荷载标准值偏高;计算偏安全..μs 风荷载体型系数个人认为一级结构在这里考的多且很到位..以规则矩形结构平面为例风荷载体型系数分为三类μs1迎风面体形系数μs2 背风面体形系数μs3 和μs4为侧风面体型系数μs1=0.80μs2=-0.48+0.03H/Lμs3=μs4=-0.60平常计算风荷载主要是以顺风方向进行计算;则μs=μs1-μs2=0.080+0.48+0.03H/L为什么上式是减号是因为迎风面的压力还是背风面的吸力其实都在一个方向上;所以要调整两者的符号;要他们绝对值加;其实上式完全可以写成：μs=/μs1/+/μs2/=0.080+0.48+0.03H/L另外工作中经常会发现一种现象对于基本矩形的建筑;有的设计院不经计算直接在正压区取1.5的体型系数;经验取值也只能进行经验的解释：多年来这个系数是这样来的;一般建筑正风压系数为+0.8;侧面-0.7;背面-0.5..假定风来袭时正面门窗开启或者时被风损坏;那么正面的风压将会作用到室内各个部分;故其侧面的风压将会是-0.7-0.8=-1.5.. 但是现代建筑功能复杂;房屋众多;一般不会容易出现这种最不利的情况..所以新版规范进行了修改;改为了内压0.2;正压提高到1.0..原规范大面风压体型系数取值1.5..注意：对于一些超高层;在需要更细致的进行风荷载计算的情况下;需要进行风洞试验;以此来确定风荷载体型系数..βz z高度处的风振系数风振系数主要是为了考虑风载波动中的动力作用脉动风力对建筑产生的振动效应..进一步说;风振系数加大了风荷载;把原来风荷载中的脉动部分加强后算在了静力荷载上;作用就可以按照静力作用计算风荷载效应了..这是一种近似的把动力问题化为静力计算的方法;可以大大简化设计工作..但是;如果建筑物的高度很大例如超过200m;特别是对于周期较长比较柔的结构;最好进行风洞试验..用通过实验得到的风对建筑物的作用作为设计依据较为安全可靠..风振系数牵连的东西最多;包括脉动增大系数;脉动影响系数;风压高度变化系数和振型系数\其中脉动增大系数又和周期;基本风载和粗糙程度有关而脉动影响系数又与H/B和粗糙程度有关。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
2.6 横向风荷载计算
2.6.1 自然情况
地区基本风压 W 0=0.70kN/m 2，地面粗糙程度B 类。
2.6.2 风荷载计算 （1） 风荷载标准值
0w w z s z k ⨯⨯⨯=μμβ，风荷载标准值见表2-6-1
表2-6-1 风荷载标准值
层数 β
Z
μ
S
μ
Zi
W 0 W k F Wki V i 6 1
1.3
1.19 0.70
1.083 8.87 8.87 5 1.14 1.037 1
2..40 21.27 4 1.063 0.965 11.71 32.98 3 1.00 0.910 10.97 4
3.95 2 1.00 0.910 10.65 5
4.60 1
1.00
0.910
12.24
66.84
注：（1）在实际工程中，对于高度不大于30M ，高宽比小于 1.5的高建筑，取风振系数βZ =1.0。
（2）
A w F ki w ki ⨯=。
1K F =0.910×3.9×（3.3+0.6）/2+0.910×3.9×1.5=12.24KN
2K F =0.910×3.9×1.5+0.910×3.9×1.5=10.65KN 3K F =0.910×3.9×1.5+0.965×3.9×1.5=10.97KN
4K F =0.965×3.9×1.5+1.037×3.9×1.5=11.711KN 5K F =1.037×3.9×1.5+1.083×3.9×1.5=12.24KN
6K F =1.083×3.9×1.5+1.083×3.9×0.6=8.87KN
（2）风荷载作用分布图，见图2-6-1
图2-6-1风荷载作用分布图
2.6.3风荷载作用下侧移计算
反弯点高度修正
()yh
+
+
y=
=
+
h
y
y
y
y
1
3
2
C柱（中框）反弯点计算，见表2-6-2
表2-6-2 C柱（中框）反弯点计算
层h(m) K y0 y1 y2 y3 y
6 3.0 0.746 0.30 0.00 0.00 0.00 0.30
5 3.0 0.74
6 0.40 0.00 0.00 0.00 0.40
4 3.0 0.746 0.40 0.00 0.00 0.00 0.40
3 3.0 0.746 0.45 0.00 0.00 0.00 0.45
2 3.0 0.746 0.50 0.00 0.00 0.00 0.50
1 4.3 0.704 0.70 0.00 0.00 0.00 0.70
B柱（中框）反弯点计算，见表2-6-3
表2-6-3 B柱（中框）反弯点计算
层h(m) K y0 y1 y2 y3 y
6 3.0 1.460 0.3
7 0.00 0.00 0.00 0.37
5 3.0 1.460 0.42 0.00 0.00 0.00 0.42
4 3.0 1.460 0.4
5 0.00 0.00 0.00 0.45
3 3.0 1.460 0.47 0.00 0.00 0.00 0.47
2 3.0 1.460 0.50 0.00 0.00 0.00 0.50
1 4.3 0.570 0.64 0.00 0.00 0.00 0.64
A柱（中框）反弯点计算，见表2-6-4
表2-6-4 A柱（中框）反弯点计算
层h(m) K y0 y1 y2 y3 y
6 3.0 0.711 0.30 0.00 0.00 0.00 0.30
5 3.0 0.711 0.40 0.00 0.00 0.00 0.40
4 3.0 0.711 0.41 0.00 0.00 0.00 0.41
3 3.0 0.711 0.41 0.00 0.00 0.00 0.41
2 3.0 0.711 0.50 0.00 0.00 0.00 0.50
1 4.3 0.669 0.70 0.00 0.00 0.00 0.70
2.6.4 风荷载作用下内力计算
（1）风荷载作用下柱端弯矩计算，见表2-6-5、表2-6-6、表2-6-7
表2-6-5 中框C柱柱端剪力和弯矩计算表
层H(m) ∑Di(KN/m) D(KN/m)D/∑Di Vi(kN) Vik(kN) y M下(KNm) M上(KNm) 6 3.0 43587 12410 0.285 8.87 2.53 0.30 2.28 5.31 5 3.0 43587 12410 0.285 21.27 6.06 0.40 7.27 10.91 4 3.0 43587 12410 0.285 32.98 9.40 0.40 11.28 16.92 3 3.0 43587 12410 0.285 43.95 12.52 0.45 16.90 20.66 2 3.0 43587 12410 0.285 54.60 15.56 0.50 23.34 23.34 1 4.3 33925 10501 0.310 66.84 20.72 0.70 62.36 26.73
表6-6 B 框中柱柱端剪力和弯矩计算表
层 H(M) ∑Di(kN/m) D(kN/m) D/∑Di Vi(kN) Vik(kN) y
M 下（kNm ） M 上(kNm) 6 3.0 43587 19225 0.441 8.87 3.91 0.37 4.34 7.39 5 3.0 43587 19225 0.441 21.27 9.38 0.42 11.82 16.32 4 3.0 43587 19225 0.441 32.98 14.54 0.45 19.63 23.99 3 3.0 43587 19225 0.441 43.95 19.38 0.47 27.32 23.84 2 3.0 43587 19225 0.441 54.60 24.07 0.50 36.11 36.11 1
4.3
33925
13668
0.403
66.84 26.94
0.64
74.14
41.70
表2-6-7 A 框中柱柱端剪力和弯矩计算表
层 H(M) ∑Di(kN/m) D(kN/m) D/∑Di Vi(kN) Vik(kN) y
M 下（kNm ） M 上(kNm) 6 3.0 43587 11952 0.274 8.87 2.43 0.30 2.19 5.10 5 3.0 43587 11952 0.274 21.27 5.83 0.40 6.99 10.49 4 3.0 43587 11952 0.274 32.98 9.04 0.41 11.12 16.00 3 3.0 43587 11952 0.274 43.95 12.04 0.41 14.81 21.31 2 3.0 43587 11952 0.274 54.60 14.96 0.50 22.44 22.44 1
4.3
33925
10328
0.304
66.84
20.32 0.70
61.16
26.21
（2） 风荷载作用下梁端弯矩、剪力和柱轴力计算 根据节点平衡由柱端弯矩求得梁轴线处弯矩
μ1=K1/K1+K2=0.51
μ2 = K2/K1+K2=0.49 M=(M 上+M 下)μ M=(M 上+M 下)μ2
风荷载作用下的梁端弯矩、剪力和柱轴力，见表2-6-8
M M V V V L
+===-
右
左右左
表2-6-8风荷载作用下的梁端弯矩、剪力和柱轴力
层
CB跨梁端剪力BA跨梁端剪力柱轴力
L
(m)
M E左M E右V E
L
(m)
M E左M E右V E
C柱
（KN)
B柱
(KN)
A柱
(KN)
6 5.
7 5.31 3.77 1.59 6.0 3.62 5.10 1.45 1.59 0.14 1.45 5 5.7 13.19 10.54 4.16 6.0 10.12 12.6
8 3.8 5.75 0.50 5.25 4 5.7 24.1
9 18.26 7.45 6.0 17.55 17.48 5.84 13.20 2.11 11.09 3 5.7 31.94 27.50 10.43 6.0 26.42 32.43 9.81 23.63 2.73 20.90 2 5.7 40.24 32.35 12.74 6.0 31.08 37.25 11.39 36.37 4.08 32.29 1 5.7 50.07 39.68 15.75 6.0 38.13 48.65 14.46 52.12 5.37 46.75
（3）风荷载作用下框架内力图如下
风荷载作用下框架内力图，图2-6-2、图2-6-3、图2-6-4
图2-6-2 风荷载作用下框架弯矩图
图2-6-3 风荷载作用下框架剪力图
图2-6-4风荷载作用下框架轴力图。