您的位置：360文档中心› 86中考数学几何专项训练及答案

86中考数学几何专项训练及答案

合集下载

中考数学几何图形专题训练50题含答案

中考数学几何图形专题训练50题含答案

中考数学几何图形专题训练50题含答案(单选、填空、解答题)一、单选题1．下列各图经过折叠后不能围成一个正方体的是（）A．B．C．D．【答案】C【分析】根据平面图形的折叠、正方体的展开图的特点即可得出答案．【详解】解：A．是正方体的展开图，经过折叠后能围成一个正方体，故A不符合题意；B．是正方体的展开图，经过折叠后能围成一个正方体，故B不符合题意；C．不是正方体的展开图，经过折叠后不能围成一个正方体，故C符合题意；D．是正方体的展开图，经过折叠后能围成一个正方体，故D不符合题意．故选：C．【点睛】本题主要考查了展开图折叠成几何体，属于基础题，要充分展开想象，注意培养自己的立体感．2．一副三角板按如图所示的方式摆放，则∠1补角的度数为（）A．45︒B．135︒C．75︒D．165︒【答案】D【分析】根据题意得出∠1=15°，再求∠1补角即可．∠=︒-︒=︒【详解】由图形可得1453015∠∠1补角的度数为18015165︒-︒=︒故选：D．【点睛】本题考查利用三角板求度数和补角的定义，熟记各个三角板的角的度数是解题的关键．3．用一个放大10倍的放大镜看一个10°的角，这个角是（）A ．100°B ．10°C ．110°D ．170° 【答案】B 【分析】根据放大镜看一个角只会改变边的长度，不会改变角本身的度数即可求解．【详解】解：用放大镜看一个角，不会改变角本身的度数，故选：B ．【点睛】本题考查角的大小比较，放大镜看到的角不会改变角本身的度数． 4．如果点C 在线段AB 所在直线上，则下列各式中AC AB =，AC CB =，2AB AC =，AC CB AB +=，能说明C 是线段AB 中点的有（ ）A ．1个B ．2个C ．3个D ．4个 【答案】A【分析】根据线段中点的定义，能判断AC=CB 的条件都能说明C 是线段AB 中点．【详解】根据分析得：若AC=AB ，则不能判断C 是线段AB 中点；若AC=CB ，则可判断C 是线段AB 中点；若AB=2AC ，则不能判断C 是线段AB 中点；若AC+CB=AB ，则不能判断C 是线段AB 中点；综上可得共有1个正确.故选A.【点睛】本题考查线段中点的定义，解题的关键是掌握线段中点的定义.5．如图，已知BD CF =，B F ∠=∠，//AC DE 下列结论不正确的是（ ）A ．FD BC =B ．EF CB =C ．//EF ABD ．AE ∠=∠【答案】B 【分析】根据全等三角形的判定和性质、平行线的判定和性质以及线段的和差进行判断即可得解．【详解】解：∠//AC DE∠ACB EDF ∠=∠∠BD CF =∠BD CD CF CD +=+∠BC DF =∠在ABC 和EFD △中B F BC FDACB EDF ∠=∠⎧⎪=⎨⎪∠=∠⎩∠()ABC EFD ASA ≌∠A E ∠=∠故说法D 正确；∠B F ∠=∠∠//EF AB故说法C 正确；∠BD CF =∠BD CD CF CD +=+∠BC DF =故说A 正确，说法B 错误．故选：B【点睛】本题考查了全等三角形的判定和性质、平行线的判定和性质以及线段的和差，熟悉各知识点是解题的关键．6．如图，OC 平分AOD ∠，30DOC AOB ∠-∠=︒，有下列结论：∠30BOC ∠=︒；∠BOC ∠的度数无法确定；∠若20AOB ∠=︒，则100AOD ∠=︒；∠若60AOB ∠=︒，则A ，O ，D 三点在同一条直线上．其中，正确的有（ ）A ．1个B ．2个C ．3个D ．4个【答案】C 【分析】根据角平分线定义得出DOC AOC ∠=∠，根据30DOC AOB ∠-∠=︒，即可求出30BOC ∠=︒，判断出∠正确，∠错误；根据30BOC ∠=︒，20AOB ∠=︒，求出50AOC AOB BOC ∠=∠+∠=︒，根据角平分线定义求出100AOD ∠=︒，即可判断∠正确；求出180AOD ∠=︒，即可判断∠正确．【详解】解：∠OC 平分AOD ∠，∠DOC AOC ∠=∠，∠30DOC AOB AOC AOB BOC ∠-∠=∠-∠=∠=︒，故∠正确，∠错误．由∠知，30BOC ∠=︒，∠50AOC AOB BOC ∠=∠+∠=︒，∠2100AOD AOC ∠=∠=︒，故∠正确．∠30BOC ∠=︒，60AOB ∠=︒，∠90AOC BOC AOB ∠=∠+∠=︒，∠2180AOD AOC ∠=∠=︒，∠A 、O 、D 三点在一条直线上，故∠正确．综上，正确的为∠∠∠，共3个，故C 正确．故选：C ．【点睛】本题主要考查了角平分线的定义，几何图形中角的计算，解题的关键是根据角平分线的定义和已知条件，求出30BOC ∠=︒．7．如图，120AOB ∠=︒，13AOC BOC ∠=∠，OM 平分BOC ∠，则AOM ∠的度数为（ ）A ．45︒B ．65︒C ．75︒D ．80︒故选C．【点睛】本题考查了角平分线定义，角的有关计算的应用，解此题的关键是求出∠AOC和∠COM的大小．8．如图，这是每个面上都有一个汉字的正方体的一种展开图，那么在原正方体的表面上，与汉字“爱”相对的面上的汉字是（）A．西B．电C．附D．中【答案】C【分析】正方体的表面展开图，相对的面之间一定相隔一个正方形，根据这一特点作答．【详解】解：正方体的表面展开图，相对的面之间一定相隔一个正方形，“我”与“电”是相对面，“爱”与“附”是相对面，“西”与“中”是相对面．故选：C．【点睛】本题主要考查了正方体相对两个面上的文字，注意正方体的空间图形，从相对面入手，分析及解答问题．9．如果A、B、C三点在同一直线上，线段AB=3cm，BC=2cm，那么A、C两点之间的距离为（）A．1cmB．5cmC．1cm或5cmD．无法确定【答案】C【详解】试题解析：由题意可知，C点分两种情况，∠C点在线段AB延长线上，如图1，AC=AB+BC=3+2=5cm；∠C点在线段AB上，如图2，AC=AB-BC=3-2=1cm．综合∠∠A、C两点之间的距离为1cm或5cm．故选C．【点睛】由题意可知，点C分两种情况，画出线段图，结合已知数据即可求出结论．本题考查了两点间的距离，解题的关键是根据题意画出线段图，找准线段间的关系．10．如图，AD平分∠BAC，点E在AB上，EF∥AC交AD于点G，若∠DGF＝40°，则∠BEF的度数为（）A．20°B．40°C．50°D．80°【答案】D【分析】由EF∥AC，∠DGF＝40°，得出∠DAC=∠DGF＝40°，∠BEF=∠BAC，又AD 平分∠BAC，则∠BEF=∠BAC=2∠DAC=80°．【详解】解：∠EF∥AC，∠DGF＝40°，∠∠DAC=∠DGF＝40°，∠BEF=∠BAC，∠AD平分∠BAC，∠∠BEF=∠BAC=2∠DAC=80°．故选：D．【点睛】本题主要考查平行线的性质以及角平分线的定义，熟练掌握平行线的性质以及角平分线的定义是解决本题的关键．11．若钟表分针走30分钟，则钟表的时针转（）A．5︒B．15︒C．30︒D．120︒【答案】B【分析】根据“整个钟面12小时，时针每小时转30︒”即可得．．将一副直角三角尺按如图所示的不同方式摆放，则图中与不一定．．．相等的是（ ）A ．B ．C ．D ．【答案】B 【分析】A 选项由图形即直角三角形的性质即可判断；B 选项由两角互余即可的判断；C 选项由对顶角相等即可判断；D 选项由同角的余角相等即可判断．【详解】A 选项中，90,45αβα∠+∠=︒∠=︒，45βα∴∠=∠=︒，故不符合题意；B 选项中，90αβ∠+∠=︒，则α∠与∠β不一定相等，故符合题意；C 选项中，,αβ∠∠是对顶角，αβ∴∠=∠，故不符合题意；D 选项如图，190,190αβ∠+∠=︒∠+∠=︒，αβ∴∠=∠，故不符合题意；故选：B ．【点睛】本题考查了对顶角相等，余角，同角的余角相等等知识点，熟练掌握这些知识是解题的关键．13．如下图的正方体，选项中哪一个图形是它的展开图（ ）A ．B ．C ．D ．【答案】A【分析】根据正方体相邻面及其表面展开图的特点解答即可．【详解】解：A 、展开图中，其三个相邻面上的线段位置，符合题意，B 、展开图中，其中有两个有线段的两个面相对，不符合题意；C 、展开图中，其中有两个面上的线段平行，不符合题意；D 、展开图中，其中有两个有线段的两个面相对，不符合题意，故选：A ．【点睛】本题考查正方体的展开图，弄清正方体展开图中哪些面相邻，哪些面相对是解答的关键．14．把立方体的六个面分别涂上六种不同的颜色，并画出朵数不等的花，各面上的颜色与花朵的朵数情况列表如下：现将上述大小相同，颜色、花朵分布完全样的四个立方体拼成一个水平放置的长方体，如图所示，那么长方体的下底面共有花朵数是（ ）A ．11B ．13C ．15D ．17 【答案】D【分析】由图中显示的规律，可分别求出，右边正方体的下边为白色，左边为绿色，后面为紫色，按此规律，可依次得出右二的立方体的下侧为绿色，右三的为黄色，左一的为紫色，即可求出下底面的花朵数．【详解】解：由题意可得，右一的立方体的下侧为白色，右二的立方体的下侧为绿色，右三的为黄色，左一的为紫色，那么长方体的下底面共有花数4＋6＋2＋5＝17朵．故长方体的下底面共有17朵花．故选D ．【点睛】本题考查生活中的立体图形与平面图形，同时考查了学生的空间思维能力．注意正方体的空间图形，从相对面入手，分析及解答问题．15．如图，在四边形ABCD 中，90A BCD ∠=∠=︒，BC DC =，CE AD ⊥，垂足为E ，若3AE CE ==．则四边形ABCD 的面积为（ ）A ．9B ．12C ．272D ．无法求出 【答案】A 【分析】过点C 作CF 垂直AB 的延长线于点F ，先证明四边形AFCE 是矩形，再证明FCB ECD △≌△，进而将四边形ABCD 的面积转化为矩形AFCE 的面积求解即可．【详解】解：如图，过点C 作CF 垂直AB 的延长线于点F ，∠90A BCD ∠=∠=︒， CE AD ⊥，CF AF ⊥，∠四边形AFCE 是矩形，90==︒CED F ∠∠，∠90FCE FCB BCE ∠=∠+∠=︒，3CF AE CE === ，∠90BCD BCE DCE ∠=∠+∠=︒，∠FCB ECD ∠=∠，在FCB 和ECD 中，CED F FCB ECD BC DC ∠=∠⎧⎪∠=∠⎨⎪=⎩，∠FCB ECD △≌△，∠==339ABCD AFCE AE CE S S ⋅=⨯=四边形矩形，故选：A ．【点睛】本题主要考查了全等三角形的判定及性质、同角的余角相等，垂直定义以及矩形的判定及性质，熟练掌握全等三角形的判定及性质是解题的关键．16．如图，在ABC 中，以A 为圆心，适当长为半径作弧，分别交AB 、AC 于点D 、E ，再分别以D 、E 为圆心，相同长为半径作弧，分别交DB、EC 于点F 、G ，连接EF 、DG ，交于点H ，连接AH 并延长交BC 于点I ，则线段AI 是( )A ．ABC 的高B ．ABC 的中线 C ．ABC 的角平分线D ．以上都不对【答案】C 【分析】根据题意利用SAS 可证AFE AGD △≌△，即可得EG DF =，再利用AAS 可证EHG DHF ≌△△，即可得EH DH =，用SSS 可证明AHE AHD △≌△，即可得EAH DAH ∠=∠，即可得．【详解】解：由作图可知，AE AD =，EG DF =，∠AE EG AD DF +=+，即AG AF =，在AFE △和AGD △中，AE AD EAF DAG AF AG =⎧⎪∠=∠⎨⎪=⎩，∠AFE AGD △≌△（SAS ），∠AFE AGD ∠=∠，在EHG 和DHF △中，EHG DHF EGH DFH EG DF ∠=∠⎧⎪∠=∠⎨⎪=⎩，∠EHG DHF ≌△△（AAS ），∠EH DH =在AHE 和AHD 中，AE AD AH AH EH DH =⎧⎪=⎨⎪=⎩，∠AHE AHD △≌△（SSS ），∠EAH DAH ∠=∠，∠AI 是ABC 的角平分线．故选：C ．【点睛】本题考查了全等三角形的判定与性质，角平分线的判定，解题的关键是掌握全等三角形的判定与性质．17．如图：∠AOB ：∠BOC ：∠COD ＝2：3：4，射线OM 、ON ，分别平分∠AOB 与∠COD ，又∠MON ＝84°，则∠AOB 为（ ）A ．28°B ．30°C ．32°D ．38°【答案】A 【分析】首先设∠AOB ＝2x °，则∠BOC ＝3x °，∠COD ＝4x °，然后利用角的和差关系和角平分线的定义列出方程，即可求出∠AOB 的度数．【详解】解：设∠AOB ＝2x °，则∠BOC ＝3x °，∠COD ＝4x °，∠射线OM 、ON 分别平分∠AOB 与∠COD ，18．如图，在ABCD 中，DAB ∠的平分线AE 交CD 于E ，6AB =，4BC =，则EC的长为（ ）A ．2B ．2.5C ．3D ．3.5【答案】A 【分析】根据平行四边形的性质及AE 为角平分线可知：BC=AD=DE=4，又有CD=AB=6，可求EC 的长．【详解】解：根据平行四边形的对边相等，得：CD=AB=6，AD=BC=4．根据平行四边形的对边平行，得：CD∠AB ，∠∠AED=∠BAE ，又∠DAE=∠BAE ，∠∠DAE=∠AED ．∠ED=AD=4，∠EC=CD-ED=6-4=2．故选：A ．【点睛】本题主要考查了平行四边形的性质，在平行四边形中，当出现角平分线时，一般可构造等腰三角形，进而利用等腰三角形的性质解题．19．如图，直线EO∠CD ，垂足为点O ，AB 平分∠EOD ，则∠BOD 的度数为（ ）A．120°B．130°C．135°D．140°【答案】C【详解】试题分析：根据直线EO∠CD，可知∠EOD=90°，根据AB平分∠EOD，可知∠AOD=45°，再根据邻补角的定义即可求出∠∠BOD=180°-45°=135°考点：垂线、角平分线的性质、邻补角定义．二、填空题20．已知：∠AOC=146°，OD为∠AOC的平分线，∠AOB=90°，∠BOD的度数_____．21．2022年10月16日，党的第二十次全国代表大会在北京召开，这是一次在全党全国各族人民迈上全面建设社会主义现代化国家新征程、向第二个百年奋斗目标进军的关键时刻召开的十分重要的大会．如图是一个正方体的展开图，请你判断，正方体上与“荣”字相对的面上的汉字是_______．【答案】祖【分析】根据正方体展开图中相对的面总是隔着一个面的特征解题即可．【详解】解：根据正方体展开图中相对的面总是隔着一个面的特征可得荣字相对的面上的汉字为“祖”，故答案为：祖．【点睛】本题主要考查正方体展开图的特征，能够根据特征得出结论是解题关键．22．用一个平面截圆锥，可以得到________、________及类似拱形形状．如图：【答案】圆等腰三角形【解析】略23．如图，要用一张长方形的纸片折成一个纸袋，两条折痕的夹角为80°（即∠POQ＝80°），就可以做成一个纸袋，那么粘胶水部分所构成的这个角∠A'OB'＝_____．【答案】20°【分析】根据折叠性质得出∠POA=∠POA′，∠QOB=∠QOB′，根据∠AOB为平角，∠POA+∠QOB=180°-∠POQ=100°，再利用∠A′OB′=∠POA′+∠QOB′-∠POQ=20°即可．【详解】解：∠OP为折痕，OQ为折痕，∠∠POA=∠POA′，∠QOB=∠QOB′，∠∠AOB为平角∠∠POA+∠QOB=180°-∠POQ=100°，∠∠A′OB′=∠POA′+∠QOB′-∠POQ=∠POA+∠QOB-∠POQ=100°-80°=20°．故答案为：20°．【点睛】本题考查折叠性质，平角，角的和差，掌握折叠性质，平角，角的和差是解题关键．24．下午三点半时，时针与分针所夹的锐角的大小为________．【答案】75︒##75度【分析】先求出时钟上，每一个大格的度数为30︒，再根据下午三点半时，时针与分针所夹的锐角为2.5个大格即可得．︒÷=︒，【详解】解：时钟上，共有12个大格，每一个大格的度数为3601230因为下午三点半时，时针与分针所夹的锐角为2.5个大格，⨯︒=︒，所以下午三点半时，时针与分针所夹的锐角的大小为2.53075故答案为：75︒．【点睛】本题考查了钟面角，熟练掌握时钟上，每一个大格的度数为30︒是解题关键．25．点C是线段AB上的一点，2=，点M、N分别是线段AC、BC的中点，BC ACMN BC等于_________．那么:26．已知∠a=50°18′，则∠a的余角是________°________′.【答案】3942【分析】互余的概念：和为90度的两个角互为余角．用90°减去一个角的余角就等于这个角的度数．【详解】根据余角的定义，知∠A的余角是90°﹣50°18'=39°42'．故答案为39，42．【点睛】本题考查了余角和角度的计算，关键是记住互为余角的两个角的和为90度．27．在一个圆形时钟的表面，OA 表示秒针，OB 表示分针（O 为两针的旋转中心）若现在时间恰好是12点整，则经过__________秒钟后，∠OAB 的面积第一次达到最大． 【答案】151559##9005928．如图，直线AB 、CD 相交于点O ，OE 平分BOD ∠，COB ∠为100︒，则AOE ∠=___________度识是解题的关键．29．小王从家出发向南偏东30°的方向走了100米到达小军家，此时小王家在小军家的_________方向． 【答案】北偏西30︒【分析】根据方向角的定义作出示意图，根据图形即可解答．【详解】解：如图所示，由题意知∠BAC ＝30°，则在∠ABC 中，∠BAC ＋∠ACB ＝90°，∠∠ACB ＝60°．又∠∠ACB ＋∠ACD ＝90°，∠∠ACD ＝30°，即小王家在小军家北偏西30°方向．故答案是：北偏西30°．【点睛】本题考查了方向角的定义，理解定义作出示意图是关键．30．如图所示，已知ABC 的周长为12，5BC =，在边AC 、AB 上有两个动点P 、Q ，它们同时从点A 分别向点C 、B 运动，速度分别为m 和n ，运动时间t 后，PC CB BQ ++=__________．【答案】()12m n t -+【分析】根据PC AC AP BQ AB AQ =-=-，，可得PC BQ AC AB AP AQ +=+--，进一步得到PC CB BQ ++，依此即可求解．【详解】解：PC AC AP BQ AB AQ =-=-，，()1257PC BQ AC AB AP AQ mt nt m n t ∴+=+--=---=-+，()()7512PC CB BQ m n t m n t ∴++=-++=-+．故答案为：()12m n t -+．【点睛】本题考查了列代数式，线段的和差关系，整式的加减运算，关键是得到PC BQ +的表达式．31．已知∠α＝60°，则∠α的补角等于_______． 【答案】120°【分析】利用互为补角的两个角之和为180°，解题即可【详解】因为∠α＝60°，所以∠α的补角是180°-60°=120°故填120°32．将三角尺按右图所示的方式放置在一张长方形纸片上，90EGF ∠=︒，30FEG ∠=︒，1130∠=︒，则BFG ∠的度数为___________．【答案】110°【分析】由长方形AD 与BC 平行，求出∠EFB ，由直角三角形求∠EFG ，再求两角的和即可．【详解】∠AD ∠BC ，∠∠1+∠EFB =180゜∠∠1=130゜∠∠EFB =180゜-130゜=50゜，∠∠EGF =90°，∠FEG =30°，∠∠EFG =180°-∠EGF -∠FEG =60°∠∠BFG =∠EFB +∠EFG =50°+60゜=110゜．故答案为：110゜．【点睛】本题考查角的度数问题，关键抓住平行线，同旁内角互补，三角形两锐角互余．33．若船A 在灯塔B 的北偏东30°方向上，则灯塔B 在船A 的_________方向上．【答案】南偏西30°【分析】本题画出A 、B 的位置，即分别以A 、B 为为原点，分别画出A 、B 的正北、正南、正西、正东方向，标出A 与B 的关系即可求解.【详解】从图中可以看出，B 在A 的南偏西30°.故答案为南偏西30°.【点睛】本题考查一个物体相对于另一物体的位置，注意这类题中“北偏东30°”的含义，是从正北方向开始，向东方向偏，偏角为30°.34．18°33′25″×3=_________．【答案】55°40′15″【分析】将度分秒分别乘以3后进位化简即可.【详解】1833253549975'''︒'"⨯==55°40′15″，故答案为：55°40′15″.【点睛】此题考查角度的计算，根据乘法法则进行计算，计算后每个单位满60向前一单位进一.35．如图，将一副三角板()90CAB DAE ∠=∠=︒按如图放置，则下列结论：∠13∠=∠；∠如果230∠=︒，则有//AC DE ；∠如果230∠=︒，则有//BC AD ；∠如果230∠=︒，必有4C ∠=∠．其中正确的有________．（填序号）【答案】∠∠∠【分析】根据两种三角板的各角的度数，利用平行线的判定与性质结合已知条件对各个结论逐一验证，即可得出答案．【详解】解：∠∠∠CAB=∠EAD=90°，∠∠1=∠CAB-∠2，∠3=∠EAD-∠2，∠∠1=∠3．∠∠正确．∠∠∠2=30°，∠∠1=90°-30°=60°，∠∠E=60°，∠∠1=∠E，∠AC∠DE．∠∠正确．∠∠∠2=30°，∠∠3=90°-30°=60°，∠∠B=45°，∠BC不平行于A D．∠∠错误．∠由∠得AC∠DE．∠∠4=∠C．∠∠正确．故答案为：∠∠∠．【点睛】此题主要考查学生对平行线判定与性质、余角和补角的理解和掌握，解答此题时要明确两种三角板各角的度数．36．如图，OC是∠AOB的平分线，如果∠AOB=130°,∠BOD=24°48＇，那么∠COD=_____.【答案】40.2°【分析】由角平分线定义，求出∠BOC的度数，然后利用角的和差关系，即可得到答案.【详解】解：∠OC是∠AOB的平分线，∠AOB=130°，37．如图，,AC BD 在AB 的同侧，2,8,8AC BD AB ===，点M 为AB 的中点，若120CMD ∠=，则CD 的最大值是_____．【答案】14 【分析】如图，作点A 关于CM 的对称点A ′，点B 关于DM 的对称点B ′，证明△A ′MB ′为等边三角形，即可解决问题．【详解】解：如图，作点A 关于CM 的对称点'A ，点B 关于DM 的对称点B'． 120CMD ∠=，60AMC DMB ∴∠+∠=，∴''60CMA DMB ∠+∠=，''60A MB ∴∠=，''MA MB =，''A MB ∴∆为等边三角形''''14CD CA A B B D CA AM BD ≤++=++=，CD ∴的最大值为14，故答案为14．【点睛】本题考查等边三角形的判定和性质，两点之间线段最短，解题的关键是学会添加常用辅助线，学会利用两点之间线段最短解决最值问题38．如图，在四边形ABCD 中，DAB ∠的角平分线与ABC ∠的外角平分线相交于点P ，且240D C ∠+∠=°，则P ∠=______．【答案】30︒##30度39．如图，在边长为2的菱形ABCD 中，60ABC ∠=︒，将BCD △沿直线BD 平移得到B C D '''，连接AC '、AD '，则AC AD ''+的最小值为________．ABC∠=由对称性可得：三、解答题∠，40．按要求补全图形并证明．如图，150∠=︒，OC垂直OB，OD平分AOCAOB∠．OE平分BOC(1)利用三角板依题意补全图形(2)求DOE∠的度数75【分析】（190，根据150，得出60，根据∠∠，即可得出EOC BOC30AOC=，4575．）解：补全图形，如图所示：90，150，60，AOC ，30AOC ∠， 45， 75．【点睛】本题主要考查了角平分线的定义，垂线的定义，解题的关键是数形结合，熟练掌握角平分线的定义．41．已知,,,AE GF BC GF EF DC EF AB ∥∥∥∥，猜想A ∠与C ∠的关系如何？并说明理由．解：因为,AE GF BC GF ∥∥（已知）所以AE BC ∥（______）所以______180(______)A ∠+=︒；同理，______180C ∠+=︒；所以______（______）．【答案】平行于同一条直线的两直线平行；∠B ；两直线平行，同旁内角互补；∠A ＝∠C ；同角的补角相等或等式性质【分析】根据平行线的判定和性质以及同角的补角相等求解即可．【详解】解：因为AE GF ∥，BC GF ∥（已知）所以AE BC ∥（平行于同一条直线的两直线平行）；所以∠A＋∠B＝180°（两直线平行，同旁内角互补）；同理，∠C＋∠B＝180°；∠∠A＝∠C（同角的补角相等或等式的性质）．故答案为：平行于同一条直线的两直线平行；∠B；两直线平行，同旁内角互补；∠A ＝∠C；同角的补角相等或等式的性质．【点睛】本题主要考查了平行线的性质与判定，同角的补角相等，熟知平行线的性质与判定是解题的关键．42．如图，点B在线段AC上，点E在线段DF上，EC，AF，DB∠EC，下面写出了说明“∠C＝∠D”的过程．说明：∠∠A＝∠F（已知），∠DF∠．根据：∠∠DEC+∠C＝180°．根据：∠DB∠EC（已知），∠∠DEC+∠＝180°．根据：∠∠C＝∠D．根据：．【答案】AC；内错角相等，两直线平行；两直线平行，同旁内角互补；D；两直线平行，同旁内角互补；同角的补角相等．【分析】根据平行线的性质与判定进行求解即可．【详解】说明：∠∠A＝∠F（已知），∠DF∥AC．根据：内错角相等，两直线平行；∠∠DEC+∠C＝180°．根据：两直线平行，同旁内角互补；∠DB∥EC（已知），∠∠DEC+∠D＝180°．根据：两直线平行，同旁内角互补；∠∠C＝∠D．根据：同角的补角相等．故答案为：AC；内错角相等，两直线平行；两直线平行，同旁内角互补；D；两直线平行，同旁内角互补；同角的补角相等．【点睛】本题主要考查了平行线的性质与判定，同角的补角相等，解题的关键在于能够熟练掌握相关知识进行求解．43．如图，O为直线AB上一点，∠BOC=α．(1)若α=40°，OD平分∠AOC，∠DOE=90°，如图（a）所示，求∠AOE的度数；(2)若∠AOD=13∠AOC，∠DOE=60°，如图（b）所示，请用α表示∠AOE的度数；(3)若∠AOD=1n∠AOC，∠DOE=180n︒（n≥2，且n为正整数），如图（c）所示，请用α和n表示∠AOE的度数（直接写出结果）．44．如图，在△ABC中，AB∠BC，BE∠AC于E，AF平分∠BAC交BE于点F，DF∠BC．（1）试说明：BF＝DF；（2）延长AF交BC于点G，试说明：BG＝DF．【答案】（1）说明见解析；（2）说明见解析．【分析】（1）由角平分线的性质可得FE=FH，由“ASA”可证∠DEF∠∠BHF，可得BF=DF；（2）由等角的余角相等可得∠AFE=∠AGB=∠BFG，可得BF=BG=DF．【详解】解：（1）如图，延长DF交AB于H，延长AF交BC于G，∠AB∠BC，DF∠BC，∠DH∠AB，∠AF平分∠BAC，BE∠AC，DH∠AB，∠FE＝FH，又∠∠DFE＝∠BFH，∠DEF＝∠BHF＝90°，∠∠DEF∠∠BHF（ASA），∠BF＝DF；（2）∠AF平分∠BAC，∠∠EAF＝∠BAG，∠∠EAF+∠AFE＝90°，∠BAG+∠AGB＝90°，∠∠AFE＝∠AGB，∠∠BFG＝∠AGB，∠BF＝BG，∠BG＝DF．【点睛】本题考查了全等三角形的判定和性质，角平分线的性质，直角三角形的性质，灵活运用全等三角形的性质是本题的关键．45．如图，在Rt∠ABC中，∠ACB＝90°，∠A＝40°，∠ABC的外角∠CBD的平分线BE 交AC的延长线于点E．(1)求∠CBE的度数；(2)过点D作DF∥BE，交AC的延长线于点F，求∠F的度数．(3)若把直线FD绕点F旋转，直线DF和直线BE相交于点M，当DF和三角形ABC的一边平行时，请直接写出∠FME的度数．【答案】(1)65°(2)25°(3)65°或115°．【分析】（1）根据三角形外角的性质得出∠CBD的度数，再根据角平分线定义即可求得∠CBE的度数；（2）先根据三角形外角的性质得出∠CEB的度数，再根据平行线的性质求出∠F的度数；（3）根据题意分别画出图形，再利用平行线的性质解决．（1）解：∠Rt∠ABC中，∠ACB＝90°，∠A＝40°，∠∠CBD=∠ACB+∠A=130°，∠BE是∠CBD的角平分线，46．已知a＝﹣（﹣2）2×3，b＝|﹣9|+7，c＝1115 53⎛⎫-⨯⎪⎝⎭．（1）求3[a﹣（b+c）]﹣2[b﹣（a﹣2c）]的值．（2）若A＝2212119272⎛⎫⎛⎫⎛⎫-÷-+-⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭×（1﹣3）2，B＝|a|﹣b+c，试比较A和B的大小．（3）如图，已知点D是线段AC的中点，点B是线段DC上的一点，且CB：BD＝2：3，若AB＝ab12ccm，求BC的长．∠BC ＝2cm ．【点睛】本题主要考查了有理数的混合运算以及与线段的中点有关的计算，熟练掌握运算法则是解答本题的关键．47．如图1，已知直线EF 与直线AB 交于点E ，直线EF 与直线CD 交于点F ，EM 平分AEF ∠交直线CD 于点M ，且FEM FME ∠=∠，点G 是射线MD 上的一个动点(不与点M F 、重合)，EH 平分FEG ∠交直线CD 于点H ，过点H 作HN EM ∥交直线AB 于点N ，设EHN a ∠=，EGF β∠=．(1)求证：AB CD ∥；(2)当点G 在点F 的右侧时，∠依据题意在图1中补全图形;∠若70β=︒，则α=________°；(3)当点G 在运动过程中，α和β之间有怎样的数量关系？直接写出你的结论． AB CD ；根据题目要求画出图形即可；110︒=，再根据，再根据ME ）分两种情况进行讨论：当点G 在点F2248．如图，上面的图形分别是下面哪个立体图形展开的形状，请你把有对应关系的平面图形与立体图形连接起来．【答案】见解析．【分析】根据常见的各种立体几何图形的展开图的特征即可得答案．【详解】∠三个长方形和两个三角形如图摆放是三棱柱的展开图，一个扇形和一个圆是圆锥如图摆放的展开图，六个长方形如图摆放是长方体的展开图，一个长方形和两个圆如图摆放是圆柱的展开图，∠连接如图：【点睛】本题考查常见立体几何图形的展开图，熟记各立体几何图形的展开图是解题关键．49．如图，把一个棱长8厘米的正方体的六个面都涂上红色，再将它的棱四等分，然后从等分点把正方体锯开．(1)能得到多少个棱长为2厘米的小正方体？(2)三个面有红色的小正方体有多少个？(3)两个面有红色的小正方体有多少个？(4)一个面有红色的小正方体有多少个？(5)有没有各面都没有红色的小正方体？如果有，那么有多少个？【答案】(1)64个(2)8个(3)24个(4)24个(5)有，8个【分析】（1）棱长是8cm的立方体体积512cm3，棱长为2cm的小正方体体积为8cm3，由此能求出共得到多少个棱长为2cm的小正方体；（2）三面涂色的小正方体是位于棱长是8cm的立方体的顶点处的小正方体，由此能求出三面涂色的小正方体有多少个；（3）二面涂色的小正方体是位于棱长是8cm的立方体的各边上的正方体，由此能求出二面涂色的小正方体有多少个；（4）一个面有红色的小正方体位于棱长是8cm的立方体的表面上既不是顶点又不是各边上的正方体，由此能求出二面涂色的小正方体有多少个；（5）六个面均没涂色的小正方体为棱长是8cm的立方体中心的正方体，由此能求出六个面均没有涂色的小正方体有多少个．【详解】（1）棱长是8cm的立方体体积为：8×8×8=512（cm3），棱长为2cm的小正方体体积为8cm3，∠共得到512÷8=64个小正方体．（2）三面涂色的小正方体是位于棱长是8cm的立方体的顶点处的小正方体，∠立方体共有8个顶点，∠三面涂色的小正方体有8个，（3）二面涂色的小正方体是位于棱长是8cm的立方体的各边上的正方体，∠立方体共有12条边，每边有2个正方体，∠二面涂色的小正方体有24个，（4）一面涂色的小正方体在棱长是8cm的立方体的表面上既不是顶点又不是各边上的正方体，∠立方体共有6个面，每个面有4个正方体，∠一面涂色的小正方体有24个，（5）六个面均没涂色的小正方体为棱长是8cm的立方体中心的正方体，共有64-8-24-24=8个，【点睛】本题考查大正方体分割成小正方体的计算，是中档题，解题时要认真审题，要熟练掌握正方体的结构特征．。

中考数学几何图形专题训练50题含参考答案

中考数学几何图形专题训练50题含参考答案

中考数学几何图形专题训练50题含答案(单选、填空、解答题)一、单选题1．如图是一正方体展开图，则有、志、者三面的对面分别是（）A．事竟成B．事成竟C．成竟事D．竟成事2．下列四个图中，每个都是由六个相同的小正方形组成，折叠后能围成正方体的是（）A．B．C．D．3．如图，下列说法正确的是（）A．直线OM与直线MN是同一条直线B．射线MO与射线MN是同一条射线C．线段OM与线段ON是同一条线段D．射线NO与射线MO是同一条射线4．如图是某同学在数学实践课上设计的正方体纸盒的展开图，每个面上都有一个汉字，其中与“明”字相对的面上的字是（）A．诚B．信C．友D．善5．图是一个正方体的表面展开图，将它折成正方体后，“法”字在上面，那么在下面的一定是（）A ．明B ．诚C ．信D ．制 6．如图，在直线l 上的点是（ ）A ．点AB ．点BC ．点CD ．点D 7．如图，C 为线段AB 上一点，点D 为AC 的中点，且2AD =，10AB =．若点E 在直线AB 上，且1BE =，则DE 的长为（ ）A ．7B ．10C ．7或9D ．10或11 8．已知3725α∠=︒'，则α∠的补角是( )A ．14235︒'B ．15235︒'C ．14275︒'D ．15275︒' 9．能解释：“用两个钉子就可以把木条固定在墙上”这实际问题的数学知识是（ ） A ．垂线段最短B ．两点确定一条直线C ．两点之间线段最短D ．同角的补角相等10．一副直角三角板如图放置，使两三角板的斜边互相平行，每块三角板的直角顶点都在另一三角板的斜边上，则∠1的度数为（ ）A ．90°B ．75°C ．65°D ．60° 11．用度、分、秒表示21.24为（ ）A ．211424'''B ．212024'''C ．21144'''D ．2114' 12．在下面的四个几何体中，它们各自的主视图、左视图与俯视图都一样的是（ ）A ．正方体B ．正四棱台C ．有正方形孔的正方体D ．底面是长方形的四棱锥 13．有5个大小一样的正方形制成如图所示的拼接图形（阴影部分），请你在图中的拼接图形上再接一个正方形，使新拼接成的图形折叠后能成为一个封闭的正方体盒子，你不能选择图中A ，B ，C ，D 中的（ ）位置拼接正方形．A ．AB ．BC ．CD ．D14．下列立体图形中，俯视图与主视图不同的是（ ）A ．B ．C ．D ．15．下列图形中，不可以作为一个正方体的表面展开图的是A ．B ．C ．D ． 16．如图，将ABC 绕点C 顺时针旋转得到DEC ，使点A 的对应点D 恰好落在边AB 上，点B 的对应点为E ，连接BE ，下列四个结论：∠AC CD =；∠A BEC ∠=∠；∠AB EB ⊥；∠CD 平分ADE ∠；其中一定正确的是（ ）A ．∠∠∠B ．∠∠∠C ．∠∠∠D ．∠∠∠∠17．下列说法中，正确的是（ ）∠射线AB 和射线BA 是同一条射线；∠等角的余角相等；∠若AB BC =，则点B 为线段AC 的中点；∠点C 在线段AB 上，M ，N 分别是线段AC ，CB 的中点，若5MN =，则线段10AB =．A ．∠∠B ．∠∠C ．∠∠D ．∠∠ 18．已知射线OC 是∠AOB 的平分线，若∠AOC=30°，则∠AOB 的度数为（ ） A ．15 B ．30 C ．45 D ．60 19．用两把常用三角板不可能拼成的角度为（ ）A ．45B ．105C ．125D ．150 20．如图，在∠ABC 中，BF 平分∠ABC ，过A 点作AF∠BF ，垂足为F 并延长交BC 于点G ，D 为AB 中点，连接DF 延长交AC 于点E ．若AB=12，BC=20，则线段EF 的长为（ ）A ．2B ．3C ．4D ．5二、填空题21．已知2437α'∠=︒，那么α∠的补角等于______．22．已知∠α=60°，则∠α的余角等于____度．23．在空间搭4个大小一样的等边三角形，至少要_______根游戏棒.24．已知线段14cm AB =，点C 是直线AB 上一点，4cm BC =，若M 是AC 的中点，N 是BC 的中点，则线段MN 的长度是___________cm ．25．下午12:20 分，钟表上时针与分针所夹角的度数为_____度（所求夹角小于180︒）．26．和都是 的余角，则______．27．图，∠AOC =∠BOD =90°，OB 在∠AOC 的内部，OC 在∠BOD 的内部，OE 是∠AOB 的一条三等分线．请从A ，B 两题中任选一题作答．A．当∠BOC＝30°时，∠EOD的度数为__________．B．当∠BOC＝α°时，∠EOD的度数为__________（用含α的代数式表示）．28．将一副三角尺如图所示叠放在一起，则∠AEC＝______度．29．对几何体分类时，首先确定标准，即：（1）从形状方面，按柱体、________、球划分；（2）从面的方面，按组成的面有无__________划分；（3）从顶点方面，按有无________划分．30．几个同学在公园玩，发现一个漂亮的“古董”. 甲：它有10个面；乙：它有24条棱；丙：它有8个面是正方形，2个面是多边形；丁：如果把它的侧面展开，是一个长方形，这个长方形有八种颜色，挺好看. 通过这四个同学的对话，从几何体的名称来看，这个“古董“的形状是_____________.31．如图，一艘船由A港沿北偏东65︒方向航行30km至B港，然后再沿北偏西40︒方向航行至C港，C港在A港北偏东20︒方向，则A，C两港之间的距离为______km．32．如图是一个正方体的展开图，将它折叠成正方体后，字母B的对面是________．（用图中字母表示）33．甲、乙两艘客轮同时离开港口，航行的速度都是40m /min ，甲客轮沿北偏东30°的方向航行15min 到达点A ，乙客轮沿南偏东60°的方向航行20min 到达点B ．则A 、B 两点的直线距离为______m ．34．平行四边形ABCD 中，AE 平分∠BAD 交BC 与点E ，且将BC 分成4cm 和6cm 两部分，则平行四边形ABCD 的周长为_____________．35．如图，AB 是∠O 的直径，点C 、D 是AB 两侧∠O 上的点，若∠CAB ＝34°，则∠ADC ＝_____°．36．点C 在直线AB 上，若AB ＝3，BC ＝2，则AC 为_____．37．由O 点引出的7条射线如图，若OA OE ⊥，OC OG ⊥，BOC FOG ∠>∠，则图中以O 为顶角的锐角共有________个．38．一个由125个同样的小正方体组成的大正方体，从这个大正方体中抽出若干个正方体，把大正方体中相对的两面打通，结果如图，则图中剩下的小正方有______个．39．如图，∠α=120°，∠β=90°，则∠γ的度数是________ °．40．Rt△ABC中，∠ACB=90°，AC=20，BC=10，D、E分别为边AB、CA上两动点，则CD+DE的最小值为______．三、解答题41．如图，AD为△ABC的角平分线，点E在AC上，点F在BC上，连接BE交AD于点G，连接EF，∠1＝∠2.(1)求证：∠BEF与∠AGB互补；(2)若∠C＝75°，EF∠BC，求∠ABC的度数．42．如图，OD平分∠BOC，OE平分∠AOC．若∠BOC＝70°，∠AOC＝50°．求出∠D0E及其补角的度数.43．小明用剪刀展开了一个长方体纸盒，可是一不小心多剪了一条棱，把纸盒剪成了两部分，即图中的∠和∠．根据你所学的知识，回答下列问题：（1）小明总共剪开了条棱．（2）现在小明想将剪断的∠重新粘贴到∠上去，而且经过折叠以后，仍然可以还原成一个长方体纸盒，请你帮助小明在∠上补全．(作图要求：先用尺和铅笔画图，再用黑色的签字笔描一遍)（3）小明说：已知这个长方形纸盒高为3cm ，底面是一个正方形，并且这个长方形纸盒所有棱长的和是92cm ，请计算，这个长方体纸盒的体积是___________cm 3．44．如图1，已知AB //CD ，点G 在AB 上，点H 在EF 上，连接CG 、CH ，CG CH ⊥，90CHE CGA ∠+∠=︒．(1)求证：AB //EF ；(2)如图2，若90BAE ∠=︒，延长HC 交BA 的延长线于点M ，请直接写出图2中所有与AGC ∠互余的角．45．如图，100AOB ∠=︒，射线OC 以2/s ︒的速度从OA 位置出发，射线OD 以10/s ︒的速度从OB 位置出发，设两条射线同时绕点O 逆时针旋转s t ．(1)当10t =时，求COD ∠的度数；(2)若015t ≤≤．∠当三条射线OA 、OC 、OD 构成的三个度数大于0︒的角中，有两个角相等，求此时t 的值；∠在射线OD ，OC 转动过程中，射线OE 始终在BOD ∠内部，且OF 平分AOC ∠，当110EOF ∠=︒，求BOE AOD∠∠的值． 46．如图：点A ，B ，E 在同一条直线上，AD AC ⊥，且BD AD AE EC ⊥⊥，，垂足分别为A ，D ，E ．(1)求证：ABD ∽CAE ；(2)若1356AB BD AC ===，，，求CE 的值．47．如图，AF BC ∥．72FAC ∠=︒，CD 平分ACB ∠，4CDE BCD ∠=∠．(1)求CDE ∠的度数．(2)求证：AED B ∠=∠．48．(1)如图1，已知点C ，D 在线段AB 上，P 是BD 的中点，线段AB ，CP 的长度m ，n 满足227(15)0m n -+-=，AD ：BC ＝5：7，求线段CD 的长度；(2)已知∠AOB ＝140°，将射线OB 绕着点O 逆时针旋转一定的角度α（0°＜α＜140°）得到射线OD ，作∠BOD 的平分线OP ，将射线OP 绕着点O 逆时针旋转60°得到射线OC ．∠AOD ：∠BOC ＝1：t ．∠如图2，若t ＜1，请直接用含有t 的式子表示出∠AOD 的度数；∠若∠COD ＝12∠AOC ，求t 的值． 49．问题提出（1）如图1，点A ，B 在直线l 的同侧，在直线l 上作一点P ，使得AP BP +的值最小．问题探究（2）如图2，正方形ABCD 的边长为6，点M 在DC 上，且2DM =，N 是AC 上的一动点，则DN MN +的最小值是_________．问题解决（3）现在各大景区都在流行“真人CS ”娱乐项目，其中有一个“快速抢点”游戏，游戏规则如图3，在用绳子围成的一个边长为12m 的正方形ABCD 场地中，游戏者从AB 边上的点E 处出发，分别先后赶往边,,BC CD DA 上插小旗子，最后回到点E ．求游戏者所跑的最少路程．50．如图，已知，在Rt ABC 中，斜边10AB =，4sin 5A = ，点P 为边AB 上一动点（不与A ，B 重合），PQ 平分CPB ∠交边BC 于点Q ，QM AB ⊥于M QN CP ⊥，于N ．(1)当AP=CP 时，求QP ；(2)若CP AB ⊥ ，求CQ ；(3)探究：AP 为何值时，四边形PMQN 与BPQ 的面积相等？参考答案：1．A【分析】正方体的表面展开图，相对的面之间一定相隔一个正方形，根据这一特点作答．【详解】解：这是一个正方体的平面展开图，共有六个面，其中面“有”与面“事”相对，面“志”与面“竟”相对，“者”与面“成”相对．故选A．【点睛】本题主要考查了正方体相对两个面上的文字，注意正方体的空间图形，从相对面入手，分析及解答问题．2．C【详解】试题解析：A、折叠后，没有上下底面，故不能围成正方体；B、折叠后，缺少一个底面，故也不能围成正方体；C、折叠后能围成正方体；D、折叠后第一行两个面无法折起来，而且下边没有面，不能折成正方体；故选C．考点：展开图折叠成几何体．3．A【分析】根据直线、射线、线段的概念求解即可【详解】解：同一条直线可由这条直线上任意两点的大写字母表示，选项A正确；同一条射线必须满足端点相同，延伸方向相同，选项B，D错误；同一条线段的两个端点相同，选项C错误.故选：A.【点睛】本题考查的知识点是线段、射线以及直线的概念，熟记概念定义是解题的关键. 4．B【分析】正方体的表面展开图，相对的面之间一定相隔一个正方形，根据这一特点作答．【详解】解：正方体的表面展开图，相对的面之间一定相隔一个正方形，在正方体盒子上与“明”字相对的面上的字是“信”．故选：B．【点睛】本题主要考查了正方体相对两个面上的文字，注意正方体的空间图形，从相对面入手，分析及解答问题．5．C【分析】根据正方体的表面展开图，相对的面之间一定相隔一个正方形，这一特点作答即可．【详解】解：正方体的表面展开图，相对的面之间一定相隔一个正方形，∠与“法”字相对的面上的汉字是“信”．故应选：C ．【点睛】本题主要考查了正方体相对两个面上的文字，从实物出发，结合具体的问题，辨析几何体的展开图，通过结合立体图形与平面图形的转化，建立空间观念，是解决此类问题的关键6．B【分析】根据图像点与线的关系可直接得出答案．【详解】解：由图像可知点A 、C 、D 在直线l 外，点B 在直线l 上故选B ．【点睛】本题考查了点线关系，比较简单．7．C【分析】由题意根据线段中点的性质，可得AD 、DC 的长，进而根据线段的和差，可得DE 的长．【详解】解：∠点D 为AC 的中点，且2AD =，∠2AD DC ==，∠10AB =，∠6BC AB AD DC =--=,∠1BE =，当E 在B 左侧，2617DE DC BC BE =+-=+-=,当E 在B 右侧，2619DE DC BC BE =++=++=.∠DE 的长为7或9.故选：C.【点睛】本题考查两点间的距离，解题的关键是利用线段的和差以及线段中点的性质． 8．A【分析】根据互补两角之和180°计算即可．【详解】∠3725α∠=︒'∠α∠的补角=1803725︒-︒'=14235︒'，故选A ．【点睛】本题考查补角定义和角度计算，需要注意角度度分秒计算时进制时60． 9．B【分析】根据两点确定一条直线解答即可．【详解】解：“用两个钉子就可以把木条固定在墙上”这实际问题的数学知识是:两点确定一条直线，故选B ．【点睛】本题考查了直线的性质，熟练掌握两点确定一条直线是解答本题的关键． 10．B【分析】根据平行线的性质可得∠FDC ＝∠F ＝30°，然后根据三角形外角的性质可得结果．【详解】解：如图，∠EF ∠BC ，∠∠FDC ＝∠F ＝30°，∠∠1＝∠FDC +∠C ＝30°+45°＝75°，故选：B ．【点睛】本题主要考查了平行线的性质以及三角形外角的性质，熟知三角板各个角的度数是解本题的关键．11．A【分析】根据度、分、秒之间的进制，先将度中的小数部分转化为分，再将分的小数部分转化为秒即得．【详解】解：21.24210.2460︒'︒=+⨯2114.4︒'=+21140.460'''=︒++⨯211424'''=︒++211424'''=︒．故选：A ．【点评】本题考查了度、分、秒运算，熟练掌握度、分、秒之间的六十进制是解题关键，六十进制与十进制易混淆．12．A【分析】主视图、左视图、俯视图是分别从物体正面、左面和上面看，所得到的图形，找到三个图形一致的几何体即可．【详解】解：A、正方体的三视图是全等的正方形，符合题意；B、正四棱台的三视图分别为梯形，梯形，两个正方形的组合图形，不符合题意；C、有正方孔的正方体的左视图与主视图都是正方形里面有两条竖直的虚线，俯视图是两个正方形的组合图形，不符合题意；D、四棱锥的三视图分别是三角形，三角形，四边形及中心，不符合题意；故选A．【点睛】本题考查了几何体的三种视图，掌握定义是关键．注意看不到的棱用虚线表示．13．A【分析】结合正方体的平面展开图的特征，只要折叠后能围成正方体即可．【详解】解：如图所示：根据立方体的展开图可知，不能选择图中A的位置接正方形．故选：A．【点睛】此题主要考查了应用与设计作图．正方体的平面展开图共有11种，应灵活掌握，不能死记硬背．14．C【分析】从正面看所得到的图形是主视图，从左面看到的图形是左视图，从上面看到的图象是俯视图．【详解】A ．俯视图与主视图都是正方形，故该选项不合题意；B ．俯视图与主视图都是矩形，故该选项不合题意；C ．俯视图是圆，左视图是三角形；故该选项符合题意；D ．俯视图与主视图都是圆，故该选项不合题意；故选C ．【点睛】此题主要考查了三视图，关键是把握好三视图所看的方向．属于基础题，中考常考题型．15．B【分析】利用不能出现同一行有多于4个正方形的情况，不能出现田字形、凹字形的情况进行判断也可．【详解】A ．可以作为一个正方体的展开图，B ．不可以作为一个正方体的展开图，C ．可以作为一个正方体的展开图，D ．可以作为一个正方体的展开图，故选B ．【点睛】本题考查了正方体的展开图，熟记展开图的11种形式是解题的关键，利用不是正方体展开图的“一线不过四、田凹应弃之”（即不能出现同一行有多于4个正方形的情况，不能出现田字形、凹字形的情况）判断也可．16．A【分析】根据旋转的性质得到AC CD =，BC CE =，A EDC ∠=∠，故∠正确；得到ACD BCE ∠=∠，CBE BEC ∠=∠，根据三角形的内角和得到1802ACD A ADC ︒-∠∠=∠=，1802BCE CBE BEC ︒-∠∠=∠=，求得A BEC ∠=∠，故∠正确；由于A ABC ∠+∠不一定等于90︒，于是得到ABC CBE ∠+∠不一定等于90︒，故∠错误，可求得ADC EDC ∠=∠，故可判定∠．【详解】解：∠ABC 绕点C 顺时针旋转得到DEC ，∠AC CD =，BC CE =，A EDC ∠=∠，ACB ECD ∠=∠，故①正确；∴A ADC EDC ∠=∠=∠，ACD DCB DCB BCE ∠+∠=∠+∠，∠CD 平分ADE ∠，ACD BCE ∠=∠，故∠正确；∠BC CE =，∠CBE BEC ∠=∠，∠根据三角形内角和定理可知1802ACDA ADC︒-∠∠=∠=，1802BCECBE BEC ︒-∠∠=∠=，∠A BEC∠=∠，故∠正确；∠A ABC∠+∠不一定等于90︒，ABC CBE∴∠+∠不一定等于90︒，故∠错误．综上，正确的由①②④，故选：A.【点睛】本题考查了旋转的性质，等腰三角形的性质、、三角形的内角和定理、角平分线的定义，正确的识别图形是解题的关键．17．C【分析】根据射线及线段的定义及特点可判断各项，从而得出答案．【详解】∠射线AB和射线BA不是同一条射线，错误；∠同角的余角相等，正确；∠若AB=BC，点B在线段AC上时，则点B为线段AC的中点，错误；∠点C在线段AB上，M，N分别是线段AC，CB的中点．若MN=5，则线段AB=10，正确．故选：C．【点睛】本题考查射线及线段的知识，注意基本概念的掌握是解题的关键．18．D【分析】根据角平分线的定义即可求解．【详解】解：∠射线OC是∠AOB的平分线，∠AOC=30°，∠∠AOB=60°．故答案选：D．【点睛】此题考查了角的计算，以及角平分线的定义，关键是熟练掌握角平分线的定义．19．C【分析】根据两个三角板可拼出的角度有15°，30°，45°，60°，75°，90°，105°，120°，135°，150°，180°【详解】∠三角板的度数为30°,60°,90°;45°,45°,90°∠可拼出的角度有15°,30°,45°,60°,75°,90°105°,120°,135°,150°,180°.故答案选：C.【点睛】本题考查的知识点是角的计算，解题的关键是熟练的掌握角之间的转换.20．CAB，由角平分线的定义可证得【分析】由直角三角形的性质可求得DF=BD=12DE∠BC，利用三角形中位线定理可求得DE的长，则可求得EF的长．【详解】解:∠AF∠BF，D为AB的中点，∠DF=DB=1AB=6，2∠∠DBF=∠DFB，∠BF平分∠ABC，∠∠DBF=∠CBF，∠∠DFB=∠CBF，∠DE∠BC，∠DE为∠ABC的中位线，∠DE=1BC=10，2∠EF=DE−DF=10−6=4，故选C.【点睛】本题考查直角三角形斜边上的中线的性质，角平分线的性质，等腰三角形的判定与性质，三角形中位线定理.根据直角三角形斜边上的中线是斜边是斜边的一半可得∠DBF 为等腰三角形，通过角平分线的性质和等角对等边可得DF//BC，即DE为∠ABC的中位线，从而计算出DE，继而求出EF.21．155°23′【分析】根据补角的概念，直接作答即可．【详解】解：根据题意，∠α=24°37′，则∠α的补角=180°-24°37′=155°23′．故答案为：155°23′．【点睛】此题考查补角的问题．解题的关键是掌握补角的定义，涉及角度问题时，需要特别注意题干中是否带有单位．22．30【详解】∠互余两角的和等于90°，∠α的余角为：90°-60°=30°.故答案为：3023．6【分析】根据题意可知在同一平面内用游戏棒搭4个大小一样的等边三角形（两个菱形），至少要9根游戏棒，在空间搭4个大小一样的等边三角形，如三棱锥，至少要6根游戏棒．【详解】由题可知：因为4个等边三角形需12根游戏棒，但可共用3根，所以至少要9根游戏棒；因为空间可以共棱，所以至少要6根游戏棒．【点睛】此题涉及到规律型：数字的变化类．主要考查了学生的分析、总结、归纳能力，规律型的习题一般是从所给的数据和运算方法进行分析，从特殊值的规律上总结出一般性的规律．24．7【分析】本题需要分两种情况讨论，∠当点C在线段AB上时，∠当点C在线段AB的延长线上时，根据线段中点的定义，计算即可．【详解】如图，当点C在线段AB上时，则14410AC=-=∠M是AC的中点，N是BC的中点，∠1152722MN MC CN AC BC=+=+=+=；如图，当点C在线段AB的延长线上时，则14418AC=+=，∠M是AC的中点，N是BC的中点，∠1192722MN MC CN AC BC=-=-=-=，综上所述，段MN的长度是7cm，故答案为：7【点睛】本题考查了两点间的距离，关键是利用了线段的中点的定义，分情况讨论．25．110【分析】因为钟表上的刻度是把一个圆平均分成了12等份，每一份是30°，借助图形，找出时针和分针之间相差的大格数，用大格数乘30°即可．【详解】解：∠时针在钟面上每分钟转0.5°，分针每分钟转6°，∠钟表上12时20分钟时，时针与分针的夹角可以看成时针转过12时0.5°×20=10°，分针在数字4上．∠钟表12个数字，每相邻两个数字之间的夹角为30°，∠12时20分钟时分针与时针的夹角4×30°-10°=110°．故答案为：110．【点睛】本题考查钟表分针所转过的角度计算．在钟表问题中，常利用时针与分针转动的度数关系：分针每转动1°时针转动（112）°，并且利用起点时间时针和分针的位置关系建立角的图形．26．=【详解】解：∠α=90°-∠AOB ，∠β=90°-∠AOB ，故∠α=∠β．故答案为=． 27． 110°或130° 1203α⎛⎫-︒ ⎪⎝⎭或21503α⎛⎫-︒ ⎪⎝⎭ 【分析】A 、根据角的和差得到∠AOB =90°-30°=60°，根据OE 是∠AOB 的一条三等分线，分类讨论，当∠AOE =13∠AOB =20°，∠当∠BOE ′=13∠AOB =20°，根据角的和差即可得到结论；B 、根据角的和差得到∠AOB ，根据OE 是∠AOB 的一条三等分线，分类讨论，当∠AOE =13∠AOB ，∠当∠BOE ′=13∠AOB ，根据角的和差即可得到结论． 【详解】解：A 、如图，∠∠AOC =90°，∠BOC =30°，∠∠AOB =90°-30°=60°，∠OE 是∠AOB 的一条三等分线，∠∠当∠AOE =13∠AOB =20°， ∠∠BOE =40°，∠∠BOD=90°，∠∠EOD=∠BOD+∠BOE=130°，∠当∠BOE′=13∠AOB=20°，∠∠DOE′=90°+20°=110°，综上所述，∠EOD的度数为130°或110°，故答案为：130°或110°；B、∠∠AOC=90°，∠BOC=α°，∠∠AOB=90°-α°，∠OE是∠AOB的一条三等分线，∠∠当∠AOE=13∠AOB=30°-13α°，∠∠BOE=90°-α-（30-13α）°=60°-23α°，∠∠BOD=90°，∠∠EOD=∠BOD+∠BOE=150°-23α°，∠当∠BOE′=13∠AOB=30°-13α°，∠∠DOE′=90°+30°-13α°=120°-13α°，综上所述，∠EOD的度数为150°-23α°或120°-13α°，故答案为：150°-23α°或120°-13α°；【点睛】本题考查了余角和补角的定义，角的倍分，熟练掌握余角和补角的性质是解题的关键．28．75【分析】由∠BAC=∠ACD=90°，可得AB∠CD，所以∠BAE=∠D=30°，利用三角形的外角关系即可求出∠AEC的度数．【详解】解：∠∠BAC=∠ACD=90°，∠AB∠CD，∠∠BAE=∠D=30°，∠∠AEC=∠B+∠BAE=75°，故答案为：75.【点睛】此题主要三角形的外角的性质，平行线的性质与判定，三角板中角度的计算，判断出AB ∠CD 是解本题的关键．29． 锥体 曲的面 顶点【分析】根据不同的分类标准的要求即可求解．【详解】解：（1）从形状方面，按柱体、__锥体______、球划分；（2）从面的方面，按组成的面有无____曲的面______划分；（3）从顶点方面，按有无____顶点____划分．故答案为（1）锥体，（2）曲的面，（3）顶点．【点睛】本题考查立体图形的不同分类方法，掌握各种分类标准及要求是解题关键． 30．八棱柱【分析】棱柱有两个面互相平行，其余各面都是多边形，并且每相邻两个四边形的公共边都互相平行；据此，再结合“这个‘古董’有8个面是正方形，2个面是多边形”，即可确定答案.【详解】根据甲：它有10个面；乙：它有24条棱；丙：它有8个面是正方形，2个面是多边形；丁：如果把它的侧面展开，是一个长方形.可知它符合棱柱的特征，可知是一个八棱柱.故答案为八棱柱.【点睛】本题考查了认识立体图形，解题的关键是熟练掌握棱柱的特征.31．【分析】根据题意得，6520CAB ∠=︒-︒，402060ACB ∠=︒+︒=︒，30AB =，过B 作BE AC ⊥于E ，解直角三角形即可得到结论．【详解】解：根据题意得，652045CAB ∠=︒-︒=︒，402060ACB ∠=︒+︒=︒，30AB =， 过B 作BE AC ⊥于E ，90AEB CEB ∴∠=∠=︒，在Rt ABE ∆中，45ABE ∠=︒，30AB =，AE BE ∴== 在Rt CBE ∆中，60ACB ∠=︒，CE ∴=AC AE CE ∴=+=∴，C两港之间的距离为km，A故答案为：【点睛】本题考查了解直角三角形的应用，方向角问题，三角形的内角和，是基础知识比较简单．32．D【分析】由平面图形的折叠及立体图形的表面展开图的特点解答即可．【详解】解：正方体的平面展开图中，相对的面一定相隔一个正方形，所以字母B的对面是D．故答案为D．【点睛】本题考查了正方体相对两个面上的文字，注意正方体的空间图形，从相对面入手，分析及解答问题．33．1000【分析】先画出草图，根据∠COA=30°，∠EOB=60°，∠EOC=180°，得到∠AOB=90°，根据路程=速度×时间，得到OA=40×15=600，OB=40×20=800，利用勾股定理计算AB即可．【详解】画出草图如下，∠∠COA=30°，∠EOB=60°，∠EOC=180°，∠∠AOB=90°，∠路程=速度×时间，∠OA =40×15=600，OB =40×20=800，∠AB =1000，故答案为：1000．【点睛】本题考查了方位角，勾股定理，正确理解方位角的意义，熟练掌握勾股定理是解题的关键．34．32cm 或28cm【分析】根据角平分线性质，得BAE DAE ∠=∠；根据平行四边形及平行线性质，得BEA DAE ∠=∠，从而得BAE BEA ∠=∠；根据等腰三角形性质，得BA BE =；根据题意，分两种情况分析，通过计算即可得到答案．【详解】根据题意，如图：∠AE 平分∠BAD 交BC 与点E ，∠BAE DAE ∠=∠∠平行四边形ABCD∠//AD BC∠BEA DAE ∠=∠∠BAE BEA ∠=∠∠BA BE =AE 将BC 分成4cm 和6cm 两部分，当6cm BE =时，得6cm BA BE ==∠10cm BC BE EC =+=∠平行四边形ABCD 的周长为2232cm BA BC +=当4cm BE =时，得4cm BA BE ==∠平行四边形ABCD 的周长为2228cm BA BC +=故答案为：32cm 或28cm ．【点睛】本题考查了角平分线、平行四边形、平行线、等腰三角形的知识；解题的关键是熟练掌握角平分线、平行四边形、等腰三角形的性质，从而完成求解．35．56【分析】先由圆周角定理得∠ACB ＝90°，求得∠ABC 的度数，然后由圆周角定理，即可求得∠ADC 的度数．【详解】解：∠AB 为∠O 的直径，∠∠ACB ＝90°，∠∠CAB ＝34°，∠∠ABC ＝90°﹣∠CAB ＝56°，∠∠ADC ＝∠ABC ＝56°．故答案为：56．【点睛】本题考查了圆周角定理以及直角三角形的性质等知识；熟练掌握圆周角定理是解题的关键．36．1或5【分析】分为两种情况，画出图形，根据线段的和差即可得出答案．【详解】解：当C 在线段AB 上时，AC=AB-BC=3-2=1，当C 在线段AB 的延长线时，AC=AB+BC=3+2=5，即AC=1或5，故答案为：1或5．【点睛】本题考查了线段的和差，能求出符合的所有情况是解此题的关键，注意要进行分类讨论．37．15【分析】分别以OA 、OB 、OC 、OD 、OE 、OF 为一边，数出所有角，找出其中的非锐角，相减即可得答案．【详解】解：以OA 、OB 、OC 、OD 、OE 、OF 为始边，分别有角6个，5个，4个，3个，2个，1个，图中共有角21个，OA OE ⊥，所以以OA 为边的非锐角有3个，分别为,,AOG AOF AOE ，,OC OG ,BOC FOG∠∠COF +∠BOC ＞90°，∠∠FOB ＞90°．所以以OB 为边的非锐角有2个，分别为,BOG BOF ，以OC 为边的非锐角有1个，为COG ∠．于是图中共有锐角21-（3+2+1）=15个．故答案为15．【点睛】此题考查了角的数法，要以每条边为始边，数出所有角，要注意，不能漏数，也不能多数，要注意去掉非锐角．38．73【分析】根据题意：我们把相对面打通需要去掉的小正方体分三种情况，按一定的顺序数去掉的小正方体数量，如前后面，上下面，左右面分别去数数，然后用总数125减掉数出来的三部分即可，注意：前面数过的后面的一定去掉，否则会重复的．【详解】解：前后面少(3+2)×5＝25(个)，上下面少的(去掉与前后面重复的)(5-3)+2×3+1×5＝13(个)，左右面少的(去掉与前后，上下重复的)(5-3)+(5-1)+(5-2)+(5-2-1)+(5-2)＝14(个)， 125-(25+13+14)＝73(个)，答：图中剩下的小正方体有73个．故答案为：73．【点睛】本题考查了正方体的对面上的数字，要注意不能重复和遗漏．39．150.【分析】根据周角的定义，利用360度减去∠α和∠β即可求解．【详解】由题意可得，∠γ=360°-∠α-∠β=360°-120°-90°=150°．故答案是：150．【点睛】本题考查了角度的计算，正确得到图中三个角之间的关系是解决问题的关键．40．16【分析】作点C关于AB的对称点C'，过点C'作C'E∠AC，交AB于点D'，即可确定C'E 就是CD+DE的最小值，然后运用勾股定理和相似三角形的知识求解即可．【详解】作点C关于AB的对称点C'，过点C'作C'E∠AC，交AB于点D'，则CD+DE的最小值为C'E的长；∠∠ACB=90°，AC=20，BC=10，，∠∠A=∠C'，∠''C E AC CC AB，∠C'E=16；故答案为16；【点睛】本题考查了相似三角形、勾股定理和最短距离问题，其中运用作对称点确定最短距离是解答的关键．41．(1)证明见解析(2)∠ABC=75°【分析】（1）先利用角平分线的定义得到∠DAC=∠1，则∠DAC=∠2，于是可判断。

中考数学总复习《几何压轴题》专项提升练习题(附答案)

中考数学总复习《几何压轴题》专项提升练习题(附答案)

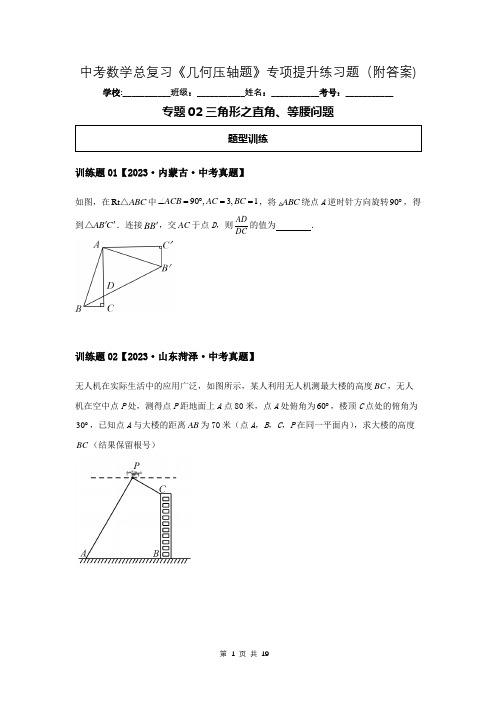
中考数学总复习《几何压轴题》专项提升练习题（附答案)学校:___________班级：___________姓名：___________考号：___________专题02三角形之直角、等腰问题 题型训练训练题01【2023·内蒙古·中考真题】如图，在Rt ABC △中90,3,1ACB AC BC ∠=︒==，将ABC 绕点A 逆时针方向旋转90︒，得到AB C ''△．连接BB '，交AC 于点D ，则AD DC 的值为 ．训练题02【2023·山东菏泽·中考真题】无人机在实际生活中的应用广泛，如图所示，某人利用无人机测最大楼的高度BC ，无人机在空中点P 处，测得点P 距地面上A 点80米，点A 处俯角为60︒，楼顶C 点处的俯角为30︒，已知点A 与大楼的距离AB 为70米（点A ，B ，C ，P 在同一平面内），求大楼的高度BC （结果保留根号）训练题03【2023·广东·中考真题】2023年5月30日，神舟十六号载人飞船发射取得圆满成功，3名航天员顺利进驻中国空间站，如图中的照片展示了中国空间站上机械臂的一种工作状态，当两臂10m AC BC ==，两臂夹角100ACB ∠=︒时，求A ，B 两点间的距离．(结果精确到0.1m ，参考数据sin500.766︒≈ cos500.643︒≈ tan50 1.192︒≈)训练题04【2023·湖北黄冈·中考真题】综合实践课上，航模小组用航拍无人机进行测高实践．如图，无人机从地面CD 的中点A 处竖直上升30米到达B 处，测得博雅楼顶部E 的俯角为45︒，尚美楼顶部F 的俯角为30︒，已知博雅楼高度CE 为15米，则尚美楼高度DF 为 米．（结果保留根号）训练题05【2023·河北沧州·模拟预测】如图1，嘉淇在量角器的圆心O 处下挂一铅锤，制作了一个简易测角仪．将此测角仪拿到眼前，使视线沿着仪器的直径刚好到达树的最高点M ．(1)在图1中，过点A 画出水平线，并标记观测M 的仰角α．若铅垂线在量角器上的读数为53︒，求α的值；(2)如图2，已知嘉淇眼睛离地1.5米，站在B 处观测M 的仰角为（1）中的α，向前走1.25米到达D 处，此时观测点M 的仰角为45︒，求树MN 的高度．（注：3tan 374︒≈ 3sin 375︒≈ 4cos375≈︒） 训练题06【2023·四川成都·八年级期末联考】如图 在等腰Rt EDF 中 90EDF ∠=︒ 2DE DF == DG EF ⊥于点G 点M N 分别是DE DG 上的动点 且DN EM = 则FM FN +的最小值为 ．训练题07【2022·陕西西安·滨河期末】如图 直线y ＝x ﹣3分别交x 轴 y 轴于B A 两点 点C （0 1）在y 轴上 点P 在x 轴上运动 则2PC ＋PB 的最小值为 ．训练题08【2021·四川甘孜·中考真题】如图 腰长为22+2的等腰ABC 中 顶角∠A ＝45° D 为腰AB 上的一个动点将ACD 沿CD 折叠 点A 落在点E 处 当CE 与ABC 的某一条腰垂直时 BD 的长为 ．训练题09【2022·福建泉州·九年级联考】如图 ABC 和AGF 是等腰直角三角形 90BAC G ∠=∠=︒ AGF 的边AF AG 交边BC 于点D E ．若4=AD 3AE = 则BEDC 的值是 ．训练题10【2021·宁夏固元·联考一模】如图在直角△BAD中延长斜边BD到点C 使得BD=2DC 连接AC 如果则的值是（）A．B．C．D．答案&解析5 tanB3=tan CAD∠3 3351315训练题01【2023·内蒙古·中考真题】【答案】5【简证】因为tan 311tan 4522ABC CD ABD α∠=⎧⇒=⇒=⎨∠=︒⎩ 故5AD DC =【常规法】解：过点D 作DF AB ⊥于点F∵90ACB ∠=︒ 3AC = 1BC =∴223110AB =+=∵将ABC 绕点A 逆时针方向旋转90︒得到AB C ''△∴==10AB AB ' 90BAB '∠=︒∴ABB '是等腰直角三角形∴45ABB '∠=︒又∵DF AB ⊥∴45FDB ∠=︒∴DFB △是等腰直角三角形∴DF BF =∵1122ADB S BC AD DF AB =⨯⨯=⨯⨯ 即=10AD DF ∵ 90C AFD ∠=∠=︒ CAB FAD ∠=∠∴AFDACB ∴DF AF BC AC= 即3AF DF = 又∵=10AF DF -45°α∴10=4 DF∴105=10=42AD⨯51=3=22CD-∴52==512ADCD故答案为：5．训练题02【2023·山东菏泽·中考真题】【答案】大楼的高度BC 为303m ．【分析】如图 过P 作PH AB ⊥于H 过C 作CQ PH ⊥于Q 而CB AB ⊥ 则四边形CQHB 是矩形 可得QH BC = BH CQ = 求解3sin 60804032PH AP =︒=⨯= cos6040AH AP =︒= 可得704030CQ BH ==-= tan 30103PQ CQ =︒= 可得403103303BC QH ==-=．【详解】解：如图 过P 作PH AB ⊥于H 过C 作CQ PH ⊥于Q 而CB AB ⊥则四边形CQHB 是矩形 ∴QH BC = BH CQ =由题意可得：80AP = 60PAH ∠=︒ 30PCQ ∠=︒ 70AB = ∴3sin 60804032PH AP =︒=⨯= cos6040AH AP =︒= ∴704030CQ BH ==-= ∴tan 30103PQ CQ =︒=∴403103303BC QH ==-= ∴大楼的高度BC 为303m ．训练题03【2023·广东·中考真题】【答案】15.3m【分析】连接AB 作作CD AB ⊥于D 由等腰三角形“三线合一”性质可知2AB AD = 1502ACD ACB ∠=∠=︒ 在Rt ACD △中利用sin AD ACD AC∠=求出AD 继而求出AB 即可．【详解】解：连接AB 作CD AB ⊥于D∵AC BC = CD AB ⊥∴CD 是边AB 边上的中线 也是ACB ∠的角平分线∴2AB AD = 1502ACD ACB ∠=∠=︒ 在Rt ACD △中 10m AC = 50ACD ∠=︒ sin AD ACD AC ∠= ∴sin 5010AD ︒= ∴10sin50100.7667.66AD =︒≈⨯=∴()227.6615.3215.3m AB AD =≈⨯=≈答：A B 两点间的距离为15.3m ．训练题04【2023·湖北黄冈·中考真题】【答案】3053-/5330-+【分析】过点E 作EM AB ⊥于点M 过点F 作FN AB ⊥于点N 首先证明出四边形ECAM 是矩形 得到15AM CE == 然后根据等腰直角三角形的性质得到15AC EM BM === 进而得到15==AD AC 然后利用30︒角直角三角形的性质和勾股定理求出53BN = 即可求解．【详解】如图所示 过点E 作EM AB ⊥于点M 过点F 作FN AB ⊥于点N由题意可得 四边形ECAM 是矩形 ∴15AM CE == ∵30AB = ∴15BM AB AM =-= ∵博雅楼顶部E 的俯角为45︒ ∴45EBM ∠=︒ ∴45BEM ∠=︒ ∴15AC EM BM ===∵点A 是CD 的中点 ∴15==AD AC 由题意可得四边形AMFN 是矩形 ∴15NF AD == ∵尚美楼顶部F 的俯角为30︒ ∴60NBF ∠=︒ ∴30BFN ∠=︒ ∴2BF BN =∴在Rt BNF △中 222BNNF BF += ∴()222152BN BN +=∴解得53BN =∴3053FD AN AB BN ==-=-．故答案为：3053-．训练题05【2023·河北沧州·模拟预测】【答案】(1)37︒(2)树MN 的高度为5.25米【分析】(1)根据互余的性质计算即可．(2) 过点A 作AP MN ⊥ 垂足为P 则 1.5PN AB ==米．设MN x =米．解直角三角形求解即可．【详解】（1）如图1；905337α=︒-︒=︒；（2）如图 过点A 作AP MN ⊥ 垂足为P 则 1.5PN AB ==米．设MN x =米． 在Rt APM △中 4( 1.5)tan 373MP AP x ==-︒（米） 在Rt MCP 中 1.5CP MP x ==-（米） 4( 1.5)( 1.5) 1.253AC AP CP x x ∴=-=---=（米） 解得 5.25x =． 答：树MN 的高度为5.25米．训练题06【2023·四川成都·八年级期末联考】【答案】23【分析】过点E 作AE EF ⊥ 使得2AE DF == 证得AEM FDN ≅ 利用全等三角形的性质证得FN AM = 求FM FN +的最小值即求FM AM +的最小值 此时只有A M F 在一条直线上时 FM AM +的最小 即为AF 的长 在Rt AEF 中利用勾股定理即可求解．【详解】解：过点E 作AE EF ⊥ 使得2AE DF == 如图所示∵等腰Rt EDF 中 90EDF ∠=︒ 2DE DF ==∴45DEF ∠=︒ 222222EF =+=∴9045AEM DEF ∠=︒-∠=︒∵等腰Rt EDF 中 90EDF ∠=︒ 2DE DF == DG EF ⊥∴45FDN ∠=︒∴FDN AEM ∠=∠在AEM △和FDN 中AE DF AEM FDN EM DN =⎧⎪∠=∠⎨⎪=⎩∴AEM FDN≅()SAS ∴FN AM =∴求FM FN +的最小值即求FM AM +的最小值 此时只有A M F 在一条直线上时 FM AM +的最小 即为AF 的长∴在Rt AEF 中()222222223AF AE EF =+=+=的最小值为23即FM FN故答案为：23训练题07【2022·陕西西安·滨河期末】【答案】4【分析】过P作PD⊥AB于D依据△AOB是等腰直角三角形可得∠BAO＝∠ABO＝45°＝∠BPD进而得到△BDP是等腰直角三角形故PD22=PB当C P D在同一直线上时CD⊥AB PC+PD的最小值等于垂线段CD的长求得CD的长即可得出结论．【详解】如图所示过P作PD⊥AB于D∵直线y＝x﹣3分别交x轴y轴于B A两点令x＝0 则y＝﹣3；令y＝0 则x＝3∴A（0 ﹣3）B（3 0）∴AO＝BO＝3又∵∠AOB＝90°∴△AOB是等腰直角三角形∴∠BAO＝∠ABO＝45°＝∠BPD∴△BDP是等腰直角三角形∴PD22=PB∴2PC+PB2=（PC22+PB）2=（PC+PD）当C P D在同一直线上即CD⊥AB时PC+PD的值最小最小值等于垂线段CD 的长此时△ACD是等腰直角三角形又∵点C（0 1）在y轴上∴AC＝1+3＝4∴CD22=AC＝22即PC+PD的最小值为22∴2PC+PB的最小值为222⨯=4 故答案为：4．训练题08【2021·四川甘孜·中考真题】【答案】2或22【分析】分两种情况：当CE ⊥AB 时 设垂足为M 在Rt △AMC 中 ∠A ＝45° 由折叠得：∠ACD ＝∠DCE ＝22.5° 证明△BCM ≌△DCM 得到BM ＝DM 证明△MDE 是等腰直角三角形 即可得解；当CE ⊥AC 时 根据折叠的性质 等腰直角三角形的判定与性质计算即可；【详解】当CE ⊥AB 时 如图设垂足为M 在Rt △AMC 中 ∠A ＝45°由折叠得：∠ACD ＝∠DCE ＝22.5°∵等腰△ABC 中 顶角∠A ＝45°∴∠B ＝∠ACB ＝67.5°∴∠BCM ＝22.5°∴∠BCM ＝∠DCM在△BCM 和△DCM 中90BMC DMC CM CM BCM DCM ∠=∠=︒⎧⎪=⎨⎪∠=∠⎩∴△BCM ≌△DCM （ASA ）∴BM ＝DM由折叠得：∠E ＝∠A ＝45° AD ＝DE∴△MDE 是等腰直角三角形∴DM ＝EM设DM ＝x 则BM ＝x DE 2=x∴AD 2=x ．∵AB＝22+2∴2x2x＝22+2 解得：x2=∴BD＝2x＝22；当CE⊥AC时如图∴∠ACE＝90°由折叠得：∠ACD＝∠DCE＝45°∵等腰△ABC中顶角∠A＝45°∴∠E＝∠A＝45°AD＝DE∴∠ADC＝∠EDC＝90°即点D E都在直线AB上且△ADC△DEC△ACE都是等腰直角三角形∵AB＝AC＝＝22+2∴AD22=AC＝22BD＝AB﹣AD＝（22+2）﹣（22）2=综上BD的长为2或22．故答案为：2或22．训练题09【2022·福建泉州·九年级联考】【答案】916【分析】利用等腰直角三角形的性质先证明AED BEA ∽ 可得34BE AE AB AD ==,设3BE x = 则4AB x AC ==,再证明ADE CDA △∽△ 可得34AC AE CD AD == 可得163CD x = 从而可得结论． 【详解】解：∵ABC 和AGF 是等腰直角三角形 ∴45,B F FAG AB AC ∠=∠=∠=︒=∵AEB AED ∠=∠∴AED BEA ∽∴AD AE DE AB BE AE ==,而4=AD 3AE = ∴34BE AE AB AD == 设3BE x = 则4AB x AC ==同理可得：ADE CDA △∽△∴AD AE DE CD AC AD == ∴34AC AE CD AD == ∴BE AC AB CD = ∴344x x x CD =,即163CD x = ∴3916163BE x CD x ==.训练题10【2021·宁夏固元·联考一模】【答案】D【详解】解：如图 延长AD 过点C 作CE ⊥AD 垂足为E∵ 即∴设AD ＝5x 则AB ＝3x∵∠CDE ＝∠BDA ∠CED ＝∠BAD∴△CDE ∽△BDA∴∴CE ＝ DE ＝∴AE ＝ ∴tan ∠CAD ＝．5tanB 3=53AD AB =12CE DE CD AB AD BD ===32x 52x 152x 15CE AE =。

中考数学几何专项训练及答案

中考数学几何专项训练及答案

中考数学几何专项训练及答案所以AD=DF=AF；AB=AD，所以△ABD为等腰三角形，∠ABD=∠BAD=30°；ABC=60°，所以∠CBD=30°；AD=DF，所以∠AFD=∠ADF=75°；ABD=∠CBD=30°，所以∠ADB=∠CDB=60°；ABD=∠BAD=30°，所以∠ADB=120°；ADB为等边三角形，BD=AD=6；XXX∠EAD+∠BAD=15°+30°=45°，∠BED=90°，所以△EBD为45°-45°-90°三角形，EB=BD/√2=3√2；AB=AD=6，所以CD=AB+2AD=18；ABC=60°，所以∠BCD=30°；CD=2AD，所以∠ADC=90°-∠ACD=60°；ADC为30°-60°-90°三角形，AD=CD/2=9，BD=6；BED=45°，所以∠BEC=45°；BE=EB=3√2，所以BC=2BE=6√2；G为BC的中点，所以BG=GC=BC/2=3√2；AD=DF=AF=9，BC=6√2，BG=GC=3√2.1）求证：DE=BC；2）连接BE，求证：∠XXX∠BAC．1）证明：∵△ABD为等边三角形。

AD=BD。

XXX为等边三角形。

AE=CE。

CAB=30°。

EAC=75°。

AEC=75°。

DEC=105°。

ACB=90°。

DBC=60°。

DCB=30°。

BDC=75°。

DBC=75°。

BDC为等腰三角形。

BC=BD。

DE=BD=BC．2）证明：∵△ABD为等边三角形。

BAD=60°。

XXX为等边三角形。

CAE=60°。

中考数学几何压轴题(有关三角形、四边形)的综合专题(含答案解析)

中考数学几何压轴题(有关三角形、四边形)的综合专题(含答案解析)

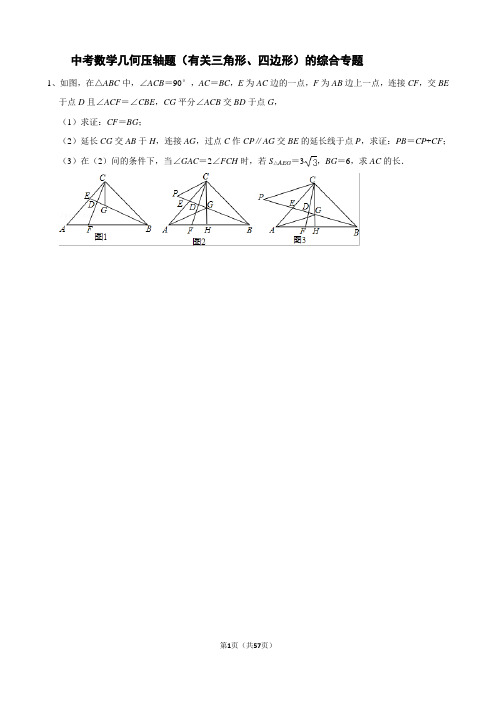
中考数学几何压轴题（有关三角形、四边形）的综合专题1、如图，在△ABC中，∠ACB＝90°，AC＝BC，E为AC边的一点，F为AB边上一点，连接CF，交BE于点D且∠ACF＝∠CBE，CG平分∠ACB交BD于点G，（1）求证：CF＝BG；（2）延长CG交AB于H，连接AG，过点C作CP∥AG交BE的延长线于点P，求证：PB＝CP+CF；（3）在（2）问的条件下，当∠GAC＝2∠FCH时，若S△AEG＝3，BG＝6，求AC的长．2、[问题背景]如图1所示，在△ABC中，AB＝BC，∠ABC＝90°，点D为直线BC上的一个动点（不与B、C重合），连结AD，将线段AD绕点D按顺时针方向旋转90°，使点A旋转到点E，连结EC．[问题初探]如果点D在线段BC上运动，通过观察、交流，小明形成了以下的解题思路：过点E作EF⊥BC 交直线BC于F，如图2所示，通过证明△DEF≌△，可推证△CEF是三角形，从而求得∠DCE＝．[继续探究]如果点D在线段CB的延长线上运动，如图3所示，求出∠DCE的度数．[拓展延伸]连接BE，当点D在直线BC上运动时，若AB＝，请直接写出BE的最小值．3、（2019秋•锦江区校级期末）在Rt△ABC中，∠ACB＝90°，∠A＝30°，BD是△ABC的角平分线．（1）如图1，求证：AD＝2DC．（2）如图2，作∠CBD的角平分线交线段CD于点M，若CM＝1，求△DBM的面积；（3）如图3，过点D作DE⊥AB于点E，点N是线段AC上一点（不与C、D重合），以BN为一边，在BN的下方作∠BNG＝60°，NG交DE延长线于点G，试探究线段ND，DG与AD之间的数量关系，并说明理由．4、（2019•镇平县三模）如图1，已知直角三角形ABC，∠ACB＝90°，∠BAC＝30°，点D是AC边上一点，过D作DE⊥AB于点E，连接BD，点F是BD中点，连接EF，CF．（1）发现问题：线段EF，CF之间的数量关系为；∠EFC的度数为；（2）拓展与探究：若将△AED绕点A按顺时针方向旋转α角（0°＜α＜30°），如图2所示，（1）中的结论还成立吗？请说明理由；（3）拓展与运用：如图3所示，若△AED绕点A旋转的过程中，当点D落到AB边上时，AB边上另有一点G，AD＝DG＝GB，BC＝3，连接EG，请直接写出EG的长度．5、（2017春•西城区校级期末）如图1，在等腰△ABC中，AB＝AC，∠BAC＝a，点P是线段AB的中点，点E是线段CB延长线上一点，且PE＝PC，将线段PC绕点P顺时针旋转α得到PD，连接BD．（1）如图2，若α＝60°，其他条件不变，先补全图形，然后探究线段BD和BC之间的数量关系，并说明理由．（2）如图3，若α＝90°，其他条件不变，探究线段BP、BD和BC之间的等量关系，并说明理由．6、【发现问题】如图1，已知△ABC，以点A为直角顶点、AB为腰向△ABC外作等腰直角△ABE．请你以A为直角顶点、AC为腰，向△ABC外作等腰直角△ACD（不写作法，保留作图痕迹）．连接BD、CE．那么BD与CE的数量关系是BD＝CE．【拓展探究】如图2，已知△ABC，以AB、AC为边向外作正方形AEFB和正方形ACGD，连接BD、CE，试判断BD与CE之间的数量关系，并说明理由．【解决问题】如图3，有一个四边形场地ABCD，∠ADC＝60°，BC＝15，AB＝8，AD＝CD，求BD的最大值．7、（1）如图1，点C为线段AB外一个动点，已知AB＝a，AC＝b．当点C位于BA的延长线上时，线段BC取得最大值，则最大值为（用含a，b的式子表示）；（2）如图2，点C为线段AB外一个动点，若AB＝10，AC＝3，分别以AC，BC为边，作等边三角形ACD和等边三角形BCE，连接AE，DB．①求证：AE＝DB；②请直接写出线段AE的最大值；（3）如图3，AB＝6，点M为线段AB外一个动点，且AM＝2，MB＝MN，∠BMN＝90°，请直接写出线段AN的最大值．8、【初步探索】（1）如图1：在四边形ABC中，AB＝AD，∠B＝∠ADC＝90°，E、F分别是BC、CD上的点，且EF ＝BE+FD，探究图中∠BAE、∠F AD、∠EAF之间的数量关系．小王同学探究此问题的方法是：延长FD到点G，使DG＝BE．连接AG，先证明△ABE≌△ADG，再证明△AEF≌△AGF，可得出结论，他的结论应是；【灵活运用】（2）如图2，若在四边形ABCD中，AB＝AD，∠B+∠D＝180°．E、F分别是BC、CD上的点，且EF＝BE+FD，上述结论是否仍然成立，并说明理由；【拓展延伸】（3）如图3，已知在四边形ABCD中，∠ABC+∠ADC＝180°AB＝AD，若点E在CB的延长线上，点F在CD的延长线上，如图3所示，仍然满足EF＝BE+FD，请写出∠EAF与∠DAB的数量关系，并给出证明过程．9、（2018•大东区一模）如图，在Rt△ABC中，∠ACB＝90°，∠A＝30°，点O为AB中点，点P为直线BC上的动点（不与点B、点C重合），连接OC、OP，将线段OP绕点P逆时针旋转60°，得到线段PQ，连接BQ．（1）如图1，当点P在线段BC上时，请直接写出线段BQ与CP的数量关系．（2）如图2，当点P在CB延长线上时，（1）中结论是否成立？若成立，请加以证明；若不成立，请说明理由；（3）如图3，当点P在BC延长线上时，若∠BPO＝45°，AC＝，请直接写出BQ的长．10、模型发现：同学们知道，三角形的两边之和大于第三边，即如图1，在△ABC中，AB+AC＞BC．对于图1，若把点C看作是线段AB外一动点，且AB＝c，AC＝b，则线段BC的长会因为点C的位置的不同而发生变化．因为AB、AC的长度固定，所以当∠BAC越大时，BC边越长．特别的，当点C位于时，线段BC的长取得最大值，且最大值为（用含b，c的式子表示）（直接填空）.模型应用：点C为线段AB外一动点，且AB＝3，AC＝2，如图2所示，分别以AC，BC为边，作等边三角形ACD 和等边三角形BCE，连接BD，AE．（1）求证：BD＝AE．（2）线段AE长的最大值为．模型拓展：如图3，在平面直角坐标系中，点A是y轴正半轴上的一动点，点B是x轴正半轴上的一动点，且AB ＝8．若AC⊥AB，AC＝3，试求OC长的最大值．11、已知：△ABC中，∠ACB＝90°，AC＝BC．（1）如图1，点D在BC的延长线上，连AD，过B作BE⊥AD于E，交AC于点F．求证：AD＝BF；（2）如图2，点D在线段BC上，连AD，过A作AE⊥AD，且AE＝AD，连BE交AC于F，连DE，问BD与CF有何数量关系，并加以证明；（3）如图3，点D在CB延长线上，AE＝AD且AE⊥AD，连接BE、AC的延长线交BE于点M，若AC ＝3MC，请直接写出的值．12、已知在△ABC中，AB＝AC，射线BM、BN在∠ABC内部，分别交线段AC于点G、H．（1）如图1，若∠ABC＝60°，∠MBN＝30°，作AE⊥BN于点D，分别交BC、BM于点E、F．①求证：∠1＝∠2；②如图2，若BF＝2AF，连接CF，求证：BF⊥CF；（2）如图3，点E为BC上一点，AE交BM于点F，连接CF，若∠BFE＝∠BAC＝2∠CFE，求的值．13、已知，△ABC中，AB＝AC，∠BAC＝90°，E为边AC任意一点，连接BE．（1）如图1，若∠ABE＝15°，O为BE中点，连接AO，且AO＝1，求BC的长；（2）如图2，F也为AC上一点，且满足AE＝CF，过A作AD⊥BE交BE于点H，交BC于点D，连接DF交BE于点G，连接AG；①若AG平分∠CAD，求证：AH＝AC；②如图3，当G落在△ABC外时，若将△EFG沿EF边翻折，点G刚好落在AB边上点P，直接写出AG与EF的数量关系．14、如图所示，Rt△ABC中，∠ACB＝90°，E为AC中点，作ED⊥AC交AB于D，连接CD；（1）如图1，求证：AB＝2CD；（2）如图2，作CF⊥AB交AB于F，点G为CF上一点，点H为DE延长线上一点，分别连接AH、GH，若∠AHG＝2∠B，求证：AH＝GH；（3）如图3，在（2）的条件下，连接DG，且有DE＝BF，∠EDG＝90°，若AC＝6，求AH的长度．15、【问题情境】一节数学课后，老师布置了一道课后练习题：如图：已知在Rt△ABC中，AC＝BC，∠ACB＝90°，CD⊥AB于点D，点E、F分别在A和BC上，∠1＝∠2，FG⊥AB于点G，求证：△CDE≌△EGF．（1）阅读理解，完成解答本题证明的思路可用下列框图表示：根据上述思路，请你完整地书写这道练习题的证明过程；（2）特殊位置，证明结论若CE平分∠ACD，其余条件不变，求证：AE＝BF；（3）知识迁移，探究发现如图，已知在Rt△ABC中，AC＝BC，∠ACB＝90°，CD⊥AB于点D，若点E是DB的中点，点F在直线CB上且满足EC＝EF，请直接写出AE与BF的数量关系．（不必写解答过程）16、在正方形ABCD和等腰直角△BGF中，∠BGF＝90°，P是DF的中点，连接PG、PC．（1）如图1，当点G在BC边上时，延长GP交DC于点E．求证：PG＝PC；（2）如图2，当点F在AB的延长线上时，（1）中的结论是否成立？请证明你的结论；（3）如图3，若四边形ABCD为菱形，且∠ABC＝60°，△BGF为等边三角形，点F在CB的延长线上时，线段PC、PG又有怎样的数量关系，请直接写出你的结论，并画出论证过程中需要添加的辅助线．17、在△ABC中，∠BAC＝60°，点D、E分别在边AC、AB上，AD＝AE，连接CE、BD相交于点F，且∠BEC＝∠ADF，连接AF．（1）如图1，连接ED，求证：∠ABD＝∠CED；（2）如图2，求证：EF+FD＝AF；（3）如图3，取BC的中点G，连接AG交BD于点H，若∠GAC＝3∠ABD，BH＝7，求△ABH的面积．18、点D，E分别在△ABC的边AC，BD上，BD，CE交于点F，连接AF，∠F AE＝∠F AD，FE＝FD．（1）如图1，若∠AEF＝∠ADF，求证：AE＝AD；（2）如图2，若∠AEF≠∠ADF，FB平分∠ABC，求∠BAC的度数；（3）在（2）的条件下，如图3，点G在BE上，∠CFG＝∠AFB若AG＝6，△ABC的周长为20，求BC长．中考数学几何压轴题（有关三角形、四边形）的综合专题参考答案1、如图，在△ABC中，∠ACB＝90°，AC＝BC，E为AC边的一点，F为AB边上一点，连接CF，交BE于点D且∠ACF＝∠CBE，CG平分∠ACB交BD于点G，（1）求证：CF＝BG；（2）延长CG交AB于H，连接AG，过点C作CP∥AG交BE的延长线于点P，求证：PB＝CP+CF；（3）在（2）问的条件下，当∠GAC＝2∠FCH时，若S△AEG＝3，BG＝6，求AC的长．证明：（1）如图1，∵∠ACB＝90°，AC＝BC，∴∠A＝45°，∵CG平分∠ACB，∴∠ACG＝∠BCG＝45°，∴∠A＝∠BCG，在△BCG和△CAF中，∵，∴△BCG≌△CAF（ASA），∴CF＝BG；（2）如图2，∵PC∥AG，∴∠PCA＝∠CAG，∵AC＝BC，∠ACG＝∠BCG，CG＝CG，∴△ACG≌△BCG，∴∠CAG＝∠CBE，∵∠PCG＝∠PCA+∠ACG＝∠CAG+45°＝∠CBE+45°，∠PGC＝∠GCB+∠CBE＝∠CBE+45°，∴∠PCG＝∠PGC，∴PC＝PG，∵PB＝BG+PG，BG＝CF，∴PB＝CF+CP；（3）解法一：如图3，过E作EM⊥AG，交AG于M，∵S△AEG＝AG•EM＝3，由（2）得：△ACG≌△BCG，∴BG＝AG＝6，∴×6×EM＝3，EM＝，设∠FCH＝x°，则∠GAC＝2x°，∴∠ACF＝∠EBC＝∠GAC＝2x°，∵∠ACH＝45°，∴2x+x＝45，x＝15，∴∠ACF＝∠GAC＝30°，在Rt△AEM中，AE＝2EM＝2，AM＝＝3，∴M是AG的中点，∴AE＝EG＝2，∴BE＝BG+EG＝6+2，在Rt△ECB中，∠EBC＝30°，∴CE＝BE＝3+，∴AC＝AE+EC＝2+3+＝3+3．解法二：同理得：∠CAG＝30°，AG＝BG＝6，如图4，过G作GM⊥AC于M，在Rt△AGM中，GM＝3，AM＝＝＝3，∵∠ACG＝45°，∠MGC＝90°，∴GM＝CM＝3，∴AC＝AM+CM＝3+3．2、[问题背景]如图1所示，在△ABC中，AB＝BC，∠ABC＝90°，点D为直线BC上的一个动点（不与B、C重合），连结AD，将线段AD绕点D按顺时针方向旋转90°，使点A旋转到点E，连结EC．[问题初探]如果点D在线段BC上运动，通过观察、交流，小明形成了以下的解题思路：过点E作EF⊥BC 交直线BC于F，如图2所示，通过证明△DEF≌△ADB，可推证△CEF是等腰直角三角形，从而求得∠DCE＝135°．[继续探究]如果点D在线段CB的延长线上运动，如图3所示，求出∠DCE的度数．[拓展延伸]连接BE，当点D在直线BC上运动时，若AB＝，请直接写出BE的最小值．解：[问题初探]如图2，过点E作EF⊥BC交直线BC于F，∴∠DFE＝90°＝∠ABD，∴∠EDF+∠DEF＝90°，由旋转知，AD＝DE，∠ADE＝90°，∴∠ADB+∠EDF＝90°，∴∠ADB＝∠DEF，∴△ABD≌△DFE（AAS），∴BD＝EF，DF＝AB，∵AB＝BC，∴BC＝DF，∴BD＝CF，∴EF＝CF，∴△CEG是等腰直角三角形，∴∠ECF＝45°，∴∠DCE＝135°，故答案为：ADB，等腰直角，135；[继续探究]如图3，过点E作EF⊥BC于F，∴∠DFE＝90°＝∠ABD，∴∠EDF+∠DEF＝90°，由旋转知，AD＝DE，∠ADE＝90°，∴∠ADB+∠EDF＝90°，∴∠ADB＝∠DEF，∴△ABD≌△DFE（AAS），∴BD＝EF，DF＝AB，∵AB＝BC，∴BC＝DF，∴BD＝CF，∴EF＝CF，∴△CEG是等腰直角三角形，∴∠ECF＝45°，∴∠DCE＝45°；[拓展延伸]如图4，在△ABC中，∠ABC＝90°，AB＝BC＝，∴∠ACB＝45°当点D在射线BC上时，由[问题初探]知，∠BCM＝135°，∴∠ACM＝∠BCM﹣∠ACB＝90°，当点D在线段CB的延长线上时，由[继续探究]知，∠BCE＝45°，∴∠ACN＝∠ACB+∠BCM＝90°，∴点E是过点C垂直于AC的直线上的点，∴当BE⊥MN时，BE最小，∵∠BCE＝45°，∴∠CBE＝45°＝∠BCE，∴BE＝CE，∴BE最小＝BC＝，即：BE的最小值为．3、在Rt△ABC中，∠ACB＝90°，∠A＝30°，BD是△ABC的角平分线．（1）如图1，求证：AD＝2DC．（2）如图2，作∠CBD的角平分线交线段CD于点M，若CM＝1，求△DBM的面积；（3）如图3，过点D作DE⊥AB于点E，点N是线段AC上一点（不与C、D重合），以BN为一边，在BN的下方作∠BNG＝60°，NG交DE延长线于点G，试探究线段ND，DG与AD之间的数量关系，并说明理由．证明：（1）如图1，过点D作DE⊥AB，∵BD是△ABC的角平分线，DE⊥AB，∠ACB＝90°，∴DC＝DE，∵∠A＝30°，DE⊥AB，∴AD＝2DE，∴AD＝2DC；（2）如图2，过点M作ME∥BD，∵∠ACB＝90°，∠A＝30°，∴∠ABC＝60°，∵BD是△ABC的角平分线，∴∠ABD＝∠DBC＝30°，∵BM平分∠CBD，∴∠CBM＝15°＝∠DBM，∵ME∥BD，∴∠MEC＝∠CBD＝30°，∠EMB＝∠DBM＝∠MBE，∴ME＝BE，∵∠MEC＝30°，∠C＝90°∴CE＝MC＝，ME＝2MC＝2＝BE，∴BC＝+2，∵∠CBD＝30°，∠C＝90°，∴BC＝CD，∴CD＝1+，∴DM＝，∴△DBM的面积＝××（+2）＝1+；（3）若点N在CD上时，AD＝DG+DN，理由如下：如图3所示：延长ED使得DW＝DN，连接NW，∵∠ACB＝90°，∠A＝30°，BD是△ABC的角平分线，DE⊥AB于点E，∴∠ADE＝∠BDE＝60°，AD＝BD，∵DN＝DW，且∠WDN＝60°∴△WDN是等边三角形，∴NW＝DN，∠W＝∠WND＝∠BNG＝∠BDN＝60°，∴∠WNG＝∠BND，在△WGN和△DBN中，∴△WGN≌△DBN（SAS），∴BD＝WG＝DG+DN，∴AD＝DG+DN．（3）若点N在AD上时，AD＝DG﹣DN，理由如下：如图4，延长BD至H，使得DH＝DN，连接HN，由（1）得DA＝DB，∠A＝30°．∵DE⊥AB于点E．∴∠2＝∠3＝60°．∴∠4＝∠5＝60°．∴△NDH是等边三角形．∴NH＝ND，∠H＝∠6＝60°．∴∠H＝∠2．∵∠BNG＝60°，∴∠BNG+∠7＝∠6+∠7．即∠DNG＝∠HNB．在△DNG和△HNB中，∴△DNG≌△HNB（ASA）．∴DG＝HB．∵HB＝HD+DB＝ND+AD，∴DG＝ND+AD．∴AD＝DG﹣ND．4、如图1，已知直角三角形ABC，∠ACB＝90°，∠BAC＝30°，点D是AC边上一点，过D作DE⊥AB于点E，连接BD，点F是BD中点，连接EF，CF．（1）发现问题：线段EF，CF之间的数量关系为EF＝CF；∠EFC的度数为120°；（2）拓展与探究：若将△AED绕点A按顺时针方向旋转α角（0°＜α＜30°），如图2所示，（1）中的结论还成立吗？请说明理由；（3）拓展与运用：如图3所示，若△AED绕点A旋转的过程中，当点D落到AB边上时，AB边上另有一点G，AD＝DG＝GB，BC＝3，连接EG，请直接写出EG的长度．解：（1）如图1中，∵DE⊥AB，∴∠BED＝90°，∵∠BCD＝90°，BF＝DF，∴FE＝FB＝FD＝CF，∴∠FBE＝∠FEB，∠FBC＝∠FCB，∴∠EFC＝∠EFD+∠CFD＝∠FBE+∠FEB+∠FBC+∠FCB＝2（∠FBE+∠FBC）＝2∠ABC＝120°，故答案为：EF＝CF，120°．（2）结论成立．理由：如图2中，取AB的中点M，AD的中点N，连接MC，MF，ED，EN，FN．∵BM＝MA，BF＝FD，∴MF∥AD，MF＝AD，∵AN＝ND，∴MF＝AN，MF∥AN，∴四边形MFNA是平行四边形，∴NF＝AM，∠FMA＝∠ANF，在Rt△ADE中，∵AN＝ND，∠AED＝90°，∴EN＝AD＝AN＝ND，同理CM＝AB＝AM＝MB，在△AEN和△ACM中，∠AEN＝∠EAN，∠MCA＝∠MAC，∵∠MAC＝∠EAN，∴∠AMC＝∠ANE，又∵∠FMA＝∠ANF，∴∠ENF＝∠FMC，在△MFC和△NEF中，，∴△MFC≌△NEF（SAS），∴FE＝FC，∠NFE＝∠MCF，∵NF∥AB，∴∠NFD＝∠ABD，∵∠ACB＝90°，∠BAC＝30°，∴∠ABC＝60°，△BMC是等边三角形，∠MCB＝60°∴∠EFC＝∠EFN+∠NFD+∠DFC＝∠MCF+∠ABD+∠FBC+∠FCB＝∠ABC+∠MCB＝60°+60°＝120°．（3）如图3中，作EH⊥AB于H．在Rt△ABC中，∵∠BAC＝30°，BC＝3，∴AB＝2BC＝6，在Rt△AED中，∠DAE＝30°，AD＝2，∴DE＝AD＝1，在Rt△DEH中，∵∠EDH＝60°，DE＝1，∴EH＝ED•sin60°＝，DH＝ED•cos60°＝，在Rt△EHG中，EG＝＝．5、如图1，在等腰△ABC中，AB＝AC，∠BAC＝a，点P是线段AB的中点，点E是线段CB延长线上一点，且PE＝PC，将线段PC绕点P顺时针旋转α得到PD，连接BD．（1）如图2，若α＝60°，其他条件不变，先补全图形，然后探究线段BD和BC之间的数量关系，并说明理由．（2）如图3，若α＝90°，其他条件不变，探究线段BP、BD和BC之间的等量关系，并说明理由．解：（1）BC＝2BD，理由：如图2，连接CD，由旋转可得，CP＝DP，∠CPD＝60°，∴△CDP是等边三角形，∴∠CDP＝60°＝∠PCD，又∵P是AB的中点，AB＝AC，∠A＝60°，∴等边三角形ABC中，∠PCB＝30°，CP⊥AB，∴∠BCD＝30°，即BC平分∠PCD，∴BC垂直平分PD，∴∠BDC＝∠BPC＝90°，∴Rt△BCD中，BC＝2BD．（2）如图3，取BC中点F，连接PF，∵∠A＝90°，AB＝AC，∴△ABC是等腰直角三角形，∵P是AB的中点，F是BC的中点，∴PF是△ABC的中位线，∴PF∥AC，∴∠PFB＝∠ACB＝45°，∠BPF＝∠A＝90°，∴△BPF是等腰直角三角形，∴BF＝BP，BP＝PF，∵∠DPC＝∠BPF＝90°，∴∠BPD＝∠FPC，又∵PD＝PC，∴△BDP≌△FCP，∴BD＝CF，∵BC＝BF+FC，∴BC＝BD+BP．6、【发现问题】如图1，已知△ABC，以点A为直角顶点、AB为腰向△ABC外作等腰直角△ABE．请你以A为直角顶点、AC为腰，向△ABC外作等腰直角△ACD（不写作法，保留作图痕迹）．连接BD、CE．那么BD与CE的数量关系是BD＝CE．【拓展探究】如图2，已知△ABC，以AB、AC为边向外作正方形AEFB和正方形ACGD，连接BD、CE，试判断BD与CE之间的数量关系，并说明理由．【解决问题】如图3，有一个四边形场地ABCD，∠ADC＝60°，BC＝15，AB＝8，AD＝CD，求BD的最大值．【发现问题】解：延长CA到M，作∠MAC的平分线AN，在AN上截取AD＝AC，连接CD，即可得到等腰直角△ACD；连接BD、CE，如图1所示：∵△ABE与△ACD都是等腰直角三角形，∴AB＝AE，AD＝AC，∠BAE＝∠CAD＝90°，∴∠BAD＝∠EAC，在△BAD和△EAC中，，∴△BAD≌△EAC（SAS），∴BD＝CE，【拓展探究】解：BD＝CE；理由如下：∵四边形AEFB与四边形ACGD都是正方形，∴AB＝AE，AD＝AC，∠BAE＝∠CAD＝90°，∴∠BAD＝∠EAC，在△BAD和△EAC中，，∴△BAD≌△EAC（SAS），∴BD＝CE；【解决问题】解：以AB为边向外作等边三角形ABE，连接CE，如图3所示：则∠BAE＝60°，BE＝AB＝AE＝8，∵AD＝CD，∠ADC＝60°，∴△ACD是等边三角形，∴∠CAD＝60°，AC＝AD，∴∠CAD+∠BAC＝∠BAE+∠BAC，即∠BAD＝∠EAC，在△BAD和△EAC中，，∴△BAD≌△EAC（SAS），∴BD＝CE；当C、B、E三点共线时，CE最大＝BC+BE＝15+8＝23，∴BD的最大值为23．7、如图1，点C为线段AB外一个动点，已知AB＝a，AC＝b．当点C位于BA的延长线上时，线段BC取得最大值，则最大值为a+b（用含a，b的式子表示）；（2）如图2，点C为线段AB外一个动点，若AB＝10，AC＝3，分别以AC，BC为边，作等边三角形ACD和等边三角形BCE，连接AE，DB．①求证：AE＝DB；②请直接写出线段AE的最大值；（3）如图3，AB＝6，点M为线段AB外一个动点，且AM＝2，MB＝MN，∠BMN＝90°，请直接写出线段AN的最大值．（1）解：∵点C为线段AB外一动点，且AC＝b，AB＝a，∴当点C位于BA的延长线上时，线段BC的长取得最大值，且最大值为AC+AB＝a+b，（2）①证明：如图2中，∵△ACD与△BCE是等边三角形，∴CD＝AC，CB＝CE，∠ACD＝∠BCE＝60°，∴∠DCB＝∠ACE，在△CAD与△EAB中，，∴△CAD≌△EAB（SAS），∴AE＝BD．②∵线段AE长的最大值＝线段BD的最大值，由（1）知，当线段BD的长取得最大值时，点D在BA的延长线上，∴最大值为AD+AB＝3+10＝13；（3）如图3中，连接BN，∵将△AMN绕着点M顺时针旋转90°得到△PBM，连接AP，则△APM是等腰直角三角形，∴MA＝MP＝2，BP＝AN，∴P A＝2，∵AB＝6，∴线段AN长的最大值＝线段BP长的最大值，∴当P在线段BA的延长线时，线段BP取得最大值最大值＝AB+AP＝6+2．8、【初步探索】（1）如图1：在四边形ABC中，AB＝AD，∠B＝∠ADC＝90°，E、F分别是BC、CD上的点，且EF ＝BE+FD，探究图中∠BAE、∠F AD、∠EAF之间的数量关系．小王同学探究此问题的方法是：延长FD到点G，使DG＝BE．连接AG，先证明△ABE≌△ADG，再证明△AEF≌△AGF，可得出结论，他的结论应是∠BAE+∠F AD＝∠EAF；【灵活运用】（2）如图2，若在四边形ABCD中，AB＝AD，∠B+∠D＝180°．E、F分别是BC、CD上的点，且EF＝BE+FD，上述结论是否仍然成立，并说明理由；【拓展延伸】（3）如图3，已知在四边形ABCD中，∠ABC+∠ADC＝180°AB＝AD，若点E在CB的延长线上，点F在CD的延长线上，如图3所示，仍然满足EF＝BE+FD，请写出∠EAF与∠DAB的数量关系，并给出证明过程．解：（1）∠BAE+∠F AD＝∠EAF．理由：如图1，延长FD到点G，使DG＝BE，连接AG，根据SAS可判定△ABE≌△ADG，进而得出∠BAE＝∠DAG，AE＝AG，再根据SSS可判定△AEF≌△AGF，可得出∠EAF＝∠GAF＝∠DAG+∠DAF＝∠BAE+∠DAF．故答案为：∠BAE+∠F AD＝∠EAF；（2）仍成立，理由：如图2，延长FD到点G，使DG＝BE，连接AG，∵∠B+∠ADF＝180°，∠ADG+∠ADF＝180°，∴∠B＝∠ADG，又∵AB＝AD，∴△ABE≌△ADG（SAS），∴∠BAE＝∠DAG，AE＝AG，∵EF＝BE+FD＝DG+FD＝GF，AF＝AF，∴△AEF≌△AGF（SSS），∴∠EAF＝∠GAF＝∠DAG+∠DAF＝∠BAE+∠DAF；（3）∠EAF＝180°﹣∠DAB．证明：如图3，在DC延长线上取一点G，使得DG＝BE，连接AG，∵∠ABC+∠ADC＝180°，∠ABC+∠ABE＝180°，∴∠ADC＝∠ABE，又∵AB＝AD，∴△ADG≌△ABE（SAS），∴AG＝AE，∠DAG＝∠BAE，∵EF＝BE+FD＝DG+FD＝GF，AF＝AF，∴△AEF≌△AGF（SSS），∴∠F AE＝∠F AG，∵∠F AE+∠F AG+∠GAE＝360°，∴2∠F AE+（∠GAB+∠BAE）＝360°，∴2∠F AE+（∠GAB+∠DAG）＝360°，即2∠F AE+∠DAB＝360°，∴∠EAF＝180°﹣∠DAB．9、如图，在Rt△ABC中，∠ACB＝90°，∠A＝30°，点O为AB中点，点P为直线BC上的动点（不与点B、点C重合），连接OC、OP，将线段OP绕点P逆时针旋转60°，得到线段PQ，连接BQ．（1）如图1，当点P在线段BC上时，请直接写出线段BQ与CP的数量关系．（2）如图2，当点P在CB延长线上时，（1）中结论是否成立？若成立，请加以证明；若不成立，请说明理由；（3）如图3，当点P在BC延长线上时，若∠BPO＝45°，AC＝，请直接写出BQ的长．解：（1）CP＝BQ，理由：如图1，连接OQ，由旋转知，PQ＝OP，∠OPQ＝60°⊅∴△POQ是等边三角形，∴OP＝OQ，∠POQ＝60°，在Rt△ABC中，O是AB中点，∴OC＝OA＝OB，∴∠BOC＝2∠A＝60°＝∠POQ，∴∠COP＝∠BOQ，在△COP和△BOQ中，，∴△COP≌△BOQ（SAS），∴CP＝BQ，（2）CP＝BQ，理由：如图2，连接OQ，由旋转知，PQ＝OP，∠OPQ＝60°∴△POQ是等边三角形，∴OP＝OQ，∠POQ＝60°，在Rt△ABC中，O是AB中点，∴OC＝OA＝OB，∴∠BOC＝2∠A＝60°＝∠POQ，∴∠COP＝∠BOQ，在△COP和△BOQ中，，∴△COP≌△BOQ（SAS），∴CP＝BQ，（3）如图3，在Rt△ABC中，∠A＝30°，AC＝，∴BC＝AC•tan∠A＝，过点O作OH⊥BC，∴∠OHB＝90°＝∠BCA，∴OH∥AB，∵O是AB中点，∴CH＝BC＝，OH＝AC＝，∵∠BPQ＝45°，∠OHP＝90°，∴∠BPQ＝∠PQH，∴PH＝OH＝，∴CP＝PH﹣CH＝﹣＝，连接BQ，同（1）的方法得，BQ＝CP＝．10、模型发现：同学们知道，三角形的两边之和大于第三边，即如图1，在△ABC中，AB+AC＞BC．对于图1，若把点C看作是线段AB外一动点，且AB＝c，AC＝b，则线段BC的长会因为点C的位置的不同而发生变化．因为AB、AC的长度固定，所以当∠BAC越大时，BC边越长．特别的，当点C位于线段BA的延长线上时，线段BC的长取得最大值，且最大值为b+c（用含b，c的式子表示）（直接填空）模型应用：点C为线段AB外一动点，且AB＝3，AC＝2，如图2所示，分别以AC，BC为边，作等边三角形ACD 和等边三角形BCE，连接BD，AE．（1）求证：BD＝AE．（2）线段AE长的最大值为5．模型拓展：如图3，在平面直角坐标系中，点A是y轴正半轴上的一动点，点B是x轴正半轴上的一动点，且AB ＝8．若AC⊥AB，AC＝3，试求OC长的最大值．解：当点C位于线段BA的延长线上时，线段BC的长取得最大值，最大值为b+c，故答案为：线段BA的延长线上；b+c；模型应用：（1）证明：∵△ACD、△BCE都是等边三角形，∴CD＝CA＝AD，CB＝CE，∠ACD＝60°，∠BCE＝60°，∴∠DCB＝∠ACE，在△DCB和△ACE中，，∴△DCB≌△ACE（SAS）∴BD＝AE；（2）当点D位于线段BA的延长线上时，线段BD的长取得最大值，最大值为AB+AD＝AB+AC＝3+2＝5，∵AE＝BD，∴线段AE长的最大值为5，模型拓展：取AB的中点G，连接OG、CG，在Rt△AOB中，G为AB的中点，∴OG＝AB＝4，在Rt△CAG中，CG＝＝＝5，当点O、G、C在同一条直线上时，OC最大，最大值为4+5＝9．11、已知：△ABC中，∠ACB＝90°，AC＝BC．（1）如图1，点D在BC的延长线上，连AD，过B作BE⊥AD于E，交AC于点F．求证：AD＝BF；（2）如图2，点D在线段BC上，连AD，过A作AE⊥AD，且AE＝AD，连BE交AC于F，连DE，问BD与CF有何数量关系，并加以证明；（3）如图3，点D在CB延长线上，AE＝AD且AE⊥AD，连接BE、AC的延长线交BE于点M，若AC ＝3MC，请直接写出的值．（1）证明：如图1中，∵BE⊥AD于E，∴∠AEF＝∠BCF＝90°，∵∠AFE＝∠CFB，∴∠DAC＝∠CBF，∵BC＝CA，∴△BCF≌△ACD，∴BF＝AD．（2）结论：BD＝2CF．理由：如图2中，作EH⊥AC于H．∵∠AHE＝∠ACD＝∠DAE＝90°，∴∠DAC+∠ADC＝90°，∠DAC+∠EAH＝90°，∴∠DAC＝∠AEH，∵AD＝AE，∴△ACD≌△EHA，∴CD＝AH，EH＝AC＝BC，∵CB＝CA，∴BD＝CH，∵∠EHF＝∠BCF＝90°，∠EFH＝∠BFC，EH＝BC，∴△EHF≌△BCF，∴FH＝CF，∴BD＝CH＝2CF．（3）如图3中，同法可证BD＝2CM．∵AC＝3CM，设CM＝a，则AC＝CB＝3a，BD＝2a，∴＝＝．12、已知在△ABC中，AB＝AC，射线BM、BN在∠ABC内部，分别交线段AC于点G、H．（1）如图1，若∠ABC＝60°，∠MBN＝30°，作AE⊥BN于点D，分别交BC、BM于点E、F．①求证：∠1＝∠2；②如图2，若BF＝2AF，连接CF，求证：BF⊥CF；（2）如图3，点E为BC上一点，AE交BM于点F，连接CF，若∠BFE＝∠BAC＝2∠CFE，求的值．（1）①证明：如图1中，∵AB＝AC，∠ABC＝60°∴△ABC是等边三角形，∴∠BAC＝60°，∵AD⊥BN，∴∠ADB＝90°，∵∠MBN＝30°，∠BFD＝60°＝∠1+∠BAF＝∠2+∠BAF，∴∠1＝∠2②证明：如图2中，在Rt△BFD中，∵∠FBD＝30°，∴BF＝2DF，∵BF＝2AF，∴BF＝AD，∵∠BAE＝∠FBC，AB＝BC，∴△BFC≌△ADB，∴∠BFC＝∠ADB＝90°，∴BF⊥CF（2）在BF上截取BK＝AF，连接AK．∵∠BFE＝∠2+∠BAF，∠CFE＝∠4+∠1，∴∠CFB＝∠2+∠4+∠BAC，∵∠BFE＝∠BAC＝2∠EFC，∴∠1+∠4＝∠2+∠4∴∠1＝∠2，∵AB＝AC，∴△ABK≌CAF，∴∠3＝∠4，S△ABK＝S△AFC，∵∠1+∠3＝∠2+∠3＝∠CFE＝∠AKB，∠BAC＝2∠CEF，∴∠KAF＝∠1+∠3＝∠AKF，∴AF＝FK＝BK，∴S△ABK＝S△AFK，∴＝2．13、已知，△ABC中，AB＝AC，∠BAC＝90°，E为边AC任意一点，连接BE．（1）如图1，若∠ABE＝15°，O为BE中点，连接AO，且AO＝1，求BC的长；（2）如图2，F也为AC上一点，且满足AE＝CF，过A作AD⊥BE交BE于点H，交BC于点D，连接DF交BE于点G，连接AG；①若AG平分∠CAD，求证：AH＝AC；②如图3，当G落在△ABC外时，若将△EFG沿EF边翻折，点G刚好落在AB边上点P，直接写出AG与EF的数量关系．（1）解：如图1中，在AB上取一点M，使得BM＝ME，连接ME．在Rt△ABE中，∵OB＝OE，∴BE＝2OA＝2，∵MB＝ME，∴∠MBE＝∠MEB＝15°，∴∠AME＝∠MBE+∠MEB＝30°，设AE＝x，则ME＝BM＝2x，AM＝x，∵AB2+AE2＝BE2，∴（2x+x）2+x2＝22，∴x＝（负根已经舍弃），∴AB＝AC＝（2+）•，∴BC＝AB＝+1．方法二：作EH⊥BC于H，求出BH，CH即可解决问题．（2）证明：如图2中，作CP⊥AC，交AD的延长线于P，GM⊥AC于M．∵BE⊥AP，∴∠AHB＝90°，∴∠ABH+∠BAH＝90°，∵∠BAH+∠P AC＝90°，∴∠ABE＝∠P AC，在△ABE和△CAP中，，∴△ABE≌△CAP，∴AE＝CP＝CF，∠AEB＝∠P，在△DCF和△DCP中，，∴△DCF≌△DCP，∴∠DFC＝∠P，∴∠GFE＝∠GEF，∴GE＝GF，∵GM⊥EF，∴FM＝ME，∵AE＝CF，∴AF＝CE，∴AM＝CM，在△GAH和△GAM中，，∴△AGH≌△AGM，∴AH＝AM＝CM＝AC（3）解：结论：AG＝EF．理由：如图3中，作CM⊥AC交AD的延长线于M，连接PG交AC于点O．由（2）可知△ACM≌△BAE，△CDF≌△CDM，∴∠AEB＝∠M＝∠GEF，∠M＝∠CFD＝∠GFE，AE＝CM＝CF，∴∠GEF＝∠GFE，∴GE＝GF，∵△EFP是由△EFG翻折得到，∴EG＝EP＝GF＝PF，∴四边形EGFP是菱形，∴PG⊥AC，OE＝OF，∵AE＝CF，∴AO＝OC，∵AB∥OP，∴BP＝PC，∵PF∥BE，∴EF＝CF＝AE，∵PB＝PC，AO＝OC，∴PO＝OG＝AB，∴AB＝PG，AB∥PG，∴四边形ABPG是平行四边形，∴AG∥BC，∴∠GAO＝∠ACB＝45°，设EO＝OF＝a，则OA＝OG＝3a，AG＝3a，∴＝＝，∴AG＝EF14、如图所示，Rt△ABC中，∠ACB＝90°，E为AC中点，作ED⊥AC交AB于D，连接CD；（1）如图1，求证：AB＝2CD；（2）如图2，作CF⊥AB交AB于F，点G为CF上一点，点H为DE延长线上一点，分别连接AH、GH，若∠AHG＝2∠B，求证：AH＝GH；（3）如图3，在（2）的条件下，连接DG，且有DE＝BF，∠EDG＝90°，若AC＝6，求AH的长度．解：（1）∵E为AC中点，作ED⊥AC交AB于D，∴AD＝CD，∵∠ACB＝90°，∴BC∥DE，∴AD＝BD，∴CD＝BD，∴AB＝2CD；（2）如图2，连接CH，∵点E是AC的中点，∴AE＝CE，∵DE⊥AC，∴CH＝AH，∴∠ACH＝∠CAH，∵∠ACB＝90°，∴∠B+∠BAC＝90°，∵CF⊥AB，∴∠BAC+∠ACF＝90°，∴∠ACF＝∠B，∴∠HCG＝∠ACH+∠ACF＝∠CAH+∠B，∠AHG＝2∠B∴在四边形AHGF中，∠AFG+∠FGH+∠AHG+∠F AH＝360°，∴∠FGH＝360°﹣（∠AFG+∠AHG+∠F AH）＝360°﹣（90°+2∠B+∠CAH+∠BAC）＝360°﹣（90°+2∠B+∠CAH+90°﹣∠B）＝360°﹣（180°+∠B+∠CAH）＝180°﹣（∠B+∠CAH），∵∠CGH＝180°﹣∠FGH＝∠B+∠CAH＝∠HCG，∴CH＝GH，∵CH＝AH，∴AH＝GH；（3）如图3，由（1）知，DE∥BC，∴∠B＝∠ADE，在△BFC和△DEA中，，∴△BFC≌△DEA，∴BC＝AD，∵AD＝BD＝CD，∴BC＝BD＝CD，∴△BCD是等边三角形，∴∠B＝60°，在Rt△ABC中，AC＝6，∴BC＝2，AB＝4，∵CF⊥BD，∴DF＝，CF＝3，∵∠BAC＝30°，∴∠ADE＝60°，∵∠EDG＝90°，∠FDG＝30°，在Rt△DFG中，DF＝，∴FG＝1，DG＝2，∴CG＝CF﹣FG＝2过点H作HN⊥CF，由（2）知，CH＝GH，∴NG＝CG＝1，∴FN＝NG+FG＝2，过点H作HM⊥AB，∴∠FMH＝∠NFM＝∠HNF＝90°，∴四边形NFMH是矩形，∴HM＝FN＝2，在Rt△DMH中，∠ADE＝60°，HM＝2，∴DH＝，在Rt△HDG中，根据勾股定理得，HG＝＝．15、【问题情境】一节数学课后，老师布置了一道课后练习题：如图：已知在Rt△ABC中，AC＝BC，∠ACB＝90°，CD⊥AB于点D，点E、F分别在A和BC上，∠1＝∠2，FG⊥AB于点G，求证：△CDE≌△EGF．（1）阅读理解，完成解答本题证明的思路可用下列框图表示：根据上述思路，请你完整地书写这道练习题的证明过程；（2）特殊位置，证明结论若CE平分∠ACD，其余条件不变，求证：AE＝BF；（3）知识迁移，探究发现如图，已知在Rt△ABC中，AC＝BC，∠ACB＝90°，CD⊥AB于点D，若点E是DB的中点，点F在直线CB上且满足EC＝EF，请直接写出AE与BF的数量关系．（不必写解答过程）（1）证明：∵AC＝BC，∠ACB＝90°，∴∠A＝∠B＝45°，∵CD⊥AB，∴∠CDB＝90°，∴∠DCB＝45°，∵∠ECF＝∠DCB+∠1＝45°+∠1，∠EFC＝∠B+∠2＝45°+∠2，∠1＝∠2，∴∠ECF＝∠EFC，∴CE＝EF，∵CD⊥AB，FG⊥AB，∴∠CDE＝∠EGF＝90°，在△CDE和△EGF中，，∴△CDE≌△EGF（AAS）；（2）证明：由（1）得：CE＝EF，∠A＝∠B，∵CE平分∠ACD，∴∠ACE＝∠1，∵∠1＝∠2，∴∠ACE＝∠2，在△ACE和△BEF中，，∴△ACE≌△BEF（AAS），∴AE＝BF；（3）AE＝BF，作EH⊥BC与H，如图3所示：设DE＝x，根据题意得：BE＝DE＝x，AD＝BD＝2x，CD＝AD＝2x，AE＝3x，根据勾股定理得：BC＝AC＝2x，∵∠ABC＝45°，EH⊥BC，∴BH＝x，∴CH＝BC﹣BH＝x，∵EC＝EF，∴FH＝CH＝x，∴BF＝x﹣x＝x，∴＝，∴AE＝．16、在正方形ABCD和等腰直角△BGF中，∠BGF＝90°，P是DF的中点，连接PG、PC．（1）如图1，当点G在BC边上时，延长GP交DC于点E．求证：PG＝PC；（2）如图2，当点F在AB的延长线上时，（1）中的结论是否成立？请证明你的结论；（3）如图3，若四边形ABCD为菱形，且∠ABC＝60°，△BGF为等边三角形，点F在CB的延长线。

中考数学模拟题《几何综合》专项测试题(附带参考答案)

中考数学模拟题《几何综合》专项测试题(附带参考答案)

中考数学模拟题《几何综合》专项测试题(附带参考答案)学校:___________班级：___________姓名：___________考号：___________考点解读在中考数学中有这么一类题它是以点线几何图形的运动为载体集合多个代数知识几何知识及数学解题思想于一题的综合性试题它就是动态几何问题。

动态几何问题经常在各地以中考试卷解答压轴题出现也常会出现在选择题最后一题的位置考察知识面较广综合性强可以提升学生的空间想象能力和综合分析问题的能力但同时难度也很大令无数初中学子闻风丧胆考场上更是丢盔弃甲解题思路1 熟练掌握平面几何知识﹕要想解决好有关几何综合题首先就是要熟练掌握关于平面几何的所有知识尤其是要重点把握三角形特殊四边形圆及函数三角函数相关知识．几何综合题重点考查的是关于三角形特殊四边形（平行四边形矩形菱形正方形）圆等相关知识2 掌握分析问题的基本方法﹕分析法综合法“两头堵”法﹕1）分析法是我们最常用的解决问题的方法也就是从问题出发执果索因去寻找解决问题所需要的条件依次向前推直至已知条件例如我们要证明某两个三角形全等先看看要证明全等需要哪些条件哪些条件已知了还缺少哪些条件然后再思考要证缺少的条件又需要哪些条件依次向前推直到所有的条件都已知为止即可综合法﹕即从已知条件出发经过推理得出结论适合比较简单的问题3）“两头堵”法﹕当我们用分析法分析到某个地方不知道如何向下分析时可以从已知条件出发看看能得到什么结论把分析法与综合法结合起来运用是我们解决综合题最常用的办策略3 注意运用数学思想方法﹕对于几何综合题的解决我们还要注意运用数学思想方法这样会大大帮助我们解决问题或者简化我们解决问题的过程加快我们解决问题的速度毕竟考场上时间是非常宝贵的．常用数学思想方法﹕转化类比归纳等等模拟预测1 （2024·江西九江·二模）如图 在矩形()ABDC AB AC >的对称轴l 上找点P 使得PAB PCD 、均为直角三角形 则符合条件的点P 的个数是（ ）A ．1B ．3C ．4D ．52 （2024·江西吉安·模拟预测）如图 在平面直角坐标系中 边长为23ABC 的顶点A B ，分别在y 轴的正半轴 x 轴的负半轴上滑动 连接OC 则OC 的最小值为（ ）A ．2B ．3C ．33D ．333 （2024·江西吉安·一模）如图 矩形ABCD 中 4AB = 6AD = 点E 在矩形的边上 则当BEC 的一个内角度数为60︒时 符合条件的点E 的个数共有（ ）A ．4个B ．5个C ．6个D ．7个4 （2023·江西·中考真题）如图 在ABCD 中 602B BC AB ∠=︒=， 将AB 绕点A 逆时针旋转角α（0360α︒<<︒）得到AP 连接PC PD ．当PCD 为直角三角形时 旋转角α的度数为 ．5 （2024·江西吉安·二模）如图 在矩形ABCD 中 6,10,AB AD E ==为CD 的中点 点P 在AE 下方矩形的边上．当APE 为直角三角形 且P 为直角顶点时 BP 的长为 ．6 （2024·江西九江·二模）如图 在平面直角坐标系中 已知矩形OABC 的顶点()20,0A ()0,8C D 为OA 的中点 点P 为矩形OABC 边上任意一点 将ODP 沿DP 折叠得EDP △ 若点E 在矩形OABC 的边上 则点E 的坐标为 ．7 （2024·江西·模拟预测）如图 ABC 中 AB AC = 30A ∠=︒ 射线CP 从射线CA 开始绕点C 逆时针旋转α角()075α︒<<︒ 与射线AB 相交于点D 将ACD 沿射线CP 翻折至A CD '△处 射线CA '与射线AB 相交于点E ．若A DE '是等腰三角形 则α∠的度数为 ．8 （2024·江西赣州·二模）在Rt ABC △中 已知90C ∠=︒ 10AB = 3cos 5B = 点M 在边AB 上 点N 在边BC 上 且AM BN = 连接MN 当BMN 为等腰三角形时 AM = ．9 （2024·江西吉安·模拟预测）如图 在矩形ABCD 中 6,10AB AD == E 为BC 边上一点 3BE = 点P 沿着边按B A D →→的路线运动．在运动过程中 若PAE △中有一个角为45︒ 则PE 的长为 ．10 （2024·江西吉安·三模）如图 在ABC 中 AB AC = 30B ∠=︒ 9BC = D 为AC上一点 2AD DC = P 为边BC 上的动点 当APD △为直角三角形时 BP 的长为 ．11 （2024·江西吉安·一模）如图 矩形ABCD 中 4AB = 6AD = E 为CD 的中点 连接BE 点P 在矩形的边上 且在BE 的上方 则当BEP △是以BE 为斜边的直角三角形时 BP 的长为 ．12 （2024·江西九江·二模）如图 在等腰ABC 中 2AB AC == 30B ∠=︒ D 是线段BC 上一动点 沿直线AD 将ADB 折叠得到ADE 连接EC ．当DEC 是以DE 为直角边的直角三角形时 则BD 的长为 ．13 （2024·江西·模拟预测）如图 在菱形ABCD 中 对角线AC BD 相交于点O 23AB = 60ABC ∠=︒ E 为BC 的中点 F 为线段OD 上一动点 当AEF △为等腰三角形时 DF 的长为 ．14 （2024·江西上饶·一模）如图 在三角形纸片ABC 中 90,60,6C B BC ∠=︒∠=︒= 将三角形纸片折叠 使点B 的对应点B '落在AC 上 折痕与,BC AB 分别相交于点E F 当AFB '为等腰三角形时 BE 的长为 ．15 （2024·江西抚州·一模）课本再现（1）如图1 CD 与BE 相交于点,A ABC 是等腰直角三角形 90C ∠=︒ 若DE BC ∥ 求证：ADE 是等腰直角三角形．类比探究（2）①如图2 AB 是等腰直角ACB △的斜边 G 为边AB 的中点 E 是BA 的延长线上一动点 过点E 分别作AC 与BC 的垂线 垂足分别为,D F 顺次连接,,DG GF FD 得到DGF △ 求证：DGF △是等腰直角三角形．②如图3 当点E 在边AB 上 且①中其他条件不变时 DGF △是等腰直角三角形是否成立？_______（填“是”或“否”）．拓展应用（3）如图4 在四边形ABCD 中 ,90,BC CD BCD BAD AC =∠=∠=︒平分BAD ∠ 当1,22AD AC == 求线段BC 的长．16 （2023·江西·中考真题）课本再现思考我们知道菱形的对角线互相垂直．反过来对角线互相垂直的平行四边形是菱形吗？可以发现并证明菱形的一个判定定理对角线互相垂直的平行四边形是菱形．(1)定理证明：为了证明该定理小明同学画出了图形（如图1）并写出了“已知”和“求证”请你完成证明过程．已知：在ABCD中对角线BD AC⊥垂足为O．求证：ABCD是菱形．(2)知识应用：如图2在ABCD中对角线AC和BD相交于点O586AD AC BD===，，．①求证：ABCD是菱形②延长BC至点E连接OE交CD于点F若12E ACD∠=∠求OFEF的值．17 （2022·江西·中考真题）问题提出：某兴趣小组在一次综合与实践活动中提出这样一个问题：将足够大的直角三角板()90,60PEF P F ∠=︒∠=︒的一个顶点放在正方形中心O 处 并绕点O 逆时针旋转 探究直角三角板PEF 与正方形ABCD 重叠部分的面积变化情况（已知正方形边长为2）．(1)操作发现：如图1 若将三角板的顶点P 放在点O 处 在旋转过程中 当OF 与OB 重合时 重叠部分的面积为__________ 当OF 与BC 垂直时 重叠部分的面积为__________ 一般地 若正方形面积为S 在旋转过程中 重叠部分的面积1S 与S 的关系为__________(2)类比探究：若将三角板的顶点F 放在点O 处 在旋转过程中 ,OE OP 分别与正方形的边相交于点M N ．①如图2 当BM CN =时 试判断重叠部分OMN 的形状 并说明理由②如图3 当CM CN =时 求重叠部分四边形OMCN 的面积（结果保留根号）(3)拓展应用：若将任意一个锐角的顶点放在正方形中心O 处 该锐角记为GOH ∠（设GOH α∠=） 将GOH ∠绕点O 逆时针旋转 在旋转过程中 GOH ∠的两边与正方形ABCD 的边所围成的图形的面积为2S 请直接写出2S 的最小值与最大值（分别用含α的式子表示）（参考数据：6262sin15tan1523-+︒=︒=︒=18 （2024·江西吉安·二模）如图 在ABC 和ADE 中 (),AB AC AD AE AD AB ==< 且BAC DAE ∠=∠．连接CE BD ．(1)求证：BD CE =．(2)在图2中 点B D E 在同一直线上 且点D 在AC 上 若,AB a BC b == 求AD CD的值（用含a b 的代数式表示）．19 （2024·江西九江·二模）初步探究（1）如图1 在四边形ABCD 中 ,AC BD 相交于点O AC BD ⊥ 且ABD CBD S S = 则OA 与OC 的数量关系为 ．迁移探究（2）如图2 在四边形ABCD 中 ,AC BD 相交于点O ABD CBD SS = （1）中OA 与OC 的数量关系还成立吗？如果成立 请说明理由．拓展探究（3）如图3 在四边形ABCD 中 ,AC BD 相交于点O 180,ABD CBD BAD BCD S S ∠∠+=︒=△△ 且 33OB OD == 求AC 的长．20 （2024·江西九江·二模）课本再现如图1 四边形ABCD 是菱形 30ACD ∠=︒ 6BD =．（1）求,AB AC 的长．应用拓展（2）如图2 E 为AB 上一动点 连接DE 将DE 绕点D 逆时针旋转120︒ 得到DF 连接EF ．①直接写出点D 到EF 距离的最小值②如图3 连接,OF CF 若OCF △的面积为6 求BE 的长．21 （2024·江西赣州·三模）某数学小组在一次数学探究活动过程中经历了如下过程：AB=P为对角线AC上的一个动点以P为直角顶问题提出：如图正方形ABCD中8△．点向右作等腰直角DPM(1)操作发现：DM的最小值为_______ 最大值为_______(2)数学思考：求证：点M在射线BC上=时求CM的长．(3)拓展应用：当CP CM22 （2024·江西赣州·二模）【课本再现】 思考我们知道 角的平分线上的点到角的两边的距离相等 反过来 角的内部到角的两边的距离相等的点在角的平分线上吗？可以发现并证明角的平分线的性质定理的逆定理角的内部到角的两边的距离相等的点在角的平分线上．【定理证明】（1）为证明此逆定理 某同学画出了图形 并写好“已知”和“求证” 请你完成证明过程．已知：如图1 在ABC ∠的内部 过射线BP 上的点P 作PD BA ⊥ PE BC ⊥ 垂足分别为D E 且PD PE =．求证：BP 平分ABC ∠．【知识应用】（2）如图2 在ABC 中 过内部一点P 作PD BC ⊥ PE AB ⊥ PF AC ⊥ 垂足分别为D E F 且PD PE PF == 120A ∠=︒ 连接PB PC ．①求BPC ∠的度数②若6PB=23PC=求BC的长．23 （2024·江西吉安·模拟预测）一块材料的形状是锐角三角形ABC下面分别对这块材料进行课题探究：课本再现：（1）在图1中若边120mmBC=高80mmAD=把它加工成正方形零件使正方形的一边在BC上其余两个顶点分别在AB AC上这个正方形零件的边长是多少?类比探究（2）如图2 若这块锐角三角形ABC材料可以加工成3个相同大小的正方形零件请你探究高AD与边BC的数量关系并说明理由．拓展延伸（3）①如图3 若这块锐角三角形ABC材料可以加工成图中所示的4个相同大小的正方形零件则ADBC的值为_______（直接写出结果）②如图4 若这块锐角三角形ABC材料可以加工成图中所示的()3n m≥相同大小的正方形零件求ADBC的值．24 （2024·江西吉安·三模）课本再现 矩形的定义 有一个角是直角的平行四边形是矩形．定义应用(1)如图1 已知：在四边形ABCD 中 90A B C ∠=∠=∠=︒用矩形的定义求证：四边形ABCD 是矩形．(2)如图2 在四边形ABCD 中 90A B ∠=∠=︒ E 是AB 的中点 连接DE CE 且DE CE = 求证：四边形ABCD 是矩形．拓展延伸(3)如图3 将矩形ABCD 沿DE 折叠 使点A 落在BC 边上的点F 处 若图中的四个三角形都相似 求AB BC的值．25 （2024·江西吉安·一模）课本再现在学习了平行四边形的概念后进一步得到平行四边形的性质：平行四边形的对角线互相平分．=（1）如图1 在平行四边形ABCD中对角线AC与BD交于点O 求证：OA OC =．OB OD知识应用=延长AC到E 使得（2）在ABC中点P为BC的中点．延长AB到D 使得BD AC∠=︒请你探究线段BE与线段AP之间的BACCE AB=连接DE．如图2 连接BE若60数量关系．写出你的结论并加以证明．26 （2024·江西九江·二模）问题提出在综合与实践课上 某数学研究小组提出了这样一个问题：如图1 在边长为4的正方形ABCD 的中心作直角EOF ∠ EOF ∠的两边分别与正方形ABCD 的边BC CD 交于点E F （点E 与点B C 不重合） 将EOF ∠绕点O 旋转．在旋转过程中 四边形OECF 的面积会发生变化吗？爱思考的浩浩和小航分别探究出了如下两种解题思路．浩浩：如图a 充分利用正方形对角线垂直 相等且互相平分等性质 证明了OEC OFD ≌ 则OEC OFD S S = OEC OCF OFD OCF OCD OECF S S S S S S =+=+=四边形．这样 就实现了四边形OECF 的面积向OCD 面积的转化．小航：如图b 考虑到正方形对角线的特征 过点O 分别作OG BC ⊥于点G OH CD ⊥于点H 证明OGE OHF ≌△△ 从而将四边形OECF 的面积转化成了小正方形OGCH 的面积．（1）通过浩浩和小航的思路点拨﹐我们可以得到OECF S =四边形__________ CE CF +=__________．类比探究（2）①如图⒉ 在矩形ABCD 中 3AB = 6AD = O 是边AD 的中点 90EOF ∠=︒ 点E 在AB 上 点F 在BC 上 则EB BF +=__________．②如图3 将问题中的正方形ABCD 改为菱形ABCD 且45ABC ∠=︒ 当45EOF ∠=︒时 其他条件不变 四边形OECF 的面积还是一个定值吗？若是 请求出四边形OECF 的面积 若不是 请说明理由．拓展延伸（3）如图4 在四边形ABCD 中 7AB = 2DC = 60BAD ∠=︒ 120BCD ∠=︒ CA 是BCD ∠的平分线 求四边形ABCD 的面积．27 （2024·江西九江·模拟预测）【课本再现】（1）如图1 四边形ABCD 是一个正方形 E 是BC 延长线上一点 且AC EC = 则DAE ∠的度数为 ．【变式探究】（2）如图2 将（1）中的ABE 沿AE 折叠 得到AB E ' 延长CD 交B E '于点F 若2AB = 求B F '的长．【延伸拓展】（3）如图3 当（2）中的点E 在射线BC 上运动时 连接B B ' B B '与AE 交于点P ．探究：当EC 的长为多少时 D P 两点间的距离最短？请求出最短距离．28 （2024·江西上饶·一模）课本再现：（1）如图1 ,D E 分别是等边三角形的两边,AB AC 上的点 且AD CE =．求证：CD BE =．下面是小涵同学的证明过程：证明：ABC 是等边三角形,60AC BC A ACB ∴=∠=∠=︒．AD CE =()SAS ADC CEB ∴≌CD BE ∴=．小涵同学认为此题还可以得到另一个结论：BFD ∠的度数是______迁移应用：（2）如图2 将图1中的CD 延长至点G 使FG FB = 连接,AG BG ．利用（1）中的结论完成下面的问题．①求证：AG BE ∥②若25CF BF = 试探究AD 与BD 之间的数量关系．参考答案考点解读在中考数学中有这么一类题它是以点线几何图形的运动为载体集合多个代数知识几何知识及数学解题思想于一题的综合性试题它就是动态几何问题。

中考数学几何图形专题训练50题(含答案)

中考数学几何图形专题训练50题(含答案)

中考数学几何图形专题训练50题含答案(单选、填空、解答题)一、单选题1．下列四个图形中，不是正方体展开图的（）A．B．C．D．2．小军从A地沿北偏西60°方向走10m到B地，再从B地向正南方向走20m到C 地，此时小军离A地().A．B．10m C．15m D．3．如图，在直线l上有A，B，C三点，则图中线段共有（）A．4条B．3条C．2条D．1条4．如图，将下面的平面图形绕直线l旋转一周，得到的立体图形是（）A．B．C．D．5．下列四个立体图形中，是棱锥的是（）A．B．C ．D ．6．已知线段10cm AB =，点C 是直线AB 上一点，4cm BC =，点M 是线段AB 的中点，点N 是线段BC 的中点，则线段MN 的长度是（ ）A ．3cmB ．5cmC ．3cm 或7cmD ．5cm 或7cm7．下列说法正确的是( )A ．一个平角就是一条直线B ．连接两点间的线段，叫做这两点的距离C ．两条射线组成的图形叫做角D ．经过两点有一条直线，并且只有一条直线8．如图，OC 平分∠AOB ，若∠AOC ＝27°32′，则∠AOB ＝（ ）A ．55°4′B ．55°24′C ．54°14′D ．54°4′ 9．图，有一块含有30︒角的直角三角板的两个顶点放在直尺的对边上．如果242∠=︒，那么1∠的度数是（ ）A ．18︒B ．17︒C ．16︒D ．15︒ 10．下列各图都是由6个正方形组成的平面图形，其中不能看做是正方体表面展开图的是（ ）A．B．C．D．11．如图是一个正方体的表面展开图，则原正方体中与“中”字所在的面相对的面上标的字是（）A．我B．的C．梦D．国12．如图所示，以O为顶点且小于180 的角有（）A．6个B．7个C．8个D．9个13．下列说法中，正确的是().A．平角是一条直线B．周角是一条射线C．两条射线组成的图形是角D．一条射线绕它的端点旋转而成的图形叫做角14．如图，是一个正方体骰子的表面展开图，将其折叠成正方体骰子（点数朝外），如果1点在上面，3点在左面，在前面的点数为（）A．2B．4C．5D．615．如图是一个小正方形的展开图，把展开图折叠成小正方形后，有“祝”字一面的相对面上的字是（）A．考B．试C．成D．功16．如图，点C，D在线段AB上，AC=13AB，CD=12CB，若AB=3，则图中所有线段长的和是（）A．6B．8C．10D．1217．下列几何体中，由曲面和平面围成的是（）A．三棱柱B．圆锥C．球体D．正方体18．已知：如图，C是线段AB的中点，D是线段BC的中点，AB＝20 cm，那么线段AD等于()A．15 cm B．16 cm C．10 cm D．5 cm19．下列说法中正确的是（）A．两条射线组成的图形叫做角；B．各边相等的多边形叫做正多边形；C．一个圆分割成圆心角度数比位1∠2∠3的三个扇形，则最小扇形的圆心角是60°；D．小于平角的角可分为锐角和钝角两类．20．A、B两辆汽车沿着笔直的公路行驶，A车从甲地出发，B车从乙地出发，行驶到途中两车相遇，各自仍朝前进的方向行驶，到了目的地后立即返回，过了某一时刻，两车又在原地点相遇，则两车必定是（）A．沿着同一条公路行驶B．沿着两条不同的公路行驶C．以上两种情况都有可能D．以上都不对二、填空题21．已知36a∠=︒,则a∠的补角的度数是__________．22．已知∠α＝65°30′，则∠α的余角大小是_______．23．图中以A 为端点的线段共有______条．24．计算：34°25′20″×3=_______________25．一个角的余角比它的补角的14还少12︒，则这个角的度数为_______． 26．如图，从A 处观测C 处仰角30CAD ∠=︒，从B 处观测C 处的仰角45CBD ∠=︒，从C 处观测A 、B 两处的视角ACB =∠______度．27．一副三角板叠在一起如图放置，最小锐角的顶点D 恰好放在等腰直角三角形的斜边上，AC 与DM 、DN 分别交于点E 、F ，把∠DEF 绕点D 旋转到一定位置，使得DE=DF ，则∠BDN 的度数是_________ ．28．数轴上的点P 对应的数是1-，将点P 向右移动8个长度单位得到点Q ，则线段PQ 的中点在数轴上对应的数是____________．29．在∠ABC 中，∠ABC 和∠ACB 的平分线交于点O ，且∠BOC =110°，则∠A 的度数是____________．30．若∠α=20°40′，则∠α的补角的大小为_____．31．如图，A 岛在B 岛的北偏东30°方向，C 岛在B 岛的北偏东80°方向，A 岛在C 岛北偏西40°方向，从A 岛看B ，C 两岛的视角∠BAC 是______ 度．32．点A 和点B 在同一平面上，如果从A 观察B ，B 在A 的北偏东14°方向，那么从B 观察A ，A 在B 的_____方向．33．已知线段AB=10cm ，直线AB 上有一点C ，且BC=4cm ，M 是线段AC 的中点，则线段BM 的长是_cm ．34．如图，O 的弦AB 长为2，CD 是O 的直径，30,15ADB ADC ∠=︒∠=︒．∠O 的半径长为_________．∠P 是CD 上的动点，则PA PB +的最小值是_________．35．如图，将一副直角三角尺按图∠放置，使三角尺∠的长直角边与三角尺∠的某直角边在同一条直线上，则图∠中的∠1=______°．36．如图，已知∠ABC 的内角∠A=α°，分别作内角∠ABC 与外角∠ACD 的平分线，两条平分线交于点A 1，得∠A 1；∠A 1BC 和∠A 1CD 的平分线交于点A 2，得∠A 2；…以此类推得到∠A 2014，则∠A 2014的度数是_______．37．一副直角三角板叠放如图，90C E ∠=∠=︒．现将含45°角的三角板ADE 固定不动，把含30°角的三角板ABC （其中30CAB ∠=︒）绕顶点A 顺时针旋转角α（0180α︒<<︒）．当旋转角在30°~180°的旋转过程中，使得两块三角板至少有一组对应边（所在的直线）互相平行，此时符合条件的α=________．38．已知∠AOB ＝80°，OC 为从O 点引出的任意一条射线，若OM 平分∠AOC ，ON 平分∠BOC ，则∠MON 的度数是_____．39．如图所示，若图中共有m 条线段，n 条射线，则m n +=__________________.40．如图，请你在有序号的方格中选出两个画出阴影，使它们与图中四个有阴影的正方形一起可以构成正方体表面的展开图，你选择的两个正方形是____________ (填序号，任填一组即可)．三、解答题41．如图，直线AB 和CD 相交于点O ，35BOD ∠=︒，OA 平分EOC ∠，求EOD ∠的度数．42．图中哪些图形是立体图形，哪些是平面图形？平面图形：_______________；立体图形：_______________．43．如图，已知长方形ABCD 的长AB x =米，宽BC y =米，x ，y 满足()2540x y -+-=，一动点P 从A 出发以每秒1米的速度沿着A D C B →→→运动，另一动点Q 从B 出发以每秒2米的速度沿B C D A →→→运动，P ，Q 同时出发，运动时间为t ．(1)x =______________，y =______________．(2)当 4.5t =时，求APQ △的面积；(3)当P ，Q 都在DC 上，且PQ 距离为1时，求t 的值44．如图1，已知A 、O 、B 三点在同一直线上，射线OD 、OE 分别平分∠AOC 、∠BOC ．（1）求∠DOE 的度数；（2）如图2，在∠AOD 内引一条射线OF OC ⊥，其他不变，设()090DOF αα∠=︒︒<<︒．∠求∠AOF 的度数（用含α的代数式表示）；∠若∠BOD 是∠AOF 的2倍，求∠DOF 的度数．45．如图，在77⨯的正方形网格中有一个格点ABC ．(1)在图中作出ABC 关于直线l 对称的111A B C △(2)在直线l 上找到一点D ，使得AD CD +的值最小（在图中标出D 点位置，保留作图痕迹）46．如图，直线,EF CD 相交于点,,O OA OB OC ⊥平分AOF ∠．（1）若40AOE ∠=︒，求∠BOD 的度数；（2）若30BOE ∠=︒，求∠DOE 的度数．47．如图，点C 是线段AB 的中点，点D 在线段AB 上，且13AD AB =．（1）若4cm AD =，求线段CD 的长．（2）若3cm CD =，求线段AB 的长．48．（1）如图1，将两个正方形的一个顶点重合放置，若40AOD ∠=︒，则COB ∠=______度；（2）如图2，将三个正方形的一个顶点重合放置，求∠1的度数；（3）如图3，将三个正方形的一个顶点重合放置，若OF 平分DOB ∠，那么OE 平分AOC ∠吗？为什么？49．如图，90,60AOB COD AOC ∠=∠=︒∠=︒，射线ON 以10度/秒的速度从OD 出发绕点O 顺时针转动到OA 时停止，同时射线OM 以25度/秒的速度从OA 出发绕点O 逆时针转动到OD 时停止，设转动时间为t 秒．(1)当OM ON 、重合时，求t 的值；(2)当ON 平分BOD ∠时，试通过计算说明OM 平分AOD ∠；(3)当t 为何值时，MON ∠与AOD ∠互补？参考答案：1．D【分析】由正方体展开图的特征即可判定出正方体的展开图．【详解】解：由正方体展开图的特征即可判定D不是正方体的展开图，故选：D．【点睛】本题主要考查了几何体的展开图，解题的关键是熟记正方体展开图的特征．2．D【详解】试题分析：根据题意可得：A、B、C三点构成直角三角形，BC为斜边，则根据直角三角形的性质可得：，故选D．3．B【详解】线段有：AB、AC、BC.故选：B.4．D【分析】根据面动成体，梯形绕下底边旋转是圆锥加圆柱，可得答案.【详解】面动成体，直角三角形绕直角边旋转一周可得圆锥，长方形绕一边旋转一周可得圆柱，那么所求的图形是下面是圆锥，上面是圆柱的组合图形．故选D．【点睛】此题考查点、线、面、体的问题，解决本题的关键是得到所求的平面图形是得到几何体的主视图的被纵向分成的一半.5．B【分析】逐一判断出各选项中的几何体的名称即可得答案．【详解】A是棱柱，不符合题意；B是棱锥，符合题意，C是球体，不符合题意；D是圆柱，不符合题意；故选B．【点睛】本题考查了几何体的识别，熟练掌握常见几何体的图形特征是解题的关键．6．C=-；点C在点B右侧时，【分析】根据题意知，点C在点B左侧时，MN BM BN+MN BM BN =，因为点M 是线段AB 的中点，点N 是线段BC 的中点，分别算出,BM BN 长度，代入计算即可．【详解】解：因为点C 是直线AB 上一点，所以需要分类讨论：（1）点C 在点B 左侧时，作图如下：∠10cm AB =，4cm BC =， ∠152BM AB cm ==，122BN BC cm ==， 又∠MN BM BN =-，∠=523MN cm -=．（2）当点C 在点B 右侧时，作图如下：由（1）知，152BM AB cm ==，122BN BC cm ==， ∠+MN BM BN =，∠+=5+2=7cm MN BM BN =，综上所述，MN 的长度是3cm 或7cm ．故选：C【点睛】本题考查线段长度的计算，根据题意分类讨论是解题关键．7．D【分析】根据平角、两点间的距离、角的定义和直线公理逐项进行解答即可得.【详解】A 、平角的两条边在一条直线上，故本选项错误；B 、连接两点的线段的长度叫做两点间的距离，故此选项错误；C 、有公共端点是两条射线组成的图形叫做角，故此选项错误；D 、经过两点有一条直线，并且只有一条直线，正确，故选：D ．【点睛】本题考查了平角、两点间的距离、角的概念以及直线公理的内容，熟练掌握相关知识是解题的关键．8．A【分析】由OC 平分∠AOB 可得到∠AOB=2∠AOC ，代入计算可得解.【详解】解：OC 平分∠AOB ，则227322?554AOB AOC ∠=∠=︒'⨯=︒'， 故选：A【点睛】本题考查了角平分线和角的计算，比较基础.9．A【分析】如解图所示，依据60ABC ∠=︒，242∠=︒，即可得到18EBC ∠=︒，再根据BE CD ，即可得出118EBC ∠=∠=︒．【详解】：如图，∠60ABC ∠=︒，242∠=︒，∠18EBC ∠=︒，∠BE CD ，∠118EBC ∠=∠=︒，故选：A ．【点睛】此题考查了平行线的性质，掌握两直线平行，内错角相等是解决此题的关键． 10．D【分析】由平面图形的折叠及正方体的展开图解题．【详解】解：正方体共有11种表面展开图，A 、B 、C 项都是正方体的展开图，D 出现了“田”字格，故不是正方体的展开图；故选择：D.【点睛】本题考查的是正方体的展开图，以及学生的立体思维能力．解题时勿忘记四棱柱的特征及正方体展开图的各种情形．11．C【分析】利用正方体及其表面展开图的特点解题．【详解】解：这是一个正方体的平面展开图，共有六个面，其中面“国”与面“我”相对，面“梦”与面“的”相对，“中”与面“梦”相对．故选：C．12．D【分析】根据图形，找出以O为顶点的所有小于180°的角即可.【详解】解：以O为顶点且小于180°的角有：∠AOC，∠COD，∠DOE，∠EOB，∠AOD，∠AOE，∠COE，∠COB，∠DOB.一共有9个；故选择：D.【点睛】本题考查了角的表示，解题的关键是要找到图中两两相交直线的交点，作为角的顶点，且找出的角要小于180°．13．D【分析】根据角的定义即可判断.【详解】如果一个角的终边继续旋转，旋转到与始边成一条直线时，所成的角叫做平角，故A错误；当终边旋转到与始边重合时，所成的角叫做周角，故B错误；有公共端点的两条不重合的射线组成的图形叫做角，故C错误；一条射线绕它的端点旋转而成的图形叫做角，故D正确.故选D.【点睛】此题考查了角的定义，掌握角的两种定义和周角、平角的定义是解题的关键. 14．A【分析】利用正方体及其表面展开图的特点可知“3点”和“4点”相对，“5点”和“2点”相对，“6点”和“1点”相对，当1点在上面，3点在左面，可知5点在后面，继而可得出2点在前面．【详解】这是一个正方体的表面展开图，共有六个面，其中面“3点”和面“4点”相对，面“5点”和面“2点”相对，面“6点”和面“1点”相对，如果1点在上面，3点在左面，可知5点在后面，2点在前面；故选A．【点睛】此题考查学生的空间想象能力，先找到每个面的对面，进而确定它们的位置. 15．D【分析】正方体的表面展开图，相对的面之间一定相隔一个正方形，根据这一特点作答即可．【详解】正方体的表面展开图，相对的面之间一定相隔一个正方形，∠“祝”与“功”是相对面．故选：D．【点睛】本题主要考查了展开与折叠，注意正方体的空间图形，从相对面入手，分析及解答问题．16．C【详解】解：∠AB=3，∠AC=13AB=13×3=1，∠BC=3-1=2，∠CD=12CB=12×2=1，∠AD=1+1=2，CB=1+1=2，DB=2-1=1，即图中所有线段长的和是AC+AD+AB+CD+CB+DB=1+2+3+1+2+1=10．故选C．17．B【分析】三棱柱由平面组成、圆锥由曲面和平面组成、球体由曲面组成、正方体由平面组成，结合各图形的特点可得出答案．【详解】解：三棱柱由平面组成、圆锥由曲面和平面组成、球体由曲面组成、正方体由平面组成；故选：B【点睛】此题考查了认识立体图形的知识，熟练掌握是解题的关键.18．A【分析】根据C点为线段AB的中点，D点为BC的中点，可知AC=CB=12AB，CD=12CB，AD=AC+CD，又AB=4cm，继而即可求出答案．【详解】∠点C是线段AB的中点，AB=20cm，∠BC=12AB=12×20cm=10cm，∠点D是线段BC的中点，∠BD=12BC=12×10cm=5cm，∠AD=AB-BD=20cm-5cm=15cm．故选A．【点睛】本题考查了两点间的距离的知识，注意理解线段的中点的概念．利用中点性质转化线段之间的倍分关系是解题的关键．19．C【详解】A. 由公共端点的两条射线组成的图形叫做角，故不正确；B. 各边相等，且各角也相等的多边形叫做正多边形，故不正确；C. 一个圆分割成圆心角度数比位1∠2∠3的三个扇形，则最小扇形的圆心角是1360123⨯++=60°，正确； D. 小于平角的角可分为锐角，直角和钝角三类，故不正确．故选C ．【点睛】本题考查了角、正多边形、圆心角的定义，以及角的分类，熟练掌握各知识点是解答本题的关键．20．A【详解】解：根据题意，两车必定沿着同一条公路行驶．故选A ．21．144°【分析】根据补角的定义即可求出a ∠的补角的度数．【详解】解: a ∠的补角的度数是180°－a ∠=180°－36°=144°故答案为: 144°．【点睛】此题考查的是求一个角的补角,掌握补角的定义是解决此题的关键．22．24°30′##24.5°【分析】如果两个角的和为90°，则这个两个角互为余角，根据互为余角的两个角的和为90°作答．【详解】解：根据定义∠α的余角度数是90°﹣65°30′＝24°30′．故答案为：24°30′．【点睛】本题考查角互余的概念：和为90度的两个角互为余角．属于基础题，较简单． 23．3【分析】根据线段的定义分别写出各条线段即可【详解】解：图中以A 为端点的线段有线段AB ，线段AC ，线段AD ，共3条故答案为：3【点睛】本题考查了线段的定义，属于基础题，较简单24．10316'︒【分析】直接根据角的运算计算即可．【详解】160',1'60''︒==3425'20''310316'∴︒⨯=︒故答案为：10316'︒．【点睛】本题主要考查角的运算，掌握度分秒之间的关系是解题的关键．25．76︒【分析】设这个角为x ，则它的余角为90x ︒-，补角为180x ︒-,根据题意列出方程即可求解．【详解】设这个角为x ，则它的余角为90x ︒-，补角为180x ︒-()190180124x x ∴-=-- 19045124x x -=-- 3574x = 4573x =⨯ 76x =︒即这个角为76︒故答案为76︒．【点睛】此题主要考查角度的计算，解题的关键是根据题意列出方程求解．26．15【分析】根据三角形外角的性质求解即可．【详解】解：∠CBD ∠是ABC 的外角，∠CBD CAD ACB ∠=∠+∠，∠453015ACB CBD CAD ∠=∠-∠=︒-︒=︒．故答案为：15【点睛】本题考查了仰角的概念和三角形外角性质，掌握三角形的外角等于与它不相邻的两个内角的和是解题关键．27．120°【分析】根据等腰三角形的性质和特殊直角三角形的角度求得∠DFC ，进一步利用三角形外角的性质即可得到结果．【详解】解：如图，∠DE=DF ，∠EDF=30°， ∠∠DFC=12（180°-∠EDF ）=75°，∠∠C=45°，∠∠BDN=∠DFC+∠C=75°+45°=120°．故答案为：120°．【点睛】本题考查了旋转的性质，直角三角形的性质，等腰三角形的性质，掌握三角形的内角和与外角的性质是解题的关键．28．3【分析】利用数轴得到点Q表示的数，再根据线段中点定义可得答案．【详解】解：∠点P对应的数是-1，将点P向右移动8个长度单位得到点Q，∠点Q表示的数为：-1+8=7，∠线段PQ的中点对应的数是1713 2-+-=故答案为：3．【点睛】本题考查了数轴，掌握数轴上两点间的距离是解决此题的关键．29．40°【分析】根据三角形内角和定理列式求出∠OBC+∠OCB，再根据角平分线的定义求出∠ABC+∠ACB，然后利用三角形的内角和定理列式计算即可得解．【详解】解：如图，在∠BOC中，∠BOC = 110°，∴∠OBC + ∠OCB = 180°- 110°= 70°，OB、OC分别是∠ABC和∠ACB的平分线，∴∠ABC = 2∠OBC，∠ACB=2∠OCB，∴∠ABC +∠ACB = 2×70°= 140°，∴在∠ABC中，∠A = 180°-(∠ABC+∠ACB)= 180°- 140°= 40°，故答案为：40°．【点睛】本题考查了三角形的内角和定理，角平分线的定义，整体思想的利用是解题的关键．30．159°20′【详解】试题分析：根据∠α的补角=180°﹣∠α，代入求出即可．解：∠∠α=20°40′，∠∠α的补角=180°﹣20°40′=159°20′，故答案为159°20′．考点：余角和补角；度分秒的换算．31．70°【详解】由题意可知∠DBC=80°，∠DBA=30°，∠∠ABC=50°，又∠DB∠EC，∠ECA=40°，∠∠ECB=100°，∠∠ACB=60°，∠∠BAC=180°-60°-50°=70°32．南偏西14°．【分析】根据方位角的概念，画图正确表示出方位角，利用平行线的性质即可求解．【详解】由题意可知，∠1＝14°，∠AC∠BD，∠∠1＝∠2＝14°，根据方向角的概念可知，由点B测点A的方向为南偏西14°方向．故答案为：南偏西14°．【点睛】此题考查的知识点是方向角，解答此类题需要从运动的角度，正确画出方位角，即可解答．33．3或7【分析】根据线段的和差，可得BC的长，根据线段中点的性质，可得答案．【详解】当点C在线段AB上时，AC＝AB−BC＝10−4＝6，点M是线段AC的中点，AC＝3，MA＝12BM＝AB−AM＝10−3＝7；当点C在线段的反向延长线上时，AC＝AB＋BC＝10＋4＝14，点M是线段AC的中点，AM＝1AC＝7，2BM＝AB−AM＝10−7＝3，故答案为：3或7．【点睛】本题考查了两点间的距离，利用线段的和差、线段中点的性质是解题关键，要分类讨论，以防遗漏．34． 2 【分析】∠连接,OA OB ，易证AOB 是等边三角形，弦AB 长为2，2OA OB ==，即可得到答案；∠先证90BOC AOB AOC ∠=∠+∠=︒，延长BO 交O 于点E ，连接AE 交CD 于点P ，连接BP ,则此时PA PB PA PE AE +=+=，即PA PB +的最小值是AE 的长，再用勾股定理求出AE 即可．【详解】解：∠连接,OA OB ，∠30,ADB ∠=︒ ∠60AOB ∠=︒, ∠OA OB =，∠AOB 是等边三角形， ∠弦AB 长为2， ∠2OA OB ==， 即O 的半径长为2， 故答案为：2 ∠∠15ADC ∠=︒， ∠230AOC ADC ︒∠=∠=, ∠90BOC AOB AOC ∠=∠+∠=︒，延长BO 交O 于点E ，连接AE 交CD 于点P ，连接BP ,则此时PA PB PA PE AE +=+=，即PA PB +的最小值是AE 的长，∠60BAO ∠=︒，∠2OA OE ==， ∠30OAE AEB ︒∠=∠=， ∠90BAE BAO OAE ∠=∠+∠=︒，∠AE ==即PA PB +的最小值是故答案为：【点睛】此题考查了圆周角定理、勾股定理、等边三角形的判定和性质、轴对称最短路径等知识，熟练掌握相关定理并灵活应用是解题的关键． 35．105【分析】利用三角形外角性质求解． 【详解】如图，∠∠2=30︒，∠3=45︒， ∠∠4=∠2+∠3=75︒， ∠∠1=1804105︒-∠=︒， 故答案为：105．．【点睛】此题考查三角板的角度计算，三角形外角的性质，观察图形掌握各角度之间的位置关系是解题的关键． 36．201420141A 2α∠=【分析】由三角形的外角性质知：∠A=∠ACD-∠ABC ，而∠A 1=12（∠ACD-∠ABC ），即∠A 1=12∠A ，同理可得，∠A 2=12∠A 1，依此类推即可． 【详解】∠∠ACD 是∠ABC 的外角， ∠∠ACD ＝∠A ＋∠ABC ，∠1B A 平分∠ABC ，1CA 平分∠ACD ，∠112A BC ABC ∠=∠，112ACD ACD ∠=∠， ∠1A CD ∠是1A CB 的外角， ∠111ACD A BC A ∠=∠+∠， ∠11122ACD ABC A ∠=∠+∠， ∠()11122A ACD ABC A ∠=∠-∠=∠， 同理可得：1212A A ∠=∠， 根据规律可得：201420141A 2α∠=【点睛】本题考查的是三角形内角和定理及三角形外角的性质，找出规律是解答此题的关键．37．60°或105°或135°【分析】分类讨论：当//BC AD 时，当//AC DE 时，当//AB DE 时，利用角度之间的关系计算即可；【详解】解：如图当//BC AD 时，，90C CAD ︒∠=∠=∠903060a DAB ︒=-︒=∠=︒， 如图，当//AC DE 时，90E CAE ︒∠=∠=，则459030105DAB α︒=∠=︒+︒-︒=， 如图，当//AB DE 时，90A E B E ∠=∠=︒，∠4590135BAD α=∠=︒+︒=︒；综上：符合条件的α为60°或105°或135°， 故答案为：60°或105°或135°．【点睛】本题考查角度之间的计算，平行的性质，解题的关键是对平行的边进行分情况讨论．38．40°或140°【分析】根据角平分线的定义求得∠MOC ＝12∠AOC ，∠CON ＝12∠BOC ；然后根据图形中的角与角间的和差关系来求∠MON 的度数． 【详解】解：∠OM 平分∠AOC ，ON 平分∠BOC ．∠∠MOC＝12∠AOC，∠CON＝∠BON＝12∠BOC．如图1，∠MON＝∠MOC-∠CON＝12（∠AOC-∠BOC）=12∠AOB＝12×80°＝40°；如图2，∠MON＝∠MOC+∠CON＝12（∠AOC+∠BOC）＝12（360°﹣∠AOB）＝12×280°＝140°．如图3，∠MON＝∠MOC+∠CON＝12（∠AOC+∠BOC）=12∠AOB＝12×80°＝40°；故答案为：40°或140°．【点睛】此题主要考查了角平分线的定义．注意“数形结合”数学思想在解题过程中的应用．39．26【分析】根据射线、线段的定义进而判断得出m，n的值再代入计算即可．【详解】解：图中共有10条线段，共有16条射线，则m=10,n=16,所以m n+=10+16=26.故答案为26.【点睛】此题主要考查了射线、线段的定义，熟练掌握它们的定义是解题关键．40．∠∠或∠∠或∠∠或∠∠【分析】观察所给图形结合正方体的平面展开图的特点进行填涂即可．【详解】根据正方体的展开图的特点，按如下方式进行填涂后可以构成正方体表面的展开图：故答案为：∠∠或∠∠或∠∠或∠∠．【点睛】本题主要考查正方体展开图的2-3-1型和2-2-2-型，掌握正方体的展开图是解题关键．41．110EOD ∠=︒．【分析】根据对顶角相等先求出∠AOC 的度数，然后根据角平分线的定义求出∠COE 的度数，最后根据∠OCE 与∠EOD 互为邻补角即可得出答案． 【详解】35BOD ∠=︒，35AOC ∴∠=︒OA 平分EOC ∠，223570COE AOC ∴∠=∠=⨯︒=︒ 180110EOD COE ∴∠=︒-∠=︒．【定睛】本题主要考查了角的和差运算，根据对顶角相等和角平分线的定义求出∠COE 是 解决此题的关键．42． ②③⑧ ①④⑤⑥⑦【分析】根据立体图形和平面图形定义分别进行判断． 【详解】解：∠∠∠是平面图形；∠∠∠∠∠是立体图形．【点睛】本题考查认识立体图形：有些几何图形（如长方体、正方体、圆柱、圆锥、球等）的各部分不都在同一个平面内，这就是立体图形． 43．(1)5，4(2)1APQ S =△平方米 (3)4t =【分析】（1）根据绝对值和乘方的非负性，即可求解；（2）根据题意得：当t =4.5时，点P 在CD 上，DP =0.5米，点Q 刚好到达点D 处，可得12PQ =米，再由12APQ S PQ AD =⋅⋅△，即可求解； （3）当P ，Q 都在DC 上，可得4 4.5t ≤≤，然后分两种情况讨论：当P 左Q 右时，当Q 左P 右时，即可求解．【详解】（1）解∠∠()2540x y -+-=， ∠50,40x y -=-=， ∠x =5，y =4， 故答案为：5，4；（2）解：当t =4.5时，P 走过的路程为4.5米，此时点P 在CD 上，DP =0.5米，Q 走过的路程为9米，刚好到达点D 处， ∠12PQ =米， ∠11141222APQ S PQ AD =⋅⋅=⨯⨯=△平方米；（3）解：点P 在DC 上，49t ≤≤，点Q 在DC 上，2 4.5t ≤≤， ∠4 4.5t ≤≤，当P 左Q 右时，4DP t =-，24CQ t =-，∠()()5424133PQ CD DP CQ t t t =--=----=-， ∠1331t -=， 解得：4t =当Q 左P 右时，4DP t =-，24CQ t =-，∠()()4245313PQ DP CQ CD t t t =+-=-+--=-， ∠3131t -=， 解得144.53t =>，不符题意，舍去． 综上，满足题意的4t =．【点睛】本题主要考查了动点问题，涉及绝对值和平方式的非负性，三角形面积的求解，解题的关键是关键题意用时间t表示出线段长度，列式求出t的值．44．（1）90°；（2）∠90°-2α°∠18°【分析】（1）根据角平分线的定义和平角的定义，即可求解；（2）∠根据余角的性质得：∠COE=∠DOF=α°，根据角平分线的定义，可得∠BOC=2α°，进而即可求解；∠用α分别表示出∠BOD和∠AOF的度数，结合∠BOD是∠AOF的2倍，列出关于α的方程，即可求解．【详解】（1）∠点A、O、B三点在同一直线上，射线OD、OE分别平分∠AOC、∠BOC，∠∠COD=12∠AOC，∠COE=12∠BOC，∠∠COD+∠COE=12∠AOC+12∠BOC=12（∠AOC+∠BOC）=12×180°=90°，∠∠DOE=∠COD+∠COE=90°；（2）∠∠OE平分∠BOC，∠∠BOC=2∠COE，∠OF∠OC，∠∠COF=∠COD+∠DOF=90°，∠∠COE+∠COD=90°，∠∠COE=∠DOF=α°，∠∠BOC=2α°，∠∠AOF+∠BOC=90°，∠∠AOF=90°-2α°；∠∠∠BOE=∠COE=α°，∠∠BOD=∠BOE+∠DOE=90°+α°，∠∠BOD=2∠AOF=2（90°-2α°）=180°-4α°，∠90°+α°=180°-4α°，∠α=18，即：∠DOF=18°．【点睛】本题主要考查角的和差倍分，涉及余角的定义和性质，平角的定义，角平分线的定义，根据题意，列出一元一次方程，是解题的关键．45．(1)图见解析(2)图见解析【分析】（1）分别作出A ，B ，C 的对应点111A B C ，，即可； （2）连接1AA ，1CA 交l 于点D ，点D 即为所求． 【详解】（1）如图所示； （2）如图所示：【点睛】本题考查了作图—轴对称变换，最短问题，解决本题的关键是熟练掌握基本知识．46．（1）20°；（2）60°【分析】（1）先求出∠AOF =140°，然后根据角平分线的定义求出∠AOC =70°，再由垂线的定义得到∠AOB =90°，则∠BOD =180°-∠AOB -∠AOC =20°；（2）先求出∠AOE =60°，从而得到∠AOF =120°，根据角平分线的性质得到∠AOC =60°，则∠COE =∠AOE +∠AOC =120°，∠DOE =180°-∠COE =60°． 【详解】解：（1）∠∠AOE =40°， ∠∠AOF =180°-∠AOE =140°， ∠OC 平分∠AOF ， ∠∠AOC =12∠AOF =70°， ∠OA ∠OB ， ∠∠AOB =90°，∠∠BOD =180°-∠AOB -∠AOC =20°；（2）∠∠BOE=30°，OA∠OB，∠∠AOE=60°，∠∠AOF=180°-∠AOE=120°，∠OC平分∠AOF，∠∠AOC=12∠AOF=60°，∠∠COE=∠AOE+∠AOC=60°+60°=120°，∠∠DOE=180°-∠COE=60°．【点睛】本题主要考查了几何中角度的计算，角平分线的定义，垂线的定义，解题的关键在于能够熟练掌握角平分线的定义．47．（1）2 cm；（2）18cm【分析】（1）先求出AB的长，再结合线段中点的定义求出AC的长，进而即可求解；（2）设AB=x cm，则13AD x=cm，根据线段的中点的定义，列出方程，进而即可求解．【详解】（1）∠13AD AB=，AD=4 cm，∠AB=3×4=12 cm，∠点C是线段AB的中点，∠AC=12AB=11262⨯=cm，∠CD=AC-AD=6-4=2 cm；（2）设AB=x cm，则13AD x=cm，∠点C是线段AB的中点，∠AB=2（AD+CD），即x=2（13x+3），解得：x=18，∠AB=18cm．【点睛】本题主要考查线段的和差倍分以及一元一次方程的应用，利用一元一次方程解决问题，是解题的关键．48．（1）140；（2）20°；（3）OE平分∠AOC，见解析【分析】（1）根据正方形各角等于90°，得出∠COD+∠AOB=180°，再根据∠AOD=40°，∠COB=∠COD+∠AOB-∠AOD，即可得出答案；（2）根据已知得出∠1+∠2，∠1+∠3的度数，再根据∠1+∠2+∠3=90°，最后用∠1+∠2+∠1+∠3-（∠1+∠2+∠3），即可求出∠1的度数；（3）根据∠COD=∠AOB和等角的余角相等得出∠COA=∠DOB，∠EOA=∠FOB，再根据角平分线的性质得出∠DOF=∠FOB=12∠DOB和∠EOA=12∠DOB=12∠COA，从而得出答案．【详解】解：（1）∠两个图形是正方形，∠∠COD＝90°，∠AOB＝90°，∠∠COD+∠AOB＝180°，∠∠AOD＝40°，∠∠COB＝∠COD+∠AOB－∠AOD＝140°故答案为：140；（2）如图，由题意知，∠1+∠2＝50°∠，∠1+∠3＝60°∠，又∠1+∠2+∠3＝90°∠，所以：∠+∠－∠得：∠1＝20°；（3）OE平分∠AOC，理由如下：∠∠COD＝∠AOB，∠∠COA＝∠DOB（等角的余角相等），同理：∠EOA＝∠FOB，∠OF平分∠DOB，∠12DOF FOB DOB∠=∠=∠，∠1122EOA DOB COA ∠=∠=∠，∠OE平分∠AOC．【点睛】本题考查了角的和差运算，与余角和补角的有关的计算，根据所给出的图形，找到角与角的关系是本题的关键．49．（1）307t =；（2）见解析；（3）247t =或367t = 【分析】（1）根据题意10,25150DON t AOM t AOD ∠=∠=∠=︒， ,当OM ON 、重合时，+DON AOM AOD ∠∠=∠，计算即可；（2）根据题意可得=60BOD AOC ∠∠=︒，由ON 平分BOD ∠可计算出3t =，故25375AOM ∠=⨯=︒,即可说明OM 平分AOD ∠；（3）根据题意可得30MON ∠=︒分两种情况说明，当OM ON 、重合之前和OM ON 、重合之后分别计算即可．【详解】由题意：10,25DON t AOM t ∠=∠=()190,60COD AOC ∠=∠=150AOD COD AOC ∴∠=∠+∠=当,ON OM 重合时，DON AOM AOD ∠+∠=∠1025150t t ∴+= 解得：307t = ()290AOB COD ∠=∠=90AOC BOC BOD BOC ∴∠+∠=∠+∠=60BOD AOC ∴∠=∠= ON 平分BOD ∠1302DON BOD ∴∠=∠= ∠30103t =÷= ∠1253752AOM AOD ∠=⨯==∠ OM ∴平分AOD ∠()3150,180AOD AOD MON ∠=∠+∠=30MON ∴∠=当OM 与ON 重合前150DON MON AOM ∠+∠+∠=103025150 t t++=解得：247 t=当OM与ON重合后150 DON AOM MON∠+∠-∠= 102530150t t+-=解得：367 t=∴当247t=或367t=时，MON∠与AOD∠互补【点睛】本题考查的是角的综合题，一元一次方程的解法，旋转的性质，有一定的难度，分情况讨论是难点．。

中考复习初中数学几何证明经典试题(含答案)

中考复习初中数学几何证明经典试题(含答案)

P CG FAD E初中几何证明题经典题（一）1、已知：如图，O 是半圆的圆心，C 、E 是圆上的两点，CD ⊥AB ，EF ⊥AB ，EG ⊥CO ． 求证：CD ＝GF ．（初二）.如下图做GH ⊥AB,连接EO 。

由于GOFE 四点共圆，所以∠GFH ＝∠OEG , 即△GHF ∽△OGE,可得EO GF =GO GH =COCD,又CO=EO ，所以CD=GF 得证。

2、已知：如图，P 是正方形ABCD 内点，∠PAD ＝∠PDA ＝150． 求证：△PBC 是正三角形．（初二）3、如图，已知四边形ABCD 、A 1B 1C 1D 1都是正方形，A CC 1、DD 1的中点．求证：四边形A 2B 2C 2D 2是正方形．（初二）4、已知：如图，在四边形ABCD 中，AD ＝BC ，M 、N 的延长线交MN 于E 、F ．求证：∠DEN ＝∠F ． 经典1、已知：△ABC 中，H 为垂心（各边高线的交点），O （1）求证：AH ＝2OM ； （2）若∠BAC ＝600，求证：AH ＝AO ．（初二）2、设MN 是圆O 外一直线，过O 作OA ⊥MN 于A 及D 、E ，直线EB 及CD 分别交MN 于P 、Q ． 求证：AP ＝AQ ．（初二）3、如果上题把直线MN 设MN 是圆O 的弦，过MN 的中点A 任作两弦于P 、Q ． 求证：AP ＝AQ ．（初二）4、如图，分别以△ABC 的AC 和BC 为一边，在△CBFG ，点P 是EF 的中点．求证：点P 到边AB 的距离等于AB 的一半．（初二） 经典题（三） 1、如图，四边形ABCD 为正方形，DE ∥AC ，AE ＝AC ，AE 与CD 相交于F ． 求证：CE ＝CF ．（初二）2、如图，四边形ABCD 为正方形，DE ∥AC ，且CE ＝CA ，直线EC 交DA 延长线于F ．AQ P NM · O B D AF D AFGCEBO D求证：AE ＝AF ．（初二）3、设P 是正方形ABCD 一边BC 上的任一点，PF ⊥AP ，CF 平分∠DCE ．求证：PA ＝PF ．（初二） 4、如图，PC 切圆O 于C ，AC 为圆的直径，PEF 为圆的割线，AE 、AF 与直线PO 相交于B 、D ．求证：AB ＝DC ，＝AD ．（初三）经典题（四）1、已知：△ABC 是正三角形，P 是三角形内一点，PA ＝3，PB ＝4，PC ＝5． 求：∠APB 的度数．（初二）2、设P 是平行四边形ABCD 内部的一点，且∠PBA ＝∠PDA ．求证：∠PAB ＝∠PCB ．（初二）3、设ABCD 为圆内接凸四边形，求证：AB ·CD ＋AD ·BC ＝AC ·BD ．（初三）4、平行四边形ABCD 中，设E 、F 分别是BC 、AB 上的一点，AE 与CF 相交于P ，且 AE ＝CF ．求证：∠DPA DPC ．（初二） 经典难题（五）1、 设P 是边长为1的正△ABC 内任一点，L ＝PA ＋PB ＋PC ， 求证：≤L ＜2．2、已知：P 是边长为1的正方形ABCD 内的一点，求PA ＋PB ＋PC 的最小值．3、P 为正方形ABCD 内的一点，并且PA ＝a ，PB ＝2a ，PC ＝3a ，求正方形的边长．4、如图，△ABC 中，∠ABC ＝∠ACB ＝800，D 、E 分别是AB 、AC 上的点，∠DCA ＝300，∠EBA ＝200，求∠BED 的度数． 经典题（一）1.如下图做GH ⊥AB,连接EO 。

中考数学模拟题汇总《几何》专项练习题

中考数学模拟题汇总《几何》专项练习题

中考数学模拟题汇总《几何》专项练习题（含答案解析）1、如图，在矩形ABCD中，动点P从点B出发，沿BC、CD、DA运动至点A停止，设点P运动的路程为x，△ABP的面积为y，如果y关于x的函数图象如图所示，则△ABC的面积是（）A．10B．16C．18D．20【分析】本题难点在于应找到面积不变的开始与结束，得到BC，CD的具体值．【解答】解：动点P从点B出发，沿BC、CD、DA运动至点A停止，而当点P运动到点C，D 之间时，△ABP的面积不变．函数图象上横轴表示点P运动的路程，x＝4时，y开始不变，说明BC＝4，x＝9时，接着变化，说明CD＝9﹣4＝5．∴△ABC的面积为＝×4×5＝10．故选：A．2、如图，点C是线段AB上的一个动点，△ACD和△BCE是在AB同侧的两个等边三角形，DM，EN分别是△ACD和△BCE的高，点C在线段AB上沿着从点A向点B的方向移动（不与点A，B重合），连接DE，得到四边形DMNE．这个四边形的面积变化情况为（）A．逐渐增大B．逐渐减小C．始终不变D．先增大后变小【分析】易得此四边形为直角梯形，AB的长度一定，那么直角梯形的高为AB的长度的一半，上下底的和也一定，所以面积不变．【解答】解：当点C在线段AB上沿着从点A向点B的方向移动时，根据等边三角形的性质，等边△ACD和△BCE的高DM和EN的和不会改变，即DM+EN＝MC+CN＝AC+CB＝AB，而且MN的长度也不会改变，即MN＝AC+CB＝AB．∴四边形DMNE面积＝AB2，∴面积不会改变．故选：C．3、如图，圆柱形容器中，高为1.2m，底面周长为1m，在容器内壁离容器底部0.3m的点B处有一蚊子，此时一只壁虎正好在容器外壁，离容器上沿0.3m与蚊子相对的点A处，则壁虎捕捉蚊子的最短距离为m（容器厚度忽略不计）．【分析】将容器侧面展开，建立A关于EF的对称点A′，根据两点之间线段最短可知A′B 的长度即为所求．【解答】解：如图：∵高为1.2m，底面周长为1m，在容器内壁离容器底部0.3m的点B处有一蚊子，此时一只壁虎正好在容器外壁，离容器上沿0.3m与蚊子相对的点A处，∴A′D＝0.5m，BD＝1.2﹣0.3+AE＝1.2m，∴将容器侧面展开，作A关于EF的对称点A′，连接A′B，则A′B即为最短距离，A′B＝＝＝1.3（m）．故答案为：1.3．4、在⊙O中，AB是⊙O的直径，AB＝8cm，＝＝，M是AB上一动点，CM+DM的最小值是cm．【分析】作点C关于AB的对称点C′，连接C′D与AB相交于点M，根据轴对称确定最短路线问题，点M为CM+DM的最小值时的位置，根据垂径定理可得＝，然后求出C′D 为直径，从而得解．【解答】解：如图，作点C关于AB的对称点C′，连接C′D与AB相交于点M，此时，点M为CM+DM的最小值时的位置，由垂径定理，＝，∴＝，∵＝＝，AB为直径，∴C′D为直径，∴CM+DM的最小值是8cm．故答案为：8．5、如图，一只蚂蚁沿着棱长为2的正方体表面从点A出发，经过3个面爬到点B，如果它运动的路径是最短的，则AC的长为．【分析】将正方体展开，右边与后面的正方形与前面正方形放在一个面上，此时AB最短，根据三角形MCB与三角形ACN相似，由相似得比例得到MC＝2NC，求出CN的长，利用勾股定理求出AC的长即可．【解答】解：将正方体展开，右边与后面的正方形与前面正方形放在一个面上，展开图如图所示，此时AB最短，∵△BCM∽△ACN，∴＝，即＝＝2，即MC＝2NC，∴CN＝MN＝，在Rt△ACN中，根据勾股定理得：AC＝＝，故答案为：．6、在平面直角坐标系中，平行四边形ABOC如图放置，点A、C的坐标分别是（0，4）、（﹣1，0），将此平行四边形绕点O顺时针旋转90°，得到平行四边形A′B′OC′．（1）若抛物线经过点C、A、A′，求此抛物线的解析式；（2）在（1）的情况下，点M是第一象限内抛物线上的一动点，问：当点M在何处时，△AMA′的面积最大？最大面积是多少？并求出此时M的坐标；（3）在（1）的情况下，若P为抛物线上一动点，N为x轴上的一动点，点Q 坐标为（1，0），当P、N、B、Q构成平行四边形时，求点P的坐标，当这个平行四边形为矩形时，求点N的坐标．【分析】（1）由平行四边形ABOC绕点O顺时针旋转90°，得到平行四边形A′B′OC′，且点A的坐标是（0，4），可求得点A′的坐标，然后利用待定系数法即可求得经过点C、A、A′的抛物线的解析式；（2）首先连接AA′，设直线AA′的解析式为：y＝kx+b，利用待定系数法即可求得直线AA′的解析式，再设点M的坐标为：（x，﹣x2+3x+4），继而可得△AMA′的面积，继而求得答案；（3）分别从BQ为边与BQ为对角线去分析求解即可求得答案．【解答】解：（1）∵平行四边形ABOC绕点O顺时针旋转90°，得到平行四边形A′B′OC′，且点A的坐标是（0，4），∴点A′的坐标为：（4，0），∵点A、C的坐标分别是（0，4）、（﹣1，0），抛物线经过点C、A、A′，设抛物线的解析式为：y＝ax2+bx+c，∴，解得：，∴此抛物线的解析式为：y＝﹣x2+3x+4；（2）连接AA′，设直线AA′的解析式为：y＝kx+b，∴，解得：，∴直线AA′的解析式为：y＝﹣x+4，设点M的坐标为：（x，﹣x2+3x+4），则S△AMA′＝×4×[﹣x2+3x+4﹣（﹣x+4）]＝﹣2x2+8x＝﹣2（x﹣2）2+8，∴当x＝2时，△AMA′的面积最大，最大值S△AMA′＝8，∴M的坐标为：（2，6）；方法二：过M点做x轴垂线和AA'交于一点E（x，﹣x+4），把△AMA'分成两个共底三角形，然后以ME为底，可以得出ME的长就是M点纵坐标减去E点纵坐标，即题目当中的﹣x2+3x+4﹣（﹣x+4），另外两个三角形的高之和就等于4，这是一种面积问题的常用方法．（3）设点P的坐标为（x，﹣x2+3x+4），当P，N，B，Q构成平行四边形时，∵平行四边形ABOC中，点A、C的坐标分别是（0，4）、（﹣1，0），∴点B的坐标为（1，4），∵点Q坐标为（1，0），P为抛物线上一动点，N为x轴上的一动点，①当BQ为边时，PN∥BQ，PN＝BQ，∵BQ＝4，∴﹣x2+3x+4＝±4，当﹣x2+3x+4＝4时，解得：x1＝0，x2＝3，∴P1（0，4），P2（3，4）；当﹣x2+3x+4＝﹣4时，解得：x3＝，x4＝，∴P3（，﹣4），P4（，﹣4）；②当BQ为对角线时，BP∥QN，BP＝QN，此时P与P1，P2重合；综上可得：点P的坐标为：P1（0，4），P2（3，4），P3（，﹣4），P4（，﹣4）；如图2，当这个平行四边形为矩形时，点N的坐标为：（0，0）或（3，0）．7、某学校数学社团遇到这样一个题目：如图1，在△ABC中，点O在线段BC上，∠BAO＝30°，∠OAC＝75°，AO＝，BO：CO＝1：3，求AB的长．经过社团成员讨论发现，过点B作BD∥AC，交AO的延长线于点D，通过构造△ABD就可以解决问题（如图2）．请回答：∠ADB＝°，AB＝．【分析】（1）根据平行线的性质可得出∠ADB＝∠OAC＝75°，结合∠BOD＝∠COA可得出△BOD∽△COA，利用相似三角形的性质可求出OD的值，进而可得出AD的值，由三角形内角和定理可得出∠ABD＝75°＝∠ADB，由等角对等边可得出AB＝AD＝4，此题得解。

中考数学几何基础、三角形与四边形复习专题训练精选试题及答案

中考数学几何基础、三角形与四边形复习专题训练精选试题及答案

立体图形的认识及角、相交线与平行线专题训练一、填空题：（每题 3 分，共 36 分）１、32.43°＝＿＿＿度＿＿＿分＿＿＿秒。

２、若∠1＝30°，则∠A 的补角是＿＿＿＿度。

３、如图，∠1和∠2是直线AB 、AC 被BC 所截而成的＿＿＿＿角。

４、如图，射线OA 表示的方向是＿＿＿＿＿＿＿。

５、锯木头时，一般先在木板上画出两个点，然后过这两点弹出一条墨线，这种做法的理由是＿＿＿＿＿＿＿＿＿＿＿＿＿＿。

６、如图，AC ⊥l 1，AB ⊥l 2，则点A 到直线 l 2 的距离是指线段＿＿＿＿＿＿＿＿的长度。

７、如图，已知：AB ∥CD ，∠1＝∠2，若∠1＝50°，则∠3＝＿＿＿＿度。

８、如图，将两块直角三角板的直角顶点重合为如图所示的形状，若∠AOD ＝127°， 则∠BOC ＝＿＿＿＿。

９、下面是一些相同的小正方体构成的几何体的三视图。

则至少要＿＿＿个正方体搭成。

主视图 左视图 俯视图10、如图，要得到AB ∥CD 的结论，则需要角相等的条件是＿＿＿＿＿＿（写出一个即可）11、直线 a ∥b ，则∠ACB ＝＿＿＿＿。

12、平面内有若干条直线，当下列情形时，可将平面最多分成几部分。

① 有一条直线时，最多分成两部分。

② 有两条直线时，最多分成 2＋2＝4 部分。

③ 有三条直线时，最多分成＿＿＿＿部分。

二、选择题。

（每题 4 分，共 24 分）A B CG D E F （第10题）A O DB C（第8题） A D E C ） ） ） 1 2 3 （第7题） ┘ ┘A B C l 1 l 2 （第6题） ） ） 1 2 A B C （第3题） 东 南西 A北 ） 30° O （第4题）（第11题） a b A B 28° 50°C１、在下列立体图形中，不属于多面体的是（ ）A 、正方体B 、三棱柱C 、长方体D 、圆锥 ２、两条直线被第三条直线所截，则（ ） A 、同位角相等 B 、同错角相等 C 、同旁内角互补 D 、无法确定 ３、在修建泉厦高速公路时，有时需将弯曲的道路改直，根据（ ）A 、直线公理B 、直线公理或线段最短公理C 、线段最短公理D 、平行公理４、如图是一个台球桌面的示意图，如果一个球按图中所示的方向被击中（球可以经过多次反射），那么该球最后将落入的球袋是（ ）A 、1号袋B 、2号袋C 、3号袋D 、4号袋５、下面图形中，不能折成正方体的是（ ）AB D ６、如果两个角的一边在同一直线上，另一边互相平行，那么这两个角的关系是（ ）A 、相等B 、互补C 、相等或互补D 、相等且互补三、解答题：（每题 8 分，共 40 分）１、已知C 为线段AB 的中点，D 在线段CB 上，且DA ＝6，DB ＝4，求CD 的长度。

中考数学几何压轴题及答案及答案

中考数学几何压轴题及答案及答案

中考数学几何压轴题及答案一、解答题（共30小题）1.观察猜想（1）如图①，在Rt△ABC中，∠BAC＝90°，AB＝AC＝3，点D与点A重合，点E在边BC上，连接DE，将线段DE绕点D顺时针旋转90°得到线段DF，连接BF，BE与BF的位置关系是，BE+BF＝；探究证明（2）在（1）中，如果将点D沿AB方向移动，使AD＝1，其余条件不变，如图②，判断BE与BF的位置关系，并求BE+BF的值，请写出你的理由或计算过程；拓展延伸（3）如图③，在△ABC中，AB＝AC，∠BAC＝α，点D在边BA的延长线上，BD＝n，连接DE，将线段DE绕着点D顺时针旋转，旋转角∠EDF＝α，连接BF，则BE+BF的值是多少？请用含有n，α的式子直接写出结论2.在△ABC的边BC上取B′、C′两点，使∠AB′B＝∠AC′C＝∠BAC（1）如图1中∠BAC为直角，∠BAC＝∠AB′B＝∠AC′C＝90°（点B′与点C′重合），则△ABC∽△B'BA∽△C'AC，，，进而可得AB2+AC2＝；（2）如图2中当∠BAC为锐角，图3中∠BAC为钝角时（1）中的结论还成立吗？若不成立，则AB2+AC2等于什么（用含用BC和B′C′的式子表示）？并说明理由（3）若在△ABC中，AB＝5，AC＝6，BC＝9，请你先判断出△ABC的类型，再求出B′C′的长3．（1）问题发现如图1，在Rt△ABC和Rt△CDE中，∠ACB＝∠DCE＝90°，∠CAB＝∠CDE＝45°，点D是线段AB上一动点，连接BE填空：①的值为；②∠DBE的度数为．（2）类比探究如图2，在Rt△ABC和Rt△CDE中，∠ACB＝∠DCE＝90°，∠CAB＝∠CDE＝60°，点D是线段AB上一动点，连接BE．请判断的值及∠DBE的度数，并说明理由；（3）拓展延伸如图3，在（2）的条件下，将点D改为直线AB上一动点，其余条件不变，取线段DE 的中点M，连接BM、CM，若AC＝2，则当△CBM是直角三角形时，线段BE的长是多少？请直接写出答案．4.（1）问题发现：如图①，在△ABC中，∠BAC＝90°，AB＝AC，点D是BC的中点，以点D为顶点作正方形DFGE，使点A、C分别在DE和DF上，连接BE、AF．则线段BE 和AF数量关系．（2）类比探究：如图②，保持△ABC固定不动，将正方形DFGE绕点D旋转α（0°＜α≤360°），则（1）中的结论是否成立？如果成立，请证明；如果不成立，请说明理由．（3）解决问题：若BC＝DF＝2，在（2）的旋转过程中，连接AE，请直接写出AE的最大值．5.如图，在平行四边形ABCD中，AC与BD交于点O，以点O为顶点的∠EOF的两边分别与边AB、AD交于点E、F，且∠EOF与∠BAD互补．（1）若四边形ABCD是正方形，则线段OE与OF有何数量关系？请直接写出结论；（2）若四边形ABCD是菱形，那么（1）中的结论是否成立？若成立，请画出图形并给出证明；若不成立，请说明理由；（3）若AB：AD＝m：n，探索线段OE与OF的数量关系，并证明你的结论.6.如图（1），已知点G在正方形ABCD的对角线AC上，GE⊥BC，垂足为点E，GF⊥CD，垂足为点F.（1）证明与推断：①求证：四边形CEGF是正方形；②推断：的值为：（2）探究与证明：将正方形CEGF绕点C顺时针方向旋转α角（0°＜α＜45°），如图（2）所示，试探究线段AG与BE之间的数量关系，并说明理由；（3）拓展与运用：正方形CEGF在旋转过程中，当B，E，F三点在一条直线上时，如图（3）所示，延长CG交AD于点H．若AG＝6，GH＝2，则BC＝．7.如图1，在△ABC中，AB＝AC＝2，∠BAC＝120°，点D、E分别是AC、BC的中点，连接DE.定理：在直角三角形中，如果一个锐角等于30°，那么它所对的直角边等于斜边的一半．探索发现：图1中，的值为；的值为．（2）拓展探完若将△CDE绕点C逆时针方向旋转一周，在旋转过程中的大小有无变化？请仅就图2的情形给出证明．（3）问题解决当△CDE旋转至A，D，E三点共线时，直接写出线段BE的长．8.已知△ABC是边长为4的等边三角形，边AB在射线OM上，且OA＝6，点D是射线OM上的动点，当点D不与点A重合时，将△ACD绕点C逆时针方向旋转60°得到△BCE，连接DE，设OD＝m．（1）问题发现如图1，△CDE的形状是三角形．（2）探究证明如图2，当6＜m＜10时，△BDE的周长是否存在最小值？若存在，求出△BDE周长的最小值；若不存在，请说明理由．（3）解决问题是否存在m的值，使△DEB是直角三角形？若存在，请直接写出m的值；若不存在，请说明理由．9.等腰直角三角形ABC和等腰直角三角形ADE中，∠BAC＝∠DAE＝90°，AB＝4，AE＝2，其中△ABC固定，△ADE绕点A作360°旋转，点F、M、N分别为线段BE、BC、CD 的中点，连接MN、NF．问题提出：（1）如图1，当AD在线段AC上时，则∠MNF的度数为，线段MN 和线段NF的数量关系为；深入讨论：（2）如图2，当AD不在线段AC上时，请求出∠MNF的度数及线段MN和线段NF的数量关系；拓展延伸：（3）如图3，△ADE持续旋转过程中，若CE与BD交点为P，则△BCP面积的最小值为．10．四边形是我们在学习和生活中常见的图形，而对角线互相垂直的四边形也比较常见，比如筝形、菱形、图1中的四边形ABCD等．它们给我们的学习和生活带来了很多的乐趣和美感．（1）如图2，在四边形ABCD中，AB＝AD，CB＝CD，则AC与BD的位置关系是，请说明理由．（2）试探究图1中四边形ABCD的两组对边AB，CD与BC，AD之间的数量关系，请写出证明过程．（3）问题解决：如图3，分别以Rt△ACB的直角边AC和斜边AB为边向外作正方形ACFG 和正方形ABDE，连接CE，BG，GE，已知AC＝4，AB＝5，求GE的长．11．问题发现：如图（1）在Rt△ABC和Rt△BDE中，∠A＝∠DEB＝30°，BC＝BE＝6，Rt△BDE绕点B逆时针旋转，H为CD的中点，当点C与点E重合时，BH与AE的位置关系为，BH与AE的数量关系为；问题证明：在Rt△BDE绕点B旋转的过程中，（1）中的结论是否仍然成立？若成立，请就图（2）的情形给出证明若不成立，请说明理由；拓展应用：在Rt△BDE绕点B旋转的过程中，当DE∥BC时，请直接写出BH2的长．12．如图1，菱形ABCD与菱形GECF的顶点C重合，点G在对角线AC上，且∠BCD＝∠ECF＝60°，（1）问题发现的值为；（2）探究与证明将菱形GECF绕点C按顺时针方向旋转α角（0°＜α＜60°），如图2所示，试探究线段AG与BE之间的数量关系，并说明理由；（3）拓展与运用：菱形GECF在旋转过程中，当点A，G，F三点在一条直线上时，如图3所示连接CG并延长，交AD于点H，若CE＝2，GH＝，则AH的长为．13．如图，在Rt△ABC中，∠ACB＝90°，＝，CD⊥AB于点D，点E是直线AC上一动点，连接DE，过点D作FD⊥ED，交直线BC于点F．（1）探究发现：如图1，若m＝n，点E在线段AC上，则＝；（2）数学思考：①如图2，若点E在线段AC上，则＝（用含m，n的代数式表示）；②当点E在直线AC上运动时，①中的结论是否仍然成立？请仅就图3的情形给出证明；（3）拓展应用：若AC＝，BC＝2，DF＝4，请直接写出CE的长．14．如图，已知点E是射线BC上的一点，以BC、CE为边作正方形ABCD和正方形CEFG，连接AF，取AF的中点M，连接DM、MG（1）如图1，判断线段DM和GM的数量关系是，位置关系是；（2）如图2，在图中的正方形CEFG绕点C逆时针旋转的过程中，其他条件不变，（1）中的结论是否成立？说明理由；（3）已知BC＝10，CE＝2，正方形CEFG绕点C旋转的过程中，当A、F、E共线时，直接写出△DMG的面积．15.在Rt△ABC中，∠ACB＝90°，AB＝，AC＝2，过点B作直线m∥AC，将△ABC绕点C顺时针旋转得到△A′B′C（点A，B的对应点分别为A'，B′），射线CA′，CB′分别交直线m于点P，Q．（1）如图1，当P与A′重合时，求∠ACA′的度数；（2）如图2，设A′B′与BC的交点为M，当M为A′B′的中点时，求线段PQ的长；（3）在旋转过程中，当点P，Q分别在CA′，CB′的延长线上时，试探究四边形P A'B′Q的面积是否存在最小值．若存在，求出四边形P A′B′Q的最小面积；若不存在，请说明理由．16.如图（1），在等边三角形ABC中，点D，E分别在边AB，AC上，AD＝AE，连接BE，CD，点M，N，P分别是BE，CD，BC的中点，连接DE，PM，PN，MN．（1）观察猜想，图（1）中△PMN是（填特殊三角形的名称）（2）探究证明，如图（2），△ADE绕点A按逆时针方向旋转，则△PMN的形状是否发生改变？并就图（2）说明理由．（3）拓展延伸，若△ADE绕点A在平面内自由旋转，AD＝2，AB＝6，请直接写出△PMN 的周长的最大值．17.已知△ABC，AB＝AC，D为直线BC上一点，E为直线AC上一点，AD＝AE，设∠BAD＝α，∠CDE＝β，（1）如图1，若点D在线段BC上，点E在线段AC上．∠ABC＝60°，∠ADE＝70°，则α＝°；β＝°.（2）如图2，若点D在线段BC上，点E在线段AC上，则α，β之间有什么关系式？说明理由．（3）是否存在不同于（2）中的α，β之间的关系式？若存在，请写出这个关系式（写出一种即可），说明理由；若不存在，请说明理由.18.问题提出：（1）如图1，在四边形ABCD中，连接AC、BD，AB＝AD，∠BAD＝∠BCD＝90°，将△ABC绕点A逆时针旋转90°，得到△ADE，点B的对应点落在点D，点C的对应点为点E，可知点C、D、E在一条直线上，则△ACE为三角形，BC、CD、AC的数量关系为；探究发现：（2）如图2，在⊙O中，AB为直径，点C为的中点，点D为圆上一个点，连接AD、CD、AC、BC、BD，且AD＜BD，请求出CD、AD、BD间的数量关系.拓展延伸：（3）如图3，在等腰直角三角形ABC中，点P为AB的中点，若AC＝13，平面内存在一点E，且AE＝10，CE＝13，当点Q为AE中点时，PQ＝.19.已知△ABC中，CA＝CB，0°＜∠ACB≤90°，点M、N分别在边CA，CB上（不与端点重合），BN＝AM，射线AG∥BC交BM延长线于点D，点E在直线AN上，EA＝ED．（1）【观察猜想】如图1，点E在射线NA上，当∠ACB＝45°时，①线段BM与AN的数量关系是；②∠BDE的度数是；（2）【探究证明】如图2点E在射线AN上，当∠ACB＝30°时，判断并证明线段BM与AN的数量关系，求∠BDE的度数；（3）【拓展延伸】如图3，点E在直线AN上，当∠ACB＝60°时，AB＝3，点N是BC 边上的三等分点，直线ED与直线BC交于点F，请直接写出线段CF的长．20.如图①，在正方形ABCD和正方形AB'C'D'中，AB＝2，AB'＝，连接CC’（1）问题发现：．（2）拓展探究：将正方形AB'C'D'绕点A逆时针旋转，记旋转角为θ，连接BB'，试判断：当0°≤θ＜360°时，的值有无变化？请仅就图②中的情形给出你的证明；（3）问题解决：请直接写出在旋转过程中，当C，C′，D'三点共线时BB′的长．21.如图1，在正方形ABCD中，点O是对角线BD的中点．（1）观察猜想将图1中的△BCD绕点O逆时针旋转至图2中△ECF的位置，连接AC，DE，则线段AC与DE的数量关系是，直线AC与DE的位置关系是．（2）类比探究将图2中的△ECF绕点O逆时针旋转至图3的位置，（1）中的结论是否成立？并说明理由．（3）拓展延伸将图2中的△ECF在平面内旋转，设直线AC与DE的交点为M，若AB＝4，请直接写出BM的最大值与最小值．22.如图1，点B在直线l上，过点B构建等腰直角三角形ABC，使∠BAC＝90°，且AB＝AC，过点C作CD⊥直线l于点D，连接AD．（1）小亮在研究这个图形时发现，∠BAC＝∠BDC＝90°，点A，D应该在以BC为直径的圆上，则∠ADB的度数为°，将射线AD顺时针旋转90°交直线l于点E，可求出线段AD，BD，CD的数量关系为；（2）小亮将等腰直角三角形ABC绕点B在平面内旋转，当旋转到图2位置时，线段AD，BD，CD的数量关系是否变化，请说明理由；（3）在旋转过程中，若CD长为1，当△ABD面积取得最大值时，请直接写AD的长．23．如图1，将三角板放在正方形ABCD上，使三角板的直角顶点E与正方形ABCD的顶点A重合，三角板的一边交CD于点F．另一边交CB的延长线于点G．（1）观察猜想：线段EF与线段EG的数量关系是；（2）探究证明：如图2，移动三角板，使顶点E始终在正方形ABCD的对角线AC上，其他条件不变，（1）中的结论是否仍然成立？若成立，请给予证明：若不成立．请说明理由：（3）拓展延伸：如图3，将（2）中的“正方形ABCD”改为“矩形ABCD”，且使三角板的一边经过点B，其他条件不变，若AB＝a、BC＝b，求的值．24．如图1，在Rt△ABC中，∠B＝90°，AB＝2，BC＝1，点D，E分别是边BC，AC的中点，连接DE．将△EDC绕点C按顺时针方向旋转，记旋转角为α．（1）问题发现①当α＝0°时，＝；②当α＝180°时，＝．（2）拓展探究试判断：当0°≤α＜360°时，的大小有无变化？请仅就图2的情况给出证明．（3）问题解决当△EDC旋转至A、B、E三点共线时，直接写出线段BD的长．25.在△ABC中，AD为BC边上的中线，E为AD上一动点，设DE＝nEA，连接CE并延长，交AB于点F．（1）尝试探究如图（1），当∠BAC＝90°，∠B＝30°，DE＝EA时，BF，BA之间的数量关系是；（2）类比延伸如图（2），当△ABC为锐角三角形，DE＝EA时，（1）中的结论是否仍然成立？若成立，请给予证明；若不成立，请说明理由；（3）拓展迁移如图（3），当△ABC为锐角三角形，DE＝nEA时，请直接写出BF，BA之间的数量关系．26.古希腊数学家毕达哥拉斯认为：“一切平面图形中最美的是圆”．请研究如下美丽的圆．如图，线段AB是⊙O的直径，延长AB至点C，使BC＝OB，点E是线段OB的中点，DE ⊥AB交⊙O于点D，点P是⊙O上一动点（不与点A，B重合），连接CD，PE，PC．（1）求证：CD是⊙O的切线；（2）小明在研究的过程中发现是一个确定的值．回答这个确定的值是多少？并对小明发现的结论加以证明．27．定义：三角形一个内角的平分线和与另一个内角相邻的外角平分线相交所成的锐角称为该三角形第三个内角的遥望角．（1）如图1，∠E是△ABC中∠A的遥望角，若∠A＝α，请用含α的代数式表示∠E．（2）如图2，四边形ABCD内接于⊙O，＝，四边形ABCD的外角平分线DF交⊙O 于点F，连结BF并延长交CD的延长线于点E．求证：∠BEC是△ABC中∠BAC的遥望角．（3）如图3，在（2）的条件下，连结AE，AF，若AC是⊙O的直径．①求∠AED的度数；②若AB＝8，CD＝5，求△DEF的面积．28.【性质探究】如图，在矩形ABCD中，对角线AC，BD相交于点O，AE平分∠BAC，交BC于点E．作DF⊥AE于点H，分别交AB，AC于点F，G．（1）判断△AFG的形状并说明理由．（2）求证：BF＝2OG．【迁移应用】（3）记△DGO的面积为S1，△DBF的面积为S2，当＝时，求的值．【拓展延伸】（4）若DF交射线AB于点F，【性质探究】中的其余条件不变，连结EF，当△BEF的面积为矩形ABCD面积的时，请直接写出tan∠BAE的值．29．如图，已知AC为正方形ABCD的对角线，点P是平面内不与点A，B重合的任意一点，连接AP，将线段AP绕点P顺时针旋转90°得到线段PE，连接AE，BP，CE．（1）求证：△APE∽△ABC；（2）当线段BP与CE相交时，设交点为M，求的值以及∠BMC的度数；（3）若正方形ABCD的边长为3，AP＝1，当点P，C，E在同一直线上时，求线段BP 的长．30．如图1和图2，在△ABC中，AB＝AC，BC＝8，tan C＝．点K在AC边上，点M，N 分别在AB，BC上，且AM＝CN＝2．点P从点M出发沿折线MB﹣BN匀速移动，到达点N时停止；而点Q在AC边上随P移动，且始终保持∠APQ＝∠B．（1）当点P在BC上时，求点P与点A的最短距离；（2）若点P在MB上，且PQ将△ABC的面积分成上下4：5两部分时，求MP的长；（3）设点P移动的路程为x，当0≤x≤3及3＜x≤9时，分别求点P到直线AC的距离（用含x的式子表示）；（4）在点P处设计并安装一扫描器，按定角∠APQ扫描△APQ区域（含边界），扫描器随点P从M到B再到N共用时36秒．若AK＝，请直接写出点K被扫描到的总时长．参考答案与试题解析一．解答题（共30小题）1．【解答】解：（1）如图①中，∵∠EAF＝∠BAC＝90°，∴∠BAF＝∠CAE，∵AF＝AE，AB＝AC，∴△BAF≌△CAE，∴∠ABF＝∠C，BF＝CE，∵AB＝AC，∠BAC＝90°，∴∠ABC＝∠C＝45°，∴∠FBE＝∠ABF+∠ABC＝90°，BC＝BE+EC＝BE+BF，故答案为：BF⊥BE，BC．（2）如图②中，作DH∥AC交BC于H．∵DH∥AC，∴∠BDH＝∠A＝90°，△DBH是等腰直角三角形，由（1）可知，BF⊥BE，BF+BE＝BH，∵AB＝AC＝3，AD＝1，∴BD＝DH＝2，∴BH＝2，∴BF+BE＝BH＝2；（3）如图③中，作DH∥AC交BC的延长线于H，作DM⊥BC于M．∵AC∥DH，∴∠ACB＝∠H，∠BDH＝∠BAC＝α，∵AB＝AC，∴∠ABC＝∠ACB∴∠DBH＝∠H，∴DB＝DH，∵∠EDF＝∠BDH＝α，∴∠BDF＝∠HDE，∵DF＝DE，DB＝DH，∴△BDF≌△HDE，∴BF＝EH，∴BF+BE＝EH+BE＝BH，∵DB＝DH，DM⊥BH，∴BM＝MH，∠BDM＝∠HDM，∴BM＝MH＝BD•sin．∴BF+BE＝BH＝2n•sin．2．【解答】解：（1）如图1中，∵△ABC∽△B'BA∽△C'AC，∴＝，＝，∴AB2＝BB′×BC，AC2＝CC′×BC，∴AB2+AC2＝BC（BB′+CC′）＝BC×BC＝BC2，故答案为BC2．（2）不成立．理由：如图2中当∠BAC为锐角时，BB′+CC′﹣B′C′＝BC，且△ABC∽△B'BA∽△C'AC，∴∴＝，＝，∴AB2＝BB′×BC，AC2＝CC′×BC，∴AB2+AC2＝BC（BB′+CC′）＝BC2+BC•B′C′．图3中∠BAC为钝角时，BB′+CC′+B′C′＝BC．AB2+AC2＝BC（BB′+CC′）＝BC2﹣BC•B′C′．（3）当AB＝5，AC＝6，BC＝9时，则AB2+AC2＜BC2，可知△ABC为钝角三角形，由图3可知：AB2+AC2＝BC2﹣BC•B′C′，∴52+62＝92﹣9B′C′，∴B′C′＝．3．【解答】解：（1）∵∠ACB＝∠DCE＝90°，∠CAB＝∠CDE＝45°，∴∠ABC＝∠CAB＝45°＝∠CDE＝∠CED，∴AC＝BC，CD＝CE，∵∠ACB＝∠DCE＝90°，∴∠ACD＝∠BCE，在△ACD和△BCE中，，∴△ACD≌△BCE（SAS），∴BE＝AD，∠CAB＝∠CBE＝45°，∴∠DBE＝∠ABC+∠CBE＝90°，＝1，故答案为：1，90°（2），∠DBE＝90°理由如下：∵∠ACB＝∠DCE＝90°，∠CAB＝∠CDE＝60°，∴∠ACD＝∠BCE，∠CED＝∠ABC＝30°∴tan∠ABC＝tan30°＝＝∵∠ACB＝∠DCE＝90°，∠CAB＝∠CDE＝60°，∴Rt△ACB∽Rt△DCE∴∴，且∠ACD＝∠BCE∴△ACD∽△BCE∴＝，∠CBE＝∠CAD＝60°∴∠DBE＝∠ABC+∠CBE＝90°（3）若点D在线段AB上，如图，由（2）知：＝，∠ABE＝90°∴BE＝AD∵AC＝2，∠ACB＝90°，∠CAB＝90°∴AB＝4，BC＝2∵∠ECD＝∠ABE＝90°，且点M是DE中点，∴CM＝BM＝DE，∵△CBM是直角三角形∴CM2+BM2＝BC2＝（2）2，∴BM＝CM＝∴DE＝2∵DB2+BE2＝DE2，∴（4﹣AD）2+（AD）2＝24∴AD＝+1∴BE＝AD＝3+若点D在线段BA延长线上，如图同理可得：DE＝2，BE＝AD∵BD2+BE2＝DE2，∴（4+AD）2+（AD）2＝24，∴AD＝﹣1∴BE＝AD＝3﹣综上所述：BE的长为3+或3﹣4．【解答】解：（1）∵△ABC中，∠BAC＝90°，AB＝AC，点D是BC的中点，∴AD＝BD＝DC，∠BDA＝90°，∵四边形DFGE是正方形，∴DE＝DF，∠EDF＝90°，∴∠BDE＝∠ADF＝90°，在△BDE和△ADF中，，∴△BDE≌△ADF（SAS），∴BE＝AF故答案为：BE＝AF；（2）成立；理由如下：当正方形DFGE在BC的上方时，如图②所示，连接AD，∵在Rt△ABC中，AB＝AC，D为斜边BC的中点，∴AD＝BD，AD⊥BC，∴∠ADE+∠EDB＝90°，∵四边形DFGE为正方形，∴DE＝DF，且∠EDF＝90°，∴∠ADE+∠ADF＝90°，∴∠BDE＝∠ADF，在△BDE和△ADF中，，∴△BDE≌△ADF（SAS），∴BE＝AF；当正方形DFGE在BC的下方时，连接AD，如图③所示：∵∠BDE＝∠BDF+90°，∠ADF＝∠BDF+90°，∴∠BDE＝∠ADF，在△BDE和△ADF中，，∴△BDE≌△ADF（SAS），∴BE＝AF；综上所述，（1）中的结论BE＝AF成立；（3）在△ADE中，∵AE＜AD+DE，∴当点A、D、E共线时，AE取得最大值，最大值为AD+DE．如图④所示：则AD＝BC＝1，DE＝DF＝2，∴AE＝AD+DE＝3，即AE的最大值为3．5．【解答】解：（1）如图1，过点O作OM⊥AB于M，ON⊥AD于N，∴∠OME＝∠ONF＝90°，∴∠BAD+∠MON＝180°，∵∠BAD+∠EOF＝180°，∴∠MON＝∠EOF，∴∠EOM＝∠FON，∵O是正方形ABCD的对角线的交点，∴∠BAO＝∠DAO，∵OM⊥AB，ON⊥AD，∴OM＝ON，∴△OME≌△ONF（AAS）∴OE＝OF；（2）（1）的结论成立；理由：如图2，过点O作OM⊥AB于M，ON⊥AD于N，∴∠OME＝∠ONF＝90°，∴∠BAD+∠MON＝180°，∵∠BAD+∠EOF＝180°，∴∠MON＝∠EOF，∴∠EOM＝∠FON，∵O是菱形ABCD的对角线的交点，∴∠BAO＝∠DAO，∵OM⊥AB，ON⊥AD，∴OM＝ON，∴△OME≌△ONF（AAS）∴OE＝OF；（3）如图3，过点O作OG⊥AB于G，OH⊥AD于H，∴∠OGE＝∠OHF＝90°，∴∠BAD+∠GOH＝180°，∵∠BAD+∠EOF＝180°，∴∠GOH＝∠EOF，∴△EOG∽△FOH，∴，∵O是▱ABCD的对角线的交点，∴S△AOB＝S△AOD，∵S△AOB＝AB•OG，S△AOD＝AD•OH，∴AB•OG＝AD•OH，∴＝，∴．6．【解答】解：（1）①∵四边形ABCD是正方形，∴∠BCD＝90°，∠BCA＝45°，∵GE⊥BC、GF⊥CD，∴∠CEG＝∠CFG＝∠ECF＝90°，∴四边形CEGF是矩形，∠CGE＝∠ECG＝45°，∴EG＝EC，∴四边形CEGF是正方形；②由①知四边形CEGF是正方形，∴∠CEG＝∠B＝90°，∠ECG＝45°，∴＝，GE∥AB，∴＝＝，故答案为：；（2）连接CG，由旋转性质知∠BCE＝∠ACG＝α，在Rt△CEG和Rt△CBA中，＝cos45°＝、＝cos45°＝，∴＝＝，∴△ACG∽△BCE，∴＝＝，∴线段AG与BE之间的数量关系为AG＝BE；（3）∵∠CEF＝45°，点B、E、F三点共线，∴∠BEC＝135°，∵△ACG∽△BCE，∴∠AGC＝∠BEC＝135°，∴∠AGH＝∠CAH＝45°，∵∠CHA＝∠AHG，∴△AHG∽△CHA，∴＝＝，设BC＝CD＝AD＝a，则AC＝a，则由＝得＝，∴AH＝a，则DH＝AD﹣AH＝a，CH＝＝a，∴＝得＝，解得：a＝3，即BC＝3，故答案为：3．7．【解答】解：（1）如图1，连接AE，∵AB＝AC＝2，点E分别是BC的中点，∴AE⊥BC，∴∠BEC＝90°，∵AB＝AC＝2，∠BAC＝120°，∴∠B＝∠C＝30°，在Rt△ABE中，AE＝AB＝1，根据勾股定理得，BE＝∵点E是BC的中点，∴BC＝2BE＝2，∴＝＝，∵点D是AC的中点，∴AD＝CD＝AC＝1，∴＝＝，故答案为：，；（2）无变化，理由：由（1）知，CD＝1，CE＝BE＝，∴＝，，∴＝，由（1）知，∠ACB＝∠DCE＝30°，∴∠ACD＝∠BCE，∴△ACD∽△BCE，∴，（3）当点D在线段AE上时，如图2，过点C作CF⊥AE于F，∠CDF＝180°﹣∠CDE＝60°，∴∠DCF＝30°，∴DF＝CD＝，∴CF＝DF＝，在Rt△AFC中，AC＝2，根据勾股定理得，AF＝＝，∴AD＝AF+DF＝，由（2）知，，∴BE＝AD＝当点D在线段AE的延长线上时，如图3，过点C作CG⊥AD交AD的延长线于G，∵∠CDG＝60°，∴∠DCG＝30°，∴DG＝CD＝，∴CG＝DG＝，在Rt△ACG中，根据勾股定理得，AG＝，∴AD＝AG﹣DG＝，由（2）知，，∴BE＝AD＝即：线段BE的长为或．8．【解答】解：（1）证明：∵将△ACD绕点C逆时针方向旋转60°得到△BCE，∴∠DCE＝60°，DC＝EC，∴△CDE是等边三角形；故答案为：等边；（2）存在，当6＜t＜10时，由旋转的性质得，BE＝AD，∴C△DBE＝BE+DB+DE＝AB+DE＝4+DE，由（1）知，△CDE是等边三角形，∴DE＝CD，∴C△DBE＝CD+4，由垂线段最短可知，当CD⊥AB时，△BDE的周长最小，此时，CD＝2，∴△BDE的最小周长＝CD+4＝2+4；（3）存在，①∵当点D与点B重合时，D，B，E不能构成三角形，∴当点D与点B重合时，不符合题意，②当0≤m＜6时，由旋转可知，∠ABE＝60°，∠BDE＜60°，∴∠BED＝90°，由（1）可知，△CDE是等边三角形，∴∠DEB＝60°，∴∠CEB＝30°，∵∠CEB＝∠CDA，∴∠CDA＝30°，∵∠CAB＝60°，∴∠ACD＝∠ADC＝30°，∴DA＝CA＝4，∴OD＝OA﹣DA＝6﹣4＝2，∴m＝2；③当6＜m＜10时，由∠DBE＝120°＞90°，∴此时不存在；④当m＞10时，由旋转的性质可知，∠DBE＝60°，又由（1）知∠CDE＝60°，∴∠BDE＝∠CDE+∠BDC＝60°+∠BDC，而∠BDC＞0°，∴∠BDE＞60°，∴只能∠BDE＝90°，从而∠BCD＝30°，∴BD＝BC＝4，∴OD＝14，∴m＝14，综上所述：当m＝2或14时，以D、E、B为顶点的三角形是直角三角形．9．【解答】解：（1）如图1中，连接DB，MF，CE，延长BD交EC于H．∵AC＝AB，AE＝AD，∠BAD＝∠CAE＝90°，∴△BAD≌△CAE（SAS），∴BD＝EC，∠ACE＝∠ABD，∵∠ABD+∠ADB＝90°，∠ADB＝∠CDH，∴∠ADH+∠DCH＝90°，∴∠CHD＝90°，∴EC⊥BH，∵BM＝MC，BF＝FE，∴MF∥EC，MF＝EC，∵CM＝MB，CN＝ND，∴MN∥BD，MN＝BD，∴MN＝MF，MN⊥MF，∴∠NMF＝90°，∴∠MNF＝45°，NF＝MN．故答案为：45°（2）：如图2中，连接MF，EC，BD．设EC交AB于O，BD交EC于H．∵AC＝AB，AE＝AD，∠BAD＝∠CAE＝90°，∴∠BAD＝∠CAE，∴△BAD≌△CAE（SAS），∴BD＝EC，∠ACE＝∠ABD，∵∠AOC+∠ACO＝90°，∠AOC＝∠BOH，∴∠OBH+∠BOH＝90°，∴∠BHO＝90°，∴EC⊥BD，∵BM＝MC，BF＝FE，∴MF∥EC，MF＝EC，∵CM＝MB，CN＝ND，∴MN∥BD，MN＝BD，∴MN＝MF，MN⊥MF，∴∠NMF＝90°，∴∠MNF＝45°，NF＝MN．（3）：如图3中，如图以A为圆心AD为半径作⊙A．当直线PB与⊙A相切时，此时∠CBP的值最小，点P到BC的距离最小，即△BCP的面积最小，∵AD＝AE，AB＝AC，∠BAC＝∠DAE＝90°，∴∠BAD＝∠CAE，∴△BAD≌△CAE（SAS），∴∠ACE＝∠ABD，BD＝EC，∵∠ABD+∠AOB＝90°，∠AOB＝∠CPO，∴∠CPB＝90°，∵PB是⊙A的切线，∴∠ADP＝90°，∵∠DPE＝∠ADP＝∠DAE＝90°，∴四边形ADPE是矩形，∵AE＝AD，∴四边形ADPE是正方形，∴AD＝AE＝PD＝PE＝2，BD＝EC＝＝2，∴PC＝2﹣2，PB＝2+2，∴S△BCP的最小值＝×PC×PB＝（2﹣2）（2+2）＝4．10．【解答】（1）解：AC⊥BD，理由如下：连接AC、BD，如图2所示：∵AB＝AD，∴点A在线段BD的垂直平分线上，∵CB＝CD，∴点C在线段BD的垂直平分线上，∴直线AC是线段BD的垂直平分线，∴AC⊥BD，故答案为：AC⊥BD；（2）解：AD2+BC2＝AB2+CD2；理由如下：如图1，已知四边形ABCD中，AC⊥BD，设BD、AC相交于E，∵AC⊥BD，∴∠AED＝∠AEB＝∠BEC＝∠CED＝90°，由勾股定理得，AD2+BC2＝AE2+DE2+BE2+CE2，AB2+CD2＝AE2+BE2+CE2+DE2，∴AD2+BC2＝AB2+CD2；（3）解：如图3，连接CG、BE，∵四边形ACFG和四边形ABDE是正方形，∴AC＝AG，AB＝AE，∠CAG＝∠BAE＝90°，∴∠CAG+∠BAC＝∠BAE+∠BAC，即∠GAB＝∠CAE，在△GAB和△CAE中，，∴△GAB≌△CAE（SAS），∴∠ABG＝∠AEC，又∠AEC+∠AME＝90°，∴∠ABG+∠AME＝90°，即CE⊥BG，由（2）得，CG2+BE2＝CB2+GE2，在Rt△ABC中，AC＝4，AB＝5，根据勾股定理得，BC2＝52﹣42＝9，∵CG和BE分别是正方形ACFG和正方形ABDG的对角线，∴CG2＝42+42＝32，BE2＝52+52＝50，∴GE2＝CG2+BE2﹣CB2＝32+50﹣9＝73，∴GE＝．11．【解答】解：问题发现：如图1中，结论：AE＝2BH，AE⊥BH．理由：在Rt△ABC中，∵BC＝6，∠A＝30°，∴AE＝2BC＝12，在Rt△CDB中，∵∠DCB＝30°，∴CD＝＝4，∵CH＝DH，∴BH＝CD＝2，∴＝＝2，∴AE＝2BH．故答案为AE⊥BH，AE＝2BH．问题证明：如图2中，（1）中结论成立．理由：延长BH到F使得HF＝BH，连接CF．设AE交BF于O．∵CH＝DH，BH＝HF，∠CHF＝∠BHD，∴△CHF≌△DHB（SAS），∴BD＝CF，∠F＝∠DBH，∴CF∥BD，∵AB＝BC，BE＝BD，∴BE＝CF，∴＝＝，∵CF∥BD，∴∠BCF+∠CBD＝180°，∵∠ABC+∠DBE＝∠ABD+∠CBD+∠CBD+∠CBE＝∠CBD+∠ABE＝180°，∴∠BCF＝∠ABE，∴△ABE∽△BCF，∴∠CBF＝∠BAE，＝＝，∴AE＝BF＝2BH，∵∠CBF+∠ABF＝90°，∴∠ABF+∠BAE＝90°，∴∠AOB＝90°，∴BH⊥AE．拓展应用：如图3﹣1中，当DE在BC的下方时，延长AB交DE于F．∵DE∥BC∴∠ABC＝∠BFD＝90°，由题意BC＝BE＝6，AB＝6，BD＝2，DE＝4，∵•BD•BE＝•DE•BF，∴BF＝＝3，∴EF＝BF＝3，∴AF＝6+3，∴AE2＝AF2+EF2＝（6+3）2+（3）2＝144+36．∵AE＝2BH，∴AE2＝12BH2，∴BH2＝12+3如图3﹣2中，当DE在BC的上方时，同法可得AF＝6﹣3，EF＝3，∴BH2＝＝（＝12﹣3．12．【解答】解：（1）如图1中，作EH⊥CG于H．∵四边形ECFG是菱形，∠ECF＝60°，∴∠ECH＝∠ECF＝30°，EC＝EG，∵EH⊥CG，∴GH＝CG，∴＝cos30°＝，∴＝2•＝，∵EG∥CD，AB∥CD，∴GE∥AB，∴＝＝．故答案为．（2）结论：AG＝BE．理由：如图2中，连接CG．∵四边形ABCD，四边形ECFG都是菱形，∠ECF＝∠DCB＝60°，∴∠ECG＝∠EGC＝∠BCA＝∠BAC＝30°，∴△ECG∽△BCE，∴＝，∵∠ECB＝∠GCA，∴△ECB∽△GCA，∴＝＝，∴AG＝BE．（3）如图3中，∵∠AGH＝∠CGF＝30°．∠AGH＝∠GAC+∠GCA，又∵∠DAC＝∠HAG+∠GAC＝30°，∴∠HAG＝∠ACH，∵∠AHG＝∠AHC，∴△HAG∽△HCA，∴HA：HC＝GH：HA，∴AH2＝HG•HC，∴FC＝2，CG＝CF，∴GC＝2，∵HG＝，∴AH2＝HG•HC＝•3＝9，∵AH＞0，∴AH＝3．故答案为3．13．【解答】解：（1）当m＝n时，即：BC＝AC，∵∠ACB＝90°，∴∠A+∠ABC＝90°，∵CD⊥AB，∴∠DCB+∠ABC＝90°，∴∠A＝∠DCB，∵∠FDE＝∠ADC＝90°，∴∠FDE﹣∠CDE＝∠ADC﹣∠CDE，即∠ADE＝∠CDF，∴△ADE∽△CDF，∴，∵∠A＝∠DCB，∠ADC＝∠BDC＝90°，∴△ADC∽△CDB，∴＝1，∴＝1（2）①∵∠ACB＝90°，∴∠A+∠ABC＝90°，∵CD⊥AB，∴∠DCB+∠ABC＝90°，∴∠A＝∠DCB，∵∠FDE＝∠ADC＝90°，∴∠FDE﹣∠CDE＝∠ADC﹣∠CDE，即∠ADE＝∠CDF，∴△ADE∽△CDF，∴，∵∠A＝∠DCB，∠ADC＝∠BDC＝90°，∴△ADC∽△CDB，∴，∴②成立．如图，∵∠ACB＝90°，∴∠A+∠ABC＝90°，又∵CD⊥AB，∴∠DCB+∠ABC＝90°，∴∠A＝∠DCB，∵∠FDE＝∠ADC＝90°，∴∠FDE+∠CDE＝∠ADC+∠CDE，即∠ADE＝∠CDF，∴△ADE∽△CDF，∴，∵∠A＝∠DCB，∠ADC＝∠BDC＝90°，∴△ADC∽△CDB，∴，∴．（3）由（2）有，△ADE∽△CDF，∵＝，∴＝，∴CF＝2AE，在Rt△DEF中，DE＝2，DF＝4，∴EF＝2，①当E在线段AC上时，在Rt△CEF中，CF＝2AE＝2（AC﹣CE）＝2（﹣CE），EF＝2，根据勾股定理得，CE2+CF2＝EF2，∴CE2+[2（﹣CE）]2＝40∴CE＝2，或CE＝﹣（舍）而AC＝＜CE，∴此种情况不存在，②当E在AC延长线上时，在Rt△CEF中，CF＝2AE＝2（AC+CE）＝2（+CE），EF＝2，根据勾股定理得，CE2+CF2＝EF2，∴CE2+[2（+CE）]2＝40，∴CE＝，或CE＝﹣2（舍），③如图1，当点E在CA延长线上时，CF＝2AE＝2（CE﹣AC）＝2（CE﹣），EF＝2，根据勾股定理得，CE2+CF2＝EF2，∴CE2+[2（CE﹣）]2＝40，∴CE＝2，或CE＝﹣（舍）即：CE＝2或CE＝．14．【解答】解：（1）如图1，延长GM交AD于H，∵AD∥GF，∴∠GFM＝∠HAM，在△FMG和△AMH中，，∴△FMG≌△AMH（ASA），∴HM＝GM，AH＝FG，∵AD＝CD，AH＝FG＝CG，∴DH＝DG，∵∠HDG＝90°，HM＝GM，∴DM＝MG，DM⊥MG，故答案为DM＝MG，DM⊥MG．（2）结论成立：DM＝MG，DM⊥MG，理由：如图2中，延长GM使得MH＝GM，连接AH、DH、DG，延长AD交GF的延长线于N，交CD于O．∵AM＝MF，∠AMH＝∠FMG，MH＝MG，∴△AMH≌△FMG（SAS），∴AH＝GF＝CG，∠AHM＝∠FGM，∴AH∥GN，∴∠HAD＝∠N，∵∠ODN＝∠OGC＝90°，∠DON＝∠GOC，∴∠N＝∠OCG，∴∠HAD＝∠DCG，∵AH＝CG，AD＝CD，∴△HAD≌△GCD（SAS），∴DH＝DG，∠HDA＝∠CDG，∴∠HDG＝∠ADC＝90°，∴△HDG是等腰直角三角形，∵MH＝MG，∴DM⊥GH，DM＝MH＝MG，（3）①如图3﹣1中，连接AC．在Rt△ABC中，AC＝＝10，在Rt△ACE中，AE＝＝14，∴AF＝AE＝EF＝14﹣2＝12，∴FM＝AM＝AF＝6，在Rt△MGF中，MG＝＝2，∴S△DMG＝×2×2＝20，②如图3﹣2中，连接AC．同法可得AE＝14，AF＝16，FM＝8，MG＝＝2，∴S△DMG＝×2×2＝34，综上所述，满足条件的△DMG的面积为20或34．15．【解答】解：（1）由旋转可得：AC＝A'C＝2，∵∠ACB＝90°，AB＝，AC＝2，∴BC＝，∵∠ACB＝90°，m∥AC，∴∠A'BC＝90°，∴cos∠A'CB＝＝，∴∠A'CB＝30°，∴∠ACA'＝60°；（2）∵M为A'B'的中点，∴∠A'CM＝∠MA'C，由旋转可得，∠MA'C＝∠A，∴∠A＝∠A'CM，∴tan∠PCB＝tan∠A＝，∴PB＝BC＝，∵∠PCQ＝∠PBC＝90°，∴∠BQC+∠BPC＝∠BCP+∠BPC＝90°，∴∠BQC＝∠BCP＝∠A，∴tan∠BQC＝tan∠A＝，∴BQ＝BC×＝2，∴PQ＝PB+BQ＝；（3）∵S四边形P A'B′Q＝S△PCQ﹣S△A'CB'＝S△PCQ﹣，∴S四边形P A'B′Q最小，即S△PCQ最小，∴S△PCQ＝PQ×BC＝PQ，法一：（几何法）取PQ的中点G，∵∠PCQ＝90°，∴CG＝PQ，即PQ＝2CG，当CG最小时，PQ最小，∴CG⊥PQ，即CG与CB重合时，CG最小，∴CG min＝，PQ min＝2，∴S△PCQ的最小值＝3，S四边形P A'B′Q＝3﹣；法二（代数法）设PB＝x，BQ＝y，由射影定理得：xy＝3，∴当PQ最小时，x+y最小，∴（x+y）2＝x2+2xy+y2＝x2+6+y2≥2xy+6＝12，当x＝y＝时，“＝”成立，∴PQ＝+＝2，∴S△PCQ的最小值＝3，S四边形P A'B′Q＝3﹣．16．【解答】解：（1）结论：△PMN是等边三角形．理由：如图1中，∵△ABC是等边三角形，∴AB＝AC，∠ABC＝∠ACB＝60°，∵AD＝AE，∴BD＝EC，∵PB＝PC，CN＝ND，BM＝EM，∴PN∥BD，PM∥EC，PN＝BD，PM＝EC，∴PM＝PN，∠NPC＝∠ABC＝60°，∠MPB＝∠ACB＝60°，∴∠MPN＝60°，∴△PMN是等边三角形，故答案为等边三角形．（2）△PMN的形状不发生改变，仍为等边三角形，理由如下：如图2中，连接BD，CE．由旋转可得∠BAD＝∠CAE，∵△ABC是等边三角形，∴AB＝AC，∠ACB＝∠ABC＝60°又∵AD＝AE，∴△ABD≌△ACE（SAS），∴BD＝CE，∠ABD＝∠ACE，∵M是BE的中点，P是BC的中点，∴PM是△BCE的中位线，∴PM＝，且PM∥CE．同理可证PN＝BD且PN∥BD，∴PM＝PN，∠MPB＝∠ECB，∠NPC＝∠DBC，∴∠MPB+∠NPC＝∠ECB+∠DBC＝（∠ACB+∠ACE）+（∠ABC﹣∠ABD）＝∠ACB+∠ABC＝120°，∴∠MPN＝60°，∴△PMN是等边三角形．（3）∵PM＝EC，∴当EC最大时，等边△PMN的周长最大，∵EC≤AE+AC，∴EC≤8，∴PM≤4，∴PM的最大值为4，∴△PMN的周长的最大值为12．17．【解答】解：（1）∵AB＝AC，∠ABC＝60°，∴∠BAC＝60°，∵AD＝AE，∠ADE＝70°，∴∠DAE＝180°﹣2∠ADE＝40°，∴α＝∠BAD＝60°﹣40°＝20°，∴∠ADC＝∠BAD+∠ABD＝60°+20°＝80°，∴β＝∠CDE＝∠ADC﹣∠ADE＝10°，故答案为：20，10；（2）设∠ABC＝x，∠AED＝y，∴∠ACB＝x，∠AED＝y，在△DEC中，y＝β+x，在△ABD中，α+x＝y+β＝β+x+β，∴α＝2β；（3）①当点E在CA的延长线上，点D在线段BC上，如图1设∠ABC＝x，∠ADE＝y，∴∠ACB＝x，∠ACE＝y，在△ABD中，x+α＝β﹣y，在△DEC中，x+y+β＝180°，∴α＝2β﹣180°，②当点E在CA的延长线上，点D在CB的延长线上，如图2，同①的方法可得α＝180°﹣2β．18．【解答】解：（1）由旋转变换的性质可知，∠CAE＝90°，AC＝AE，∴△ACE为等腰直角三角形，∴CE＝AC，∵CE＝CD+DE＝CD+BC，∴BC+CD＝AC，故答案为：等腰直角；BC+CD＝AC；（2）延长CO交⊙O于E，连接AE、BE、DE，则∠CDE＝90°，∵点C为的中点，∴点E为的中点，∴EA＝EB，∵AB为⊙O的直径，∴∠ADB＝90°，由（1）得，DE＝（AD+BD），由勾股定理得，CD2＝CE2﹣DE2＝AD2+BD2﹣（AD+BD）2＝（AD﹣BD）2，∴CD＝（BD﹣AD）；（3）如图3，当点E在直线AC的左侧时，连接CQ、PC，∵CA＝CB，点P为AB的中点，∴CP⊥AB，∵CA＝CE，点Q为AE中点，∴CQ⊥AE，AQ＝QE＝AE＝5，∴由勾股定理得，CQ＝＝12，由（1）得，AQ+CQ＝PQ，。

中考数学几何综合题 练习(附答案)

中考数学几何综合题 练习(附答案)

几何专题综合训练1如图，四边形ABCD 是正方形，△ECF 是等腰直角三角形，其中CE=CF ，G 是CD 与EF 的交点．（1）求证：△BCF ≌△DCE ．（2）若BC=5，CF=3，∠BFC=900，求DG ：GC 的值．2正方形ABCD 边长为4，M 、N 分别是BC 、CD 上的两个动点，当M 点在BC 上运动时，保持AM 和MN 垂直，（1）证明：Rt Rt ABM MCN △∽△；（2）设BM x ，梯形ABCN 的面积为y ，求y 与x 之间的函数关系式；当M 点运动到什么位置时，四边形ABCN 面积最大，并求出最大面积； （3）当M 点运动到什么位置时Rt Rt ABM AMN △∽△，求x 的值．NDA CBM第2题图3在图3-1至图3-3中，点B是线段AC的中点，点D是线段CE的中点．四边形BCGF和CDHN都是正方形．AE的中点是M．（1）如图3-1，点E在AC的延长线上，点N与点G重合时，点M与点C重合，求证：FM = MH，FM⊥MH；（2）将图3-1中的CE绕点C顺时针旋转一个锐角，得到图3-2，求证：△FMH是等腰直角三角形；（3）将图3-2中的CE缩短到图3-3的情况，△FMH还是等腰直角三角形吗？（不必说明理由）图3-1AHC(M) D E BF G(N)G图3-2AHCDEBF NMAHCDE图3-3BF GMN4如图（1），已知正方形ABCD 在直线MN 的上方，BC 在直线MN 上，E 是BC 上一点，以AE 为边在直线MN 的上方作正方形AEFG ． （1）连接GD ，求证：△ADG ≌△ABE ；(4分) （2）连接FC ，观察并猜测∠FCN 的度数，并说明理由；(4分)（3）如图（2），将图（1）中正方形ABCD 改为矩形ABCD ，AB =a ，BC =b （a 、b 为常数），E 是线段BC 上一动点（不含端点B 、C ），以AE 为边在直线MN 的上方作矩形AEFG ，使顶点G 恰好落在射线CD 上．判断当点E 由B 向C 运动时，∠FCN 的大小是否总保持不变，若∠FCN 的大小不变，请用含a 、b 的代数式表示tan ∠FCN 的值；若∠FCN 的大小发生改变，请举例说明N M B E A C D F G图（1）图（2） M B E A C D F G N5如图2－5－7，矩形ABCD中，AB＝8，BC＝6，对角线AC上有一个动点P（不包括点A和点C）．设AP＝x，四边形PBCD的面积为y．（1）写出y与x的函数关系，并确定自变量x的范围．（2）有人提出一个判断：“关于动点P，⊿PBC面积与⊿PAD面积之和为常数”．请你说明此判断是否正确，并说明理由．．答案1. 分析与解答 （1）∵四边形 ABCD 是正方形，∴∠BCF+∠FCD=900，BC=CD ．∵△ECF 是等腰直角三角形，CF=CE ．∴∠ECD+∠FCD=900．∴∠BCF=∠ECD ．∴△BCF ≌△DCE（2）在△BFC 中，BC=5，CF=3，∠BFC=900． ∴4==．∵△BCF ≌△DCE ，∴DE=BF=4，∠BFC=∠DEC=∠FCE=900． ∴DE ∥FC ．∴△DGE ∽△CGF ．∴DG ：GC=DE ：CF=4：3．2. ．解：（1）在正方形ABCD 中，490AB BC CD B C ===∠=∠=，°， AM MN ⊥ ，90AMN ∴∠=°，90CMN AMB ∴∠+∠=°．在Rt ABM △中，90MAB AMB ∠+∠=°， CMN MAB ∴∠=∠，Rt Rt ABM MCN ∴△∽△． ······················································· 2分 （2）Rt Rt ABM MCN △∽△，44AB BM xMC CN x CN∴=∴=-，， 244x x CN -+∴=， ···················································································································· 4分22214114428(2)102422ABCNx x y S x x x ⎛⎫-+∴==+=-++=--+ ⎪⎝⎭梯形， 当2x =时，y 取最大值，最大值为10． ··················································································· 6分 （3）90B AMN ∠=∠= °，∴要使ABM AMN △∽△，必须有AM ABMN BM=， ································································ 7分 由（1）知AM ABMN MC=， BM MC ∴=，∴当点M 运动到BC 的中点时，ABM AMN △∽△，此时2x =． ···································· 9分3（1）证明：∵四边形BCGF 和CDHN 都是正方形，又∵点N 与点G 重合，点M 与点C 重合，∴FB = BM = MG = MD = DH ，∠FBM =∠MDH = 90°． ∴△FBM ≌ △MDH ． ∴FM = MH ．NDA CBM答案第2题图∵∠FMB =∠DMH = 45°，∴∠FMH = 90°．∴FM ⊥HM ．（2）证明：连接MB 、MD ，如图2，设FM 与AC 交于点P ． ∵B 、D 、M 分别是AC 、CE 、AE 的中点， ∴MD ∥BC ，且MD = BC = BF ；MB ∥CD ， 且MB =CD =DH ．∴四边形BCDM 是平行四边形． ∴ ∠CBM =∠CDM ．又∵∠FBP =∠HDC ，∴∠FBM =∠MDH ． ∴△FBM ≌ △MDH ． ∴FM = MH ， 且∠MFB =∠HMD ．∴∠FMH =∠FMD －∠HMD =∠APM －∠MFB =∠FBP = 90°． ∴△FMH 是等腰直角三角形．（3）是．。

中考数学几何图形专题训练50题-含答案

中考数学几何图形专题训练50题-含答案

中考数学几何图形专题训练50题含答案(单选、填空、解答题)一、单选题1．如图，是某个几何体的展开图，该几何体是（ ）A ．三棱柱B ．三棱锥C ．球D ．圆锥 2．如图，把一块三角板ABC 的直角顶点B 放在直线EF 上，30C ∠=︒，AC ∥EF ，则1∠=（ ）A ．30°B ．45°C ．60°D ．75°3．如图是每个面上都标有一个汉字的正方体的表面展开图，在此正方体上与“爱”字相对的面上的汉字是（ ）A ．保B ．定C ．古D ．城 4．如图，已知AC BC ⊥，190A ∠+∠=︒，则2∠与A ∠的关系是（ ）A．2∠大C．相等D．无法确定∠大B．A5．若一个锐角的余角比这个角大30°，则这个锐角的度数是（）A．30︒B．150︒C．60︒D．155︒6．图中的立方体展开后，应是下图中的（）A．B．C．D．7．如图，直线与相交于点，，则与（）A．是对顶角B．相等C．互余D．互补8．如图由四个相同的小立方体组成的立体图像，它的主视图是（）．A ．B ．C ．D ． 9．如图，钟表上10点整时，时针与分针所成的角是（ ）A ．30︒B ．60︒C ．90︒D ．120︒ 10．如图，将直角三角形绕其一条直角边所在直线l 旋转一周，得到的几何体是（ ）A ．B ．C ．D ． 11．如图，在长方形ABCD 中，点E ，点F 分别为BC 和AB 上任意一点，点B 和点M 关于EF 对称，EN 是MEC ∠的平分线，若60BFE ∠=︒，则MEN ∠的度数是( )A ．30︒B ．60︒C ．45︒D ．50︒12．如图是正方形纸盒展开图，那么在原正方体中，与“沉”字所在面相对面的汉字是（）A．冷B．静C．应D．考13．如图是一块带有圆形空洞和矩形空洞的小木板，则下列物体中最有可能既可以堵住圆形空洞，又可以堵住矩形空洞的是（）A．正方体B．球C．圆锥D．圆柱体14．如图，用平面去截一个正方体，所得截面的形状应是（）A．A B．B C．C D．D15．如图，点O在直线AB上，∠COE=90°，OD平分∠AOE，∠COD=25°，则∠BOD=（）A．110°B．115°C．120°D．135°16．下列说法正确的是（）A．射线PA和射线AP是同一条射线B．射线OA的长度是3cmC．直线,AB CD相交于点P D．两点确定一条直线17．如图，一个底面直径为30cm，高为20cm的糖罐子，一只蚂蚁从A处沿着糖罐的表面爬行到B处，则蚂蚁爬行的最短距离是（）A ．24cmB ．C ．25cmD ．30cm 18．如图，等边ABC 的边长为1，过点B 的直线l AB ⊥，且ABC 与A BC ''△关于直线l 对称，D 为线段BC '上的一个动点，则AD CD +的最小值为（ ）A ．1B ．2C ．3D ．419．如图，在ABC 中，90C ∠=︒，30B ∠=︒，如图：（1）以A 为圆心，任意长为半径画弧分别交AB 、AC 于点M 和N ；（2）分别以M 、N 为圆心，大于MN 的长为半径画弧，两弧交于点P ；（3）连结AP 并延长交BC 于点D ．根据以上作图过程，下列结论中错误的是（ ）A ．AD 是BAC ∠的平分线B ．60ADC ∠=︒ C ．点D 在AB 的中垂线上 D ．:1:3DAC ABD S S =△△20．如图，在Rt 直角△ABC 中，45B ∠=︒，AB =AC ，点D 为BC 中点，直角MDN ∠绕点D 旋转，DM ，DN 分别与边AB ，AC 交于E ，F 两点，下列结论：△△DEF 是等腰直角三角形；△ AE =CF ；△△BDE △△ADF ；△ BE +CF =EF ，其中正确结论是（ ）A ．△△△B ．△△△C ．△△△D ．△△△△二、填空题21．在_______内填上适当的分数：135等于________平角．22．如图，AB △CD ，CB 平分△ABD ，若△ABC ＝40°，则△D 的度数为_______．23．如果△α＝26°，那么△α的余角等于__________．24．如图，点A在点O北偏东32︒方向上，点B在点O南偏东43︒方向上，则AOB∠= ______．25．如图，是一副三角板拼成的图案，则AED=∠____．26．如图是一个正方体的表面展开图，则原正方体中与“建”字所在的面相对的面上标的字是___________．27．如图是一个长方体的表面展开图，每个面上都标注了字母和数据，请根据要求回答（1）如果A面在长方体的底部，那么_________面会在上面；（2）这个长方体的体积为_________米3．28．若α∠的补角是它的3倍，则α∠的度数为________________．29．两根长度分别为8cm 和10cm 的直木条，将它们一端重合且放在同一条直线上，此时两根木条中点之间的距离为________．30．已知，如图4090COD AOC BOD ∠∠∠=︒==︒，，则AOB ∠=_______度．31．若一个直棱柱共有10个面，所有侧棱长的和等于64，则每条侧棱的长为______．32．小红从O 点出发向北偏西32°17＇方向走到A 点，小明从O 点出发向南偏西54°28＇方向走到B 点，则∠AOB 的度数是_____．33．如图是一个正方体的展开图，它的六个面上分别写有“构建和谐社会”六个字，将其围成正方体后，与“社”在相对面上的字是_____．34．5400秒化成度数是____________度35．如图，OA 的方向是北偏东20°，OC 的方向是北偏西40°，若AOC AOB ∠=∠，则OB 的方向是______．36．已知，如图，A 、O 、B 在同一直线上，OF 平分AOB ∠，12∠=∠，3=4∠∠．（1）射线OD 是_______的角平分线；（2）AOC ∠的补角是_______；（3）AOC ∠的余角是_______；（4）_______是2∠的余角；（5）DOB ∠的补角是_______；（6）_______是COF ∠的补角．37．线段AB ＝12cm ，点C 在线段AB 上，且AC ＝13BC ，M 为BC 的中点，则AM 的长为_______cm.38．如图，在△O 中，AB 是△O 的直径，10,AB AC CD DB ===，点E 是点D 关于AB 的对称点，M 是AB 上的一动点，下列结论：△60BOE ︒∠=；△12CED DOB ∠=∠；△DM CE ⊥；△CM DM +的最小值是10．上述结论中正确的个数是_________．39．如图，在Rt ABC △中，90ABC ∠=︒，以AC 为边，作ACD ，满足AD AC =，点E 为BC 上一点，连接AE ，12BAE CAD ∠=∠，连接DE ．下列结论中正确的是__________．（填序号）△AC DE ⊥；△ADE ACB ∠=∠；△若//CD AB ，则AE AD ⊥；△2DE CE BE =+．40．如图，在△ABC 中，AB = AC = 8，S △ABC = 16，点P 为角平分线AD 上任意一点，PE △AB ，连接PB ，则PB+PE 的最小值为_____．三、解答题41．线段4AB =cm ，延长线段AB 到C ，使BC =14AB ，再反向延长AB 到D ，使AD=3cm ，E 是AD 中点，F 是CD 的中点，求EF 的长度．42．已知图为一几何体从不同方向看的图形．(1)写出这个几何体的名称；(2)任意画出这个几何体的一种表面展开图；(3)若长方形的高为10厘米，三角形的边长为4厘米，求这个几何体的侧面积． 43．如图△，点O 为直线MN 上一点，过点O 作直线OC ，使60NOC ︒∠=．将一把直角三角尺的直角顶点放在点O 处，一边 OA 在射线OM 上，另一边OB 在直线AB 的下方，其中30OBA ︒∠=()1将图△中的三角尺沿直线OC 翻折至''A B O ∆， 求'A ON ∠的度数；()2将图△中的三角尺绕点O 按每秒10︒的速度沿顺时针方向旋转，旋转角为()0360αα︒︒<<， 在旋转的过程中，在第几秒时，直线OA 恰好平分锐角NOC ∠． ()3将图△中的三角尺绕点O 顺时针旋转；当点A 点B 均在直线MN 上方时(如图△所示)，请探究MOB ∠与AOC ∠之间的数量关系，请直接写出结论，不必写出理由．44．如图，在直线AB 上，线段20AB =，动点P 从A 出发，以每秒2个单位长度的速度在直线AB 上运动，M 为AP 的中点，N 为BP 的中点，设点P 的运动吋间为t 秒．(1)若点P 在线段AB 上运动，当7MP =时，NP = ；(2)若点P 在射线AB 上运动，当2MP NP =时，求点P 的运动时间t 的值；(3)当点P 在线段AB 的反向延长线上运动时，线段AB 、MP 、NP 有怎样的数量关系？请写出你的结论，并说明你的理由．45．已知：点M ，N ，P 在同一条直线上，线段MN a =，线段()PN b a b =>，点A 是MP 的中点．求线段MP 与线段AN 的长．（用含a ，b 的代数式表示） 46．如图所示，l 为河岸，B 处为草地，牧马人要将A 处的马牵到河边喝水，再牵到B 地吃草，问怎样走路程最短？47．如图，在ABC 中，CD 、CE 分别是ABC 的高和角平分线，,()BAC B ∠α∠βαβ==>．(1)若70,40αβ=︒=︒，求DCE ∠的度数；(2)试用α、β的代数式表示DCE ∠的度数_________．48．某产品的形状是长方体，长为8cm ，它的展开图如图所示，求长方体的体积．49．如图，已知线段AB 上有两点C ，D ，且AC△CD△DB ＝2△3△4，E ，F 分别为AC ，DB 的中点，EF ＝2.4 cm ，求线段AB 的长．50．综合与探究已知△AOB 、△BOC ，△AOB ＝90°，(1)若△BOC 为锐角，OE 、OD 分别平分△AOB 和△BOC ，△如图1，当射线OC 在△AOB 外部，△BOC ＝40°时，求△EOD 的度数；△当△BOC ＝α(090α︒<<︒)时，则△EOD 的度数是_____；(2)若△AOC 和△BOC 均为小于平角的角，OE 、OD 分别平分△AOC 和△BOC ，△当△BOC ＝40°，OC 位置如图2所示时，求△EOD 的度数．△当△BOC ＝α时（0°＜α＜180°），则△EOD 的度数是_____．参考答案：1．A【分析】侧面为三个长方形，底面为三角形，故原几何体为三棱柱．【详解】解：观察图形可知，这个几何体是三棱柱，故A 正确．故选：A ．【点睛】本题考查的是三棱柱的展开图，熟练掌握三棱柱的展开图，是解题的关键． 2．C【分析】根据三角板的角度，可得60A ∠=︒，根据平行线的性质即可求解． 【详解】解：30C ∠=︒，9060A C ∴∠=︒-∠=︒AC ∥EF ，160A ∴∠=∠=︒故选C【点睛】本题考查了平行线的性质，掌握平行线的性质是解题的关键．3．A【分析】本题考查了正方体的平面展开图，对于正方体的平面展开图中相对的面一定相隔一个小正方形，据此作答．【详解】正方体的表面展开图中，相对的面之间一定相隔一个正方形，所以在此正方体上与“爱”字相对的面上的汉字是“保”，故选A ．【点睛】本题考查正方体的展开图，解题的关键是掌握正方体相对两个面上的文字的知识．4．C【分析】由190A ∠+∠=︒，1290∠+∠=︒，可知2A ∠=∠，进而可得答案．【详解】解：△190A ∠+∠=︒，1290∠+∠=︒△2A ∠=∠故选C ．【点睛】本题考查了余角．解题的关键在于明确同角的余角相等．5．A【分析】根据余角的定义解决此题．【详解】解：设这个角的度数为x ．由题意得，9030x x -=+︒︒．△30x =︒．△这个角的度数为30︒．故选：A ．【点睛】本题主要考查余角，熟练掌握余角的定义是解决本题的关键．6．D【详解】由正方体的展开图可知，D 项符合题意，故选D ．7．C【详解】试题分析：因为CD 是一条直线，又，所以△AOE=90°所以△1+△2=180°-90°=90°，所以他们的关系是互余考点：角的互余关系点评：难度小，理解角与角的各种的关系是关键．8．A【分析】从正面看作出相应图象即可得.【详解】解：从正面看，共2列，左边是1个正方形，右边是2个正方形，且下齐．故选A.【点睛】题目主要考查小正方体的主视图的作法，理解题意，掌握视图的作法是解题关键. 9．B【分析】根据钟面分成12个大格，每格的度数为30°即可解答．【详解】解：△钟面分成12个大格，每格的度数为30°，△钟表上10点整时，时针与分针所成的角是60°故选B ．【点睛】考核知识点：钟面角.了解钟面特点是关键.10．B【分析】根据直角三角形绕直角边旋转是圆锥，即可解得．【详解】将直角三角形绕其一条直角边所在直线l 旋转一周，得到的几何体是圆锥；故答案为：B．【点睛】本题考查了点、线、面、体，熟记各种平面图形旋转得到的立体图形是解题的关键．11．B∠的平分线，可算出△MEN 【分析】根据对称的性质可得△MEF的度数，再由EN是MEC的度数.【详解】解：由题意可得：△B=90°，△△BFE=60°，△△BEF=30°，△点B和点M关于EF对称，△△BEF=△MEF=30°，△△MEC=180-30°×2=120°，∠的平分线，又△EN是MEC△△MEN=120÷2=60°.故选B.【点睛】本题考查了轴对称的性质和角平分线的性质，根据已知角利用三角形内角和、角平分线的性质计算相关角度即可，难度不大.12．B【分析】根据正方体的展开图的特点，确定出相对的面即可．【详解】解：根据正方体表面展开图可知，与“沉”字所在面相对面的汉字是“静”．故答案为B．【点睛】本题考查正方体的表面展开图的特征，掌握正方体展开图的对面的判定方法是解答本题的关键．13．D【分析】本题中，圆柱的俯视图是个圆，可以堵住圆形空洞，它的正视图和左视图是个矩形，可以堵住方形空洞．【详解】根据三视图的知识来解答．圆柱的俯视图是一个圆，可以堵住圆形空洞，而它的正视图以及侧视图都为一个矩形，可以堵住方形的空洞，故圆柱是最佳选项．故选D．【点睛】此题考查立体图形，本题将立体图形的三视图运用到了实际中，只要弄清楚了立体图形的三视图，解决这类问题其实并不难．14．B【详解】试题解析：正方体的截面，经过正方体的四个侧面，正方体中，对边平行，故可确定为平行四边形，交点垂直于底边，故为矩形．故选B．点睛：截面的形状既与被截的几何体有关，还与截面的角度和方向有关．15．B【分析】先根据△COE=90°，△COD=25°，由角的和差关系求得△DOE=90°﹣25°=65°，再根据OD平分△AOE，由角平分线的定义得出△AOD=△DOE=65°，最后根据邻补角的定义得出△BOD=180°﹣△AOD=115°．【详解】△△COE=90°，△COD=25°，△△DOE=90°﹣25°=65°．△OD平分△AOE，△△AOD=△DOE=65°，△△BOD=180°﹣△AOD=115°．故选B．【点睛】本题考查了角的计算以及角平分线的定义的综合应用，解决问题的关键是运用角平分线以及直角的定义，求得△AOD的度数，再根据邻补角进行计算．16．D【分析】根据直线、射线、线段的性质对各选项分析判断后利用排除法．【详解】解：A、射线PA和射线AP不是同一条射线，故本选项错误；B、射线是无限长的，故本选项错误；C、直线AB、CD可能平行，没有交点，故本选项错误；D、两点确定一条直线是正确的．故选：D．【点睛】本题主要考查了直线、射线、线段的特性，是基础题，需熟练掌握．17．C【分析】根据题意首先将此圆柱展成平面图，根据两点间线段最短，可得AB最短，由勾股定理即可求得需要爬行的最短路程．【详解】解：将此圆柱展成平面图得：△有一圆柱，它的高等于20cm ，底面直径等于30πcm ， △底面周长＝3030ππ⋅=cm ，△BC ＝20cm ，AC ＝12×30＝15（cm ），△AB 25=（cm ）．答：它需要爬行的最短路程为25cm ．故选：C ．【点睛】本题主要考查平面展开图求最短路径问题，将圆柱体展开，根据两点之间线段最短，运用勾股定理解答是解题关键．18．B【分析】连接CA '交BC '于点E ，C ，A '关于直线BC '对称，推出当点D 与B 重合时，AD CD +的值最小，最小值为线段AA '的长2=．【详解】解：连接CA '交BC '于点E ，直线l AB ⊥，且ABC ∆与△A BC ''关于直线l 对称，A ∴，B ，A '共线，60ABC A BC ∠=∠''=︒，60CBC ∴∠'=︒，C BA C BC ∴∠''=∠'，BA BC '=，'BE CA ∴⊥，CD DA ='，C ∴，A '关于直线BC '对称，∴当点D与B重合时，AD CD+的值最小，最小值为线段AA'的长2=，故选B．【点睛】本题考查轴对称-最短问题，等边三角形的性质等知识，解题的关键是学会利用轴对称解决最短问题，属于中考常考题型．19．D【分析】根据作图的过程可以判定AD是△BAC的角平分线；利用角平分线的定义可以推知△CAD=30°，则由直角三角形的性质来求△ADC的度数；利用等角对等边可以证得△ADB的等腰三角形，由等腰三角形的“三线合一”的性质可以证明点D在AB的中垂线上；利用30度角所对的直角边是斜边的一半、三角形的面积计算公式来求两个三角形的面积之比．【详解】解：A、根据作图方法可得AD是△BAC的平分线，正确；B、△△C=90°，△B=30°，△△CAB=60°，△AD是△BAC的平分线，△△DAC=△DAB=30°，△△ADC=60°，正确；C、△△B=30°，△DAB=30°，△AD=DB，△点D在AB的中垂线上，正确；D、△△CAD=30°，△CD=12AD，△AD=DB，△CD=12DB，△CD=13 CB，S△ACD=12CD•AC，S△ACB=12CB•AC，△S△ACD：S△ACB=1：3，△S△DAC：S△ABD≠1：3，错误，故选：D．【点睛】本题考查了角平分线的性质、线段垂直平分线的性质以及作图—基本作图．解题时，需要熟悉等腰三角形的判定与性质．20．C【分析】根据等腰直角三角形的性质可得△CAD=△B=45°，根据同角的余角相等求出△ADF=△BDE，然后利用“角边角”证明△BDE和△ADF全等，判断出△正确；根据全等三角形对应边相等可得DE=DF、BE=AF，从而得到△DEF是等腰直角三角形，判断出△正确；再求出AE=CF，判断出△正确；根据BE+CF=AF+AE，利用三角形的任意两边之和大于第三边可得BE+CF＞EF，判断出△错误．【详解】△△B=45°，AB=AC，△△ABC是等腰直角三角形，△点D为BC中点，△AD=CD=BD，AD△BC，△CAD=45°，△△CAD=△B，△△MDN是直角，△△ADF+△ADE=90°，△△BDE+△ADE=△ADB=90°，△△ADF=△BDE，在△BDE和△ADF中，CAD BAD BDADF BDE∠=∠⎧⎪=⎨⎪∠=∠⎩，△△BDE△△ADF（ASA），故△正确；△DE=DF、BE=AF，又△△MDN是直角，△△DEF是等腰直角三角形，故△正确；△AE=AB-BE，CF=AC-AF，△AE=CF，故△正确；△BE+CF=AF+AE＞EF，△BE+CF＞EF，故△错误；综上所述，正确的结论有△△△；故选：C．【点睛】本题考查了全等三角形的判定与性质、等腰直角三角形的性质、同角的余角相等的性质、三角形三边的关系；熟练掌握等腰直角三角形的性质，并能进行推理论证是解决问题的关键．21．3 4【分析】根据一平角等于180°解答即可.【详解】△135÷180=34，△135等于34平角．故答案为3 4 .【点睛】本题考查了平角的定义，熟练掌握一平角等于180°是解答本题的关键. 22．100°【分析】根据角平分线定义和平行线的性质即可求出△D的度数．【详解】解：△CB平分△ABD，△ABC＝40°，△△ABD＝2△ABC＝80°，△AB△CD，△△ABD+△D＝180°，△△D＝180°﹣80°＝100°，则△D的度数为100°．故答案为：100°．【点睛】本题主要考查了角平分线的定义，平行线的性质，熟练掌握角平分线的定义，平行线的性质是解题的关键．23．64°【详解】△△α＝26°，△△α的余角=90°-26°=64°．故答案为：64°【点睛】本题考查了余角的定义，是基础题，熟记互为余角的两个角的和等于90°是解题的关键．24．105°【分析】直接利用方向角结合互补的性质得出答案．【详解】解：如图所示：由题意可得，△1=32°，△2=43°，则△AOB=180°-△1-△2=105°．故答案为：105°．【点睛】此题主要考查了方向角，正确把握方向角的定义是解题关键．25．135°【详解】本题主要考查了三角板的知识及平角的定义根据三角板的知识可知△DEC的度数，再根据平角的定义即可求得结果．由题意得△DEC=45°，则△AED=180°-△DEC=135°.思路拓展：解答本题的关键是掌握好三角板的知识及平角的定义．26．明【分析】这种展开图是属于“1，4，1”的类型，其中，上面的1和下面的1是相对的2个面.【详解】由正方体的展开图特点可得：“建”和“明”相对；“设”和“丽”相对；“美”和“三”相对；故答案为：明.【点睛】此题考查正方体相对两个面上的文字的知识；掌握常见类型展开图相对面上的两个字的特点是解决本题的关键.27．F6【分析】（1）根据展开图，可得几何体，、、A B C 是邻面，D F E 、、是邻面，根据A 面在底面，F 会在上面，可得答案；（2）由体积计算公式解答．【详解】解：（1）如图所示，A 与F 是对面，所以如果A 面在长方体的底部，那么 F 面会在上面；故答案是：F ；（2）这个长方体的体积是：1236⨯⨯=（米3）．故答案是：6【点睛】本题考查了几何体的展开图，利用了几何体展开图组成几何体时面与面之间的关系．28．45︒##45度【分析】设α∠为x ，根据互为补角的两个角的和等于180︒表示出这个角的补角，然后列出方程求解即可．【详解】解：设α∠为x ，则α∠的补角为180x ︒-，根据题意得1803x x ︒-=，解得45x =︒，故答案为：45︒．【点睛】本题考查了互为补角的定义，根据题意表示出这个角的补角，然后列出方程是解题的关键．29．1cm 或9cm##9cm 或1cm【分析】设较长的木条为AB ，较短的木条为BC ，根据中点定义求出BM 、BN 的长度，然后分两种情况：BC 不在AB 上和BC 在AB 上时，分别代入数据进行计算即可得解．【详解】解：设较长的木条为AB =10cm ，较短的木条为BC =8cm ，△M 、N 分别为AB 、BC 的中点，△BM =5cm ，BN =4cm ，△如图1，BC 不在AB 上时，MN =BM +BN =5+4=9(cm)，△如图2，BC 在AB 上时，MN =BM −BN =5−4=1(cm)，综上所述，两根木条的中点间的距离是1cm 或9cm ，故答案为：1cm 或9cm ．如图，【点睛】本题考查了两点间的距离，主要利用了线段的中点定义，难点在于要分情况讨论，作出图形更形象直观．30．140【分析】利用角的和差关系先求出50COB ∠=︒，，再利用角的和差关系求出AOB ∠的度数．【详解】解：△4090COD AOC BOD ∠∠∠=︒==︒，，△ 50COB BOD COD ∠∠∠=-=︒，△ 140AOB AOC COB ∠∠∠=+=︒．故答案为：140．【点睛】本题主要考查了角的和差，关键是熟练掌握角的运算中的和差关系．31．8【分析】先根据这个棱柱有10个面，求出这个棱柱是8棱柱，有8条侧棱，再根据所有侧棱的和为64cm ，即可得出答案．【详解】解：△这个棱柱有10个面，△这个棱柱是8棱柱，有8条侧棱，△所有侧棱的和为64cm ，△每条侧棱长为64÷8=8（cm ）；故答案为：8【点睛】本题主要利用了棱柱面的个数比侧棱的条数多２的关系求解，是一道基础题． 32．93°15＇【分析】利用平角的定义计算即可．【详解】△从O 点出发向北偏西32°17＇方向走到A 点，小明从O 点出发向南偏西54°28＇方向走到B 点，△∠AOB =180°-54°28＇-32°17＇=93°15＇．【点睛】本题考查了方位角，平角，角的和与差，熟练掌握方位角和平角的定义是解题的关键．33．和．【分析】本题考查了正方体的展开图，一般从相对面入手进行分析与解答；【详解】解：正方体的表面展开图，相对的面之间一定相隔一个正方形，所以“建”与“谐”是相对面，“社”与“和”是相对面，“会”与“构”是相对面，由此可知与“社”相对的面上的字是“和”．【点睛】本题主要考查学生对正方体展开图形的理解和掌握，解答本题的关键是根据相对的面相隔一个面得到相对的两个面．34．1.5【详解】试题解析：△5400÷60=90，90÷60=1.5，△5400″=1.5°．35．北偏东80°【分析】先根据角的和差得到△AOC 的度数，根据△AOC =△AOB 得到△AOB 的度数，再根据角的和差得到OB 的方向．【详解】解：△OA 的方向是北偏东20°，OC 的方向是北偏西40°，△△AOC =20°+40°=60°，△△AOC =△AOB ，△△AOB =60°，20°+60°=80°，故OB 的方向是北偏东80°．故答案为：北偏东80°．【点睛】考查了方位角，方位角是表示方向的角；以正北，正南方向为基准，来描述物体所处的方向．利用角的和差得出OB 与正北方的夹角是解题关键．36． AOC ∠ COB ∠ 3∠和4∠ DOF ∠ 1∠和2∠ EOA ∠【分析】由角平分线的定义，补角、余角的定义，分别进行计算，即可得到答案．【详解】解：根据题意，（1）△12∠=∠△射线OD 是AOC ∠的角平分线；（2）△180AOC BOC ∠+∠=︒，△AOC ∠的补角是COB ∠；（3）△OF 平分AOB ∠，180AOB ∠=︒，△90AOF BOF ∠=∠=︒，△390AOC ∠+∠=︒，△3=4∠∠，△490AOC ∠+∠=︒；△AOC ∠的余角是3∠和4∠；（4）△12∠=∠，190DOF ∠+∠=︒，△290DOF ∠+∠=︒，△DOF ∠是2∠的余角；（5）△1180DOB ∠+∠=︒，12∠=∠△2180DOB ∠+∠=︒，△DOB ∠的补角是1∠和2∠；（6）△4180AOE ∠+∠=︒，4COF ∠=∠，△180COF EOA ∠+∠=︒，△EOA ∠是COF ∠的补角．故答案为：AOC ∠；COB ∠；3∠和4∠；DOF ∠；1∠和2∠；EOA ∠．【点睛】本题考查了角平分线的定义，补角、余角的定义，解题的关键是熟练掌握几何图形中角的运算．37．7.5【分析】可先作出简单的图形，进而依据图形分析求解．【详解】解：如图，△点C 在AB 上，且AC=13BC ， △AC=14AB=3cm ，△BC=9cm ，又M 为BC 的中点， △CM=12BC=4.5cm ，△AM=AC+CM=7.5cm ．故答案为7.5.【点睛】本题考查的是两点间的距离的计算，掌握线段中点的定义、灵活运用数形结合思想是解题的关键．38．3【分析】△根据点E 是点D 关于AB 的对称点可知BD BE ，进而可得1180603DOB BOE COD ︒︒∠=∠=∠=⨯=； △根据一条弧所对的圆周角等于圆心角的一半即可得结论；△根据等弧对等角，可知只有当M 和A 重合时，60,30MDE CED ︒︒∠=∠=，DM CE ⊥； △作点C 关于AB 的对称点F ，连接CF ，DF ，此时CM DM +的值最短，等于DF 的长，然后证明DF 是O 的直径即可得到结论．【详解】解：AC CD DB ==，点E 是点D 关于AB 的对称点，BD BE ∴=， 1180603DOB BOE COD ︒︒∴∠=∠=∠=⨯=，△正确；1116030222CED COD DOB ︒︒∠=∠=⨯==∠，△△正确； BE 的度数是60°，AE ∴的度数是120°，△只有当M 和A 重合时，60,︒∠=MDE ，30︒∠=CED△只有M 和A 重合时，DM CE ⊥，△错误；作C 关于AB 的对称点F ，连接CF ，交AB 于点N ，连接DF 交AB 于点M ，此时CM DM +的值最短，等于DF 的长．连接,CD AC CD DB AF ===，并且弧的度数都是60°，1112060,6030,22︒︒︒︒∴∠=⨯=∠=⨯=D CFD 180603090,︒︒︒︒∴∠=--=FCDDF ∴是O 的直径，即10DF AB ==，△当点M 与点O 重合时，CM DM +的值最小，最小值是10，△△正确．故答案为：3．【点睛】本题考查了圆的综合知识，涉及圆周角、圆心角、弧、弦的关系、最短距离的确定等，掌握圆的基本性质并灵活运用是解题关键．39．△△△【分析】因为12BAE DAC ∠=∠，且90ABC ∠=︒，所以需要构造2倍的BAC ∠，故延长EB 至G ，使BE BG =，从而得到GAE CAD ∠=∠，进一步证明GAC EAD ∠=∠，且AE AG =，接着证明GAC EAD ≌，则ADE ACG ∠=∠，DE CG =，所以△是正确的，也可以通过线段的等量代换运算推导出△是正确的，设BAE x ∠=，则2DAC x ∠=，因为//CD AB ，所以90BAC ACD x ∠=∠=︒-，接着用x 表示出EAC ∠，再计算出=90DAE ∠︒，故△是正确的，当CAE BAE ∠=∠时，可以推导出AC DE ⊥，否则AC 不垂直于DE ，故△是错误的．【详解】解：如图，延长EB 至G ，使BE BG =，设AC 与DE 交于点M ，90ABC ∠=︒，AB GE ∴⊥，AB ∴垂直平分GE ，AG AE ∴=，12GAB BAE DAC ∠=∠=∠， 12BAE GAE ∠=∠， GAE CAD ∴∠=∠，GAE EAC CAD EAC ∴∠+∠=∠+∠，GAC EAD ∴∠=∠，在GAC 与EAD 中，AG AE GAC EAD AC AD =⎧⎪∠=∠⎨⎪=⎩，GAC EAD ∴≌（SAS ），G AED ∴∠=∠，ACB ADE ∠=∠，故△是正确的；AG AE =，G AEG AED ∴∠=∠=∠，AE ∴平分BED ∠，当BAE EAC ∠=∠时，90AME ABE ∠=∠=︒，则AC DE ⊥，当BAE EAC ∠≠∠时，AME ABE ∠≠∠，则无法说明AC DE ⊥，故△是不正确的； 设BAE x ∠=，则2CAD x ∠=，1802902x ACD ADC x ︒-∴∠=∠==︒-， //AB CD ，90BAC ACD x ∴∠=∠=︒-，90902CAE BAC EAB x x x ∴∠=∠-∠=︒--=︒-，902290DAE CAE DAC x x ∴∠=∠+∠=︒-+=︒，AE AD ∴⊥，故△是正确的；GAC EAD ≌，CG DE ∴=，2CG CE GE CE BE =+=+，2DE CE BE ∴=+，DE BE BE CE ∴-=+，2DE CE BE ∴=+，故△是正确的．故答案为：△△△．【点睛】本题考查了全等三角形的判定与性质，角平分线的定义，角度的计算，构造两倍的BAE ∠，是本题解题的关键．40．4【分析】利用角平分线定理确定当BF△AC 时，PB+PE 的值最小，再利用三角形面积公式，即可求得.【详解】如图，△AB = AC = 8，AD 平分CAB ∠△'''P E P F =△当BF△AC 时，PB+PE 的值最小=BF1162ABC S AC BF ∆== △BF=4 △PB+PE 的最小值为4.【点睛】本题考查了轴对称-最短路径问题，也可以用角平分线定理考虑，找到PE+PB 最小值的情况并画出图形，是解题的关键.41．2.5cm ．【分析】结合图形和题意，利用线段的和差知CD ＝AD ＋AB ＋BC ，即可求CD 的长度；再利用中点的定义，求得DF 和DE 的长度，又EF ＝DF−DE ，即可求得EF 的长度．【详解】△4AB =cm ，BC =14AB ， △BC=1cm ，△CD ＝AD ＋AB ＋BC ＝3＋4＋1＝8cm ；△E 是AD 中点，F 是CD 的中点，△DF ＝12CD ＝8×12＝4cm ，DE ＝12AD ＝12×3＝1.5cm ．△EF ＝DF−DE ＝4−1.5＝2.5cm ．【点睛】本题主要考查了两点间的距离和中点的定义，解题的关键是运用数形结合思想． 42．(1)直三棱柱(2)见解析(3)这个几何体的侧面积为120cm 2【分析】（1）只有棱柱的主视图和左视图才能出现长方形，根据俯视图是三角形，可得到此几何体为直三棱柱；（2）画出三个长方形，两个三角形；（3）侧面积为长方形，计算出3个长方形的面积求和即可．【详解】（1）解：由主视图和左视图都是长方形，且俯视图是三角形，故该立体图形是直三棱柱；（2）解：展开图如图所示：；（3）解：这个几何体的侧面积23104120cm ⨯⨯＝．【点睛】本题主要考查了由三视图判断几何体、几何体的展开图、棱柱的侧面积等知识点，根据题意得到该几何体是直三棱柱是解答本题的关键．43．（1） '60A ON ︒∠=；（2）15秒或33秒；（3）30MOB AOC ︒∠-∠=或30MOB AOC ︒∠+∠=【分析】（1）如图△中，延长CO 到C′．利用翻折不变性求出△A′O′C′即可解决问题； （2）设t 秒时，直线OA 恰好平分锐角△NOC ．构建方程即可解决问题；（3）分两种情形分别求解即可解决问题，△当OB ，OA 在OC 的两旁时，△当OB ，OA 在OC 的同侧时，求出MOB ∠与AOC ∠之间的数量关系即可.【详解】解：（1）如图△中，延长CO 到C′，△三角尺沿直线OC 翻折至△A′B′O ，△△A′OC′=△AOC′=△CON=60°，△△A′ON=180°-60°-60°=60°；（2）设t 秒时，直线OA 恰好平分锐角△NOC ，由题意10t=150或10t=330，解得t=15或33s ，则第15或33秒时，直线OA 恰好平分锐角△NOC ；（3）△当OB ，OA 在OC 的两旁时，△△AOB=90°，△120°-△MOB+△AOC=90°，△△MOB-△AOC=30°；△当OB ，OA 在OC 的同侧时，△MOB+△AOC=120°-90°=30°.综上，30MOB AOC ︒∠-∠=或30MOB AOC ︒∠+∠=.【点睛】本题考查翻折变换，旋转变换，三角形的内角和定理等知识，解题的关键是理解题意，学会利用参数构建方程解决问题，学会用分类讨论的思想思考问题．44．(1)3； (2)203或20； (3)12NP MP AB -=，理由见解析． 【分析】（1）由中点的含义先求解7AM MP ==，证明12PN BN BP ==，再求解6PB AB AB =-=，从而可得答案；（2）△当点P 在线段AB 上，2MP NP =， △当点P 在线段AB 的延长线上，2MP NP =，再建立方程求解即可；（3）先证明12MP AP t ==，()1102NP AB AP t =+=+，可得()1010NP MP t t -=+-=，从而可得结论．【详解】（1）解：△M 为AP 的中点，N 为BP 的中点，7MP =，△7AM MP ==，12PN BN BP ==， △14AP =，。

初三几何测试题及答案

初三几何测试题及答案

初三几何测试题及答案一、选择题（每题3分，共30分）1. 下列哪个选项是直角三角形的判定条件？A. 两条边相等B. 一条边是另一条边的两倍C. 一个角是90度D. 三角形的周长是固定的答案：C2. 一个圆的半径是5厘米，那么它的周长是多少厘米？A. 31.4B. 15.7C. 10D. 25答案：A3. 一个等腰三角形的底边长为6厘米，腰长为8厘米，那么它的高是多少厘米？A. 4B. 6C. 8D. 10答案：A4. 下列哪个图形是轴对称图形？A. 正方形B. 矩形C. 梯形D. 所有选项答案：D5. 一个三角形的三个内角之和是多少度？A. 90度B. 180度C. 360度D. 720度答案：B6. 一个长方形的长是10厘米，宽是5厘米，那么它的面积是多少平方厘米？A. 20B. 30C. 50D. 100答案：C7. 一个圆的直径是10厘米，那么它的面积是多少平方厘米？A. 78.5B. 39.25C. 25D. 100答案：B8. 一个等边三角形的边长是6厘米，那么它的高是多少厘米？A. 3B. 6C. 9D. 12答案：B9. 一个平行四边形的对角线互相垂直，那么这个平行四边形是什么形状？A. 矩形B. 菱形C. 正方形D. 任意四边形答案：B10. 一个三角形的三个顶点分别在圆上，那么这个三角形是什么形状？A. 直角三角形B. 等腰三角形C. 等边三角形D. 任意三角形答案：C二、填空题（每题3分，共30分）1. 一个三角形的两个内角分别是40度和70度，那么第三个内角是______度。

答案：702. 一个圆的半径是8厘米，那么它的直径是______厘米。

答案：163. 一个正方形的对角线长是10厘米，那么它的边长是______厘米。

答案：5√24. 一个长方形的长是12厘米，宽是8厘米，那么它的周长是______厘米。

答案：405. 一个等腰直角三角形的直角边长是5厘米，那么它的斜边长是______厘米。

中考数学《几何中的最值问题》专项练习(附答案解析)

中考数学《几何中的最值问题》专项练习(附答案解析)

中考数学《几何中的最值问题》专项练习(附答案解析)一、单选题1．如图1，点P从△ABC的顶点B出发，沿B→C→A匀速运动到点A，图2是点P运动时，线段BP的长度y随时间x变化的关系图象，其中M是曲线部分的最低点，则△ABC的面积是（）A．12 B．24 C．36 D．482．将一张宽为4cm的长方形纸片（足够长）折叠成如图所示图形，重叠部分是一个三角形，则这个三角形面积的最小值是（）A．4cm2B．8cm2C．12cm2D．16cm23．如图，已知直线5-512y x与x轴、y轴分别交于B、C两点，点A是以D（0，2）为圆心，2为半径的⊙D上的一个动点，连接AC、AB，则△ABC面积的最小值是（）A．30 B．29 C．28 D．274．如图，∠AOB＝45°，点M、N分别在射线OA、OB上，MN＝6，△OMN的面积为12，P是直线MN上的动点，点P关于OA对称的点为P1，点P关于OB对称点为P2，当点P在直线NM上运动时，△OP1P2的面积最小值为（）A．6 B．8 C．12 D．185．如图，矩形ABCD中，AB=8，AD=4，E为边AD上一个动点，连接BE，取BE的中点G，点G 绕点E逆时针旋转90°得到点F，连接CF，则△CEF面积的最小值是（）A．16 B．15 C．12 D．11二、填空题6．如图，在△ABC中，AB＝AC，∠BAC＝120°，点D为AB边上一点（不与点B重合），连接CD，将线段CD绕点D逆时针旋转90°，点C的对应点为E，连接BE．若AB＝6，则△BDE面积的最大值为_________．7．如图，⊙O的直径为5，在⊙O上位于直径AB的异侧有定点C和动点P，已知BC：CA＝4：3，点P在半圆弧AB上运动（不与A，B重合），过C作CP的垂线CD交PB的延长线于D点．则△PCD的面积最大为______________．8．已知AB为半圆的直径，AB＝2，DA⊥AB，CB⊥AB，AD＝1，BC＝3，点P为半圆上的动点，则AD，AB，BC，CP，PD围成的图形的面积的最大值是_____．9．如图，在矩形ABCD中，∠ACB=30°，，点E是边BC上一动点（点E不与B，C重合），连接AE，AE的中垂线FG分别交AE于点F，交AC于点G，连接DG，GE．设AG=a，则点G到BC边的距离为_____（用含a的代数式表示），ADG的面积的最小值为_____．10．如图，直线AB交坐标轴于A(-2，0)，B(0，-4)，点P在抛物线1(2)(4)2y x x=--上，则△ABP面积的最小值为__________．三、解答题11．如图，已知抛物线23y ax bx =++与x 轴交于A 、B 两点，过点A 的直线l 与抛物线交于点C ，其中A 点的坐标是(1，0)，C 点坐标是(4，3)．（1）求抛物线的解析式；（2）抛物线的对称轴上是否存在点D ，使△BCD 的周长最小？若存在，求出点D 的坐标，若不存在，请说明理由；（3）点P 是抛物线上AC 下方的一个动点，是否存在点p ，使△PAC 的面积最大？若存在，求出点P 的坐标，若不存在，请说明理由．12．已知，如图，矩形ABCD 中，AD ＝6，DC ＝7，菱形EFGH 的三个顶点E ，G ，H 分别在矩形ABCD 的边AB ，CD ，AD 上，AH ＝2，连接CF ．（1）当四边形EFGH 为正方形时，求DG 的长；（2）当DG ＝6时，求△FCG 的面积；（3）求△FCG 的面积的最小值．13．如图，抛物线2y ax bx c =++与x 轴交于点(1,0)A -，点(3,0)B ，与y 轴交于点C ，且过点(2,3)D -．点P 、Q 是抛物线2y ax bx c =++上的动点．(1)求抛物线的解析式；(2)当点P 在直线OD 下方时，求POD ∆面积的最大值．(3)直线OQ 与线段BC 相交于点E ，当OBE ∆与ABC ∆相似时，求点Q 的坐标．14．已知抛物线y ＝a （x ﹣1）2过点（3，4），D 为抛物线的顶点．（1）求抛物线的解析式；（2）若点B 、C 均在抛物线上，其中点B （0，1），且∠BDC ＝90°，求点C 的坐标：（3）如图，直线y ＝kx +1﹣k 与抛物线交于P 、Q 两点，∠PDQ ＝90°，求△PDQ 面积的最小值．15．如图，已知二次函数213222y x x =-++的图象交x 轴于A (－1，0),B (4，0)，交y 轴于点C ，点P 是直线BC 上方抛物线上一动点（不与B ,C 重合），过点P 作PE ⊥BC ，PF ∥y 轴交BC 与F ，则△PEF 面积的最大值是___________．16．如图，已知点P 是∠AOB 内一点，过点P 的直线MN 分别交射线OA ，OB 于点M ，N ，将直线MN 绕点P 旋转，△MON 的形状与面积都随之变化．（1）请在图1中用尺规作出△MON ，使得△MON 是以OM 为斜边的直角三角形；（2）如图2，在OP 的延长线上截取PC ＝OP ，过点C 作CM ∥OB 交射线OA 于点M ，连接MP 并延长交OB 于点N ．求证：OP 平分△MON 的面积；（3）小亮发现：在直线MN 旋转过程中，（2）中所作的△MON 的面积最小．请利用图2帮助小亮说明理由．17．如图，已知A ，B 是线段MN 上的两点，4MN =，1MA =，1MB >，以A 为中心顺时针旋转点M ，以B 为中心逆时针旋转点N ，使M ，N 两点重合成一点C ，构成ABC ，设AB x =．（1）求x 的取值范围；（2）求ABC 面积的最大值．18．如图1，在Rt △ABC 中，∠A ＝90°，AB ＝AC ，点D ，E 分别在边AB ，AC 上，AD ＝AE ，连接DC ，点M ，P ，N 分别为DE ，DC ，BC 的中点．（1）观察猜想：图1中，线段PM与PN的数量关系是，位置关系是；（2）探究证明：把△ADE绕点A逆时针方向旋转到图2的位置，连接MN，BD，CE，判断△PMN 的形状，并说明理由；（3）拓展延伸：把△ADE绕点A在平面内自由旋转，若AD＝4，AB＝10，请直接写出△PMN面积的最大值．19．问题提出（1）如图①，在Rt△ABC中，∠ABC＝90°，AB＝12，BC＝16，则AC＝；问题探究（2）如图②，在Rt△ABC中，∠ABC＝90°，AC＝10，点D是AC边上一点，且满足DA＝DB，则CD＝；问题解决（3）如图③，在Rt△ABC中，过点B作射线BP，将∠C折叠，折痕为EF，其中E为BC中点，点F在AC边上，点C的对应点落在BP上的点D处，连接ED、FD，若BC＝8，求△BCD面积的最大值，及面积最大时∠BCD的度数．20．如图，已知边长为6的菱形ABCD 中，∠ABC ＝60°，点E ，F 分别为AB ，AD 边上的动点，满足BE AF =，连接EF 交AC 于点G ，CE 、CF 分别交BD 于点M ，N ，给出下列结论：①△CEF 是等边三角形；②∠DFC ＝∠EGC ； ③若BE ＝3，则BM ＝MN ＝DN ；④222EF BE DF =+； ⑤△ECF ．其中所有正确结论的序号是______21．如图，抛物线2y ax bx c =++与坐标轴交于点()()()0, 31,03,0A B E --、、,点P 为抛物线上动点,设点P 的横坐标为t ．（1）若点C 与点A 关于抛物线的对称轴对称,求C 点的坐标及抛物线的解析式；（2）若点P 在第四象限,连接PA PE 、及AE ,当t 为何值时,PAE ∆的面积最大?最大面积是多少?（3）是否存在点P ,使PAE ∆为以AE 为直角边的直角三角形，若存在，直接写出点P 的坐标；若不存在，请说明理由．22．如图，在平面直角坐标系xOy 中，抛物线y ＝ax 2﹣2ax ﹣3a （a ＜0）与x 轴交于A 、B 两点（点A 在点B 的左侧），经过点A 的直线l ：y ＝kx+b 与y 轴负半轴交于点C ，与抛物线的另一个交点为D ，且CD ＝4AC ．（1）直接写出点A 的坐标，并求直线l 的函数表达式（其中k 、b 用含a 的式子表示）；（2）点E 是直线l 上方的抛物线上的动点，若△ACE 的面积的最大值为54，求a 的值； （3）设P 是抛物线的对称轴上的一点，点Q 在抛物线上，当以点A 、D 、P 、Q 为顶点的四边形为矩形时，请直接写出点P 的坐标．23．如图1，抛物线2y x bx c =-++与x 轴交于A 、B 两点，与y 轴交于点C ，已知点B 坐标为(3,0)，点C 坐标为(0,3)．（1）求抛物线的表达式；（2）点P 为直线BC 上方抛物线上的一个动点，当PBC 的面积最大时，求点P 的坐标；（3）如图2，点M 为该抛物线的顶点，直线MD x ⊥轴于点D ，在直线MD 上是否存在点N ，使点N 到直线MC 的距离等于点N 到点A 的距离？若存在，求出点A 的坐标；若不存在，请说明理由．24．如图，已知边长为10的正方形ABCD E ，是BC 边上一动点（与B C 、不重合），连结AE G ，是BC 延长线上的点，过点E 作AE 的垂线交DCG ∠的角平分线于点F ，若FG BG ⊥．（1）求证：ABE EGF ∽△△； （2）若2EC =，求CEF △的面积；（3）请直接写出EC 为何值时，CEF △的面积最大．参考答案与解析一、单选题1．【答案】D【解答】由图2知，AB＝BC＝10，当BP⊥AC时，y的值最小，即△ABC中，BC边上的高为8（即此时BP＝8），即可求解．【解答】解：由图2知，AB＝BC＝10，当BP⊥AC时，y的值最小，即△ABC中，BC边上的高为8（即此时BP＝8），当y＝8时，PC＝＝＝6，△ABC的面积＝×AC×BP＝×8×12＝48，故选：D．【点评】本题是运动型综合题，考查了动点问题的函数图象、解直角三角形、图形面积等知识点．解题关键是深刻理解动点的函数图象，了解图象中关键点所代表的实际意义，理解动点的完整运动过程．2．【答案】B【分析】当AC⊥AB时，重叠三角形面积最小，此时△ABC是等腰直角三角形，面积为8cm2．【解答】解：如图，当AC⊥AB时，三角形面积最小，∵∠BAC=90°∠ACB=45°∴AB=AC=4cm，∴S△ABC =12×4×4=8cm2．故选：B．【点评】本题考查了折叠的性质，发现当AC⊥AB时，重叠三角形的面积最小是解决问题的关键．3．【答案】B【分析】过D作DM⊥BC于M，连接BD，则由三角形面积公式得，12BC×DM=12OB×CD，可得DM，可知圆D上点到直线5-512y x的最小距离，由此即可解决问题．【解答】过D作DM⊥BC于M，连接BD，如图，令0y =，则12x =，令0x =，则5y =-，∴B （12，0），C （0，-5），∴OB=12，OC=5，=， 则由三角形面积公式得，12BC ×DM=12OB ×CD ， ∴DM=8413， ∴圆D 上点到直线5-512y x =的最小距离是845821313-=， ∴△ABC 面积的最小值是1581329213⨯⨯=． 故选：B ．【点评】本题考查了一次函数的应用、勾股定理的应用、圆的有关性质，解此题的关键是求出圆上的点到直线BC 的最大距离以及最小距离．4．【答案】B【分析】连接OP ，过点O 作OH ⊥NM 交NM 的延长线于H ．首先利用三角形的面积公式求出OH ，再证明△OP 1P 2是等腰直角三角形，OP 最小时，△OP 1P 2的面积最小．【解答】解：连接OP ，过点O 作OH ⊥NM 交NM 的延长线于H ．∵S △OMN ＝12•MN •OH ＝12，MN ＝6，∴OH ＝4，∵点P 关于OA 对称的点为P 1，点P 关于OB 对称点为P 2，∴∠AOP ＝∠AOP 1，∠POB ＝∠P 2OB ，OP ＝OP 1＝OP 2∵∠AOB ＝45°，∴∠P 1OP 2＝2（∠POA+∠POB ）＝90°，∴△OP 1P 2是等腰直角三角形，∴OP ＝OP 1最小时，△OP 1P 2的面积最小，根据垂线段最短可知，OP 的最小值为4，∴△OP 1P 2的面积的最小值＝12×4×4＝8， 故选：B ．【点评】本题考查轴对称，三角形的面积，垂线段最短等知识，解题的关键是证明△OP 1P 2是等腰直角三角形，属于中考常考题型．5．【答案】B【分析】过点F 作AD 的垂线交AD 的延长线于点H ，则△FEH ∽△EBA ，设AE=x ，可得出△CEF 面积与x 的函数关系式，再根据二次函数图象的性质求得最小值．【解答】解：过点F 作AD 的垂线交AD 的延长线于点H ，∵∠A=∠H=90°，∠FEB=90°，∴∠FEH=90°-∠BEA=∠EBA ，∴△FEH ∽△EBA ，∴ ,HF HE EF AE AB BE == G 为BE 的中点，1,2FE GE BE ∴==∴ 1,2HF HE EF AE AB BE === 设AE=x ， ∵AB 8,4,AD ==∴HF 1,4,2x EH == ,DH AE x ∴==CEF DHFC CED EHF S S S S ∆∆∆∴=+-11111(8)8(4)422222x x x x =++⨯--⨯• 2141644x x x x =+--- 2116,4x x =-+ ∴当12124x -=-=⨯ 时，△CEF 面积的最小值1421615.4=⨯-+= 故选：B ．【点评】本题通过构造K 形图，考查了相似三角形的判定与性质．建立△CEF 面积与AE 长度的函数关系式是解题的关键．二、填空题6．【答案】818【分析】作CM ⊥AB 于M ，EN ⊥AB 于N ，根据AAS证得EDN ≌DCM ，得出EN ＝DM ，然后解直角三角形求得AM ＝3，得到BM ＝9，设BD ＝x ，则EN ＝DM ＝9﹣x ，根据三角形面积公式得到S △BDE ＝12BD EN ⋅＝12x （9﹣x ）＝﹣12（x ﹣4.5）2+818，根据二次函数的性质即可求得． 【解答】解：作CM ⊥AB 于M ，EN ⊥AB 于N ，∴∠EDN +∠DEN ＝90°，∵∠EDC ＝90°，∴∠EDN +∠CDM ＝90°，∴∠DEN ＝∠CDM ， 在EDN 和DCM 中DEN CDM END DMC 90ED DC ︒∠=∠⎧⎪∠=∠=⎨⎪=⎩∴EDN ≌DCM （AAS ），∴EN ＝DM ，∵∠BAC ＝120°，∴∠MAC ＝60°，∴∠ACM ＝30°，∴AM ＝12AC ＝12⨯6＝3， ∴BM ＝AB +AM ＝6+3＝9，设BD ＝x ，则EN ＝DM ＝9﹣x ，∴S △BDE ＝12BD EN ⋅＝12x （9﹣x ）＝﹣12（x ﹣4.5）2+818， ∴当BD ＝4.5时，S △BDE 有最大值为818， 故答案为：818． 【点评】此题主要考查旋转综合题、全等三角形的判定及性质、直角三角形的性质和求最值，解题的关键是熟知全等三角形的判定与性质和利用二次函数求最值．7．【答案】503【分析】由圆周角定理可知A P ∠=∠，再由90ACB PCD ∠=∠=︒可证明~ACB PDC ，最后根据相似三角形对应边成比例，及已知条件BC ：CA ＝4：3，结合三角形面积公式解题即可．【解答】AB 为直径，90ACB ∴∠=︒PC CD ⊥，90PCD ∴∠=︒又CAB CPD ∠=∠~ACB PDC ∴AC BC CP CD∴= BC ：CA ＝4：3，43CD PC ∴= 当点P 在弧AB 上运动时，12PCD S PC CD =⋅△ 2142233PCD S PC PC PC ∴=⨯⋅= 当PC 最大时，PCD S 取得最大值而当PC 为直径时最大，22505=33PCD S ∴=⨯． 【点评】本题考查圆周角定理、三角形面积、相似三角形的判定与性质等知识，是重要考点，难度较易，掌握相关知识是解题关键．8．【答案】【分析】五边形ABCDP 的面积＝四边形ABCD 的面积﹣△CPD 的面积只要求出△CDP 面积的最小值，作EF//CD ，且与⊙O 相切于点P ，连接OP 延长OP 交AD 于H ，易知此时点P 到CD 的距离最小，此时△CDP 的面积最小．【解答】解：∵五边形ABCDP 的面积＝四边形ABCD 的面积﹣△CPD 的面积，∴只要求出△CDP 面积的最小值，作EF//CD ，且与⊙O 相切于点P ，连接OP 延长OP 交AD 于H ，易知此时点P 到CD 的距离最小，此时△CDP 的面积最小，易知AD ＝，∵四边形ABCD 的面积＝12（1+3）×2＝4＝12×1×1+12•AD •OH+12•1•3，∴OH ，∴PH ﹣11，∴△CAD 的面积最小值为2，∴五边形ABCDP 面积的最大值是4﹣（2）＝．故答案为．【点评】本题主要考查了求解多边形的面积知识点，结合圆的切线的性质进行求解是解题的重要步骤．9．【答案】42a - 【分析】先根据直角三角形含30度角的性质和勾股定理得AB=2，AC=4，从而得CG 的长，作辅助线，构建矩形ABHM 和高线GM ，如图2，通过画图发现：当GE ⊥BC 时，AG 最小，即a 最小，可计算a 的值，从而得结论．【解答】∵四边形ABCD 是矩形，∴∠B=90°，∵∠ACB=30°，，∴AB=2，AC=4，∵AG=a ，∴CG=4a -，如图1，过G 作MH ⊥BC 于H ，交AD 于M ，Rt△CGH中，∠ACB=30°，∴GH=12CG=42a-，则点G到BC边的距离为42a-，∵HM⊥BC，AD∥BC，∴HM⊥AD，∴∠AMG=90°，∵∠B=∠BHM=90°，∴四边形ABHM是矩形，∴HM=AB=2，∴GM=2﹣GH=422a--=2a，∴S△ADG11222a AD MG=⋅=⨯=当a最小时，△ADG的面积最小，如图2，当GE⊥BC时，AG最小，即a最小，∵FG是AE的垂直平分线，∴AG=EG，∴42aa -=，∴43a =，∴△ADG 的面积的最小值为4233=，故答案为：42a -． 【点评】本题主要考查了垂直平分线的性质、矩形的判定和性质、含30度角的直角三角形的性质以及勾股定理，确定△ADG 的面积最小时点G 的位置是解答此题的关键．10．【答案】152【分析】根据直线AB 交坐标轴于A(-2，0)，B(0，-4)，计算得直线AB 解析式；平移直线AB 到直线CD ，直线CD 当抛物线相交并只有一个交点P 时，△ABP 面积为最小值，通过一元二次方程和抛物线的性质求得点P 坐标；再利用勾股定理逆定理，证明ABP △为直角三角形，从而计算得到△ABP 面积的最小值．【解答】设直线AB 为y kx b =+∵直线AB 交坐标轴于A(-2，0)，B(0，-4)∴024k b b=-+⎧⎨-=⎩ ∴24k b =-⎧⎨=-⎩∴直线AB 为24y x =--如图，平移直线AB 到直线CD ，直线CD 为2y x p =-+当2y x p =-+与抛物线1(2)(4)2y x x =--相交并只有一个交点P 时，△ABP 面积为最小值∴()()21242y x p y x x =-+⎧⎪⎨=--⎪⎩∴22820x x p -+-= ∴()44820p ∆=--=∴72p =∴2210x x -+= ∴1x =将1x =代入1(2)(4)2y x x =--，得32y =∴31,2P ⎛⎫⎪⎝⎭∴()2223451224AP ⎛⎫=++= ⎪⎝⎭2231251424BP ⎛⎫=++=⎪⎝⎭2222420AB∴222AB AP BP +=∴ABP △为直角三角形，90BAP ∠=∴1115=2222ABP AB A S P ⨯=⨯=△ 即△ABP 面积的最小值为152故答案为：152． 【点评】本题考查了二次函数、一次函数、平移、一元二次方程、勾股定理逆定理的知识；解题的关键是熟练掌握二次函数、一次函数、平移、一元二次方程、勾股定理逆定理的性质，从而完成求解．三、解答题11．【答案】（1）抛物线y ＝x 2-4x +3;（2）D(2，1)；（3）点P 的坐标为5(2，3)4- 【分析】（1）（1） 将A 、C 坐标代入即可；（2）由于BC 长度不变， 要周长最小， 就是让DB DC 最小， 而A 、B 关于对称轴对称， 所以AC 就是DB DC 的最小值， 此时D 点就是AC 与抛物线对称轴的交点； 【解答】解：（1）抛物线23y ax bx =++经过点(1,0)A ，点(4,3)C ，∴3016433a bab，解得14a b ==-⎧⎨⎩，所以，抛物线的解析式为243y x x =-+；（2）243(1)(3)yx xx x ，(3,0)∴B ，抛物线的对称轴为2x =；BC 长度不变，BDDC 最小时，BCD ∆的周长最小，A 、B 是关于抛物线对称轴对称的，∴当D 点为对称轴与AC 的交点时，BD DC +最小， 即BCD ∆的周长最小， 如图，∴21x yx ，解得：21x y =⎧⎨=⎩，(2,1)D ∴，∴抛物线对称轴上存在点(2,1)D ，使BCD ∆的周长最小；（3）存在，如图，设过点P 与直线AC 平行线的直线为y x m =+，联立243y x m yx x，消掉y 得，2530x x m ，2(5)41(3)0m ，解得：134m =-， 即134m =-时，点P 到AC 的距离最大，ACP ∆的面积最大， 此时52x =，5133244y ， ∴点P 的坐标为5(2，3)4-，设过点P 的直线与x 轴交点为F ，则13(4F ，0)， 139144AF， 直线AC 的解析式为1y x =-，45CAB ∴∠=︒，∴点F 到AC 的距离为9292sin 45428AF ， 又223(41)32AC ，∴∆的最大面积127ACE=⨯=．28【点评】本题考查了二次函数综合题型，主要考查了待定系数法求二次函数解析式，待定系数法求一次函数解析式，利用轴对称确定最短路线问题，联立两函数解析式求交点坐标，利用平行线确定点到直线的最大距离问题，熟悉相关性质是解题的关键．12．【答案】（1）2‘（2）1；（3）（．【分析】（1）当四边形EFGH为正方形时，则易证AHE≌△DGH，则DG=AH=2；（2）过F作FM⊥DC，交DC延长线于M，连接GE，由于AB∥CD，可得∠AEG=∠MGE，同理有∠HEG=∠FGE，利用等式性质有∠AEH=∠MGF，再结合∠A=∠M=90°，HE=FG，可证△AHE≌△MFG，从而有FM=HA=2（即无论菱形EFGH如何变化，点F到直线CD的距离始终为定值2），进而可求三角形面积；=7-x，在△AHE中，AE≤AB=7，利用勾股定理可得HE2（3）先设DG=x，由第（2）小题得，S△FCG≤53，在Rt△DHG中，再利用勾股定理可得x2+16≤53，进而可求x，从而可得当时，△GCF的面积最小．【解答】解：（1）∵四边形EFGH为正方形，∴HG=HE，∠EAH=∠D=90°，∵∠DHG+∠AHE=90°，∠DHG+∠DGH=90°，∴∠DGH=∠AHE，∴△AHE≌△DGH（AAS），∴DG=AH=2；（2）过F作FM⊥DC，交DC延长线于M，连接GE，∵AB∥CD，∴∠AEG=∠MGE，∵HE∥GF，∴∠HEG=∠FGE ， ∴∠AEH=∠MGF ，在△AHE 和△MFG 中，∠A=∠M=90°，HE=FG ， ∴△AHE ≌△MFG （AAS ）， ∴FM=HA=2，即无论菱形EFGH 如何变化，点F 到直线CD 的距离始终为定值2， 因此S △FCG =12×FM ×GC=12×2×（7-6）=1； （3）设DG=x ，则由（2）得，S △FCG =7-x ， 在△AHE 中，AE ≤AB=7， ∴HE 2≤53， ∴x 2+16≤53，∴x∴S △FCG 的最小值为，此时，∴当时，△FCG 的面积最小为（．【点评】本题属于四边形综合题，考查了矩形、菱形的性质、全等三角形的判定和性质、勾股定理．解题的关键是学会添加常用辅助线，构造全等三角形解决问题． 13．【答案】(1)抛物线的表达式为：223y x x =--；(2)POD S ∆有最大值，当14m =时，其最大值为4916；(3) Q -或(或1122⎛⎫-+- ⎪ ⎪⎝⎭或1322⎛⎫-+ ⎪ ⎪⎝⎭． 【分析】（1）函数的表达式为：y=a （x+1）（x-3），将点D 坐标代入上式，即可求解；（2）设点()2,23P m m m --，求出32OG m =+，根据()12POD D P S OG x x ∆=⨯-1(32)(2)2m m =+-2132m m =-++，利用二次函数的性质即可求解；（3）分∠ACB=∠BOQ 、∠BAC=∠BOQ ，两种情况分别求解，通过角的关系，确定直线OQ 倾斜角，进而求解．【解答】解：(1)函数的表达式为：(1)(3)y a x x =+-，将点D 坐标代入上式并解得：1a =，故抛物线的表达式为：223y x x =--…①；(2)设直线PD 与y 轴交于点G ，设点()2,23P m m m --，将点P 、D 的坐标代入一次函数表达式：y sx t =+并解得，直线PD 的表达式为：32y mx m =--，则32OG m =+，()12POD D P S OG x x ∆=⨯-1(32)(2)2m m =+-2132m m =-++， ∵10-<，故POD S ∆有最大值，当14m =时，其最大值为4916； (3)∵3OB OC ==，∴45OCB OBC ︒∠=∠=，∵ABC OBE ∠=∠，故OBE ∆与ABC ∆相似时，分为两种情况：①当ACB BOQ ∠=∠时，4AB =，BC =，AC =， 过点A 作AH ⊥BC 与点H ，1122ABC S AH BC AB OC ∆=⨯⨯=⨯，解得：AH =， ∴CH则tan 2ACB ∠=，则直线OQ 的表达式为： 2 y x =-…②，联立①②并解得：x =故点Q -或(； ②BAC BOQ ∠=∠时，3tan 3tan 1OC BAC BOQ OA ∠====∠， 则直线OQ 的表达式为： 3 y x =-…③，联立①③并解得：12x -±=，故点1322Q ⎛-- ⎝⎭或⎝⎭；综上，点Q -或(或⎝⎭或⎝⎭． 【点评】本题考查的是二次函数综合运用，涉及到解直角三角形、三角形相似、面积的计算等，其中（3），要注意分类求解，避免遗漏．14．【答案】（1）y ＝（x ﹣1）2；（2）点C 的坐标为（2，1）；（3）1 【分析】（1）将点（3，4）代入解析式求得a 的值即可；（2）设点C 的坐标为（x 0，y 0），其中y 0＝（x 0﹣1）2，作CF ⊥x 轴，证△BDO ∽△DCF 得BO DFDO CF=，即1＝00x 1y -＝()01x 1-，据此求得x 0的值即可得；（3）过点D 作x 轴的垂线交直线PQ 于点G ，则DG ＝4，根据S △PDQ ＝12DG •MN 列出关于k 的等式求解可得．【解答】解：（1）将点（3，4）代入解析式，得：4a ＝4，解得：a ＝1，所以抛物线解析式为y ＝（x ﹣1）2； （2）由（1）知点D 坐标为（1，0）， 设点C 的坐标为（x 0，y 0），（x 0＞1、y 0＞0）， 则y 0＝（x 0﹣1）2，如图1，过点C 作CF ⊥x 轴，∴∠BOD ＝∠DFC ＝90°，∠DCF+∠CDF ＝90°， ∵∠BDC ＝90°， ∴∠BDO+∠CDF ＝90°， ∴∠BDO ＝∠DCF ， ∴△BDO ∽△DCF ， ∴BO DFDO CF=， ∴1＝00x 1y -＝()01x 1-，解得：x 0＝2，此时y 0＝1， ∴点C 的坐标为（2，1）．（3）设点P 的坐标为（x 1，y 1），点Q 为（x 2，y 2），（其中x 1＜1＜x 2，y 1＞0，y 2＞0）， 如图2，分别过点P 、Q 作x 轴的垂线，垂足分别为M 、N ， 由y=(x-1)2 ，y=kx+1-k ，得x 2﹣（2+k ）x+k ＝0． ∴x 1+x 2＝2+k ，x 1•x 2＝k ． ∴MN ＝|x 1﹣x 2|＝|2﹣k|．则过点D 作x 轴的垂线交直线PQ 于点G ，则点G 的坐标为（1，1）， 所以DG ＝1，∴S △PDQ ＝12DG •MN ＝12×1×|x 1﹣x 2|12|2﹣k|， ∴当k ＝0时，S △PDQ 取得最小值1．【点评】本题主要考查二次函数的综合问题，解题的关键是熟练掌握待定系数法求函数解析式、相似三角形的判定与性质及一元二次方程根与系数的关系等知识点．15．【答案】45【分析】先证明△PEF ∽△BOC,得出PE EF PF BO OC BC ==，再根据122y x =-+，得出关于x 的二次函数方程，根据顶点坐标公式，求得则△PEF 面积最大值．【解答】解：设213,222P x x x ⎛⎫-++⎪⎝⎭(0<x<4)， 抛物线213222y x x =-++与y 轴交于C 点，故C(0,2)，∵PF ∥y 轴，PE ⊥BC ， ∴∠PFE=∠BCO, 又∵∠PEF=∠BOC=90°, ∴△PEF ∽△BOC, ∴PE EF PF BO OC BC== ,把B(4,0),C(0,2)代入直线BC 的解析式为122y x =-+， 点1,22F x x ⎛⎫-+ ⎪⎝⎭，∴221312(2)22222P F x PF y y x x x x =-=-++--+=-+，∴PE=BO ·PF BC =42212x x -+== ， EF=OC ·PFBC=222211122(2)x x x x x x -+-+-== ， ∴221(2)1225PEFx x SPE EF -=⋅= =2221(2)(2)42520x x x ⎡⎤-⎢⎥⎡⎤--+⎣⎦⎣⎦=， 当2x =时，PEF S △取值最大，∴PEF S △的最大值为244205=， 故答案为45． 【点评】本题考查了三角形的面积及相似三角形的判定与性质．熟练掌握相似三角形的判定与性质及用含x 的代数式表示出三角形的面积是解题的关键．16．【答案】（1）见解析；（2）见解析；（3）当点P 是MN 的中点时S △MON 最小．理由见解析． 【分析】（1）根据尺规作图，过P 点作PN ⊥OB 于N ，交OA 于点M ； （2）证明三角形全等得P 为MN 的中点，便可得到结论；（3）过点P 作另一条直线EF 交OA 、OB 于点E 、F ，设PF ＜PE ，与MC 交于于G ，证明△PGM ≌△PFN ，得△PGM 与△PFN 的面积相等，进而得S 四边形MOFG ＝S △MON ． 便可得S △MON ＜S △EOF ，问题得以解决．【解答】（1）①在OB 下方取一点K ，②以P 为圆心，PK 长为半径画弧，与OB 交于C 、D 两点，③分别以C 、D 为圆心，大于12CD 长为半径画弧，两弧交于E 点， ④作直线PE ，分别与OA 、OB 交于点M 、N ，故△OMN 就是所求作的三角形；（2）∵CM ∥OB ，∴∠C ＝∠PON ，在△PCM 和△PON 中，C PON PC POCPH OPN ∠=∠⎧⎪=⎨⎪∠=∠⎩， ∴△PCM ≌△PON （ASA ），∴PM ＝PN ，∴OP 平分△MON 的面积；（3）过点P 作另一条直线EF 交OA 、OB 于点E 、F ，设PF ＜PE ，与MC 交于于G ，∵CM ∥OB ，∴∠GMP ＝∠FNP ，在△PGM 和△PFM 中，PMG PNF PM PNMPG NPF ∠=∠⎧⎪=⎨⎪∠=∠⎩， ∴△PGM ≌△PFN （ASA ），∴S △PGM ＝S △PFN∴S 四边形MOFG ＝S △MON ．∵S 四边形MOFG ＜S △EOF ，∴S △MON ＜S △EOF ，∴当点P 是MN 的中点时S △MON 最小．【点评】本题主要考查了图形的旋转性质，全等三角形的性质与判定，三角形的中线性质，关键证明三角形全等．17．【答案】（1）12x <<；（2）2． 【分析】（1）由旋转可得到AC=MA=x ，BC=BN=3-x ，利用三角形三边关系可求得x 的取值范围；（2）过点C 作CD ⊥AB 于D ，设CD=h ，利用勾股定理表示出AD 、BD ，再根据BD=AB-AD 列方程求出h 2，然后求出△ABC 的面积的平方，再根据二次函数的最值问题解答．【解答】解：（1）∵4MN =，1MA =，AB x =，∴413BN x x =--=-．由旋转的性质，得1MA AC ==，3BN BC x ==-，由三角形的三边关系，得31,31,x x x x --<⎧⎨-+>⎩①② 解不等式①得1x >，解不等式②得2x <，∴x 的取值范围是12x <<．（2）如图，过点C 作CD AB ⊥于点D ，设CD h =，由勾股定理，得AD =，BD ==， ∵BD AB AD =-，x =-34=-x ，两边平方整理，得()222832=x x h x -+-．∵ABC 的面积为1122AB CD xh ⋅=， ∴()2222113183222422S xh x x x ⎛⎫⎛⎫==-⨯-+=--+ ⎪ ⎪⎝⎭⎝⎭， ∴当32x =时，ABC 面积最大值的平方为12，∴ABC ． 【点评】本题考查了旋转的性质，三角形的三边关系，勾股定理，二次函数的最值问题，（1）难点在于考虑利用三角形的三边关系列出不等式组，（2）难点在于求解利用勾股定理列出的无理方程．18．【答案】（1）PM ＝PN ，PM ⊥PN ；（2）△PMN 是等腰直角三角形．理由见解析；（3）S △PMN 最大＝492． 【分析】（1）由已知易得BD CE =，利用三角形的中位线得出12PM CE =，12PN BD =，即可得出数量关系，再利用三角形的中位线得出//PM CE 得出DPM DCA ∠=∠，最后用互余即可得出位置关系；（2）先判断出ABD ACE ∆≅∆，得出BD CE =，同（1）的方法得出12PM BD =，12PN BD =，即可得出PM PN =，同（1）的方法由MPN DCE DCB DBC ACB ABC ∠=∠+∠+∠=∠+∠，即可得出结论；（3）方法1：先判断出MN 最大时，PMN ∆的面积最大，进而求出AN ，AM ，即可得出MN 最大AM AN =+，最后用面积公式即可得出结论．方法2：先判断出BD 最大时，PMN ∆的面积最大，而BD 最大是14AB AD +=，即可得出结论．【解答】解：（1）点P ，N 是BC ，CD 的中点，//PN BD ∴，12PN BD =， 点P ，M 是CD ，DE 的中点，//PM CE ∴，12PM CE =， AB AC =，AD AE =，BD CE ∴=，PM PN ∴=，//PN BD ，DPN ADC ∴∠=∠，//PM CE ，DPM DCA ∴∠=∠，90BAC ∠=︒，90ADC ACD ∴∠+∠=︒，90MPN DPM DPN DCA ADC ∴∠=∠+∠=∠+∠=︒，PM PN ∴⊥，故答案为：PM PN =，PM PN ⊥；（2）PMN ∆是等腰直角三角形．由旋转知，BAD CAE ∠=∠，AB AC =，AD AE =，()ABD ACE SAS ∴∆≅∆，ABD ACE ∴∠=∠，BD CE =， 利用三角形的中位线得，12PN BD =，12PM CE =，PM PN ∴=，PMN ∴∆是等腰三角形，同（1）的方法得，//PM CE ，DPM DCE ∴∠=∠，同（1）的方法得，//PN BD ，PNC DBC ∴∠=∠，DPN DCB PNC DCB DBC ∠=∠+∠=∠+∠，MPN DPM DPN DCE DCB DBC ∴∠=∠+∠=∠+∠+∠BCE DBC ACB ACE DBC =∠+∠=∠+∠+∠ACB ABD DBC ACB ABC =∠+∠+∠=∠+∠，90BAC ∠=︒，90ACB ABC ∴∠+∠=︒，90MPN ∴∠=︒，PMN ∴∆是等腰直角三角形；（3）方法1：如图2，同（2）的方法得，PMN ∆是等腰直角三角形，MN ∴最大时，PMN ∆的面积最大，//DE BC ∴且DE 在顶点A 上面，MN ∴最大AM AN =+，连接AM ，AN ，在ADE ∆中，4AD AE ==，90DAE ∠=︒，AM ∴=在Rt ABC ∆中，10AB AC ==，AN =MN ∴=最大，22211114922242PMN S PM MN ∆∴==⨯=⨯=最大． 方法2：由（2）知，PMN ∆是等腰直角三角形，12PM PN BD ==， PM ∴最大时，PMN ∆面积最大，∴点D 在BA 的延长线上，14BD AB AD ∴=+=，7PM ∴=，2211497222PMN S PM ∆∴==⨯=最大． 【点评】此题属于几何变换综合题，主要考查了三角形的中位线定理，等腰直角三角形的判定和性质，全等三角形的判断和性质，直角三角形的性质的综合运用；解（1）的关键是判断出12PM CE =，12PN BD =，解（2）的关键是判断出ABD ACE ∆≅∆，解（3）的关键是判断出MN 最大时，PMN ∆的面积最大．19．【答案】（1）20；（2）5；（3）S △BCD ＝16；∠BCD ＝45°【分析】（1）由勾股定理可求解；（2）由等腰三角形的性质可得∠A ＝∠DBA ，由余角的性质可得∠DBC ＝∠C ，可得DB ＝DC ＝AD ＝12AC ＝5； （3）由中点的性质和折叠的性质可得DE ＝EC ＝4，则当DE ⊥BC 时，S △BCD 有最大值，由三角形面积公式和等腰直角三角形的性质可求解．【解答】解：（1）∵∠ABC ＝90°，AB ＝12，BC ＝16，∴20AC ==，故答案为：20；（2）∵DA ＝DB ，∴∠A ＝∠DBA ，∵∠ABC ＝90°∴∠A +∠C ＝90°，∠ABD +∠DBC ＝90°，∴∠DBC ＝∠C ，∴DB＝DC，∴DB＝DC＝AD＝12AC＝5，故答案为：5；（3）∵E为BC中点，BC＝8，∴BE＝EC＝4，∵将∠C折叠，折痕为EF，∴DE＝EC＝4，当DE⊥BC时，S△BCD有最大值，S△BCD＝12×BC×DE＝12×8×4＝16，此时∵DE⊥BC，DE＝EC，∴∠BCD＝45°．故答案为：S△BCD＝16；∠BCD＝45°．【点评】本题主要考查了勾股定理、直角三角形斜边中线问题以及三角形中的折叠问题；题目较为综合，其中熟练掌握定义定理是解题的关键．20．【答案】①②③⑤【分析】由“SAS”可证△BEC≌△AFC，可得CF＝CE，∠BCE＝∠ACF，可证△EFC是等边三角形，由三角形内角和定理可证∠DFC＝∠EGC；由等边三角形的性质和菱形的性质可求MN＝DN＝BM＝由勾股定理即可求解EF2＝BE2＋DF2不成立；由等边三角形的性质可得△ECF面积2，则当EC⊥AB时，△ECF【解答】解：∵四边形ABCD是菱形，∴AB＝BC＝CD＝AD＝6，∵AC＝BC，∴AB＝BC＝CD＝AD＝AC，∴△ABC，△ACD是等边三角形，∴∠ABC＝∠BAC＝∠ACB＝∠DAC＝60°，∵AC＝BC，∠ABC＝∠DAC，AF＝BE，∴△BEC≌△AFC（SAS）∴CF＝CE，∠BCE＝∠ACF，∴∠ECF ＝∠BCA ＝60°，∴△EFC 是等边三角形，故①正确；∵∠ECF ＝∠ACD ＝60°，∴∠ECG ＝∠FCD ，∵∠FEC ＝∠ADC ＝60°，∴∠DFC ＝∠EGC ，故②正确；若BE ＝3，菱形ABCD 的边长为6，∴点E 为AB 中点，点F 为AD 中点，∵四边形ABCD 是菱形，∴AC ⊥BD ，AO ＝CO ，BO ＝DO ，∠ABO ＝12∠ABC ＝30°，∴AO ＝12AB ＝3，BO ＝∴BD ＝，∵△ABC 是等边三角形，BE ＝AE ＝3，∴CE ⊥AB ，且∠ABO ＝30°，∴BE EM ＝3，BM ＝2EM ，∴BM ＝同理可得DN ＝∴MN ＝BD −BM −DN ＝∴BM ＝MN ＝DN ，故③正确；∵△BEC ≌△AFC ，∴AF ＝BE ，同理△ACE ≌△DCF ，∴AE ＝DF ，∵∠BAD ≠90°，∴EF 2＝AE 2＋AF 2不成立，∴EF 2＝BE 2＋DF 2不成立，故④错误，∵△ECF 是等边三角形，∴△ECF 2， ∴当EC ⊥AB 时，△ECF 面积有最小值，此时，EC ＝ECF 面积的最小值为4，故⑤正确； 故答案为：①②③⑤．【点评】本题是四边形综合题，考查菱形的性质，全等三角形的判定和性质，等边三角形的判定和性质，勾股定理等知识，熟练掌握性质定理是解题的关键．21．【答案】（1）223;y x x =--（2）当32t =时，S 有最大值278；（3）()()2,5,1,4-- 【分析】（1）根据抛物线上的对称点B 和E ，求出对称轴从而可求出C 点坐标．然后设出抛物线的交点式，再把点A 代入求出a 值即可求出抛物线的解析式；（2）过点P 作y 轴的平行线交AE 于点H ，分别根据抛物线和直线AE 的解析式表示出点P 和点H 的坐标，从而求出线段PH 的长，最后用含t 的式子表示∆APE 的面积，利用二次函数的性质求解；（3）根据两直线垂直时，它们的斜率之积为-1，可求得与直线AE 垂直的直线方程，最后联立方程组可求点P 的坐标．【解答】解：（1）抛物线2y ax bx c =++经过点()()1,03,0,B E -、∴抛物线的对称轴为1,x =点()0,3A -，点()2,3C -抛物线表达式为()()()23123,.y a x x a x x =-+=--33a ∴-=-,解得1,a =∴抛物线的表达式为223;y x x =--()2如图,过点P 作y 轴的平行线交AE 于点H由点,A E 的坐标得直线AE 的表达式为3,y x =-设点()2,23P t t t --，则(),3H t t -()()22213333273233222228PAES PH OE t t t t t t ∆⎛⎫∴=•=--++=-+=--+ ⎪⎝⎭ 当32t =时，S 有最大值278()3直线AE 表达式中的k 值为1,则与之垂直的直线表达式中的k 值为1-① 当90PEA ︒∠=时，直线PE 的表达式为1,y x b =-+将点E 的坐标代人并解得13b =,直线PE 的表达式为3,y x =-+联立得2233y x x y x ⎧=--⎨=-+⎩解得2x =-或3（不合题意，舍去）故点P 的坐标为()2,5-② 当90PAE ︒∠=时，直线PA 的表达式为2,y x b =-+将点A 的坐标代人并解得23b =,直线PE 的表达式为3,y x =--联立得2233y x x y x ⎧=--⎨=--⎩ 解得1x =或0（不合题意，舍去）故点()1,4P -综上，点P 的坐标为()2,5-或（1,-4)【点评】本题考查了二次函数的综合题：熟练掌握二次函数图象上点的坐标特征、二次函数的性质；会利用待定系数法求二次函数解析式；会解一元二次方程；理解坐标与图形性质，记住两直线垂直时它们的斜率之积为-1；会利用分类讨论的思想解决数学问题．。

初中数学几何题练习与参考答案

初中数学几何题练习与参考答案

初中数学几何题练习与参考答案答案如下：初中数学几何题练习与参考答案练习题一：直角三角形的性质1. 在直角三角形ABC中，已知∠A=90°，BC=6cm，AC=8cm，求AB的长。

解：根据勾股定理，有AB² + BC² = AC²代入已知数据，得到AB² + 6² = 8²化简得AB² = 64 - 36 = 28再开方得到AB = √28 cm练习题二：相似三角形的特征2. 若△ABC ~ △DEF，且AB=10cm，BC=6cm，DE=12cm，求DF 的长度。

解：由相似三角形的性质，可以得到以下比例：AB/DE = BC/DF 代入已知数据，得到10/12 = 6/DF交叉相乘得到DF = 6*12/10 = 7.2cm练习题三：平行线和梯形的性质3. 若AB // CD, AB = 8cm, CD = 10cm，且ABCD为梯形，高为6cm，求梯形的面积。

解：由梯形的面积公式，可以得到以下计算步骤：梯形面积 = (底1 + 底2) * 高 / 2代入已知数据，得到梯形面积 = (8 + 10) * 6 / 2 = 54cm²练习题四：圆的性质4. 已知半径为3cm的圆，求其周长和面积。

解：圆的周长公式为2πr，圆的面积公式为πr²。

代入已知半径3cm，得到周长= 2π * 3 = 6π cm，面积= π * 3² = 9π cm²练习题五：体积与表面积的计算5. 已知正方体的棱长为4cm，求其体积和表面积。

解：正方体的体积公式为边长的立方，表面积公式为边长的平方乘以6。

代入已知边长4cm，得到体积 = 4³ = 64cm³，表面积 = 4² * 6 =96cm²练习题六：二次曲线的图像探究6. 若抛物线y = ax² + bx + c的顶点为(-2, 3)，且过点(1, 5)，求a、b、c的值。

相关主题
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

中考数学几何专题训练含答案1、如图，在直角梯形ABCD中，AD∥BC，∠ABC=90°，E为AB延长线上一点，连接ED，与BC交点H．过E作CD的垂线，垂足为CD上的一点F，并与BC交于点G．已知G为CH的中点，且∠BEH=∠HEG．（1）若HE=HG，求证：△EBH≌△GFC；（2）若CD=4，BH=1，求AD的长．2、已知，Rt△ABC中，∠ACB=90°，∠CAB=30°．分别以AB、AC为边，向形外作等边△ABD和等边△ACE．（1）如图1，连接线段BE、CD．求证：BE=CD；（2）如图2，连接DE交AB于点F．求证：F为DE中点．3、如图，在梯形ABCD中，AD∥BC，∠C=90°，E为CD的中点，EF∥AB交BC于点F（1）求证：BF=AD+CF；（2）当AD=1，BC=7，且BE平分∠ABC时，求EF的长．4、在等腰梯形ABCD中，AD∥BC，AB=AD=CD,∠ABC=60°,延长AD到E,使DE=AD,延长DC到F，使DC=CF,连接BE、BF和EF.⑴求证：△ABE≌△CFB;⑵如果AD=6,tan∠EBC的值.ABDECF5、已知：AC是矩形ABCD的对角线，延长CB至E，使CE=CA，F是AE的中点，连接DF、CF 分别交AB于G、H点（1）求证：FG=FH；（2）若∠E=60°，且AE=8时，求梯形AECD的面积．6、如图，直角梯形ABCD中，AD∥BC，∠BCD=90°，且CD=2AD，tan∠ABC=2，过点D作DE ∥AB，交∠BCD的平分线于点E，连接BE．（1）求证：BC=CD；（2）将△BCE绕点C，顺时针旋转90°得到△DCG，连接EG．求证：CD垂直平分EG；（3）延长BE交CD于点P．求证：P是CD的中点．7、如图，直角梯形ABCD中，∠DAB=90°，AB∥CD，AB=AD，∠ABC=60度．以AD为边在直角梯形ABCD外作等边三角形ADF，点E是直角梯形ABCD内一点，且∠EAD=∠EDA=15°，连接EB、EF．（1）求证：EB=EF；（2）延长FE交BC于点G，点G恰好是BC的中点，若AB=6，求BC的长．（1）证明：∵△ADF为等边三角形，8、已知，矩形ABCD中，延长BC至E，使BE=BD，F为DE的中点，连结AF、CF.求证：(1)∠ADF=∠BCF；(2) AF⊥CF.9、如图，在直角梯形ABCD中，AD⊥DC，AB∥DC，AB=BC，AD与BC延长线交于点F，G是DC延长线上一点，AG⊥BC于E．（1）求证：CF=CG；（2）连接DE，若BE=4CE，CD=2，求DE的长．10、如图，在正方形ABCD中，E、F分别为BC、AB上两点，且BE=BF，过点B作AE的垂线交AC于点G，过点G作CF的垂线交BC于点H延长线段AE、GH交于点M．（1）求证：∠BFC=∠BEA；（2）求证：AM=BG+GM．11、直角梯形ABCD中，AB∥CD，∠C=90°，AB=BC，M为BC边上一点．（1）若∠DMC=45°，求证：AD=AM．（2）若∠DAM=45°，AB=7，CD=4，求BM的值．12、如图，AC是正方形ABCD的对角线，点O是AC的中点，点Q是AB上一点，连接CQ，DP ⊥CQ于点E，交BC于点P，连接OP，OQ；求证：（1）△BCQ≌△CDP；（2）OP=OQ．中考数学几何专题训练（24）答案1、如图，在直角梯形ABCD中，AD∥BC，∠ABC=90°，E为AB延长线上一点，连接ED，与BC交于点H．过E作CD的垂线，垂足为CD上的一点F，并与BC交于点G．已知G为CH的中点，且∠BEH=∠HEG．（1）若HE=HG，求证：△EBH≌△GFC；（2）若CD=4，BH=1，求AD的长．（1）证明：∵HE=HG，∴∠HEG=∠HGE，∵∠HGE=∠FGC，∠BEH=∠HEG，∴∠BEH=∠FGC，∵G是HC的中点，∴HG=GC，∴HE=GC，∵∠HBE=∠CFG=90°．∴△EBH≌△GFC；（2）解：过点H作HI⊥EG于I，∵G为CH的中点，∴HG=GC，∵EF⊥DC，HI⊥EF，∴∠HIG=∠GFC=90°，∠FGC=∠HGI，∴△GIH≌△GFC，∵△EBH≌△EIH（AAS），∴FC=HI=BH=1，∴AD=4-1=3．2、已知，Rt△ABC中，∠ACB=90°，∠CAB=30°．分别以AB、AC为边，向形外作等边△ABD和等边△ACE．（1）如图1，连接线段BE、CD．求证：BE=CD；（2）如图2，连接DE交AB于点F．求证：F为DE中点．证明：（1）∵△ABD和△ACE是等边三角形，∴AB=AD，AC=AE，∠DAB=∠EAC=60°，∴∠DAB+∠BAC=∠EAC+∠BAC，即∠DAC=∠BAE，在△DAC和△BAE中， AC=AE ∠DAC=∠BAE AD=AB ，∴△DAC≌△BAE（SAS），∴DC=BE；（2）如图，作DG∥AE，交AB于点G，由∠EAC=60°，∠CAB=30°得：∠FAE=∠EAC+∠CAB=90°，∴∠DGF=∠FAE=90°，又∵∠ACB=90°，∠CAB=30°，∴∠ABC=60°，又∵△ABD为等边三角形，∠DBG=60°，DB=AB，∴∠DBG=∠ABC=60°，在△DGB和△ACB中，∠DGB=∠ACB ∠DBG=∠ABC DB=AB ，∴△DGB≌△ACB（AAS），∴DG=AC，又∵△AEC为等边三角形，∴AE=AC，∴DG=AE，在△DGF和△EAF 中，∠DGF=∠EAF ∠DFG=∠EFA DG=EA ，∴△DGF≌△EAF（AAS），∴DF=EF，即F为DE中点．3、如图，在梯形ABCD中，AD∥BC，∠C=90°，E为CD的中点，EF∥AB交BC于点F（1）求证：BF=AD+CF；（2）当AD=1，BC=7，且BE平分∠ABC时，求EF的长．（1）证明：如图（1），延长AD交FE的延长线于N∵∠NDE=∠FCE=90°∠DEN=∠FECDE=EC∴△NDE≌△FCE∴DN=CF∵AB∥FN，AN∥BF∴四边形ABFN是平行四边形∴BF=AD+DN=AD+FC（2）解：∵AB∥EF，∴∠ABN=∠EFC，即∠1+∠2=∠3，又∵∠2+∠BEF=∠3，∴∠1=∠BEF，∴BF=EF，∵∠1=∠2，∴∠BEF=∠2，∴EF=BF，又∵BC+AD=7+1∴BF+CF+AD=8而由（1）知CF+AD=BF∴BF+BF=8∴2BF=8，∴BF=4，∴BF=EF=44、在等腰梯形ABCD中，AD∥BC，AB=AD=CD,∠ABC=60°,延长AD到E,使DE=AD,延长DC到F，使DC=CF,连接BE、BF和EF.⑴求证：△ABE≌△CFB;⑵如果AD=6,tan∠EBC的值.解：（1）证明：连结CE，在△BAE与△FCB中，∵ BA=FC，∠A=∠BCF，， AE=BC，∴△BAE≌△FCB；（2）延长BC交EF于点G，作AH⊥BG于H，作AM⊥BG，∵△BAE≌△FCB，∴∠AEB=∠FBG，BE=BF，∴△BEF为等腰三角形，AB DECF又∵AE∥BC，∴∠AEB=∠EBG，∴∠EBG=∠FBG，∴BG⊥EF，∵∠AMG=∠EGM=∠AEG=90°，∴四边形AMGE为矩形，∴AM=EG，在Rt△ABM中，AM=AB•sin60°=6× =，∴EG=AM=，BG=BM+MG=6×2+6×cos60°=15，∴tan∠EBC=5、已知：AC是矩形ABCD的对角线，延长CB至E，使CE=CA，F是AE的中点，连接DF、CF 分别交AB于G、H点（1）求证：FG=FH；（2）若∠E=60°，且AE=8时，求梯形AECD的面积．（1）证明：连接BF∵ABCD为矩形∴AB⊥BC AB⊥AD AD=BC∴△ABE为直角三角形∵F是AE的中点∴AF=BF=BE∴∠FAB=∠FBA∴∠DAF=∠CBF∵AD=BC, ∠DAF=∠CBF ,AF=BF ,∴△DAF≌△CBF∴∠ADF=∠BCF∴∠FDC=∠FCD∴∠FGH=∠FHG∴FG=FH；（2）解：∵AC=CE∠E=60°∴△ACE为等边三角形∴CE=AE=8∵AB⊥BC∴BC=BE==4∴根据勾股定理AB=∴梯形AECD的面积=×(AD+CE)×CD=×(4+8)×=6、如图，直角梯形ABCD中，AD∥BC，∠BCD=90°，且CD=2AD，tan∠ABC=2，过点D作DE ∥AB，交∠BCD的平分线于点E，连接BE．（1）求证：BC=CD；（2）将△BCE绕点C，顺时针旋转90°得到△DCG，连接EG．求证：CD垂直平分EG；（3）延长BE交CD于点P．求证：P是CD的中点．证明：（1）延长DE交BC于F，∵AD∥BC，AB∥DF，∴AD=BF，∠ABC=∠DFC．在Rt△DCF中，∵tan∠DFC=tan∠ABC=2，∴=2，即CD=2CF，∵CD=2AD=2BF，∴BF=CF，∴BC=BF+CF=CD+CD=CD．即BC=CD．（2）∵CE平分∠BCD，∴∠BCE=∠DCE，由（1）知BC=CD，∵CE=CE，∴△BCE≌△DCE，∴BE=DE，由图形旋转的性质知CE=CG，BE=DG，∴DE=DG，∴C，D都在EG的垂直平分线上，∴CD垂直平分EG．（3）连接BD，由（2）知BE=DE，∴∠1=∠2．∵AB∥DE，∴∠3=∠2．∴∠1=∠3．∵AD∥BC，∴∠4=∠DBC．由（1）知BC=CD，∴∠DBC=∠BDC，∴∠4=∠BDP．又∵BD=BD，∴△BAD≌△BPD(ASA)∴DP=AD．∵AD=CD，∴DP=CD．∴P是CD的中点．7、如图，直角梯形ABCD中，∠DAB=90°，AB∥CD，AB=AD，∠ABC=60度．以AD为边在直角梯形ABCD外作等边三角形ADF，点E是直角梯形ABCD内一点，且∠EAD=∠EDA=15°，连接EB、EF．（1）求证：EB=EF；（2）延长FE交BC于点G，点G恰好是BC的中点，若AB=6，求BC的长．（1）证明：∵△ADF为等边三角形，∴AF=AD，∠FAD=60°∵∠DAB=90°，∠EAD=15°，AD=AB∴∠FAE=∠BAE=75°，AB=AF，∵AE为公共边∴△FAE≌△BAE∴EF=EB（2）过C作CQ⊥AB于Q，∵CQ=AB=AD=6，∵∠ABC=60°，∴BC=6÷=．8、已知，矩形ABCD中，延长BC至E，使BE=BD，F为DE的中点，连结AF、CF.求证：(1)∠ADF=∠BCF；(2) AF⊥CF.证明：（1）在矩形ABCD中，∵∠ADC=∠BCD=90°，∴∠DCE=90°，在Rt△DCE中，∵F为DE中点，∴DF=CF，∴∠FDC=∠DCF，∴∠ADC+∠CDF=∠BCD+∠DCF，即∠ADF=∠BCF；（2）连接BF，∵BE=BD，F为DE的中点，∴BF⊥DE，∴∠BFD=90°，即∠BFA+∠AFD=90°，在△AFD和△BFC中AD=BC ∠ADF=∠BCF CF=DF ，∴△ADF≌△BCF，∴∠AFD=∠BFC，∵∠AFD+∠BFA=90°，∴∠BFC+∠BFA=90°，即∠AFC=90°，∴AF⊥FC．9、如图，在直角梯形ABCD中，AD⊥DC，AB∥DC，AB=BC，AD与BC延长线交于点F，G是DC延长线上一点，AG⊥BC于E．（1）求证：CF=CG；（2）连接DE，若BE=4CE，CD=2，求DE的长．解答：（1）证明：连接AC，∵DC∥AB，AB=BC，∴∠1=∠CAB，∠CAB=∠2，∴∠1=∠2；∵∠ADC=∠AEC=90°，AC=AC，∴△ADC≌△AEC，∴CD=CE；∵∠FDC=∠GEC=90°，∠3=∠4，∴△FDC≌△GEC，∴CF=CG．（2）解：由（1）知，CE=CD=2，∴BE=4CE=8，∴AB=BC=CE+BE=10，∴在Rt△ABE中，AE= AB2-BE2 =6，∴在Rt△ACE中，AC= AE2+CE2 =由（1）知，△ADC≌△AEC，∴CD=CE，AD=AE，∴C、A分别是DE垂直平分线上的点，∴DE⊥AC，DE=2EH；（8分）在Rt△AEC中，S△AEC=AE•CE=AC•EH，∴EH===∴DE=2EH=2×=10、如图，在正方形ABCD中，E、F分别为BC、AB上两点，且BE=BF，过点B作AE的垂线交AC于点G，过点G作CF的垂线交BC于点H延长线段AE、GH交于点M．（1）求证：∠BFC=∠BEA；（2）求证：AM=BG+GM．证明：（1）在正方形ABCD中，AB=BC，∠ABC=90°，在△ABE和△CBF中，AB=BC ∠ABC=∠ABC BE=BF ，∴△ABE≌△CBF（SAS），∴∠BFC=∠BEA；（2）连接DG，在△ABG和△ADG中，AB=AD ∠DAC=∠BAC=45°AG=AG ，∴△ABG≌△ADG（SAS），∴BG=DG，∠2=∠3，∵BG⊥AE，∴∠BAE+∠2=90°，∵∠BAD=∠BAE+∠4=90°，∴∠2=∠3=∠4，∵GM⊥CF，∴∠BCF+∠1=90°，又∠BCF+∠BFC=90°，∴∠1=∠BFC=∠2，∴∠1=∠3，在△ADG中，∠DGC=∠3+45°，∴∠DGC也是△CGH的外角，∴D、G、M三点共线，∵∠3=∠4（已证），∴AM=DM，∵DM=DG+GM=BG+GM，∴AM=BG+GM．11、直角梯形ABCD中，AB∥CD，∠C=90°，AB=BC，M为BC边上一点．（1）若∠DMC=45°，求证：AD=AM．（2）若∠DAM=45°，AB=7，CD=4，求BM的值．（1）证明：作AF⊥CD交延长线于点F．∵∠DMC=45°，∠C=90°∴CM=CD，又∵∠B=∠C=∠AFD=90°，AB=BC，∴四边形ABCF为正方形，∴BC=CF，∴BM=DF，在Rt△ABM和Rt△AFD中，AB=AF，∠B=∠AFD=90°，BM=DF，∴△ABM≌△AFD，∴AD=AM．（2）解：把Rt△ABM绕点A顺时针旋转90°，使AB与AE重合，得Rt△AFN．∵∠DAM=45°，∴∠BAM+∠DAF=45°，由旋转知∠BAM=∠NAF，∴∠DAF+∠NAF=45°，即∠DAM=∠DAN，由旋转知AM=AN，∴△ADM≌△ADN，∴DM=DN，设BM=x，∵AB=BC=CF=7，∴CM=7-x又∵CD=4，∴DF=3，BM=FN=x，∴MD=DN=3+x，在Rt△CDM中，（7-x）2+42=（3+x）2，解得：x=∴BM的值为．答：BM的值为．12、如图，AC是正方形ABCD的对角线，点O是AC的中点，点Q是AB上一点，连接CQ，DP ⊥CQ于点E，交BC于点P，连接OP，OQ；求证：（1）△BCQ≌△CDP；（2）OP=OQ．证明：∵四边形ABCD是正方形，∴∠B=∠PCD=90°，BC=CD，∴∠2+∠3=90°，又∵DP⊥CQ，∴∠2+∠1=90°，∴∠1=∠3，在△BCQ和△CDP中，∠B=∠PCD BC=CD ∠1=∠3 ．∴△BCQ≌△CDP．（2）连接OB．由（1）：△BCQ≌△CDP可知：BQ=PC，∵四边形ABCD是正方形，∴∠ABC=90°，AB=BC，而点O是AC中点，∴BO=AC=CO，∠4=∠ABC=45°=∠PCO，在△BCQ和△CDP中，BQ=CP ∠4=∠PCO BO=CO∴△BOQ≌△COP，∴OQ=OP．。

相关文档
最新文档