第6讲分式方程

合集下载

第6讲一元一次方程与分式方程及其应用PPT课件

A．1 B．－1 C．0 D．2
类型二一元一次方程的解法例2 解下列方程：x－x－2 1＝2－x＋3 2.
【思路分析】根据解一元一次方程的基本步骤解答即可．
【答案】6x－3(x－1)＝12－2(x＋2)， 6x－3x＋3＝12－2x－4，3x＋3＝8－2x， 3x＋2x＝8－3，5x＝5，∴x＝1.
【解后感悟】(1)去分母，方程两边同乘各分母的最小公倍数时，不要漏乘没有分母的项 (尤其是常数项)，若分子是多项式，则要把它看成一个整体加上括号；(2)去括号可用分配律，注意符号，勿漏乘．
4．解方程：(1)(2016·贺州)解方程：x6－30－ 4 x＝5.
【答案】x＝30
(2)7x－12x－21（x－1）＝23(x－1)．
【答案】方程两边都乘以(x－3)得，2－x－m＝ 2(x－3)，∵分式方程有增根，∴x－3＝0，
解得x＝3，
∴2－3－m＝2(3－3)，解得m＝－1.故选A.
【答案】x＝－753.
类型三分式方程的解法
例3 (1)(2015·营口)若关于x的分式方程x－2 3＋3x－＋xm ＝2有增根，则m的值是( )
A．m＝－1 B．m＝0 C．m＝3 D．m＝0或m＝3 【思路分析】方程两边都乘以最简公分母(x－3)，
把分式方程化为整式方程，再根据分式方程的增根就是使最简公分母等于0的未知数的值求出x的值，然后代入进行计算即可求出m的值．
3x＋n 【答案】解方程 2x＋1 ＝2得x＝n－2. ∵关于x的
3x＋n 方程2x＋1＝2的解是负数，∴n－2＜0.解得：n＜2.
1 又∵原方程有意义的条件为：x≠－ 2 ，∴n－2≠
1
3
3
－2，即n≠2.∴n＜2且n≠2.

第6讲：分式方程

２％” 等量关系：５得
解答时要注意验根；二是已知方程有增根，方程中求字母系数；三是分式方程的应用题．外分式方程与此
一
元二次方程相结合的问题也时有出现．
原来每位工人的工作效率 ×（＋２％）１５一现在每位工人的工作效率，而每位工人的工作效率一每天工
５“ 一” ．五江北水城文化旅游节期间，名同学包几
租一辆面包车前去旅游，面包车的租价为１０元，８出
发时又增加了两名同学，结果每个同学比原来少摊了
３元钱车费，设参加游览的同学共人，所列方程则
为（）．
点评本题是以工作效率为背景的常见的分式方程实际问题．实际背景比较复杂，重在考查学生理解能力、分析能力．意在检验时，注还应该考虑是否符合实际．
数学Ｚ鬟Ｈ
。
ＯＧＬＫ，ＮＥｉＸＥ￣
露黧
例３（典题）若解＋一（于关
去分母，到一个整式方程；２解这个整式方程；３得（）（）
检验：把所得的整式方程的解代入
，
— —
使
（）１按此计划，公司平均每天应生产帐篷多少该
顶？
不为０的根就是原方程的根，否则为增
根，根必须增
— —
．
（）产２后，司又从其他部门抽调了５２生天公Ｏ名
４在解分式方程的应用题时，了要检验所列方．除程的根是否为增根外，还要检验．

讲义6：分式方程

七年级上：初一数学提高（1）班辅导讲义6：分式方程及整数指数幂姓名______________辅导时间______【知识要点】1、分式方程：分母中含有未知数的方程。

.解分式方程的基本思想：去分母，把分式方程转化为整式方程解分式方程的一般步骤：（1）去分母：在原方程的两边同时乘以最简公分母，把分式方程转化成整式方程（2）解这个整式方程：得到整式方程的根（3）验根：检验整式方程的根是否为原分式方程的根（把整式方程的根代入最简公分母检验，使最简公分母等于零的根是原方程的增根，必须舍去）（4）写结论：原方程的根为……，或原方程无解列分式方程解应用题和列整式方程解应用题步骤基本相同，但必须注意，要检验求得的解是否为原方程的根，以及是否符合题意。

2、整数指数幂：正整数、0、负整数都可以作指数；幂的有关运算法则依然成立（0和负整数作指数时要求底数不等于0）3、科学计数法的简单应用【基础自测】1、下列方程中是分式方程的是（）A.2413x x +-+ B. 5042x x -+= C. ()34243x x -= D. 142x x +=+ 2、1a =-是下列哪个方程的根？（）A. 21012a a -=++B. 2201a a-=- C. 21012a a +=-+ D. 2212a a =-+ 3、下列运算正确的是（）A. ()224--=B. 2124--=C. 22155x x -=D. ()122xy xy-= 4、下列等式正确的是（）A. ()311--=B. ()()236222-⨯-=C. ()()826555-÷-=-D. ()0241-=5、分式方程5231x x=-的解是______________ 6、若分式方程()()2815x a a x +=--的解为15x =-，则a ＝____________； 7、x ＝1_________（是、不是）方程1111x x x +=--的根8、去分母解关于x 的方程3022x m x x --=--时会产生增根，则m ＝ _______ 9、科学计数法表示：1340000＝ _________________；0.0001034＝ __________________10、写出原数：65.7110-⨯=______________；84.0310-⨯=______________； 11、大小比较：24--，20.2-，0133⎛⎫- ⎪⎝⎭，334-⎛⎫ ⎪⎝⎭：___________________________________ 12、用50克盐加水调制成浓度为25%的盐水，需要加水____________克13、炎炎夏日，甲安装队为A 小区安装66台空调，乙安装队为B 小区安装60台空调，两队恰好同时开工同时完工；甲队比乙队每天多安装2台，设乙队每天安装x 台空调，根据题意，可以列出方程为____________【例题选讲】：1、解方程（1）21211x x =-- （2）3233x x x =+--（3）22254212343x x x x x -=-+-++ （4）23251x x x x x +-=+-2、（1）m 为何值时，关于x 的方程22432x mx x x -+-=+2会产生增根？（2）已知关于x 的方程323-=--x m x x 解为正数,求m 的取值范围.3、计算：（1）()11xy x y --+；（2）()()1122x y x y ----+÷-（3）2110162123733---⎛⎫⎛⎫⎛⎫⎛⎫⋅-+-⋅- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭ （4）()110111432232---⎡⎤⎡⎤⎛⎫⎛⎫-⨯÷+--⎢⎥⎢⎥ ⎪ ⎪⎝⎭⎝⎭⎢⎥⎢⎥⎣⎦⎣⎦4、应用题：（1）轿车和货车同时从上海出发，轿车行270千米到达南京时，货车才行120千米到达无锡，如果轿车每小时比货车多行50千米，那么求轿车的速度（2）一个分数的分母比它的分子大5；如果这个分数的分子加上14，分母减去1，那么所得的分数为原分数的倒数，去这个分数（3）某文具厂加工一种学生画图工具2500套，在加工了1000套后，采用了新技术，使每天的工作效率提高到原来的1.5倍，结果提前5天完成任务。

2014中考总复习第6讲一元一次方程与分式方程

第一部分
复习目标
知识回顾
重点解析
探究拓展
真题演练
一、一元一次方程和分式方程的有关概念 1. 一元一次方程: 只含有这样的方程叫做一元一次方程. 一元一次方程的一般形式为 2. 分式方程: 分母中含有二、等式的性质 1. 性质 1 等式两边加( 或减) a± c= . , 结果仍相等. 用式子表示: 如果 a=b, 那么 . 的方程叫做分式方程. 未知数( 元) , 并且含有未知数的项的次数是 ,
第一部分
复习目标
2. 性质 2 等式两边乘 ac=
知识回顾
重点解析
探究拓展
真题演练
或除以 ( c≠0) .
, 结果仍相等. 用式子表示: 如果 a=b, 那么
c ; 如果 a=b, 那么 a =
三、解一元一次方程的一般步骤 1. 2. 3.
: 在方程两边都乘以各分母的最小公倍数, 注意别漏乘; : 注意括号前的系数与符号; : 把含有未知数的项移到方程的一边, 其他项移到方程的另一边, 注意移项要
第一部分
复习目标
知识回顾
重点解析
探究拓展
真题演练
9. (2013·三明中考)兴发服装店老板用 4 500 元购进一批某款 T 恤衫, 由于深受顾客喜爱, 很快售完, 老板又用 4 950 元购进第二批该款式 T 恤衫, 所购数量与第一批相同, 但每件进价比第一批多了 9 元. ( 1) 第一批该款式 T 恤衫每件进价是多少元?
=0,
则原方程可化为 y2- 2 y+ 2 =0, 解得 y=1 或 y= 2 , 若若
x2 1 y=1, 则 x =1, 此方程无实数解;
5 y= 2
5
5
5

《分式方程》讲义

《分式方程》讲义一、什么是分式方程在我们学习数学的过程中，方程是一个非常重要的概念。

之前我们接触过一元一次方程、二元一次方程等，今天我们要来认识一种新的方程类型——分式方程。

那到底什么是分式方程呢？分式方程是指方程里含有分式，并且分母里含有未知数或含有未知数整式的有理方程。

比如说，像这样的方程：＄＼frac{x}｛x-1} ＝ 2$ ，＄＼frac{2}｛x} ＋ 3 ＝ 5$ ，它们都是分式方程。

因为在这些方程中，分母中都含有未知数。

二、分式方程的解法接下来，我们重点来学习一下分式方程的解法。

解分式方程的一般步骤可以总结为以下几步：1、去分母这是解分式方程最为关键的一步。

我们要找到所有分式的最简公分母，然后将方程两边同时乘以这个最简公分母，把分式方程化为整式方程。

例如，对于方程＄＼frac{x}｛x-1} ＝ 2$ ，最简公分母是＄x 1$ ，方程两边同时乘以＄x 1$ ，得到＄x ＝ 2(x 1)＄。

2、解整式方程完成去分母后，我们得到了一个整式方程。

接下来，按照解整式方程的方法求解这个方程。

就以上面得到的整式方程＄x ＝ 2(x 1)＄为例，展开得到＄x ＝2x 2$ ，移项可得＄2x x ＝ 2$ ，即＄x ＝ 2$ 。

3、检验这一步非常重要，却很容易被忽略。

我们将求得的解代入原分式方程的分母中，如果分母不为零，那么这个解就是原分式方程的解；如果分母为零，那么这个解就是增根，原分式方程无解。

还是以方程＄＼frac{x}｛x-1} ＝ 2$ 为例，把＄x ＝ 2$ 代入分母＄x 1$ ，＄2 1 ＝ 1$ ，不为零，所以＄x ＝ 2$ 是原方程的解。

三、分式方程的增根在解分式方程的过程中，增根是一个需要特别关注的概念。

增根是分式方程化为整式方程后，产生的使分式方程的分母为零的根。

为什么会产生增根呢？这是因为在去分母的过程中，我们乘以了一个含有未知数的式子，这个式子有可能为零。

而等式两边同乘以零是不符合数学规则的，所以可能会产生额外的根，也就是增根。

第06课时分式方程及其应用PPT课件

根据题意得:26a+35(200-a)=6280,
(2)若两种芯片共购买了 200 条,且购买的总费用为 6280 元,求购
解得:a=80.
买了多少条 A 型芯片?
答:购买了 80 条 A 型芯片.
+3
例 1 [2017·宁夏] 解方程:
-
4
-3 +3
=1.
[方法模型] 解分式方程时易出现的错误:
(1)漏乘没有分母的项;
(2)没有验根;
(3)去分母时,没有注意符号的变化.
解:去分母,得 x2+6x+9-4x+12=x2-9,
移项、合并同类项,得 2x=-30,
系数化为 1,得 x=-15,
)
B.4
=1 的解为 x=2,则 m
C.3
D.2
-1
=1 的解
为 x=2,∴x=2 满足关于 x 的分式方程
-3
-1
-3
=1,∴
2-1
=1,解得 m=4.故选 B.
高频考向探究
探究三分式方程的应用
例 3 [2018·岳阳] 为落实党中央“长江大保护”新发展理念,我
市持续推进长江岸线保护,还洞庭湖和长江水清岸绿的自然
完成的绿化面积的 2 倍,并且甲工程队完成 300 平方米的绿化
面积比乙工程队完成 300 平方米的绿化面积少用 3 小时.乙工
程队每小时能完成多少平方米的绿化面积?
解:设乙工程队每小时能完成 x 平方米的
300 300
绿化面积.根据题意,得

-
2
=3.
解得 x=50.
经检验,x=50 是分式方程的解且符合题意.

一元一次方程与分式方程及其应用

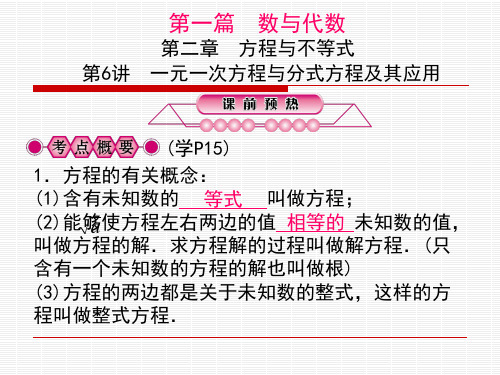
C．x＝2
4．(2014·扬州)某漆器厂接到制作480件漆器的订单，为了尽快完成任务，该厂实际每天制作的件数比原来每天多50%，结果提前10天完成任务，则 16 原来每天制作件．
第一篇数与代数
第二章方程与不等式第6讲一元一次方程与分式方程及其应用
(学P15) 1．方程的有关概念： (1)含有未知数的等式叫做方程； (2)能够使方程左右两边的值相等的未知数的值， a 叫做方程的解．求方程解的过程叫做解方程．(只含有一个未知数的方程的解也叫做根) (3)方程的两边都是关于未知数的整式，这样的方程叫做整式方程．
2．一元一次方程和分式方程 (1)只含有一个未知数，且未知数的次数是一次，这样的整式方程叫做一元一次方程；一元一次方程的一般式形式是ax＋b＝0(a≠0)． (2)分母里含有未知数的方程叫做分式方程． 3．一元一次方程和分式方程的解法 (1)解一元一次方程主要有以下步骤：去分母；去括号；移项；合并同类项；未知数的系数化为1； (2)解分式方程的步骤：①去分母，转化为整式方程； ②解整式方程，得根；③验根．
【答案】解：设九(1)班人均捐款x元，则九(2)班人均捐款(1＋20%)x＝1.2x元，根据题意列方程得：
1200 1200 ＝8，解之得x＝25. x 1.2 x
检验：当x＝25，分母不为0， ∴x＝25是原方程的根．当x＝25时，1.2x＝30. 答：这两个班级每班的人均捐款数分别为25元和30元．
【解后感悟】本题是分式方程的解和解一元一次不等式，关键是得出n－2＜0和n－2≠－，注意题目中的隐含条件2x＋1≠0，不要忽略．
1．如果方程x＋2＝0与方程2x－a＝0的解相同，那么a＝－4 ． a x 2．已知关于x的方程2＋ x 1 x 1 有增根，则a的值是( A )

第06讲分式方程(讲义)(原卷版)-2024年中考数学一轮复习讲义

第06讲分式方程目录一、考情分析二、知识建构考点一解分式方程题型01 判断分式方程题型02 分式方程的一般解法题型03 分式方程的特殊解法类型一分组通分法类型二分离分式法类型三列项相消法类型四消元法题型04 错看或错解分式方程问题题型05 解分式方程的运用（新定义运算）题型06 根据分式方程解的情况求值题型07 根据分式方程有解或无解求参数题型08 已知分式方程有增根求参数题型09 已知分式方程有整数解求参数考点二分式方程的应用题型01 列分式方程题型02 利用分式方程解决实际问题类型一行程问题类型二工程问题类型三和差倍分问题类型四销售利润问题考点一解分式方程分式方程的概念：分母中含有未知数的方程叫做分式方程．增根的概念：在方程变形时，有时可能产生不适合原方程的根，这种根叫做方程的增根.1.分式方程与整式方程的根本区别：分母中含有未知数，也是判断分式方程的依据.2. 去分母时要把方程两边的式子作为一个整体，记得不要漏乘整式项.3. 分式方程的结果还要代回方程的最简公分母中，只有最简公分母不是零的解才是原方程的解．4. 分式方程的增根是去分母后的整式方程的根，也是使分式方程的公分母为0的根，它不是原分式方程的根．5. 解分式方程可能产生使分式方程无意义的根，检验是解分式方程的必要步骤.6. 分式方程有增根与无解并非是同一个概念．分式方程无解，需分类讨论：可能是解为增根，也可能是去分母后的整式方程无解.题型01 判断分式方程题型02 分式方程的一般解法解分式方程方法：先通过方程两边同乘最简公分母将分式方程化为整式方程，再解整式方程，最后需要检验整式方程的解是不是分式方程的解.题型03 分式方程的特殊解法类型一分组通分法方法简介：如果整个方程一起通分，计算量大又易出错，观察方程中分母的特点可联想分组通分求解.类型二分离分式法方法简介：每个分式的分母与分子相差1，利用这个特点可采用分类分式法求解类型三列项相消法方法简介：根据分式方程的结果特点，依据公式“1n(n+1)=1n−1n+1”化积为差，裂项相消，简化难度.类型四消元法方法简介：当方程中的分式互为倒数,或不同分式中的分母互为相反式,或方程中分子、分母的二次项与一次项分别相同时,可考虑用换元法.题型04 错看或错解分式方程问题+1，其中x=先化简，再求值：3−xx−4⋅(x−4)+(x−4)解：原式=3−xx−4=3−x+x−4=−1题型05 解分式方程的运用（新定义运算）题型06 根据分式方程解的情况求值由分式方程的解的情况求字母系数的取值范围，一般解法是：①根据未知数的范围求出字母的范围；②把使分母为0的未知数的值代入到去分母后的整式方程中，求出对应的字母系数的值；③综合①②，求出字母系数的范围.题型07 根据分式方程有解或无解求参数已知分式方程的解确定字母参数，首先将分式方程化为整式方程，用含字母参数的代数式表x，再根据解的情况确定字母参数的取值. 同时要注意原分式方程的最简公分母不能为零.题型08 已知分式方程有增根求参数依据分式方程的增根确定字母参数的值的一般步骤：1)先将分式方程转化为整式方程;2)由题意求出增根;3)将增根代入所化得的整式方程，解之就可得到字母参数的值.题型09 已知分式方程有整数解求参数考点二分式方程的应用用分式方程解决实际问题的步骤：审：理解并找出实际问题中的等量关系;设：用代数式表示实际问题中的基础数据;列：找到所列代数式中的等量关系，以此为依据列出方程;解：求解方程;验：考虑求出的解是否具有实际意义;+1）检验所求的解是否是所列分式方程的解.2）检验所求的解是否符合实际意义.答：实际问题的答案.与分式方程有关应用题的常见类型：题型01 列分式方程【例1】（2022·云南·中考真题）某地开展建设绿色家园活动，活动期间，计划每天种植相同数量的树木，该A．1.4−x=8 1.4+x=8 1.4−2x=8 1.4+2x=8题型02 利用分式方程解决实际问题类型一行程问题【例2】（2022·四川自贡·统考中考真题）学校师生去距学校45千米的吴玉章故居开展研学活动，骑行爱好者张老师骑自行车先行2小时后，其余师生乘汽车出发，结果同时到达；已知汽车速度是自行车速度的3倍，求张老师骑车的速度．【变式2-1】（2023青岛市一模）小李从A地出发去相距4.5千米的B地上班，他每天出发的时间都相同．第一天步行去上班结果迟到了5分钟．第二天骑自行车去上班结果早到10分钟．已知骑自行车的速度是步行速度的1.5倍：(1)求小李步行的速度和骑自行车的速度分别为多少千米每小时；(2)有一天小李骑自行车出发，出发1.5千米后自行车发生故障．小李立即跑步去上班（耽误时间忽略不计）为了至少提前5分钟到达．则跑步的速度至少为多少千米每小时？类型二工程问题【例3】（2023重庆市模拟预测）为方便群众出行，甲、乙两个工程队负责修建某段通往高铁站的快线，已知甲队每天修路的长度是乙队的1.5倍，如果两队各自修建快线600m，甲队比乙队少用4天．(1)求甲，乙两个工程队每天各修路多少米？(2)现计划再修建长度为3000m的快线，由甲、乙两个工程队来完成．若甲队每天所需费用为1万元，乙队每天所需费用为0.6万元，求在总费用不超过38万元的情况下，至少安排乙工程队施工多少天？【变式3-1】（2023·重庆渝中·重庆巴蜀中学校考一模）重庆市潼南区是中国西部绿色菜都，为全市人民提供了新鲜多样的蔬菜．今年，区政府着力打造一个新的蔬菜基地，计划修建灌溉水渠1920米，由甲、乙两，而乙施工队单独修建这个施工队合作完成．已知乙施工队每天修建的长度是甲施工队每天修建的长度的43项工程需要的天数比甲施工队单独修建这项工程需要的天数少4天．(1)求甲、乙两施工队每天各修建多少米？(2)若甲施工队每天的修建费用为13万元，乙施工队每天的修建费用为15万元，实际修建时先由甲施工队单独修建若干天，再由甲、乙两个施工队合作修建，恰好12天完成修建任务，求共需修建费用多少万元？类型三和差倍分问题【例4】（2022·广东深圳·深圳中学校考一模）2022年北京冬奥会吉祥物冰墩墩深受大家的喜欢．某商家两次购进冰墩墩进行销售，第一次用22000元，很快销售一空，第二次又用48000元购进同款冰墩墩，所购进数量是第一次的2倍，但单价贵了10元．(1)求该商家第一次购进冰墩墩多少个？(2)若所有冰墩墩都按相同的标价销售，要求全部销售完后的利润率不低于20%（不考虑其他因素），那么每个冰墩墩的标价至少为多少元？【变式4-1】（2022·河南·统考中考真题）近日，教育部印发《义务教育课程方案》和课程标准（2022年版），将劳动从原来的综合实践活动课程中独立出来．某中学为了让学生体验农耕劳动，开辟了一处耕种园，需倍，用300元在市场上要采购一批菜苗开展种植活动．据了解，市场上每捆A种菜苗的价格是菜苗基地的54购买的A种菜苗比在菜苗基地购买的少3捆．(1)求菜苗基地每捆A种菜苗的价格．(2)菜苗基地每捆B种菜苗的价格是30元．学校决定在菜苗基地购买A，B两种菜苗共100捆，且A种菜苗的捆数不超过B种菜苗的捆数．菜苗基地为支持该校活动，对A，B两种菜苗均提供九折优惠．求本次购买最少花费多少钱．【变式4-2】（2021·山东济南·统考中考真题）端午节吃粽子是中华民族的传统习俗．某超市节前购进了甲、乙两种畅销口味的粽子．已知购进甲种粽子的金额是1200元，购进乙种粽子的金额是800元，购进甲种粽子的数量比乙种粽子的数量少50个，甲种粽子的单价是乙种粽子单价的2倍．（1）求甲、乙两种粽子的单价分别是多少元？（2）为满足消费者需求，该超市准备再次购进甲、乙两种粽子共200个，若总金额不超过1150元，问最多购进多少个甲种粽子？【变式4-3】（2022·山东烟台·统考中考真题）扫地机器人具备敏捷的转弯、制动能力和强大的自主感知、规划能力，深受人们喜爱．某商场根据市场需求，采购了A，B两种型号扫地机器人．已知B型每个进价比A型的2倍少400元．采购相同数量的A，B两种型号扫地机器人，分别用了96000元和168000元．请问A，B两种型号扫地机器人每个进价分别为多少元？类型四销售利润问题【例5】（2023梁山县三模）某商场计划销售A，B两种型号的商品，经调查，用1500元采购A型商品的件数是用600元采购B型商品的件数的2倍，一件A型商品的进价比一件B型商品的进价多30元．（1）求一件A，B型商品的进价分别为多少元？（2）若该商场购进A，B型商品共100件进行试销，其中A型商品的件数不大于B型的件数，已知A型商品的售价为200元/件，B型商品的售价为180元/件，且全部能售出，求该商品能获得的利润最小是多少？【变式5-1】（2023银川市二模）某商场购进甲、乙两种商品，甲种商品共用了2000元，乙种商品共用了2400元．已知乙种商品每件进价比甲种商品每件进价多8元，且购进的甲、乙两种商品件数相同．（1）求甲、乙两种商品的每件进价；（2）该商场将购进的甲、乙两种商品进行销售，甲种商品的销售单价为60元，乙种商品的销售单价为88元，销售过程中发现甲种商品销量不好，商场决定：甲种商品销售一定数量后，将剩余的甲种商品按原销售单价的七折销售；乙种商品销售单价保持不变．要使两种商品全部售完后共获利不少于2460元，问甲种商品按原销售单价至少销售多少件？。

第6讲分式方程(讲义)解析版

第6讲分式方程模块一：分式方程及其解法知识精讲1、分式方程的概念分母中含有未知数的方程叫做分式方程．2、解分式方程的方法通过去分母把分式方程转化为整式方程，再求解．3、增根的概念分式方程在化整式方程求解过程中，整式方程的解如果使得分式方程中的分母为0，那么这个解就是方程的增根．4、解分式方程的一般步骤（1）方程两边都乘以最简公分母，去分母，化成整式方程；（2）解这个整式方程，求出整式方程的根；（3）检验．有两种方法：①将求得的整式方程的根代入最简公分母，如果最简公分母等于0，则这个根为增根，方程无解；如果最简公分母不等于0，则这个根为原方程的根，从而解出原方程的解；②直接代入原方程中，看其是否成立．如果成立，则这个根为原方程的根，从而解出原方程的解；如果不成立，则这个根为增根，方程无解．5、分式方程组的概念由两个或两个以上的分式方程构成的方程组叫做分式方程组．6、解分式方程组的方法找出分式方程组中相同的分式进行换元，将分式方程组转化为整式方程组，解方程组，然后进行检验．例题解析例1．（1）下列方程中，是分式方程的为（）A ．12x -=B 1=C 10-=D 1=【答案】C【分析】根据分式方程的定义：分母里含有字母的方程叫做分式方程进行判断．【详解】A. 是整式方程，故选项错误；B. 是整式方程，故选项错误；分母中含有未知数x ，所以是分式方程，故选项正确；D. 是整式方程，故选项错误.故选C.【点睛】此题考查分式方程的判定，掌握分式方程的定义是解题的关键.（2）在3253x +=；11(1)(1)432x x ++-=；21x -=；2371x x x ++=-；1(37)x x-中，分式方程有（）．A ．1个B ．2个C ．3个D ．4个【难度】★【答案】B【解析】根据分式方程的定义，分母中含有未知数的方程是分式方程，（1）（2）两个方程分母中不含未知数，（5）不是方程，（3）（4）满足定义，故选B ．【总结】考查分式方程的定义，注意前提是方程，且方程分母中必含有字母．例2．（1）用换元法解分式方程251x x +21x x+-+1=0，如果设21x x +=y ，那么原方程可以化为（）A ．2+y y -5=0B ．2y -5y+1=0C ．25y y 10++=D ．25y 10y +-=【答案】D【分析】直接把21xx +换成y ，整理即可．【详解】解：设21xy x =+，则原方程化为1510y y -+=，去分母得，25y 10y +-=，故选：D ．【点睛】本题考查的是换元法解分式方程，换元的实质是转化，关键是构造元和设元，理论依据是等量代换，目的是变换研究对象，将问题移至新对象的知识背景中去研究，从而使非标准型问题标准化、复杂问题简单化，变得容易处理．（2）.用换元法解方程221165380x x x x æöæö+++-=ç÷ç÷èøèø，设1y x x =+，则方程变为()A ．265380y y +-=B ．265400y y +-=C ．265260y y +-=D ．265500y y +-=【难度】★【答案】D【解析】1y x x =+，则有22221122x x y x x æö+=+-=-ç÷èø，原方程即为()2625380y y -+-=，展开整理即为265500y y +-=，故选D ．【总结】考查分式方程中换元法的应用，注意含有未知数部分的恒等变形转化．例3.分式方程2227381x x x x x +=+--的最简公分母是____________．【难度】★【答案】3x x -．【解析】分式方程中三个分母位置上分别为2x x +，2x x -，21x -，分解因式的结果分别为()1x x +，()1x x -，()()11x x +-，由此可得方程的最简公分母为()()311x x x x x +-=-．【总结】考查分式方程的最简公分母，将每个分母因式分解，取相同因式的最高次数乘积即为分式方程的最简公分母．例4.直接写出下列分式方程的根：（1）11211x x x -=---：_________________；（2）11111x x x -=---：_________________；（3）2121x x -=-：_________________；（4）2111x x -=-：_________________．【难度】★【答案】（1）2x =；（2）无解；（3）无解；（4）0x =．【解析】（1）根据等式性质，两边同时加上分式部分，即得2x =，检验得2x =是原分式方程的根；（2）根据等式性质，两边同时加上分式部分，即得1x =，检验得1x =为方程的增根，即方程无解；（3）约分得12x +=，解得1x =，检验得1x =为方程的增根，即方程无解；（4）约分得11x +=，解得0x =，检验得0x =是原分式方程的根．【总结】考查根据等式的性质求解简单的分式方程，注意求解结果是否是增根．例5.解方程：（1）3363142x x -=-+；（2）43252x xx x =++；（3）23312222x x x x x ++=--+-．【难度】★★【答案】（1）123x =，29x =-；（2）10x =，267x =-；（3）无解．【解析】（1）方程两边同乘()()43123x x -+，得()()()()42312831x x x x +--+=-，整理得2325180x x +-=，解得123x =，29x =-，经检验，123x =，29x =-都是原方程的根；（2）方程两边同乘()()3252x x ++，得()()52432x x x x +=+，整理得2760x x +=，解得：10x =，267x =-，经检验，10x =，267x =-都是原方程的根；（3）方程两边同乘()()212x x +-，得()()()63221x x x ++-=+，整理得220x x --=，解得：11x =-，22x =，经检验，11x =-，22x =都是原方程的增根，即原方程无解．例6.解方程：（1）2213211x x x x -=+--；（2）24221422x x x x =++--+；（3）23211214124x x x x++=+--．【难度】★★【答案】（1）13x =-；（2）6x =；（3）54x =．【解析】（1）方程两边同乘21x -，得()221213x x x x +=-+-，整理得23210x x --=，解得：113x =-，21x =，经检验，21x =是原方程的增根，即原方程的根为13x =-；（2）方程两边同乘24x -，得()()2442222x x x x =--++-，整理得24120x x --=，解得：16x =，22x =-，经检验，22x =-是原方程的增根，即原方程的根为6x =；（3）两边同乘()2241x -，得()()()2621421241x x x x -+-+=-，整理得281450x x -+=，解得：112x =，254x =，经检验，112x =是原方程的增根，即原方程的根为54x =．【总结】考查分式方程的解法，注意检验所求是否为增根．例7.已知关于x 的方程22312x m x x x +-=-+-有增根，求m 的值．【难度】★★【答案】12m =或3m =．【解析】分式方程两边同乘22x x +-，得()223x m +=-，分式方程有增根，由220x x +-=，解得：11x =，22x =-，即为原分式方程的增根，代入相应整式方程得39m -=或30m -=，解得12m =或3m =．【总结】考查分式方程的增根，代入相应的整式方程可使得方程成立且使得分式分母为0的未知数的值．例8.已知关于x 的方程7155x m xx x--=---无解，求m 的值．【难度】★★【答案】3m =．【解析】分式方程两边同乘5x -，得()75x x m x -=---，整理解得：2x m =+，因为原分式方程无解，则相应解应为分式方程的增根，即得25x m =+=，解得3m =．【总结】考查分式方程的无解，即由相应整式方程求得的解是分式方程的增根．例9.已知关于x 的方程301a xx +-=+的根是负数，求a 的取值范围．【难度】★★【答案】3a <且1a ≠．【解析】分式方程两边同乘1x +，得()310a x x +-+=，整理解得：32a x -=，方程的根是负数，则有302a x -=<，得3a <，同时分式方程的根不能为相应增根，即312a x -=≠-，得1a ≠，由此即得3a <且1a ≠．【总结】考查分式方程的解满足条件的求解，注意方程的解不能为相应的增根．例10.解方程：（1）2220383x x x x+-=+；（2）2191502x x x x æöæö+-++=ç÷ç÷èøèø．【难度】★★【答案】（1）15x =-，22x =，31x =-，42x =-；（2）11x =，22x =，312x =．【解析】（1）令23x x a +=，原方程即为208a a-=，两边同乘a 整理得28200a a --=，解得：110a =，22a =-；由2310x x +=，解得：15x =-，22x =；由232x x +=-，解得：11x =-，22x =-；经检验，15x =-，22x =，31x =-，42x =-都是原方程的根；（2）令1x a x +=，原方程即为29502a a -+=，解得12a =，252a =；由12x x+=，整理得2210x x -+=，解得：121x x ==；由152x x +=，整理得22520x x -+=，解得12x =，212x =；经检验，11x =，22x =，312x =都是原方程的根．【总结】考查用换元法求解具有特殊形式的分式方程，注意对方法的总结．例11.解方程：（1）225(16(1)1711x x x x +++=++）；（2）2216104()933x x x x+=-．【难度】★★【答案】（1）1x =2x =（2）13x =，23x =，32x =-，46x =．【解析】（1）令211x a x +=+，原方程即为6517a a +=，两边同乘a 整理得251760a a -+=，解得：125a =，23a =；由21215x x +=+，整理得25230x x -+=，方程无解；由2131x x +=+，整理得2320x x --=，解得：1x 2x =经检验，1x =2x = （2）令43x a x -=，则有2222164889333x x a x x æö+=-+=+ç÷èø，原方程即为281033a a +=，整理得231080a a -+=，解得：12a =，243a =；由423x x-=，整理得26120x x --=，解得：13x =，23x =；由4433x x -=，整理得24120x x --=，解得：12x =-，26x =；经检验，13x =+23x =-，32x =-，46x =都是原方程的根．【总结】考查用换元法求解有特殊形式的分式方程．例12.解方程组：（1）413538x y x y x y x y ì+=ï+-ïíï-=ï+-î；（2）132013251x y x y ì+=ï-ïíï-=-ï-î．【难度】★★【答案】（1）01x y =ìí=î；（2）565x y =ìïí=ïî．【解析】（1）令1a x y =+，1b x y =-，原方程组即为43538a b a b +=ìí-=î，解得：11a b =ìí=-î，由此可得11x y =+，11x y =--，由此得11x y x y +=ìí-=-î，解得：01x y =ìí=î，经检验，01x y =ìí=î是原分式方程的根；（2）令11a y =-，原方程组即为320235x a x a +=ìí-=-î，解得：55x a =ìí=î，由此可得：151y =-，解得：65y =， ∴565x y =ìïí=ïî，经检验，565x y =ìïí=ïî是原分式方程的根．【总结】考查利用换元法求分式方程组的解，注意解完之后要检验．例13.解方程组：（1）253489156x x x x +=+++++；（2）11212736x x x x x x ++-=-++++．【难度】★★【答案】（1）16x =，2334x =-；（2）92x =-．【解析】（1）对分式方程移项通分得()()()()()()()()21538495681569x x x x x x x x +-++-+=++++，展开即得2266231201554x x x x x x -+-+=++++，由此即得60x -+=或22231201554x x x x ++=++，解得：16x =，2334x =-，经检验，16x =，2334x =-都是原分式方程的根；（2）对分式方程变形得1111112736x x x x --=--++++，由此得11112736x x x x +=+++++，两边分别通分即得222929914918x x x x x x ++=++++，两边分母不同，则必有290x +=，解得92x =-，经检验，92x =-是原分式方程的根．【总结】考查特殊形式分式方程的解法，注意相应分母的关系，分组两边分别通分计算．例14.解方程：226205x x +-=+．【难度】★★【答案】11x =，21x =-．【解析】令25x a +=，则有25x a =-，原方程即为6520a a+--=，两边同乘a 整理，得2760a a -+=，解得：11a =，26a =；由251x +=，方程无解；由256x +=，解得：11x =，21x =-；经检验，11x =，21x =-都是原方程的根．【总结】考查用换元法解分式方程，注意取值范围和增根．例15.a 为何值时，关于x 的方程211a a x +=+无解?【难度】★★【答案】12a =-或0a =．【解析】分式方程两边同乘1x +，得：()211a a x +=+，展开移项得1ax a =+，当0a =时，方程无解；当0a ≠时，1a x a +=，方程无解，即得11a x a+==-，解得12a =-；综上，12a =-或0a =．【总结】考查分式方程的无解，即由相应整式方程求得的解是分式方程的增根，注意考虑未知项系数为0的情况．例16.已知关于x 的方程222022x x x k x x x x-+++=--只有一个解，求k 的值及这个解．【难度】★★★【答案】72k =-时，1212x x ==或4k =-时，1x =或8k =-时，1x =-．【解析】方程两边同乘22x x -，得()22220x x x k +-++=，展开整理得：22240x x k -++=，分式方程可能产生增根，即当相应整式方程有两解时，分式方程仅有一解，由此需进行分类讨论：①当整式方程有两相等实数根时，()()224240k ∆=--⨯+=，解得：72k =-，此时方程为212202x x -+=，解得：1212x x ==，此时分式方程只有一个解，符合题意；②当整式方程有一根为分式方程增根0x =时，此时有40k +=，解得：4k =-，此时方程为2220x x -=，解得：10x =，21x =，此时分式方程只有一个解1x =，符合题意；③当整式方程有一根为分式方程增根2x =时，此时有2222240k ⨯-⨯++=，解得：8k =-，此时方程为22240x x --=，解得：12x =，21x =-，此时分式方程只有一个解1x =-，符合题意；综上，72k =-或4k =-或8k =-．【总结】考查分式方程只有一个解的情况，方程为二次方程时，注意包含方程有一个根为分式方程的增根的情形．例17.解关于x 的方程：22112(3()1x x x x+-+= 【难度】★★★【答案】12x =，212x =．【解析】令1x a x +=，则有22221122x x a x x æö+=+-=-ç÷èø，原方程即为()22231a a --=，展开整理得22350a a --=，解得：11a =-，252a =；由11x x+=-，整理得210x x ++=，方程无解；由152x x +=，整理得22520x x -+=，解得：12x =，212x =；经检验，12x =，212x =都是原方程的根．【总结】考查用换元法求解有特殊形式的分式方程，注意解完之后进行检验．例18.解关于x 的方程()()450b x a xa b b x a x+-=-+≠+-．【难度】★★★【答案】12a b x -=，245a bx -=．【解析】令a x kb x -=+，原方程即为45k k=-，两边同乘k 整理，得2540k k -+=，解得：11k =，24k =；由1a x b x -=+，又0a b +≠，可解得：2a bx -=；由4a x b x -=+，又0a b +≠，可解得：45a bx -=；经检验，12a b x -=，245a bx -=都是原方程的根．【总结】考查用换元法求解有特殊形式的分式方程．例19.已知方程22222(1)21()x ax a a x a +-++=+有实数根，求实数a 的取值范围．【难度】★★★【答案】1122a -≤≤且0a ≠．【解析】展开得()()22222222121x ax a ax a a x a +--+++=+，根据等式性质移项得()()222220x ax a ax x a +-+=+，即为()20x a x a x a ⎡⎤+-=⎢⎥+⎣⎦，由此得()0xa x a x a+-=+，移项得()2a x a x +=，展开整理得()223210ax a x a +-+=，当0a =时，方程有实数根0x =是分式方程的增根，应舍去；当0a ≠时，方程为一元二次方程，此时根据韦达定理可得2122112a x x a a a-+=-=-，可知1x 、2x 不可能同时为a -，分式方程有实数根，则相应的整式方程应满足()2232214410a a a a ∆=--⋅=-+≥，得1122a -≤≤；综上，实数a 的取值范围为：1122a -≤≤且0a ≠．【总结】考查分式方程有实数根的情形，对分式方程整理变形满足相应的条件即可．模块二分式方程应用题知识精讲1、列方程（组）解应用题时，如何找“相等关系”（1）利用题目中的关键语句寻找相等关系；（2）利用公式、定理寻找相等关系；（3）从生活、生产实际经验中寻找相等关系．例题解析例1.要在规定日期内完成一项工程，如甲队单独做，刚好按期完成；如乙队单独做，则要超过规定时间3天才能完成；甲、乙两队合作2天，剩下的工程由乙队单独做，则刚好按期完成.那么求规定日期为x天的方程是（）．A．2213xx x-+=+B．233x x=+C．2213xx x++=+D．213xx x+=+【难度】★【答案】D【解析】设工作总量为“1”，则甲工作量+乙工作量=1，根据工作总量=工作效率×工作天数，乙工作天数为x天，由此可知选D．【总结】考查工程问题中的单位“1”，注意分清对应的工作效率和工作时间．例2.某车间加工300个零件，在加工80个以后，改进了操作方法，每天能多加工15个，一共用6天完成了任务.如果设改进操作后每天加工x个零件，那么下列根据题意列出的方程中，错误的是（）A．8030080615x x-+=-B．30080615x-=-C．80(6)8030015xx-+=-D．8015300806xx-=--【难度】★【答案】B 【解析】略【总结】考查根据题意列方程的应用，根据工作量和工作效率、工作时间之间的相互关系进行列方程的应用．例3.甲、乙两个工程队合做一项工程，6天可以完成．如果单独工作，甲队比乙队少用5天完成．两队单独工作各需多少天完成?【难度】★★【答案】甲单独需10天完成，乙单独需15天完成．【解析】设甲单独需用x天完成，则乙单独需用()5x+天完成，依题意可得11615x xæö+=ç÷+èø，整理得27300x x--=，解得：13x=-，210x=，经检验，13x=-，210x=都是原方程的根，但13x=-不合题意应舍去，即得10x=，即甲单独需10天完成，乙单独需10515+=天完成．【总结】考查工程问题中的列方程解应用题，把工作总量当作单位“1”解题．例4.登山比赛时，小明上山时的速度为a米/分，下山的速度是b米/分，已知上山和下山的路径是一样的，求小明在全程中的平均速度?【难度】★★【答案】2aba b+．【解析】设小明上山的路程为sm，则整个过程中小明总行程为2sm，根据平均速度=总行程÷总时间，即得平均速度22s abvs s a ba b==++．【总结】考查平均速度的求取，平均速度==总行程÷总时间，与行程远近无关，注意平均速度的求法．例5.甲、乙两人分别从相距9千米的A、B两地同时出发，相向而行，1小时后相遇．相遇后，各自继续以原有的速度前进，已知甲到B地比乙到A地早27分钟，求两人的速度各是多少?【难度】★★★【答案】甲速度为5/km h，乙速度为4/km h．【解析】设甲速度为/xkm h，则乙速度为()9/x km h-，927min20h=，依题意可得999920x x-=-，整理得2311800x x+-=，解得：136x=-，25x=，经检验，136x=-，25x=都是原方程的根，但136x=-不合题意应舍去，即得5x=，即甲速度为5/km h，乙速度为954/km h-=．【总结】考查行程问题中的列方程解应用题，根据相遇问题的基本关系一个条件作设一个条件列式进行求解．例6.甲、乙两辆车同时从A地出发开往距A地240千米的B地，结果甲车比乙车早到了60分钟；第二次，乙车提速30千米/时，结果比甲车早到了20分钟，求第一次甲、乙两车的速度各是多少?【难度】★★★【答案】甲速度为80/km h，乙速度为60/km h．【解析】设甲车xh到达B地，60min1h=，120min3h=，依题意可得24024030113xx-=+-，整理得232330x x+-=，解得1113x=-，23x=，经检验，111 3x=-，23x=都是原方程的根，但111 3x=-不合题意应舍去，即得3x=，可得甲速度为24080/3km h=，乙速度为24060/31km h=+．【总结】考查行程问题中的列方程解应用题，根据行程问题的基本等量关系一个条件作设一个条件列式进行求解，注意本题中用时间作设速度列式解题更方便．例7.某服装厂接到一宗生产13万套衣服的业务，在生产了4万套后，接到了买方急需货物的通知，为满足买方的要求，该厂改进了操作方法，每月能多生产1万套，一共5个月完成了这宗业务．求改进操作方案后每月能生产多少万套衣服?【难度】★★★【答案】3万套．【解析】设改进操作方案后每月能生产x 万套衣服，则改进之前每月生产()1x -万套，依题意可得413451x x -+=-，整理得251890x x -+=，解得：135x =，23x =，经检验，135x =，23x =都是原方程的根，但135x =不合题意应舍去，即得：3x =，即改进操作方案后每月能生产3万套衣服．【总结】考查工作总量问题，一个条件作设一个条件列式进行求解．随堂检测1.已知方程：（1）2412x x -=-；（2）221x x =-；（3）11x x x æö-=ç÷èø；（43x -=，其中是分式方程的有_____________．【难度】★【答案】（1）、（2）、（3）．【解析】根据分式方程的定义，分母中含有未知数的方程是分式方程，（1）、（2）、（3）满足条件，（4）方程中不含有分式，故答案为（1）、（2）、（3）．【总结】考查分式方程的定义，注意前提是方程，且方程分母中必含有字母．2.当x 取何值时，分式方程1112x x x +=--的最简公分母的值等于0?【难度】★【答案】1x =或2x =．【解析】分式方程的最简公分母为()()12x x --，最简公分母值为0，即()()120x x --=，解得：1x =或2x =．【总结】考查分式方程的最简公分母，将每个分母因式分解，取相同因式的最高次数乘积即为分式方程的最简公分母．3.分式方程22228(2)331112x x x x x x +-+=-+，如果设2221x xy x +=-，那么原方程可以化为关于y 的整式方程为．【难度】★【答案】281130y y -+=．【解析】2221x x y x +=-，则有22112x x x y-=+，原方程即为3811y y +=，整理化作关于y 的整式方程即为281130y y -+=．【总结】考查利用换元法对复杂形式的分式方程进行转化，注意最终要化成整式方程的形式．4.解方程：（1）26531111x x x x =++--+；（2）22161242x x x x +-=--+；（3）243455121760x x x x x x --+=---+．【难度】★★【答案】（1）9x =；（2）5x =-；（3）12x =，29x =．【解析】（1）方程两边同乘21x -，得()()2615131x x x x =--++-，整理得2890x x --=，解得：11x =-，29x =，经检验，11x =-是原方程的增根，即原方程的根为9x =；（2）方程两边同乘24x -，得()22162x x +-=-，整理得23100x x +-=，解得：12x =，25x =-，经检验，12x =是原方程的增根，即原方程的根为5x =-；（3）两边同乘21760x x -+，得()()()4123545x x x x ----=-，整理得211180x x -+=，解得“”12x =，29x =，经检验，12x =，29x =都是原方程的根．【总结】考查分式方程的解法，注意检验所求是否为增根．5.解方程：221313x x x x ++=+．【难度】★★【答案】11x =，21x =+．【解析】令1x a x =+，原方程即为2133a a +=，整理即为231060a a -+=，解得：1a =2a =由1x x =+，解得：1x =；由1x x =+，解得：1x =+经检验11x =，21x =【总结】考查利用换元法解分式方程．6.解方程组311332412463324x y x y x y y x ì+=ï+-ïíï-=ï+-î【难度】★★【答案】1011711x y ì=ïïíï=ïî．【解析】令132a x y =+，14b x y =-，原方程组即为13312463a b a b ì+=ïíï+=î，解得：1413a b ì=ïïíï=ïî，由此可得113241143x y x y ì=ï+ïíï=ï-î，去分母得32443x y x y +=ìí-=î，解得：1011711x y ì=ïïíï=ïî，经检验，1011711x y ì=ïïíï=ïî是原分式方程的根．【总结】考查用换元法解有特殊形式的分式方程组，注意验根．7.若分式方程22111x m x x x x x++-=++产生增根，求m 的值．【难度】★★【答案】2m =-或1m =．【解析】方程两边同乘2x x +，得()()22211x m x -+=+，展开整理得2220x x m ---=，分式方程产生增根，即当相应整式方程有两解时，分式方程仅有一解，由此需进行分类讨论：①整式方程有一根为分式方程增根0x =时，此时有20m --=，解得：2m =-；②整式方程有一根为分式方程增根1x =-时，此时有()()212120m --⨯---=，解得：1m =；综上，2m =-或1m =．【总结】考查分式方程有增根的情况，即对应的整式方程有一个根为分式方程的增根．8.甲、乙两地间铁路长400千米，现将火车的行驶速度每小时比原来提高了45千米，因此，火车由甲地到乙地的行驶时间缩短了2小时．求火车原来的速度．【难度】★★【答案】75/km h ．【解析】设火车原来的速度为/xkm h ，依题意可得400400245x x -=+，整理得24590000x x +-=，解得：1120x =-，275x =，经检验，1120x =-，275x =都是原方程的根，但1120x =-不合题意应舍去，即得75x =，即可得火车原来速度为75/km h ．【总结】考查行程问题中的列方程解应用题，根据行程问题的基本等量关系一个条件作设一个条件列式进行求解．9.某市为了美化环境，计划在一定的时间内完成绿化面积200万亩的任务，后来市政府调整了原定计划，不但绿化面积要在原计划的基础上增加20%，而且要提前1年完成任务．经测算，要完成新的计划，平均每年的绿化面积必须比原计划多20万亩，求原计划平均每年的绿化面积．【难度】★★★【答案】原计划平均每年绿化面积40万亩．【解析】设原计划平均每年的绿化面积为x 万亩，则新计划每年()20x +万亩，依题意可得()200120%200120x x ⨯+-=+，整理得26040000x x +-=，解得：1100x =-，240x =，经检验，1100x =-，240x =都是原方程的根，但1100x =-不合题意应舍去，即得40x =，即原计划平均每年的绿化面积为40万亩．【总结】考查工作量的问题，根据相应的等量关系式列方程求解．10.解方程：221114(4)12()12433x x x -=-++．【难度】★★★【答案】11x =+，21x =，33x =+，43x =【解析】方程两边同乘12展开得22364881616x x x x-+=--+，根据等式的性质移项变形得2668120x x x x æöæö---+=ç÷ç÷èøèø，因式分解得：66260x x x x æöæö----=ç÷ç÷èøèø，由此可得620x x --=或660x x --=；由620x x--=，整理得2260x x --=，解得：11x =+21x =-；由660x x --=，整理得2660x x --=，解得：13x =+23x =经检验，11x =21x =-33x =43x =-都是原方程的根．【总结】考查用整体思想先对分式方程变形，然后求解分式方程的根，注意对方法的总结．11.解方程：596841922119968x x x x x x x x ----+=+----．【难度】★★★【答案】12314x =．【解析】对分式方程变形得1155514219968x x x x -++=++-----，根据等式的性质可变形得115519986x x x x -=-----，两边分别通分即得221010281711448x x x x =-+-+，由此可得22281711448x x x x -+=-+，解得：12314x =，经检验，12314x =是原分式方程的根．【总结】考查特殊形式分式方程的解法，注意相应分母的关系，分组两边分别通分计算．12.已知关于x 的方程21221232a a x x x x ++=---+有增根，求a ．【难度】★★★【答案】32a =-或2a =-．【解析】方程两边同乘232x x -+，得()2122x a x a -+-=+，展开整理得()134a x a +=+，当10a +≠，即1a ≠-时，得341a x a +=+，分式方程可能产生增根，由此进行分类讨论：①整式方程根为分式方程增根1x =时，此时有3411a a +=+，解得32a =-；②整式方程有一根为分式方程增根2x =时，此时有3421a a +=+，解得2a =-；综上，32a =-或2a =-．【总结】考查分式方程有增根的情况，即对应的整式方程根为分式方程的增根．13.已知：关于x 的方程227()72120a a x x a x x+--++=只有一个实数根，求a ．【难度】★★★【答案】94a =或4a =．【解析】整理原方程得27120a a x x x x æöæö+-++=ç÷ç÷èøèø，因式分解得340a a x x x x æöæö+-+-=ç÷ç÷èøèø，由此可得30a x x +-=或40a x x +-=，分别整理得：230x x a -+=和240x x a -+=，两方程根的判别式分别为194a ∆=-，2164a ∆=-．因为方程仅有一实数根，所以940a -=或1640a -=，解得：94a =或4a =．【总结】考查分式方程的根与对应整式方程的根相结合的问题，根据实际题目进行问题的分析转化，解决问题．。

中考数学专题训练第6讲分式1(解析版)

分式题型一分式的概念1．（2021·浙江平阳·九年级期中）已知要使分式32x x +-有意义.则x 的取值应满足（）A ．2x ≠B ．3x ≠-C ．3x =-D ．2x =【答案】A 【分析】要使分式32x x +-有意义.则20x -≠.所以2x ≠．故选：A ． 2．（2021·内蒙古·包头市第四十八中学九年级月考）下面是某同学在一次数学测验中解答的填空题.其中答对的是（） A ．若x 2＝4.则x ＝2 B ．若分式2232x x x --+的值为零.则x ＝2C ．x 2+x ﹣k ＝0的一个根是1.则k ＝2D ．若3x 2＝6x .则x ＝2 【答案】C【分析】解：A 、x 2＝4.则2x =±.选项错误.不符合题意；B 、分式2232x x x --+的值为零.则220320x x x -=⎧⎨-+≠⎩.21,2x x x =⎧⎨≠≠⎩.无解.选项错误.不符合题意；C 、x 2+x ﹣k ＝0的一个根是1.则110k +-=.解得2k =.选项正确.符合题意；D 、3x 2＝6x .解得0x =或2x =.选项错误.不符合题意；故选C3．（2021·陕西·西安高新一中实验中学九年级开学考试）如果分式||11x x -+的值为0.那么x 的值为（） A ．0 B ．1 C ．1- D ．±1【答案】B 【分析】分式||11x x -+的值为0.10x ∴-=.1x =.解得1x =±.又10x +≠.1x ∴≠-.1x ∴=.故选：B ． 4．若代数式(2)(1)||1x x x ---的值为零.则x 的取值是（）A ．2x =或1x =B ．2x =且1x =C ．2x =D ．1x =-【答案】C【分析】(2)(1)0x x --=且||1x ≠.解得x =2或x =1.且x ≠±1∴2x =．故选C ．5．（2021·广西百色·中考真题）当x ＝﹣2时.分式2232796x x x -++的值是（）A ．﹣15B ．﹣3C ．3D ．15【答案】A【分析】解：2232796x x x -++()()22393x x -=+()()()23333x x x +-+=()333x x -=+ 把2x =-代入上式中.原式()3231523--==--+.故选A.6．（2021·四川省隆昌市第一中学九年级月考）3311a a a a --=++ ）A ．1a ≠-B ．3a ≥-且1a ≠C ．1a >-D ．3a ≥【答案】D【分析】解：根据题意得.30-≥a .10a +> ∴3a ≥.1a >- ∴3a ≥.故选D ． 7．（2021·云南昭通·二模）1x-.则实数x 的取值范围是（） A ．1x ≤ B ．1x ≤且0x ≠ C ．1x <且0x ≠ D ．1x <【答案】D【分析】由题意可得：10x -≥10x -≠.解得：1x <.故选：D 8．（2021·浙江瓯海·三模）若a b＝12.则a bb+的值是（） A ．3 B ．23C ．32D ．2【答案】C【分析】解：∵ab＝12.∴2b a =.将2b a =代入a bb +中.得2322a a a +=.故选：C ． 9．（2021·浙江浙江·九年级期末）下列分式一定有意义的是（）A ．11x -B ．1xC ．211x - D ．211x + 【答案】D【分析】∵当x =1时.|1-x |=0,∴A 不符合题意；∵当x =0时.分母为0.∴B 不符合题意；∵当x =1或-1时.21x -=0,∴C 不符合题意；∵220+110x x ≥，≥≠.∴D 符合题意；故选D 10．（2021·广东·执信中学模拟预测）不论x 取何值.下列代数式的值不可能为0的是（）A ．1x +B ．21x -C ．11x + D ．()21x +【答案】C【分析】解：A 、当x =-1时.x +1=0.故不合题意；B 、当x =±1时.x 2-1=0.故不合题意；C 、分子是1.而1≠0.则11x +≠0.故符合题意；D 、当x =-1时.()210x +=.故不合题意；故选C ．题型二分式的性质、约分、通分11．（2021·贵州·贵阳市第十九中学九年级月考）若把x .y 的值同时缩小x 为原来的13倍.则下列分式的值保持不变的是（）A ．xy x y+B ．22y x ++C ．()22x y x + D ．222xy x - 【答案】C【分析】A.1111333==11333x y xyxy x y x y x y ⨯⨯+++.选项说法错误.不符合题意；B. 61263=3616233y y x x y x +++=+++.选项说法错误.不符合题意；C. 22222222111()()()33311()()33x y x y x y x x x ⎛⎫++ ⎪+⎝⎭==.选项说法正确.符合题意；D. 22222213112261())(33()3xx x y x y x y x ⨯==---⨯.选项说法错误.不符合题意.故选C12．（2021·重庆一中九年级开学考试）把代数式3xyx y+中的x 、y 同时扩大五倍后.代数式的值（） A ．扩大为原来的3倍 B ．不变 C ．缩小为原来的15D ．扩大为原来的5倍【答案】D 【分析】解：3xyx y+中的x 、y 都扩大为原来的5倍.得3557515555()x y xy xy x y x y x y ⨯⋅==+++.故选：D ． 13．分式11x--可变形为（）． A ．11x -- B ．11x+ C ．11x -+ D ．11x -【答案】D 【分析】解：1111=1(1)11x x x x -==----+-.故选项A 、B 、C 均不符合题意.选项D 符合题意.故选：D ．14．（2021·河北张家口·一模）下列各式从左到右的变形中.不正确的是（） A ．2233a a-=- B ．66b ba a-=- C ．3344a ab b=- D ．8833a ab b--=-- 【答案】C 【分析】解：A 、2233a a-=-.符号改变了两处.改变了分子与分式的符号.分式的值不变.正确.故选项A 不符合题意；B 、66b ba a-=-.符号改变了两处.改变了分子与分母的符号.分式的值不变.正确.故选项B 不符合题意；C 、3344a ab b=-.符号改变了一处.改变了分母的符号.分式的值发生改变.不正确.故选项C 符合题意； D 、8833--=a ab b. 符号改变了两处.改变了分子与分式的符号.分式的值不变.正确.故选项D 不符合题意；故选：C ． 15．下列各式中.正确的有（）①263333()22=b b a a ；②222224()=++x x x y x y ；③a b a b a b a b -++=---；④1x y x y -+=--；⑤0x y x y +=+；⑥2222()()()()---+=+-x y x y x y x y ．A ．1个B ．2个C ．3个D ．4个【答案】B【分析】①2633327()28b b a a =.故不符合题意；②222224()2x x x y x xy y =+++.故不符合题意；③a b a ba b a b-+-=--+.故不符合题意；④1x y x y -+=--.故符合题意；⑤1x y x y +=+.故不符合题意；⑥2222()()()()---+=+-x y x y x y x y .故符合题意；所以正确的有2个．故选：B ．16．下列分式中属于最简分式的是（） A ．42xB ．11xx -- C ．211x x -- D ．221xx + 【答案】D 【分析】解：A 、42=2x x.不是最简分式.故此选项不符合题意；B 、111x x -=--.不是最简分式.故此选项不符合题意；C 、211x x --=11(1)(1)1x x x x -=+-+.不是最简分式.故此选项不符合题意；D 、221xx +是最简分式.故此选项符合题意.故选：D ． 17．（2021·河北唐山·一模）若221()3m n m n m n -=≠-.则m n +=（） A ．3 B ．-3 C ．13D ．13-【答案】C【分析】∵()()22,m n m n m n m n m n m n +--=≠--.∴2213m n m n m n -=+=-.故选：C ． 18．（2021·江苏·苏州市南环实验中学校二模）分式222()a b a b --化简为最简分式的结果为（） A ．a b + B ．-a b C ．a ba b+- D ．a ba b-+ 【答案】C【分析】解：222()a b a b --=2()()()a b a b a b +--=a ba b+-．故选C ．19．（2021·广东·广州市第十六中学二模）分式3x y xy +.232yx .26xy xy 的最简分母是（） A ．3x B ．xC ．26xD ．226x y【答案】D 【分析】解：3x y xy +.232y x .26xy xy的分母分别是3xy 、22x 、26xy .故最简公分母为226x y ．故选：D ．20．（2021·河北唐山·一模）要把分式232a b 与2a bab c-通分.分式的最简公分母是（） A ．222a b c B ．332a b C ．332a b c D ．336a b c【答案】A【分析】解：根据最简公分母是各分母的最小公倍数.∵系数2与1的公倍数是2.2a 与a 的最高次幂是2a .b 与2b 的最高次幂是2b .对于只在一个单项式中出现的字母c 直接作公分母中的因式.∴公分母为：222a b c ．故选择：A ．21．能使分式2321020224x x x x ---+-的值为正整数的所有x 的值的和为（） A ．10 B ．0 C ．8- D ．10-【答案】D【分析】∵20x ≥.∴220x +>.()()()22322102102010224222x x x x x x x x -+---==-+---+.若分式的值为正整数.则210x -=-.1-.2-.5-.所以8x =-.1.0.3-.所以()810310-+++-=-.故选D. 22．关于分式的约分或通分.下列哪个说法正确（） A ．211x x +-约分的结果是1x B ．分式211x -与11x -的最简公分母是x ﹣1 C ．22xx约分的结果是1D ．化简221x x -﹣211x -的结果是1【答案】D 【分析】解：A 、211x x +-＝11x - .故本选项错误；B 、分式211x -与11x -的最简公分母是x 2﹣1.故本选项错误；C 、22x x ＝2x .故本选项错误；D 、221x x -﹣211x -＝1.故本选项正确；故选D ．题型三分式的运算23．（2021·四川蓬安·九年级月考）卵细胞是人体中最大的细胞.直径约为0.0002米.直径用科学记数法表示为（）米． A ．0.2×10﹣3 B ．0.2×10﹣4 C ．2×10﹣4 D ．2×10﹣3【答案】C【分析】解：直径约为0.0002米.用科学记数法表示为2×10﹣4米．故选：C ． 24．（2021·河南·郑州外国语中学九年级开学考试）化简22111a a a+--的结果正确的是（） A ．2311a a +- B ．2311a a -- C ．11a + D ．11a - 【答案】C 【分析】221212(1)111(1)(1)1(1)(1)1a a a a a a a a a a a a -++=-==--+--+-+；故选：C ． 25．（2021·北京市陈经纶中学分校九年级月考）如果a ﹣b ＝3那么代数式（222a b a+﹣b ）•aa b-的值为（） A 3B ．3C ．3 D ．3【答案】A【分析】解：原式222()22a b ab aa a ab +=-⋅-2()2a b a a a b-=⋅-2a b -=. 当23a b -=.原式233==故选：A ． 26．（2021·湖北·老河口市教学研究室九年级月考）化简2b a ba a a ⎛⎫+-÷ ⎪⎝⎭的结果是（）A ．-a bB ．a b +C ．1a b- D ．1a b+ 【答案】A【分析】解：2b a b a a a ⎛⎫+-÷ ⎪⎝⎭=22a b aa ab -⨯+ =()()a b a b a a a b +-⨯+ =-a b ．故选：A ．27．（2021·山东乳山·模拟预测）如果2320a a +-=.那么代数式2231933a a a a ⎛⎫+÷ ⎪-+-⎝⎭的值为（） A ．1 B ．12C ．13D ．14【答案】B【分析】解：2231933a a a a ⎛⎫+÷⎪-+-⎝⎭＝2333(3)(3)(3)(3)a a a a a a a ⎡⎤--+⋅⎢⎥+-+-⎣⎦.23(3)(3)a a a a a -=⋅+-213a a =+ 由a 2+3a ﹣2＝0.得到a 2+3a ＝2.则原式＝12.故选B ． 28．已知实数a .b 满足1a b ⋅=.那么221111a b +++的值为（） A ．14B ．12C ．1D ．2【答案】C【分析】解：∵•1a b =.∴()2221a b ab ==.∴22222222112111a b a b a b b a +++=+++++2222211a b b a ++=+++1=．故选：C ． 29．（2021·重庆市天星桥中学九年级开学考试）化简2111a a a +--的结果为（）A ．211a a +-B ．211a a+-C ．1a +D ．1a -【答案】C【分析】解：原式=2111a a a ---=211a a --=()()111a a a +--=1a +．故选C ． 30．（2021·河北桥东·二模）当2ab =-时.计算2b a ba a a ⎛⎫--÷ ⎪⎝⎭的值为（）A ．2B ．2-C ．12D ．12-【答案】A【分析】2b a b a a a ⎛⎫--÷⎪⎝⎭22a b a b a a --=÷()()a b a b aa ab -+=⋅-a b =+.把2a b =-代入得22a b b b +=-+=故选A ．31．（2021·河南·二模）下列各式计算正确的是（） A 42±B ．11011a a+=+- C ．2333122x y x x y ⎛⎫÷= ⎪⎝⎭D ．22()()a b b a b a +-=-【答案】D【分析】42=.故该选项计算错误.不符合题意.B.21111211(1)(1)1a a a a a a a -+++==+-+--.故该选项计算错误.不符合题意.C.233122x y x xy ⎛⎫÷= ⎪⎝⎭.故该选项计算错误.不符合题意.D.22()()a b b a b a +-=-.故该选项计算正确.符合题意.故选：D ． 32．（2021·山东诸城·二模）下列计算正确的是（） A ．1a ba b-+=-- B ．5333= C ．23193x x x -=-- D ．1122a a-=【答案】A 【分析】A.()1a b a b a b a b-+--==---.符合题意；B. 532333不符合题意；C. 23193x x x -=-+.不符合题意；D.1122a a -=.不符合题意．故选A ． 33．（2021·广东高要·二模）下列运算错误的是（） A ．224a a a += B ．34a a a ÷= C ．1a bb a-=-- D ．123ccc+=【答案】A【分析】A 、2222a a a +=.原式计算错误.符合题意；B 、34a a a ÷=.正确.不合题意；C 、1a b b a -=--.正确.不合题意；D 、123c c c+=.正确.不合题意；故选：A ．34．（2021·黑龙江大庆·中考真题）已知0b a >>.则分式a b 与11a b ++的大小关系是（）A ．11a ab b +<+B ．11a ab b +=+ C ．11a ab b +>+ D ．不能确定【答案】A 【分析】解：()()()()111111a b b a a a a bb b b b b b +-++--==+++.∵0b a >>.∴()1011a a a b b b b b +--=<++.∴11a ab b +<+.故选：A ．题型四分式方程的概念与解法35．下列关于x 的方程.其中不是分式方程的是（） A ．1a ba xa++=B ．11b a a x b x-=+ C ．1x a x a b+-= D ．1x n x mx m x n-++=+- 【答案】C【分析】分式方程是分母含有未知数的等式．A 、1a ba xa++=分母含未知数.是分式方程.不符合题意；B 、11b a ax b x -=+分母含未知数.是分式方程.不符合题意；C 、1x a x a b+-=分母不含未知数.不是分式方程.符合题意；D 、1x n x mx m x n-++=+-分母含未知数.是分式方程.不符合题意；故选：C ． 36．下列结论正确的是（） A ．153y y+=是分式方程 B ．方程221624x x x --+-＝1无解 C ．方程223x xx x x x=++的根为x ＝0 D ．解分式方程时.一定会出现增根【答案】B【分析】解：A ．原方程中分母不含未知数.不是分式方程.所以A 选项不符合题意；B ．解方程.得x ＝﹣2.经检验x ＝﹣2是原方程的增根.所以原方程无解.所以B 选项符合题意；C ．解方程.得x ＝0.经检验x ＝0是原方程的增根.所以原方程无解.所以C 选项不符合题意；D ．解分式方程时.不一定会出现增根.只有使分式方程分母的值为0的根是增根.所以D 选项不符合题意．故选：B ．37．（2021·黑龙江·哈尔滨市萧红中学九年级期中）方程5113x x =-+的解是（） A ．2x =- B ．2x =C ．4x =-D ．4x =【答案】C【分析】解：去分母得：5（x +3）=x -1. 去括号得：5x +15=x -1. 解得：x =-4.检验：把x =-4代入得：（x -1）（x +3）≠0. ∴分式方程的解为x =-4．故选：C ．38．（2021·重庆八中九年级月考）若关于x 的一元一次不等式组()31212x x x a ⎧-<+⎨≤+⎩的解集为4x <.且关于y 的分式方程2422y a ay y++=--的解是非负整数解.则所有满足条件的整数a 的值之和是（）A ．5B ．7C ．13D ．15【答案】C【分析】解不等式()3121x x -<+得.4x <.2x a ≤+不等式组的解集为：4x < 24a ∴+≥2a ∴≥解分式方程2422y a ay y++=--得 2422y a ay y +-=-- 24(2)y a a y ∴+-=-整理得8=3ay -. 20,y -≠ 则82,3a-≠ 2,a ∴≠分式方程的解是非负整数解.803a-∴≥ 8a ∴≤.且8a -是3的倍数. 28a ∴<≤.且8a -是3的倍数.∴整数a 的值为58，5813∴+=.故选：C ．39．（2021·重庆实验外国语学校九年级月考）关于x的分式方程114211a xx x---=++有整数解.且关于y的不等式组116232(1)5y yy a-⎧->-⎪⎨⎪-≤-⎩有解.则所有满足条件的正整数a的和是（）A．6 B．12 C．14 D．20 【答案】A【分析】解：∵11 623 2(1)5y yy a-⎧->-⎪⎨⎪-≤-⎩∴y＜52.y≥32a-∵关于y的不等式组116232(1)5y yy a-⎧->-⎪⎨⎪-≤-⎩有解∴不等式组的解集为32a-≤y＜52.∴32a-＜52.即a-3＜5.可得a＜8由114211a xx x---=++有整数解,可得：x=22a-,即a为偶数∵x≠-1∴x≠6∵正整数a∴a=2或a=4∴4+2=6．故选A．40．（2021·重庆一中九年级期中）若关于x的不等式组4213222()x xx x a+-⎧-≥⎪⎨⎪+≤-⎩有解.且关于y的分式方程1211y a yy y--+--＝﹣3的解为非负数.则所有满足条件的整数a的值之积是（）A．﹣6 B．0 C．4 D．12 【答案】D【分析】解：不等式组整理得：822xx a≤⎧⎨≥+⎩.∵关于x的不等式组4213222()x xx x a+-⎧-≥⎪⎨⎪+≤-⎩有解.∴2a+2≤8.即a≤3.解分式方程1211y a yy y--+--＝﹣3得y＝22a+.∵关于y 的分式方程1211y a yy y--+--＝﹣3的解为非负数. ∴22a +≥0.且22a +≠1. 解得.a ≥﹣2.且a ≠0. ∴﹣2≤a ≤3.且a ≠0. ∵a 为整数.∴a ＝﹣2或﹣1或1或2或3.∴满足条件的所有整数a 的值之积：（﹣2）×（﹣1）×1×2×3＝12．故选：D ． 41．（2021·重庆实验外国语学校九年级月考）若关于x 的一元一次不等式组3214x x x a+⎧>-⎪⎨⎪≤⎩的解集为x a ≤.且关于y 的分式方程52122y a yy y--+=--有正整数解.则所有满足条件的整数a 的个数为（） A ．2 B ．3 C ．4 D ．5【答案】B【分析】解：3214x x x a +⎧>-⎪⎨⎪≤⎩①②. 解不等式①.得：x ＜6. 解不等式②.得：x ≤a . ∵该不等式解集为x ≤a . ∴a ＜6；由52122y a yy y--+=-- 分式方程去分母.得：y -a -（5-2y ）=y -2. 解得：y =32a +. ∵分式方程有正整数解.且y ≠2.∴满足条件的整数a 可以取5；3；-1；共3个；故选：B ． 42．（2021·重庆·西南大学附中九年级月考）已知关于x 的分式方程()()232626mx x x x x +=--+-无解.且关于y 不等式组()4434m y y y ->⎧⎨-≤+⎩有且只有三个偶数解.则符合条件的整数m 有（）个A ．0B ．1C ．2D ．3【答案】B【分析】解：分式方程无解的情况有两种.分式方程去分母得：(2)2(2)(6)3(2)(2)mx x x x x x ++--=+-.整理得：2(1)2(8)360m x m x -+-+=.情况一：整式方程无解时.即()()24843610m m ∆=--⨯-<且10m -≠时.方程无解. ∴2521000m m -+<. 解得250m <<.即当250m <<时方程无解；情况二：当整式方程有解.是分式方程的增根.即2x =.或6x =.或2x =-. ①当2x =时.4(1)4(8)360m m -+-+=.解得0m =. ②当6x =时.36(1)12(8)360m m -+-+=.解得2m =. ③当2x =-时.4(1)4(8)360m m ---+=.此方程无解. 综合两种情况得.当0m =或250m <≤时.分式方程无解.解不等式得48y m y <-⎧⎨≥-⎩. 根据题意得不等式的解集为84y m -<-. ∵不等式组有且只有三个偶数解为8-.6-.4-. ∴442m -<--≤. ∴02m <≤.综上所述当2m =时符合题目中所有要求．故选：B ．43．（2021·四川省成都市七中育才学校九年级月考）若关于x 的分式方程211x kx x-=--有增根.则k 的值为（） A ．1 B ．0 C ．﹣2 D ．﹣1【答案】D【分析】解：去分母得： ()21--=-x x k .∴22x x k -+=-.∴2x k =+∵分式方程有增根.10x -=.解得x =1.即210k +-=解得：k ＝﹣1.故选D ．44．（2021·重庆酉阳·九年级期末）在321012-,-,-,,,这六个数中.随机取出一个数记为a .那么使得关于x 的一元二次方程2420x x a --=有解.且使得关于x 的方程1311x a x x+-=--有整数解的所有a 的值之和为（） A ．2B ．1C ．0D ．1-【答案】A【分析】解：要使得关于x 的一元二次方程2420x x a --=有解.则Δ≥16-4×（-2a ）≥0.解得a ≥-2,∴a 的可能值为-2.-1、0、1、2.解1311x a x x+-=--可得.22a x=+.1,x ≠ 21,2a∴+≠2,a ∴≠- 使得方程有整数解满足条件的a 的值为0、2.综上所述满足条件的a 的值为0、2.0+2=2.故选：A ．45．（2021·广东·深圳市罗湖区翠园初级中学九年级开学考试）关于x 的分式方程311x mx x -=--有增根.则m 的值是（） A ．﹣2 B ．3 C ．﹣3 D ．2【答案】A【分析】解：去分母.得：x -3=m .由分式方程有增根.得到x -1=0.即x =1.把x =1代入整式方程.可得：m =-2．故选：A ．46．（2021·黑龙江佳木斯·三模）已知关于x 的分式方程3102112kx x x-+=--有解.则k 的取值范围为（） A ．2k ≠- B ．6k ≠- C ．2k ≠-且6k ≠- D ．2k <-且6k ≠-【答案】C 【分析】解：3102112kx x x-+=--. 去分母得.3210kx x ++-=. 解得.22x k -=+. ∵关于x 的分式方程3102112kx x x-+=--有解. ∴2122k -≠+且20k +≠. 解得.2k ≠-且6k ≠-.故选：C ．题型五分式方程的应用47．（2021·湖南·长沙市开福区青竹湖湘一外国语学校九年级期中）高铁为居民出行提供了便利.从铁路沿线相距360km 的甲地到乙地.乘坐高铁列车比乘坐普通列车少用3h ．已知高铁列车的平均速度是普通列车平均速度的3倍.设普通列车的平均速度为x km/h.依题意.下面所列方程正确的是（）A．36036033x x-=B．36036033x x-=C．360360313x x-=D．360360313xx-=【答案】A【分析】根据题意可得：列车的平均速度为x km/h.则高铁列车的平均速度为3x km/h.高铁列车所用的时间为：3603x.普通列车的时间为：360x.所列方程为：36036033x x-=.故选：A．48．（2021·陕西·交大附中分校模拟预测）某修路队计划x天内铺设铁路120km.由于采用新技术.每天多铺设铁路3km.因此提前2天完成计划.根据题意.可列方程为（）A．12012032x x=+-B．12012032x x=+-C．12012032x x=++D．12012032x x=++【答案】B【分析】解：原计划每天修建道路120xm.则实际用了（x﹣2）天.每天修建道路为1202x-m.根据采用新技术.每天多铺设铁路3km得.12012032x x=+-．故选：B．49．（2021·辽宁·沈阳市第四十三中学九年级月考）随着快递业务的增加.某快递公司为快递员更换了快捷的交通工具.公司投递快件的能力由每周6000件提高到8400件.平均每人每周比原来多投递80件.若快递公司的快递人数不变.求原来平均每人每周投递快件多少件？设原来平均每人每周投递快件x件.根据题意可列方程为（）A．6000x＝840080x+B．6000x+80＝8400xC．8400x＝6000x﹣80 D．6000x＝840080x-【答案】A【分析】解：设原来平均每人每周投递快件x件.则更换交通工具后平均每人每周投递快件（x+80）件.依题意得：6000x＝840080x+.故选：A．50．（2021·福建省厦门第六中学三模）某次列车平均提速v km/h.用相同的时间.列车提速前行驶s km.提速后比提速前多行驶50km.则方程50s svx x++=所表达的等量关系是（）A．提速前列车行驶s km与提速后行驶(s＋50)km的时间相等B ．提速后列车每小时比提速前列车每小时多开v kmC ．提速后列车行驶(s ＋50)km 的时间比提速前列车行驶s km 多v hD ．提速后列车用相同的时间可以比提速前多开50km 【答案】B【分析】解：∵用相同的时间.列车提速前行驶s km.提速后比提速前多行驶50km .∴s +50表示列车提速后同样的时间内行驶的路程.∵某次列车平均提速v km/h.路程=速度×时间.∴方程50s s v xx++=表达的含义提速后列车每小时比提速前列车每小时多开v km.故选B.51．（2021·山东淄博·中考真题）甲、乙两人沿着总长度为10km 的“健身步道”健步走.甲的速度是乙的1.2倍.甲比乙提前12分钟走完全程．设乙的速度为km/h x .则下列方程中正确的是（） A ．1010121.2x x-= B ．10100.21.2x x-= C ．1010121.2x x-= D ．10100.21.2x x-= 【答案】D【分析】解：由题意得：10100.21.2x x-=；故选D ． 52．（2021·重庆市育才中学九年级月考）每年中秋节.某商家生产的甲、乙、丙三种月饼礼盒一直深受消费者喜爱．今年中秋节.该商家继续售卖甲、乙、丙三种月饼礼盒.已知去年该商家售卖甲、乙、丙三种月饼礼盒的营业额之比为4:9:7．今年.由于商家加大了促销宣传力度.预计三种月饼礼盒的营业额都会增加.其中甲种礼盒增加的营业额占总增加的营业额的815.此时.甲种月饼礼盒的营业额与今年三种月饼礼盒总营业额之比为4:15.为使今年乙、丙两种月饼礼盒的营业额之比为6:5.则今年乙种月饼礼盒增加的营业额与今年总营业额之比为______．【答案】1:25【分析】解：∵甲种月饼礼盒的营业额与今年三种月饼礼盒总营业额之比为4:15.且乙、丙两种月饼礼盒的营业额之比为6:5.∴今年甲、乙、丙三种月饼礼盒的营业额之比为4∶6∶5.设今年甲、乙、丙三种月饼礼盒的营业额分别为4a .6a .5a .则今年总营业额为15a .∵去年该商家售卖甲、乙、丙三种月饼礼盒的营业额之比为4:9:7.∴设去年甲、乙、丙三种月饼礼盒的营业额分别为4b .9b .7b .则去年总营业额为20b .∴今年甲、乙、丙三种月饼礼盒的营业额分别增加了44a b -.69a b -.57a b -.总营业额增加了1520a b -.∵甲种礼盒增加的营业额占总增加的营业额的815.∴448152015a b a b -=-.解得：0.6b a =.经检验：b＝0.6a 符合题意.∴今年乙种月饼礼盒增加的营业额与今年总营业额之比为69690.66 5.4115151525a b a a a a a a a --⨯-===.故答案为：1∶25． 53．（2021·重庆实验外国语学校九年级开学考试）重庆某笔记本电脑公司每年都会组织员工出国学习旅行.今年有A 、B 、C 、D 四个国家可供员工们选择（每名员工只能选择一个国家旅行）.但要求选择A 、C 两个国家的人数相同.选择B 、D 两个国家的人数也相同.选择A 、B 两国的人数总和为100人.A 、D 两国的费用单价相等.B 、C 两个国的费用单价也相等.A 、B 两国的费用单价之和不超过8万元.且选择A 、B 两个国家的员工总费用比选择C 、D 两个国家员工总费用多20万元.则选择A 、B 两个国家员工总费用的最大值为__万元．【答案】410【分析】解：设有x 人选择A .A 单价为1y 万元.B 单价为2y 万元.依题意可知.B 有(100)x -人.即100x <.128y y +①.1221(100)[(100)]20xy x y xy x y +--+-=.即121050y y x -=-.100x .5050x ∴-.101505x -. 即1215y y -②.①+②得24125y .解得24110y .代入①中.13910y .代入②中.13910y .13910y ∴=.24110y ∴=.A ∴、B 两个国家员工总费用为12(100)xy x y +-.B 单价A >单价.0x ∴=时总费用最大.最大值为410(1000)41010+-⨯=（万元）．故选择A 、B 两个国家员工总费用的最大值为410万元．故答案为：410．54．（2021·四川省宜宾市第二中学校三模）某服装厂准备加工400套运动装.在加工完160套后.采用了新技术.使得工作效率比原计划提高了20%.结果共用了18天完成任务.问计划每天加工服装多少套？在这个问题中.设计划每天加工x 套.则根据题意可得方程为__________________．【答案】160x +()400160120%x -+=18【分析】根据题意.采用新技术前所用时间为：160x天.采用新技术后所用时间为：()400160120%x -+天.∴所列方程为：160x +()400160120%x -+=18.故答案为：160x +()400160120%x -+=18．55．（2021·辽宁鞍山·中考真题）习近平总书记指出.中华优秀传统文化是中华民族的“根”和“魂”．为了大力弘扬中华优秀传统文化.某校决定开展名著阅读活动．用3600元购买“四大名著”若干套后.发现这批图书满足不了学生的阅读需求.图书管理员在购买第二批时正赶上图书城八折销售该套书.于是用2400元购买的套数只比第一批少4套．设第一批购买的“四大名著”每套的价格为x 元.则符合题意的方程是___________________．【答案】3600240040.8x x-= 【分析】解：设第一批购买的“四大名著”每套的价格为x 元.则设第二批购买的“四大名著”每套的价格为0.8x 元.依题意得：3600240040.8x x -=．故答案为：3600240040.8x x-=． 56．（2021·吉林省第二实验学校九年级月考）2021年4月8日世界园艺博览会在扬州拉开了帷幕.世园会以“绿色城市.健康生活”为主题.吸引了大批游客游览.世园会成人一日票分为平日票和指定日票.其中平日票比指定日票便宜30元/张.某一售票点在5月份售出平日票4万元.指定日票2.6万元.且售出的平日票数量是指定日票的2倍.这一售票点在5月份售出的平日票和指定日票各多少张？【答案】这一售票点在5月份售出的平日票和指定日票各400张.200张．【分析】解：设这一售票点在5月份售出的指定日票为x 张.则平日票为2x 张.由题意得：2600040000302x x-=. 解得：200x =.经检验200x =是原方程的解.∴2400x =.答：这一售票点在5月份售出的平日票和指定日票各400张.200张．57．某公司生产开发了960件新产品.需要经过加工后才能投放市场.现在有A .B 两个工厂都想参加加工这批产品.已知A 工厂单独加工这批产品比B 工厂单独加工这批产品要多用20天.而B 工厂每天比A 工厂多加工8件产品.公司需要支付给A 工厂每天80元的加工费.B 工厂每天120元的加工费．（1）A .B 两个工厂每天各能加工多少件新产品？（2）公司制定产品方案如下：可以由每个厂家单独完成；也可以由两个厂家同时合作完成．在加工过程中.公司需要派一名工程师每天到厂进行技术指导.并负担每天5元的午餐补助费．请帮助公司选择哪家工厂加工比较省钱.并说明理由．【答案】（1）A 每天加工16件.B 每天加工24件；（2）两个工厂合作完成.理由见解析【分析】解：（1）设A 每天加工x 件产品.则B 每天加工x ＋8件产品.由题意得960960208x x -=+.解得x ＝16件.答：A 每天加工16件产品.则B 每天加工24件产品；（2）A 单独加工完成需要960÷16=60天.费用为：60×（80+5）=5100元.B 单独加工完成需要960÷24=40天.费用为：40×（120+5）=5000元；A 、B 合作完成需要960÷（16+24）=24天.费用为：24×（120+80+5）=4920元．所以既省时又省钱的加工方案是A 、B 合作．58．（2021·黑龙江·哈尔滨市虹桥初级中学校九年级月考）某单位在疫情期间用6000元购进A 、B 两种口罩1100包.购买A 种口罩与购买B 种口罩的费用相同.且一包A 种口罩的单价是一包B 种口罩单价的1.2倍．（1）求A .B 两种口罩一包的单价各是多少元？（2）若计划用不超过11000元的资金再次购进A 、B 两种口罩共2000包.已知A 、B 两种口罩的进价不变.求A 种口罩最多能购进多少包？【答案】（1）A 种口罩一包的单价为6元.B 种口罩一包的单价为5元（2）A 种口罩最多能购进1000包【分析】(1) 设B 种口罩一包的单价为x 元.则A 种口罩一包的单价为1.2x 元.根据题意.得：3000300011001.2x x+=.解得：x = 5.经检验.x = 5是原方程的解.且符合题意.则1.2 x = 6.答：A 种口罩一包的单价为6元.B 种口罩一包的单价为5元；(2)设购进A 种口罩m 包.则购进B 种口罩(2000-m )包. 依题意.得：6m +5 (2000 - m )≤ 11000.解得：m ≤ 1000.答：A 种口罩最多能购进1000包．59．（2021·黑龙江·哈尔滨市第六十九中学校九年级月考）杭州国际动漫节开幕前.某动漫公司预测某种动漫玩具能够畅销.就用32000元购进了一批这种玩具.上市后很快脱销.动漫公司又用68000元购进第二批这种玩具.所购数量是第一批购进数量的2倍.但每套进价多了10元．（1）该动漫公司两次共购进这种玩具多少套？（2）如果这两批玩具每套的售价相同.且全部售完后总利润率不低于20%.那么每套售价至少是多少元？【答案】（1）600套；（2）200元【分析】解：（1）设动漫公司第一次购x 套玩具.由题意得：6800032000102x x-=.解这个方程.200x =.经检验.200x =是原方程的根．∴22200200600x x +=⨯+=.答：动漫公司两次共购进这种玩具600套．（2）设每套玩具的售价y 元.由题意得：600y 320006800020%3200068000--≥+.解这个不等式.200y ≥.答：每套玩具的售价至少是200元．60．（2021·山东青岛·中考真题）某超市经销甲、乙两种品牌的洗衣液.进货时发现.甲品牌洗衣液每瓶的进价比乙品牌高6元.用1800元购进甲品牌洗衣液的数量是用100元购进乙品牌洗衣液数量的45．销售时.甲品牌洗衣液的售价为36元/瓶.乙品牌洗衣液的售价为28元/瓶．（1）求两种品牌洗衣液的进价；（2）若超市需要购进甲、乙两种品牌的洗衣液共120瓶.且购进两种洗衣液的总成本不超过3120元.超市应购进甲、乙两种品牌洗衣液各多少瓶.才能在两种洗衣液完全售出后所获利润最大？最大利润是多少元？【答案】（1）甲品牌洗衣液进价为30元/瓶.乙品牌洗衣液进价为24元/瓶；（2）购进甲品牌洗衣液40瓶.乙品牌洗衣液80瓶时所获利润最大.最大利润是560元【分析】解：（1）设甲品牌洗衣液进价为x 元/瓶.则乙品牌洗衣液进价为()6x -元/瓶. 由题意可得.18004180056x x =⋅-. 解得30x =.经检验30x =是原方程的解.答：甲品牌洗衣液进价为30元/瓶.乙品牌洗衣液进价为24元/瓶. （2）设利润为y 元.购进甲品牌洗衣液m 瓶. 则购进乙品牌洗衣液()120m -瓶. 由题意可得.()30241203120m m +-≤. 解得40m ≤.由题意可得.()()()363028*********y m m m =-+--=+. ∵20k =>.∴y 随m 的增大而增大.∴当40m =时.y 取最大值.240480560y =⨯+=最大值.答：购进甲品牌洗衣液40瓶.乙品牌洗衣液80瓶时所获利润最大.最大利润是560元． 61．（2021·重庆八中九年级月考）巫溪某村民承包土地发展李子种植.2020年开始大量投产增收.其中早熟李种植面积亩数是晚熟李种植面积亩数的3倍.早熟李、晚熟李分别收益60000元和40000元.而早熟李平均每亩收益比晚熟李少1000元．（1）2020年早熟李、晚熟李种植面积分别有多少亩？（2）在扶贫专家小组的精准帮助下.优化管理.淘汰了部分低产李子林改种其他经济作物增加收益.2021年.早熟李、晚熟李的种植面积比2020年分别降低了1%3a 和%a .然而平均每亩早熟李和晚熟李的收益在2020年基础上分别增加了%a 和1%2a .2021年两种李子的总收益与2020年两种李子总收益相等.求a 的值．【答案】（1）早熟李种60亩.晚熟李种20亩；（2）50．【分析】解：（1）设2020年晚熟李种植面积有x 亩.则早熟李种植面积为3x 亩. 根据题意.得40006000010003x x-= . 解方程.得20x. 经检验.20x是分式方程式得解.360x ∴= . 即2020年早熟李、晚熟李种植面积分别有60亩、20亩．（2）由（1）可得: 2020年早熟李、晚熟李种植面积分别有60亩、20亩.2020年早熟李平均每亩收益为60000100060=元.晚熟李平均每亩收益为40000200020=元. 由题意可得：2021 年早熟李、晚熟李种植面积分别有1601%3a ⎛⎫- ⎪⎝⎭亩、()201%a -亩. 2021 年早熟李平均每亩收益为()10001%a + 元.晚熟李平均每亩收益为120001%2a ⎛⎫+ ⎪⎝⎭元. 由2021 年两种李子的总收益与2020 年两种李子总收益相等.得.()()11601%10001%201%20001%600004000032a a a a ⎛⎫⎛⎫-⨯++-⨯+=+ ⎪ ⎪⎝⎭⎝⎭令%t a =.则()()11600001140000111000032t t t t ⎛⎫⎛⎫-++-+= ⎪ ⎪⎝⎭⎝⎭. ()()()()31125t t t t -++-+= .223225t t t t +-+--=.220t t -=.()210t t -=.0t =或0.5=t .0a =（舍）.50a =．答：50a =．62．（2021·湖南·长沙市开福区青竹湖湘一外国语学校九年级期中）某学校计划从商店购买测温枪和洗手液.已知购买一个测温枪比购买一瓶洗手液多用20元.若用400元购买测温枪和用160元购买洗手液.则购买测温枪的数量是购买洗手液数量的一半．（1）求购买一个测温枪、一瓶洗手液各需多少元；（2）经商谈.商店给予该学校购买一个测温枪赠送一瓶洗手液的优惠.如果该学校需要洗手液的数量是测温枪数量的2倍还多8个.且该学校购买测温枪和洗手液的总费用不超过1540元.那么该学校最多可购买多少个测温枪？【答案】（1）购买一个测温枪需要25元.购买一瓶洗手液需要5元；（2）该学校最多可购买50个测温枪．【分析】（1）设购买一瓶洗手液需要x 元.则购买一个测温枪需要(20)x +元.依题意.得：4001160202x x=⨯+. 解得：5x =.经检验.5x =是原方程的解.且符合题意.2025x ∴+=．答：购买一个测温枪需要25元.购买一瓶洗手液需要5元．（2）设该学校购买m 个测温枪.则购买(28)m +瓶洗手液.依题意.得：255(28)1540m m m ++-.解得：50m ．答：该学校最多可购买50个测温枪．63．（2021·山东·青岛大学附属中学二模）扶贫工作小组对果农进行精准扶贫.帮助果农将一种有机生态水果拓宽了市场．与去年相比.今年这种水果的产量增加了1000千克.每千克的平均批发价比去年降低了125.批发销售总额比去年增加了20%．（1）已知去年这种水果批发销售总额为10万元.求这种水果今年每千克的平均批发价是多少元?（2）今年某水果店从果农处直接批发.专营这种水果.调查发现.若每千克的平均销售价为41元.则每天可售出300千克；若每千克的平均销售价每降低3元.每天可多卖出180千克．工商部门规定.该水果利润率不得超过40%.设水果店一天的利润为W 元.当每千克的平均销售价为多少元时.该水果店一天的利润最大.最大利润是多少?（利润计算时.其他费用忽略不计.并且售价为整数）【答案】（1）24元；（2）每千克平均售价为33元.最大利润为7020元．【分析】解：（1）由题意.设这种水果去年每千克的平均批发价是x 元.则今年的批发价为1125x ⎛⎫- ⎪⎝⎭元 .今年的批发销售总额为10（1+20%）=12万元 ∴ 1000001200001000,1125x x +=⎛⎫- ⎪⎝⎭解得x =25经检验x =25是分式方程的解．。

分式方程知识讲解

分式方程知识讲解分式方程是一种包含分数的方程，其中未知数出现在分数中的分子或分母中。

解分式方程的关键是通过消除分母，将方程转化为一个整式方程，并找到未知数的解。

一般来说，分式方程的解可以分为两种情况：分母不为0的情况和分母为0的情况。

对于分母不为0的情况，我们可以通过消除分母，将方程转化为一个整式方程来求解。

以下是一些常见的分式方程的解法：1.一次分式方程：形如a/x+b=c的方程。

这类方程可以通过先将方程两边都乘以x，然后移项化简得到解。

2.二次分式方程：形如a/(x^2)+b/x+c=d的方程。

这类方程可以通过将方程两边都乘以x^2，然后移项化简得到一个二次方程，进而求解。

3.分式方程组：包含多个分式方程的方程组。

解决这类方程组的关键是通过消去未知数的分母，将方程组转化为一个整式方程组，并求解。

对于分母为0的情况，我们需要特殊处理。

一般地，当分母为0时，方程无解或者方程的解为未知数的取值范围。

在解分式方程时，我们需要遵守以下一些基本规则：1.分式方程的等式两边都要乘以一个非零的数，以保持方程的等价性。

2.消去分式方程的分母时，要确保不会出现除以0的情况。

3.当两个方程的等式两边都乘以相同的非零数时，等式仍然成立。

下面我们通过一些具体的例子来进一步讲解分式方程的解法。

例1：求解分式方程2/x+3=5解法：将方程两边都乘以x，得到2+3x=5x。

将变量项移到一边，常数项移到另一边，得到3x-5x=-2、合并同类项，得到-2x=-2、再将方程两边都除以-2，得到x=1、所以方程的解为x=1例2：求解分式方程1/(x+1)+1/x=1/2解法：首先将方程两边的分式相加，得到(x+1+x)/(x(x+1))=1/2、化简得到2x+1=x(x+1)。

将方程转化为二次方程形式，得到x^2+x-1=0。

利用求根公式，我们可以解得x=(-1±√5)/2、所以方程的解为x=(-1+√5)/2或x=(-1-√5)/2例3：求解分式方程组1/x+1/y=1/2，x-y=1解法：将第一个方程移项，得到1/x-1/2=-1/y。

中考数学专题复习课件 --- 第六讲一元一次方程与分式方程

3
【解析】选A.把x=2代入方程2x+3m-1=0,解得m=-1.
2.(2010 ·东营中考)分式方程 (A)-3 (B)2 (C)3
1 3 的解是( x2 x
)
(D)-2
【解析】选C.原方程去分母,得x=3x-6,解得x=3,经检验x=3是
原方程的根,或者把选项代入原方程检验即可.
3.(2010·河北中考)小悦买书需用48元钱，付款时恰好用了 1元和5元的纸币共12张.设所用的1元纸币为x张，根据题意，
去分母，得(2x-8)-4=8, 去括号，得2x-8-4=8, 移项，合并同类项，得2x=20, 系数化为1，得x=10.
【纠错空间】上述解题过程出现了三个常见错误： (1)不会利用分式的符号法则对分式进行等值变形，这个法则是“分式的分子、分母和分式本身的符号，任意改变两处，分式的值不变”，按此法则，下列变形应该是：
3
检验：当 x 26 时，x-7≠0,且原方程的左右两边相等，
∴原方程的解为 x 26 .
3
3
x 1.(2010·江西中考)解方程： 2 x2
4 1. x2 4
【解析】去分母，得(x-2)2+4=x2-4, 解得x=3. 检验：当x=3时，x2-4≠0, ∴x=3是原方程的解.
【解析】设原计划每天修水渠 x 米.
3 根据题意得： 600 3 600 20, x 1.8x
解得：x=80, 经检验：x=80是原分式方程的解. 答：原计划每天修水渠80米.
解分式方程常见的错误
【例】解分式方程 2x 8 4 8.
x7 7x 2x 8 4Байду номын сангаас【错误解析】变形，得 8 , x 7 x 7

第六讲浙教版七年级下册分式方程应用题汇总(二)

17．A、B两城铁路长240千米，为使行驶时间减少20分，需要提速10千米/时，但在现有条件下安全行驶限速100千米/时，问能否实现提速目标．
18．A、B两地间的路程为150千米，甲、乙两车分别从A、B两地同时出发，相向而行，2小时相遇；相遇后，各以原来速度继续行驶，甲车到达B地立即原路返回，返回时的速度是原来的2倍，结果甲、乙两车同时到达A地，求甲车的原速度和乙车的速度．
（2）如果甲车间的生产费用为每天6500元，乙车间的生产费用为每天4500元，有以下三种方案可供选择：
方案一：由甲车间单独生产这批产品；
方案二：由乙车间单独生产这批产品；
方案三：甲乙两车间同时合作生产这批产品．
如从节约生产费用的角度考虑，工厂应选择哪个方案？请说明理由．
7．某校初三年级学生参加赈灾义演活动，甲班捐款200元，乙班30名同学捐款200元，这样，两班人均捐款比甲班人均捐款多1元，甲班有多名学生参加这次赈灾活动？（规定班级人数不超过60人）
3．甲、乙两公司各为“希望工程”捐款20000元．已知乙公司比甲公司人均多捐20元，且乙公司的人数比甲公司的人数少20%．问甲、乙两公司人均捐款各为多少元？
4．甲乙二人周末到惠州红花湖环湖旅行，同时从起点（0公理处）出发，环湖步行18千米后回到起点处，甲比乙每小时多走1千米，结果比乙早到36分钟．问二人每小时各走几千米？
5、甲容器中有15%的盐水30升，乙容器中有18%的盐水20升，如果向两个容器各加入等量的水，使它们的浓度相等，那么加入的水是多少升？
6、某市为治理污水，需要铺设一段全长位3000m的污水输送管道，为了尽量减少施工队城市交通所造成的影响，实际施工时每天的工效比原计划提高25%，结果提前30天完成任务。若设原计划每天铺设xm，则依题意可列方程

利用换元法解方程(组)

第6讲利用换元法解方程一、方法技巧（一）换元法解方程是用新元代替方程中含有未知数的某个部分，达到化简的目的.（二）运用换元法解方程，主要有三种类型：分式方程、无理方程、整式（高次）方程.解分式方程、无理方程、整式(高次)方程的基本思想是将分式方程化为整式方程、无理方程化为有理方程、整式（高次）方程逐步降次.（三）换元的方法是以所讨论方程的特有性质为依据的，不同的方程就有不同的换元方法，因此，这种方法灵活性大，技巧性强．恰当地换元，可将复杂方程化简，以便寻求解题的途径．常用换元方法有局部换元、均值换元、倒数换元、常数换元等．例如：① 256011x x x x ⎛⎫⎛⎫++= ⎪ ⎪++⎝⎭⎝⎭ ，可使用局部换元法，设1x y x =+ ②22110x x x x +++=，变形后也可使用局部换元法，设1x t x +=③222212219116x x x x x x x +++++=+++，看着很繁冗，变形整理成222211191116x x x x x x +++++=+++时，就可使用局部换元法. ④()()443182x x +++=，可设()()3122x x y x +++==+，方程变成()()441182y y ++-=，使方程变得易解，这是均值换元法.⑤4326538560x x x x +-++=，符合与中间项等距离的项的系数相等，如46x 与6，35x 与5x 系数相等，可构造1x x+换元，是倒数换元法.⑥32310x x +++=，不易求解，若反过来看，把设x 看作已t ，则方程就变成()()2232110x t x t x ⋅+++-=，数字换元法不常用，但不失为一种巧妙的解题方法.有时根据方程各部分特点可设双元，达到化繁为简，求解的目的.例如：()()()()()222222223232321321451x x x x x x x x x x -++-+--+--=-+观察发现()()22232321451x x x x x x -++--=-+，故可设232x x u -+=，2321x x v --=，原方程变为()222u uv v u v ++=+，方程由繁变简，可得解.（四）本讲注重研究用换元法解方程的技能、技巧．拓宽学生知识面，培养学生学习和研究数学的兴趣.二、应用举例类型一局部换元（高次方程）【例题1】解方程：42320x x -+=【答案】11x =，21x =-，3x =4x =【解析】试题分析：通过观察发现()242x x =，故设2x y =，原方程变形为2320y y -+=，可把高次方程降次，转化为可解的一元二次方程.试题解析：解：设2x y =，则原方程变形为2320y y -+=，解得，11y =，22y =，由11y =得21x =，解得11x =，21x =-，由22y =得22x =，解得3x =，4x =∴方程的解是11x =，21x =-，3x =4x =【难度】较易（分式方程）【例题2】解方程：256011x x x x ⎛⎫⎛⎫++= ⎪ ⎪++⎝⎭⎝⎭【答案】134x =-，223x =- 【解析】试题分析：括号里的分式相同，由这个特点，可以用换元法来解.试题解析：解：设1x y x =+，于是原方程变形为2560y y ++= 解得13y =-，22y =-当13y =-时，31x x =-+，解得134x =-，当22y =-时，21x x =-+，解得223x =- 经检验134x =-，223x =-均为原方程的根. ∴方程的解是134x =-，223x =- 【难度】较易【例题3】已知实数x 满足22110x x x x +++=，那么1x x+的值是（）【答案】2-【解析】试题分析：由于222112x x x x ⎛⎫+=+- ⎪⎝⎭，故设1x t x +=，可解. 试题解析：解：设1x t x+=，原方程化简得21120x x x x ⎛⎫+-++= ⎪⎝⎭， ∴220t t -+=，解得11t =，22t =- 由11x x+=化简得210x x -+=，△＜0 ，无解，舍去 ∴12x x +=- 点评：方程中并无“相同”的部分时，可通过代数式间的关系变形构造出“相同”部分，设元.【难度】一般（无理方程）【例题4103= 【答案】114x =，294x =- 【解析】试题分析：这是一个根号里含有分式的无理方程，也可通过换元后求解，通过变形发现221x x x++=，与2x x +互为倒数，y =，则原方程变形为1103y y +=，无理方程化为有理方程. 试题解析：()0y y = ＞，则原方程变形为1103y y +=整理得231030y y -+=解得13y =，213y =当13y =3=，解得114x =当213y =13=，解得294x =- 经检验114x =，294x =-都是原方程的根. 原方程的解是114x =，294x =- 【难度】一般【例题510=【答案】11x =21x = 【解析】试题分析：1=，可设两个未知数，利用韦达定理求解.试题解析：m = n = ，原方程变为1m n +=又∵()2222m n m n mn +=++∴142mn =+，即32mn =- 根据韦达定理，m n 、是方程2302z z --=的根解得1z =2z =0， ∴2z 舍去即m =n =12= 12=解得112x =+， 212x =-经检验11x =+212x =-是原方程的解∴ 方程的解是11x =+21x =- 【难度】一般类型二均值换元【例题6】解方程：()()443182x x +++= 【答案】10x =，24x =-【解析】试题分析：观察方程可知()()312x x +-+=，适合使用均值法换元，故设()()3122x x y x +++==+可达到降次目的.试题解析：解：设()()3122x x y x +++==+，原方程变为()()441182y y ++-=整理得()()()()222221121182y y y y ⎡⎤++--+-=⎣⎦ ()()2222412182y y +--=426400y y +-= 解得210y =-（舍），24y =即12y =，12y =-由22x +=，得10x =由22x +=-，得24x =-∴原方程的解为10x =，24x =-点评：一般形如()()44x a x b c +++=的方程可用均值法，设22x a x b a b y x ++++==+进行代换，化原方程为双二次方程求解.【难度】较难类型三倒数换元【例题7】解方程：4326538560x x x x +-++= 【答案】112x =，22x =, 33x =-，413x =- 【解析】试题分析：本题的特点是：按x 降幂排列后，与中间项等距离的项的系数相等，如46x 与6，35x 与5x 系数相等，可构造1x x +换元. 试题解析：解：显然0x =不是方程的解，故用2x 除方程两边，整理得221165380x x x x ⎛⎫⎛⎫+++-= ⎪ ⎪⎝⎭⎝⎭，设1y x x =+，则22212x y x+=-，上式变为()2625380y y -+-=，整理得265500y y +-= 解得152y =，2103y =-，由152x x +=，解得112x =，22x = 由1103x x +=-，解得33x =-，413x =- 点评：形如4320ax bx cx bx a ++++=的方程称为倒数方程，其特点是，按某一字母降幂排列后，与中间项等距离的项的绝对值相等，其解法是，用2x 除各项，构造1x x±，使原方程变为一元二次方程得解.【难度】较难类型四常数换元【例题8】解方程32310x x ++=【答案】11x =，212x -=，312x --= 【解析】试题分析：这是三次方程，且系数中含无理数，不易求解，若反过来看，把设x 设为设t ，则方程就变成关于t 的一元二次方程.试题解析：t=则原方程变形为322210x x t xt t +++-=即()()2232110x t x t x ⋅+++-= ()()2110x t x x t x ⎡⎤⋅++++-=⎡⎤⎣⎦⎣⎦ ()()2110x x x x ⎡⎤⎤++-=⎣⎦⎦整理得)21110x x x ⎡⎤⎡⎤+++=⎣⎦⎣⎦)2110x x ++=或10x +=解得11x =，2x =，3x = 【难度】困难三、实战演练类型一局部换元（高次方程）1.已知()()2222138x y x y ++++=，则22x y +的值为（）【答案】1【解析】试题分析：解题时把22x y +当成一个整体考虑，再求解就比较简单.试题解析：解：设22x y t +=，()0t ≥，则原方程变形为()()138t t ++=，整理得()()510t t +-=，解得15t =-，21t =，∵0t ≥∴1t =∴22x y +的值是1【难度】较易2.解方程：()2222360x x x x +--=【答案】10x =，22x =-，33x =-，41x =【解析】试题分析：观察可知，方程整理后()()2222320x xx x +-+=，可用换元法降次.试题解析：解：方程整理后()()2222320x xx x +-+=设22x x y +=，则原方程变为230y y -= 解得10y =，23y =由10y =，得220x x +=，解得10x =，22x =-由23y =，得223x x +=，解得33x =-，41x =∴原方程的解是10x =，22x =-，33x =-，41x =【难度】较易3.方程()()22235320x x ---+=，如果设23x y -=，那么原方程可变形为（） A ．2520y y -+= B. 2520y y +-= C. 2520y y --= D. 2520y y ++=【答案】D【解析】试题分析:注意到23x -与23x -互为相反数，只有符号要变化，可利用换元法变形.试题解析：解：设23x y -=，则23x y -=-用y 表示23x -后代入方程得2520y y ++=故选D.【难度】较易4.解方程：()22213x x +=+【答案】11x =，21x =- 【解析】试题分析：1.以21x +为一个整体换元，因此要对方程进行变形使其含有21x +.2.把方程展开成标准的双次方程，再对2x 进行换元.试题解析：解法一：原方程可化为()()2221120x x +-+-=，设21x y +=，得220y y --=，解得12y =，21y =-由212x +=，解得11x =，21x =-由211x +=-，22x =-无实根∴方程的解是11x =，21x =-解法二：由方程得4220x x +-=，设2x y =得220y y +-=，解得11y =，22y =-（舍去）由21x =，解得11x =，21x =-∴方程的解是11x =，21x =-点评：换元的关键是善于发现或构造方程中表达形式相同的部分作为换元对象.在解方程的过程中换元的方法常常不是唯一的，解高次方程时，只要能达到将次目的的换元方法都可以应用. 【难度】较易（分式方程）5.解方程2261x x x x=+++ 【答案】12x =-，21x =【解析】试题分析：方程左边分式分母为2x x +，可将右边2x x +看成一个整体，然后用换元法解.试题解析：解：设2x x y +=，则原方程变形为61y y=+ 解得13y =-，22y =当13y =-时，23x x +=-，△＜0，此方程无实根当22y =时， 22x x +=，解得12x =-，21x =经检验，12x =-，21x =都是原方程的根.【难度】较易【解析】试题分析：整理后发现()222x x x x +=+，故()()2211x x x ++=+，就可换元解题了试题解析：设()21x y +=，则整理得220y y --=解得12y =，21y =-（舍去）【难度】较易7.解方程222212219116x x x x x x x +++++=+++【答案】121x x ==，332x -+=，432x --= 【解析】试题分析：观察到()2222222112211111x x x x x x x x x x x x +++++++==+++++++，设2211x x y x ++=+，原方程可化为11916y y ++=，由繁变简，可解. 试题解析：解：原方程变形得222211191116x x x x x x +++++=+++，即22221113116x x x x x x ++++=+++ 设2211x x y x ++=+，则原方程变为1136y y += 整理得261360y y -+= 解得132y =，223y = 由132y =得221312x x x ++=+，解得121x x ==由223y =得221213x x x ++=+，解得3x =，4x =经检验121x x ==，3x =4x =.∴原方程的解是121x x ==，332x -+=，432x --= 【难度】一般8.解方程：22272720x x x x+-++=【答案】11x =，21x =， 312x =-，42x = 【解析】试题分析：观察可发现22222711272272x x x x x x x x ⎛⎫⎛⎫+-++=+--+ ⎪ ⎪⎝⎭⎝⎭，而222112x x x x ⎛⎫+=-+ ⎪⎝⎭，故可设1x x -为辅助元，可得解. 试题解析：解：将原方程转化为21122720x x x x ⎡⎤⎛⎫⎛⎫-+--+=⎢⎥ ⎪ ⎪⎝⎭⎝⎭⎢⎥⎣⎦设1x y x-=，则原方程转化为22760y y -+=解得12y =，232y =当12y =时，12x x-=，解得11x =，21x = 当232y =时，132x x -=，解得312x =-，42x =经检验11x =21x = 312x =-，42x =都是原方程的解所以，原方程的解是11x =，21x =， 312x =-，42x = 【难度】一般9.解方程:222322322x x x x-+=-【答案】1x =2x = 【解析】试题分析：这个方程左边两个分式互为倒数关系，抓住这一特点，可设2232x y x =- 试题解析：解：设2232x y x =-，则原方程可化为12y y +=，即2210y y -+=∴()210y -=，解得1y = 由22132x x =-，得23220x x --=解得：1x =，213x =经检验1x =，2x =都是原方程的根点评：解有倒数关系的分式方程时，常把原方程中的一个分式作为整体进行换元，换元时要注意分子、分母互换时分式可以用一个新元和它的倒数来表示，即形如()()0b a f x c f x ++=的方程，可设()y f x = 【难度】较易10.解方程：222122272221x x x x x x +=+-+-+-【答案】11x =-21x =-【解析】试题分析：观察方程的分母，发现各分母均是关于x 的二次三项式，仅常数项不同，抓住这一特点，可设22y x x =+ 试题解析：解：设22y x x =+，原方程可化为122721y y y +=---，即()()12721y y y -=---，即2120y y --=，解得：14y =，23y =-由224x x +=，解得11x =-21x =- 由223x x +=-，△＜0，方程无解经检验11x =-21x =-.∴方程的解是11x =-21x =-【难度】较难11.解方程：222111011102101310x x x x x x ++=++++-+ 【答案】15x =，22x =，35x =-，42x =-【解析】试题分析：观察方程的分母，发现三个分母都是关于x 的二次三项式，仅一次项不同，抓住这一特点，可设2210y x x =++试题解析：解：设2210y x x =++，则原方程可化为1110915y x y y x ++=+-整理得：224450y xy x --=解得：19y x =，25y x =-由22109x x x ++=，解得15x =，22x =由22105x x x ++=-，解得35x =-，42x =-经检验知，它们都是原方程的解.点评：以上三个例子可以看出，换元时必须对原方程仔细观察、分析，抓住方程的特点，恰当换元，花繁为简，达到解方程的目的.【难度】较难（双元换元） 12.解方程： 213134211x x x x x x --⎛⎫+= ⎪++⎝⎭【答案】11x =，26x =，33x =，43x =【解析】试题分析：本题整理后2213134211x x x x x ⎛⎫⎛⎫-+= ⎪⎪++⎝⎭⎝⎭，发现221313131313111x x x x x x x ⎛⎫⎛⎫-+++== ⎪ ⎪+++⎝⎭⎝⎭，设2131x x a x -=+，2131x b x +=+，可得13a b +=，42ab =，利用韦达定理可求解. 试题解析：解：设2131x x a x -=+，2131x b x +=+ 可得13a b +=，42ab =由韦达定理，知a ，b 是方程213420z z -+=的两根解得16z =，27z =即67a b =⎧⎨=⎩或76a b =⎧⎨=⎩即2213611371x x x x x ⎧-=⎪⎪+⎨+⎪=⎪+⎩或2213711361x x x x x ⎧-=⎪⎪+⎨+⎪=⎪+⎩ 经检验11x =，26x =，33x =，43x =.所以方程的解是11x =，26x =，33x =，43x =【难度】较难13()()()()()222222223232321321451x x x x x x x x x x -++-+--+--=-+ 【答案】131x x ==，22x =，413x =-【解析】试题分析：观察发现()()22232321451x x x x x x -++--=-+，故可设232x x u -+=，2321x x v --=，原方程变为()222u uv v u v ++=+，方程由繁变简，可得解试题解析：解：∵()()22232321451x x x x x x -++--=-+设232x x u -+=，2321x x v --= 原方程变为()222u uv v u v ++=+∵()2222u uv v u v ++=+∴0uv =，即0u =或0v =即2320x x -+=或23210x x --=解得11x =，22x =，31x =，413x =-∴方程的解是131x x ==，22x =，413x =- 点评：对于本题这样繁冗的方程，直接展开求解不可取，可通过观察，找到代数式间的联系，不妨设两个辅助元，将方程变形，目的是使方程有繁变简，可解.【难度】较难（无理方程）14.1=【答案】1x =-【解析】试题分析：解无理方程的基本思想是将其转化为有理方程，通常是设根式为元，本题的两根式存在()()1+12x x +=+的关系，故设一个辅助元即可.试题解析：解：设y =21x y +=，即221x y +=+1y =1y =-两边平方，并整理得0y =0=，解得1x =-经检验1x =-是原方程的解点评：解无理方程时，常把方程中的一个含有未知数的根式作为整体换元，达到化去根号转化为可解的方程的目的.【难度】一般15.解方程组：183x y +=⎧⎪-=【答案】191x y =⎧⎨=-⎩【解析】试题分析：此题是整式方程与无理方程合并的方程组，解题时应从无理方程出发，将其化为有理方程求解.试题解析：u =v =，则原方程组可化为：22173u v u v ⎧+=⎨-=⎩()()12 由（2）得，3u v =+，（3）将（3）代入（1），得()22317v v ++=，解得，11v =，24v =-∴4u =得41==，解得191x y =⎧⎨=-⎩经检验，知191x y =⎧⎨=-⎩是原方程组的解 ∴原方程组的解为191x y =⎧⎨=-⎩点评：妙用换元法，将无理方程组化为有理方程组，从而把繁杂而生疏的问题转化为简单而熟悉的问题.【难度】一般16.解方程：22650x x --=【答案】15x =，22x =-【解析】试题分析：由于根号里面23x x -与根号外面226x x -，对应系数成比例，故可以将其变形()223130x x ---=，不难找到辅助元.试题解析：y =，则原方程可以化为22530y y --=解得112y =-（舍去），23y =3=，解得15x =，22x =-经检验15x =，22x =-是原方程的解.点评：以前学过的取平方去根号法解无理方程，是种普遍方法.现在的换元法必须构造出根号内外两个相同的式子才行.【难度】较难类型二均值换元17.解方程：()()()()214719x x x x -+++=【答案】1x =2x =3x =，4x = 【解析】试题分析：方程的左边是四个二项式乘积，故展开求解不可取，应通过观察找突破口，左边重组后，()()()()2714x x x x -+++⎡⎤⎡⎤⎣⎦⎣⎦()()2251454x x x x =+-++，可设元求解.试题解析：解：原方程变形后()()()()271419x x x x -+++=⎡⎤⎡⎤⎣⎦⎣⎦整理后得()()225145419x x x x +-++=设()()22251454552x x x x y x x +-+++==+-方程可变为()()9919y y -+=，即2100y =解得110y =，210y =-由110y =得25510x x +-=，解得1x =2x =由210y =-得25510x x +-=-，解得3x =4x =∴方程的解是152x -=，252x --=，352x -+=，452x --= 点评：本题也可设25x x +为辅助元，但没有均值法计算快捷，恰当的重组变形得到()()()()2714x x x x -+++⎡⎤⎡⎤⎣⎦⎣⎦是解本题的关键.【难度】一般18.解方程：()()()2673416x x x +++= 【答案】123x =-，253x =- 【解析】试题分析：方程左边四个二次项的乘积，显然展开求解不可取，可尝试变形后()()()267686672x x x +++=，取均值，将其由繁变简.试题解析：解：方程变形为()()()267686672x x x +++= 设()()()()67676866674x x x x y x +++++++==+原方程变成()()21172yy y +-= 整理得42720y y --=解得29y =或28y =-（舍去）∴13y =，23y =-即673x +=或673x +=- 解得123x =-，253x =- 【难度】较难类型三倒数换元19.解方程：4322316320x x x x +-++=【答案】12x =-，22x =-32x =，412x = 【解析】试题分析：此题符合倒数方程的特点：按x 降幂排列后，与中间项等距离的项的系数相等，两边同时除以2x ，可构造1x x+为元得解. 试题解析：解：∵这是个倒数方程，且知0x ≠，两边除以2x ，并整理得221123160x x x x ⎛⎫⎛⎫+++-= ⎪ ⎪⎝⎭⎝⎭ 设1x y x +=，则22212x y x+=- 原方程化为223200y y +-=解得14y =-，252y =由14y =-得14x x+=-，解得12x =-，22x =- 由252y =得152x x +=，解得32x =，412x =∴方程的解是12x =-，22x =-32x =，412x = 【难度】较难20.解方程((5598y y ++-= 【答案】2y =±【解析】试题分析：此题无法用通常的方法解决，但注意到5+5-互为倒数且指数均为y ，因此，利用换元法换元后再利用根与系数的关系就可以顺利解决此题了.试题解析：解：设(5y a =+，(5y b =-，则981a b ab +=⎧⎨=⎩a 、b 可看作29810t t -+=的根解得149t =+，249t =-则4949a b ⎧=+⎪⎨=-⎪⎩4949a b ⎧=-⎪⎨=+⎪⎩∴(((2254955y a ±=+=±=±=+∴2y =±点评：本题是指数方程，不是中考考点，但解法巧妙，可用来拓展思路，不妨试试！【难度】较难。

分式方程说课稿

分式方程说课稿分式方程说课稿1一、教材分析：1、__与本节的地位与作用： __是在学生已掌握了整式的四则运算，多项式的因式分解的基础上，通过对比分数的知识来学习的，包括分式的概念、分式的基本性质、分式的四则运算，这一章的内容对于今后进一步学习函数和方程等知识有着重要的作用。

可化为一元一次方程的分式方程是在学生已熟练地掌握了一元一次方程的解法、分式四则运算等有关知识的基础进行学习的。

它既可看着是分式有关知识在解方程中的应用；也可看着是进一步学习研究其它分式方程的基础（可化为一元二次方程的分式方程）。

同时学习了分式方程后也为解决实际问题拓宽了路子，打破了列方程解应用题时代数式必须是整式这一限制。

解分式方程的基本思想是：“把分式方程转化为整式方程”，基本方法是：“去分母”。

让学生进一步体会“转化”这一数学思想，对提高学生的数学素质是非常重要的。

2、教学目标：根据学生已有的知识基础及本节在教材中的地位与作用，依据大纲的要求确定本课时的教学目标为：（1）了解分式方程的概念，会识别分式方程与整式方程。

（2）理解分式方程的解法，会熟练地解分式方程。

（3）体会解分式方程的“转化”思想。

3、教学重点、难点、关键：根据大纲要求及学生的认知水平，确定本节课的教学重点为：分式方程的解法。

重中之重是去分母实现分式方程到整式方程的转化与验根。

由于学生去分母时涉及等式的基本性质、整式运算、分式运算等知识，学生容易出错，而一旦顺利地实现了去分母，即实现了分式方程到整式方程的转化，解整式方程是学生早已熟悉的知识。

因此确定正确去分母既是教学的难点，也是教学的关键。

由于解分式方程可能产生增根，学生第一次遇到，所以分式方程的验根也是难点，二、教学方法：（一）学生分析：根据七年级学生的知识水平和年龄特征，考虑到素质教育的要求，结合本节课的特点，主要采用启导式教学法、讲练法，引导学生去观察、去思考、去探索，尽量让学生自己寻找、归纳出解分式方程的一般步骤。

第6讲分式方程及其应用

经检验,x=40 是分式方程的根.
∴B 采样点送检车的平均速度为 40×1.5=60(km/h),
∴B 采样点送检车的行驶时间为 45÷60=0.75(h).
∵3.2+0.75=3.95<4,∴B 采样点采集的样本不会失效.
1.(2021 恩施)分式方程
A.x=1

C.x=

+1=
-

的解是( D )

A.x=
B.x=
C.x=
D.x=

[变式 2](2021 连云港)解方程:
+
(x+1)2-4=(x+1)(x-1),
整理,得2x-2=0,解得x=1.
检验:当x=1时,(x+1)(x-1)=0,
∴原方程无解.

=1.
- -
解:方程两边同乘(x+1)(x-1),得
∴x=1是增根,应舍去.
-
8.(2021 潍坊)若 x<2,且

0
+|x-2|+x-1=0,则 x=
-
.
1 .
9.(2021 东营)某地积极响应“把绿水青山变成金山银山,用绿色杠杆撬动经济转型”发展理念,开展
荒山绿化,打造美好家园,促进旅游发展.某工程队承接了 90 万平方米的荒山绿化任务,为了迎接雨
季的到来,实际工作时每天的工作效率比原计划提高了 25%,结果提前 30 天完成了任务.设原计划每
1.(2022 方城期中)给出下列方程:
-

+

+

2014年广东中考高分突破课件：第二章第6讲分式方程

★课堂精讲★
考点 1 ．分式方程的解法(2009、2010 年考)
1 3 =0 1. （ 2013 玉林）方程 x-1 x+1 的解是（ A ）
A．x=2 B．x=1 C．x= 2
1
D．x=-2
思路点拨：本题考查了解分式方程，解分式方程的基本思想是“转化思想”，把分式方程转化为整式方程求解．解分式方程一定注意要验根．
x2 4 =0 2．（ 2013 莱芜）方程 x-2 的解为（ A ）
A．-2 B．2 C．±2
1 D．- 2
x 的值，经检
思路点拨：分式方程去分母转化为整式方程，求出整式方程的解得到验即可得到分式方程的解．
3．（2013 珠海）解方程：
．
思路点拨：观察可得最简公分母是（x+2）(x-2)，方程两边同时乘以最简公分母，可以把分式转化为整式方程求解.注意：（1）解分式方程的基本思想是 “转化思想” ，把分式方程转化为整式方程求解.（2）解分式方程一定要验根.
思路点拨：（1）先设苹果进价为每千克 x 元，根据两超市将苹果全部售完，其中甲超市获利 2100 元列出方程，求出 x 的值，再进行检验即可求出答案；（2）根据（1）求出每个超市苹果总量，再根据大、小苹果售价分别为 10 元和 5.5 元，求出乙超市获利，再与甲超市获利 2100 元相比较即可．
思路点拨：设每人每小时的绿化面积 x 平方米，根据增加 2 人后完成的时间比原来的时间少 3 小时为等量关系建立方程求出其解即可．
4. 解：设每人每小时的绿化面积 x 平方米，由题意，得
180 180 =3 6x （6 2）x ，
解得：x=2.5．经检验，x=2.5 是原方程的解，且符合题意．答：每人每小时的绿化面积 2.5 平方米．

【2014中考复习方案】(江西专版)中考数学复习权威课件：6分式方程

解分式方程的一般步骤是：①方程两边都乘各个分母的
考点1
最简公分母，把分式方程转化为整式方程；②解这个整式方 ________________
程；③检验：把求得的未知数的取值代入最简公分母，看是否等于 0，使最简公分母为0的根是原方程的增根，增根必须舍去．
赣考解读考点聚焦赣考探究
第6讲┃分式方程
赣考解读
考点聚焦
赣考探究
第6讲┃分式方程
解析
(1)首先把总工作量看作单位“1”，设出甲车、乙车单独运完此堆
垃圾所需的趟数，表示出甲车、乙车的工作效率，再表示出甲车、乙车12趟完成的工作量，根据等量关系“甲车的工作量＋乙车的工作量＝总工作量”列出方程． (2)根据“甲车12趟所需费用＋乙车12趟所需费用＝4800”求出甲车、乙车每趟所需费用，再计算单独租用一种车所需车间原计划在x天内生产120个零件，由于采用了新技术，每天
120 120 － x ＝3 ．多生产零件3个，因此提前2天完成任务，则列方程为______________ x－ 2
赣考解读
考点聚焦
赣考探究
第6讲┃分式方程
2．某校为了进一步开展“阳光体育”活动，购买了一批乒乓球拍和羽毛球拍．已知一副羽毛球拍比一副乒乓球拍贵20 元，购买羽毛球拍的费用比购买乒乓球拍的2000元要多，多出的部分能购买25副乒乓球拍．若每副乒乓球拍的价格为x 元，购买的两种球拍数一样，求x.
赣考解读
考点聚焦
赣考探究
第6讲┃分式方程
探究三分式方程的应用
例3 [2013·娄底] 为了创建全国卫生城市，某社区要清理一个卫生死角内的堆垃圾，租用甲、乙两车运送，两车各运12趟可完成，需支付运费4800元．已知甲、乙两车单独运完此堆垃圾，乙车所运趟数是甲车的2倍，且乙车每趟运费比甲车少200 元． (1)求甲、乙两车单独运完此堆垃圾各需运多少趟？ (2)若单独租用一台车，租用哪台车合算？

解分式方程课件

THANKS
感谢观看
化学反应速率问题
通过解分式方程，可以计算化学反应的速率、反应时间等参数，有助于分析和解决化学反应速率问题。
溶液浓度问题
利用分式方程，可以计算溶液的浓度、溶质的质量等参数，有助于分析和解决溶液浓度问题。
06
练习题与答案解析
练习题一：一元一次分式方程求解
练习题1
解方程 $frac{x}{x-2} - frac{3}{x+2} = 1$
未知数位不同
整式方程的未知数通常出现在分子中，而分式方程的未知数出现在分母中。
方程形式不同
解法不同
整式方程通常通过合并同类项、移项等方法求解，而分式方程则需要通过去分母等方法转化为整式方程后求解。
整式方程通常是多项式等式，而分式方程则包含分式。
02
解分式方程方法
去分母法
原理
通过去分母，将分式方程转化为整式方程，从而简化求解过程。
找公共分母
观察分式方程中的各个分式，找出它们的公共分母。
消去分母
通过两边同时乘以公共分母，将分式方程转化为整式方程。
求解整式方程，得到解集
整理方程
将整式方程进行整理，化简为标准形式。
求解方程
运用整式方程的求解方法，如因式分解、配方法等，求出方程的解集。
检验解集，确定最终解
检验解的合法性
将求得的解代入原方程进行检验，确保解满足原方程。
练习题2
解方程 $frac{x^3+2x^2+x}{x^2+x} - frac{x^2+3x+2}{x+2} = frac{2}{x}$
练习题3
解方程 $frac{x^4-16}{x^2-4} - frac{2(x^2+4)}{x^2+4x+4} = frac{8}{x^2-4}$

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

第6讲分式方程表头加底纹注意事项：只是章首页考纲要求命题趋势1．理解分式方程的概念，会解可化为一元一次(二次)方程的分式方程(方程中的分式不超过两个)，知道解分式方程的基本思想是把分式方程化为整式方程． 2．了解解分式方程产生增根的原因，能解决有关字母系数的问题． 3．会列分式方程解决实际问题. 中考中多以选择题、填空题、解答题的形式考查以下几点：(1)找分式方程的最简公分母，将分式方程化成整式方程；(2)已知方程有增根，确定有关字母的值；(3)解分式方程．列分式方程解决实际问题是中考的重点.知识梳理一、分式方程1．分母里含有________的有理方程叫做分式方程．2．使分式方程分母为零的未知数的值即为__________；分式方程的增根有两个特征：(1)增根使__________为零；(2)增根是分式方程化成的__________方程的根．二、分式方程的基本解法解分式方程的一般步骤：(1)去分母，把分式方程转化为__________方程．(2)解这个整式方程，求得方程的根．(3)检验，把解得整式方程的根代入最简公分母，如果最简公分母为零，则它不是原方程的根，而是方程的__________，必须舍去；如果使最简公分母不为零，则它是原分式方程的根．三、分式方程的实际应用分式方程的应用题与一元一次方程应用题类似，不同的是要注意检验：(1)检验所求的解是否是所列分式方程的解；(2)检验所求的解是否符合实际．自主测试1．分式方程32x －4－x x －2＝12的解为( ) A ．x ＝52 B ．x ＝53 C ．x ＝5 D ．无解 2．货车行驶25千米与小车行驶35千米所用时间相同，已知小车每小时比货车多行驶20千米，那么两车的速度各为多少？设货车的速度为x 千米/时，依题意列方程正确的是( )A ．25x ＝35x －20 B ．25x －20＝35xC ．25x ＝35x ＋20D ．25x ＋20＝35x3．已知关于x 的分式方程a ＋2x ＋1＝1的解是非正数，则a 的取值范围是__________．考点一、分式方程的解法【例1】解方程：x ＋12x ＝x ＋13.分析：把分式方程转化为整式方程，通过解整式方程求得分式方程的解．解：原方程两边同乘6x ，得3(x ＋1)＝2x ·(x ＋1)，整理得2x 2－x －3＝0，解得x ＝－1或x ＝32.经验证知它们都是原方程的解，故原方程的解为x ＝－1或x ＝32. 方法总结解分式方程时应注意以下两点：(1)去分母时，要将最简公分母乘以每一个式子，不要“漏乘”；(2)解分式方程时必须检验，检验时只要代入最简公分母看其是否为0即可．若能使最简公分母为0，则该解是原方程的增根．触类旁通1 解方程：x x ＋2＋x ＋2x －2＝8x 2－4. 【例2】解方程：x －1x ＋x x －1＝52. 解：设x －1x ＝y ，则原方程化为y ＋1y ＝52. 解得y 1＝2，y 2＝12.当y ＝2时，x －1x＝2，解得x ＝－1；当y ＝12时，x －1x ＝12，解得x ＝2. 经检验，x 1＝－1，x 2＝2均符合题意，所以原方程的解为x 1＝－1，x 2＝2.方法总结解分式方程时，如按常规用约去分母的方法解，所得到的整式方程比较复杂，不易继续求解，我们可采用换元法求解．一般分式方程有以下两种情况时，可考虑换元法：第一种情况是“倒数型”，如2x x －1＋x －1x ＝52，由于x x －1与x －1x 互为倒数，当设x x －1＝y 时，原方程可化为2y ＋1y ＝52；第二种情况是“平方型”，如⎝⎛⎭⎫x －1x 2－2⎝⎛⎭⎫x －1x －3＝0，此时设x －1x＝y ，则原方程可化为y 2－2y －3＝0. 触类旁通2 方程66x ＋3－60x＝0的根是________．考点二、分式方程的增根【例3】分式方程x x －1－1＝m (x －1)(x ＋2)有增根，则m 的值为( ) A ．0或3 B ．1C ．1或－2D ．3解析：由(x －1)(x ＋2)＝0得增根可能是x ＝1或x ＝－2，把方程两边都乘(x －1)(x ＋2)得x (x ＋2)－(x －1)·(x ＋2)＝m ，当x ＝1时，得m ＝3，当x ＝－2时，得m ＝0，此时方程变为x x －1－1＝0，即x ＝x －1，此时方程无解，故m ＝0舍去，∴当m ＝3时，原方程有增根x ＝1.答案：D方法总结利用增根求分式方程中字母的值：(1)确定增根；(2)将原分式方程化成整式方程；(3)增根代入变形后的整式方程，求出字母的值．触类旁通3 若解分式方程mx ＋1x －1＝－1时产生增根，则m 的值是( ) A ．0 B ．1 C ．－1 D ．±1考点三、分式方程的应用【例4】某品牌瓶装饮料每箱价格26元．某商店对该瓶装饮料进行“买一送三”促销活动，若整箱购买，则买一箱送三瓶，这相当于每瓶比原价便宜了0.6元．问该品牌饮料一箱有多少瓶？解：设该品牌饮料一箱有x 瓶，依题意，得26x －26x ＋3＝0.6，化简，得x 2＋3x －130＝0，解得x 1＝－13(不合题意，舍去)，x 2＝10.经检验：x ＝10符合题意．答：该品牌饮料一箱有10瓶．方法总结列分式方程解决实际问题关键是找到“等量关系”，将实际问题抽象为方程问题．同时，既要注意求得的根是否是原分式方程的根，又要根据具体问题的实际意义，检验是否合理．触类旁通4 某镇道路改造工程，由甲、乙两工程队合作20天可完成．甲工程队单独施工比乙工程队单独施工要多用30天才可完成．(1)求甲、乙两工程队单独完成此项工程各需要多少天；(2)若甲工程队独做a 天后，再由甲、乙两工程队合作__________天(用含a 的代数式表示)可完成此项工程；(3)如果甲工程队施工每天需付施工费1万元，乙工程队施工每天需付施工费2.5万元，甲工程队至少要单独施工多少天后，再由甲、乙两工程队合作施工完成剩下的工程，才能使施工费不超过64万元？1．(2012浙江丽水)把分式方程2x ＋4＝1x 转化为一元一次方程时，方程两边需同乘以( ) A ．x B ．2xC ．x ＋4D ．x (x ＋4)2．(2012四川宜宾)分式方程12x 2－9－2x －3＝1x ＋3的解为( ) A ．3 B ．－3 C ．无解 D ．3或－33．(2012浙江台州)小王乘公共汽车从甲地到相距40千米的乙地办事，然后乘出租车返回，出租车的平均速度比公共汽车多20千米/时，回来时路上所花时间比去时节省了14，设公共汽车的平均速度为x 千米/时，则下面列出的方程中正确的是( ) A ．40x ＋20＝34×40xB ．40x ＝34×40x ＋20C ．40x ＋20＋14＝40xD ．40x ＝40x ＋20－14 4．(2012四川攀枝花)若分式方程：2＋1－kx x －2＝12－x有增根，则k ＝__________. 5．(2012广东梅州)解方程：4x 2－1＋x ＋21－x＝－1. 6．(2012山东临沂)某工厂加工某种产品，机器每小时加工产品的数量比手工每小时加工产品的数量的2倍多9件．若加工1 800件这样的产品，机器加工所用的时间是手工加工所用时间的37倍．求手工每小时加工产品的数量．1．解方程x x 2－1＋2(x 2－1)x ＝3时，设x x 2－1＝y ，则原方程化为y 的整式方程为( ) A ．2y 2－6y ＋1＝0 B ．y 2－3y ＋2＝0C ．2y 2－3y ＋1＝0D ．y 2＋2y －3＝02．分式方程2x －5x －2＝32－x的解是( ) A ．x ＝－2 B ．x ＝2C ．x ＝1D ．x ＝1或x ＝23．若关于x 的方程m －1x －1－x x －1＝0没有增根，则m 的值不能是( )A ．3B ．2C ．1D ．－14．某单位向一所希望小学赠送1 080件文具，现用A ，B 两种不同的包装箱进行包装，已知每个B 型包装箱比A 型包装箱多装15件文具，单独使用B 型包装箱比单独使用A 型包装箱可少用12个．设B 型包装箱每个可以装x 件文具，根据题意列方程为( )A ．1 080x ＝1 080x －15＋12B ．1 080x ＝1 080x －15－12 C ．1 080x ＝1 080x ＋15－12 D ．1 080x ＝1 080x ＋15＋12 5．已知x ＝1是分式方程1x ＋1＝3k x的根，则实数k ＝________. 6．若2x －1与1互为相反数，则x 的值是__________． 7．已知关于x 的方程2x ＋m x －2＝3的解是正数，则m 的取值范围为__________． 8．解分式方程：(1)x x ＋1＋1＝2x ＋1x ； (2)1x ＋1－2x x 2－1＝1. 9．某市为了治理城市污水，需要铺设一段全长为300米的污水排放管道，铺设120米后，为了尽可能减少施工对城市交通所造成的影响，后来每天的工作量比原计划增加20%，结果共用了27天完成了这一任务，求原计划每天铺设管道多少米．参考答案导学必备知识自主测试1．B 去分母，得3－2x ＝x －2，解得x ＝53.经检验x ＝53是原方程的解． 2．C 相等关系为：货车行驶25千米所用时间＝小车行驶35千米所用时间．3．a ≤－1 去分母，得a ＋2＝x ＋1，解得x ＝a ＋1，由题意得a ＋1≤0，所以a ≤－1. 探究考点方法触类旁通1．解：去分母，得x (x －2)＋(x ＋2)2＝8.去括号，得x 2－2x ＋x 2＋4x ＋4＝8.整理，得x 2＋x －2＝0.解得x 1＝－2，x 2＝1.检验，当x 1＝－2时，x 2－4＝4－4＝0，∴x 1＝－2是增根；当x 2＝1时，x 2－4＝1－4＝－3≠0，∴原方程的根是x ＝1.触类旁通2．解：66x ＋3－60x＝0， 60x ＋180＝66x ，x ＝30.触类旁通3．C 使分母为零的未知数的值即为增根，增根一定是分式方程转化为整式方程后的这个整式方程的根．∵mx ＋1x －1＝－1有增根，∴x －1＝0，∴x ＝1，∴mx ＋1＝－x ＋1.当x ＝1时，解得m ＝－1.触类旁通4．解：(1)设乙单独做x 天完成此项工程，则甲单独做(x ＋30)天完成此项工程．由题意，得20⎝⎛⎭⎫1x ＋1x ＋30＝1，整理，得x 2－10x －600＝0，解得x 1＝30，x 2＝－20.经检验：x 1＝30，x 2＝－20都是分式方程的解．但x 2＝－20不符合题意舍去，x ＋30＝60.答：甲、乙两工程队单独完成此项工程各需要60天、30天．(2)设甲单独做a 天后，甲、乙再合作⎝⎛⎭⎫20－a 3天，可以完成此项工程． (3)由题意，得1×a ＋(1＋2.5)⎝⎛⎭⎫20－a 3≤64，解得a ≥36.答：甲工程队至少要单独做36天后，再由甲、乙两队合作完成剩下的此项工程，才能使施工费不超过64万元．品鉴经典考题1．D2．C 解方程去分母得12－2(x ＋3)＝x －3解得x ＝3，经检验x ＝3是原方程的增根，原方程无解．3．A 因为公共汽车的平均速度为x 千米/时，则出租车的平均速度为(x ＋20)千米/时，小王乘公共汽车从甲地到乙地所花的时间为40x 小时，回来时路上所花时间为40x ＋20小时，根据相等关系：回来时路上所花时间＝去时路上所花时间×34，列方程为40x ＋20＝34×40x. 4．1 解方程去分母得2(x －2)＋1－kx ＝－1，由于原方程有增根，则x ＝2，解得k ＝1.5．解：方程两边都乘以(x ＋1)(x －1)，得4－(x ＋1)(x ＋2)＝－(x 2－1)，整理，得3x ＝1，解得x ＝13. 经检验，x ＝13是原方程的解．故原方程的解是x ＝13. 6．解：设手工每小时加工产品x 件，则机器每小时加工产品(2x ＋9)件．根据题意，得1 800x ×37＝1 8002x ＋9. 解这个方程，得x ＝27.经检验，x ＝27是原方程的解．答：手工每小时加工产品27件．研习预测试题1．B 设x x 2－1＝y ，则原方程化为y ＋2y ＝3，去分母移项得y 2－3y ＋2＝0. 2．C 去分母，得2x －5＝－3，解得x ＝1.检验，当x ＝1时，x －2≠0，所以原方程的解为x ＝1.3．B 将分式方程两边都乘以(x －1)，得m －1－x ＝0，把x ＝1代入m －1－x ＝0，解得m ＝2.所以若原分式方程没有增根，则m ≠2.4．B 因为B 型包装箱每个可以装x 件文具，则A 型包装箱每个可以装(x －15)件文具．相等关系为：单独使用B 型包装箱数＝单独使用A 型包装箱数－12，列方程为1 080x ＝1 080x －15－12.5．16 把x ＝1代入方程，得12＝3k ，解得k ＝16. 6．－1 由题意，得2x －1＋1＝0，所以2＋(x －1)＝0，所以x ＝－1.经检验x ＝－1是方程2x －1＋1＝0的解． 7．m ＞－6且m ≠－4 由2x ＋m x －2＝3，得x ＝m ＋6，∴m ＋6＞0，m ＞－6.又∵x －2≠0，即x ≠2，∴m ≠－4，故m ＞－6且m ≠－4.8．解：(1)去分母，得x 2＋x (x ＋1)＝(2x ＋1)(x ＋1)，解得x ＝－12.经检验：x ＝－12是原方程的解，所以原方程的解为x ＝－12. (2)去分母，得x －1－2x ＝x 2－1，化简，得x 2＋x ＝0，解得x 1＝0，x 2＝－1.经检验：x ＝－1不是原方程的解．所以原方程的解为x ＝0.9．解：设原计划每天铺设管道x 米．则120x ＋300－120x (1＋20%)＝27.解得x ＝10(米)．经检验，x ＝10是原方程的解．答：原计划每天铺设管道10米．。