广东省普宁市第二中学2016-2017学年高二第一学期期末考试数学试卷理
2016-2017年高二上第一次月考理科试卷(含答案)解析
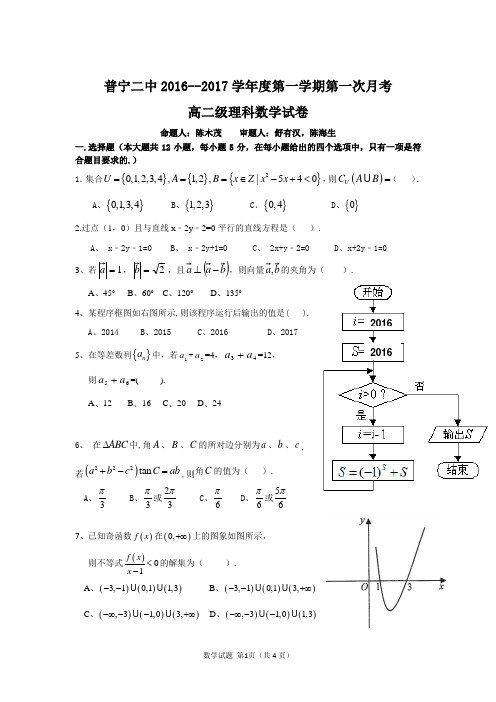
普宁二中2016--2017学年度第一学期第一次月考高二级理科数学试卷命题人:陈木茂 审题人:舒有汉,陈海生一.选择题(本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.)1.集合{}{}{}20,1,2,3,4,1,2,|540U A B x Z x x ===∈-+<,则()U C A B=( ). A 、{}0,1,3,4 B 、{}1,2,3 C 、{}0,4 D 、{}0 2.过点(1,0)且与直线x ﹣2y ﹣2=0平行的直线方程是( ). A 、 x ﹣2y ﹣1=0 B 、 x ﹣2y+1=0C 、 2x+y ﹣2=0D 、x+2y﹣1=031=2=,且()-⊥,则向量,的夹角为( ).A 、45°B 、60°C 、120°D 、135°4、某程序框图如右图所示,则该程序运行后输出的值是( ). A 、2014 B 、2015 C 、2016 D 、20175、在等差数列{}n a 中,若1a +2a =4,43a a +=12, 则65a a +=( ). A 、12 B 、16 C 、20 D 、246、 在ABC ∆中,角A 、B 、C 的所对边分别为a 、b 、c , 若()222tan a b c C ab +-=,则角C 的值为( ).A、3π B7、已知奇函数()f x 在()0,+∞上的图象如图所示, 则不等式()01f x x <-的解集为( ).A 、()()()3,10,11,3--B 、()()()3,10,13,--+∞C 、()()(),31,03,-∞--+∞ D 、()()(),31,01,3-∞--2016 20168、已知等比数列{}n a 中,各项都是正数,且31a ,321a ,22a 成等差数列, 则7698a a a a ++等于( ).A 、6B 、7C 、8D 、99、已知数列{}n a 、{}n b 满足n n a b 2log =,n ∈N *,其中{}n b 是等差数列,且2120089=⋅a a ,则=+++++20162015321b b b b b ( ). A 、2017 B 、-2016 C 、1009 D 、-1008 10.某三棱锥的三视图如右图所示,图中网格小正方形的边长为1,则该三棱锥的体积为( )A 、5B 、4C 、3D 、211、已知圆C :()2211x y ++=,P ()00,y x 为圆上任一点, 则00342x y -+的最大值为( ). A 、5 B 、6 C 、7 D 、812、设函数f (x )=a x +b x -c x ,其中c >a >0,c >b >0.若a ,b ,c 是△ABC 的三条边长, 则下列命题正确的有几个。
广东普宁市第一中学2016-2017学年高二数学上学期第二次月考试题 理

普宁市第一中学2016-2017学年度上学期第二次月考高二数学(理科)注意事项:1.本试题共4页,满分150分,考试时间90分钟。
2.答卷前,考生务必用黑色字迹的钢笔或签字笔将自己的姓名、考生号等相关信息填写在答题卷密封线内,并在“座位号”栏内填写座位号。
3. 所有题目必须用黑色字迹的钢笔或签字笔作答,答案必须写在答题卷上各题目指定区域内的相应位置上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液。
不按以上要求作答的答案无效。
一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一个是符合题目要求的.)1.已知全集,则正确表示集合和关系的韦恩(Venn)图是( )2.复数等于()A.B.C.D.3.若的值等于()A.2 B.3 C.4 D.64.已知,,且,则A. B.C.或 D.5.如图,网格纸上小正方形的边长为,粗线画出的是某几何体的三视图,则此几何体的体积为()6.椭圆的焦点在y轴上,长轴长是短轴长的两倍,则的值为A.B.C.2 D.47.程序框图如图所示,输出S的值是( )A.7B.11C. 12D.258在同一坐标系中,函数f(x)=x a(x>0),g(x)=log a x的图象可能是9.设x,y满足约束条件,则目标函数的最大值是A.5B. -1C.-5D.010已知函数在上有两个零点,则实数的取值范围为()A. B. C. D.11.已知函数f(x)=x2+bx的图象在点A(1,f(1))处的切线l与直线3x﹣y+2=0平行,若数列{}的前n项和为S n,则S2014的值为()A.B.C.D.12已知定义在R上的奇函数f(x),设其导函数为f′(x),当x∈(-∞,0]时,恒有xf′(x)<f(-x),令F(x)=xf(x),则满足F(3)>F(2x-1)的实数x的取值范围是()A(,2) B(-2,1)C(-1,2) D(-1,)二、填空题(本大题共4小题,每小题5分,共20分. 把答案填在答题卡内.)13.若实数,满足则S=2x+y-1的最大值为--------14.已知数列{a n}满足:a n≤a n+1,a n=n2+λn,n∈N*,则实数λ的最小值是________.15.如图,一辆汽车在一条水平的公路上向正西行驶,到处时测得公路北侧一山顶D在西偏北的方向上,行驶600m后到达处,测得此山顶在西偏北的方向上,仰角为,则此山的高度_________m.16.△ABC中,∠A=60°,M为边BC的中点,AM=,则2AB+AC的取值范围是________.三、解答题(本大题共6小题,17题10分,18-22题12分.解答时应写出必要的文字说明、证明过程或演算步骤)17.(10分).在中,角、、的对边分别为,且满足,,边上中线的长为.(I)求角和角的大小;(II)求的各边长。
广东省普宁市第二中学高二数学下学期第一次月考试题理

2016—2017学年度高二级下学期第一次月考理科数学试题注意事项:1。
答卷前,考生务必用黑色字迹的钢笔或签字笔将自己的姓名和考生号填写在答题卷上。
2.用2B 铅笔将选择题答案在答题卷对应位置涂黑;答案不能答在试卷上。
3。
非选择题必须用黑色字迹钢笔或签字笔作答,答案必须写在答题卷各题目指定区域内的相应位置上;不准使用铅笔或涂改液。
不按以上要求作答的答案无效。
4.考生必须保持答题卷的整洁。
一、选择题(本大题共12小题,每小题5分,共60分.)1.已知复数z 满足(5+12i )z=169,则=( ) A .-5﹣12i B .5﹣12i C .—5+12iD .5+12i2.已知集合M ={x|013≤+-x x },N ={—3,—1,1,3,5},则M ∩N =( ) A.{-1,1,3} B 。
{1,3} C.{—3,1} D.{—3,-1,1} 3. “0cos =α”是“1sin =α"的( ).A.充分不必要条件B.必要不充分条件C 。
充分必要条件 D.既不充分也不必要条件 4。
已知向量a =(—1,0),b =(2123,),则向量a 与b 的夹角为( ) A .6π B .65πC .3πD .32π 5。
设函数34)(2-+-=x x x f ,若从区间上任取一个数0x ,则所选取的实数0x 满足0)(0≥x f 的概率为( )A 。
41B .31C .21D .436。
椭圆C 的焦点在x 轴上,一个顶点是抛物线E:x y 162=的焦点,过焦点且垂直于长轴的弦长为2,则椭圆的离心率为( )A .21B .414 C .22 D .237。
一个几何体的三视图如右图所示,其中正视图和侧视图是腰长为2的两个全等的等腰直角三角形,俯视图是圆心角为2π的扇形,则该几何体的侧面积...为( ) A .2 B .π+4 C .π24+D .ππ24++8.已知)cos()2tan(,135cos 2παπααππα++-=∈则),且,(=( ) A .1312 B .1312- C .1213 D .1213- 9.已知函数()()sin f x A ωx φ=+002πA ωφ⎛⎫>>< ⎪⎝⎭,,的部分图象如图所示,若将()f x 图像上的所有点向右平移6π个单位得到函数()g x 的图像,则函数()g x 的单调递增区间为( ) A .Z k k k ∈⎥⎦⎤⎢⎣⎡+-,4,4ππππB .Z k k k ∈⎥⎦⎤⎢⎣⎡+-,42,42ππππC . Z k k k ∈⎥⎦⎤⎢⎣⎡+-,6,3ππππ D .Z k k k ∈⎥⎦⎤⎢⎣⎡+-,62,32ππππ10。
广东省普宁市第二中学2016-2017学年高二上学期期末考试数学(理)试题 含答案

普宁市第二中学2018届高二级上学期·期末考试理科数学试题注意事项:1。
答卷前,考生务必用黑色字迹的钢笔或签字笔将自己的姓名和考生号填写在答题卷上。
2.用2B铅笔将选择题答案在答题卷对应位置涂黑;答案不能答在试卷上.3。
非选择题必须用黑色字迹钢笔或签字笔作答,答案必须写在答题卷各题目指定区域内的相应位置上;不准使用铅笔或涂改液.不按以上要求作答的答案无效。
4.考生必须保持答题卷的整洁。
第I卷选择题(每题5分,共60分)本卷共12题,每题5分,共60分,在每题后面所给的四个选项中,只有一个是正确的.1.已知集合A⊆{0,1,2},且集合A中至少含有一个偶数,则这样的集合A的个数为()A.6 B.5 C.4 D.32。
已知复数的实部为﹣1,则复数z﹣b在复平面上对应的点在()A.第一象限 B.第二象限 C.第三象限 D.第四象限3。
已知△ABC的三内角A、B、C的对边边长分别为a、b、c.若A .B .C .D .4.甲、乙、丙、丁、戊五位同学站成一排照相留念,则在甲乙相邻的条件下,甲丙也相邻的概率为( ) A .1 B . C . D .5.当0,0>>y x ,191=+yx 时,y x +的最小值为( )A .10B .12C .14D .166.如图直三棱柱ABC ﹣A 1B 1C 1的体积为V,点P 、Q 分别在侧棱AA 1和CC 1上,AP=C 1Q ,则四棱锥B ﹣APQC 的体积为( )A .B .C .D .7。
过点A (﹣2,﹣4)作倾斜角为45°的直线交抛物线y 2=2px (p >0)于点P 1、P 2,若|P 1P 2|2=|AP 1|•|AP 2|,则实数p 的值为( ) A .1 B .2 C .3 D .48.如图的程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”,执行该程序框图,若输入的a ,b 分别为16,28,则输出的a=( )A.0 B.2 C.4 D.149。
广东省普宁市第一中学高二数学上学期期末考试试题文

普宁一中2016--2017学年度第一学期高二级 期末考试文科数学试题卷注意事项:1.答卷前,考生务必用黑色字迹的钢笔或签字笔将自己的姓名和考生号填写在答题卷上。
2.用2B 铅笔将选择题答案在答题卷对应位置涂黑;答案不能答在试卷上。
3.非选择题必须用黑色字迹钢笔或签字笔作答,答案必须写在答题卷各题目指定区域内的相应位置上;不准使用铅笔或涂改液。
不按以上要求作答的答案无效。
4.考生必须保持答题卷的整洁。
一、选择题(每小题5分,共60分.在所给的四个选项中,只有一项是符合题目要求的) 1.O600cos 的值为A 、21B 、21-C 、23D 、23-2.设集合{}0652<+-=x x x A ,{}052>-=x x B ,则=⋂B AA 、)25,3(-- B 、)25,2( C 、)3,25( D 、)25,3(- 3.复数i z +=14(i 是虚数单位)的共轭复数在复平面内对应的点是A 、()2,2-B 、()2,2C 、()2,2--D 、()2,2-4.已知数列()*++∈-===N n a a a a a n n n 1221,5,1,则=2016a A 、1 B 、4 C 、-4 D 、55.取一根长度为4m 的绳子,拉直后在任意位置剪断,则剪得的两段长度都不小于1.5m 的 概率是A 、41B 、31C 、21D 、326.已知||a =||b =2,且它们的夹角为π3,则||b a += A 、32 B 、23 C 、1 D 、27.给出下列命题:①22bc ac b a >⇒>; ②22b a b a >⇒>;③22b a b a >⇒>; ④33b a b a >⇒>其中正确的命题是A 、①②B 、②③C 、③④D 、②④ 8.如右图所示的程序的输出结果为S=1320,则判断框中应填A 、9≥iB 、9≤iC 、10≤iD 、10≥i 9.定义在R 上的函数)(x f 在),6(+∞上为增函数,且函数)6(+=x f y 为偶函数,则A 、)7()4(f f <B 、)7()4(f f >(第8题图)C 、)7()5(f f >D 、)7()5(f f <10.已知一个几何体的三视图如右图所示,则该几何体的体积是A 、32B 、332C 、334 D 、3411.气象意义上的春季进入夏季的标志为:“连续五天每天日平均 温度不低于22℃”,现在甲、乙、丙三地连续五天的日平均温度的记录数据(记录数据都是正整数,单位℃): (第10题图) 甲地:五个数据的中位数是24,众数为22; 乙地:五个数据的中位数是27,平均数为24;丙地:五个数据中有一个数据是30,平均数是24,方差为10. 则肯定进入夏季的地区有A 、0个B 、1个C 、2个D 、3个12.已知圆O 的半径为2,PA ,PB 为圆O 的两条切线,A 、B 为切点(A 与B 不重合),则PB PA ⋅ 的最小值为A 、2412+-B 、2416+-C 、2812+-D 、2816+- 二. 填空题:本大题共4小题,每小题5分。
普宁高二期末数学试卷真题

一、选择题(每题5分,共50分)1. 下列各数中,绝对值最小的是()A. -3B. 2C. -1D. 02. 已知函数f(x) = 2x - 3,那么f(-1)的值为()A. -5B. -2C. 0D. 23. 如果等差数列{an}的首项为a1,公差为d,那么第n项an的表达式为()A. an = a1 + (n-1)dB. an = a1 - (n-1)dC. an = a1 + ndD. an = a1 - nd4. 已知函数y = x^2 - 4x + 4,那么它的图像与x轴的交点个数为()A. 1B. 2C. 3D. 05. 在△ABC中,已知∠A = 60°,∠B = 45°,那么∠C的度数为()A. 60°B. 45°C. 75°D. 90°6. 下列不等式中,正确的是()A. 2x + 3 > 5x - 1B. 3x - 2 < 4x + 1C. -2x + 5 > -x - 3D. x + 2 < 2x + 37. 已知等比数列{bn}的首项为b1,公比为q,那么第n项bn的表达式为()A. bn = b1 q^(n-1)B. bn = b1 / q^(n-1)C. bn = b1 q^nD. bn = b1 / q^n8. 函数y = |x - 2| + 1的图像与x轴的交点个数为()A. 1B. 2C. 3D. 09. 在直角坐标系中,点A(2, 3)关于x轴的对称点为()A. (2, -3)B. (-2, 3)C. (2, 3)D. (-2, -3)10. 下列数列中,是等差数列的是()A. 1, 3, 5, 7, 9...B. 1, 2, 4, 8, 16...C. 2, 4, 8, 16, 32...D. 1, 4, 9, 16, 25...二、填空题(每题5分,共50分)11. 若等差数列{an}的首项为a1,公差为d,那么第n项an = _______。
广东省普宁市第一中学高二数学上学期期末考试试题文

普宁一中2016--2017学年度第一学期高二级 期末考试文科数学试题卷注意事项:1.答卷前,考生务必用黑色字迹的钢笔或签字笔将自己的姓名和考生号填写在答题卷上。
2.用2B 铅笔将选择题答案在答题卷对应位置涂黑;答案不能答在试卷上。
3.非选择题必须用黑色字迹钢笔或签字笔作答,答案必须写在答题卷各题目指定区域内的相应位置上;不准使用铅笔或涂改液。
不按以上要求作答的答案无效。
4.考生必须保持答题卷的整洁。
一、选择题(每小题5分,共60分.在所给的四个选项中,只有一项是符合题目要求的) 1.O600cos 的值为A 、21B 、21-C 、23D 、23- 2.设集合{}0652<+-=x x x A ,{}052>-=x x B ,则=⋂B AA 、)25,3(-- B 、)25,2( C 、)3,25( D 、)25,3(- 3.复数i z +=14(i 是虚数单位)的共轭复数在复平面内对应的点是A 、()2,2-B 、()2,2C 、()2,2--D 、()2,2- 4.已知数列()*++∈-===N n a a a a a n n n 1221,5,1,则=2016aA 、1B 、4C 、-4D 、55.取一根长度为4m 的绳子,拉直后在任意位置剪断,则剪得的两段长度都不小于1.5m 的 概率是A 、41B 、31C 、21D 、326.已知||=||=2,且它们的夹角为π3,则||+= A 、32 B 、23 C 、1 D 、27.给出下列命题:①22bc ac b a >⇒>; ②22b a b a >⇒>;③22b a b a >⇒>; ④33b a b a >⇒>其中正确的命题是A 、①②B 、②③C 、③④D 、②④ 8.如右图所示的程序的输出结果为S=1320,则判断框中应填 A 、9≥i B 、9≤i C 、10≤i D 、10≥i 9.定义在R 上的函数)(x f 在),6(+∞上为增函数,且函数)6(+=x f y 为偶函数,则A 、)7()4(f f <B 、)7()4(f f >(第8题图)C 、)7()5(f f >D 、)7()5(f f <10.已知一个几何体的三视图如右图所示,则该几何体的体积是A 、32B 、332C 、334 D 、3411.气象意义上的春季进入夏季的标志为:“连续五天每天日平均 温度不低于22℃”,现在甲、乙、丙三地连续五天的日平均温度的记录数据(记录数据都是正整数,单位℃): (第10题图) 甲地:五个数据的中位数是24,众数为22; 乙地:五个数据的中位数是27,平均数为24;丙地:五个数据中有一个数据是30,平均数是24,方差为10. 则肯定进入夏季的地区有A 、0个B 、1个C 、2个D 、3个12.已知圆O 的半径为2,PA ,PB 为圆O 的两条切线,A 、B 为切点(A 与B 不重合),则PB PA ⋅ 的最小值为A 、2412+-B 、2416+-C 、2812+-D 、2816+- 二. 填空题:本大题共4小题,每小题5分。
数学---广东省揭阳市普宁二中2016-2017学年高二(上)试卷(文)(解析版)

2016-2017学年广东省揭阳市普宁二中高二(上)数学试卷(文科)一.选择题1.(5分)抛物线y=x2的焦点坐标为()A.B.C.D.2.(5分)函数f(x)=1﹣e x的图象与x轴相交于点P,则曲线在点P处的切线的方程为()A.y=﹣e•x+1 B.y=﹣x+1 C.y=﹣x D.y=﹣e•x3.(5分)又曲线﹣=1上一点P到它的一个焦点的距离等于3,那么点P与两个焦点所构成三角形的周长等于()A.42 B.36 C.28 D.264.(5分)在棱长为2的正四面体ABCD中,E,F分别是BC,AD的中点,则=()A.0 B.﹣2 C.2 D.﹣35.(5分)已知函数y=x n e﹣x,则其导数y'=()A.nx n﹣1e﹣x B.x n e﹣x C.2x n e﹣x D.(n﹣x)x n﹣1e﹣x6.(5分)已知直线l的方向向量,平面α的一个法向量为,则直线l与平面α所成的角为()A.120°B.60°C.30°D.150°7.(5分)当x在(﹣∞,+∞)上变化时,导函数f′(x)的符号变化如下表:则函数f(x)的图象的大致形状为()A.B.C.D.8.(5分)若函数f(x)=kx﹣ln x在区间(1,+∞)单调递增,则k的取值范围是()A.(﹣∞,﹣2] B.(﹣∞,﹣1] C.[2,+∞)D.[1,+∞)9.(5分)若a>0,b>0,且函数f(x)=4x3﹣ax2﹣2bx+2在x=1处有极值,则ab的最大值等于()A.2 B.3 C.6 D.910.(5分)已知函数f(x)=x3﹣12x,若f(x)在区间(2m,m+1)上单调递减,则实数m 的取值范围是()A.[﹣1,1] B.(﹣1,1] C.(﹣1,1)D.[﹣1,1)11.(5分)在棱长为2的正方体ABCD﹣A1B1C1D1中,正方形BCC1B1所在平面内的动点P 到直线D1C1DC的距离之和为2,∠CPC1=60°,则点P到直线CC1的距离为()A.B.C.D.12.(5分)已知函数f(x)=x3+ax2+bx+c,x∈[﹣2,2]表示的曲线过原点,且在x=±1处的切线斜率均为﹣1,有以下命题:①f(x)的解析式为:f(x)=x3﹣4x,x∈[﹣2,2];②f(x)的极值点有且仅有一个;③f(x)的最大值与最小值之和等于零,则下列选项正确的是()A.①②B.①③C.②③D.①②③二.填空题13.(5分)已知点P(x,y)的坐标满足条件,那么(x+1)2+y2的取值范围为.14.(5分)已知三棱锥S﹣ABC的所有顶点都在球O的球面上,SC为球O的直径,且SC ⊥OA,SC⊥OB,△OAB为等边三角形,三棱锥S﹣ABC的体积为,则球O的表面积为.三.解答题15.(12分)数列{a n}的前n项和为S n,a1=1,a n+1=2S n+1(n∈N*),等差数列{b n}满足b3=3,b5=9.(1)分别求数列{a n},{b n}的通项公式;(2)设C n=(n∈N*),求证C n+1<C n.16.(12分)如图所示,异面直线AB,CD互相垂直,AB=,BC=,CD=1,BD=2,AC=3,截面EFGH分别与BD,AD,AC,BC相交于点E,F,G,H,且AB∥平面EFGH,CD∥平面EFGH.(1)求证:BC⊥平面EFGH;(2)求二面角B﹣AD﹣C的正弦值.17.(12分)某校高三数学竞赛初赛考试结束后,对考生成绩进行统计(考生成绩均不低于90分,满分150分),将成绩按如下方式分为六组,第一组.如图为其频率分布直方图的一部分,若第四、五、六组的人数依次成等差数列,且第六组有4人.(1)请补充完整频率分布直方图,并估计这组数据的平均数M;(2)现根据初赛成绩从第四组和第六组中任意选2人,记他们的成绩分别为x,y.若|x﹣y|≥10,则称此二人为“黄金帮扶组”,试求选出的二人为“黄金帮扶组”的概率P1;(3)以此样本的频率当作概率,现随机在这组样本中选出3名学生,求成绩不低于120分的人数ξ的分布列及期望.18.(12分)设函数f(x)=(1+x)2﹣2ln(1+x)(1)若关于x的不等式f(x)﹣m≥0在[0,e﹣1]有实数解,求实数m的取值范围.(2)设g(x)=f(x)﹣x2﹣1,若关于x的方程g(x)=p至少有一个解,求p的最小值.(3)证明不等式:(n∈N*).19.(12分)在空中,取直线l为轴,直线l与l′相交于O点,夹角为30°,l′围绕l旋转得到以O为顶点,l′为母线的圆锥面.已知直线l∥平面α,l与α的距离为2,平面α与圆锥面相交得到双曲线Γ.在平面α内,以双曲线Γ的中心为原点,以双曲线的两个焦点所在直线为y轴,建立直角坐标系.(Ⅰ)求双曲线Γ的方程;(Ⅱ)在平面α内,以双曲线Γ的中心为圆心,半径为2的圆记为曲线Γ′,在Γ′上任取一点P,过点P作双曲线Γ的两条切线交曲线Γ′于两点M、N,试证明线段MN的长为定值,并求出这个定值.(选修4-4:坐标系与参数方程)20.(10分)在直角坐标系xOy中,直线l的参数方程为(t为参数),若以原点O为极点,x轴正半轴为极轴建立极坐标系,已知圆C的极坐标方程为ρ=4cosθ,设M是圆C上任一点,连结OM并延长到Q,使|OM|=|MQ|.(Ⅰ)求点Q轨迹的直角坐标方程;(Ⅱ)若直线l与点Q轨迹相交于A,B两点,点P的直角坐标为(0,2),求|P A|+|PB|的值.(选修4-5:不等式选讲)21.设函数f(x)=|2x+1|﹣|x﹣4|.(1)解不等式f(x)>0;(2)若f(x)+3|x﹣4|≥m对一切实数x均成立,求m的取值范围.参考答案一.选择题1.D【解析】∵抛物线y=x2的标准形式是x2=y,∴抛物线焦点在y轴上,开口向上,可得2p=1,=因此,抛物线的焦点坐标为:(0,)故选D2.C【解析】由f(x)=1﹣e x,可令f(x)=0,即e x=1,解得x=0可得P(0,0),又f′(x)=﹣e x,∴f′(0)=﹣e0=﹣1.∴f(x)=1﹣e x在点P(0,0)处的切线方程为y﹣0=﹣1×(x﹣0),即y=﹣x.故选:C.3.A【解析】双曲线﹣=1的a=8,b=6,则c==10,设P到它的上焦点F的距离等于3,由于3>c﹣a=2,3<c+a=18,则P为上支上一点,则由双曲线的定义可得PF'﹣PF=2a=16,(F'为下焦点).则有PF'=19.则点P与两个焦点所构成三角形的周长为PF+PF'+FF'=3+19+20=42.故选A.4.D【解析】如图所示,棱长为2的正四面体ABCD中,E,F分别是BC,AD的中点,则=(+)•(+)=(•+•+•+•)=(2×2×cos120°+2×2×2×cos90°+2×2×2×cos180°+2×2×cos120°)=﹣3.故选:D.5.D【解析】y′=nx n﹣1e﹣x﹣x n e﹣x=(n﹣x)x n﹣1e﹣x,故选:D.6.C【解析】直线l的方向向量,平面α的一个法向量为,直线l与平面α所成的角的正弦值=|cos<,>|===.直线l与平面α所成的角为:30°.故选:C.7.C【解析】由图表可得函数f′(x)在(﹣∞,1)上小于0,在(1,4)上大于0,即函数f(x)在(﹣∞,1)上是减函数,在(1,4)上是增函数,故f(0)是函数的极小值.同理,由图表可得函数f′(x)在(1,4)上大于0,在(1,4)上小于0,即函数f(x)在(1,4)上是增函数,在(4,+∞)上是增函数,可得f(4)是函数的极大值,故选C.8.D【解析】f′(x)=k﹣,∵函数f(x)=kx﹣ln x在区间(1,+∞)单调递增,∴f′(x)≥0在区间(1,+∞)上恒成立.∴,而y=在区间(1,+∞)上单调递减,∴k≥1.∴k的取值范围是[1,+∞).故选:D.9.D【解析】∵f′(x)=12x2﹣2ax﹣2b,又因为在x=1处有极值,∴a+b=6,∵a>0,b>0,∴,当且仅当a=b=3时取等号,所以ab的最大值等于9.故选:D.10.D【解析】∵函数f(x)=x3﹣12x在(2m,m+1)上单调递减,∴f'(x)=3x2﹣12≤0在(2m,m+1)上恒成立.故,即成立.解得:﹣1≤m<1,故选:D.11.A【解析】在面BCC1B1内到直线D1C1、DC的距离即为P到点C1,C的距离,故有面BCC1B1内的点P到直线C1、C的距离之和为2,由椭圆的定义即知点P的轨迹是椭圆的一部分.以CC1所在的直线为x轴,线段CC1的中心为坐标原点,建立直角坐标系,则C(﹣1,0),C1(1,0),∴c=1,a=,b=1.设P(x,y),得椭圆的方程为:+y2=1.∵∠CPC1=60°,∴=1×tan30°=,设点P到直线CC1的距离为h,则=,解得h=,∴点P到直线CC1的距离为.故选:A.12.B【解析】∵函数f(x)=x3+ax2+bx+c,x∈[﹣2,2]表示的曲线过原点,∴c=0对函数f(x)求导,得,f′(x)=3x2+2ax+b,∵在x=±1处的切线斜率均为﹣1,∴f′(1)=1,f′(﹣1)=1,即,3+2a+b=﹣1,3﹣2a+b=﹣1解得a=0,b=﹣4∴f(x)=x3﹣4x,x∈[﹣2,2],①正确.f′(x)=3x2﹣4,令f′(x)=0,得,x=,∴f(x)的极值点有两个,②错误f(﹣2)=0,f(﹣)=,f()=﹣,f(2)=0∴f(x)的最大值为,最小值为﹣,最大值与最小值之和等于零.③正确.故选B二.填空题13.(,8]【解析】画出表示的平面区域如图:,而(x+1)2+y2的表示区域内点P(x,y)与点M(﹣1,0)的距离的平方,由图知:|MC|2=(1+1)2+22=8最大;M到直线2x+y﹣2=0的距离的平方:最小.由于2x+y﹣2>0不取等号,所以不是最小值,故答案为:(,8].14.16π【解析】根据题意作出图形:设球心为O,球的半径r.∵SC⊥OA,SC⊥OB,∴SC⊥平面AOB,三棱锥S﹣ABC的体积可看成是两个小三棱锥S﹣ABO和C﹣ABO的体积和.∴V三棱锥S﹣ABC=V三棱锥S﹣ABO+V三棱锥C﹣ABO=××r2×r×2=,∴r=2,∴球O的表面积为4π×22=16π.三.解答题15.解:(1)①当n≥2时,由a n+1=2S n+1,a n=2S n﹣1+1,得a n+1﹣a n=2a n,即a n+1=3a n.由a1=1,∴a2=2a1+1=3=3a1.∵a1=1≠0,∴数列{a n}是以1为首项,3为公比的等比数列.∴.②等差数列{b n}满足b3=3,b5=9.设公差为d,则,解得.∴b n=﹣3+(n﹣1)×3=3n﹣6.(2)由(1)可得=.∴=c n.∵3n=(1+2)n=…+2n≥3n,∴.16.证明:(1)∵AB∥平面EFGH,又∵AB⊂平面ABD,平面ABD∩平面EFGH=EF,∴AB∥EF,同理CD∥HE,∵,∴AB2+BC2=AC2,∴AB⊥BC,同理BC⊥DC,∴BC⊥EF,同理BC⊥EH,又∵EF,EH是平面EFGH内的两相交直线,∴BC⊥平面EFGH.(2)由(1)及异面直线AB,CD互相垂直知,直线AB,BC,CD两两垂直,作,以C为原点,CD为x轴,CB为y轴,Cz为z轴,建立空间直角坐标系C﹣xyz,如图所示,则,∵x轴⊂平面ACD,∴平面ACD的一个法向量可设为,∵,∴,得:,即,又∵z轴∥平面ABD,∴平面ABD的一个法向量可设为,∴,得,即,设二面角B﹣AD﹣C的大小为θ,那么,∴,∴二面角B﹣AD﹣C的正弦值为.17.解:(1)频率分布直方图见解析,M=95×0.2+105×0.15+115×0.35+125×0.15+135×0.1+145×0.05=114.5;(2)依题意可得:第四组人数为:=12,故P1==;(3)依题意可得:样本总人数为:=80,成绩不低于120分的人数为:80×(0.05+0.10+0.15)=24,故在样本中任选1人,其成绩不低于120分的概率==.由已知ξ的可能取值为0,1,2,3.ξ~B,P(ξ=0)==,P(ξ=1)==,P(ξ=2)==,P(ξ=3)==.ξ的分布列如下P故Eξ==.18.(1)解:依题意得f(x)max≥m,x∈[0,e﹣1]∵,而函数f(x)的定义域为(﹣1,+∞)∴f(x)在(﹣1,0)上为减函数,在(0,+∞)上为增函数,∴f(x)在[0,e﹣1]上为增函数,∴∴实数m的取值范围为m≤e2﹣2(2)解:g(x)=f(x)﹣x2﹣1=2x﹣2ln(1+x)=2[x﹣ln(1+x)],∴显然,函数g(x)在(﹣1,0)上为减函数,在(0,+∞)上为增函数∴函数g(x)的最小值为g(0)=0∴要使方程g(x)=p至少有一个解,则p≥0,即p的最小值为0(3)证明:由(2)可知:g(x)=2[x﹣ln(1+x)]≥0在(﹣1,+∞)上恒成立所以ln(1+x)≤x,当且仅当x=0时等号成立令,则x∈(0,1)代入上面不等式得:即,即所以ln2﹣ln1<1,,,…,将以上n个等式相加即可得到:19.解:(Ⅰ)如右图,O'为双曲线的中心,OO'为轴l与平面α的距离|OO'|=2,A为双曲线的顶点,∠AOO'=60°,∴.在轴l上取点C,使得|OC|=4,过C作与轴l垂直的平面,交圆锥面得到圆C,圆C与双曲线相交于D、E,DE的中点为B,由题意知,|CB|=2,|CD|=4,得|BD|=2,从而双曲线的实半轴长为2,且过点(2,4).设双曲线的标准方程为,将点(2,4)代入方程得b2=4,所以双曲线的标准方程为证明:(Ⅱ)在条件(Ⅰ)下,双曲线Γ的两切线PM、PN都不垂直x轴,设点P的坐标为(x0,y0),令过点P的切线的斜率为k,则切线方程为y=k(x﹣x0)+y0,:由△=0,化简得:令PM、PN的斜率分别为k1、k2,,因点P(x0,y0)在圆Γ'上,则有,得:,∴k1k2=﹣1,知PM⊥PN,线段MN是圆O的直径,|MN|=4.20.解:(Ⅰ)圆C的极坐标方程为ρ=4cosθ,化为ρ2=4ρcosθ,可得直角坐标方程:x2+y2=4x,配方为(x﹣2)2+y2=4,设Q(x,y),则,代入圆的方程可得,化为(x﹣4)2+y2=16.即为点Q的直角坐标方程.(Ⅱ)把直线l的参数方程(t为参数)代入(x﹣4)2+y2=16.得令A,B对应参数分别为t1,t2,则,t1t2>0.∴.21.解:(1)当x≥4时,f(x)=2x+1﹣(x﹣4)=x+5>0,得x>﹣5,所以x≥4成立;当﹣≤x<4时,f(x)=2x+1+x﹣4=3x﹣3>0,得x>1,所以1<x<4成立;当x<﹣时,f(x)=﹣x﹣5>0,得x<﹣5,所以x<﹣5成立.综上,原不等式的解集为{x|x>1或x<﹣5};(2)令F(x)=f(x)+3|x﹣4|=|2x+1|+2|x﹣4|≥|2x+1﹣(2x﹣8)|=9,当﹣时等号成立.即有F(x)的最小值为9,所以m≤9.即m的取值范围为(﹣∞,9].。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
普宁市第二中学2018届高二级上学期·期末考试
理科数学试题
注意事项:
1.答卷前,考生务必用黑色字迹的钢笔或签字笔将自己的姓名和考生号填写在答题卷上。
2.用2B 铅笔将选择题答案在答题卷对应位置涂黑;答案不能答在试卷上。
3.非选择题必须用黑色字迹钢笔或签字笔作答,答案必须写在答题卷各题目指定区域内的相应位置上;不准使用铅笔或涂改液。
不按以上要求作答的答案无效。
4.考生必须保持答题卷的整洁。
第I 卷 选择题(每题5分,共60分)
本卷共12题,每题5分,共60分,在每题后面所给的四个选项中,只有一个是正确的。
1.已知集合A ⊆{0,1,2},且集合A 中至少含有一个偶数,则这样的集合A 的个数为( )
A .6
B .5
C .4
D .3
2.已知复数的实部为﹣1,则复数z ﹣b 在复平面上对应的点在( )
A .第一象限
B .第二象限
C .第三象限
D .第四象限
3.已知△ABC 的三内角A 、B 、C 的对边边长分别为a 、b 、c .若a=
b ,A=2B ,则cos B=( )
A .
B .
C .
D . 4.甲、乙、丙、丁、戊五位同学站成一排照相留念,则在甲乙相邻的条件下,甲丙也相邻的概率为( )
A .1
B .
C .
D .
5.当 0,0>>y x ,191=+y
x 时,y x +的最小值为( ) A .10 B .12 C .14 D .16
6.如图直三棱柱ABC ﹣A 1B 1C 1的体积为V ,点P 、Q 分别在侧棱AA 1和CC 1上,AP=C 1Q ,则四棱锥B ﹣APQC 的体积为( )
A .
B .
C .
D .
7.过点A (﹣2,﹣4)作倾斜角为45°的直线交抛物线y 2=2px (p >0)于点P 1、P 2,若|P 1P 2|2=|AP 1|•|AP 2|,
则实数p 的值为( )
A .1
B .2
C .3
D .4
8.如图的程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”,执行该程序框图,若输入的a ,b 分别为16,28,则输出的a=( )
A .0
B .2
C .4
D .14 9.已知a n =log (n+1)(n+2)(n∈N *).我们把使乘积a 1•a 2•a 3•…•a n 为整数的数n 叫做“优数”,则
在区间(1,2004)内的所有优数的和为( )
A .1024
B .2003
C .2026
D .2048
10.右图所示,点P 在边长为1的正方形的边上运动,设M 是CD 边的中点,则当点P 沿着A ﹣B ﹣C ﹣M 运动时,以点P 经过的路程x 为自变量,三角形APM 的面积函数的图象形状大致是( )
A .
B .
C .
D .
11.设两条直线的方程分别为x+y+a=0,x+y+b=0,已知a ,b 是方程x 2+x+c=0的两个实根,且0≤c≤,则这两条直线之间的距离的最大值和最小值分别是( )
A .,
B .,
C .,
D .,。
