北京市石景山区2013届高三一模 数学理试题
【解析分类汇编系列二:北京2013(一模)数学理】11:概率与统计 Word版含答

【解析分类汇编系列二:北京2013(一模)数学理】11概率与统计1.(2013届北京丰台区一模理科)某校从高一年级学生中随机抽取100名学生,将他们期中考试的数学成绩(均为整数)分成六段:[40,50),[50,60),…,[90,100]后得到频率分布直方图(如图所示).则分数在[70,80)内的人数是________。
【答案】30由题意,分数在[70,80)内的频率为:1﹣(0.010+0.015+0.015+0.025+0.005)×10=1﹣0.7=0.3.则分数在[70,80)内的人数是0.3×100=30人。
2.(2013届东城区一模理科)如图是甲、乙两名同学进入高中以来5次体育测试成绩的茎叶图,则甲5次测试成绩的平均数是 ,乙5次测试成绩的平均数与中位数之差是 .【答案】84 2甲的测试成绩的平均数是180(434710)845+-++++=,乙的测试成绩的平均数是180(12811)845+-+++=,乙的测试成绩的中位数为82,所以乙5次测试成绩的平均数与中位数之差是84822-=。
专题:概率 一、选择题1.(2013届北京石景山区一模理科)3.将一颗骰子掷两次,观察出现的点数,并记第一次出现的点数为m ,第二次出现的点数为n ,向量p =(m ,n ),q =(3,6),则向量p 与q共线的概率为( )A .13B .14C .16D .112【答案】D由题意可得,基本事件(m ,n )(m ,n=1,2,…,6)的个数=6×6=36. 若,p q 共线,则630m n -=,得到2n m =.满足此条件的共有(1,2),(2,4),(3,6)三个基本事件.因此向量,p q 共线的概率313612P ==,选D. 2.(2013届北京大兴区一模理科)若实数,a b 满足221a b +≤,则关于x 的方程220x x a b -++=有实数根的概率是( ) A .14 B .34 C .3π24π+ D .π24π-【答案】C要使方程有实根,则判别式44()a b ∆=-+>,即10a b +-<,,如图,阴影部分。
北京市2013届高三数学理试题分类汇编(含9区一模及上学期期末试题)专题:选修部分(含答案)

北京2013届高三最新模拟试题分类汇编(含9区一模及上学期期末试题精选)专题:选修部分一、选择题1 .(2013届北京海滨一模理科)在极坐标系中, 曲线4cos ρθ=围成的图形面积为A.π B .4 C.4π D.162 .(2013届北京市延庆县一模数学理)在极坐标系下,圆03sin 4:2=++θρρC 的圆心坐标为 ( )A .)0,2(B .)2,2(πC .),2(πD .)2,2(π-3 .(2013届房山区一模理科数学)在极坐标系中,圆2sin ρθ=的圆心到直线co s 2sin 10ρθρθ-+=的距离为( )A5B5C5D54 .(2013届门头沟区一模理科)下列直线中,平行于极轴且与圆2co s ρθ=相切的是A .c o s 1ρθ=B .sin 1ρθ=C .c o s 2ρθ=D .sin 2ρθ=5 .(2013届门头沟区一模理科)如图:圆O 的割线P AB 经过圆心O ,C 是圆上一点,P A =AC =12AB ,则以下结论不正确...的是 A .CB =CP B .PC ⋅AC =P A ⋅BC C .PC 是圆O 的切线 D .BC 2=BA ⋅BP6 .(北京市东城区普通高中示范校2013届高三3月联考综合练习(二)数学(理)试题 )在极坐标系中,过点(3,)3π且垂直于极轴的直线方程 ( )A .3s in 2=ρθB .3c o s 2=ρθC .3s in 2=ρθ D .3c o s 2=ρθ7 .(北京市东城区普通校2013届高三3月联考数学(理)试题 )极坐标方程4cos ρθ=化为直角坐标方程是( )A .22(2)4x y -+=B .224x y +=PC .22(2)4x y +-=D .22(1)(1)4x y -+-=8 .(北京市东城区普通校2013届高三3月联考数学(理)试题 )AB COP 如图,已知AB 是⊙O 的一条弦,点P 为AB 上一点, PC OP ⊥,PC 交⊙O 于C ,若4AP =,2PB =,则PC 的长是 ( ) A.3B .C.2D9 .(北京市西城区2013届高三上学期期末考试数学理科试题)在极坐标系中,已知点(2,)6P π,则过点P 且平行于极轴的直线的方程是 ( )A .sin 1=ρθB .s in =ρθC .c o s 1=ρθD .c o s =ρθ10.(北京市顺义区2013届高三第一次统练数学理科试卷(解析))参数方程⎩⎨⎧--=-=ty t x 21,2(为参数)与极坐标方程θρsin =所表示的图形分别是 ( )A .直线、直线B .直线、圆C .圆、圆D .圆、直线11.(北京市顺义区2013届高三第一次统练数学理科试卷(解析))如图,AC AB ,分别与圆O 相切于点ADEC B ,,是⊙O 的割线,连接CE BEBD CD ,,,.则( )A .DE AD AB ⋅=2B .CE AC DE CD ⋅=⋅C .CE BD CD BE ⋅=⋅ D .CD BD AE AD ⋅=⋅12.(北京市通州区2013届高三上学期期末考试理科数学试题 )已知圆的直角坐标方程为2220x y x +-=.在以原点为极点,x 轴非负半轴为极轴的极坐标系中,该圆的方程为 ( )A .2c o s ρθ=B .2sin ρθ=C .2c o s ρθ=-D .2sin ρθ=-13.(【解析】北京市海淀区2013届高三上学期期末考试数学理试题 )已知直线2,:2x t l y t=+⎧⎨=--⎩(t 为参数)与圆2c o s 1,:2s in x C y θθ=+⎧⎨=⎩(θ为参数),则直线l 的倾斜角及圆心C 的直角坐标分别是( )A .π,(1,0)4B .π,(1,0)4- C .3π,(1,0)4 D .3π,(1,0)4-14.(【解析】北京市海淀区2013届高三上学期期末考试数学理试题 )如图,P C 与圆O 相切于点C ,直线P O 交圆O 于,A B 两点,弦C D 垂直A B 于E . 则下面结论中,错误..的结论是 A.B E C ∆∽D EA∆ B .A C E A C P ∠=∠C .2D EO E E P=⋅D .2P CP A A B=⋅二、填空题15.(2013届北京大兴区一模理科)已知直线y k x =与曲线42c o s ()2sin x y qq q ì=+ïïíï=ïî为参数有且仅有一个公共点,则k=16.(2013届北京大兴区一模理科)如图,在圆O 中,直径AB 与弦CD 垂直,垂足为E(E 在A ,O 之间),E FB C^,垂足为F .若6A B=,5C FC B ?,则A E=。
北京市2013各区数学一模试题--数列及解析几何

2013年北京市各区高三一模试题编--数列一填空选择(2013年东城一模文科)(7)对于函数)(x f y =,部分x 与y 的对应关系如下表:x 1 2 3 4 5 6 7 8 9 y7 4 5 8 1 3 5 2 6数列}{n x 满足21=x ,且对任意*n ∈N ,点),(1+n n x x 都在函数)(x f y =的图象上,则201320124321x x x x x x ++++++ 的值为(A )9394 (B )9380 (C )9396 (D )9400 (2013年东城一模文科理科)(14)数列{a n }的各项排成如图所示的三角形形状,其中每一行比上一行增加两项,若n n a a =(0)a ≠, 则位于第10行的第8列的项等于 ,2013a 在图中位于 .(填第几行的第几列)(2013年东城一模理科)(5)已知数列{}n a 中,12a =,120n n a a +-=,2log n n b a =,那么数列{}n b 的前10项和等于(A )130 (B )120 (C )55 (D )50(2013西城一模文科理科)4.设等比数列{}n a 的公比为q ,前n 项和为n S ,且10a >.若232S a >,则q 的取值范围是(A )1(1,0)(0,)2- (B )1(,0)(0,1)2-(C )1(,1)(,)2-∞-+∞(D )1(,)(1,)2-∞-+∞(2013西城一模文科)14.已知数列{}n a 的各项均为正整数,其前n 项和为n S .若1, ,231,,nn n nn a a a a a +⎧⎪=⎨⎪+⎩是偶数是奇数且329S =,则1a =______;3n S =______. (2013西城一模理科)10.设等差数列{}n a 的公差不为0,其前n 项和是n S .若23S S =,0k S =,则k =______.(2013海淀一模文科)2.等差数列{}n a 中, 2343,9,a a a =+= 则16a a 的值为 A. 14 B. 18 C. 21 D.2(2013海淀一模理科)10.等差数列{}n a 中,34259,18a a a a +==, 则16_____.a a = (2013丰台一模文科理科)3. 设n S 为等比数列{}n a 的前n 项和,3420a a +=,则31S a ( )(A) 2 (B) 3 (C) 4 (D) 5(2013年石景山一模文科理科)11.在等差数列{a n }中,a l =-2013,其前n 项和为S n ,若10121210S S -=2,则2013S 的值等于 。
北京市石景山区2013届高三一模数学理试题

2013年石家庄市高中毕业班教学质量检测(一)高三数学(理科)一、选择题(60分)1、若集合A={x|x>-2},B={x|-3<x<3},则A B=A、{x|x>-3}B、{x|-3<x<3}C、{x|x>-2}D、{x|-2<x<3}2、若,a b R∈,i为虚数单位,且a+2i=i(b+i),则a+b=A、-1B、1C、2D、33、双曲线3x2-y2=12的实轴长是A 、4B、6C、D、4、采用系系统抽样方法从480人中抽取16人做问卷调查,为此将他们随机编号为1 、2、…、480,分组后在第一组采用简单随机抽样的方法抽到的号码为8抽到的16人中,编号落人区间[1,160]的人做问卷A,编号落入区问[161,320]的人做问卷B,其余的人做问卷C,则被抽到的人中,做问卷B的人数为A、4B、5C、6D、75、如右图所示,程序框图输出的结果为A、15B、16C、136D、1536、在平面直角坐标系中,不等式组1040xx yx y-≤⎧⎪+≥⎨⎪-+≥⎩,表示的平面区域的面积是A、3B、92C、6D、97、如图所示,若向正方形ABCD内随机投入一质点,则所投的质点恰好落在CE与y轴及抛物线y=x2所围成的阴影区域内的概率是A、15B、16C、17D、238、函数2cos23xy x=-的图象大致是9、若7cos(2)38xπ-=-,则sin()3xπ+学科网的值为A、14B、78C、±14D、±7810、已知圆x2+y2-2x-4y+a-5=0上有且仅有两个点到直线3x-4y-15=0的距离为1,则实数a的取值范围为A、(5,7)B、(-15,1)C、(5,10)D、(-∞,1)11、如图,棱长为1的正方体ABC-A1B1C1D1中,E,F为A1C1上两动点,且EF=12,则下列结论中错误的是A、BD⊥CEB、△CEF的面积为定值C、直线BC与平面CEF所成的角为定值D、直线BE与CF所成的角为定值12、已知单位向量e 与向量a ,b 满足:|a -e |=|a |,(a -b )²(b -e )=0,对每一个确定的向量a ,都有与其对应的向量b 满足以上条件,设M ,m 分别为|b |的最大值和最小值,令t =|M -m |,则对任意的向量a ,实数t 的取值范围是A 、[0,1]B 、[0,12]C 、[1,2+∞] D [1,+∞] 二、填空题(20分) 13、在621()x x +的展开式中,常数项为_____(用数字作答)。
北京市石景山区2013届高三上学期期末考试理科数学试题

北京市石景山区2013届高三上学期期末考试理科数学试题石景山区2012—2013学年第一学期期末考试试卷高三数学(理)本试卷共6页,150分.考试时长120分钟.请务必将答案答在答题卡上,在试卷上作答无效.考试结束后上交答题卡.第一部分(选择题 共40分) 一、选择题共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项.1.设集合{}4,3,2,1=U ,{}2,1=A ,{}4,2=B ,则=⋃B A C U)(( )A . {}2,1B . {}4,32,C . {}4,3D .{}4,3,2,12. 若复数iZ=1,iZ -=32,则=12ZZ( ) A . 13i -- B .i +2C .13i +D .i +33.AC 为平行四边形ABCD 的一条对角线,(2,4),(1,3),AB AC AD 则===u u u r u u u r u u u r ( )A .(2,4)B .(3,7)C .(1,1)D .(1,1)--4. 设,m n 是不同的直线,,αβ是不同的平面,下列命题中正确的是( )A .若//,,m n m n αβ⊥⊥,则αβ⊥B .若//,,m n m n αβ⊥⊥,则//αβC .若//,,//m n m n αβ⊥,则α⊥βD .若//,,//m n m n αβ⊥,则//αβ5.执行右面的框图,若输出结果为3,则可输入的实数x 值的个数为( ) A .1 B .2C .3D .46.若从1,2,3,…,9这9个整数中同时取4个 不同的数,其和为奇数,则不同的取法共有( ) A .60种 B .63种 C .65种 D .66种7.某三棱锥的三视图如图所示,该三棱锥的体积是( )A .38B .4C .2D .34正(主)视图 侧(左)视图俯视图2 23 2 3 1 开输出输否 是 结>2x 2=-1y x 2=log y x8. 在整数集Z 中,被5除所得余数为k 的所有整数组成一个“类”,记为[]k ,即[]{}5k n k n =+∈Z ,0,1,2,3,4k =.给出如下四个结论: ① []20133∈;② []22-∈;③[][][][][]01234Z =∪∪∪∪;④ 整数,a b 属于同一“类”的充要条件是“[]0a b -∈”.其中,正确结论的个数为( ). A .1 B .2C .3D .4第二部分(非选择题 共110分)二、填空题共6小题,每小题5分,共30分. 9.已知不等式组y x y x x a ≤⎧⎪≥-⎨⎪≤⎩,,表示的平面区域S 的面积为4,则=a ; 若点Sy x P ∈),(,则yx z +=2 的最大值为 .10.如右图,从圆O 外一点P 引圆O 的割线PAB 和P A BC O •DPCD ,PCD过圆心O ,已知1,2,3PA AB PO ===,则圆O 的半径等于 . 11.在等比数列{}na 中,141=,=42a a -,则公比=q ;123++++=n a a a a L .12. 在ABC ∆中,若2,60,7a Bb =∠=︒=BC 边上的高等于 .13.已知定点A 的坐标为(1,4),点F 是双曲线221412x y -=的左焦点,点P 是双曲线右支上的动点,则PF PA+的最小值为 .14. 给出定义:若11< +22m x m -≤ (其中m 为整数),则m 叫做离实数x 最近的整数,记作{}x ,即{}=x m. 在此基础上给出下列关于函数()={}f x x x -的四个命题:①=()y f x 的定义域是R ,值域是11(,]22-; ②点(,0)k 是=()y f x 的图像的对称中心,其中k Z∈;③函数=()y f x 的最小正周期为1;④ 函数=()y f x 在13(,]22-上是增函数. 则上述命题中真命题的序号是 .三、解答题共6小题,共80分.解答应写出文字说明,演算步骤或证明过程. 15.(本小题共13分)已知函数sin 2(sin cos )()cos x x x f x x +=. (Ⅰ)求)(x f 的定义域及最小正周期;(Ⅱ)求)(x f 在区间⎥⎦⎤⎢⎣⎡-46ππ,上的最大值和最小值.16.(本小题共14分)如图1,在Rt ABC ∆中,90C ∠=︒,36BC AC ==,.D 、E 分别是AC AB 、上的点,且//DE BC ,将ADE ∆沿DE 折起到1A DE ∆的位置,使1A D CD ⊥,如图2.(Ⅰ)求证:BC ⊥平面1A DC ;(Ⅱ)若2CD =,求BE 与平面1A BC 所成角的正弦值; (Ⅲ) 当D 点在何处时,1A B 的长度最小,并求出最小值.17.(本小题共13分)甲、乙、丙三人独立破译同一份密码,已知甲、乙、丙各自破译出密码的概率分别为1123p 、、,且他们是否破译出密码互不影响.若三人中只有甲破译出密码的概率为14. (Ⅰ)求甲乙二人中至少有一人破译出密码的概率;(Ⅱ)求p 的值;(Ⅲ)设甲、乙、丙三人中破译出密码的人数为X,求X 的分布列和数学期望EX .18.(本小题共13分)ABC D E图图ABC D E已知函数()=ln+1,f x x ax a R-∈是常数.(Ⅰ)求函数=()y f x的图象在点(1,(1))P f处的切线l的方程;(Ⅱ)证明函数=()(1)y f x x≠的图象在直线l的下方;(Ⅲ)讨论函数=()y f x零点的个数.19.(本小题共14分)已知椭圆的中心在原点,焦点在x轴上,离心率为32,且经过点(4,1)M,直线:=+l y x m交椭圆于不同的两点A B、.(Ⅰ)求椭圆的方程;(Ⅱ)求m的取值范围;(Ⅲ)若直线l不过点M,求证:直线MA MB、的斜率互为相反数.20.(本小题共13分)定义:如果数列{}na的任意连续三项均能构成一个三角形的三边长,则称{}na为“三角形”数列.对于“三角形”数列{}na ,如果函数()y f x =使得()nn bf a =仍为一个“三角形”数列,则称()y f x =是数列{}na 的“保三角形函数”(*)n N ∈.(Ⅰ)已知{}na 是首项为2,公差为1的等差数列,若()(1)xf x kk =>是数列{}na 的“保三角形函数”,求k 的取值范围;(Ⅱ)已知数列{}nc 的首项为2013,nS 是数列{}nc 的前n 项和,且满足+1438052n n S S -=,证明{}nc 是“三角形”数列;(Ⅲ)若()lg g x x =是(Ⅱ)中数列{}nc 的“保三角形函数”,问数列{}nc 最多有多少项?(解题中可用以下数据 :lg20.301,lg30.477,lg2013 3.304≈≈≈)石景山区2012—2013学年第一学期期末考试高三数学(理科)参考答案一、选择题共8小题,每小题5分,共40分.题号 1 2 3 4 5 6 7 8 答案 B A D C C A B C二、填空题共6小题,每小题5分,共30分.(9题、11题第一空2分,第二空3分) 三、解答题共6小题,共80分. 15.(本小题共13分)(Ⅰ)因为cos 0x ≠,所以+,2x k k Z ππ≠∈. 所以函数)(x f 的定义域为{+,}2x x k k Z ππ≠∈| ……………2分 题号 9 101112 13 14 答案2;6611222n ;---3329①③sin 2sin cos ()cos x x x f x x +=()()2sin sin +cos =2sin +sin2x x x x x =22-)14x π=+……………5分π=T……………7分(Ⅱ)因为46ππ≤≤-x ,所以7-2-1244x πππ≤≤ ……………9分当2-44x ππ=时,即4x π=时,)(x f 的最大值为2; ……………11分当2--42x ππ=时,即8x π=-时,)(x f 的最小值为-2+1. ………13分 16.(本小题共14分)(Ⅰ)证明: 在△ABC 中,90,//,C DE BC AD DE ∠=︒∴⊥1A D DE∴⊥.又11,,A D CD CD DE D A D BCDE ⊥⋂=∴⊥面.由1,.BC BCDE A D BC ⊂∴⊥面1,,BC CD CD BC C BC A DC⊥⋂=∴⊥面. …………………………4分(Ⅱ)如图,以C 为原点,建立空间直角坐标系. ……………………5分1(2,0,0),(2,2,0),(0,3,0),(2,0,4)D E B A .AC D Ex z设(,,)x y z =n 为平面1A BC 的一个法向量,因为(0,3,0),CB =u u u r1(2,0,4)CA =u u u r所以30240y x z =⎧⎨+=⎩,令2x =,得=0,=1y z -. 所以(2,0,1)=-n 为平面1A BC的一个法向量. ……………………7分设BE 与平面1A BC 所成角为θ.则4sin =cos 555BE θ<⋅>==⋅u u u rn .所以BE与平面1A BC所成角的正弦值为45. …………………9分(Ⅲ)设(,0,0)D x ,则1(,0,6)A x x -,2221(-0)(0-3)(6--0)A B x x =++22-1245x x =+…………………12分当=3x 时,1A B 的最小值是33即D 为AC 中点时, 1A B 的长度最小,最小值为33…………………14分 17.(本小题共13分)记“甲、乙、丙三人各自破译出密码”分别为事件321,,A A A ,依题意有12311(),(),(),23P A P A P A p ===且321,,A A A 相互独立.(Ⅰ)甲、乙二人中至少有一人破译出密码的概率为121()P A A -⋅1221233=-⨯=.…………………3分(Ⅱ)设“三人中只有甲破译出密码”为事件B ,则有()P B =123()P A A A ⋅⋅=121(1)233p p -⨯⨯-=, …………………5分所以1134p -=,14p =. ……………………7分 (Ⅲ)X的所有可能取值为3,2,1,0. ……………………8分所以1(0)4P X ==, (1)P X ==P 123()A A A ⋅⋅+P 123()A A A ⋅⋅+P 123()A A A ⋅⋅111312111423423424=+⨯⨯+⨯⨯=,(2)P X ==P 123()A A A ⋅⋅+P 123()A A A ⋅⋅+P 123()A A A ⋅⋅11312111112342342344=⨯⨯+⨯⨯+⨯⨯=,(3)P X ==P123()A A A ⋅⋅=111123424⨯⨯= . ……………………11分X分布列为:X 0 1 2 3 P14112414124…………………12分所以,1111113()012342442412E X =⨯+⨯+⨯+⨯=. (13)分1. (本小题共13分) (Ⅰ)1()=f x ax'-…………………1分(1)=+1f a -,=(1)=1lk f a '-,所以切线 l 的方程为(1)=(1)l y f k x --,即=(1)y a x-. …………………3分(Ⅱ)令()=()(1-)=ln +1>0F x f x a x x x x --,,则11()=1=(1)()=0=1.F x x F x x x x''--, 解得 x)1 , 0(1) , 1(∞+()F x ' +-)(x F↗最大值↘………………6分(1)<0F ,所以>0x ∀且1x ≠,()<0F x ,()<(1)f x a x -,即函数=()(1)y f x x ≠的图像在直线 l 的下方. …………………8分(Ⅲ)令()=ln +1=0f x x ax -,ln +1=x a x. 令ln +1()=x g x x ,22ln +11(ln +1)ln ()=()==x x xg x x x x-''-, 则()g x 在(0,1)上单调递增,在(1,+)∞上单调递减,当=1x 时,()g x 的最大值为(1)=1g .所以若>1a ,则()f x 无零点;若()f x 有零点,则1a ≤.………………10分若=1a ,()=ln +1=0f x x ax -,由(Ⅰ)知()f x 有且仅有一个零点=1x .若0a ≤,()=ln +1f x x ax -单调递增,由幂函数与对数函数单调性比较,知()f x 有且仅有一个零点(或:直线=1y ax -与曲线=ln y x 有一个交点).若0<<1a ,解1()==0f x a x '-得1=x a,由函数的单调性得知()f x 在1=x a 处取最大值,11()=ln >0f a a,由幂函数与对数函数单调性比较知,当x 充分大时()<0f x ,即()f x 在单调递减区间1(,+)a ∞有且仅有一个零点;又因为1()=<0a f e e -,所以()f x 在单调递增区间1(0)a,有且仅有一个零点.综上所述,当>1a 时,()f x 无零点; 当=1a 或0a ≤时,()f x 有且仅有一个零点; 当0<<1a 时,()f x 有两个零点. …………………13分 19.(本小题共14分) (Ⅰ)设椭圆的方程为22221x y a b+=,因为32e =,所以224a b =,又因为(4,1)M ,所以221611a b+=,解得225,20ba ==,故椭圆方程为221205x y +=. …………………4分 (Ⅱ)将y x m =+代入221205x y +=并整理得22584200x mx m ++-=,22=(8)-20(4-20)>0m m ∆,解得55m -<<. …………………7分(Ⅲ)设直线,MA MB 的斜率分别为1k 和2k ,只要证明12k k+=.设11(,)A x y ,22(,)B x y , 则212128420,55m m x x x x -+=-=. …………………9分12122112121211(1)(4)(1)(4)44(4)(4)y y y x y x k k x x x x ----+--+=+=----122112122(1)(4)(1)(4)2(5)()8(1)2(420)8(5)8(1)055x m x x m x x x m x x m m m m m =+--++--=+-+----=---=分子所以直线MA MB 、的斜率互为相反数. …………………14分20.(本小题共13分) (Ⅰ)显然121,nn n n an a a a ++=++>对任意正整数都成立,即{}na 是三角形数列。
2013年北京高三(一模)数学(理)分类汇编系列二解析版12.程序与框图
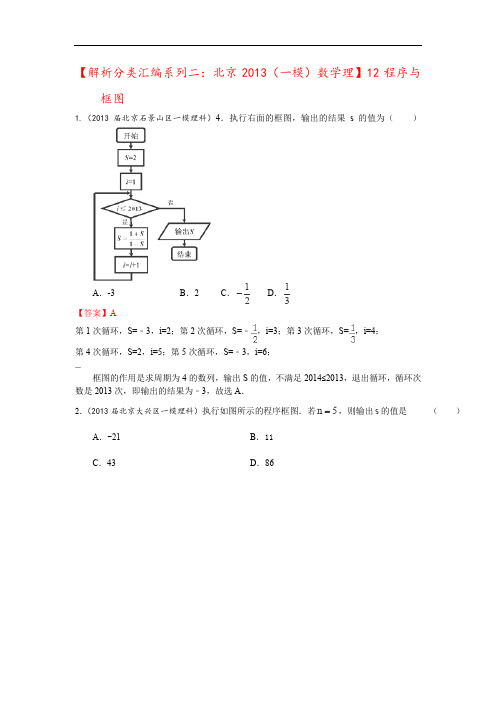
【解析分类汇编系列二:北京2013(一模)数学理】12程序与框图1.(2013届北京石景山区一模理科)4.执行右面的框图,输出的结果s的值为()A.-3 B.2 C.12-D.13【答案】A第1次循环,S=﹣3,i=2;第2次循环,S=﹣,i=3;第3次循环,S=,i=4;第4次循环,S=2,i=5;第5次循环,S=﹣3,i=6;…框图的作用是求周期为4的数列,输出S的值,不满足2014≤2013,退出循环,循环次数是2013次,即输出的结果为﹣3,故选A.2.(2013届北京大兴区一模理科)执行如图所示的程序框图.若5n=,则输出s的值是()A.-21 B.11C.43 D.86【答案】A第一次循环,11(2)1,2s i =+-=-=;第二次循环,21(2)3,3s i =-+-==;第三次循环,33(2)5,4s i =+-=-=;第四次循环,41(2)11,5s i =-+-==,第五次循环,511(2)21,6s i =+-=-=,此时不满足条件,输出21s =-,所以选A.3.(2013届北京丰台区一模理科)执行右边的程序框图,输出k 的值是( )A .3B .4C .5D .6【答案】A第一次循环,2,03ba a ==,不满足条件,循环,此时22,3k b ==。
第二次循环,22832(),394b a a =⨯==,不满足条件,循环,此时83,9k b ==。
第三次循环,3283(),139ba a =⨯==,满足条件,此时输出3k =。
选A.4.(2013届北京海淀一模理科)某程序的框图如图所示,执行该程序, 若输入的x 值为5,则输出的y 值为A.2- B .1- C .12 D .2【答案】C若5x =,则第一次循环,523x =-=,第二次循环,321x =-=,第三次循环121x =-=-,此时满足条件,输出1122y -==,选C.5.(2013届北京西城区一模理科)执行如图所示的程序框图.若输出y =,则输入角=θ( )A .π6 B .π6- C .π3 D .π3-【答案】D由题意知sin ,4tan ,42y πθθππθθ⎧<⎪⎪=⎨⎪≤≤⎪⎩。
【解析分类汇编系列二:北京2013(一模)数学理】1:集合 Word版含答案

【解析分类汇编系列二:北京2013(一模)数学理】1:集合1.(2013届北京石景山区一模理科)1.设集合M= {x|x 2≤4),N={x|log 2 x≥1},则M N 等于( )A . [-2,2]B .{2}C .[2,+∞)D . [-2,+∞)【答案】B{22}M x x =-≤≤,{2}N x x =≥,所以{2}{2}M N x x === ,选B.2.(2013届北京朝阳区一模理科)(2)已知集合{}23M x x =-<<,{}lg(2)0N x x =+≥,则M N =A. (2,)-+∞B. (2,3)-C. (2,1]--D. [1,3)- 【答案】D{}lg(2)0{21}{1}N x x x x x x =+≥=+≥=≥-,所以{13}M N x x =-≤< ,选D.3.(2013届北京海淀一模理科)集合2{6},{30}A x x B x x x =∈≤=∈->N|R|,则A B =( )A .{3,4,5}B .{4,5,6}C .{|36}x x <≤D .{|36}x x ≤<【答案】B{0,1,2,3,4,5,6}A =,{30}B x x x =><或,所以{4,5,6}A B = ,选B.4.(2013届北京市延庆县一模数学理)已知集合},3,1{m A =,},1{m B =,A B A = ,则=m ( )A .0或3B .0或3C .1或3D .1或3【答案】B因为A B A = ,所以B A ⊆,即3m =或m =解得3m =,0m =或1m =,当1m =时,集合,A B 不成立。
所以3m =或0m =,选B.5.(2013届北京西城区一模理科)已知全集U=R ,集合{|02}A x x =<<,2{|10}B x x =->,那么U A B = ð( )A .{|01}x x <<B .{|01}x x <≤C .{|12}x x <<D .{|12}x x ≤< 【答案】B2{|10}={11}B x x x x x =->><-或,所以{|11}U B x x =-≤≤ð,所以{01}U A B x x =<≤ ð,选B.6.(2013届东城区一模理科)已知全集{1,2,3,4}U =,集合{1,2}A =,那么集合U A ð为( )A .{3}B .{3,4}C .{1,2}D .{2,3}【答案】B因为{1,2}A =,所以={3,4}U A ð,选B.7.(2013届房山区一模理科数学)已知全集U =R ,集合2{|1},{|4}M x x N x x =≤=>,则()M C N =R( )A .(2,1]-B .[2,1]-C .(,1]-∞-D .(,2)-∞-【答案】B{22}N x x x =><-或,所以(){22}C N =x x -≤≤R ,所以(){21}M C N =x x -≤≤R ,选B.8.(2013届房山区一模理科数学)设集合M 是R 的子集,如果点0x ∈R 满足:00,,0a x M x x a ∀>∃∈<-<,称0x 为集合M 的聚点.则下列集合中以1为聚点的有:{|}1n n n ∈+N ; ②*2{|}n n∈N ; ③Z ; ④{|2}x y y = ( )A .①④B .②③C .①②D .①②④【答案】A ①中,集合{|}1nn n ∈+N 中的元素是极限为1的数列, 除了第一项0之外,其余的都至少比0大, ∴在12a <的时候,不存在满足得0<|x|<a 的x , ∴0不是集合{|}1nn n ∈+N 的聚点 ②集合*2{|}n n∈N 中的元素是极限为0的数列, 对于任意的a >0,存在2n a >,使0<|x|=2a n<,∴0是集合*2{|}n n ∈N 的聚点③对于某个a <1,比如a=0.5,此时对任意的x ∈Z ,都有|x ﹣0|=0或者|x ﹣0|≥1,也就是说不可能0<|x ﹣0|<0.5,从而0不是整数集Z 的聚点 ④故选A9.(2013届门头沟区一模理科)已知全集U = R ,集合A {}24x x =≤,B {}1x x =<,则集合AB 等于( )A .{}2x x ≥-B .{}12x x ≤≤ C .{}1x x ≥D .R【答案】A{}24{22}A x x x x =≤=-≤≤,{1}U B x x =≥ð,所以={2}U A B x x ≥- ð,选A.10.(2013届北京丰台区一模理科)已知M 是集合{}1,2,3,,21(*,2)k k N k -∈≥ 的非空子集,且当x M ∈时,有2k x M -∈.记满足条件的集合M 的个数为()f k ,则(2)f = ;()f k = 。
【解析分类汇编系列二:北京2013(一模)数学理】12.程序与框图 Word版含答案

【解析分类汇编系列二:北京2013(一模)数学理】12程序与框图
1.(2013届北京石景山区一模理科)4.执行右面的框图,输出的结果s的值为()
A.-3 B.2 C.
1
2
-D.
1
3
【答案】A
第1次循环,S=﹣3,i=2;第2次循环,S=﹣,i=3;第3次循环,S=,i=4;
第4次循环,S=2,i=5;第5次循环,S=﹣3,i=6;
…
框图的作用是求周期为4的数列,输出S的值,不满足2014≤2013,退出循环,循环次
数是2013次,即输出的结果为﹣3,故选A.
2.(2013届北京大兴区一模理科)执行如图所示的程序框图.若5
n=,则输出s的值是()A.-21 B.11
C.43 D.86
【答案】A
第一次循环,11(2)1,2s i =+-=-=;第二次循环,21(2)3,3s i =-+-==;
第三次循环,33(2)5,4s i =+-=-=;第四次循环,41(2)11,5s i =-+-==,第五次循环,511(2)21,6s i =+-=-=,此时不满足条件,输出21s =-,所以选A.
3.(2013届北京丰台区一模理科)执行右边的程序框图,输出k 的值是
( ) A .3 B .4 C .5 D .6
【答案】A。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2013年石家庄市高中毕业班教学质量检测(一)高三数学(理科)一、选择题(60分)1、若集合A={x|x>-2},B={x|-3<x<3},则A B=A、{x|x>-3}B、{x|-3<x<3}C、{x|x>-2}D、{x|-2<x<3}2、若,a b R∈,i为虚数单位,且a+2i=i(b+i),则a+b=A、-1B、1C、2D、33、双曲线3x2-y2=12的实轴长是A 、4B、6C、D、4、采用系系统抽样方法从480人中抽取16人做问卷调查,为此将他们随机编号为1 、2、…、480,分组后在第一组采用简单随机抽样的方法抽到的号码为8抽到的16人中,编号落人区间[1,160]的人做问卷A,编号落入区问[161,320]的人做问卷B,其余的人做问卷C,则被抽到的人中,做问卷B的人数为A、4B、5C、6D、75、如右图所示,程序框图输出的结果为A、15B、16C、136D、1536、在平面直角坐标系中,不等式组1040xx yx y-≤⎧⎪+≥⎨⎪-+≥⎩,表示的平面区域的面积是A、3B、92C、6D、97、如图所示,若向正方形ABCD内随机投入一质点,则所投的质点恰好落在CE 与y轴及抛物线y=x2所围成的阴影区域内的概率是A、15B、16C、17D、238、函数2cos23xy x=-的图象大致是9、若7cos(2)38x π-=-,则sin()3x π+学科网的值为 A 、14 B 、78 C 、±14 D 、±7810、已知圆x 2+y 2-2x -4y +a -5=0上有且仅有两个点到直线3x -4y -15=0的距离为1,则实数a 的取值范围为 A 、(5,7) B 、(-15,1) C 、(5,10) D 、(-∞,1) 11、如图,棱长为1的正方体ABC -A 1B 1C 1D 1中,E ,F 为A 1C 1上两动点,且EF =12,则下列结论中错误的是A 、BD ⊥CEB 、△CEF 的面积为定值C 、直线BC 与平面CEF 所成的角为定值D 、直线BE 与CF 所成的角为定值 12、已知单位向量e 与向量a ,b 满足:|a -e |=|a |,(a -b )²(b -e )=0,对每一个确定的向量a ,都有与其对应的向量b 满足以上条件,设M ,m 分别为|b |的最大值和最小值,令t =|M -m |,则对任意的向量a ,实数t的取值范围是A 、[0,1]B 、[0,12]C 、[1,2+∞] D [1,+∞] 二、填空题(20分) 13、在621()x x +的展开式中,常数项为_____(用数字作答)。
14、某几何体的三视图如右图所示,则该几何体的体积为___15、若函数21(),1()2log ,1xx f x x x ⎧≤⎪=⎨⎪>⎩,则f (x )≥2的解集为___16、当*n N ∈时,定义函数N (n )表示n 的最大奇因数,如则S (n )=____(用关于n 的代数式表示)。
三、解答题(70分)17、(本小题满分10分)已知等差数列{n a }的前n 项和为n S ,且372a a =,417S = (1)求数列{n a }的通项公式。
(2)求数列{n a }的前n 项和n S 的最大值。
18、(本小题满分12分)在一次抗雪救灾中,需要在A ,B 两地之间架设高压电线,为测量A ,B 两地的距离,救援人员在相距l 米的C ,D 两地(A ,B ,C ,D 在同一平面上),没得∠ACD =45°,∠ADC =75°,∠BCD =30°,∠BDC =15°(如右图)。
考虑到电线的自然下垂和施工损耗等原因,实际所需电线长度大约应该是A ,B 距离的1.2倍,问救援人员至少应该准备多长的电线?19、(本小题满分12分)如图,已知四棱锥P -ABCD 的底面为矩形,PA ⊥底面ABCD ,且AB BC =1,点E ,F 分别为AB ,PC 中点。
(I )当PA 的长度为多少时,EF ⊥PD ;(II )在(I )的前提下,求二面角B -PC -D 的余弦值。
20、(本小题满分12分)为参加部队射击比赛,甲、乙两人进行了4天的集中训练,每天的射击数据如下表 甲射击数据表: 乙射击数据表:将射击环数的频率视为概率,估计他们的比赛成绩。
(I )求甲、乙两人射击环数X 1,X 2的分布列,根据射击环数的期望与方差比较两人的射击水平; (II )若射击成绩在9环以上(含9环)为成绩优秀,求甲在3次射击中至少有2次成绩优秀的概率。
21、(本小题满分12分)已知椭圆C :22221(0)x y a b a b+=>>的右顶点、上顶点分别为M ,N ,过其左焦点F (-c ,0)作垂直于x 轴的直线l ,且与椭圆在第二象限交于P 点,MN OP λ=。
(1)求椭圆C 的离心率;(2)若椭圆的弦AB 过点E (5,0)且不与坐标轴垂直,设点A 关于x 轴的对称点A 1,直线A 1B 与x 轴交于点R (5,0),求椭圆C 的方程。
22、(本小题满分12分)已知函数()ln af x x x=-。
(I )若f (x )在x =1处取得极值,求实数a 的值; (II )若f (x )≥5-3x 恒成立,求实数a 的取值范围。
数学(理科答案)一、选择题:共12小题,每小题5分,共60分. 1-5ABABC 6-10DBCCB 11-12DC二、填空题:本大题共4小题,每小题5分,共20分.13. 15 14. 3 15. (,1][8,)-∞-+∞ 16.4233n + 三、解答题:17.解:(Ⅰ)设等差数列{}n a 的公差为d . 由已知732a a =,174=S ,得11122(6)434172a d a d a d +=+⎧⎪⎨⨯+=⎪⎩,………………2分 解得1512a d =⎧⎪⎨=-⎪⎩,1122n n a -∴=+.……………5分 (Ⅱ)法一:2(1)11214415.224216n n n S n n -⎛⎫⎛⎫=+-=--+⎪ ⎪⎝⎭⎝⎭ ……………8分 ∴当n 取10或11时,n S 取最大值1272.……………10分法二: 数列{}n a 的10,a >公差0d <,∴此等差数列{}n a 是首项为正数的递减数列.当11n =时,1102n na -==; 所以当111n n N *≤≤∈且时,有0;n a ≥当n 12n N *≥∈且时,有0n a <.………………8分 综上:当n 取10或11时,1110S S ==1272. 所以n S 取最大值1272.………10分 18.解:依题意,CD l =,045=∠ACD ,在ACD ∆中,0060180CAD =∠-∠-=∠ADC ACD ,根据正弦定理60sin 45sin CDAD =,∴sin 45sin 60CD AD == , ……….4分 在BCD ∆中,00135180=∠-∠-=∠BDC BCD CBD ,030=∠BCD根据正弦定理BD =sin 30sin135CD ︒=︒ , sin 30sin135CD BD ==…………………….8分 又在ABD ∆中,090=∠+∠=∠BDC ADC ADB 根据勾股定理有AB ===l 642…………………………10分实际所需电线长度约为l AB 5422.1=………………………….12分 19.解:(Ⅰ)以A 为原点,建立如图所示的空间直角坐标系. 设PA x =, 则1(0,0,),(1,0,0),(()22x P x D E C F --- ……………2分又1(,0,),(1,0,)22x EF PD x =-=--210022x EF PD ⋅=+-= ,所以1x =,当PA 的长度为1时,EF ⊥PD .………………5分(Ⅱ)法一:在Rt PBC ∆中作BN ⊥PC ,∴21,23==CN BN . CF=1∴N 为CF 中点。
取CD中点M,连结MN∴MN//DF。
又 DF⊥P C,∴MN⊥P C∴MNB ∠为二面角B -PC -D的平面角.…………9分 在MNB ∆中23,21,26===BN MN BM , ∴cos MNB ∠=33-∴二面角B -PC -D的余弦值为33-.…………12分 法二:如图建立空间直角坐标系A-xyz ,则B (0,2,0)P (1,0,0)C (0,2,1-)D(0,0,1-) 则)1,2,0(-=PB ,)1,2,1(--=PC ,)1,0,1(--=PD 设平面PBC 的法向量1(,,)x y z =n∴10PB ⋅= n ,10PC ⋅= n∴02,02=-+-=-z y x z y ,令1=y ,则 1=n ,……………8分同理可得平面PCD 的一个法向量2(1,0,1)=-n ,………………10分则二面角B -PC -D的余弦值cos 12,n n =33-,……………12分 20.解:(Ⅰ) 由甲射击数据表可知,总共射击400次,其中射击7环的频数为40次,8环频数为80次,9环频数为120次,10环的频数为160次.故 ()14070.1400P X === ()18080.2400P X === ()112090.3400P X === ()1160100.4400P X ===所以,甲射击环数1X 的分布列为同理可计算乙射击环数2X 的分布列 (4)分()()119,1E X D X ==;()()229, 1.4E X D X ==…………………………………………………………6分甲乙两人射击环数均值相等,甲射击环数方差比乙射击环数方差小,因此甲乙射击的平均水平没有差别,但甲发挥比乙稳定. ………………8分(Ⅱ)甲在一次射击成绩优秀的概率0.30.40.7P =+= 甲在3次目标射击中至少有2次成绩优秀的概率为:2233330.70.30.7C C ⨯⨯+⨯=0.784 …………………………12分21.解:(Ⅰ)由椭圆方程22221(0)x y a b a b+=>>得M 、N 的坐标为M (,0)a ,N (0,)b ,则(,)MN a b =- ,又由22221x c x y ab =-⎧⎪⎨+=⎪⎩,得2(,)b P c a-1X7 8 9 10P 0.1 0.2 0.3 0.42X7 8 9 10P 0.2 0.1 0.2 0.5由(0)MN OP λλ=>得b c =……………….2分.…………….4分 (Ⅱ)设1122(,),(,)A x y B x y ,由1A R BR k k =得121255y y x x -=--,又AE BE k k ==,则221155x y x y --==-121220(2)c x c x x +=++.…………8分设直线:(AB y k x =,则由22222(x y c y k x ⎧+=⎪⎨=-⎪⎩得2222(810)(12)05k c k x x -+-+=.12x x +=,22122(810)5(12)k c x x k -=+.…………10分代入得220(2c c +=+.解得c = 所以椭圆方程为221105x y +=.…………12分 22.解:(Ⅰ)函数()f x 定义域为(0,)+∞,2'()x af x x +=-. '(1)0f =,即1a =-.…………2分经检验,1a =-符合题意.………………….4分 (Ⅱ)设()()35ln 35a g x f x x x x x=+-=-+-,则当0x >时,()0g x ≥恒成立. (1)20g a =-≥,所以2a ≥.…………6分223'()x x a g x x --=.方程'()0g x =有一负根1x 和一正根2x .120x x <<.其中1x 不在函数定义域内. ()g x 在2(0,)x 上是减函数,在2(,)x +∞上是增函数.即()g x 在定义域上的最小值为2()g x .………8分 依题意2()0g x ≥.即2222()ln 350a g x x x x =-+-≥.又22230x x a --=,所以2231a x x =-,因为02>x a ,312>x 。
