001——北京市2008年高级中等学校招生考试(答案部分) 数学
2008年普通高等学校校招生全国统一考试数学北京卷(理科)
2008年普通高等学校校招生全国统一考试数学北京卷(理科)第Ⅰ卷(选择题 共40分)一、本题共8小题。
每小题5分,共40分。
在每小题列出的四个选项中,选出符合题目要求的一项。
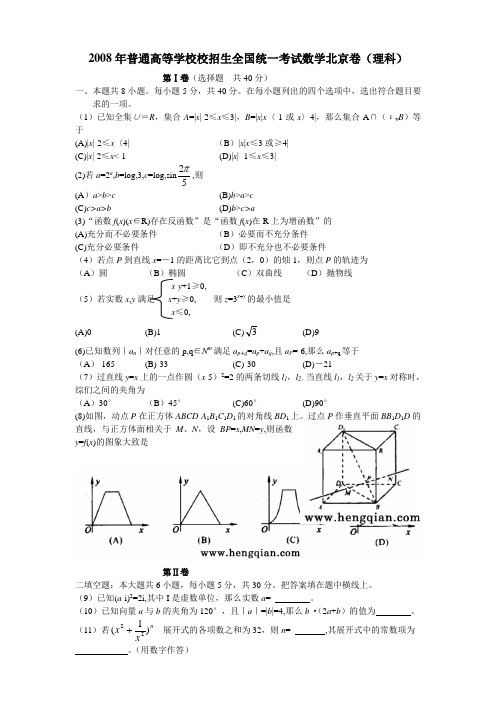
(1)已知全集∪=R ,集合A =|x |-2≤x ≤3|,B =|x |x 〈-1或x 〉4|,那么集合A ∩(εv B )等于(A)|x |-2≤x 〈4| (B )|x |x ≤3或≥4| (C)|x |-2≤x <-1 (D)|x | -1≤x ≤3| (2)若a =2a ,b =log,3,c =log,sin52π,则 (A )a >b >c (B)b >a >c (C)c>a>b (D)b >c>a(3)“函数f (x )(x ∈R)存在反函数”是“函数f (x )在R 上为增函数”的 (A)充分而不必要条件 (B )必要而不充分条件 (C)充分必要条件 (D )即不充分也不必要条件(4)若点P 到直线x =-1的距离比它到点(2,0)的烛1,则点P 的轨迹为 (A )圆 (B )椭圆 (C )双曲线 (D )抛物线x -y +1≥0,(5)若实数x ,y 满足 x +y ≥0, 则z =3x +y 的最小值是x ≤0, (A)0(B)1(C)3(D)9(6)已知数列|a n |对任意的p,q ∈N m 满足a p+q =a p +a q ,且a P =-6,那么a p +q 等于 (A )-165 (B)-33 (C)-30 (D)-21(7)过直线y =x 上的一点作圆(x -5)2=2的两条切线l 1,l 2,当直线l 1,l 2关于y =x 对称时,综们之间的夹角为 (A )30° (B )45° (C)60° (D)90°(8)如图,动点P 在正方体ABCD -A 1B 1C 1D 1的对角线BD 1上。
过点P 作垂直平面BB 1D 1D 的直线,与正方体面相关于M 、N ,设BP =x ,MN =y ,则函数y =f (x )的图象大致是第Ⅱ卷二填空题:本大题共6小题,每小题5分,共30分。
2008年普通高等学校招生全国统一考试数学卷(北京.理)含详解

绝密★使用完毕前2008年普通高等学校校招生全国统一考试 数学(理工农医类)(北京卷)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,第Ⅰ卷1至2页,第Ⅱ卷3至9页,共150分。
考试时间120分钟。
考试结束,将本试卷和答题卡一并交回。
第Ⅰ卷(选择题 共40分)注意事项:1答第Ⅰ卷前,考生务必将自己的姓名、准考证号、考试科目涂写在答题卡上。
2.每小题选出答案后,用钢笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案。
不能答在试卷上。
一、本题共8小题。
每小题5分,共40分。
在每小题列出的四个选项中,选出符合题目要求的一项。
(1)已知全集∪=R ,集合A =|x |-2≤x ≤3|,B =|x |x 〈-1或x 〉4|,那么集合A ∩(εv B )等于(A)|x |-2≤x 〈4| (B )|x |x ≤3或≥4| (C)|x |-2≤x <-1(D)|x | -1≤x ≤3|(2)若a =2a ,b =log,3,c =log,sin 52 ,则 (A )a >b >c(B)b >a >c(C)c>a>b (D)b >c>a(3)“函数f (x )(x ∈R)存在反函数”是“函数f (x )在R 上为增函数”的(A)充分而不必要条件 (B )必要而不充分条件 (C)充分必要条件 (D )即不充分也不必要条件(4)若点P 到直线x =-1的距离比它到点(2,0)的烛1,则点P 的轨迹为 (A )圆 (B )椭圆 (C )双曲线 (D )抛物线 x -y +1≥0,(5)若实数x ,y 满足 x +y ≥0, 则z =3x +y 的最小值是x ≤0,(A)0(B)1(C)3 (D)9(6)已知数列|a n |对任意的p,q ∈N m满足a p+q =a p +a q ,且a P =-6,那么a p +q 等于 (A )-165 (B)-33 (C)-30 (D)-21(7)过直线y =x 上的一点作圆(x -5)2=2的两条切线l 1,l 2,当直线l 1,l 2关于y =x 对称时,综们之间的夹角为(A )30° (B )45° (C)60° (D)90°(8)如图,动点P 在正方体ABCD -A 1B 1C 1D 1的对角线BD 1上。
2008年普通高等学校招生全国统一考试数学(北京卷·理科)(附答案,完全word版)

2008年普通高等学校招生全国统一考试数学(理工农医类)(北京卷)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,第Ⅰ卷1至2页,第Ⅱ卷3至9页,共150分.考试时间120分钟.考试结束,将本试卷和答题卡一并交回.第Ⅰ卷(选择题 共40分)注意事项: 1.答第Ⅰ卷前,考生务必将自己的姓名、准考证号、考试科目涂写在答题卡上. 2.每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其他答案.不能答在试卷上.一、本大题共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项.1.已知全集U =R ,集合{}|23A x x =-≤≤,{}|14B x x x =<->或,那么集合()UA B ð等于( ) A .{}|24x x -<≤ B .{}|34x x x 或≤≥ C .{}|21x x -<-≤D .{}|13x x -≤≤2.若0.52a =,πlog 3b =,22πlog sin 5c =,则( ) A .a b c >>B .b a c >>C .c a b >>D .b c a >>3.“函数()()f x x ∈R 存在反函数”是“函数()f x 在R 上为增函数”的( ) A .充分而不必要条件B .必要而不充分条件C .充分必要条件D .既不充分也不必要条件4.若点P 到直线1x =-的距离比它到点(20),的距离小1,则点P 的轨迹为( ) A .圆B .椭圆C .双曲线D .抛物线5.若实数x y ,满足1000x y x y x ⎧-+⎪+⎨⎪⎩,,,≥≥≤则23x yz +=的最小值是( )A .0B .1CD .96.已知数列{}n a 对任意的*p q ∈N ,满足p q p q a a a +=+,且26a =-,那么10a 等于( )A .165-B .33-C .30-D .21-7.过直线y x =上的一点作圆22(5)(1)2x y -+-=的两条切线12l l ,,当直线12l l ,关于y x =对称时,它们之间的夹角为( ) A .30B .45C .60D .908.如图,动点P 在正方体1111ABCD A BC D -的对角线1BD 上.过点P 作垂直于平面11BB D D 的直线,与正方体表面相交于M N ,.设B P x =,MN y =,则函数()y f x =的图象大致是( )A BC DMNP A 1B 1C 1D 1第 3 页 共 12 页2008年普通高等学校招生全国统一考试数学(理工农医类)(北京卷)第Ⅱ卷(共110分)注意事项:1.用钢笔或圆珠笔将答案直接写在试卷上.2.答卷前将密封线内的项目填写清楚.二、填空题:本大题共6小题,每小题5分,共30分.把答案填在题中横线上. 9.已知2()2a i i -=,其中i 是虚数单位,那么实数a = .10.已知向量a 与b 的夹角为120,且4==a b ,那么(2)+b a b 的值为 .11.若231nx x ⎛⎫+ ⎪⎝⎭展开式的各项系数之和为32,则n = ,其展开式中的常数项为 .(用数字作答)12.如图,函数()f x 的图象是折线段ABC ,其中A B C ,,的坐标分别为(04)(20)(64),,,,,,则((0))f f = ; 0(1)(1)limx f x f x∆→+∆-=∆ .(用数字作答)13.已知函数2()cos f x x x =-,对于ππ22⎡⎤-⎢⎥⎣⎦,上的任意12x x ,,有如下条件:①12x x >; ②2212x x >; ③12x x >. 其中能使12()()f x f x >恒成立的条件序号是 .14.某校数学课外小组在坐标纸上,为学校的一块空地设计植树方案如下:第k 棵树种植在点()k k k P x y ,处,其中11x =,11y =,当2k ≥时,111215551255k k k k k k x x T T k k y y T T --⎧⎡--⎤⎛⎫⎛⎫=+--⎪ ⎪ ⎪⎢⎥⎪⎝⎭⎝⎭⎣⎦⎨--⎛⎫⎛⎫⎪=+- ⎪ ⎪⎪⎝⎭⎝⎭⎩,. ()T a 表示非负实数a 的整数部分,例如(2.6)2T =,(0.2)0T =.按此方案,第6棵树种植点的坐标应为 ;第2008棵树种植点的坐标应为 . 三、解答题:本大题共6小题,共80分.解答应写出文字说明,演算步骤或证明过程. 15.(本小题共13分)已知函数2π()sin sin 2f x x x x ωωω⎛⎫=+ ⎪⎝⎭(0ω>)的最小正周期为π. (Ⅰ)求ω的值;(Ⅱ)求函数()f x 在区间2π03⎡⎤⎢⎥⎣⎦,上的取值范围.16.(本小题共14分)如图,在三棱锥P ABC -中,2AC BC ==,90ACB ∠=,AP BP AB ==,PC AC ⊥. (Ⅰ)求证:PC AB ⊥;(Ⅱ)求二面角B AP C --的大小; (Ⅲ)求点C 到平面APB 的距离.17.(本小题共13分)甲、乙等五名奥运志愿者被随机地分到A B C D ,,,四个不同的岗位服务,每个岗位至少有一名志愿者.(Ⅰ)求甲、乙两人同时参加A 岗位服务的概率; (Ⅱ)求甲、乙两人不在同一个岗位服务的概率;(Ⅲ)设随机变量ξ为这五名志愿者中参加A 岗位服务的人数,求ξ的分布列.A CB P第 5 页 共 12 页18.(本小题共13分)已知函数22()(1)x bf x x -=-,求导函数()f x ',并确定()f x 的单调区间. 19.(本小题共14分)已知菱形ABCD 的顶点A C ,在椭圆2234x y +=上,对角线BD 所在直线的斜率为1.(Ⅰ)当直线BD 过点(01),时,求直线AC 的方程; (Ⅱ)当60ABC ∠=时,求菱形ABCD 面积的最大值.20.(本小题共13分)对于每项均是正整数的数列12n A a a a :,,,,定义变换1T ,1T 将数列A 变换成数列1()T A :12111n n a a a ---,,,,.对于每项均是非负整数的数列12m B b b b :,,,,定义变换2T ,2T 将数列B 各项从大到小排列,然后去掉所有为零的项,得到数列2()T B ; 又定义2221212()2(2)m mS B b b mb b b b =+++++++. 设0A 是每项均为正整数的有穷数列,令121(())(012)k k A T T A k +==,,,. (Ⅰ)如果数列0A 为5,3,2,写出数列12A A ,;(Ⅱ)对于每项均是正整数的有穷数列A ,证明1(())()S T A S A =;(Ⅲ)证明:对于任意给定的每项均为正整数的有穷数列0A ,存在正整数K ,当k K ≥时,1()()k k S A S A +=.2008年普通高等学校招生全国统一考试 数学(理工农医类)(北京卷)参考答案一、选择题(本大题共8小题,每小题5分,共40分)1.D 2.A 3.B 4.D 5.B 6.C 7.C 8.B 二、填空题(本大题共6小题,每小题5分,共30分) 9.1- 10.0 11.5 10 12.2 2-13.②14.(12), (3402), 三、解答题(本大题共6小题,共80分) 15.(共13分) 解:(Ⅰ)1cos 2()222x f x x ωω-=+112cos 2222x x ωω=-+π1sin 262x ω⎛⎫=-+ ⎪⎝⎭.因为函数()f x 的最小正周期为π,且0ω>, 所以2ππ2ω=,解得1ω=. (Ⅱ)由(Ⅰ)得π1()sin 262f x x ⎛⎫=-+ ⎪⎝⎭. 因为2π03x ≤≤, 所以ππ7π2666x --≤≤,所以1πsin 2126x ⎛⎫-- ⎪⎝⎭≤≤, 因此π130sin 2622x ⎛⎫-+ ⎪⎝⎭≤≤,即()f x 的取值范围为302⎡⎤⎢⎥⎣⎦,. ABDP第 7 页 共 12 页16.(共14分) 解法一:(Ⅰ)取AB 中点D ,连结PD CD ,. AP BP =, PD AB ∴⊥. AC BC =, CD AB ∴⊥. PD CD D =,AB ∴⊥平面PCD . PC ⊂平面PCD , PC AB ∴⊥.(Ⅱ)AC BC =,AP BP =, APC BPC ∴△≌△. 又PC AC ⊥, PC BC ∴⊥.又90ACB ∠=,即AC BC ⊥,且ACPC C =,BC ∴⊥平面PAC .取AP 中点E .连结BE CE ,. AB BP =,BE AP ∴⊥.EC 是BE 在平面PAC 内的射影, CE AP ∴⊥.BEC ∴∠是二面角B AP C --的平面角.在BCE △中,90BCE ∠=,2BC =,2BE AB ==sin BC BEC BE ∴∠==. ∴二面角B AP C --的大小为. (Ⅲ)由(Ⅰ)知AB ⊥平面PCD ,∴平面APB ⊥平面PCD .过C 作CH PD ⊥,垂足为H . 平面APB 平面PCD PD =,CH ∴⊥平面APB .CH ∴的长即为点C 到平面APB 的距离. 由(Ⅰ)知PC AB ⊥,又PC AC ⊥,且AB AC A =,PC ∴⊥平面ABC . CD ⊂平面ABC , PC CD ∴⊥.ABE P ABDPH在Rt PCD △中,12CD AB ==2PD PB ==2PC ∴==.233PC CD CH PD ∴==.∴点C 到平面APB 的距离为3. 解法二:(Ⅰ)AC BC =,AP BP =, APC BPC ∴△≌△. 又PC AC ⊥, PC BC ∴⊥. AC BC C =,PC ∴⊥平面ABC . AB ⊂平面ABC , PC AB ∴⊥.(Ⅱ)如图,以C 为原点建立空间直角坐标系C xyz -.则(000)(020)(200)C A B ,,,,,,,,. 设(00)P t ,,. PB AB ==,2t ∴=,(002)P ,,.取AP 中点E ,连结BE CE ,.AC PC =,AB BP =,CE AP ∴⊥,BE AP ⊥.BEC ∴∠是二面角B AP C --的平面角.(011)E ,,,(011)EC =--,,,(211)EB =--,,,cos 26EC EB BEC EC EB∴∠===. ∴二面角B AP C--的大小为arccos3.第 9 页 共 12 页(Ⅲ)AC BC PC ==,C ∴在平面APB 内的射影为正APB △的中心H ,且CH 的长为点C 到平面APB 的距离. 如(Ⅱ)建立空间直角坐标系C xyz -.2BH HE =,∴点H 的坐标为222333⎛⎫⎪⎝⎭,,.23CH ∴=. ∴点C到平面APB 17.(共13分)解:(Ⅰ)记甲、乙两人同时参加A 岗位服务为事件A E ,那么3324541()40A A P E C A ==,即甲、乙两人同时参加A 岗位服务的概率是140. (Ⅱ)记甲、乙两人同时参加同一岗位服务为事件E ,那么4424541()10A P E C A ==,所以,甲、乙两人不在同一岗位服务的概率是9()1()10P E P E =-=. (Ⅲ)随机变量ξ可能取的值为1,2.事件“2ξ=”是指有两人同时参加A 岗位服务,则235334541(2)4C A P C A ξ===.所以3(1)1(2)P P ξξ==-==,ξ的分布列是 18.(共13分)解:242(1)(2)2(1)()(1)x x b x f x x ----'=-3222(1)x b x -+-=- 32[(1)](1)x b x --=--.令()0f x '=,得1x b =-.当11b -<,即2b <时,()f x '的变化情况如下表:当11b ->,即2b >时,()f x '的变化情况如下表:所以,当2b <时,函数()f x 在(1)b -∞-,上单调递减,在(11)b -,上单调递增, 在(1)+∞,上单调递减. 当2b >时,函数()f x 在(1)-∞,上单调递减,在(11)b -,上单调递增,在(1)b -+∞,上单调递减.当11b -=,即2b =时,2()1f x x =-,所以函数()f x 在(1)-∞,上单调递减,在(1)+∞,上单调递减.19.(共14分)解:(Ⅰ)由题意得直线BD 的方程为1y x=+. 因为四边形ABCD 为菱形,所以AC BD ⊥. 于是可设直线AC 的方程为y x n =-+.由2234x y y x n⎧+=⎨=-+⎩,得2246340x nx n -+-=. 因为A C ,在椭圆上,所以212640n ∆=-+>,解得33n -<<.第 11 页 共 12 页设A C ,两点坐标分别为1122()()x y x y ,,,, 则1232n x x +=,212344n x x -=,11y x n =-+,22y x n =-+. 所以122n y y +=. 所以AC 的中点坐标为344n n ⎛⎫ ⎪⎝⎭,. 由四边形ABCD 为菱形可知,点344n n ⎛⎫⎪⎝⎭,在直线1y x =+上, 所以3144n n =+,解得2n =-. 所以直线AC 的方程为2y x =--,即20x y ++=.(Ⅱ)因为四边形ABCD 为菱形,且60ABC ∠=, 所以AB BC CA ==.所以菱形ABCD的面积2S =. 由(Ⅰ)可得22221212316()()2n AC x x y y -+=-+-=,所以2316)S n n ⎛=-+<< ⎝⎭. 所以当0n =时,菱形ABCD的面积取得最大值20.(共13分)(Ⅰ)解:0532A :,,,10()3421T A :,,,, 1210(())4321A T T A =:,,,; 11()43210T A :,,,,,2211(())4321A T T A =:,,,.(Ⅱ)证明:设每项均是正整数的有穷数列A 为12n a a a ,,,, 则1()T A 为n ,11a -,21a -,,1n a -,从而 112(())2[2(1)3(1)(1)(1)]n S T A n a a n a =+-+-+++-222212(1)(1)(1)n n a a a ++-+-++-. 又2221212()2(2)n n S A a a na a a a =+++++++, 所以1(())()S T A S A - 122[23(1)]2()n n n a a a =----+++++2122()n n a a a n +-++++ 2(1)0n n n n =-+++=,故1(())()S T A S A =.(Ⅲ)证明:设A 是每项均为非负整数的数列12n a a a ,,,. 当存在1i j n <≤≤,使得i j a a ≤时,交换数列A 的第i 项与第j 项得到数列B , 则()()2()j i i j S B S A ia ja ia ja -=+--2()()0j i i j a a =--≤. 当存在1m n <≤,使得120m m n a a a ++====时,若记数列12m a a a ,,,为C , 则()()S C S A =.所以2(())()S T A S A ≤.从而对于任意给定的数列0A ,由121(())(012)k k A T T A k +==,,, 可知11()(())k k S A S T A +≤.又由(Ⅱ)可知1(())()k k S T A S A =,所以1()()k k S A S A +≤. 即对于k ∈N ,要么有1()()k k S A S A +=,要么有1()()1k k S A S A +-≤. 因为()k S A 是大于2的整数,所以经过有限步后,必有12()()()k k k S A S A S A ++===. 即存在正整数K ,当k K ≥时,1()()k k S A S A +=.。
2008年北京中考数学试卷解析

2008年北京市高级中等学校招生考试数学试卷答案及评分参考阅卷须知:1.一律用红钢笔或红圆珠笔批阅,按要求签名.2.第Ⅰ卷是选择题,机读阅卷.3.第Ⅱ卷包括填空题和解答题.为了阅卷方便,解答题中的推导步骤写得较为详细,考生只要写明主要过程即可.若考生的解法与本解法不同,正确者可参照评分参考给分.解答右端所注分数,表示考生正确做到这一步应得的累加分数.第Ⅰ卷(机读卷共32分)一、选择题(共8道小题,每小题4分,共32分)题号 1 2 3 4 5 6 7 8 答案ADCCBBBD第Ⅱ卷(非机读卷共88分)二、填空题(共4道小题,每小题4分,共16分)题号9101112答案12x()()a ab a b 4207ba31(1)n nnba三、解答题(共5道小题,共25分)13.(本小题满分5分)解:1182sin 45(2π)32222132··················································································· 4分22. ································································································· 5分14.(本小题满分5分)解:去括号,得51286x x ≤.···································································· 1分移项,得58612x x ≤.··········································································· 2分合并,得36x ≤. ······················································································ 3分系数化为1,得2x ≥.················································································· 4分不等式的解集在数轴上表示如下:················································································································· 5分15.(本小题满分5分)证明:AB ED ∥,B E . ····························································································· 2分在ABC △和CED △中,1 2 30 123AB CE B E BCED ,,,ABC CED △≌△.···················································································· 4分AC CD . ····························································································· 5分16.(本小题满分5分)解:由图象可知,点(21)M ,在直线3y kx 上, ············································· 1分231k .解得2k . ······························································································· 2分直线的解析式为23y x .······································································· 3分令0y,可得32x.直线与x 轴的交点坐标为302,. ······························································ 4分令0x ,可得3y.直线与y 轴的交点坐标为(03),. ······························································· 5分17.(本小题满分5分)解:222()2x y x y xxy y22()()x y x y x y ························································································ 2分2x yxy . ································································································· 3分当30xy时,3x y .·············································································· 4分原式677322y y y yyy.··············································································· 5分四、解答题(共2道小题,共10分)18.(本小题满分5分)解法一:如图1,分别过点A D ,作AEBC 于点E ,DF BC 于点F .······································1分AE DF ∥.又AD BC ∥,四边形AEFD 是矩形.2EF AD .······································2分ABCDFE 图1AB AC ,45B,42BC ,AB AC .1222AEECBC .22DF AE ,2CFECEF···················································································· 4分在Rt DFC △中,90DFC ,2222(22)(2)10DC DFCF. ··········································· 5分解法二:如图2,过点D 作DF AB ∥,分别交AC BC ,于点E F ,.···················· 1分ABAC ,90AEDBAC.AD BC ∥,18045DAEB BAC .在Rt ABC △中,90BAC,45B,42BC,2sin 454242AC BC ································································· 2分在Rt ADE △中,90AED ,45DAE,2AD ,1DEAE .3CE AC AE.·················································································· 4分在Rt DEC △中,90CED,22221310DC DECE.························································· 5分19.(本小题满分5分)解:(1)直线BD 与O 相切. ······································································· 1分证明:如图1,连结OD .OA OD ,A ADO .90C,90CBD CDB .又CBDA ,90ADO CDB .90ODB.直线BD 与O 相切.················································································· 2分DCOABE图1ABCDFE图2(2)解法一:如图1,连结DE .AE 是O 的直径,90ADE .:8:5AD AO ,4cos 5AD A AE . ···················································································· 3分90C,CBD A ,4cos 5BC CBD BD. ············································································· 4分2BC,52BD.······································································ 5分解法二:如图2,过点O 作OH AD 于点H .12AH DHAD .:8:5AD AO ,4cos 5AH A AO . ···················3分90C,CBD A ,4cos 5BC CBD BD. ································4分2BC ,52BD.································································································· 5分五、解答题(本题满分6分)解:(1)补全图1见下图. ············································································· 1分9137226311410546373003100100(个).这100位顾客平均一次购物使用塑料购物袋的平均数为3个.································· 3分200036000.估计这个超市每天需要为顾客提供6000个塑料购物袋. ········································ 4分(2)图2中,使用收费塑料购物袋的人数所占百分比为25%. ······························ 5分根据图表回答正确给1分,例如:由图2和统计表可知,购物时应尽量使用自备袋和押金式环保袋,少用塑料购物袋;塑料购物袋应尽量循环使用,以便减少塑料购物袋的使用量,为环保做贡献.6分D COABH图240 35 30 25 20 15 10 5 0图1123 4 567 4311 26379 塑料袋数/个人数/位“限塑令”实施前,平均一次购物使用不同数量塑料..购物袋的人数统计图10六、解答题(共2道小题,共9分)21.解:设这次试车时,由北京到天津的平均速度是每小时x 千米,则由天津返回北京的平均速度是每小时(40)x千米. ·························································································· 1分依题意,得3061(40)602xx . ··································································· 3分解得200x.······························································································ 4分答:这次试车时,由北京到天津的平均速度是每小时200千米.······························ 5分22.解:(1)重叠三角形A B C 的面积为3. ·················································· 1分(2)用含m 的代数式表示重叠三角形A B C 的面积为23(4)m ; ····················· 2分m 的取值范围为843m ≤.··········································································· 4分七、解答题(本题满分7分)23.(1)证明:2(32)220mxm x m 是关于x 的一元二次方程,222[(32)]4(22)44(2)m m m mm m .当0m时,2(2)0m ,即0.方程有两个不相等的实数根.········································································ 2分(2)解:由求根公式,得(32)(2)2m m xm.22m x m 或1x . ················································································· 3分0m ,222(1)1mm mm.12x x ,11x ,222m x m . ··············································································· 4分21222221m yx x m m.即2(0)ymm 为所求. ·······················5分(3)解:在同一平面直角坐标系中分别画出2(0)y mm与2(0)y m m 的图象.····························································6分由图象可得,当1m ≥时,2y m ≤. ··········7分八、解答题(本题满分7分)24.解:(1)ykx 沿y 轴向上平移3个单位长度后经过y 轴上的点C ,1 2 3 44 3 21xy O -1 -2 -3 -4 -4-3 -2-1 2(0)ymm 2(0)ym m(03)C ,.设直线BC 的解析式为3ykx .(30)B ,在直线BC 上,330k.解得1k.直线BC 的解析式为3yx. ································································· 1分抛物线2y xbx c 过点B C ,,9303b c c,.解得43b c,.抛物线的解析式为243yxx . ······························································ 2分(2)由243y xx .可得(21)(10)D A ,,,.3OB ,3OC ,1OA ,2AB.可得OBC △是等腰直角三角形.45OBC,32CB.如图1,设抛物线对称轴与x 轴交于点F ,112AF AB .过点A 作AEBC 于点E .90AEB.可得2BE AE ,22CE .在AEC △与AFP △中,90AECAFP,ACEAPF ,AEC AFP △∽△.AE CE AFPF,2221PF.解得2PF.点P 在抛物线的对称轴上,点P 的坐标为(22),或(22),. ··································································· 5分1 Oy x2 344 3 2 1-1 -2 -2-1P EBD P ACF 图1(3)解法一:如图2,作点(10)A ,关于y 轴的对称点A ,则(10)A ,.连结A C A D ,,可得10A C AC,OCAOCA .由勾股定理可得220CD,210A D .又210A C,222A DA CCD .A DC △是等腰直角三角形,90CA D,45DCA .45OCA OCD .45OCAOCD.即OCA 与OCD 两角和的度数为45. ························································ 7分解法二:如图3,连结BD .同解法一可得20CD ,10AC.在Rt DBF △中,90DFB,1BFDF,222DB DFBF.在CBD △和COA △中,221DB AO ,3223BC OC,20210CD CA.DBBCCDAO OC CA .CBD COA △∽△.BCD OCA .45OCB ,45OCAOCD.即OCA 与OCD 两角和的度数为45. ························································ 7分九、解答题(本题满分8分)25.解:(1)线段PG 与PC 的位置关系是PG PC ;1 O yx2 3 4 43 2 1-1 -2-1BDA C F 图2A 1 O y x2 3 443 2 1-1 -2 -2-1BDA C F 图3PG PC3.································································································· 2分(2)猜想:(1)中的结论没有发生变化.证明:如图,延长GP 交AD 于点H ,连结CH CG ,.P 是线段DF 的中点,FP DP .由题意可知AD FG ∥.GFP HDP .GPF HPD ,GFP HDP △≌△.GPHP ,GF HD .四边形ABCD 是菱形,CDCB ,60HDC ABC.由60ABC BEF ,且菱形BEFG 的对角线BF 恰好与菱形ABCD 的边AB 在同一条直线上,可得60GBC .HDCGBC .四边形BEFG 是菱形,GF GB .HD GB .HDC GBC △≌△.CH CG ,DCH BCG .120DCHHCB BCGHCB.即120HCG .CH CG ,PH PG ,PG PC ,60GCPHCP.3PG PC.······························································································· 6分(3)PG PCtan(90). ············································································ 8分D CG P ABEFH。
北京市高级中等学校招生统一考试数学试卷及答案2

2008年北京市高级中等学校招生考试数 学 试 卷一、选择题(共8道小题,每小题4分,共32分) 下列各题均有四个选项,其中只有一个..是符合题意的.用铅笔把“机读答题卡”上对应题目答案的相应字母处涂黑. 1.6-的绝对值等于( ) A .6B .16C .16-D .6-2.截止到2008年5月19日,已有21 600名中外记者成为北京奥运会的注册记者,创历届奥运会之最.将21 600用科学记数法表示应为( ) A .50.21610⨯B .321.610⨯C .32.1610⨯D .42.1610⨯3.若两圆的半径分别是1cm 和5cm ,圆心距为6cm ,则这两圆的位置关系是( ) A .内切 B .相交 C .外切 D .外离4.众志成城,抗震救灾.某小组7名同学积极捐出自己的零花钱支援灾区,他们捐款的数额分别是(单位:元):50,20,50,30,50,25,135.这组数据的众数和中位数分别是( ) A .50,20 B .50,30 C .50,50D .135,50 5.若一个多边形的内角和等于720,则这个多边形的边数是( )A .5B .6C .7D .86.如图,有5张形状、大小、质地均相同的卡片,正面分别印有北京奥运会的会徽、吉祥物(福娃)、火炬和奖牌等四种不同的图案,背面完全相同.现将这5张卡片洗匀后正面向下放在桌子上,从中随机抽取一张,抽出的卡片正面图案恰好是吉祥物(福娃)的概率是( )A .15B .25C .12D .357.若20x +=,则xy 的值为( )A .8-B .6-C .5D .68.已知O 为圆锥的顶点,M 为圆锥底面上一点,点P 在OM 上.一只蜗牛从P 点出发,绕圆锥侧面爬行,回到P 点时所爬过的最短路线的痕迹如右图所示.若沿OM 将圆锥侧面剪开并展开,所得侧面展开图是( )2008年北京市高级中等学校招生考试数 学 试 卷二、填空题(共4道小题,每小题4分,共16分) 9.在函数121y x =-中,自变量x 的取值范围是 . 10.分解因式:32a ab -= .11.如图,在ABC △中,D E ,分别是AB AC ,的中点, 若2cm DE =,则BC = cm .12.一组按规律排列的式子:2b a -,53b a ,83b a -,114b a,…(0ab ≠),其中第7个式子是 ,第n 个式子是 (n 为正整数).三、解答题(共5道小题,共25分) 13.(本小题满分5分)1012sin 45(2)3-⎛⎫+-π- ⎪⎝⎭.解:CA E D BOP M OM 'MPA .OM 'MPB .OM 'MPC .OM 'MPD .14.(本小题满分5分)解不等式5122(43)x x --≤,并把它的解集在数轴上表示出来. 解:15.(本小题满分5分) 已知:如图,C 为BE 上一点,点A D ,分别在BE 两侧.AB ED ∥,AB CE =,BC ED =. 求证:AC CD =.证明:16.(本小题满分5分)如图,已知直线3y kx =-经过点M ,求此直线与x 轴,y 轴的交点坐标. 解:17.(本小题满分5分) 已知30x y -=,求222()2x yx y x xy y +--+的值.解:四、解答题(共2道小题,共10分) 18.(本小题满分5分)如图,在梯形ABCD 中,AD BC ∥,AB AC ⊥,45B ∠=,AD =BC =求DC 的长. 解:ACE DB1- 2-y ABCD19.(本小题满分5分)已知:如图,在Rt ABC △中,90C ∠=,点O 在AB 上,以O 为圆心,OA 长为半径的圆与AC AB ,分别交于点D E ,,且CBD A ∠=∠. (1)判断直线BD 与O 的位置关系,并证明你的结论; (2)若:8:5AD AO =,2BC =,求BD 的长. 解:(1)(2)五、解答题(本题满分6分)20.为减少环境污染,自2008年6月1日起,全国的商品零售场所开始实行“塑料购物袋有偿使用制度”(以下简称“限塑令”).某班同学于6月上旬的一天,在某超市门口采用问卷调查的方式,随机调查了“限塑令”实施前后,顾客在该超市用购物袋的情况,以下是根据100位顾客的100份有效答卷画出的统计图表的一部分:请你根据以上信息解答下列问题:(1)补全图1,“限塑令”实施前,如果每天约有2 000人次到该超市购物.根据这100位顾客平均一次购物使用塑料购物袋的平均数,估计这个超市每天需要为顾客提供多少个塑料购物袋?(2)补全图2,并根据统计图和统计表说明...........,购物时怎样选用购物袋,塑料购物袋使用后怎样处理,能对环境保护带来积极的影响. 解:(1)A图1 塑料袋数/个 “限塑令”实施前,平均一次购物使用不同数量塑料..购物袋的人数统计图 “限塑令”实施后,使用各种 购物袋的人数分布统计图 其它% 46%24%(2)六、解答题(共2道小题,共9分)21.(本小题满分5分)列方程或方程组解应用题:京津城际铁路将于2008年8月1日开通运营,预计高速列车在北京、天津间单程直达运行时间为半小时.某次试车时,试验列车由北京到天津的行驶时间比预计时间多用了6分钟,由天津返回北京的行驶时间与预计时间相同.如果这次试车时,由天津返回北京比去天津时平均每小时多行驶40千米,那么这次试车时由北京到天津的平均速度是每小时多少千米? 解:22.(本小题满分4分)已知等边三角形纸片ABC 的边长为8,D 为AB 边上的点,过点D 作DG BC ∥交AC 于点G .DE BC ⊥于点E ,过点G 作GF BC ⊥于点F ,把三角形纸片ABC 分别沿DG DE GF ,,按图1所示方式折叠,点A B C ,,分别落在点A ',B ',C '处.若点A ',B ',C '在矩形DEFG 内或其边上,且互不重合,此时我们称A B C '''△(即图中阴影部分)为“重叠三角形”.(1)若把三角形纸片ABC 放在等边三角形网格中(图中每个小三角形都是边长为1的等边三角形),点A B C D ,,,恰好落在网格图中的格点上.如图2所示,请直接写出此时重叠三角形A B C '''的面积;(2)实验探究:设AD 的长为m ,若重叠三角形A B C '''存在.试用含m 的代数式表示重叠三角形A B C '''的面积,并写出m 的取值范围(直接写出结果,备用图供实验,探究使用).解:(1)重叠三角形A B C '''的面积为 ;(2)用含m 的代数式表示重叠三角形A B C '''的面积为 ;m 的取值范围为 .F B ' C ' E B 图1图2 A C B 备用图 A C B备用图七、解答题(本题满分7分)23.已知:关于x 的一元二次方程2(32)220(0)mx m x m m -+++=>. (1)求证:方程有两个不相等的实数根;(2)设方程的两个实数根分别为1x ,2x (其中12x x <).若y 是关于m 的函数,且212y x x =-,求这个函数的解析式;(3)在(2)的条件下,结合函数的图象回答:当自变量m 的取值范围满足什么条件时,2y m ≤.(1)证明:(2)解:(3)解:八、解答题(本题满分7分)24.在平面直角坐标系xOy 中,抛物线2y x bx c =++与x 轴交于A B ,两点(点A 在点B的左侧),与y 轴交于点C ,点B 的坐标为(30),,将直线y kx =沿y 轴向上平移3个单位长度后恰好经过B C ,两点.(1)求直线BC 及抛物线的解析式;(2)设抛物线的顶点为D ,点P 在抛物线的对称轴上,且APD ACB ∠=∠,求点P 的坐标;(3)连结CD ,求OCA ∠与OCD ∠两角和的度数.解:(1)(2)x(3)九、解答题(本题满分8分) 25.请阅读下列材料: 问题:如图1,在菱形ABCD 和菱形BEFG 中,点A B E ,,在同一条直线上,P 是线段DF 的中点,连结PG PC ,.若60ABC BEF ∠=∠=,探究PG 与PC 的位置关系及PGPC的值.小聪同学的思路是:延长GP 交DC 于点H ,构造全等三角形,经过推理使问题得到解决.请你参考小聪同学的思路,探究并解决下列问题:(1)写出上面问题中线段PG 与PC 的位置关系及PGPC的值; (2)将图1中的菱形BEFG 绕点B 顺时针旋转,使菱形BEFG 的对角线BF 恰好与菱形ABCD 的边AB 在同一条直线上,原问题中的其他条件不变(如图2).你在(1)中得到的两个结论是否发生变化?写出你的猜想并加以证明.(3)若图1中2(090)ABC BEF αα∠=∠=<<,将菱形BEFG 绕点B 顺时针旋转任意角度,原问题中的其他条件不变,请你直接写出PGPC 的值(用含α的式子表示). 解:(1)线段PG 与PC 的位置关系是 ;PGPC= .(2)D A BE F C P G 图1 D C G PA B E F图22008年北京市高级中等学校招生考试数学试卷答案及评分参考阅卷须知:1.一律用红钢笔或红圆珠笔批阅,按要求签名.2.第Ⅰ卷是选择题,机读阅卷.3.第Ⅱ卷包括填空题和解答题.为了阅卷方便,解答题中的推导步骤写得较为详细,考生只要写明主要过程即可.若考生的解法与本解法不同,正确者可参照评分参考给分.解答右端所注分数,表示考生正确做到这一步应得的累加分数.第Ⅰ卷(机读卷共32分)第Ⅱ卷(非机读卷共88分)三、解答题(共5道小题,共25分)13.(本小题满分5分)112sin45(2π)3-⎛⎫+-- ⎪⎝⎭2132=⨯+-····················································································4分2 =.···································································································5分14.(本小题满分5分)解:去括号,得51286x x--≤. ····································································1分移项,得58612x x--+≤. ···········································································2分合并,得36x-≤. ·······················································································3分系数化为1,得2x-≥. ·················································································4分···················································································································5分15.(本小题满分5分)证明:AB ED ∥,B E ∴∠=∠. ······························································································· 2分 在ABC △和CED △中,AB CE B E BC ED =⎧⎪∠=∠⎨⎪=⎩,,, ABC CED ∴△≌△. ···················································································· 4分 AC CD ∴=. ······························································································· 5分 16.(本小题满分5分)解:由图象可知,点(21)M -,在直线3y kx =-上, ·············································· 1分 231k ∴--=.解得2k =-.································································································ 2分∴直线的解析式为23y x =--. ······································································· 3分令0y =,可得32x =-. ∴直线与x 轴的交点坐标为302⎛⎫- ⎪⎝⎭,. ······························································· 4分令0x =,可得3y =-.∴直线与y 轴的交点坐标为(03)-,. ································································· 5分17.(本小题满分5分) 解:222()2x yx y x xy y+--+ 22()()x yx y x y +=-- ························································································· 2分2x yx y+=-. ··································································································· 3分 当30x y -=时,3x y =. ·············································································· 4分原式677322y y y y y y +===-. ··············································································· 5分四、解答题(共2道小题,共10分) 18.(本小题满分5分) 解法一:如图1,分别过点A D ,作AE BC ⊥于点E ,DF BC ⊥于点F . ····································· 1分 ∴AE DF ∥. 又AD BC ∥,∴四边形AEFD 是矩形.EF AD ∴== ····································· 2分AB AC ⊥,45B ∠=,BC = AB AC ∴=.12AE EC BC ∴===DF AE ∴==CF EC EF =-=···················································································· 4分在Rt DFC △中,90DFC ∠=,DC ∴=== ············································· 5分 解法二:如图2,过点D 作DF AB ∥,分别交AC BC ,于点E F ,. ···················· 1分 AB AC ⊥,90AED BAC ∴∠=∠=.AD BC ∥,18045DAE B BAC ∴∠=-∠-∠=.在Rt ABC △中,90BAC ∠=,45B ∠=,BC =sin 45424AC BC ∴=== ································································· 2分 在Rt ADE △中,90AED ∠=,45DAE ∠=,AD =1DE AE ∴==.3CE AC AE ∴=-=. ·················································································· 4分 在Rt DEC △中,90CED ∠=,DC ∴===. ························································· 5分 19. (本小题满分5分)解:(1)直线BD 与O 相切. ······································································· 1分 证明:如图1,连结OD . OA OD =, A ADO ∴∠=∠.ABCDFE图2A BCDFE 图190C ∠=, 90CBD CDB ∴∠+∠=.又CBD A ∠=∠,90ADO CDB ∴∠+∠=. 90ODB ∴∠=.∴直线BD 与O 相切. ················································································· 2分 (2)解法一:如图1,连结DE .AE 是O 的直径, 90ADE ∴∠=.:8:5AD AO =,4cos 5AD A AE ∴==. ······················································································ 3分 90C ∠=,CBD A ∠=∠,4cos 5BC CBD BD ∴∠==. ··············································································· 4分 2BC =, 52BD ∴=. ······································································ 5分 解法二:如图2,过点O 作OH AD ⊥于点H . 12AH DH AD ∴==.:8:5AD AO =,4cos 5AH A AO ∴==. ··················· 3分 90C ∠=,CBD A ∠=∠,4cos 5BC CBD BD ∴∠==. ································· 4分 2BC =,52BD ∴=. ································································································· 5分 五、解答题(本题满分6分) 解:(1)补全图1见下图. ············································································· 1分AA图1塑料袋数/个“限塑令”实施前,平均一次购物使用不同数量塑料..购物袋的人数统计图9137226311410546373003100100⨯+⨯+⨯+⨯+⨯+⨯+⨯==(个).这100位顾客平均一次购物使用塑料购物袋的平均数为3个. ································· 3分200036000⨯=.估计这个超市每天需要为顾客提供6000个塑料购物袋. ········································· 4分 (2)图2中,使用收费塑料购物袋的人数所占百分比为25%. ······························· 5分 根据图表回答正确给1分,例如:由图2和统计表可知,购物时应尽量使用自备袋和押金式环保袋,少用塑料购物袋;塑料购物袋应尽量循环使用,以便减少塑料购物袋的使用量,为环保做贡献. ································································································· 6分 六、解答题(共2道小题,共9分)21.解:设这次试车时,由北京到天津的平均速度是每小时x 千米,则由天津返回北京的平均速度是每小时(40)x +千米. ········································································· 1分依题意,得3061(40)602x x +=+. ···································································· 3分 解得200x =. ······························································································ 4分答:这次试车时,由北京到天津的平均速度是每小时200千米. ······························ 5分22.解:(1)重叠三角形A B C '''. ················································· 1分(2)用含m 的代数式表示重叠三角形A B C '''2)m -; ······················· 2分m 的取值范围为843m <≤. ··········································································· 4分七、解答题(本题满分7分) 23.(1)证明:2(32)220mx m x m -+++=是关于x 的一元二次方程,222[(32)]4(22)44(2)m m m m m m ∴∆=-+-+=++=+.当0m >时,2(2)0m +>,即0∆>.∴方程有两个不相等的实数根. ········································································ 2分(2)解:由求根公式,得(32)(2)2m m x m+±+=.22m x m +∴=或1x =. ·················································································· 3分 0m >,222(1)1m m m m++∴=>.12x x <,11x ∴=,222m x m +=. ················································································ 4分 21222221m y x x m m+∴=-=-⨯=.。
2008年普通高等学校招生全国统一考试数学(北京卷·文科)(附答案,完全word版)

2008年普通高等学校招生全国统一考试数学(文史类)(北京卷)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,第Ⅰ卷1至2页,第Ⅱ卷3至9页,共150分.考试时间120分钟.考试结束,将本试卷和答题卡一并交回.第Ⅰ卷(选择题 共40分)注意事项: 1.答第Ⅰ卷前,考生务必将自己的姓名、准考证号、考试科目涂写在答题卡上. 2.每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其他答案.不能答在试卷上.一、本大题共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项.1.若集合{|23}A x x =-≤≤,{|14}B x x x =<->或,则集合A B 等于( )A .{}|34x x x >或≤ B .{}|13x x -<≤ C .{}|34x x <≤D .{}|21x x --<≤2.若372log πlog 6log 0.8a b c ===,,,则( ) A .a b c >>B .b a c >>C .c a b >>D .b c a >>3.“双曲线的方程为221916x y -=”是“双曲线的准线方程为95x =±”的( ) A .充分而不必要条件B .必要而不充分条件C .充分必要条件D .既不充分也不必要条件4.已知ABC △中,a =b =60B =,那么角A 等于( )A .135B .90C .45D .305.函数2()(1)1(1)f x x x =-+<的反函数为( )A .1()11)fx x -=>B .1()11)fx x -=>C .1()11)f x x -=+≥D .1()11)f x x -=-≥6.若实数x y ,满足1000x y x y x ⎧-+⎪+⎨⎪⎩,,,≥≥≤则2z x y =+的最小值是( )A .0B .12C .1D .27.已知等差数列{}n a 中,26a =,515a =,若2n n b a =,则数列{}n b 的前5项和等于( ) A .30B .45C .90D .1868.如图,动点P 在正方体1111ABCD A B C D -的对角线1BD 上,过点P 作垂直于平面11BB D D 的直线,与正方体表面相交于M N ,.设B P x =,MN y =,则函数()y f x =的图象大致是( )A BC DMNP A 1B 1C 1D 12008年普通高等学校招生全国统一考试数学(文史类)(北京卷)第Ⅱ卷(共110分)注意事项:1.用钢笔或圆珠笔将答案直接写在试卷上.2.答卷前将密封线内的项目填写清楚.二、填空题:本大题共6小题,每小题5分,共30分.把答案填在题中横线上. 9.若角α的终边经过点(12)P -,,则tan 2α的值为 . 10.不等式112x x ->+的解集是 . 11.已知向量a 与b 的夹角为120,且4==a b ,那么a b 的值为 .12.5231x x ⎛⎫+ ⎪⎝⎭的展开式中常数项为 ;各项系数之和为 .(用数字作答)13.如图,函数()f x 的图象是折线段ABC ,其中A B C ,,的坐标分别为(04)(20)(64),,,,,,则((0))f f = ;函数()f x 在1x =处的导数(1)f '= .14.已知函数2()cos f x x x =-,对于ππ22⎡⎤-⎢⎥⎣⎦,上的任意12x x ,,有如下条件:①12x x >; ②2212x x >; ③12x x >.其中能使12()()f x f x >恒成立的条件序号是 .三、解答题:本大题共6小题,共80分.解答应写出文字说明,演算步骤或证明过程.15.(本小题共13分)已知函数2π()sin sin 2f x x x x ωωω⎛⎫=+ ⎪⎝⎭(0ω>)的最小正周期为π. (Ⅰ)求ω的值;(Ⅱ)求函数()f x 在区间2π03⎡⎤⎢⎥⎣⎦,上的取值范围.16.(本小题共14分)如图,在三棱锥P ABC -中,2AC BC ==,90ACB ∠=,AP BP AB ==,PC AC ⊥. (Ⅰ)求证:PC AB ⊥;(Ⅱ)求二面角B AP C --的大小. 17.(本小题共13分)已知函数32()3(0)f x x ax bx c b =+++≠,且()()2g x f x =-是奇函数. (Ⅰ)求a ,c 的值;(Ⅱ)求函数()f x 的单调区间.18.(本小题共13分)甲、乙等五名奥运志愿者被随机地分到A B C D ,,,四个不同的岗位服务,每个岗位至少有一名志愿者.(Ⅰ)求甲、乙两人同时参加A 岗位服务的概率; (Ⅱ)求甲、乙两人不在同一个岗位服务的概率. 19.(本小题共14分) 已知ABC △的顶点A B ,在椭圆2234x y +=上,C 在直线2l y x =+:上,且AB l ∥. (Ⅰ)当AB 边通过坐标原点O 时,求AB 的长及ABC △的面积; (Ⅱ)当90ABC ∠=,且斜边AC 的长最大时,求AB 所在直线的方程. 20.(本小题共13分)数列{}n a 满足11a =,21()n n a n n a λ+=+-(12n =,,),λ是常数. (Ⅰ)当21a =-时,求λ及3a 的值;(Ⅱ)数列{}n a 是否可能为等差数列?若可能,求出它的通项公式;若不可能,说明理由; (Ⅲ)求λ的取值范围,使得存在正整数m ,当n m >时总有0n a <.ACBP2008年普通高等学校招生全国统一考试数学(文史类)(北京卷)参考答案一、选择题(本大题共8小题,每小题5分,共40分)1.D 2.A 3.A 4.C 5.B 6.A 7.C 8.B二、填空题(本大题共6小题,每小题5分,共30分)9.4310.{}|2x x <-11.8-12.10 3213.2 2-14.②三、解答题(本大题共6小题,共80分) 15.(共13分) 解:(Ⅰ)1cos 2()22x f x x ωω-=11sin 2cos 2222x x ωω=-+π1sin 262x ω⎛⎫=-+ ⎪⎝⎭. 因为函数()f x 的最小正周期为π,且0ω>, 所以2ππ2ω=,解得1ω=. (Ⅱ)由(Ⅰ)得π1()sin 262f x x ⎛⎫=-+ ⎪⎝⎭. 因为2π03x ≤≤, 所以ππ7π2666x --≤≤,所以1πsin 2126x ⎛⎫-- ⎪⎝⎭≤≤. 因此π130sin 2622x ⎛⎫-+ ⎪⎝⎭≤≤,即()f x 的取值范围为302⎡⎤⎢⎥⎣⎦,. 16.(共14分)解法一:(Ⅰ)取AB 中点D ,连结PD CD ,. AP BP =, PD AB ∴⊥. AC BC =, CD AB ∴⊥. PD CD D =,ACBDPAB ∴⊥平面PCD . PC ⊂平面PCD , PC AB ∴⊥.(Ⅱ)AC BC =,AP BP =, APC BPC ∴△≌△. 又PC AC ⊥, PC BC ∴⊥.又90ACB ∠=,即AC BC ⊥,且ACPC C =,BC ∴⊥平面PAC .取AP 中点E .连结BE CE ,. AB BP =,BE AP ∴⊥.EC 是BE 在平面PAC 内的射影, CE AP ∴⊥.BEC ∴∠是二面角B AP C --的平面角.在BCE △中,90BCE ∠=,2BC =,BE AB ==sin 3BC BEC BE ∴∠==. ∴二面角B AP C --的大小为arcsin3. 解法二:(Ⅰ)AC BC =,AP BP =, APC BPC ∴△≌△. 又PC AC ⊥, PC BC ∴⊥. AC BC C =,PC ∴⊥平面ABC . AB ⊂平面ABC , PC AB ∴⊥.(Ⅱ)如图,以C 为原点建立空间直角坐标系C xyz -.则(000)(020)(200)C A B ,,,,,,,,. 设(00)P t ,,.PB AB ==,2t ∴=,(002)P ,,. ACBEPy取AP 中点E ,连结BE CE ,.AC PC =,AB BP =,CE AP ∴⊥,BE AP ⊥.BEC ∴∠是二面角B AP C --的平面角.(011)E ,,,(011)EC =--,,,(211)EB =--,,,cos 26EC EB BEC EC EB∴∠===. ∴二面角B AP C --的大小为arccos17.(共13分)解:(Ⅰ)因为函数()()2g x f x =-为奇函数,所以,对任意的x ∈R ,()()g x g x -=-,即()2()2f x f x --=-+. 又32()3f x x ax bx c =+++所以32323232x ax bx c x ax bx c -+-+-=----+. 所以22a a c c =-⎧⎨-=-+⎩,.解得02a c ==,.(Ⅱ)由(Ⅰ)得3()32f x x bx =++.所以2()33(0)f x x b b '=+≠.当0b <时,由()0f x '=得x =x 变化时,()f x '的变化情况如下表:所以,当0b <时,函数()f x 在(-∞,上单调递增,在(上单调递减,在)+∞上单调递增.当0b >时,()0f x '>,所以函数()f x 在()-∞+∞,上单调递增. 18.(共13分)解:(Ⅰ)记甲、乙两人同时参加A 岗位服务为事件A E ,那么3324541()40A A P E C A ==,即甲、乙两人同时参加A 岗位服务的概率是140. (Ⅱ)设甲、乙两人同时参加同一岗位服务为事件E ,那么4424541()10A P E C A ==,所以,甲、乙两人不在同一岗位服务的概率是9()1()10P E P E =-=. 19.(共14分)解:(Ⅰ)因为AB l ∥,且AB 边通过点(00),,所以AB 所在直线的方程为y x =.设A B ,两点坐标分别为1122()()x y x y ,,,. 由2234x y y x⎧+=⎨=⎩,得1x =±.所以12AB x =-=.又因为AB 边上的高h 等于原点到直线l 的距离.所以h =122ABC S AB h ==△. (Ⅱ)设AB 所在直线的方程为y x m =+,由2234x y y x m⎧+=⎨=+⎩,得2246340x mx m ++-=. 因为A B ,在椭圆上, 所以212640m ∆=-+>.设A B ,两点坐标分别为1122()()x y x y ,,,, 则1232mx x +=-,212344m x x -=,所以12AB x =-=.又因为BC 的长等于点(0)m ,到直线l 的距离,即BC =所以22222210(1)11AC AB BC m m m =+=--+=-++. 所以当1m =-时,AC 边最长,(这时12640∆=-+>) 此时AB 所在直线的方程为1y x =-. 20.(共13分)解:(Ⅰ)由于21()(12)n n a n n a n λ+=+-=,,,且11a =. 所以当21a =-时,得12λ-=-, 故3λ=.从而23(223)(1)3a =+-⨯-=-.(Ⅱ)数列{}n a 不可能为等差数列,证明如下:由11a =,21()n n a n n a λ+=+-得22a λ=-,3(6)(2)a λλ=--,4(12)(6)(2)a λλλ=---.若存在λ,使{}n a 为等差数列,则3221a a a a -=-,即(5)(2)1λλλ--=-, 解得3λ=.于是2112a a λ-=-=-,43(11)(6)(2)24a a λλλ-=---=-. 这与{}n a 为等差数列矛盾.所以,对任意λ,{}n a 都不可能是等差数列.(Ⅲ)记2(12)n b n n n λ=+-=,,,根据题意可知,10b <且0n b ≠,即2λ>且2*()n n n λ≠+∈N ,这时总存在*0n ∈N ,满足:当0n n ≥时,0n b >;当01n n -≤时,0n b <.所以由1n n n a b a +=及110a =>可知,若0n 为偶数,则00n a <,从而当0n n >时,0n a <;若0n 为奇数,则00n a >,从而当0n n >时0n a >.因此“存在*m ∈N ,当n m >时总有0n a <”的充分必要条件是:0n 为偶数,记02(12)n k k ==,,,则λ满足22221(2)20(21)210k k b k k b k k λλ-⎧=+->⎪⎨=-+--<⎪⎩. 故λ的取值范围是22*4242()k k k k k λ-<<+∈N .。
2008年普通高等学校招生全国统一考试数学理试题(北京卷)(含答案)

绝密★使用完毕前2008年普通高等学校校招生全国统一考试数学(理工农医类)(北京卷)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,第Ⅰ卷1至2页,第Ⅱ卷3至9页,共150分。
考试时间120分钟。
考试结束,将本试卷和答题卡一并交回。
第Ⅰ卷(选择题 共40分) 注意事项:1答第Ⅰ卷前,考生务必将自己的姓名、准考证号、考试科目涂写在答题卡上。
2.每小题选出答案后,用钢笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案。
不能答在试卷上。
一、本题共8小题。
每小题5分,共40分。
在每小题列出的四个选项中,选出符合题目要求的一项。
(1)已知全集∪=R ,集合A =|x |-2≤x ≤3|,B =|x |x 〈-1或x 〉4|,那么集合A ∩(εv B )等于 (A)|x |-2≤x 〈4| (B )|x |x ≤3或≥4| (C)|x |-2≤x <-1 (D)|x | -1≤x ≤3| (2)若a =2a ,b =log,3,c =log,sin52,则 (A )a >b >c (B)b >a >c (C)c>a>b (D)b >c>a(3)“函数f (x )(x ∈R)存在反函数”是“函数f (x )在R 上为增函数”的 (A)充分而不必要条件 (B )必要而不充分条件 (C)充分必要条件 (D )即不充分也不必要条件(4)若点P 到直线x =-1的距离比它到点(2,0)的烛1,则点P 的轨迹为 (A )圆 (B )椭圆 (C )双曲线 (D )抛物线x -y +1≥0,(5)若实数x ,y 满足 x +y ≥0, 则z =3x +y 的最小值是x ≤0, (A)0(B)1(C)3(D)9(6)已知数列|a n |对任意的p,q ∈N m 满足a p+q =a p +a q ,且a P =-6,那么a p +q 等于 (A )-165 (B)-33 (C)-30 (D)-21(7)过直线y =x 上的一点作圆(x -5)2=2的两条切线l 1,l 2,当直线l 1,l 2关于y =x 对称时,综们之间的夹角为 (A )30° (B )45° (C)60° (D)90° (8)如图,动点P 在正方体ABCD -A 1B 1C 1D 1的对角线BD 1上。
(精编精校)2008年普通高等学校招生全国统一考试(北京卷) 理科数学 解析版

2008年高考北京理科数学详解一、本大题共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项. 1.已知全集U =R ,集合{}|23A x x =-≤≤,{}|14B x x x =<->或,那么集合()UA B 等于( )A .{}|24x x -<≤ B .{}|34x x x 或≤≥ C .{}|21x x -<-≤ D .{}|13x x -≤≤【标准答案】: D【试题分析】: C U B=[-1, 4],()UA B ={}|13x x -≤≤【高考考点】:集合 【易错提醒】: 补集求错 【备考提示】: 高考基本得分点 2.若0.52a =,πlog 3b =,22πlog sin 5c =,则( ) A .a b c >> B .b a c >>C .c a b >>D .b c a >>【标准答案】: A【试题分析】:利用估值法知a 大于1,b 在0与1之间,c 小于0. 【高考考点】: 函数的映射关系,函数的图像。
【易错提醒】: 估值出现错误。
【备考提示】: 大小比较也是高考较常见的题型,希望引起注意。
3.“函数()()f x x ∈R 存在反函数”是“函数()f x 在R 上为增函数”的( ) A .充分而不必要条件 B .必要而不充分条件 C .充分必要条件D .既不充分也不必要条件【标准答案】: B【试题分析】: 函数()()f x x ∈R 存在反函数,至少还有可能函数()f x 在R 上为减函数,充分条件不成立;而必有条件显然成立。
【高考考点】: 充要条件,反函数,映射关系,函数单调性。
【易错提醒】: 单调性与一一对应之间的关系不清楚 【备考提示】: 平时注意数形结合训练。
4.若点P 到直线1x =-的距离比它到点(20),的距离小1,则点P 的轨迹为( ) A .圆B .椭圆C .双曲线D .抛物线【标准答案】: D【试题分析】: 把P 到直线1x =-向左平移一个单位,两个距离就相等了,它就是抛物线的定义。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1 北京市2008年高级中等学校招生考试1.A 【解析】|-6|=-(-6)=6.本题考查了绝对值的意义,求一个数的绝对值要注意它的非负性,一个负数的绝对值是它的相反数,所以-6的绝对值等于6.学生易混淆倒数、相反数和绝对值的概念,错误地认为-6的绝对值等于61,而误选B .2.D 【解析】4102.16600 21⨯=.本题考查的是科学记数法的概念.对于较大数用科学记数法表示时,n 10a ⨯ (n 为整数)中的a 必须满足1≤|a|<10,n 应为整数位数减1.如果学生忽视a 的条件,或把n 10a ⨯中的a 错记为0<|a|<1了,就会误选A .3.C 【解析】由题意可知圆心距d=R +r ,所以两圆外切.本题考查的是利用数量关系判断两圆的位置关系.两圆的位置关系一共有五种(外离、外切、相交、内切、内含),判断两圆的位置关系可由圆心距d 与两圆半径R 、r(R >r)间的数量关系来确定.学生经常把内切d=R -r 与外切d=R +r 之间的数量关系记混,故此题易误选A .4.C 【解析】众数是一组数据中出现次数最多的数,在这一组数据中50是出现次数最多的,故众数是50,从而排除了选项D ;而将这组数据从小到大的顺序排列后,处于中间位置的那个数是50,那么由中位数的定义可知,这组数据的中位数是50,所以应选C .本题为统计题,考查众数与中位数的意义.中位数是将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(或最中间两个数的平均数),叫做这组数据的中位数.如果中位数的概念掌握得不好,不把数据按要求重新排列,就会错误地将这组数据最中间的那个数30当作中位数,因而误选B .5.B 【解析】利用多边形内角和公式:(n -2)×180°=720°,解得n=6.所以这个多边形是六边形.本题考查的是多边形的有关性质—多边形的内角和.本题是基础题,但由于有些学生对此公式没有记熟,故误选了A 或D .其实如果公式不熟,可以利用“多边形的边数每增加一条,内角和就增加180°”这一特性,由三角形内角和是180°,依次递推,也可以求出这个多边形的边数.6.B 【解析】因为5张卡片中,吉祥物卡片只有两张,因此抽出的卡片正面图案恰好是吉祥物(福娃)的概率52P =.本题是以奥运为载体,考查等可能事件的概率,题目简单明了,利用公式n m P(A)=,可直接求得. 7.B 【解析】因为03-y ,0|2x |≥≥+,由03-y | 2x |=++,可以得到x +2=0,y -3=0.所以x=-2,y=3.所以xy=(-2)×3=-6.本题考查的是代数式的非负性,一元一次方程的解法及代数式的求值.题目注重基础比较简单.8.D 【解析】蜗牛绕圆锥侧面爬行的最短路线应该是一条线段,因此选项A 和B 错误.又因为蜗牛从P 点出发,绕圆锥侧面爬行后,又回到起始点P 处,那么如果将选项C 、D 的圆锥侧面展开图还原成圆锥后,位于母线OM 上的点P 应该能够与母线OM′上的点(P′)重合,而选项C 还原后两个点不能够重合,故只有选项D 正确.本题结合圆锥侧面展开图的有关知识,把立体图形问题转化为平面图形问题来解决,它考查了“两点之间线段最短”的特性与空间想象能力和转化的数学思想方法.题目属中档题.9.21x ≠【解析】因为1x 21-是分式,根据分式的意义可知,分母2x -1不能为0,由2x -1≠0得21x ≠.本题属于基础题,它考查的是函数自变量的取值范围,分式的概念.有的学生审题不认真,把函数1x 21y -=误认为2x -1≥0,因此将答案错写成21x ≥. 10.a(a +b)(a -b)【解析】多项式23b a -a 只有两项,可以考虑两种方法,提公因式法和平方差公式,观察题目可知此题这两种方法均要用到,即首先提取公因式,然后再用平方差公式.所以b)-b)(a a(a )b -a(a ab -a 2223+==.本题考查的是因式分解的概念,用提取公因式法和运用公式法进行因式分解,还考查了乘法公式.题目设置注重基础,同时考查了学生思维的严密性和认真程度.学生常犯的错误是将多项式只分解到)b -a(a 22就不再分解了,没有分解完.在填空题中,如果将一个多项式进行因式分解,没有分解完,是不会给分的,所以遇到这种题目,一定要仔细观察,所给的多项式是否还能分解,一定要分解到再也不能分解为止.11.4 【解析】由题意可知,DE 是△ABC 的中位线,不仅有DE ∥BC ,而且有DE=21BC .所以BC=2DE=2×2=4.本题考查了三角形中位线的性质,比较简单.如果三角形中位线的性质没有记住,还可以利用△ADE 与△ABC 的相似比为1∶2,得出正确结论.12.720ab - n 1n 3n a b )1(--【解析】观察给出的一列数,发现这一列数的分母a 的指数分别是1,2,3,4,…,与这列数的项数相同,故第7个式子的分母是7a ,第n 个式子的分母是n a ;这一列数的分子b 的指数分别是2,5,8,11,…,即第一个数是3×1-1=2,第二个数是3×2-1=5,第三个数是3×3-1=8,第四个数是3×4-1=11,…,每个数都比项数的3倍少1,故第7个式子的分子是201-73b b =⨯,第n 个式子的分子是1-3n b ;特别要注意的是这列数字每一项的符号,它们的规律是奇数项为负,偶数项为正,故第7个式子的符号为负,第n 个式子的符号为n 1)-(.这是一道规律探索型问题,考查学生分析数字、观察规律的探究能力及归纳猜想能力.此题设计了两个空,这两个空的探索充分的体现了由“特殊”到“一般”的思维过程,第一个空只要读懂题目都能回答正确,而第二个空的符号是个难点,若不认真观察,将其结果写成n 13n ab -±,分不清奇偶项为正还是为负,就错了.13.解:1-0)31-()π-(22sin45-8 +︒ 223122222-=-+⨯-=. 【解析】本题是一道常见的且难度不大的代数基础题,主要考查了二次根式的化简、特殊角的锐角三角函数值、零指数的意义、负整数指数幂的概念等有关知识和实数的有关运算,是对学生基本概念和基本技能的一种考查.14.解:去括号,得5x -12≤8x -6.移项,得5x -8x≤-6+12.合并,得-3x≤6.系数化为1,得x≥-2.不等式的解集在数轴上表示如下:【解析】本题考查的是一元一次不等式的解法及其解集的数轴表示.学生在去括号时易出现漏乘-3项、移项时不变号、合并时的计算错误,系数化1同除以-3时,不等号没改变方向及在数轴上表示解集时,画成空心圆圈的错误.本题属于容易题,是对学生基本技能(运算方法、运算法则、基本性质的运用)的一种考查.15.证明:∵AB ∥ED ,∴∠B=∠E .在△ABC 和△CED 中,,⎪⎩⎪⎨⎧=∠=∠=ED ,BC ,E B ,CE AB∴△ABC ≌△CED .∴AC=CD .【解析】这是一道简单的几何题,此题主要考查了平行线的性质,全等三角形的性质与判定,简单的推理论证能力,题目设置注重基础,没有设坎儿.学生易犯的错误有:(1)全等的符号与相似的符号混淆,将“≌”写成“∽”;(2)推理过程跳跃性较大,没有“∵AB ∥ED ,∴∠B=∠E”,这一步,而直接运用∠B=∠E 这个条件.16.解:由图象可知,点M(-2,1)在直线y=kx -3上,∴-2k -3=1.解得k=-2.∴直线的解析式为y=-2x -3.令y=0,可得23-x =. ∴直线与x 轴的交点坐标为0),23-(. 令x=0,可得y=-3.∴直线与y 轴的交点坐标为(0,-3).【解析】本题考查的是从图形中获取信息的能力,一次函数的图象和性质,运用待定系数法求一次函数的解析式,由解析式求函数图象与两坐标轴的交点坐标的函数基本知识与基本技能,体现了数形结合的数学思想方法.解题方法比较简捷.学生在做此题时,易出现在求函数图象与两坐标轴的交点坐标时,横纵坐标究竟谁为0的混乱思维.由于x 轴上的点纵坐标为0,因此在求函数图象与x 轴的交点坐标时,应该先令y=0,之后解关于x 的方程即可.17.解:22y xy 2x y x 2+-+·(x -y) =2)y x (y x 2-+·(x -y)= y x y x 2-+. 当x -3y=0时,x=3y .原式=27y 2y 7y y 3y y 6==-+. 【解析】本题在求解过程中运用了整体代入求值的策略.由于此题不能直接求出x 与y 的值,所以需要先将x -3y=0整理为x=3y 之后再整体代入.它可以按照上面的方法先将原式化简后代入求值;也可以将x=3y 直接带入原式进行化简求值.有些学生由于不会整体代入,因此只做到将原式化简,求值就做不下去了.18.解法一:如图1,分别过点A 、D 作AE ⊥BC 于点E ,DF ⊥BC 于点F .∴AE ∥DF .又AD ∥BC ,∴四边形AEFD 是矩形.∴EF=AD=2.∵AB ⊥AC ,∠B=45°,BC=24,∴AB=AC .∴.22BC 21EC AE === ∴22AE DF ==,2EF =-EC CF =.在Rt △DFC 中,∠DFC=90°,∴10)2()2(2CF DF DC 2222=+=+=.解法二:如图2,过点D 作DF ∥AB ,分别交AC 、BC 于点E 、F .∵AB ⊥AC ,∴∠AED=∠BAC=90°.∵AD ∥BC ,∴∠DAE=180°-∠B -∠BAC=45°.在Rt △ABC 中,∠BAC=90°,∠B=45°,24BC =,∴ 4.2224sin45BC AC =⨯=︒=⋅ 在Rt △ADE 中,∠AED=90°,∠DAE=45°,2AD =,∴DE=AE=1. ∴CE=AC -AE=3.在Rt △DEC 中,∠CED=90°,∴.10 31CE DE DC 2222=+=+=【解析】此题需要添加适当的辅助线,构造特殊的三角形,然后运用勾股定理求出结论.下面又给了四种添加辅助线的不同方法(如:图1,图2,图3,图4),说明此题的解法还有很多.此题考查了特殊四边形的有关知识(梯形、矩形等),梯形中常见的辅助线的做法,锐角三角函数和勾股定理等知识.学生在辅助线的添加与叙述时,经常犯同时满足多个条件的错误,如:解法二中的辅助线,常常会出现“过点D 作DF ∥AB ,使DF ⊥AC”等的错误.另外此题需要用二次根式的运算解决问题,由于学生二次根式的计算不熟练,因此会出现方法正确,计算结果错误的现象.19.解:(1)直线BD 与⊙O 相切.证明:如图1,连接OD .∵OA=OD ,∴∠A=∠ADO .∵∠C=90°,∴∠CBD +∠CDB=90°.又∵∠CBD=∠A ,∴∠ADO +∠CDB=90°.∴∠ODB=90°.∴直线BD 与⊙O 相切.(2)解法一:如图1,连接DE .∵AE 是⊙O 的直径,∴∠ADE=90°.∵AD ∶AO=8∶5,∴54AE AD cosA ==.∵∠C=90°,∠CBD=∠A ,∴54BD BC CBD cos ==∠. ∵BC=2∴25BD =. 解法二:如图2,过点O 作OH ⊥AD 于点H .∴AD 21DH AH ==. ∵AD ∶AO=8∶5,∴54AO AH cosA ==. ∵∠C=90°,∠CBD=∠A , ∴54BD BC CBD cos ==∠. ∵BC=2,∴25BD =. 【解析】此题目还可以由△ADE ∽△BCD(图1),或由△AHO ∽△BCD(图2),利用对应边的比相等求出BD 的长.此题是圆的综合题,既考查了直线与圆的位置关系,切线的判定,圆周角的有关性质,又考查了相似三角形的判定与性质,锐角三角函数及直角三角形的有关性质,培养了学生综合分析问题的能力和逻辑推理能力.学生在解决此题目时易犯的错误是:(1)易受思维定势的干扰,见着直角三角形就用30°和60°角来解决问题;(2)相似三角形对应边找不准;(3)由线段的比不会转化为三角函数间的关系;(4)相似与全等的符号混淆,将“∽”写成“≌”;(5)思维混乱,推理过程跳跃性较大.20.解:(1)补全图见下图.“限塑令”实施前,平均一次购物使用不同数量塑料购物袋的人数统计图100300100736451041132623719=⨯+⨯+⨯+⨯+⨯+⨯+⨯=3(个).这100位顾客平均一次购物使用塑料购物袋的平均数为3个.2 000×3=6 000.估计这个超市每天需要为顾客提供6 000个塑料购物袋.(2)图2中,使用收费塑料购物袋的人数所占百分比为25%.根据图表回答正确给1分,例如:由图2和统计表可知,购物时应尽量使用自备袋和押金式环保袋,少用塑料购物袋;塑料购物袋应尽量循环使用,以便减少塑料购物袋的使用量,为环保做贡献.【解析】通过设计“限塑令”的实际问题背景,考查学生对统计图表的识图、读图能力,及加权平均数的计算和用样本估计总体的统计思想,由于题目文字叙述较长,还考查了学生的阅读理解能力.特别是题目最后一问,让学生通过反思,提出合理化建议,能够让学生明白环境保护是我们每一个人的义务,做到了寓德育于平时的教学之中.此题主要丢分在计算算式9×1+37×2+26×3+11×4+10×5+4×6+3×7时不细心.21.解:设这次试车时,由北京到天津的平均速度是每小时x 千米,则由天津返回北京的平均速度是每小时(x +40)千米.依题意,得40)(x 21x 60630+=+. 解得x=200.答:这次试车时,由北京到天津的平均速度是每小时200千米.【解析】这是一道传统的行程问题的应用题,考查了学生分析问题,列方程解决实际问题的能力.仔细分析发现题目虽然只要求一个未知量,但实际上有两个未知量:北京到天津的平均速度和由天津返回北京的平均速度.题中的等量关系有两个:(1)由天津返回北京比去天津时平均每小时多行驶40千米;(2)北京到天津、天津返回到北京的路程相同.用(1)设未知量,用(2)列方程.列方程时,还要注意到题中的两个关键词:(1)由天津返回北京的行驶时间与预计时间(半小时,即21小时)相同,则天津返回到北京的路程为(21(x +40)千米;(2)由北京到天津的行驶时间比预计时间(21小时)多用了6分钟101小时).则北京到天津的路程为)10121(+x 千米. 根据以上分析可以便得到一个一元一次方程:40)(x 21x )10121(+=+.此题还可列式为:)60x 604030(60x 30+=⨯,或40)(x 21=x 60630++,或10121x )40x (21+=+(此方程为分式方程,注意结果要进行检验),或⎪⎩⎪⎨⎧+=+=)x 21101(2y ,x 40y 等. 学生容易出现的问题是:(1)阅读能力差,对题意不理解;(2)找不到等量关系;(3)时间单位不统一;(4)基本功不扎实,如:将方程化简应为36x=30(x +40),却化为36x=30x +40等;(5)计算出错;(6)书写不规范,如“设北京到天津是x”等等.22.4m 38 m)-(43 32<≤ 【解析】(1)观察图形可知重叠三角形A′B′C′是边长为2的等边三角形,则这个三角形底边上的高为3,所以重叠三角形A′B′C′的面积33221=⨯⨯=;(2)如图1,由折叠的性质和已知可知:A′D=AD=m ,B′D=BD=8-m ,所以A′B′=B′C′=8-2m ,A′B′边上的高=m)-(43,所以重叠三角形A′B′C′的面积2m)-(43m)-(432m)-(821=⨯⨯=;当D 为AB 边中点时“重叠三角形”不存在,故m <4.而当D 在AB 的31点处,即AD=38时,点B′和点C′恰在矩形DEFG 边上,符合题意;当38AD <时,点B′和点C′就在矩形DEFG 外了,这与已知不符,故38m ≥,因此m 的取值范围为4m 38<≤.此题是一道图形折叠的实验探究题,它考查了等边三角形的概念,三角形的面积公式,用代数式表示图形的阴影面积,动点中自变量m 的取值范围,图形变换—折叠、轴对称的性质,格点图形的特性等知识,考查了学生的动手操作能力,想象能力,探究问题的能力,由于题目文字叙述较长,还考查了学生的阅读理解能力及对新定义的理解能力.学生易出现的问题:(1)不会利用格点图形的特性求边长;(2)对等边三角形认识不够全面,等边三角形面积的求法不熟练;(3)对折叠图形的特性掌握不好,不知道折叠前后两个图形之间的关系,如A′D=AD=m ,B′D=BD=8-m ;(4)对“重叠三角形”存在的条件审题不全面,m 的取值范围中38m ≥考虑不到,因此多数学生都会错误地认为:m 的取值范围为0<m <4.23.证明:(1)∵022m 2)x (3m -mx 2=+++是关于x 的一元二次方程, ∴△=2222)(m 44m m 2)4m(2m -2)](3m -[+=+++=++.∵当m >0时,02)(m 2>+,即△>0.∴方程有两个不相等的实数根.(2)由求根公式,得x=m2)2m ()2m 3(+±+ ∴m 2)(2m x +=或x=1. ∵m >0,∴m1)2(m m 22m +=+>1. ∵21x x <,∴1x 1=,m22m x 2+=. ∴m212m 22m 2x x y 12=⨯-+=-=. 即m 2y =(m >0)为所求. (3)在同一平面直角坐标系中分别画出m2y =(m >0)与y=2m(m >0)的图象.由图象可得,当m≥1时,y≤2m .【解析】(1)要证明方程有两个不相等的实数根,应从根的判别式入手,只要能够说明根的判别式△>0即可.这里用到了配方、非负数的性质及题目中的附加条件m >0.(2)要求函数122x -x y =的解析式,需要先求出1x 与2x 的值,由于△>0,所以方程的根一定是有理数,因此用求根公式可求出方程的根,再代入122x -x y =中即可.注意求出的两个根要区分大小,否则会得出错误的结论. 这是一道代数综合题,它以方程知识为载体,重点考查一元二次方程的概念和根的判别式,一元二次方程的解法(字母方程),配方法,求函数解析式,函数的大小比较和实数的大小比较,并要求学生会正确画出一次函数和反比例函数的图象,且能通过函数图象解决两个函数的大小比较问题.学生易出现的问题:(1)证明的思路不明确,直接用△>0,来说明△>0;(2)判别式的计算错误;(3)不会用求根公式解字母方程;(4)求出2m2)(m 2)(3m x +±+=后不会化简;(5)求出两个根后,没有区分大小;(6)第(3)问不会用图象解决问题,想用代数方法解决却又不会求二次不等式的解集.24解:(1)∵y=kx 沿y 轴向上平移3个单位长度后经过y 轴上的点C , ∴C(0,3).设直线BC 的解析式为y=kx +3,∵B(3,0)在直线BC 上,∴3k +3=0. 解得k=-1.∴直线BC 的解析式为y=-x +3.∵抛物线c bx x y 2++=过点B 、C ,∴⎩⎨⎧==++3.c 0,c 3b 9 解得⎩⎨⎧=-=3.c 4,b∴抛物线的解析式为3?x x y 2+=.(2)由-4x+3x y 2=,可得D(2,-1),A(1,0).∴OB=3,OC=3,OA=1,AB=2.可得△OBC 是等腰直角三角形.∴∠OBC=45°,CB=23.如图1,设抛物线对称轴与x 轴交于点F ,∴AF=21AB=1. 过点A 作AE ⊥BC 于点E .∴∠AEB=90°.可得BE=AE=2,CE=22.在△AEC 与△AFP 中,∠AEC=∠AFP=90°,∠ACE=∠APF ,∴△AEC ∽△AFP .∴PF CE AF AE =,PF2212=.解得PF=2.∵点P 在抛物线的对称轴上,∴点P 的坐标为(2,2)或(2,-2).(3)解法一:如图2,作点A(1,0)关于y 轴的对称点A′,则A′(-1,0).连接A′C 、A′D ,可得10AC C A'==,∠OCA′=∠OCA .由勾股定理可得20CD 2=,10D A'2=.又10C A'2=,∴222CD C A'D A'=+.∴△A′DC 是等腰直角三角形,∠CA′D=90°.∴∠DCA′=45°.∴∠OCA′+∠OCD=45°.∴∠OCA +∠OCD=45°.即∠OCA 与∠OCD 两角和的度数为45°.解法二:如图3,连接BD .同解法一可得CD=20,AC=10.在Rt △DBF 中,∠DFB=90°,BF=DF=1,∴2BF DF DB 22=+=.在△CBD 和△COA 中,212AO DB ==,2323OC BC ==,21020CA CD ==. ∴CA CD OC BC AO DB ==. ∴△CBD ∽△COA .∴∠BCD=∠OCA .∵∠OCB=45°,∴∠OCA +∠OCD=45°.即∠OCA 与∠OCD 两角和的度数为45°.【解析】本题为代数与几何的综合题,它综合考查了一次函数与二次函数解析式的求法,并将函数与几何图形有机地结合起来,重点考查学生能否认真审题、挖掘出题中的隐含条件,(如:可从解题过程中得到△OBC 是等腰直角三角形等),综合运用数学知识解决问题的能力,以及运用方程的思想、数形结合的思想、分类讨论的思想和转化的思想解决数学问题的能力.本题考查的知识点很多,有图形变换—平移、轴对称概念与性质,用待定系数法确定一次函数与二次函数的解析式,相似三角形的性质与判定,直角三角形的解法,勾股定理等.学生易出现的问题:(1)所求的直线解析式应是平移后的,学生只求出平移前的直线y=kx ;(2)第二问中,由于没发现△OBC 是等腰直角三角形,因此找不齐证明相似三角形的条件,于是就出现用一个已知条件∠APD=∠ACB 来判定△AEC ∽△AFP 的错误方法;(3)考虑问题不全面,只求出一个P 点的坐标,不会用对称性得出P 点的另一个坐标;(4)对(2)(3)两问不能将学过的数学知识和方法综合运用,对综合题不知如何分析,无从下手.25.解:(1)线段PG 与PC 的位置关系是PG ⊥PC ;3PCPG . (2)猜想:(1)中的结论没有发生变化.证明:如图,延长GP 交AD 于点H ,连接CH 、CG .∵P 是线段DF 的中点,∴FP=DP .由题意可知AD ∥FG .∴∠GFP=∠HDP .∵∠GPF=∠HPD ,∴△GFP ≌△HDP .∴GP=HP ,GF=HD .∵四边形ABCD 是菱形,∴CD=CB ,∠HDC=∠ABC=60°.由∠ABC=∠BEF=60°,且菱形BEFG 的对角线BF 恰好与菱形ABCD 的边AB 在同一条直线上,可得∠GBC=60°.∴∠HDC=∠GBC .∵四边形BEFG 是菱形,∴GF=GB .∴HD=GB .∴△HDC ≌△GBC .∴CH=CG ,∠DCH=∠BCG .∴∠DCH +∠HCB=∠BCG +∠HCB=120°.即∠HCG=120°.∵CH=CG ,PH=PG ,∴PG ⊥ PC ,∠GCP=∠HCP=60°.∴3PCPG =. (3)tan PC PG =(90°-α). 【解析】(1)由题目中的已知和小聪的提示“延长GP 交DC 于点H ,构造全等三角形.”可知△GFP ≌△HDP ,从而得到CH=CG ,PH=PG ,∠HCP=∠GCP=60°.根据等腰三角形的性质有PG ⊥PC ,再由30°角的直角三角形的性质,可得3PCPG =;(2)用(1)的提示即可得出结论不变及推理过程;(3)若图1中∠ABC=∠BEF=2α(0°<α<90°),由(1)和(2)的推理,可以得到PG ⊥PC 和∠PCG=90°-α,在直角三角形PCG 中,因为PC PG PCG tan =∠,所以t an PCPG =(90°-α).这是一道阅读理解题,需要学生仔细阅读,从中悟出解题的思路与方法.它考查了图形变换——图形旋转的性质,菱形的性质,全等三角形的判定与性质,等腰三角形的判定与性质,直角三角形的判定与性质,锐角三角函数等.题目设了三问,三个填空、一个推理论证,由易到难,层层递进,问题(1)可由提示得出,问题(2)又由问题(1)的提示进行推理,问题(3)由问题(1)和(2)可以得到结论.虽然每一问的难度在逐渐上升,但只要第一问能仔细地想一想结论是如何得出的,而不是猜,那么就能很快地解决(2)与(3)的问题.这也告诉我们,读题时一定要认真仔细,每一步的来龙去脉一定要弄明白,答案就会轻松得到.学生易出现的问题:(1)由于问题(1)的结论是猜出来的,因此到第二问就做不下去了,所以第三问还错误地认为3PCPG =;(2)跳跃性太大,做第二问时,用题目中的提示不先证明△GFP ≌△HDP ,而直接得出△CDH ≌△CBG 的结论;(3)不会读题,不会用题目中小聪的提示,不知如何添加辅助线,因而找不到条件与问题之间的关系;(4)思维混乱,证明无条理,如用边边角证全等,或想用哪个角,就把哪个角作为已知相等来用的错误等等.综评:本份试卷知识与能力考查得比较全面,符合考纲要求,能够依托教材,难易度适中,具有一定的区分度,没有偏、难、怪题,有利于各层次学生的发挥(对部分想有挑战性的学生来说,题略显容易).此份试题有新题型(8,22,25),但步子较稳,多数学生能够接受.题目能够与奥运挂钩、与抗震救灾和环保挂钩(2,4,6,20题),贴近生活.但此份试题阅读量较大(20,21,22,25题,一共有4道),对于阅读能力稍差一些的学生,会造成一定的阅读理解障碍,影响得分.(北京王建国袁芝馨)。
