七年级平行线的判定与性质精选练习题
七年级数学-平行线的性质与判定的证明-练习题及答案

七年级数学-平行线的性质与判定的证明-练习题及答案--------------------------------------------------------------------------作者: _____________--------------------------------------------------------------------------日期: _____________平行线的性质与判定的证明温故而知新可以为师以:重点1.平行线的性质(1)两直线平行,同位角相等;(2)两直线平行,内错角相等;(3)两直线平行,同旁内角互补.2.平行线的判定(1)同位角相等,两直线平行;(2)内错角相等,两直线平行;(3)同旁内角互补,两直线平行互补.例1 已知如图2-2,AB∥CD∥EF,点M,N,P分别在AB,CD,EF上,NQ平分∠MNP.(1)若∠AMN=60°,∠EPN=80°,分别求∠MNP,∠DNQ的度数;(2)探求∠DNQ与∠AMN,∠EPN的数量关系.解析:根据两直线平行,内错角相等及角平分线定义求解.(标注∠MND=∠AMN,∠DNP=∠EPN)答案:(标注∠MND=∠AMN=60°,∠DNP=∠EPN=80°)解:(1)∵AB∥CD∥EF,∴∠MND=∠AMN=60°,∠DNP=∠EPN=80°,∴∠MNP=∠MND+∠DNP=60°+80°=140°,又NQ平分∠MNP,∴∠MNQ=12∠MNP=12×140°=70°,∴∠DNQ=∠MNQ-∠MND=70°-60°=10°,∴∠MNP,∠DNQ的度数分别为140°,10°.(下一步) (2)(标注∠MND=∠AMN,∠DNP=∠EPN)由(1)得∠MNP=∠MND+∠DNP=∠AMN+∠EPN,∴∠MNQ=12∠MNP=12(∠AMN+∠EPN),∴∠DNQ=∠MNQ-∠MND=12(∠AMN+∠EPN)-∠AMN=12(∠EPN-∠AMN),即2∠DNQ=∠EPN-∠AMN.小结:在我们完成涉及平行线性质的相关问题时,注意实现同位角、内错角、同旁内角之间的角度转换,即同位角相等,内错角相等,同旁内角互补.例2 如图,∠AGD=∠ACB,CD⊥AB,EF⊥AB,证明:∠1=∠2.解析:(标注:∠1=∠2=∠DCB,DG∥BC,CD∥EF)答案:(标注:∠1=∠2=∠DCB)证明:因为∠AGD=∠ACB,所以DG∥BC,所以∠1=∠DCB,又因为CD⊥AB,EF⊥AB,所以CD∥EF,所以∠2=∠DCB,所以∠1=∠2.小结:在完成证明的问题时,我们可以由角的关系可以得到直线之间的关系,由直线之间的关系也可得到角的关系.例3 (1)已知:如图2-4①,直线AB∥ED,求证:∠ABC+∠CDE=∠BCD;(2)当点C位于如图2-4②所示时,∠ABC,∠CDE与∠BCD存在什么等量关系?并证明.(1)解析:动画过点C作CF∥AB由平行线性质找到角的关系.(标注∠1=∠ABC,∠2=∠CDE)答案:证明:如图,过点C作CF∥AB,∵直线AB∥ED,∴AB∥CF∥DE,∴∠1=∠ABC,∠2=∠CDE.∵∠BCD=∠1+∠2,∴∠ABC+∠CDE=∠BCD;(2)解析:动画过点C作CF∥AB,由平行线性质找到角的关系.(标注∠ABC+∠1=180°,∠2+∠CDE=180°)答案:∠ABC+∠BCD+∠CDE=360°.证明:如图,过点C作CF∥AB,∵直线AB∥ED,∴AB∥CF∥DE,∴∠ABC+∠1=180°,∠2+∠CDE=180°.∵∠BCD=∠1+∠2,∴∠ABC+∠BCD+∠CDE=360°.小结:在运用平行线性质时,有时需要作平行线,取到桥梁的作用,实现已知条件的转化.例4 如图2-5,一条公路修到湖边时,需绕道,如果第一次拐的角∠A是120°,第二次拐的角∠B是150°,第三次拐的角是∠C,这时的道路恰好和第一次拐弯之前的道路平行,那么∠C应为多少度?解析:动画过点B作BD∥AE,答案:解:过点B作BD∥AE,∵AE∥CF,∴AE∥BD∥CF,∴∠A=∠1,∠2+∠C=180°∵∠A=120°,∠1+∠2=∠ABC=150°,∴∠2=30°,∴∠C=180°-30°=150°.小结:把关于角度的问题转化为平行线问题,利用平行线的性质与判定予以解答.举一反三:1.如图2-9,FG∥HI,则∠x的度数为()A.60°B. 72°C. 90°D. 100°解析:∠AEG=180°-120°=60°,由外凸角和等于内凹角和有60°+30°+30°=x+48°,解得x=72°. 答案:B.2.已知如图所示,AB∥EF∥CD,EG平分∠BEF,∠B+∠BED+∠D=192°,∠B-∠D=24°,求∠GEF的度数.解析:解:∵AB∥EF∥CD,∴∠B=∠BEF,∠DEF=∠D.∵∠B+∠BED+∠D=192°,即∠B+∠BEF+∠DEF+∠D=192°,∴2(∠B+∠D)=192°,即∠B+∠D=96°.∵∠B-∠D=24°,∴∠B=60°,即∠BEF=60°.∵EG平分∠BEF,∴∠GEF=12∠BEF=30°.3.已知:如图2-10,AB∥EF,BC∥ED,AB,DE交于点G.求证:∠B=∠E.解析:标注AB∥EF,BC∥ED答案:证明:∵AB∥EF,∴∠E=∠AGD.∵BC∥ED,∴∠B=∠AGD,∴∠B=∠E.例5如图2-6,已知AB∥CD,试再添上一个条件,使∠1=∠2成立,并说明理由.解析:标注 AB∥CD,∠1=∠2答案:方法一:(标注CF∥BE)解:需添加的条件为CF∥BE ,理由:∵AB∥CD,∴∠DCB=∠ABC.∵CF∥BE,∴∠FCB=∠EBC,∴∠1=∠2;方法二:(标注CF,BE,∠1=∠2=∠DCF=∠ABE)解:添加的条件为CF,BE分别为∠BCD,∠CBA的平分线.理由:∵AB∥CD,∴∠DCB=∠ABC.∵CF ,BE 分别为∠BCD ,∠CBA 的平分线,∴∠1=∠2.小结:解决此类条件开放性问题需要从结果出发,找出结果成立所需要的条件,由果溯因.例6 如图1-7,已知直线1l 2l P ,且3l 和1l 、2l 分别交于A 、两点,点P 在AB 上,4l 和1l 、2l 分别交于C 、D 两点,连接PC 、PD 。
(完整word版)七年级平行线的判定与性质练习题带答案
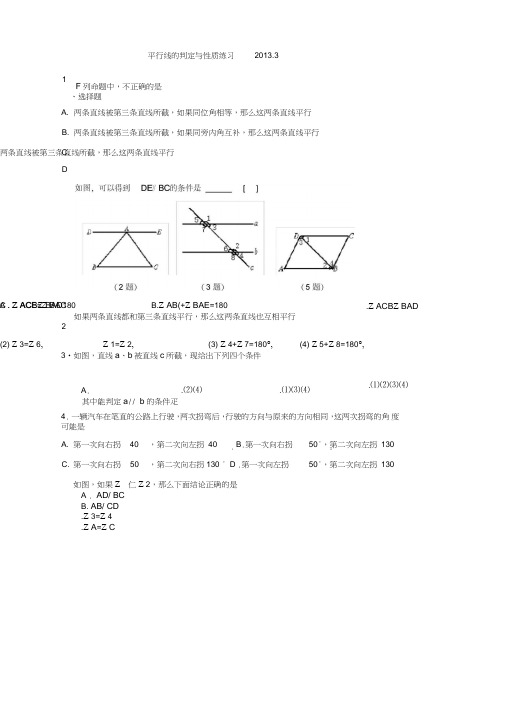
、选择题两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行 两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行如果两条直线都和第三条直线平行,那么这两条直线也互相平行3•如图,直线a 、b 被直线c 所截,现给出下列四个条件其中能判定a // b 的条件疋4. 一辆汽车在笔直的公路上行驶,两次拐弯后,行驶的方向与原来的方向相同,这两次拐弯的角 度可能是A . AD/ BC B. AB/ CD .Z 3=Z 4 .Z A =Z C平行线的判定与性质练习 2013.3A. 第一次向右拐 40 ,第二次向左拐 40B .第一次向右拐 50°,第二次向左拐 130C. 第一次向右拐 50 ,第二次向右拐130 ° D .第一次向左拐 50°,第二次向左拐 130如图,如果Z 仁Z 2,那么下面结论正确的是1. F 列命题中,不正确的是 A. C.两条直线被第三条直线所截,那么这两条直线平行 B. D.A . Z ACE =Z BAC B.Z AB(+Z BAE =180 C ACB Z BAD 180 .Z ACB Z BADZ 1=Z 2, (2) Z 3=Z 6, (3) Z 4+Z 7=180°, (4) Z 5+Z 8=180°,A .(1)(3) .⑵⑷ .⑴⑶⑷.⑴⑵⑶⑷2.OOA .两直线平行,同位角相等B .两直线平行,内错角相等C .同位角相等,两直线平行 A .互相垂直 8.如图,AB// CD 那么二、填空题11.如图,由下列条件可判定哪两条直线平行,并说明根据.7 C =180°,6.如图,a IIb , a 、 b 被c 所截, 得到/仁/2的依据是(A.Z 仁/4 B .Z 2=7 3 D . Z 1 = / 59.如图,在平行四边形ABCD 中,下列各式不一定正确的是(C. 7 10 .如图, 1 + 7 2=180° 3+7 4=180°AD// BC, 7 B=30°.7 2+7 3=180° .7 2+7 4=180°,DB 平分7 ADE 则7 DEC 的度数为((1) 7 1 = 7 2,.(2) 7 A =7 3, .(3) 7 AB (+D .内错角相等,两直线平行D .无法确定B .互相平行.相交C 7.同c 、d 的位置关系为((10 题)A. 30° B . 60°直线的位置关系是13 .同垂直于一条直线的两条直线12 .如果两条直线被第三条直线所截,一组同旁内角的度数之比为3 : 2,差为 36°,那么这两条14.如图,直线EF分别交ABCD于GH Z仁60°,/ 2=120°,那么直线AB与CD的关系是____________理由是:________________________________________________ .15 .如图,AB// EF, BC// DE 则Z E+Z B 的度数为(14 题)(15 题)求证:EF// CD.B,且Z BED Z D =180三、解答题BE // CF .OA、20.如图,已知/ AMB=/ EBF / BCN 2 BDE 求证:/ CAF=/ AFD23. (1)如图,若 AB// DE / B=135°,Z D=145°,你能求出/ C 的度数吗?(2)在AB// DE 的条件下,你能得出/ B 、/ C 、/ D 之间的数量关系吗?并说明理由.24. 如图,在折线 ABCDEF 叩,已知/ 1 = / 2=/ 3=/ 4=?/ 5, ?延长AB GF 交于点 M.试探索/ AMG与/ 3的关系,并说明理由.25.(开放题)已知如图,四边形 ABCD 中, AB// CD BC// AD,那么/ A 与/ C,/B 与/ D 的大小关系如何?请说明你的理由.21.如图,一条公路修到湖边时,需拐弯绕湖而过,如果第一次拐的角 A 是120。
七年级下数学《平行线的判定与性质》练习题 (24)

七年级下数学《平行线的判定与性质》练习题
1.下列正确的有()
①过一点有且只有一条直线与已知直线垂直.②过一点有且只有一条直线平行于已知直
线.③两条直线相交线若有3个角相等,那么这两条直线互相垂直.④同位角相等,两直线平行.
A.4个B.3个C.2个D.1个
【分析】根据垂直、平行线的判定和性质判断即可.
【解答】解:①在同一平面内,过一点有且只有一条直线与已知直线垂直,是假命题.
②过直线外一点有且只有一条直线平行于已知直线,是假命题.
③两条直线相交线若有3个角相等,那么这两条直线互相垂直是真命题.
④同位角相等,两直线平行是真命题;
故选:C.
1。
平行线的判定与性质的综合应用 专题练习

平行线的判定与性质的综合应用专题练习平行线的判定与性质的综合运用专题一、推理填空题1.已知:如图,DE∥BC,∠ADE=∠XXX,将说明∠1=∠2成立的理由填写完整。
解:因为DE∥BC,所以∠ADE=∠XXX。
又因为DE∥BC,所以DB∥EF。
由平行线性质可知,∠1=∠ADE=∠XXX∠2.2.已知:如图所示,∠1=∠2,∠A=∠3.求证:XXX。
证明:因为∠1=∠2,所以XXX。
又因为∠A=∠3,所以AC∥BD。
由平行线性质可知,AC∥DE。
3.已知:如图,∠XXX∠ADC,BF、DE分别平分∠ABC 与∠ADC,且∠1=∠3.求证:AB∥DC。
证明:因为∠XXX∠ADC,所以∠XXX∠ADC。
又因为BF、DE分别平分∠ABC与∠ADC,所以∠1=∠ABC,∠3=∠ADC。
由∠1=∠3可得,∠2=∠ADC。
由平行线性质可知,AB∥DC。
二、证明题4.如图,AB∥CD,AE交CD于点C,DE⊥AE,垂足为E,∠A=37º,求∠D的度数。
证明:因为AB∥CD,所以∠A+∠D=180º。
又因为DE⊥AE,所以∠ADE=90º。
由∠A=37º可得,∠ADE=53º。
由三角形内角和定理可得,∠D=80º。
5.如图,已知AB∥CD,∠1=100°,∠2=120°,求∠α的度数。
证明:因为AB∥CD,所以∠1+∠α+∠2=180º。
由∠1=100º,∠2=120º可得,∠α= -40º。
由于∠α是角度,所以∠α=320º。
6.如图,XXX,AE平分∠BAD,求证:XXX与AE相交于F,∠XXX∠EAF。
证明:因为XXX,所以∠BAD=∠ACD。
又因为AE平分∠BAD,所以∠XXX∠DAF。
由相邻角的性质可得,∠EAF+∠DAF=∠BAD=∠ACD。
又因为CD与AE相交于F,所以∠CFE+∠EAF+∠ACD=180º。
人教版七年级下册数学平行线的判定与性质综合题集

人教版七年级下册数学平行线的判定与性质综合题集一.平行线的判定(共1小题)1.将一副三角板中的两个直角顶点C叠放在一起(如图),其中∠A=30°,∠B=60°,∠D=∠E=45°.(1)若∠BCD=112°,求∠ACE的度数;(2)试猜想∠BCD与∠ACE的数量关系,请说明理由;(3)若三角板ABC保持不动,绕顶点C转动三角板DCE,在转动过程中,试探究∠BCD等于多少度时,CD ∥AB?请你直接写出答案.二.平行线的性质(共20小题)2.(2021春•阜南县期末)如图,已知AM∥BN,∠A=60°,点P是射线AM上一动点(与点A不重合),BC,BD分别平分∠ABP和∠PBN,分别交射线AM于点C,D.(1)求∠CBD的度数;(2)当点P运动时,∠APB:∠ADB的比值是否随之变化?若不变,请求出这个比值;若变化,请找出变化规律;(3)当点P运动到某处时,∠ACB=∠ABD,求此时∠ABC的度数.3.(2021春•铁锋区期末)背景阅读:在同一平面内,两条不重合的直线的位置关系有相交、平行,若两条不重合的直线只有一个公共点,我们就说这两条直线相交,若两条直线不相交,我们就说这两条直线互相平行,两条直线的位置关系的性质和判定是几何的重要知识,是初中阶段几何合情推理的基础.已知:AM∥CN,点B为平面内一点,AB⊥BC于B.问题解决:(1)如图1,直接写出∠A和∠C之间的数量关系;(2)如图2,过点B作BD⊥AM于点D,求证:∠ABD=∠C;(3)如图3,在(2)问的条件下,点E、F在DM上,连接BE、BF、CF,BF平分∠DBC,BE平分∠ABD,若∠FCB+∠NCF=180°,∠BFC=3∠DBE,则∠EBC=.4.(2017秋•雨花区期末)已知AM∥CN,点B为平面内一点,AB⊥BC于B(1)如图1,直接写出∠A和∠C之间的数量关系;(2)如图2,过点B作BD⊥AM于点D,求证:∠ABD=∠C;(3)如图3,在(2)问的条件下,点E、F在DM上,连接BE、BF、CF,BF平分∠DBC,BE平分∠ABD,若∠FCB+∠NCF=180°,∠ABF=2∠ABE,求∠EBC的度数.5.(2019春•韶关期末)将一副三角板中的两个直角顶点C叠放在一起(如图①),其中∠A=30°,∠B=60°,∠D=∠E=45°.(1)猜想∠BCD与∠ACE的数量关系,并说明理由;(2)若∠BCD=3∠ACE,求∠BCD的度数;(3)若按住三角板ABC不动,绕顶点C转动三角板DCE,试探究∠BCD等于多少度时CE∥AB,并简要说明理由.6.(2021春•龙岗区校级期中)如图,已知直线AB∥射线CD,∠CEB=100°,P是射线EB上一动点,过点P作PQ∥EC交射线CD于点Q,连接CP,作∠PCF=∠PCQ,交直线AB于点F,CG平分∠ECF,交直线AB于点G.(1)若点P,F,G都在点E的右侧,求∠PCG的度数;(2)在(1)的条件下,若∠EGC﹣∠ECG=40°,求∠CPQ的度数;(3)在点P的运动过程中,是否存在这样的情形,使=?若存在,求出∠CPQ的度数;若不存在,请说明理由.7.(2021秋•揭东区期末)已知:如图所示,直线MN∥GH,另一直线交GH于A,交MN于B,且∠MBA=80°,点C为直线GH上一动点,点D为直线MN上一动点,且∠GCD=50°.(1)如图1,当点C在点A右边且点D在点B左边时,∠DBA的平分线交∠DCA的平分线于点P,求∠BPC 的度数;(2)如图2,当点C在点A右边且点D在点B右边时,∠DBA的平分线交∠DCA的平分线于点P,求∠BPC 的度数;(3)当点C在点A左边且点D在点B左边时,∠DBA的平分线交∠DCA的平分线所在直线交于点P,请直接写出∠BPC的度数,不说明理由.8.(2021春•奉化区校级期末)已知,直线AB∥DC,点P为平面上一点,连接AP与CP.(1)如图1,点P在直线AB、CD之间,当∠BAP=60°,∠DCP=20°时,求∠APC.(2)如图2,点P在直线AB、CD之间,∠BAP与∠DCP的角平分线相交于点K,写出∠AKC与∠APC之间的数量关系,并说明理由.(3)如图3,点P落在CD外,∠BAP与∠DCP的角平分线相交于点K,∠AKC与∠APC有何数量关系?并说明理由.9.(2020秋•罗湖区校级期末)如图,已知AB∥CD,现将一直角三角形PMN放入图中,其中∠P=90°,PM交AB于点E,PN交CD于点F(1)当△PMN所放位置如图①所示时,则∠PFD与∠AEM的数量关系为;(2)当△PMN所放位置如图②所示时,求证:∠PFD﹣∠AEM=90°;(3)在(2)的条件下,若MN与CD交于点O,且∠DON=30°,∠PEB=15°,求∠N的度数.10.(2021春•临邑县期末)如图,直线CB∥OA,∠C=∠OAB=100°,E、F在CB上,且满足∠FOB=∠AOB,OE平分∠COF(1)求∠EOB的度数;(2)若平行移动AB,那么∠OBC:∠OFC的值是否随之发生变化?若变化,找出变化规律或求出变化范围;若不变,求出这个比值.(3)在平行移动AB的过程中,是否存在某种情况,使∠OEC=∠OBA?若存在,求出其度数;若不存在,说明理由.11.(2017春•南安市期末)“一带一路”让中国和世界更紧密,“中欧铁路”为了安全起见在某段铁路两旁安置了两座可旋转探照灯.如图1所示,灯A射线从AM开始顺时针旋转至AN便立即回转,灯B射线从BP开始顺时针旋转至BQ便立即回转,两灯不停交叉照射巡视.若灯A转动的速度是每秒2度,灯B转动的速度是每秒1度.假定主道路是平行的,即PQ∥MN,且∠BAM:∠BAN=2:1.(1)填空:∠BAN=°;(2)若灯B射线先转动30秒,灯A射线才开始转动,在灯B射线到达BQ之前,A灯转动几秒,两灯的光束互相平行?(3)如图2,若两灯同时转动,在灯A射线到达AN之前.若射出的光束交于点C,过C作∠ACD交PQ于点D,且∠ACD=120°,则在转动过程中,请探究∠BAC与∠BCD的数量关系是否发生变化?若不变,请求出其数量关系;若改变,请说明理由.12.(2021春•奉化区校级期末)如图,已知直线AB∥射线CD,∠CEB=100°.P是射线EB上一动点,过点P 作PQ∥EC交射线CD于点Q,连接CP.作∠PCF=∠PCQ,交直线AB于点F,CG平分∠ECF.(1)若点P,F,G都在点E的右侧.①求∠PCG的度数;②若∠EGC﹣∠ECG=40°,求∠CPQ的度数.(2)在点P的运动过程中,是否存在这样的情形,使?若存在,求出∠CPQ的度数;若不存在,请说明理由.13.(2019春•河东区期末)已知:点A、C、B不在同一条直线上,AD∥BE(1)如图①,当∠A=58°,∠B=118°时,求∠C的度数;(2)如图②,AQ、BQ分别为∠DAC、∠EBC的平分线所在直线,试探究∠C与∠AQB的数量关系;(3)如图③,在(2)的前提下,且有AC∥QB,QP⊥PB,直接写出∠DAC:∠ACB:∠CBE的值.14.(2021春•济南期中)如图,直线PQ∥MN,点C是PQ、MN之间(不在直线PQ,MN上)的一个动点.(1)如图1,若∠1与∠2都是锐角,请写出∠C与∠1,∠2之间的数量关系并说明理由.(2)把直角三角形ABC如图2摆放,直角顶点C在两条平行线之间,CB与PQ交于点D,CA与MN交于点E,BA与PQ交于点F,点G在线段CE上,连接DG,有∠BDF=∠GDF,求的值.(3)如图3,若点D是MN下方一点,BC平分∠PBD,AM平分∠CAD,已知∠PBC=25°,求∠ACB+∠ADB 的度数.15.(2016春•深圳校级期中)平面内的两条直线有相交和平行两种位置关系(1)已知AB平行于CD,如a图,当点P在AB、CD外部时,∠BPD+∠D=∠B即∠BPD=∠B﹣∠D,为什么?请说明理由.如b图,将点P移动到AB、CD内部,以上结论是否仍然成立?若不成立,则∠BPD、∠B、∠D之间有何数量关系?请说明结论;(2)在图b中,将直线AB绕点B逆时针方向旋转一定角度交直线CD于点Q,如图c,则∠BPD、∠B、∠D、∠BQD之间有何数量关系?(不需证明)(3)根据(2)的结论求图d中∠A+∠B+∠C+∠D+∠E+∠F的度数.16.(2019秋•道里区校级期中)已知:AF平分∠BAE,CF平分∠DCE.(1)如图①,已知AB∥CD,求证:∠AEC=∠C﹣∠A;(2)如图②,在(1)的条件下,直接写出∠E与∠F的关系.∠E=(用含有∠F的式子表示);(3)如图③,BD⊥AB,垂足为B,∠BDC=110°,∠AEC=40°,求∠AFC的度数.17.(2019春•荔湾区期末)如图,已知AB∥CD,直线FG分别与AB、CD交于点F、点G.(1)如图1,当点E在线段FG上,若∠EAF=40°,∠EDG=30°,则∠AED=°.(2)如图2,当点E在线段FG的延长线上,CD与AE交于点H,则∠AED、∠EAF、∠EDG之间满足怎样的关系,请证明你的结论;(3)如图3,在(2)的条件下,DM平分∠EDG,交AE于点K,射线AN将∠EAB分成∠EAN:∠NAB=1:2,且与DM交于点I,若∠DEA=22°,∠DIA=20°,求∠DKE的度数.18.(2019春•香洲区期末)如图1.直线AD∥EF,点B,C分别在EF和AD上,∠A=∠ABC,BD平分∠CBF.(1)求证:AB⊥BD;(2)如图2,BG⊥AD于点G,求证:∠ACB=2∠ABG;(3)在(2)的条件下,如图3,CH平分∠ACB交BG于点H,设∠ABG=α,请直接写出∠BHC的度数.(用含α的式子表示)19.(2020春•阳西县期末)已知AB∥CD,点C在点D的右侧,连接AD,BC,BE平分∠ABC,DE平分∠ADC,BE,DE相交于点E.(1)如图1,当点B在点A的左侧时,①若∠ABC=50°,∠ADC=70°,求∠BED的度数;②请直接写出∠BED与∠ABC,∠ADC的数量关系;(2)如图2,当点B在点A的右侧时,试猜想∠BED与∠ABC,∠ADC的数量关系,并说明理由.20.(2021春•利州区期末)小明同学在完成七年级上册数学的学习后,遇到了一些问题,请你帮他解决下.(1)如图1,已知AB∥CD,则∠AEC=∠BAE+∠DCE成立吗?请说明理由;(2)如图2,已知AB∥CD,BE平分∠ABC,DE平分∠ADC.BE、DE所在直线交于点E,若∠FAD=60°,∠ABC=40°,求∠BED的度数;(3)将图2中的点B移到点A的右侧,得到图3,其他条件不变,若∠FAD=α°,∠ABC=β°,请你求出∠BED的度数(用含α,β的式子表示).21.(2019春•赣州期末)如图1,已知AB∥CD,∠B=20°,∠D=110°.(1)若∠E=50°,请直接写出∠F的度数;(2)探索∠E与∠F之间满足的数量关系,并说明理由;(3)如图2,EP平分∠BEF,FG平分∠EFD,FG的反向延长线交EP于点P,求∠P的度数.三.平行线的性质(共1小题)22.(2021春•鼓楼区校级期中)如图,已知:点A、C、B不在同一条直线,AD∥BE.(1)求证:∠B+∠C﹣∠A=180°.(2)如图②,AQ、BQ分别为∠DAC、∠EBC的平分线所在直线,试探究∠C与∠AQB的数量关系;(3)如图③,在(2)的前提下,且有AC∥QB,直线AQ、BC交于点P,QP⊥PB,请求出∠DAC:∠ACB:∠CBE的值.四.平行线的判定与性质(共22小题)23.(2021秋•深圳期末)如图,AB⊥BC,AE平分∠BAD交BC于E,AE⊥DE,∠1+∠2=90°,M,N分别是BA,CD延长线上的点,∠EAM和∠EDN的平分线交于点F.下列结论:①AB∥CD;②∠AEB+∠ADC=180°;③DE平分∠ADC;④∠F=135°,其中正确的有()A.1个B.2个C.3个D.4个24.(2021秋•禅城区期末)已知:如图,点B、C在线段AD的异侧,点E、F分别是线段AB、CD上的点,∠AEG =∠AGE,∠C=∠DGC.(1)求证:AB∥CD;(2)若∠AGE+∠AHF=180°,求证:∠B=∠C;(3)在(2)的条件下,若∠BFC=4∠C,求∠D的度数.25.(2021秋•福田区校级期末)点E在射线DA上,点F、G为射线BC上两个动点,满足∠DBF=∠DEF,∠BDG =∠BGD,DG平分∠BDE.(1)如图1,当点G在F右侧时,求证:BD∥EF;(2)如图2,当点G在F左侧时,求证:∠DGE=∠BDG+∠FEG;(3)如图3,在(2)的条件下,P为BD延长线上一点,DM平分∠BDG,交BC于点M,DN平分∠PDM,交EF于点N,连接NG,若DG⊥NG,∠B﹣∠DNG=∠EDN,则∠B的度数为.26.(2021秋•嵩县期末)图1展示了光线反射定律:EF是镜面AB的垂线,一束光线m射到平面镜AB上,被AB 反射后的光线为n,则入射光线m,反射光线n与垂线EF所夹的锐角θ1=θ2.(1)在图1中,证明:∠1=∠2.(2)图2中,AB,BC是平面镜,入射光线m经过两次反射后得到反射光线n,已知∠1=30°,∠4=60°,判断直线m与直线n的位置关系,并说明理由.(3)图3是潜望镜工作原理示意图,AB,CD是平行放置的两面平面镜.请解释进入潜望镜的光线m为什么和离开潜望镜的光线n是平行的?27.(2021秋•九龙县期末)如图,已知点A在EF上,点P,Q在BC上,∠E=∠EMA,∠BQM=∠BMQ.(1)求证:EF∥BC;(2)若FP⊥AC,∠2+∠C=90°,求证:∠1=∠B;(3)若∠3+∠4=180°,∠BAF=3∠F﹣20°,求∠B的度数.28.(2019•重庆开学)如图1,直线MN与直线AB、CD分别交于点E、F,∠MEB与∠DFN互补.(1)若∠BEF与∠EFD的角平分线交于点P,EP与CD交于点G,点H是MN上一点,且GH⊥EG,求证:PF∥GH;(2)如图2,在(1)的条件下,连接PH,K是GH上一点使∠PHK=∠HPK,作PQ平分∠EPK,问∠HPQ 的大小是否发生变化?若不变,请求出其值;若变化,请说明理由.29.(2021秋•南岗区校级期末)已知:直线AB∥CD,一块三角板EFH,其中∠EFH=90°,∠EHF=60°.(1)如图1,三角板EFH的顶点H落在直线CD上,并使EH与直线AB相交于点G,若∠2=2∠1,求∠1的度数;(2)如图2,当三角板EFH的顶点F落在直线AB上,且顶点H仍在直线CD上时,EF与直线CD相交于点M,试确定∠E、∠AFE、∠MHE的数量关系;(3)如图3,当三角板EFH的顶点F落在直线AB上,顶点H在AB、CD之间,而顶点E恰好落在直线CD上时得△EFH,在线段EH上取点P,连接FP并延长交直线CD于点T,在线段EF上取点K,连接PK并延长交∠CEH的角平分线于点Q,若∠Q﹣∠HFT=15°,且∠EFT=∠ETF,求证:PQ∥FH.30.(2021春•庆云县期末)已知:如图(1)直线AB、CD被直线MN所截,∠1=∠2.(1)求证:AB∥CD;(2)如图(2),点E在AB,CD之间的直线MN上,P、Q分别在直线AB、CD上,连接PE、EQ,PF平分∠BPE,QF平分∠EQD,则∠PEQ和∠PFQ之间有什么数量关系,请直接写出你的结论;(3)如图(3),在(2)的条件下,过P点作PH∥EQ交CD于点H,连接PQ,若PQ平分∠EPH,∠QPF:∠EQF=1:5,求∠PHQ的度数.31.(2021春•鼓楼区期末)珠江某河段两岸安置了两座可旋转探照灯A,B.如图1,2所示,假如河道两岸是平行的,PQ∥MN,且∠BAM=2∠BAN,灯A射线从AM开始顺时针旋转至AN便立即回转,灯B射线从BP开始顺时针旋转至BQ便立即回转,两灯不停交叉照射巡视,且灯A转动的速度是每秒2度,灯B转动的速度是每秒1度.(1)填空:∠BAN=°;(2)若灯B射线先转动30秒,灯A射线才开始转动,在灯B射线到达BQ之前,A灯转动几秒,两灯的光束互相平行?(3)如图3,若两灯同时转动,在灯A射线到达AN之前,若两灯发出的射线AC与BC交于点C,过C作∠ACD 交PQ于点D,且∠ACD=120°,则在转动过程中,请探究∠BAC与∠BCD的数量关系,并说明理由.32.(2021春•福田区校级月考)某学习小组发现一个结论:已知直线a∥b,若直线c∥a,则c∥b.他们发现这个结论运用很广,请你利用这个结论解决以下问题:已知直线AB∥CD,点E在AB、CD之间,点P、Q分别在直线AB、CD上,连接PE、EQ.(1)如图1,运用上述结论,探究∠PEQ与∠APE+∠CQE之间的数量关系.并说明理由;(2)如图2,PF平分∠BPE,QF平分∠EQD,当∠PEQ=130°时,求出∠PFQ的度数;(3)如图3,若点E在CD的下方,PF平分∠BPE,QH平分∠EQD,QH的反向延长线交PF于点F,当∠PEQ =80°时,请直接写出∠PFQ的度数.33.(2021春•罗湖区校级期末)如图1,BC⊥AF于点C,∠A+∠1=90°.(1)求证:AB∥DE;(2)如图2,点P从点A出发,沿线段AF运动到点F停止,连接PB,PE.则∠ABP,∠DEP,∠BPE三个角之间具有怎样的数量关系(不考虑点P与点A,D,C重合的情况)?并说明理由.34.(2021春•饶平县校级期末)已知AM∥CN,点B为平面内一点,AB⊥BC于B.(1)如图1,直接写出∠A和∠C之间的数量关系;(2)如图2,过点B作BD⊥AM于点D,求证:∠ABD=∠C;(3)如图3,在(2)问的条件下,点E、F在DM上,连接BE、BF、CF,BF平分∠DBC,BE平分∠ABD,若∠FCB+∠NCF=180°,∠BFC=3∠DBE,求∠EBC的度数.35.(2020春•湘桥区期末)(1)如图1,AB∥CD,∠AEP=40°,∠PFD=130°.求∠EPF的度数.小明想到了以下方法(不完整),请填写以下结论的依据:如图1,过点P作PM∥AB,∴∠1=∠AEP=40°()∵AB∥CD,(已知)∴PM∥CD,()∴∠2+∠PFD=180°.()∵∠PFD=130°,∴∠2=180°﹣130°=50°.∴∠1+∠2=40°+50°=90°.即∠EPF=90°.(2)如图2,AB∥CD,点P在AB,CD外,问∠PEA,∠PFC,∠P之间有何数量关系?请说明理由;(3)如图3所示,在(2)的条件下,已知∠P=α,∠PEA的平分线和∠PFC的平分线交于点G,用含有α的式子表示∠G的度数是.(直接写出答案,不需要写出过程)36.(2020春•香洲区校级期中)如图,AD交BC于点D,点F在BA的延长线上,点E在线段CD上,EF与AC 相交于点G,∠BDA+∠CEG=180°.(1)证明AD∥EF;(2)若点H在FE的延长线上,且∠EDH=∠C,∠F=∠H,则∠BAD和∠CAD相等吗?请说明理由;(3)在(2)的条件下,若FH⊥BC,∠C=30°,求∠F的度数.37.(2020春•海勃湾区期末)如图1,直线MN与直线AB、CD分别交于点E、F,∠1与∠2互补.(1)试判断直线AB与直线CD的位置关系,并说明理由;(2)如图2,∠BEF与∠EFD的角平分线交于点P,EP与CD交于点G,点H是MN上一点,且GH⊥EG,求证:PF∥GH;(3)如图3,在(2)的条件下,连接PH,K是GH上一点使∠PHK=∠HPK,作PQ平分∠EPK,求∠HPQ 的度数.38.(2020春•广宁县期末)探索:小明在研究数学问题:已知AB∥CD,AB和CD都不经过点P,探索∠P与∠C 的数量关系.发现:在图1中,:∠APC=∠A+∠C;如图5小明是这样证明的:过点P作PQ∥AB∴∠APQ=∠A()∵PQ∥AB,AB∥CD.∴PQ∥CD()∴∠CPQ=∠C∴∠APQ+∠CPQ=∠A+∠C即∠APC=∠A+∠C(1)为小明的证明填上推理的依据;(2)应用:①在图2中,∠P与∠A、∠C的数量关系为;②在图3中,若∠A=30°,∠C=70°,则∠P的度数为;(3)拓展:在图4中,探究∠P与∠A,∠C的数量关系,并说明理由.39.(2019春•茂名期中)如图1,CE平分∠ACD,AE平分∠BAC,∠EAC+∠ACE=90°.(1)请判断AB与CD的位置关系,并说明理由;(2)如图2,在(1)的结论下,当∠E=90°保持不变时,移动直角顶点E,使∠MCE=∠ECD,当直角顶点E点移动时,请确定∠BAE与∠MCD的数量关系,并说明理由;(3)如图3,在(1)的结论下,P为线段AC上的一个定点,点Q为直线CD上的一个动点,当点Q在射线CD上运动时(点C除外)∠BAC与∠CPQ+∠CQP有何数量关系?为什么?40.(2019春•东莞市校级月考)(1)如图①,AB∥CD,点E在直线AB与CD之间,连接AE、CE.证明:∠A+∠C=∠E;(2)当点E在如图②的位置时,AB∥CD,证明:∠A+∠E+∠C=360°;(3)如图③,点E、F、G在直线AB与CD之间,AB∥CD,连接AE、EF、FG、CG,若∠EFG=28°,则∠A+∠E+∠G+∠C=°.41.(2017春•广州期末)图1展示了光线反射定律:EF是镜面AB的垂线,一束光线m射到平面镜AB上,被AB 反射后的光线为n,则入射光线m,反射光线n与垂线EF所夹的锐角θ1=θ2.(1)在图1中,证明:∠1=∠2.(2)图2是潜望镜工作原理示意图,AB,CD是平行放置的两面平面镜.请解释进入潜望镜的光线m为什么和离开潜望镜的光线n是平行的?(3)图3中,AB,BC是平面镜,入射光线m经过两次反射后,反射光线n与m平行但方向相反,求∠ABC的度数.42.(2017春•长兴县期末)如图甲所示,已知点E在直线AB上,点F,G在直线CD上,且∠EFG=∠FEG,EF 平分∠AEG.(1)判断直线AB与直线CD是否平行,并说明理由.(2)如图乙所示,H是AB上点E右侧一动点,∠EGH的平分线GQ交FE的延长线于点Q,设∠Q=α,∠EHG =β①若∠HEG=40°,∠QGH=20°,求∠Q的度数.②判断:点H在运动过程中,α和β的数量关系是否发生变化?若不变,求出α和β的数量关系;若变化,请说明理由.43.(2015春•越秀区期末)如图1,在四边形ABCD中,∠ABC+∠ADC=180°,BE、DF分别是∠ABC与∠ADC 的平分线,∠ADF与∠AFD互余.(1)试判断直线BE与DF的位置关系,并说明理由;(2)如图2,延长CB、DF相交于点G,过点B作BH⊥FG,垂足为点H,试判断∠FBH与∠GBH的大小关系,并说明理由.44.(2013春•福田区期末)把下面的说理过程补充完整.已知:如图,∠1+∠2=180°,∠3=∠B,试判断∠AED与∠C的关系,并说明理由.解:∠AED=∠C∵∠1+∠ADG=180°(平角定义),∠1+∠2=180°(已知)∴∠2=∠ADG()∴EF∥AB()∴∠3=∠ADE()∵∠3=∠B(已知)∴∠B=()∴DE∥BC()∴∠AED=∠C()五.平移的性质(共2小题)45.(2017春•硚口区期末)如图1,将线段AB平移至DC,使点A与点D对应,点B与点C对应,连AD、BC.(1)填空:AB与CD的位置关系为,BC与AD的位置关系为;(2)点E、G都在直线CD上,∠AGE=∠GAE,AF平分∠DAE交直线CD于F,①如图2,若G、E为射线DC上的点,∠FAG=30°,求∠B的度数;②如图3,若G、E为射线CD上的点,∠FAG=α,求∠C的度数.46.(2016秋•吉林期末)如图,点C、M、N在射线DQ上,点B在射线AP上,且AP∥DQ,∠D=∠ABC=80°,∠1=∠2,AN平分∠DAM.(1)试说明AD∥BC的理由;(2)试求∠CAN的度数;(3)平移线段BC.①试问∠AMD:∠ACD的值是否发生变化?若不会,请求出这个比值;若会,请找出相应变化规律;②若在平移过程中存在某种位置,使得∠AND=∠ACB,试求此时∠ACB的度数.。
平行线的判定及性质 例题及练习

平行线的判定及性质一、【基础知识精讲】1、平行线的判定(1)平行公理:经过直线外一点,有且只有一条直线与已知直线平行. (2)平行公理的推论:平行于同一条直线的两条直线. (3)在同一平面内,垂直于同一条直线的两条直线. (4)同位角相等,两直线平行. (5)内错角相等,两直线平行.(6)同旁内角互补,两直线平行.3、平行线的性质(1)两直线平行,同位角相等. (2)两直线平行,内错角相等.(3)两直线平行,同旁内角互补.二、【例题精讲】专题一:余角、补角、对顶角与三线八角例题1:∠A的余角与∠A的补角互为补角,那么2∠A是()A.直角 B.锐角 C.钝角 D.以上三种都有可能【活学活用1】如图2-79中,下列判断正确的是()A.4对同位角,2对内错角,4对同旁内角B.4对同位角,2对内错角,2对同旁内角C.6对同位角,4对内错角,4对同旁内角D.6对同位角,4对内错角,2对同旁内角【活学活用2】如图2-82,下列说法中错误的是( )A.∠3和∠5是同位角B.∠4和∠5是同旁内角C.∠2和∠4是对顶角D.∠1和∠2是同位角【活学活用3】如图,直线AB与CD交于点O,OE⊥AB于O,图中∠1与∠2的关系是()A.对顶角B.互余C.互补D相等例题2:如果两个角的两边分别平行,而其中一个角比另一个角的4倍少30°,那么这两个角分别是_______.【活学活用4】如图,∠AOC +∠DOE +∠BOF = .专题二:平行线的判定例题3:如图,已知∠EFB+∠ADC=180°,且∠1=∠2,试说明DG ∥AB.1 2A BCDF E G【活学活用】1、长方体的每一对棱相互平行,那么这样的平行棱共有 ( )A .9对B .16对 C.18对 D .以上答案都不对2、已知:如图2-96,DE ⊥AO 于E,BO ⊥AO,FC ⊥AB 于C ,∠1=∠2,求证:DO ⊥AB.3、如图2-97,已知:∠1=∠2=,∠3=∠4,∠5=∠6.求证:AD ∥BC.4、如图2—101,若要能使AB ∥ED ,∠B 、∠C 、∠D 应满足什么条件?ABCDOE F5、同一平面内有四条直线a 、b 、c 、d ,若a ∥b ,a ⊥c ,b ⊥d ,则c 、d 的位置关系为( ) A.互相垂直 B .互相平行 C.相交 D .没有确定关系专题三:平行线的性质1、如图,110,ABC ACB BO ∠+∠=、CO 分别平分ABC ∠和,ACB EF ∠过点O 与BC 平行,则BOC ∠= . 2、如图,AB //CD ,BC //DE ,则∠B+∠D = .3、如图,直线AB 与CD 相交于点O ,OB 平分∠DOE .若60DOE ∠=,则∠AOC 的度数是 .4、 如图,175,2120,375∠=∠=∠=,则4∠= .13 425、如图,//AB CD ,直线EF 分别交AB 、CD 于E 、F ,ED 平分BEF ∠,若172∠=,则2∠= .【例题讲解】例1:如图,已知:AD ∥BC, ∠AEF=∠B,求证:AD ∥EF 。
2、平行线的判定和性质练习题
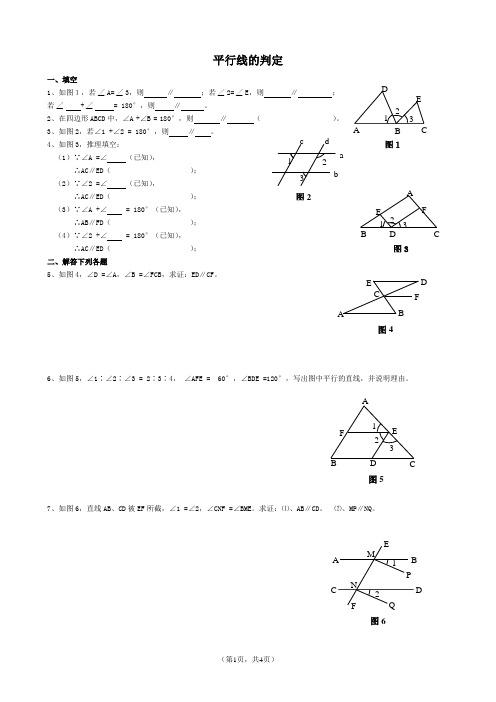
一、填空1、如图1,若∠A=∠3,则 ∥ ;若∠2=∠E ,则 ∥ ;若∠ +∠ = 180°,则 ∥ 。
2、在四边形ABCD 中,∠A +∠B = 180°,则 ∥ ( )。
3、如图2,若∠1 +∠2 = 180°,则 ∥ 。
4、如图3,推理填空:(1)∵∠A =∠ (已知),∴AC∥ED( ); (2)∵∠2 =∠ (已知),∴AC∥ED( ); (3)∵∠A +∠ = 180°(已知), ∴AB∥FD( ); (4)∵∠2 +∠ = 180°(已知), ∴AC∥ED( ); 二、解答下列各题5、如图4,∠D =∠A,∠B =∠FCB,求证:ED∥CF。
6、如图5,∠1∶∠2∶∠3 = 2∶3∶4, ∠AFE = 60°,∠BDE =120°,写出图中平行的直线,并说明理由。
7、如图6,直线AB 、CD 被EF 所截,∠1 =∠2,∠CNF =∠BME。
求证:⑴、AB∥CD。
⑵、MP∥NQ。
a bc d 1 23 图2AB CED12 3 图11 2 3 AF CDB E图3E BAFD C图41 32 A E CD BF 图5F2A B CDQE1 P MN 图6一、填空1、如图1,已知∠1 = 100°,AB∥CD,则∠2 = ,∠3 = ,∠4 = 。
2、如图2,直线AB 、CD 被EF 所截,若∠1 =∠2,则∠AEF +∠CFE = 。
3、如图3所示:⑴、若EF∥AC,则∠A +∠ = 180°,∠F + ∠ = 180°( )。
⑵、若∠2 =∠ ,则AE∥BF。
⑶、若∠A +∠ = 180°,则AE∥BF。
4、如图4,AB∥CD,∠2 = 2∠1,则∠2 = 。
5、如图5,AB∥CD,EG⊥AB 于G ,∠1 = 50°,则∠E = 。
6、如图6,AB∥CD,AC⊥BC,图中与∠CAB 互余的角有 。
七年级平行线的判定与性质精选练习题

1 / 31 32 A E CD B F图10七年级--平行线的判定与性质精选题一.完成推理,填写推理依据:1.如图⑩ ∵∠B=∠_______,∴ AB ∥CD ( ) ∵∠BGC=∠_______,∴ CD ∥EF ( )∵AB ∥CD ,CD ∥EF ,∴ AB ∥_______( )2.如图⑾ 填空: (1)∵∠2=∠3(已知)∴ AB__________( )(2)∵∠1=∠A (已知)__________( )(3)∵∠1=∠D (已知)∴ __________( )(4)∵_______=∠F ∴ AC ∥DF ( ))二.证明题1.已知:如图⑿,CE 平分∠ACD ,∠1=∠B ,求证:AB ∥CE2.如图:∠1=︒53,∠2=︒127,∠3=︒53, 试说明直线AB 与CD ,BC 与DE 的位置关系。
3.如图:已知∠A=∠D ,∠B=∠FCB ,能否确定ED 与CF 的位置关系,请说明理由。
4.已知:如图,,,且.求证:EC ∥DF.5.如图10,∠1∶∠2∶∠3 = 2∶3∶4, ∠AFE = 60°,∠BDE =120°,2 / 3写出图中平行的直线,并说明理由.6如图11,直线AB 、CD 被EF 所截,∠1 =∠2,∠CNF =∠BME。
求证:AB∥CD,MP∥NQ.7.已知:如图,∠1=∠2,且BD 平分∠ABC .求证:AB ∥CD.8.已知:如图,∠1=∠2,∠3=100°,∠B =80°.求证:EF ∥C D .9.如图12,∠ABD 和∠BDC 的平分线交于E ,BE 交CD 于点F ,∠1 +∠2 = 90°.求证:(1)AB∥CD; (2)∠2 +∠3 = 90°.10.如图,一条公路修到湖边时,需拐弯绕湖而过,如果第一次拐的角A 是120°,第二次拐的角B 是150°,第三次拐的角是∠C ,这时的道路恰好和第一次拐弯之前的道路平行问∠C 是多少度?说明你的理由.13.如图9,已知∠ABE +∠DEB = 180°,∠1 =∠2,求证:∠F =∠G. F2 A B C D Q E 1 PMN 图11 图91 2A C BF G EDC图1212 3A B DF3 / 3。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
七年级--平行线的判定与性质精选题一.完成推理,填写推理依据:
1.如图⑩∵∠B=∠_______,∴AB∥CD()∵∠BGC=∠_______,∴CD∥EF()
∵AB∥CD ,CD∥EF,
∴AB∥_______()
2.如图⑾填空:
(1)∵∠2=∠3(已知)∴AB__________()(2)∵∠1=∠A(已知)__________()(3)∵∠1=∠D(已知)∴__________()(4)∵_______=∠F∴AC∥DF()
)
二.证明题
1.已知:如图⑿,CE平分∠ACD,∠1=∠B,
求证:AB∥CE
2.如图:∠1=︒
53,
53,∠2=︒
127,∠3=︒
试说明直线AB与CD,BC与DE的位置关系。
3.如图:已知∠A=∠D,∠B=∠FCB,能否确定ED与CF的位置关系,请说明理由。
1 3
2 A E C
D B F
图10 4.已知:如图,
,,
且
.
求证:EC ∥DF.
5.如图10,∠1∶∠2∶∠3 = 2∶3∶4, ∠AFE = 60°,∠BDE =120°,
写出图中平行的直线,并说明理由.
6如图11,直线AB 、CD 被EF 所截,∠1 =∠2,∠CNF =∠BME。
求证:AB∥CD,MP∥NQ.
7.已知:如图,∠1=∠2,且BD 平分∠ABC .求证:AB ∥CD.
F
2 A B C D Q E 1 P
M
N 图11
8.已知:如图,∠1=∠2,∠3=100°,∠B =80°.求证:EF ∥C D .
9.如图12,∠ABD 和∠BDC 的平分线交于E ,BE 交CD 于点F ,∠1 +∠2 = 90°.
求证:(1)AB∥CD; (2)∠2 +∠3 = 90°.
10.如图,一条公路修到湖边时,需拐弯绕湖而过,如果第一次拐的角A 是120°,第二次拐的角B 是150°,第三次拐的角是∠C ,这时的道路恰好和第一次拐弯之前的道路平行问∠C 是多少度?说明你的理由.
13.如图9,已知∠ABE +∠DEB = 180°,∠1 =∠2,求证:∠F =∠G.
图9
1 2 A C B
F G E
D
C
图12
1
2 3
A B D
F。
