【内供】2019届高三8月内部特供卷 理科数学(二)学生版
2019年高考理科数学全国2卷(附答案)(2)[2]
![2019年高考理科数学全国2卷(附答案)(2)[2]](https://img.taocdn.com/s3/m/3b065c981711cc7931b716f4.png)
20 19年高考理科数学全国2卷(附答案)( 2) (w or d 版可编辑修改是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔(2)( wo rd 版可编辑修改))的内容能够给您的工作和学习带来便利。
同时也真诚如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以_ —理科数学 全国 II 卷___ - 本试卷共 23 小题,满分150 分,考试用时120 分钟:号 -(适用地区:内蒙古 / 黑龙江 /辽宁 /吉林 /重庆 /陕西 / 甘肃 /宁/新疆 / 西藏 /海南 )学 —注意事项:_-__1. 答卷前,考生务必将自己的姓名、考生号等填写在答题卡和试卷指定位置_-__2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案__ —如需改动,用橡皮擦干净后,再选涂其它答案标号。
回答非选择题时写在___答题卡上。
写在本试卷上无效。
_ 线__ 封_3. 考试结束后,将本试卷和答题卡一并交回。
_密__ —__12 小题,每小题 5 分,共 60 分.在每个小题给选 : —一、 选择题:本题共名 — 项中,只有一项是符合题目要求的。
姓—2— 1.设集合 A={ x|x —5x+6>0} , B={ x|x-1<0} ,则 A∩B=班 -A . (-∞, 1)B . (-2, 1)C .(-3 , —1)D . (3, +∞___ —_2 .设 z=—3+2i ,则在复平面内 z 对应的点位于_—__ A .第一象限B .第二象限C .第三象限D .第四象限年 -____线 3 .已知 AB =(2,3) , AC =(3 ,t), BC =1,则 AB BC = __ 封_ A .—3 B .—2 C . 2D . 3 _ 密_-__4. 2019 年 1 月 3 日嫦娥四号探测器成功实现人类历史上首次月球背面软_ -__R,L2点到月球的距离为r ,根据牛顿运动定律和万有引力定律,地月连长线上.设地球质量为M1,月球质量为M2,地月距离为R, L2点到月距离为 r,根据牛顿运动定律和万有引力定律,r 满足方程:M1M 2M1(R r)2r2(R r )3。
(2021年整理)2019届全国高考高三模拟考试卷数学(理)试题(二)(解析版)

2019届全国高考高三模拟考试卷数学(理)试题(二)(解析版)编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(2019届全国高考高三模拟考试卷数学(理)试题(二)(解析版))的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为2019届全国高考高三模拟考试卷数学(理)试题(二)(解析版)的全部内容。
2019届全国高考高三模拟考试卷数学(理)试题(二)(解析版)注意事项:1.答题前,先将自己的姓名、准考证号填写在试题卷和答题卡上,并将准考证号条形码粘贴在答题卡上的指定位置。
2.选择题的作答:每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑,写在试题卷、草稿纸和答题卡上的非答题区域均无效.3.非选择题的作答:用签字笔直接答在答题卡上对应的答题区域内。
写在试题卷、草稿纸和答题卡上的非答题区域均无效.4.考试结束后,请将本试题卷和答题卡一并上交.一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.[2019·南昌一模]已知复数()i2ia z a +=∈R 的实部等于虚部,则a =( ) A .12-B .12C .1-D .12.[2019·梅州质检]已知集合{}31,A x x n n ==-∈N ,{}6,8,10,12,14B =,则集合A B 中元素的个数为( ) A .2B .3C .4D .53.[2019·菏泽一模]已知向量()1,1=-a ,()2,3=-b ,且()m ⊥+a a b ,则m =( ) A .25B .25-C .0D .154.[2019·台州期末]已知圆C :()()22128x y -+-=,则过点()3,0P 的圆C 的切线方程为( ) A .30x y +-=B .30x y --=C .230x y --=D .230x y +-=5.[2019·东北三校]中国有十二生肖,又叫十二属相,每一个人的出生年份对应了十二种动物(鼠、牛、虎、兔、龙、蛇、马、羊、猴、鸡、狗、猪)中的一种,现有十二生肖的吉祥物各一个,三位同学依次选一个作为礼物,甲同学喜欢牛和马,乙同学喜欢牛、狗和羊,丙同学哪个吉祥物都喜欢,如果让三位同学选取礼物都满意,则选法有( ) A .30种B .50种C .60种D .90种6.[2019·汕尾质检]某空间几何体的三视图如图所示,正视图是底边长为3的等腰三角形,侧视图是直角边长为1的等腰直角三角形,俯视图是扇形,则该几何体的体积为( )A .π9B .π3C .π6D .π187.[2019合肥质检]将函数()π2sin 16f x x ⎛⎫=+- ⎪⎝⎭的图象上各点横坐标缩短到原来的12(纵坐标不变)得到函数()g x 的图象,则下列说法正确的是( ) A .函数()g x 的图象关于点π,012⎛⎫- ⎪⎝⎭对称 B .函数()g x 的周期是π2C .函数()g x 在π0,6⎛⎫ ⎪⎝⎭上单调递增D .函数()g x 在π0,6⎛⎫ ⎪⎝⎭上最大值是18.[2019·临沂质检]执行如图所示的程序框图,输出的值为( )A .0B .12C .1D .1-9.[2019·重庆一中]2sin80cos70cos20︒︒-=︒( )A .B .1CD .210.[2019·揭阳一模]函数()f x 在[)0,+∞单调递减,且为偶函数.若()21f =-,则满足()31f x -≥-的x 的取值范围是( ) A .[]1,5B .[]1,3C .[]3,5D .[]2,2-11.[2019·陕西联考]已知双曲线()2222:10,0x y C a b a b-=>>的右焦点为2F ,若C 的左支上存在点M ,使得直线0bx ay -=是线段2MF 的垂直平分线,则C 的离心率为( )AB .2CD .512.[2019·临川一中]若函数()f x 在其图象上存在不同的两点()11,A x y ,()22,B x y ,其坐标满足条件:1212x x y y +0,则称()f x 为“柯西函数",则下列函数:①()()10f x x x x=+>;②()()ln 0e f x x x =<<;③()cos f x x =;④()21f x x =-.其中为“柯西函数”的个数为( ) A .1B .2C .3D .4二、填空题:本大题共4小题,每小题5分,共20分.13.[2019·江门一模]已知a 、b 、c 是锐角ABC △内角A 、B 、C 的对边,S 是ABC △的面积,若8a =,5b =,S =,则c =_________.14.[2019·景山中学]已知a ,b 表示直线,α,β,γ表示不重合平面. ①若a αβ=,b α⊂,a b ⊥,则αβ⊥;②若a α⊂,a 垂直于β内任意一条直线,则αβ⊥; ③若αβ⊥,a αβ=,b αγ=,则a b ⊥;④若a α⊥,b β⊥,a b ∥,则αβ∥.上述命题中,正确命题的序号是__________.15.[2019·林芝二中]某传媒大学的甲、乙、丙、丁四位同学分别从影视配音、广播电视、公共演讲、播音主持四门课程中选修一门,且这四位同学选修的课程互不相同.下面是关于他们选课的一些信息:①甲同学和丙同学均不选播音主持,也不选广播电视;②乙同学不选广播电视,也不选公共演讲;③如果甲同学不选公共演讲,那么丁同学就不选广播电视.若这些信息都是正确的,依据以上信息可推断丙同学选修的课程是_______(填影视配音、广播电视、公共演讲、播音主持)16.[2019·河南联考]若一直线与曲线eln y x =和曲线2y mx =相切于同一点P ,则实数m =________.三、解答题:本大题共6大题,共70分,解答应写出文字说明、证明过程或演算步骤. 17.(12分)[2019·长郡中学]设正项数列{}n a 的前n 项和为n S是n a 与1n a +的等比中项,其中*n ∈N .(1)求数列{}n a 的通项公式; (2)设()11211n n n n n a b a a +++=-⋅,记数列{}n b 的前n 项和为n T ,求证:21n T <.18.(12分)[2019·维吾尔一模]港珠澳大桥是中国建设史上里程最长,投资最多,难度最大的跨海桥梁项目,大桥建设需要许多桥梁构件.从某企业生产的桥梁构件中抽取100件,测量这些桥梁构件的质量指标值,由测量结果得到如图所示的频率分布直方图,质量指标值落(1)求这些桥梁构件质量指标值落在区间[]75,85内的频率;(2)若将频率视为概率,从该企业生产的这种桥梁构件中随机抽取3件,记这3件桥梁构件中质量指标值位于区间[)45,75内的桥梁构件件数为X ,求X 的分布列与数学期望.19.(12分)[2019·淄博模拟]如图,在四棱锥P ABCD -中,AB CD ∥,1AB =,3CD =,2AP =,23DP =60PAD ∠=︒,AB ⊥平面PAD ,点M 在棱PC 上.(1)求证:平面PAB ⊥平面PCD ;20.(12分)[2019·泰安期末]已知椭圆()22122:10x y C a b a b+=>>的离心率为22,抛物线22:4C y x =-的准线被椭圆1C 截得的线段长为2.(1)求椭圆1C 的方程;(2)如图,点A 、F 分别是椭圆1C 的左顶点、左焦点直线l 与椭圆1C 交于不同的两点M 、N (M 、N 都在x 轴上方).且AFM OFN ∠=∠.证明:直线l 过定点,并求出该定点的坐标.21.(12分)[2019·衡水中学]已知函数()23ln f x x ax x =+-,a ∈R .(1)当13a =-时,求函数()f x 的单调区间;(2)令函数()()2x x f x ϕ'=,若函数()x ϕ的最小值为32-,求实数a 的值.请考生在22、23两题中任选一题作答,如果多做,则按所做的第一题记分. 22.(10分)【选修4—4:坐标系与参数方程】[2019·揭阳一模]以原点O 为极点,x 轴的非负半轴为极轴建立极坐标系,已知曲线C 的极坐标方程为22cos 2a ρθ=(a ∈R ,a 为常数)),过点()2,1P 、倾斜角为30︒的直线l 的参数方程满足2x =+,(t 为参数). (1)求曲线C 的普通方程和直线l 的参数方程;(2)若直线l 与曲线C 相交于A 、B 两点(点P 在A 、B 之间),且2PA PB ⋅=,求a 和PA PB -的值.23.(10分)【选修4—5:不等式选讲】[2019·汕尾质检]已知()221f x x x =++-的最小值为t .求t 的值;若实数a ,b 满足2222a b t +=,求221112a b +++的最小值.2019届高三第三次模拟考试卷理 科 数 学(二)答 案一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的. 1.【答案】C 【解析】∵()2i i i 1i 2i 2i 22a a a z -++===--的实部等于虚部,∴122a=-,即1a =-.故选C . 2.【答案】A【解析】由题意,集合{}31,A x x n n ==-∈N ,{}6,8,10,12,14B =, ∴{}8,14A B =,∴集合A B 中元素的个数为2.故选A . 3.【答案】A【解析】()()()1,12,312,31m m m m m +=-+-=--a b ,结合向量垂直判定,建立方程,可得12310m m --+=,解得25m =,故选A . 4.【答案】B【解析】根据题意,圆C :()()22128x y -+-=,P 的坐标为()3,0,则有()()2231028-+-=,则P 在圆C 上,此时20113CP K -==--,则切线的斜率1k =,则切线的方程为3y x =-,即30x y --=,故选B . 5.【答案】B【解析】若同学甲选牛,那么同学乙只能选狗和羊中的一种,丙同学可以从剩下的10中任意选,∴共有11210C C 20⋅=, 若同学甲选马,那么同学乙能选牛、狗和羊中的一种,丙同学可以从剩下的10中任意选,∴共有11310C C 30⋅=,∴共有203050+=种.故选B .6.【答案】A【解析】由三视图可知,该几何体是圆锥的一部分,正视图是底边长为3的等腰三角形, 侧视图是直角边长为1的等腰直角三角形,圆锥的高为1,底面半径为1, 俯视图是扇形,圆心角为2π3,几何体的体积为112ππ113239⨯⨯⨯⨯=.故选A . 7.【答案】C【解析】将函数()f x 横坐标缩短到原来的12后,得到()π2sin 216g x x ⎛⎫=+- ⎪⎝⎭,当π12x =-时,π112f ⎛⎫-=- ⎪⎝⎭,即函数()g x 的图象关于点π,112⎛⎫-- ⎪⎝⎭对称,故选项A 错误; 周期2ππ2T ==,故选项B 错误; 当π0,6x ⎛⎫∈ ⎪⎝⎭时,πππ2662x ⎛⎫+∈ ⎪⎝⎭,,∴函数()g x 在π0,6⎛⎫⎪⎝⎭上单调递增,故选项C 正确;∵函数()g x 在π0,6⎛⎫ ⎪⎝⎭上单调递增,∴()π16g x g ⎛⎫<= ⎪⎝⎭,即函数()g x 在π0,6⎛⎫ ⎪⎝⎭上没有最大值,故选项D 错误.故选C .8.【答案】A【解析】第一次循环,1k =,cos01S ==,112k =+=,4k >不成立; 第二次循环,2k =,π131cos 1322S =+=+=,213k =+=,4k >不成立; 第三次循环,3k =,32π31cos12322S =+=-=,314k =+=,4k >不成立; 第四次循环,4k =,1cos π110S =+=-=,415k =+=,4k >成立, 退出循环,输出0S =,故选A . 9.【答案】C 【解析】∵()2sin 6020cos702sin80cos70cos20cos20︒+︒︒-︒-︒=︒︒2sin 60cos202cos60sin 20cos70cos20︒︒+︒︒-︒=︒2sin 60cos20sin 20cos70cos20︒︒+︒-︒=︒2sin 60cos202sin 603cos20︒︒==︒=︒.故选C . 10.【答案】A【解析】∵函数()f x 为偶函数,∴()()312f x f -≥-=等价于()()32f x f -≥, ∵函数()f x 在[)0,+∞单调递减,∴32x -≤,232x -≤-≤,15x ≤≤,故选A . 11.【答案】C【解析】()2,0F c ,直线0bx ay -=是线段2MF 的垂直平分线, 可得2F 到渐近线的距离为222F P b b a ==+,即有22OP c b a =-=,由OP 为12MF F △的中位线,可得122MF OP a ==,22MF b =,可得212MF MF a -=,即为222b a a -=,即2b a =,可得221145c b e a a==+=+=.故选C .12.【答案】B【解析】由柯西不等式得:对任意实数1x ,1y ,2x ,2y ,2222121211220x x y y x y x y +-+⋅+≤恒成立, (当且仅当1221x y x y =取等号)若函数()f x 在其图象上存在不同的两点()11,A x y ,()22,B x y ,其坐标满足条件:222212121122x x y y x y x y +-+⋅+的最大值为0,则函数()f x 在其图象上存在不同的两点()11,A x y ,()22,B x y ,使得OA ,OB 共线, 即存在过原点的直线y kx =与()y f x =的图象有两个不同的交点:对于①,方程()10kx x x x=+>,即()211k x -=,不可能有两个正根,故不存在;对于②,,由图可知不存在;对于③,,由图可知存在;对于④,,由图可知存在,∴“柯西函数”的个数为2,故选B .二、填空题:本大题共4小题,每小题5分,共20分. 13.【答案】7【解析】根据三角形面积公式得到13sin sin 2S ab C C =⨯⇒= ∵三角形为锐角三角形,故得到角C 为π3,再由余弦定理得到222π1cos 7322a b c c ab+-==⇒=.故答案为7.14.【答案】②④【解析】对于①,根据线面垂直的判定定理,需要一条直线垂直于两条相交的直线,故不正确,对于②,a α⊂,a 垂直于β内任意一条直线,满足线面垂直的定理,即可得到αβ⊥, 又a α⊂,则αβ⊥,故正确,对于③,αβ⊥,a αβ=,b αγ=,则a b ⊥或a b ∥,或相交,故不正确, 对于④,可以证明αβ∥,故正确. 故答案为②④. 15.【答案】影视配音【解析】由①知甲和丙均不选播音主持,也不选广播电视; 由②知乙不选广播电视,也不选公共演讲;由③知如果甲不选公共演讲,那么丁就不选广播电视,综上得甲、乙、丙均不选广播电视,故丁选广播电视,从而甲选公共演讲,丙选影视配音, 故答案为影视配音. 16.【答案】12【解析】曲线eln y x =的导数为e 'y x=,曲线2y mx =的导数为2y mx '=,由e 2mx x=,0x >且0m >,得x =e 2⎫⎪⎪⎭,代入eln y x =得e 2=,解得12m =,故答案为12. 三、解答题:本大题共6大题,共70分,解答应写出文字说明、证明过程或演算步骤. 17.【答案】(1)n a n =;(2)见解析.【解析】(1n a 与1n a +的等比中项,∴()221n n n n n S a a a a =+=+, 当1n =时,21112a a a =+,∴11a =.当2n ≥时,22111222n n n n n n n a S S a a a a ---=-=+--,整理得()()1110n n n n a a a a --+--=. 又0n a >,∴()112n n a a n --=≥,即数列{}n a 是首项为1,公差为1的等差数列. ∴()()1111n a a n d n n =+-=+-=. (2)()()()1121111111n n n n b n n n n +++⎛⎫=-⋅=-+ ⎪++⎝⎭,∴21232111111111122334212221n n T b b b b n n n n ⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫=++++=+-+++-++-+ ⎪ ⎪ ⎪ ⎪ ⎪-+⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭11121n =-<+. 18.【答案】(1)0.05;(2)见解析.【解析】(1)设区间[]75,85内的频率为x ,则区间[)55,65,[)65,75内的频率分别为4x 和2x . 依题意得()0.0040.0120.0190.0310421x x x +++⨯+++=,解得0.05x =. ∴这些桥梁构件质量指标值落在区间[]75,85内的频率为0.05.(2)从该企业生产的该种桥梁构件中随机抽取3件,相当于进行了3次独立重复实验,∴X 服从二项分布(),B n p ,其中3n =.由(1)得,区间[]45,75内的频率为0.30.20.10.6++=,将频率视为概率得0.6p =.∵X 的所有可能取值为0,1,2,3,且()00330C 0.60.40.064P X ==⨯⨯=,()11231C 0.60.40.288P X ==⨯⨯=,()22132C 0.60.40.432P X ==⨯⨯=,()33033C 0.60.40.216P X ==⨯⨯=.∴X 的分布列为:X P0.0640.2880.4320.216X 服从二项分布(),B n p ,∴X 的数学期望为30.6 1.8EX =⨯=.19.【答案】(1)见解析;(2)219565. 【解析】(1)∵AB ⊥平面PAD ,∴AB DP ⊥, 又∵23DP =,2AP =,60PAD ∠=︒, 由sin sin PD PA PAD PDA =∠∠,可得1sin 2PDA ∠=,∴30PDA ∠=︒,90APD ∠=︒,即DP AP ⊥, ∵AB AP A =,∴DP ⊥平面PAB , ∵DP ⊂平面PCD ,∴平面PAB ⊥平面PCD ;(2)以点A 为坐标原点,AD 所在的直线为y 轴,AB 所在的直线为z 轴, 如图所示,建立空间直角坐标系,其中()0,0,0A ,()0,0,1B ,()0,4,3C ,()0,4,0D ,)3,1,0P . 从而()0,4,1BD =-,()3,1,0AP =,()3,3,3PC =-,设PM PC λ=,从而得)33,31,3M λλλ+,()33,31,31BM λλλ=+-,设平面MBD 的法向量为(),,x y z =n ,若直线PA ∥平面MBD ,满足000BM BD AP ⎧⋅=⎪⎪⋅=⎨⎪⋅=⎪⎩n n n,即)()()131310400x y z y z y λλλ-+++-=-=⎨+=, 得14λ=,取)3,12=--n ,且()3,1,1BP =-, 直线BP 与平面MBD所成角的正弦值等于3sin 156BP BPθ⋅-===⋅n n 20.【答案】(1)2212x y +=;(2)直线l 过定点()2,0.【解析】(1)由题意可知,抛物线2C 的准线方程为1x =, 又椭圆1C ,∴点⎛⎝⎭在椭圆上,∴221112a b +=,① 又c e a ==,∴222212a b e a -==,∴222a b =,②,由①②联立,解得22a =,21b =,∴椭圆1C 的标准方程为2212x y +=.(2)设直线:l y kx m =+,设()11,M x y ,()22,N x y ,把直线l 代入椭圆方程,整理可得()222214220k x km m +++-=,()()222222164212216880k m k m k m ∆=-+-=-+>,即22210k m -+>,∴122421kmx x k +=-+,21222221m x x k -=+,∵111FM y k x =+,221FN yk x =+,M 、N 都在x 轴上方,且AFM OFN ∠=∠,∴FM FN k k =-,∴121211y yx x =-++,即()()()()122111kx m x kx m x ++=-++, 整理可得()()1212220kx x k m x x m ++++=,∴()2222242202121m km k k m m k k -⎛⎫⋅++-+= ⎪++⎝⎭,即22224444420km k k m km k m m ---++=,整理可得2m k =, ∴直线l 为()22y kx k k x =+=+,∴直线l 过定点()2,0. 21.【答案】(1)见解析;(2)56-.【解析】(1)13a =-时,()2ln f x x x x =--,则()()()221121x x x x f x x x +---'==, 令()'0f x =,解得12x =-或1x =,而0x >,故1x =,则当()0,1x ∈时,()0f x '<,即()f x 在区间内递减,当()1,x ∈+∞时,()0f x '>,即()f x 在区间内递增.(2)由()23ln f x x ax x =+-,()123f x x a x'=+-,则()()23223x x f x x ax x ϕ'==+-,故()2661x x ax ϕ'=+-,又()()264610a ∆=-⨯⨯->,故方程()0x ϕ'=有2个不同的实根, 不妨记为1x ,2x ,且12x x <, 又∵12106x x =-<,故120x x <<, 当()20,x x ∈时,()0x ϕ'<,()x ϕ递减, 当()2,x x ∈+∞时,()0x ϕ'>,()x ϕ递增, 故()()322222min 23x x x ax x ϕϕ==+-,①又()20x ϕ'=,∴2226610x ax +-=,即222166x a x -=,②将222166x a x -=代入式,得2222222222222233316112323622x x x x x x x x x x x -+⋅⋅-=+--=--, 由题意得3221322x x --=-,即322230x x +-=, 即()()222212230x x x -++=,解得21x =, 将21x =代入式中,得56a =-.请考生在22、23两题中任选一题作答,如果多做,则按所做的第一题记分.22.【答案】(1)222x y a -=,3212x t y ==+⎧⎪⎪⎨⎪⎪⎩(t 为参数);(2)2a =±,432. 【解析】(1)由22cos 2a ρθ=得()2222cos sin a ρθθ-=,又cos x ρθ=,sin y ρθ=,得222x y a -=,∴C 的普通方程为222x y a -=, ∵过点()2,1P 、倾斜角为30︒的直线l 的普通方程为)321y x =-+, 由32x =+得112y t =+,∴直线l 的参数方程为3212x t y =+=+⎧⎪⎪⎨⎪⎪⎩(t 为参数).(2)将212x t y =+=+⎧⎪⎪⎨⎪⎪⎩代入222x y a -=,得()()2221230t t a +-+-=,依题意知()()2221830a ∆⎡⎤=-->⎣⎦,则上方程的根1t 、2t 就是交点A 、对应的参数, ∵()21223t t a ⋅=-,由参数t 的几何意义知1212PA PB t t t t ⋅=⋅=⋅,得122t t ⋅=, ∵点P 在A 、B 之间,∴120t t ⋅<,∴122t t ⋅=-,即()2232a -=-,解得24a =(满足0∆>),∴2a =±, ∵1212PA PB t t t t -=-=+,又()1221t t +=-,∴2PA PB -=. 23.【答案】(1)2;(2)1.【解析】(1)()31,12213,1131,1x x f x x x x x x x +≥⎧⎪=++-=+-<<⎨⎪--≤-⎩,故当1x =-时,函数()f x 有最小值2,∴2t =. (2)由(1)可知22222a b +=,故22124a b +++=,∴2222222222212111112121121244b a a b a b a b a b +++++++⎛⎫+++=+⋅=≥ ⎪++++⎝⎭, 当且仅当22122a b +=+=,即21a =,20b =时等号成立,故221112a b +++的最小值为1.。
2019届高三理科数学测试卷(二)附答案

第1页(共8页) 第2页(共8页)2019届高三文科数学测试卷(二)附答案注意事项:1.答题前,先将自己的姓名、准考证号填写在试题卷和答题卡上,并将准考证号条形码粘贴在答题卡上的指定位置。
2.选择题的作答:每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑,写在试题卷、草稿纸和答题卡上的非答题区域均无效。
3.非选择题的作答:用签字笔直接答在答题卡上对应的答题区域内。
写在试题卷、草稿纸和答题卡上的非答题区域均无效。
4.考试结束后,请将本试题卷和答题卡一并上交。
第Ⅰ卷一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.设集合{}20A x x =->,{}2320B x x x =-+<,若全集U A =,则U B =ð( ) A .(],1-∞B .(),1-∞C .()2,+∞D .[)2,+∞2.总体由编号为00,01,02,...,48,49的50个个体组成,利用下面的随机数表选取8个个体,选取方法是从随机数表第6行的第9列和第10列数字开始从左到右依次选取两个数字,则选出的第4个个体的编号为( ) 附:第6行至第9列的随机数表:A .3B .16C .38D .493.设i 是虚数单位,若复数()5i12ia a +∈-R 是纯虚数,则a =( ) A .1-B .1C .2-D .24.已知等差数列{}n a 的前n 项和为n S ,若341118a a a ++=,则11S =( ) A .9B .22C .36D .665.如图所示程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”,执行该程序框图,若输入a,b 的分别为10,4,则输出的a =( )A .0B .14C .4D .26.如图,在正方体1111ABCD A B C D -中,M,N 分别是1BC ,1CD 的中点,则下列说法错误的是( )A .1MN CC ⊥B .MN ⊥平面11ACC A C .MN AB ∥D .MN ∥平面ABCD7.函数()()e e cos x x f x x -=-在区间[]5,5-上的图象大致为( )A .B .C .D .8.某旅行社租用A ,B 两种型号的客车安排900名客人旅行,A ,B 两种车辆的载客量分别为36人和60人,租金分别为1600元/辆和2400元/辆,旅行社要求租车总数不超过21辆,且B 型车不多于A 型车7辆,则租金最少为( )第3页(共8页) 第4页(共8页)A .31200元B .36000元C .36800元D .38400元9.点P 是双曲线22221x y a b-=右支上一点,1F 、2F 分别为左、右焦点.12PF F △的内切圆与x 轴相切于点N ,若点N 为线段2OF 中点,则双曲线的离心率为( ) A .3B .2CD10.已知函数()()π2sin 0,2f x x ωϕωϕ⎛⎫=+>< ⎪⎝⎭的图象经过点()0,1B -,在区间ππ,183⎛⎫⎪⎝⎭上为单调函数,且()f x 的图象向左平移π个单位后与原来的图象重合,则ϕω=( )A .π12-B .π12C .π6 D .π6-11.已知函数()()2e 0x f x x x =+<与()()2ln g x x x a =++的图象上存在关于y 轴对称的点,则实数a 的取值范围是( ) A .(),e -∞B .1,e ⎛⎫-∞ ⎪⎝⎭C .1,e e ⎛⎫- ⎪⎝⎭D .1e,e ⎛⎫- ⎪⎝⎭12.已知数列{}n a ,定义数列{}12n n a a +-为数列{}n a 的“2倍差数列”,若{}n a 的“2倍差数列”的通项公式为1122n n n a a ++-=,且12a =,若函数{}n a 的前n 项和为n S ,则33S =( ) A .3821+B .3922+C .3822+D .392第Ⅱ卷二、填空题:本大题共4小题,每小题5分.13.已知向量a ,b ,其中=a ,2=b ,且()+⊥a b a ,则向量a ,b 的夹角为______.14.已知曲线cos sin y a x x =+在π,12⎛⎫⎪⎝⎭处的切线方程为π102x y -+-=,则实数a =______.15.下列命题中,正确的命题序号是__________.(请填上所有正确的序号)①已知a ∈R ,两直线1:1l ax y +=,2:2l x ay a +=,则“1a =-”是“12l l ∥”的充分条件;②“0x ∀≥,22x x >”的否定是“00x ∃≥,0202x x <”;③“1sin 2α=”是“π2π6k α=+,k ∈Z ”的必要条件; ④已知0a >,0b >,则“1ab >”的充要条件是“1a b>”16.已知三角形PBD 所在平面与矩形ABCD 所在平面互相垂直,2PD BD ==,120BDP ∠=︒,若点P 、A 、B 、C 、D 都在同一球面上,则此球的表面积等于_________. 三、解答题:解答应写出文字说明、证明过程或演算步骤.17.(12分)在ABC △中,角A 、B 、C 的对边分别为a 、b 、c ,已知cos cos cos 2cos sin C A B A B +=, (1)求tan A ;(2)若b =AB边上的中线CD =ABC △的面积.18.(12分)在如图所示的多面体ABCDE 中,AB ⊥平面ACD ,DE ⊥平面ACD ,且2AC AD CD DE ====,1AB =.(1)请在线段CE 上找到点F 的位置,使得恰有直线BF ⊥平面CDE ,并证明; (2)在(1)的条件下,求多面体ABCDF 的体积.19.(12分)近年来,随着我国汽车消费水平的提高,二手车行业得到迅猛发展,某汽第5页(共8页) 第6页(共8页)车交易市场对2017年成交的二手车交易前的使用时间(以下简称“使用时间”)进行统计,得到频率分布直方图如图1.(1)记“在2017年成交的二手车中随机选取一辆,该车的使用年限在(]8,16”为事件A ,试估计A 的概率;(2)根据该汽车交易市场的历史资料,得到散点图如图2,其中x (单位:年)表示二手车的使用时间,y (单位:万元)表示相应的二手车的平均交易价格.由散点图看出,可采用e a bx y +=作为二手车平均交易价格y 关于其使用年限x 的回归方程,相关数据如下表(表中ln i i Y y =,101110i i Y Y ==∑);①根据回归方程类型及表中数据,建立y 关于x 的回归方程;②该汽车交易市场对使用8年以内(含8年)的二手车收取成交价格4%的佣金,对使用时间8年以上(不含8年)的二手车收取成交价格10%的佣金.在图1对使用时间的分组中,以各组的区间中点值代表该组的各个值.若以2017年的数据作为决策依据,计算该汽车交易市场对成交的每辆车收取的平均佣金.附注:①对于一组数据()11,u v ,()22,u v ,...,(),n n u v ,其回归直线v u αβ=+的斜率和截距的最小二乘估计分别为1221ˆni i i nii u v nuvunuβ==-=-∑∑,ˆˆv u αβ=-, ②参考数据: 2.95e 19.1≈, 1.75e 5.75≈,0.55e 1.73≈,0.65e 0.52-≈, 1.85e 0.16-≈.20.(12分)已知M 是直线:1l x =-上的动点,点F 的坐标是(1,0),过M 的直线'l 与l 垂直,并且'l 与线段MF 的垂直平分线相交于点N . (1)求点N 的轨迹C 的方程;(2)设曲线N 上的动点A 关于x 轴的对称点为'A ,点P 的坐标为(2,0),直线AP 与曲线C 的另一个交点为B (B 与'A 不重合),是否存在一个定点T ,使得T 、A '、B 三点共线?若存在,求出点T 的坐标;若不存在,请说明理由.21.(12分)已知a ∈R ,函数()e x f x ax =-(e 2.71828...≈是自然对数的底数)第7页(共8页) 第8页(共8页)(1)求函数()f x 的单调区间;(2)若函数()()()e 22ln x F xf x ax x a =--++在区间10,2⎛⎫⎪⎝⎭内无零点,求a 的最大值.请考生在22、23两题中任选一题作答,如果多做,则按所做的第一题记分.22.(10分)【选修4-4:坐标系与参数方程】在平面直角坐标系xOy 中,曲线1C 的参数方程为cos sin x a y b ϕϕ=⎧⎨=⎩(0a b >>,ϕ为参数),在以O 为极点,x 轴的正半轴为极轴的极坐标系中,曲线2C 是圆心在极轴上,且经过极点的圆.已知曲线1C上的点1,2M ⎛ ⎝⎭对应的参数π3ϕ=,射线π3θ=与曲线2C 交于点π1,3D ⎛⎫ ⎪⎝⎭(1)求曲线1C 的普通方程和2C 的直角坐标方程;(2)若点()1,A ρθ,2π,2B ρθ⎛⎫+ ⎪⎝⎭在曲线1C 上,求221211ρρ+的值.23.(10分)【选修4-5:不等式选讲】 已知函数()34f x x x =-++. (1)求()()4f x f ≥的解集;(2)设函数()()()3g x k x k =-∈R ,若()()f x g x >对x ∀∈R 成立,求实数k 的取值范围.高三文科数学(二)答案一、选择题.1.【答案】A2.【答案】C3.【答案】D4.【答案】D5.【答案】D6.【答案】C7.【答案】B8.【答案】C9.【答案】B10.【答案】A11.【答案】A12.【答案】B二、填空题.13.【答案】5π614.【答案】1-15.【答案】①③④16.【答案】16π三、解答题17.【答案】(1)tan2A=;(2)当2c=时,1sin42ABCS bc A==△;当6c=时,12ABCS=△.【解析】(1)由已知得()cos cos cos cosπcos cosC A B A B A B+=-++⎡⎤⎣⎦()cos cos cos sin sinA B A B A B=-++=,所以sin sin2cos sinA B A B=,因为在ABC△中,sin0B≠,所以sin2cosA A=,则tan2A=.(2)由(1)得,cos A=,sin A=,在ACD△中,2222cos22c cCD b b A⎛⎫=+-⋅⋅⋅⎪⎝⎭,代入条件得28120c c-+=,解得2c=或6,当2c=时,1sin42ABCS bc A==△;当6c=时,12ABCS=△.18.【答案】(1)见解析;(2)3.【解析】(1)F为线段CE的中点.证明如下:由已知AB⊥平面ACD,DE⊥平面ACD,∴AB ED∥,设H是线段CD的中点,连接FH,则12FH DE∥,且12FH DE=,∵12AB DE∥,且12AB DE=,∴四边形ABFE是平行四边形,∴BF AH∥,∵AH CD⊥,AH DE⊥,CD DE D=,∴AH⊥平面CDE,∴BF⊥平面CDE.(2)∵ABCDF A BCD F BCD B ACD B CDFV V V V V----=+=+1133ACD CDFS AB S AH=⨯⨯+⨯⨯==△△,∴多面体ABCDF.19.【答案】(1)0.40;(2)0.29万元.【解析】(1)由频率分布直方图得,该汽车交易市场2017年成交的二手车使用时间在(]8,12的频率为0.0740.28⨯=,在(]12,16的频率为0.0340.12⨯=,所以()0.280.120.40P A=+=.(2)①由e a bxy+=得ln y a bx=+,即Y关于x的线性回归方程为ˆY a bx=+答案第1页(共8页)答案第2页(共8页)答案 第3页(共8页) 答案 第4页(共8页)因为1011022211079.7510 5.5 1.9ˆ0.338510 5.510i i i i i x Y x Ybx x==-⋅-⨯⨯===--⨯-∑∑, ()ˆˆ 1.90.3 5.5 3.55aY bx =-=--⨯=, 所以Y 关于x 的线性回归方程为ˆ 3.550.3Y x =-, 即y 关于x 的回归方程为 3.550.3ˆe x y-=; ②根据①中的回归方程 3.550.3ˆe x y-=和图1,对成交的二手车可预测: 使用时间在(]0,4的平均成交价格为 3.550.32 2.95e e 19.1-⨯=≈,对应的频率为0.2; 使用时间在(]4,8的平均成交价格为 3.550.36 1.75e e 5.75-⨯=≈,对应的频率为0.36; 使用时间在(]8,12的平均成交价格为 3.550.3100.55e e 1.73-⨯=≈,对应的频率为0.28; 使用时间在(]12,16的平均成交价格为 3.550.3140.65e e 0.52-⨯-=≈,对应的频率为0.12; 使用时间在(]16,20的平均成交价格为 3.550.318 1.85e e 0.16-⨯-=≈,对应的频率为0.04; 所以该汽车交易市场对于成交的每辆车可获得的平均佣金为:()0.219.10.36 5.754%⨯+⨯⨯()0.28 1.730.120.520.040.1610%+⨯+⨯+⨯⨯0.290920.29=≈万元.20.【答案】(1)24y x =;(2)见解析.【解析】(1)由题意可知:NM NF =,即曲线C 为抛物线,焦点坐标为(1,0)F , 准线方程为:1l x =-,∴点N 的轨迹C 的方程24y x =.(2)设2,4a A a ⎛⎫ ⎪⎝⎭,则2,4a A a ⎛⎫'- ⎪⎝⎭,直线AB 的斜率224824AP a ak a a ==--, 直线AB 的方程()2428ay x a =--,由()224428y xay x a ⎧=⎪⎨=-⎪-⎩,整理得:()22880ay a y a ---=, 设()22,B x y ,则28a y ⋅=-,则28y a =-,2216x a =,则2168,B a a ⎛⎫- ⎪⎝⎭,又2,4a A a ⎛⎫'- ⎪⎝⎭'222841684A Baa a k a a a -+==-+-,∴A B '的方程为22484a a y a x a ⎛⎫+=-- ⎪+⎝⎭, 令0y =,则2x =-,直线A B '与x 轴交于定点()2,0-, 因此存在定点()2,0-,使得T ,A ',B 三点共线.21.【答案】(1)见解析;(2)4ln 2.【解析】(1)∵()e x f x ax =-,∴()e x f x a '=-,当0a ≤时,在()0f x '>上R 恒成立,()f x 增区间为(),-∞+∞,无减区间; 当0a >时,令()0f x '=得ln x a =,()f x 的增区间为()ln ,a +∞,减区间为(),ln a -∞.(2)函数()()()e 22ln 2ln x F x f x ax x a ax x a =--++=--,10,2x ⎛⎫∈ ⎪⎝⎭,∴()22ax F x a x x-'=-=, ①当0a ≤时,()0F x '<在10,2⎛⎫ ⎪⎝⎭上恒成立,函数()F x 在区间10,2⎛⎫⎪⎝⎭上单调递减,则()112ln ln 402222aa F x F a ⎛⎫>=--=-> ⎪⎝⎭,∴0a ≤时,函数()F x 在区间10,2⎛⎫⎪⎝⎭上无零点;答案 第5页(共8页) 答案 第6页(共8页)②当0a >时,令()'0F x =得,2x a= 令()'0F x >,得2x a >,令()'0F x <,得20x a<<, 因此,函数()F x 的单调递增区间是2,a ⎛⎫+∞ ⎪⎝⎭,单调递减区间是20,a ⎛⎫⎪⎝⎭.(i )当212a ≥,即时04a <≤, 函数()F x 的单调递减区间是10,2⎛⎫ ⎪⎝⎭,∴()112ln ln 42222aa F x F a ⎛⎫>=--=- ⎪⎝⎭,要使函数()F x 在区间10,2⎛⎫⎪⎝⎭内无零点,则ln 402a -≥,得4ln 2a ≤;(ii )当212a <,即4a >时, 函数()F x 的单调递减区间是20,a ⎛⎫ ⎪⎝⎭,单调递增区间是21,2a ⎛⎫⎪⎝⎭,∴()min 2222ln 2ln 42ln F x F a a a a a ⎛⎫==--=-+- ⎪⎝⎭,设()2ln 42ln g a a a =-+-,∴()2210ag a a a-'=-=<,∴()g a 在()4,+∞上单调递减,∴()()()g 42ln 42ln 44ln 422ln 2lne 0g a <=-+-=-=-<, 而当120e a x a <=<时,()0e aaF x a =+>, ∴函数()F x 在区间10,2⎛⎫⎪⎝⎭内有零点,不合题意.综上,要使函数()()()e 22ln x F x f x ax x a =--++在区间10,2⎛⎫⎪⎝⎭内无零点,则a 的最大值为4ln 2. 22.【答案】(1)见解析;(2)54. 【解析】(1)将M ⎛ ⎝⎭及对应的参数π3ϕ=,代入cos sin x a y b ϕϕ=⎧⎨=⎩,得π1cos 3πsin 3a b ⎧=⎪⎪=, 即21a b =⎧⎨=⎩,∴曲线1C 的普通方程为2214x y +=.设圆2C 的半径为R ,由题意可得,圆2C 的极坐标方程为2cos R ρθ=.将点π1,3D ⎛⎫⎪⎝⎭代入2cos R ρθ=,得π12cos 3R =,即1R =,∴曲线2C 的极坐标方程为2cos ρθ=,∴曲线2C 的直角坐标方程为()2211x y -+=.(2)∵曲线1C 的普通方程为2214x y +=,点()1,A ρθ,2π,2B ρθ⎛⎫+ ⎪⎝⎭在曲线1C 上,∴222211cos sin 14ρθρθ+=,222222sin cos 14ρθρθ+=,∴22221211cos sin 4θθρρ⎛⎫+=+ ⎪⎝⎭22sin 5cos 44θθ⎛⎫++= ⎪⎝⎭. 23.【答案】(1){5x x ≤-或}4x ≥;(2)12k -<≤. 【解析】(1)()34f x x x =-++, ∴()()4f x f ≥,即349x x -++≥,∴4349x x x ≤-⎧⎨---≥⎩①或43349x x x -<<⎧⎨-++≥⎩②或3349x x x ≥⎧⎨-++≥⎩③, 解不等式①:5x ≤-;②:无解;③:4x ≥, 所以()()4f x f ≥的解集为{5x x ≤-或}4x ≥.(2)()()f x g x >即()34f x x x =-++的图象恒在()()3g x k x =-,k ∈R 图象的上方,可以作出()21,4347,4321,3x x f x x x x x x --≤-⎧⎪=-++=-<<⎨⎪+≥⎩的图象,而()()3g x k x =-,k ∈R 图象为恒过定点()3,0P ,且斜率k 变化的一条直线, 作出函数()y f x =,()y g x =图象如图,其中2PB k =,可得()4,7A -,∴1PA k =-,由图可知,要使得()f x 的图象恒在()g x 图象的上方, 实数k 的取值范围为12k -<≤.答案第7页(共8页)答案第8页(共8页)。
【高考模拟】2019理科数学试卷(二)及答案解析

2019年普通高等学校招生全国统一考试模拟卷理科数学(二)本试题卷共7页,23题(含选考题)。
全卷满分150分。
考试用时120分钟。
★祝考试顺利★注意事项:1、答题前,先将自己的姓名、准考证号填写在试题卷和答题卡上,并将准考证号条形码粘贴在答题卡上的指定位置。
用2B铅笔将答题卡上试卷类型A后的方框涂黑。
2、选择题的作答:每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑。
写在试题卷、草稿纸和答题卡上的非答题区域均无效。
3、填空题和解答题的作答:用签字笔直接答在答题卡上对应的答题区域内。
写在试题卷、草稿纸和答题卡上的非答题区域均无效。
4、选考题的作答:先把所选题目的题号在答题卡上指定的位置用2B铅笔涂黑。
答案写在答题卡上对应的答题区域内,写在试题卷、草稿纸和答题卡上的非答题区域均无效。
5、考试结束后,请将本试题卷和答题卡一并上交。
第Ⅰ卷一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的。
1.设i是虚数单位,若复数z的共轭复数为()A B C D2.若双曲线221yxm-=的一个焦点为()3,0-,则m=()A.B.8C.9D.643.得到函数()f x的图像,()A B C D4.函数()12xf x ⎛⎫= ⎪⎝⎭,()0,x ∈+∞的值域为D ,在区间()1,2-上随机取一个数x ,则x D ∈的概率是( ) A .12B .13C .14D .15.记()()()()72701272111x a a x a x a x -=+++++⋅⋅⋅++,则012a a a +++6a ⋅+的值为( )A .1B .2C .129D .21886.一个几何体的三视图如图所示,则该几何体的体积为( )A .83B .163C .203D .87.《九章算术》是我国古代的数学名著,书中有如下问题:“今有大夫、不更、簪裹、上造、公士,凡五人,共猎得五鹿,欲以爵次分之,问各得几何?”其意思:“共有五头鹿,5人以爵次进行分配(古代数学中“以爵次分之”这种表述,一般表示等差分配,在本题中表示等差分配).”在这个问题中,若大夫得“一鹿、三分鹿之二”,则簪裹得( ) A .一鹿、三分鹿之一 B .一鹿 C .三分鹿之二D .三分鹿之一8 )A .B .C .D .9.阅读如图所示的程序框图,运行相应程序,输出的结果是( )A .12B .18C .120D .12510.当实数x ,y 满足约束条件3310x y x y y +⎧⎪-⎨⎪⎩≤≥≥,表示的平面区域为C ,目标函数2z x y =-的最小值为1p ,而由曲线()230y x y =≥,直线3x =及x 轴围成的平面区域为D ,向区域D 内任投入一个质点,该质点落入C 的概率为2p ,则1224p p -的值为( ) A .12B .23 C .35D .4311.已知点1F 是抛物线C :22x py =的焦点,点2F 为抛物线C 的对称轴与其准线的交点,过2F 作抛物线C 的切线,切点为A ,若点A 恰好在以1F ,2F 为焦点的双曲线上,则双曲线的离心率为( ) A.2B1 C1D.212.已知函数()e e x x f x -=+(其中e 是自然对数的底数),若当0x >时,()e 1x mf x m -+-≤恒成立,则实数m 的取值范围为( )A .10,3⎛⎫ ⎪⎝⎭B .1,3⎛⎤-∞- ⎥⎝⎦C .1,3⎡⎫+∞⎪⎢⎣⎭D .11,33⎡⎤-⎢⎥⎣⎦第Ⅱ卷本卷包括必考题和选考题两部分。
高考高三3月内部特供卷 理科数学(二)学生版

-------------------------天才是百分之一的灵感加百分之九十九的勤奋------------------------------金戈铁骑 2019届高三3月份内部特供卷理科数学(二) 注意事项: 1.答题前,先将自己的姓名、准考证号填写在试题卷和答题卡上,并将准考证号条形码粘贴在答题卡上的指定位置.2.选择题的作答:每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑,写在试题卷、草稿纸和答题卡上的非答题区域均无效.3.非选择题的作答:用签字笔直接答在答题卡上对应的答题区域内。
写在试题卷、草稿纸和答题卡上的非答题区域均无效.4.考试结束后,请将本试题卷和答题卡一并上交.第Ⅰ卷一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的. 1.已知集合U =R ,{}26A x x =∈<Z ,(){}220B x x x =-<,则图中阴影部分表示的集合为( ) A .{}0,1,2 B .{}0,2 C .{}1,2 D .{}22.已知()()log 32a x f x x -=-,则函数()f x 的定义域为( )A .(),3-∞B .()(],22,3-∞UC .()(),22,3-∞UD .()3,+∞3.已知函数()211x f x x +=-,其定义域是[)8,4--,则下列说法正确的是( )A .()f x 有最大值53,无最小值 B .()f x 有最大值53,最小值75C .()fx 有最大值75,无最小值 D .()f x 有最大值2,最小值754.函数111f x x ⎛⎫= ⎪+⎝⎭,则函数()f x 的解析式是( )A .1xx + B .1x + C .11x + D .x5.若 2.1log 0.6a =,0.62.1b =,0.5log 0.6c =,则a ,b ,c 的大小关系是( )A .a b c >>B .b c a >>C .c b a >>D .b a c >> 6.在三角形ABC 中,“sin sin A B >”是“tan tan A B >”的( )条件 A .充分不必要 B .必要不充分 C .充要 D .既不充分也不必要 7.已知函数()f x 是定义在R 内的奇函数,且满足()()2f x f x +=-,当()0,2x ∈时,()22f x x =,则()2015f =( ) A .2- B .2 C .98- D .98 8.已知函数()()1211log 3,,1x a a x f x x x ⎧-≤⎪=⎨+>⎪⎩,当12x x ≠时,()()12120f x f x x x -<-,则a 的取值范围是( )A .10,3⎛⎤ ⎥⎝⎦B .11,32⎡⎤⎢⎥⎣⎦C .10,2⎛⎤ ⎥⎝⎦D .11,43⎡⎤⎢⎥⎣⎦ 9.函数()2x f x x a =+的图象可能是( ) A .(1)(3) B .(1)(2)(4) C .(2)(3)(4) D .(1)(2)(3)(4) 10.函数()22368f x x x x =---+-的值域是( ) A .35,5⎡⎤-⎣⎦ B .[]1,5 C .2,35⎡⎤+⎣⎦ D .35,35⎡⎤-+⎣⎦ 11.已知()222,02,0x x x f x x x x ⎧-≥⎪=⎨+<⎪⎩,则不等式()()6f x f x +->的解集为( ) 此卷只装订不密封 班级姓名准考证号考场号座位号-------------------------天才是百分之一的灵感加百分之九十九的勤奋------------------------------A .(),3-∞-B .()3,+∞C .()(),33,-∞-+∞UD .()3,3-12.已知函数()1sin 212x f x x x ⎛⎫=+- ⎪-⎝⎭,则实数201812019k kf =⎛⎫⎪⎝⎭∑的值是( )A .4036B .2018C .1009D .1007第Ⅱ卷二、填空题:本大题共4小题,每小题5分,共20分.13.已知()y f x =是定义在()2,2-上的增函数,若()()112f m f m -<-,则m 的取值范围是____.14.已知函数()2f x x x m =++,若()f x 在区间[]0,1上单调,则实数m 的取值范围为____.15.已知()2sin 21x f x x =++,则()()()()()21012f f f f f -+-+++=______.16.如图,已知过原点O 的直线与函数8log y x =的图象交于A ,B 两点,分别过A ,B 作y 轴的 平行线与函数2log y x =图象交于C ,D 两点,若BC x ∥轴,则四边形ABCD 的面积为_____.三、解答题:本大题共6个大题,共70分.解答应写出文字说明、证明过程或演算步骤.17.(12分)已知等差数列{}n a 的首项为1a ,公差为()1,d a d ∈∈Z Z ,前n 项的和为n S ,且749S =,52426S <<.(1)求数列{}n a 的通项公式;(2)设数列11n n a a +⎧⎫⎨⎬⋅⎩⎭的前n 项的和为n T ,求n T .18.(12分)在ABC △中,角A ,B ,C 的对边分别是a ,b ,c ()3cos 23cos a C b c A =.(1)求角A 的大小; (2)若2a =,求ABC △面积的最大值.-------------------------天才是百分之一的灵感加百分之九十九的勤奋------------------------------金戈铁骑19.(12分)已知函数()()ln x a f x x -=.(1)若1a =-,证明:函数()f x 是()0,+∞上的减函数;(2)若曲线()y f x =在点()()1,1f 处的切线与直线0x y -=平行,求a 的值;(3)若0x >,证明:()e ln 11x x xx +>-(其中e 2.71828=⋯是自然对数的底数).20.(12分)设椭圆22:12x C y +=的右焦点为F ,过F 的直线l 与C 交于A ,B 两点,点M 的坐标为()2,0. (1)当l 与x 轴垂直时,求直线AM 的方程; (2)设O 为坐标原点,求OMA OMB ∠∠的值.-------------------------天才是百分之一的灵感加百分之九十九的勤奋------------------------------21.(12分)设函数()()212e 2x f x x ax ax =-+-.(1)讨论()f x 的单调性;(2)设1a =,当0x ≥时,()2f x kx ≥-,求k 的取值范围.请考生在22、23两题中任选一题作答,如果多做,则按所做的第一题记分. 22.(10分)【选修4-4:坐标系与参数方程】 以直角坐标系的原点O 为极点,x 轴的正半轴为极轴,已知点P 的直角坐标为()1,5-,点M 的极坐标为4,π2⎛⎫ ⎪⎝⎭.若直线l 过点P ,且倾斜角为π3,圆C 以M 为圆心、4为半径. (1)求直线l 的参数方程和圆C 的极坐标方程; (2)试判定直线l 和圆C 的位置关系. 23.(10分)【选修4-5:不等式选讲】 已知函数()2f x x a =-,()1g x bx =+. (1)当1b =时,若()()12f x g x +的最小值为3,求实数a 的值; (2)当1b =-时,若不等式()()1f x g x +<的解集包含1,12⎡⎤⎢⎥⎣⎦,求实数a 的取值范围.-------------------------天才是百分之一的灵感加百分之九十九的勤奋------------------------------ 金戈铁骑-------------------------天才是百分之一的灵感加百分之九十九的勤奋------------------------------金戈铁骑金戈铁骑 2019届高三3月份内部特供卷理科数学(二)答 案一、选择题.1.【答案】B 【解析】{}{}262,1,0,1,2A x x =∈<=--Z ,(){}()()220,00,2B x x x =-<=-∞U , {}[)02, U B =+∞U ð,图中阴影部分表示的集合为(){}0,2U A B =I ð,故选B .2.【答案】C【解析】由题易得()()30,22,320x x ->⎧⇒-∞⎨-≠⎩U ,故选C .3.【答案】A【解析】()()213211x f x f x x x +==+⇒--在[)8,4--上是减函数()f x ⇒有最大值()583f -=,无最小值,故选A .4.【答案】A【解析】令1t x =,0t ≠,1-.则有1x t =,所以()1111tf t t t==++,0t ≠,1-,所以()1xf x x =+,0t ≠,1-,故选A .5.【答案】B【解析】 2.1log 0.60a =<,0.62.11b =>,0.50log 0.61c <=<,b c a ∴>>,故选B .6.【答案】D【解析】sin sin π0A B a b A B >⇔>⇔>>>,π0A B >>>Q 推不出tan tan A B >,tan tan A B >推不出π0A B >>>,∴“sin sin A B >”是“tan tan A B >”的既不充分也不必要条件,故选D .7.【答案】A【解析】根据题意,函数()f x 满足()()2f x f x +=-,则()()()42f x f x f x +=-+=, 则函数是周期为4的周期函数,则()()()2015145041f f f =-+⨯=-,又由函数为奇函数,则()()()211212f f -=-=-⨯=-,故()20152f =-,故选A .8.【答案】A【解析】∵当12x x ≠时,()()12120f x f x x x -<-,∴()f x 是R 上的单调减函数, ∵()()1211log 3,,1x a a x f x x x ⎧-≤⎪=⎨+>⎪⎩,∴0121011123a a a <-<<<-≥⎧⎪⎪⎨⎪⎪⎩,∴103a <≤,故选A . 9.【答案】C 【解析】首先函数为奇函数,当0a =时,()21x f x x x ==,故(4)满足条件; 当0a <时,函数()()222a x f x x a -'=+,函数()0f x '<恒成立,令20x a +=,解得x a =±-, 故函数()f x 在(),a -∞--,(),a a ---,(),a -+∞上单调递减,故(3)满足条件; 当0a >时,()()222a x f x x a -'=+,令()0f x '=,解得x a =±, 当()0f x '>,即(),x a a ∈-时,函数单调递增;当()0f x '<,即(),x a ∈-∞-,(),a +∞时, 函数单调递减,故(2)满足条件, 所以函数()2x f x x a =+的图象可能是(2)、(3)、(4),故选C . 10.【答案】A 【解析】由()()2223682313f x x x x x x =---+-=----,知2680x x -+-≥,解得[]2,4x ∈.令()22313t x x =----,则()21323x x t --=--, 即为()213y x =--和23y x t =--两函数图象的交点,作出函数图象,如图所示: 由图可知,当直线和半圆相切时t 最小,当直线过点()4,0A 时,t 最大. 3114t -=+,解得35t =±35t =.-------------------------天才是百分之一的灵感加百分之九十九的勤奋------------------------------当直线过点()4,0A 时,2430t ⨯--=,解得5t =.所以3t ⎡⎤∈⎣⎦,即()3f x ⎡⎤∈⎣⎦.故选A .11.【答案】C【解析】Q 当0x <时,0x ->,()()()2222f x x x x x -=---=+,又有当0x <时,()22f x x x =+,()00f =,()()f x f x ∴-=,即函数()f x 为偶函数.不等式()()6f x f x +->转化为不等式()3f x >,可得2023x xx ≥->⎧⎪⎨⎪⎩或2023x x x <+>⎧⎪⎨⎪⎩,解得3x >或3x <-,∴不等式()()6f x f x +->的解集为()(),33,-∞-+∞U .故选C .12.【答案】C【解析】由题意,函数()1sin 212xf x x x ⎛⎫=+- ⎪-⎝⎭,令()()1112112222121221x x g x x x x -+===+---,则()g x 的对称中心为11,22⎛⎫⎪⎝⎭,所以()()11g x g x +-=,则2018112018*********k k g =⎛⎫=⨯= ⎪⎝⎭∑,令()1sin 2h x x ⎛⎫=- ⎪⎝⎭,则()h x 的对称中心为()1π,02k k ⎛⎫+∈ ⎪⎝⎭Z , 所以1,02⎛⎫ ⎪⎝⎭为函数()h x 的对称中心,则()()10h x h x +-=,所以2018102019k k h =⎛⎫= ⎪⎝⎭∑, 所以2018201820181111009201920192019k k k k k k f g h ===⎛⎫⎛⎫⎛⎫=+= ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭∑∑∑,故选C .二、填空题.13.【答案】12,23⎛⎫- ⎪⎝⎭【解析】由已知可得122112223m m m -<-<-<⇒-<<.14.【答案】(][),20,-∞-+∞U 【解析】由题得二次函数的对称轴为12x =-. 因为函数()f x 在区间[]0,1上单调, 所以当函数单调递增时,()14014000Δm Δm f m =->⎧⎪=-≤⎨=≥⎪⎩或,解之得0m ≥. 当函数单调递减时,()140120Δm f m =->=+≤⎧⎪⎨⎪⎩,解之得2m ≤-, 综合得m 的取值范围为(][),20,-∞-+∞U ,故答案为(][),20,-∞-+∞U . 15.【答案】5 【解析】∵()()12222sin sin 221212112x x x x x f x f x x x +-+-=++-=+=++++, 且()01f =,∴()()()()()210125f f f f f -+-+++=. 16.23 【解析】设点A ,B 的横坐标分别为1x 、2x ,由题设知,11x >,21x >. 则点A ,B 纵坐标分别为81log x 、82log x . 因为A ,B 在过点O 的直线上,所以818212log log x x x x =, 点C 、D 坐标分别为()121log ,x x ,()222log ,x x . 由于BC 平行于x 轴,知2182log log x x =,即得21221log log 3x x =,∴321x x =. 代入281182log log x x x x =,得3181181log 3log x x x x =. 由于11x >,知81log 0x ≠,∴3113x x =.考虑11x >,解得1x =. 于是点A的坐标为,即21log 36A ⎫⎪⎭,∴21log 32B ⎛⎫ ⎪⎝⎭,21log 32C ⎫⎪⎭,23log 32D ⎛⎫ ⎪⎝⎭. ∴梯形ABCD 的面积为()222111log 3log 33232S AC BD BC ⎛⎫=+⨯=+⨯= ⎪⎝⎭.23.-------------------------天才是百分之一的灵感加百分之九十九的勤奋------------------------------金戈铁骑金戈铁骑三、解答题.17.【答案】(1)21n a n =-;(2)21n nT n =+.【解析】(1)由题意得1176749254245262a d a d ⨯+=⨯<+<⎧⎪⎪⎨⎪⎪⎩,1a ∈Z Q ,d ∈Z ,解得112a d ==⎧⎨⎩,()1121n a a n d n ∴=+-=-.(2)()()111111212122121n n a a n n n n +⎛⎫==- ⎪⋅-+-+⎝⎭Q ,111111111233557212121n nT n n n ⎛⎫∴=-+-+-++-= ⎪-++⎝⎭L .18.【答案】(1)π6;(2)2【解析】(1cos 2sin cos cos A C B A C A =,()2sin cos A C B A +=2sin cos B B A =,又B 为三角形内角,所以sin 0B ≠,于是cos A =,又A 为三角形内角,所以π6A =.(2)由余弦定理2222cos a b c bc A =+-,得22422b c bc =+-≥-,所以(42bc ≤,所以1sin 22S bc A ==19.【答案】(1)见解析;(2)0a =;(3)见解析.【解析】(1)当1a =-时,函数()f x 的定义域是()()1,00,-+∞U ,所以()()2ln 11xx x f x x -++'=,令()()ln 11xg x x x =-++,只需证0x >时,()0g x ≤.又()()()22110111xg x x x x '=-=-<+++,故()g x 在()0,+∞上为减函数,所以()()0ln10g x g <=-=,所以()0f x '<,函数()f x 是()0,+∞上的减函数.(2)由题意知,()1|1x f x ='=,且()()2ln x x a x a f x x ---'=, 所以()()11ln 111f a a '=--=-,即有()ln 101a a a --=-, 令()()ln 11a t a a a =---,1a <,则()()211011t a a a '=+>--,故()t a 是(),1-∞上的增函数, 又()00t =,因此0是()t a 的唯一零点,即方程()ln 101a a a --=-有唯一实根0,所以0a =. (3)因为()ln 11lne 11e e 1e e x x x x x x -+==---,故原不等式等价于()()e ln 11n 1e l 1x x x x -++>-, 由(1)知,当1a =-时,()()ln 1x f x x +=是()0,+∞上的减函数, 故要证原不等式成立,只需证明:当0x >时,e 1x x <-, 令()e 1x h x x =--,则()e 10x h x '=->,()h x 在()0,+∞上的增函数, 所以()()00h x h >=,即e 1x x <-,故()()1e x f x f >-, 即()()ln 11l 11e n e 1e x x x x x x -++>=--. 20.【答案】(1)AM的方程为y x =或y ;(2)1OMA OMB ∠=∠. 【解析】(1)由已知得()1,0F ,l 的方程为1x =, 由已知可得,点A的坐标为⎛ ⎝⎭或1,⎛ ⎝⎭. 所以AM的方程为2y x =2y x =-. (2)当l 与x 轴重合时,0OMA OMB ∠=∠=︒, 当l 与x 轴不重合也不垂直时,设l 的方程为()()10y k x k =-≠,()11,A x y ,()22,B x y ,当1x <2x <MA ,MB 的斜率之和为121222MA MB y y k k x x +=+--, 由()111y k x =-,()221y k x =-,得()()()12121223422MA MB kx x k x x k k k x x -+++=--, 将()1y k x =-代入2212x y +=,得()2222214220k x k x k +-+-=, 所以2122421k x x k +=+,21222221k x x k -=+.-------------------------天才是百分之一的灵感加百分之九十九的勤奋------------------------------则()33312122441284234021k k k k kkx x k x x k k --++-++==+,从而0MA MB k k +=,故MA ,MB 的倾斜角互补,所以OMA OMB ∠=∠,所以1OMAOMB ∠=∠.21.【答案】(1)见解析;(2)(],2-∞-.【解析】(1)由题意得x ∈R ,()()()1e x f x x a =-+',①当0a ≥时,当(),1x ∈-∞,()0f x '<;当()1,x ∈+∞时,()0f x '>, 所以()f x 在(),1-∞单调递减,在()1,+∞单调递增,②当0a <时,令()0f x '=,得1x =,()ln x a =-,(i )当e a <-时,(),1x ∈-∞,()0f x '>;当()()1,ln x a ∈-时,()0f x '<; 当()()ln ,x a ∈-+∞时,()0f x '>,所以()f x 在(),1-∞,()()ln ,a -+∞单调递增,在()()1,ln a -单调递减; (ii )当e a =-时,()0f x '≥,所以()f x 在R 单调递增;(iii )当e 0a -<<时,()(),ln x a ∈-∞-,()0f x '>;当()()ln ,1x a ∈-时,()0f x '<;当()1,x ∈+∞时,()0f x '>,∴()f x 在()(),ln a -∞-,()1,+∞单调递增,在()()ln ,1a -单调递减.(2)令()()()2122e 22x g x f x kx x x x kx =-+=-+--+,有()()1e 1x g x x x k =-+--',令()()1e 1x h x x x k =-+--,有()e 1x h x x '=+,①当0x ≥时,()e 10x h x x '=+>,()h x 单调递增.∴()()02h x h k ≥=--,即()2g x k '≥--.(i )当20k --≥,即2k ≤-时,()0g x '≥,()g x 在()0,+∞单调递增, ()()00g x g ≥=,不等式()2f x kx ≥-恒成立,(ii )当20k --<,2k >-时,()0g x '=有一个解,设为0x 根, ∴有()00,x x ∈,()0g x '<,()g x 单调递减;当()0,x x ∈+∞时,()0g x '>,()g x 单调递增, 有()()000g x g <=,∴当0x ≥时,()2f x kx ≥-不恒成立,综上所述,k 的取值范围是(],2-∞-. 请考生在22、23两题中任选一题作答,如果多做,则按所做的第一题记分. 22.【答案】(1)1125x t y =+=-⎧⎪⎪⎨⎪⎪⎩(t 为参数),8sin ρθ=;(2)直线l 与圆C 相离. 【解析】(1)直线l的参数方程111cos 23 5sin ππ53x t x t y t y ⎧⎪⎪⎨⎪⎪⎩⎧=+=+⋅⎪⎪⇒⎨⎪=-+⋅=-+⎪⎩(t 为参数), M 点的直角坐标为()0,4,4为半径, 所以圆C 方程()22416x y +-=,由cos sin x p y p θθ==⎧⎨⎩,代入得圆C 极坐标方程8sin p θ=. (2)直线l50y ---=, 圆心M 到l的距离为4d ==>,∴直线l 与圆C 相离. 23.【答案】(1)8a =-或4;(2)31,2⎛⎫ ⎪⎝⎭. 【解析】(1)当1b =时,()()11112222a a a f x g x x x x x +=-++≥---=+, 因为()()12f x g x +的最小值为3,所以132a +=,解得8a =-或4. (2)当1b =-时,()()1f x g x +<,即211x a x -+-<, 当1,12x ⎡⎤∈⎢⎥⎣⎦时,2112112x a x x a x x a x -+-<⇔-+-<⇔-<,即3a x a <<, 因为不等式()()1f x g x +<的解集包含1,12⎡⎤⎢⎥⎣⎦,所以1a >且132a <, 即312a <<,故实数a 的取值范围是31,2⎛⎫ ⎪⎝⎭.。
2019届高三8月考理科数学试卷(二)
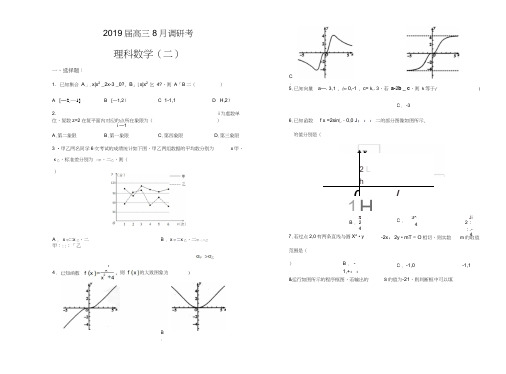
2019届高三8月调研考理科数学(二)一、选择题:1. 已知集合A」.x|x2 _2x-3 _0?, B」[x|x2乞4?,则A「B 二()A . [―2,—1]B . [―1,2)C. 1-1,1 D . H,2)2. i为虚数单位,复数z=2 在复平面内对应的点所在象限为()i —1A.第二象限B.第一象限C.第四象限D.第三象限3 •甲乙两名同学6次考试的成绩统计如下图,甲乙两组数据的平均数分别为x甲、C.5.已知向量6.已知函数a—. 3,1 , b= 0,-1 , c= k,. 3,若a-2b _ c,则k等于()C. -3x乙,标准差分别为二甲,二乙,则()A . x甲:::x乙,二甲:::;「乙B . x甲:::x乙,二甲-:二乙f x =2sin L、0,0 J;::二的部分图像如图所示,的值分别是(2 Lh0/1HJIB . 243^C .4Ji2::.-47.若过点2,0有两条直线与圆X2• y-2x,2y • mT = O相切,则实数m的取值范围是() B . -1,+::C . -1,0 -1,14.3B.)&运行如图所示的程序框图,若输出的S的值为-21,则判断框中可以填2A . a ::: 64? 9.抛物线E:y 2 线上,则BF 10 .将半径为 i" rIB . a 乞64?C . a :::128?a 乞128?=2px p 0的焦点为F ,点A (Q2 ),若线段 AF 的中点 B 在抛物3,圆心角为 11. △ ABC 的内角 则C 为( 12 .已知可导函数 —的扇形围成一个圆锥,则该圆锥的内切球的体积为3C 的对边分别为a , b , c ,且sin B +sin Csin A b1 , a cJTf x 的定义域为 -::,0,其导函数f x 满足2x 厂(x )—2f (x )A O ,则不等式 f (2017 +x )—(x +2017) f (—1)v 0 的解集为( A . -::, -2018B . -2018-2017C . -2018,0 二、填空题D . -2017,0 2x_ y _ 013 .已知实数x , y 满足约束条件 x ・y_6乞0 ,则z=2x_3y 的最小值是 _____________x - 2y - 3 _ 014 .春节期间,某销售公司每天销售某种取暖商品的销售额y (单位:万元)与当天的平均气温x (单位:C )有关.现收集了春节期间这个销售公司 4天的x 与y的数据列于下表:平均气温(C )-2 -3 -5 -6 销售额(万元)20232730根据以上数据,求得 y 与x 之间的线性回归方程 ynbxr 的系数b = _匹,515 .已知某三棱柱的三视图如图所示, 那么该三棱柱最大侧面的面积为16 .在直角坐标系xOy 中,如果相异两点图象上,那么称A , B 为函数f x 的一对关于原点成中心对称的点(A , B 与B ,A 为同一对)函数』.|Sin —x f x 二2lOg 6xx_ 0的图象上有 对关于原点成中心对称的点.三、解答题17 .已知数列「aj 的前n 项和S n 满足S n 二(1)求数列;的通项公式;(2)设b n =an 3a n n e\*,求数列b 啲前n项和T n .18.某少儿游泳队需对队员进行限时的仰卧起坐达标测试. 已知队员的测试分数y0,0 乞x :: 30与仰卧起坐个数X之间的关系如下:y W60,30 'X " 40;测试规则:每位队员最j80,40 Ex<50100,x _50多进行三组测试,每组限时1分钟,当一组测完,测试成绩达到60分或以上时,就以此组测试成绩作为该队员的成绩,无需再进行后续的测试,最多进行三组;根据以往的训练统计,队员“喵儿”在一分钟内限时测试的频率分布直方图如下:(1)计算a值;(2)以此样本的频率作为概率,求①在本次达标测试中,“喵儿”得分等于80的概率;②“喵儿”在本次达标测试中可能得分的分布列及数学期望.2u 汕40 50的19.如图,正三棱柱ABC —A i B i C i的所有棱长都为2, D为CC i中点.(1)求证:AB」平面A1BD ;(2)求锐二面角 A —A1D—B的余弦值;£请考生在22、23两题中任选一题作答,如果多做,则按所做的第一题记分.22.【选修4-4 :坐标系与参数方程】以平面直角坐标系的原点为极点,x轴的正半轴为极轴,建立极坐标系,已知直线20.已知f x =_x1 2 -3 , g x =2x1nx _ax且函数f x与g x在x =1处的切线平行.(1)求函数g x在1,g 1处的切线方程;(2)当xGO ;时,g x - f x _0 恒成立,求实数a的取值范围.(1)求直线丨的普通方程和曲线C的直角坐标方程;(2)若直线I与x轴交于点P,与曲线C交于点A , B,且PA FB =1 ,求实数1 求椭圆的方程;2 设直线I : y =kx(k :::0)与椭圆交于P , Q两点,l与直线AB交于点M ,且点P, M均在第四象限.若△ BPM的面积是△ BPQ面积的2倍,求k的值. 的值.21 .设椭圆x y2 2 =1(a b 0)的右顶点为a bA,上顶点为B .已知椭圆的离心率为AB = 13 .23 .【选修4-5 :不等式选讲】设函数 f x[= 2x-1 - x • 2 .(1) 解不等式f x • 0;(2) 若x0:= R,使得f x o厂2m2::: 4m,求实数m的取值范围.,曲线C的极坐标方程为亍=2cosr l的参数方程是t m(m > 0,t为参数。
2019届北京市海淀八模高三模拟测(二)数学(理)试题(解析版)

2019届北京市海淀八模高三模拟测(二)数学(理)试题一、单选题1.已知集合,,则下图中阴影部分所表示的集合为( )A .B .C .D .【答案】B【解析】由图象可知阴影部分对应的集合为A ∩(∁U B ),然后根据集合的基本运算即可.【详解】∵B ={x |x 2﹣1≥0}={x |x ≥1或x ≤﹣1},∴∁U B ={x |﹣1<x <1},又由图象可知阴影部分对应的集合为A ∩(∁U B ),∴A ∩(∁U B )={0},故选:B .【点睛】本题主要考查集合的基本运算,利用图象先确定集合关系是解决本题的关键,比较基础.2.已知复数z 在复平面内对应点是()1,2-, i 为虚数单位,则21z z +=-( ) A .1i -- B .1i + C .312i -D .312i + 【答案】D 【解析】21z z +=- 323122i i i -=+- ,选D. 3.等比数列中,若,且成等差数列,则其前5项和为( ) A .30 B .32 C .62 D .64【答案】C【解析】设等比数列{a n }的公比为q ,a 4=8a 1,可得a 1q 3=8a 1,解可得q .又a 1,a 2+1,a 3成等差数列,可得2(a 2+1)=a 1+a 3,解可得a 1,由等比数列前n 项和公式计算可得答案.【详解】根据题意,设等比数列{a n }的公比为q ,∵a4=8a1,∴a1q3=8a1,a1≠0,解得q=2.又a1,a2+1,a3成等差数列,∴2(a2+1)=a1+a3,∴2(2a1+1)=a1(1+22),解得a1=2;则其前5项和S562;故选:C.【点睛】本题考查等比数列的通项公式与求和公式,掌握等比数列的通项公式和前n项和公式即可.4.如图给出的是2000年至2016年我国实际利用外资情况,以下结论正确的是()A.2000年以来我国实际利用外资规模与年份呈负相关B.2010年以来我国实际利用外资规模逐年增大C.2008年以来我国实际利用外资同比增速最大D.2010年以来我国实际利用外资同比增速最大【答案】C【解析】根据图表中的数据对选项逐项分析.【详解】从图表中可以看出,2000年以来我国实际利用外资规模基本上是逐年上升的,因此实际利用外资规模与年份正相关,选项A错误;我国实际利用外资规模2012年比2011年少,所以选项B错误;从图表中的折线可以看出,2008年实际利用外资同比增速最大,所以选项C正确;2008年实际利用外资同比增速最大,所以选项D错误;故选:C.【点睛】本题主要考查对图表信息的提取能力,难度不大,属于基础题.5.如图,在长方体中,,,点在侧面上,满足到直线和的距离相等的点()A.不存在B.恰有1个C.恰有2个D.有无数个【答案】B【解析】设P到AB的距离为x,到AA1的距离为y,求出P到直线CD的距离,列方程得出P点轨迹,得出答案.【详解】设P到AB的距离为x(x,到AA1的距离为y(0≤y,则P到直线CD的距离为,∴y,即y2﹣x2=1(y≥1),又0≤y∴y=1,x=0,此时只有一个B点满足,故选:B.【点睛】本题考查了空间距离的计算,属于中档题.6.数学名著《算学启蒙》中有关于“松竹并生”的问题:松长四尺,竹长两尺,松日自半,竹日自倍,松竹何日而长等.如图,是源于其思想的一个程序框图.若输入的分别为8、2,则输出的()A.2 B.3 C.4 D.5【答案】D【解析】由已知中的程序框图可知:该程序的功能是利用循环结构计算并输出变量n的值,模拟程序的运行过程,可得答案.【详解】输入的a、b分别为8、2,n=1第一次执行循环体后a=12,b=4,不满足退出循环的条件,第二次执行循环体后n=2,a=18,b=8,不满足退出循环的条件,第三次执行循环体后n=3,a=27,b=16,不满足退出循环的条件,第四次执行循环体后n=4,a,b=32,不满足退出循环的条件,第五次执行循环体后n=5,a,b=64,满足退出循环的条件,故输出的n=5,故选:D.【点睛】本题考查的知识点是程序框图,当循环的次数不多,或有规律时,常采用模拟循环的方法解答.7.小李从网上购买了一件商品,快递员计划在下午5:00-6:00之间送货上门.已知小李下班到家的时间为下午5:30-6:00.快递员到小李家时,如果小李未到家,则快递员会电话联系小李.若小李能在10分钟之内到家,则快递员等小李回来;否则,就将商品存放在快递柜中.则小李需要去快递柜收取商品的概率为()A.B.C.D.【答案】D【解析】设快递员送达的时刻为x,小李到家的时刻为y,根据题意列出有序实数对(x,y)满足的区域,以及小李去快递柜收取商品对应的平面区域,计算面积比即可得出答案.【详解】假设快递员送达的时刻为x,小李到家的时刻为y,则有序实数对(x,y)满足的区域为{(x,y)|},小李需要去快递柜收取商品,即序实数对(x,y)满足的区域为{(x,y)|},如图所示;∴小李需要去快递柜收取商品的概率为P.故选:D.【点睛】本题考查几何概型概率的求法,考查数形结合的解题思想方法,是中档题.8.将函数图象上所有点的横坐标缩短为原来的,纵坐标不变,再向右平移个单位长度,得到函数的图象,则下列说法正确的是()A.函数的一条对称轴是B.函数的一个对称中心是C.函数的一条对称轴是D.函数的一个对称中心是【答案】C【解析】利用诱导公式、函数y=A sin(ωx+φ)的图象变换规律,正弦函数、余弦函数的图象的对称性,判断各个选项是否正确,从而得出结论.【详解】将函数图象上所有点的横坐标缩短为原来的,可得y=2sin(2x)的图象,然后纵坐标不变,再向右平移个单位长度,得到函数y=g(x)=2sin(2x)=2cos2x的图象,令x,求得g(x)=0,可得(,0)是g(x)的一个对称中心,故排除A;令x,求得g(x)=﹣1,可得x是g(x)的图象的一条对称轴,故排除B,故C正确;令x,求得g(x),可得x不是g(x)的图象的对称中心,故排除D,故选:C.【点睛】本题主要考查诱导公式、函数y=A sin(ωx+φ)的图象变换规律,以及正弦函数、余弦函数的图象的对称性,属于基础题.9.设函数,,“是偶函数”是“的图象关于原点对称”()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件【答案】B【解析】“y=f(x)的图象关于原点对称”,x∈R,可得y=|f(x)|是偶函数.反之不成立,例如f(x)=x2.【详解】“y=f(x)的图象关于原点对称”,x∈R,可得y=|f(x)|是偶函数.反之不成立,例如f(x)=x2,满足y=|f(x)|是偶函数,x∈R.因此,“y=|f(x)|是偶函数”是“y=f(x)的图象关于原点对称”的必要不充分条件.故选:B.【点睛】本题考查了函数的奇偶性、简易逻辑的判定方法,考查了推理能力与计算能力,属于基础题.10.已知椭圆的左、右焦点分别为、,过的直线交椭圆、两点,若的最大值为5,则b的值为()A.1 B.C.D.2【答案】C【解析】由题意可知椭圆是焦点在x轴上的椭圆,利用椭圆定义得到|BF2|+|AF2|=8﹣|AB|,再由过椭圆焦点的弦中通径的长最短,可知当AB垂直于x轴时|AB|最小,把|AB|的最小值b2代入|BF2|+|AF2|=8﹣|AB|,由|BF2|+|AF2|的最大值等于5列式求b的值即可.【详解】由0<b<2可知,焦点在x轴上,∵过F1的直线l交椭圆于A,B两点,则|BF2|+|AF2|+|BF1|+|AF1|=2a+2a=4a=8∴|BF2|+|AF2|=8﹣|AB|.当AB垂直x轴时|AB|最小,|BF2|+|AF2|值最大,此时|AB|=b2,则5=8﹣b2,解得b,故选:C.【点睛】本题考查直线与圆锥曲线的关系,考查了椭圆的定义,考查椭圆的通径公式,考查计算能力,属于中档题.11.已知过球面上三点、、的截面到球心距离等于球半径的一半,且,,则球面面积为()A.B.C.D.【答案】C【解析】设出球的半径,小圆半径,通过已知条件求出两个半径,再求球的表面积.【详解】如图,设球的半径为R,O′是△ABC的外心,外接圆半径为r,则OO′⊥面ABC.在Rt△ACD中,cos A,则sin A.在△ABC中,由正弦定理得2r,r,△ABC外接圆的半径,.故选:C.【点睛】本题考查立体几何中的球的截面问题和球的表面积问题,考查球面距离弦长问题,正弦定理的应用,考查学生分析问题解决问题能力,空间想象能力,属于难题.12.数学上称函数(,,)为线性函数.对于非线性可导函数,在点附近一点的函数值,可以用如下方法求其近似代替值:.利用这一方法,的近似代替值()A.大于B.小于C.等于D.与的大小关系无法确定【答案】A【解析】设,令,则,,故近似值大于.点睛:本题主要考查新定义概念的理解,考查基本初等函数的导数的求法,考查近似值的一种求法,考查比较大小的方法.题目所给新定义是一种近似值的求法,阅读理解后,将所求的近似值利用新定义的概念来表示,即,然后利用平方的方法进行大小的比较.二、填空题13.设满足约束条件,则的最小值为__________.【答案】-5【解析】由约束条件作出可行域,由图得到最优解,求出最优解的坐标,数形结合得答案.【详解】由x,y满足约束条件作出可行域如图,由图可知,目标函数的最优解为A,联立,解得A(﹣1,1).∴z=3x﹣2y的最小值为﹣3×1﹣2×1=﹣5.故答案为:﹣5.【点睛】本题考查了简单的线性规划,考查了数形结合的解题思想方法,是中档题.14.已知向量满足,,,则向量在向量上的投影为__________.【答案】-1【解析】由已知结合向量数量积的性质可求,然后代入到向量在向量上的投影公式可求.【详解】,,,,5,则向量在向量上的投影为1,故答案为:﹣1.【点睛】本题主要考查了平面向量数量积的性质的简单应用,熟练掌握基本性质是求解问题的关键.15.已知双曲线的右焦点为,左顶点为.以为圆心,为半径的圆交的右支于、两点,的一个内角为60°,则的离心率为__________.【答案】【解析】由题意可得P A⊥PB,又,△APQ的一个内角为60°,即有△PFB为等腰三角形,PF=P A=a+c,运用双曲线的定义和离心率公式,计算即可得到所求.【详解】如图,设左焦点为F1,圆于x轴的另一个交点为B,∵△APQ的一个内角为60°∴∠P AF=30°,∠PBF=60°⇒PF=AF=a+c,⇒PF1=3a+c,在△PFF1中,由余弦定理可得.⇒3c2﹣ac﹣4a2=0⇒3e2﹣e﹣4=0⇒,故答案为:.【点睛】本题考查双曲线的定义、方程和性质,考查直径所对的圆周角为直角,以及等腰三角形的性质,考查离心率公式的运用,属于中档题.16.已知数列满足,,表示不超过的最大整数(如,记,数列的前项和为).①若数列是公差为1的等差数列,则__________;②若数列是公比为的等比数列,则__________.【答案】6【解析】①若数列是公差为的等差数列,且,,则,所以,则;故填6.②若数列是公比为的等比数列,且,,则,则,;故填.【点睛】本题考查等差数列、等比数列、二项式定理和新定义型数列的求解;本题的难点是第二问如何确定数列的通项公式,采用了二项式展开式,利用二项式的性质进行求解,难度较大.三、解答题17.在中,内角、、的对边分别为,,.若的面积为,且,. (1)求角的大小;(2)若,求角的大小.【答案】(1);(2).【解析】(1)根据余弦定理和三角形的面积公式化简即可得出,从而得出B 的值;(2)利用正弦定理及B,直接求出C.【详解】(1)在中,由余弦定理,得,,,,,,,;(2)由正弦定理得,,,,,,,.【点睛】本题考查了正弦定理,余弦定理的应用,属于中档题.18.在如图所示的多面体中,平面,,,,,,,是的中点.(1)求证:;(2)求平面与平面所成锐二角的余弦值.【答案】(Ⅰ)证明见解析;(Ⅱ).【解析】试题分析:(Ⅰ)由题意可知,,两两垂直,以点为坐标原点,,,分别为轴,建立空间直角坐标系,由已知得,,即证得(Ⅱ)由已知得是平面的法向量,设平面的法向量为,计算得令,得设平面与平面所成锐二面角的大小为,则通过计算即得结果.试题解析:(Ⅰ)∵平面,平面,平面,∴,.又,∴,,两两垂直.以点为坐标原点,,,分别为轴,建立空间直角坐标系,由已知得,,,,,,,∴,.∴,∴.(Ⅱ)由已知得是平面的法向量,设平面的法向量为,∵,,∴,即,令,得,设平面与平面所成锐二面角的大小为,则.∴平面与平面所成锐二面角的余弦值为.19.(本小题满分13分)某产品按行业生产标准分成8个等级,等级系数X依次为1,2,……,8,其中X≥5为标准A,X≥3为标准B,已知甲厂执行标准A生产该产品,产品的零售价为6元/件;乙厂执行标准B生产该产品,产品的零售价为4元/件,假定甲、乙两厂得产品都符合相应的执行标准(I)已知甲厂产品的等级系数X1的概率分布列如下所示:且X1的数字期望EX1=6,求a,b的值;(II)为分析乙厂产品的等级系数X2,从该厂生产的产品中随机抽取30件,相应的等级系数组成一个样本,数据如下:3 5 3 3 8 5 5 6 3 46 3 47 5 3 48 5 38 3 4 3 4 4 7 5 6 7用这个样本的频率分布估计总体分布,将频率视为概率,求等级系数X2的数学期望.在(I)、(II)的条件下,若以“性价比”为判断标准,则哪个工厂的产品更具可购买性?说明理由.注:(1)产品的“性价比”=;(2)“性价比”大的产品更具可购买性.【答案】【解析】略20.已知过抛物线2:2(0)C y px p =>的焦点F ,斜率为的直线交抛物线于()()112212,,,()A x y B x y x x <两点,且6AB =.(1)求该抛物线C 的方程;(2)已知抛物线上一点(),4M t ,过点M 作抛物线的两条弦MD 和ME ,且MD ME ⊥,判断直线DE 是否过定点?并说明理由.【答案】(1)24y x =;(2)定点()8,4-【解析】试题分析:(1)利用点斜式设直线直线AB 的方程,与抛物线联立方程组,结合韦达定理与弦长公式求AB ,再根据6AB =解得2p =.(2)先设直线DE 方程x my t =+, 与抛物线联立方程组,结合韦达定理化简MD ME ⊥,得48t m =+或44t m =-+,代入DE 方程可得直线DE 过定点()8,4-试题解析:(1)拋物线的焦点,02p F ⎛⎫⎪⎝⎭ ,∴直线AB 的方程为: 2p y x ⎫=-⎪⎭.联立方程组22{ 2y pxp y x =⎫=-⎪⎭,消元得: 22204p x px -+=, ∴212122,4p x x p x x +==.∴6AB ===解得2p =.∴抛物线C 的方程为: 24y x =.(2)由(1)可得点()4,4M ,可得直线DE 的斜率不为0, 设直线DE 的方程为: x my t =+,联立2{ 4x my t y x=+=,得2440y my t --=,则216160m t ∆=+>①.设()()1122,,,D x y E x y ,则12124,4y y m y y t +==-. ∵()()11224,44,4MD ME x y x y ⋅=--⋅--()()12121212416416x x x x y y y y =-+++-++()2222121212124164164444y y y y y y y y ⎛⎫=⋅-+++-++ ⎪⎝⎭ ()()()2212121212343216y y y y y y y y =-++-++22161232160t m t m =--+-=即2212321616t t m m -+=+,得: ()()226421t m -=+,∴()6221t m -=±+,即48t m =+或44t m =-+, 代人①式检验均满足0∆>,∴直线DE 的方程为: ()4848x my m m y =++=++或()44x m y =-+. ∴直线过定点()8,4-(定点()4,4不满足题意,故舍去).点睛:定点、定值问题通常是通过设参数或取特殊值来确定“定点”是什么、“定值”是多少,或者将该问题涉及的几何式转化为代数式或三角问题,证明该式是恒定的. 定点、定值问题同证明问题类似,在求定点、定值之前已知该值的结果,因此求解时应设参数,运用推理,到最后必定参数统消,定点、定值显现.21.已知函数.(1)讨论函数的单调性;(2)若函数存在两个极值点且满足,求的取值范围.【答案】(1)见解析;(2)【解析】试题分析:(1)求出,分五种情况讨论的范围,分别令求得的范围,可得函数增区间,求得的范围,可得函数的减区间;(2)由(1)可知,,不等式化为,令,则,,利用导数研究函数的单调性,证明当时,不等式不成立,当时,可证明,适量题意,即.试题解析:(1)定义域为,,当或时,恒成立,当时,由得或,于是结合函数定义域的分析可得:当时,函数在定义域上是增函数;当时,函数定义域为,此时有,于是在上是增函数,在上是减函数,在上是增函数,当时,函数定义域为,于是在上为减函数,在上为增函数,当时,函数定义域为,此时有,于是在上是增函数,在上是减函数,在上是减函数,在上是增函数,当时,函数定义域为,于是在上是增函数,在上是增函数.(2)由(1)知存在两个极值点时,的取值范围是,由(1)可知,,;不等式化为,令,所以,令,,当时,,,,所以,不合题意;当时,,,所以在上是减函数,所以,适量题意,即.综上,若,此时正数的取值范围是.22.在平面直角坐标系中,曲线的参数方程为(,为参数),以坐标原点为极点,轴正半轴为极轴建立极坐标系,直线的坐标方程为,若直线与曲线相切.(1)求曲线的极坐标方程;(2)在曲线上取两点、于原点构成,且满足,求面积的最大值.【答案】(1);(2).【解析】(1)求出直线l的直角坐标方程为y2,曲线C是圆心为(,1),半径为r的圆,直线l与曲线C相切,求出r=2,曲线C的普通方程为(x)2+(y﹣1)2=4,由此能求出曲线C的极坐标方程.(2)设M(ρ1,θ),N(ρ2,),(ρ1>0,ρ2>0),由2sin(2),由此能求出△MON面积的最大值.【详解】(1)由题意可知将直线的直角坐标方程为,曲线是圆心为,半径为的圆,直线与曲线相切,可得:;可知曲线的方程为,曲线的极坐标方程为,即.(2)由(1)不妨设,,.当时,,面积的最大值为.本题考查曲线的极坐标方程的求法,考查三角形的面积的最大值的求法,考查参数方程、极坐标方程、直角坐标方程的互化等基础知识,考查运算求解能力,考查函数与方程思想,是中档题.23.若,且.(1)求的最小值;(2)是否存在,使得的值为?并说明理由.【答案】(1);(2)不存在,使得的值为.【解析】(1)由条件利用基本不等式求得,再利用基本不等式求得的最小值.(2)根据及基本不等式求得,从而可得不存在a,b,使得=.【详解】(1),,,,当且仅当时等号,,.,,当且仅当时取等号;(2),,,,不存在,使得的值为.【点睛】本题主要考查基本不等式在最值中的应用,要注意检验等号成立条件是否具备,属于基。
【内供】2019届高三8月内部特供卷 理科数学(二)学生版

2019届高三好教育云平台8月份内部特供卷高三理科数学(二)注意事项:1.答题前,先将自己的姓名、准考证号填写在试题卷和答题卡上,并将准考证号条形码粘贴在答题卡上的指定位置。
2.选择题的作答:每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑,写在试题卷、草稿纸和答题卡上的非答题区域均无效。
3.非选择题的作答:用签字笔直接答在答题卡上对应的答题区域内。
写在试题卷、草稿纸和答题卡上的非答题区域均无效。
4.考试结束后,请将本试题卷和答题卡一并上交。
第Ⅰ卷一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合{}|24,x A x x =≤∈N ,6=|1,Z 1B x x x ⎧⎫>∈⎨⎬+⎩⎭,则满足条件A C B ⊆⊆集合C 的个数为( ) A .4B .3C .2D .12.已知p :“R x ∀∈,233x +≥”,则p ⌝是( ) A .R x ∀∈,233x +< B .R x ∃∈,233x +≤ C .R x ∃∈,233x +<D .R x ∃∈,233x +≥3.下列命题中正确命题的个数是( )(1)对分类变量X 与Y 的随机变量2K 的观测值k 来说,k 越小,判断“X 与Y 有关系”的把握越大;(2)若将一组样本数据中的每个数据都加上同一个常数后,则样本的方差不变; (3)在残差图,残差点分布的带状区域的宽度越狭窄,其模型拟合的精度越高;(4)设随机变量ξ服从正态分布()0,1N ,若()1P p ξ>=,则()1102P p ξ-<<=-;A .4B .3C .2D .14.《张丘建算经》卷上第22题为:“今有女善织,日益功疾,且从第2天起,每天比前一天多织相同量的布,若第一天织5尺布,现在一月(按30天计),共织390尺布”,则该女最后一天织多少尺布?( ) A .18 B .20 C .21 D .255.某几何体的三视图如图所示,则这个几何体最长的一条棱长为( )A.B.C .4D.6.设n S 是数列{}n a 的前n 项和,且11a =-,11n n n a S S ++=,则10S =( ) A .110B .110-C .10D .10-7.设0sin d a x x π=⎰,则()622x ⎛⋅+ ⎝的展开式中常数项是( ) A .332 B .332- C . 320 D .320-8.设sin 390a =︒,函数()0log 0xa ax f x x x ⎧<⎪=⎨≥⎪⎩,则211log 108f f ⎛⎫⎛⎫+ ⎪ ⎪⎝⎭⎝⎭的值等于( )A .9B .10C .11D .129.现有一个不透明的口袋中装有标号为1,2,2,3的四个小球,他们除数字外完全相同,现从中随机取出一球记下号码后放回,均匀搅拌后再随机取出一球,则两次取出小球所标号码不同的概率为( )A .16B .56 C .38D .5810.已知定义在区间,2π⎡⎤-π⎢⎥⎣⎦上的函数()y f x =的图像关于直线4x π=对称,当4x π≥时,()sin f x x =,如果关于x 的方程()f x a =有解,记所有解的和为S ,则S 不可能为( )A .34πB .2π C .π D .2π11.已知直线l 与双曲线2214x y -=相切于点P ,l 与双曲线两条渐近线交于M ,N 两点,则OM ON⋅ 的值为( ) A .3B .4C .5D .与.P 的位置有关12.设()()210n n f x x x x x =++++> ,其中n ∈N ,2n ≥,则函数()()2n n G x f x =-在1,12n ⎛⎫⎪⎝⎭内的零点个数是( ) A .0 B .1C .2D .与n 有关此卷只装订不密封班级 姓名 准考证号 考场号 座位号二、填空题:(本大题共4题,每小题5分,满分20分,将答案填在答题纸上)13.已知复数1i z =+,则221z z z -=-__________.14.从抛物线214y x =上一点P 引抛物线准线的垂线,垂足为M ,且5PM =.设抛物线的焦点为F ,则MPF △的面积为__________.15.过平面区域202020x y y x y -+≥⎧⎪+≥⎨⎪++≤⎩内一点P 作圆22:1O x y +=的两条切线,切点分别为A ,B ,记APB α∠=,当α最大时,点P 坐标为__________.16.设()3f x x x =-,过下列点()0,0A ,()0,2B ,()2,1C -,D ⎝⎭,()2,0E -分别作曲线()f x 的切线,其中存在三条直线与曲线()y f x =相切的点是__________.三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17.(12分)在平面直角坐标系xoy 中,已知向量sin ,cos 4x x ⎛π⎫⎛⎫=+ ⎪ ⎪⎝⎭⎝⎭m ,cos ,sin 4x x ⎛π⎫⎛⎫=- ⎪ ⎪⎝⎭⎝⎭n ,设()f x =⋅m n(1)求()f x 的最小正周期;(2)在锐角三角形ABC △中,角A ,B ,C 的对边分别为a ,b ,c ,若02C f ⎛⎫= ⎪⎝⎭,1c =,求ABC△面积的最大值.18.(12分)郑州一中社团为调查学生学习围棋的情况,随机抽取了100名学生进行调查.根据调查结果绘制的学生日均学习围棋时间的频率分布直方图:将日均学习围棋时间不低于40分钟的学生称为“围棋迷”.(1)根据已知条件完成下面的2×2列联表,并据此资料你是否认为“围棋迷”与性别有关?(2)将上述调查所得到的频率视为概率.现在从该地区大量学生中,采用随机抽样方法每次抽取1名学生,抽取3次,记被抽取的3名学生中的“围棋迷”人数为X .若每次抽取的结果是相互独立的,求X 的分布列与期望.附:()()()()()22n ad bc K a b c d a c b d -=++++,19.(12分)如图1,在直角梯形ABCD 中,90ADC ∠=︒,CD AB ∥,2AB =,1AD CD ==,M 为线段AB 的中点.将ADC △沿AC 折起,使平面ADC ⊥平面ABC ,得到几何体D ABC -,如图2所示.(1)求证:平面DBC ⊥平面ACD ; (2)求二面角B CD M --的余弦值.20.(12分)已知椭圆2222:1x y C a b+=的离心率为12,1F ,2F 是椭圆的两个焦点,P 是椭圆上任意一点,且12PF F △的周长是6. (1)求椭圆C 的方程; (2)设圆:()224:9T x t y -+=,过椭圆的上顶点作圆T 的两条切线交椭圆于E ,F 两点,当圆心在x 轴上移动且()0,1t ∈时,求EF 的斜率的取值范围.21.(12分)已知函数()ln f x x x =-.(1)证明:()ln x f x x >;(2)设0m n >>,比较()()()f m m f n n m n+-+-与22mm n+的大小,并说明理由.请考生在22、23两题中任选一题作答,如果多做,则按所做的第一题记分. 22.(10分)【选修4-4:坐标系与参数方程】已知直线l 的参数方程:1cos sin x t y t θθ=+⎧⎨=⎩(θ为参数),曲线C的参数方程:sin x y αα⎧=⎪⎨=⎪⎩(α为参数),且直线交曲线C 于A ,B 两点.(1)将曲线C 的参数方程化为普通方程,并求3θπ=时,AB 的长度; (2)已知点()1,0P ,求当直线倾斜角θ变化时,PA PB ⋅的范围.23.(10分)【选修4-5:不等式选讲】已知实数0a >,0b >,且228a b +=,若a b m +≤恒成立. (1)求实数m 的最小值;(2)若21x x a b -+≥+对任意的a ,b 恒成立,求实数x 的取值范围.2019届高三好教育云平台8月份内部特供卷高三理科数学(二)答 案一、选择题.1.【答案】A2.【答案】C3.【答案】B4.【答案】C 5.【答案】A 6.【答案】B 7.【答案】B 8.【答案】C 9.【答案】D 10.【答案】D 11.【答案】B 12.【答案】B二、填空题.13.【答案】2i 14.【答案】10 15.【答案】()1,1-- 16.【答案】C ,E三、解答题.17.【答案】(1)T =π;(2. 【解析】(1)()sin cos sin cos 44f x x x x x ππ⎛⎫⎛⎫=⋅=⋅+-+ ⎪ ⎪⎝⎭⎝⎭m n ,sin cos sin cos 442x x x x πππ⎛⎫⎛⎫=⋅+--+ ⎪ ⎪⎝⎭⎝⎭sin cos sin sin 44x x x x ππ⎛⎫⎛⎫=⋅--- ⎪ ⎪⎝⎭⎝⎭,1cos 2sin 212sin 2222x x x π⎛⎫-- ⎪⎝⎭=-=-,故()f x 的最小正周期T =π; (2)1sin 022C f C ⎛⎫=-= ⎪⎝⎭,又三角形为锐角三角形,故6C π=,11sin 264S ab ab π==,(22212cos 226c a b ab ab ab π==+-≥=,∴2ab ≤∴11sin 264S ab ab π==≤.18.【答案】(1)见解析;(2)()34E X =,见解析. 【解析】解:(1)由频率分布直方图可知,在抽取的100人中,“围棋迷”有25人,从而2×2列联表如下:将2×2列联表中的数据代入公式计算,得:()()221112122121212100301045151003.0307525455533n n n n n n n n n χ++++-⨯⨯-⨯===≈⨯⨯⨯, 因为3.030 3.841<,所以没有理由认为“围棋迷”与性别有关;(2)由频率分布直方图知抽到“围棋迷”的频率为0.25,将频率视为概率,即从观众中抽取一名“围棋迷”的概率为1.由题意13,3X B ⎛⎫⎪ ,从而X 的分布列为()13344E X np ==⨯=.19.【答案】(1)见解析;(2) 【解析】(1)在图1中,可得AC BC ==222AC BC AB +=,故AC BC ⊥, 取AC 中点O 连结DO ,则DO AC ⊥,又面ADE ⊥面ABC ,面ADE 面ABC AC =,DO⊂面ACD ,从而OD ⊥平面ABC ,∴OD BC ⊥,又AC BC ⊥,AC OD O = ,∴BC ⊥平面ACD ,故平面DBC ⊥平面ACD ; (2)建立空间直角坐标系O xyz -如图所示,则M ⎛⎫ ⎪ ⎪⎝⎭,C ⎫⎪⎪⎝⎭,D ⎛ ⎝⎭,,CM ⎫=⎪⎪⎝⎭,CD =⎝⎭, 设()1,,x y z =n 为面CDM 的法向量,则1100CM CD ⎧=⎪⎨=⎪⎩n n即00+==,解得y x z x =-⎧⎨=-⎩, 令1x =-,可得()11,1,1=-n ,又()20,1,0=n 为面ACD 的一个法向量,∴121212cos ,⋅===n n n n n n ,∴二面角B CD M --的余弦值为.20.【答案】(1)22143x y +=;(2)⎛ ⎝⎭. 【解析】(1)由12e =,可知2a c =, 因为12PF F △的周长是6,所以226a c +=,所以2a =,1c =,所求椭圆方程为22143x y +=; (2)椭圆的上顶点为(M ,设过点M 与圆T相切的直线方程为y kx =由直线1y kx =+与T23=,()2294230t k -++=,∴12k k +=,1222394k k t =-,由122143y k x x y ⎧=+⎪⎨+=⎪⎩得()2211340k x x ++=,∴1E x =,同理2F x =,((1212EF E F E FEF E FE FE Fk x k x y y k xk x k x x x x x x ---===---,()1212334k k k k +=-,当01t <<时,()f t =EF的斜率的范围为⎛ ⎝⎭. 21.【答案】(1)见解析;(2)()()()22f m m f n n mm nm n +-+>-+,见解析.【解析】(1)因为()1xf x x-'=,故()f x 在()0,1上是增加的,在()1,+∞上是减少的, ()()max 1ln111f x f ==-=-,()min 1f x =,设()ln x G x x =,则()21ln xG x x -'=,故()G x 在()0,e 上是增加的, 在()e,+∞上是减少的,故()()max 1e 1eG x G ==<,()()max min G x f x <, 所以()ln xf x x>对任意()0,x ∈+∞恒成立; (2)()()lnln ln 11mf m f n m n m n n m n m n n n-+--==⨯---,2211m n mm n n m n =⨯++, ∵0m n >>,∴10m n ->,故只需比较ln m n 与1mn n m m n-+的大小令()1m t t n =>,设()()211ln ln 11t t t G t t t t t t--=-=-++,()()()()()3243222222111211111t t t t t t t t G t t t t t t t -+++--++'=-==+++, 因为1t >,所以()0G t '>,所以函数()G t 在()1,+∞上是增加的, 故()()10G t G >=,所以()0G t >对任意1t >恒成立, 即1ln mm n n m n->+,从而有()()()22f m m f n n m m n m n +-+>-+. 22.【答案】(1)2213x y +=,3;(2)1,13⎡⎤⎢⎥⎣⎦.【解析】(1)曲线C 的普通方程为2213x y +=;当3θπ=时,直线l的参数方程:112x t y ⎧=+⎪⎪⎨⎪=⎪⎩(t 为参数),将l 的参数方程代入2213x y +=,得220t t +-=,解得12t =-,21t =,所以123AB t t =-=. (2)直线l 参数方程代入得()222cos 3sin 2cos 20t t θθθ++-=,1222221cos 3sin 12sin PA PB t t θθθ⋅=-==++,20sin 1θ≤≤,113PA PB ≤⋅≤,所以PA PB ⋅的范围是1,13⎡⎤⎢⎥⎣⎦.23.【答案】(1)4;(2)2|23x x x ⎧⎫≤-≥⎨⎬⎩⎭或.【解析】(1)∵222a b ab +≥,∴()22222a b a b +≥+,∴()216a b +≤, ∴()4a b +≤,故4m ≥;(2)由21x x a b -+≥+恒成立,故只需214x x -+≥, 解得实数x 的取值范围是2|23x x x ⎧⎫≤-≥⎨⎬⎩⎭或.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2019届高三好教育云平台8月份内部特供卷高三理科数学(二)注意事项:1.答题前,先将自己的姓名、准考证号填写在试题卷和答题卡上,并将准考证号条形码粘贴在答题卡上的指定位置。
2.选择题的作答:每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑,写在试题卷、草稿纸和答题卡上的非答题区域均无效。
3.非选择题的作答:用签字笔直接答在答题卡上对应的答题区域内。
写在试题卷、草稿纸和答题卡上的非答题区域均无效。
4.考试结束后,请将本试题卷和答题卡一并上交。
第Ⅰ卷一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合{}|24,x A x x =≤∈N ,6=|1,Z 1B x x x ⎧⎫>∈⎨⎬+⎩⎭,则满足条件A C B ⊆⊆集合C 的个数为( ) A .4B .3C .2D .12.已知p :“R x ∀∈,233x +≥”,则p ⌝是( ) A .R x ∀∈,233x +< B .R x ∃∈,233x +≤ C .R x ∃∈,233x +<D .R x ∃∈,233x +≥3.下列命题中正确命题的个数是( )(1)对分类变量X 与Y 的随机变量2K 的观测值k 来说,k 越小,判断“X 与Y 有关系”的把握越大;(2)若将一组样本数据中的每个数据都加上同一个常数后,则样本的方差不变; (3)在残差图,残差点分布的带状区域的宽度越狭窄,其模型拟合的精度越高;(4)设随机变量ξ服从正态分布()0,1N ,若()1P p ξ>=,则()1102P p ξ-<<=-;A .4B .3C .2D .14.《张丘建算经》卷上第22题为:“今有女善织,日益功疾,且从第2天起,每天比前一天多织相同量的布,若第一天织5尺布,现在一月(按30天计),共织390尺布”,则该女最后一天织多少尺布?( ) A .18 B .20 C .21 D .255.某几何体的三视图如图所示,则这个几何体最长的一条棱长为( )A.B.C .4D.6.设n S 是数列{}n a 的前n 项和,且11a =-,11n n n a S S ++=,则10S =( ) A .110B .110-C .10D .10-7.设0sin d a x x π=⎰,则()622x ⎛⋅+ ⎝的展开式中常数项是( ) A .332 B .332- C . 320 D .320-8.设sin 390a =︒,函数()0log 0xa ax f x x x ⎧<⎪=⎨≥⎪⎩,则211log 108f f ⎛⎫⎛⎫+ ⎪ ⎪⎝⎭⎝⎭的值等于( )A .9B .10C .11D .129.现有一个不透明的口袋中装有标号为1,2,2,3的四个小球,他们除数字外完全相同,现从中随机取出一球记下号码后放回,均匀搅拌后再随机取出一球,则两次取出小球所标号码不同的概率为( )A .16B .56 C .38D .5810.已知定义在区间,2π⎡⎤-π⎢⎥⎣⎦上的函数()y f x =的图像关于直线4x π=对称,当4x π≥时,()sin f x x =,如果关于x 的方程()f x a =有解,记所有解的和为S ,则S 不可能为( )A .34πB .2π C .π D .2π11.已知直线l 与双曲线2214x y -=相切于点P ,l 与双曲线两条渐近线交于M ,N 两点,则OM ON⋅的值为( ) A .3B .4C .5D .与.P 的位置有关12.设()()210n n f x x x x x =++++>,其中n ∈N ,2n ≥,则函数()()2n n G x f x =-在1,12n ⎛⎫⎪⎝⎭内的零点个数是( ) A .0 B .1 C .2 D .与n 有关此卷只装订不密封班级 姓名 准考证号 考场号 座位号二、填空题:(本大题共4题,每小题5分,满分20分,将答案填在答题纸上)13.已知复数1i z =+,则221z z z -=-__________.14.从抛物线214y x =上一点P 引抛物线准线的垂线,垂足为M ,且5PM =.设抛物线的焦点为F ,则MPF △的面积为__________.15.过平面区域202020x y y x y -+≥⎧⎪+≥⎨⎪++≤⎩内一点P 作圆22:1O x y +=的两条切线,切点分别为A ,B ,记APB α∠=,当α最大时,点P 坐标为__________.16.设()3f x x x =-,过下列点()0,0A ,()0,2B ,()2,1C -,D ⎝⎭,()2,0E -分别作曲线()f x 的切线,其中存在三条直线与曲线()y f x =相切的点是__________.三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17.(12分)在平面直角坐标系xoy 中,已知向量sin ,cos 4x x ⎛π⎫⎛⎫=+ ⎪ ⎪⎝⎭⎝⎭m ,cos ,sin 4x x ⎛π⎫⎛⎫=- ⎪ ⎪⎝⎭⎝⎭n ,设()f x =⋅m n(1)求()f x 的最小正周期;(2)在锐角三角形ABC △中,角A ,B ,C 的对边分别为a ,b ,c ,若02C f ⎛⎫= ⎪⎝⎭,1c =,求ABC△面积的最大值.18.(12分)郑州一中社团为调查学生学习围棋的情况,随机抽取了100名学生进行调查.根据调查结果绘制的学生日均学习围棋时间的频率分布直方图:将日均学习围棋时间不低于40分钟的学生称为“围棋迷”.(1)根据已知条件完成下面的2×2列联表,并据此资料你是否认为“围棋迷”与性别有关?(2)将上述调查所得到的频率视为概率.现在从该地区大量学生中,采用随机抽样方法每次抽取1名学生,抽取3次,记被抽取的3名学生中的“围棋迷”人数为X .若每次抽取的结果是相互独立的,求X 的分布列与期望.附:()()()()()22n ad bc K a b c d a c b d -=++++,19.(12分)如图1,在直角梯形ABCD 中,90ADC ∠=︒,CD AB ∥,2AB =,1AD CD ==,M 为线段AB 的中点.将ADC △沿AC 折起,使平面ADC ⊥平面ABC ,得到几何体D ABC -,如图2所示.(1)求证:平面DBC ⊥平面ACD ; (2)求二面角B CD M --的余弦值.20.(12分)已知椭圆2222:1x y C a b+=的离心率为12,1F ,2F 是椭圆的两个焦点,P 是椭圆上任意一点,且12PF F △的周长是6. (1)求椭圆C 的方程; (2)设圆:()224:9T x t y -+=,过椭圆的上顶点作圆T 的两条切线交椭圆于E ,F 两点,当圆心在x 轴上移动且()0,1t ∈时,求EF 的斜率的取值范围.21.(12分)已知函数()ln f x x x =-.(1)证明:()ln x f x x >;(2)设0m n >>,比较()()()f m m f n n m n+-+-与22mm n+的大小,并说明理由.请考生在22、23两题中任选一题作答,如果多做,则按所做的第一题记分. 22.(10分)【选修4-4:坐标系与参数方程】已知直线l 的参数方程:1cos sin x t y t θθ=+⎧⎨=⎩(θ为参数),曲线C的参数方程:sin x y αα⎧=⎪⎨=⎪⎩(α为参数),且直线交曲线C 于A ,B 两点.(1)将曲线C 的参数方程化为普通方程,并求3θπ=时,AB 的长度; (2)已知点()1,0P ,求当直线倾斜角θ变化时,PA PB ⋅的范围.23.(10分)【选修4-5:不等式选讲】已知实数0a >,0b >,且228a b +=,若a b m +≤恒成立. (1)求实数m 的最小值;(2)若21x x a b -+≥+对任意的a ,b 恒成立,求实数x 的取值范围.2019届高三好教育云平台8月份内部特供卷高三理科数学(二)答 案一、选择题.1.【答案】A2.【答案】C3.【答案】B4.【答案】C 5.【答案】A 6.【答案】B 7.【答案】B 8.【答案】C 9.【答案】D 10.【答案】D 11.【答案】B 12.【答案】B二、填空题.13.【答案】2i 14.【答案】10 15.【答案】()1,1-- 16.【答案】C ,E三、解答题.17.【答案】(1)T =π;(2. 【解析】(1)()sin cos sin cos 44f x x x x x ππ⎛⎫⎛⎫=⋅=⋅+-+ ⎪ ⎪⎝⎭⎝⎭m n ,sin cos sin cos 442x x x x πππ⎛⎫⎛⎫=⋅+--+ ⎪ ⎪⎝⎭⎝⎭sin cos sin sin 44x x x x ππ⎛⎫⎛⎫=⋅--- ⎪ ⎪⎝⎭⎝⎭,1cos 2sin 212sin 2222x x x π⎛⎫-- ⎪⎝⎭=-=-,故()f x 的最小正周期T =π; (2)1sin 022C f C ⎛⎫=-= ⎪⎝⎭,又三角形为锐角三角形,故6C π=,11sin 264S ab ab π==,(22212cos 226c a b ab ab ab π==+-≥=,∴2ab ≤∴11sin 264S ab ab π==≤.18.【答案】(1)见解析;(2)()34E X =,见解析. 【解析】解:(1)由频率分布直方图可知,在抽取的100人中,“围棋迷”有25人,从而2×2列联表如下:将2×2列联表中的数据代入公式计算,得:()()221112122121212100301045151003.0307525455533n n n n n n n n n χ++++-⨯⨯-⨯===≈⨯⨯⨯, 因为3.030 3.841<,所以没有理由认为“围棋迷”与性别有关;(2)由频率分布直方图知抽到“围棋迷”的频率为0.25,将频率视为概率,即从观众中抽取一名“围棋迷”的概率为1.由题意13,3X B ⎛⎫⎪⎭,从而X 的分布列为()13344E X np ==⨯=.19.【答案】(1)见解析;(2) 【解析】(1)在图1中,可得AC BC ==222AC BC AB +=,故AC BC ⊥, 取AC 中点O 连结DO ,则DO AC ⊥,又面ADE ⊥面ABC , 面ADE面ABC AC =,DO⊂面ACD ,从而OD ⊥平面ABC ,∴OD BC ⊥,又AC BC ⊥,AC OD O =,∴BC ⊥平面ACD ,故平面DBC ⊥平面ACD ;(2)建立空间直角坐标系O xyz -如图所示,则M ⎛⎫ ⎪ ⎪⎝⎭,C ⎫⎪⎪⎝⎭,D ⎛ ⎝⎭,2,CM ⎛⎫= ⎪⎪⎝⎭,2CD ⎛= ⎝⎭, 设()1,,x y z =n 为面CDM 的法向量,则1100CM CD⎧=⎪⎨=⎪⎩n n即00+==,解得y x z x =-⎧⎨=-⎩,令1x =-,可得()11,1,1=-n ,又()20,1,0=n 为面ACD 的一个法向量,∴121212cos ,⋅===n n n n n n ,∴二面角B CD M --的余弦值为.20.【答案】(1)22143x y +=;(2)⎛ ⎝⎭. 【解析】(1)由12e =,可知2a c =, 因为12PF F △的周长是6,所以226a c +=,所以2a =,1c =,所求椭圆方程为22143x y +=; (2)椭圆的上顶点为(M ,设过点M 与圆T 相切的直线方程为y kx =由直线1ykx =+与T23=,()2294230t k -++=, ∴12k k +=,1222394k k t =-, 由122143y k x xy ⎧=+⎪⎨+=⎪⎩得()2211340k x x ++=,∴1E x =,同理2F x=, ((1212EF E F E FEF E FE FE Fk x k x y y k xk x k x x x x x x ---===---,()1212334k k k k +=-,当01t <<时,()f t =EF 的斜率的范围为⎛ ⎝⎭. 21.【答案】(1)见解析;(2)()()()22f m m f n n mm nm n +-+>-+,见解析.【解析】(1)因为()1xf x x-'=,故()f x 在()0,1上是增加的,在()1,+∞上是减少的, ()()max 1ln111f x f ==-=-,()min 1f x =,设()ln x G x x =,则()21ln xG x x -'=,故()G x 在()0,e 上是增加的, 在()e,+∞上是减少的,故()()max 1e 1eG x G ==<,()()max min G x f x <, 所以()ln xf x x>对任意()0,x ∈+∞恒成立; (2)()()lnln ln 11mf m f n m n m n n m n m n n n-+--==⨯---,2211m n mm n n m n =⨯++, ∵0m n >>,∴10m n ->,故只需比较ln m n 与1mn n m m n-+的大小令()1m t t n =>,设()()211ln ln 11t t t G t t t t t t--=-=-++,()()()()()3243222222111211111t t t t t t t t G t t t t t t t -+++--++'=-==+++, 因为1t >,所以()0G t '>,所以函数()G t 在()1,+∞上是增加的, 故()()10G t G >=,所以()0G t >对任意1t >恒成立, 即1ln mm n n m n->+,从而有()()()22f m m f n n m m n m n +-+>-+. 22.【答案】(1)2213x y +=,3;(2)1,13⎡⎤⎢⎥⎣⎦.【解析】(1)曲线C 的普通方程为2213x y +=;当3θπ=时,直线l 的参数方程:112x t y ⎧=+⎪⎪⎨⎪=⎪⎩(t 为参数),将l 的参数方程代入2213x y +=,得220t t +-=,解得12t =-,21t =,所以123AB t t =-=. (2)直线l 参数方程代入得()222cos 3sin 2cos 20t t θθθ++-=,1222221cos 3sin 12sin PA PB t t θθθ⋅=-==++,20sin 1θ≤≤,113PA PB ≤⋅≤,所以PA PB ⋅的范围是1,13⎡⎤⎢⎥⎣⎦.23.【答案】(1)4;(2)2|23x x x ⎧⎫≤-≥⎨⎬⎩⎭或.【解析】(1)∵222a b ab +≥,∴()22222a b a b +≥+,∴()216a b +≤, ∴()4a b +≤,故4m ≥;(2)由21x x a b -+≥+恒成立,故只需214x x -+≥, 解得实数x 的取值范围是2|23x x x ⎧⎫≤-≥⎨⎬⎩⎭或.。
