空间向量的坐标运算练习
高中数学人教A版(2019)选择性必修一第一章空间向量及运算的坐标表示同步练习

高中数学人教A 版(2019)选择性必修一第一章空间向量及运算的坐标表示同步练习一、单选题(共8题;共16分)1.(2分)空间直角坐标系中,已知 A(1,−2,3) , B(3,2,−5) ,则线段 AB 的中点为( )A .(−1,−2,4)B .(−2,0,1)C .(2,0,−2)D .(2,0,−1)2.(2分)已知 a ⃗ =(1,1,0),b ⃗ =(0,1,1),c ⃗ =(1,0,1) , p ⃗ =a ⃗ −b ⃗ ,q ⃗ =a ⃗ +2b ⃗ −c ⃗ ,则 p⃗ ⋅q ⃗ = ( ) A .-1 B .1 C .0 D .-23.(2分)已知向量 a ⃗ =(3,5,−1) , b ⃗ =(2,2,3) , c ⃗ =(1,−1,2) ,则向量 a ⃗ −b ⃗ +4c ⃗ 的坐标为( ).A .(5,−1,4)B .(5,1,−4)C .(−5,1,4)D .(−5,−1,4)4.(2分)已知向量 a ⃗ =(1,1,0),则与 a⃗ 共线的单位向量 e ⃗ =( ) A .(√22,−√22,0)B .(0, 1, 0)C .(√22,√22,0)D .(1, 1, 1)5.(2分)在空间直角坐标系中,向量 a ⃗ =(2,−3,5) , b ⃗ =(−2,4,5) ,则向量 a ⃗ +b⃗ = ( ) A .(0,1,10) B .(−4,7,0) C .(4,−7,0)D .(−4,−12,25)6.(2分)已知向量 a ⃗ =(2,3,1) , b ⃗ =(1,2,0) ,则 |a +b⃗ | 等于( ) A .√3 B .3 C .√35D .97.(2分)已如向量 a ⃗ =(1,1,0) , b ⃗ =(−1,0,1) ,且 ka +b⃗ 与 a ⃗ 互相垂直,则 k = ( ). A .13B .12C .−13D .−128.(2分)已知空间向量 m ⃗⃗⃗ =(3,1,3) , n ⃗ =(−1,λ,−1) ,且 m⃗⃗⃗ //n ⃗ ,则实数 λ= ( ) A .−13B .-3C .13D .6二、多选题(共4题;共12分)9.(3分)以下命题正确的是( )A .若 p → 是平面 α 的一个法向量,直线 b 上有不同的两点 A ,B ,则 b//α 的充要条件是 p →⋅AB⃗⃗⃗⃗⃗⃗ =0B .已知 A , B ,C 三点不共线,对于空间任意一点 O ,若 OP ⃗⃗⃗⃗⃗⃗ =25OA ⃗⃗⃗⃗⃗⃗ +15OB ⃗⃗⃗⃗⃗⃗ +25OC ⃗⃗⃗⃗⃗ ,则 P , A , B , C 四点共面C .已知 a →=(−1,1,2) , b →=(0,2,3) ,若 ka →+b →与 2a →−b →垂直,则 k =−34D .已知 △ABC 的顶点坐标分别为 A(−1,1,2) , B(4,1,4) , C(3,−2,2) ,则 AC 边上的高 BD 的长为 √1310.(3分)下列四个结论正确的是( )A .任意向量 a ⃗ , b →,若 a ⃗ ⋅b ⃗ =0 ,则 a →=0→或 b →=0→或 〈a →,b →〉=π2 B .若空间中点 O , A , B , C 满足 OC ⃗⃗⃗⃗⃗ =13OA ⃗⃗⃗⃗⃗⃗ +23OB ⃗⃗⃗⃗⃗⃗ ,则 A , B , C 三点共线C .空间中任意向量 a →,b →,c →都满足 (a →⋅b →)⋅c →=a →⋅(b →⋅c →)D .已知向量 a →=(1,1,x) , b →=(−2,x,4) ,若 x <25,则 〈a →,b →〉 为钝角 11.(3分)如图,在长方体 ABCD −A 1B 1C 1D 1 中, AB =5 , AD =4 , AA 1=3 ,以直线 DA ,DC , DD 1 分别为 x 轴、 y 轴、 z 轴建立空间直角坐标系,则( )A .点B 1 的坐标为 (5,4,3)B .点C 1 关于点 B 对称的点为 (8,5,−3)C .点 A 关于直线 BD 1 对称的点为 (0,5,3) D .点 C 关于平面 ABB 1A 1 对称的点为 (8,−5,0)12.(3分)已知向量 a⃗ =(1,1,0) ,则与 a ⃗ 共线的单位向量 e ⃗ = ( ) A .(−√22,−√22,0)B .(0,1,0)C .(√22,√22,0) D .(−1,−1,0)三、填空题(共4题;共5分)13.(1分)已知向量 a⃗ =(1,2,3) , b ⃗ =(x,x 2+y −2,y) ,并且 a ⃗ , b ⃗ 同向,则 x , y 的值分别为 .14.(1分)若向量 a ⃗ = (1,λ,2), b ⃗ = (﹣2,1,1), a⃗ , b ⃗ 夹角的余弦值为 16,则λ= . 15.(2分)已知 a ⃗ =(3,2λ−1,1) , b ⃗ =(μ+1,0,2μ) .若 a ⃗ ⊥b ⃗ ,则μ= ;若 a ⃗ //b⃗ ,则λ+μ= .16.(1分)已知向量 a ⇀=(0,−1,1),b ⇀=(4,1,0),|λa ⇀+b ⇀|=√29 ,且 λ>0 ,则 λ= .四、解答题(共4题;共45分)17.(10分)如图,建立空间直角坐标系 Oxyz .单位正方体 ABCD −A ′B ′C ′D ′ 顶点A 位于坐标原点,其中点B(1,0,0) ,点 D(0,1,0) ,点 A ′(0,0,1) .(1)(5分)若点E 是棱 B ′C ′ 的中点,点F 是棱 B ′B 的中点,点G 是侧面 CDD ′C ′ 的中心,则分别求出向量 OE⇀,OG ⇀,FG ⇀ 的坐标; (2)(5分)在(1)的条件下,分别求出 (OE ⃗⃗⃗⃗⃗ +OG ⃗⃗⃗⃗⃗ )⋅FG⃗⃗⃗⃗⃗ , |EG ⃗⃗⃗⃗⃗ | 的值. 18.(10分)已知点 A(0,1,2) , B(1,−1,3) , C(1,5,−1) .(1)(5分)若D 为线段 BC 的中点,求线段 AD 的长;(2)(5分)若 AD ⇀=(2,a,1) ,且 AB ⃗⃗⃗⃗⃗⃗ ⋅AD ⃗⃗⃗⃗⃗⃗ =1 ,求a 的值,并求此时向量 AB ⃗⃗⃗⃗⃗⃗ 与 AD ⃗⃗⃗⃗⃗⃗ 夹角的余弦值. 19.(20分)已知点 A(0,1,−1) , B(2,2,1) ,向量 a ⃗ =OA ⃗⃗⃗⃗⃗⃗ ,b ⃗ =OB ⃗⃗⃗⃗⃗⃗ ,计算: (1)(5分)求向量 b ⃗ 的单位向量 b 0⃗⃗⃗⃗ ;(2)(5分)求 |2a −b ⃗ | , |−3a | ; (3)(5分)cos <a ,b⃗ > ; (4)(5分)求点 B 到直线 OA 的距离.20.(5分)已知正方形ABCD 的边长为2, PA ⊥ 平面 ABCD ,且PA=2,E 是PD 中点.以A 为原点,建立如图所示的空间直角坐标系 A −xyz .(Ⅰ)求点 A,B,C,D,P,E 的坐标; (Ⅱ)求 |CE⃗⃗⃗⃗⃗ | .答案解析部分1.【答案】D【解析】【解答】根据中点坐标公式,中点坐标为(2,0,−1).故答案为:D.【分析】由空间直角坐标系中点的公式代入数值计算出结果即可。
高三数学空间向量基本定理与坐标运算试题
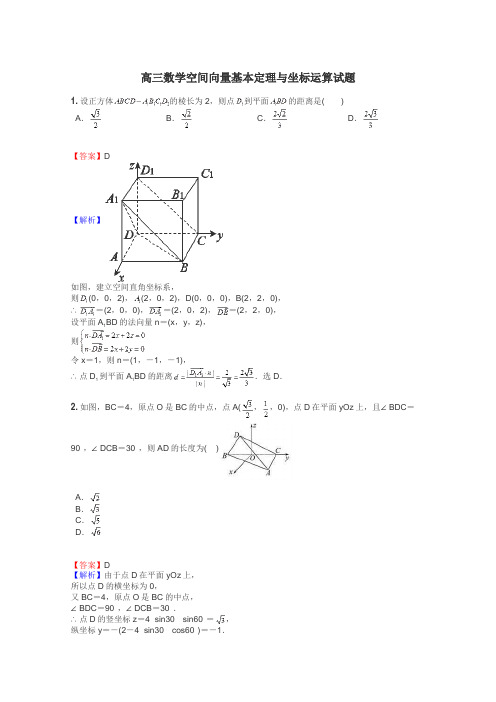
高三数学空间向量基本定理与坐标运算试题1.设正方体的棱长为2,则点到平面的距离是() A.B.C.D.【答案】D【解析】如图,建立空间直角坐标系,则(0,0,2),(2,0,2),D(0,0,0),B(2,2,0),∴=(2,0,0),=(2,0,2),=(2,2,0),设平面A1BD的法向量n=(x,y,z),则令x=1,则n=(1,-1,-1),∴点D1到平面A1BD的距离.选D.2.如图,BC=4,原点O是BC的中点,点A(,,0),点D在平面yOz上,且∠BDC=90°,∠DCB=30°,则AD的长度为( )A.B.C.D.【答案】D【解析】由于点D在平面yOz上,所以点D的横坐标为0,又BC=4,原点O是BC的中点,∠BDC=90°,∠DCB=30°.∴点D的竖坐标z=4×sin30°×sin60°=,纵坐标y=-(2-4×sin30°×cos60°)=-1.∴D(0,-1,).∴|AD|==,选D.3.在四棱锥中,,,,则这个四棱锥的高A.1B. 2C. 13D. 26【答案】B【解析】根据tiyi,由于四棱锥中,,,,那么可知设平面ABCD的法向量为,则根据在上投影的绝对值可知得到锥体的高度为,故可知h=2,故选B.【考点】向量的运用点评:主要是考查了向量的数量积的运用,求解距离,属于基础题。
4.已知、、为两两垂直的单位向量,非零向量,若向量与向量、、的夹角分别为、、,则.【答案】1【解析】设、、为长方体的共顶点的三条棱的方向向量,因非零向量,故可为长方体体对角线的方向向量,则、、分别为则有5.(理)已知向量=(2,4,x),=(2,y,2),若||=6,⊥,则x+y的值是()A.-3或1B.3或-1C.-3D.1【答案】A【解析】则故选A6.点是棱长为1的正方体内一点,且满足,则点到棱的距离为A.B.C.D.【答案】A【解析】略7.已知a+3b与7a-5b垂直,且a-4b与7a-2b垂直,则〈a,b〉=_______【答案】60°【解析】略8.已知空间向量,且,则()A.B.C.D.【答案】C【解析】略9.以下向量中,能成为以行列式形式表示的直线方程的一个法向量的是()A.B.C.D.【答案】A【解析】【考点】三阶矩阵.分析:此题要求方程的解集,主要还是化简方程左边的行列式得直线方程,最后求出一个法向量即可.解:因为得到方程:2+x-2y-1=0化简得:x-2y+1=0其一个方向向量为(2,1).故它的法向量为:(1,-2)故选A.10.的三个内角的对边分别为,已知,向量,。
人教A版选修2-1第三章第六课时同步练习3-1-5空间向量运算的坐标表示

§3.1. 5空间向量运算的坐标表示一、选择题1.已知a =(cos α,1,sin α),b =(sin α,1,cos α) ,且a 不平行 b ,则向量a +b 与a -b 的夹角是( )A .90°B .60°C .30°D .0°2.已知空间四点A (4,1,3),B (2,3,1),C (3,7,-5),D (x ,-1,3)共面,则x 的值为( )A .4B .1C .10D .113.下列各组向量中共面的组数为( )①a =(1,2,3),b =(3,0,2),c =(4,2,5)②a =(1,2,-1),b (0,2,-4),c =(0,-1,2)③a =(1,1,0),b =(1,0,1),c =(0,1,-1)④a =(1,1,1),b (1,1,0),c =(1,0,1)A .0B .1C .2D .34.下列各组向量不平行的是( )A .a =(1,2,-2),b =(-2,-4,4)B .c =(1,0,0),d =(-3,0,0)C .e =(2,3,0),f =(0,0,0)D .g =(-2,3,5),h =(16,-24,40)5.若两点的坐标是A (3cos α,3sin α,1),B (2cos θ,2sin θ,1),则|AB →|的取值范围是( )A .[0,5]B .[1,5]C .(1,5)D .[1,25]6.已知a =(x,2,0),b =(3,2-x ,x ),且a 与b 的夹角为钝角,则x 的取值范围是( )A .x <-4B .-4<x <0C .0<x <4D .x >47.如图所示的空间直角坐标系中,正方体ABCD -A 1B 1C 1D 1棱长为1,B 1E 1=14A 1B 1,则BE 1→等于( ) A .(0,14,-1) B .(-14,0,1) C .(0,-14,1) D .(14,0,-1) 8.已知a =(1,2,-y ),b =(x,1,2),且(a +2b )∥(2a -b ),则( )A .x =13,y =1B .x =12,y =-4C .x =2,y =-14D .x =1,y =-19.如图AC 1是正方体的一条体对角线,点P 、Q 分别为其所在棱的中点,则PQ 与AC 1所成的角为( )A .4πB .12π C.π3 D.π210.已知向量OA →=(2,-2,3),向量OB →=(x,1-y,4z ),且平行四边形OACB对角线的中点坐标为(0,32,-12),则(x ,y ,z )=( ) A .(-2,-4,-1) B .(-2,-4,1)C .(-2,4,-1)D .(2,-4,-1)二、填空题11.已知a =(1,0,-1),b =(1,-1,0),单位向量n 满足n ⊥a ,n ⊥b ,则n =________.12.已知空间三点A (1,1,1)、B (-1,0,4)、C (2,-2,3),则AB →与CA →的夹角θ的大小是________.13.已知向量a =(-3,2,5),b =(1,-3,0),c =(7,-2,1),则:(1)a +b +c =________; (2)(a +b )·c =________; (3)|a -b +c |2=________.14.已知a ,b ,c 不共面,且m =3a +2b +c ,n =x (a -b )+y (b -c )-2(c -a ),若m ∥n ,则x +y =__________________.三、解答题15.已知点A (2,3,-1),B (8,-2,4),C (3,0,5),是否存在实数x ,使AB →与AB →+xAC →垂直?16.正方体ABCD -A 1B 1C 1D 1中,E 、F 分别是BB 1、DC 的中点.求证:(1)AE ⊥D 1F ; (2)AE ⊥平面A 1D 1F .18.已知空间三点A (0,2,3)、B (-2,1,6)、C (1,-1,5).(1)求以AB →、AC →为邻边的平行四边形面积;(2)若|a |=3,且a 分别与AB →、AC →垂直,求向量a 的坐标.参考答案一、选择题1.[答案] A[解析] ∵|a |2=2,|b |2=2,(a +b )·(a -b )=|a |2-|b |2=0,∴(a +b )⊥(a -b ).2.[解析] AB →=(-2,2,-2),AC →=(-1,6,-8),AD →=(x -4,-2,0),∵A 、B 、C 、D 共面,∴AB →、AC →、AD →共面,∴存在λ、μ,使AD →=λAB →+μAC →,即(x -4,-2,0)=(-2λ-μ,2λ+6μ,-2λ-8μ),∴⎩⎪⎨⎪⎧ x -4=-2λ-μ-2=2λ+6μ0=-2λ-8μ,∴⎩⎪⎨⎪⎧ λ=-4μ=1x =11. 3.[答案] D[解析] ①设a =x b +y c ,则⎩⎪⎨⎪⎧ 1=3x +4y 2=0·x +2y 3=2x +5y ,解得⎩⎪⎨⎪⎧x =-1y =1. 故存在实数x =-1,y =1使得a =-b +c ,∴a ,b ,c 共面.②中b =-2c ,③中c =a -b .故②③中三个向量共面.4.[答案] D[解析] b =-2a ,d =-3c ,f =0e ,只有D 不存在实数λ,使g =λh .5.[答案] B[解析] |AB →|2=(2cos θ-3cos α)2+(2sin θ-3sin α)2=13-12cos θcos α-12sin θsin α =13-12cos(θ-α)∈[1,25],∴1≤|AB →|≤5.6.[答案] A[解析] ∵a 、b 的夹角为钝角,∴a ·b <0,即3x +2(2-x )+0·x =4+x <0.∴x <-4.又当夹角为π时,存在λ<0,使b =λa ,∴⎩⎪⎨⎪⎧ 3=λx 2-x =2λx =0,此方程组无解,因此选A. 7.[答案] C[解析] B (1,1,0)、E 1(1,34,1),BE 1→=(0,-14,1). 8.[答案] B[解析] a +2b =(2x +1,4,4-y ),2a -b =(2-x,3,-2y -2),∵(a +2b )∥(2a -b ),∴⎩⎪⎨⎪⎧ 2x +1=λ(2-x )4=3λ4-y =(-2y -2)λ,∴⎩⎪⎨⎪⎧x =12y =-4 9.[答案] D[分析] 建立空间直角坐标系,求出AC 1→与PQ →的坐标,转化为求AC 1→与PQ →的夹角.[解析] 设正方体棱长为1,以点A 1为坐标原点,A 1B 1、A 1D 1、A 1A 所在直线分别为x轴、y 轴、z 轴建立空间直角坐标系,则P ⎝⎛⎭⎫12,0,0,Q ⎝⎛⎭⎫0,1,12,A (0,0,1),C 1(1,1,0),所以PQ →=⎝⎛⎭⎫-12,1,12,AC 1→=(1,1,-1),故PQ →·AC 1→=-12×1+1×1+12×(-1)=0, ∴PQ →⊥AC 1→,即PQ 与AC 1所成的角为π2. 10.[答案] A[解析] 由条件(2,-2,3)+(x,1-y,4z )=2⎝⎛⎭⎫0,32,-12, ∴(x +2,-1-y,3+4z )=(0,3,-1),∴⎩⎪⎨⎪⎧x =-2y =-4z =-1.二、填空题11.[答案] ⎝⎛⎭⎫33,33,33 ⎝⎛⎭⎫-33,-33,-33[解析] 设n =(x ,y ,z ),由条件⎩⎪⎨⎪⎧ x -z =0x -y =0x 2+y 2+z 2=1,∴x =y =z =33或-33.12.[答案] 120°[解析] AB →=(-2,-1,3),CA →=(-1,3,-2),AB →·CA →=-7,|AB →|=14,|CA →|=14,∴cos θ=-714×14=-12,∴θ=120°.13.[答案] (5,-3,6) -7 54[解析] (1)a +b +c =(-3,2,5)+(1,-3,0)+(7,-2,1)=(5,-3,6).(2)a +b =(-2,-1,5),(a +b )·c =(-2,-1,5)·(7,-2,1)=-7.(3)a -b +c =(3,3,6),|a -b +c |2=54.14.[答案] -4[解析] ∵a 、b 、c 不共面,m ∥n , ∴x +23=-x +y 2=-y -21,∴⎩⎪⎨⎪⎧ x =-2y =-2.三、解答题15.[解析] AB →=(6,-5,5),AC →=(1,-3,6),AB →+xAC →=(6+x ,-5-3x,5+6x ),∵AB →⊥(AB →+xAC →)∴6(6+x )-5(-5-3x )+5(5+6x )=0,∴x =-9651=-3217,∴存在实数x =-3217, 使AB →与AB →+xAC →垂直.16.[证明] 设正方体的棱长为1,以DA →、DC →、DD 1→为坐标向量,建立空间直角坐标系D -xyz ,如图所示.(1)易知A (1,0,0)、E (1,1,12)、F (0,12,0)、D 1(0,0,1).∵AE →=(0,1,12),D 1F →=(0,12,-1).又AE →·D 1F →=(0,1,12)·(0,12,-1)=0,∴AE ⊥D 1F .(2)DA →=(1,0,0)=D 1A 1→,∴D 1A 1→·AE →=(1,0,0)·(0,1,12)=0,∴AE ⊥D 1A 1,由(1)知AE ⊥D 1F ,且D 1A ∩D 1F =D 1,∴AE ⊥平面A 1D 1F .17.[解析] (1)∵c ∥BC →,BC →=(-2,-1,2).∴设c =(-2λ,-λ,2λ),∴|c |=(-2λ)2+(-λ)2+(2λ)2=3|λ|=3∴λ=±1∴c =(-2,-1,2)或c =(2,1,-2).(2)a =AB →=(-1+2,1-0,2-2)=(1,1,0)b =AC →=(-3+2,0-0,4-2)=(-1,0,2).∴cos<a ,b >=a·b|a|·|b| =(1,1,0)·(-1,0,2)2×5=-1010.(3)k a +b =(k -1,k,2),k a -2b =(k +2,k ,-4).又(k a +b )⊥(k a -2b ),则(k a +b )·(k a -2b )=(k -1,k,2)·(k +2,k ,-4)=2k 2+k -10=0,∴k =2或k =-52. 18.[解析] (1)由题中条件可知AB →=(-2,-1,3),AC →=(1,-3,2),∴cos 〈AB →,AC →〉=AB →·AC →|AB →|·|AC →|=-2+3+614×14=12, ∴sin 〈AB →,AC →〉=32, ∴以AB →,AC →为邻边的平行四边形面积S =|AB →|·|AC →|·sin 〈AB →,AC →〉=7 3.(2)设a =(x ,y ,z ),由题意得⎩⎪⎨⎪⎧ x 2+y 2+z 2=3,-2x -y +3z =0,x -3y +2z =0.解得⎩⎪⎨⎪⎧ x =1,y =1,z =1,或⎩⎪⎨⎪⎧ x =-1,y =-1,z =-1.∴a =(1,1,1)或a =(-1,-1,-1)。
空间向量的坐标运算

空间向量的坐标运算 1一.选择题1.在空间直角坐标系中,已知点(,,)P x y z ,那么下列说法正确..的是( )A . 点p 关于x 轴对称的坐标是()1,,p x y z -B . 点p 关于yoz 平面对称的坐标是()2,,p x y z --C . 点p 关于y 轴对称点的坐标是()3,,p x y z -D . 点p 关于原点对称点的坐标是(),,x y z ---2.下列命题是真命题的是( )A. 分别表示空间向量的有向线段所在的直线是异面直线,则这两个向量不是共面向量.B. 若a b = ,则,a b 的长度相等而方向相同或相反.C. 若向量,AB CD 满足CD AB 〉 ,且AB CD 与同向,则AB CD 〉 .D. 若两个非零向量AB CD 与满足0AB CD +=,则AB ‖CD .3.已知点()1,3,4p --,且该点在三个坐标平面yoz 平面,zox 平面,xoy 平面上的射影的坐标依次为()111,,x y z ,()222,,x y z 和()333,,x y z ,则( )A .2221230x y z ++= B.2222310x y z ++=C. 2223120x y z ++= D.以4.到定点()1,0,0的距离小于或等于1的点集合为( )A.()(){}222,,|11x y z x y z -++≤B.()(){}222,,|11x y z x y z -++=C.()(){},,|11x y z x y z -++≤D.(){}222,,|1x y z x y z ++≤5.已知()()3cos ,3sin ,12cos ,2sin ,1P ααββ==和Q ,则PQ 的取值范围是()A.[]0,5B.[]0,25C.[]1,5D.()1,56.已知()()()2,5,1,2,2,4,1,4,1A B C ---,则向量AB AC 与的夹角为( )A. 030B.045C.060D.090二.填空题7.已知{},,i j k 为单位正交基,且3,232a i j k b i j k =-++=-- ,则向量a b + 与 向量2a b - 的坐标分别是______________;_________________.8.若(1,1,0),(1,0,2),a b a b ==-+ 则同方向的单位向量是_________________.9. 已知()()1,1,,2,,a t t t b t t =--= ,则b a - 的最小值是_______________.10.若向量 ()()1,,2,2,1,2a b λ==- ,,a b 夹角的余弦值为89,则λ等于__________. 11.已知(c o s ,1,s i n ),(s i n ,a b αααα== 则向量a ba b +- 与的夹角是_________. 12.()()(),2,4,1,,3,1,2,,,,a x b y c z a b c =-=-=- 且两两垂直,则_______,x =_________________y z ==13.设1,2,,a b a b == 且的夹角为0120;则2a b + 等于______________.空间向量的坐标运算21.已知▱ABCD ,且A (4,1,3)、B (2,-5,1)、C (3,7,-5),则顶点D 的坐标为( )A .(72,4,-1) B .(2,3,1) C .(-3,1,5) D .(5,13,-3) 2.已知△ABC 的三个顶点坐标分别为A (2,3,1)、B (4,1,-2)、C (6,3,7),则△ABC 的重心坐标为( )A .(6,72,3)B .(4,73,2)C .(8,143,4)D .(2,76,1) 3.若向量a =(1,λ,2),b =(2,-1,2),cos 〈a ,b 〉=89,则λ等于( ) A .2 B .-2 C .-2或255 D .2或-2554. 已知两空间向量a =(2,cos θ,sin θ),b =(sin θ,2,cos θ),则a +b 与a -b 的夹角为( )A .30°B .45°C .60°D .90°二、填空题5.与A (-1,2,3)、B (0,0,5)两点距离相等的点满足的等式为________.6.已知向量a =(-1,2,3),b =(1,1,1),则向量a 在向量b 方向上的投影为________.7.已知a =(2,-1,2),b =(2,2,1),则以a ,b 为邻边的平行四边形的面积为________.。
空间向量及其运算的坐标表示(解析版)-高二数学新教材同步题型+能力+素养练

1.3 空间向量及其运算的坐标表示题型一:空间向量的坐标运算1.已知空间点(3,1,4)P --,则点P 关于y 轴对称的点的坐标为( ) A .(3,1,4)--- B .(3,1,4)-- C .(3,1,4)- D .(3,1,4)【答案】D【点拨】利用空间直角坐标系点关于坐标轴对称的特点求解作答. 【详解】依题意,点(3,1,4)P --关于y 轴对称的点的坐标为(3,1,4). 故选:D2.平行六面体1111ABCD A B C D -中,()()11,2,3,1,2,4AC C =-,则点1A 的坐标为( ) A .()0,4,7 B .()2,0,1- C .()2,0,1- D .()2,0,1【答案】B【点拨】利用空间向量的坐标表示,即得. 【详解】设()1,,A x y z ,∵()()11,2,3,1,2,4AC C =-,又11AC AC =, ∴()()1,2,31,2,4x y z =----, 解得2,0,1x y z =-==,即()12,0,1A -. 故选:B.3.如图所示的空间直角坐标系中,四棱锥P ABCD -的底面ABCD 是正方形,PB ⊥平面ABCD ,且2PB AB ==,若3PC PQ =,则点Q 的空间直角坐标为( )一维练基础A .()3,2,1B .44,2,33⎛⎫ ⎪⎝⎭C .()1,2,3D .()1,2,1【答案】B【点拨】根据空间向量的坐标运算直接计算.【详解】由题意得()0,2,0C ,()2,2,2P ,所以()2,0,23PC PQ =--=,所以()22,0,33PQ =--,所以Q 的坐标为()()()2244,0,2,2,2,2,3333--+=.故选:B .4.已知向量a =(3,0,1),b =(﹣2,4,0),则3a +2b 等于( )A .(5,8,3)B .(5,﹣6,4)C .(8,16,4)D .(16,0,4)【答案】A【点拨】直接根据空间向量的线性运算,即可得到答案; 【详解】32(9,0,3)(4,8,0)(5,8,3)a b +=+-=,故选:A5.若(2,0,1),(3,1,1),(1,1,0)a b c ==--=,则22a b c -+=( ) A .()2,4,1- B .()10,0,3--C .()2,4,1--D .()10,0,3【答案】D【点拨】直接利用向量的坐标运算求解即可 【详解】因为(2,0,1),(3,1,1),(1,1,0)a b c ==--=, 所以22(2,0,1)2(3,1,1)2(1,1,0)(10,0,3)a b c -+=---+=, 故选:D题型二:空间向量模长的坐标表示1.已知向量()1,2,1a =-,()2,2,0b =-,则a 在b 的方向上的数量投影为( ) A .6-B .a - C .32D .34-b【答案】C【点拨】直接由数量投影的公式求解即可. 【详解】由题意知:a 在b 的方向上的数量投影为()22122232a b b-⨯⋅==+-. 故选:C.2.若向量()1,2,3a =-,()2,3,1b =--,则2a b +=( ) A .27B .5 C 26D .42【答案】C【点拨】求出2a b +的坐标,利用空间向量的模长公式可求得结果. 【详解】由已知可得()23,4,1a b +=-,故()222234126a b +=-++=.故选:C.3.在空间直角坐标系Oxyz 中,点(345)A ,,在坐标平面Oxy ,Oxz 内的射影分别为点B ,C ,则BC →=( )A .5B 34C 41D .52【答案】C【点拨】写出点A 在坐标平面Oxy ,Oxz 内的射影分别为点B ,C ,再计算BC →的值.【详解】解:在空间直角坐标系Oxyz 中,点(3A ,4,5)在坐标平面Oxy ,Oxz 内的射影分别为点B ,C ,则(3B ,4,0),(3C ,0,5), ∴(0BC →=,4-,5),||0162541BC →∴++故选:C .4.已知()1,1,0a t =-,()2,,b t t =,则b a -的最小值是( ) A .1 B 2C 3D 5【答案】B【点拨】利用空间向量坐标的减法求出b a -,然后利用求模公式求出b a -. 【详解】解:()()1,1,0,2,,a t b t t =-= (1,1,)b a t t t -=+-∴2222(1)(1)32b a t t t t ∴-=++-+=+∴当0=t 时,b a -取最小值2故选:B5.已知向量()1,21a →=-,,()3,,1b x =,且a b →→⊥,那么b →等于( )A 10B 11C .3D .5【答案】B【详解】解:因为向量()1,21a →=-,,()3,,1b x =,且a b →→⊥,所以13210x -⨯++=,解得1x =, 所以()3,1,1b =,所以22231111b →=++故选:B题型三:空间向量平行的坐标表示1.已知()1,4,4a =--,(),2,21b m m =-+,若a b ∥,则m 的值为( ) A .-2 B .2C .12-D .12【答案】C【点拨】根据向量共线的性质即可求解. 【详解】因为a b ∥,所以221144m m -+==--,解得12m =-, 故选:C.2.已知()1,2,a y =,(),1,2b x =,且//a b ,则x y ⋅=( ) A .1 B .1-C .2-D .2【答案】D【点拨】利用空间向量共线的坐标表示可求得x 、y 的值,即可得解.【详解】因为//a b ,则214x y =⎧⎨=⎩,所以,12x =,4y =,因此,2x y ⋅=.故选:D.3.已知空间三点()0,1,2A ,()2,3,1B ,()1,2,C m ,若,,A B C 三点共线,则m =( ). A .12B .1C .32D .2【答案】C【点拨】求出向量AB 与向量AC 的坐标,根据,,A B C 三点共线,可得向量AB 与向量AC 共线,由此即可求出结果.【详解】因为()2,2,1AB =-,()1,1,2AC m =-,且,,A B C 三点共线, 所以向量AB 与向量AC 共线, 所以1221m -=-,得32m =.故选:C.4.已知()2,1,3A ,()1,3,1B ,()4,,C y z ,若AB AC ∥,则2y z -=( ) A .20- B .17- C .11 D .4【答案】B【点拨】根据空间向量共线的性质进行求解即可. 【详解】()1,2,2AB =--,()2,1,3AC y z =--, 因为AB AC ∥,所以122213y z --==--, 解得3y =-,7z =,故217y z -=-. 故选:B5.已知两个向量()2,1,3a =-,(),2,b s t =,且//a b ,则s t -的值为( ) A .-2 B .2C .10D .-10【答案】C【点拨】根据向量共线可得,s t 满足的关系,从而可求它们的值,据此可得正确的选项. 【详解】因为//a b ,故存在常数λ,使得a b λ=,所以2123s t λλλ=⎧⎪=⎨⎪-=⎩,故4,6s t ==-,所以10s t -=,故选:C.题型四:空间向量垂直的坐标表示1.已知向量(2,1,3),(,2,6)a b x →→=-=-,若a b →→⊥,则实数x 的值为( ) A .7 B .8 C .9 D .10【答案】D【点拨】解方程2123(6)0x -⨯+⨯-=即得解.【详解】解:因为a b →→⊥,所以2123(6)0,10x x -⨯+⨯-=∴=. 故选:D2.设,x y ∈R ,向量(,1,1),(1,,1),(2,4,2)a x b y c ===-,且,a c b c ⊥∥,则||x y +=( ) A .1 B .2 C .3 D .4【答案】A【点拨】根据向量平行和垂直的坐标表示求出y 和x 即可. 【详解】024201a c a c x x ⊥⇒⋅=⇒-+=⇒=, b ∥1224y c y ⇒=⇒=--, ∴1x y +=. 故选:A.3.已知()1,2,1u =是直线l 的方向向量,()2,,2v y =为平面α的法向量,若l ∥α,则y 的值为( ) A .2- B .12-C .4D .14【答案】A【点拨】由l ∥α,可得u v ⊥,再计算即可求解.【详解】由题意可知u v ⊥,所以=0u v ⋅,即12+21202y y ⨯+⨯=⇒=-. 故选:A4.已知点()1,1,2A -在平面α上,其法向量()2,1,2n =-,则下列点不在平面α上的是( ) A .()2,3,3B .()3,7,4C .()1,7,1--D .()2,0,1-【答案】D【点拨】根据法向量的定义,利用向量垂直对四个选项一一验证即可. 【详解】()1,1,2A -对于A :记()12,3,3A ,则()11,4,1AA =.因为()()11,4,12,1,22420AA n =-=-+=,所以点()12,3,3A 在平面α上 对于B :记()3,7,4B ,则()2,8,2AB =.因为()()2,8,22,1,24840AB n =-=-+=,所以点()3,7,4B 在平面α上 对于C :记()1,7,1C --,则()2,6,1AC =---.因为()()2,6,12,1,24620AC n =----=-+-=,所以点()1,7,1C --在平面α上 对于D :记()2,0,1D -,则()3,1,1AD =--.因为()()3,1,12,1,26120AD n =---=---≠,所以点()2,0,1D -不在平面α上. 故选:D5.已知()1,1,3a =-,(),,1b x y =,若a b ⊥,则x y +=( ) A .9 B .6 C .5 D .3【答案】D【点拨】根据空间向量垂直的坐标表示即可求解. 【详解】0303a b a b x y x y ⊥⇒⋅=⇒+-=⇒+=. 故选:D.题型五:空间向量夹角余弦的坐标表示1.若向量()1,,0a λ=,(2,1,2)b =-且a 与b 的夹角余弦值为23,则实数λ等于( ) A .0 B .-43C .0或-43D .0或43【答案】C【点拨】由空间向量夹角余弦的坐标表示直接计算可得. 【详解】由题知,22cos ,31414a b a b a bλ⋅<>===+++即2340λλ+=,解得0λ=或43λ=-.故选:C2.已知向量()1,0,1a =-,则下列向量中与a 成3π夹角的是( ) A .()1,1,0- B .()1,1,0- C .()0,1,1- D .()1,0,1--【答案】B【点拨】利用空间向量夹角公式进行逐一判断即可.【详解】A :因为向量()1,0,1a =-与向量()1,1,0-2222121(1)(1)1=-+-⨯-+, 所以向量()1,0,1a =-与向量()1,1,0-夹角为23π,故不符合题意; B :因为向量()1,0,1a =-与向量()1,1,0-2222121(1)1(1)=+-⨯+-,所以向量()1,0,1a =-与向量()1,1,0-夹角为3π,故符合题意; C :因为向量()1,0,1a =-与向量()0,1,1-2222121(1)(1)1=-+-⨯-+,所以向量()1,0,1a =-与向量()0,1,1-夹角为23π,故不符合题意; D :因为向量()1,0,1a =-与向量()1,0,1--夹角的余弦值为222201(1)(1)(1)=+-⨯-+-,所以向量()1,0,1a =-与向量()1,0,1--夹角为2π,故不符合题意,故选:B4.若()1,,2a λ=,()2,1,2b =-,且a ,b 的夹角的余弦值为89,则λ等于( )A .2B .2-C .2-或255D .2或255-【答案】C【点拨】根据8cos ,9a b a b a b⋅==,解得即可得出答案.【详解】解:因为()1,,2a λ=,()2,1,2b =-, 所以2248cos ,935a b a b a bλλ⋅-+===+,解得:=λ2-或255. 故选:C.4.已知空间向量()()2,3,63,1,,4a b ==-,则,a b =( ) A .2π B .3π C .4π D .6π【答案】A【点拨】求得0a b ⋅=,即可得出. 【详解】()()2,3,63,1,,4a b ==-,()2334610a b ∴⋅=⨯+⨯-+⨯=,a b ∴⊥,,2a b π∴=.故选:A.5.已知空间向量()1,0,1a =,()1,1,b n =,3a b ⋅=则向量a 与b λ(0λ≠)的夹角为( ) A .6πB .6π或56π C .3π D .3π或23π 【答案】B【详解】,13a b a b cos a b n ⋅==+=解得2n =,222,?3n cos a b ⨯+= 代入得32cos a b ⋅=,又向量夹角范围:[]0,π 故,a b 的夹角为6π,则a 与b λ的夹角, 当0λ>时为6π;0λ<时为56π. 故选:B.1.已知向量()(),1,1,1,2,0a k b ==,且a 与b 互相垂直,则k 的值为( )二维练能力A .-2B .-12C .12D .2【答案】A【点拨】由题意0a b ⋅=,由空间向量的数量积运算可得答案. 【详解】由a 与b 互相垂直,则20a b k ⋅=+=,解得2k =- 故选:A2.已知(2,2,3)a =--,(2,0,4)=b ,则cos ,a b 〈〉=( ) A 485B .485C .0D .1【答案】B【点拨】利用空间向量的夹角余弦值公式cos ,||||a ba b a b ⋅<>=⋅即可求得.【详解】解:(2,2,3)a =--,(2,0,4)=b ,40485cos ,||||1725a b a b a b ⋅+-∴<>===⋅⋅故选:B.3.已知向量()1,0,a m =,(2,0,23b =-,若a b ∥,则a =( ) A .1 B 2C 3D .2【答案】D【点拨】由空间平行向量,先求出m 的值,再由模长公式求解模长. 【详解】由//a b ,则λa b ,即(1,0,)(2,0,23)m λ=-, 有1223m λλ==-,, 所以1123322m λ==-=-, 所以(1,0,3a =-,则()2221032a =++-故选:D4.下列四个结论正确的是 ( )A .任意向量,a b ,若0a b ⋅=,则0a =或0b =B .若空间中点O ,A ,B ,C 满足1233OC OA OB =+,则A ,B ,C 三点共线C .空间中任意向量,,a b c 都满足()()a b c a b c ⋅⋅=⋅⋅ D .已知向量()()1,1,,2,,4a x b x ==-,若25x <,则,a b 为钝角 【答案】B【点拨】A 选项,0a b ⋅=也可以是0,0a b ≠≠,a b ⊥;B 选项,利用向量线性运算得到2AC CB =,从而得到三点共线;C 选项可以举出反例;D 选项,求出,a b 为钝角时x 的取值范围,从而得到答案. 【详解】0a b ⋅=则0a =或0b =或0,0a b ≠≠,a b ⊥,故A 错误; 若空间中点O ,A ,B ,C 满足1233OC OA OB =+,即()()1233OC OA OB OC -=-, 所以1233AC CB =,化简得:2AC CB =,则A ,B ,C 三点共线,B 正确;设()()()1,1,1,2,2,1a b c ===。
人教A版高中数学选择性必修第一册1.3空间向量及其运算的坐标表示 经典例题及配套练习题

C1D1 上,
B1E1
1 4
A1B1 ,
D1F1
1 4
C1D1 .
图 1.3-9
(1)求 AM 长.
的 (2)求BE1与 DF1所成角的余弦值.
分析:(1)利用条件建立适当的空间直角坐标系,写出点 A,M 的坐标,利用空间两点间的距离公式
求出 AM 的长.(2)BE1 与 DF1 所成的角就是 BE1 ,DF1 所成的角或它的补角.因此,可以通过 BE1 ,
(2)写出点 P 2,3, 4 在三个坐标平面内的射影的坐标. (3)写出点 P 1,3,5 关于原点成中心对称的点的坐标. 【答案】(1)平面 yoz 与 x 轴垂直,平面 xoz 与 y 轴垂直,平面 xoy 与 z 轴垂直;(2)点 P 2,3, 4 在平面 yoz 的射影的坐标 P0,3, 4 ,点 P 2,3, 4 在平面 xoy 的射影的坐标 P2,3,0 ;点 P 2, 3, 4 在平面 xoz 的射影的坐标 P2, 0, 4 ;(3)点 P 1, 3, 5 关于原点对称点的坐标是 P1, 3, 5 .
1.3 空间向量及其运算的坐标表示
1.3.1 空间直角坐标系 例 1 如图 1.3-6,在长方体 OABC DABC 中, OA 3, OC 4 , OD 2 ,以
1 3
OA,
1 4
OC,
1 2
OD
为单位正交基底,建立如图所示的空间直角坐标系
Oxyz
.
图 1.3-6
(1)写出 D¢,C, A , B 四点的坐标; (2)写出向量 AB , BB , AC , AC 坐标.
图 1.3-8
分析:要证明 EF DA1 ,只要证明 EF DA1 ,即证 EF DA1 0 .我们只要用坐标表示 EF ,DA1 ,
空间向量运算的坐标表示 专题训练

空间向量运算的坐标表示 专题训练[A 基础达标]1.已知向量a =(1,1,0),b =(-1,0,2),则|3a +b |为( ) A.15 B .4C .5 D.17解析:选D.3a +b =3(1,1,0)+(-1,0,2)=(3,3,0)+(-1,0,2)=(2,3,2),故|3a +b |=4+9+4=17.2.若向量a =(1,1,x ),b =(1,2,1),c =(1,1,1),满足条件(c -a )·(2b )=-2,则x 的值为( )A .2B .-2C .0D .1解析:选A.因为c -a =(0,0,1-x ),2b =(2,4,2), 所以(c -a )·(2b )=2(1-x )=2-2x =-2.所以x =2.3.若△ABC 中,∠C =90°,A (1,2,-3k ),B (-2,1,0),C (4,0,-2k ),则k 的值为( ) A.10 B .-10C .2 5D .±10解析:选D.CB→=(-6,1,2k ), CA→=(-3,2,-k ), 则CB→·CA →=(-6)×(-3)+2+2k ×(-k ) =-2k 2+20=0,所以k =±10.4.已知a =(x ,1,2),b =(1,2,-y ),且(2a +b )∥(-a +2b ),则( )A .x =13,y =1B .x =12,y =-4C .x =2,y =-14D .x =1,y =-1解析:选B.2a +b =(2x +1,4,4-y ),-a +2b =(2-x ,3,-2y -2),因为(2a +b )∥(-a +2b ),则存在非零实数λ,使得2a +b =λ(-a +2b ),所以⎩⎪⎨⎪⎧2x +1=(2-x )λ,4=3λ,4-y =(-2y -2)λ,所以⎩⎨⎧x =12,y =-4. 5.若A (x ,5-x ,2x -1),B (1,x +2,2-x ),则当|AB→|取最小值时,x 的值等于( )A .19B .-87C.87D.1914解析:选C.因为AB→=(1-x ,2x -3,3-3x ), 所以|AB →|= (1-x )2+(2x -3)2+(3-3x )2= 14⎝ ⎛⎭⎪⎫x -872+57. 故当x =87时,|AB→|有最小值. 6.已知a =(1,m ,3),b =(-2,4,n ),若a ∥b ,则m -n =________. 解析:因为a ∥b ,所以b =λa .所以⎩⎪⎨⎪⎧λ=-2,m λ=4,3λ=n .所以⎩⎪⎨⎪⎧λ=-2,m =-2,n =-6.所以m -n =4.答案:47.已知2a +b =(0,-5,10),c =(1,-2,-2),a ·c =4,|b |=12,则〈b ,c 〉=________.解析:由题意,得|c |=3,(2a +b )·c =0×1+(-5)×(-2)+10×(-2)=-10,所以2a ·c +b ·c =-10.又a ·c =4,所以b ·c =-18,所以cos〈b ,c 〉=b ·c |b |·|c |=-12,所以〈b ,c 〉=120°. 答案:120°8.若a =(x ,2,2),b =(2,-3,5)的夹角为钝角,则实数x 的取值范围是________.解析:a·b =2x -2×3+2×5=2x +4,设a ,b 的夹角为θ,因为θ为钝角,所以cos θ=a·b |a ||b |<0,又|a |>0,|b |>0,所以a·b <0,即2x +4<0,所以x <-2.又a ,b 不会反向,所以实数x 的取值范围是(-∞,-2).答案:(-∞,-2)9.已知向量a =(6,-3,2),b =(4,-2,-4).求:(1)|a |;(2)(3a +2b )·(-2a +b ).解:(1)|a |=a 2=62+(-3)2+22=7.(2)因为|b |=b 2=42+(-2)2+(-4)2=6,a ·b =6×4+(-3)×(-2)+2×(-4)=22,所以(3a +2b )·(-2a +b )=-6a 2+3a ·b -4a ·b +2b 2=-244.10.已知四边形ABCD 的顶点坐标分别是A (3,-1,2),B (1,2,-1),C (-1,1,-3),D (3,-5,3),求证:四边形ABCD 是一个梯形.证明:因为AB→=(1,2,-1)-(3,-1,2)=(-2,3,-3), CD→=(3,-5,3)-(-1,1,-3)=(4,-6,6), 且-24=3-6=-36,所以AB →与CD →共线. 又因为AB 与CD 不共线,所以AB ∥CD .又因为AD→=(3,-5,3)-(3,-1,2)=(0,-4,1), BC→=(-1,1,-3)-(1,2,-1)=(-2,-1,-2), 且0-2≠-4-1≠1-2,所以AD →与BC →不平行. 所以四边形ABCD 为梯形.[B 能力提升]1.已知a =(1,2,3),b =(2,1,2),c =(1,1,2),且向量p ∥c ,则当(p -a )·(p -b )取得最小值时,向量p 的坐标为( )A.⎝ ⎛⎭⎪⎫12,34,13B.⎝ ⎛⎭⎪⎫12,23,34 C.⎝ ⎛⎭⎪⎫43,43,83 D.⎝ ⎛⎭⎪⎫43,43,73 解析:选C.设p =λc ,则p -a =λc -a =(λ-1,λ-2,2λ-3),p -b =λc -b =(λ-2,λ-1,2λ-2),所以(p -a )·(p -b )=2(3λ2-8λ+5)=2⎣⎢⎡⎦⎥⎤3⎝⎛⎭⎪⎫λ-432-13,所以当λ=43时,(p -a )·(p -b )取得最小值,此时p =λc =⎝ ⎛⎭⎪⎫43,43,83. 2.若a =(1,t ,2),b =(-2,t ,1),则a 与b 夹角θ的范围为________.解析:cos θ=t 2t 2+5·t 2+5=t 2t 2+5, 当t =0时,cos θ=0; 当t ≠0时,cos θ=11+5t 2<1,所以0≤cos θ<1.因为θ∈[0,π],所以0<θ≤π2.答案:⎝⎛⎦⎥⎤0,π2 3.若a =(2,3,-1),b =(-2,1,3),求以a ,b 为邻边的平行四边形的面积.解:|a |=|b |=14,a ·b =|a ||b |cos a ,b =2×(-2)+3×1+(-1)×3=-4,得cos a ,b =-27,故sin a ,b =357,所求平行四边形的面积为|a ||b |sin a ,b =14×14×357=6 5.4.(选做题)已知空间三点A (0,2,3),B (-2,1,6),C (1,-1,5). (1)若AP→∥BC →,且|AP →|=214,求点P 的坐标; (2)求以AB→,AC →为邻边的平行四边形的面积. 解:(1)因为AP→∥BC →,所以可设AP →=λBC →(λ∈R ). 因为BC→=(3,-2,-1),所以AP →=(3λ,-2λ,-λ). 又|AP→|=214, 所以(3λ)2+(-2λ)2+(-λ)2=214,解得λ=±2.所以AP→=(6,-4,-2)或AP →=(-6,4,2). 设点P 的坐标为(x ,y ,z ),则AP→=(x ,y -2,z -3). 所以⎩⎪⎨⎪⎧x =6,y -2=-4,z -3=-2或⎩⎪⎨⎪⎧x =-6,y -2=4,z -3=2.解得⎩⎪⎨⎪⎧x =6,y =-2,z =1或⎩⎪⎨⎪⎧x =-6,y =6,z =5.故所求点P 的坐标为(6,-2,1)或(-6,6,5).(2)因为AB→=(-2,-1,3),AC →=(1,-3,2), 所以cos 〈AB →,AC →〉=AB →·AC →|AB →||AC →|=-2+3+614×14=714=12. 所以sin 〈AB →,AC →〉=32.故以AB →,AC →为邻边的平行四边形的面积S =|AB →||AC →|sin 〈AB →,AC →〉=14×32=7 3.。
空间向量例题及解答

C空间向量及其坐标运算例1:在平行六面体ABCD —A 1B 1C 1D 1中,M 为AC 与BD 的交点,若B A 1=a ,11D A =b ,A A 1=c .则下列向量中与BM 相等的向量是( )A .1122a b c -+- B .++2121C .1122a b c -- D .+--2121练习:已知长方体ABCD-A'B'C'D',设M 是底面ABCD 的中心,N 是侧面BCC'B'对角线BC'上的点,且BN ∶NC'=3∶1,并且MN AB AD AA αβγ'=++,试求α,β,γ例2 :已知:,28)1(,0423p y n m x b p n m a +++=≠--=且p n m ,,不共面.若a ∥b求y x ,的值.练习1:点M 在平面ABC 内,并且对空间任意一点O ,=++xOM OA OB OC , 则x =练习2:下面命题正确的个数是 ( )①若23p x y =+,则p 与x 、y 共面;②若23MP MA MB =+,则M 、P 、A 、B 共面;③若0OA OB OC OD +++=,则A 、B 、C 、D 共面;④若151263OP OA OB OC =+-,则P 、A 、B 、C 共面; A.1 B. 2 C.3 D.4练习3:如图,已知空间四边形ABCD 中,向量AB a =,AC b =,AD c =若M 为BC 的中点,G 为BCD △ 的重心,GM xa yb zc =++, 则(),,x y z =练习4:一正方体1111ABCD A BC D -,P 、M 为空间中任意两点,若1167PM PB AA BA AD =++-,那么点M 一定在 平面内例3:已知4,135,λ===⊥a b m =a +b,n =a +b,a,b m n ,则λ=练习1:若OA 、OB 、OC 三个单位向量两两之间夹角为60°,则|OA -OB +2OC |=C1练习2:若(3)a b +⊥)57(b a -,且(4)a b -⊥)57(b a -,则a 与b的夹角为____________。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
空间向量的坐标运算练
习
SANY标准化小组 #QS8QHH-HHGX8Q8-GNHHJ8-HHMHGN#
空间向量的坐标运算——1
1、已知向量b ,a 分别平行于x 、y 轴,则它们的坐标各有什么特点 答:a 的__________________________; b 的________________________________
2、如果的横坐标为0,其它坐标都不为0,则与哪个坐标平面平行答:_________
4、点P(2,-3,4)在xoy 面上的射影坐标是___________;在xoz 面上的射影坐标是
___________;
在yoz 面上的射影坐标是___________
5、点Q (-3,2,5)关于原点对称的点的坐
标是___________;关于xoz 面对称的点的坐标是__________________
6、已知A (3,4,5),B (0,2,1),若
AB 5
2OC =,则C 点的坐标是______________
7、写出与原点距离等于3的点所满足的条件________________________________
8、已知A(2,0,0),B(6,2,2),C(4,0,
2)
A :2
D 3C 4B 6ππππ
::: 9、如图,ABC-A 1B 1C 1是正三棱柱(即底面是正三角形,沿着垂直于底面的向量平移所得到的轨迹),若AB =2,AA 1=4,R 是BB 1的中点,取AB 的中点为原点建立坐标系如图,写出下列向量的坐标:
______________=
______________=______________=A A'
'A
R
_________
10、已知A(3,4,4),B(-2,-1,5),C(4,5,0),若D在线段AC上,且三角形ABD的面积是三角形ABC面积的四分之一,(1)求D点的坐标;(2)求向量BD的坐标。
