8-Fundamental of estimation theory
伍德里奇---计量经济学第8章部分计算机习题详解(STATA)
伍德⾥奇---计量经济学第8章部分计算机习题详解(STATA)班级:⾦融学×××班姓名:××学号:×××××××C8.1SLEEP75.RAWsleep=β0+β1totwork+β2educ+β3age+β4age2+β5yngkid+β6male+u 解:(ⅰ)写出⼀个模型,容许u的⽅差在男⼥之间有所不同。
这个⽅差不应该取决于其他因素。
在sleep=β0+β1totwork+β2educ+β3age+β4age2+β5yngkid+β6male+u模型下,u⽅差要取决于性别,则可以写成:Var u︳totwork,educ,age,yngkid,male =Var u︳male =δ0+δ1male。
所以,当⽅差在male=1时,即为男性时,结果为δ0+δ1;当为⼥性时,结果为δ0。
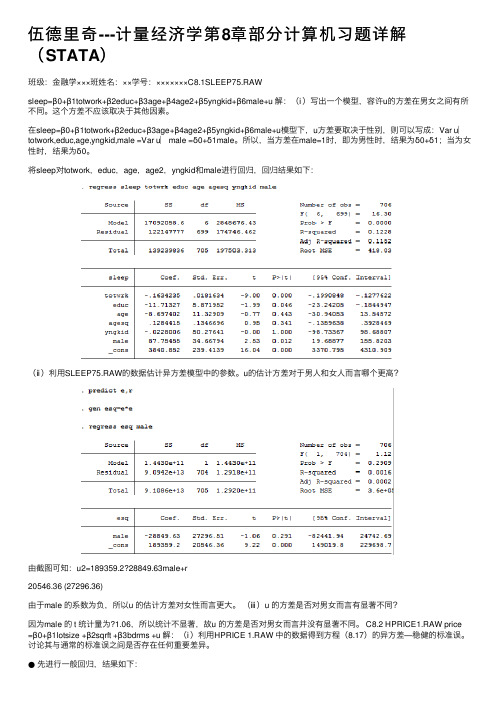
将sleep对totwork,educ,age,age2,yngkid和male进⾏回归,回归结果如下:(ⅱ)利⽤SLEEP75.RAW的数据估计异⽅差模型中的参数。
u的估计⽅差对于男⼈和⼥⼈⽽⾔哪个更⾼?由截图可知:u2=189359.2?28849.63male+r20546.36 (27296.36)由于male 的系数为负,所以u 的估计⽅差对⼥性⽽⾔更⼤。
(ⅲ)u 的⽅差是否对男⼥⽽⾔有显著不同?因为male 的 t 统计量为?1.06,所以统计不显著,故u 的⽅差是否对男⼥⽽⾔并没有显著不同。
C8.2 HPRICE1.RAW price =β0+β1lotsize +β2sqrft +β3bdrms +u 解:(ⅰ)利⽤HPRICE 1.RAW 中的数据得到⽅程(8.17)的异⽅差—稳健的标准误。
讨论其与通常的标准误之间是否存在任何重要差异。
●先进⾏⼀般回归,结果如下:●再进⾏稳健回归,结果如下:由两个截图可得:price =?21.77+0.00207lotsize +0.123sqrft +13.85bdrms29.48 0.00064 0.013 (9.01)37.13 0.00122 0.018 [8.48]n =88,R 2=0.672⽐较稳健标准误和通常标准误,发现lotsize 的稳健标准误是通常下的2倍,使得 t 统计量相差较⼤。
确定论与随机论

确定论与随机论方法论(methodology)不同于方法(method),它是具体方法的总和与升华,它往往代表了人们对一门具体学科的思维定势和知识结构及其教育模式的总体认识,由此而产生其研究方法的主导思想,以致形成该学科领域的各种具体的研究方法和方案。
在科学发展史上,方法论具有举足轻重的地位和作用。
实践表明,海口特价机票预订,许多学科领域的进展,转折或突破几乎都与一种新的方法论的建立悉悉相关(1)。
在大气科学的发展历程中,关于"确定论"与"随机论"的争论更比其他学科突出,由于其内涵的复杂性,迄今仍值得探讨。
众所周知,一切科学的发展总是经历着:纯经验→半经验→定性规律→定量规律→理论(数学)模型→实验(物理或数值)方案→新事实(新定律、新理论)→再实践→再认识,…这样的发展过程。
大气科学也不例外。
自从牛顿力学建立以来,大气科学已不再是半经验的经典气象学了。
随着大量观测事实的积累,传统的气象学早已派生出各种分支学科并有了长足的进展。
例如,动力气象学、辐射气象学、大气热力学、大力动力学、数值天气预报等。
尤其是牛顿力学应用于旋转流体而导出的Navie-stokes方程及热力学第一定律所导出的热力学方程,迄今已成为确定论的大气体科学方法论的坚实基础。
近二十多年来,在大气动力学基础上发展起来的动力气候数值模拟更加支持了确定论的研究方法和思想。
然而,事实上,任何一门科学,人们所考察的都只是"有限现象"。
自然辩证法认为,一切有限现象都包含有偶然性的成分,因此,科学所研究的一切(物理、化学、生物)过程都包含着偶然性成分。
"偶然性"并不阻碍对于各种现象的科学认识,它是相对于必然性的新的生长点,随着人类认识世界的深化,各个必然过程的交叉点上所出现的偶然性将逐渐减少,但是,人类对于无穷世界的认识,永远不可能到达那个"终结真理"的顶点。
An Introduction to Estimation Theory

45
Appendix B The Lognormal Distribution
48
Appendix C Filtering Theory on the Continuum
49
References
55
iv
An Introduction to Estimation Theory May 1997, DAO O ce Note 97-01
3 Conditional mean and conditional mode estimation
8
3.1 Introduction . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 8
3.2 Conditional mean estimation . . . . . . . . . . . . . . . . . . . . . . . . . . 9
6.2 The continuum problem . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 32
6.3 A nite-dimensional problem . . . . . . . . . . . . . . . . . . . . . . . . . . 38
5.3 Lognormal observation errors . . . . . . . . . . . . . . . . . . . . . . . . . . 28
6 A simple illustrative example
31
6.1 Introduction . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 31
Review of 'Detection, Estimation, and Modulation Theory, Part I'

预定论名词解释(二)

预定论名词解释(二)资深创作者预定论名词解释预定论(Determinism)是一种哲学观点,认为一切事件都有一个确定的原因,世界的发展和运行按照确定的规律进行。
预定论涉及到许多相关的名词和概念,下面是一些相关名词及其解释。
1.因果律(Causality)因果律是指一切事件都有其因果关系,即每一个事件都是由前面的某个或某些事件所引起的。
在预定论中,因果律是决定一切事件的原因,它认为每个事件的发生都有一个确定的原因。
例如,如果一个苹果从树上掉下来砸到了地面,这个事件的原因可以是重力的作用,也就是因果律。
根据这个观点,如果我们知道了某个事件的所有相关因素,那么我们就可以预测和解释这个事件的发生。
2.宇宙决定论(Cosmic Determinism)宇宙决定论是预定论的一个更加广义的形式,它认为整个宇宙的发展和运行都是按照确定的规律进行的。
它不仅包括了人类的行为,也包括了自然界的各种现象和事件。
例如,宇宙决定论认为所有自然界的运行都遵循一定的规律,比如行星绕太阳运行的轨迹,植物的生长与季节变化等等。
宇宙决定论认为这些现象的发生都有其确定的原因,能够被科学方法所解释和预测。
3.必然性(Necessity)必然性是指一件事情不可避免或者无法改变的性质。
在预定论中,必然性是事件按照确定的规律进行的结果,即事件发生是不可避免的。
例如,如果一个人在燃气炉上点火,那么燃气炉会产生火焰。
这个事件的发生是按照燃烧物质与氧气反应产生的规律进行的,是一个必然的结果。
4.自由意志(Free Will)自由意志是指个体能够自主做出决策和选择的能力。
与预定论相对立,自由意志认为人类有能力在某种程度上摆脱因果律的束缚,做出不受先前因果关系限制的决策。
例如,如果一个人在超市里面面临购买两种商品的选择,自由意志认为个体可以独立地做出选择,并不受到先前事件的影响。
5.唯物主义(Materialism)唯物主义是一种哲学观点,认为物质是世界的唯一本原和实在。
伍德里奇计量经济学笔记

伍德里奇计量经济学笔记伍德里奇计量经济学(Wooldridge Econometrics)是一门应用计量经济学的学科,它结合了经济学和数理统计学的理论和方法。
1. 引言- 计量经济学的定义:利用数理统计学和计量经济模型来分析经济问题。
- 经济学模型包括描述经济系统和理论关系的方程。
- 计量经济学的目标是估计和测试经济模型中的参数。
2. 统计学基础- 假设检验:用统计方法来验证经济理论。
- 最小二乘法(OLS):估计经济模型中未知参数的方法。
- OLS估计结果的性质和假设:无偏性、一致性和有效性。
3. 单变量回归模型- 简单线性回归模型:一个自变量和一个因变量之间的线性关系。
- 估计参数和评估模型:OLS估计、t统计量、R方和调整的R 方。
- 解释和预测:利用估计的模型进行解释和预测。
4. 多变量回归模型- 多元线性回归模型:多个自变量和一个因变量之间的线性关系。
- 估计参数和评估模型:OLS估计、t统计量、F统计量、R方和调整的R方。
- 控制变量和决策:利用控制变量来减少混淆因素,做出更准确的决策。
5. 动态模型- 差分方程:描述变量随时间变化的关系。
- 滞后变量和滞后因变量:引入滞后变量来解释变量之间的时序关系。
- 动态因果关系:解释一些经济变量之间的长期和短期关系。
6. 面板数据模型- 面板数据:包含多个个体和多个时间观测的数据集。
- 固定效应模型和随机效应模型:解释面板数据中个体效应和时间效应。
- 引入个体和时间固定效应:控制个体特征和时间变化对变量关系的影响。
7. 工具变量估计- 决定性和随机性端变量:用于解决内生性问题的变量。
- 工具变量的选择和检验:选择有效的工具变量来估计内生性模型。
- 两阶段最小二乘法(2SLS):用工具变量估计内生性模型。
8. 非线性回归模型- 非线性函数:描述实际经济关系的复杂性。
- 估计非线性模型:使用非线性最小二乘法(NLS)估计非线性模型。
- 非线性回归模型的解释和预测:利用估计的非线性模型进行解释和预测。
伍德里奇 计量经济学导论

伍德里奇计量经济学导论一、导论计量经济学是经济学的一个重要分支,旨在通过运用数理统计方法和经济理论来分析经济现象。
伍德里奇(Woodridge)是一位著名的计量经济学家,他的著作《计量经济学导论》是该领域的经典教材之一。
本文将对伍德里奇的计量经济学导论进行全面详细、完整深入的介绍。
二、计量经济学的基本概念计量经济学是研究经济现象的定量方法。
它通过建立数学模型,运用统计学原理和经济理论,对经济现象进行量化分析。
计量经济学的基本概念包括:1.回归分析:回归分析是计量经济学的核心方法之一。
它通过建立经济模型,利用样本数据来估计模型中的参数,从而对经济关系进行分析和预测。
2.假设检验:假设检验是计量经济学中的一种统计推断方法。
它用于检验经济模型中的假设是否成立,判断经济关系的显著性。
3.时间序列分析:时间序列分析是计量经济学中研究时间相关性的方法。
它通过对时间序列数据的观察和分析,揭示经济现象的演变规律和趋势。
4.面板数据分析:面板数据分析是计量经济学中研究面板数据(即跨时期和跨个体的数据)的方法。
它可以同时考虑个体特征和时间变动,对经济关系进行更全面的分析。
三、伍德里奇计量经济学导论的内容伍德里奇的《计量经济学导论》是一本系统介绍计量经济学基本理论和方法的教材。
该书的主要内容包括:1.回归分析基础:介绍了回归分析的基本概念和原理,包括线性回归模型、最小二乘法估计、假设检验等内容。
2.多元回归分析:扩展了回归分析的内容,引入了多个自变量的情况,讨论了多元回归模型的估计和推断。
3.回归模型的假设检验:详细介绍了回归模型中各项假设的检验方法,包括正态性检验、异方差性检验等。
4.回归模型的问题和解决方法:讨论了回归模型中可能出现的问题,如多重共线性、异方差等,并提出了相应的解决方法。
5.时间序列分析:介绍了时间序列分析的基本原理和方法,包括平稳性、自相关性、移动平均模型、自回归模型等。
6.面板数据分析:讲解了面板数据分析的基本概念和方法,包括固定效应模型、随机效应模型等。
离散数学及其应用英文版第八版课程设计

Discrete Mathematics and Its Applications, 8th Edition CourseDesignBackgroundDiscrete mathematics is a foundation for many computer science and mathematics-related fields. It deals with objects that can only take distinct values, such as integers, graphs, and propositions. The applications of discrete mathematicsare diverse and important, including cryptography, computer algorithms, and database systems.The book Discrete Mathematics and Its Applications,written by Kenneth H. Rosen, is a widely accepted textbook on the subject. In this course design, we will use the book’s8th edition, which covers a vast range of topics in discrete mathematics.Course DescriptionThe course ms to provide students with a comprehensive understanding of discrete mathematics and its applications. The course will cover major topics in the field, including:1.Propositional logic and predicate logic2.Set theory and relationsbinatorics and discrete probability4.Graph theory5.Trees, spanning trees, and graph traversals6.Boolean algebra and switching circuits7.The theory of computation and formal languages8.Number theory and cryptographySpecial emphasis will be placed on developing problem-solving skills, logical reasoning, and mathematical maturity. Students will learn to apply the tools and techniques learned in this course to real-world problems.Course GoalsUpon completion of this course, students should be able to:1.Understand and apply the fundamental principles ofdiscrete mathematics2.Identify and solve problems involving logic, sets,and relations3.Analyze and solve problems in combinatorics anddiscrete probability4.Understand the properties and applications ofgraphs, trees, and circuits5.Understand the principles and applications of thetheory of computation and formal languages6.Demonstrate knowledge of number theory and itsapplications to cryptographyCourse OutlineThe course will be delivered through lectures, problem-solving sessions, and assignments. The course outline is as follows:Week 1: Propositional Logic and Predicate Logic•Introduction to logic•Propositional logic–Logical connectives and truth tables–Tautologies, contradictions, and logical equivalence–Logical inference and proof techniques •Predicate logic–Predicates and quantifiers–Universal and existential quantifiers–Translating English statements into predicate logicWeek 2: Set Theory and Relations•Introduction to sets and set operations•Relations–Binary relations and their properties–Equivalence relations and partitions–Partial orders and Hasse diagramsWeek 3: Combinatorics and Discrete Probability•Counting principles–The multiplication rule–The addition rule–Permutations and combinations•Discrete probability–Probability spaces and events–Conditional probability and independence–Random variables and their distributions Week 4: Graph Theory•Introduction to graphs and their representations •Basic terminology•Walks, paths, and cycles•Connectivity and components•Directed graphsWeek 5: Trees, Spanning Trees, and Graph Traversals •Trees and their properties•Spanning trees and their properties•Minimum spanning trees and algorithms•Graph traversals–Breadth-first search–Depth-first searchWeek 6: Boolean Algebra and Switching Circuits •Boolean algebra and its operations•Boolean functions and their representations•Canonical forms and minimization•Switching circuits and their designWeek 7: The Theory of Computation and Formal Languages •Introduction to automata theory•Finite automata and regular languages•Regular expressions•Pushdown automata and context-free languages Week 8: Number Theory and Cryptography•Principles of number theory–Divisibility and prime numbers–Modular arithmetic and congruences •Cryptography–Cryptographic algorithms and protocols–Public-key cryptography and RSAAssessmentAssessment will be based on a combination of quizzes, assignments, and exams. The final grade will be determined based on the following:•Quizzes: 20%•Assignments: 40%•Midterm exam: 20%•Final exam: 20%ConclusionThis course design provides a comprehensive overview of the topics covered in the book Discrete Mathematics and Its Applications, 8th edition. The course ms to develop problem-solving skills, logical reasoning, and mathematical maturity. Students will learn to apply discrete mathematics to real-world problems, with a focus on computer science and mathematics-related fields.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Unbiased
• The sample variance
m 1 2 2 ˆ ˆ yi m i 1
UESTC-何子述等
9
However, From(10.9)-(10.14)
2 m
1 2 ˆ E yi E m i 1 m m 1 2 m m
In this case
Depends only on the parameter estimate & p
UESTC-何子述等
Independent of parameter
15
Both are sufficient estimates!
10.5.5 Minimum-variance estimates
13
Consider the sample p mean where the individual random variables are independent and each is normally ll distributed di t ib t d with ith mean and d variance i 2 joint pdf p of measurements is given g by y . The j
p y1 , ,... ym ; g T y1 ,... , ym , h y1 ,... , ym
Depends p only y on the UESTC-何子述等 estimate & parameter Independent of parameter
2
2
2
m 1 2 2 ˆ lim E lim m m m
2
The sample variance is biased but asymptotically unbiased estimate estimate.
UESTC-何子述等 10
10.5.2 Consistent estimates
p y1 , ,... ym ;
2
i
1
As
m 2 i 1 i
2
2
m 2 2
m yi 2 exp p 2 i 1 2
2
y y y y
i 1 m
ˆ y α
.
UESTC-何子述等
7
10.5.1 Unbiased estimates
ˆ An estimate y is unbiased, , if
ˆ is i a constant vector ˆ E = is i a random d vector t
UESTC-何子述等 17
An alternative form of the Cramer-Rao inequality Is
ˆ V 1
2 ln p y1 ,..., ym ; E
The equality condition is obtained when
The Proof for CRLB Proof:
p y; dy = 1
p y; p y; d y dy = 0
Th pdf The df can be b expressed d as
p y1 , ,... ym ; 2
h y1 , y2 , , ym 1
2 2 s y 1 y exp m 1 exp m 2 m /2 2 2 2 2 2
T y is a sufficient statistic for if the conditional pdf p y1 , y2 ,, ym T y , does not depend on .
A method used to determine whether or not an estimate is a sufficient estimate is to see if the Fisher factorization theorem is satisfied. satisfied
The variance of an unbiased estimate is a estimate performance measure . A i An important t t bound b d on the th variance i is i the th Cramer-Rao inequality q y CRB or CRLB (Cramer-Rao Low Bound)
Asymptotically unbiased estimate
m
UESTC-何子述等
ˆ lim E =
8
10.5.1 Unbiased estimates
In the example 10.1 • the sample mean
1 m ˆ y yi ˆ =α m i 1
2
In practice practice, it is more useful. useful
UESTC-何子述等
12
10.5.4 Estimators based on sufficient statistics
ˆ T y in the y ? Whether the full information is used to estimate
UESTC-何子述等 2
10.2 Formulation of the general g parameter estimation problem
The parameter estimation problem is to find a parameter estimate vector that depends on the Estimator observables.
• The Th parameter t α may be b random d vector t or a
nonrandom parameter vector. • The parameter estimation occur depending on whether pdf is known or unknown.
ˆ V 1 2 E 2 ln p y1 ,..., ym ;
Fisher information
UESTC-何子述等 16
Therefore, the inequality q y can be expressed p as
ˆ F 1 V
ˆ m is consistent if it converges An estimate g stochastically to as m becomes large. A explicit An li it statement t t t of f consistency it is i that th t for f ˆm every y small number, , 0 , the estimate concentrates on the parameter as m becomes l large
The estimate can be defined by
A direct estimation way 1 m ˆ y yi ˆ =α m i 1
UESTC-何子述等
1 m 2 ˆ yi ˆ m i 1
(估计子)
ˆ y to estimate a parameter! Construct a function α
UESTC-何子述等 3
• The p parameter estimate α p on the ˆ y depends
random observables and is itself a random variable.
m
ˆ m 1 lim P
ˆ m lim P 1 m
or
UESTC-何子述等
11
10.5.2 Consistent estimates
Mean square consistent estimate
ˆm 0 lim E m
UESTC-何子述等 4
Example 10.1
Constant number p plus zero mean noise are
yi ni ,
1 ˆ yi m i 1
m
i 1,...., m
2 y 1 i p yi ; exp 2 2
where h
2 F E 2 ln p y1 ,..., ym ;
If the estimate of the parameter satisfies the Cramer-Rao bound with equality, then it is termed a most efficient estimate.(优效估计)
Chapter 10 Fundamentals of Estimation Theory
UESTC-何子述等
1
10.1 Chapter highlights
• Parameter estimation problem formulation • Types of estimation problems • Bayes yes es estimation o • Minimax estimation • Maximum-likelihood estimation • Comparison of estimators of parameters
