湖北省荆州中学09-10学年高二上学期期中考试(数学文)
湖北省荆州市高二上学期期中数学试卷

湖北省荆州市高二上学期期中数学试卷姓名:________ 班级:________ 成绩:________一、选择题 (共15题;共30分)1. (2分)(2019·贵州模拟) 已知集合,,则()A .B .C .D .2. (2分)(2018·自贡模拟) 若,则()A .B .C .D .3. (2分)函数是R上的奇函数,,则的解集是()A .B .C .D .4. (2分)将函数的图象向左平移个长度单位,得到函数g(x)的图象,则g(x)的单调递增区间是()A .B .C .D .5. (2分)(2017·赣州模拟) 已知函数f(x)=|2x﹣2|+b的两个零点分别为x1 , x2(x1>x2),则下列结论正确的是()A . 1<x1<2,x1+x2<2B . 1<x1<2,x1+x2<1C . x1>1,x1+x2<2D . x1>1,x1+x2<16. (2分) (2020高二上·百色期末) 甲、乙两人8次测评成绩的茎叶图如图,由茎叶图知甲的成绩的中位数和乙的成绩的平均数分别是()A . 23,22B . 23,22. 5C . 22,22. 5D . 22,237. (2分)为了调查学生每天零花钱的数量(钱数取整数元),以便引导学生树立正确的消费观.在某校抽取样本容量为1000的频率分布直方图如图所示,则样本数据落在[6,14)内的频数为()A . 780B . 680C . 648D . 4608. (2分)(2020·鄂尔多斯模拟) 下边程序框图的算法源于我国古代的中国剩余定理.把运算“正整数除以正整数所得的余数是”记为“ ”,例如 .执行该程序框图,则输出的等于()A . 16B . 17C . 18D . 199. (2分)函数y=的图象如图,则()A . k=,ω=,φ=B . k=,ω=,φ=C . k=﹣,ω=2,φ=D . k=﹣2,ω=2,φ=10. (2分) (2017高一上·黄石期末) f(x)是定义在R上的奇函数,满足f(x+2)=f(x),当x∈(0,1)时,f(x)=2x﹣1,则的值等于()A . -B . ﹣6C . -D . ﹣411. (2分)某单位在月份用电量(单位:千度)的数据如表:月份x2356用电量3 4.5 5.57已知用电量y与月份x之间有较好的线性相关关系,其回归方程 = x+1,由此可预测7月份用电量(单位:千度)约为()A . 6B . 7C . 8D . 912. (2分)已知函数,若,且,则的最小值为()A .B .C .D .13. (2分) (2019高一上·儋州期中) 已知函数在定义域上是奇函数又是减函数,若,则的取值范围是()A .B .C .D .14. (2分) (2018高二上·浙江月考) 已知函数,则下列说法正确的是A . 的最小正周期为B . 的图象关于中心对称C . 在区间上单调递减D . 的值域为15. (2分) (2015高一下·嘉兴开学考) 已知函数,若g(x)=[f(x)]2+bf(x)+c (其中b,c为常数)恰有5个不同的零点x1 , x2 , x3 , x4 , x5 ,则f(x1+x2+x3+x4+x5)=()A . 3lg2B . 2lg2C . 0D . 1二、填空题 (共5题;共6分)16. (1分) (2016高一下·滕州期末) 某校有男生1200人,女生900人,为了解该校学生对某项体育运动的喜爱情况,采用按性别分层抽样的方法,从该校学生中抽取一个容量为70的样本,则样本中女生的人数为________.17. (2分) (2018高一上·温州期中) 函数y=ln(x-1)的定义域为________;函数y=ln(x-1)的值域为________.18. (1分) (2017高一下·广东期末) cos45°sin15°﹣sin45°cos15°的值为________.19. (1分) (2020高一下·潮州期中) 已知函数,记函数在区间上的最大值为M,最小值为m,设函数 .若,则函数的值域为________.20. (1分) (2018高一上·天门月考) 已知函数,的图象关于原点对称,则的零点为________.三、解答题 (共4题;共35分)21. (10分) (2018高三上·汕头模拟) 在△ 中,角的对边分别为,,(1)若,求的值;(2)设,当取最大值时求的值.22. (10分)(2020·兴平模拟) 已知函数 .(1)求函数的最小正周期和单调递增区间;(2)将函数的图像向右平移个单位长度,得到函数的图像,求使得的的取值范围.23. (10分)某大学新闻系有男生45名,女生15名,按照分层抽样的方法组建了一个4人的青奥会采访小组.(1)求某学生被抽到的概率及采访小组中男、女生的人数;(2)经过半个月的实地采访,这个采访小组决定选出2名学生做后期整理编辑,方法是先从小组里选出1名学生对信息分类,该学生整理结束,再从小组内剩下的学生中选1名做后期剪辑,求选出的2名学生中恰有1名女生的概率.24. (5分) (2016高二上·船营期中) 已知a>0,a≠1,设p:函数y=loga(x+1)在(0,+∞)上单调递减;q:曲线y=x2+(2a﹣3)x+1与x轴交于不同的两点.如果p且q为假命题,p或q为真命题,求a的取值范围.参考答案一、选择题 (共15题;共30分)答案:1-1、考点:解析:答案:2-1、考点:解析:答案:3-1、考点:解析:答案:4-1、考点:解析:答案:5-1、考点:解析:答案:6-1、考点:解析:答案:7-1、考点:解析:答案:8-1、考点:解析:答案:9-1、考点:解析:答案:10-1、考点:解析:答案:11-1、考点:解析:答案:12-1、考点:解析:答案:13-1、考点:解析:答案:14-1、考点:解析:答案:15-1、考点:解析:二、填空题 (共5题;共6分)答案:16-1、考点:解析:答案:17-1、考点:解析:答案:18-1、考点:解析:答案:19-1、考点:解析:答案:20-1、考点:解析:三、解答题 (共4题;共35分)答案:21-1、答案:21-2、考点:解析:答案:22-1、答案:22-2、考点:解析:答案:23-1、答案:23-2、考点:解析:答案:24-1、考点:解析:。
湖北省荆州中学高二数学上学期第二次质量检测试题 文

荆州中学高二年级第二次质量检测考试数学卷(文科)一、选择题(本题满分60分,共12个小题,每题5分,在每小题给出的四个选项中,只有一个选项是符合题目要求的)1.一个人打靶时连续射击两次,事件“至少有一次中靶”的互斥事件是( ) A .至多有一次中靶 B .两次都中靶 C .只有一次中靶 D .两次都不中靶2.若两条直线34120x y +-=和8110ax y ++=平行,则它们之间的距离为( )A .235 B .2310C .72D .523.已知x 与y 之间的一组数据如下表,根据表中提供的数据,求出y 关于x 的线性回归方程为ˆ0.35ybx =+ , 那么b 的值为( )A .0.5B .0.6C .0.7D .0.754.在面积为S 的△ABC 内任投一点P ,则△PBC 的面积大于2S的概率是( ) A.31 B.21 C.43 D.415.如图给出的是计算1001614121++++Λ的值的一个程序框图,其中判断框中应填入的是( ) A .100>i B .100≤iC .50>iD .50≤i6.已知k ∈[-2,1],则k 的值使得过A (1,1)可以作两条直线与圆045222=--++k y kx y x 相切的概率等于( ) A .31 B .21 C .32 D .437.集合{(,)||1|}A x y y x =≥-,集合{(,)|||6}B x y y x =≤-+,先后掷两颗骰子,掷第一颗骰子得点数为a ,掷第二颗骰子得点数为b ,则B A b a ⋂∈),(的概率等于( )A.14B.29C.736D.1136x 34 5 6 y 2.5 344.58.当曲线241x y --=与直线033=+--k y kx 有两个相异的交点时,实数k 的取值范围是( )A .212,55⎛⎫⎪⎝⎭B .⎥⎦⎤ ⎝⎛2,52C .⎥⎦⎤ ⎝⎛52,0D .⎪⎭⎫⎢⎣⎡512,29.给出下面四个命题:①“b a 直线直线//”的充要条件是“a 平行于b 所在的平面”; ②“直线⊥l 平面α内所有直线”的充要条件是“⊥l 平面α”; ③“直线b a ,为异面直线”的充分而不必要条件是“直线b a ,不相交”;④“平面α//平面β”的必要而不充分条件是“α内存在不共线三点到β的距离相等”. 其中正确命题的序号是( )A.①②B.②③C.③④D.②④10.棱长为1的正方体1111ABCD A B C D -的8个顶点都在球O 的表面上,E F ,分别是棱1AA ,1DD 的中点,则直线EF 被球O 截得的线段长为( )A .22B .1C .212+D .211.设P 是椭圆上的一点,F 1、F 2是焦点,若∠F 1PF 2=30°,则△PF 1F 2的面积为( )A. B. C. D.1612.设22:(2)(3)1p x y -+-≤,12:23110x y q y x ty +≤⎧⎪≥⎨⎪-+≤⎩若p 是q 的充分不必要条件则( )A.4t ≥B.3544t ≤≤C.04t <≤D.354t ≥ 二、填空题(本题满分20分,共4个小题,每小题5分,只要求写出结果)13.如果双曲线221369x y -=的弦被点(2,4)p 平分,则这条弦所在的直线方程为 . 14.从区间[]0,2随机抽取2n 个数1212,,,,,,n n x x x y y y L L 构成n 个数对1122(,),(,),,(,)n n x y x y x y L ,其中两数的平方和小于4的数对共有m 个,则用随机模拟的方法得到的圆周率π的近似值为 .15.用秦九韶算法计算多项式5432()7125635f x x x x x x =+--+-在计算(5)f 时所需进行的加法和乘法的运算总次数是 .16.以下命题中,正确命题是 .①函数44sin cos y x x =-的最小正周期是π;②四面体ABCD 中,和A B C D 、、、距离相等的平面共有4个;③命题“若a b <,则22a b <”的否定是“若a b <,则22a b ≥”;④用三个不等式:0,0,0c dab bc ad a b>->->(其中a b c d 、、、均为实数)中的两个作为条件,另一个作为结论组成一个命题,得到的真命题有3个. 三、解答题(共70分,要求写出解答过程)17.(本题满分12分)已知命题p :方程2221212x y m m -=--表示焦点在y 轴上的椭圆;命题q :双曲线2215y x m-=的离心率(1,2)e ∈,若p 或q 为真命题,p 且q 为假命题,求实数m 的取值范围.18.(本题满分12分)荆州市政府为了鼓励居民节约用水,计划调整居民用水收费方案,拟确定一个合理的月用水量标准x (吨).一位居民的月用水量不超过x 的部分按平价收费,超出x 的部分按议价收费。
湖北荆州中学2024年高二9月月考数学试题+答案

荆州中学2024-2025学年高二上学期9月月考数学试卷时间:150分钟 满分:150分一、选择题:本题共8小题,每小题5分,共40分,在每小题给出的四个选项中,只有一项是符合要求的.1.已知复数z 满足1i 2i z z +=−,则z =( )A .32B .52C D2. 图为某地2014年至2023年的粮食年产量折线图,则下列说法不正确...的是( )A. 这10年粮食年产量的极差为15B. 这10年粮食年产量的平均数为31C. 前5年的粮食年产量的方差大于后5年粮食年产量的方差D. 这10年粮食年产量的中位数为293.正四棱台的上、下底面的边长分别为2,4,侧棱长为2,则其体积为( )A .20+B C .563D .4.已知2b a = ,若a 与b 的夹角为60°,则2a b − 在b 上的投影向量为( )A .12bB .12b − C .32b − D .32b5.向量{},,a b c 是空间的一个单位正交基底,向量p 在基底a ,b ,c下的坐标为(1,2,3)−,则p 在基底{},,a b a b c +−的坐标为( )A .13,,322 −B .13,,322 −−C .13,,322 −D .13,,322 −−6. 某商场开展20周年店庆购物抽奖活动(100%中奖),凡购物满500元的顾客均可参加该活动,活动方式是在电脑上设置一个包含1,2,3,4,5,6的6个数字编号的滚动盘,随机按下启动键后,滚动盘上的数字开始滚动,当停止时滚动盘上出现一个数字,若该数字是大于5的数,则获得一等奖,奖金为150元;若该数字是小于4的奇数,则获得二等奖,奖金为100元;若该数字出现其它情况,则获得三等奖,奖金为50元.现某顾客依次操作两次,则该顾客奖金之和为200元的概率为( ) A.536B.518C.29D.127. 在锐角ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,S 为ABC 的面积,且()224S a b c =−−,则22b c bc +的取值范围为( ) A .3522 ,B .3,22C .522,D .[)2,+∞8.在三棱锥P ABC −中,AC ⊥平面PAB ,3AB =,4AC =,BP =45ABP ∠=°,则三棱锥P ABC −外接球的表面积为( ) A .8πB .16πC .26πD .32π二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.9. 在平面直角坐标系中,下列说法不正确的是( )A .任意一条直线都有倾斜角和斜率B .直线的倾斜角越大,则该直线的斜率越大C .若一条直线的倾斜角为α,则该直线的斜率为tan αD .与坐标轴垂直的直线的倾斜角是0°或90° 10. 一个不透明的盒子中装有大小和质地都相同的编号分别为1,2,3,4的4个小球,从中任意摸出两个球.设事件1A =“摸出的两个球的编号之和小于5”,事件2A =“摸出的两个球的编号都大于2”,事件3A =“摸出的两个球中有编号为3的球”,则( ) A .事件1A 与事件2A 是互斥事件 B .事件1A 与事件3A 是对立事件C .事件1A 与事件3A 是相互独立事件D .事件23A A 与事件13A A ∩是互斥事件11.如图,在直三棱柱111ABC A B C −中,已知190,2,ACB AC BC CC E ∠=°===为11B C 的中点,过AE 的截面与棱111,BB AC 分别交于点,F G ,则下列说法正确的是( )A .三棱锥1A AEF −的体积为定值B .线段1C G 长度的取值范围是10,2C .当点F 为1BB 中点时,截面AFEG 3++D .存在点F ,使得1A F AE ⊥三、填空题:本题共3小题,每小题5分,共15分.12. 在平行六面体1111ABCD A B C D −中,1π3A AB DAB ∠=∠=,1π2A AD ∠=,12ABAD AA ===,则13.已知(1,0,0)A ,(2,1,0)B ,(1,1,1)C 三点,则A 到直线BC 的距离为 .14.如图,已知ABC ∆为等边三角形,点 G 是ABC ∆的重心.过点G 的直线l 与线段AB 交于点D ,与线段 AC 交于点E .设AD AB λ= ,AE AC µ=,且0λµ≠设ADE ∆的周长为1c ,ABC ∆的周长为2c ,设t λµ=,记()12c f t t c =−,则()f t 的值域为__________.四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.15.为了选拔培养有志于服务国家重大战略需求且综合素质优秀或基础学科拔尖的学生,教育部启动了“强基计划”的招生改革工作.某校强基招生面试有两道题,两道题都答对者才能通过强基招生面试.假设两题作答相互独立,现有甲、乙、丙三名学生通过考核进入面试环节,他们答对第一题的概率分别是111,,324,答对第二题的概率分别是112,,233.(1)求甲、乙两位考生中有且只有一位考生通过强基招生面试的概率; (2)求甲、乙、丙三人中至少有一人通过强基招生面试的概率.16.已知ABC 的内角,,A B C 所对的边分别为,,a b c ,且π22sin 6c b a C−=−. (1)求角A ;(2)若a D =为边BC 上一点,AD 为BAC ∠的平分线,且1AD =,求ABC 的面积.17.如图,在四棱锥P ABCD −中,平面PAD ⊥平面ABCD ,PAD △为等边三角形,PD AB ⊥,//AD BC ,2,1,ADAB BC M ===为PA 的中点. (1)证明:DM ⊥平面PAB ;(2)求平面PCD 与平面PAB 夹角的余弦值.18.对800名参加竞赛选拔学生的成绩作统计(满分:100分),将数据分成五组,从左到右依次记为[50,60),[60,70),[)70,80,[80,90),[90,100],并绘制成如图所示的频率分布直方图.(1)根据频率分布直方图估计这800名学生成绩的众数和平均数(求平均数时同一组数据用该组区间的中点值作代表);(2)现从以上各组中采用按比例分配的分层随机抽样的方法抽取40人.若分数在区间[)70,90的学生实际成绩的平均数与方差分别为78分和2775,第三组[)70,80的学生实际成绩的平均数与方差分别为72分和1,求第四组[80,90)的学生实际成绩的平均数与方差.19.在空间直角坐标系O xyz −中,己知向量(),,u a b c =,点()0000,,P x y z .若直线l 以u为方向向量且经过点0P ,则直线l 的标准式方程可表示为()0000x xy y z z abc a b c−−−==≠;若平面α以u 为法向量且经过点0P ,则平面α的点法式方程表示为()()()0000a x x b y y c z z −+−+−=.(1)已知直线l 2z ,平面1α50y z +−+=,求直线l 与平面1α所成角的余弦值;(2)已知平面2α的点法式方程可表示为2320x y z ++−=,平面外一点()1,2,1P ,点P 到平面2α的距离;(3)(i )若集合{(,,)|||||2,||1}M x y z x y z =+≤≤,记集合M 中所有点构成的几何体为S ,求几何体S 的体积;(ii )若集合(){,,|2,2,2}N x y z x y y z z x =+≤+≤+≤.记集合N 中所有点构成的几何体为T ,求几何体T 相邻两个面(有公共棱)所成二面角的大小.荆州中学2023级高二上学期九月月考数学试卷参考答案1-8 CCBBA BCC 9.ABC 10.ACD 11.AC14.2915.(1)518(2)91216【详解】(1)甲通过考核进入面试环节,答对第一题的概率分别是13,答对第二题的概率分别是12,甲考生通过某校强基招生面试的概率为1111326P =×=. 乙考生通过某校强基招生面试的概率为2111236P =×=, ∴甲、乙两位考生中有且只有一位考生通过强基招生面试的概率为:11115(1)(1)666618P =×−+−×=.(2)丙考生通过某校强基招生面试的概率为3121436P =×=,∴甲、乙、丙三人中至少有一人通过强基招生面试的概率为:11191'1111666216P =−−×−×−= .16.(1)π3A =(2【小问1详解】因π22sin sin cos 6c b a C C a C−=−=−,由正弦定理可得2sin sin sin sin cos C BA C A C −=−,且()sin sin sin cos cos sin B A C A C A C =+=+,即2sin sin cos cos sin sin sin cos C A C A C A C A C −−=−,整理可得π2sin sin cos sin 2sin sin 6C A C A C C A=+=+,且()0,πC ∈,则sin 0C ≠,可得πsin 16A+=, 又因为()0,πA ∈,则ππ7π666A <+<,可得ππ62A +=,所以π3A =.为【小问2详解】因为AD 为BAC ∠的平分线,则π6BAD CAD ∠=∠=, 因为ABCBAD CAD S S S =+ ,则111sin sin sin 222AB AC BAC AB AD BAD AD AC CAD ⋅⋅∠=⋅⋅∠+⋅⋅∠,即111111122222bc c b ××+×××,可得b c +, 在BAC 中,由余弦定理可得()22222cos 22cos a b c bc BAC b c bc bc BAC =+−∠=+−−∠, 即()2632bc bc bc =−−,整理可得()220bc bc −−=,解得2bc =或bc 1−(舍去), 所以ABC的面积11sin 222ABC S bc BAC =⋅∠=×=△17.(1)证明见解析【详解】(1)取AD 的中点O ,连接,PO CO , 因为PAD △为等边三角形,所以PO AD ⊥,又因为平面PAD ⊥平面ABCD ,平面PAD ∩平面ABCD AD =,PO ⊂平面PAD ,所以⊥PO 平面ABCD ,因为AB ⊂平面ABCD ,所以AB PO ⊥,又,,,PD AB PD PO P PD PO ⊥∩=⊂平面PAD ,所以AB ⊥平面PAD , 因为DM ⊂平面PAD ,所以AB DM ⊥, 因为M 是PA 的中点,所以DM PA ⊥, 因为,AB PA ⊂平面PAB ,且AB PA A = , 所以DM ⊥平面PAB .(2)因为2,1AD BC ==,由(1)知四边形ABCO 为矩形,则//AB OC , 又AB ⊥平面PAD ,所以CO ⊥平面PAD ,以O 为坐标原点,分别以,,OC OD OP 所在直线为x 轴,y 轴,z 轴建立空间直角坐标系,则(()()(()1,0,,1,0,0,0,1,0,0,1,,1,1,02P M C D PD CD −=− , 取平面PAB的法向量为30,2DM =−,设平面PCD 的法向量为(),,m x y z = ,则00m PD m CD ⋅= ⋅=,即00y x y = −+= ,令1z =,则x y =)m =. cos ,m DM m DM m DM ⋅==⋅ PCD 与平面PAB.18.(1)众数为65;平均数为67(2)平均数为87;方差为2【详解】(1)解:根据频率分布直方图的众数的定义,可得这800名学生成绩的众数为6070652+=, 这800名学生成绩的的平均数为:(550.030650.040750.015850.010950.005)1067x =×+×+×+×+××=(分).(2)解:根据题意,采用按比例分配的分层随机抽样的方法抽取40人, 各段抽取的人生分别为:12人,16人,6人,4人和2人, 其中分数在区间[)70,90的学生为10人,分别为(1,2,,10)i i µ= , 其中平均成绩与方差分别为2,u s ,则227778,5u s ==, 设第三组学生实际成绩分别为(1,2,,6)i x i = ,其平均数和方差为2,xx s ,则272,1x x s ==, 设第四组学生实际成绩分别为(1,2,3,4)i y i =,其平均数和方差为2,y y s ,由67247810y ×+=,可得87y =,由222221{[()][()]}x y s m s x u n s y u m n =⋅⋅+−+⋅+−+, 可得2222771{6[1(7278)]4[(8778)]}564y s =⋅×+−+⋅+−+,解得22y s =, 所以第四组[)80,90的学生实际成绩的平均数为87与方差为2. 19.(1(2(3)(i)16;(ii )2π3 (1)由题可知,直线l的一个方向向量坐标为()1,2m=,平面1α的一个法向量为)1n =−,设直线l 与平面1α所成角为β,则有·sin m n m nβ==cos β=, 直线l 与平面1α(2)由题可知平面2α的法向量为()22,3,1n =,且过点()0,0,2A ,因为()1,2,1P ,所以()1,2,1AP =− ,所以点P 到平面2α的距离为22·n AP n =(3)(i )建立空间直角坐标系,先分别画平面2,0,02,0,02,0,02,0,011x y x y x y x y x y x y x y x y z z +=>> −=><−+= −−=<< ==− ,然后得到几何体S 为几何体S是底面边长为的正方形,高为2的长方体,故几何体S的体积为216=,(ii )由(i )可知,(){,,|2,2,2}N x y z x y y z z x =+≤+≤+≤的图像是一个完全对称的图像,所以我们只需讨论第一卦限的相邻两个平面的二面角即可, 此时0,0,0x y z >>>,得{}(,,)2,2,2,0,0,0Nx y z x y y z z x x y z =+≤+≤+≤>>>,画出第一卦限图像,显然其二面角为钝角,计算平面2,2x y y z +=+=得二面角,所以两个平面的法向量分别为()()23,0,1,1n n ==,所以其二面角的余弦值为2323·12n n n n −=−,所以二面角为2π3.。
湖北省荆州市高二上学期期中数学试卷

湖北省荆州市高二上学期期中数学试卷姓名:________班级:________成绩:________一、 选择题 (共 18 题;共 36 分)1. (2 分) (2018 高一下·六安期末) 若,则不等式的解集是( )A.B.C.D. 2. (2 分) (2018 高二下·甘肃期末) “大自然是懂数学的”,自然界中大量存在如下数列:1,1,2,3, ,8,13,21, ,则其中 的值是( ) A.4 B.5 C.6 D.7 3. (2 分) 已知四棱锥 P﹣ABCD 的顶点都在球 O 上,底面 ABCD 是矩形,平面 PAD⊥平面 ABCD,△PAD 为正三 角形,AB=2AD=4,则球 O 的表面积为( )A.B. C . 32π D . 64π 4. (2 分) 若 f(x)=x2-2x-4lnx 则 f′(x)>0 的解集为( )第 1 页 共 12 页A.B . (-1,0)C.D . (-1,0)5. (2 分) 设 是等差数列.下列结论中正确的是( )A.若,则B.若,则C.若,则D.若, 则( ) ( )6. (2 分) (2017·莱芜模拟) 已知 m、n 是两条不同的直线,α、β 是两个不同的平面,给出下列命题:①若 α⊥β,m∥α,则 m⊥β;②若 m⊥α,n⊥β,且 m⊥n,则 α⊥β;③若 m⊥β,m∥α,则 α⊥β;④若 m∥α,n∥β,且 m∥n,则 α∥β.其中正确命题的个数是( )A.1B.2C.3D.47. (2 分) (2017 高一下·黄冈期末) 下列结论正确的是( )A . 若 a>b,则 ac2>bc2B . 若 a2>b2 , 则 a>b第 2 页 共 12 页C . 若 a>b,c<0,则 a+c<b+c D . 若 < ,则 a<b8. (2 分) 设实数 x,y 满足 A.3 B.2, 则 的最小值是( )C.D. 9. (2 分) (2017 高一下·双鸭山期末) 如下图是一个正方体的平面展开图,在这个正方体中①③与为异面直线④以上四个命题中,正确的序号是( )A . ①②③B . ②④C . ③④D . ②③④②与成角10. (2 分) 已知数列满足 且是函数的两个零点,则 等于( )A . 24第 3 页 共 12 页B . 32 C . 48 D . 64 11. (2 分) 正方体 ABCD﹣A′B′C′D′中,AB 的中点为 M,DD′的中点为 N,正方形 A′B′C′D′的中心 为 R,则异面直线 MR 与 CN 所成的角的余弦值是( ) A.0 B.1 C. D. 12. (2 分) (2018 高二上·遵义月考) 某空间几何体的三视图如图所示,该空间几何体的体积是( )A.8 B . 10 C. D. 13. (2 分) 正三棱锥的底面边长为 2,侧面均为直角三角形,则此棱锥的体积为( ) A. B.第 4 页 共 12 页C.D.14. (2 分) 已知数列中, ()A.B., 等比数列 的公比 q 满足C.D.15. (2 分) (2019 高二上·宁波期中) 等腰梯形中,线 将平面折起,折叠过程中, 与 夹角的取值范围为( )A. B. C. D. 16. (2 分) (2019 高一上·三亚期中) 函数 取值范围为( ) A. B.在区间C.D.第 5 页 共 12 页且,则,沿对角上为减函数,则 的17. (2 分) 设数列{an}是集合{3s+3t|0≤s<t,且 s,t∈Z}中所有的数从小到大排列成的数列,即 a1=4, a2=10,a3=12,a4=28,a5=30,a6=36,…,将数列{an}中各项按照上小下大,左小右大的原则排成如图等腰直角 三角形数表,a200 的值为( )A . 39+319 B . 310+319 C . 319+320 D . 310+32018. (2 分) 已知不等式 A.2对任意正实数 x , y 恒成立,则正实数 a 的最小值为( )B.4C.8D . 16二、 填空题 (共 4 题;共 4 分)19. (1 分) 某几何体三视图如图所示,则该几何体的体积为________第 6 页 共 12 页20. (1 分) (2018 高三下·滨海模拟) 等比数列 中,各项都是正数,且 ,则=________., 成等差数列,21. (1 分) (2017 高一下·扬州期末) 已知正数 a,b 满足 + =,则 ab 的最小值为________.22. (1 分) 若 a,b 是两条异面直线,且 a∥平面 α,则 b 与 α 的位置关系是________.三、 解答题 (共 3 题;共 25 分)23. (5 分) 已知二次函数 f(x)满足 f(1+x)=f(1﹣x),且 f(0)=0,f(1)=1,若 x∈[m,n]时 f(x) 的值域也为[m,n],求 m,n.24. (10 分) 如图,在正三棱柱 ABC﹣A1B1C1 中,点 D 是棱 AB 的中点,BC=2,AA1=2 .(1) 求证:BC1∥平面 A1DC; (2) 求二面角 D﹣A1C﹣A 的平面角的正弦值. 25. (10 分) (2016 高一下·赣州期中) 已知 Sn 为等比数列{an}的前 n 项和•且 S4=S3+3a3 , a2=9. (1) 求数列{an}的通项公式 (2) 设 bn=(2n﹣1)an,求数列{bn}的前 n 项和 Tn.第 7 页 共 12 页一、 选择题 (共 18 题;共 36 分)1-1、 2-1、 3-1、 4-1、 5-1、 6-1、 7-1、 8-1、 9-1、 10-1、 11-1、 12-1、 13-1、 14-1、 15-1、 16-1、参考答案第 8 页 共 12 页17-1、 18-1、二、 填空题 (共 4 题;共 4 分)19-1、 20-1、 21-1、 22-1、三、 解答题 (共 3 题;共 25 分)23-1、第 9 页 共 12 页24-1、第 10 页 共 12 页24-2、25-1、25-2、。
湖北省荆州市高二上学期数学期中考试试卷

湖北省荆州市高二上学期数学期中考试试卷姓名:________ 班级:________ 成绩:________一、单选题 (共4题;共8分)1. (2分) (2016高二下·汕头期中) 已知AB为圆x2+y2=1的一条直径,点P为直线x﹣y+2=0上任意一点,则的最小值为()A . 1B .C . 2D . 22. (2分) (2016高二上·福州期中) 已知0<x<,则﹣<0是﹣x>0成立的()A . 充要条件B . 充分不必要条件C . 必要不充分条件D . 既不充分也不必要条件3. (2分) (2018·泉州模拟) 实数满足,则的最大值为()A .B .C .D .4. (2分) (2019高二上·四川期中) 在圆内,过点的最长弦和最短弦分别为AC和BD,则四边形ABCD的面积为A .B .C .D .二、填空题 (共12题;共12分)5. (1分) (2018高一下·瓦房店期末) 与向量垂直的单位向量为________.6. (1分) (2019高二上·上海期中) 若矩阵,,则 ________.7. (1分)当a>0,b>0且a+b=2时,行列式的值的最大值是________ .8. (1分) (2017高一下·泰州期中) 已知直线l1:ax﹣y﹣1=0,若直线l1的倾斜角为,则a=________.9. (1分) A=, f(x)=x2+3x,则f(A)=________ .10. (1分) (2018高三上·镇海期中) 已知直线,其中,若,则 =________,若,则 =________.11. (1分)已知点A(﹣5,0),B(﹣1,﹣3),若圆x2+y2=r2(r>0)上恰有两点M,N,使得△MAB和△NAB 的面积均为5,则r的取值范围是________12. (1分) (2016高一上·郑州期末) 已知圆的方程为x2+y2+ax+2y+a2=0,要使过定点A(1,2)作圆的切线有两条,则a的取值范围是________13. (1分) (2018高一下·雅安期中) 某企业生产甲,乙两种产品均需用两种原料,已知生产1吨每种产品需用原料及每天原料的可用限额如下表所示,如果生产1吨甲,乙产品可获利润分别为3万元、4万元,则该企业可获得最大利润为________万元.甲乙原料限额A(吨)3212B(吨)12814. (1分) (2018高一下·重庆期末) 已知圆,直线,如果圆上总存在点,它关于直线的对称点在轴上,则的取值范围是________.15. (1分) (2018高二下·磁县期末) 若直线l:与x轴相交于点A,与y轴相交于B,被圆截得的弦长为4,则为坐标原点的最小值为________.16. (1分)(2017·山东) 在平面直角坐标系xOy中,双曲线 =1(a>0,b>0)的右支与焦点为F 的抛物线x2=2py(p>0)交于A,B两点,若|AF|+|BF|=4|OF|,则该双曲线的渐近线方程为________.三、解答题 (共5题;共65分)17. (10分)(2018·河北模拟) 在矩形中,,,点是线段上靠近点的一个三等分点,点是线段上的一个动点,且 .如图,将沿折起至,使得平面平面 .(1)当时,求证:;(2)是否存在,使得与平面所成的角的正弦值为?若存在,求出的值;若不存在,请说明理由.18. (10分) (2016高三上·西安期中) 已知三角形ABC中,.(1)若.求三角形ABC的面积S△;(2)求三角形ABC的面积S△.19. (15分)某人在塔的正东处沿着南偏西的方向前进米后到达处,望见塔在东北方向,若沿途测得塔的最大仰角为,求塔高.20. (15分) (2019高二上·上海期中) 如图,已知直线和直线,射线的一个法向量为,点为坐标原点,,,点、分别是直线、上的动点,直线和之间的距离为2,于点,于点;(1)若,求的值;(2)若,求的最大值;(3)若,,求的最小值.21. (15分)(2017·潍坊模拟) 已知抛物线C顶点在原点,焦点在y轴上,抛物线C上一点Q(a,2)到焦点的距离为3,线段AB的两端点A(x1 , y1)、B(x2 , y2)在抛物线C上.(1)求抛物线C的方程;(2)若y轴上存在一点M(0,m)(m>0),使线段AB经过点M时,以AB为直径的圆经过原点,求m的值;(3)在抛物线C上存在点D(x3,y3),满足x3<x1<x2,若△ABD是以角A为直角的等腰直角三角形,求△ABD面积的最小值.参考答案一、单选题 (共4题;共8分)1-1、2-1、3-1、4-1、二、填空题 (共12题;共12分)5-1、6-1、7-1、8-1、9-1、10-1、11-1、12-1、13-1、14-1、15-1、16-1、三、解答题 (共5题;共65分) 17-1、17-2、18-1、18-2、19-1、20-1、20-2、20-3、21-1、21-2、21-3、。
(全优试卷)湖北省高二数学(文)上学期期中试题word版
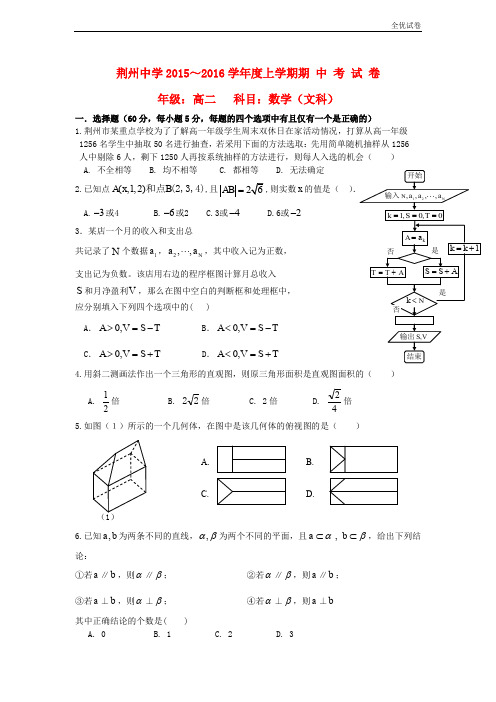
荆州中学2015~2016学年度上学期期 中 考 试 卷年级:高二 科目:数学(文科)一.选择题(60分,每小题5分,每题的四个选项中有且仅有一个是正确的)1.荆州市某重点学校为了了解高一年级学生周末双休日在家活动情况,打算从高一年级1256名学生中抽取50名进行抽查,若采用下面的方法选取:先用简单随机抽样从1256人中剔除6人,剩下1250人再按系统抽样的方法进行,则每人入选的机会( ) A. 不全相等 B. 均不相等 C. 都相等 D. 无法确定2.已知点(,1,2)A x B 和点(2,3,4),且AB =,则实数x 的值是( )A.3-或4B.6-或2C.3或4-D.6或2- 3.某店一个月的收入和支出总共记录了N 个数据1a ,2,,N a a⋅⋅⋅,其中收入记为正数,支出记为负数。
该店用右边的程序框图计算月总收入S 和月净盈利V ,那么在图中空白的判断框和处理框中,应分别填入下列四个选项中的( )A .0,A V S T >=-B .0,A V S T <=-C .0,A V S T >=+D .0,A V S T <=+4.用斜二测画法作出一个三角形的直观图,则原三角形面积是直观图面积的( ) A.21倍 B. 22倍 C. 2倍 D. 42倍5.如图(1)所示的一个几何体,在图中是该几何体的俯视图的是( )(1)6.已知,a b 为两条不同的直线,,αβ为两个不同的平面,且,a b αβ⊂⊂,给出下列结论:①若a ∥b ,则α∥β; ②若α∥β,则a ∥b ; ③若a ⊥b ,则α⊥β; ④若α⊥β,则a ⊥b 其中正确结论的个数是( )A. 0B. 1C. 2D. 3A. B. C. D.x y O x y O x y O xyO7.将一圆形纸片沿半径剪开为两个扇形,其圆心角之比为3∶4. 再将它们卷成两个圆锥侧面,则两圆锥的之底面积比为( ) A. 3∶4 B. 9∶16 C. 4:3 D. 16:9 8.在同一直角坐标系中,方程y ax =与y x a =+的图形正确的是( )A. B. C. D.9.若()2,1P -为圆()22125x y -+=的弦AB 的中点,则直线AB 的方程为 ( )A. 230x y +-=B. 10x y +-=C. 30x y --=D. 250x y --=10.已知点)3,2(-A 、(3,2),B --若直线l 过点)1,1(P ,且与线段AB 相交,则直线l 的斜率的取值k 范围是 ( )A. (]3,4,4⎡⎫-∞-+∞⎪⎢⎣⎭ B. 13,,44⎛⎤⎡⎫-∞-+∞ ⎪⎥⎢⎝⎦⎣⎭C. 34,4⎡⎤-⎢⎥⎣⎦D. 3,44⎡⎤⎢⎥⎣⎦11.若直线42y kx k =++与曲线y =k 的取值范围是( )A. [)1,+∞B. 31,4⎡⎫--⎪⎢⎣⎭ C. 3,14⎛⎤ ⎥⎝⎦D. (],1-∞- 12.若圆C 与圆()()22:261D x y ++-=关于直线:0l x y -=对称,则圆C 的方程为( ) A. 22(2)(6)1x y ++-= B. 22(6)(2)1x y -++= C. 22(1)(3)1x y -+-= D. 22(1)(3)1x y +++=二、填空题(共20分,每小题5分)13.过圆22:1O x y +=外一点()1,2M -的切线方程为 .14.已知x 与y 之间的一组数据如右图所示,当m 变化时,y 与x 的回归直线方程ˆy b x a =+必过定点 .15.在三棱锥的四个面中,直角三角形最多可有 个.16.荆州市为了解7080-岁的老人的日平均睡眠时间(单位:h ),随机选择了50位老人进行调查,下表是这50位老人睡眠时间的频率分布表:的值为 .三、解答题17. (本小题满分10分)某地区100位居民的人均月用水量(单位:t )的频率分布直方图及频数分布表如下:(1)根据频率分布直方图估计这组数据的众数与平均数;(2)当地政府制定了人均月用水量为3t 的标准,若超出标准加倍收费,当地政府解释说,85%以上的居民不超出这个标准,这个解释对吗?为什么?18.(本小题满分12分)已知一条光线从点()2,3A -射出,经过x 轴反射后,反射光线与圆()()22:321C x y -+-=相切,求反射光线所在直线的方程.19.(本小题满分12分)在2015年全运会上两名射击运动员甲、乙在比赛中打出如下成绩:甲:9.4,8.7,7.5,8.4,10.1,10.5,10.7,7.2,7.8,10.8; 乙:9.1,8.7,7.1,9.8,9.7,8.5,10.1,9.2,10.1,9.1;(1)用茎叶图表示甲、乙两人的成绩;并根据茎叶图估计他们的中位数;(2)已知甲、乙两人成绩的方差分别为1.69与0.81,分别计算两个样本的平均数x x 乙甲、和标准差s s 乙甲、,并根据计算结果估计哪位运动员的成绩比较好,哪位运动员的成绩比较稳定.20.(本小题满分12分)已知点()3,4,(6,3)A B --到直线:10l ax y ++=的距离相等,求a 得值.21.(本小题满分12分)在三棱锥A BCD -中,AB BCD ⊥面,BC CD ⊥,点E 在棱AC 上,且BE AC ⊥.(Ⅰ)试证明:BE ACD ⊥面;(Ⅱ)若2AB BC CD ===,过直线BE 任作一个平面与直线 AD 相交于点P ,得到三棱锥A BCD -的一个截面BEP ∆, 求BEP ∆面积的最小值;(Ⅲ)若2AB BC CD ===,求二面角B AD C --的正弦值.22.(本小题满分12分)已知圆22:1O x y +=和定点()2,1A ,由圆O 外一点(,)P a b 向圆O 引切线PQ ,切点为Q ,且满足PQ PA =. (1) 求实数,a b 间满足的等量关系; (2) 求线段PQ 长的最小值;(3) 若以P 为圆心的圆P 与圆O 有公共点,试求圆P 的半径最小时圆P 的方程.PABCDE荆州中学2015~2016学年度上学期期 中 考 试 卷年级:高二 科目:数学(文科) 出题人:审题人:参考答案一、选择题CDCBC ABCCA BB 二、填空题34501x y x ++==和; )4,23(; 4; 6.42三、解答题17. 解:(1)由图知,这组数据的众数为2.25, 平均数为2.02.(2)人均月用水量在3t 以上的居民的比例为6%+4%+2%=12%,即大约是有12%的居民月均用水量在3t 以上,88%的居民月均用水量在3t 以下,因此,政府的解释是正确的.18.解:A 关于x 轴的对称点(2,3)A '--。
2023-2024学年湖北省荆州市荆州中学高二(上)期中数学试卷【答案版】

2023-2024学年湖北省荆州市荆州中学高二(上)期中数学试卷一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项符合题目要求. 1.(3﹣2i )(1+2i )=( ) A .﹣1+4iB .7﹣4iC .7+4iD .﹣1﹣4i2.已知集合A ={x |x ﹣2>0},B ={x |x 2﹣x +m =0},若A ∩B ≠∅,则m 的取值范围为( ) A .(﹣∞,﹣2)B .(﹣∞,2]C .(﹣∞,2)D .(﹣∞,﹣2]3.如图,在三棱锥P ﹣ABC 中,P A ⊥平面ABC ,AB ⊥AC ,且PD →=3DC →,则BD →在AC →方向上的投影向量为( )A .34AC →B .−23AC →C .−34AC →D .23AC →4.抛掷两枚质地均匀的骰子,设事件A =“两枚骰子的点数之和为偶数”,事件B =“恰有一枚骰子的点数为偶数”,则( ) A .P (A )>P (B )B .P (A )<P (B )C .A 与B 互为对立事件D .A 与B 互为互斥但不对立事件5.在△ABC 中,AB =1,BC =√5,cosA =56,则AC =( )A .2B .73C .3D .526.若A (2,2,1),B (0,0,1),C (2,0,0),则点A 到直线BC 的距离为( ) A .2√305B .√305C .2√55D .√557.定义在R 上的奇函数f (x )在区间(0,+∞)上单调递减,且f (6)=0,则不等式xf (x ﹣4)<0的解集为( )A .(﹣2,0)∪(4,10)B .(﹣2,0)∪(0,4)∪(10,+∞)C .(﹣∞,﹣2)∪(10,+∞)D .(﹣∞,﹣2)∪(0,4)∪(10,+∞)8.已知实数x ,y 满足2x ﹣y +2=0,则√(x −9)2+y 2+√x 2+y 2−4x −4y +8的最小值为( ) A .3√13B .10+√13C .108D .117二、选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求. 9.已知一组数据x ,x +2,3x ﹣3,2x +1,9的平均数为6,则( ) A .x =2B .x =3C .这组数据的第70百分位数为7D .这组数据的第70百分位数为6.510.已知点A (1,4),B (3,2),C (2,﹣1),若直线l 经过点C ,且A ,B 到l 的距离相等,则l 的方程可能是( ) A .x +y ﹣1=0B .x ﹣y ﹣3=0C .x ﹣2=0D .y +1=011.已知直线l :(√3m +1)x −(m −√3)y −4=0与圆O :x 2+y 2=16相交于A ,B 两点,则△OAB 的面积可能为( ) A .8B .4√3C .4D .2√312.苏州博物馆(图一)是地方历史艺术性博物馆,建筑物的顶端可抽象为如图二所示的上、下两层等高的几何体,其中上层EFGH ﹣NPQM 是正四棱柱,下层底面ABCD 是边长为4的正方形,E ,F ,G ,H 在底面ABCD 的投影分别为AD ,AB ,BC ,CD 的中点,若AF =√5,则下列结论正确的有( )A .该几何体的表面积为32+8√2+4√6B .将该几何体放置在一个球体内,则该球体体积的最小值为36πC .直线CP 与平面ABF 所成角的正弦值为√63D .点M 到平面BFG 的距离为√63三、填空题:本题共4小题,每小题5分,共20分.13.过点M(√3,0)作圆C :x 2+(y ﹣1)2=1的两条切线,切点分别为A ,B ,则直线AB 的方程为 .14.若直线l 1:ax +4y +7=0与l 2:2x ﹣3y ﹣1=0垂直,则a = .15.已知函数f(x)=√3sin(ωx +π3)+sin(ωx −π6)(ω>0),若函数g (x )=f (x )﹣1在(0,π)上恰有两个零点,则ω的取值范围为 .16.如图,在正方体ABCD ﹣A 1B 1C 1D 1中,AM =2MB ,N 为DD 1的中点,记平面CMN 与平面ADD 1A 1的交线为l ,则直线l 与直线AC 1所成角的余弦值为 .四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤. 17.(10分)已知直线l 1:x +ay ﹣a +2=0与l 2:2ax +(a +3)y +a ﹣5=0. (1)当a =1时,求直线l 1与l 2的交点坐标; (2)若l 1∥l 2,求a 的值.18.(12分)如图,这是某圆弧形山体隧道的示意图,其中底面AB 的长为16米,最大高度CD 的长为4米,以C 为坐标原点,AB 所在的直线为x 轴建立直角坐标系. (1)求该圆弧所在圆的方程;(2)若某种汽车的宽约为2.5米,高约为1.6米,车辆行驶时两车的间距要求不小于0.5米以保证安全,同时车顶不能与隧道有剐蹭,则该隧道最多可以并排通过多少辆该种汽车?(将汽车看作长方体)19.(12分)甲、乙准备进行一局羽毛球比赛,比赛规定:一回合中赢球的一方作为下一回合的发球方.若甲发球,则本回合甲赢的概率为34,若乙发球,则本回合甲赢的概率为14,每回合比赛的结果相互独立.经抽签决定,第1回合由甲发球. (1)求第3回合由乙发球的概率;(2)求前3个回合中甲赢的回合数不低于乙的概率.20.(12分)如图,在正四棱锥P ﹣ABCD 中,E ,F 分别为P A ,PC 的中点,DG →=2GP →. (1)证明:B ,E ,G ,F 四点共面.(2)记四棱锥P ﹣BEGF 的体积为V 1,四棱锥P ﹣ABCD 的体积为V 2,求V 1V 2的值.21.(12分)已知O 为坐标原点,A (0,4),P 是平面内一动点,且PA →•PO →=0,记动点P 的轨迹为C . (1)求C 的方程.(2)已知不经过原点且斜率存在的直线l 与C 相交于M ,N 两点,且k OM •k ON =﹣3,试问l 是否经过定点?若经过,求出该定点坐标;若不经过,说明理由.22.(12分)如图,在斜三棱柱ABC ﹣A 1B 1C 1中,△ABC 是边长为2的等边三角形,M ,Q 分别为AC ,A 1B 1的中点,且MQ ⊥AB . (1)证明:MC 1⊥AB .(2)若BB 1=4,MQ =√15,求平面MB 1C 1与平面MC 1Q 夹角的余弦值.2023-2024学年湖北省荆州市荆州中学高二(上)期中数学试卷参考答案与试题解析一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项符合题目要求. 1.(3﹣2i )(1+2i )=( ) A .﹣1+4iB .7﹣4iC .7+4iD .﹣1﹣4i解:(3﹣2i )(1+2i )=3+6i ﹣2i ﹣4i 2=7+4i . 故选:C .2.已知集合A ={x |x ﹣2>0},B ={x |x 2﹣x +m =0},若A ∩B ≠∅,则m 的取值范围为( ) A .(﹣∞,﹣2)B .(﹣∞,2]C .(﹣∞,2)D .(﹣∞,﹣2]解:因为A ={x |x ﹣2>0}={x |x >2},A ∩B ≠∅,所以B ≠∅,而B ={x |x 2﹣x +m =0},当Δ=(﹣1)2﹣4m =0,即m =14时,B ={x|x 2−x +14=0}={12},则A ∩B =∅,不合题意;当Δ=(﹣1)2﹣4m >0,即m <14时,方程x 2﹣x +m =0有两个不等实根,又二次函数y =x 2﹣x +m 的对称轴为x =12<2,则要使A ∩B ≠∅,只须22﹣2+m <0,解得m <﹣2; 综上,m 的取值范围为(﹣∞,﹣2). 故选:A .3.如图,在三棱锥P ﹣ABC 中,P A ⊥平面ABC ,AB ⊥AC ,且PD →=3DC →,则BD →在AC →方向上的投影向量为( )A .34AC →B .−23AC →C .−34AC →D .23AC →解:因为P A ⊥平面ABC ,AB ⊥AC ,所以P A ⊥AB ,P A ⊥AC ,故以A 为坐标原点,AB ,AC ,P A 所在直线分别为x ,y ,z 轴建立空间直角坐标系,令AB =a ,AC =b ,P A =c ,则A (0,0,0),B (a ,0,0),C (0,b ,0),D(0,34b ,14c),则AC →=(0,b ,0),BD →=(−a ,34b ,14c),所以BD →在AC →方向上的投影向量为AC →⋅BD →|AC →|⋅AC →|AC →|=34b 2|b|⋅AC →|b|=34AC →.故选:A .4.抛掷两枚质地均匀的骰子,设事件A =“两枚骰子的点数之和为偶数”,事件B =“恰有一枚骰子的点数为偶数”,则( ) A .P (A )>P (B )B .P (A )<P (B )C .A 与B 互为对立事件D .A 与B 互为互斥但不对立事件解:因为事件A =“两枚骰子的点数之和为偶数”,即事件A 包括两枚骰子的点数之和为偶数分为两枚骰子都为奇数和偶数,P(A)=3×3+3×36×6=12,事件B =“恰有一枚骰子的点数为偶数”,即事件B 为两枚骰子一枚为奇数,一枚偶数,即两枚骰子的点数之和为奇数.所以P(B)=2×3×36×6=12, 所以A 与B 互为对立事件,且P(A)=P(B)=12.故A ,B ,D 错误;C 正确.故选:C .5.在△ABC 中,AB =1,BC =√5,cosA =56,则AC =( )A .2B .73C .3D .52解:因为在△ABC 中,AB =1,BC =√5,cosA =56,由余弦定理知cosA =AB 2+AC 2−BC22AB⋅AC ,所以56=12+AC 2−(√5)22×1×AC,则3AC 2﹣5AC ﹣12=0,解得AC =3或AC =−43(舍去).故选:C .6.若A (2,2,1),B (0,0,1),C (2,0,0),则点A 到直线BC 的距离为( ) A .2√305B .√305C .2√55D .√55解:由题意得,BA →=(2,2,0),BC →=(2,0,−1),则BA →在BC →上的投影向量的模为|BA →⋅BC →||BC →|=√5, 则点A 到直线BC 的距离为√|BA →|2−(|BA →⋅BC →||BC →|)2=√(√8)2−(45)2=2√305.故选:A .7.定义在R 上的奇函数f (x )在区间(0,+∞)上单调递减,且f (6)=0,则不等式xf (x ﹣4)<0的解集为( )A .(﹣2,0)∪(4,10)B .(﹣2,0)∪(0,4)∪(10,+∞)C .(﹣∞,﹣2)∪(10,+∞)D .(﹣∞,﹣2)∪(0,4)∪(10,+∞)解:因为定义在R 上的奇函数f (x ) 在区间 (0,+∞)上单调递减,且f (6)=0, 所以f (x )的图象大致如图所示:由xf(x﹣4)<0,①当x>0时,f(x﹣4)<0,即﹣6<x﹣4<0或x﹣4>6,解得0<x<4或x>10;②当x<0时,f(x﹣4)>0,即x﹣4<﹣6或0<x﹣4<6(舍),解得x<﹣2;综上,0<x<4,或x>10或x<﹣2.故选:D.8.已知实数x,y满足2x﹣y+2=0,则√(x−9)2+y2+√x2+y2−4x−4y+8的最小值为()A.3√13B.10+√13C.108D.117解:√(x−9)2+y2+√x2+y2−4x−4y+8=√(x−9)2+y2+√(x−2)2+(y−2)2,该式表示直线l:2x﹣y+2=0上一点到P(9,0),Q(2,2)两点距离之和的最小值.而P,Q两点在l的同一侧,设点P关于l对称的点P′(x0,y0),则{y0−0x0−9=−122×x0+92−y0+02+2=0,解得{x0=−7y0=8,∴P′(﹣7,8),故√(x−9)2+y2+√x2+y2−4x−4y+8≥|P′Q|=√(−7−2)+(8−2)2=3√13.故选:A.二、选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.9.已知一组数据x,x+2,3x﹣3,2x+1,9的平均数为6,则()A.x=2B.x=3C.这组数据的第70百分位数为7D.这组数据的第70百分位数为6.5解:x,x+2,3x﹣3,2x+1,9的平均数为6,则x+x+2+3x﹣3+2x+1+9=30,解得x=3,故A错误,B正确;这组数据为3,5,6,7,9,由5×0.7=3.5,则这组数据的第70百分位数为7,故C正确,D错误.故选:BC.10.已知点A(1,4),B(3,2),C(2,﹣1),若直线l经过点C,且A,B到l的距离相等,则l的方程可能是()A.x+y﹣1=0B.x﹣y﹣3=0C.x﹣2=0D.y+1=0解:若A,B在l的同侧,则l∥AB,A(1,4),B(3,2),则k AB=2−43−1=−1,所以l的方程为x+y﹣1=0,若A,B在l的两侧,则l经过线段AB的中点M(2,3),此时l的方程为x﹣2=0,综上所述,l的方程可能是x+y﹣1=0或x﹣2=0.故选:AC.11.已知直线l:(√3m+1)x−(m−√3)y−4=0与圆O:x2+y2=16相交于A,B两点,则△OAB的面积可能为()A.8B.4√3C.4D.2√3解:将l的方程转化为(√3x−y)m+x+√3y−4=0,令{√3x−y=0x+√3y−4=0,解得{x=1y=√3,即1经过定点P(1,√3),则圆心O到l的距离d≤|OP|=2,设∠AOB=θ,则cos θ2=d4≤12,故60°≤θ<90°,即120°≤2θ<180°,△OAB的面积S=12×42×sin2θ∈(0,4√3].故选:BCD.12.苏州博物馆(图一)是地方历史艺术性博物馆,建筑物的顶端可抽象为如图二所示的上、下两层等高的几何体,其中上层EFGH﹣NPQM是正四棱柱,下层底面ABCD是边长为4的正方形,E,F,G,H 在底面ABCD的投影分别为AD,AB,BC,CD的中点,若AF=√5,则下列结论正确的有()A.该几何体的表面积为32+8√2+4√6B.将该几何体放置在一个球体内,则该球体体积的最小值为36πC.直线CP与平面ABF所成角的正弦值为√6 3D.点M到平面BFG的距离为√6 3解:设F,G在平面ABCD的投影分别为AB,BC的中点R,S,由于AF=√5,AB=4,所以F到平面ABCD的距离为FR=√AF2−(12AB)2=1,由于上、下两层等高,所以P到平面ABCD的距离为2,又FG =RS =12AC =2√2,由于GS =FR =1,BS =RB =12×4=2所以BG =GC =√GS 2+BS 2=√5=BF =AF ,所以△AFB ≌△BGC ,同理可得△CDH ≌△ADE ≌△AFB ≌△BGC ,△BFG ≌△CHG ≌△DEH ≌△AEF , 则点B 到FG 的距离为√BF 2−(12FG)2=√(√5)2−(√2)2=√3,则△ABF 的面积为12AB ⋅FR =12×4×1=2,△BFG 的面积为12×2√2×√3=√6,故该几何体的表面积4×2+4×√6+4×4+2√2×2√2+2√2×4=32+8√2+4√6,故A 正确; 将该几何体放置在一个球体内,要使该球体体积最小,则球心在该几何体上下底面中心所连直线上, 且A 、B 、C 、D ,N 、P 、Q 、M 均在球面上,设球心到下底面ABCD 的距离为x , 由于四边形MNPQ 为边长为2√2的正方形,四边形ABCD 为边长为4的正方形, 则其对角线长度分别为4,4√2,则(2√2)2+x 2=22+(2−x)2, 解得x =0,则该球体的半径为2√2,体积为4π3×(2√2)3=64√2π3,故B 错误;以A 为坐标原点建立如图所示的空间直角坐标系,则C (4,4,0),P (2,0,2),B (4,0,0),F (2,0,1),G (4,2,1),M (2,4,2),CP →=(−2,−4,2),BF →=(﹣2,0,1),BG →=(0,2,1),BM →=(﹣2,4,2), 平面ABF 的一个法向量为m →=(0,1,0),则cos <CP →,m →>=−42√6=−√63,设直线CP 与平面ABF 所成角为θ,则sinθ=|cos <CP →,m →>|=√63,故直线CP 与平面ABF 所成角的正弦值为√63,故C 正确; 设平面BFG 的法向量为n →=(x 1,y 1,z 1),则{n →⋅BF →=−2x 1+z 1=0n →⋅BG →=2y 1+z 1=0,令x 1=1,得n →=(1,﹣1,2), 则点M 到平面BFG 的距离为|n →⋅BM →||n →|=√12+(−1)2+22=√63,故D 正确. 故选:ACD .三、填空题:本题共4小题,每小题5分,共20分.13.过点M(√3,0)作圆C :x 2+(y ﹣1)2=1的两条切线,切点分别为A ,B ,则直线AB 的方程为 √3x −y =0 .解:圆C :x 2+(y ﹣1)2=1①,则圆心C (0,1), 以C (0,1),M (√3,0)为直径的圆的方程为:(x −√32)2+(y −12)2=1②, ①﹣②可得,√3x −y =0,故直线AB 的方程为√3x −y =0. 故答案为:√3x −y =0.14.若直线l 1:ax +4y +7=0与l 2:2x ﹣3y ﹣1=0垂直,则a = 6 . 解:因为l 1⊥l 2,所以2a ﹣12=0,解得a =6. 故答案为:6.15.已知函数f(x)=√3sin(ωx +π3)+sin(ωx −π6)(ω>0),若函数g (x )=f (x )﹣1在(0,π)上恰有两个零点,则ω的取值范围为 (2,83] .解:由题意可知,f(x)=√3sin(ωx +π3)+sin(ωx −π6)=√3sin(ωx +π3)−cos(ωx +π3)=2sin(ωx +π6),由g (x )=0,得sin(ωx +π6)=12.由0<x <π,得π6<ωx +π6<ωπ+π6;由在(0,π)上恰有两个零点可得13π6<ωπ+π6≤17π6,解得2<ω≤83.故答案为:(2,83].16.如图,在正方体ABCD ﹣A 1B 1C 1D 1中,AM =2MB ,N 为DD 1的中点,记平面CMN 与平面ADD 1A 1的交线为l ,则直线l 与直线AC 1所成角的余弦值为7√111111.解:设I ∩AA 1=P ,连接NP ,MP ,直线NP 即为直线l .易证得MP ∥CN ,由AM =2MB ,N 为DD 1的中点,得AP =13AA 1,以D 为坐标原点,DA .DC ,DD 1所在直线分别为x ,y ,z 轴建立如图所示的空间直角坐标系,设AB =6,则得:N (0,0,3),P (6,0,2),A (6,0,0),C 1(0,6,6), NP →=(6,0,﹣1),AC 1→=(﹣6,6,6), 所以得:|cos <NP →,AC 1→>|=|NP →⋅AC 1→||NP →|⋅|AC 1→|=√37×6√3=7√111111,故直线与直线 AC 1 所成角的余弦值为7√111111. 故答案为:7√111111. 四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤. 17.(10分)已知直线l 1:x +ay ﹣a +2=0与l 2:2ax +(a +3)y +a ﹣5=0. (1)当a =1时,求直线l 1与l 2的交点坐标; (2)若l 1∥l 2,求a 的值.解:(1)因为a =1,所以l 1:x +y +1=0,l 2:2x +4y ﹣4=0,即x +2y ﹣2=0, 联立{x +y +1=0x +2y −2=0解得{x =−4y =3,故直线l 1与l 2的交点坐标为(﹣4,3).(2)因为l 1∥l 2,所以2a 2﹣a ﹣3=0,解得a =﹣1或a =32,当a =﹣1时,l 1与l 2重合,不符合题意. 当a =32时,l 1与l 2不重合,符合题意.故a =32.18.(12分)如图,这是某圆弧形山体隧道的示意图,其中底面AB 的长为16米,最大高度CD 的长为4米,以C 为坐标原点,AB 所在的直线为x 轴建立直角坐标系. (1)求该圆弧所在圆的方程;(2)若某种汽车的宽约为2.5米,高约为1.6米,车辆行驶时两车的间距要求不小于0.5米以保证安全,同时车顶不能与隧道有剐蹭,则该隧道最多可以并排通过多少辆该种汽车?(将汽车看作长方体)解:(1)由圆的对称性可知,该圆弧所在圆的圆心在y 轴上, 由图形可得A (﹣8,0),B (8,0),D (0,4),设该圆的半径为r 米,则r 2=82+(r ﹣4)2,解得r =10,圆心为(0,﹣6), 故该圆弧所在圆的方程为x 2+(y +6)2=100.(2)设与该种汽车等高且能通过该隧道的最大宽度为d 米,则(d 2)2+(6+1.6)2=102,解得d =2√42.24.若并排通过4辆该种汽车,则安全通行的宽度为4×2.5+3×0.5=11.5<2√42.24.隧道能并排通过4辆该种汽车;若并排通过5辆该种汽车,则安全通行的宽度为5×2.5+4×0.5=14.5>2√42.24,故该隧道不能并排通过5辆该种汽车.综上所述,该隧道最多可以并排通过4辆该种汽车.19.(12分)甲、乙准备进行一局羽毛球比赛,比赛规定:一回合中赢球的一方作为下一回合的发球方.若甲发球,则本回合甲赢的概率为34,若乙发球,则本回合甲赢的概率为14,每回合比赛的结果相互独立.经抽签决定,第1回合由甲发球. (1)求第3回合由乙发球的概率;(2)求前3个回合中甲赢的回合数不低于乙的概率. 解:(1)由题可知,第3回合由乙发球的概率为34×14+14×34=38; (2)前3个回合中甲赢的回合数不低于乙,则前3个回合中甲赢的回合数为2或3, 甲赢的回合数为2的概率为 34×34×14+34×14×14+14×14×34=1564, 甲赢的回合数为3的概率为34×34×34=2764, 故前3个回合中甲赢的回合数不低于乙的概率为 2764+1564=2132. 20.(12分)如图,在正四棱锥P ﹣ABCD 中,E ,F 分别为P A ,PC 的中点,DG →=2GP →. (1)证明:B ,E ,G ,F 四点共面.(2)记四棱锥P ﹣BEGF 的体积为V 1,四棱锥P ﹣ABCD 的体积为V 2,求V 1V 2的值.解:(1)证明:因为E ,F 分别为P A ,PC 的中点,所以BE →=12BA →+12BP →,BF →=12BC →+12BP →,所以BG →=BD →+DG →=BD →+23DP →=BD →+23(BP →−BD →)=13BD →+23BP →=13BA →+13BC →+23BP →=23(12BA →+12BP →)+23(12BC →+12BP →)=23BE →+23BF →, 故B ,E ,G ,F 四点共面;(2)由正四棱锥的对称性知,V 1=2V E ﹣PBG ,V 2=2V A ﹣PBD , 设点E 到平面PBG 的距离为d 1,点A 到平面PBD 的距离为d 2, 由E 是P A 的中点得d 2=2d 1, 由DG →=2GP →得S △PBD =3S △PBG ,所以V 1V 2=V E−PBG V A−PBD=13S △PBG ⋅d 113S △PBD ⋅d 2=16. 21.(12分)已知O 为坐标原点,A (0,4),P 是平面内一动点,且PA →•PO →=0,记动点P 的轨迹为C . (1)求C 的方程.(2)已知不经过原点且斜率存在的直线l 与C 相交于M ,N 两点,且k OM •k ON =﹣3,试问l 是否经过定点?若经过,求出该定点坐标;若不经过,说明理由. 解:(1)设P (x ,y ),由A (0,4),PA →•PO →=0,可得(﹣x ,4﹣y )•(﹣x ,﹣y )=x 2﹣y (4﹣y )=0,化为x 2+y 2﹣4y =0, 则C 的方程为x 2+y 2﹣4y =0;(2)设直线l 的方程为y =kx +m (m ≠0), 由直线l 与圆相交,可得√1+k22,即1+k 2>14(m ﹣2)2, 直线l 的方程与圆x 2+y 2﹣4y =0联立,可得(1+k 2)x 2+(2km ﹣4k )x +m 2﹣4m =0, 设M (x 1,y 1),N (x 2,y 2),由韦达定理可得x 1x 2=m 2−4m 1+k2,由x =y−mk代入圆x 2+y 2﹣4y =0,可得(1+k 2)y 2﹣(2m +4k 2)y +m 2=0,由韦达定理可得y1y2=m21+k2,由k OM•k ON=﹣3,可得y1y2x1x2=m2m2−4m=−3,解得m=3,即有直线l的方程为y=kx+3,则直线l恒过定点(0,3).22.(12分)如图,在斜三棱柱ABC﹣A1B1C1中,△ABC是边长为2的等边三角形,M,Q分别为AC,A1B1的中点,且MQ⊥AB.(1)证明:MC1⊥AB.(2)若BB1=4,MQ=√15,求平面MB1C1与平面MC1Q夹角的余弦值.(1)证明:因为△A1B1C1是等边三角形,Q为A1B1的中点,所以C1Q⊥A1B1,又AB∥A1B1,所以C1Q⊥AB,因为MQ⊥AB,C1Q∩MQ=Q,所以AB⊥平面MC1Q,又MC1⊂平面C1MQ,所以MC1⊥AB;(2)解:取AB靠近点A的四等分点N,连接MN,NQ,易证得MN∥C1Q,则MN⊥AB,且MN=√32,由BB1=4,得QN=3√72,因为MQ=√15,所以MQ2+MN2=QN2,即MQ⊥MN,又MQ⊥AB,从而MQ⊥平面ABC,以M为坐标原点,MN所在直线为x轴,MQ所在直线为z轴,建立如图所示的空间直角坐标系,则M(0,0,0),B1(0,1,√15),C1(−√3,0,√15),则MB 1→=(0,1,√15),MC 1→=(−√3,0,√15), 设平面MB 1C 1的法向量为m →=(x ,y ,z ),则有{m →⋅MB 1→=y +√15z =0m →⋅MC 1→=−√3x +√15z =0,令z =1,得m →=(√5,−√15,1),由图可知,n →=(0,1,0)是平面MC 1Q 的一个法向量,设平面MB 1C 1与平面MC 1Q 的夹角为θ,则cosθ=|m →⋅n →||m →||n →|=√15√21=√357.。
湖北省荆州中学高二数学上学期期中考试 文【会员独享】

荆州中学2010~2011学年度上学期期 中 考 试 卷一、选择题(每小题5分,共50分)1.某企业有职工150人,其中高级职称15人,中级职称45人,一般职员90人, 现抽取30人进行分层抽样,则各职称人数分别为( )A .5,10,15B .3,9,18C .3,10,17D .5,9,162.有五条线段长度分别为1,3,5,7,9,从这5条线段中任取3条,则所取3条线段能构成一个三角形的概率为( )A .101 B .103 C .21 D .107 3.一次函数nx n m y 1+-=的图象同时经过第一、三、四象限的必要但不充分条件是( )A .1,1m n ><且B .0mn <C .0,0m n ><且D .0,0m n <<且4.在发生某公共卫生事件期间,有专业机构认为该事件在一段时间没有发生在规模群体感染的标志为“连续10天,每天新增疑似病例不超过7人”。
根据过去10天甲、乙、丙、丁四地新增疑似病例数据,一定符合该标志的是)( )A 甲地:总体均值为3,中位数为4B 乙地:总体均值为1,总体方差大于0C 丙地:中位数为2,3为众数D 丁地:总体均值为2,总体方差为35.过点(0,4)的直线与双曲线221412x y -=的右支交于A ,B 两点,则直线AB 的斜率k 的取值范围是( )A .)7,3(B . )3,7(--C )(,+∞-∞UD .(U6.统计某校1000名学生的数学水平测试成绩,得到样本频率分布直方图如图所示,若满分为100分,规定不低于60分为及格,则及格率是( ) A .20% B .25% C .6%D .80%7.抛物线22x y =上两点),(11y x A 、),(22y x B 关于直线m x y +=对称,且2121-=⋅x x ,则m 等于( )A .23 B .2 C .25D .3 8.“0m n >>”是“方程221mx ny +=”表示焦点在y 轴上的椭圆”的 ( )A.充分而不必要条件B.必要而不充分条件C.充要条件D.既不充分也不必要条件9.已知方程0,,0(022>≠≠=++=+c b a ab c by ax ab by ax 其中和,它们所表示的曲线可能是( )A. B. C. D.10.点P 在直线:1l y x =-上,若存在过P 的直线交抛物线2y x =于,A B 两点,且|||PA AB =,则称点P 为“点”,那么下列结论中正确的是( ) A .直线l 上的所有点都是“点” B .直线l 上仅有有限个点是“点”C .直线l 上的所有点都不是“点”D .直线l 上有无穷多个点(点不是所有的点)是“点”二、填空题(每小题5分,共25分)11.点A 为周长等于3的圆周上的一个定点,若在该圆周上随机取一点B ,则劣弧AB 的长度小于1的概率为 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
荆州中学2009~2010学年度上学期期 中 试 卷(文科)年级:高二 科目:数学 命题人:马玮 审题人:徐法章一、选择题:本大题10小题,每小题5分,共50分,在每小题给出的四个选项中,只有一项是符合题目要求的。
1、对于实数,,,c b a 下列命题正确的是( )A 、若b a >,则22bc ac >B 、若,0<<b a 则22b ab a >>C 、若0<<b a ,则ba 11< D 、若0<<b a ,则ba ab >2、直线03=-y x 的倾斜角为( )A 、3πB 、6πC 、32π D 、65π3、若直线0=++C By Ax 在第一、二、三象限,则( ) A、0,0>>BC AB B、0,0<>BC AB C、0,0><BC AB D 、0,0<<BC AB4、若不等式6|2|<+ax 的解集为(-1,2),则实数a 等于( )A 、8B 、2C 、-4D 、-85、已知直线的倾斜角为θ,且54sin =θ,则此直线的斜率是( )A、34 B 、34-C 、±43 D 、±346、平面内有两定点B A ,,且4=AB ,动点P 4=+,则点P 的轨迹是( )A 、线段B 、直线C 、圆D 、以上都不对7、两个圆0222:221=-+++y x y x C 与0124:222=+--+y x y x C 的公切线有且仅有( )A 、1条B 、2条C 、3条D 、4条8、过点⎪⎪⎭⎫⎝⎛33,1且与直线03=-y x 所成角为060的直线方程为( )A 、023=-+y xB 、023=++y xC 、1=xD 、023=-+y x 或1=x9、当y x 、满足条件1<+y x 时,变量3-=y x u 的取值范围是( )A 、⎥⎦⎤⎢⎣⎡-31,31 B 、⎪⎭⎫ ⎝⎛-31,31 C 、()3,3- D 、⎪⎭⎫⎝⎛⋃⎪⎭⎫ ⎝⎛-31,00,31二、填空题:本大题共5小题,每小题5分,共25分,把答案填在答题卡的相应位置。
11、若直线l 经过()4,3P 且在坐标轴上的截距相等,则直线l 的方程为________________。
12、若直线062:1=++y ax L 与直线()011:22=-+-+a y a x L ,则21//L L 时,=a _____________。
13、已知圆012422=++++y x y x 上任意点关于直线()0,001>>=++n m ny mx 的对称点均在圆上,则nm11+的最小值是__________________。
14、若方程m x x +=-21有解,则实数m 的取值范围是_____________________。
15、由实数,x y 满足不等式组2132y x y kx k ≤⎧⎪≥⎨⎪≥-+⎩所确定的可行域内,若目标函数z x y =-+仅在点(3,2)取得最小值,则正实数k 的取值范围是 。
三.解答题:本大题共6小题,共75分。
解答应写出文字说明、证明过程或演算步骤。
16、(本小题12分)解关于x的不等式:()()1221≥>--axxa17、(本小题12分)在等腰直角ABC∆中,090=∠C,一条直角边BC所在的直线方程为0532=++yx,点A坐标为()2,2,求直线BCAC、的方程。
18、(本小题12分)已知圆过两点()(),3,11,3-BA、且它的圆心在直线023=--yx上,求此圆的方程。
19、(本小题12分)某研究所计划利用“神七”宇宙飞船进行新产品搭载实验,计划搭载新产品A、B,该所要根据该产品的研制成本、产品重量、搭载实验费用、和预计产生收益来决定具体安排.通过调查,有关数据如下表:20、(本小题13分)已知圆084422=-++-+k y x y x 关于直线02=--y x 对称的圆是圆C ,且圆C 与直线04043=-+y x 相切,求实数k 的值。
21、(本小题14分)过点()0,3M 作直线l 与圆2522=+y x 交于B A 、两点, (1)若点P 是线段AB 的中点,求点P 的轨迹方程。
(2)求直线l 的倾斜角为何值时AOB ∆的面积最大,并求这个最大值。
荆州中学2009~2010学年度上学期期中卷参 考 答 案年级:高二 科目:数学(文科) 命题人:马玮 审题人:徐法章一、选择题:(本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的).二、填空题:(本大题共5小题,每小题5分,共25分)11. 43y x =或7y x =-+ 12. 1- 13.3+14.[- 15.(0,1)三、解答题:(本大题共6小题,共75分,解答应写出文字说明、证明过程或演算步骤.) 16.(本题12分)解:不等式可化为(2)(4)02a x a x --->- ………………………2分① 当12a ≤<时,原不等式等价于4()(2)02a x x a ---<-12a ≤< ∴422a a ->- 解得 422a x a -<<- …………4分②当2a =时,原不等式等价于202x >- 解得 2x > …………6分③当2a >时原不等式等价于()0224>-⎪⎭⎫⎝⎛---x a a x 2a > 422a a -∴<- 解得42a x a -<- 或2x >. …………10分综上可知:当12a ≤<时,解集为422a x x a -⎧⎫<<⎨⎬-⎩⎭当2a =时,解集为{}2x x >; 当2a >时,解集为4{2a x x a -<- 或2}x > ………………12分17.(本题12分)解:由题意知23B C k =-A CBC ⊥32A C k ∴=又(2,2)A∴直线A C 的方程为32(2)2y x -=-即312y x =- ……………4分设直线A B 的斜率为k 045CAB ∠=tan 4511AC ACk k k k -∴==+⋅ 即321312k k -=+解得5k =- 或 15k = ……………6分当5k =-时,直线:25(2)AB y x -=-- 即 512y x =-+当15k =时,直线1:2(2)5A B y x -=-- 即 1855y x =+……………10分综上知:直线A C 的方程为:312y x =-直线A B 的方程为:512y x =-+ 或 1855y x =+……………12分18.(本题12分)解:由题意知:圆心即为线段A B 的中垂线和直线320x y --= 交点A B 、的中点311(1,2),132A B M k -==---∴线段A B 的中垂线为:22(1)y x -=- 即2y x = ………………6分 由2320y x x y =⎧⎨--=⎩ 解得 24x y =⎧⎨=⎩即圆心(2,4)O O A γ===∴圆的方程为22(2)(4)10x y -+-=19.(本题12分)由图象得,当直线经过M 点时能z 取得最大值,⎩⎨⎧2x +3y =30,2x +y =22, 解得⎩⎨⎧x =9,y =4,即(9,4)M , 所以z =80×9+60×4=960(万元)答:应供应产品A 9件,产品B 4件,可使得利润最多达到960万元. 20.(本题12分)解:由题意知:22(2)(2)x y k -++=,若圆心(2,2)-关于直线20x y --=对称的点C 为(,)C a b 则212222022b a a b +⎧=-⎪⎪-⎨+-⎪--=⎪⎩ 解得 00a b =⎧⎨=⎩ …………6分∴圆C 为:22x y k +=又圆C 与直线34400x y +-=相切∴=60k = ……………………12分21.(本题12分)解:①P 是A B 中点O P A B ∴⊥,取O M 中点G ,则在R t O M P ∆中必有13.22G P O M ==P ∴点的轨迹为以G 为圆心32为半径的圆,令(,)P x y 则2239()24x y -+=即2230x x y -+=经检验知:A B 为x 轴及AB y 轴均满足上式P ∴点的轨迹为2230x x y -+= ……………………………6分②令OP h =,由题意知03h <≤ 在R t A P O ∆中AP =即AB =113)22A B O S A B O P h h ∆=⋅=⨯=<≤=(03)h <≤令2t h = 则 09t <≤易知ABO S ∆=在 09t <≤时单调递增∴当9=t 即直线A B 垂直x 轴时m ax 12ABO S ∆=,此时l 的倾斜角为090。
