特殊角的三角函数值讲义
初中数学《特殊角的三角函数值》试讲逐字稿(附教案)

《特殊角的三角函数值》试讲逐字稿(附教案)简案一、教学目标【知识与技能目标】学生能够掌握锐角三角形函数值及其计算方法,并能熟练运用。
【过程与方法目标】通过自主探究、合作交流的过程,培养数感,提升推理运算能力。
【情感态度与价值观目标】体会数学的乐趣,培养学习数学的趣味。
二、教学重难点【教学重点】学生能够掌握锐角三角形函数值及其计算方法,并能熟练运用。
【教学难点】运用锐角三角函数进行计算。
三、教学方法讲授法,讨论法,练习法四、教学过程(一)复习导入引导回忆锐角三角函数的定义,以及锐角三角函数它们的正弦余弦和正切的求法,学生回答,引入新课。
(二)新课讲授1.动手操作,解决问题拿出事先发给学生的三角尺,学生测量出三角尺的角度,确定三个特殊角30°、45°、60°2.小组合作,探究新知教师组织学生小组讨论,推导出30度,45度和60 度角的三角函数值,并且填写任务单,提示学生设最短的边为1。
小组汇报,详细讲解其中一个角预设一:学生设最短的边为1预设二:学生设最短边位a最后总结角度规律,从左到右加15°;45 度角的三角函数;30°、60°三角函数值之间的关系。
3.灵活运用,例题讲解出示例题,让学生计算,多媒体出示答案,同桌之间互相纠正。
(三)巩固总结求适合下列条件的锐角的度数(1)tan B=√33(2)2sin a-√2= 0(四)课堂小结教师引导学生对本节课所学知识进行小结,学生畅谈本节课的收获,教师给予点评和补充。
(五)布置作业作业1:完成剩余课后练习题;作业2:学有余力的同学预习下节课的知识《特殊的三角函数值》试讲逐字稿各位老师上午好,我试讲的题目是《特殊的三角函数值》,下面开始我的试讲。
上课,同学们好,请坐一、导入上课前老师来考考大家,之前我们学习了锐角三角函数的定义,有同学知道锐角三角函数它们的正弦余弦和正切分别是怎样求的呢?课代表你来说,课代表说的非常正确,他说在直角三角形ABC中<c=90度,那么<A,它对应的正弦sinA就是,对边比上斜边,cosA等于邻边比上斜边,tanA等于对边比上邻边。
锐角三角函数的计算-特殊角的三角函数值(知识讲解)-2022-2023学年九年级数学下册基础知识讲练
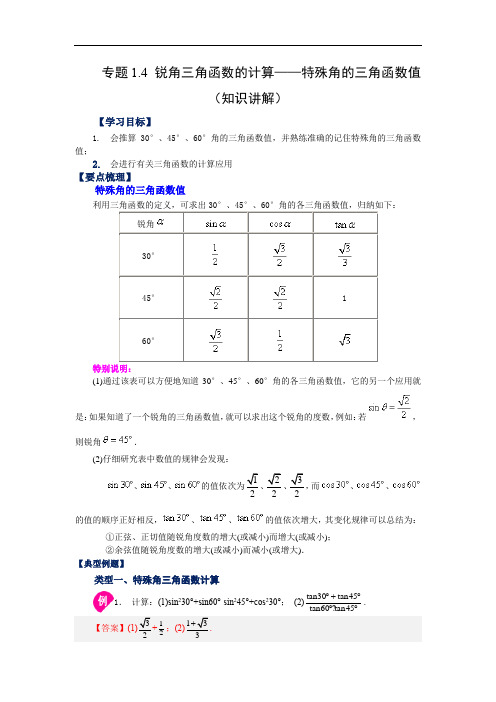
专题1.4 锐角三角函数的计算——特殊角的三角函数值(知识讲解)【学习目标】1.会推算30°、45°、60°角的三角函数值,并熟练准确的记住特殊角的三角函数值;2.会进行有关三角函数的计算应用【要点梳理】特殊角的三角函数值锐角30°45° 160°特别说明:(1)通过该表可以方便地知道30°、45°、60°角的各三角函数值,它的另一个应用就是:如果知道了一个锐角的三角函数值,就可以求出这个锐角的度数,例如:若,则锐角.(2)仔细研究表中数值的规律会发现:、、的值依次为12、22、32,而、、的值的顺序正好相反,、、的值依次增大,其变化规律可以总结为:①正弦、正切值随锐角度数的增大(或减小)而增大(或减小);②余弦值随锐角度数的增大(或减小)而减小(或增大).【典型例题】类型一、特殊角三角函数计算1.计算:(1)sin230°+sin60°-sin245°+cos230°;(2)tan30tan45 tan60?tan45︒+︒︒︒.【答案】(1)32+12;(2)133+.【分析】(1)将特殊角的三角函数值代入求解;(2)将特殊角的三角函数值代入求解.特殊值:sin 30° =12;sin 60° = 32;sin 45° = 22;cos 30° = 32;tan 60° = 3;tan 45° = 1解:(1)原式=1342+-12+34=32 + 12; 3133?1+(2)原式= =133+. 【点拨】本题考查了特殊角的三角函数值,解答本题的关键是掌握几个特殊角的三角函数值.举一反三:【变式1】计算:222sin 60cos 60︒︒︒︒-﹣sin45°•tan45° 【答案】3232+ 【分析】把特殊角的三角函数值代入计算即可.解:222sin 60cos 60tan 604cos 45︒︒︒︒--﹣sin45°•tan45° ()22312222122342⎛⎫⨯- ⎪⎝⎭=-⨯-⨯ 122322=-- 23222=+-=3232+. 【点拨】本题考查了特殊角的三角函数值及分母有理化、二次根式的化简,牢记特殊角的三角函数值,是解决本题的关键.【变式2】计算:2cos45°﹣tan60°+sin30°﹣12tan45°【答案】2-3【分析】将各特殊角的三角函数值代入即可得出答案.解:原式=2×22﹣3+12﹣12×1 =2-3【点拨】此题考查特殊角的三角函数值,属于基础题,熟练记忆一些特殊角的三角函数值是关键.类型二、特殊角三角函数计算2.计算:()2012sin 451220202π-︒⎛⎫----+- ⎪⎝⎭ 【答案】-2【分析】直接利用特殊角的三角函数值、绝对值的性质、零指数幂的性质、负整数指数幂的性质分别代入化简即可.解:原式=24121-+-+=-2【点拨】此题主要考查了实数运算,正确化简各数是解题关键.举一反三:【变式1】计算:0113tan 30(2014π)32()3-︒---. 【答案】-2试题分析:分别计算033tan3033=⨯,(2014-π)0=1,32-=2﹣11333-⎛⎫= ⎪⎝⎭,,再用实数的混合运算法则计算.解:原式=3×33﹣1+2﹣3﹣3=﹣2. 【变式2】计算:()()2(31)3tan3052522sin60+--++. 【答案】3试题分析:用完全平方公式、平方差公式去括号,计算出特殊角三角函数值,再进行乘法运算,最后进行加减运算即可.解:(3-1)2+3tan 30°-(5-2)( 5+2)+2sin 60°=4-23+3×33-(5-4)+2×32=4-23+3-1+3=3.【点拨】掌握二次根式的加减乘除运算法则.类型三、三角函数计算3. 已知A ∠为锐角,且24sin 30A -=,则A ∠=______. 【答案】60︒【分析】计算,并结合A ∠是个锐角,即可求解.解:∵24sin 30A -=,∵23sin 4A =, ∵3sin 2A =±, ∵A ∠为锐角,∵3sin 2A =, ∵60A ∠=︒故答案是:60°【点拨】本题主要考察计算和锐角三角函数与角度关系,属于基础的计算题,难度不大.解题的关键是结合角度范围确定三角函数值范围.举一反三:【变式1】已知矩形ABCD 的周长为()232cm ,对角线2cm AC =,求BAC ∠与DAC ∠的度数. 【答案】30BAC ∠=︒,60=︒∠DAC 或60BAC ∠=︒,30DAC ∠=︒.【分析】设AB=x,将BC 表示出来,再利用勾股定理可求出x=1或x=3,再利用三角函数求出一个角为30°,另一个角为60°.解:∵矩形ABCD 的周长为232+,∵AB+BC= 3+1,∵对角线AC=2,∵设AB=x,则BC=3+1-x,∵AB 2+BA 2=AC 2,∵x 2+(3+1-x)2=22,解得:x 1=1,x 2=3,∵当AB=1,则BC=3,∵tan∵BAC=3,∵∵BAC=60°,∵DAC=30°,当AB=3,则BC=1,∵tan∵BAC= 33, ∵∵BAC=30°,∵DAC=60°,故30BAC ∠=︒,60=︒∠DAC 或60BAC ∠=︒,30DAC ∠=︒. 【点拨】此题主要考查了勾股定理和特殊角的三角函数值,解答本题的关键是掌握特殊角的三角函数值.【变式2】计算(1)23602cos 30tan 45︒-︒+︒(2)已知α是锐角,且()1sin 152α-︒=84cos α的值. 【答案】(1)1 (2)0【分析】(1)把特殊角的三角函数值代入代数式进行计算即可;(2)先利用锐角的正弦求解α的大小,再代入代数式进行计算即可.(1)解:23sin 602cos 30tan 45︒-︒+︒ 23332122331122(2) α是锐角,且()1sin 152α-︒=,1530,=45,∴ 84cos α-2224222220=-=【点拨】本题考查的是特殊角的三角函数值的混合运算,已知三角函数值求解锐角的大小,熟记特殊角的三角函数值是解本题的关键.类型四、三角函数计算4.(1)计算:21122cos453-⎛⎫--︒+-⎪⎝⎭.(2)如图,在△ABC中,∵ACB=90°,角平分线AE与高CD交于点F,求证:CE=CF.【答案】(1)8;(2)见分析【分析】(1)计算绝对值、特殊角的三角函数值、负整数指数幂,再合并即可;(2)根据直角三角形两锐角互余求得∵B=∵ACD,然后根据三角形外角的性质求得∵CEF=∵CFE,根据等角对等边求得CE=CF.(1)解:21 122cos453-⎛⎫--︒+-⎪⎝⎭221292=--⨯+2129=--+=8;(2)证明:∵在△ABC中,∵ACB=90°,∵∵B+∵BAC=90°,∵CD是AB边上的高,∵∵ACD+∵BAC=90°,∵∵B=∵ACD,∵AE是∵BAC的角平分线,∵∵BAE=∵EAC,∵∵B +∵BAE =∵ACD +∵EAC ,即∵CEF =∵CFE ,∵CE =CF .【点拨】本题考查了特殊角的三角函数值,负整数指数幂,直角三角形的性质,三角形外角的性质,等腰三角形的判定等,熟练掌握性质定理是解题的关键.举一反三:【变式1】如图,将∵ABC 沿射线AB 平移4cm 后能与∵BDE 完全重合,连接CE 、CD 交BE 于点O ,OB =OC .(1)求证:四边形CBDE 为矩形;(2)若S △BOC 432,求∵ACD 的度数. 【答案】(1)见分析(2)120°【分析】(1)由平移的性质及ASA判定定理可证得OCE ODB ≌,根据全等三角形的性质即可求证结论.(2)根据矩形的性质及面积公式即可求得BC ,进而可利用特殊三角函数值可求得60BCD ∠=︒,根据垂直平分线的性质即可求解.(1)证明:由题意可知:△BDE 由△ABC 平移后得到,∵//BC DE ,且BC DE =,∵四边形CBDE 是平行四边形,∵//CE BD ,且CE BD =,∵ECD CDB ∠=∠,CEB EBD ∠=∠,在OCE 和ODB △中 ECD CDB CE BDCEB EBD ∠=∠⎧⎪=⎨⎪∠=∠⎩, ∵ ()OCE ODB ASA ≌∵OC OD =,OB OE =,又∵OB OC =,∵CD BE =,∵ 平行四边形CBDE 为矩形.(2)由(1)可知四边形CBDE 为矩形,∵90CBD ∠=︒,且4BD =cm ,在OBC 中过点O 作BC 的垂线,垂足为F ,则2OF =,∵143223BOC S BC =⨯⨯=,∵433BC =cm , ∵在Rt CBD △,43433BD tan BCD CB ∠===,∵60BCD ∠=︒,又∵在△ACD 中,BC 是AD 的垂直平分线,∵60ACB BCD ∠=∠=︒,∵120ACD ∠=︒,∴∵ACD 的度数为120︒.【点拨】本题考查了平移的性质、全等三角形的判定及性质、矩形的判定及性质、特殊三角函数值求角度,熟练掌握相关性质及判定定理是解题的关键.【变式2】将矩形ABCD 对折,使AD 与BC 重合,得到折痕EF ,展开后再一次折叠,使点A 落在EF 上的点A '处,并使得折痕经过点B ,得到折痕BG ,连接AA ',如图1,问题解决:(1)试判断图1中ABA '△是什么特殊的三角形?并说明理由;(2)如图2,在图1的基础上,AA '与BG 相交于点N ,点P 是BN 的中点,连接AP 并延长交BA '于点Q ,求BQ BA '的值.【答案】(1)ABA '△是等边三角形,理由见分析(2)13BQ BA =' 【分析】(1)等边三角形,解法一利用垂直平分线性质得出AA ′=BA ′,利用折叠得出BA BA '=即可,解法二:根据折叠得出12BE BA =,BA BA '=,90A EB '∠=︒然后利用锐角三角函数定义得出1cos 2BE A BE BA '∠==' ,求出60A BE '∠=︒即可; (2)解法一:过点N 作NH A B '∥交AP 于H ,先证PHN PQB ≌△△(AAS ),再证AHN AQA '∽△△,得出12BQ QA =' 即可 解法二:由折叠可知A N AN '=,由点P 是BN 的中点 ,得出BP PN =,利用平行线等分性质得出1A M A N QM AN ''==,1BQ BP QM PN ==,证出BQ QM A M '==即可.(1)解:ABA '△是等边三角形.解法一:理由是:由折叠可知EF 垂直平分AB ;∵AA ′=BA ′,∵∵ABG 折叠得△A ′BG ,∵BA BA '=,∵AA BA BA ''==;∵ABA '△是等边三角形;解法二:理由是:由折叠可知12BE BA =,BA BA '=,90A EB '∠=︒, ∵1cos 2BE A BE BA '∠==' , ∵60A BE '∠=︒,∵ABA '△是等边三角形;(2)解法一:过点N 作NH A B '∥交AP 于H ,∵HNP QBP ∠=∠,NHP BOP ∠=∠, 又∵点P 是BN 的中点 , ∵BP NP =,在△PHN 和△PQB 中, HNP QBP NHP BQP PN PB ∠=∠⎧⎪∠=∠⎨⎪=⎩, ∵PHN PQB ≌△△(AAS ), ∵HN BQ =,又∵NH A B '∥,∵ANH AA Q '∠=∠,AHN AQA '∠=∠, ∵AHN AQA '∽△△, 由折叠可知12A N AN AA ''==, ∵12HN AN QA AA =='' , ∵12BQ QA =', ∵13BQ BA ='; 解法二:由折叠可知A N AN '=, 又∵点P 是BN 的中点 , ∵BP PN =,过点N 作NM AQ ∥交BA '于M , ∵1A M A N QM AN''==,1BQ BP QM PN ==, ∵BQ QM A M '==, ∵13BQ BA ='.【点拨】本题考查一题多解,等边三角形的判定,折叠性质,线段垂直平分线性质,平行线等分线段定理,三角形相似判定与性质,锐角三角函数值求角,掌握一题多解,等边三角形的判定,折叠性质,线段垂直平分线性质,平行线等分线段定理,三角形相似判定与性质是解题关键.。
人教版九年级数学课件《特殊角的三角函数值》

第二十八章第1节
特殊角的三角函数值
PEOPLE
EDUCATION
学校:XXXX
VERSION
OF
THE
老师:XXXX
NINTH
GRADE
MATH
VOLUME
学习目标
人教版数学九年级下册
1.运用三角函数的知识,自主探索,推导出30°、45°、60°角的三角函数
值.(重点)
2.熟记三个特殊锐角的三角函数值,并能准确地加以运用.(难点)
1
A.
2
B.
3
2
C.
3
3
3.在△ABC中,若cosA=
A.锐角三角形
D. 3
2
,tanB=
2
B.直角三角形
3,则这个三角形一定是( A)
C.钝角三角形
D.等腰三角形
人教版数学九年级下册
达标检测
4.在△ABC中,若 sinA −
1
2
1 2
+(cosB- ) =0,则∠C为(
2
D)
A.30° B.45° C.60° D.90°
BC
7
∴ ∠B=60°
∴ ∠A=90°-∠B=30°
人教版数学九年级下册
人教版数学九年级下册
人教版数学九年级下册
针对练习
已知△ABC中的∠A与∠B满足(1-tanA)2 +|sinB-
试判断△ABC的形状.
3
解:∵
|sinB-
|=0,
2
3
∴ tanA=1,sinB= ,
2
(1-tanA)2 +
∴sin2A+cos2A=
三角函数特殊角

三角函数特殊角引言在学习三角函数的过程中,我们经常会遇到一些特殊角。
这些特殊角具有一些特殊的性质和计算方法,对于求解三角函数的值以及解题起到了重要作用。
本文将介绍三角函数的特殊角,包括零度角、30度角、45度角、60度角和90度角,以及它们的性质与计算方法。
一、零度角(0°)零度角是最简单的特殊角之一,即角度为0°。
在三角函数中,零度角的正弦、余弦、正切和余切的值具有特殊的计算方法和性质:•正弦值(sin):零度角的正弦值为0,即sin(0°) = 0;•余弦值(cos):零度角的余弦值为1,即cos(0°) = 1;•正切值(tan):由于正切是正弦与余弦的比值,因此零度角的正切值为0,即tan(0°) = 0;•余切值(cot):由于余切是余弦与正弦的比值,零度角的余切值不存在。
二、三十度角(30°)三十度角是一个重要的特殊角,它的角度为30°。
在三角函数中,三十度角的正弦、余弦、正切和余切的值也具有特殊的计算方法和性质:•余弦值(cos):三十度角的余弦值为√3/2,即c os(30°) = √3/2;•正切值(tan):三十度角的正切值为√3/3,即tan(30°) = √3/3;•余切值(cot):三十度角的余切值为√3,即cot(30°) = √3。
三十度角在三角函数中的值是非常常见且重要的,它在几何图形的计算、物理学等领域中都有广泛的应用。
三、四十五度角(45°)四十五度角也是一个特殊角,它的角度为45°。
在三角函数中,四十五度角的正弦、余弦、正切和余切的值同样具有特殊的计算方法和性质:•正弦值(sin):四十五度角的正弦值为√2/2,即sin(45°) = √2/2;•余弦值(cos):四十五度角的余弦值为√2/2,即cos(45°) = √2/2;•正切值(tan):四十五度角的正切值为1,即tan(45°) = 1;•余切值(cot):四十五度角的余切值为1,即cot(45°) = 1。
初中数学知识点三角函数特殊三角函数值

初中数学知识点三角函数特殊三角函数值特殊三角函数值是指在特定角度下三角函数的值。
这些特殊角度是常见的,学好特殊三角函数值可以帮助我们更好地理解三角函数的性质和应用。
在初中数学中,最常见的特殊三角函数值包括:1.0度、30度、45度、60度和90度角的正弦、余弦和正切值。
0度角的正弦值为0,余弦和正切值均为1、这是因为三角函数中的正弦函数在0度时取最小值,余弦和正切函数在0度时取最大值。
30度角的正弦值为1/2,余弦值为√3/2,正切值为√3/3、在30度角下,正弦值表示对边与斜边的比值,余弦值表示邻边与斜边的比值,正切值表示对边与邻边的比值。
45度角的正弦值为1/√2,余弦值为1/√2,正切值为1、在45度角下,正弦和余弦值相等,均表示对边和斜边的比值,正切值表示对边和邻边的比值。
60度角的正弦值为√3/2,余弦值为1/2,正切值为√3、在60度角下,正弦值表示对边和斜边的比值,余弦值表示邻边和斜边的比值,正切值表示对边和邻边的比值。
90度角的正弦值为1,余弦值为0,正切值为无穷大(不存在)。
在90度角下,正弦函数的值最大为1,余弦值最小为0,正切函数不存在。
2.180度、270度和360度角的正弦、余弦和正切值。
由于三角函数是周期性函数,同一角度模360度之后,三角函数的值又会重复出现。
因此,180度角和0度角的三角函数值相同,270度角和90度角的三角函数值相同,360度角和0度角的三角函数值相同。
180度角的正弦和余弦值均为0,正切值不存在。
270度角的正弦值为-1,余弦值为0,正切值不存在。
360度角的正弦和余弦值均为0,正切值不存在。
通过掌握这些特殊三角函数值,我们可以在计算中更方便地使用三角函数,加深对三角函数的理解和应用。
需要注意的是,在初中数学中,一般使用这些特殊三角函数值进行计算,而不会涉及到更高阶的三角函数值。
掌握这些特殊三角函数值的计算方法,是学好数学和物理的基础。
进一步深入研究三角函数和其他特殊三角函数值的计算方法,是高中及以上学习中的内容。
九年级数学PPT特殊角的三角函数值课件

2 1
2
tan 300 3 3
cot 300 3
tan 600 3
cot 600 3 3
300
2
3
1
如图,求
角的四个
sin 450 4三520 角函数值,
2
cos 450 2450 2
450
tan 450 1
2
1
cot 450 1
1
请记住:
30的0 三450角6函00 数值
22
2 6 2
6
6 cot2 600 tan 600
4.
3 tan 300
6 ( 3 )2 3
解:原式
3
(2 3) 3 3 3
3
3 3
2 33 3
2 3 3
练习:计算
1.sin 30 cos2 45 0
3
2.2cos45 2 3
2.在ABC中,A 300, tan B 3, BC 2 3
则AB ________ .
如图,在△ABC中,∠C=90°,
AC=8cm,AB的垂直平分线MN交AC
于D,连结BD,若cos∠BDC=3 ,
求BC的长
5
B
N
5x 4x
C
3x
M
D
5x
A
如图,△ABC中,AB=AC,∠A =30度,AC的垂直平分线分别交
3 3 22
0
例:计算下列各值:
2.sin2 60 cos2 60
解:原式 ( 3 )2 ( 1 )2 22
3 1 sin 2 600 (sin 600)2
44
1
特殊角的三角函数值

28.1.3 特殊角的三角函数值教学目标1.知识与技能(1)通过实例认识直角三角形的边角关系,即锐角三角函数(sinA,cosA,tanA),知道30°,45°,60°角的三角函数值.(2)记住30°,45°,60°锐角的三角函数值,从而达到知道特殊角能求三角函数和知道特殊三角函数值来求锐角的效果。
(3)运用特殊角三角函数值解决直角三角形有关的简单的实际问题.(4)能综合运用直角三角形的勾股定理与边角关系解决简单的实际问题.2.过程与方法经历探索30°,45°,60°角的三角函数值的过程,发展学生观察、分析,•解决问题的能力.贯彻在实践活动中发现问题,提出问题,再探究问题的过程中找出规律。
3.情感、态度与价值观通过用30°,45°,60°角的特殊三角函数值的应用过程,发展学生观察、分析,•解决问题的能力.培养学生数形结合的思想.重点与难点1.重点运用三角函数的知识,自主探索,推导出30°、45°、60°角的三角函数值.2.难点熟记三个特殊锐角的三角函数值,并能准确地加以运用.复习引入如图在Rt △ABC 中,∠C=900AB BCA sinA =∠=斜边的对边AB ACA cosA =∠=斜边的邻边ACBCA A tanA =∠∠=的邻边的对边1. 对于sin α与tan α,角度越大,函数值越 ; 对于cos α,角度越大,函数值越 .2. 互余的两角之间的三角函数关系:若∠A+∠B=90°,则sinA cosB ,cosA sinB , tanA · tanB = .在学生回答了这个问题后,教师再复述一遍,提出新问题:两块三角尺中有几个不同的锐角?是多少度?分别求出这几个锐角的正弦值、余弦值和正切值.提醒学生:在300,600,900为角三角板时可以设300角所对的边长为a ,•利用勾股定理和三角函数的定义可以求出这些三角函数值.在450,450,900为角三角板时可以设450角所对的边长为a ,•利用勾股定理和三角函数的定义可以求出这些三角函数值. 探究新知(一)特殊值的三角函数学生在求完这些角的正弦值、余弦值和正切值后教师加以总结. 30°、45°、60°的正弦值、余弦值和正切值如下表:∠A的邻边b∠A的对边a 斜边c CBA通过上表,让学生观察上表中数字变化的规律并加以总结:对于正弦值,分母都是22,.对于正切,60•,即是下一个角的正切值. 要求学生记住上述特殊角的三角函数值.教师强调:(sin60°)2用sin 260°表示,即为(sin60°)·(sin60°). (二)特殊角三角函数的应用1.师生共同完成课本第114页(盲文课本第314页)例3:求下列各式的值.(1)cos 260°+sin 260°. (2)cos 45sin 45︒︒-tan45°.教师以提问方式一步一步解上面两题.学生回答,教师板书.解:(1)cos 260°+sin 260°=(12)2+(2)2=1(2)cos 45sin 45︒︒-tan45°=2÷2-1=0巩固练习 一、选择题.1.已知:Rt △ABC 中,∠C=90°,∠A=600,则sinA 是( ).A .21 B .22 C .23D .1 2.已知:Rt △ABC 中,∠C=90°,tanB=33,则∠A 是( ). A .300 B .450 C .600 D .900二、计算:(1) sin30°+ cos45°; (2) sin 230°+ cos 230°-tan45° 解:原式 =2212221+=+解:原式 =01232122=-+)()(2.师生共同完成课本第115页(盲文课本第315页)例4:教师解答题意:(1)如课本图28.1-9(1),在Rt △ABC 中,∠C=90,AB=6,BC=3,求∠A 的度数.(2)如课本图28.1-9(2),已知圆锥的高AO 等于圆锥的底面半径OB 的3倍,求a .教师分析解题方法:要求一个直角三角形中一个锐角的度数,可以先求它的某一个三角函数的值,如果这个值是一个特殊解,那么我们就可以求出这个角的度数.解:(1)在课本图28.1-9(1)中,∵sinA=BC AB =, ∴∠A=45°.(2)在课本图28.1-9(2)中,∵tana=AO OB OB=∴a=60°. 当堂练习1.tan α=1,锐角 α 的度数应是 ( )A .40°B .30°C .20°D .10°2. 已知sinA =21,则下列正确的是 ( )A. cosA =22B. cosA =23C. tanA = 1D. tanA =33. tan (α+10°),锐角 α 的度数应是 ( ) A .60° B .50° C .40° D .30° . 4. 求下列各式的值:(1) 1-2 sin30°cos30°;(2) 3tan30°-tan45°+2sin60°;课时总结 学生要牢记下表:对于sina 与tana,角度越大函数值也越大;对于cosa ,角度越大函数值越小. 拓展延伸1. 已知:| tanB -| + (2 sinA - )2 =0, 求∠A ,∠B 的度数.解:∵ | tanB - | + (2 sinA - )2 =0, ∴ tanB - =0 ,2 sinA =0, ∴ tanB = ,sinA=2∴ ∠B =60°,∠A =60°.2.已知 △ABC 中的 ∠A 与 ∠B满足 (1-tanA)2 +|sinB - 2|=0,试判断 △ABC 的形状.解:∵ (1-tanA)2 + | sinB -2|=0, ∴ 1-tanA=0 , sinB - =0 ∴ tanA =1,sinB ∴ ∠A =45°,∠B =60°, ∠C =180°-45°-60°=75°,∴ △ABC 是锐角三角形. 课堂小结特殊角的三角函数值⎪⎩⎪⎨⎧三角函数值角函数通角的三角函数值60、45、30000过作业设计 课本练习做课本第114页习题28.1复习巩固第3题. 1.下列各式中不正确的是( ).A .sin 260°+cos 260°=1B .sin30°+cos30°=1C .sin35°=cos55°D .tan45°>sin45° 2.计算2sin30°-2cos60°+tan45°的结果是( ). A .2 BCD .1 3.已知∠A 为锐角,且cosA ≤12,那么( ) A .0°<∠A ≤60° B .60°≤∠A<90° C .0°<∠A ≤30° D .30°≤∠A<90° 4.在△ABC 中,∠A 、∠B 都是锐角,且sinA=12,ABC 的形状是( )A .直角三角形B .钝角三角形C .锐角三角形D .不能确定5.如图Rt △ABC 中,∠ACB=90°,CD ⊥AB 于D ,BC=3,AC=4,设∠BCD=a ,则tana•的值为( ).A .34 B .43 C .35 D .456.当锐角a>60°时,cosa 的值( ). A .小于12 B .大于12CD .大于17.在△ABC 中,三边之比为a :b :c=1:2,则sinA+tanA 等于( ).A1.2B C D + 8.sin 272°+sin 218°的值是( ). A .1 B .0 C .12D9)2+││=0,则△ABC ( ). A .是直角三角形 B .是等边三角形C .是含有60°的任意三角形D .是顶角为钝角的等腰三角形 二、填空题.10.设α、β均为锐角,且sin α-cos β=0,则α+β=_______. 11.cos 45sin 301cos 60tan 452︒-︒︒+︒的值是_______.12.已知,等腰△ABC•的腰长为,•底为30•°,•则底边上的高为______,•周长为______.13.在Rt △ABC 中,∠C=90°,已知cosA=________. 三、解答题.14.求下列各式的值.(1)sin30°·cos45°+cos60°;(2)2sin60°-2cos30°·sin45°(3)2cos602sin 302︒︒-; (4)sin 45cos3032cos 60︒+︒-︒-sin60°(1-sin30°).(5)tan45°·sin60°-4sin30°·cos45°·tan30°(6)sin 45tan 30tan 60︒︒-︒+cos45°·cos30°15.若方程2x 2+(4sin θ)x+1=0(0<θ<90°)有两个相等的实数根,求θ的值.班主任经验介绍班主任是份繁琐的工作,我于2008年参加教师工作以来,一直在乡镇学校任教并且一直当班主任,整整十二年了,在这十二年里我想我付出了很多也得到了很多,谈谈以下几点:1.首先,作为班主任要明确自己的身份和责任,以自身来讲,要不断的学习,提高自身的业务水平,特别是勤于参加各种培训学习,如国培,外出跟班学习,参加名校,名师的学习,理论知识的学习等。
特殊角的三角函数值表ppt课件
1
0 不存在
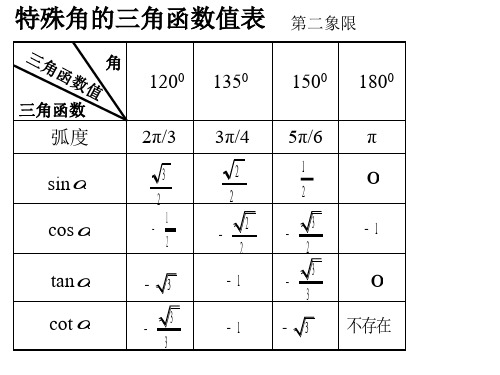
特殊角的三角函数值表 认识到了贫困户贫困的根本原因,才能开始对症下药,然后药到病除。近年来国家对扶贫工作高度重视,已经展开了“精准扶贫”项目
第三象限
角
三角函数
弧度
2100 7π/6
sin
1 2
cos
3
2
tan
3
3
cot
3
2250
5π/4
2 2
2 2 1
1
2400 2700
4π/3 3π/2
3
1
2
1 2
0
3 不存在
3
0
3
特殊角的三角函数值表 认识到了贫困户贫困的根本原因,才能开始对症下药,然后药到病除。近年来国家对扶贫工作高度重视,已经展开了“精准扶贫”项目
第四象限
角
三角函数
弧度
3000 5π/3
sin
3
2
cos
1
2
tan
3
cot
3
3
3150
7π/4
2 2 2 2
1
1
3300 3600
11π/6 2π
1
0
2
3
1
2
3
0
3
3 不存在
特殊角的三角函数值总表 认识到了贫困户贫困的根本原因,才能开始对症下药,然后药到病除。近年来国家对扶贫工作高度重视,已经展开了“精准扶贫”项目
认识到了贫困户贫困的根本原因,才 能开始 对症下 药,然 后药到 病除。 近年来 国家对 扶贫工 作高度 重视, 已经展 开了“ 精准扶 贫”项 目
特殊角的三角函数值表 认识到了贫困户贫困的根本原因,才能开始对症下药,然后药到病除。近年来国家对扶贫工作高度重视,已经展开了“精准扶贫”项目
