计量经济学实验报告模板 简单线性模型回归分析
计量经济学实验一 一元回归模型
实验二一元回归模型【实验目的】掌握一元线性、非线性回归模型的建模方法【实验内容】建立我国税收预测模型【实验步骤】【例1】建立我国税收预测模型。
表1列出了我国1985-1998年间税收收入Y和国内生产总值(GDP)x的时间序列数据,请利用统计软件Eviews建立一元线性回归模型。
一、建立工作文件⒈菜单方式在录入和分析数据之前,应先创建一个工作文件(Workfile)。
启动Eviews软件之后,在主菜单上依次点击File\New\Workfile(菜单选择方式如图1所示),将弹出一个对话框(如图2所示)。
用户可以选择数据的时间频率(Frequency)、起始期和终止期。
图1 Eviews菜单方式创建工作文件示意图图2 工作文件定义对话框本例中选择时间频率为Annual(年度数据),在起始栏和终止栏分别输入相应的日期85和98。
然后点击OK,在Eviews软件的主显示窗口将显示相应的工作文件窗口(如图3所示)。
图3 Eviews工作文件窗口一个新建的工作文件窗口内只有2个对象(Object),分别为c(系数向量)和resid(残差)。
它们当前的取值分别是0和NA(空值)。
可以通过鼠标左键双击对象名打开该对象查看其数据,也可以用相同的方法查看工作文件窗口中其它对象的数值。
⒉命令方式还可以用输入命令的方式建立工作文件。
在Eviews软件的命令窗口中直接键入CREATE命令,其格式为:CREATE 时间频率类型起始期终止期本例应为:CREATE A 85 98二、输入数据在Eviews软件的命令窗口中键入数据输入/编辑命令:DA TA Y X此时将显示一个数组窗口(如图4所示),即可以输入每个变量的数值图4 Eviews数组窗口三、图形分析借助图形分析可以直观地观察经济变量的变动规律和相关关系,以便合理地确定模型的数学形式。
⒈趋势图分析命令格式:PLOT 变量1 变量2 ……变量K作用:⑴分析经济变量的发展变化趋势⑵观察是否存在异常值本例为:PLOT Y X⒉相关图分析命令格式:SCAT 变量1 变量2作用:⑴观察变量之间的相关程度⑵观察变量之间的相关类型,即为线性相关还是曲线相关,曲线相关时大致是哪种类型的曲线说明:⑴SCAT命令中,第一个变量为横轴变量,一般取为解释变量;第二个变量为纵轴变量,一般取为被解释变量⑵SCAT命令每次只能显示两个变量之间的相关图,若模型中含有多个解释变量,可以逐个进行分析⑶通过改变图形的类型,可以将趋势图转变为相关图本例为:SCA T Y X图5 税收与GDP趋势图图5、图6分别是我国税收与GDP时间序列趋势图和相关图分析结果。
计量经济学实验二 多元线性回归分析 完成版

计量经济学实验二 多元线性回归分析 完成版 第一篇: 《多元线性回归分析,带你探索数据的奥秘》 朋友们,今天咱们来聊聊计量经济学里的多元线性回归分析。这东西听起来挺玄乎,其实啊,没那么复杂。 比如说,咱们想知道房价到底是由啥决定的。是房子的面积、周边的配套设施,还是小区的环境?这时候多元线性回归分析就派上用场啦。 就像我有个朋友,他想买房子,可搞不清为啥有的房子贵,有的便宜。后来我们用多元线性回归分析一研究,发现房子面积越大、周边学校越好,房价就越高。 所以说,这多元线性回归分析能帮咱们弄明白好多事儿背后的原因呢! 第二篇: 《走进多元线性回归分析的奇妙世界》 大伙们,今天咱们一起走进多元线性回归分析的世界。 想象一下,你开了个小店,想知道为啥有的月份生意好,有的月份不行。是天气的原因?还是促销活动的影响?这就像个谜团,而多元线性回归分析就是解开谜团的钥匙。 我认识个大姐,她开水果店的,一直搞不明白为啥夏天水果卖得好,冬天就差些。用了多元线性回归分析后发现,气温高的时候大家买水果多,而且节假日搞促销也能多卖不少。 这下她心里就有底啦,知道啥时候该多进货,啥时候该少进点。 第三篇: 《搞懂多元线性回归分析,让生活更明白》 亲爱的朋友们,今天咱们来弄清楚多元线性回归分析是咋回事。 比如说,你想知道自己的体重和啥有关系。是吃的东西?还是运动的量?这时候多元线性回归分析就能告诉你答案。 我邻居大哥,一直减肥减不下来,特别苦恼。后来我们一起用这个方法分析,发现他吃的高热量食物太多,运动又太少。找到原因后,大哥调整了饮食和运动习惯,体重慢慢就下来了。 所以啊,多元线性回归分析能让咱们的生活更有方向! 第四篇: 《多元线性回归分析,为您揭示隐藏的规律》 朋友们,今天咱们来聊聊这个多元线性回归分析。 好比说,一个工厂想提高产量,不知道是机器设备的问题,还是工人操作的问题。这时候用多元线性回归分析一研究,就能找出关键因素。 我有个亲戚在工厂上班,他们厂之前产量上不去,后来用这个方法发现是机器老化影响了效率。换了新机器后,产量一下子就提高了。 可见,多元线性回归分析能帮我们发现那些隐藏的规律,解决好多难题! 第五篇: 《探索多元线性回归分析,让决策更明智》 大伙们,咱们来探索一下多元线性回归分析。 比如说你要投资,不知道选哪个项目好。是看项目的利润?还是风险?多元线性回归分析就能帮你权衡。 我有个朋友想投资开饭店,拿不准主意。我们用这个方法分析了市场数据,发现地段好、菜品有特色的饭店更容易赚钱。朋友按照这个方向去找,饭店开得红红火火。 所以,学会多元线性回归分析,能让咱们做出更明智的决策!
多元线性回归模型实验报告计量经济学

多元线性回归模型实验报告计量经济学Revised by BLUE on the afternoon of December 12,2020.实验报告课程名称金融计量学实验项目名称多元线性回归模型班级与班级代码实验室名称(或课室)专业任课教师xxx学号: xxx姓名: xxx 实验日期: 2012年 5 月3日广东商学院教务处制姓名 xxx 实验报告成绩评语:指导教师(签名)年月日说明:指导教师评分后,实验报告交院(系)办公室保存多元线性回归模型一、实验目的通过上机实验,使学生能够使用 Eviews 软件估计可化为线性回归模型的非线性模型,并对线性回归模型的参数线性约束条件进行检验。
二、实验内容(一)根据中国某年按行业分的全部制造业国有企业及规模以上制造业非国有企业的工业总产值Y,资产合计K及职工人数L进行回归分析。
(二)掌握可化为线性多元非线性回归模型的估计和多元线性回归模型的线性约束条件的检验方法(三)根据实验结果判断中国该年制造业总体的规模报酬状态如何三、实验步骤(一)收集数据下表列示出来中国某年按行业分的全部制造业国有企业及规模以上制造业非国有企业的工业总产值Y,资产合计K及职工人数L。
序号工业总产值Y(亿元)资产合计K(亿元)职工人数L(万人)序号工业总产值Y(亿元)资产合计K(亿元)职工人数L(万人)1 113 17 432 67 18 613 84 19 2404 27 20 2225 327 21 806 120 22 967 58 23 2228 31 24 1639 16 25 24410 66 26 14511 58 27 13812 28 28 4613 61 29 21814 254 30 1915 83 31 4516 33表1(二)创建工作文件(Workfile)。
1、启动Eviews5,在主菜单上依次点击File\New\Workfile(如图),按确定。
2、在弹出的对话框中选择数据的时间频率(本实验为序列数据),输入数据数为31(如图1),然后点击OK(如图2)。
线性回归分析实验报告

线性回归分析实验报告线性回归分析实验报告引言线性回归分析是一种常用的统计方法,用于研究因变量与一个或多个自变量之间的关系。
本实验旨在通过线性回归分析方法,探究自变量与因变量之间的线性关系,并通过实验数据进行验证。
实验设计本实验采用了一组实验数据,其中自变量为X,因变量为Y。
通过对这组数据进行线性回归分析,我们将得到回归方程,从而可以预测因变量Y在给定自变量X的情况下的取值。
数据收集与处理首先,我们收集了一组与自变量X和因变量Y相关的数据。
这些数据可以是实际观测得到的,也可以是通过实验或调查获得的。
然后,我们对这组数据进行了处理,包括数据清洗、异常值处理等,以确保数据的准确性和可靠性。
线性回归模型在进行线性回归分析之前,我们需要确定一个线性回归模型。
线性回归模型的一般形式为Y = β0 + β1X + ε,其中Y是因变量,X是自变量,β0和β1是回归系数,ε是误差项。
回归系数β0和β1可以通过最小二乘法进行估计,最小化实际观测值与模型预测值之间的误差平方和。
模型拟合与评估通过最小二乘法估计回归系数后,我们将得到一个拟合的线性回归模型。
为了评估模型的拟合程度,我们可以计算回归方程的决定系数R²。
决定系数反映了自变量对因变量的解释程度,取值范围为0到1,越接近1表示模型的拟合程度越好。
实验结果与讨论根据我们的实验数据,进行线性回归分析后得到的回归方程为Y = 2.5 + 0.8X。
通过计算决定系数R²,我们得到了0.85的值,说明该模型能够解释因变量85%的变异程度。
这表明自变量X对因变量Y的影响较大,且呈现出较强的线性关系。
进一步分析除了计算决定系数R²之外,我们还可以对回归模型进行其他分析,例如残差分析、假设检验等。
残差分析可以用来检验模型的假设是否成立,以及检测是否存在模型中未考虑的其他因素。
假设检验可以用来验证回归系数是否显著不为零,从而判断自变量对因变量的影响是否存在。
简单计量经济学回归分析课程论文模板

论文题目:大学生GPA的影响因素分析****:**学号:G*********专业:金融班级:5班本文基于美国密歇根州多所高校大学生调查的数据,循序渐进的建立回归模型探究了影响大学生GPA的一些主要因素,并根据分析得出的结果给出了一些相关的建议。
运用Eviews软件与OLS法过对高中毕业学校规模、毕业年集中学术排名、SAT成绩、性别、是否是运动员等可能对大学GPA产生较大影响的因素进行回归分析,得出其中较为明显的影响因素,从而为我国高校大学生成绩的提高提出有效的建议与看法。
关键词:大学GPA,回归分析,共线性,异方差1.研究背景概述 (4)2.模型的设计 (5)2.1影响因素的分析及符号说明 (5)2.2数据的选择 (5)2.3研究报告的基本步骤 (7)3.计量模型建立及分析 (8)3.1.1简单影响因素的分析 (8)3.2加入平方项对问题进行分析 (9)3.3引入二值变量对问题进行分析 (10)4.模型检验 (12)4.1回归方程的标准差的评价 (12)4.2回归模型的总体显著性检验 (12)4.3计量经济学检验 (12)4.3.1多重共线性检验 (12)4.3.2 White检验方法检验模型异方差性 (13)4.3.3 DW检验检验模型自相关性 (13)5.对模型进一步的讨论 (14)5.1检验SAT成绩对大学成绩的影响是否取决于性别 (14)5.2对女性运动员与女性非运动员之间成绩差别的探讨 (15)6.结论 (17)参考文献 (19)附录1 (20)1.研究背景概述自国家大力发展高等教育以来,我国各大高校不断扩招。
近年来,我国高等教育的毛入学率已经达到了21%,实现了高等教育的大众化。
但是,伴随着高校招生规模的不断扩大,也出现了一些新问题。
很大一部分教师及管理人员认为,随着办学规模的扩大,大学新生的整体素质在逐年下降。
因为扩招使得学校的入学门槛逐步降低,使得参加高考的考生进本都有大学可上,虽然长期来看可能对中国的劳动力素质的提高有好处,但是使通过高考进入大学的学生整体学术基础素质持续下滑,如何提高大学生学术素质受到了社会各界的广泛关注。
计量经济学-简单线性回归模型
S.E. of regression
175.2325
Akaike info criterion
13.22880
Sum squared resid
951899.7
Schwarz criterion
13.31949
Log likelihood
-216.2751
Hannan-Quinn criter.
已经得到 =800, =8000, =300, (10)=2.23
则n=12, =30, =40000,
= =8000
=
650 2.23* * =650 30.1256411
即在95%的置信概率下消费支出C平均值的预测区间为(619.874359,680.125641)
2.4解:
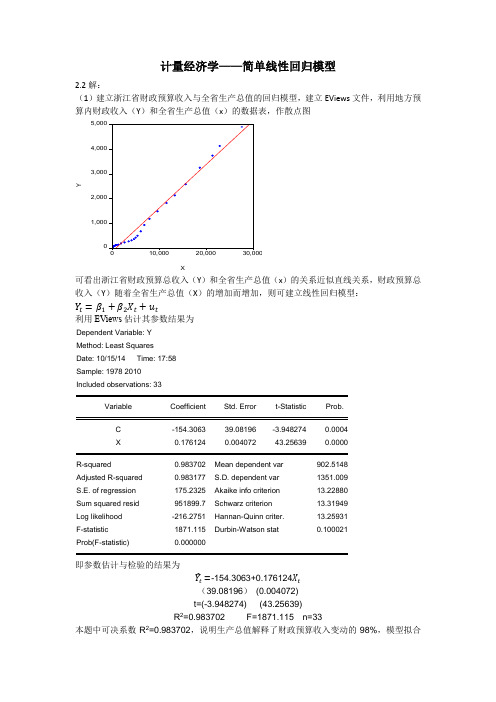
(1)建立建筑面积与建造单位成本回归模型,建立EViews文件,利用建造单位成本(Y)和建筑面积(x)的数据表,作散点图
10071.74
Schwarz criterion
9.984610
Log likelihood
-57.42275
Hannan-Quinn criter.
9.873871
F-statistic
178.0715
Durbin-Watson stat
1.172407
Prob(F-statistic)
0.000000
Kurtosis
1.664917
2.346511
Jarque-Bera
0.898454
0.213547
Probability
0.638121
0.898729
Sum
42.28000
19432.00
计量经济学实验报告---多元回归模型实验

2011-2012学年第1学期计量经济学实验报告实验(二):多元回归模型实验(1)估计参数利用EViews6估计模型的参数,方法是:1、建立工作文件:首先,双击EViews6图标,进入EViews6主页。
在菜单一次点击File\New\Workfile,出现对话框“Workfile Create”。
在“Workfile structure type ”中选择数据频率:Datad-regular frequency.在“Data specification”中Start data输入“1980”,在End data中输入“2002”点击“ok”出现“Workfile UNTITLED”工作框。
其中已有变量:“c”—截距项“resid”—剩余项。
2、Eviews命令:data y x p1 p2 p3 回车,输入数据,得到如图:图2-1 数据的输入3.对数据进行回归分析,eviews命令:LS Y C X P1 P2 P3图2-2根据上图,模型的估计的结果为:lnY=3.616+0.001lnX-0.506lnP1+0.119lnP2+0.048lnP3(0.450) (0) (0.162) (0.086) 0.051)t=(0.805) (4.652) (-3.115) (1.388) (0.942)R2=0.940 2 r=0.926 F=70.105(2)作对家庭人均鸡肉年消费量Y与猪肉价格P2、牛肉价格P3的散点图,图2-3和图2-4图2-3 图2-4图2-3 家庭人均鸡肉年消费量Y与猪肉价格P2的散点图图2-4 家庭人均鸡肉年消费量Y与牛肉价格P3的散点图由上面两张图可知都呈现线性关系,建立线性回归方程:i i i u X X Y +++=22110i βββi=1,2, .....,23 输入LS Y C P2 P3,用eviews6进行估计的输出结果如图:模型的估计结果为: Y=2.111+0.168P2+0.031P3(0.371)(0.060)(0.077) t=(5.689) (2.813) (0.402)R 2=0.834 2-r =0.817 F=50.150模型检验:①经济意义检验该地区家庭人均鸡肉消费量与鸡肉价格和牛肉价格成正相关,当牛肉价格不变时,猪肉价格上涨1单位,该地区家庭人均鸡肉消费量增加0.168单位;当猪肉价格不变时,牛肉价格上涨1单位,该地区家庭人均鸡肉消费量增加0.031单位,与猪肉价格成更大正相关关系符合一般情况。
计量经济学回归模型实验报告定稿版

计量经济学回归模型实验报告HUA system office room 【HUA16H-TTMS2A-HUAS8Q8-HUAH1688】回归模型分析报告背景意义:教育是立国之本,强国之基。
随着改革开放的进行、经济的快速发展和人们生活水平的逐步提高,“教育”越来越受到人们的重视。
一方面,人均国内生产总值的增加与教育经费收入的增加有着某种联系,而人口的增长也必定会对教育经费收入产生影响。
本报告将从这两个方面进行分析。
我国1991年~2013年的教育经费收入、人均国内生产总值指数、年末城镇人口数的统计资料如下表所示。
试建立教育经费收入Y关于人均国内生产总值指数X1和年末城镇人口数X2的回归模型,并进行回归分析。
年份教育经费收入Y(亿元)人均国内生产总值指数 X1(1978年=100)年末城镇人口数 X2(万人)1991731.50282256.6731203 1992867.04905289.7232175 19931059.93744326.323317319941488.78126364.9134169 19951877.95011400.635174 19962262.33935435.7637304 19972531.73257471.1339449 19982949.05918503.2541608 19993349.04164536.9443748 20003849.08058577.6445906 20014637.66262621.0948064 20025480.02776672.9950212 20036208.2653735.8452376 20047242.59892805.254283 20058418.83905891.315621220069815.30865998.7958288200712148.06631134.6760633200814500.737421237.4862403200916502.70651345.0764512201019561.847071480.8766978201123869.293561613.6169079201228655.305191730.1871182201330364.718151853.9773111资料来源:中经网统计数据库。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
简单线性模型回归分析
一、实验目的与要求:
目的:影响某市货物运输量的因素可能有很多,比如国内生产总值,
经济增长,零售物价指,等。为研究国内生产总值对货物运输量是否
有影响,二者有何关系。
二、实验内容
根据1985-1998年某市货物运适量Y和当年国内生产总值GDP数据,
运用EV软件,做简单线性回归分析,包括模型设定,估计参数,模
型检验,模型应用,得出回归结果。
三、实验过程:
(一)模型设定
为研究中国国内生产总值对货物运输量的关系,根据1985-1998年
中国国内生产总值GDP和货物运输量Y,如图1:
年份 Y GDP
1985 18249 161.69
1986 18252 171.07
1987 18400 184.07
1988 16693 194.75
1989 15543 197.86
1990 15929 208.55
1991 18308 221.06
1992 17522 246.92
1993 21640 276.8
1994 23783 316.38
1995 24040 363.52
1996 24133 415.51
1997 25090 465.78
1998 24505 509.1
根据以上数据,作货物运输量Y和国内生产总值GDP的散点图,如图
2:
从散点图可以看出,货物运输量Y和国内生产总值GDP大体呈现为线
性关系,所以建立的计量经济模型为以下线性模型:01iiiYXu
(二)估计参数
1、双击“Eviews”,进入主页。输入数据:点击主菜单中的File/Open /EV Workfile—Excel
—GDP.xls;
2、在EV主页界面点击“Quick”菜单,点击“Estimate Equation”,出现“Equation
Specification”对话框,选择OLS估计,输入“y c x”,点击“OK”。即出现回归结果图3:
参数回归结果为:
Yt=12596.27+26.95GDP
(10.1) (6.5)
R^2=0.78 –R^2=0.78
1.对回归方程的结构分析:
B^1=26.95是这个样本回归方程的斜率,它表示GDP每增加1亿
元,某市将增加26,95吨的货物运输量,B^0=12596.27是样本回归
方程的截距,它表示不受GDP影响的某市货物运输量。
2.统计检验:
B^=0.78说明总离差平方和的78%被样本回归解释,有22%未被解
释,因此,样本回归直线的拟合优度是可以的。
给出显著水平a=0.05,查自由度v=14-2=12的t分布表,得出临界值T0.025(12)=2.18,
t0=10.1大于t0.025(12),t1=6.5大于t0.025(12),故回归系数均显著部位零,回归模
型中应包含常数项,GDP对Y有显著影响。
3.预测2000年的某市货物运输量:
加入2000年某市以1980年为不变价的国内生产总值为629亿元,
2000年货物运输量预测值是29307.84吨。
