(完整版)初中几何中线段和差的最大值与最小值典型分析(最全).doc
最新初中几何中线段和差的最大值与最小值练习题(最全)打印版

初中几何中线段和(差)的最值问题一、两条线段和的最小值。
基本图形解析: 一)、已知两个定点:1、在一条直线m 上,求一点P ,使PA+PB 最小; (1)点A 、B 在直线m 两侧:(2)点A 、B 在直线同侧:A 、A ’ 是关于直线m 的对称点。
2、在直线m 、n 上分别找两点P 、Q ,使PA+PQ+QB 最小。
(1)两个点都在直线外侧:(2)一个点在内侧,一个点在外侧:(3)两个点都在内侧:mmB mA Bmn mnn mnnnm(4)、台球两次碰壁模型变式一:已知点A 、B 位于直线m,n 的内侧,在直线n 、m 分别上求点D 、E 点,使得围成的四边形ADEB 周长最短.填空:最短周长=________________变式二:已知点A 位于直线m,n 的内侧, 在直线m 、n 分别上求点P 、Q 点PA+PQ+QA 周长最短.二)、一个动点,一个定点: (一)动点在直线上运动:点B 在直线n 上运动,在直线m 上找一点P ,使PA+PB 最小(在图中画出点P 和点B )1、两点在直线两侧:2、两点在直线同侧:mnm nm nm(二)动点在圆上运动点B 在⊙O 上运动,在直线m 上找一点P ,使PA+PB 最小(在图中画出点P 和点B ) 1、点与圆在直线两侧:2、点与圆在直线同侧:三)、已知A 、B 是两个定点,P 、Q 是直线m 上的两个动点,P 在Q 的左侧,且PQ 间长度恒定,在直线m 上要求P 、Q 两点,使得PA+PQ+QB 的值最小。
(原理用平移知识解) (1)点A 、B 在直线m 两侧:过A 点作AC ∥m,且AC 长等于PQ 长,连接BC,交直线m 于Q,Q 向左平移PQ 长,即为P 点,此时P 、Q 即为所求的点。
(2)点A 、B 在直线m 同侧:mmmmQ Q练习题1.如图,∠AOB =45°,P 是∠AOB 内一点,PO =10,Q 、R 分别是OA 、OB 上的动点,求△PQR 周长的最小值为 .2、 如图1,在锐角三角形ABC 中,AB=4,∠BAC=45°,∠BAC 的平分线交BC 于点D ,M,N 分别是AD 和AB 上的动点,则BM+MN 的最小值为 . 3、如图,在锐角三角形ABC 中 ,AB=BAC=45,BAC 的平分线交BC 于D ,M 、N 分别是AD 和AB 上的动点,则BM+MN 的最小值是多少?4、如图4所示,等边△ABC 的边长为6,AD 是BC 边上的中线,M 是AD 上的动点,E 是AC 边上一点.若AE=2,EM+CM 的最小值为 .5、如图3,在直角梯形ABCD 中,∠ABC =90°,AD ∥BC ,AD =4,AB =5,BC =6,点P 是AB 上一个动点,当PC +PD 的和最小时,PB 的长为__________.6、 如图4,等腰梯形ABCD 中,AB=AD=CD=1,∠ABC=60°,P 是上底,下底中点EF 直线上的一点,则PA+PB 的最小值为 .Q二、求两线段差的最大值问题 (运用三角形两边之差小于第三边) 基本图形解析:1、在一条直线m 上,求一点P ,使PA 与PB 的差最大; (1)点A 、B 在直线m 同侧:解析:延长AB 交直线m 于点P ,根据三角形两边之差小于第三边,P ’A —P ’B <AB ,而PA —PB=AB 此时最大,因此点P 为所求的点。
(完整版)初中几何中线段和与差最值问题
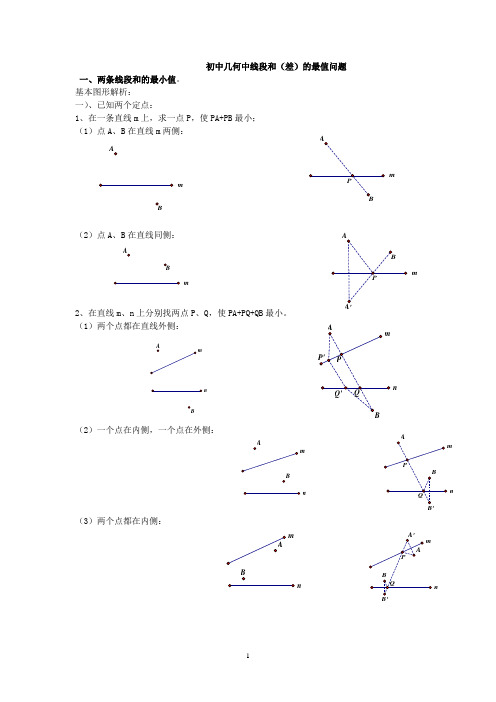
三、其它非基本图形类线段和差最值问题
1、求线段的最大值与最小值需要将该条线段转化到一个三角形中,在该三角形中,其他两边是已知的,则所求线段的最大值为其他两线段之和,最小值为其他两线段之差。
点B在直线n上运动,在直线m上找一点P,使PA+PB最小(在图中画出点P和点B)
1、两点在直线两侧:
2、两点在直线同侧:
(二)动点在圆上运动
点B在⊙O上运动,在直线m上找一点P,使PA+PB最小(在图中画出点P和点B)
1、点与圆在直线两侧:
2、点与圆在直线同侧:
三)、已知A、B是两个定点,P、Q是直线m上的两个动点,P在Q的左侧,且PQ间长度恒定,在直线m上要求P、Q两点,使得PA+PQ+QB的值最小。(原理用平移知识解)
压轴题
1、如图,正比例函数 的图象与反比例函数 (k≠0)在第一象限的图象交于A点,过A点作x轴的垂线,垂足为M,已知三角形OAM的面积为1.
(1)求反比例函数的解析式;
(2)如果B为反比例函数在第一象限图象上的点(点B与点A不重合),且B点的横坐标为1,在x轴上求一点P,使PA+PB最小.
2、如图,一元二次方程 的二根 , ( < )是抛物线 与x轴的两个交点B,C的横坐标,且此抛物线过点A(3,6).
(1)求点D的坐标;
(2)过O,C,D三点作抛物线,在抛物线的对称轴上是否存在一点P,使线段PO与PD之差的值最大?
若存在,请求出这个最大值和点P的坐标.若不存在,请说明理由.
初中几何中线段和差的最大值与最小值模型解析之欧阳术创编

欧阳术创编 2021.02.02初中几何中线段和(差)的最值问题一、两条线段和的最小值。
基本图形解析: 一)已知两个定点:1、在一条直线m 上,求一点P ,使PA+PB 最小; (1)点A 、B 在直线m 两侧: (2)点A 、B 在直线同侧: A 、A ’ 是关于直线m 的对称点。
2、在直线m 、n 上分别找两点P 、Q ,使PA+PQ+QB 最小。
(1)两个点都在直线外侧:(2)一个点在内侧,一个点在外侧: (3)两个点都在内侧: (4)台球两次碰壁模型变式一:已知点A 、B 位于直线m,n 的内侧,在直线n 、m 分别上求点D 、E点,mnn m欧阳术创编 2021.02.02 欧阳美创编使得围成的四边形ADEB 周长最短.填空:最短周长=________________ 变式二:已知点A 位于直线m,n 的内侧,在直线m 、n 分别上求点P 、Q 点PA+PQ+QA 周长最短. 二)一个动点,一个定点: (一)动点在直线上运动:点B 在直线n 上运动,在直线m 上找一点P ,使PA+PB 最小(在图中画出点P 和点B ) 1、两点在直线两侧: 2、两点在直线同侧: (二)动点在圆上运动点B 在⊙O 上运动,在直线m 上找一点P ,使PA+PB 最小(在图中画出点P 和点B ) 1、点与圆在直线两侧: 2、点与圆在直线同侧:(三)已知A 、B 是两个定点,P 、Q 是直线m 上的两个动点,P 在Q 的左侧,且PQ 间长度恒定,在直线m 上要求P 、Q 两点,使得PA+PQ+QB 的值最小。
(原理用平移知识解) (1)点A 、B 在直线m 两侧:过A 点作AC ∥m,且AC 长等于PQ 长,连接m欧阳术创编 2021.02.02 欧阳美创编 2021.02.02BC,交直线m 于Q,Q 向左平移PQ 长,即为P 点,此时P 、Q 即为所求的点。
(2)点A 、B 在直线m 同侧:二、求两线段差的最大值问题 (运用三角形两边之差小于第三边) 基本图形解析:1、在一条直线m 上,求一点P ,使PA 与PB 的差最大;(1)点A 、B 在直线m 同侧:解析:延长AB 交直线m 于点P ,根据三角形两边之差小于第三边,P ’A —P ’B <AB ,而PA —PB=AB 此时最大,因此点P 为所求的点。
线段差的最大值与线段和的最小值问题
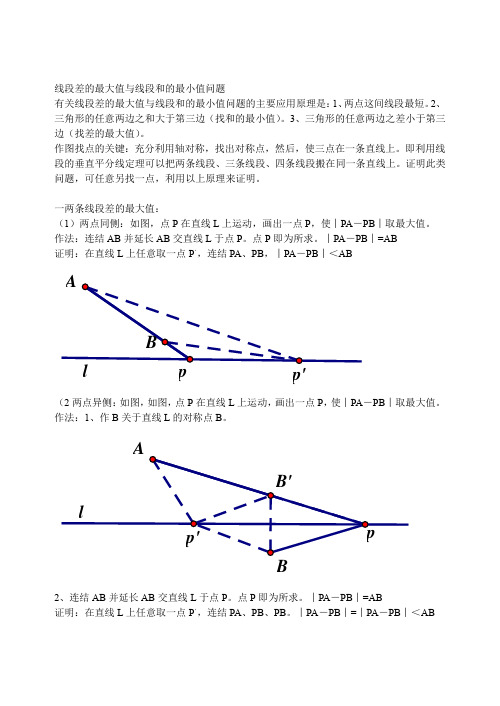
线段差的最大值与线段和的最小值问题有关线段差的最大值与线段和的最小值问题的主要应用原理是:1、两点这间线段最短。
2、三角形的任意两边之和大于第三边(找和的最小值)。
3、三角形的任意两边之差小于第三边(找差的最大值)。
作图找点的关键:充分利用轴对称,找出对称点,然后,使三点在一条直线上。
即利用线段的垂直平分线定理可以把两条线段、三条线段、四条线段搬在同一条直线上。
证明此类问题,可任意另找一点,利用以上原理来证明。
一两条线段差的最大值:(1)两点同侧:如图,点P在直线L上运动,画出一点P,使︱PA-PB︱取最大值。
作法:连结AB并延长AB交直线L于点P。
点P即为所求。
︱PA-PB︱=AB证明:在直线L上任意取一点P。
,连结PA、PB,︱PA-PB︱<ABp'(2两点异侧:如图,如图,点P在直线L上运动,画出一点P,使︱PA-PB︱取最大值。
作法:1、作B关于直线L的对称点B。
B2、连结AB并延长AB交直线L于点P。
点P即为所求。
︱PA-PB︱=AB证明:在直线L上任意取一点P。
,连结PA、PB、PB。
︱PA-PB︱=︱PA-PB︱<AB(三角形任意两边之差小于第三边)二、两条线段和的最小值问题:(1))两点同侧:如图,点P在直线L上运动,画出一点P使P A+PB取最小值。
(三角形的任意两边之和大于第三边(找和的最小值),P A+PB=AB(2)两点异侧:如图,点P在直线L上运动,画出一点P使P A+PB取最小值。
(两点之间线段最短)三、中考考点:08年林金钟老师的最后一题:如图,在矩形ABCO中,B(3,2),E(3,1),F(1,2)在X轴与Y轴上是否分别存在点M、N,使得四边形EFNM的周长最小?若存在,请求出周长的最小值,若不存在,请说明理由。
提示:EF长不变。
即求F N+NM+MF的最小值。
利用E关于X轴的对称点E,F的对称点F,把这三条线段搬到同一条直线上。
一、以正方形为载体,求线段和的最小值例1. 如图1,四边形ABCD 是正方形,边长是4,E 是BC 上一点,且CE =1,P 是对角线BD 上任一点,则PE +PC 的最小值是_____________。
(完整版)初中几何中线段和与差最值问题

初中几何中线段和(差)的最值问题一、两条线段和的最小值。
基本图形解析:一)、已知两个定点:1、在一条直线m上,求一点P,使PA+PB最小; (1 )点A B在直线m两侧:■: m(2)点A B在直线同侧:2、在直线m n上分别找两点P、Q,(1)两个点都在直线外侧: 使PA+PQ+Q最小。
BPA'B(2)一个点在内侧,一个点在外侧:Q (3)两个点都在内侧:B'B'* 2(4 )、台球两次碰壁模型变式一:已知点 A 、B 位于直线m,n 的内侧,在直线n 、m 分别上求点D 、E 点,使得 围成的四边形ADEB 周长最短.二)、一个动点,一个定点: (一)动点在直线上运动:点B 在直线n 上运动,在直线 m 上找一点P ,使PA+PB 最小(在图中画出点 P 和点B ) 1两点在直线两侧:(二)动点在圆上运动点B 在O O 上运动,在直线 m 上找一点P ,使PA+PB 最小(在图中画出点 P 和点B ) 1点与圆在直线两侧:变式二:已知点 A 位于直线m,n 的内侧,在直线 m n 分别上求点 周长最短.P 、Q 点 PA+PQ+QA 2、两点在直线同侧:-:mP'A"B'2、点与圆在直线同侧:三)、已知A B是两个定点,P、Q是直线m上的两个动点,P在Q的左侧,且PQ间长度恒定在直线m上要求P、Q两点,使得PA+PQ+Q的值最小。
(原理用平移知识解)(1 )点A、B在直线m两侧:A■作法:过A点作AC// m,且AC长等于PQ长,连接BC,交直线m于Q,Q向左平移PQ长,即为P点,此时P、Q即为所求的点。
B'(2)点A B在直线m同侧:1.如图1, / AOB45。
,P是/ AOB^一点,PO10, Q R分别是OA 0B上的动点,求厶PQR周长的最小值为______________________________2、如图2,在锐角三角形ABC中,AB=4』^, / BAC=45,/ BAC的平分线交BC于点D, M,N分别是AD和AB上的动点,贝U BM+M的最小值为 ___________________________ .3、如图3,在锐角三角形ABC中,AB=5j2,/ BAC=45 BAC的平分线交BC于D, M N分别是AD和AB上的动点,贝U BM+MN勺最小值是______________ 。
初中几何中线段和差的最大值与最小值模型解析学习资料
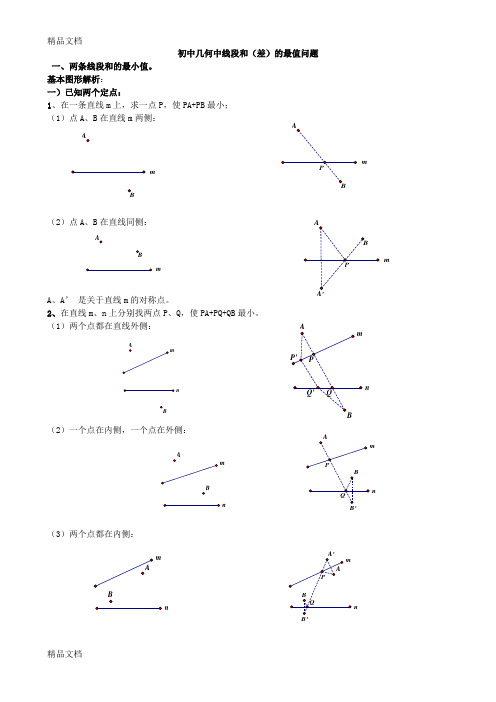
精品文档初中几何中线段和(差)的最值问题一、两条线段和的最小值。
基本图形解析:一)已知两个定点:1、在一条直线m 上,求一点P ,使PA+PB 最小; (1)点A 、B 在直线m 两侧:(2)点A 、B 在直线同侧:A 、A ’ 是关于直线m 的对称点。
2、在直线m 、n 上分别找两点P 、Q ,使PA+PQ+QB 最小。
(1)两个点都在直线外侧:(2)一个点在内侧,一个点在外侧:(3)两个点都在内侧:mmB mA Bmn mnnmnnnm(4)台球两次碰壁模型变式一:已知点A、B位于直线m,n 的内侧,在直线n、m分别上求点D、E点,使得围成的四边形ADEB周长最短.填空:最短周长=________________变式二:已知点A位于直线m,n 的内侧, 在直线m、n分别上求点P、Q点PA+PQ+QA周长最短.二)一个动点,一个定点:(一)动点在直线上运动:点B在直线n上运动,在直线m上找一点P,使PA+PB最小(在图中画出点P和点B)1、两点在直线两侧:2、两点在直线同侧:(二)动点在圆上运动点B在⊙O上运动,在直线m上找一点P,使PA+PB最小(在图中画出点P和点B)1、点与圆在直线两侧:mnmnmnmm m精品文档2、点与圆在直线同侧:(三)已知A 、B 是两个定点,P 、Q 是直线m 上的两个动点,P 在Q 的左侧,且PQ 间长度恒定,在直线m 上要求P 、Q 两点,使得PA+PQ+QB 的值最小。
(原理用平移知识解) (1)点A 、B 在直线m 两侧:过A 点作AC ∥m,且AC 长等于PQ 长,连接BC,交直线m 于Q,Q 向左平移PQ 长,即为P 点,此时P 、Q 即为所求的点。
(2)点A 、B 在直线m 同侧:二、求两线段差的最大值问题 (运用三角形两边之差小于第三边) 基本图形解析:1、在一条直线m 上,求一点P ,使PA 与PB 的差最大;(1)点A 、B 在直线m 同侧:解析:延长AB 交直线m 于点P ,根据三角形两边之差小于第三边,P ’A —P ’B <AB ,而PA —PB=AB 此时最大,因此点P 为所求的点。
完整word版,初中几何中线段和与差最值问题
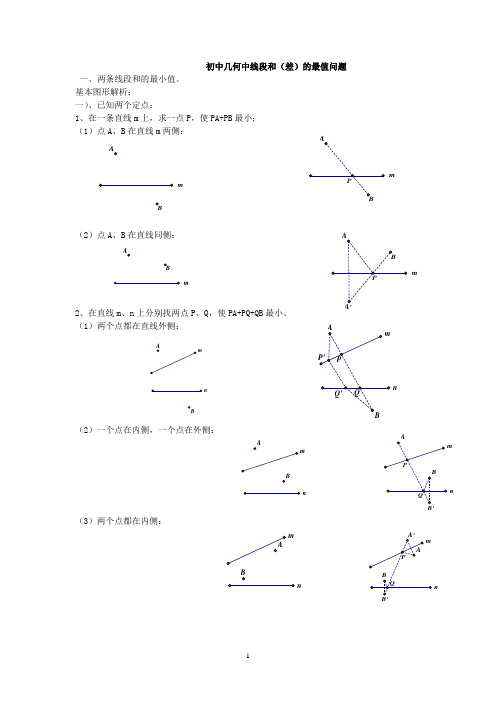
初中几何中线段和(差)的最值问题一、两条线段和的最小值。
基本图形解析: 一)、已知两个定点:1、在一条直线m 上,求一点P ,使PA+PB 最小; (1)点A 、B 在直线m 两侧:(2)点A 、B 在直线同侧:2、在直线m 、n 上分别找两点P 、Q ,使PA+PQ+QB 最小。
(1)两个点都在直线外侧:(2)一个点在内侧,一个点在外侧:(3)两个点都在内侧:mm B mA Bmn mnn mnnn m(4)、台球两次碰壁模型变式一:已知点A 、B 位于直线m,n 的内侧,在直线n 、m 分别上求点D 、E 点,使得围成的四边形ADEB 周长最短.变式二:已知点A 位于直线m,n 的内侧, 在直线m 、n 分别上求点P 、Q 点PA+PQ+QA 周长最短.二)、一个动点,一个定点: (一)动点在直线上运动:点B 在直线n 上运动,在直线m 上找一点P ,使PA+PB 最小(在图中画出点P 和点B ) 1、两点在直线两侧:2、两点在直线同侧:(二)动点在圆上运动点B 在⊙O 上运动,在直线m 上找一点P ,使PA+PB 最小(在图中画出点P 和点B ) 1、点与圆在直线两侧:m nmnm nmm2、点与圆在直线同侧:三)、已知A 、B 是两个定点,P 、Q 是直线m 上的两个动点,P 在Q 的左侧,且PQ 间长度恒定,在直线m 上要求P 、Q 两点,使得PA+PQ+QB 的值最小。
(原理用平移知识解) (1)点A 、B 在直线m 两侧:作法:过A 点作AC ∥m,且AC 长等于PQ 长,连接BC,交直线m 于Q,Q 向左平移PQ 长,即为P 点,此时P 、Q 即为所求的点。
(2)点A 、B 在直线m 同侧:练习题 1.如图1,∠AOB =45°,P 是∠AOB 内一点,PO =10,Q 、R 分别是OA 、OB 上的动点,求△PQR 周长的最小值为.2、如图2,在锐角三角形ABC 中,AB=4,∠BAC=45°,∠BAC 的平分线交BC 于点D ,M,N分别是AD 和AB 上的动点,则BM+MN 的最小值为 .3、如图3,在锐角三角形ABC 中 ,AB=52,∠BAC=45,BAC 的平分线交BC 于D ,M 、N 分别是AD 和AB 上的动点,则BM+MN 的最小值是 。
初中几何中线段和差的最大值与最小值模型解析

初中几何中线段和(差)的最值问题一、两条线段和的最小值。
基本图形解析: 一)已知两个定点:1、在一条直线m 上,求一点P ,使PA+PB 最小; (1)点A 、B 在直线m 两侧: (2)点A 、B 在直线同侧: A 、A ’ 是关于直线m 的对称点。
2、在直线m 、n 上分别找两点P 、Q ,使PA+PQ+QB 最小。
(1)两个点都在直线外侧:(2)一个点在内侧,一个点在外侧:(3)两个点都在内侧: (4)台球两次碰壁模型变式一:已知点A 、B 位于直线m,n 的内侧,在直线n 、m 分别上求点D 、E 点,使得围成的四边形ADEB 周长最短.mnnm填空:最短周长=________________变式二:已知点A 位于直线m,n 的内侧, 在直线m 、n 分别上求点P 、Q 点PA+PQ+QA 周长最短. 二)一个动点,一个定点: (一)动点在直线上运动:点B 在直线n 上运动,在直线m 上找一点P ,使PA+PB 最小(在图中画出点P 和点B ) 1、两点在直线两侧: 2、两点在直线同侧: (二)动点在圆上运动点B 在⊙O 上运动,在直线m 上找一点P ,使PA+PB 最小(在图中画出点P 和点B )1、点与圆在直线两侧:2、点与圆在直线同侧:(三)已知A 、B 是两个定点,P 、Q 是直线m 上的两个动点,P 在Q 的左侧,且PQ 间长度恒定,在直线m 上要求P 、Q 两点,使得PA+PQ+QB 的值最小。
(原理用平移知识解)m(1)点A 、B 在直线m 两侧:过A 点作AC ∥m,且AC 长等于PQ 长,连接BC,交直线m 于Q,Q 向左平移PQ 长,即为P 点,此时P 、Q 即为所求的点。
(2)点A 、B 在直线m 同侧:二、求两线段差的最大值问题 (运用三角形两边之差小于第三边)基本图形解析:1、在一条直线m 上,求一点P ,使PA 与PB 的差最大;(1)点A 、B 在直线m 同侧:解析:延长AB 交直线m于点P ,根据三角形两边之差小于第三边,P ’A —P ’B <AB ,而PA —PB=AB 此时最大,因此点P 为所求的点。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
初中几何中线段和(差)的最值问题 一、两条线段和的最小值。 基本图形解析 :(对称轴为:动点所在的直线上
一)、已知两个定点: 1、在一条直线 m 上,求一点 P,使 PA+PB 最小; (1)点 A、 B 在直线 m 两侧: A A A
P m m
B B
(2)点 A、 B 在直线同侧: A
A B m
A' A 、 A’是关于直线 m 的对称点。
2、在直线 m、n 上分别找两点 P、 Q,使 PA+PQ+QB 最小。 (1)两个点都在直线外侧: A
A m
P'P
) m B
B m P
m n B (2)一个点在内侧,一个点在外侧:
Q' Q
A n
B m A P m
B n
B n Q
B'
(3)两个点都在内侧: m A' m
A A
P
B B
n Q
n B' (4)、台球两次碰壁模型 变式一:已知点 A 、B 位于直线 m,n 的内侧,在直线 n、m 分别上求点 D、 E 点,使 得围成的四边形 ADEB 周长最短 . n n A'
A
B A
B D
m m E
B'
填空:最短周长 =________________ 变式二:已知点 A 位于直线 m,n 的内侧 , 在直线 m、n 分别上求点 P、Q 点 PA+PQ+QA 周长最短 . n
n A' A A Q
m P m
A" 二)、一个动点,一个定点: (一) 动点 在直线上运动: 点 B 在直线 n 上运动,在直线 m 上找一点 P,使 PA+PB 最小(在图中画出点 P 和点 B) 1、两点在直线两侧:
n n B
m m P A A
2、两点在直线同侧: n n B
A A m
P m
A' (二)动点在圆上运动 点 B 在⊙ O 上运动,在直线 m 上找一点 P,使 PA+PB 最小(在图中画出点 P 和点 B ) 1、点与圆在直线两侧:
O O B'
B m P
P' m
A A
2、点与圆在直线同侧: O O
A B A
m m P A'
三)、已知 A 、 B 是两个定点, P、 Q 是直线 m 上的两个动点, P 在 Q 的左侧 ,且 PQ 间长度恒定 ,在直线 m 上要求 P、 Q 两点,使得 PA+PQ+QB 的值最小。 (原理用平移知识解 ) ( 1)点 A 、B 在直线 m 两侧:
A A C
m m P Q
P Q
B B
过 A 点作 AC ∥ m,且 AC长等于 PQ长,连接 BC, 交直线 m 于 Q,Q 向左平移 PQ 长,即为 P 点,此时 P、 Q 即为所求的点。 ( 2)点 A 、 B 在直线 m 同侧:
A A E B B
P m P m Q Q B' 练习题 1.如图,∠ AOB=45 °, P 是∠ AOB 内一点, PO=10 , Q、 R 分别是 OA、 OB 上的动点,求 △PQR 周长的最小值为 .
Q 2、 如图 1,在锐角三角形 ABC中, AB=4 , ∠ BAC=45°,∠ BAC的平分线交 BC于
点 D,
M,N分别是 AD和 AB上的动点,则 BM+MN的最小值为
.
3、如图,在锐角三角形 ABC 中 ,AB= 5 2 ,∠ BAC=45
,BAC
N 分别是 AD 和 AB 上的动点,则 BM+MN 的最小值是多少?
的平分线交 BC 于 D ,M 、
4、如图 4 所示,等边△ ABC的边长为 6,AD 是 BC边上的中线 ,M 是 AD上的动点 ,E 是 AC边上
一点 . 若 AE=2,EM+CM的最小值为 .
5、如图 3,在直角梯形 ABCD中,∠ ABC= 90°, AD∥BC,AD= 4,AB= 5,BC= 6,点 P 是 AB 上一个动点,当 PC+ PD的和最小时, PB 的长为 __________ .
6、 如图 4,等腰梯形 ABCD中, AB=AD=CD=1,∠ ABC=60°, P 是上底,下底中点 EF直线上
的一点,则 PA+PB的最小值为 . 7、如图 5 菱形 ABCD中, AB=2,∠ BAD=60°, E 是 AB
的中
点, P是对角线 AC上的一个动点,则 PE+PB的最小值 为 .
8、如图,菱形 ABCD 的两条对角线分别长 6和 8,点 P是对角线 AC 上的一个动点,点 M 、N分别是边 AB 、BC 的中点,则 PM+PN 的最小值是
9、如图,圆柱形玻璃杯,高为 12cm,底面周长为 18cm,在杯内离杯底 3cm 的点 C 处有一 滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿 4cm 与蜂蜜相对的点 A 处,则蚂蚁到达蜂 蜜的最短距离为 ________cm.
10 、如 图 ,菱 形 ABCD 中 , AB=2 ,∠ A=120° ,点 P,Q , K 分 别 为线 段 BC , CD ,
BD 上 的 任 意 一 点 , 则 11、如图,正方形 ABCD PK+QK 的边长为 的 最 小 值 为 2,E 为 AB 的中点, P 是 AC 上一动点.则 PB+PE 的最
小值是
12、 如图 6 所示,已知正方形 DN+MN ABCD的边长为 8,点 M在 DC上,且 DM=2, N 是 AC上的一 13、如图,正方形 ABCD 的边长是 2,∠ DAC
AD 和 AE 上的动点,则 DQ+PQ 的最小值为 的平分线交 . DC 于点 E,若点 P、 Q 分别是 14、如图 7,在边长为 2cm 的正方形 ABCD中,点 Q为 BC边的中点,点 P 为对角线 AC上一 动点,连接 PB、 PQ,则△ PBQ周长的最小值
为 cm.(结果不取近似值).
15、如图,⊙ O 的半径为 2,点 A、 B、C 在⊙ O 上, OA⊥ OB,∠ AOC=60 °, P 是 OB 上一
动点,则 PA+PC 的最小值是 .
16、如图 P 是直径 8,MN是半径为MN上一动点,则 1 的⊙ O的直径,点PA+ PB的最小值为 A 在⊙ O上,∠ ( ) AMN= 30°, B 为 AN弧的中点, (A)2 (B) (C)1 (D)2 解答题
1、如图 9,正比例函数 y= x 的图象与反比例函数 y= ( k≠ 0)在第一象限的图象交于 A
点,过 A 点作 x 轴的垂线,垂足为 M,已知三角形 OAM的面积为 1.
( 1)求反比例函数的解析式;
( 2)如果 B 为反比例函数在第一象限图象上的点(点 B 与点 A 不重合),且 B 点的横坐标为 1,在 x 轴上求一点 P,使 PA+PB最小 . 2 、如 图 ,一 元 二 次 方 程 x 2+2x-3=0 的 二 根 x 1 , x2 ( x 1< x 2 )是 抛 物 线 y=ax 2+bx+c
与 x 轴 的 两 个 交 点 B, C 的 横 坐 标 , 且 此 抛 物 线 过 点 A( 3 , 6 ).( 1) 求 此 二 次 函 数 的 解 析 式 ;
( 2) 设 此 抛 物 线 的 顶 点 为 P, 对 称 轴 与 AC 相 交 于 点 Q, 求 点 P 和 点 Q 的 坐 标 ;( 3) 在 x 轴 上 有 一 动 点 M, 当 MQ+MA取 得 最小值时 , 求 M 点 的 坐 标 .
3、如图 10,在平面直角坐标系中,点 A 的坐标为 ( 1, ) , △AOB的面积是 .
( 1)求点 B 的坐标; ( 2)求过点 A、 O、 B 的抛物线的解析式;
( 3)在( 2)中抛物线的对称轴上是否存在点 C,使△ AOC的周长最小?若存在,求出 点 C 的 坐标;若不存在,请说明理由;
