重力加速度表
用单摆测定重力加速度 (30张ppt)

T
t n
2
2t n
为了测量周期,摆球到达哪个位置的时刻作为计
时开始与停止的时刻比较好?
应以摆球变一次摆长,将相应的l和T代入公式 中求出g值,最后求出g的平均值.如下表处理数据:
表1-5-1
摆长(m)
实验次数
l线 d
l
时间
振次
周期
周期平 重力加
【实验步骤】
1、做单摆:让细线的一端穿过摆球的小孔,然后打 一个比孔大的线结,制成一个单摆.
×
【实验步骤】
2、测摆长: 摆长为l=l线+d/2 (1)用米尺量出悬线长l线,准确到mm
(2)用游标卡尺测摆球直径d,准确到mm L
0 0
1
5
10
【实验步骤】
3、测周期: 把单摆从平衡位置拉开一个很小角度(<5o)后释放 用停表测量单摆的周期。
高中物理
实 验 九
用 单 摆 测 定 重 力 加 速 度
如皋市第一中学
学生实验课件
【实验目的】 【实验原理】 【实验器材】 【实验内容】 【注意事项】 【减小误差】 【实验练习】
0
10
【实验目的】
用单摆测定当地重力加速度
【实验原理】
单摆做简谐运动时,其周期为 T 2,l 故有 以求g 出4,当2因Tl地2此的测重出力单加摆速的度摆g长的l和数振值动。周g期T,就可
11
4
10
5
9
6
87
53
33 4 35 6
37
22 51
20 49 18 47 16
8 39
10 41 12 43 45 14
【实验步骤】 3、测周期:
把单摆从平衡位置拉开一个很小角度(<5o)后释放
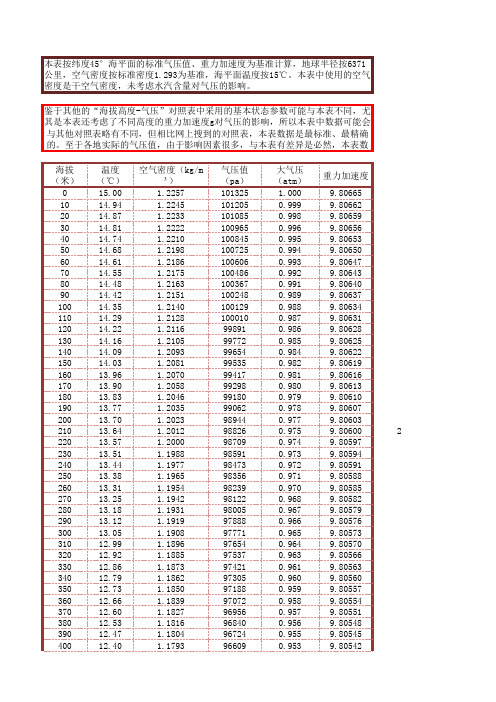
海拔高度与气压、空气密度、重力加速度对照表
2
本表按纬度45°海平面的标准气压值、重力加速度为基准计算,地球半径按6371公里,空气密度按标准密度1.293为基准,海平面温度按15℃。
本表中使用的空气密度是干空气密度,未考虑水汽含量对气压的影响。
鉴于其他的“海拔高度-气压”对照表中采用的基本状态参数可能与本表不同,尤其是本表还考虑了不同高度的重力加速度g对气压的影响,所以本表中数据可能会与其他对照表略有不同,但相比网上搜到的对照表,本表数据是最标准、最精确的。
至于各地实际的气压值,由于影响因素很多,与本表有差异是必然,本表数
1。
地球引力高度变化表

地球引力高度变化表地球引力高度变化表是一个显示不同高度上地球引力加速度(通常称为“g”)变化的表格。
地球引力加速度是由于地球的质量而产生的向心加速度,它随着海拔高度的增加而减小。
以下是一个简化的地球引力高度变化表的示例。
请注意,这个表格是基于一些简化的假设,并且实际值可能会因地理位置(例如纬度和经度)和地球内部密度的变化而有所不同。
这个表格显示了随着海拔的增加,地球引力加速度逐渐减小。
在海拔10000米以上,地球引力加速度的减小变得更为显著。
要生成更精确的地球引力高度变化表,您需要使用更复杂的数学模型,例如考虑地球的形状(不是完美的球体)和地球内部密度的变化。
此外,您还可以使用地理信息系统(GIS)软件或在线工具来生成特定地理位置的地球引力高度变化表。
地球引力随高度的变化而变化,但具体的引力高度变化表可能因地理位置、地球模型、大气条件等多种因素而有所不同。
通常情况下,地球引力随高度的增加而减小,因为引力与距离的平方成反比。
在地球表面附近,重力加速度约为9.81 m/s²,这意味着物体自由下落的速度将每秒增加约9.81米。
然而,随着高度的增加,地球引力逐渐减弱,重力加速度也会逐渐减小。
据估计,每升高1000米,重力加速度约减小3.1 m/s²。
需要注意的是,这个变化率并不是线性的,因为地球是一个球体,所以引力随高度的变化是非线性的。
此外,地球自转也会对引力产生影响,导致赤道处的重力加速度略低于两极处的重力加速度。
总的来说,地球引力的具体高度变化表需要根据具体的地理位置和地球模型进行计算。
在实际应用中,可以使用重力加速度随高度的变化公式进行计算,或者使用地球重力场模型进行更精确的预测。
物理:地球表面的重力与重力加速度ppt课件

得到加速度为
a
GM E R2
4.地球表面加速度: (1)条件:因地球质量 ME 及地球半径 RE
都是定值。
(2)结果:地球表面加速度 a 是一定值﹐ 常以 g 表示﹐由实验测得重力加速度
g =9.80 m/s2。
(3)推导由地球半径 6.40x103 km﹐即可计算出 地球质量
5.讨论:
(1)原因: g
(2)星球表面与地球表面之重力加速度比
g:gE(b GE R )2 M :G R E2E M a b23b:1 1a:b 1
3
2.质量 M 与体积 V 的关系:M =V。
3.星球表面重力加速度 g 与星球半径 R ﹑星球
质量
M
的关系: g
GM R2
。
设地球密度为ρE ,半径为 RE ,质量为 ME 则星球密度为aρE ,半径为 bRE,质量为 M (1)星球与地球之质量比
M :M E aE3 4(bE )R 3:E3 4 πE 3 R a3:b 1
27
2.火箭出发时质量为 m ,在地面上空 h 高度处
的质量为 1 m。
3
3.在地面上空 h 高度处与地心距离为 RE+h 。
火火箭箭在在地地球面表上面 空的h 高重度量处:的F 重G量RM:EE2m ‧‧‧‧‧
1 27
F
GME
(
1 3
m)
(RE h)2
‧‧‧‧‧ ‧‧‧‧‧ ‧‧‧‧‧ ‧‧‧
2 73(R R EE 2h)2, h2RE, 即 R hE2
(a)物体至星体中心的距离平方成反比。 (b)与星体的质量成正比。
范例7-3
如下图,设地球的半径为 RE,火箭由地面垂
直升高,当其质量剩为出发时的 1 时,其重
重力加速度几种测量方法比较(论文)

重力加速度几种测量方法的比较引言:重力加速度是物理学中的一个十分重要的物理量,在地面上不同的地区,重力加速度g值不相同,它是由物体所在地区的纬度、海拔等因素决定,随着地球纬度和海拔高度的变化而变化,准确地确定它的量值,无论从理论上、还是科研上、生产上以及军事上都有极其重大的意义。
测量重力加速度的方法有很多,我所要做的就是通过学习前人的理论知识,经过思考,在现有的实验室条件下,进行实验,做出归纳和总结,提出自己的看法与体会。
且实验方法虽然多,但有的测量仪器的精确度受环境因素的影响比较大,不是每种方法都适用,所以有必要对测量方法进行研究,找出一种适合测量本地重力加速度的方法。
一、重力加速度的测量方法(一)用自由落体法测量重力加速度1.实验仪器:自由落体装置(如图一),数字毫秒计,光电门(两个),铁球。
图一自由落体装置2.实验原理、步骤、注意事项实验原理:设光电门A 、B 间的距离为s ,球下落到A 门时的速度为0v ,通过A 、B 间的时间为t ,则成立:2/20gt t v s += (1)两边除以t ,得:2//0gt v t s += (2)设t x =,t s y /=,则:2/0gx v y += (3)这是一直线方程,当测出若干不同s 的t 值,用t x =和t s y /=进行直线拟合,设所得斜率为b ,则由2/g b =可求出g ,b g 2=(4) 实验步骤:(1)调节实验装置的支架,使立柱为铅直,再使落球能通过A 门B 门的中点。
(2)测量A 、B 两光电门之间的距离s 。
(3)测量时间t 。
(4)计算各组的x ,y 值,用最小二乘法做直线拟合,求出斜率b 及其标准偏差b S 、)(b u (注意:在取b 的时,由于立柱调整不完善,落球中心未通过光电门的中点,立柱上米尺的误差均给s 值引入误差,也是b 的不确定度来源,一般此项不确定度(B 类评定)较小,可略去不计,所以b S b u =)()。
主要城市重力加速度2
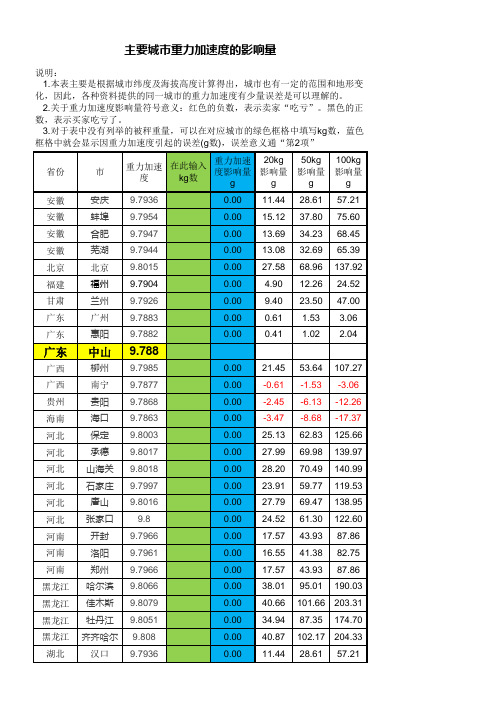
11.44 10.83 7.15 5.52 34.33 34.33 14.10 17.78 9.81 8.17 26.77 28.40 31.06 30.04 31.67 21.66 41.07 38.01 23.29 16.55 6.33 23.50 22.07 21.45 21.25 18.39 10.83 14.51 13.08 15.32 14.51 13.49 6.74 26.77 -16.55 25.75 29.42 27.58
湖北 湖北 湖南 湖南 吉林 吉林 江苏 江苏 江西 江西 辽宁 辽宁 辽宁 辽宁 辽宁 内蒙 内蒙 内蒙 内蒙 宁夏 青海 山东 山东 山东 山西 山西 陕西 陕西 陕西 陕西 上海 上海 四川 天津 西藏 新疆 新疆 新疆
武汉 宜昌 长沙 衡阳 长春 吉林 南京 徐州 九江 南昌 大连 丹东 阜新 锦州 沈阳 包头 海拉尔 乌兰浩特 乌兰里哈 银川 西宁 德州 济南 青岛 大同 太原 宝鸡 潼关 西安 延安 浦口 上海 成都 天津 拉萨 哈密 吐鲁番 乌鲁木齐
0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00
9.7936 9.7933 9.7915 9.7907 9.8048 9.8048 9.7949 9.7967 9.7928 9.792 9.8011 9.8019 9.8032 9.8027 9.8035 9.7986 9.8081 9.8066 9.7994 9.7961 9.7911 9.7995 9.7988 9.7985 9.7984 9.797 9.7933 9.7951 9.7944 9.7955 9.7951 9.7946 9.7913 9.8011 9.7799 9.8006 9.8024 9.8015
海拔高度与气压、空气密度、重力加速度对照表
2
本表按纬度45°海平面的标准气压值、重力加速度为基准计算,地球半径按6371公里,空气密度按标准密度1.293为基准,海平面温度按15℃。
本表中使用的空气密度是干空气密度,未考虑水汽含量对气压的影响。
鉴于其他的“海拔高度-气压”对照表中采用的基本状态参数可能与本表不同,尤其是本表还考虑了不同高度的重力加速度g对气压的影响,所以本表中数据可能会与其他对照表略有不同,但相比网上搜到的对照表,本表数据是最标准、最精确的。
至于各地实际的气压值,由于影响因素很多,与本表有差异是必然,本表数
1。
凯特摆测重力加速度
凯特摆测重力加速度PB09206016 肖啸实验目的:(1)学习凯特摆的实验设计思想和技巧(2)掌握一种比较精确的测量重力加速度的方法实验仪器:凯特摆,光电探头,米尺,V AFN 多用数字测试仪数据处理:(1) 计算l 和1h 的平均值与不确定度由原始数据可得下表表一:l -1h 数值表a) 计算l 的平均值与不确定度 统计计算结果:l=∑l i3i=13=74.260cmσ(l )=√∑(l i −l )23i=1n−1=0.010cml 的A 类不确定度:P=0.683 n=3 取p t =1.32u A (l )=t p√n=1.32×√3=7.62×10−3cml 的B 类不确定度:∆仪=0.1cm k p =1 C =3 P=0.683u B (l )=k p∆仪C=1×0.13=0.033cm合成不确定度:u (l )=√u A (l )2+u B (l )2=√0.007622+0.0332=0.034cm综上,实验测得:l=l ±u (l )=(74.260±0.034)cm (P =0.683)b) 计算1h 的平均值与不确定度统计计算结果:1h =∑1h i3i=13=29.923cm σ(1h )=√∑(1h i −1h )23i=1n−1=0.025cm1h 的A 类不确定度:P=0.683 n=3 取p t =1.32u A (1h )=t pσ(1h )√n=1.32×√3=0.019cm1h 的B 类不确定度:∆仪=0.1cm k p =1 C =3 P=0.683u B (1h )=k p∆仪C=1×0.13=0.033cm合成不确定度:u(1h )=√u A (1h )2+u B (1h )2=√0.0192+0.0332=0.038cm综上,实验测得:1h =1h ±u (1h )=(29.923±0.038)cm (P =0.683)(2) 计算1T 和2T 的平均值与不确定度由原始数据可得下表表二:摆动周期数值表a) 计算1T 的平均值与不确定度 统计计算结果:T 1=110×∑T 1i5i=15=1.73505sσ(T 1)=110×√∑(T 1i −T 1)25i=1n−1=0.000046s1T 的A 类不确定度:P=0.683 n=5 取p t =1.14u A (T 1)=t p 1√n=1.14×√5=0.000023s1T 的B 类不确定度:∆仪=0.0001s k p =1 C =3 P=0.683u B (T 1)=k p∆仪C=1×0.00013=0.000033s合成不确定度:u (T 1)=√u A (T 1)2+u B (T 1)2=√0.0000232+0.0000332 =0.000040s综上,实验测得T 1=T 1±u (T 1)=(1.73503±0.00004)s (P =0.683)b) 计算2T 的平均值与不确定度 统计计算结果:T 2=110×∑T 2i5i=15=1.73429sσ(T 2)=110×√∑(T 2i −T 2)25i=1n−1=0.000032s2T 的A 类不确定度:P=0.683 n=5 取p t =1.14u A (T 2)=t p 2√n=1.14×√5=0.000016s2T 的B 类不确定度:∆仪=0.0001s k p =1 C =3 P=0.683u B (T 2)=k p∆仪C=1×0.00013=0.000033s合成不确定度:u (T 2)=√u A (T 2)2+u B (T 2)2=√0.0000162+0.0000332 =0.000037s综上,实验测得T 2=T 2±u (T 2)=(1.73429±0.00004)s (P =0.683)(3)计算重力加速度g 的平均值与不确定度由公式 2222212121422(2)T T T T a b g l h l π+-=+=+- 带入数值,得到重力加速度g :1222221221214422(2)T T T T g a b l h l ππ-⎡⎤-+==+⎢⎥+-⎢⎥⎣⎦=4π2[1.735032+1.7342922×0.74260+1.735032−1.7342922×(2×0.29923−0.74260)]−1=9.7795m/s 2下面计算g 的不确定度由于221212(2)T T b h l -=- 的大小相对22122T T a l +=非常小因此 12222122212842T T l g l T T ππ-⎡⎤+≈⨯=⎢⎥+⎣⎦两边取对数 22221222128ln ln 8ln ()l g ln l ln T T T T ππ==+-++ 两边取全微分11222222121222T dT T dT dg dl g l T T T T =--++ 因此有()u g g =得到g 的合成不确定度公式()u g g =⨯=0.0045m/s2不确定度保留一位有效数字,因此:综上,实验测得g=g ±u (g )=(9.780±0.005) m/s 2 (P=0.683)误差分析:(1)本实验对周期的测量较精确,但是对等效摆长的测量却有很大的误差,由于钢卷尺较软,加之凯特摆形状的限制,对两刀口间距离(即l )德德良存在很大误差。
重力加速度PPT课件
重力加速度的大小还受到地球 自转、地形等因素的影响。
02
重力加速度的物理意义
自由落体运动
01
02
03
ቤተ መጻሕፍቲ ባይዱ定义
自由落体运动是指物体仅 受重力作用,从静止开始 下落的运动。
特点
自由落体运动是初速度为 零的匀加速直线运动,加 速度为重力加速度g。
公式
$h = frac{1}{2}gt^{2}$ (下落高度与时间的平方 成正比)
实验步骤
1. 制作一个摆,使摆长$L$可调。
2. 调整摆长,使摆球达到平衡位置。 3. 释放摆球,用秒表测量摆球的周期 $T$。
4. 根据公式计算重力加速度$g$。
物体在月球上的重力加速度
原理:月球绕地球做匀速圆周运动,根据万有引力定律 和向心力公式,可以推导出月球上的重力加速度$g = frac{GM}{R^{2}}$。 1. 选取一个合适的月球探测器,使其在月球表面着陆。
02
计算自由落体运动的高度
自由落体运动中,物体只受到重力的作用,其下落的高度可以通过上述
公式计算得出。
03
计算抛物线运动的高度
抛物线运动中,物体在垂直方向上受到重力的作用,其最高点的高度也
可以通过上述公式计算得出。
计算落地速度
利用重力加速度计算物体落地时的速度
物体落地时的速度(v)与下落时间(t)和重力加速度(g)的关系可以用公式 v = gt 来表 示。
实验步骤 2. 测量探测器的质量$m$和月球半径$R$。
3. 记录探测器在月球表面的运动数据,包括位移、速度 等。
4. 根据公式计算重力加速度$g$。
04
重力加速度的应用
计算高度
01
利用重力加速度计算物体下落的高度
地球表面重力加速度公式
地球表面重力加速度公式
地球表面重力加速度的公式是:g=GM/r²。
其中,g为重力加速度,G为万有引力常数,M为地球质量,r为距离地球表面的半径。
这个公式基于牛顿第二定律,表明重力加速度与距离的平方成反比,与质量M成正比。
另一个常用的公式是:g=9.7803(1+0.0052884sin²φ-
0.0000059sin²2φ)m/s²。
其中,φ为物体所在处的地理纬度。
这个公式将地球视为旋转椭球,并考虑了地球自转的影响。
请注意,地球表面重力加速度的值会随纬度和海拔的变化而变化。
在地球表面,重力加速度的平均值约为9.8m/s²,但在不同地方可能会有所不同。
因此,在实际应用中,需要根据具体情况选择合适的公式和参数进行计算。
