初三专题-四点共圆
初三 关于圆 四点共圆
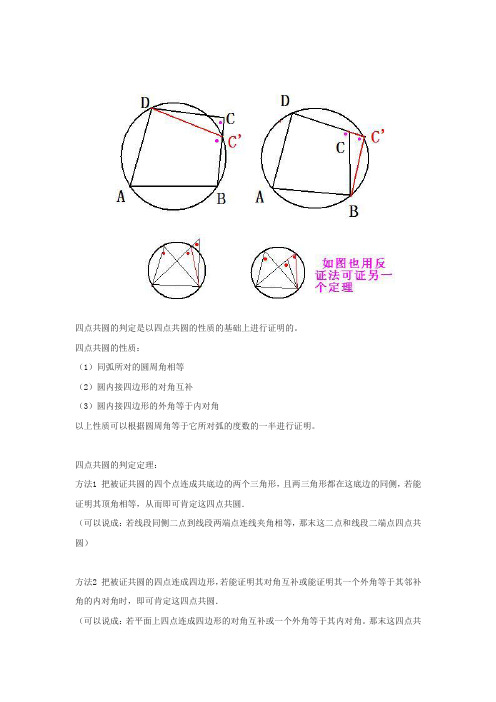
四点共圆的判定是以四点共圆的性质的基础上进行证明的。
四点共圆的性质:
(1)同弧所对的圆周角相等
(2)圆内接四边形的对角互补
(3)圆内接四边形的外角等于内对角
以上性质可以根据圆周角等于它所对弧的度数的一半进行证明。
四点共圆的判定定理:
方法1 把被证共圆的四个点连成共底边的两个三角形,且两三角形都在这底边的同侧,若能证明其顶角相等,从而即可肯定这四点共圆.
(可以说成:若线段同侧二点到线段两端点连线夹角相等,那末这二点和线段二端点四点共圆)
方法2 把被证共圆的四点连成四边形,若能证明其对角互补或能证明其一个外角等于其邻补角的内对角时,即可肯定这四点共圆.
(可以说成:若平面上四点连成四边形的对角互补或一个外角等于其内对角。
那末这四点共
圆)
我们可都可以用数学中的一种方法;反证法开进行证明。
现就“若平面上四点连成四边形的对角互补。
那末这四点共圆”证明如下(其它画个证明图如后)
已知:四边形ABCD中,∠A+∠C=180°
求证:四边形ABCD内接于一个圆(A,B,C,D四点共圆)
证明:用反证法
过A,B,D作圆O,假设C不在圆O上,刚C在圆外或圆内,
若C在圆外,设BC交圆O于C’,连结DC’,根据圆内接四边形的性质得∠A+∠DC’B=180°,∵∠A+∠C=180°∴∠DC’B=∠C
这与三角形外角定理矛盾,故C不可能在圆外。
类似地可证C不可能在圆内。
∴C在圆O上,也即A,B,C,D四点共圆。
专题29 四点共圆问题(教师版)-2021年中考数学模型技巧讲义(二轮)

专题29 四点共圆问题【规律总结】1、四点共圆:如果同一平面内的四个点在同一个圆上,则称这四个点共圆,一般简称为“四点共圆”。
四点共圆有三个性质:(1)共圆的四个点所连成同侧共底的两个三角形的顶角相等;(2)圆内接四边形的对角互补;(3)圆内接四边形的外角等于内对角。
2、判定定理:方法1:把被证共圆的四个点连成共底边的两个三角形,且两三角形都在这底边的同侧,若能证明其顶角相等,从而即可肯定这四点共圆。
(可以说成:若线段同侧二点到线段两端点连线夹角相等,那么这二点和线段二端点四点共圆)方法2 :把被证共圆的四点连成四边形,若能证明其对角互补或能证明其一个外角等于其邻补角的内对角时,即可肯定这四点共圆。
(可以说成:若平面上四点连成四边形的对角互补或一个外角等于其内对角,那么这四点共圆)【典例分析】例1.(2021·沭阳红岩学校九年级期末)如图,在Rt ABC △中,90ACB ∠=,3BC =,4AC =,点P 为平面内一点,且CPB A ∠=∠,过C 作CQ CP ⊥交PB 的延长线于点Q ,则CQ 的最大值为( )A .175B .154CD 【答案】B【分析】根据题意可得A 、B 、C 、P 四点共圆,由AA 定理判定三角形相似,由此得到CQ 的值与PC 有关,当PC 最大时CQ 即取最大值.【详解】解:∵在Rt ABC △中,90ACB ∠=,CPB A ∠=∠,3BC =,4AC =∵A 、B 、C 、P 四点共圆,AB 为圆的直径,5=∵CQ CP ⊥∵90ACB PCQ ∠=∠=∵∵ABC∵∵PQC ∵AC PC BC CQ =, 43PC CQ =,即34CQ=PC ∵当PC 取得最大值时,CQ 即为最大值∵当PC=AB=5时,CQ 取得最大值为154故选:B .【点睛】本题考查相似三角形的判定和性质以及四点共圆,掌握同圆或等圆中,同弧所对的圆周角相等确定四点共圆,利用相似三角形性质得到线段间等量关系是解题关键.例2.(2019·上海市市西初级中学八年级期末)如图,AB 是Rt ABC 和Rt ABD △的公共斜边,AC=BC ,32BAD ∠=,E 是AB 的中点,联结DE 、CE 、CD ,那么ECD ∠=___________________.【答案】13【分析】先证明A、C、B、D四点共圆,得到∵DCB与∵BAD的是同弧所对的圆周角的关系,得到∵DCB 的度数,再证∵ECB=45°,得出结论.【详解】解:∵AB是Rt∵ABC和Rt∵ABD的公共斜边,E是AB中点,∵AE=EB=EC=ED,∵A、C、B、D在以E为圆心的圆上,∵∵BAD=32°,∵∵DCB=∵BAD=32°,又∵AC=BC,E是Rt∵ABC的中点,∵∵ECB=45°,∵∵ECD=∵ECB-∵DCB=13°.故答案为:13.【点睛】本题考查直角三角形的性质、等腰三角形性质、圆周角定理和四点共圆问题,综合性较强.例3.(2020·北京市三帆中学九年级期中)已知:过O上一点A作两条弦AB、AC,且∠=︒,(AB、AC都不经过O)过A作AC的垂线AF,交O于D,直线BD,45AAC 交于点E ,直线BC ,AD 交于点F .(1)请在图1中,按要求补全图形;(2)在图2中探索线段BE 和BF 的数量关系,并证明你的结论;(3)探索线段AB 、AE 、AF 的数量关系,并直接写出你的结论________.【答案】(1)见解析;(2)BE BF =,理由见解析;(3)AE AF =【分析】(1)根据题意补全图形即可;(2)连接EF ,CD ,取EF 中点G 连接BG 、AG ,证明B 、E 、A 、F 四点共圆进而可证出结论;(3)由(2)知,点A 、B 、E 、F 四点共圆,连接CD ,交AB 于点P ,则CD 过圆心O ,由证得出∵ACB∵∵APD∵CPB ,进而可证AC AD +=,由等量代换可得出结论.【详解】解:(1)补全图形(2)BE BF =证明:连接EF ,CD ,CD 过圆心O ,CD 为直径,取EF 中点G 连接BG 、AG ∵AF AE ⊥,∵DBF=90°,∵90EBF FAE ∠=∠=︒∵EG AG =∵EG BG AG GF ===∵B 、E 、A 、F 在圆G 上,∵∵1=∵2,∵∵DAE=90°,∵BAD=45°,∵∵2=∵BAD=45°,又∵∵EBF=90°,∵∵BEF=45°=∵1,∵BE BF =,故答案为:BE BF =;(3)由(2)知,点A 、B 、E 、F 四点共圆,连接CD ,交AB 于点P ,则CD 过圆心O , ∵∵BEA=∵BFA ,BE BF =,∵EBC=∵DBF=∵DAE=90°,∵∵EBC∵∵FBD ,∵BC=BD ,CE=DF ,在∵ACB 和∵APD 中,∵CAB=∵DAB=45°,∵ABC=∵ADC ,∵BCD=45°,∵∵ACB∵∵APD∵CPB , ∵,AC AB BC AB AP AD BE BC==, ∵2,AC AD AP AB BC BP AB ⋅=⋅=⋅,CD 为直径,2222==2AC AD CD BC +,∵()222+2AC AD AC AD AC AD =++⋅=222BC AC AD +⋅=22BP AB AP AB ⋅+⋅=()2AB BP AP ⋅+=22AB ,∵AC AD +=,,∵AE AF =+,故答案为:AE AF =+.【点睛】本题考查了四点共圆的证明,圆的性质以及性质应用,勾股定理的应用,熟练掌握圆的性质是解题的关键.【好题演练】一、单选题1.(2020·浙江杭州市·九年级专题练习)如图,圆上有A 、B 、C 、D 四点,其中80BAD ∠=︒,若弧ABC 、弧ADC 的长度分别为7π、11π,则弧BAD 的长度为( )A .4πB .8πC .10πD .15π【答案】C【分析】先求出圆的周长,再根据圆内接四边形的性质可得100C ∠=︒,然后根据圆周角定理可得弧BAD 所对圆心角的度数,最后根据弧长的定义即可得.【详解】弧ABC 、弧ADC 的长度分别为7π、11π∴圆的周长为71118πππ+=80BAD ∠=︒100C ∴∠=︒(圆内接四边形的对角互补)∴弧BAD 所对圆心角的度数为2200C ∠=︒则弧BAD 的长度为2001810360ππ⨯= 故选:C .【点睛】本题考查了圆周角定理、弧长的定义、圆内接四边形的性质,熟记圆的相关定理与性质是解题关键.2.(2019·浙江绍兴市·九年级期中)如图1,在等腰三角形ABC 中,AB=AC=4,BC=6.如图2,在底边BC 上取一点D ,连结AD ,使得∠DAC=∠ACD .如图3,将∠ACD 沿着AD 所在直线折叠,使得点C 落在点E 处,连结BE ,得到四边形ABED .则BE 的长是( )A .1B .65C .3215D .174【答案】A【分析】只要证明ABD MBE ∆∆∽,得AB BD BM BE =,求出BM 、BD 即可解决问题. 【详解】解:AB AC =,ABC C ∴∠=∠,DAC ACD ∠=∠,DAC ABC ∴∠=∠,C C ∠=∠,CAD CBA ∴∆∆∽, ∴CA CD CB CA , ∴464CD =, 83CD ∴=,810633BD BC CD =-=-=, DAM DAC DBA ∠=∠=∠,ADM ADB ∠=∠,ADM BDA ∴∆∆∽,∴AD DM BD DA =,即8310833DM =, 3215DM ∴=,103263155MB BD DM =-=-=, ABM C MED ∠=∠=∠,A ∴、B 、E 、D 四点共圆,ADB BEM ∴∠=∠,EBM EAD ABD ∠=∠=∠,ABD MBE ∴∆∆∽, ∴AB BD BM BE=, 6105314BM BD BE AB ⨯∴===.故选:A .【点睛】本题考查翻折变换、等腰三角形的判定和性质、相似三角形的判定和性质等知识,解题的关键是充分利用相似三角形的性质解决问题,本题需要三次相似解决问题,题目比较难,属于中考选择题中的压轴题.二、填空题3.(2020·黑龙江哈尔滨市·)如图,等边∠ABC 中,D 在BC 上,E 在AC 上,BD =CE ,连BE 、AD 交于F ,T 在EF 上,且DT =CE ,AF=50,TE =16,则FT =_____.【答案】17【分析】用“SAS”可判定∵ABD∵∵BCE ,得到∵AFE=60°,延长FE 至点G ,使得FG=FA ,连AG ,AT ,得到∵AFG 是等边三角形,证明A 、B 、D 、T 四点共圆,设法证明∵FAT∵∵GAE (ASA ),即可求得答案.【详解】∵∵ABC 为等边三角形,∵AB=AC=BC ,∵ABD=∵BCE=60°,在∵ABD 和∵BCE 中,60AB BC ABD BCE BD CE =⎧⎪∠=∠=︒⎨⎪=⎩,∵∵ABD∵∵BCE (SAS ),∵∵BAD=∵CBE ,∵∵ADC=∵CBE+∵BFD=∵BAD+∵B ,∵∵BFD=∵B=∵AFE=60°;延长FE 至点G ,使得FG=FA ,连AG ,AT ,∵∵AFE=60°,∵∵AFG 是等边三角形,∵AG=AF=FG=50,∵AGF=∵FAG=60°,∵∵BAF+∵EAF =∵CAG+∵EAF =60°,∵∵BAF=∵CAG ,∵DT=CE ,∵∵DBT=∵BTD ,∵∵BAD=∵CBE ,∵∵BAD=∵BTD ,∵A 、B 、D 、T 四点共圆,∵∵BAD=∵DAT ,∵∵FAT=∵GAE ,在∵FAT 和∵GAE 中,60FAT GAE AF AG AFG AGF ∠=∠⎧⎪=⎨⎪∠=∠=︒⎩, ∵∵FAT∵∵GAE (ASA ),∵FT= GE ,∵FG=50,TE=16, ∵FT=12(FG - TE)=17. 故答案为:17.【点睛】本题主要考查了等边三角形的判定和性质,全等三角形的判定和性质,圆周角定理等,作出辅助线,判断出∵FAT∵∵GAE 是解本题的关键.4.(2020·西安市铁一中学九年级二模)如图,正方形ABCD 中,9AB =,点E 为AD 上一点,且:1:2AE ED =,点P 为边AB 上一动点,连接PE ,过点E 作EF PE ⊥,交射线BC 于点F ,连接PF ,点M 为PF 中点,连接DM ,则DM 的最小值为________.【答案】10【分析】由已知可得AE=3,DE=6,又AB=9,90A ︒∠=,由勾股定理得=90PEF ︒∠=,90PBF ︒∠=,M 为PF 中点,可知M 为四边形BFEP 外接圆的圆心,BE 为圆M 的弦,故圆心M 在线段BE 的垂直平分线上,作线段BE 的垂直平分线GH 交BE 于G ,交CD 于H ,过点D 作DM GH ⊥于M ,此时的线段DM 即为所求最小值,过点E 作EN DM ⊥于N ,则四边形EGMN 为矩形,可得90GEN ︒∠=,GE=MN ,可证ABE NED ,可得AE BE DN DE =,代入数据得:,又,可得DM 的长度.【详解】∵:1:2AE ED =,AD=AB=9,∵AE=3,DE=6,又∵AB=9,90A ︒∠=,=∵90PEF ︒∠=,90PBF ︒∠=,∵B 、F 、E 、P 四点共圆,且PF 为直径,∵M 为PF 中点,∵M 为四边形BFEP 外接圆的圆心,∵E 、B 为定点,∵BE 为圆M 的弦,∵圆心M 在线段BE 的垂直平分线上,如下图,作线段BE 的垂直平分线GH 交BE 于G ,交CD 于H ,过点D 作DM GH ⊥于M ,此时的线段DM 即为所求最小值,过点E 作EN DM ⊥于N ,则四边形EGMN 为矩形,∵90GEN ︒∠=,GE=MN,∵90AEB DEN ︒∠+∠=,∵90A ︒∠=,∵90ABE AEB ︒∠+∠=,∵=DEN ABE ∠∠,又∵==90A DNE ︒∠∠,∵ABE NED , ∵AE BE DN DE=,即3DN =解得:∵BE=∵EG= ,,+2=10.【点睛】本题考查了圆内接四边形,圆的对称性,相似三角形的判定和性质,熟练掌握圆周角定理及其逆定理确定四点共圆是解题的关键.三、解答题5.(2020·沭阳县修远中学九年级期中)在边长为12cm 的正方形ABCD 中,点E 从点D 出发,沿边DC 以1cm/s 的速度向点C 运动,同时,点F 从点C 出发,沿边CB 以1cm/s 的速度向点B 运动,当点E 达到点C 时,两点同时停止运动,连接AE 、DF 交于点P ,设点E . F 运动时间为t 秒.回答下列问题:(1)如图1,当t 为多少时,EF 的长等于(2)如图2,在点E 、F 运动过程中,①求证:点A 、B 、F 、P 在同一个圆(∠O)上;②是否存在这样的t 值,使得问题①中的∠O 与正方形ABCD 的一边相切?若存在,求出t值;若不存在,请说明理由;③请直接写出问题①中,圆心O 的运动的路径长为_________.【答案】(1)t=4或8;(2)①证明见解析;②存在,t=3或12;③6cm .【分析】(1)由题意易得DE=CF=t ,则有EC=12-t ,然后利用勾股定理求解即可;(2)①由题意易证∵ADE∵∵DCF ,则有∵CDF=∵DAE ,然后根据平行线的性质可得∵APF=90°,进而可得∵B+∵APF=180°,则问题得证;②由题意可知当∵O 与正方形ABCD 的一边相切时,可分两种情况进行分类讨论求解:一是当圆与AD 相切时,一是当圆与边DC 相切时;③由动点E 、F 在特殊位置时得出圆心O 的运动轨迹,进而求解即可.【详解】解:(1)由题意易得:DE=CF=t ,四边形ABCD 是正方形,∴AB=CD=BC=AD=12cm ,∵C=∵B=∵ADC=∵DAB=90°,∴ EC=12-t ,EF 的长等于,∴在Rt∵CEF 中,222EF EC CF =+,即(()22212t t =-+解得124,8t t ==;(2)①由(1)可得AB=CD=BC=AD=12cm ,∵C=∵B=∵ADC=∵DAB=90°,DE=CF=t , ∴∵ADE∵∵DCF ,∴∵CDF=∵DAE ,∵CDF+∵PDA=90°,∴∵DAE+∵PDA=90°,∴∵ADP=∵APF=90°,∴∵APF+∵B=180°,由四边形APFB 内角和为360°可得:∵PAB+∵PFB=180°,∴点A 、B 、F 、P 在同一个圆(∵O)上;②由题意易得:当∵O 与正方形ABCD 的一边相切时,只有两种情况;a 、当∵O 与正方形ABCD 的边AD 相切时,如图所示:由题意可得AB 为∵O 的直径,∴t=12;b 、当∵O 与正方形ABCD 的边DC 相切于点G 时,连接OG 并延长交AB 于点M ,过点O 作OH∵BC 交BC 于点H ,连接OF ,如图所示:∴OG∵DC ,GM∵AB ,HF=HB ,∴四边形OMBH 、GOHC 是矩形,∴OH=BM=GC ,OG=HC ,AB=BC=12cm ,∴OH=6,CF=t ,BF=12-t , ∴126,662222t t t t HF CH OG OF t -==-===+-=+, 在Rt∵FOH 中,222OF OH FH =+,即2226+6622t t ⎛⎫⎛⎫=+- ⎪ ⎪⎝⎭⎝⎭, 解得:3t =;综上所述:当3t =或t=12时,∵O 与正方形ABCD 的边相切;③由(1)(2)可得:当点E 与点D 重合及点F 与点C 重合时,圆心在正方形的中心上;当点E 与点C 重合及点F 与点B 重合时,圆心在AB 的中点上,故圆心的运动轨迹为一条线段,如图所示:∴OP 即为圆心的运动轨迹,即OP=6cm .故答案为6cm .【点睛】本题主要考查圆的综合,熟练掌握圆的性质及切线定理解题的关键,注意运用分类讨论思想解决问题.6.(2020·安徽芜湖市·芜湖一中九年级)已知AD 为锐角ABC ∆的高,G 为AC 中点,DE AB ⊥于点E ,延长ED 至F ,使得GF GD =.(1)证明:AED AFC ∆∆;(2)证明:22AE CF BE AF ⋅=⋅;(3)若6,7,8AB BC CA ===,求四边形ACFD 的面积.【答案】(1)见解析;(2)见解析;(3)16【分析】(1)通过GA GD GC GF ===得A ,D ,F ,C 四点共圆,得到ADE ACF ∠=∠,结合90AED AFC ︒∠=∠=,证得AEDAFC ∆∆; (2)通过Rt AED Rt AFC ∆∆,Rt AED Rt DEB ∆∆证得22AE CF BE AF ⋅=⋅; (3)利用勾股定理求得AD ,BD ,CD ,在Rt ADB ∆中,求出DE ,AE ,得出ADE S ∆,借助2()ACF ADE S AC S AD∆∆=,求得ACF S ∆,再用Rt AEF Rt ADC ∆∆,得到2()AEF ADC AE S S AD ∆∆=⋅,最后ACFD AEF ACF AED S S S S ∆∆∆∆=+-.【详解】解:(1)∵GA GD GC GF ===∵,,,A D F C 四点共圆∵90AFC ADC ︒∠=∠=又∵ADE ACF ∠=∠∵Rt AED Rt AFC ∆∆(2)由(1)Rt AEDRt AFC ∆∆ ∵AF AE CF ED= 又∵Rt AEDRt DEB ∆∆ ∵AF AE DE CF ED EB== ∵2()AF AE DE AE CF ED EB EB =⋅= 即22AE CF BE AF ⋅=⋅(3)∵222236(7)64AD BD AD BD ⎧+=⎨+-=⎩∵311,22AD BD CD === ∵Rt ADB ∆中,2458AD BD AD DE AE AB AB ⋅====∵128ADE S ∆=而2()ACF ADE S AC S AD∆∆=∵ACF S ∆=同理利用Rt AEF Rt ADC ∆∆得到2()AEF ADC AE S S AD ∆∆=⋅=∵ACFD AEF ACF AED S S S S ∆∆∆∆=+-=. 【点睛】本题考查了四点共圆的判断,圆内接四边形的性质,圆周角定理的应用,相似三角形的证明,不规则图形的面积的求法,熟练掌握其中的联系,是解题的关键.。
四点共圆的7种判定方法证明

四点共圆的7种判定方法证明要证明四个点共圆,可以使用以下七种判定方法。
方法1:使用相交弧的性质假设四个点A、B、C、D共圆。
我们可以通过观察四个点连线所形成的相交弧的性质来进行判定。
即如果从A到B的弧和从C到D的弧的起点和终点重合,或者从B到C的弧和从D到A的弧的起点和终点重合,或者从C到D的弧和从A到B的弧的起点和终点重合,则可以证明四个点共圆。
方法2:使用余弦定理假设四个点A、B、C、D共圆,并且以A为圆心,AB为半径做圆,那么可以使用余弦定理证明。
首先,假设O为C到D的中点,我们可以根据余弦定理得出:AC² = AO² + OC² - 2 * AO * OC * cos∠AOC,同样地,我们可以得出:BD² = BO² + OD² - 2 * BO * OD * cos∠BOD。
由于共圆的性质,我们可以得到∠AOC = ∠BOD,因此AC² = BD²,从而可以证明四个点共圆。
方法3:使用向量运算假设四个点A、B、C、D共圆,我们可以使用向量运算进行证明。
首先,我们可以构建向量AB和向量AC,然后计算它们的叉乘,得到一个向量N。
同样地,我们可以构建向量AD和向量AC,并计算它们的叉乘,得到另一个向量M。
如果向量N和向量M垂直(即内积等于0),那么可以证明四个点共圆。
方法4:使用角平分线的性质假设四个点A、B、C、D共圆,并且AC和BD相交于点P。
那么根据角平分线的性质,我们可以得知∠APC=∠BPD。
同样地,由于共圆的性质,我们可以得到∠APC=∠BPC,因此∠BPD=∠BPC。
这意味着点P在角BPD的角平分线上,所以我们可以得出AD与BC也相交于点P,从而可以证明四个点共圆。
方法5:使用Miquel点的性质假设四个点A、B、C、D共圆,并且以AC为直径作圆,那么D一定在这个圆上。
同样地,以BD为直径作圆,C也一定在这个圆上。
初三:第14课 四点共圆

第14课 四点共圆一、基本结论与方法:判断四点共圆的方法有:1.到定点等距离的几个点在同一个圆上;2.同斜边的直角三角形的各顶点共圆;3.同底同侧张角相等的三角形的各顶点共圆;4、如果一个四边形的一组对角互补,那么它的四个顶点共圆;5、如果四边形的一个外角等于它的内对角,则它的四个顶点共圆;6、四边形的对角线相交于点P ,且PA•PC=PB•PD,那么四个顶点共圆;7、四边形ABCD 的一组对边AB 、DC 的延长线交于点P ,若PA•PB=PC•PD, 那么四个顶点共圆.托勒密定理:圆内接四边形的对边之积的和,等于对角线之积。
即:如图,四边形ABCD 内接于圆,求证:BD AC BC AD CD AB ⋅=⋅+⋅.DB二、例题与习题例1、如图,ABCD 是等腰梯形,求证:BD 2=AB•CD+BC 2.CD 例2、△ABC 中,∠A:∠B:∠C=1:2:4,:求证:BC AC AB 111=+A D例3、在边长为1的正七边形中,对角线AD=a,BG=b,求证:22)()(ab b a b a =-+.C 例4、两圆相交于A 、B,P 是BA 延长线上一点,PCD 、PEF 分别是两圆的割线,求证:C 、D 、E 、F 四点共圆。
F例5、由圆外定直线上任意点,引圆的两条切线,求证:两切点的连线必经过某定点。
CA例6、点P 是正三角形外接圆的劣弧AB 上一点,连接PC 交AB 于D ,求证:(1)PA+PB=PC;(2)111PA PBPD +=.例7、P为△ABC内一点,D、E、F分别在三角形的边上,已知P、D、C、E四点共圆,P、E、A、F四点共圆,求证:B、D、P、F四点共圆。
例8、设凸四边形ABCD的对角线互相垂直,垂足为E,证明:点E关于AB、BC、CD、DA 的对称点也共圆。
A例9、两个圆彼此相交,从它们的对称中心引出两条射线交圆周于不在同一直线上的四个点,证明:这四个点共圆。
例10、梯形ABCD的两条对角线相交于点K,分别以梯形的两腰围直径作圆,点K位于两圆之外,证明:由K向两圆所作的切线长度相等。
2024年广东九年级中考数学专题复习课件专题七+++隐圆与四点共圆

10. 如图,在矩形ABCD中,AB=2,BC=3,现有一根 长为2的木棒EF紧贴着矩形的边(即两个端点始终在矩 形的边上),按逆时针方向滑动一周,则木棒EF的中 点P在运动过程中所产生 的运动轨迹长度为__2_π_+__2__.
11.(2023·广州)如图,在正方形ABCD中,E为边AD上 的动点(不与点A,D重合),边BC关于BE对称的线段 为BF,连接AF.
解:∵∠ADE=∠ABE=90°, ∴A,D,B,E四点共圆,AE为四点所在圆的直径. 又∵△ABC为等腰直角三角形, ∴∠AED=∠ABD=45°. ∴△DAE为等腰直角三角形.
∴AE= 2 AD=2 2 .
5 对角互补的四边形的顶点共圆 8.如图,在四边形ABCD中,AB=AD=6,∠BAD=
1 到定点距离相等的各点共圆 几何语言:如图,∵OA=OB=OC=OD, ∴A,B,C,D四点共圆.
2 同斜边的两个直角三角形的顶点共圆 几何语言:如图,∵∠B=∠D=90°,∴A,B,C,D 四点共圆.证明提示:取斜边中点,
连接OD,OB.
3 对角互补的四边形的顶点共圆 几何语言:如图,∵∠A+∠C=180°,∴A,B,C, D四点共圆.
=∠CBN+∠ABN ∴∠AGC==9900°°.. ∴A,B,C,D,G五点共圆. ∵△GBF≌△GBC,
∴当G为 AD 的中点时,边BC上的高最大,S△GBC最 大.如图,过点G作GH⊥BC于点H.
则GH过圆心O,即过正方形中心O.
∴GH=OH+OG=
1 2
AB+
2 2
AB.
∴S△BGF=S△GBC=
60°,∠BCD=120°,四边形ABCD的周长是否存 在最大值?若存在,求出最大值;若不存在,请说 明理由.
成都石室中学初三数学-课件-中考专题冲刺一 四点共圆问题

(1)如图 1,若 A ,O ,C 三点在同一直线上,且 ABO 60 ,则 PMN 的形状是
.此
时 AD
.
BCBiblioteka 、知识点(2)如图 2,若 A , O , C 三点在同一直线上,且 AO 2 ,证明 PMN∽BAO ,并计算 BO 3
AD 的值; BC (3)在图 2 中,固定 AOB ,将 COD 绕点 O 旋转,直接写出 PM 的最大值
一、知识点
(2014 秋•诸暨市期末)如图,以 RtABC的斜边 BC 为一边在 ABC 的同侧作正方形 BCEF , 设正方形的中心为 O ,连结 AO ,如果 AB 2 , AO 3 2 ,则 tanAOB 的值为 ( )
一、知识点
已知:(如图)边长为 1 的正方形 ABCD 内接于 e O ,点 L 为劣弧 CD(不含端点)上任意一 点.直线 AL 交线段 CD 于点 K ,直线 CL 交直线 AD 于点 M ,直线 MK 交线段 BC 于点 N ,线段 LB 交线段 KN 于点 P .
谢 谢!
(1)求证: MN 2 ; (2)求证: B , M , L , N 四点共圆; (3)求证: KP NP .
一、知识点
已知:AOB 中,AB OB 2 ,COD 中,CD OC 3,ABO DCO ,连接 AD ,BC ,
点 M 、 N 、 P 分别为 OA 、 OD 、 BC 的中点.
北京师范大学出版社
% +
sin ������ =
−������ ± ������2 − 4������������ 2������
中考专题复习: 四点共圆问题
成都石室中学 张烁
一、知识点
如图所示在△ABC 中,∠ACB=65°,BD⊥AC 于点 D,CE⊥AB 于点 E,则∠AED=
中考数学圆中的重要模型四点共圆模型

圆中的重要模型-四点共圆模型四点共圆是初中数学的常考知识点,近年来,特别是四点共圆判定的题目出现频率较高。
相对四点共圆性质的应用,四点共圆的判定往往难度较大,往往是填空题或选择题的压轴题,而计算题或选择中四点共圆模型的应用(特别是最值问题),通常能简化运算或证明的步骤,使问题变得简单。
本文主要介绍四点共圆的四种重要模型。
四点共圆:若在同一平面内,有四个点在同一个圆上,则称这四个点共圆,一般简称为“四点共圆”。
模型1、定点定长共圆模型(圆的定义)【模型解读】若四个点到一定点的距离相等,则这四个点共圆。
这也是圆的基本定义,到定点的距离等于定长点的集合。
条件:如图,平面内有五个点O、A、B、C、D,使得OA=OB=OC=OD,结论:A、B、C、D四点共圆(其中圆心为O)。
例1、(2023•连云港期中)如图,点O为线段BC的中点,点A、C、D到点O的距离相等,若∠ABC=40°,则∠ADC的度数是.例2.(2022秋·江西赣州·九年级校联考期中)如图,点O为线段AB的中点,点B,C,D到点O的距离相等,连接AC,BD.则下面结论不一定成立的是()A.∠ACB=90°B.∠BDC=∠BAC C.AC平分∠BAD D.∠BCD+∠BAD=180°例3.(2021·湖北随州·统考中考真题)如图,在R t A B C中,90∠A C B∠=︒,O为A B的中点,O D平分A O COF例4.(2022·北京·清华附中九年级阶段练习)如图,四边形A B C D 中,D A D B D C==,72BD C ∠=︒,则B A C∠的度数为______.模型2、定边对双直角共圆模型同侧型 异侧型 1)定边对双直角模型(同侧型)条件:若平面上A 、B 、C 、D 四个点满足90A B DA C D ∠=∠=︒,结论:A 、B 、C 、D 四点共圆,其中AD 为直径。
【中考】四点共圆问题

2021年中考数学复习专题:四点共圆问题一、证明四点共圆1、如图,点E 、F 、G 、H 分别是菱形ABCD 各边的中点。
求证:E 、F 、G 、H 四点共圆。
2、如图,在△ABC 中,A D ⊥BC 于D ,DE ⊥AB 于E ,DF ⊥AC 于F. 求证:点B 、E 、F 、C 四点共圆。
(提示:点A 、E 、D 、F 共圆,△AEF = △ADF = △C )二、利用四点共圆解决问题1、已知:如图,AB = AC = AD ,△BAC = 2△CAD .求证:△BDC = 2△CBD .2、E FGH F E C B A DD C BA4、已知:如图,Rt△ABC 中,AB ⊥BC ,AB = 6,BC = 4 .点P 是△ABC 内部一动点,且满足△PAB = △PBC ,求线段CP 长的最小值。
PC B A 1 3、56789 101113 121415、已知:如下左图,在四边形ABCD 中,△A = 900,AB = AD, AB 上有一点E ,且CB = CD = CE = 1 , 连接DE,求△CDE 的周长。
16、如上中图,在四边形ABCD 中,AC ,BD 是它的对角线,相交于点O ,∠ABC =∠ADC =90°,∠BCD 是锐角,BD =BC .求证:sin ∠BCD =BDAC.17、已知:如上右图,BE 、CD 是△ABC 的高,连接DE 。
(1)求证:ΔABE ∽ ΔACD.(2)若∠BAC =120°,点M 是BC 的中点,若DM = 1 ,求DE 的长。
CB A DE AMDECB。
