高考数学(理)总复习：利用导数解决函数零点问题

合集下载

高考数学总复习考点知识与题型专题讲解22 利用导数研究函数的零点

高考数学总复习考点知识与题型专题讲解§3.7 利用导数研究函数的零点考试要求函数零点问题在高考中占有很重要的地位，主要涉及判断函数零点的个数或范围．高考常考查三次函数与复合函数的零点问题，以及函数零点与其他知识的交汇问题，一般作为解答题的压轴题出现．题型一利用函数性质研究函数的零点例1已知函数f (x )＝x sin x －1.(1)讨论函数f (x )在区间⎣⎢⎡⎦⎥⎤－π2，π2上的单调性；(2)证明：函数y ＝f (x )在[0，π]上有两个零点． (1)解因为函数f (x )的定义域为R ，f (－x )＝－x sin(－x )－1＝f (x )，所以函数f (x )为偶函数，又f ′(x )＝sin x ＋x cos x ，且当x ∈⎣⎢⎡⎦⎥⎤0，π2时，f ′(x )≥0，所以函数f (x )在⎣⎢⎡⎦⎥⎤0，π2上单调递增，又函数f (x )为偶函数，所以f (x )在⎣⎢⎡⎭⎪⎫－π2，0上单调递减，综上，函数f (x )在⎣⎢⎡⎦⎥⎤0，π2上单调递增，在⎣⎢⎡⎭⎪⎫－π2，0上单调递减．(2)证明由(1)得，f (x )在⎣⎢⎡⎦⎥⎤0，π2上单调递增，又f (0)＝－1<0，f ⎝ ⎛⎭⎪⎫π2＝π2－1>0，所以f (x )在⎣⎢⎡⎦⎥⎤0，π2内有且只有一个零点，当x ∈⎝ ⎛⎦⎥⎤π2，π时，令g (x )＝f ′(x )＝sin x ＋x cos x ，则g ′(x )＝2cos x －x sin x ，当x ∈⎝ ⎛⎦⎥⎤π2，π时，g ′(x )<0恒成立，即g (x )在⎝ ⎛⎦⎥⎤π2，π上单调递减，又g ⎝ ⎛⎭⎪⎫π2＝1>0，g (π)＝－π<0，则存在m ∈⎝ ⎛⎦⎥⎤π2，π，使得g (m )＝0，且当x ∈⎝ ⎛⎭⎪⎫π2，m 时，g (x )>g (m )＝0，即f ′(x )>0，则f (x )在⎝ ⎛⎭⎪⎫π2，m 上单调递增，当x ∈(m ，π]时，有g (x )<g (m )＝0，即f ′(x )<0，则f (x )在(m ，π]上单调递减，又f ⎝ ⎛⎭⎪⎫π2＝π2－1>0，f (π)＝－1<0，所以f (x )在(m ，π]上有且只有一个零点，综上，函数y ＝f (x )在[0，π]上有2个零点．思维升华利用函数性质研究函数的零点，主要是根据函数单调性、奇偶性、最值或极值的符号确定函数零点的个数，此类问题在求解过程中可以通过数形结合的方法确定函数存在零点的条件．跟踪训练1(2023·芜湖模拟)已知函数f (x )＝ax ＋(a －1)ln x ＋1x －2，a ∈R . (1)讨论f (x )的单调性；(2)若f (x )只有一个零点，求a 的取值范围．解 (1)函数f (x )的定义域为(0，＋∞)，f ′(x )＝a ＋a －1x －1x 2＝(ax －1)(x ＋1)x 2，①若a ≤0，则f ′(x )<0，f (x )在(0，＋∞)上单调递减；②若a >0，则当x ∈⎝ ⎛⎭⎪⎫0，1a 时，f ′(x )<0，f (x )单调递减，当x ∈⎝ ⎛⎭⎪⎫1a ，＋∞时，f ′(x )>0，f (x )单调递增．综上，当a ≤0时，f (x )在(0，＋∞)上单调递减；当a >0时，f (x )在⎝ ⎛⎭⎪⎫0，1a 上单调递减，在⎝ ⎛⎭⎪⎫1a ，＋∞上单调递增．(2)若a ≤0，f ⎝ ⎛⎭⎪⎫1e ＝a e ＋1－a ＋e －2＝⎝ ⎛⎭⎪⎫1e －1a ＋e －1>0，f (1)＝a －1<0.结合函数的单调性可知，f (x )有唯一零点．若a >0，因为函数在⎝ ⎛⎭⎪⎫0，1a 上单调递减，在⎝ ⎛⎭⎪⎫1a ，＋∞上单调递增，所以要使得函数有唯一零点，只需f (x )min ＝f ⎝ ⎛⎭⎪⎫1a ＝1－(a －1)ln a ＋a －2＝(a －1)(1－ln a )＝0，解得a ＝1或a＝e.综上，a ≤0或a ＝1或a ＝e. 题型二数形结合法研究函数的零点例2(2023·郑州质检)已知函数f (x )＝e x －ax ＋2a ，a ∈R . (1)讨论函数f (x )的单调性； (2)求函数f (x )的零点个数．解 (1)f (x )＝e x －ax ＋2a ，定义域为R ，且f ′(x )＝e x －a ，当a ≤0时，f ′(x )>0，则f (x )在R 上单调递增；当a >0时，令f ′(x )＝0，则x ＝ln a ，当x <ln a 时，f ′(x )<0，f (x )单调递减；当x >ln a 时，f ′(x )>0，f (x )单调递增．综上所述，当a ≤0时，f (x )在R 上单调递增；当a >0时，f (x )在(－∞，ln a )上单调递减，在(ln a ，＋∞)上单调递增． (2)令f (x )＝0，得e x ＝a (x －2)，当a ＝0时，e x ＝a (x －2)无解，∴f (x )无零点，当a ≠0时，1a ＝x －2e x ，令φ(x )＝x －2e x ，x ∈R ，∴φ′(x )＝3－xe x ，当x ∈(－∞，3)时，φ′(x )>0；当x ∈(3，＋∞)时，φ′(x )<0，∴φ(x )在(－∞，3)上单调递增，在(3，＋∞)上单调递减，且φ(x )max ＝φ(3)＝1e 3，又x →＋∞时，φ(x )→0， x →－∞时，φ(x )→－∞， ∴φ(x )的图象如图所示．当1a >1e 3，即0<a <e 3时，f (x )无零点；当1a ＝1e 3，即a ＝e 3时，f (x )有一个零点；当0<1a <1e 3，即a >e 3时，f (x )有两个零点；当1a <0，即a <0时，f (x )有一个零点．综上所述，当a ∈[0，e 3)时，f (x )无零点；当a ∈(－∞，0)∪{e 3}时，f (x )有一个零点；当a ∈(e 3，＋∞)时，f (x )有两个零点．思维升华含参数的函数零点个数，可转化为方程解的个数，若能分离参数，可将参数分离出来后，用x 表示参数的函数，作出该函数的图象，根据图象特征求参数的范围或判断零点个数．跟踪训练2(2023·长沙模拟)已知函数f (x )＝a ln x －2x . (1)若a ＝2，求曲线y ＝f (x )在x ＝1处的切线方程； (2)若函数f (x )在(0,16]上有两个零点，求a 的取值范围．解 (1)当a ＝2时，f (x )＝2ln x －2x ，该函数的定义域为(0，＋∞)，f ′(x )＝2x －1x ，又f (1)＝－2，f ′(1)＝1，因此，曲线y ＝f (x )在x ＝1处的切线方程为y ＋2＝x －1，即x －y －3＝0. (2)①当a ≤0时，f ′(x )＝a x －1x<0，则f (x )在(0，＋∞)上单调递减，不符合题意； ②当a >0时，由f (x )＝a ln x －2x ＝0可得2a ＝ln xx ，令g (x )＝ln x x，其中x >0，则直线y ＝2a 与曲线y ＝g (x )的图象在(0,16]内有两个交点， g ′(x )＝x x －ln x2x x ＝2－ln x2x x，令g ′(x )＝0，可得x ＝e 2<16，列表如下，所以函数g (x )在区间(0,16]上的极大值为g (e 2)＝2e ，且g (16)＝ln 2，作出g (x )的图象如图所示．由图可知，当ln 2≤2a <2e ，即e<a ≤2ln 2时，直线y ＝2a 与曲线y ＝g (x )的图象在(0,16]内有两个交点，即f (x )在(0,16]上有两个零点，因此，实数a 的取值范围是⎝ ⎛⎦⎥⎤e ，2ln 2.题型三构造函数法研究函数的零点例3(12分)(2022·新高考全国Ⅰ)已知函数f (x )＝e x －ax 和g (x )＝ax －ln x 有相同的最小值． (1)求a ；[切入点：求f (x )，g (x )的最小值](2)证明：存在直线y ＝b ，其与两条曲线y ＝f (x )和y ＝g (x )共有三个不同的交点，并且从左到右的三个交点的横坐标成等差数列．[关键点：利用函数的性质与图象判断e x －x ＝b ，x －ln x ＝b 的解的个数及解的关系]思维升华涉及函数的零点(方程的根)问题，主要利用导数确定函数的单调区间和极值点，根据函数零点的个数寻找函数在给定区间内的极值以及区间端点的函数值与0的关系，从而求得参数的取值范围．跟踪训练3(2021·全国甲卷)已知a>0且a≠1，函数f(x)＝x aa x(x>0)．(1)当a＝2时，求f(x)的单调区间；(2)若曲线y＝f(x)与直线y＝1有且仅有两个交点，求a的取值范围．解(1)当a＝2时，f(x)＝x22x(x>0)，f′(x)＝x(2－x ln 2)2x(x>0)，令f′(x)>0，则0<x<2ln 2，此时函数f(x)单调递增，令f ′(x )<0，则x >2ln 2，此时函数f (x )单调递减，所以函数f (x )的单调递增区间为⎝ ⎛⎭⎪⎫0，2ln 2，单调递减区间为⎝ ⎛⎭⎪⎫2ln 2，＋∞.(2)曲线y ＝f (x )与直线y ＝1有且仅有两个交点，可转化为方程x a a x ＝1(x >0)有两个不同的解，即方程ln x x ＝ln aa 有两个不同的解．设g (x )＝ln xx (x >0)，则g ′(x )＝1－ln x x 2(x >0)，令g ′(x )＝1－ln xx 2＝0，得x ＝e ，当0<x <e 时，g ′(x )>0，函数g (x )单调递增，当x >e 时，g ′(x )<0，函数g (x )单调递减，故g (x )max ＝g (e)＝1e ，且当x >e 时，g (x )∈⎝ ⎛⎭⎪⎫0，1e ，又g (1)＝0，所以0<ln a a <1e ，所以a >1且a ≠e ，即a 的取值范围为(1，e)∪(e ，＋∞)．课时精练1．(2023·济南质检)已知函数f (x )＝ln x ＋axx ，a ∈R . (1)若a ＝0，求f (x )的最大值；(2)若0<a <1，求证：f (x )有且只有一个零点．(1)解若a ＝0，则f (x )＝ln x x ，其定义域为(0，＋∞)，∴f ′(x )＝1－ln xx 2，由f ′(x )＝0，得x ＝e ，∴当0<x <e 时，f ′(x )>0；当x >e 时，f ′(x )<0，∴f (x )在(0，e)上单调递增，在(e ，＋∞)上单调递减，∴f (x )max ＝f (e)＝1e .(2)证明 f ′(x )＝⎝ ⎛⎭⎪⎫1x ＋a x －ln x －ax x 2＝1－ln x x 2，由(1)知，f (x )在(0，e)上单调递增，在(e ，＋∞)上单调递减，∵0<a <1，∴当x >e 时，f (x )＝ln x ＋ax x ＝a ＋ln x x>0，故f (x )在(e ，＋∞)上无零点；当0<x <e 时，f (x )＝ln x ＋ax x ，∵f ⎝ ⎛⎭⎪⎫1e ＝a －e<0，f (e)＝a ＋1e >0，且f (x )在(0，e)上单调递增，∴f (x )在(0，e)上有且只有一个零点，综上，f (x )有且只有一个零点．2．函数f (x )＝ax ＋x ln x 在x ＝1处取得极值．(1)求f (x )的单调区间；(2)若y ＝f (x )－m －1在定义域内有两个不同的零点，求实数m 的取值范围．解(1)f(x)的定义域为(0，＋∞)，f′(x)＝a＋ln x＋1，由f′(1)＝a＋1＝0，解得a＝－1.则f(x)＝－x＋x ln x，∴f′(x)＝ln x，令f′(x)>0，解得x>1；令f′(x)<0，解得0<x<1.∴f(x)的单调递增区间为(1，＋∞)，单调递减区间为(0,1)．(2)y＝f(x)－m－1在(0，＋∞)内有两个不同的零点，则函数y＝f(x)与y＝m＋1的图象在(0，＋∞)内有两个不同的交点．由(1)知，f(x)在(0,1)上单调递减，在(1，＋∞)上单调递增，f(x)min＝f(1)＝－1，f(e)＝0，作出f(x)图象如图．由图可知，当－1<m＋1<0，即－2<m<－1时，y＝f(x)与y＝m＋1的图象有两个不同的交点．因此实数m的取值范围是(－2，－1)．3．(2022·河南名校联盟模拟)已知f(x)＝(x－1)e x－13ax3＋13a(a∈R)．(1)若函数f(x)在[0，＋∞)上单调递增，求a的取值范围；(2)当a≤e时，讨论函数f(x)零点的个数．解(1)f(x)＝(x－1)e x－13ax3＋13a，则f′(x)＝x(e x－ax)．∵函数f(x)在[0，＋∞)上单调递增，∴f′(x)＝x(e x－ax)≥0在[0，＋∞)上恒成立，则e x－ax≥0，x≥0.当x＝0时，则1≥0，即a∈R；当x>0时，则a≤e x x，构建g(x)＝e xx(x>0)，则g′(x)＝(x－1)e xx2(x>0)，令g′(x)>0，则x>1，令g′(x)<0，则0<x<1，∴g(x)在(0,1)上单调递减，在(1，＋∞)上单调递增，则g(x)≥g(1)＝e，∴a≤e，综上所述，a≤e.(2)f(x)＝(x－1)e x－13ax3＋13a＝(x－1)⎣⎢⎡⎦⎥⎤e x－13a(x2＋x＋1)，令f(x)＝0，则x＝1或e x－13a(x2＋x＋1)＝0，对于e x－13a(x2＋x＋1)＝0，即e xx2＋x＋1＝13a，构建h(x)＝e xx2＋x＋1，则h′(x)＝x(x－1)e x (x2＋x＋1)2，令h′(x)>0，则x>1或x<0，令h′(x)<0，则0<x<1，∴h(x)在(－∞，0)，(1，＋∞)上单调递增，在(0,1)上单调递减，h(0)＝1，h(1)＝e3且h(x)>0，当x∈R时恒成立，则当a＝e时，e xx2＋x＋1＝13a有两个根x1＝1，x2<0；当0<a<e时，e xx2＋x＋1＝13a只有一个根x3<0；当a≤0时，e xx2＋x＋1＝13a无根．综上所述，当a≤0时，f(x)只有一个零点；当0<a≤e时，f(x)有两个零点．4．(2022·全国乙卷)已知函数f(x)＝ax－1x－(a＋1)ln x.(1)当a＝0时，求f(x)的最大值；(2)若f(x)恰有一个零点，求a的取值范围．解(1)当a＝0时，f(x)＝－1x－ln x(x＞0)，所以f′(x)＝1x2－1x＝1－xx2.当x∈(0,1)时，f′(x)＞0，f(x)单调递增；当x∈(1，＋∞)时，f′(x)＜0，f(x)单调递减，所以f(x)max＝f(1)＝－1.(2)由f (x )＝ax －1x －(a ＋1)ln x (x ＞0)，得f ′(x )＝a ＋1x 2－a ＋1x ＝(ax －1)(x －1)x 2(x ＞0)．当a ＝0时，由(1)可知，f (x )不存在零点；当a ＜0时，f ′(x )＝a ⎝ ⎛⎭⎪⎫x －1a (x －1)x 2，当x ∈(0,1)时，f ′(x )＞0，f (x )单调递增，当x ∈(1，＋∞)时，f ′(x )＜0，f (x )单调递减，所以f (x )max ＝f (1)＝a －1＜0，所以f (x )不存在零点；当a ＞0时，f ′(x )＝a ⎝ ⎛⎭⎪⎫x －1a (x －1)x 2，当a ＝1时，f ′(x )≥0，f (x )在(0，＋∞)上单调递增，因为f (1)＝a －1＝0，所以函数f (x )恰有一个零点；当a ＞1时，0＜1a ＜1，故f (x )在⎝ ⎛⎭⎪⎫0，1a ，(1，＋∞)上单调递增，在⎝ ⎛⎭⎪⎫1a ，1上单调递减．因为f (1)＝a －1＞0，所以f ⎝ ⎛⎭⎪⎫1a ＞f (1)＞0，当x →0＋时，f (x )→－∞，由零点存在定理可知f (x )在⎝ ⎛⎭⎪⎫0，1a 上必有一个零点，所以a ＞1满足条件，当0＜a ＜1时，1a ＞1，故f (x )在(0,1)，⎝ ⎛⎭⎪⎫1a ，＋∞上单调递增，在⎝ ⎛⎭⎪⎫1，1a 上单调递减．因为f (1)＝a －1＜0，所以f ⎝ ⎛⎭⎪⎫1a ＜f (1)＜0，当x →＋∞时，f (x )→＋∞，由零点存在定理可知f (x )在⎝ ⎛⎭⎪⎫1a ，＋∞上必有一个零点，即0＜a ＜1满足条件．综上，若f (x )恰有一个零点，则a 的取值范围为(0，＋∞)．。

高考数学一轮总复习课件：专题研究利用导数研究函数的零点

g′(x)＝－sinx＋（1＋1 x）2.
当x∈－1，π2 时，g′(x)单调递减，
由g′(0)＝1>0，g′
π 2
＝－1＋
1 1＋π2 2
<0，可得g′(x)在
－1，π2 上有唯一零点，设为α.
当x∈(－1，α)时，g′(x)>0；当x∈α，π2 时，g′(x)<0. 所以g(x)在(－1，α)上单调递增，在α，π2 上单调递减．故g(x)在－1，π2 上存在唯一极大值点，即f′(x)在－1，π2 上存在唯一极大值点．
①当 a>1 时，方程 g(x)＝a 无解，即 f(x)没有零点； ②当 a＝1 时，方程 g(x)＝a 有且只有一解，即 f(x)有唯一的零点； ③当 0<a<1 时，方程 g(x)＝a 有两解，即 f(x)有两个零点； ④当 a≤0 时，方程 g(x)＝a 有且只有一解，即 f(x)有唯一的零点．综上，当 a>1 时，f(x)没有零点；当 a＝1 或 a≤0 时，f(x)有唯一的零点；当 0<a<1 时，f(x)有两个零点而f
π 2
>0，f(π)＝－ln(1＋π)<0，所以f(x)在
π2 ，π
上有
唯一零点．
④当x∈(π，＋∞)时，ln(x＋1)>1，
所以f(x)<0，从而f(x)在(π，＋∞)上没有零点．
综上，f(x)有且仅有2个零点．
【答案】略
状元笔记
证明与零点有关的不等式，函数的零点本身就是一个条件，即零点对应的函数值为0，证明的思路一般对条件等价转化，构造合适的新函数，利用导数知识探讨该函数的性质(如单调性、极值情况等)再结合函数图象来解决．

第3章第6课时利用导数解决函数的零点问题-备战2025年高考数学一轮复习(解析版)

第6课时利用导数解决函数的零点问题考点一判断、证明或讨论函数零点的个数[典例1]已知函数f(x)＝x sin x－32.判断函数f(x)在(0，π)内的零点个数，并加以证明．[解]f(x)在(0，π)内有且只有两个零点．证明如下：因为f′(x)＝sin x＋x cos x，当x∈0f′(x)＞0.又f(x)＝x sin x－32，从而有f(0)＝－32＜0，f＝π−32＞0，且f(x)在0所以f(x)在0又f(x)在0f(x)在0当xπ时，令g(x)＝f′(x)＝sin x＋x cos x.由1＞0，g(π)＝－π＜0，且g(x)π上的图象是连续不断的，故存在mπ，使得g(m)＝0.由g′(x)＝2cos x－x sin x，知xπ时，有g′(x)＜0，从而g(x)2π上单调递减．当x时，g(x)＞g(m)＝0，即f′(x)＞0，从而f(x)上单调递增，故当x时，f(x)＞f＝π−32＞0，故f(x)上无零点；当x∈(m，π)时，有g(x)＜g(m)＝0，即f′(x)＜0，从而f(x)在(m，π)上单调递减．又f(m)＞0，f(π)＜0，且f(x)在(m，π)上的图象是连续不断的，从而f(x)在(m，π)内有且仅有一个零点．综上所述，f(x)在(0，π)内有且只有两个零点．利用导数求函数的零点个数的常用方法(1)数形结合法．利用导数研究函数的性质，画出相应函数的图象，数形结合求解．(2)零点存在定理法．先判断函数在某区间有零点，再结合图象与性质确定函数有多少个零点．(3)分离参数法．转化为一条直线与一个复杂函数图象交点个数问题．[跟进训练]1．(2023·湖南师大附中三模节选)已知函数f(x)＝e x－(a∈R)，试讨论函数f(x)零点个数．[解]由f(x)＝e x－＝0，得x e x＝a(x≠0)，设h(x)＝x e x，则h′(x)＝(x＋1)e x，当x＜－1时，h′(x)＜0，当－1＜x＜0，x＞0时，h′(x)＞0，所以h(x)＝x e x在(－1，0)，(0，＋∞)上单调递增；在(－∞，－1)上单调递减，所以h(x)min＝h(－1)＝－1e，据此可画出h(x)＝x e x的大致图象如图，所以，①当a＜－1e或a＝0时，f(x)无零点；②当a＝－1e或a＞0时，f(x)有一个零点；③1＜a＜0时，f(x)有两个零点．[典例2](2022·全国乙卷)已知函数f(x)＝ln(1＋x)＋ax e－x.(1)当a＝1时，求曲线y＝f(x)在点(0，f(0))处的切线方程；(2)若f(x)在区间(－1，0)，(0，＋∞)各恰有一个零点，求a的取值范围．[思维流程][解](1)f(x)的定义域为(－1，＋∞)，当a＝1时，f(x)＝ln(1＋x)＋e，f(0)＝0，所以切点为(0，0)．f′(x)＝11++1−e，f′(0)＝2，所以切线斜率为2，所以曲线y＝f(x)在点(0，f(0))处的切线方程为y＝2x.(2)f(x)＝ln(1＋x)＋B，f′(x)＝11++设g(x)＝e x＋a(1－x2)，①若a>0，当x∈(－1，0)时，g(x)＝e x＋a(1－x2)>0，即f′(x)>0，所以f(x)在(－1，0)上单调递增，f(x)<f(0)＝0，故f(x)在(－1，0)上没有零点，不合题意．②若－1<a<0，当x∈(0，＋∞)时，则g′(x)＝e x－2ax>0，所以g(x)在(0，＋∞)上单调递增，所以g(x)>g(0)＝1＋a>0，即f′(x)>0，所以f(x)在(0，＋∞)上单调递增，f(x)>f(0)＝0，故f(x)在(0，＋∞)上没有零点，不合题意．③若a<－1，(ⅰ)当x∈(0，＋∞)时，则g′(x)＝e x－2ax>0，所以g(x)在(0，＋∞)上单调递增，g(0)＝1＋a<0，g(1)＝e>0，所以存在m∈(0，1)，使得g(m)＝0，即f′(m)＝0，当x∈(0，m)时，f′(x)<0，f(x)单调递减，当x∈(m，＋∞)时，f′(x)>0，f(x)单调递增，所以当x∈(0，m)时，f(x)<f(0)＝0，当x→＋∞，f(x)→＋∞，所以f(x)在(m，＋∞)上有唯一零点，在(0，m)上没有零点，即f(x)在(0，＋∞)上有唯一零点．(ⅱ)当x∈(－1，0)时，g(x)＝e x＋a(1－x2)，设h(x)＝g′(x)＝e x－2ax，h′(x)＝e x－2a>0，所以g′(x)在(－1，0)上单调递增，g′(－1)＝1e＋2a<0，g′(0)＝1>0，所以存在n∈(－1，0)，使得g′(n)＝0，当x∈(－1，n)时，g′(x)<0，g(x)单调递减，当x∈(n，0)时，g′(x)>0，g(x)单调递增，g(x)<g(0)＝1＋a<0，又g(－1)＝1e>0，所以存在t∈(－1，n)，使得g(t)＝0，即f′(t)＝0，当x∈(－1，t)时，f(x)单调递增，当x∈(t，0)时，f(x)单调递减，又x→－1，f(x)→－∞，而f(0)＝0，所以当x∈(t，0)时，f(x)>0，所以f(x)在(－1，t)上有唯一零点，在(t，0)上无零点，即f(x)在(－1，0)上有唯一零点，所以a<－1，符合题意．④当a＝0时，f(x)＝ln(1＋x)在(－1，＋∞)上单调递增，不符合题意．⑤当a＝－1时，f′(x)＝e+2−11+·e，令k(x)＝e x＋x2－1，则k′(x)＝e x＋2x，当x>0时，k′(x)>0，k(x)单调递增，k(x)>k(0)＝0，即f′(x)>0，f(x)单调递增，f(x)>f(0)＝0，不合题意．所以若f(x)在区间(－1，0)，(0，＋∞)各恰有一个零点，则a的取值范围为(－∞，－1)．【教师备选资源】(2020·全国Ⅰ卷)已知函数f(x)＝e x－a(x＋2)．(1)当a＝1时，讨论f(x)的单调性；(2)若f(x)有两个零点，求a的取值范围．[思维流程][解](1)当a＝1时，f(x)＝e x－x－2，则f′(x)＝e x－1.当x<0时，f′(x)<0；当x>0时，f′(x)>0.所以f(x)在(－∞，0)上单调递减，在(0，＋∞)上单调递增．(2)f′(x)＝e x－a.当a≤0时，f′(x)>0，所以f(x)在(－∞，＋∞)上单调递增，故f(x)至多存在一个零点，不合题意．当a>0时，由f′(x)＝0可得x＝ln a．当x∈(－∞，ln a)时，f′(x)<0；当x∈(ln a，＋∞)时，f′(x)>0．所以f(x)在(－∞，ln a)上单调递减，在(ln a，＋∞)上单调递增．故当x＝ln a时，f(x)取得最小值，最小值为f(ln a)＝－a(1＋ln a)．(ⅰ)若0<a ≤1e ，则f (ln a )≥0，f (x )在(－∞，＋∞)至多存在一个零点，不合题意．(ⅱ)若a >1e ，则f (ln a )<0.由于f (－2)＝e -2>0，所以f (x )在(－∞，ln a )上存在唯一零点．由(1)知，当x >2时，e x －x －2>0，所以当x >4且x >2ln (2a )时，f (x )＝e 2·e 2−+2>e ln2·+2－a (x＋2)＝2a >0.故f (x )在(ln a ，＋∞)上存在唯一零点．从而f (x )在(－∞，＋∞)上有两个零点．综上，a+∞.与函数零点有关的参数范围问题，往往利用导数研究函数的单调区间和极值点，并结合特殊点，从而判断函数的大致图象，讨论其图象与x 轴的位置关系，进而确定参数的取值范围或通过对方程等价变形转化为两个函数图象的交点问题．[跟进训练]2．(1)(2023·全国乙卷)函数f (x )＝x 3＋ax ＋2存在3个零点，则a 的取值范围是()A ．(－∞，－2)B ．(－∞，－3)C ．(－4，－1)D ．(－3，0)(2)已知函数f (x )＝12x 2－a ln x ，若a >0，函数f (x )在区间(1，e)上恰有两个零点，求a 的取值范围．(1)B[由题意知f ′(x )＝3x 2＋a ，要使函数f (x )存在3个零点，则f ′(x )＝0要有2个不同的根，则a <0．令3x 2＋a ＝0，解得x ＝令f ′(x )>0，则x <x令f ′(x )<0x 所以f (x )在−∞，−+∞上单调递增，在−上单调递减，所以要使f (x )存在3个零点，则>0，<0，+2>0，+2<0，解得a <－3.故选B.](2)[解]函数f (x )＝12x 2－a ln x 的定义域为(0，＋∞)，f ′(x )＝x －＝2−.因为a >0，由f ′(x )>0，得x >，由f ′(x )<0，得0<x <.即f (x )在(0，)上单调递减，在(，＋∞)上单调递增．①若≤1，即0<a ≤1时，f (x )在(1，e)上单调递增，f (1)＝12，f (x )在区间(1，e)上无零点．②若1<<e ，即1<a <e 2时，f (x )在(1，)上单调递减，在(，e)上单调递增，f (x )min ＝f ()＝12a (1－ln a )．∵f (x )在区间(1，e)上恰有两个零点，∴1=12＞0，=121−ln ＜0，e =12e 2−＞0，∴e<a <12e 2.③若≥e ，即a ≥e 2时，f (x )在(1，e)上单调递减，f (1)＝12>0，f (e)＝12e 2－a <0，f (x )在区间(1，e)上只有一个零点．综上，f (x )在区间(1，e)上恰有两个零点时，a 的取值范围是e ，12e 2.在解导数综合题时，经常会碰到这种情形：导函数存在零点，但是不能求出具体的解，这种零点我们称之为隐零点，相应的问题称为隐零点问题．这类问题的解题思路是对函数的零点设而不求，通过整体代换和过渡，再结合题目条件解决问题．[典例]已知函数f (x )＝x e x －ln x －1，若f (x )≥mx 恒成立，求实数m 的取值范围．[赏析]法一(分离变量法)：由f (x )≥mx 得x e x －ln x －1≥mx (x ＞0)，即m≤x−ln K1，令φ(x)＝x−ln K1，则φ′(x)＝2e+ln2，令h(x)＝x2e x＋ln x，则h′(x)＝(2x＋x2)e x＋1＞0，所以h(x)在(0，＋∞)上单调递增．切入点：零点存在定理，发现零点，设而不求又＝1e2e1e－1＜e2e2－1＝0，h(1)＝e＞0，所以h(x)1存在零点x0，即h(x0)＝02e0＋ln x0＝0，突破点：等价变形，寻找等量关系02e0＋ln x0＝0⇔0e0＝－ln00＝ln(e ln10)，关键点：辅助函数，得出等量关系令y＝x e x(x＞0)，因为y′＝(x＋1)e x＞0，所以y＝x e x在(0，＋∞)上单调递增，故x0＝ln10＝－ln x0，即e0＝10，所以φ(x)在(0，x0)上单调递减，在(x0，＋∞)上单调递增．落脚点：整体代换，代入求值所以φ(x)min＝φ(x0)＝0e0−ln0−10＝1+0−10＝1，所以m≤1.法二(朗博同构法)：由f(x)≥mx得x e x－ln x－1≥mx(x＞0)，所以e rln−ln−1≥B＞0，由切线不等式得e rln−+ln−1≥0，故(1－m)x≥0(x＞0)恒成立，所以1－m≥0，即m≤1.函数零点存在但不可求时，常虚设零点，利用零点存在定理估计所设零点所在的一个小范围(区间长度小于1个单位)，然后利用零点所满足的关系进行代换化简．[跟进训练]1．若a ln x－(2a＋1)x<1－2ax在x∈(1，＋∞)上恒成立，求整数a的最大值．参考数据：ln3<43，ln4>[解]因为a ln x－(2a＋1)x<1－2ax在(1，＋∞)上恒成立，即a<r1ln在x∈(1，＋∞)上恒成立．令h(x)＝r1ln，x>1，可得h′(x)＝ln K1−1ln2，令t(x)＝ln x－1－1(x>1)，可得t(x)在(1，＋∞)上单调递增，且t(3)<0，t(4)>0，所以存在x0∈(3，4)，使得t(x0)＝ln x0－10－1＝0，从而h(x)在(1，x0)上单调递减，在(x0，＋∞)上单调递增，所以h(x)min＝h(x0)＝0+1ln0＝0+110+1＝x0∈(3，4)．因为a<r1ln在(1，＋∞)上恒成立，所以a<h(x)min＝x0，所以整数a的最大值为3. 2．设函数f(x)＝e x－x－2，k为整数，且当x>0时，(x－k)·f′(x)＋x＋1>0，求k 的最大值．[解]由题意知f′(x)＝e x－1.(x－k)·f′(x)＋x＋1＞0，即(x－k)(e x－1)＋x＋1>0，得k<x＋r1e−1(x>0)恒成立，令g(x)＝r1e＋x(x>0)，得g′(x)1x>0)．令h(x)＝e x－x－2(x>0)，则h′(x)＝e x－1>0，故h(x)在(0，＋∞)上单调递增．又因为h(1)<0，h(2)>0，所以函数h(x)存在唯一零点α∈(1，2)．当x∈(0，α)时，g′(x)<0；当x∈(α，＋∞)时，g′(x)>0，所以g(x)min＝g(α)＝r1e−1＋α.又h(α)＝eα－α－2＝0，所以eα＝α＋2且α∈(1，2)，则g(x)min＝g(α)＝1＋α∈(2，3)，所以k的最大值为2.课时分层作业(二十二)利用导数解决函数的零点问题1．(2024·河南郑州模拟)已知函数f(x)＝x ln x＋a－ax(a∈R)．(1)若a＝1，求函数f(x)的极值；(2)若函数f(x)在区间[1，e]上有且只有一个零点，求实数a的取值范围．[解](1)由题可得，函数f(x)的定义域为(0，＋∞)，f′(x)＝ln x＋1－a.若a＝1，则f′(x)＝ln x，当0＜x＜1时，f′(x)＜0，f(x)在(0，1)上单调递减；当x＞1时，f′(x)＞0，f(x)在(1，＋∞)上单调递增．所以f(x)的极小值为f(1)＝ln1＋1－1＝0，无极大值．(2)f(x)＝x ln x－ax＋a，易知f(1)＝0，所求问题等价于函数f(x)＝x ln x－ax＋a在区间(1，e]上没有零点．因为f′(x)＝ln x＋1－a，当0＜x＜e a-1时，f′(x)＜0，所以f(x)在(0，e a-1)上单调递减；当x＞e a-1时，f′(x)＞0，所以f(x)在(e a-1，＋∞)上单调递增．①当e a-1≤1，即a≤1时，函数f(x)在区间(1，e]上单调递增，所以f(x)＞f(1)＝0，此时函数f(x)在区间(1，e]上没有零点，满足题意．②当1＜e a-1＜e，即1＜a＜2时，f(x)在区间(1，e a-1)上单调递减，在区间(e a-1，e]上单调递增，要使f(x)在(1，e]上没有零点，只需f(e)＜0，即e－e a＋a＜0，解得a＞e e−1，所e e−1＜a＜2.③当e≤e a-1，即a≥2时，函数f(x)在区间(1，e]上单调递减，在区间(1，e]上满足f(x)＜f(1)＝0，此时函数f(x)在区间(1，e]上没有零点，满足题意．综上所述，实数a的取值范围是a≤1或a＞e e−1.2．(2024·广东佛山模拟)已知函数f(x)＝ln x＋sin x.(1)求函数f(x)在区间[1，e]上的最小值；(2)判断函数f(x)的零点个数，并证明．[解](1)f(x)＝ln x＋sin x的定义域为(0，＋∞)，f′(x)＝1＋cos x，令g(x)＝f′(x)＝1＋cos x，g′(x)＝－12－sin x，当x∈[1，e]时，g′(x)＝－12－sin x＜0，所以g(x)在[1，e]上单调递减，且g(1)＝1＋cos1＞0，g(e)＝1e＋cos e＜1e＋cos2π3＝1e−12＜0，所以由零点存在定理可知，在区间[1，e]存在唯一的a，使g(a)＝f′(a)＝0.又当x∈(1，a)时，g(x)＝f′(x)＞0；当x∈(a，e)时，g(x)＝f′(x)＜0，所以f(x)在x∈(1，a)上单调递增，在x∈(a，e)上单调递减，又因为f(1)＝ln1＋sin1＝sin1，f(e)＝ln e＋sin e＝1＋sin e＞f(1)，所以函数f(x)在区间[1，e]上的最小值为f(1)＝sin1.(2)函数f(x)有一个零点，证明如下：因为f(x)＝ln x＋sin x，x∈(0，＋∞)，若0＜x≤1，f′(x)＝1＋cos x＞0，所以f(x)在区间(0，1]上单调递增，又f(1)＝sin1＞0，f1＋sin1e＜0，结合零点存在定理可知，f(x)在区间(0，1]上有且仅有一个零点．若1＜x≤π，则ln x＞0，sin x≥0，则f(x)＞0，若x＞π，因为ln x＞lnπ＞1≥－sin x，所以f(x)＞0，所以f(x)在区间(1，＋∞)上没有零点．综上，函数f(x)在(0，＋∞)上有且仅有一个零点．3．(2021·全国甲卷)已知a＞0且a≠1，函数f(x)＝(x＞0)．(1)当a＝2时，求f(x)的单调区间；(2)若曲线y＝f(x)与直线y＝1有且仅有两个交点，求a的取值范围．[解](1)当a＝2时，f(x)＝22(x＞0)，f′(x)x＞0)，令f′(x)＞0，则0＜x＜2ln2，此时函数f(x)单调递增，令f′(x)＜0，则x＞2ln2，此时函数f(x)单调递减，所以函数f(x)的单调递增区间为0+∞.(2)曲线y＝f(x)与直线y＝1有且仅有两个交点，＝1(x>0)有两个不同的解，即方程ln＝ln有两个不同的解．设g(x)＝ln(x＞0)，则g′(x)＝1−ln2(x＞0)，令g′(x)＝1−ln2＝0，得x＝e，当0<x<e时，g′(x)>0，函数g(x)单调递增，当x＞e时，g′(x)＜0，函数g(x)单调递减，故g(x)max＝g(e)＝1e，且当x>e时，g(x)∈0又g(1)＝0，所以0＜ln＜1e，所以a＞1且a≠e，即a的取值范围为(1，e)∪(e，＋∞)．4．(2024·四川成都模拟)已知函数f(x)＝B e(a＞0)和函数g(x)＝ln，且f(x)有最1x.(1)求实数a的值；(2)直线y＝m与两曲线y＝f(x)和y＝g(x)恰好有三个不同的交点，其横坐标分别为x1，x2，x3，且x1＜x2＜x3，证明：x1x3＝.[解](1)f(x)＝B e的定义域为R，且f′(x)a＞0，当x＜1时，f′(x)＞0，f(x)单调递增；当x＞1时，f′(x)＜0，f(x)单调递减，所以f(x)max＝f(1)＝e，所以e＝1x，解得a＝±1，又a＞0，所以a＝1.(2)证明：由(1)可知，f(x)＝e在(－∞，1)上单调递增，在(1，＋∞)上单调递减，又g′(x)＝1−ln2，所以g(x)＝ln在(0，e)上单调递增，在(e，＋∞)上单调递减，f (x )＝e 和g (x )＝ln 的图象如图所示．设f (x )和g (x )的图象交于点A ，则当直线y ＝m 经过点A 时，直线y ＝m 与两条曲线y ＝f (x )和y ＝g (x )共有三个不同的交点，则0＜x 1＜1＜x 2＜e ＜x 3，且2e 2＝ln 22＝m ，ln 33＝m .因为m ＝1e 1＝ln 22，所以1e 1＝ln 2e ln 2，即f (x 1)＝f (ln x 2)，因为x 1＜1，ln x 2＜ln e ＝1，且f (x )＝e 在(－∞，1)上单调递增，所以x 1＝ln x 2，21＝2ln 2＝1.因为m ＝2e 2＝ln 33，所以2e 2＝ln 3e ln 3，即f (x 2)＝f (ln x 3)，因为x 2＞1，ln x 3＞ln e ＝1，且f (x )＝e 在(1，＋∞)上单调递减，所以x 2＝ln x 3，所以32＝3ln 3＝1.21＝32＝1，即x 1x 3＝22。

利用导数解决函数的零点问题

第六节利用导数解决函数的零点问题考点1 判断、证明或讨论函数零点的个数判断函数零点个数的3种方法直接法令f (x )＝0，则方程解的个数即为零点的个数画图法转化为两个易画出图象的函数，看其交点的个数即可定理法利用零点存在性定理判定，可结合最值、极值去解决(2019·全国卷Ⅰ)已知函数f (x )＝sin x －ln(1＋x )，f ′(x )为f (x )的导数．证明： (1)f ′(x )在区间⎝ ⎛⎭⎪⎫－1，π2存在唯一极大值点； (2)f (x )有且仅有2个零点．[证明] (1)设g (x )＝f ′(x )，则g (x )＝cos x －11＋x ，g ′(x )＝－sin x ＋1（1＋x ）2.当x ∈⎝ ⎛⎭⎪⎫－1，π2时，g ′(x )单调递减，而g ′(0)＞0，g ′⎝ ⎛⎭⎪⎫π2＜0，可得g ′(x )在⎝ ⎛⎭⎪⎫－1，π2有唯一零点，设为α.则当x ∈(－1，α)时，g ′(x )＞0；当x ∈⎝ ⎛⎭⎪⎫α，π2时，g ′(x )＜0. 所以g (x )在(－1，α)单调递增，在⎝ ⎛⎭⎪⎫α，π2单调递减，故g (x )在⎝ ⎛⎭⎪⎫－1，π2存在唯一极大值点，即f ′(x )在⎝ ⎛⎭⎪⎫－1，π2存在唯一极大值点． (2)f (x )的定义域为(－1，＋∞)．(ⅰ)当x ∈(－1，0]时，由(1)知，f ′(x )在(－1，0)单调递增，而f ′(0)＝0，所以当x ∈(－1，0)时，f ′(x )＜0，故f (x )在(－1，0)单调递减．又f (0)＝0，从而x ＝0是f (x )在(－1，0]的唯一零点．(ⅱ)当x ∈⎝ ⎛⎦⎥⎤0，π2时，由(1)知，f ′(x )在(0，α)单调递增，在⎝ ⎛⎭⎪⎫α，π2单调递减，而f ′(0)＝0，f ′⎝ ⎛⎭⎪⎫π2＜0，所以存在β∈⎝ ⎛⎭⎪⎫α，π2，使得f ′(β)＝0，且当x ∈(0，β)时，f ′(x )＞0；当x ∈⎝ ⎛⎭⎪⎫β，π2时，f ′(x )＜0.故f (x )在(0，β)单调递增，在⎝ ⎛⎭⎪⎫β，π2单调递减．又f (0)＝0，f ⎝ ⎛⎭⎪⎫π2＝1－ln ⎝ ⎛⎭⎪⎫1＋π2＞0，所以当x ∈⎝ ⎛⎦⎥⎤0，π2时，f (x )＞0.从而，f (x )在⎝ ⎛⎦⎥⎤0，π2没有零点． (ⅲ)当x ∈⎝ ⎛⎦⎥⎤π2，π时，f ′(x )＜0，所以f (x )在⎝ ⎛⎭⎪⎫π2，π单调递减．而f ⎝ ⎛⎭⎪⎫π2＞0，f (π)＜0，所以f (x )在⎝ ⎛⎦⎥⎤π2，π有唯一零点． (ⅳ)当x ∈(π，＋∞)时，ln(x ＋1)＞1，所以f (x )＜0，从而f (x )在(π，＋∞)没有零点．综上，f (x )有且仅有2个零点．根据参数确定函数零点的个数，解题的基本思想是“数形结合”，即通过研究函数的性质(单调性、极值、函数值的极限位置等)，作出函数的大致图象，然后通过函数图象得出其与x 轴交点的个数，或者两个相关函数图象交点的个数，基本步骤是“先数后形”．设函数f (x )＝ln x ＋m x ，m ∈R .(1)当m ＝e(e 为自然对数的底数)时，求f (x )的极小值；(2)讨论函数g (x )＝f ′(x )－x 3零点的个数．[解] (1)由题意知，当m ＝e 时，f (x )＝ln x ＋e x (x ＞0)，则f ′(x )＝x －e x 2，∴当x ∈(0，e)时，f ′(x )＜0，f (x )在(0，e)上单调递减；当x ∈(e ，＋∞)时，f ′(x )＞0，f (x )在(e ，＋∞)上单调递增，∴当x＝e时，f(x)取得极小值f(e)＝ln e＋ee＝2，∴f(x)的极小值为2.(2)由题意知g(x)＝f′(x)－x3＝1x－mx2－x3(x＞0)，令g(x)＝0，得m＝－13x3＋x(x＞0)．设φ(x)＝－13x3＋x(x≥0)，则φ′(x)＝－x2＋1＝－(x－1)(x＋1)．当x∈(0，1)时，φ′(x)＞0，φ(x)在(0，1)上单调递增；当x∈(1，＋∞)时，φ′(x)＜0，φ(x)在(1，＋∞)上单调递减．∴x＝1是φ(x)的唯一极值点，且是极大值点，因此x＝1也是φ(x)的最大值点，∴φ(x)的最大值为φ(1)＝23，又∵φ(0)＝0.结合y＝φ(x)的图象(如图)，可知，①当m＞23时，函数g(x)无零点；②当m＝23时，函数g(x)有且只有一个零点；③当0＜m＜23时，函数g(x)有两个零点；④当m≤0时，函数g(x)有且只有一个零点．综上所述，当m＞23时，函数g(x)无零点；当m＝23或m≤0时，函数g(x)有且只有一个零点；当0＜m＜23时，函数g(x)有两个零点．考点2 已知函数零点个数求参数解决此类问题常从以下两个方面考虑(1)根据区间上零点的个数情况，估计出函数图象的大致形状，从而推导出导数需要满足的条件，进而求出参数满足条件．(2)先求导，通过求导分析函数的单调情况，再依据函数在区间内的零点情况，推导出函数本身需要满足的条件，此时，由于函数比较复杂，常常需要构造新函数，通过多次求导，层层推理得解．设函数f (x )＝－x 2＋ax ＋ln x (a ∈R )．(1)当a ＝－1时，求函数f (x )的单调区间；(2)若函数f (x )在[13，3]上有两个零点，求实数a 的取值范围．[解] (1)函数f (x )的定义域为(0，＋∞)，当a ＝－1时，f ′(x )＝－2x －1＋1x ＝－2x 2－x ＋1x，令f ′(x )＝0，得x ＝12(负值舍去)，当0＜x ＜12时，f ′(x )＞0；当x ＞12时，f ′(x )＜0.∴f (x )的单调递增区间为(0，12)，单调递减区间为(12，＋∞)．(2)令f (x )＝－x 2＋ax ＋ln x ＝0，得a ＝x －ln x x .令g (x )＝x －ln x x ，其中x ∈[13，3]，则g ′(x )＝1－1－ln x x 2＝x 2＋ln x －1x 2，令g ′(x )＝0，得x ＝1，当13≤x ＜1时，g ′(x )＜0；当1＜x ≤3时，g ′(x )＞0，∴g (x )的单调递减区间为[13，1)，单调递增区间为(1，3]，∴g (x )min ＝g (1)＝1，∴函数f (x )在[13，3]上有两个零点，g (13)＝3ln 3＋13，g (3)＝3－ln 33，3ln 3＋13＞3－ln 33，∴实数a 的取值范围是(1，3－ln 33]．与函数零点有关的参数范围问题，往往利用导数研究函数的单调区间和极值点，并结合特殊点，从而判断函数的大致图象，讨论其图象与x 轴的位置关系，进而确定参数的取值范围；或通过对方程等价变形转化为两个函数图象的交点问题．(2018·全国卷Ⅱ)已知函数f (x )＝e x －ax 2.(1)若a ＝1，证明：当x ≥0时，f (x )≥1；(2)若f (x )在(0，＋∞)只有一个零点，求a .[解] (1)当a ＝1时，f (x )≥1等价于(x 2＋1)e －x －1≤0.设函数g (x )＝(x 2＋1)e －x －1，则g ′(x )＝－(x 2－2x ＋1)e －x ＝－(x －1)2e －x . 当x ≠1时，g ′(x )＜0，所以g (x )在(0，＋∞)上单调递减．而g (0)＝0，故当x ≥0时，g (x )≤0，即f (x )≥1.(2)设函数h (x )＝1－ax 2e －x .f (x )在(0，＋∞)只有一个零点等价于h (x )在(0，＋∞)只有一个零点．(ⅰ)当a ≤0时，h (x )＞0，h (x )没有零点；(ⅱ)当a ＞0时，h ′(x )＝ax (x －2)e －x .当x ∈(0，2)时，h ′(x )＜0；当x ∈(2，＋∞)时，h ′(x )＞0.所以h (x )在(0，2)上单调递减，在(2，＋∞)上单调递增．故h(2)＝1－4ae2是h(x)在(0，＋∞)的最小值．①若h(2)＞0，即a＜e24，h(x)在(0，＋∞)没有零点；②若h(2)＝0，即a＝e24，h(x)在(0，＋∞)只有一个零点；③若h(2)＜0，即a＞e24，由于h(0)＝1，所以h(x)在(0，2)有一个零点．由(1)知，当x＞0时，e x＞x2，所以h(4a)＝1－16a3e4a＝1－16a3（e2a）2＞1－16a3（2a）4＝1－1a＞0，故h(x)在(2，4a)有一个零点．因此h(x)在(0，＋∞)有两个零点．综上，f(x)在(0，＋∞)只有一个零点时，a＝e24.考点3函数零点性质研究本考点包括两个方向：一是与函数零点性质有关的问题(更多涉及构造函数法)；二是可以转化为函数零点的函数问题(更多涉及整体转化、数形结合等方法技巧)．能够利用等价转换构造函数法求解的问题常涉及参数的最值、曲线交点、零点的大小关系等．求解时一般先通过等价转换，将已知转化为函数零点问题，再构造函数，然后利用导数研究函数的单调性、极值、最值等，并结合分类讨论，通过确定函数的零点达到解决问题的目的．已知函数f(x)＝12x2＋(1－a)x－a ln x，a∈R.(1)若f(x)存在极值点为1，求a的值；(2)若f(x)存在两个不同的零点x1，x2，求证：x1＋x2＞2.[解](1)由已知得f′(x)＝x＋1－a－ax，因为f(x)存在极值点为1，所以f′(1)＝0，即2－2a＝0，a＝1，经检验符合题意，所以a＝1.(2)证明：f′(x)＝x＋1－a－ax＝(x＋1)(1－ax)(x＞0)，①当a≤0时，f′(x)＞0恒成立，所以f(x)在(0，＋∞)上为增函数，不符合题意；②当a＞0时，由f′(x)＝0得x＝a，当x＞a时，f′(x)＞0，所以f(x)单调递增，当0＜x＜a时，f′(x)＜0，所以f(x)单调递减，所以当x＝a时，f(x)取得极小值f(a)．又f(x)存在两个不同的零点x1，x2，所以f(a)＜0，即12a2＋(1－a)a－a ln a＜0，整理得ln a＞1－12a，作y＝f(x)关于直线x＝a的对称曲线g(x)＝f(2a－x)，令h(x)＝g(x)－f(x)＝f(2a－x)－f(x)＝2a－2x－a ln 2a－x x，则h′(x)＝－2＋2a2（2a－x）x ＝－2＋2a2－（x－a）2＋a2≥0，所以h(x)在(0，2a)上单调递增，不妨设x1＜a＜x2，则h(x2)＞h(a)＝0，即g(x2)＝f(2a－x2)＞f(x2)＝f(x1)，又2a－x2∈(0，a)，x1∈(0，a)，且f(x)在(0，a)上为减函数，所以2a－x2＜x1，即x1＋x2＞2a，又ln a＞1－12a，易知a＞1成立，故x1＋x2＞2.(1)研究函数零点问题，要通过数的计算(函数性质、特殊点的函数值等)和形的辅助，得出函数零点的可能情况；(2)函数可变零点(函数中含有参数)性质的研究，要抓住函数在不同零点处函数值均为零，建立不同零点之间的关系，把多元问题转化为一元问题，再使用一元函数的方法进行研究．已知函数f(x)＝ln x－x.(1)判断函数f(x)的单调性；(2)若函数g(x)＝f(x)＋x＋12x－m有两个零点x1，x2，且x1＜x2，求证：x1＋x2＞1.[解](1)函数f(x)的定义域为(0，＋∞)，f′(x)＝1x－1＝1－xx.令f′(x)＝1－xx＞0，得0＜x＜1，令f′(x)＝1－xx＜0，得x＞1.所以函数f(x)的单调递增区间为(0，1)，单调递减区间为(1，＋∞)．(2)证明：根据题意知g(x)＝ln x＋12x－m(x＞0)，因为x1，x2是函数g(x)＝ln x＋12x－m的两个零点，所以ln x1＋12x1－m＝0，ln x2＋12x2－m＝0，两式相减，可得ln x1x2＝12x2－12x1，即ln x1x2＝x1－x22x1x2，故x1x2＝x1－x22lnx1x2，则x1＝x1x2－12lnx1x2，x2＝1－x2x12lnx1x2.令t＝x1x2，其中0＜t＜1，则x1＋x2＝t－12ln t ＋1－1t2ln t＝t－1t2ln t.构造函数h(t)＝t－1t－2ln t(0＜t＜1)，则h′(t)＝（t－1）2t2.因为0＜t＜1，所以h′(t)＞0恒成立，故h(t)＜h(1)，即t－1t －2ln t＜0，可知t－1t2ln t＞1，故x1＋x2＞1.课外素养提升④逻辑推理——构造法求f(x)与f′(x)共存问题在导数及其应用的客观题中，有一个热点考查点，即不给出具体的函数解析式，而是给出函数f(x)及其导数满足的条件，需要据此条件构造抽象函数，再根据条件得出构造的函数的单调性，应用单调性解决问题的题目，该类题目具有一定的难度．下面总结其基本类型及其处理方法.f′(x)g(x)±f(x)g′(x)型【例1】(1)定义在R上的函数f(x)，满足f(1)＝1，且对任意的x∈R都有f′(x)＜12，则不等式f(lg x)＞lg x＋12的解集为________．(2)设f(x)，g(x)分别是定义在R上的奇函数和偶函数，当x＜0时，f′(x)g(x)＋f(x)g′(x)＞0，且g(－3)＝0，则不等式f(x)g(x)＜0的解集为________．(1)(0，10)(2)(－∞，－3)∪(0，3)[(1)由题意构造函数g(x)＝f(x)－12x，则g′(x)＝f′(x)－12＜0，所以g(x)在定义域内是减函数．因为f(1)＝1，所以g(1)＝f(1)－12＝1 2，由f(lg x)＞lg x＋12，得f(lg x)－12lg x＞12.即g(lg x)＝f(lg x)－12lg x＞12＝g(1)，所以lg x＜1，解得0＜x＜10.所以原不等式的解集为(0，10)．(2)借助导数的运算法则，f′(x)g(x)＋f(x)g′(x)＞0⇔[f(x)g(x)]′＞0，所以函数y ＝f(x)g(x)在(－∞，0)上单调递增．又由题意知函数y＝f(x)g(x)为奇函数，所以其图象关于原点对称，且过点(－3，0)，(3，0)．数形结合可求得不等式f(x)g(x)＜0的解集为(－∞，－3)∪(0，3)．][评析](1)对于不等式f′(x)＋g′(x)＞0(或＜0)，构造函数F(x)＝f(x)＋g(x)．(2)对于不等式f′(x)－g′(x)＞0(或＜0)，构造函数F(x)＝f(x)－g(x)．特别地，对于不等式f′(x)＞k(或＜k)(k≠0)，构造函数F(x)＝f(x)－kx.(3)对于不等式f′(x)g(x)＋f(x)g′(x)＞0(或＜0)，构造函数F(x)＝f(x)g(x)．(4)对于不等式f′(x)g(x)－f(x)g′(x)＞0(或＜0)，构造函数F(x)＝f（x）g（x）(g(x)≠0)．xf′(x)±nf(x)(n为常数)型【例2】(1)设f′(x)是奇函数f(x)(x∈R)的导函数，f(－1)＝0，当x＞0时，xf′(x)－f(x)＜0，则使得f(x)＞0成立的x的取值范围是()A．(－∞，－1)∪(0，1)B．(－1，0)∪(1，＋∞)C．(－∞，－1)∪(－1，0) D．(0，1)∪(1，＋∞)(2)设函数f(x)在R上的导函数为f′(x)，且2f(x)＋xf′(x)＞x2，则下列不等式在R上恒成立的是()A．f(x)＞0 B．f(x)＜0C．f(x)＞x D．f(x)＜x(1)A(2)A[(1)令g(x)＝f（x）x，则g′(x)＝xf′（x）－f（x）x2.由题意知，当x＞0时，g′(x)＜0，∴g(x)在(0，＋∞)上是减函数．∵f(x)是奇函数，f(－1)＝0，∴f(1)＝－f(－1)＝0，∴g(1)＝f(1)＝0，∴当x∈(0，1)时，g(x)＞0，从而f(x)＞0；当x∈(1，＋∞)时，g(x)＜0，从而f(x)＜0.又∵f(x)是奇函数，∴当x∈(－∞，－1)时，f(x)＞0；当x∈(－1，0)时，f(x)＜0.综上，使f(x)＞0成立的x的取值范围是(－∞，－1)∪(0，1)．(2)令g(x)＝x2f(x)－14x4，则g′(x)＝2xf(x)＋x2f′(x)－x3＝x[2f(x)＋xf′(x)－x2]．当x＞0时，g′(x)＞0，∴g(x)＞g(0)，即x2f(x)－14x4＞0，从而f(x)＞14x2＞0；当x＜0时，g′(x)＜0，∴g(x)＞g(0)，即x2f(x)－14x4＞0，从而f(x)＞14x2＞0；当x＝0时，由题意可得2f(0)＞0，∴f(0)＞0.综上可知，f(x)＞0.][评析](1)对于xf′(x)＋nf(x)＞0型，构造F(x)＝x n f(x)，则F′(x)＝x n－1[xf′(x)＋nf(x)](注意对x n－1的符号进行讨论)，特别地，当n＝1时，xf′(x)＋f(x)＞0，构造F(x)＝xf(x)，则F′(x)＝xf′(x)＋f(x)＞0.(2)对于xf ′(x )－nf (x )＞0(x ≠0)型，构造F (x )＝f （x ）x n ，则F ′(x )＝xf ′（x ）－nf （x ）x n ＋1(注意对x n ＋1的符号进行讨论)，特别地，当n ＝1时，xf ′(x )－f (x )＞0，构造F (x )＝f （x ）x ，则F ′(x )＝xf ′（x ）－f （x ）x 2＞0.f ′(x )±λf (x )(λ为常数)型【例3】 (1)已知f (x )在R 上的可导函数，且∀x ∈R ，均有f (x )＞f ′(x )，则有( )A ．e 2 019f (－2 019)＜f (0)，f (2 019)＞e 2 019f (0)B ．e 2 019f (－2 019)＜f (0)，f (2 019)＜e 2 019f (0)C ．e 2 019f (－2 019)＞f (0)，f (2 019)＞e 2 019f (0)D ．e 2 019f (－2 019)＞f (0)，f (2 019)＜e 2 019f (0)(2)已知定义在R 上的函数f (x )满足f (x )＋2f ′(x )＞0恒成立，且f (2)＝1e (e 为自然对数的底数)，则不等式e x f (x )－e x2＞0的解集为________．(1)D (2)(2，＋∞) [(1)构造函数h (x )＝f （x ）e x ，则h ′(x )＝f ′（x ）－f （x ）e x＜0，即h (x )在R 上单调递减，故h (－2 019)＞h (0)，即f （－2 019）e －2 019＞f （0）e 0⇒e 2 019f (－2 019)＞f (0)；同理，h (2 019)＜h (0)，即f (2 019)＜e 2 019f (0)，故选D.(2)由f (x )＋2f ′(x )＞0，得2[12f (x )＋f ′(x )]＞0，可构造函数h (x )＝e x 2f (x )，则h ′(x )＝12e x 2[f (x )＋2f ′(x )]＞0，所以函数h (x )＝e x 2f (x )在R 上单调递增，且h (2)＝e f (2)＝1.不等式ex f (x )－e x 2＞0等价于e x 2f (x )＞1，即h (x )＞h (2)⇒x ＞2，所以不等式e x f (x )－e x2＞0的解集为(2，＋∞)．][评析](1)对于不等式f′(x)＋f(x)＞0(或＜0)，构造函数F(x)＝e x f(x)．(2)对于不等式f′(x)－f(x)＞0(或＜0)，构造函数F(x)＝f（x）e x.。

专题11 利用导数解决零点问题(解析版)

专题11 利用导数解决零点问题1．（2022·全国·高考真题（理））已知函数()()ln 1e xf x x ax -=++(1)当1a =时，求曲线()y f x =在点()()0,0f 处的切线方程； (2)若()f x 在区间()()1,0,0,-+∞各恰有一个零点，求a 的取值范围．【答案】(1)2y x = (2)(,1)-∞- 【解析】【分析】（1）先算出切点,再求导算出斜率即可（2）求导,对a 分类讨论,对x 分(1,0),(0,)-+∞两部分研究 (1)()f x 的定义域为(1,)-+∞当1a =时,()ln(1),(0)0e x x f x x f =++=,所以切点为(0,0)11(),(0)21e xx f x f x ''-=+=+,所以切线斜率为2 所以曲线()y f x =在点(0,(0))f 处的切线方程为2y x = (2)()ln(1)e xaxf x x =++()2e 11(1)()1e (1)e x x x a x a xf x x x '+--=+=++设()2()e 1x g x a x =+-1︒若0a >,当()2(1,0),()e 10x x g x a x ∈-=+->,即()0f x '>所以()f x 在(1,0)-上单调递增,()(0)0f x f <= 故()f x 在(1,0)-上没有零点,不合题意2︒若10a -,当,()0x ∈+∞,则()e 20xg x ax '=->所以()g x 在(0,)+∞上单调递增所以()(0)10g x g a >=+,即()0f x '> 所以()f x 在(0,)+∞上单调递增,()(0)0f x f >= 故()f x 在(0,)+∞上没有零点,不合题意 3︒若1a <-(1)当,()0x ∈+∞,则()e 20x g x ax '=->,所以()g x 在(0,)+∞上单调递增 (0)10,(1)e 0g a g =+<=>所以存在(0,1)m ∈,使得()0g m =,即()0'=f m 当(0,),()0,()x m f x f x '∈<单调递减当(,),()0,()x m f x f x '∈+∞>单调递增所以当(0,),()(0)0x m f x f ∈<= 当,()x f x →+∞→+∞所以()f x 在(,)m +∞上有唯一零点又(0,)m 没有零点,即()f x 在(0,)+∞上有唯一零点(2)当()2(1,0),()e 1x x g x a x ∈-=+-设()()e 2x h x g x ax '==-()e 20x h x a '=->所以()g x '在(1,0)-单调递增 1(1)20,(0)10eg a g ''-=+<=>所以存在(1,0)n ∈-,使得()0g n '= 当(1,),()0,()x n g x g x '∈-<单调递减当(,0),()0,()x n g x g x '∈>单调递增,()(0)10g x g a <=+< 又1(1)0eg -=> 所以存在(1,)t n ∈-,使得()0g t =,即()0f t '= 当(1,),()x t f x ∈-单调递增,当(,0),()x t f x ∈单调递减有1,()x f x →-→-∞而(0)0f =,所以当(,0),()0x t f x ∈>所以()f x 在(1,)t -上有唯一零点,(,0)t 上无零点即()f x 在(1,0)-上有唯一零点所以1a <-,符合题意所以若()f x 在区间(1,0),(0,)-+∞各恰有一个零点,求a 的取值范围为(,1)-∞-2．（2022·全国·高考真题（理））已知函数()ln xf x x a x x e -=+-．(1)若()0f x ≥，求a 的取值范围；(2)证明：若()f x 有两个零点12,x x ，则121x x <．【答案】(1)(,1]e -∞+ (2)证明见的解析【解析】【分析】（1）由导数确定函数单调性及最值，即可得解；（2）利用分析法，转化要证明条件为1e 11e 2ln 02x x x x x x x ⎡⎤⎛⎫----> ⎪⎢⎥⎝⎭⎣⎦，再利用导数即可得证.(1)()f x 的定义域为(0,)+∞，2111()e 1x f x x x x ⎛⎫'=--+ ⎪⎝⎭1111e 1e 11x x x x x x x x ⎛⎫-⎛⎫⎛⎫=-+-=+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭令()0f x =,得1x =当(0,1),()0,()x f x f x '∈<单调递减当(1,),()0,()x f x f x >'∈+∞单调递增()(1)e 1f x f a ≥=+-，若()0f x ≥,则e 10a +-≥,即1a e ≤+ 所以a 的取值范围为(,1]e -∞+ (2)由题知,()f x 一个零点小于1,一个零点大于1 不妨设121x x 要证121x x <,即证121x x < 因为121,(0,1)x x ∈,即证()121f x f x ⎛⎫> ⎪⎝⎭因为()()12f x f x =,即证()221f x f x ⎛⎫> ⎪⎝⎭即证1e 1ln e ln 0,(1,)x x x x x x x x x-+--->∈+∞即证1e 11e 2ln 02x x x x x x x ⎡⎤⎛⎫----> ⎪⎢⎥⎝⎭⎣⎦下面证明1x >时，1e 11e 0,ln 02x x x x x x x ⎛⎫->--< ⎪⎝⎭设11(),e e xx g x x xx =->，则11122111111()e e e 1e e 1x x x xx g x x x x x x x x ⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫'=--+⋅-=--- ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭111e 1e 1e e xx x xx x x x x ⎛⎫⎛⎫-⎛⎫=--=- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭设()()()22e 1111,e e 0x x xx x x x x x x x ϕϕ-⎛⎫=>=-=⎪⎭'> ⎝所以()()1e x ϕϕ>=,而1e e x <所以1e e 0xx x->,所以()0g x '>所以()g x 在(1,)+∞单调递增即()(1)0g x g >=,所以1e e 0xx x x-> 令11()ln ,12h x x x x x ⎛⎫=--> ⎪⎝⎭2222211121(1)()10222x x x h x x x x x ----⎛⎫'=-+==< ⎪⎝⎭所以()h x 在(1,)+∞单调递减即()(1)0h x h <=,所以11ln 02x x x ⎛⎫--< ⎪⎝⎭；综上, 1e 11e 2ln 02x x x x x x x ⎡⎤⎛⎫----> ⎪⎢⎥⎝⎭⎣⎦,所以121x x <. 3．（2022·全国·高考真题（文））已知函数1()(1)ln f x ax a x x=--+．(1)当0a =时，求()f x 的最大值；(2)若()f x 恰有一个零点，求a 的取值范围．【答案】(1)1- (2)()0,+∞ 【解析】【分析】（1）由导数确定函数的单调性，即可得解；（2）求导得()()()211ax x f x x --'=，按照0a ≤、01a <<及1a >结合导数讨论函数的单调性，求得函数的极值，即可得解. (1)当0a =时，()1ln ,0f x x x x =-->，则()22111xf x x x x-'=-=，当()0,1∈x 时，0f x ，()f x 单调递增；当()1,x ∈+∞时，0fx，()f x 单调递减；所以()()max 11f x f ==-；(2)()()11ln ,0f x ax a x x x =--+>，则()()()221111ax x a f x a x x x--+'=+-=，当0a ≤时，10-≤ax ，所以当()0,1∈x 时，0f x，()f x 单调递增；当()1,x ∈+∞时，0fx，()f x 单调递减；所以()()max 110f x f a ==-<，此时函数无零点，不合题意；当01a <<时，11a >，在()10,1,,a ⎛⎫+∞ ⎪⎝⎭上，0f x，()f x 单调递增；在11,a ⎛⎫⎪⎝⎭上，0f x，()f x 单调递减；又()110f a =-<，由（1）得1ln 1x x +≥，即1ln 1x x ≥-，所以ln x x x <<<当1x >时，11()(1)ln 2((2f x ax a x ax a ax a x x=--+>--+-+则存在2312m a a⎛⎫=+> ⎪⎝⎭，使得()0f m >，所以()f x 仅在1,a ⎛⎫+∞ ⎪⎝⎭有唯一零点，符合题意；当1a =时，()()2210x f x x-'=≥，所以()f x 单调递增，又()110f a =-=，所以()f x 有唯一零点，符合题意；当1a >时，11a <，在()10,,1,a ⎛⎫+∞ ⎪⎝⎭上，0f x，()f x 单调递增；在1,1a ⎛⎫⎪⎝⎭上，0f x，()f x 单调递减；此时()110f a =->，由（1）得当01x <<时，1ln 1xx>-，1>ln 21x ⎛> ⎝，此时11()(1)ln 2(11)1f x ax a x ax ax x x ⎛=--+<--+-< ⎝ 存在2114(1)n a a=<+，使得()0f n <，所以()f x 在10,a ⎛⎫ ⎪⎝⎭有一个零点，在1,a ⎛⎫+∞ ⎪⎝⎭无零点，所以()f x 有唯一零点，符合题意；综上，a 的取值范围为()0,+∞.4．（2022·全国·模拟预测）已知函数()()ln 13f x a x x =+-．(1)讨论函数()f x 的单调性；(2)证明：当1a =时，方程()sin 3f x x x =-在,2π⎛⎫+∞ ⎪⎝⎭上有且仅有一个实数解．【答案】(1)答案不唯一，具体见解析 (2)证明见解析【解析】【分析】（1）先求出函数的定义域，再求出()31af x x '=-+，然后分0a >，0a ≤可得出函数的单调性. （2）设()()ln 1sin g x x x =+-，将问题转化为函数()g x 在,2π⎛⎫+∞ ⎪⎝⎭上有且仅有一个零点，又当e 1x >-时，()ln 1lne 1sin x x +>=≥，所以只需证()g x 在,e 12π⎛⎤- ⎥⎝⎦上有且仅有一个零点，求出其导数，由零点存在原理即可证明. (1)函数()()ln 13f x a x x =+-的定义域是()1,-+∞，()31af x x '=-+．当0a >时，令()0f x '<，得33a x ->；令()0f x '>，得313a x --<<，故()f x 在31,3a -⎛⎫- ⎪⎝⎭上单调递增，在3,3a -⎛⎫+∞ ⎪⎝⎭上单调递减；当0a ≤时，()0f x '<恒成立，故()f x 在()1,-+∞上单调递减． (2)当1a =时，方程()sin 3f x x x =-即为()ln 13sin 3x x x x +-=-，即()ln 1sin 0x x +-=．令()()ln 1sin g x x x =+-，则()1cos 1g x x x '=-+，则“方程()sin 3f x x x =-在,2π⎛⎫+∞ ⎪⎝⎭上有且仅有一个实数解”等价于“函数()g x 在,2π⎛⎫+∞ ⎪⎝⎭上有且仅有一个零点”．当e 1x >-时，()ln 1lne 1sin x x +>=≥，所以()0g x >在()e 1,-+∞上恒成立，所以只需证()g x 在,e 12π⎛⎤- ⎥⎝⎦上有且仅有一个零点．因为e 1π-<，所以当,e 12x π⎛⎤∈- ⎥⎝⎦时，cos 0x <，101x >+，所以()0g x '>在,e 12π⎛⎤- ⎥⎝⎦上恒成立．所以()g x 在,e 12π⎛⎤- ⎥⎝⎦上单调递增，又ln 1sin ln 1102222g ππππ⎛⎫⎛⎫⎛⎫=+-=+-< ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，()()e 11sin e 1g -=--，所以()g x 在,e 12π⎛⎤- ⎥⎝⎦上有且仅有一个零点，即()g x 在,2π⎛⎫+∞ ⎪⎝⎭上有且仅有一个零点．故方程()sin 3f x x x =-在,2π⎛⎫+∞ ⎪⎝⎭上有且仅有一个实数解．5．（2022·湖北·大冶市第一中学模拟预测）已知函数()e sin xf x x ax =+，其中e 是自然对数的底数.(1)若1a =时，试判断f （x ）在区间（2π-，0）的单调性，并予以证明；(2)从下面两个条件中任意选一个，试求实数a 的取值范围. ①函数()f x 在区间[0，2π]上有且只有2个零点； ①当2,0x π⎡⎤∈⎢⎥⎣⎦时，()2f x x ≥.【答案】(1)f （x ）在（π2-，0）上单调递增，证明见解析；(2)选择①：π22e 1πa -≤<-；选择①：1a ≥-.【解析】【分析】（1）求导，通过判定导函数在（π2-，0）上的正负确定单调性；（2）选择①：易得()00f =，则因此f （x ）在π0,2x ⎛⎤∈ ⎥⎝⎦上有且只有1个零点，求导通过讨论找出符合条件的a 的取值范围；选择①：构造函数2π()e sin ,0,2x m x x ax x x ⎡⎤=+-∈⎢⎥⎣⎦，此时()00m =，可通过端点效应或隐零点等思路求a的取值范围. (1)当1a =时，()e sin ,(,0)2xf x x ax x π=+∈-()πe sin e cos 1sin 14x x xf x x x x ⎛⎫=++=++ ⎪⎝⎭'.当π,02x ⎛⎫∈- ⎪⎝⎭时，πππ,444x ⎛⎫+∈- ⎪⎝⎭，所以sin 1144x x ππ⎛⎫⎛⎫<+<-+< ⎪ ⎪⎝⎭⎝⎭，又0e 1x <<，πsin 14xx ⎛⎫+>- ⎪⎝⎭，从而()0f x '>，所以，f （x ）在（π2-，0）上单调递增. (2) 选择①，由函数()e sin 0π,2xf x x ax x ⎡⎤=+∈⎢⎥⎣⎦，，可知()00f =因此f （x ）在π0,2x ⎛⎤∈ ⎥⎝⎦上有且只有1个零点.()e sin e cos x x f x x x a +'=+，令()e sin e cos x x h x x x a =++，则()2e cos 0xh x x '=≥在[0.π2]上恒成立.即()f x '在[0，π2]上单调递增，()2ππ01e 2f a f a ⎛'⎫=+=⎪⎭'+ ⎝，，当1a ≥-时，()()00f x f '≥'≥，f （x ）在[0.π2]上单调递增.则f （x ）在（0，π2]上无零点，不合题意，舍去，当π2e a ≤-时，()0π2f x f ⎛⎫'≤'≤ ⎪⎝⎭，()f x 在[0，π2]上单调递减，则()f x 在（0，π2]上无零点，不合题意，舍去，当2e 1a π-<<-时，π2(0)10,()e 2π0f a f a '=+<'=+≥则()f x '在（0，π2）上只有1个零点，设为0x .且当0(0,)x x ∈时，()0f x <′；当0,2x x π⎛⎫∈ ⎪⎝⎭时，()0f x >′ 所以当()00x x ∈，时，()f x 在（0，0x ）上单调递减，在（x0，π2）上单调递增，又()π200e ππ22f f a ⎛⎫==+ ⎪⎝⎭，因此只需20π22πe f a ⎛⎫=+≥ ⎪⎝⎭即可，即π22e 1πa -≤<-，综上所述：2π2e 1πα-≤<-选择①，构造函数2π()e sin ,0,2x m x x ax x x ⎡⎤=+-∈⎢⎥⎣⎦此时()2π2e π244π00x m m a ⎛⎫==+- ⎪⎝⎭，则2π()e sin e cos 2(0)π1,(e 2π)xxm x x x a x m a m a'=++-'=+'=-+，易知(1)π)(2m m '>'令()e sin e cos 2,()2e cos 2,(0)0,()2π2x x xt x x x a x t x x t t =++-'=-'='=-令2π()2e cos 2,()2e (cos sin ),(0)2,()2πe 2xxp x x p x x x p p =-=-'='=-＇，令()2e (cos sin )x q x x x =-，则()4e sin 0x q x x '=-≤ 所以()2e (cos sin )x q x x x =-在（0，π2）上单调递减.又π20π(0)(0)20,()()2e 22πq p q p ='=>='=-<在（0，π2）上存在唯一实数1x 使得()10q x =，且满足当()10,x x ∈时，()0q x >当1π(,)2x x ∈时.()0q x <即p （x ）在（0，x 1）上单调递增，在（x 1，π2）上单调递减.又()()ππ0002022p t p t ⎛⎫⎛⎫==-=-< ⎪'' ⎪⎝⎭⎝⎭，，所以()2e cos 2x p x x =-在1π(,)2x 上存在一实数2x 使得()20p x =，且满足当2(0,)x x ∈时，()0p x >；当2π()2x x ∈⋅时，()0p x <即()()t x m x ='在（0，x2）上单调递增，在（2x ，2π）上单调递减，当()010m a ='+≥时，即()10a m x ≥-'≥，，函数()2e sin x m x x ax x =+-在[0，π2]上单调递增，又()00m =，因此()2e sin 0x m x x ax x =+-≥恒成立，符合题意，当()010m a '=+<，即1a <-，在π20,x ⎛⎫∈ ⎪⎝⎭上必存在实数3x ，使得当()30,x x ∈时，()0m x '<，又()00m =，因此在()30,x x ∈上存在实数()0m x <，不合题意，舍去综上所述1a ≥-.6．（2022·浙江湖州·模拟预测）已知函数12()e x f x =（e 为自然对数的底数）． (1)令1()||()()g x a x f x f x =--，若不等式()0g x ≤恒成立，求实数a 的取值范围； (2)令3()()x xf x m ϕ=-，若函数()ϕx 有两不同零点()1212,x x x x <． ①求实数m 的取值范围；①证明：21e e 21x x m -<+．【答案】(1)(,1]-∞；(2)①2,03e m ⎛⎫∈- ⎪⎝⎭；①证明见解析.【解析】【分析】（1）根据()g x 为偶函数，将问题转化为0x ≥时()0g x ≤恒成立，根据(0)0g =及参变分离求0x >有1122ee x x a x--≤恒成立，求参数范围；（2）①利用导数研究()ϕx 的单调性，及区间值域情况，进而判断()0x ϕ=有两不同解时m 的范围即可；①由（1）知：0x <时1122e e x x x -≥-且120x x <<，应用放缩法有2()e e x x x ϕ≥-，构造2()e e x x F x =-研究极值并判断()F x m =的两根与12,x x 大小关系得到3214e e e e x x x x -<-即可证结论. (1)由题设，1122()||e ex x g x a x -=--，则()()g x g x =-，所以()g x 为偶函数，故只需0x ≥时，()0g x ≤恒成立，而(0)0g =满足，所以0x >有1122ee x x a x--≤恒成立，令02t x =>，则e e 2t ta t--≤，若()e e 2t t h t t -=--，则()e e 220t t h t -'=+-≥=，仅当0=t 时等号成立，所以()0h t '>，即()h t 在(0,)+∞上递增，则()(0)0h t h >=，即e e 2t t t -->，所以，在(0,)+∞上e e 12t tt-->，则1a ≤，综上：a 的范围为(,1]-∞． (2)①由题设，323()1e 2x x x ϕ⎛⎫=+ ⎪'⎝⎭，若()0x ϕ'>得：23x >-，故()ϕx 在2,3⎛⎫-∞- ⎪⎝⎭单调减，在2,3⎛⎫-+∞ ⎪⎝⎭单调增，且x 趋向负无穷()ϕx 趋向于0，x 趋向正无穷()ϕx 趋向于正无穷，又2233e ϕ⎛⎫-=- ⎪⎝⎭，()00ϕ=，则0x <时，()0x ϕ<；0x >时，()0x ϕ>，要使()0x ϕ=有两个不同解12,x x 且120x x <<，则2,03e m ⎛⎫∈- ⎪⎝⎭；①由（1）知：0x <时1122e ex x x -≥-，则1132222()e e e e e x x x x xx ϕ-⎛⎫≥-=- ⎪⎝⎭；记2()e e x x F x =-且0x <，则(()e e 1)2x x F x '=-，所以(,ln 2)-∞-上()0F x '<，(ln 2,0)-上()0F x '>，故()F x 在(,ln 2)-∞-上递减，(ln 2,0)-上递增，且12()(ln 2),043e F x F ⎛⎫≥-=-∈- ⎪⎝⎭，所以()F x m =也有两根，记为34x x <，又(,0)-∞上)(()x F x ϕ≥，则31240x x x x <<<<，令e x t =，则34e ,e xx 为20t t m --=的两根，故34e e 1x x +=，34e e x x m =-，所以34e e x x -=3124e e e e x x x x <<<，所以3214(41)1e e e e 212x x x xm m ++-<-==+． 7．（2022·湖北·模拟预测）已知()()1ln af x a x x x=-++(1)若0a <，讨论函数()f x 的单调性； (2)()()ln a g x f x x x =+-有两个不同的零点1x ，()2120x x x <<，若12202x x g λλ+⎛⎫'> ⎪+⎝⎭恒成立，求λ的范围．【答案】(1)单调性见解析 (2)(][),22,λ∈-∞-+∞【解析】【分析】（1）求导可得()()()21x a x f x x +-'=，再根据a -与0,1的关系分类讨论即可；（2）由题()ln g x a x x =+，，设()120,1x t x =∈根据零点关系可得21ln x x a t -=，再代入1222x x g λλ+⎛⎫' ⎪+⎝⎭化简可得()()21ln 02t t t λλ+-+<+恒成立，设()()()21ln 2t ht t t λλ+-=++，再求导分析单调性与最值即可(1)()f x 定义域为()0,∞+()()()()()222211111x a x a x a x a f x a x x x x+--+-'=-+-== ①）01a <-<即10a -<<时，()01f x a x '<⇒-<<，()00f x x a '>⇒<<-或1x > ①）1a -=即1a =-时，()0,x ∈+∞，()0f x '≥恒成立 ①）1a ->即1a <-，()01f x x a '<⇒<<-，()001f x x '>⇒<<或x a >- 综上：10a -<<时，(),1x a ∈-，()f x 单调递减；()0,a -、()1,+∞，()f x 单调递增 1a =-时，()0,x ∈+∞，()f x 单调递增1a <-时，()1,x a ∈-，()f x 单调递减；()0,1、(),a -+∞，()f x 单调递增(2)()ln g x a x x =+，由题1122ln 0ln 0a x x a x x +=⎧⎨+=⎩，120x x <<则()1221ln ln a x x x x -=-，设()120,1x t x =∈ ①212112ln ln ln x x x xa x x t--==-()1a g x x'=+ ①122112122221122ln 2x x x x g a x x t x x λλλλλλ+-++⎛⎫'=+=⋅+ ⎪+++⎝⎭()()()21102ln t t tλλ+-=+>+恒成立()0,1t ∈，①ln 0t < ①()()21ln 02t t t λλ+-+<+恒成立设()()()21ln 2t h t t t λλ+-=++，①()0h t <恒成立()()()()()()()()22222224122241222t t t t h t t t t t t t λλλλλλλ⎛⎫-- ⎪++-+⎝⎭'=-==+++ ①）24λ≥时，204t λ-<，①()0h t '>，①()h t 在()0,1上单调递增 ①()()10h t h <=恒成立， ①(][),22,λ∈-∞-+∞合题①）24λ<，20,4t λ⎛⎫∈ ⎪⎝⎭，①()0h t '>，①()h t 在20,4λ⎛⎫⎪⎝⎭上单调递增2,14t λ⎛⎫∈ ⎪⎝⎭时，()0h t '<， ①()h t 在2,14λ⎛⎫⎪⎝⎭上单调递减①2,14t λ⎛⎫∈ ⎪⎝⎭，()()10h t h >=，不满足()0h t <恒成立综上：(][),22,λ∈-∞-+∞【点睛】本题主要考查了分类讨论分析函数单调性的问题，同时也考查了双零点与恒成立问题的综合，需要根据题意消去参数a ，令()120,1x t x =∈，再化简所求式关于t 的解析式，再构造函数分析最值.属于难题 8．（2022·浙江绍兴·模拟预测）设a 为实数，函数()e ln 1=++x f x a x x ． (1)当1a e=-时，求函数()f x 的单调区间；(2)判断函数()f x 零点的个数．【答案】(1)减区间为()0,∞+，无增区间. (2)当0a ≥，函数()f x 在(0,)+∞上没有零点；当210e a -≤<，函数()f x 在(0,)+∞上有1个零点；当21e a <-，函数()f x 在(0,)+∞上有2个零点. 【解析】【分析】(1)利用二次求导研究函数()f x 的单调性，进而得出结果； (2)利用分类讨论的思想，根据函数()f x 与()()f x g x x=具有相同的零点，结合导数分别研究当0a ≥、210e a -≤<、21e a <-时()g x 的单调性，利用零点的存在性定理即可判断函数()g x 的零点个数，进而得出结果. (1)函数()f x 的定义域为(0,)+∞，当1a e=-时，1()e ln 1e xf x x x =-++，则1()e ln 1x f x x -'=-++，且()01f '=，有1111e ()ex x x f x x x---''=-+=，令()01f x x ''=⇒=，所以当(0,1)x ∈时()0f x ''>，则()'f x 单调递增，当(1,)x ∈+∞时()0f x ''<，则()'f x 单调递减，所以max ()(1)0f x f ''==，即()0f x '≤，则函数()f x 在(0,)+∞上单调递减，即函数()f x 的减区间为(0,)+∞，无增区间； (2)由(1)知当1a e=-时函数()f x 在(0,)+∞上单调递减，又(1)0f =，此时函数()f x 只有1个零点；因为函数()f x 的定义域为(0,)+∞，所以()f x 与()f x x具有相同的零点，令()e 1()ln (0)x f x a g x x x x x x ==++>，则222(1)e 11(1)(e 1)()x x a x x a g x x x x x --+'=+-=，当0a ≥时，e 10x a +>，令()01g x x '=⇒=，则函数()g x 在(0,1)上单调递减，在(1,)+∞上单调递增，所以min ()(1)e 10g x g a ==+>，此时函数()g x 无零点，即函数()f x 无零点；当0a <时，令()01g x x '=⇒=或1ln()x a=-，若10e a -<<，则11ln()a<-，列表如下：当211e ea -≤≤-时，222e 2e 222e 4222e e e (e )2e 2e e 2e 0e ea g ------=++<++=-++<，当210e a -<<即21e a ->时，131e ()a a->-，1121111()e ln()[e ln()1]aa g a a a a a a a a---=-+--=---+3111[()(1)1]0a a a a a <-----+<，又(1)0g >，此时函数()g x 有1个零点，则函数()f x 有1个零点；若1e <-a ，则11ln()a>-，列表如下：所以ln()min 1e 111()(ln())ln ln()ln ln()ln1011ln()ln()aa g x g a a a a a -=-=+-+=-<=--，又(1)0g >，2(e )0g <，则此时函数()g x 有2个零点，即函数()f x 有2个零点；综上，当0a ≥时，函数()f x 在(0,)+∞上没有零点，当210ea -≤<时，函数()f x 在(0,)+∞上有1个零点，当21e a <-时，函数()f x 在(0,)+∞上有2个零点.【点睛】与函数零点有关的参数范围问题，往往利用导数研究函数的单调区间和极值点，并结合特殊点，从而判断函数的大致图像，讨论其图像与x 轴的位置关系，进而确定参数的取值范围；或通过对方程等价变形转化为两个函数图像的交点问题．9．（2022·河南·开封市东信学校模拟预测（理））已知函数()ln 12a af x x x =+-+，其中R a ∈． (1)讨论函数()f x 的单调性；(2)讨论函数()f x零点的个数．【答案】(1)当4a ≤时，函数()f x 的增区间为(0,)+∞，没有减区间；当4a >时，函数()f x 的增区间为,⎛⎫+∞ ⎪ ⎪⎝⎭⎝⎭，减区间为⎝⎭(2)当4a ≤，函数()f x 有且仅有一个零点；当4a >时，函数()f x 有且仅有3个零点【解析】【分析】（1）求导，再分0a <，04a ≤≤和4a >分类讨论即可；（2）根据单调性及零点存在性定理分析即可. (1)函数()f x 的定义域为(0,)+∞，2221(2)1()(1)(1)a x a x f x x x x x +-+'=-=++，在一元二次方程2(2)10x a x +-+=中，22Δ(2)44(4)a a a a a =--=-=-， ①当0a <时，()0f x '≥，此时函数()f x 单调递增，增区间为(0,)+∞，没有减区间； ①当04a ≤≤时，()0f x '≥，此时函数()f x 单调递增，增区间为(0,)+∞，没有减区间； ①当4a >时，一元二次方程2(2)10x a x +-+=有两个不相等的根，分别记为()1221,x x x x >，有122x x a +=-，1210x x =>，可得210x x >>，有12x x ==可得此时函数()f x 的增区间为()()120,,,x x +∞减区间为()12,x x ，综上可知，当4a ≤时，函数()f x 的增区间为(0,)+∞，没有减区间；当4a >时，函数()f x 的增区间为,⎛⎫+∞ ⎪ ⎪⎝⎭⎝⎭，减区间为⎝⎭； (2)由（1）可知：①当4a ≤时，函数()f x 单调递增，又由(1)0f =，可得此时函数只有一个零点为1x =； ①当4a >时，由122110,x x x x =>>，可得1201x x <<<，又由(1)0f =，由函数的单调性可知()()12(1)0,(1)0f x f f x f >=<=，当01x <<且20e ax -<<时，可得2ln ln e ax -<，有ln 02ax +<，可得()ln ln 022a af x x a x <+-=+<，当2e ax >时，2()ln ln e 02222aa a a af x x >->-=-=可知此时函数()f x 有且仅有3个零点，由上知，当4a ≤时，函数()f x 有且仅有一个零点；当4a >时，函数()f x 有且仅有3个零点．10．（2022·贵州·贵阳一中模拟预测（文））已知函数()323.f x ax x a b =-++(1)讨论()f x 的单调性；(2)当()f x 有三个零点时a 的取值范围恰好是()()()3,22,00,1,--⋃-⋃求b 的值. 【答案】(1)答案见解析 (2)3b = 【解析】【分析】(1)求函数()f x 的导函数()'f x ，讨论a ，并解不等式()0f x '>，()0f x '<可得函数的单调区间；(2)由(1)结合零点存在性定理可求b . (1)()f x 的定义域为R ，()()23632,f x ax x x ax =-=-'若0a =，则()0600f x x x '>⇒->⇒<，()00f x x <⇒>'∴ ()f x 在(),0∞-单调递增，()0,∞+单调递减，若0a >，则()00'>⇒<f x x 或2x a>， ()200f x x a>⇒<<'， ()f x ∴在(),0∞-单调递增，20,a ⎛⎫ ⎪⎝⎭单调递减，2,a ⎛⎫+∞ ⎪⎝⎭单调递增，若0a <，则()200f x x a'>⇒<< ()20f x x a>⇒<'或0x >， ()f x ∴在2,a ⎛⎫-∞ ⎪⎝⎭单调递减，2,0a ⎛⎫⎪⎝⎭单调递增，()0,∞+单调递减.(2)可知()f x 要有三个零点，则0a ≠，且2(0)0f f a ⎛⎫< ⎪⎝⎭由题意也即是()200f f a ⎛⎫< ⎪⎝⎭的解集就是()()()3,22,00,1--⋃-⋃，也就是关于a 的不等式()()()32224400a b a ba a b a b a a ++-⎛⎫++-<⇒< ⎪⎝⎭的解集就是()()()3,22,00,1--⋃-⋃，令()()()32240a b a ba h a a+++=<，时()()()()()1114130h b b b b =++-=+-=，所以有1b =-或3b =，当3b =时，()()()()()323222233434400a a a a a a a h a aa++-+-+-=<⇒<，()()()2231440a a a a a+-++<的解是()()()3,22,00,1--⋃-⋃，满足条件，当1b =-时，()()()322140a a a h a a---=<，当1a =-时，()1120h -=>，不满足条件，故1b ≠-，综合上述3b =.11．（2022·河南·平顶山市第一高级中学模拟预测（理））已知函数()()e 12()exx xf x a a =+--∈R ． (1)若()e ()=⋅x g x f x ，讨论()g x 的单调性； (2)若()f x 有两个零点，求实数a 的取值范围．【答案】(1)答案见解析；(2)()0,1. 【解析】【分析】（1）对函数进行求导，分为0a ≤和0a >两种情形，根据导数与0的关系可得单调性；（2）函数有两个零点即()e ()=⋅x g x f x 有两个零点，根据（1）中的单调性结合零点存在定理即可得结果. (1)由题意知，()()()e ()e e 12e e 12e e x x x x x xx x g x f x a a x ⎡⎤=⋅=⋅+--=+--⎢⎥⎣⎦，()g x 的定义域为(,)-∞+∞，()e (e 1)e e 2e 1(2e 1)(e 1)x x x x x x x g x a a a '=++⋅--=+-．若0a ≤，则()0g x '<，所以()g x 在(,)-∞+∞上单调递减；若0a >，令()0g x '=，解得ln x a =-．当(,ln )x a ∈-∞-时，()0g x '<；当(ln ,)x a ∈-+∞时，()0g x '>，所以()g x 在(,ln )a -∞-上单调递减，在(ln ,)a -+∞上单调递增． (2)因为e 0x >，所以()f x 有两个零点，即()e ()=⋅x g x f x 有两个零点．若0a ≤，由（1）知，()g x 至多有一个零点．若0a >，由（1）知，当ln x a =-时，()g x 取得最小值，最小值为1(ln )1ln g a a a-=-+． ①当1a =时，由于(ln )0g a -=，故()g x 只有一个零点： ①当(1,)∈+∞a 时，由于11ln 0a a-+>，即(ln )0g a ->，故()g x 没有零点； ①当(0,1)a ∈时，11ln 0a a-+<，即(ln )0g a -<．又2222(2)e (e 1)2e 22e 20g a -----=+-+>-+>，故()g x 在(,ln )a -∞-上有一个零点．存在03ln 1,x a ⎛⎫⎛⎫∈-+∞ ⎪ ⎪⎝⎭⎝⎭，则0000000000()e (e 1)2e e (e 2)e 0x x x x x xg x a x a a x x =+--=+-->->．又3ln 1ln a a ⎛⎫->- ⎪⎝⎭，因此()g x 在(ln ,)a -+∞上有一个零点．综上，实数a 的取值范围为(0,1)．12．（2022·青海·大通回族土族自治县教学研究室三模（理））已知函数()ln 1f x ax x =++． (1)若()f x 在(0,)+∞上仅有一个零点，求实数a 的取值范围； (2)若对任意的0x >，2()e x f x x ≤恒成立，求实数a 的取值范围．【答案】(1)0a ≥或1a =- (2)(,2]-∞ 【解析】【分析】（1）求导1()f x a x'=+，0x >，分0a ≥和0a <讨论求解；（2）对任意的0x >，2()e x f x x ≤恒成立，转化为2ln 1e xx a x+≤-在(0,)+∞上恒成立求解． (1)解：1()f x a x'=+，0x >，当0a ≥时，()0f x '>恒成立，所以()f x 在(0,)+∞上单调递增．又()11ee 11a af a a ----=--+()1e 10a a --=-≤，(1)10f a =+>，所以此时()f x 在(0,)+∞上仅有一个零点，符合题意；当0a <时，令()0f x '>，解得10x a <<-；令()0f x '<，解得1x a>-，所以()f x 在10,a ⎛⎫- ⎪⎝⎭上单调递增，所以()f x 在1,a ∞⎛⎫-+ ⎪⎝⎭上单调递减．要使()f x 在(0,)+∞上仅有一个零点，则必有10f a ⎛⎫-= ⎪⎝⎭，解得1a =-．综上，当0a ≥或1a =-时，()f x 在(0,)+∞上仅有一个零点． (2)因为()ln 1f x ax x =++，所以对任意的0x >，2()e x f x x ≤恒成立，等价于2ln 1e xx a x+≤-在(0,)+∞上恒成立．令2ln 1()e (0)xx m x x x+=->，则只需min ()a m x ≤即可，则2222e ln ()+'=x x xm x x ，再令22()2e ln (0)x g x x x x =+>，则()221()4e 0'=++>xg x x x x，所以()g x 在(0,)+∞上单调递增．因为12ln 204g ⎛⎫=< ⎪⎝⎭，2(1)2e 0g =>，所以()g x 有唯一的零点0x ，且0114x <<，所以当00x x <<时，()0m x '<，当0x x >时，()0m x '>，所以()m x 在()00,x 上单调递减，在()0,x +∞上单调递增．因为022002eln 0x x x +=，所以()()()00002ln 2ln ln ln x x x x +=-+-，设()ln (0)S x x x x =+>，则1()10'=+>S x x，所以函数()S x 在(0,)+∞上单调递增．因为()()002ln S x S x =-，所以002ln x x =-，即0201ex x =．所以()0()m x m x ≥=02000000ln 1ln 11e 2x x x x x x x +-=--=，则有2a ≤．所以实数a 的取值范围为(,2]-∞．13．（2022·福建省福州第一中学三模）已知函数()e sin 1x f x a x =--在区间0,2π⎛⎫⎪⎝⎭内有唯一极值点1x .(1)求实数a 的取值范围；(2)证明：()f x 在区间(0,)π内有唯一零点2x ，且212x x <. 【答案】(1)(1,)+∞ (2)证明见解析【解析】【分析】（1）先求导，再讨论1a 时，函数单增不合题意，1a >时，由导数的正负确定函数单调性知符合题意；（2）先由导数确定函数()f x 在区间(0,)π上的单调性，再由零点存在定理即可确定在区间(0,)π内有唯一零点；表示出()12f x ，构造函数求导，求得()120f x >，又由()20f x =，结合()f x 在()1,x x π∈上的单调性即可求解. (1)()e cos x f x a x '=-，当0,2x π⎛⎫∈ ⎪⎝⎭时，cos (0,1)x ∈，21e e x π<<，①当1a 时，()0f x '>，()f x 在0,2π⎛⎫⎪⎝⎭上单调递增，没有极值点，不合题意，舍去；①当1a >时，显然()'f x 在0,2π⎛⎫ ⎪⎝⎭上递增，又因为(0)10f a '=-<，2e 02f ππ⎛⎫'=> ⎪⎝⎭，所以()'f x 在0,2π⎛⎫ ⎪⎝⎭上有唯一零点1x ，所以()10,x x ∈，()0f x '<；1,2x x π⎛⎫∈ ⎪⎝⎭，()0f x '>，所以()f x 在0,2π⎛⎫⎪⎝⎭上有唯一极值点，符合题意.综上，(1,)∈+∞a .(2)由（1）知1a >，所以,2x ππ⎡⎫∈⎪⎢⎣⎭时，()e cos 0x f x a x '=->，所以()10,x x ∈，()0f x '<，()f x 单调递减；()1,x x π∈，()0f x '>，()f x 单调递增，所以()10,x x ∈时，()(0)0f x f <=，则()10<f x ，又因为()e 10f ππ=->，所以()f x 在()1,πx 上有唯一零点2x ，即()f x 在(0,)π上有唯一零点2x .因为()112211112e sin 21e 2sin cos 1x x f x a x a x x =--=--，由（1）知()10f x '=，所以11e cos xa x =，则()112112e 2e sin 1x xf x x =--，构造2()e 2e sin 1,0,2t t p t t t π⎛⎫=--∈ ⎪⎝⎭，所以()2()2e 2e (sin cos )2e e sin cos t t t t p t t t t t '=-+=--，记()e sin cos ,0,2tt t t t πϕ⎛⎫=--∈ ⎪⎝⎭，则()e cos sin t t t t ϕ'=-+，显然()t ϕ'在0,2π⎛⎫ ⎪⎝⎭上单调递增，所以()(0)0t ϕϕ''>=，所以()t ϕ在0,2π⎛⎫ ⎪⎝⎭上单调递增，所以()(0)0t ϕϕ>=，所以()0p t '>，所以()p t 在0,2π⎛⎫⎪⎝⎭上单调递增，所以()(0)0p t p >=，所以()()1220f x f x >=，由前面讨论可知：112x x π<<，12x x π<<，且()f x 在()1,x x π∈单调递增，所以122x x >.【点睛】本题关键点在于先表示出()12f x ，构造函数()p t 求导，令导数为新的函数再次求导，进而确定函数()p t 的单调性，从而得到()120f x >，再结合()20f x =以及()f x 在()1,x x π∈上的单调性即可证得结论. 14．（2022·安徽·合肥市第八中学模拟预测（文））已知函数()e (sin cos )sin .x f x x x a x =+-.(1)当1a =时，求函数f （x ）在区间[0]2π，上零点的个数； (2)若函数()y f x =在（0，2π）上有唯一的极小值点，求实数a 的取值范围【答案】(1)2个(2)2]∞-⋃（，3222[2e ,)2e ,2e πππ⎧⎫+∞⋃⎨⎬⎩⎭【解析】【分析】(1)利用导数判断函数f x （）在[0]2π，上的单调性，结合零点存在性定理确定零点个数；(2)利用导数，通过分类讨论确定函数f x （）的单调性及极值，由此确定a 的取值范围.(1)因为1a =，所以()e (sin cos )sin .x f x x x x =+-()(2e 1)cos x f x x '=-，则当02x π⎛⎫∈ ⎪⎝⎭，时，()0f x '>，f x （）在02π⎛⎫⎪⎝⎭，上单调递增，当322x ππ⎛⎫∈ ⎪⎝⎭，时，()0f x '<，f x （）在322ππ⎛⎫⎪⎝⎭，上单调递减，当322x ππ⎛⎫∈ ⎪⎝⎭，时，()0f x '>，f x （）在322ππ⎛⎫⎪⎝⎭，单词递增，又32223(0)10,()e 10,()1e 0,(2)e 022f f f f ππππππ=>=->=-<=>，则f x （）在322ππ⎛⎫ ⎪⎝⎭，，322ππ⎛⎫⎪⎝⎭，上各有一个零点，所以f x （）在区间[0]2π，上共有两个零点， (2)2()(2e )cos ,(02),22e 2e x x f x a x x ππ'=-∈<<，①当2a ≤时，当02x π⎛⎫∈ ⎪⎝⎭，时，()0f x '>，f x （）在02π⎛⎫⎪⎝⎭，上单调递增，当322x ππ⎛⎫∈ ⎪⎝⎭，时，()0f x '<，f x （）在322ππ⎛⎫⎪⎝⎭，上单调递减，当322x ππ⎛⎫∈ ⎪⎝⎭，时，()0f x '>，f x （）在322ππ⎛⎫⎪⎝⎭，单词递增，此时f x （）在32x π=的时候取得极小值，则2a ≤时符合题意： ①当22e a π≥时，当02x π⎛⎫∈ ⎪⎝⎭，时，()0f x '<，f x （）在02π⎛⎫⎪⎝⎭，上单调递减，当322x ππ⎛⎫∈ ⎪⎝⎭，时，()0f x '>，f x （）在322ππ⎛⎫⎪⎝⎭，上单调递增，当322x ππ⎛⎫∈ ⎪⎝⎭，时，()0f x '<，f x （）在322ππ⎛⎫⎪⎝⎭，单词递减，此时f x （）在2x π=的时候取得极小值，则22a e π≥时符合题意①当222e a π<<时，0ln 22a π<<，此时f x （）在0,ln 2a ⎛⎫ ⎪⎝⎭上单调递减，在ln ,22a π⎛⎫ ⎪⎝⎭，上单调递增，在3,22ππ⎛⎫ ⎪⎝⎭上单调递减，在3(,2)2ππ上单调递增，此时有两个极小值点，不符合题意： ①当22e a π=时，ln22a π=，此时f x （）在（0，32π）上单调递减，在3,22ππ⎛⎫ ⎪⎝⎭上单调递增，此时f x （）在32x π=的时候取得极小值，则22e a π=时符合题意；①当3222e 2e a ππ<<时，3ln 222a ππ<<，此时f x （）在02π⎛⎫ ⎪⎝⎭，上单调递减，在,ln 22a π⎛⎫ ⎪⎝⎭上单调递增，在3ln 22a π⎛⎫⎪⎝⎭，上单调递减，在3,22ππ⎛⎫⎪⎝⎭上单调递增，此时有两个极小值点，不符合题意； ①当322e a π=时，3ln22a π=，此时f x （）在02π⎛⎫ ⎪⎝⎭，上单调递减，在22ππ⎛⎫ ⎪⎝⎭，上单调递增，此时f x （）在2x π=的时候取得极小值，则322e a π=时符合题意；①当322e 2e a ππ<<时，3ln 222a ππ<<，此时f x （）在02π⎛⎫ ⎪⎝⎭，上单调递减，在322ππ⎛⎫⎪⎝⎭，上单调递增，在3(,ln )22a π上单调递减，在(ln ,2)2aπ上单调递增，此时有两个极小值点，不符合题意；综上所述3222(,22e ,)2 ][e ,2e a πππ⎧⎫∈-∞+∞⎨⎬⎩⎭.【点睛】(1)可导函数y ＝f (x )在点x 0处取得极值的充要条件是f ′(x 0)＝0，且在x 0左侧与右侧f ′(x )的符号不同． (2)若f (x )在(a ，b )内有极值，那么f (x )在(a ，b )内绝不是单调函数，即在某区间上单调增或减的函数没有极值．15．（2022·江西·上高二中模拟预测（理））已知函数()()2ln 0ax af x x a x -=->.(1)讨论()f x 的单调性；(2)设()()2ag x f x x=-+有两个零点12,x x ，若212x x >，证明：3312672e x x +>．【答案】(1)答案见解析 (2)证明见解析【解析】【分析】（1）求导得()2221b ax x af x a x x x -+-=--='，对导函数进行分情况讨论其正负，即可得()f x 的单调性. （2）通过函数有两个零点，转化成1212ln 2ln 2x x a x x ++==，然后根据比例，构造出221111ln 2ln()2ln 2ln 2x x tx x x x ++==++，得到122111,e t x t x t x --==，进而构造函数33313ln ()ln[(1)]ln(1)1t t h t t t t t -=+=++-，利用导数处理单调性，进而可求. (1)）()2221b ax x af x a x x x -+-=--=' 令2()F x ax x a =-+- ，则()00F a =-< ，且对称轴102x a=> 而214a ∆=-易知当10,2a ⎛⎫∈ ⎪⎝⎭ 时()f x 在0⎛⎫+∞ ⎪ ⎪⎝⎭⎝⎭ 单调递减，在⎝⎭单调递增当)12a ∞⎡∈+⎢⎣，时()f x 在()0+∞，单调递减. (2)()g x 有两个零点12,x x 且0x >，则1212ln 2ln 2ln 2ln 20x x x x ax a a x x x +++-+=⇒=⇒==，设21x t x =， 212x x >，2t ∴> ∴221111ln 2ln()2ln 2ln 2x x tx x x x ++==++，∴11ln ln 2ln 2t x t x ++=+，所以12111ln ln 2e 1t t x x t t --=-⇒=-， ∴33333631121(1)e (1)t x x t x t t --+=+=+，设33313ln ()ln[(1)]ln(1)1t t h t tt t t -=+=++-，2t >，则222331(1)()[1ln ](1)1t t h t t t t t -'=--+-+，设2231(1)()1ln 1t t t t t tϕ-=--++，则7437323223211()(441)[(1)4(1)](1)(1)t t t t t t t t t t t t t ϕ--'=+--=-+-++，当(1,)t ∈+∞时，()0t ϕ'>，所以函数()t ϕ在(1,)t ∈+∞上递增，()()10t ϕϕ∴>=，则()0h t '>，()h t ∴在(1,)+∞递增，又2t >，∴()(2)ln72h t h >=，故3361272e x x -+>．【点睛】本题考查了含参函数的单调性，最值问题，方程与函数零点的综合问题，利用导数解决单调性的问题，分情况讨论，转化，构造函数证明不等式，二阶求导等综合性的函数知识，在做题时要理清思路，是一道导数的综合题.16．（2022·山东师范大学附中模拟预测）已知函数()()ln h x x a x a =-∈R . (1)若()h x 有两个零点，a 的取值范围；(2)若方程()e ln 0xx a x x -+=有两个实根1x 、2x ，且12x x ≠，证明：12212e ex x x x +>. 【答案】(1)()e,+∞ (2)证明见解析【解析】【分析】（1）分析可知0a ≠，由参变量分离法可知直线1y a=与函数()ln xf x x=的图象有两个交点，利用导数分析函数()f x 的单调性与极值，数形结合可求得实数a 的取值范围；（2）令e 0x t x =>，其中0x >，令111e x t x =，222e xt x =，分析可知关于t 的方程ln 0t a t -=也有两个实根1t 、2t ，且12t t ≠，设120t t >>，将所求不等式等价变形为12112221ln 1t t t t t t ⎛⎫- ⎪⎝⎭>+，令121t s t =>，即证()21ln 1s s s ->+，令()()21ln 1s g s s s -=-+，其中1s >，利用导数分析函数()g s 的单调性，即可证得结论成立. (1)解：函数()h x 的定义域为()0,∞+.。

高考数学(理)总复习：利用导数解决函数零点问题(解析版)

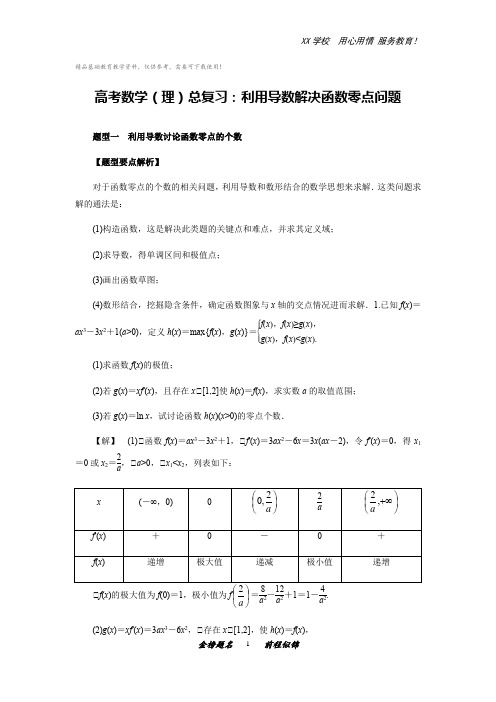
精品基础教育教学资料，仅供参考，需要可下载使用！高考数学（理）总复习：利用导数解决函数零点问题题型一利用导数讨论函数零点的个数【题型要点解析】对于函数零点的个数的相关问题，利用导数和数形结合的数学思想来求解．这类问题求解的通法是：(1)构造函数，这是解决此类题的关键点和难点，并求其定义域； (2)求导数，得单调区间和极值点； (3)画出函数草图；(4)数形结合，挖掘隐含条件，确定函数图象与x 轴的交点情况进而求解．1.已知f (x )＝ax 3－3x 2＋1(a >0)，定义h (x )＝max{f (x )，g (x )}＝⎩⎪⎨⎪⎧f (x )，f (x )≥g (x )，g (x )，f (x )<g (x ).(1)求函数f (x )的极值；(2)若g (x )＝xf ′(x )，且存在x ∈[1,2]使h (x )＝f (x )，求实数a 的取值范围； (3)若g (x )＝ln x ，试讨论函数h (x )(x >0)的零点个数．【解】 (1)∈函数f (x )＝ax 3－3x 2＋1，∈f ′(x )＝3ax 2－6x ＝3x (ax －2)，令f ′(x )＝0，得x 1＝0或x 2＝2a，∈a >0，∈x 1<x 2，列表如下：∈f (x )的极大值为f (0)＝1，极小值为f ⎪⎭⎫⎝⎛a ＝8a 2－12a 2＋1＝1－4a 2. (2)g (x )＝xf ′(x )＝3ax 3－6x 2，∈存在x ∈[1,2]，使h (x )＝f (x )，∈f (x )≥g (x )在x ∈[1,2]上有解，即ax 3－3x 2＋1≥3ax 3－6x 2在x ∈[1,2]上有解，即不等式2a ≤1x 3＋3x 在x ∈[1,2]上有解．设y ＝1x 3＋3x ＝3x 2＋1x 3(x ∈[1,2])，∈y ′＝－3x 2－3x 4<0对x ∈[1,2]恒成立，∈y ＝1x 3＋3x 在x ∈[1,2]上单调递减，∈当x ＝1时，y ＝1x 3＋3x 的最大值为4，∈2a ≤4，即a ≤2.(3)由(1)知，f (x )在(0，＋∞)上的最小值为f ⎪⎭⎫⎝⎛a 2＝1－4a 2， ∈当1－4a 2>0，即a >2时，f (x )>0在(0，＋∞)上恒成立，∈h (x )＝max{f (x )，g (x )}在(0，＋∞)上无零点．∈当1－4a2＝0，即a ＝2时，f (x )min ＝f (1)＝0.又g (1)＝0，∈h (x )＝max{f (x )，g (x )}在(0，＋∞)上有一个零点． ∈当1－4a2<0，即0<a <2时，设φ(x )＝f (x )－g (x )＝ax 3－3x 2＋1－ln x (0<x <1)， ∈φ′(x )＝3ax 2－6x －1x <6x (x －1)－1x <0，∈φ(x )在(0,1)上单调递减．又φ(1)＝a －2<0，φ⎪⎭⎫ ⎝⎛e 1＝a e3＋2e 2－3e 2>0，∈存在唯一的x 0∈⎪⎭⎫⎝⎛1,1e ，使得φ(x 0)＝0，(∈)当0<x ≤x 0时，∈φ(x )＝f (x )－g (x )≥φ(x 0)＝0， ∈h (x )＝f (x )且h (x )为减函数．又h (x 0)＝f (x 0)＝g (x 0)＝ln x 0<ln 1＝0， f (0)＝1>0，∈h (x )在(0，x 0)上有一个零点； (∈)当x >x 0时，∈φ(x )＝f (x )－g (x )<φ(x 0)＝0， ∈h (x )＝g (x )且h (x )为增函数，∈g (1)＝0，∈h (x )在(x 0，＋∞)上有一零点；从而h (x )＝max{f (x )，g (x )}在(0，＋∞)上有两个零点，综上所述，当0<a <2时，h (x )有两个零点；当a ＝2时，h (x )有一个零点；当a >2时，h (x )无零点．题组训练一利用导数讨论函数零点的个数已知函数f (x )＝ln x －12ax ＋a －2，a ∈R .(1)求函数f (x )的单调区间；(2)当a <0时，试判断g (x )＝xf (x )＋2的零点个数．【解析】 (1)f ′(x )＝1x －a 2＝2－ax2x(x >0)．若a ≤0，则f ′(x )>0，∈函数f (x )的单调递增区间为(0，＋∞)；若a >0，当0<x <2a 时，f ′(x )>0，函数f (x )单调递增，当x >2a 时，f ′(x )<0，函数f (x )单调递减，综上，若a ≤0时，函数f (x )的单调递增区间为(0，＋∞)；若a >0时，函数f (x )的单调递增区间为⎪⎭⎫ ⎝⎛a 2,0，单调递减区间为⎪⎭⎫ ⎝⎛∞+a 2.(2)g (x )＝x ln x －12ax 2＋ax －2x ＋2，g ′(x )＝－ax ＋ln x ＋a －1.又a <0，易知g ′(x )在(0，＋∞)上单调递增， g ′(1)＝－1<0，g ′(e)＝－a e ＋a ＝a (1－e)>0，故而g ′(x )在(1，e)上存在唯一的零点x 0，使得g ′(x 0)＝0.当0<x <x 0时，g ′(x )<0，g (x )单调递减；当x >x 0时，g ′(x )>0，g (x )单调递增，取x 1＝e a ，又a <0，∈0<x 1<1，∈g (x 1)＝x 1)2221(ln 111x a ax x +-+-＝e a⎪⎭⎫ ⎝⎛+-+-a a e a ae a 2221，设h (a )＝a －12a e a ＋a －2＋2e a ，(a <0)，h ′(a )＝－12a e a －12e a －2e a ＋2，(a <0)，h ′(0)＝－12，h ″(a )＝e －a －e a ＋e －a －12a e a >0，∈h ′(a )在(－∞，0)上单调递增，h ′(a )<h ′(0)<0， ∈h (a )在(－∞，0)上单调递减，∈h (a )>h (0)＝0， ∈g (x 1)>0，即当a <0时，g (e a )>0.当x 趋于＋∞时，g (x )趋于＋∞，且g (2)＝2ln2－2<0. ∈函数g (x )在(0，＋∞)上始终有两个零点．题型二由函数零点个数求参数的取值范围【题型要点解析】研究方程的根(或函数零点)的情况，可以通过导数研究函数的单调性、最大值、最小值、变化趋势等，并借助函数的大致图象判断方程根(函数零点)的情况，这是导数这一工具在研究方程中的重要应用．已知函数f (x )＝mxln x ，曲线y ＝f (x )在点(e 2，f (e 2))处的切线与直线2x ＋y ＝0垂直(其中e为自然对数的底数)．(1)求f (x )的解析式及单调减区间；(2)若函数g (x )＝f (x )－kx 2x －1无零点，求k 的取值范围．【解析】 (1)函数f (x )＝mx ln x 的导数为f ′(x )＝m (ln x －1)(ln x )2，又由题意有：f ′(e2)＝12∈m 4＝12∈m ＝2，故f (x )＝2xln x.此时f ′(x )＝2(ln x －1)(ln x )2，由f ′(x )≤0∈0<x <1或1<x ≤e ，所以函数f (x )的单调减区间为(0,1)和(1，e]．(2)g (x )＝f (x )－kx 2x －1∈g (x )＝x ⎪⎭⎫ ⎝⎛--1ln 2x kx x ，且定义域为(0,1)∈(1，＋∞)，要函数g (x )无零点，即要2ln x ＝kxx －1在x ∈(0,1)∈(1，＋∞)内无解，亦即要k ln x －2(x －1)x ＝0在x ∈(0,1)∈(1，＋∞)内无解．构造函数h (x )＝k ln x －2(x －1)x ∈h ′(x )＝kx －2x2.∈当k ≤0时，h ′(x )<0在x ∈(0,1)∈(1，＋∞)内恒成立，所以函数h (x )在(0,1)内单调递减，h (x )在(1，＋∞)内也单调递减.又h (1)＝0，所以在(0,1)内无零点，在(1，＋∞)内也无零点，故满足条件；∈当k >0时，h ′(x )＝kx －2x 2∈h ′(x )＝22x k x k ⎪⎭⎫ ⎝⎛-， (i)若0<k <2，则函数h (x )在(0,1)内单调递减，在⎪⎭⎫⎝⎛k 2,1内也单调递减，在⎪⎭⎫ ⎝⎛+∞,2k 内单调递增，又h (1)＝0，所以在(0,1)内无零点；易知h ⎪⎭⎫ ⎝⎛k 2<0，而h (e 2k )＝k ·2k －2＋2e2k>0，故在⎪⎭⎫⎝⎛+∞,2k 内有一个零点，所以不满足条件；(ii)若k ＝2，则函数h (x )在(0,1)内单调递减，在(1，＋∞)内单调递增．又h (1)＝0，所以x ∈(0,1)∈(1，＋∞)时，h (x )>0恒成立，故无零点，满足条件；(iii)若k >2，则函数h (x )在⎪⎭⎫ ⎝⎛k 2,0内单调递减，在⎪⎭⎫⎝⎛1,2k 内单调递增，在(1，＋∞)内单调递增，又h (1)＝0，所以在⎪⎭⎫⎝⎛1,2k 及(1，＋∞)内均无零点．又易知h ⎪⎭⎫⎝⎛k 2<0，而h (e －k )＝k (－k )－2＋2e k ＝2e k －k 2－2，又易证当k >2时，h (e －k )>0，所以函数h (x )在⎪⎭⎫ ⎝⎛k 2,0内有一零点，故不满足条件．综上可得：k 的取值范围为：k ≤0或k ＝2.题组训练二由函数零点个数求参数的取值范围已知函数f (x )＝ln x －ax (ax ＋1)，其中a ∈R . (1)讨论函数f (x )的单调性；(2)若函数f (x )在(0,1]内至少有1个零点，求实数a 的取值范围．【解析】(1)依题意知，函数f (x )的定义域为(0，＋∞)，且f ′(x )＝1x－2a 2x －a＝2a 2x 2＋ax －1－x ＝(2ax －1)(ax ＋1)－x，当a ＝0时，f (x )＝ln x ，函数f (x )在(0，＋∞)上单调递增；当a >0时，由f ′(x )>0，得0<x <12a，由f ′(x )<0，得x >12a ，函数f (x )⎪⎭⎫⎝⎛a 21,0上单调递增，在⎪⎭⎫⎝⎛+∞,21a 上单调递减．当a <0时，由f ′(x )>0，得0<x <－1a ，由f ′(x )<0，得x >－1a，函数f (x )在⎪⎭⎫ ⎝⎛-a 1,0上单调递增，在⎪⎭⎫⎝⎛+∞-,1a 上单调递减． (2)当a ＝0时，函数f (x )在(]0，1内有1个零点x 0＝1；当a >0时，由(1)知函数f (x )在⎪⎭⎫ ⎝⎛a 21,0上单调递增，在⎪⎭⎫⎝⎛+∞,21a 上单调递减． ∈若12a ≥1，即0<a ≤12时，f (x )在(0,1]上单调递增，由于当x →0时，f (x )→－∞且f (1)＝－a 2－a <0知，函数f (x )在(0,1]内无零点；∈若0<12a <1，即当a >12时，f (x )在⎪⎭⎫ ⎝⎛a 21,0上单调递增，在⎥⎦⎤ ⎝⎛1,21a 上单调递减，要使函数f (x )在(0,1]内至少有1个零点，只需满足f ⎪⎭⎫⎝⎛a 21≥0，即ln 12a ≥34，又∈a >12，∈ln 12a <0，∈不等式不成立．∈f (x )在(0,1]内无零点；当a <0时，由(1)知函数f (x )在⎪⎭⎫ ⎝⎛-a 1,0上单调递增，在⎪⎭⎫⎝⎛+∞-,1a 上单调递减． ∈若－1a ≥1，即－1≤a <0时，f (x )在(0,1]上单调递增，由于当x →0时，f (x )→－∞，且f (1)＝－a 2－a >0，知函数f (x )在(0,1]内有1个零点；∈若0<－1a <1，即a <－1时，函数f (x )在⎪⎭⎫ ⎝⎛-a 1,0上单调递增，在⎥⎦⎤⎝⎛-1,1a 上单调递减，由于当x →0时，f (x )→－∞，且当a <－1时，f ⎪⎭⎫⎝⎛-a 1＝ln ⎪⎭⎫⎝⎛-a 1<0，知函数f (x )在(0,1]内无零点．综上可得a 的取值范围是[－1,0]．题型三利用导数证明复杂方程在某区间上仅有一解【题型要点解析】证明复杂方程在某区间上有且仅有一解的步骤： (1)在该区间上构造与方程相应的函数； (2)利用导数研究该函数在该区间上的单调性； (3)判断该函数在该区间端点处的函数值的符号； (4)作出结论．已知函数f (x )＝(x 2－2x )ln x ＋ax 2＋2.(1)当a ＝－1时，求f (x )在点(1，f (1))处的切线方程；(2)当a >0时，设函数g (x )＝f (x )－x －2，且函数g (x )有且仅有一个零点，若e －2<x <e ，g (x )≤m ，求m 的取值范围．【解析】 (1)当a ＝－1时，f (x )＝(x 2－2x )ln x －x 2＋2，定义域为(0，＋∞)，∈f ′(x )＝(2x －2)ln x ＋x －2－2x ＝(2x －2)ln x －x －2.∈f ′(1)＝－3，又f (1)＝1，f (x )在(1，f (1))处的切线方程3x ＋y －4＝0.(2)令g (x )＝f (x )－x －2＝0，则(x 2－2x )ln x ＋ax 2＋2＝x ＋2，即a ＝1－(x －2)·ln xx ，令h (x )＝1－(x －2)·ln xx，则h ′(x )＝－1x 2－1x ＋2－2ln x x 2＝1－x －2ln xx 2.令t (x )＝1－x －2ln x ，t ′(x )＝－1－2x ＝－x －2x ，∈t ′(x )<0，t (x )在(0，＋∞)上是减函数，又∈t (1)＝h ′(1)＝0，所以当0<x <1时，h ′(x )>0，当x >1时，h ′(x )<0，所以h (x )在(0,1)上单调递增，在(1，＋∞)上单调递减，∈h (x )max ＝h (1)＝1.因为a >0，所以当函数g (x )有且仅有一个零点时，a ＝1.g (x )＝(x 2－2x )ln x ＋x 2－x ，若e －2<x <e ，g (x )≤m ，只需g (x )max ≤m ， g ′(x )＝(x －1)(3＋2ln x )，令g ′(x )＝0得x ＝1，或x ＝e －32，又∈e －2<x <e∈函数g (x )在(e －2，e －32)上单调递增，在(e －32，1)上单调递减，在(1，e)上单调递增，又g (e －32)＝－12e －3＋2e －32，g (e)＝2e 2－3e ，∈g (e －32)＝－12e －3＋2e －32<2e －32<2e<2e ⎪⎭⎫ ⎝⎛-23e ＝g (e)，即g (e －32)<g (e)，g (x )max ＝g (e)＝2e 2－3e ，∈m ≥2e 2－3e .题组训练三利用导数证明复杂方程在某区间上仅有一解已知y ＝4x 3＋3tx 2－6t 2x ＋t －1，x ∈R ，t ∈R .(1)当x 为常数时，t 在区间⎥⎦⎤⎢⎣⎡32,0变化时，求y 的最小值φ(x )；(2)证明：对任意的t ∈(0，＋∞)，总存在x 0∈(0,1)，使得y ＝0.【解析】 (1)当x 为常数时，设f (t )＝4x 3＋3tx 2－6t 2x ＋t －1＝－6xt 2＋(3x 2＋1)t ＋4x 3－1，f ′(t )＝－12xt ＋3x 2＋1.∈当x ≤0时，由t ∈⎥⎦⎤⎢⎣⎡32,0知f (t )>0，f (t )在⎥⎦⎤⎢⎣⎡32,0上递增，其最小值φ(x )＝f (0)＝4x 3－1；∈当x >0时，f (t )的图象是开口向下的抛物线，其对称轴为直线；t ＝－3x 2＋1－12x ＝3x 2＋112x ，若⎩⎪⎨⎪⎧x >0，3x 2＋112x ≤13，即13≤x ≤1，则f (t )在⎥⎦⎤⎢⎣⎡32,0上的最小值为 φ(x )＝f ⎪⎭⎫⎝⎛32＝4x 3＋2x 2－83x －13.若⎩⎪⎨⎪⎧x >0，3x 2＋112x >13，即0<x <13或x >1，则f (t )在⎥⎦⎤⎢⎣⎡32,0上的最小值为φ(x )＝f (0)＝4x 3－1.综合∈∈，得φ(x )＝⎩⎨⎧4x 3－1，x <13或x >1，4x 3＋2x 2－83x －13，13≤x ≤1.(2)证明：设g (x )＝4x 3＋3tx 2－6t 2x ＋t －1，则g ′(x )＝12x 2＋6tx －6t 2＝12(x ＋t )⎪⎭⎫ ⎝⎛-2t x 由t ∈(0，＋∞)，当x 在区间(0，＋∞)内变化时，g ′(x )，g (x )取值的变化情况如下表：∈当t2≥1，即t ≥2时，g (x )在区间(0,1)内单调递减，g (0)＝t －1>0，g (1)＝－6t 2＋4t ＋3＝－2t (3t －2)＋3≤－4(3－2)＋3<0.所以对任意t ∈[2，＋∞)，g (x )在区间(0,1)内均存在零点，即存在x 0∈(0,1)，使得g (x 0)＝0.∈当0<t 2<1，即0<t <2时，g (x )在⎪⎭⎫ ⎝⎛2,0t 内单调递减，在⎪⎭⎫ ⎝⎛1,2t 内单调递增，若t ∈(0,1)，则g ⎪⎭⎫⎝⎛2t ＝－74t 3＋t －1≤－74t 3<0，g (1)＝－6t 2＋4t ＋3≥－6t ＋4t ＋3＝－2t ＋3≥1>0，所以g (x )在⎪⎭⎫⎝⎛1,2t 内存在零点；若t ∈(1,2)，则g (0)＝t －1>0，g ⎪⎭⎫ ⎝⎛2t ＝－74t 3＋t －1<－74×13＋2－1<0，所以g (x )在⎪⎭⎫ ⎝⎛2,0t 内存在零点．所以，对任意t ∈(0,2)，g (x )在区间(0,1)内均存在零点，即存在x 0∈(0,1)，使得g (x 0)＝0，综合∈∈，对任意的t ∈(0，＋∞)，总存在x 0∈(0,1)，使得y ＝0.【专题训练】1．已知函数f (x )＝xln x＋ax ，x >1.(1)若f (x )在(1，＋∞)上单调递减，求实数a 的取值范围； (2)若a ＝2，求函数f (x )的极小值；(3)若方程(2x －m )ln x ＋x ＝0，在(1，e]上有两个不等实根，求实数m 的取值范围． [解析] (1)f ′(x )＝ln x －1ln 2x ＋a ，由题意可得f ′(x )≤0在(1，＋∞)上恒成立，∈a ≤1ln 2x －1ln x＝221ln 1⎪⎭⎫⎝⎛-x －14.∈x ∈(1，＋∞)，∈ln x ∈(0，＋∞)， ∈当1ln x －12＝0时，函数t ＝221ln 1⎪⎭⎫ ⎝⎛-x －14的最小值为－14，∈a ≤－14. 故实数a 的取值范围为⎥⎦⎤ ⎝⎛∞-41,(2)当a ＝2时，f (x )＝xln x ＋2x ，f ′(x )＝ln x －1＋2ln 2x ln 2x，令f ′(x )＝0，得2ln 2x ＋ln x －1＝0，解得ln x ＝12或ln x ＝－1(舍)，即x ＝e 12.当1<x <e 12时，f ′(x )<0，当x >e 12时，f ′(x )>0，∈f (x )的极小值为f (e 12)＝e 1212＋2e 1e ＝4e 12.(3)将方程(2x －m )ln x ＋x ＝0两边同除以ln x 得(2x －m )＋x ln x ＝0，整理得xln x＋2x ＝m ，即函数g (x )＝xln x ＋2x 的图象与函数y ＝m 的图象在(1，e]上有两个不同的交点．由(2)可知，g (x )在(1，e 12)上单调递减，在(e 12，e]上单调递增，g (e 12)＝4e 12，g (e)＝3e ，在(1，e]上，当x →1时，x ln x →＋∞，∈4e 12<m ≤3e ，故实数m 的取值范围为(4e 12，3e]．2．已知f (x )＝2x ln x ，g (x )＝x 3＋ax 2－x ＋2.(1)如果函数g (x )的单调递减区间为⎪⎭⎫⎝⎛-1,31，求函数g (x )的解析式； (2)在(1)的条件下，求函数y ＝g (x )的图象在点P (－1，g (－1))处的切线方程； (3)已知不等式f (x )≤g ′(x )＋2恒成立，若方程a e a －m ＝0恰有两个不等实根，求m 的取值范围．【解】 (1)g ′(x )＝3x 2＋2ax －1，由题意知，3x 2＋2ax －1<0的解集为⎪⎭⎫⎝⎛-1,31，即3x 2＋2ax －1＝0的两根分别是－13，1，代入得a ＝－1，∈g (x )＝x 3－x 2－x ＋2. (2)由(1)知，g (－1)＝1，∈g ′(x )＝3x 2－2x －1，g ′(－1)＝4，∈点P (－1,1)处的切线斜率k ＝g ′(－1)＝4，∈函数y ＝g (x )的图象在点P (－1,1)处的切线方程为y －1＝4(x ＋1)，即4x －y ＋5＝0.(3)由题意知，2x ln x ≤3x 2＋2ax ＋1对x ∈(0，＋∞)恒成立，可得a ≥ln x －32x －12x 对x ∈(0，＋∞)恒成立．设h (x )＝ln x －32x －12x，则h ′(x )＝1x －32＋12x 2＝－(x －1)(3x ＋1)2x 2，令h ′(x )＝0，得x ＝1，x ＝－13(舍)，当0<x <1时，h ′(x )>0；当x >1时，h ′(x )<0， ∈当x ＝1时，h (x )取得最大值，h (x )max ＝h (1)＝－2， ∈a ≥－2.令φ(a )＝a e a ，则φ′(a )＝e a ＋a e a ＝e a (a ＋1)， ∈φ(a )在[－2，－1]上单调递减，在(－1，＋∞)上单调递增，∈φ(－2)＝－2e －2＝－2e 2，φ(－1)＝－e －1＝－1e ，当a →＋∞时，φ(a )→＋∞，∈方程a e a －m ＝0恰有两个不等实根，只需－1e <m ≤－2e 2.3．设函数f (x )＝x 3＋ax 2＋bx ＋c .(1)求曲线y ＝f (x )在点(0，f (0))处的切线方程；(2)设a ＝b ＝4，若函数f (x )有三个不同零点，求c 的取值范围； (3)求证：a 2－3b >0是f (x )有三个不同零点的必要而不充分条件．【解析】 (1)由f (x )＝x 3＋ax 2＋bx ＋c ，得f ′(x )＝3x 2＋2ax ＋b .因为f (0)＝c ，f ′(0)＝b ，所以曲线y ＝f (x )在点(0，f (0))处的切线方程为y ＝bx ＋c .(2)当a ＝b ＝4时，f (x )＝x 3＋4x 2＋4x ＋c ，所以f ′(x )＝3x 2＋8x ＋4. 令f ′(x )＝0，得3x 2＋8x ＋4＝0，解得x ＝－2或x ＝－23.f (x )与f ′(x )在区间(－∞，＋∞)上的情况如下：所以，当c >0且c －3227<0时，存在x 1∈(－4，－2)，x 2∈⎪⎭⎫ ⎝⎛--3,2，x 3∈⎪⎭⎫⎝⎛-0,3，使得f (x 1)＝f (x 2)＝f (x 3)＝0.由f (x )的单调性知，当且仅当c ∈⎪⎭⎫⎝⎛2732,0时，函数f (x )＝x 3＋4x 2＋4x ＋c 有三个不同零点．(3)证明：当Δ＝4a 2－12b <0时，f ′(x )＝3x 2＋2ax ＋b >0，x ∈(－∞，＋∞)，此时函数f (x )在区间(－∞，＋∞)上单调递增，所以f (x )不可能有三个不同零点．当Δ＝4a 2－12b ＝0时，f ′(x )＝3x 2＋2ax ＋b 只有一个零点，记作x 0. 当x ∈(－∞，x 0)时，f ′(x )>0，f (x )在区间(－∞，x 0)上单调递增；当x ∈(x 0，＋∞)时，f ′(x )>0，f (x )在的区间(x 0，＋∞)上单调递增．所以f (x )不可能有三个不同零点．综上所述，若函数f (x )有三个不同零点，则必有Δ＝4a 2－12b >0. 故a 2－3b >0是f (x )有三个不同零点的必要条件．当a ＝b ＝4，c ＝0时，a 2－3b >0，f (x )＝x 3＋4x 2＋4x ＝x (x ＋2)2只有两个不同零点，所以a 2－3b >0不是f (x )有三个不同零点的充分条件．因此a 2－3b >0是f (x )有三个不同零点的必要而不充分条件．。

2023年高考数学总复习第三章导数及其应用第5节：利用导数研究函数的零点问题(教师版)

2023年高考数学总复习第三章导数及其应用利用导数研究函数的零点问题题型一判断、证明或讨论函数零点的个数例1已知函数f (x )＝13x 3－a (x 2＋x ＋1).(1)若a ＝3，求f (x )的单调区间；(2)证明：f (x )只有一个零点.(1)解当a ＝3时，f (x )＝13x 3－3x 2－3x －3，f ′(x )＝x 2－6x －3.令f ′(x )＝0，解得x ＝3－23或x ＝3＋2 3.当x ∈(－∞，3－23)∪(3＋23，＋∞)时，f ′(x )>0；当x ∈(3－23，3＋23)时，f ′(x )<0.故f (x )在(－∞，3－23)，(3＋23，＋∞)单调递增，在(3－23，3＋23)单调递减.(2)证明由于x 2＋x ＋1>0，所以f (x )＝0等价于x 3x 2＋x ＋1－3a ＝0.设g (x )＝x 3x 2＋x ＋1－3a ，则g ′(x )＝x 2（x 2＋2x ＋3）（x 2＋x ＋1）2≥0，仅当x ＝0时g ′(x )＝0，所以g (x )在(－∞，＋∞)单调递增.故g (x )至多有一个零点，从而f (x )至多有一个零点.又f (3a －1)＝－6a 2＋2a －13＝－a －162－16<0，f (3a ＋1)＝13>0，故f (x )有一个零点.综上，f (x )只有一个零点.感悟提升利用导数研究方程根(函数零点)的一般方法(1)研究方程根的情况，可以通过导数研究函数的单调性、最大值、最小值、变化趋势等.(2)根据题目要求，画出函数图像的走势规律，标明函数极(最)值的位置.(3)数形结合法分析问题，可以使问题的求解过程有一个清晰、直观的整体展现.训练1设函数f (x )＝ln x ＋m x ，m 为正数.试讨论函数g (x )＝f ′(x )－x 3零点的个数.解由题设g (x )＝f ′(x )－x 3＝1x －m x 2－x 3(x >0)，令g (x )＝0，得m ＝－13x 3＋x (x >0).转化为函数y ＝m 与y ＝－13x 3＋x 的图像的交点情况.设φ(x )＝－13x 3＋x (x >0)，则φ′(x )＝－x 2＋1＝－(x －1)(x ＋1)，当x ∈(0，1)时，φ′(x )>0，φ(x )在(0，1)上单调递增；当x ∈(1，＋∞)时，φ′(x )<0，φ(x )在(1，＋∞)上单调递减，∴x ＝1是φ(x )唯一的极值点，且是极大值点，因此x ＝1也是φ(x )的最大值点，∴φ(x )的最大值为φ(1)＝23.结合y ＝φ(x )的图像(如图)，可知①当m >23时，函数g (x )无零点；②当m ＝23时，函数g (x )有且只有一个零点；③当0<m <23时，函数g (x )有两个零点；综上所述，当m >23时，函数g (x )无零点；当实数m ＝23时，函数g (x )有且只有一个零点；当0<m <23时，函数g (x )有两个零点.题型二根据零点个数确定参数范围例2(2021·全国甲卷)已知a ＞0且a ≠1，函数f (x )＝x a ax (x ＞0).(1)当a ＝2时，求f (x )的单调区间；(2)若函数φ(x )＝f (x )－1有且仅有两个零点，求a 的取值范围.解(1)当a ＝2时，f (x )＝x 22x ，定义域为(0，＋∞)，f ′(x )＝x （2－x ln 2）2x(x ＞0)，令f ′(x )＞0，则0＜x ＜2ln 2，此时函数f (x )单调递增，令f ′(x )＜0，则x ＞2ln 2，此时函数f (x )单调递减，所以函数f (x )(2)函数φ(x )＝f (x )－1有且仅有两个零点，则转化为方程x a a x ＝1(x ＞0)有两个不同的解，即方程ln x x ＝ln a a 有两个不同的解.设g (x )＝ln x x (x ＞0)，则g ′(x )＝1－ln x x2(x >0)，令g ′(x )＝1－ln x x 2＝0，得x ＝e ，当0＜x ＜e 时，g ′(x )＞0，函数g (x )单调递增，当x ＞e 时，g ′(x )＜0，函数g (x )单调递减，故g (x )max ＝g (e)＝1e，且当x ＞e 时，g (x )g (1)＝0，所以0＜ln a a ＜1e，所以a ＞1且a ≠e ，故a 的取值范围为(1，e)∪(e ，＋∞).感悟提升在解决已知函数y ＝f (x )有几个零点求f (x )中参数t 的取值范围问题时，经常从f (x )中分离出参数t ＝g (x )，然后用求导的方法判断g (x )的单调性，再根据题意求出参数t 的值或取值范围.解题时要充分利用导数工具和数形结合思想.训练2已知函数f (x )＝ax －2ln x －a x(a ∈R ).(1)讨论函数f (x )的单调性；(2)若函数h (x )＝1－a 2x －f （x ）2恰有两个不同的零点，求实数a 的取值范围.解(1)函数f(x)＝ax－2ln x－ax的定义域是(0，＋∞)，求导可得f′(x)＝a－2x＋ax2＝ax2－2x＋ax2.当a≤0时，f′(x)<0，故函数f(x)在(0，＋∞)上单调递减.当a≥1时，4(1－a2)≤0，此时f′(x)＝ax2－2x＋ax2≥0，故函数f(x)在(0，＋∞)上单调递增.当0<a<1时，4(1－a2)>0，令f′(x)＝0，得x1＝1－1－a2a，x2＝1＋1－a2a，所以函数f(x)在(0，x1)，(x2，＋∞)上单调递增；在(x1，x2)上单调递减.综上所述，当a≤0时，函数f(x)在(0，＋∞)上单调递减；当a≥1时，函数f(x)在(0，＋∞)上单调递增；当0<a<1时，函数f(x)(1－1－a2a，1＋1－a2a)上单调递减.(2)由题意得函数h(x)＝1－a2x－f（x）2＝1－a2x＋ln x(x>0)，则函数h(x)＝1－a2xf（x）2恰有两个不同的零点即方程1－a2x＋ln x＝0恰有两个不同的根.由1－a2x＋ln x＝0得a＝2（1＋ln x）x，所以直线y＝a与函数g(x)＝2（1＋ln x）x的图像有两个不同的交点.由g(x)＝2（1＋ln x）x，得g′(x)＝－2ln xx2，当0<x<1时，g′(x)>0，g(x)单调递增，当x>1时，g′(x)<0，g(x)单调递减，所以g(x)max＝g(1)＝2.又e－2<1，g(e－2)＝2（1＋ln e－2）e－2＝－2e－2<0，x>1时，g(x)>0，所以实数a的取值范围为(0，2).题型三可化为函数零点的个数问题例3已知函数f(x)＝ln x(0<x≤1)与函数g(x)＝x2＋a的图像有两条公切线，求实数a的取值范围.解设公切线与函数f(x)＝ln x的图像切于点A(x1，ln x1)(0<x1≤1)，因为f(x)＝ln x，所以f′(x)＝1 x，所以在点A(x1，ln x1)处切线的斜率k1＝f′(x1)＝1 x1，所以切线方程为y－ln x1＝1x1(x－x1)，即y＝xx1＋ln x1－1，设公切线与函数g(x)＝x2＋a的图像切于点B(x2，x22＋a)，因为g(x)＝x2＋a，所以g′(x)＝2x，所以在点B(x2，x22＋a)处切线的斜率k2＝g′(x)＝2x2，所以切线方程为y－(x22＋a)＝2x2(x－x2)，即y＝2x2x－x22＋a，1x1＝2x2，ln x1－1＝－x22＋a.因为0<x1≤1，所以1x1＝2x2≥1，x2≥12.又a＝－ln2x2＋x22－1，令t＝x2∈12，＋∞，则h(t)＝－ln2t＋t2－1＝－ln2－ln t＋t2－1，所以h′(t)＝2t2－1 t.令h′(t)>0且t≥12，得t>22；令h ′(t )<0且t ≥1，得12≤t <22.所以h (t )在12，所以函数f (x )＝ln x (0<x ≤1)与函数g (x )＝x 2＋a 有两条公切线，满足h (t )≤ln2－12<h (t )≤－34，所以a ln 2－12，－34.感悟提升解决曲线的切线条数、两曲线的交点个数、方程根的个数等问题的关键是转化为对应函数的零点个数问题，利用数形结合思想，通过研究函数的零点个数解决相关问题.训练3已知函数f (x )＝1＋ln x x.(1)求函数f (x )的图像在x ＝1e 2处的切线方程(e 为自然对数的底数)；(2)当x >1时，方程f (x )＝a (x －1)＋1x(a >0)有唯一实数根，求a 的取值范围.解(1)函数f (x )的定义域为(0，＋∞)，f ′(x )＝－ln x x 2，所以f 2e 4，又e 2，所以函数f (x )的图像在x ＝1e2处的切线方程为y ＋e 2＝2e 即y ＝2e 4x －3e 2.(2)当x >1时，f (x )＝a (x －1)＋1x，即ln x －a (x 2－x )＝0.令h (x )＝ln x －a (x 2－x )，有h (1)＝0，h ′(x )＝－2ax 2＋ax ＋1x.令r (x )＝－2ax 2＋ax ＋1(a >0)，则r (0)＝1，r (1)＝1－a ，①当a≥1时，r(1)≤0，r(x)在(1，＋∞)上单调递减，所以x∈(1，＋∞)时，r(x)<0，即h′(x)<0，所以h(x)在(1，＋∞)上单调递减，故当x>1时，h(x)<h(1)＝0，所以方程f(x)＝a(x－1)＋1x无实根.②当0<a<1时，r(1)＝1－a>0，r(x)在(1，＋∞)上单调递减，所以存在x0∈(1，＋∞)，使得x∈(1，x0)时，r(x)>0，即h(x)单调递增；x∈(x0，＋∞)时，r(x)<0，即h(x)单调递减.所以h(x)max＝h(x0)>h(1)＝0.取x＝1＋1(x>2)，则1＋1a ln1＋1a a1＋1a＋a1＋1a ln1＋1a－1＋1a.令t＝1＋1a>0，故m(t)＝ln t－t(t>2)，则m′(t)＝1t－1<0，所以m(t)在(2，＋∞)单调递减，所以m(t)<ln2－2<0，即h 1＋1a故存在唯一x1x0，1＋1a，使得h(x1)＝0.综上，a的取值范围为(0，1).隐零点问题在求解函数问题时，很多时候都需要求函数f(x)在区间I上的零点，但所述情形都难以求出其准确值，导致解题过程无法继续进行时，可这样尝试求解：先证明函数f(x)在区间I上存在唯一的零点(例如，函数f(x)在区间I上是单调函数且在区间I的两个端点的函数值异号时就可证明存在唯一的零点)，这时可设出其零点是x0.因为x0不易求出(当然，有时是可以求出但无需求出)，所以把零点x0叫作隐零点；若x0容易求出，就叫作显零点，而后解答就可继续进行，实际上，此解法类似于解析几何中“设而不求”的方法.例1设函数f(x)＝e x－ax－2.(1)求f(x)的单调区间；(2)若a＝1，k为整数，且当x>0时，(x－k)f′(x)＋x＋1>0，求k的最大值.解(1)f(x)的定义域为R，f′(x)＝e x－a.当a≤0时，f′(x)>0恒成立，所以f(x)单调增区间为(－∞，＋∞)，无单调减区间.当a>0时，令f′(x)<0，得x<ln a，令f′(x)>0，得x>ln a，所以f(x)的单调递减区间为(－∞，ln a)，单调递增区间为(ln a，＋∞). (2)由题设可得(x－k)(e x－1)＋x＋1>0，即k<x＋x＋1e x－1(x>0)恒成立，令g(x)＝x＋1e x－1＋x(x>0)，得g′(x)＝e x－1－（x＋1）e x（e x－1）2＋1＝e x（e x－x－2）（e x－1）2(x>0).由(1)的结论可知，函数h(x)＝e x－x－2(x>0)是增函数.又因为h(1)<0，h(2)>0，所以函数h(x)的唯一零点α∈(1，2)(该零点就是h(x)的隐零点).当x∈(0，α)时，g′(x)<0；当x∈(α，＋∞)时，g′(x)>0，所以g(x)min＝g(α)＝α＋1eα－1＋α.又h(α)＝eα－α－2＝0，所以eα＝α＋2且α∈(1，2)，则g(x)min＝g(α)＝1＋α∈(2，3)，所以k的最大值为2.例2已知函数f(x)＝(x－1)e x－ax的图像在x＝0处的切线方程是x＋y＋b＝0.(1)求a，b的值；(2)求证函数f(x)有唯一的极值点x0，且f(x0)>－32.(1)解因为f′(x)＝x e x－a，由f′(0)＝－1得a＝1，又f(0)＝－1，所以切线方程为y－(－1)＝－1(x－0)，即x＋y＋1＝0，所以b＝1.(2)证明令g(x)＝f′(x)＝x e x－1，则g′(x)＝(x＋1)e x，所以当x<－1时，g(x)单调递减，且此时g(x)<0，则g(x)在(－∞，－1)内无零点；当x≥－1时，g(x)单调递增，且g(－1)<0，g(1)＝e－1>0，所以g(x)＝0有唯一解x0，f(x)有唯一的极值点x0.由x0e x0＝1⇒e x0＝1 x0，f(x0)＝x0－1x0－x0＝1x又＝e2－1<0，g(1)＝e－1>0⇒12<x0<1⇒2<1x0＋x0<52，所以f(x0)>－3 2 .1.已知函数f(x)＝e x＋(a－e)x－ax2.(1)当a＝0时，求函数f(x)的极值；(2)若函数f(x)在区间(0，1)内存在零点，求实数a的取值范围.解(1)当a＝0时，f(x)＝e x－e x，则f′(x)＝e x－e，f′(1)＝0，当x<1时，f′(x)<0，f(x)单调递减；当x>1时，f′(x)>0，f(x)单调递增，所以f(x)在x＝1处取得极小值，且极小值为f(1)＝0，无极大值.(2)由题意得f′(x)＝e x－2ax＋a－e，设g(x)＝e x－2ax＋a－e，则g′(x)＝e x－2a.若a＝0，则f(x)的最大值f(1)＝0，故由(1)得f(x)在区间(0，1)内没有零点.若a<0，则g′(x)＝e x－2a>0，故函数g(x)在区间(0，1)内单调递增.又g(0)＝1＋a－e<0，g(1)＝－a>0，所以存在x0∈(0，1)，使g(x0)＝0.故当x∈(0，x0)时，f′(x)<0，f(x)单调递减；当x∈(x0，1)时，f′(x)>0，f(x)单调递增.因为f(0)＝1，f(1)＝0，所以当a<0时，f(x)在区间(0，1)内存在零点.若a>0，由(1)得当x∈(0，1)时，e x>e x.则f(x)＝e x＋(a－e)x－ax2>e x＋(a－e)x－ax2＝a(x－x2)>0，此时函数f(x)在区间(0，1)内没有零点.综上，实数a的取值范围为(－∞，0).2.设函数f(x)＝12x2－m ln x，g(x)＝x2－(m＋1)x，m>0.(1)求函数f(x)的单调区间；(2)当m≥1时，讨论f(x)与g(x)图像的交点个数.解(1)函数f(x)的定义域为(0，＋∞)，f′(x)＝（x＋m）（x－m）x.当0<x<m时，f′(x)<0，函数f(x)单调递减；当x>m时，f′(x)>0，函数f(x)单调递增.综上，函数f(x)的单调递增区间是(m，＋∞)，单调递减区间是(0，m).(2)令F(x)＝f(x)－g(x)＝－12x2＋(m＋1)x－m ln x，x>0，题中问题等价于求函数F(x)的零点个数.F′(x)＝－（x－1）（x－m）x，当m＝1时，F′(x)≤0，函数F(x)为减函数，因为F(1)＝32>0，F(4)＝－ln4<0，所以F(x)有唯一零点；当m>1时，0<x<1或x>m时，F′(x)<0；1<x<m时，F′(x)>0，所以函数F(x)在(0，1)和(m，＋∞)上单调递减，在(1，m)上单调递增，因为F(1)＝m＋12>0，F(2m＋2)＝－m ln(2m＋2)<0，所以F(x)有唯一零点.综上，函数F(x)有唯一零点，即函数f(x)与g(x)的图像总有一个交点.3.已知函数f(x)＝(x－1)e x－ax2＋b＋12.(1)若a＝1，求函数f(x)的单调区间；(2)当a＝12时，f(x)的图像与直线y＝bx有3个交点，求b的取值范围.解(1)当a＝1时，f(x)＝(x－1)e x－x2＋b＋12(x∈R)，则f′(x)＝e x＋(x－1)e x－2x＝x(e x－2).令f′(x)>0，解得x<0或x>ln2；令f′(x)<0，解得0<x<ln2，所以函数f(x)的单调递增区间为(－∞，0)和(ln2，＋∞)，单调递减区间为(0，ln2).(2)因为a＝12，所以f(x)＝(x－1)e x－12x2＋b＋12.由(x－1)e x－12x2＋b＋12＝bx，得(x－1)e x－12(x2－1)＝b(x－1).当x＝1时，方程成立.当x≠1时，只需要方程e x－12(x＋1)＝b有2个实根.令g(x)＝e x－12(x＋1)，则g′(x)＝e x－12.当x <ln 12时，g ′(x )<0，当x >ln 12且x ≠1时，g ′(x )>0，所以g (x )∞，ln 12，(1，＋∞)上单调递增，因为＝12－12＋＝12ln 2，g (1)＝e －1≠0，所以b 2，e －(e －1，＋∞).4.已知函数f (x )＝ax cos x －1在0，π6上的最大值为3π6－1.(1)求a 的值；(2)证明：函数f (x )2个零点.(1)解f ′(x )＝a (cos x －x sin x )，因为x ∈0，π6，所以cos x >sin x ≥0，又1>x ≥0，所以1·cos x >x sin x ，即cos x －x sin x >0.当a >0时，f ′(x )>0，所以f (x )在区间0，π6上单调递增，所以f (x )max ＝a ·π6×32－1＝3π6－1，解得a ＝2.当a <0时，f ′(x )<0，所以f (x )在区间0，π6上单调递减，所以f (x )max ＝f (0)＝－1，不符合题意，当a ＝0时，f (x )＝－1，不符合题意.综上，a ＝2.(2)证明设g (x )＝cos x －x sin x ，则g ′(x )＝－2sin x －x cos x x所以g (x )又g (0)＝1>0，＝－π2<0，所以存在唯一的x0g(x0)＝0，当0<x<x0时，g(x)>0，即f′(x)＝2g(x)>0，所以f(x)在(0，x0)上单调递增；当x0<x<π2时，g(x)<0，即f′(x)＝2g(x)<0，所以f(x)0又f(0)＝－1<0，＝2π4－1>0，1<0，所以f(x)综上，函数f(x).。

专题05 利用导数研究函数零点问题 (解析版)

导数及其应用专题五：利用导数研究函数零点问题一、知识储备1、利用导数确定函数零点的常用方法(1)图象法：根据题目要求画出函数的图象，标明函数极(最)值的位置，借助数形结合的思想分析问题（画草图时注意有时候需使用极限）．(2)利用函数零点存在定理：先用该定理判定函数在某区间上有零点，然后利用导数研究函数的单调性、极值(最值)及区间端点值的符号，进而判断函数在该区间上零点的个数． 2、利用函数的零点求参数范围的方法(1)分离参数(()a g x =)后，将原问题转化为()y g x =的值域(最值)问题或转化为直线y a =与()y g x =的图象的交点个数问题(优选分离、次选分类)求解； (2)利用函数零点存在定理构建不等式求解；(3)转化为两个熟悉的函数图象的位置关系问题，从而构建不等式求解．二、例题讲解1．（2022·重庆市秀山高级中学校高三月考）已知函数()e e x x f x x =+. （1）求函数()f x 的单调区间和极值；（2）讨论函数()()()g x f x a a =-∈R 的零点的个数.【答案】（1）单调递减区间是(,2)-∞-，单调递增区间是(2,)-+∞，极小值为21e -，无极大值；（2）详见解析. 【分析】（1）利用导数求得()f x 的单调区间，进而求得极值.（2）由（1）画出()f x 大致图象，由此对a 进行分类讨论，求得()g x 的零点个数. 【详解】（1）函数()f x 的定义域为R ，且()(2)e x f x x '=+，令()0f x '=得2x =-，则()'f x ，()f x 的变化情况如下表示：(2,)-+∞.当2x =-，()f x 有极小值为21(2)e f -=-，无极大值. （2）令()0f x =有1x =-：当1x <-时，()0f x <；当1x >-时，()0f x >，且()f x 经过212,e A ⎛⎫-- ⎪⎝⎭，(1,0)B -，(0,1)C .当x →-∞，与一次函数相比，指数函数e x y -=增长更快，从而1()0e xx f x -+=→；当x →+∞时，()f x →+∞，()f x '→+∞，根据以上信息，画出大致图象如下图所示.函数()()()g x f x a a =-∈R 的零点的个数为()y f x =与y a =的交点个数. 当2x =-时，()f x 有极小值21(2)e f -=-. ∴关于函数()()()g x f x a a =-∈R 的零点个数有如下结论：当21e a <-时，零点的个数为0个；当21e a =-或0a ≥，零点的个数为1个；当210ea -<<时，零点的个数为2个. 【点睛】求解含参数零点问题，可利用分离常数法，结合函数图象进行求解.感悟升华（核心秘籍）本题讨论()()()g x f x a a =-∈R 零点的个数，将问题分解为()y f x =与y a =交点的个数，注意在利用导函数求()f x 单调性，极值后，画出草图，容易出错，本题利用极限x →-∞时，()0f x →，从而将草图画的更准确；三、实战练习1．（2022·河南高三开学考试（文））若函数()34f x ax bx =+－，当2x =时，函数()f x 有极值43-．（1）求函数的递减区间；（2）若关于x 的方程()0f x k -=有一个零点，求实数k 的取值范围．【答案】（1）递减区间为()2,2-；（2）428,,33⎛⎫⎛⎫-∞-⋃+∞ ⎪ ⎪⎝⎭⎝⎭.【分析】（1）对函数进行求导，利用()()2120,42824,3f a b f a b ⎧=-='⎪⎨=-+=-⎪⎩，解方程即可得1,34.a b ⎧=⎪⎨⎪=⎩，对函数求导，根据导数的性质列表，即可得答案；（2）作出函数的图象，直线与函数图象需有1个交点，即可得答案；【详解】（1）()23f x ax b '=-，由题意知()()2120,42824,3f a b f a b ⎧=-='⎪⎨=-+=-⎪⎩解得1,34.a b ⎧=⎪⎨⎪=⎩ 故所求的解析式为()31443f x x x =-+，可得()()()2422f x x x x '=-=-+，令()0f x '=，得2x =或2x =-，由此可得所以函数的递减区间为2,2-.(2)由(1)知，得到当2x <-或2x >时， ()f x 为增函数; 当22x -<<时， ()f x 为减函数，∴函数()31443f x x x =-+的图象大致如图，由图可知当43k <-或283k >时， ()f x 与y k =有一个交点，所以实数k 的取值范围为428,,33⎛⎫⎛⎫-∞-⋃+∞ ⎪ ⎪⎝⎭⎝⎭.【点睛】关键点睛：根据函数的单调性做出该函数的大致图像，进而利用数形结合求解，考查利用导数研究函数的极值、单调性、零点，考查函数与方程思想、转化与化归思想、分类讨论思想、数形结合思想，考查逻辑推理能力、运算求解能力.2．（2022·陕西西安中学高三月考（理））已知函数()()1xf x e ax a R =--∈.（1）试讨论函数()f x 的零点个数；（2）若函数()()ln 1ln xg x e x =--，且()()f g x f x <⎡⎤⎣⎦在()0,x ∈+∞上恒成立，求实数a 的取值范围.【答案】（1）当0a 或1a =时，函数()f x 只有一个零点；当()()0,11,a ∈+∞时，函数()f x 有两个零点．（2）(],1-∞【分析】（1）通过求解函数的单调性，然后根据零点存在定理，通过讨论求解得出函数零点的个数；（2）根据（1）中结论，得到函数()f x 在(0,)+∞上单调递增，将不等式转换为自变量的比较，最后得出结论．【详解】解：（1）根据题意，可得()x f x e a '=-，则有：①若0a ，则()0x f x e a '=->，此时可得函数()f x 在R 上单调递增，又因为(0)0f =，所以函数只有一个零点； ②若0a >，令()0f x '=，则有ln x a =，所以()0ln f x x a '>⇒>，此时函数()f x 在(ln ,)a +∞上单调递增；()0ln f x x a '<⇒<，此时函数()f x 在(,ln )a -∞上单调递减；即()(ln )1ln min f x f a a a a ==--，则有：()i 当ln 01a a =⇒=时，则()0f x ，此时函数()f x 只有一个零点；()ii 当ln 0a ≠时，即1a ≠时，则(ln )(0)0f a f <=，又因为x →-∞时，()f x →+∞；x →+∞时，()f x →+∞，根据零点存在定理可得，此时函数()f x 在R 上有两个零点．综上可得，当0a 或1a =时，函数()f x 只有一个零点；当()()0,11,a ∈+∞时，函数()f x 有两个零点．（2）下面证明：0x ∀>，有()0g x x <<，先证：0x ∀>，有()0g x >，由（1）可知当1a =时，()()00min f x f ==，即当0x >时，1x e x ->，故0x ∀>，()()()1ln 1ln ln ln10x xe g x e x g x x ⎛⎫-=--==>= ⎪⎝⎭，再证0x ∀>，()g x x <；要证0x ∀>，()g x x <，只需证明0x ∀>，1x xe e x-<，即证0x ∀>，1x x e xe -<，即证0x ∀>，10x x xe e -+> 令()1(0)x x H x xe e x =-+>()0x H x xe '=>在(0,)+∞上恒成立，即得函数()H x 在(0,)+∞上单调递增，故有()(0)0H x H >=，即0x ∀>，10x x xe e -+>恒成立，即0x ∀>，有()0g x x <<，当1a ≤时，由（1）得，()f x 在(0,)+∞上单调递增，则由上结论可知，[()]()f g x f x <在(0,)x ∈+∞上恒成立，符合题意；当1a >时，由（1）得，()f x 在(0,ln )a 上单调递减，在(ln ,)a +∞上单调递增，此时当0ln x a <<时，0()ln [()]()g x x a f g x f x <<<⇔>，不合题意，综上可得，1a ，即(],1a ∈-∞．【点睛】导函数中常用的两种常用的转化方法：一是利用导数研究含参函数的单调性，常化为不等式恒成立问题．注意分类讨论与数形结合思想的应用；二是函数的零点、不等式证明常转化为函数的单调性、极(最)值问题处理．3．（2022·榆林市第十中学高三月考（文））已知函数()2ln f x ax x x =--，0a ≠．（1）试讨论函数()f x 的单调性；（2）若函数()f x 有两个零点，求实数a 的取值范围．【答案】（1）当0a <时，函数()f x 在()0,∞+上单调递减；当0a >时，()f x 在⎛ ⎝⎭上单调递减，在⎫+∞⎪⎪⎝⎭上单调递增．（2）()0,1. 【分析】（1）求出导函数()212121ax x f x ax x x-'-=--=，设()221g x ax x =--，对a 分类讨论：当0a <时，函数()f x在()0,∞+上单调递减；当0a >时，()f x 在⎛ ⎝⎭上单调递减，在⎫+∞⎪⎪⎝⎭上单调递增．（2）把()f x 有两个零点，转化为2ln x xa x +=有两个解，令()2ln x x h x x+=，二次求导后得到函数()h x 的单调性和极值，即可求出实数a 的取值范围. 【详解】函数()2ln f x ax x x =--的定义域为()0+∞，. （1）()212121ax x f x ax x x-'-=--=，设()221g x ax x =--当0a <时，因为函数()g x 图象的对称轴为104x a=<，()01g =-．所以当0x >时，()0g x <，()0f x '<，函数()f x 在()0,∞+上单调递减；当0a >时，令()0g x =．得1x =2x =当20x x <<时，()0<g x ，()0f x '<，当2x x >时，()0>g x ，()0f x '>．所以函数()f x 在⎛ ⎝⎭上单调递减，在⎫+∞⎪⎪⎝⎭上单调递增．（2）若()f x 有两个零点，即2ln 0ax x x --=有两个解，2ln x x a x +=．设()2ln x x h x x +=，()312ln x h x xx '-=-，设()12ln F x x x =--，因为函数()F x 在()0,∞+上单调递减，且()10F =，所以当01x <<时，()0F x >，()0h x '>，当1x >时，()0F x <，()0h x '<．以函数()h x 在()0,1上单调递增，在()1,+∞上单调递减，且 x →+∞时，()0h x →，()11h =，所以01a <<．即实数a 的取值范围为()0,1.4．（2022·沙坪坝·重庆南开中学）已知函数()e 1xf x x a -=++（R a ∈）．（1）讨论()f x 的单调性；（2）若函数()f x 有两个零点，求a 的取值范围．【答案】（1）当0a ≤时，()f x 在R 上单调递增；当0a >时，()f x 在(),ln a -∞上单调递减，在()ln ,a +∞上单调递增；（2）()20,e -.【分析】（1）对函数求导，进而讨论a 的符号，进而得到函数的单调区间；（2）由（1）可以判断0a >，根据（1）可知()()min ln 0f x f a =<，进而根据零点存在定理结合放缩法得到答案. 【详解】（1）()f x 的定义域为R ，()1e xf x a -'=-，①当0a ≤时，()0f x '>恒成立，所以()f x 在R 上单调递增； ②当0a >时，令()0f x '=得ln x a =，当ln x a <时，()0f x '<，()f x 单调递减，当ln x a >时，()0f x '>，()f x 单调递增，所以()f x 在(),ln a -∞上单调递减，在()ln ,a +∞上单调递增综上所述，当0a ≤时，()f x 在R 上单调递增；当0a >时，()f x 在(),ln a -∞上单调递减，在()ln ,a +∞上单调递增.（2）由（1）可知，0a ≤时，()f x 在R 上单调递增，函数至多有一个零点，不合题意.0a >时，()f x 在(),ln a -∞上单调递减，在()ln ,a +∞上单调递增，因为函数有2个零点，所以()()2min ln ln 200e f x f a a a -==+<⇒<<，且()11e 02f a -+>=.记()()e 0x g x x x =-<，则()e 1xg x '=-，所以(),0x ∈-∞时，()0g x '<，()g x 单调递减，所以()()010g x g >=>，则e xx >，于是2e2x x ->-，则x <0时，2e 4xx ->. 所以当x <0时，()214ax f x x >++，限定1x <-，则()()212844ax f x x x ax >+=+，所以当1x <-且8x a<-时，()0f x >.于是，若函数有2个零点，则()20,e a -∈.【点睛】在“()()2min ln ln 200e f x f a a a -==+<⇒<<，且()11e 02f a -+>=”这一步之后，另一个特值不太好找，这时候需要利用e xx >得到2e2x x->-，进而根据放缩法得到结论. 5．（2022·赣州市第十四中学高三月考（文））已知函数()e 2xf x x =+. （1）求函数()y f x =的单调区间；（2）若函数()()()g x f x ax a =-∈R ，在定义域内恰有三个不同的零点，求实数a 的取值范围.【答案】（1）()f x 在(),2-∞-和()2,1--上为减函数，在()1,-+∞上为增函数；（2）⎛⎫+∞⎪⎪⎭. 【分析】（1）求出函数()f x 的定义域，利用导数与函数单调性的关系可求得函数()f x 的增区间和减区间；（2）分析可知，直线y a =与函数()22xeh x x x=+（0x ≠且2x ≠-）的图象有三个交点，利用导数分析函数()22xe h x x x=+的单调性与极值，数形结合可得出实数a 的取值范围.【详解】（1）因为()e 2xf x x =+的定义域为{}2x x ≠-，且()()()212x e x f x x +'=+，则当2x <-时，()0f x '<，()f x 为减函数；当21x -<<-时，()0f x '<，()f x 为减函数；当1x >-时，()0f x '>，()f x 为增函数，综上可得：()f x 在(),2-∞-和()2,1--上为减函数，在()1,-+∞上为增函数；（2）令函数()()0g x f x ax =-=，因为0x =不是方程的解，所以可得22xe a x x=+，构造函数()22xeh x x x =+（0x ≠且2x ≠-），则()()()22222x e x h x x x -'=+，由()0h x '=可得x =作出函数()h x 的图象如下图所示：由图可知，当a >时，函数y a =与函数()y h x =的图象有三个不同的交点，因此实数a 的取值范围是⎛⎫+∞⎪⎪⎭.【点睛】方法点睛：利用导数解决函数零点问题的方法：（1）直接法：先对函数求导，根据导数的方法求出函数的单调区间与极值，根据函数的基本性质作出图象，然后将问题转化为函数图象与x 轴的交点问题，突出导数的工具作用，体现了转化与化归思想、数形结合思想和分类讨论思想的应用；（2）构造新函数法：将问题转化为研究两函数图象的交点问题；（3）参变量分离法：由()0f x =分离变量得出()a g x =，将问题等价转化为直线y a =与函数()y g x =的图象的交点问题.6．（2022·天津静海一中高三月考）已知函数32()3f x x x ax b =-++在1x =-处的切线与x 轴平行．（1）求a 的值和函数()f x 的单调区间；（2）若函数()y f x =的图象与抛物线231532y x x =-+恰有三个不同交点，求b 的取值范围．【答案】（1）-9，单调增区间为(,1)-∞-和(3,)+∞；单调减区间为(1,3)-；（2）1,12⎛⎫⎪⎝⎭.【分析】（1）根据(1)0f '-=即可求得a 的值，利用导函数求解单调区间；（2）令23239()()1536322g x f x x x x x x b ⎛⎫=--+=-++- ⎪⎝⎭，转化为()g x 有三个不同的零点.【详解】（1）由已知得2()36f x x x a '=-+， ∵在1x =-处的切线与x 轴平行 ∴(1)0f '-=，解得9a =-．这时2()3693(1)(3)f x x x x x ==+'--- 由()0f x '>，解得3x >或1x <-；由()0f x '<，解13x ．∴()f x 的单调增区间为(,1)-∞-和(3,)+∞；单调减区间为(1,3)-．（2）令23239()()1536322g x f x x x x x x b ⎛⎫=--+=-++- ⎪⎝⎭，则原题意等价于()g x 图象与x 轴有三个交点． ∵2()3963(1)(2)g x x x x x '=-+=--， ∴由()0g x '>，解得2x >或1x <；由()0g x '<，解得12x <<．∴()g x 在1x =时取得极大值1(1)2g b =-；()g x 在2x =时取得极小值(2)1g b =-．依题意得10210b b ⎧->⎪⎨⎪-<⎩，解得112b <<．故b 的取值范围为1,12⎛⎫⎪⎝⎭．7．（2022·沙坪坝·重庆南开中学高三月考）已知函数()()2ln =+-∈f x ax x x a R ．（1）当1a =时，求()f x 在区间1[,1]3上的最值；（2）若()()g x f x x =-在定义域内有两个零点，求a 的取值范围．【答案】（1）3()=ln 24min f x +，()2max f x =；（2）10,2e ⎛⎫⎪⎝⎭.【分析】（1）当1a =时，求出导函数，求出函数得单调区间，即可求出()f x 在区间1[,1]3上的最值；（2）由()()0g x f x x =-=，分离参数得2ln ()x a h x x ==，根据函数2ln ()xh x x =得单调性作图，结合图像即可得出答案. 【详解】解：（1）当1a =时，()2ln f x x x x =+-，(21)(1)()x x f x x-+'=，∴()f x 在11[,)32单调递减，在1(,1]2单调递增，11114ln ln 339339f ⎛⎫=+-=+ ⎪⎝⎭，()414112ln 993f e f ⎛⎫==+> ⎪⎝⎭，∴13()()ln 224min f x f ==+，()(1)2max f x f ==.（2）()()0g x f x x =-=2ln ()x a h x x ⇔==，则312ln ()xh x x -'=，∴()h x在单调递增，在)+∞单调递减，12h e=，当0x →时，()h x →-∞，当x →+∞时，()0h x →，作出函数2ln ()x h x x =和y a=得图像， ∴由图象可得，1(0,)2a e∈.8．（2022·全国高三专题练习）已知函数()ln f x a x bx =+的图象在点(1,3)-处的切线方程为21y x =--. （1）若对任意1[,)3x ∈+∞有()f x m 恒成立，求实数m 的取值范围；（2）若函数2()()2g x f x x k =+++在区间(0,)+∞内有3个零点，求实数k 的范围. 【答案】（1）[ln31--，)+∞；（2）3(ln2,0)4-.【分析】（1）()af x b x'=+，(0)x >，根据函数()f x 的图象在点(1,3)-处的切线的方程为21y x =--．可得f '（1）2=-，f （1）3=-，解得a ，b ，利用导数研究函数的单调性极值与最值即可得出实数m 的取值范围．（2）由（1）可得：2()ln 32g x x x x k =-+++，利用导数研究函数的单调性极值与最值，根据函数2()()2g x f x x k =+++在区间(0,)+∞内有3个零点，可得最值满足的条件，进而得出实数k 的取值范围．【详解】解：（1）()a f x b x'=+，(0)x >.函数()f x 的图象在点(1,3)-处的切线的方程为21y x =--. f '∴（1）2=-，f （1）3=-，∴23a b b +=-⎧⎨=-⎩，解得3b =-，1a =.()ln 3f x x x ∴=-.13()13()3x f x x x --=-='，1[,)3x ∈+∞，()0f x '∴.∴当13x =时，函数()f x 取得最大值，1()ln313f =--.对任意1[,)3x ∈+∞有()f x m 恒成立，所以()max m f x ，1[,)3x ∈+∞.ln31m ∴--.∴实数m 的取值范围是[ln31--，)+∞.（2）由（1）可得：2()ln 32g x x x x k =-+++，∴1(21)(1)()23x x g x x x x--'=+-=，令()0g x '=，解得12x =，1. 列表如下：由表格可知：当1x =时，函数()f x 取得极小值g （1）k =；当2x =时，函数()g x 取得极大值13()ln224g k =-++.要满足函数2()()2g x f x x k =+++在区间(0,)+∞内有3个零点， 3ln2040k k ⎧-++>⎪⎨⎪<⎩，解得3ln204k -<<，则实数k 的取值范围3(ln2,0)4-.【点睛】本题考查了利用导数研究函数的单调性极值与最值、方程与不等式的解法、转化方法，考查了推理能力于计算能力，属于难题．9．（2022·全国高三开学考试）已知函数()()()21102f x x a x x =-+>. （1）若()()ln g x f x a x =+，讨论函数()g x 的单调性；（2）已知()()()2ln 222m x f x x x a x a =-++-+，若()m x 在1,2⎡⎫+∞⎪⎢⎣⎭内有两个零点，求a 的取值范围.【答案】（1）答案见解析；（2）9ln 21,105⎛⎤+ ⎥⎝⎦ 【分析】（1）求出导函数，对a 进行分类讨论：①0a ≤；②01a <<；③a =1；④a >1，利用导数研究单调性. （2）把()m x 在1,2⎡⎫+∞⎪⎢⎣⎭内有两个零点转化为关于x 方程2ln 2=2x x x a x -++在1,2⎡⎫+∞⎪⎢⎣⎭上有两个不相等的实数根.令()2ln 21=,,22x x x h x x x -+⎡⎫∈+∞⎪⎢+⎣⎭利用导数判断单调性，求出值域，即可求出a 的范围. 【详解】（1）()f x 的定义域为(0,+∞)，()()()()11x x a a f x x a x x--'=-++=. ①当0a ≤时，令()0f x '<，得到01x <<；令()0f x '>，得到1x >，此时()f x 在(0,1)上为减函数，在(1,+∞)上为增函数；②当01a <<时，令()0f x '<，得到1<<a x ；令()0f x '>，得到0x a <<或1x >，此时()f x 在(a ,1)上为减函数，在(0,a )和()1,+∞上为增函数；③当a =1时,显然()0f x '≥恒成立，此时()f x 在0,+∞)上为增函数；④当a >1时,令()0f x '<，得到1x a <<；令()0f x '>，得到01x <<或x a >.此时()f x 在(1,a )上为减函数,在(0,1)和(a ,+∞)上为增函数.综上：①当0a ≤时， ()f x 在(0,1)上为减函数，在(1,+∞)上为增函数； ②当01a <<时， ()f x 在(a ,1)上为减函数，在(0,a )和()1,+∞上为增函数； ③当a =1时，()f x 在0,+∞)上为增函数；④当a >1时，()f x 在(1,a )上为减函数,在(0,1)和(a ,+∞)上为增函数.（2）()()()22ln 222ln 22m x f x x x a x a x ax x x a =-++-+=---+在1,2⎡⎫+∞⎪⎢⎣⎭内有两个零点，即关于x 方程2ln 2=2x x x a x -++在1,2⎡⎫+∞⎪⎢⎣⎭上有两个不相等的实数根.令()2ln 21=,,22x x x h x x x -+⎡⎫∈+∞⎪⎢+⎣⎭则()()2232ln 4=2x x x h x x +--'+，令()2132ln 4,2p x x x x x ⎡⎫=+--∈+∞⎪⎢⎣⎭，，则()()()212x x p x x-+'=，显然()0p x '≥在1,2⎡⎫+∞⎪⎢⎣⎭上恒成立,故()p x 在1,2⎡⎫+∞⎪⎢⎣⎭上单调递增.因为p (1)=0，所以当1,12x ⎡⎫∈⎪⎢⎣⎭，有()0p x <，即()0h x '<所以()h x 单调递减；当()1x ∈+∞，，有()0p x >，即()0h x '>所以()h x 单调递增；因为()()9ln 24=,1,0111423ln 21532h h h h ⎛⎫⎛⎫+==-> ⎪ ⎪⎝⎭⎝⎭，所以a 的取值范围9ln 21,105⎛⎤+ ⎥⎝⎦ 10．（2022·贵州贵阳一中（文））已知函数3211()()32f x x ax a =-∈R 在[0,1]上的最小值为16-．（1）求a 的值；（2）若函数()()2()g x f x x b b =-+∈R 有1个零点，求b 的取值范围．【答案】（1）1a =；（2）76b <-或103b >．【分析】（1）利用导数分0a ，01a <<，1a =和1a >四种情况求出函数的最小值，然后列方程可求出a 的值；（2）由（1）3211()232g x x x x b =--+，可得3211232b x x x =-++，构造函数3211()232h x x x x =-++，利用导数求出函数的单调区间和极值，结合函数图像可得答案【详解】解：（1）由3211()32f x x ax =-，2()()f x x ax x x a =--'=，当0a 时，()'f x 在[0,)+∞上恒大于等于0，所以()f x 在[0,1]上单调递增， min ()(0)0f x f ==，不合题意；当01a <<时，则[0,]x a ∈时，()0f x '<，()f x 单调递减； [,1]x a ∈时，()0f x '>，()f x 单调递增，所以333min 111()()326f x f a a a a ==-=-，31166a -=-，所以1a =，不满足01a <<；当1a =时，在[0,1]上，()0f x '且不恒为0，所以()f x 在[0,1]上单调递减，min 111()(1)326f x f ==-=-，适合题意；当1a >时，在[0,1]上，()0f x '<，所以()f x 在[0,1]上单调递减，min 111()(1)326f x f a ==-=-，所以1a =，不满足1a >；综上，1a =．（2）由（1）3211()232g x x x x b =--+，所以3211232b x x x =-++，令3211()232h x x x x =-++，则2()2(2)(1)h x x x x x =-++=--+'，所以(2)0,(1)0h h ''=-=，且当1x <-时，()0h x '<；当12x -<<时，()0h x '>；当2x >时，()0h x '<，所以 117()(1)2326h x h =-=+-=-极小， 1110()(2)844323h x h ==-⨯+⨯+=极大，如图：函数()g x 有1个零点，所以76b <-或103b >．。

高考数学科学复习创新方案：利用导数研究函数的零点问题

利用导数研究函数的零点问题例1(2022·新高考Ⅰ卷改编)已知函数f(x)＝e x－x，g(x)＝x－ln x.(1)判断直线y＝b与曲线y＝f(x)和y＝g(x)的交点分别有几个；(2)证明：曲线y＝f(x)和y＝g(x)有且只有一个公共点；(3)证明：存在直线y＝b，其与两条曲线y＝f(x)和y＝g(x)共有三个不同的交点，并且从左到右的三个交点的横坐标成等差数列．解(1)设S(x)＝e x－x－b，S′(x)＝e x－1，当x<0时，S′(x)<0，当x>0时，S′(x)>0，故S(x)在(－∞，0)上为减函数，在(0，＋∞)上为增函数，所以S(x)min＝S(0)＝1－b.当b<1时，S(x)min＝1－b>0，S(x)无零点；当b＝1时，S(x)min＝1－b＝0，S(x)有1个零点；当b>1时，S(x)min＝1－b<0，而S(－b)＝e－b>0，S(b)＝e b－2b，设u(b)＝e b－2b，则当b>1时，u′(b)＝e b－2>0，故u(b)在(1，＋∞)上为增函数，故u(b)>u(1)＝e－2>0，故S(b)>0，故S(x)＝e x－x－b有两个不同的零点．，设T(x)＝x－ln x－b，T′(x)＝x－1x当0<x<1时，T′(x)<0，当x>1时，T′(x)>0，故T(x)在(0，1)上为减函数，在(1，＋∞)上为增函数，所以T(x)min＝T(1)＝1－b.当b<1时，T(x)min＝1－b>0，T(x)无零点；当b＝1时，T(x)min＝1－b＝0，T(x)有1个零点；当b>1时，T(x)min＝1－b<0，而T(e－b)＝e－b>0，T(e b)＝e b－2b>0，所以T(x)＝x－ln x－b有两个不同的零点．综上可知，当b<1时，直线y＝b与曲线y＝f(x)和y＝g(x)的交点个数都是0；当b＝1时，直线y＝b与曲线y＝f(x)和y＝g(x)的交点个数都是1；当b>1时，直线y＝b与曲线y＝f(x)和y＝g(x)的交点个数都是2.(2)证明：由f(x)＝g(x)得e x－x＝x－ln x，即e x＋ln x－2x＝0，设h(x)＝e x＋ln x－2x，其中x>0，故h′(x)＝e x＋1x－2，设s(x)＝e x－x－1，则当x>0时，s′(x)＝e x－1>0，故s(x)在(0，＋∞)上为增函数，故s(x)＞s(0)＝0，即e x>x＋1，所以h′(x)>x＋1x－1≥2－1>0，所以h(x)在(0，＋∞)上为增函数，而h(1)＝e－2>0，e1e3－3－2e3<e－3－2e3＜0，故h(x)在(0，＋∞)上有且只有一个零点x0，且1e3<x0<1，当0<x<x0时，h(x)<0，即e x－x<x－ln x，即f(x)<g(x)，当x>x0时，h(x)>0，即e x－x>x－ln x，即f(x)>g(x)，所以曲线y＝f(x)和y＝g(x)有且只有一个公共点．(3)证明：由(2)知，若存在直线y＝b与曲线y＝f(x)，y＝g(x)有三个不同的交点，则b＝f(x0)＝g(x0)>1，此时e x－x＝b有两个不同的解x1，x0(x1<0<x0)，x－ln x＝b有两个不同的解x0，x2(0<x0<1<x2)，故e x1－x1＝b，e x0－x0＝b，x2－ln x2－b＝0，x0－ln x0－b＝0，所以x2－b＝ln x2，即e x2－b＝x2，即e x2－b－(x2－b)－b＝0，故x2－b为方程e x－x＝b的解，同理x0－b也为方程e x－x＝b的解，所以{x1，x0}＝{x0－b，x2－b}，而b>10＝x2－b，1＝x0－b，即x1＋x2＝2x0.利用导数确定函数零点或方程根的个数的常用方法(1)构建函数g(x)(需g′(x)易求，g′(x)＝0可解)，转化为确定g(x)的零点个数问题求解，利用导数研究该函数的单调性、极值，并确定定义域区间端点值的符号(或变化趋势)等，画出g(x)的图象草图，数形结合求解函数零点的个数．(2)利用函数零点存在定理：先用该定理判断函数在某区间上有零点，然后利用导数研究函数的单调性、极值(最值)及区间端点值符号，进而判断函数在该区间上零点的个数．(2024·衡水模拟)已知函数f(x)＝(x－2)e x.(1)求函数f(x)的单调区间和极值；(2)若g(x)＝f(x)－a，讨论函数g(x)的零点个数．解(1)f(x)的定义域为R，f′(x)＝e x＋(x－2)e x＝(x－1)e x，又e x>0恒成立，∴当x∈(－∞，1)时，f′(x)<0；当x∈(1，＋∞)时，f′(x)>0，∴函数f(x)的单调递减区间为(－∞，1)，单调递增区间为(1，＋∞)．函数f(x)的极小值为f(1)＝－e，无极大值．(2)当x<2时，f(x)<0，当x>2时，f(x)>0，结合(1)中结论作出函数图象如图，∴g(x)的零点个数等价于f(x)的图象与直线y＝a的交点个数．当a≥0时，f(x)的图象与直线y＝a有且仅有一个交点；当－e<a<0时，f(x)的图象与直线y＝a有两个不同的交点；当a＝－e时，f(x)的图象与直线y＝a有且仅有一个交点；当a<－e时，f(x)的图象与直线y＝a无交点．综上所述，当a∈[0，＋∞)∪{－e}时，g(x)有唯一零点；当a∈(－e，0)时，g(x)有两个不同的零点；当a∈(－∞，－e)时，g(x)无零点．例2(2022·全国乙卷)已知函数f(x)＝ax－1x－(a＋1)ln x.(1)当a＝0时，求f(x)的最大值；(2)若f(x)恰有一个零点，求a的取值范围．解(1)当a＝0时，f(x)＝－1x －ln x(x＞0)，则f′(x)＝1x2－1x＝1－xx2，当x∈(0，1)时，f′(x)＞0，f(x)单调递增；当x∈(1，＋∞)时，f′(x)＜0，f(x)单调递减，所以f(x)max＝f(1)＝－1.(2)由f(x)＝ax－1x －(a＋1)ln x(x＞0)，得f′(x)＝a＋1x2－a＋1x＝（ax－1）（x－1）x2(x＞0)．当a＝0时，由(1)可知，f(x)不存在零点；当a<0时，f′(x)＝x－1）x2，若x∈(0，1)，f′(x)＞0，f(x)单调递增，若x∈(1，＋∞)，f′(x)＜0，f(x)单调递减，所以f(x)max＝f(1)＝a－1＜0，所以f(x)不存在零点；当a＞0时，f′(x)＝x－1）x2，若a＝1，则f′(x)≥0，f(x)在(0，＋∞)上单调递增，因为f(1)＝a－1＝0，所以函数f(x)恰有一个零点，若a＞1，则f(x)(1，＋∞)为f(1)＝a－1＞0，所以f(1)＞0，当x→0＋时，f(x)→－∞，由零点存在定理可知，f(x)a＞1满足条件．若0＜a＜1，则f(x)在(0，1)因为f(1)＝a－1＜0，所以f(1)＜0，当x→＋∞时，f(x)→＋∞，由零点存在定理可知，f(x)0＜a＜1满足条件．综上，若f(x)恰有一个零点，则a的取值范围为(0，＋∞)．根据函数零点个数确定参数取值范围的核心思想是“数形结合”，即通过函数图象与x轴的交点个数，或者两个相关函数图象的交点个数确定参数满足的条件，进而求得参数的取值范围，解决问题的步骤是“先形后数”．(2024·南阳一中月考)设函数f(x)＝(x－2)ln(x－1)－ax，a∈R.(1)若f(x)在(2，＋∞)上单调递增，求a的取值范围；(2)若f(x)有两个不同的零点，求a的取值范围．解(1)∵f′(x)＝ln(x－1)＋1－1x－1－a(x>1)，令H(x)＝ln(x－1)＋1－1x－1－a(x>1)，则H′(x)＝1x－1＋1（x－1）2>0，∴f′(x)在(1，＋∞)上单调递增，∵f(x)在(2，＋∞)上单调递增，∴f′(2)≥0，∴－a≥0⇒a≤0.∴a的取值范围是(－∞，0]．(2)f(x)＝0⇒a＝（x－2）ln（x－1）x，令g(x)＝（x－2）ln（x－1）x，故g′(x)＝1x－1－2·xx－1－ln（x－1）x2＝（x－1）－1x－1＋2ln（x－1）x2，令h(x)＝(x－1)－1x－1＋2ln(x－1)，∴h′(x)＝1＋1（x－1）2＋2x－1>0，∴h(x)在(1，＋∞)上单调递增，又h(2)＝0，∴当1<x<2时，h(x)<0，即g′(x)<0，当x>2时，h(x)>0，即g′(x)>0，∴g(x)在(1，2)上单调递减，在(2，＋∞)上单调递增，∴g(x)≥g(2)＝0，又由当x→1时，x－2x→－1，ln(x－1)→－∞，则g(x)→＋∞；当x→＋∞时，x－2x→1，ln(x－1)→＋∞，则g(x)→＋∞，若f(x)有两个不同的零点，则需满足a>0.∴a的取值范围为(0，＋∞)．例3(2023·泰州模拟)已知函数f(x)＝e x－ax2＋bx－1，其中a，b为常数，e 为自然对数的底数，e＝2.71828….(1)当a＝0时，若函数f(x)≥0，求实数b的取值范围；(2)当b＝2a时，若函数f(x)有两个极值点x1，x2，现有如下三个命题：①7x1＋bx2＞28；②2a(x1＋x2)>3x1x2；③x1－1＋x2－1>2.请从①②③中任选一个进行证明．解(1)当a＝0时，f(x)＝e x＋bx－1，f′(x)＝e x＋b，当b≥0时，因为f(－1)b<0，所以此时不符合题意；当b＜0时，当x∈(－∞，ln(－b))时，f′(x)＜0，f(x)单调递减，当x ∈(ln (－b )，＋∞)时，f ′(x )＞0，f (x )单调递增，所以f (x )min ＝f (ln (－b ))＝－b ＋b ln (－b )－1，要使f (x )≥0，只需f (x )min ＝－b ＋b ln (－b )－1≥0，令g (x )＝x －x ln x －1，则g ′(x )＝－ln x ，当x ∈(0，1)时，g ′(x )＞0，g (x )单调递增，当x ∈(1，＋∞)时，g ′(x )＜0，g (x )单调递减，所以g (x )≤g (1)＝0，则由g (－b )＝－b ＋b ln (－b )－1≥0，得－b ＝1，所以b ＝－1，故实数b 的取值范围为{－1}．(2)证明：当b ＝2a 时，f (x )＝e x －ax 2＋2ax －1，f ′(x )＝e x －2ax ＋2a ，令φ(x )＝f ′(x )＝e x －2ax ＋2a ，则φ′(x )＝e x －2a ，因为函数f (x )有两个极值点x 1，x 2，所以φ(x )＝f ′(x )＝e x －2ax ＋2a 有两个零点，若a ≤0，则φ′(x )＞0，φ(x )单调递增，不可能有两个零点，所以a ＞0，令φ′(x )＝e x －2a ＝0，得x ＝ln (2a )，当x ∈(－∞，ln (2a ))时，φ′(x )＜0，φ(x )单调递减；当x ∈(ln (2a )，＋∞)时，φ′(x )＞0，φ(x )单调递增，所以φ(x )min ＝φ(ln (2a ))＝4a －2a ln (2a )，因为φ(x )有两个零点，所以4a －2a ln (2a )＜0，则a >12e 2.设x 1＜x 2，因为φ(1)＝e ＞0，φ(2)＝e 2－2a ＜0，所以1＜x 1＜2＜x 2，因为φ(x 1)＝φ(x 2)＝0，所以e x 1＝2ax 1－2a ，e x 2＝2ax 2－2a ，则e x 2e x 1＝x 2－1x 1－1，取对数得x 2－x 1＝ln (x 2－1)－ln (x 1－1)，令x 1－1＝t 1，x 2－1＝t 2，则t 2－t 1＝ln t 2－ln t 1，即t 2－ln t 2＝t 1－ln t 1(0＜t 1＜1＜t 2)．若选择命题①：令u (t )＝t －ln t ，则u (t 1)＝u (t 2)，u ′(t )＝1－1t，当0<t <1时，u ′(t )<0，当t >1时，u ′(t )>0，所以u (t )＝t －ln t 在(0，1)上单调递减，在(1，＋∞)上单调递增，令v (t )＝u (t )－u (2－t )＝2t －ln t ＋ln (2－t )－2(0＜t ＜2)，则v ′(t )＝2（t －1）2t （t －2）≤0，v (t )在(0，2)上单调递减，因为0＜t 1＜1，所以v (t 1)＞v (1)＝0，即u (t 1)－u (2－t 1)＞0，亦即u (t 2)＝u (t 1)＞u (2－t 1)，因为t 2＞1，2－t 1＞1，u (t )＝t －ln t 在(1，＋∞)上单调递增，所以t 2＞2－t 1，则x 2－1＞2－(x 1－1)，整理得x 1＋x 2＞4，所以7x 1＋bx 2＝7x 1＋2ax 2＞7x 1＋7x 2＞28，故①成立，得证．若选择命题②：令u (t )＝t －ln t ，则u (t 1)＝u (t 2)，u ′(t )＝1－1t，当0<t <1时，u ′(t )<0，当t >1时，u ′(t )>0，所以u (t )＝t －ln t 在(0，1)上单调递减，在(1，＋∞)上单调递增，令v (t )＝u (t )－t －1t －2ln t ，则v ′(t )＝（t －1）2t2≥0，v (t )在(0，＋∞)上单调递增，又v (1)＝0，所以当t ∈(0，1)时，v (t )＝u (t )－v (1)＝0，即u (t )<因为0<t 1<1，所以u (t 2)＝u (t 1)<因为t 2＞1，1t 1＞1，u (t )＝t －ln t 在(1，＋∞)上单调递增，所以t 2<1t 1，所以x 2－1<1x 1－1，即x 1x 2＜x 1＋x 2，所以x1x2<x1＋x2<2312e2(x1＋x2)<23a(x1＋x2)，所以2a(x1＋x2)>3x1x2，故②成立，得证．若选择命题③：因为x1－1＝t1，x2－1＝t2，则t2－t1＝ln t2－ln t1＝2ln t2t1，因为0<t1<1<t2，所以t2t1>1.令F(t)＝ln t－2（t－1）t＋1，则当t>1时，F′(t)＝（t－1）2t（t＋1）2>0，所以F(t)＝ln t－2（t－1）t＋1在(1，＋∞)上单调递增，则F(t)＝ln t－2（t－1）t＋1>F(1)＝0，所以ln t>2（t－1）t＋1，则t2－t1＝2ln t2t1>4·t2－t1t2＋t1，两边约去t2－t1后，化简整理得t1＋t2>2，即x1－1＋x2－1>2，故③成立，得证．(1)研究函数零点问题，要通过数的计算(函数性质、特殊点的函数值等)和形的辅助，得出函数零点的可能情况．(2)函数可变零点(函数中含有参数)性质的研究，要抓住函数在不同零点处函数值均为零，建立不同零点之间的关系，把多元问题转化为一元问题，再使用一元函数的方法进行研究．已知函数f(x)＝a e－x＋ln x－1(a∈R)．(1)当a≤e时，讨论函数f(x)的单调性；(2)若函数f(x)恰有两个极值点x1，x2(x1<x2)，且x1＋x2≤2ln3，求x2x1的最大值．解(1)函数的定义域为(0，＋∞)，f ′(x )＝－a e －x＋1x ＝e x －ax x e x ，∵a ≤e ，∴e x －ax ≥e x －e x .设g (x )＝e x －e x ，则g ′(x )＝e x －e ，当0<x <1时，g ′(x )<0，g (x )单调递减，当x >1时，g ′(x )>0，g (x )单调递增，∴g (x )≥g (1)＝0，∴f ′(x )≥0，f (x )在(0，＋∞)上单调递增．∴当a ≤e 时，函数f (x )在(0，＋∞)上单调递增．(2)依题意，f ′(x 1)＝f ′(x 2)＝0x 1＝ax 1，x 2＝ax 2，两式相除得，e x 2－x 1＝x 2x 1，设x 2x 1＝t ，则t >1，x 2＝tx 1，e (t －1)x 1＝t ，∴x 1＝ln t t －1，x 2＝t ln t t －1，∴x 1＋x 2＝（t ＋1）ln tt －1.设h (t )＝（t ＋1）ln t t －1(t >1)，则h ′(t )＝t －1t －2ln t （t －1）2，设φ(t )＝t －1t－2ln t (t >1)，则φ′(t )＝1＋1t 2－2t ＝（t －1）2t 2>0，∴φ(t )在(1，＋∞)上单调递增，则φ(t )>1－11－2ln 1＝0，∴h ′(t )>0，则h (t )在(1，＋∞)上单调递增，又x 1＋x 2≤2ln 3，即h (t )≤2ln 3，又h (3)＝2ln 3，∴t ∈(1，3]，即x 2x 1的最大值为3.课时作业一、单项选择题1．(2023·全国乙卷)函数f (x )＝x 3＋ax ＋2存在3个零点，则a 的取值范围是()A ．(－∞，－2)B ．(－∞，－3)C ．(－4，－1)D ．(－3，0)答案B解析f (x )＝x 3＋ax ＋2，则f ′(x )＝3x 2＋a ，若f (x )存在3个零点，则f (x )存在极大值和极小值，则a <0.令f ′(x )＝3x 2＋a ＝0，解得x ＝－－a3或x ＝－a 3，且当x ∈∞∪时，f ′(x )>0，当x ∈－－a 3，f ′(x )<0，故f (x )的极大值为f，若f (x )存在3个零点，则，即a －a3＋2>0，a －a3＋2<0，解得a <－3.故选B.2．(2023·济宁二模)已知函数f (x )，x ≤0，ln x ，x >0，若函数g (x )＝f (x )－f (－x )有5个零点，则实数a 的取值范围是()A ．(－e ，0)－1e ，C ．(－∞，－e)∞答案C解析y ＝f (－x )与y ＝f (x )的图象关于y 轴对称，且f (0)＝0，要想g (x )＝f (x )－f (－x )有5个零点，则当x ＞0时，－x ＝a ln x 要有2个根，结合对称性可知，x＜0时也有2个零点，故满足有5个零点．当x ＝1时，－1＝0，不符合题意；当x ≠1时，a ＝－x ln x ，令h (x )＝－xln x ，定义域为(0，1)∪(1，＋∞)，h ′(x )＝1－ln x （ln x ）2，令h ′(x )＞0得0＜x ＜1，1＜x ＜e ，令h ′(x )＜0得x ＞e ，故h (x )＝－xln x在(0，1)，(1，e)上单调递增，在(e ，＋∞)上单调递减，且当x ∈(0，1)时，h (x )＝－x ln x>0恒成立，h (x )＝－xln x在x ＝e 处取得极大值，其中h (e)＝－e ，故a ∈(－∞，－e)，此时直线y ＝a 与h (x )＝－xln x的图象有两个交点．故选C.3．(2023·银川三模)已知函数f (x )＝mx －ln x ＋m 在区间(e －1，e)上有唯一零点，则实数m 的取值范围为()A.－e e 2＋1，e 2＋1－1e ＋1，－ee ＋1，1，e 2＋答案B解析函数f (x )＝mx －ln x ＋m ，令f (x )＝0，则ln x ，即m ＝x ln x x ＋1，令h (x )＝x ln x x ＋1，则h ′(x )＝x ＋1＋ln x （x ＋1）2，令k (x )＝x ＋1＋ln x ，则k ′(x )＝1＋1x >0，所以函数y ＝k (x )在区间(e －1，e)上单调递增，故k (x )>k (e －1)＝e －1>0，所以h ′(x )>0，故函数y ＝h (x )在区间(e －1，e)上单调递增，故h (e －1)<h (x )<h (e)，即－1e ＋1<h (x )<e e ＋1，所以－1e ＋1<m <ee ＋1，故实数m －1e ＋1，故选B.4．(2023·邢台二模)已知函数f (x )＝x －ln x ＋m (m ∈R )，若f (x )有两个零点x 1，x 2(x 1<x 2)，则下列关系式不正确的是()A ．m <－1B ．x 1＋x 2≤2C ．0<x 1<1D ．e x 1－x 2＝x 1x 2答案B解析f ′(x )＝1－1x ＝x －1x，令f ′(x )＝0，解得x ＝1，故函数f (x )在(0，1)上单调递减，在(1，＋∞)上单调递增，如图，故f (x )min ＝f (1)＝1＋m <0，即m <－1，并且0<x 1<1，故A ，C 正确；由于x 1，x 2为f (x )的零点，故有x 1－ln x 1＋m ＝0①，x 2－ln x 2＋m ＝0②，两式相减得，x 1－x 2＝lnx 1x 2，即e x 1－x 2＝x 1x 2，故D 正确；由①②可知，m ＝ln x 1－x 1＝ln x 2－x 2，令g (x )＝ln x －x ，则g (x 1)＝g (x 2)，g ′(x )＝1x －1＝1－x x ，所以在(0，1)上，g ′(x )>0，g (x )单调递增，在(1，＋∞)上，g ′(x )<0，g (x )单调递减，令h (x )＝g (x )－g (2－x )＝ln x －x －ln (2－x )＋2－x ＝ln x －ln (2－x )－2x ＋2，则h ′(x )＝1x＋12－x －2＝2x 2－4x ＋2x （2－x ）＝2（x －1）2x （2－x ），所以当0＜x ＜1时，h ′(x )>0，所以h (x )在(0，1)上单调递增，所以h (x )<h (1)＝0，所以g (x 1)<g (2－x 1)，又因为g (x )在(1，＋∞)上单调递减，且g (x 2)＝g (x 1)，所以x 2>2－x 1，即x 1＋x 2>2，故B 不正确．故选B.二、多项选择题5．(2022·新高考Ⅰ卷)已知函数f (x )＝x 3－x ＋1，则()A ．f (x )有两个极值点B ．f (x )有三个零点C ．点(0，1)是曲线y ＝f (x )的对称中心D ．直线y ＝2x 是曲线y ＝f (x )的切线答案AC解析因为f (x )＝x 3－x ＋1，所以f ′(x )＝3x 2－1，令f ′(x )＝3x 2－1＝0，得x＝±33.由f ′(x )＝3x 2－1＞0，得x ＜－33或x ＞33；由f ′(x )＝3x 2－1＜0，得－33＜x ＜33.所以f (x )＝x 3－x ＋1∞在－33，f (x )有两个极值点，故A 正确；因为f (x )的极小值－33＋1＝1－239＞0，f (－2)＝(－2)3－(－2)＋1＝－5＜0，所以函数f (x )在R 上有且只有一个零点，故B 错误；因为函数g (x )＝x 3－x 的图象向上平移一个单位长度得函数f (x )＝x 3－x ＋1的图象，函数g (x )＝x 3－x 的图象关于原点(0，0)中心对称，所以点(0，1)是曲线f (x )＝x 3－x ＋1的对称中心，故C 正确；假设直线y ＝2x 是曲线y ＝f (x )的切线，切点为(x 0，y 0)，则f ′(x 0)＝3x 20－1＝2，解得x 0＝±1.若x 0＝1，则切点坐标为(1，1)，但点(1，1)不在直线y ＝2x 上，若x 0＝－1，则切点坐标为(－1，1)，但点(－1，1)不在直线y ＝2x 上，所以假设不成立，故D 错误．故选AC.6．(2023·秦皇岛二模)已知函数f (x )＝ln x －ax 有两个零点x 1，x 2，且x 1<x 2，则下列说法正确的是()A ．aB ．y ＝f (x )在(0，e)上单调递增C ．x 1＋x 2>6D ．若a x 2－x 1<2－aa答案ABD解析由f (x )＝ln x －ax ，可得f ′(x )＝1x－a (x >0)，当a ≤0时，f ′(x )>0，∴f (x )在x ∈(0，＋∞)上单调递增，与题意不符；当a >0时，令f ′(x )＝1x －a ＝0，解得x ＝1a ，∴当x f ′(x )>0，f (x )单调递增，当x f ′(x )<0，f (x )单调递减，∴当x ＝1a 时，f (x )取得极大值，又函数f (x )＝ln x －ax 有两个零点x 1，x 2(x 1<x 2)，∴ln 1a －1>0，可得0<a <1e .综上可得，0<a <1e ，故A 正确；当a →1e时，x 1＋x 2→2e<6，故C 错误；∵当x f (x )单调递增，a ∴(0，e)B 正确；∵f (x )a 1，x 1，2a ，x 2f (1)＝－a <0＝f (x 1)，∴x 1>1.∵ln 2a －2<ln e 2－2＝0＝f (x 2)，∴x 2<2a ，∴x 2－x 1<2a －1＝2－a a ，故D 正确．故选ABD.7．(2024·福建省名校联盟模拟)机械制图中经常用到渐开线函数inv x ＝tan x －x ，其中x 的单位为弧度，则下列说法正确的是()A ．x ·inv x 是偶函数B ．inv x －π2－k π，π2＋k 2k ＋1个零点(k ∈N )C ．inv x －π2－k π，π2＋k 4k ＋1个极值点(k ∈N )D ．当－π2<x <0时，inv x <x －sin x答案ABD解析函数inv x ＝tan x －x ∈R|x ≠n π＋π2，n ∈显然y ＝x 和inv x 均为奇函数，因此x ·inv x 是偶函数，A 正确；当x －π2，令h (x )＝inv x ，h ′(x )＝1cos 2x －1≥0，函数inv x －π2，x ＝0时，inv x ＝0，即函数inv x －π2，x －π2＋k 1π，π2＋k 1k 1∈Z 时，令x＝t ＋k 1π，t －π2，则tan x －x ＝tan(t ＋k 1π)－(t ＋k 1π)＝tan t －t －k 1π，令y ＝tan t －t ，t －π2，y ＝tan t －t －π2，R ，直线y ＝k 1π(k 1∈Z )与y ＝tan t －t ，t －π2唯一交点，因此函数inv x 在－π2＋k 1π，π2＋k 1k 1∈Z 上有唯一零点，所以inv x －π2－k π，π2＋k2k ＋1个零点(k ∈N )，B 正确；由B 项知，函数inv x －π2＋k 1π，π2＋k 1k 1∈Z 上为增函数，因此inv x 不存在极值点，C 错误；令函数f (x )＝inv x －x ＋sin x ，求导得f ′(x )＝1cos 2x －2＋cos x ，当－π2<x <0时，设u ＝cos x ∈(0，1)，g (u )＝1u2－2＋u ，求导得g ′(u )＝1－2u 3<0，函数g (u )在(0，1)上单调递减，g (u )>112－2＋1＝0，即f ′(x )>0，因此f (x )π2，f (x )<f (0)＝0，即inv x <x －sin x ，D 正确．故选ABD.8．(2024·日照模拟)已知函数f (x )＝x 2＋x －1e x ，则()A ．函数f (x )只有两个极值点B ．若关于x 的方程f (x )＝k 有且只有两个实根，则k 的取值范围为(－e ，0)C ．方程f (f (x ))＝－1共有4个实根D ．若关于x 的不等式f (x )≥a (x ＋1)的解集内恰有两个正整数，则a 的取值范，12e答案ACD解析对f (x )求导得f ′(x )＝－x 2－x －2e x ＝－（x ＋1）（x －2）ex，当x <－1或x >2时，f ′(x )<0，当－1<x <2时，f ′(x )>0，即f (x )在(－∞，－1)，(2，＋∞)上单调递减，在(－1，2)上单调递增，因此f (x )在x ＝－1处取得极小值f (－1)＝－e ，在x ＝2处取得极大值f (2)＝5e 2，A 正确；由上述分析可知，曲线y ＝f (x )及直线y＝k 如图所示，由图可知，当－e<k≤0或k＝5e2时，直线y＝k与曲线y＝f(x)有2个交点，所以若方程f(x)＝k有且只有两个实根，则k的取值范围为(－e，0]∪5e2，B错误；由f(x)＝0，得x2＋x－1＝0，解得x＝－1±52，令f(x)＝t且f(t)＝－1，由图可知，f(t)＝－1有两解分别为－1－52<t1<－1，t2＝0，所以f(x)＝t1或f(x)＝t2，而1＋5<2e，则－1－52>－e，则f(x)＝t1有两解．又t2＝0，由图可知f(x)＝t2也有两解．综上，方程f(f(x))＝－1共有4个实根，C正确；因为直线y＝a(x＋1)过定点(－1，0)，且f(1)＝1e ，f(2)＝5e2，f(3)＝11e3，记k1＝f（1）－01－（－1）＝12e，k2＝f（2）－02－（－1）＝53e2，k3＝f（3）－03－（－1）＝114e3，所以k3<a≤k1，D正确．故选ACD.三、填空题9．(2024·长沙模拟)已知函数f(x)＝e x－2ax＋a，若f(x)恰有两个零点，则实数a的取值范围是________．答案12e32，＋∞解析函数f(x)＝e x－2ax＋a，定义域为R，显然x＝12不是f(x)的零点，令f(x)＝0，得a＝e x2x－1，设g(x)＝e x2x－1，则g′(x)＝（2x－3）e x（2x－1）2，令g′(x)<0，解得x<32且x≠12，令g ′(x )>0，解得x >32，故g (x )∞递增．当x <12时，g (x )<0，当x >12时，g (x )>0，当x ＝32时，g (x )取得极小值＝12e 32，作出函数g (x )的大致图象如图所示，结合图象可知，实数a 的取值范围是e 32，＋10．(2023·福州三模)如果两个函数分别存在零点α，β，满足|α－β|＜n ，则称两个函数互为“n 度零点函数”．若f (x )＝ln (x －2)与g (x )＝ax 2－ln x 互为“2度零点函数”，则实数a 的最大值为________．答案12e解析因为函数f (x )的零点为3，所以设函数g (x )的零点为x 0，则|x 0－3|＜2，解得1＜x 0＜5.g (x 0)＝ax 20－ln x 0＝0，a ＝ln x 0x 20(1<x 0<5)，令h (x )＝ln xx 2(1<x <5)，求导得h ′(x )＝1－2ln xx3，令h ′(x )＝0，得x ＝e ，所以当x ∈(1，e)时，h ′(x )＞0，h (x )单调递增；当x ∈(e ，5)时，h ′(x )＜0，h (x )单调递减，所以h (x )max ＝h (e)＝12e .所以实数a 的最大值为12e.四、解答题11．(2023·广州模拟)已知函数f (x )＝e x －1＋e －x ＋1，g (x )＝a (x 2－2x )(a <0)．(1)求函数f (x )的单调区间；(2)讨论函数h (x )＝f (x )－g (x )的零点个数．解(1)由f (x )＝ex －1＋e－x ＋1，可得f ′(x )＝ex －1－e－x ＋1＝e 2（x －1）－1ex －1，令f ′(x )＝0，解得x ＝1，当x <1时，则x －1<0，可得f ′(x )<0，f (x )在(－∞，1)上单调递减；当x >1时，则x －1>0，可得f ′(x )>0，f (x )在(1，＋∞)上单调递增．故函数f (x )的单调递减区间是(－∞，1)，单调递增区间是(1，＋∞)．(2)由h(x)＝0，得f(x)＝g(x)，因此函数h(x)的零点个数等价于函数f(x)与g(x)图象的交点个数．因为g(x)＝a(x2－2x)(a<0)，所以g(x)的单调递增区间是(－∞，1)，单调递减区间是(1，＋∞)，所以当x＝1时，g(x)取得最大值g(1)＝－a.由(1)可知，当x＝1时，f(x)取得最小值f(1)＝2，当－a<2，即－2<a<0时，函数f(x)与g(x)的图象没有交点，即函数h(x)没有零点；当－a＝2，即a＝－2时，函数f(x)与g(x)的图象只有一个交点，即函数h(x)只有一个零点；当－a>2，即a<－2时，函数h(x)有两个零点，理由如下：因为h(x)＝f(x)－g(x)＝e x－1＋e－x＋1－a(x2－2x)，所以h(1)＝2＋a<0，h(2)＝e＋e－1>0，由函数零点存在定理，知h(x)在(1，2)内有零点．又f(x)在(1，＋∞)上单调递增，g(x)在(1，＋∞)上单调递减，所以h(x)＝f(x)－g(x)在(1，＋∞)上单调递增，所以h(x)＝f(x)－g(x)在(1，＋∞)上只有一个零点．又因为f(2－x)＝e(2－x)－1＋e－(2－x)＋1＝e1－x＋e x－1＝f(x)，所以f(x)的图象关于直线x＝1对称，因为g(x)的图象关于直线x＝1对称，所以f(x)与g(x)的图象都关于直线x＝1对称，所以h(x)＝f(x)－g(x)在(－∞，1)上也只有一个零点．所以当a<－2时，函数h(x)＝f(x)－g(x)有两个零点．ax2－ln x.12．(2024·镇江模拟)已知函数f(x)＝12(1)若a＝1，求f(x)的极值；(2)若方程f(x)＝1在区间[1，2]上有解，求实数a的取值范围．解(1)当a＝1时，f(x)＝12x2－ln x，f′(x)＝x2－1x，令f′(x)＝0，得x＝1，当0<x<1时，f′(x)<0，当x>1时，f′(x)>0，所以f(x)在(0，1)上单调递减，在(1，＋∞)上单调递增，所以f(x)的极小值为f(1)＝12，无极大值．(2)因为f′(x)＝ax－1x ＝ax2－1x，①若a≥1，当x∈[1，2]时，f′(x)≥0恒成立，所以f(x)在[1，2]上单调递增，要使方程f(x)＝1在[1，2]1）≤1，2）≥1，1，－ln2≥1，得1＋ln22≤a≤2，因为1＋ln22<1，所以1≤a≤2.②若a≤14，当x∈[1，2]时，f′(x)≤0恒成立，所以f(x)在[1，2]上单调递减，此时f(x)≤f(1)＝a2≤18，不符合题意．③若14<a<1，当1≤x<1a时，f′(x)<0，当1a<x≤2时，f′(x)>0，所以f(x)在12上单调递增，此时f(1)＝a2<12，f(1)<12，要使方程f(x)＝1在[1，2]上有解，则需f(2)＝2a－ln2≥1，解得a≥1＋ln22，所以1＋ln22≤a<1.综上可知，实数a的取值范围为1＋ln22，2.13．(2021·全国甲卷)已知a>0且a≠1，函数f(x)＝x aa x(x>0)．(1)当a＝2时，求f(x)的单调区间；(2)若曲线y＝f(x)与直线y＝1有且仅有两个交点，求a的取值范围．解(1)当a＝2时，f(x)＝x22x(x>0)，f′(x)＝x（2－x ln2）2x(x>0)．令f′(x)>0，得0<x<2ln2；令f′(x)<0，得x>2ln2，故函数f(x)(2)要使曲线y＝f(x)与直线y＝1有且仅有两个交点，即方程x aa x ＝1(x>0)有两个不同的解，故方程ln xx＝ln aa有两个不同的解．设g(x)＝ln xx(x>0)，则g′(x)＝1－ln xx2(x>0)．令g′(x)＝1－ln xx2＝0，解得x＝e.令g′(x)>0，则0<x<e，此时函数g(x)单调递增．令g′(x)<0，则x>e，此时函数g(x)单调递减．故g(x)max＝g(e)＝1e，且当x>e时，g(x)又g(1)＝0，故要使方程ln xx ＝ln aa有两个不同的解，则0<ln aa<1e.即0<g(a)<g(e)，所以a∈(1，e)∪(e，＋∞)．综上，a的取值范围为(1，e)∪(e，＋∞)．14．(2023·济南模拟)已知函数f(x)＝x ln x－ax2－x，g(x)＝f（x）x，a∈R.(1)讨论g(x)的单调性；(2)设f(x)有两个极值点x1，x2(x1＜x2)，证明：x41x2>e3(e＝2.71828…为自然对数的底数)．解(1)g(x)＝f（x）x ＝ln x－ax－1，g′(x)＝1x－a，①当a≤0时，g′(x)＞0，g(x)在(0，＋∞)上单调递增；②当a＞0时，令g′(x)＝0，解得x＝1a，当x g′(x)＞0，g(x)单调递增，当x g′(x)＜0，g(x)单调递减．综上，当a≤0时，g(x)在(0，＋∞)上单调递增；当a＞0时，g(x)(2)证明：由题意知，f′(x)＝ln x－2ax，x1，x2是f′(x)＝0的两根，即ln x1－2ax1＝0，ln x2－2ax2＝0，解得2a＝ln x1－ln x2x1－x2，(*)要证x41x2>e3，即证4ln x1＋ln x2＞3，即证4·2ax1＋2ax2＞3，把(*)式代入得ln x1－ln x2x1－x2(4x1＋x2)>3，所以应证ln x1x2<3（x1－x2）4x1＋x2＝4·x1x2＋1令t＝x1x2，0＜t＜1，即证h(t)＝ln t－3（t－1）4t＋1<0(0<t<1)成立，而h′(t)＝1t －15（4t＋1）2＝16t2－7t＋1t（4t＋1）2>0，所以h(t)在(0，1)上单调递增，h(t)＜ln1－3×（1－1）4×1＋1＝0，不等式得证．。

导数与零点问题解题技巧

导数与零点问题解题技巧
1. 嘿，你想知道怎么通过导数来巧妙找到函数的零点吗？就像在一片迷雾中找到那关键的线索！比如求函数f(x)=x³-3x+2 的零点，咱通过求导找到极值点，就能逐步逼近零点啦，是不是很神奇？
2. 哇哦，注意啦！导数可是解决零点问题的一把利器呀！好比你找宝藏有了精确的地图。

像对于函数 g(x)=e^x-x-1，用导数不就能轻松分析它零点的情况嘛！
3. 嘿呀，有没有觉得导数和零点问题之间像是有一条神秘的纽带呀！就像侦探和线索一样。

比如分析函数 h(x)=sinx+x 在某个区间的零点，导数能帮大忙呢！
4. 哎呀，学会这些解题技巧那可真是太棒啦！简直像是掌握了绝世武功。

想想函数i(x)=lnx+x²，用导数去攻克零点问题，多有成就感！
5. 天呐，导数与零点问题的结合简直妙不可言！就如同给你一双慧眼。

拿函数 j(x)=x^4-4x² 来说，导数能让我们快速看清零点的分布呢。

6. 哇塞，这些解题技巧你可不能错过呀！这就好比游戏里的通关秘籍。

像是函数 k(x)=x+cosx ，利用导数去求解零点，厉害吧！
7. 嘿，你知道用导数解决零点问题能带来多大的乐趣吗？那可比发现新大陆还让人兴奋！好比函数l(x)=x³/3-x²+2x 的零点求解。

8. 总之，导数与零点问题解题技巧真的超有用的啦！你一定要好好掌握哦！就像拥有了一把打开数学难题大门的钥匙！不管遇到什么函数，都能轻松应对！。

2023年人教版高考数学总复习第一部分考点指导第四章导数及其应用第四节第2课时导数与函数零点

【加练备选】 1.函数 f(x)＝ex－|x|3 的零点个数是( ) A．1 B．2 C．3 D．4
【解析】选 C.当 x≤0 时，f(x)＝ex＋x3，因为 f′(x)＝ex＋3x2＞0，所以函数此时单调递增，而 f(－1)＝e－1－1＜0，f(0)＝1＞0，所以此时函数 f(x)＝ex＋x3 有唯一零点；当 x＞0 时，令 f(x)＝ex－x3＝0，解得 ex＝x3⇒x＝3ln x，此时原函数的零点为函数 g(x)＝x－3ln x 的零点，g′(x) ＝1－3x ，因此当 x＞3 时 g′(x)＝1－3x ＞0，函数单调递增，当 0<x<3 时，g′(x)＝1－3x ＜0，函数单调递减， g(3)＝3－3ln 3＝3(1－ln 3)＜0，g(1)＝1＞0， g(6)＝6－3ln 6＝3(2－ln 2)＞0，所以函数在(0，3)和(3，＋∞)内各有一个零点，所以一共有 3 个零点．
当 x＞0 时，两图象必须有两个交点，
假设两图象当
x＞0
时至多只有一个交点，则
ex≥ax2
恒成立，即
ex a≤x2
，
令 g(x)＝exx2
ex（x－2），则 g′(x)＝ x3
，当 g′(x)＞0 时，x＞2，当 g′(x)＜0 时，0＜x＜2，
则 g(x)min＝g(2)＝e42
，即若
e2 a≤ 4
考点二零点与参数的值或范围讲练互动
[典例 1](1)已知关于 x 的方程 ax＝xa(其中 a＞1，x＞0)有且仅有一个解，令 h(x)＝ ax－xa(a＞1，x＞0)，则下列结论错误的是( ) A．a＝e B．h(x)在区间(1，e)上单调递减 C．x＝e 是 h(x)的零点 D．h(1)是 h(x)的极小值，x＝e 是 h(x)的极大值点

利用导数研究函数零点问题

利用导数研究函数零点问题f(0)＝0，所以切线方程为y＝－3＋4x；2)将g(x)＝2exf(x)化为g(x)－2exf(x)＝0，即(－x2＋ax－3)ex－2xlnx＝0。

令φ(x)＝(－x2＋ax－3)ex，ψ(x)＝2xlnx，所以φ′(x)＝ex(2－2x＋a)，ψ′(x)＝2lnx＋2。

由φ′(x)＝0，得x＝1，由ψ′(x)＝0，得x＝e－1。

当x＜1时，φ(x)单调递减，当x＞1时，φ(x)单调递增，所以φ(x)在[0，1)和(1，＋∞)上单调递减。

在(－∞，1]和[1，＋∞)上单调递增，ψ(x)在(0，＋∞)上单调递增。

所以当x＜1时，φ(x)＞ψ(x)，当x＞e－1时，φ(x)＜ψ(x)。

所以方程g(x)＝2exf(x)在(0，1)和(e－1，＋∞)上无解，在(1，e－1)上有两个解。

所以a的取值范围为[2，6]。

当$m>1$时，当$0m$时，$F'(x)0$。

因此，函数$F(x)$在区间$(0,1)$和$(m,+\infty)$上单调递减，在区间$(1,m)$上单调递增。

注意到$F(1)=m$，$F(2m+2)=-m\ln(2m+2)$，因此$F(x)$有唯一零点。

综上，函数$F(x)$有唯一零点，即两函数图像只有一个交点。

1) 针对函数的零点问题，我们可以利用导数确定函数的单调区间和极值点，通过求解函数在给定区间的极值和端点的函数值，来确定参数的取值范围。

2) 解决这类问题的关键在于将函数零点、方程的根、曲线交点相互转化，突出导数的作用，运用转化和化归的思想方法。

1) 确定零点的个数问题：我们可以利用数形结合的方法来判断交点个数。

如果函数比较复杂，可以结合导数知识确定极值点和单调区间，从而确定其大致图像。

2) 方程是否有解问题就是判断是否存在零点的问题。

我们可以通过分离变量，将其转化为求函数值域的问题来处理。

可以通过构造函数$g(x)$的方法，将问题转化为研究构造的函数$g(x)$的零点问题。

高考数学复习课件：利用导数解决函数的零点问题

利用导数解决函数的零点问题
01 探本朔源·技法示例
技法阐释 1.利用导数研究高次式、分式、指数式、对数式、三角式及绝对值式结构函数零点个数(或方程根的个数)问题的一般思路 (1)可转化为用导数研究其函数的图象与x轴(或直线y＝k)在该区间上的交点问题； (2)证明有几个零点时，需要利用导数研究函数的单调性，确定分类讨论的标准，确定函数在每一个区间上的极值(最值)、端点函数值等性质，进而画出函数的大致图象．再利用零点存在性定理，在每个单调区间内取值证明f(a)·f(b)＜0.
[解] (1)由题意知，当m＝e时，f(x)＝ln x＋ex(x＞0)，则f′(x)＝ x－x2 e，
∴当x∈(0，e)时，f′(x)＜0，f(x)在(0，e)上单调递减；当x∈(e，＋∞)时，f′(x)＞0，f(x)在(e，＋∞)上单调递增， ∴当x＝e时，f(x)取得极小值f(e)＝ln e＋ee＝2， ∴f(x)的极小值为2.
(2)方法一：由题意知，方程 kx－ln x＝0 仅有一个实根，
由 kx－ln x＝0，得 k＝lnxx(x＞0)．令g(x)＝lnxx(x＞0)，则g′(x)＝1－xl2n x，当x＝e时，g′(x)＝0；当0＜x＜e时，g′(x)＞0；当x＞e时， g′(x)＜0.
∴g(x)在(0，e)上单调递增，在(e，＋∞)上单调递减， ∴g(x)max＝g(e)＝1e. 当x→＋∞时，g(x)→0. 又∵k＞0，∴要使f(x)仅有一个零点，则k＝1e.
谢谢观论法：一般命题情境为没有固定区间，求满足函数零点个数的参数范围，通常解法为结合单调性，先确定参数分类的标准，在每个小范围内研究零点的个数是否符合题意，将满足题意的参数的各小范围并在一起，即为所求参数范围．
高考示例 (2020·全国卷Ⅲ)设函数f(x)＝x3＋bx＋c，曲线y＝f(x)在点12，f 12处的切线与y轴垂直． (1)求b； (2)若f(x)有一个绝对值不大于1的零点，证明：f(x)所有零点的绝对值都不大于1.

导数专题：利用导数研究函数零点的4种常见考法(原卷版)

导数专题：利用导数研究函数零点的4种常见考法一、函数零点问题常规求解步骤：第一步：将问题转化为函数的零点问题，进而转化为函数的图象与x 轴（或y=k）在某区间上的交点问题；第二步：利用导数研究该函数在此区间上的单调性、极值、端点值等性质，进而画出其图象；第三步：结合图象判断零点或根据零点分析参数。

二、利用导数确定函数零点的常用方法1、图象法：根据题目要求画出函数的图象，标明函数极（最）值的位置，借助数形结合的思想分析问题（画草图时注意有时候需要使用极限）；2、利用函数零点存在定理：先用该定理判定函数在某区间上有零点，然后利用导数研究函数的单调性、极值（最值）及区间端点值的符号，进而判断函数在该区间上零点的个数。

三、利用函数的零点求参数范围的方法1、分离参数（a=g(x)）后，将原问题转化为y=g(x)的值域（最值）问题或转化为直线y=a 与y=g(x)的图象的交点个数问题（优先分离、次选分类）求解；2、利用函数零点存在定理构造不等式求解；3、转化为两个熟悉的函数图象的位置关系问题，从而构建不等式求解。

四、导函数的零点不可直接求时的应对策略1、“特值试探法”：当导函数的零点不可求时，可尝试利用特殊值试探，此时特殊值的选取应遵循一下原则：①当含有ln x 的函数中，通常选取k x e =，特别的，选当0k =时，1x =来试探；②在含有x e 的函数中，通常选取ln x k =，特别的，选取当1k =时，0x =来试探，在探得导函数的一个零点后，结合导函数的单调性，确定导函数在零点左右的符号，进而确定原函数的单调性和极值，使问题得到解决。

2、“虚设和代换法”：当导函数()f x '的零点无法求出显性的表达式时，我们可以先证明零点的存在，再虚设为0x ，接下来通常有两个方向：①由0()0f x '=得到一个关于0x 的方程，再将这个关于0x 的方程的整体或局部代入0()f x ，从而求得0()f x ，然后解决相关的问题；②根据导函数()f x '的单调性，得出0x 两侧导函数的正负，进而得出原函数的单调性和极值，使问题得解。

高考数学一轮总复习第3章导数及其应用第2节导数的应用第5课时利用导数研究函数的零点问题教师用书

第5课时　利用导数研究函数的零点问题考点1　讨论函数的零点个数——综合性(2021·海口模拟)已知函数f(x)＝．(1)判断f(x)的单调性，并比较2 0202 021与2 0212 020的大小；(2)若函数g(x)＝(x－2)2＋x(2f(x)－1)，其中≤a≤，判断g(x)的零点的个数，并说明理由．参考数据：ln 2≈0.693．解：(1)函数f(x)＝，定义域是(0，＋∞)，故f′(x)＝．令f′(x)＞0，解得0＜x＜e；令f′(x)＜0，解得x＞e，故f(x)在(0，e)上单调递增，在(e，＋∞)上单调递减，则f(2 020)＞f(2 021)，即＞，故2 021ln 2 020＞2 020ln 2 021，故ln 2 0202 021＞ln 2 0212 020，故2 0202 021＞2 0212 020．(2)因为g(x)＝(x2－4x＋4)＋2ln x－x，所以g′(x)＝ax＋－2a－1＝．令g′(x)＝0，解得x＝2或x＝，①当a＝时，则g′(x)＝≥0，g(x)在(0，＋∞)上单调递增，且g(2)＝2ln 2－2＜0，g(6)＝2ln 6－2＞0，故g(2)g(6)＜0，故存在x0∈(2,6)，使得g(x0)＝0，故g(x)在(0，＋∞)上只有1个零点；②当<a<时，则＜2，则g(x)在上单调递增，在上单调递减，在(2，＋∞)上单调递增，故g(x)在(0，＋∞)上有极小值g(2)，g(2)＝2ln 2－2<0，有极大值g＝2a－－2ln a－2，且g(2)＝2ln 2－2＜0，g(6)＝8a＋2ln 6－6＞2ln 6－2＞0，故g(2)g(6)＜0，故存在x1∈(2,6)，使得g(x1)＝0，故g(x)在(2，＋∞)上只有1个零点，另一方面令h(a)＝g＝2a－－2ln a－2，h′(a)＝2＋－＝2>0，所以h(a)在上单调递增，所以h(a)<h＝e－－2－2ln <0，则g＜0，故g(x)在上没有零点．综上：当≤a≤时，g(x)只有1个零点．已知函数f(x)＝x－(e为自然常数)．(1)若f(x)在(0，＋∞)上单调递增，求实数a的取值范围；(2)设a∈R，讨论函数g(x)＝x－ln x－f(x)的零点个数．解：(1)f(x)＝x－，则f′(x)＝．因为f(x)在(0，＋∞)上单调递增，所以f′(x)≥0在(0，＋∞)上恒成立．记φ(x)＝e x＋ax－a，则φ(x)≥0在(0，＋∞)上恒成立，φ′(x)＝e x＋a．当a≥－1时，φ′(x)＝e x＋a＞1＋a≥0，即φ(x)在(0，＋∞)上单调递增，所以φ(x)＞φ(0)＝1－a≥0，所以－1≤a≤1；当a＜－1时，令φ′(x)＝e x＋a＝0，解得x＝ln(－a)．当0＜x＜ln(－a)时，φ′(x)＜0，φ(x)在(0，ln(－a))上单调递减；当x＞ln(－a)时，φ′(x)＞0，φ(x)在(ln(－a)，＋∞)上单调递增，所以φ(x)≥φ(ln(－a))＝－2a＋a ln(－a)≥0，解得－e2≤a＜－1．综上可得，实数a的取值范围是[－e2,1]．(2)g(x)＝x－ln x－f(x)＝－ln x(x＞0)，令g(x)＝0，得a＝(x＞0)．令h(x)＝，则h′(x)＝，当x∈(0,1]时，ln x≤0，x－1≤0，所以h′(x)≥0，h(x)单调递增；当x∈(1，＋∞)时，h′(x)＞0，h(x)单调递增．所以h(x)在(0，＋∞)单调递增，又h(x)＝∈R，a∈R，所以y＝a与h(x)＝的图象只有一个交点，所以a∈R，g(x)只有唯一一个零点．考点2　由函数的零点个数求参数的范围——综合性(2022·湖南模拟)已知函数f(x)＝x3＋3a(x＋1)(a∈R)．(1)讨论f(x)的单调性；(2)若函数g(x)＝f(x)－x ln x－3a在上有两个不同的零点，求a的取值范围．解：(1)f′(x)＝3x2＋3a．①当a≥0时，f′(x)≥0，f(x)在R上单调递增；②当a＜0时，令f′(x)＞0，解得x<－或x>，令f′(x)＜0，解得－<x<，所以f(x)在(－∞，－)，(，＋∞)上单调递增，在(－，)上单调递减．综上，当a≥0时，f(x)在R上单调递增；当a＜0时，f(x)在(－∞，－)，(，＋∞)上单调递增，在(－，)上单调递减．(2)g(x)＝x3＋3ax－x ln x，依题意，x3＋3ax－x ln x＝0在上有两个不同的解，即3a＝ln x－x2在上有两个不同的解．设h(x)＝ln x－x2，x∈，则h′(x)＝－2x＝．当x∈时，h′(x)≥0，h(x)单调递增；当x∈时，h′(x)＜0，h(x)单调递减，所以h(x)max＝h＝－ln 2－，且h＝－ln 2－，h(2)＝ln 2－4，h>h(2)，所以－ln 2－≤3a<－ln 2－，所以－ln 2－≤a<－ln 2－，即实数a的取值范围为．已知函数f(x)＝x2＋ax＋1－，a∈R．(1)若f(x)在(0,1)上单调递减，求a的取值范围；(2)设函数g(x)＝f(x)－x－a－1，若g(x)在(1，＋∞)上无零点，求整数a的最小值．解：(1)由题知f′(x)＝2x＋a＋≤0在(0,1)上恒成立，即a≤－2x恒成立．令h(x)＝－2x，则h′(x)＝－2＝－2>0，所以h(x)在(0,1)上单调递增，所以a≤h(x)min＝h(0)＝1．故a的取值范围是(－∞，1]．(2)由已知x>1，假设g(x)＝0⇔－a＝x＋，记φ(x)＝x＋，则φ′(x)＝1＋．令φ′(x)＞0，解得x>1＋，所以φ(x)在(1,1＋)上单调递减，在(1＋，＋∞)上单调递增，φ(1＋)＝1＋＋＝1＋＝1＋∈(2,3)，由题知－a＝φ(x)在(1，＋∞)内无解，故－a<φ(1＋)<3，所以a>－φ(1＋)，所以整数a的最小值为－2．考点3　函数极值点的偏移问题——综合性(2021·新高考全国Ⅰ卷)已知函数f(x)＝x(1－ln x)．(1)讨论f(x)的单调性；(2)设a，b为两个不相等的正数，且b ln a－a ln b＝a－b，证明：2<＋<e．(1)解：函数f(x)的定义域为(0，＋∞)，又f′(x)＝1－ln x－1＝－ln x，当x∈(0,1)时，f′(x)>0，当x∈(1，＋∞)时，f′(x)<0，故f(x)的单调递增区间为(0,1)，单调递减区间为(1，＋∞)．(2)证明：因为b ln a－a ln b＝a－b，故b(ln a＋1)＝a(ln b＋1)，即＝，故f ＝f ．设＝x1，＝x2，由(1)可知不妨设0<x1<1，x2>1．因为x∈(0,1)时，f(x)＝x(1－ln x)>0，x∈(e，＋∞)时，f(x)＝x(1－ln x)<0，故1<x2<e．先证：x1＋x2>2，若x2≥2，x1＋x2>2必成立．若x2<2,要证x1＋x2>2，即证x1>2－x2，而0<2－x2<1，故即证f(x1)>f(2－x2)，即证f(x2)>f(2－x2)，其中1<x2<2．设g(x)＝f(x)－f(2－x)，1<x<2，则g′(x)＝f′(x)＋f′(2－x)＝－ln x－ln(2－x)＝－ln[x(2－x)]．因为1<x<2，故0<x(2－x)<1，故－ln x(2－x)>0，所以g′(x)>0，故g(x)在(1,2)上单调递增，所以g(x)>g(1)＝0，故f(x)>f(2－x)，即f(x2)>f(2－x2)成立，所以x1＋x2>2成立，综上，x1＋x2>2成立．设x2＝tx1，则t>1，结合＝，＝x1，＝x2，可得x1(1－ln x1)＝x2(1－ln x2)，即1－ln x1＝t(1－ln t－ln x1)，故ln x1＝，要证x1＋x2<e，即证(t＋1)x1<e，即证ln (t＋1)＋ln x1<1，即证ln (t＋1)＋<1，即证(t－1)ln (t＋1)－t ln t<0．令S(t)＝(t－1)ln (t＋1)－t ln t，t>1，则S′(t)＝ln (t＋1)＋－1－ln t＝ln －．先证明一个不等式：ln(x＋1)≤x．设u(x)＝ln(x＋1)－x，则u′(x)＝－1＝，当－1<x<0时，u′(x)>0；当x>0时，u′(x)<0，故u(x)在(－1,0)上为增函数，在(0，＋∞)上为减函数，故u(x)ma x＝u(0)＝0，故ln(x＋1)≤x成立．由上述不等式可得当t>1时，ln ≤<，故S′(t)<0恒成立，故S(t)在(1，＋∞)上为减函数，故S(t)<S(1)＝0，故(t－1)ln (t＋1)－t ln t<0成立，即x1＋x2<e成立．综上所述，2<＋<e．对称化构造是解决极值点偏移问题的方法，该方法可分为以下三步：已知函数f(x)＝ln x－ax有两个零点x1，x2(x1<x2)．(1)求实数a的取值范围；(2)求证：x1·x2>e2．(1)解：f′(x)＝－a＝(x>0)，①若a≤0，则f′(x)>0，不符合题意．②若a>0，令f′(x)＝0，解得x＝．当x∈时，f′(x)>0；当x∈时，f′(x)<0．由题意知f(x)有两个零点的必要条件为f(x)＝ln x－ax的极大值f＝ln －1>0，解得0<a<．显然e∈，f(e)＝1－a e<0，∈，f＝2ln－．设t＝>e，g(t)＝2ln t－t，g′(t)＝－1<0，所以g(t)在(e，＋∞)上单调递减，g(t)<g(e)＝2－e<0，即f <0．所以实数a的取值范围为．(2)证明：因为f(1)＝－a<0，所以1<x1<<x2．构造函数H(x)＝f－f＝ln －ln －2ax,0<x<．H′(x)＝＋－2a＝>0，所以H(x)在上单调递增，故H(x)>H(0)＝0，即f >f．由1<x1<<x2，知－x1>，故f(x2)＝f(x1)＝f <f＝f．因为f(x)在上单调递减，所以x2>－x1，即x1＋x2>．故ln (x1x2)＝ln x1＋ln x2＝a(x1＋x2)>2，即x1·x2>e2．拓展考点　隐零点求解问题已知函数f(x)＝ax2－ax－x ln x，且f(x)≥0．(1)求a；(2)证明：f(x)存在唯一的极大值点x0，且e－2<f(x0)<2－2．(1)解：f(x)的定义域为(0，＋∞)，设g(x)＝ax－a－ln x，则f(x)＝xg(x)，f(x)≥0等价于g(x)≥0．因为g(1)＝0，g(x)≥0，故g′(1)＝0，而g′(x)＝a－，g′(1)＝a－1＝0，得a＝1．若a＝1，则g′(x)＝1－．当0<x<1时，g′(x)<0，g(x)单调递减；当x>1时，g′(x)>0，g(x)单调递增，所以x＝1是g(x)的极小值点，故g(x)≥g(1)＝0．综上，a＝1．(2)证明：由(1)知f(x)＝x2－x－x ln x，f′(x)＝2x－2－ln x(x>0)．设h(x)＝2x－2－ln x，h′(x)＝2－．当x∈时，h′(x)<0；当x∈时，h′(x)>0，所以h(x)在上单调递减，在上单调递增．又h(e－2)>0，h<0，h(1)＝0，所以h(x)在上有唯一零点x0，在上有唯一零点1，且当x∈(0，x0)时，h(x)>0；当x∈(x0，1)时，h(x)<0；当x∈(1，＋∞)时，h(x)>0．因为f′(x)＝h(x)，所以x＝x0是f(x)的唯一极大值点．由f′(x0)＝0得ln x0＝2(x0－1)，故f(x0)＝x0(1－x0)．由x0∈得f(x0)<．因为x＝x0是f(x)在(0,1)上的最大值点，由e－1∈(0,1)，f′(e－1)≠0得f(x0)>f(e－1)＝e－2，所以e－2<f(x0)<2－2．设函数f(x)＝e x－ax－2．(1)求f(x)的单调区间；(2)若a＝1，k为整数，且当x>0时，(x－k)·f′(x)＋x＋1>0，求k的最大值．解：(1)当a≤0时，f(x)的单调递增区间是(－∞，＋∞)，无单调递减区间；当a>0时，函数f(x)的单调递减区间是(－∞，ln a)，单调递增区间是(ln a，＋∞)．(解答过程略)(2)由题设可得(x－k)(e x－1)＋x＋1>0，即k<x＋(x>0)恒成立．令g(x)＝＋x(x>0)，得g′(x)＝＋1＝(x>0)．由(1)的结论可知，函数h(x)＝e x－x－2(x>0)是增函数．又因为h(1)<0，h(2)>0，所以函数h(x)的唯一零点α∈(1,2)(该零点就是h(x)的隐零点)，且eα＝α＋2．当x∈(0，α)时，g′(x)<0；当x∈(α，＋∞)时，g′(x)>0，所以g(x)min＝g(α)＝＋α．又eα＝α＋2且α∈(1,2)，则g(x)min＝g(α)＝1＋α∈(2,3)，所以k的最大值为2．1．按导函数零点能否精确求解可以把零点分为两类：1．已知函数f(x)＝e x－a－eln(e x＋a)，若关于x的不等式f(x)≥0恒成立，求实数a的取值范围．解：由函数f(x)＝e x－a－eln(e x＋a)，求得定义域为，对函数求导可得：f′(x)＝e x－，则存在一个x0，使得f′(x0)＝0，且－＜x＜x0时，f′(x)＜0，x＞x0时，f′(x)＞0，则f(x)≥f(x0)＝e x0－a－eln(e x0＋a)＝－a－e·ln e＝e x0＋－2e－a＝e x0＋a＋－2e－2a．因为e x0＋a＋≥2e，所以f(x0)≥2e－2e－2a＝－2a≥0，则a≤0，所以实数a的取值范围为(－∞，0]．2．已知函数f(x)＝．(1)求函数f(x)的零点及单调区间；(2)求证：曲线y＝存在斜率为6的切线，且切点的纵坐标y0<－1．(1)解：函数f(x)的零点为e．函数f(x)的单调递增区间为(e，＋∞)，单调递减区间为(0，e)．(解答过程略)(2)证明：要证曲线y＝存在斜率为6的切线，即证y′＝＝6有解，等价于1－ln x－6x2＝0在x>0时有解．构造辅助函数g(x)＝1－ln x－6x2(x>0)，g′(x)＝－－12x<0，函数g(x)在(0，＋∞)上单调递减，且g(1)＝－5<0，g＝1＋ln 2－>0，所以∃x0∈，使得g(x0)＝1－ln x0－6x＝0．即证明曲线y＝存在斜率为6的切线．设切点坐标为，则y＝＝＝－6x0，x0∈．令h(x)＝－6x，x∈，由h(x)在区间上单调递减，则h(x)<h＝－1，．所以y0<－1求证：x1x2>e2(e为自然对数的底数)．[四字程序]思路参考：转化为证明ln x1＋ln x2>2，根据x1，x2是方程f′(x)＝0的根建立等量关系．令t＝，将ln x1＋ln x2变形为关于t的函数，将ln x1＋ln x2>2转化为关于t的不等式进行证明．证明：欲证x1x2>e2，需证ln x1＋ln x2>2．若f(x)有两个极值点x1，x2，则函数f′(x)有两个零点．又f′(x)＝ln x－mx(x>0)，所以x1，x2是方程f′(x)＝0的两个不等实根．于是，有解得m＝．另一方面，由得ln x2－ln x1＝m(x2－x1)，从而得＝，于是，ln x1＋ln x2＝＝．又0<x1<x2，设t＝，则t>1．因此，ln x1＋ln x2＝，t>1．要证ln x1＋ln x2>2，即证>2，t>1．即当t>1时，有ln t>．设函数h(t)＝ln t－，t＞1，则h′(t)＝－＝≥0，所以，h(t)为(1，＋∞)上的增函数．又h(1)＝0，因此，h(t)＞h(1)＝0．于是，当t>1时，有ln t>．所以ln x1＋ln x2>2成立，即x1x2>e2．思路参考：将证明x1x2>e2转化为证明x1>．依据x1，x2是方程f′(x)＝0的两个不等实根，构造函数g(x)＝，结合函数g(x)的单调性，只需证明g(x2)＝g(x1)<g．证明：由x1，x2是方程f′(x)＝0的两个不等实根，且f′(x)＝ln x－mx(x>0)，所以mx1＝ln x1，mx2＝ln x2．令g(x)＝，g(x1)＝g(x2)，由于g′(x)＝，因此，g(x)在(0，e)上单调递增，在(e，＋∞)上单调递减．又x1<x2，所以0<x1<e<x2．令h(x)＝g(x)－g(x∈(0，e))，h′(x)＝>0，故h(x)在(0，e)上单调递增，故h(x)<h(e)＝0，即g(x)<g．令x＝x1，则g(x2)＝g(x1)<g．因为x2，∈(e，＋∞)，g(x)在(e，＋∞)上单调递减，所以x2>，即x1x2>e2．思路参考：设t1＝ln x1∈(0,1)，t2＝ln x2∈(1，＋∞)，推出＝e t1－t2．将证明x1x2>e2转化为证明t1＋t2>2，引入变量k＝t1－t2<0构建函数进行证明．证明：设t1＝ln x1∈(0,1)，t2＝ln x2∈(1，＋∞)．由得⇒＝e t1－t2．设k＝t1－t2<0，则t1＝，t2＝．欲证x1x2>e2，需证ln x1＋ln x2>2．即只需证明t1＋t2＞2，即>2⇔k(1＋e k)<2(e k－1)⇔k(1＋e k)－2(e k－1)<0．设g(k)＝k(1＋e k)－2(e k－1)(k<0)，则g′(k)＝k e k－e k＋1．令m(k)＝k e k－e k＋1，则m′(k)＝k e k<0，故g′(k)在(－∞，0)上单调递减，故g′(k)>g′(0)＝0，故g(k)在(－∞，0)上单调递增，因此g(k)<g(0)＝0，命题得证．思路参考：设t1＝ln x1∈(0,1)，t2＝ln x2∈(1，＋∞)，推出＝e t1－t2．将证明x1x2>e2转化为证明t1＋t2>2，引入变量＝k∈(0,1)构建函数进行证明．证明：设t1＝ln x1∈(0,1)，t2＝ln x2∈(1，＋∞)．由得⇒＝e t1－t2．设＝k∈(0,1)，则t1＝，t2＝．欲证x1x2>e2，需证ln x1＋ln x2>2，即只需证明t1＋t2>2，即>2⇔ln k<⇔ln k－<0．设g(k)＝ln k－(k∈(0,1))，g′(k)＝>0，故g(k)在(0,1)上单调递增，因此g(k)<g(1)＝0，命题得证．1．本题考查应用导数研究极值点偏移问题，基本解题方法是把双变量的等式或不等式转化为一元变量问题求解，途径都是构造一元函数．2．基于课程标准，解答本题一般需要具有良好的转化与化归能力、运算求解能力、逻辑思维能力．本题的解答体现了逻辑推理、数学运算的核心素养．3．基于高考数学评价体系，本题涉及函数与方程、不等式、导数的计算与应用等知识，渗透着函数与方程、转化与化归、分类讨论等思想方法，有一定的综合性，属于能力题，在提升学生思维的灵活性、创造性等数学素养中起到了积极的作用．已知函数f(x)＝x ln x－2ax2＋x，a∈R．(1)若f(x)在(0，＋∞)内单调递减，求实数a的取值范围；(2)若函数f(x)有两个极值点分别为x1，x2，证明：x1＋x2>．(1)解：f′(x)＝ln x＋2－4ax．因为f(x)在(0，＋∞)内单调递减，所以f′(x)＝ln x＋2－4ax≤0在(0，＋∞)内恒成立，即4a≥＋在(0，＋∞)内恒成立．令g(x)＝＋，则g′(x)＝．所以，当0<x<时，g′(x)>0，即g(x)在内单调递增；当x>时，g′(x)<0，即g(x)在内单调递减．所以g(x)的最大值为g＝e，所以实数a的取值范围是．(2)证明：若函数f(x)有两个极值点分别为x1，x2，则f′(x)＝ln x＋2－4ax＝0在(0，＋∞)内有两个不等根x1，x2．由(1)，知0<a<．由两式相减，得ln x1－ln x2＝4a(x1－x2)．不妨设0<x1<x2，则<1，所以要证明x1＋x2>，只需证明<，即证明>ln x1－ln x2，亦即证明>ln．令函数h(x)＝－ln x,0<x<1，所以h′(x)＝<0，即函数h(x)在(0,1)内单调递减．所以当x∈(0,1)时，有h(x)>h(1)＝0，所以>ln x，即不等式>ln成立．综上，x1＋x2>，命题得证．。

第10讲利用导数研究函数的零点问题高考数学

′
=
−

−

=

得

=

，构造函数

=

，求导得

, ＞
在 −∞, 上单调递减，在 , 上单调递增， , +∞ 上单调递减，
且 = ，
试卷讲评课件
=

＞及

→ +∞ 时 → ，
的图像如图，得到 =
当＜或 = 时，有一个零点；
当＞时，有两个零点.
试卷讲评课件
练1
f x = 2ex − 5x 2 的零点的个数为(
A.0
B.1
)
D.3
√
C.2
【分析】先把零点个数转化为函数交点个数，再构造函数 =

,结

合导函数求解单调性及极值最后应用数形结合求解.
【详解】由
π
4
2e
a =______

【分析】常数分离得

=

= 有唯一的解，求出的单调性与

极值，由有且仅有一个零点可得 = .
试卷讲评课件
【详解】当 = 时， = ≥ 恒成立，在[, ]上无零点.
1
, +∞
e
【分析】由 ′
2
3 1
,
2
2e e
3
0, 2
2e
−
，令

1
∪ , +∞
e
−
=
＜＜

，则直
上的图象有两个交点，利用导数分析函数

专题20 利用导数研究零点问题(解析版)

．
【解析】 ①当 a 0 时， 3x2 1 0 时， x 3 ，所以此时不符合题意； 3
②当 a 0 时， f '(x) 3ax2 6x 3x(ax 2) ，当 f '(x) 0 时，解得 x 2 或 x 0 ，则 f (x) 在 (,0) 上单 a
调递增，因为 f (0) 1 ， f (1) a 2 0 ，则存在一零点在 (,0) 上，所以此时不符合题意；
lnlnx
x,
0 2
x 1, x2 ,1
x
2, 分情况讨论：
ln x x2 6 , x 2.
当 0 x 1 时， f (x) g(x) 1有 1 个解 x 1 ，此时有一个根. e
当1 x 2 时， f (x) g(x) 单调递增，且 f (1) g(1) 1， f (2) g(2) 2 ln 2 1，此时有一个
∈ ,f(x)>0 恒成立,即对 x∈ ,a>2- 恒成立.
令 l(x)=2- ,x∈ ,则 l'(x)=-
=
.
再令 m(x)=2ln x+ -2,x∈ ,m'(x)=- + = <0,m(x)在上为减函数,于是 m(x)>m =2-2ln 2>0,
从而 l'(x)>0,于是 l(x)在上为增函数,l(x)<l =2-4ln 2,
咨询电话 18100655369 陈老师 18118913693 张老师 18112398139 叶老师
中高考数理化思维训练尖子生培优艺考生文化课辅导三步作文法全国名校名师一对一精品小班授课
＝－e－x0，y0＝k(x0－2)＝e－x0＝－e－x0(x0－2)，解得 x0＝1，k＝－1e；因此，当 x＜2 时，f(x)＝

高考数学一轮复习第4讲第3课时利用导数研究函数的零点问题

第3课时利用导数研究函数的零点问题考向一判断函数零点或方程的根个数问题例1已知函数f(x)＝e x－1，g(x)＝x＋x，其中e是自然对数的底数，e＝2.71828….(1)证明：函数h(x)＝f(x)－g(x)在区间(1,2)上有零点；(2)求方程f(x)＝g(x)的根的个数，并说明理由．解(1)证明：由题意可得h(x)＝f(x)－g(x)＝e x－1－x－x，所以h(1)＝e－3<0，h(2)＝e2－3－2>0，所以h(1)h(2)<0，所以函数h(x)在区间(1,2)上有零点．(2)由(1)可知h(x)＝f(x)－g(x)＝e x－1－x－x.由g(x)＝x＋x知x∈[0，＋∞)，而h(0)＝0，则x＝0为h(x)的一个零点．又h(x)在(1,2)内有零点，因此h(x)在[0，＋∞)上至少有两个零点．h′(x)＝e x－12x－12－1，记φ(x)＝e x－12x－12－1，则φ′(x)＝e x＋14x－32，当x∈(0，＋∞)时，φ′(x)>0，因此φ(x)在(0，＋∞)上单调递增，易知φ(x)在(0，＋∞)内至多有一个零点，即h(x)在[0，＋∞)内至多有两个零点，则h(x)在[0，＋∞)上有且只有两个零点，所以方程f(x)＝g(x)的根的个数为2.利用导数确定函数零点或方程根个数的常用方法(1)构建函数g(x)(要求g′(x)易求，g′(x)＝0可解)，转化确定g(x)的零点个数问题求解，利用导数研究该函数的单调性、极值，并确定定义域区间端点值的符号(或变化趋势)等，画出g(x)的图象草图，数形结合求解函数零点的个数．(2)利用函数零点存在定理：先用该定理判断函数在某区间上有零点，然后利用导数研究函数的单调性、极值(最值)及区间端点值符号，进而判断函数在该区间上零点的个数．1.(2020·潍坊检测)已知函数f(x)＝ln x－x2＋ax，a∈R.(1)证明：ln x≤x－1；(2)若a≥1，讨论函数f(x)的零点个数．解(1)证明：令g(x)＝ln x－x＋1(x>0)，则g(1)＝0，g′(x)＝1x－1＝1－xx，可得x∈(0,1)时，g′(x)>0，函数g(x)单调递增；x∈(1，＋∞)时，g′(x)<0，函数g(x)单调递减．∴当x＝1时，函数g(x)取得极大值也是最大值，∴g(x)≤g(1)＝0，即ln x≤x－1.(2)f′(x)＝1x－2x＋a＝－2x2＋ax＋1x，x>0.令－2x20＋ax0＋1＝0，解得x0＝a＋a2＋84(负值舍去)，在(0，x 0)上，f ′(x )>0，函数f (x )单调递增；在(x 0，＋∞)上，f ′(x )<0，函数f (x )单调递减． ∴f (x )max ＝f (x 0)．当a ＝1时，x 0＝1，f (x )max ＝f (1)＝0，此时函数f (x )只有一个零点x ＝1. 当a >1时，f (1)＝a －1>0，f ⎝ ⎛⎭⎪⎪⎫12a ＝ln 12a －14a2＋12<12a －1－14a2＋12＝－⎝ ⎛⎭⎪⎪⎫12a －122－14<0，f (2a )＝ln 2a －2a 2<2a －1－2a 2＝－2⎝ ⎛⎭⎪⎪⎫a －122－12<0.∴函数f (x )在区间⎝ ⎛⎭⎪⎪⎫12a ，1和区间(1,2a )上各有一个零点．综上可得，当a ＝1时，函数f (x )只有一个零点x ＝1；当a >1时，函数f (x )有两个零点．考向二由函数零点个数求解参数取值范围问题例2 (2020·全国卷Ⅰ)已知函数f (x )＝e x －a (x ＋2)． (1)当a ＝1时，讨论f (x )的单调性； (2)若f (x )有两个零点，求a 的取值范围．解 (1)当a ＝1时，f (x )＝e x －(x ＋2)，f ′(x )＝e x －1，令f ′(x )＜0，解得x ＜0，令f ′(x )＞0，解得x ＞0，所以f (x )的单调递减区间为(－∞，0)，单调递增区间为(0，＋∞)．(2)解法一：当a ≤0时，f ′(x )＝e x －a >0恒成立，f (x )在(－∞，＋∞)上单调递增，不符合题意；当a >0时，令f ′(x )＝0，解得x ＝ln a ，当x ∈(－∞，ln a )时，f ′(x )<0，f (x )单调递减，当x ∈(ln a ，＋∞)时，f ′(x )>0，f (x )单调递增．所以f (x )的极小值也是最小值为f (ln a )＝a －a (ln a ＋2)＝－a (1＋ln a )．又当x →－∞时，f (x )→＋∞，当x →＋∞时，f (x )→＋∞.所以要使f (x )有两个零点，只要f (ln a )<0即可，则1＋ln a >0，可得a >1e.综上，若f (x )有两个零点，则a 的取值范围是⎝ ⎛⎭⎪⎪⎫1e ，＋∞.解法二：若f (x )有两个零点，即e x －a (x ＋2)＝0有两个解，显然x ＝－2不成立，即a ＝ex x ＋2(x ≠－2)有两个解，令h (x )＝exx ＋2(x ≠－2)，则有h ′(x )＝错误!＝错误!，令h ′(x )＞0，解得x ＞－1，令h ′(x )＜0，解得x ＜－2或－2＜x ＜－1，所以函数h (x )在(－∞，－2)和(－2，－1)上单调递减，在(－1，＋∞)上单调递增，且当x ＜－2时，h (x )＜0，而当x →－2＋(从右侧趋近于－2)时，h (x )→＋∞，当x →＋∞时，h (x )→＋∞，所以当a ＝exx ＋2有两个解时，有a ＞h (－1)＝1e ，所以满足条件的a 的取值范围是⎝ ⎛⎭⎪⎪⎫1e ，＋∞.根据函数零点个数确定参数取值范围的核心思想是“数形结合”，即通过函数图象与x 轴的交点个数，或者两个相关函数图象的交点个数确定参数满足的条件，进而求得参数的取值范围，解决问题的步骤是“先形后数”．2.(2021·大庆实验中学月考)设k ∈R ，函数f (x )＝ln x －kx .(1)若k ＝2，求曲线y ＝f (x )在P (1，－2)处的切线方程； (2)若f (x )无零点，求实数k 的取值范围．解 (1)在区间(0，＋∞)上，f ′(x )＝1x －k ＝1－kx x，当k ＝2时，f ′(1)＝1－2＝－1，则切线方程为y －(－2)＝－(x －1)，即x ＋y ＋1＝0.(2)①若k <0，则f ′(x )>0，f (x )是区间(0，＋∞)上的增函数，因为f (1)＝－k >0，f (e k )＝k －k e k ＝k (1－e k )<0，所以f (1)·f (e k )<0，函数f (x )在区间(0，＋∞)上有唯一零点； ②若k ＝0，f (x )＝ln x 有唯一零点x ＝1； ③若k >0，令f ′(x )＝0，得x ＝1k，在区间⎝ ⎛⎭⎪⎪⎫0，1k 上，f ′(x )>0，函数f (x )是增函数；在区间⎝ ⎛⎭⎪⎪⎫1k ，＋∞上，f ′(x )<0，函数f (x )是减函数；故在区间(0，＋∞)上，f (x )的极大值为f ⎝ ⎛⎭⎪⎪⎫1k ＝ln 1k －1＝－ln k －1，由于f (x )无零点，须使f ⎝ ⎛⎭⎪⎪⎫1k ＝－ln k －1<0，解得k >1e ，故所求实数k 的取值范围是⎝ ⎛⎭⎪⎪⎫1e ，＋∞.考向三涉及函数零点、极值点的综合问题例3 (2019·全国卷Ⅱ)已知函数f (x )＝(x －1)ln x －x －1.证明：(1)f (x )存在唯一的极值点；(2)f (x )＝0有且仅有两个实根，且两个实根互为倒数．证明 (1)f (x )的定义域为(0，＋∞)． f ′(x )＝x －1x ＋ln x －1＝ln x －1x .因为y ＝ln x 在(0，＋∞)上单调递增， y ＝1x 在(0，＋∞)上单调递减，所以f ′(x )在(0，＋∞)上单调递增．又f ′(1)＝－1<0，f ′(2)＝ln 2－12＝ln 4－12>0，故存在唯一x 0∈(1,2)，使得f ′(x 0)＝0. 又当0<x <x 0时，f ′(x )<0，f (x )单调递减，当x >x 0时，f ′(x )>0，f (x )单调递增，因此，f (x )存在唯一的极值点．(2)由(1)知f (x 0)<f (1)＝－2，又f (e 2)＝e 2－3>0，所以f (x )＝0在(x 0，＋∞)内存在唯一根x ＝α. 由α>x 0>1得1α<1<x 0.又f ⎝ ⎛⎭⎪⎪⎫1α＝⎝ ⎛⎭⎪⎪⎫1α－1ln 1α－1α－1＝错误!＝0，故1α是f (x )＝0在(0，x 0)内的唯一根．综上，f (x )＝0有且仅有两个实根，且两个实根互为倒数．(1)研究函数零点问题，要通过数的计算(函数性质、特殊点的函数值等)和形的辅助，得出函数零点的可能情况．(2)函数可变零点(函数中含有参数)性质的研究，要抓住函数在不同零点处函数值均为零，建立不同零点之间的关系，把多元问题转化为一元问题，再使用一元函数的方法进行研究．3.已知函数f(x)＝12x2＋(1－a)x－a ln x，a∈R.(1)若f(x)存在极值点为1，求a的值；(2)若f(x)存在两个不同的零点x1，x2，求证：x1＋x2>2.解(1)由已知得f′(x)＝x＋1－a－ax，因为f(x)存在极值点为1，所以f′(1)＝0，即2－2a＝0，a＝1，经检验符合题意，所以a＝1.(2)证明：f′(x)＝x＋1－a－ax＝(x＋1)⎝⎛⎭⎪⎪⎫1－ax(x>0)，①当a≤0时，f′(x)>0恒成立，所以f(x)在(0，＋∞)上为增函数，不符合题意；②当a>0时，由f′(x)＝0得x＝a，当x>a时，f′(x)>0，所以f(x)单调递增，当0<x<a时，f′(x)<0，所以f(x)单调递减，所以当x＝a时，f(x)取得极小值f(a)．又f(x)存在两个不同的零点x1，x2，所以f(a)<0，即12a2＋(1－a)a－a ln a<0，整理得ln a>1－12a，作y＝f(x)关于直线x＝a的对称曲线g(x)＝f(2a－x)，令h(x)＝g(x)－f(x)＝f(2a－x)－f(x)＝2a－2x－a ln 2a－x x，则h ′(x )＝－2＋错误!＝－2＋错误!≥0，所以h (x )在(0,2a )上单调递增，不妨设x 1<a <x 2，则h (x 2)>h (a )＝0，即g (x 2)＝f (2a －x 2)>f (x 2)＝f (x 1)，又2a －x 2∈(0，a )，x 1∈(0，a )，且f (x )在(0，a )上为减函数，所以2a －x 2<x 1，即x 1＋x 2>2a ，又ln a >1－12a ，易知a >1成立，故x 1＋x 2>2.一、单项选择题1．已知函数f (x )＝ln xx2.若方程f (x )－a ＝0恰有两个不同的实数根，则实数a 的取值范围是( )A.⎝⎛⎭⎪⎪⎫0，12eB ．⎝ ⎛⎭⎪⎪⎫－∞，12eC.⎝ ⎛⎭⎪⎪⎫－∞，2eD ．⎝ ⎛⎭⎪⎪⎫12e ，＋∞答案 A 解析 f (x )＝ln x x2的定义域为(0，＋∞)，f ′(x )＝x －2xln xx4＝1－2ln x x3，令f ′(x )≥0可得0<x ≤e ，函数f (x )在(0，e )上单调递增，令f ′(x )<0可得x >e ，函数f (x )在(e ，＋∞)上单调递减，当x ＝e 时，函数f (x )取极大值，也为最大值，f (e )＝12e，又x →0＋(x 从右侧趋近于0)时，f (x )→－∞；x →＋∞时，f (x )→0，若方程f (x )＝a 恰有两个不同的实数根，则0<a <12e. 2．(2020·河北区二模)已知函数f (x )＝x －ln x ＋m (m ∈R )，若f (x )有两个零点x 1，x 2(x 1<x 2)，则下列选项中不正确的是( )A ．m <－1B ．x 1＋x 2≤2C ．0<x 1<1D ．e x 1－x 2＝x1x2答案 B解析 f ′(x )＝1－1x ＝x －1x ，令f ′(x )＝0，解得x ＝1，故函数f (x )在(0,1)上单调递减，在(1，＋∞)上单调递增，如图，故f (x )min ＝f (1)＝1＋m <0，即m <－1，并且0<x 1<1，故A ，C 正确；由于x 1，x 2为f (x )的零点，故有x 1－ln x 1＋m ＝0 ①，x 2－ln x 2＋m ＝0 ②，两式相减得，x 1－x 2＝ln x1x2，即e x 1－x 2＝x1x2，故D 正确；由于当m <－1时，0<x 1<1，x 2>1,1<2－x 1<2，由①②可知，m ＝ln x 1－x 1＝ln x 2－x 2，令g (x )＝ln x －x ，则g (x 1)＝g (x 2)，g ′(x )＝1x －1＝1－xx ，所以在(0,1)上，g ′(x )>0，g (x )单调递增，在(1，＋∞)上，g ′(x )<0，g (x )单调递减，g (x 2)－g (2－x 1)＝g (x 1)－g (2－x 1)＝ln x 1－x 1－ln (2－x 1)＋(2－x 1)，0<x 1<1，令h (x )＝ln x －x －ln (2－x )＋2－x,0<x <1，h ′(x )＝1x－1＋12－x－1＝错误!＝错误!＝错误!>0，所以h (x )在(0,1)上单调递增，所以h (x )<h (1)＝0，所以g (x 1)<g (2－x 1)，又因为g (x )在(1，＋∞)上单调递减，且g (x 2)＝g (x 1)，所以x 2>2－x 1，即x 1＋x 2>2，故B 不正确．故选B.二、多项选择题3．(2020·聊城二模)下列关于函数f (x )＝x 3－3x 2＋2x 的叙述，正确的为( ) A ．函数f (x )有三个零点B ．点(1,0)是函数f (x )图象的对称中心C ．函数f (x )的极大值点为x ＝1－33D ．存在实数a ，使得函数g (x )＝[f (x )]2＋af (x )为增函数答案 ABC解析 f (x )＝x 3－3x 2＋2x ＝x (x －1)(x －2)，令f (x )＝0，则x ＝0或x ＝1或x ＝2，所以函数f (x )有三个零点，所以A 正确；f (1＋x )＝(1＋x )3－3(1＋x )2＋2(1＋x )＝x 3－x ，f (1－x )＝(1－x )3－3(1－x )2＋2(1－x )＝－x 3＋x ，所以f (1＋x )＋f (1－x )＝0，所以函数f (x )的图象关于点(1,0)中心对称，所以B 正确；求出f (x )＝x 3－3x 2＋2x 的导函数f ′(x )＝3x 2－6x ＋2，令f ′(x )＝3x 2－6x ＋2>0，则x <1－33或x >1＋33，令f ′(x )＝3x 2－6x ＋2<0，则1－33<x <1＋33，所以函数f (x )＝x 3－3x 2＋2x 在⎝⎛⎭⎪⎪⎫－∞，1－33和⎝ ⎛⎭⎪⎪⎫1＋33，＋∞上单调递增，在⎝ ⎛⎭⎪⎪⎫1－33，1＋33上单调递减，所以当x ＝1－33时，函数f (x )＝x 3－3x 2＋2x 有极大值，所以函数f (x )的极大值点为x ＝1－33，所以C正确；假设函数g (x )＝[f (x )]2＋af (x )为增函数，则g ′(x )＝f ′(x )·(2f (x )＋a )>0恒成立，由上可知当x <1－33或x >1＋33时，f ′(x )>0，若要满足g ′(x )＝f ′(x )(2f (x )＋a )>0，则需在⎝ ⎛⎭⎪⎪⎫－∞，1－33和⎝ ⎛⎭⎪⎪⎫1＋33，＋∞上2f (x )＋a >0恒成立，f (x )＝x 3－3x 2＋2x 的图象如图，如图所示函数2f (x )＋a >0在⎝ ⎛⎭⎪⎪⎫－∞，1－33上不可能恒成立，所以不存在这样的实数a ，所以D 错误．故选ABC.4．(2020·烟台一模)关于函数f (x )＝e x ＋a sin x ，x ∈(－π，＋∞)，下列说法正确的是( )A ．当a ＝1时，f (x )在(0，f (0))处的切线方程为2x －y ＋1＝0B ．当a ＝1时，f (x )存在唯一极小值点x 0且－1＜f (x 0)＜0C ．对任意a ＞0，f (x )在(－π，＋∞)上均存在零点D ．存在a ＜0，使f (x )在(－π，＋∞)上有且只有一个零点答案 ABD解析当a ＝1时，f (x )＝e x ＋sin x ，f ′(x )＝e x ＋cos x ，f (0)＝1，f ′(0)＝2，∴所求切线方程为y －1＝2(x －0)，即2x －y ＋1＝0，故A 正确；当x ∈(0，＋∞)时，f ′(x )＝e x ＋cos x ＞0恒成立，∴f (x )在(0，＋∞)上无极值；当x ∈(－π，0]时，令g (x )＝f ′(x )＝e x＋cos x ，则g ′(x )＝e x－sin x ＞0恒成立，∴g (x )在(－π，0]上单调递增，又f ′⎝ ⎛⎭⎪⎪⎫－π2＝e －π2＞0，f ′⎝ ⎛⎭⎪⎪⎫－3π4＝e －3π4－22＜0，∴存在x 0∈⎝ ⎛⎭⎪⎪⎫－3π4，－π2，使f ′(x 0)＝e x 0＋cos x 0＝0，即e x 0＝－cos x 0，∴f (x )极小值＝f (x 0)＝e x 0＋sin x 0＝－cos x 0＋sin x 0＝2sin ⎝ ⎛⎭⎪⎪⎫x0－π4，∵－3π4＜x 0＜－π2，∴－π＜x 0－π4＜－3π4，∴－22＜sin ⎝ ⎛⎭⎪⎪⎫x0－π4＜0，∴－1＜f (x 0)＜0，故B 正确；当a ＝1e4时，f (x )＝e x＋sinx e4，f ′(x )＝e x＋cosxe4，当x ∈(0，＋∞)时，f ′(x )＝e x＋cosx e4＞0恒成立，∴f (x )在(0，＋∞)上单调递增，∴f (x )＞f (0)＞0，∴f (x )在(0，＋∞)上不存在零点；当x ∈(－π，0]时，令h (x )＝f ′(x )＝e x＋cosxe4，h ′(x )＝e x－sinxe4＞0恒成立，∴h (x )在(－π，0]上单调递增，又h (－π)＝f ′(－π)＝e －π－1e4＞0，∴f (x )在(－π，0]上单调递增，又f (－π)＝e －π>0，∴f (x )在(－π，0]上不存在零点，故C 错误；f (x )零点个数可以转化为y ＝e x 与y ＝－a sin x 的图象交点个数问题，如图，显然存在a ＜0，使y ＝e x 与y ＝－a sin x 的图象有一个交点，即f (x )有且只有一个零点，故D 正确．故选ABD.三、填空题5．(2020·海南省高三第一次联考)已知函数f (x )＝ax 3－3x 2＋2，若函数f (x )只有一个零点x 0，且x 0>0，则实数a 的取值范围为________.答案 (－∞，－2)解析 f (x )＝ax 3－3x 2＋2，∴f ′(x )＝3ax 2－6x ＝3x (ax －2)．又f (0)＝2.①当a ＝0时，f (x )＝－3x 2＋2有两个零点，不符合题意；②当a >0时，令f ′(x )＝0，x ＝0或x ＝2a，当f ′(x )>0时，x <0或x >2a，∴f (x )在(－∞，0)上单调递增，f (0)＝2，x →－∞时，f (x )→－∞，f (x )在(－∞，0)存在一个零点，不符合题意；③当a <0时，f (x )的递减区间为⎝ ⎛⎭⎪⎪⎫－∞，2a ，(0，＋∞)，递增区间是⎝ ⎛⎭⎪⎪⎫2a ，0，f (0)＝2，x →＋∞时，f (x )→－∞，∴f (x )在(0，＋∞)存在唯一零点，当x ＝2a 时，f (x )在(－∞，0)上取得最小值，而f (x )＝ax 3－3x 2＋2在(－∞，0)上不能有零点，故f ⎝ ⎛⎭⎪⎪⎫2a ＝a ⎝ ⎛⎭⎪⎪⎫2a 3－3⎝ ⎛⎭⎪⎪⎫2a 2＋2>0，解得a <－2.6．(2020·延边州模拟)若函数f (x )与g (x )满足：存在实数t ，使得f (t )＝g ′(t )，则称函数g (x )为f (x )的“友导”函数．已知函数g (x )＝12kx 2－x ＋3为函数f (x )＝x 2ln x ＋x 的“友导”函数，则k 的取值范围是________.答案 [2，＋∞)解析由g (x )＝12kx 2－x ＋3可得g ′(x )＝kx －1，∵函数g (x )＝12kx 2－x ＋3为函数f (x )＝x 2ln x ＋x 的“友导”函数，∴kx －1＝x 2ln x ＋x 有解，即k ＝x ln x ＋1＋1x有解．令h (x )＝x ln x ＋1＋1x ，则h ′(x )＝1＋ln x －1x2，再令φ(x )＝1＋ln x －1x2，∴φ′(x )＝1x ＋2x3>0，∴φ(x )＝1＋ln x －1x2在(0，＋∞)上单调递增，∵h ′(1)＝φ(1)＝0，∴x >1时，h ′(x )>0,0<x <1时，h ′(x )<0，∴h (x )在(0,1)上单调递减，在(1，＋∞)上单调递增，∴h (x )min ＝h (1)＝2，∴a ≥2.四、解答题7．(2020·海南省高三第一次联考)已知f (x )＝x 3＋3ax 2＋bx ＋a 2(a >1)的图象在x ＝－1处的切线方程为y ＝0.(1)求常数a ，b 的值；(2)若方程f (x )＝c 在区间[－4,1]上有两个不同的实根，求实数c 的值．解 (1)f ′(x )＝3x 2＋6ax ＋b ，由题意知错误!⇒错误!解得⎩⎪⎨⎪⎧a ＝1，b ＝3(舍去)或⎩⎪⎨⎪⎧a ＝2，b ＝9.(2)当a ＝2，b ＝9时，f ′(x )＝3x 2＋12x ＋9＝3(x ＋3)(x ＋1)，故方程f ′(x )＝0有根，根为x ＝－3或x ＝－1，x (－∞，－3)－3 (－3，－1)－1 (－1，＋∞)f ′(x ) ＋0 － 0 ＋f (x )极大值极小值由表可见，当x ＝－1时，f (x )有极小值0. 由上表可知f (x )的递减区间为(－3，－1)，递增区间为(－∞，－3)，(－1，＋∞)．因为f (－4)＝0，f (－3)＝4，f (－1)＝0，f (0)＝4，f (1)＝20.由数形结合可得c ＝0或c ＝4.8．(2020·山东青岛期中)已知二次函数f(x)的最小值为－4，且关于x的不等式f(x)≤0的解集为{x|－1≤x≤3，x∈R}．(1)求函数f(x)的解析式；(2)求函数g(x)＝错误!－4ln x的零点个数．解(1)因为f(x)是二次函数，且关于x的不等式f(x)≤0的解集为{x|－1≤x≤3，x ∈R}，所以设f(x)＝a(x＋1)(x－3)＝ax2－2ax－3a，且a>0.所以f(x)min＝f(1)＝－4a＝－4，解得a＝1.故函数f(x)的解析式为f(x)＝x2－2x－3.(2)由(1)知g(x)＝x2－2x－3x－4ln x＝x－3x－4ln x－2，所以g(x)的定义域为(0，＋∞)，g′(x)＝1＋3x2－4x＝错误!，令g′(x)＝0，得x1＝1，x2＝3.当x变化时，g′(x)，g(x)的取值变化情况如表所示．当当x>3时，g(3)＝3－1－4ln 3－2＝－4ln 3<0，g(e5)＝e5－3e5－20－2>25－1－22＝9>0.又因为g(x)在(3，＋∞)上单调递增，因而g(x)在(3，＋∞)上只有1个零点，故g(x)仅有1个零点．9．(2020·滨州三模)已知函数f(x)＝e x(x＋a)，其中e是自然对数的底数，a∈R.(1)求函数f(x)的单调区间；(2)设g(x)＝f(x－a)－x2，讨论函数g(x)零点的个数，并说明理由．解(1)因为f(x)＝e x(x＋a)，所以f′(x)＝e x(x＋a＋1)．由f′(x)>0，得x>－a－1；由f′(x)<0，得x<－a－1.所以f(x)的增区间是(－a－1，＋∞)，减区间是(－∞，－a－1)．(2)因为g(x)＝f(x－a)－x2＝x e x－a－x2＝x(e x－a－x)．由g(x)＝0，得x＝0或e x－a－x＝0.设h(x)＝e x－a－x，又h(0)＝e－a≠0，即x＝0不是h(x)的零点，故只需再讨论函数h(x)零点的个数．因为h′(x)＝e x－a－1，所以当x∈(－∞，a)时，h′(x)<0，h(x)单调递减；当x∈(a，＋∞)时，h′(x)>0，h(x)单调递增．所以当x＝a时，h(x)取得最小值h(a)＝1－a.①当h(a)>0，即a<1时，h(x)>0，h(x)无零点；②当h(a)＝0，即a＝1时，h(x)有唯一零点；③当h(a)<0，即a>1时，因为h(0)＝e－a>0，所以h(x)在(－∞，a)上有且只有一个零点．令x＝2a，则h(2a)＝e a－2a.设φ(a)＝h(2a)＝e a－2a(a>1)，则φ′(a)＝e a－2>0，所以φ(a)在(1，＋∞)上单调递增，所以∀a∈(1，＋∞)，都有φ(a)≥φ(1)＝e－2>0.所以h(2a)＝φ(a)＝e a－2a>0.所以h(x)在(a，＋∞)上有且只有一个零点．所以当a>1时，h(x)有两个零点．综上所述，当a<1时，g(x)有一个零点；当a＝1时，g(x)有两个零点；当a>1时，g(x)有三个零点．10．(2020·青岛市高三上学期期末)已知函数f(x)＝ln x－x＋2sin x，f′(x)为f(x)的导函数．求证：(1)f′(x)在(0，π)上存在唯一零点；(2)f(x)有且仅有两个不同的零点．证明(1)设g(x)＝f′(x)＝1x－1＋2cos x，当x∈(0，π)时，g′(x)＝－2sin x－1x2＜0，所以g(x)在(0，π)上单调递减．又因为g ⎝ ⎛⎭⎪⎪⎫π3＝3π－1＋1＞0，g ⎝ ⎛⎭⎪⎪⎫π2＝2π－1＜0，所以g (x )在⎝ ⎛⎭⎪⎪⎫π3，π2上有唯一的零点α，所以命题得证．(2)①由(1)知，当x ∈(0，α)时，f ′(x )＞0，f (x )在(0，α)上单调递增；当x ∈(α，π)时，f ′(x )＜0，f (x )在(α，π)上单调递减，所以f (x )在(0，π)上存在唯一的极大值点α⎝ ⎛⎭⎪⎪⎫π3＜α＜π2，所以f (α)＞f ⎝ ⎛⎭⎪⎪⎫π2＝ln π2－π2＋2＞2－π2＞0.又因为f ⎝ ⎛⎭⎪⎪⎫1e2＝－2－1e2＋2sin 1e2＜－2－1e2＋2＜0，所以f (x )在(0，α)上恰有一个零点．又因为f (π)＝ln π－π＜2－π＜0，所以f (x )在(α，π)上也恰有一个零点． ②当x ∈[π，2π)时，sin x ≤0，f (x )≤ln x －x . 设h (x )＝ln x －x ，h ′(x )＝1x－1＜0，所以h (x )在[π，2π)上单调递减，所以h (x )≤h (π)＜0. 所以当x ∈[π，2π)时，f (x )≤h (x )≤h (π)＜0恒成立，所以f (x )在[π，2π)上没有零点．③当x ∈[2π，＋∞)时，f (x )≤ln x －x ＋2，设φ(x )＝ln x －x ＋2，φ′(x )＝1x－1＜0，所以φ(x )在[2π，＋∞)上单调递减，所以φ(x )≤φ(2π)＜0，所以当x ∈[2π，＋∞)时，f (x )≤φ(x )≤φ(2π)＜0恒成立，所以f(x)在[2π，＋∞)上没有零点．综上，f(x)有且仅有两个不同的零点．11．(2020·海口模拟)已知函数f(x)＝错误!，其中k≠0.(1)求f(x)的单调区间；(2)若k>0，讨论关于x的方程|ln x|＝f(x)在区间(0,2)上实根的个数．解(1)由条件，得f′(x)＝错误!＝错误!.令f′(x)＝0，得x＝2.当k>0时，由f′(x)>0，得x<2，由f′(x)<0，得x>2.所以f(x)的单调递增区间是(－∞，2)，单调递减区间是(2，＋∞)．当k<0时，由f′(x)>0，得x>2，由f′(x)<0，得x<2.所以f(x)的单调递增区间是(2，＋∞)，单调递减区间是(－∞，2)．(2)因为|ln 1|＝f(1)＝0，所以x＝1是方程|ln x|＝f(x)的实根．当0<x<1时，由(1)知f(x)单调递增，所以f(x)<f(1)＝0.而|ln x|＝－ln x>0，所以方程|ln x|＝f(x)在区间(0,1)上无实根．当1<x<2时，|ln x|＝ln x.设F(x)＝ln x－错误!，则F′(x)＝1x－2k－kxex＝ex＋kx2－2kxxex.设u(x)＝e x＋kx2－2kx，当1<x<2时，u′(x)＝e x＋2kx－2k>0，所以u(x)在(1,2)上单调递增．①当u(1)＝e－k≥0，即k≤e时，在区间(1,2)上，总有u(x)>u(1)≥0，从而F′(x)>0，所以F(x)在(1,2)上单调递增，F(x)>F(1)＝0，即原方程在(1,2)上无实根．②当u(1)＝e－k<0，即k>e时，因为u(2)＝e2>0，所以存在x0∈(1，2)，满足u(x0)＝0.所以在(1，x 0)上，u (x )<0，F (x )单调递减，在(x 0,2)上，u (x )>0，F (x )单调递增．又因为F (1)＝0，F (2)＝ln 2－ke2，所以当F (2)>0，即e<k <e 2ln 2时，原方程在(1,2)上有唯一实根，当F (2)≤0，即k ≥e 2ln 2时，原方程在(1,2)上无实根．综上所述，当0<k ≤e 或k ≥e 2ln 2时，原方程在(0,2)上仅有一个实根；当e<k <e 2ln 2时，原方程在(0,2)上有两个实根．12．(2020·烟台一模)已知函数f (x )＝1＋ln xx－a (a ∈R )．(1)若f (x )≤0在(0，＋∞)上恒成立，求a 的取值范围，并证明对任意的n ∈N *，都有1＋12＋13＋…＋1n＞ln (n ＋1)；(2)设g (x )＝(x －1)2e x ，讨论方程f (x )＝g (x )实数根的个数．解 (1)由f (x )≤0可得，a ≥1＋ln x x (x ＞0)，令h (x )＝1＋ln xx ，则h ′(x )＝错误!＝错误!，当x ∈(0,1)时，h ′(x )＞0，h (x )单调递增，当x ∈(1，＋∞)时，h ′(x )＜0，h (x )单调递减，故h (x )在x ＝1处取得最大值，要使a ≥1＋ln xx ，只需a ≥h (1)＝1，故a 的取值范围为a ≥1.显然，当a＝1时，有1＋ln xx≤1，即不等式ln x<x－1在(1，＋∞)上恒成立，令x＝n＋1n>1(n∈N*)，则有lnn＋1n<n＋1n－1＝1n，所以ln 21＋ln32＋…＋lnn＋1n<1＋12＋13＋…＋1n，即1＋12＋13＋…＋1n>ln (n＋1)．(2)由f(x)＝g(x)可得，1＋ln xx－a＝(x－1)2e x，即a＝1＋ln xx－(x－1)2e x，令t(x)＝1＋ln xx－(x－1)2e x，则t′(x)＝－ln xx2－(x2－1)e x，当x∈(0,1)时，t′(x)>0，t(x)单调递增，当x∈(1，＋∞)时，t′(x)<0，t(x)单调递减，故t(x)在x＝1处取得最大值t(1)＝1，又当x→0＋(x从右侧趋近于0)时，t(x)→－∞，当x→＋∞时，t(x)→－∞，所以当a＝1时，方程f(x)＝g(x)有一个实数解；当a<1时，方程f(x)＝g(x)有两个不同的实数解；当a>1时，方程f(x)＝g(x)没有实数解．21 / 21。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

题型一利用导数讨论函数零点的个数【题型要点解析】对于函数零点的个数的相关问题，利用导数和数形结合的数学思想来求解．这类问题求解的通法是：(1)构造函数，这是解决此类题的关键点和难点，并求其定义域； (2)求导数，得单调区间和极值点； (3)画出函数草图；(4)数形结合，挖掘隐含条件，确定函数图象与x 轴的交点情况进而求解．1.已知f (x )＝ax 3－3x 2＋1(a >0)，定义h (x )＝max{f (x )，g (x )}＝⎩⎪⎨⎪⎧f (x )，f (x )≥g (x )，g (x )，f (x )<g (x ).(1)求函数f (x )的极值；(2)若g (x )＝xf ′(x )，且存在x ∈[1,2]使h (x )＝f (x )，求实数a 的取值范围； (3)若g (x )＝ln x ，试讨论函数h (x )(x >0)的零点个数．【解】 (1)∈函数f (x )＝ax 3－3x 2＋1，∈f ′(x )＝3ax 2－6x ＝3x (ax －2)，令f ′(x )＝0，得x 1＝0或x 2＝2a，∈a >0，∈x 1<x 2，列表如下：∈f (x )的极大值为f (0)＝1，极小值为f ⎪⎭⎫⎝⎛a ＝8a 2－12a 2＋1＝1－4a 2. (2)g (x )＝xf ′(x )＝3ax 3－6x 2，∈存在x ∈[1,2]，使h (x )＝f (x )，∈f (x )≥g (x )在x ∈[1,2]上有解，即ax 3－3x 2＋1≥3ax 3－6x 2在x ∈[1,2]上有解，即不等式2a ≤1x 3＋3x 在x ∈[1,2]上有解．设y ＝1x 3＋3x ＝3x 2＋1x 3(x ∈[1,2])，∈y ′＝－3x 2－3x 4<0对x ∈[1,2]恒成立，∈y ＝1x 3＋3x 在x ∈[1,2]上单调递减，∈当x ＝1时，y ＝1x 3＋3x 的最大值为4，∈2a ≤4，即a ≤2.(3)由(1)知，f (x )在(0，＋∞)上的最小值为f ⎪⎭⎫⎝⎛a 2＝1－4a 2， ∈当1－4a 2>0，即a >2时，f (x )>0在(0，＋∞)上恒成立，∈h (x )＝max{f (x )，g (x )}在(0，＋∞)上无零点．∈当1－4a2＝0，即a ＝2时，f (x )min ＝f (1)＝0.又g (1)＝0，∈h (x )＝max{f (x )，g (x )}在(0，＋∞)上有一个零点． ∈当1－4a2<0，即0<a <2时，设φ(x )＝f (x )－g (x )＝ax 3－3x 2＋1－ln x (0<x <1)， ∈φ′(x )＝3ax 2－6x －1x <6x (x －1)－1x <0，∈φ(x )在(0,1)上单调递减．又φ(1)＝a －2<0，φ⎪⎭⎫ ⎝⎛e 1＝a e3＋2e 2－3e 2>0，∈存在唯一的x 0∈⎪⎭⎫⎝⎛1,1e ，使得φ(x 0)＝0，(∈)当0<x ≤x 0时，∈φ(x )＝f (x )－g (x )≥φ(x 0)＝0，∈h (x )＝f (x )且h (x )为减函数．又h (x 0)＝f (x 0)＝g (x 0)＝ln x 0<ln 1＝0， f (0)＝1>0，∈h (x )在(0，x 0)上有一个零点； (∈)当x >x 0时，∈φ(x )＝f (x )－g (x )<φ(x 0)＝0， ∈h (x )＝g (x )且h (x )为增函数，∈g (1)＝0，∈h (x )在(x 0，＋∞)上有一零点；从而h (x )＝max{f (x )，g (x )}在(0，＋∞)上有两个零点，综上所述，当0<a <2时，h (x )有两个零点；当a ＝2时，h (x )有一个零点；当a >2时，h (x )无零点．题组训练一利用导数讨论函数零点的个数已知函数f (x )＝ln x －12ax ＋a －2，a ∈R .(1)求函数f (x )的单调区间；(2)当a <0时，试判断g (x )＝xf (x )＋2的零点个数．【解析】 (1)f ′(x )＝1x －a 2＝2－ax2x(x >0)．若a ≤0，则f ′(x )>0，∈函数f (x )的单调递增区间为(0，＋∞)；若a >0，当0<x <2a 时，f ′(x )>0，函数f (x )单调递增，当x >2a 时，f ′(x )<0，函数f (x )单调递减，综上，若a ≤0时，函数f (x )的单调递增区间为(0，＋∞)；若a >0时，函数f (x )的单调递增区间为⎪⎭⎫ ⎝⎛a 2,0，单调递减区间为⎪⎭⎫ ⎝⎛∞+a 2. (2)g (x )＝x ln x －12ax 2＋ax －2x ＋2，g ′(x )＝－ax ＋ln x ＋a －1.又a <0，易知g ′(x )在(0，＋∞)上单调递增， g ′(1)＝－1<0，g ′(e)＝－a e ＋a ＝a (1－e)>0，故而g ′(x )在(1，e)上存在唯一的零点x 0，使得g ′(x 0)＝0.当0<x <x 0时，g ′(x )<0，g (x )单调递减；当x >x 0时，g ′(x )>0，g (x )单调递增，取x 1＝e a ，又a <0，∈0<x 1<1，∈g (x 1)＝x 1)2221(ln 111x a ax x +-+-＝e a⎪⎭⎫ ⎝⎛+-+-a a e a ae a 2221，设h (a )＝a －12a e a ＋a －2＋2e a ，(a <0)，h ′(a )＝－12a e a －12e a －2e a ＋2，(a <0)，h ′(0)＝－12，h ″(a )＝e －a －e a ＋e －a －12a e a >0，∈h ′(a )在(－∞，0)上单调递增，h ′(a )<h ′(0)<0， ∈h (a )在(－∞，0)上单调递减，∈h (a )>h (0)＝0， ∈g (x 1)>0，即当a <0时，g (e a )>0.当x 趋于＋∞时，g (x )趋于＋∞，且g (2)＝2ln2－2<0. ∈函数g (x )在(0，＋∞)上始终有两个零点．题型二由函数零点个数求参数的取值范围【题型要点解析】研究方程的根(或函数零点)的情况，可以通过导数研究函数的单调性、最大值、最小值、变化趋势等，并借助函数的大致图象判断方程根(函数零点)的情况，这是导数这一工具在研究方程中的重要应用．已知函数f (x )＝mxln x ，曲线y ＝f (x )在点(e 2，f (e 2))处的切线与直线2x ＋y ＝0垂直(其中e为自然对数的底数)．(1)求f (x )的解析式及单调减区间；(2)若函数g (x )＝f (x )－kx 2x －1无零点，求k 的取值范围．【解析】 (1)函数f (x )＝mx ln x 的导数为f ′(x )＝m (ln x －1)(ln x )2，又由题意有：f ′(e 2)＝12∈m 4＝12∈m ＝2，故f (x )＝2x ln x.此时f ′(x )＝2(ln x －1)(ln x )2，由f ′(x )≤0∈0<x <1或1<x ≤e ，所以函数f (x )的单调减区间为(0,1)和(1，e]．(2)g (x )＝f (x )－kx 2x －1∈g (x )＝x ⎪⎭⎫ ⎝⎛--1ln 2x kx x ，且定义域为(0,1)∈(1，＋∞)，要函数g (x )无零点，即要2ln x ＝kxx －1在x ∈(0,1)∈(1，＋∞)内无解，亦即要k ln x －2(x －1)x ＝0在x ∈(0,1)∈(1，＋∞)内无解．构造函数h (x )＝k ln x －2(x －1)x ∈h ′(x )＝kx －2x2.∈当k ≤0时，h ′(x )<0在x ∈(0,1)∈(1，＋∞)内恒成立，所以函数h (x )在(0,1)内单调递减，h (x )在(1，＋∞)内也单调递减.又h (1)＝0，所以在(0,1)内无零点，在(1，＋∞)内也无零点，故满足条件；∈当k >0时，h ′(x )＝kx －2x 2∈h ′(x )＝22x k x k ⎪⎭⎫ ⎝⎛-， (i)若0<k <2，则函数h (x )在(0,1)内单调递减，在⎪⎭⎫⎝⎛k 2,1内也单调递减，在⎪⎭⎫ ⎝⎛+∞,2k 内单调递增，又h (1)＝0，所以在(0,1)内无零点；易知h ⎪⎭⎫ ⎝⎛k 2<0，而h (e 2k )＝k ·2k －2＋2e2k>0，故在⎪⎭⎫⎝⎛+∞,2k 内有一个零点，所以不满足条件；(ii)若k ＝2，则函数h (x )在(0,1)内单调递减，在(1，＋∞)内单调递增．又h (1)＝0，所以x ∈(0,1)∈(1，＋∞)时，h (x )>0恒成立，故无零点，满足条件；(iii)若k >2，则函数h (x )在⎪⎭⎫ ⎝⎛k 2,0内单调递减，在⎪⎭⎫⎝⎛1,2k 内单调递增，在(1，＋∞)内单调递增，又h (1)＝0，所以在⎪⎭⎫⎝⎛1,2k 及(1，＋∞)内均无零点．又易知h ⎪⎭⎫⎝⎛k 2<0，而h (e －k )＝k (－k )－2＋2e k ＝2e k －k 2－2，又易证当k >2时，h (e －k )>0，所以函数h (x )在⎪⎭⎫ ⎝⎛k 2,0内有一零点，故不满足条件．综上可得：k 的取值范围为：k ≤0或k ＝2.题组训练二由函数零点个数求参数的取值范围已知函数f (x )＝ln x －ax (ax ＋1)，其中a ∈R . (1)讨论函数f (x )的单调性；(2)若函数f (x )在(0,1]内至少有1个零点，求实数a 的取值范围．【解析】(1)依题意知，函数f (x )的定义域为(0，＋∞)，且f ′(x )＝1x－2a 2x －a＝2a 2x 2＋ax －1－x ＝(2ax －1)(ax ＋1)－x，当a ＝0时，f (x )＝ln x ，函数f (x )在(0，＋∞)上单调递增；当a >0时，由f ′(x )>0，得0<x <12a，由f ′(x )<0，得x >12a ，函数f (x )⎪⎭⎫⎝⎛a 21,0上单调递增，在⎪⎭⎫⎝⎛+∞,21a 上单调递减．当a <0时，由f ′(x )>0，得0<x <－1a ，由f ′(x )<0，得x >－1a，函数f (x )在⎪⎭⎫ ⎝⎛-a 1,0上单调递增，在⎪⎭⎫⎝⎛+∞-,1a 上单调递减． (2)当a ＝0时，函数f (x )在(]0，1内有1个零点x 0＝1；当a >0时，由(1)知函数f (x )在⎪⎭⎫ ⎝⎛a 21,0上单调递增，在⎪⎭⎫⎝⎛+∞,21a 上单调递减． ∈若12a ≥1，即0<a ≤12时，f (x )在(0,1]上单调递增，由于当x →0时，f (x )→－∞且f (1)＝－a 2－a <0知，函数f (x )在(0,1]内无零点；∈若0<12a <1，即当a >12时，f (x )在⎪⎭⎫ ⎝⎛a 21,0上单调递增，在⎥⎦⎤ ⎝⎛1,21a 上单调递减，要使函数f (x )在(0,1]内至少有1个零点，只需满足f ⎪⎭⎫⎝⎛a 21≥0，即ln 12a ≥34，又∈a >12，∈ln 12a <0，∈不等式不成立．∈f (x )在(0,1]内无零点；当a <0时，由(1)知函数f (x )在⎪⎭⎫ ⎝⎛-a 1,0上单调递增，在⎪⎭⎫⎝⎛+∞-,1a 上单调递减． ∈若－1a ≥1，即－1≤a <0时，f (x )在(0,1]上单调递增，由于当x →0时，f (x )→－∞，且f (1)＝－a 2－a >0，知函数f (x )在(0,1]内有1个零点；∈若0<－1a <1，即a <－1时，函数f (x )在⎪⎭⎫ ⎝⎛-a 1,0上单调递增，在⎥⎦⎤⎝⎛-1,1a 上单调递减，由于当x →0时，f (x )→－∞，且当a <－1时，f ⎪⎭⎫ ⎝⎛-a 1＝ln ⎪⎭⎫⎝⎛-a 1<0，知函数f (x )在(0,1]内无零点．综上可得a 的取值范围是[－1,0]．题型三利用导数证明复杂方程在某区间上仅有一解【题型要点解析】证明复杂方程在某区间上有且仅有一解的步骤： (1)在该区间上构造与方程相应的函数； (2)利用导数研究该函数在该区间上的单调性； (3)判断该函数在该区间端点处的函数值的符号； (4)作出结论．已知函数f (x )＝(x 2－2x )ln x ＋ax 2＋2.(1)当a ＝－1时，求f (x )在点(1，f (1))处的切线方程；(2)当a >0时，设函数g (x )＝f (x )－x －2，且函数g (x )有且仅有一个零点，若e －2<x <e ，g (x )≤m ，求m 的取值范围．【解析】 (1)当a ＝－1时，f (x )＝(x 2－2x )ln x －x 2＋2，定义域为(0，＋∞)，∈f ′(x )＝(2x －2)ln x ＋x －2－2x ＝(2x －2)ln x －x －2.∈f ′(1)＝－3，又f (1)＝1，f (x )在(1，f (1))处的切线方程3x ＋y －4＝0.(2)令g (x )＝f (x )－x －2＝0，则(x 2－2x )ln x ＋ax 2＋2＝x ＋2，即a ＝1－(x －2)·ln x x ，令h (x )＝1－(x －2)·ln xx，则h ′(x )＝－1x 2－1x ＋2－2ln x x 2＝1－x －2ln xx 2.令t (x )＝1－x －2ln x ，t ′(x )＝－1－2x ＝－x －2x ，∈t ′(x )<0，t (x )在(0，＋∞)上是减函数，又∈t (1)＝h ′(1)＝0，所以当0<x <1时，h ′(x )>0，当x >1时，h ′(x )<0，所以h (x )在(0,1)上单调递增，在(1，＋∞)上单调递减，∈h (x )max ＝h (1)＝1.因为a >0，所以当函数g (x )有且仅有一个零点时，a ＝1.g (x )＝(x 2－2x )ln x ＋x 2－x ，若e －2<x <e ，g (x )≤m ，只需g (x )max ≤m ， g ′(x )＝(x －1)(3＋2ln x )，令g ′(x )＝0得x ＝1，或x ＝e －32，又∈e －2<x <e∈函数g (x )在(e －2，e －32)上单调递增，在(e －32，1)上单调递减，在(1，e)上单调递增，又g (e －32)＝－12e －3＋2e －32，g (e)＝2e 2－3e ，∈g (e －32)＝－12e －3＋2e －32<2e －32<2e<2e ⎪⎭⎫ ⎝⎛-23e ＝g (e)，即g (e －32)<g (e)，g (x )max ＝g (e)＝2e 2－3e ，∈m ≥2e 2－3e .题组训练三利用导数证明复杂方程在某区间上仅有一解已知y ＝4x 3＋3tx 2－6t 2x ＋t －1，x ∈R ，t ∈R .(1)当x 为常数时，t 在区间⎥⎦⎤⎢⎣⎡32,0变化时，求y 的最小值φ(x )；(2)证明：对任意的t ∈(0，＋∞)，总存在x 0∈(0,1)，使得y ＝0.【解析】 (1)当x 为常数时，设f (t )＝4x 3＋3tx 2－6t 2x ＋t －1＝－6xt 2＋(3x 2＋1)t ＋4x 3－1，f ′(t )＝－12xt ＋3x 2＋1.∈当x ≤0时，由t ∈⎥⎦⎤⎢⎣⎡32,0知f (t )>0，f (t )在⎥⎦⎤⎢⎣⎡32,0上递增，其最小值φ(x )＝f (0)＝4x 3－1；∈当x >0时，f (t )的图象是开口向下的抛物线，其对称轴为直线；t ＝－3x 2＋1－12x ＝3x 2＋112x ，若⎩⎪⎨⎪⎧x >0，3x 2＋112x ≤13，即13≤x ≤1，则f (t )在⎥⎦⎤⎢⎣⎡32,0上的最小值为 φ(x )＝f ⎪⎭⎫⎝⎛32＝4x 3＋2x 2－83x －13.若⎩⎪⎨⎪⎧x >0，3x 2＋112x >13，即0<x <13或x >1，则f (t )在⎥⎦⎤⎢⎣⎡32,0上的最小值为φ(x )＝f (0)＝4x 3－1.综合∈∈，得φ(x )＝⎩⎨⎧4x 3－1，x <13或x >1，4x 3＋2x 2－83x －13，13≤x ≤1.(2)证明：设g (x )＝4x 3＋3tx 2－6t 2x ＋t －1，则g ′(x )＝12x 2＋6tx －6t 2＝12(x ＋t )⎪⎭⎫ ⎝⎛-2t x 由t ∈(0，＋∞)，当x 在区间(0，＋∞)内变化时，g ′(x )，g (x )取值的变化情况如下表：∈当t2≥1，即t ≥2时，g (x )在区间(0,1)内单调递减，g (0)＝t －1>0，g (1)＝－6t 2＋4t ＋3＝－2t (3t －2)＋3≤－4(3－2)＋3<0.所以对任意t ∈[2，＋∞)，g (x )在区间(0,1)内均存在零点，即存在x 0∈(0,1)，使得g (x 0)＝0.∈当0<t 2<1，即0<t <2时，g (x )在⎪⎭⎫ ⎝⎛2,0t 内单调递减，在⎪⎭⎫ ⎝⎛1,2t 内单调递增，若t ∈(0,1)，则g ⎪⎭⎫⎝⎛2t ＝－74t 3＋t －1≤－74t 3<0，g (1)＝－6t 2＋4t ＋3≥－6t ＋4t ＋3＝－2t ＋3≥1>0，所以g (x )在⎪⎭⎫⎝⎛1,2t 内存在零点；若t ∈(1,2)，则g (0)＝t －1>0，g ⎪⎭⎫ ⎝⎛2t ＝－74t 3＋t －1<－74×13＋2－1<0，所以g (x )在⎪⎭⎫⎝⎛2,0t 内存在零点．所以，对任意t ∈(0,2)，g (x )在区间(0,1)内均存在零点，即存在x 0∈(0,1)，使得g (x 0)＝0，综合∈∈，对任意的t ∈(0，＋∞)，总存在x 0∈(0,1)，使得y ＝0.【专题训练】1．已知函数f (x )＝xln x＋ax ，x >1.(1)若f (x )在(1，＋∞)上单调递减，求实数a 的取值范围； (2)若a ＝2，求函数f (x )的极小值；(3)若方程(2x －m )ln x ＋x ＝0，在(1，e]上有两个不等实根，求实数m 的取值范围． [解析] (1)f ′(x )＝ln x －1ln 2x ＋a ，由题意可得f ′(x )≤0在(1，＋∞)上恒成立，∈a ≤1ln 2x －1ln x＝221ln 1⎪⎭⎫ ⎝⎛-x －14.∈x ∈(1，＋∞)，∈ln x ∈(0，＋∞)， ∈当1ln x －12＝0时，函数t ＝221ln 1⎪⎭⎫ ⎝⎛-x －14的最小值为－14，∈a ≤－14. 故实数a 的取值范围为⎥⎦⎤ ⎝⎛∞-41,(2)当a ＝2时，f (x )＝xln x ＋2x ，f ′(x )＝ln x －1＋2ln 2x ln 2x，令f ′(x )＝0，得2ln 2x ＋ln x －1＝0，解得ln x ＝12或ln x ＝－1(舍)，即x ＝e 12.当1<x <e 12时，f ′(x )<0，当x >e 12时，f ′(x )>0，∈f (x )的极小值为f (e 12)＝e 1212＋2e 1e ＝4e 12.(3)将方程(2x －m )ln x ＋x ＝0两边同除以ln x 得(2x －m )＋x ln x ＝0，整理得xln x ＋2x ＝m ，即函数g (x )＝xln x ＋2x 的图象与函数y ＝m 的图象在(1，e]上有两个不同的交点．由(2)可知，g (x )在(1，e 12)上单调递减，在(e 12，e]上单调递增，g (e 12)＝4e 12，g (e)＝3e ，在(1，e]上，当x →1时，x ln x →＋∞，∈4e 12<m ≤3e ，故实数m 的取值范围为(4e 12，3e]．2．已知f (x )＝2x ln x ，g (x )＝x 3＋ax 2－x ＋2.(1)如果函数g (x )的单调递减区间为⎪⎭⎫⎝⎛-1,31，求函数g (x )的解析式； (2)在(1)的条件下，求函数y ＝g (x )的图象在点P (－1，g (－1))处的切线方程； (3)已知不等式f (x )≤g ′(x )＋2恒成立，若方程a e a －m ＝0恰有两个不等实根，求m 的取值范围．【解】 (1)g ′(x )＝3x 2＋2ax －1，由题意知，3x 2＋2ax －1<0的解集为⎪⎭⎫⎝⎛-1,31，即3x 2＋2ax －1＝0的两根分别是－13，1，代入得a ＝－1，∈g (x )＝x 3－x 2－x ＋2. (2)由(1)知，g (－1)＝1，∈g ′(x )＝3x 2－2x －1，g ′(－1)＝4，∈点P (－1,1)处的切线斜率k ＝g ′(－1)＝4，∈函数y ＝g (x )的图象在点P (－1,1)处的切线方程为y －1＝4(x ＋1)，即4x －y ＋5＝0.(3)由题意知，2x ln x ≤3x 2＋2ax ＋1对x ∈(0，＋∞)恒成立，可得a ≥ln x －32x －12x 对x ∈(0，＋∞)恒成立．设h (x )＝ln x －32x －12x，则h ′(x )＝1x －32＋12x 2＝－(x －1)(3x ＋1)2x 2，令h ′(x )＝0，得x ＝1，x ＝－13(舍)，当0<x <1时，h ′(x )>0；当x >1时，h ′(x )<0， ∈当x ＝1时，h (x )取得最大值，h (x )max ＝h (1)＝－2， ∈a ≥－2.令φ(a )＝a e a ，则φ′(a )＝e a ＋a e a ＝e a (a ＋1)， ∈φ(a )在[－2，－1]上单调递减，在(－1，＋∞)上单调递增，∈φ(－2)＝－2e －2＝－2e 2，φ(－1)＝－e －1＝－1e ，当a →＋∞时，φ(a )→＋∞，∈方程a e a －m ＝0恰有两个不等实根，只需－1e <m ≤－2e 2.3．设函数f (x )＝x 3＋ax 2＋bx ＋c .(1)求曲线y ＝f (x )在点(0，f (0))处的切线方程；(2)设a ＝b ＝4，若函数f (x )有三个不同零点，求c 的取值范围； (3)求证：a 2－3b >0是f (x )有三个不同零点的必要而不充分条件．【解析】 (1)由f (x )＝x 3＋ax 2＋bx ＋c ，得f ′(x )＝3x 2＋2ax ＋b .因为f (0)＝c ，f ′(0)＝b ，所以曲线y ＝f (x )在点(0，f (0))处的切线方程为y ＝bx ＋c .(2)当a ＝b ＝4时，f (x )＝x 3＋4x 2＋4x ＋c ，所以f ′(x )＝3x 2＋8x ＋4. 令f ′(x )＝0，得3x 2＋8x ＋4＝0，解得x ＝－2或x ＝－23.f (x )与f ′(x )在区间(－∞，＋∞)上的情况如下：所以，当c >0且c －3227<0时，存在x 1∈(－4，－2)，x 2∈⎪⎭⎫ ⎝⎛--3,2，x 3∈⎪⎭⎫⎝⎛-0,3，使得f (x 1)＝f (x 2)＝f (x 3)＝0.由f (x )的单调性知，当且仅当c ∈⎪⎭⎫⎝⎛2732,0时，函数f (x )＝x 3＋4x 2＋4x ＋c 有三个不同零点．(3)证明：当Δ＝4a 2－12b <0时，f ′(x )＝3x 2＋2ax ＋b >0，x ∈(－∞，＋∞)，此时函数f (x )在区间(－∞，＋∞)上单调递增，所以f (x )不可能有三个不同零点．当Δ＝4a 2－12b ＝0时，f ′(x )＝3x 2＋2ax ＋b 只有一个零点，记作x 0. 当x ∈(－∞，x 0)时，f ′(x )>0，f (x )在区间(－∞，x 0)上单调递增；当x ∈(x 0，＋∞)时，f ′(x )>0，f (x )在的区间(x 0，＋∞)上单调递增．所以f (x )不可能有三个不同零点．综上所述，若函数f (x )有三个不同零点，则必有Δ＝4a 2－12b >0. 故a 2－3b >0是f (x )有三个不同零点的必要条件．当a ＝b ＝4，c ＝0时，a 2－3b >0，f (x )＝x 3＋4x 2＋4x ＝x (x ＋2)2只有两个不同零点，所以a 2－3b >0不是f (x )有三个不同零点的充分条件．因此a 2－3b >0是f (x )有三个不同零点的必要而不充分条件．。