2012年北京市东城区高考数学二模试卷(理科)(解析版)
2012年北京市各区二模试题分类解析【数学理】(5)三角函数
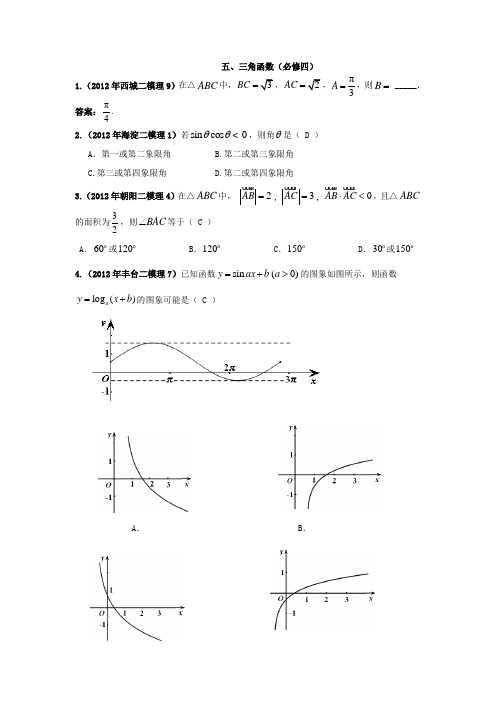
五、三角函数(必修四)1.(2012年西城二模理9)在△ABC 中,BC =,AC =,π3A =,则B = _____. 答案:π4. 2.(2012年海淀二模理1)若sin cos 0θθ<,则角θ是( D ) A .第一或第二象限角 B.第二或第三象限角 C.第三或第四象限角 D.第二或第四象限角3.(2012年朝阳二模理4)在△ABC 中, 2AB =,3AC =,0AB AC ⋅<,且△ABC 的面积为32,则BAC ∠等于( C ) A .60或120 B .120 C .150 D .30或150 4.(2012年丰台二模理7)已知函数sin (0)y ax b a =+>的图象如图所示,则函数log ()a y x b =+的图象可能是( C )A .B .C .D .5.(2012年昌平二模理9)在∆ABC 中,4,2,2π===A b a 那么角C =_________.答案:127π。
6.(2012年东城二模理11)在平面直角坐标系xOy 中,将点A 绕原点O 逆时针旋转90到点B ,那么点B 的坐标为____,若直线OB 的倾斜角为α,则sin2α的值为 .答案:)3,1(-2-7.(2012年海淀二模理11)在ABC ∆中,若120=∠A ,5c =,ABC ∆的面积为,则a = .。
8.(2012年西城二模理15)已知函数22π()cos ()sin 6f x x x =--.(Ⅰ)求π()12f 的值; (Ⅱ)若对于任意的π[0,]2x ∈,都有()f x c ≤,求实数c 的取值范围. 解:(Ⅰ)22ππππ()cos ()sin cos 12121262f =--==. ………………5分 (Ⅱ) 1π1()[1cos(2)](1cos 2)232f x x x =+--- ………………7分1π13[cos(2)cos 2]2cos 2)2322x x x x =-+=+ ………………8分π)3x =+. ………………9分 因为 π[0,]2x ∈,所以 ππ4π2[,]333x +∈, ………………10分所以当 ππ232x +=,即 π12x =时,()f x 取得最大值2. ………………11分所以 π[0,]2x ∀∈,()f x c ≤ 等价于c ≤.故当 π[0,]2x ∀∈,()f x c ≤时,c的取值范围是)+∞. ………………13分 9.(2012年朝阳二模理15) 已知函数()2cos cos f x x x x m =-+()R m ∈的图象过点π(,0)12M .(Ⅰ)求m 的值;(Ⅱ)在△ABC 中,角A ,B ,C 的对边分别是a ,b ,c .若cos +cos =2cos c B b C a B ,求()f A 的取值范围.解:(Ⅰ)由()12(cos 21)2f x x x m =-++π1sin(2)62x m =--+.…3分因为点π(,0)12M 在函数()f x 的图象上, 所以ππ1sin(2)01262m ⋅--+=,解得12m =. …5分 (Ⅱ) 因为cos +cos =2cos c B b C a B ,所以sin cos sin cos C B B C +=2sin cos A B ,所以sin(+)2sin cos B C A B =,即sin 2sin cos A A B =. ……7分 又因为(0,A ∈π),所以sin 0A ≠,所以1cos 2B =. ……8分 又因为(0,B ∈π),所以π3B =,2π3A C +=. ……10分所以2π03A <<, ππ7π2666A -<-<,所以πsin(2)6A -∈1(,1]2-.…12分所以()f A 的取值范围是1(,1]2-. ……13分10.(2012年丰台二模理15)已知函数()cos sin )f x x x x =-(Ⅰ)求()3f π的值;(Ⅱ)求函数()y f x =在区间[0,]2π上的最小值,并求使()y f x =取得最小值时的x 的值. 解:因为()cos sin )f x x x x =-2sin cos x x x -=1cos 21)sin 222x x +--12sin 22x x -=cos(2)6x π+(Ⅰ)()cos(2)336f πππ=⨯+==7分 (Ⅱ)因为 [0,]2x π∈, 所以2666x ππ7π≤+≤.当 26x π+=π,即512x π=时,函数()y f x =有最小值是12--. 当512x π=时,函数()y f x =有最小值是12--. …13分 11.(2012年昌平二模理15)已知向量a (cos ,sin ),θθ= b = (13-,), 22π≤θ≤π-.(Ⅰ)当b a ⊥时,求θ的值;(Ⅱ)求||b a +的取值范围.解:(Ⅰ) a ⊥b ∴b a ⋅0sin cos 3=-=θθ ……… 2分 得3tan =θ 又∵22π≤θ≤π-……… 4分 即:θ=3π……6分 (Ⅱ)||b a +=4)sin cos 3(21||2||22+-+=+⋅+θθb b a a )3sin(45π--=θ ……… 9分22π≤≤π-θ 6365π≤π-≤π-∴θ … 11分 21)3sin(1≤π-≤-∴θ 4)3sin(42≤π--≤-∴θ∴33≤+≤||b a … 13分12.(2012年东城二模理15)已知函数()sin()f x A x =+ωϕ(其中∈R x ,0A >,ππ0,22ωϕ>-<<)的部分图象如图所示.(Ⅰ)求函数()f x 的解析式;(Ⅱ)已知在函数()f x 的图象上的三点,,M N P 的横坐标分别为-解:(Ⅰ)由图可知,1A =,最小正周期428T =⨯=.由2π8T ==ω,得4π=ω. ………3分又π(1)sin()14f ϕ=+= ,且ππ22ϕ-<<,所以ππ42+=ϕ, 即4π=ϕ . ………5分 所以π()sin()sin (1)444f x x x =+=+ππ. ………6分(Ⅱ)因为(1)0,(1)1,f f -==π(5)sin (51)1,4f =+=-所以(1,0),(1,1),(5,1)M N P --. …………7分所以MN PN MP ===由余弦定理得3cos5MNP ∠==-. ………11分因为[)0,MNP ∠∈π, 所以4sin 5MNP ∠=. ……13分。
2012年北京市各区二模试题分类解析【数学理】(10):平面向量.pdf

课题使用人编号07课型新授课课时1主备人石伟锋 备课 时间教 学 目 标(一)情感、态度、价值观:树立正确的资源环境意识和对自然环境的忧患意识。
以保护环境为荣,以破坏环境为耻,树立人与自然和谐共处的人生价值。
有意识的控制人对自然的破坏行为。
(二)能力:能从自我做起,珍爱和保护大自然的一切生命。
提高保护自然、保护环境的能力。
(三)知识:了解人与大自然的不和谐之音的表现,懂得人与大自然和谐相处的重要性。
重点 难点 教学难点:自然景观遭到人为的破坏教具多媒体 电子白板教法学法 讨论、欣赏、感悟、体验历年考点 展示 交流 自然物种在减少 自然景观遭到人为破坏 教师引导,PPT出示材料,阅读思考、讨论: 大自然物种不断减少、甚至灭绝的原因是什么? 如何保护物种,我们能做些什么? 教师引导,PPT出示材料, 这些自然景观为什么遭到人为破坏? 如何去改变这种状况? 教师引导归纳总结 结合本地实际,探讨如何保护自然景观 学生先阅读课本和PPT材料 ⑴、思考讨论,学生畅所欲言 ⑵讨论:如何保护物种,我们能做些什么? 分小组交流: 结合本地实际,探讨如何保护自然景观 15教 学 过 程环节知识点教师活动学生活动估时合作 探究 展示 交流3、环境状况 不容乐观教师:PPT出示,环境的一些恶化状况的图片, 然后让学生谈谈所知道的情况 在观察的基础上, 让学生总结,什么是环境问题?有什么危害? 并初步探讨如何解决这些问题? 老师对一些有创意的观点和看法做法及时鼓励和表扬,激发学生探究和参与环保的热情,进行有效的情感教育和升华。
积极思考 结合实际 总结归纳 建言献策 11强化 应用 形成 能力巩固训练投放课堂练习 限时规范训练 巩固学习成果 规范答题 反馈补偿12 构建 网络知识结构1、先由学生谈谈观点、收获、体会。
2、老师总结2教后反思 初中学习网,资料共分享!我们负责传递知识! 含义:是指人类不合理地开发利用自然资源所造成的环境污染与破坏。
2012高考北京数学(理科)真题答案及简析

2012高考北京数学真题答案及简析三、解答题 15、 解:(sin cos )sin 2(sin cos )2sin cos ()2(sin cos )cos sin sin x x x x x x xf x x x x x x--===-{}πsin 21cos221|π4x x x x x k k ⎛⎫=-+=--≠∈ ⎪⎝⎭Z ,,(1)原函数的定义域为{}|πx x k k ≠∈Z ,,最小正周期为π、(2)原函数的单调递增区间为πππ8k k ⎡⎫-+⎪⎢⎣⎭,k ∈Z ,3πππ8k k ⎛⎤+⎥⎝⎦,k ∈Z16、 解:(1)CD DE ⊥,1A E DE ⊥∴DE ⊥平面1A CD , 又1A C ⊂平面1A CD , ∴1A C ⊥DE 又1A C CD ⊥,∴1A C ⊥平面BCDEy C(2)如图建系C xyz -,则()200D -,,,(00A ,,,()030B ,,,()220E -,,∴(103A B =-,,,()1210A E =--,,设平面1A BE 法向量为()n x y z =,,则1100A B n A E n ⎧⋅=⎪⎨⋅=⎪⎩∴3020y x y ⎧-=⎪⎨--=⎪⎩∴2z y y x ⎧=⎪⎪⎨⎪=-⎪⎩∴(12n =-,又∵(10M -,∴(10CM =-,∴cos ||||1CM n CM n θ⋅====⋅∴CM 与平面1A BE 所成角的大小45︒(3)设线段BC 上存在点P ,设P 点坐标为()00a ,,,则[]03a ∈,则(10A P a =-,,,()20DP a=,, 设平面1A DP 法向量为()1111n x y z =,,则1111020ay x ay ⎧-=⎪⎨+=⎪⎩∴111112z x ay ⎧=⎪⎪⎨⎪=-⎪⎩∴()136n a =-,假设平面1A DP 与平面1A BE 垂直则10n n ⋅=,∴31230a a ++=,612a =-,2a =- ∵03a <<∴不存在线段BC 上存在点P ,使平面1A DP 与平面1A BE 垂直17、(1)由题意可知:4002=6003(2)由题意可知:200+60+403=100010(3)由题意可知:22221(120000)3s a b c =++-,因此有当600a =,0b =,0c =时,有280000s =、18、 解:(1)由()1c ,为公共切点可得:2()1(0)f x ax a =+>,则()2f x ax '=,12k a =, 3()g x x bx =+,则2()=3f x x b '+,23k b =+,∴23a b =+⎺又(1)1f a =+,(1)1g b =+,∴11a b +=+,即a b =,代入①式可得:33a b =⎧⎨=⎩、(2)24a b =,∴设3221()()()14h x f x g x x ax a x =+=+++则221()324h x x ax a '=++,令()0h x '=,解得:12a x =-,26a x =-;0a >,∴26a a -<-, ∴原函数在2a ⎛⎫-∞- ⎪⎝⎭,单调递增,在26a a ⎛⎫-- ⎪⎝⎭,单调递减,在6a ⎛⎫-+∞ ⎪⎝⎭,上单调递增 ①若12a--≤,即2a ≤时,最大值为2(1)4a h a =-;②若126a a-<-<-,即26a <<时,最大值为12a h ⎛⎫-= ⎪⎝⎭③若16a--≥时,即6a ≥时,最大值为12a h ⎛⎫-= ⎪⎝⎭、综上所述:当(]02a ∈,时,最大值为2(1)4a h a =-;当()2,a ∈+∞时,最大值为12a h ⎛⎫-= ⎪⎝⎭、19、(1)原曲线方程可化简得:2218852x y m m +=--由题意可得:8852805802m m mm ⎧>⎪--⎪⎪>⎨-⎪⎪>⎪-⎩,解得:752m <<(2)由已知直线代入椭圆方程化简得:22(21)16240k x kx +++=,2=32(23)k ∆-,解得:232k >由韦达定理得:21621M N k x x k +=+①,22421M Nx x k =+,② 设(,4)N N N x k x +,(,4)M M M x kx +,(1)G G x ,MB 方程为:62M M kx y x x +=-,则316M M x G kx ⎛⎫⎪+⎝⎭,, ∴316M M x AG x k ⎛⎫=-⎪+⎝⎭,,()2N N AN x x k =+,,欲证A G N ,,三点共线,只需证AG ,AN 共线 即3(2)6MN N M x x k x x k +=-+成立,化简得:(3)6()M N M N k k x x x x +=-+ 将①②代入易知等式成立,则A G N ,,三点共线得证。
2012年3月北京市东城区示范校联考高三数学理科试题

2012年3月北京市东城区示范校联考高三数学理科试题东城区普通高中示范校高三综合练习(二)高三数学(理科) 2012.3 学校_____________班级_______________姓名______________考号___________本试卷分第Ⅰ卷和第Ⅱ卷两部分,第Ⅰ卷1至2页,第Ⅱ卷3至5页,共150分。
考试时长120分钟。
考生务必将答案答在答题卡上,在试卷上作答无效。
考试结束后,将本试卷和答题卡一并交回。
第Ⅰ卷(选择题共40分)一、本大题共8小题,每小题5分,共40分。
在每小题列出的四个选项中,选出符合题目要求的一项。
1.设全集2R,则图中阴影部分表示==-->=<-U A x x x B x x,{|30},{|1}的集合为 ( )A.}0{-<-xx<||{>xx B.}13C.}0|{-<xxx D.}13|{<<-x2.已知直线l过定点(-1,1),则“直线l的斜率为0”与圆12=2x相切”的+y23A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件 3. 已知直线m ,n 与平面α,β,下列命题正确的是( )A .βα//,//n m 且βα//,则n m //B .βα//,n m ⊥且β⊥α,则n m ⊥C .,βm n m=⊥I α且βα⊥,则α⊥n D .βα⊥⊥n m ,且βα⊥,则n m ⊥4.甲从正四面体的四个顶点中任意选择两个顶点连成直线,乙从该正四面体四个顶点中任意选择两个顶点连成直线,则所得的两条直线相互垂直的概率是 ( )A.61B. 92C. 185 D. 31 5. 执行如图所示的程序框图,若输出的结果是8,则判断框内m 的取值范围是 ( )4A.(30,42]B.(42,56]C.(56,72]D.(30,72)6.一个几何体的三视图如图所示,则此几何体的体积是 ( ) A .112 B.80 C.72D.64(第5题图)(第6题图) 7. 已知约束条件340,210,380,x y x y x y -+≥⎧⎪+-≥⎨⎪+-≤⎩若目标函数)0(>+=a ay x z 恰好在点(2,2)处取得最大值,则a 的取值范围为 ( )4 俯正侧4 435mO PQ MNA. 310<<aB.31≥aC. 31>a D. 210<<a8.如图,半径为2的⊙O 与直线MN 相切于点P ,射线PK 从PN 出发绕点P 逆时针方向旋转到PM ,旋转过程中,PK 交⊙O 于点Q ,设POQ ∠为x ,弓 形 PmQ 的面积为()S f x =,那么()f x 的图象大致是( )A B CD第Ⅱ卷(共110分)二、填空题:本大题共6小题,每小题5分,共30分。
2012东城二模理科数学带详细答案

北京市东城区2011-2012学年度第二学期高三综合练习(二)数学 (理科)本试卷分第Ⅰ卷和第Ⅱ卷两部分,第Ⅰ卷1至2页,第Ⅱ卷3至5页,共150分。
考试时长120分钟。
考生务必将答案答在答题卡上,在试卷上作答无效。
考试结束,将本试卷和答题卡一并交回。
第Ⅰ卷(选择题 共40分)一、本大题共8小题,每小题5分,共40分。
在每小题列出的四个选项中,选出符合题目要求的一项。
(1)下列命题中,真命题是(A )x ∀∈R ,210x --< (B )0x ∃∈R ,2001x x +=-(C )21,04x x x ∀∈-+>R (D )2000,220x x x ∃∈++<R (2)将容量为n 的样本中的数据分成6组,若第一组至第六组数据的频率之比为2:3:4:6:4:1,且前三组数据的频数之和等于27,则n 的值为(A )70 (B )60 (C )50 (D )40(3)41(2)x x-的展开式中的常数项为(A )24- (B )6- (C )6 (D )24(4)若一个三棱柱的底面是正三角形,其正(主)视图如图所示,则它的体积为(A (B )2(C )(D )4(5)若向量a ,b 满足1=a,=b ,且()⊥a a +b ,则a 与b 的夹角为(A )2π (B )23π (C )34π (D )56π (6)已知m 和n 是两条不同的直线,α和β是两个不重合的平面,那么下面给出的条件中一定能推出m ⊥β 的是(A )⊥αβ,且m ⊂α (B )m ∥n ,且n ⊥β (C )⊥αβ,且m ∥α (D )m ⊥n ,且n ∥β(7)若m 是2和8的等比中项,则圆锥曲线221y x m+=的离心率为 (A )2(B(C )2或2(D )2(8)定义:()00>>=y ,x y)y ,x (F x,已知数列{}n a 满足:()()n ,F ,n F a n22=()n *∈N ,若对任意正整数n ,都有k n a a ≥()k *∈N 成立,则k a 的值为(A )12 (B )2 (C )89 (D )98第Ⅱ卷(共110分)二、填空题:本大题共6小题,每小题5分,共30分。
2012年北京市高考数学试卷(理科)答案与解析

2012年北京市高考数学试卷(理科)参考答案与试题解析一、选择题共8小题.每小题5分.共40分.在每小题列出的四个选项中,选出符合胜目要求的一项.1.(5分)(2012•北京)已知集合A={x∈R|3x+2>0},B={x∈R|(x+1)(x﹣3)>0},则A∩B=),}}2.(5分)(2012•北京)设不等式组,表示的平面区域为D,在区域D内随机取B=44.(5分)(2012•北京)执行如图所示的程序框图,输出的S值为()5.(5分)(2012•北京)如图,∠ACB=90°,CD⊥AB于点D,以BD为直径的圆与BC交于点E.则()6.(5分)(2012•北京)从0、2中选一个数字.从1、3、5中选两个数字,组成无重复数=6=6中选两个数字排在个位与十位,共有=637.(5分)(2012•北京)某三棱锥的三视图如图所示,该三棱锥的表面积是()8+60+66+120+12=,=10=6.8.(5分)(2012•北京)某棵果树前n年的总产量S n与n之间的关系如图所示.从目前记录的结果看,前m年的年平均产量最高,则m的值为()二.填空题共6小题.每小题5分.共30分.9.(5分)(2012•北京)直线(t为参数)与曲线(α为参数)的交点个数为2.解:直线d=10.(5分)(2012•北京)已知﹛a n﹜是等差数列,s n为其前n项和.若a1=,s2=a3,则a2= 1.,,知,解得d==,d=11.(5分)(2012•北京)在△ABC中,若a=2,b+c=7,cosB=﹣,则b=4.,利用余弦定理可得﹣12.(5分)(2012•北京)在直角坐标系xOy中.直线l过抛物线y2=4x的焦点F.且与该抛物线相交于A、B两点.其中点A在x轴上方.若直线l的倾斜角为60°.则△OAF的面积为.的方程为:,即代入抛物线方程,化简可得,或的面积为故答案为:13.(5分)(2012•北京)己知正方形ABCD的边长为1,点E是AB边上的动点.则的值为1.解:因为==114.(5分)(2012•北京)已知f(x)=m(x﹣2m)(x+m+3),g(x)=2x﹣2,若同时满足条件:①∀x∈R,f(x)<0或g(x)<0;②∃x∈(﹣∞,﹣4),f(x)g(x)<0.则m的取值范围是(﹣4,﹣2).三、解答题公6小题,共80分.解答应写出文字说明,演算步骤或证明过程.15.(13分)(2012•北京)已知函数f(x)=.(1)求f(x)的定义域及最小正周期;(2)求f(x)的单调递增区间.sin)﹣)由,解得原函数的单调递增区间为16.(14分)(2012•北京)如图1,在Rt△ABC中,∠C=90°,BC=3,AC=6,D,E分别是AC,AB上的点,且DE∥BC,DE=2,将△ADE沿DE折起到△A1DE的位置,使A1C⊥CD,如图2.(1)求证:A1C⊥平面BCDE;(2)若M是A1D的中点,求CM与平面A1BE所成角的大小;(3)线段BC上是否存在点P,使平面A1DP与平面A1BE垂直?说明理由.,,法向量为垂直,则,可求得2,法向量为∴∴,,∴,,法向量为∴垂直,则,17.(13分)(2012•北京)近年来,某市为促进生活垃圾的分类处理,将生活垃圾分为厨余垃圾、可回收物和其他垃圾三类,并分别设置了相应的垃圾箱,为调查居民生活垃圾分类投(2)试估计生活垃圾投放错误的概率;(3)假设厨余垃圾在“厨余垃圾”箱、“可回收物”箱、“其他垃圾”箱的投放量分别为a,b,c,其中a>0,a+b+c=600.当数据a,b,c的方差s2最大时,写出a,b,c的值(结论不要求证明),并求此时s2的值.(求:S2=[++…+],其中为数据x1,x2,…,x n的平均数),因此有当正确的概率为率为,18.(13分)(2012•北京)已知函数f(x)=ax2+1(a>0),g(x)=x3+bx(1)若曲线y=f(x)与曲线y=g(x)在它们的交点(1,c)处具有公共切线,求a、b的值;(2)当a2=4b时,求函数f(x)+g(x)的单调区间,并求其在区间(﹣∞,﹣1)上的最大值.,求导函式可得:.,设,解得:,,∴))﹣在在;<﹣时,即(﹣时,最大值为19.(14分)(2012•北京)已知曲线C:(5﹣m)x2+(m﹣2)y2=8(m∈R)(1)若曲线C是焦点在x轴点上的椭圆,求m的取值范围;(2)设m=4,曲线c与y轴的交点为A,B(点A位于点B的上方),直线y=kx+4与曲线c交于不同的两点M、N,直线y=1与直线BM交于点G.求证:A,G,N三点共线.则,从而可得,三点共线,只需证,,解得:,解得:,方程为:,,三点共线,只需证,20.(13分)(2012•北京)设A是由m×n个实数组成的m行n列的数表,满足:每个数的绝对值不大于1,且所有数的和为零,记s(m,n)为所有这样的数表构成的集合.对于A∈S (m,n),记r i(A)为A的第ⅰ行各数之和(1≤ⅰ≤m),C j(A)为A的第j列各数之和(1≤j≤n);记K(A)为|r1(A)|,|R2(A)|,…,|Rm(A)|,|C1(A)|,|C2(A)|,…,|Cn(A)|中的最小值.(3)给定正整数t,对于所有的A∈S(2,2t+1),求K(A)的最大值.)首先构造满足是最大值即可.)的最大值为.的下面证明)的最大值为。
2012年北京市各区二模试题分类解析【数学理】(1):集合.pdf

1、认识生态环境破坏对我们将来生活的影响并提高环保意识。
2、学习报告文学写作手法的运用;并以此写作倡导书。
教学难点: 1、真正意义上认识到环保的重要性。
2、认识到环保是我们每个公民的职责;并制止环境破坏者的行为。
过程和方法: 朗读课文后揣摩文章字里行间充盈的感情和中心的关系,体味文中所设置的悬念。
教学方法: 诵读法与讨论法 教学过程: 一、导入: 当我们眼见一个广阔、美丽、充满生机的地方变为荒漠;原本牛马成群,绿林环绕,河流清澈的生命绿洲,现在却是一片死寂,寸草不生,不见飞鸟,令人恐怖;我们会深思,这种生态的巨变,就发生在我们的身边,这就是我们今天要认识的一个地方——罗布泊。
二、初读课文:1、正确识读、理解文中生字: 萧瑟(sè)和煦(xù)干涸(hé)吞噬(shì)裸露(luǒ)戈壁(gē)荡漾(yàng)娱乐(yú) 2、词语释义: 萧瑟:①形容风吹树木的声音;②形容冷落,凄凉。
和煦:温暖,多指阳光、风等。
干涸:(河道、池塘等)没有水了。
吞噬:蚕食、并吞。
裸露:没有东西遮盖。
戈壁滩:蒙古或新疆人称沙漠地区,这种地区尽是沙子和石块,地面缺水,植物稀少。
沧海桑田:大海变成农田,农田变成大海。
比喻世事变化很大。
也说桑田沧海。
3、内容提要: 要比较具体地把握课文内容,可以做一份内容提要,就下面几个问题画出要点:①今日罗布泊是怎样的一个地方?关键词是“沙漠”“神秘”。
②过去罗布泊是怎样的一个地方?关键词是“绿洲”“仙湖”。
③罗布泊为什么会消亡?关键词是“改道”“四盲”。
④同样的悲剧还有哪些?关键词是“青海湖”“月牙泉”。
全文充满了痛惜之情,为罗布泊生态环境的破坏而痛惜,为人们的盲目性造成的悲剧而痛惜。
生态意识,环保意识,可持续发展意识,是课文的基本理念。
课文又涉及西部大开发战略问题,用历史的教训,说明生态环境保护的重要。
2012年北京市高考数学试卷(理科)(含解析版)
17.(13 分)近年来,某市为促进生活垃圾的分类处理,将生活垃圾分为厨余垃圾、可回收物和其 他垃圾三类,并分别设置了相应的垃圾箱,为调查居民生活垃圾分类投放情况,先随机抽取了
该市三类垃圾箱总计 1000 吨生活垃圾,数据统计如下(单位:吨);
“厨余垃圾”箱
“可回收物”箱
“其他垃圾”箱
厨余垃圾
400
CE•EB=CD2
6.(5 分)从 0、2 中选一个数字.从 1、3、5 中选两个数字,组成无重复数字的三位数.其中奇
数的个数为( )
A.24
B.18
C.12
D.6
7.(5 分)某三棱锥的三视图如图所示,该三棱锥的表面积是( )
第 1页(共 14页)
则 m 的取值范围是
.
三、解答题公 6 小题,共 80 分.解答应写出文字说明,演算步骤或证明过程.
15.(13 分)已知函数 f(x)=
.
(1)求 f(x)的定义域及最小正周期; (2)求 f(x)的单调递增区间.
A.28+6
B.30+6
C.56+12
D.60+12
8.(5 分)某棵果树前 n 年的总产量 Sn 与 n 之间的关系如图所示.从目前记录的结果看,前 m 年
的年平均产量最高,则 m 的值为( )
(1)求证:A1C⊥平面 BCDE; (2)若 M 是 A1D 的中点,求 CM 与平面 A1BE 所成角的大小; (3)线段 BC 上是否存在点 P,使平面 A1DP 与平面 A1BE 垂直?说明理由.
第 2页(共 14页)
18.(13 分)已知函数 f(x)=ax2+1(a>0),g(x)=x3+bx (1)若曲线 y=f(x)与曲线 y=g(x)在它们的交点(1,c)处具有公共切线,求 a、b 的值; (2)当 a2=4b 时,求函数 f(x)+g(x)的单调区间,并求其在区间(﹣∞,﹣1)上的最大值.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2012年北京市东城区高考数学二模试卷(理科)一、本大题共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项.1. 下列命题中,真命题是( ) A.∀x ∈R ,−x 2−1<0 B.∃x 0∈R ,x 20 +x 0=−1C.∀x ∈R ,x 2−x +14>0D.∃x 0∈R ,x 2 +2x 0+2<02. 将容量为n 的样本中的数据分成6组,若第一组至第六组数据的频率之比为2:3:4:6:4:1,且前三组数据的频数之和等于27,则n 的值为( ) A.70 B.60 C.50 D.403. (理)(2x −1x )4的展开式中的常数项为( )A.−24B.−6C.6D.244. 若一个三棱柱的底面是正三角形,其正(主)视图如图所示,则它的体积为( )A.√3B.2C.2√3D.45. 若向量a →,b →满足|a →|=1,|b →|=√2,且a →⊥(a →+b →),则a →与b →的夹角为( ) A.π2B.2π3C.3π4D.5π66. 已知m 和n 是两条不同的直线,α和β是两个不重合的平面,那么下面给出的条件中一定能推出m ⊥β的是( )A.α⊥β,且m ⊂αB.m // n ,且n ⊥βC.α⊥β,且m // αD.m ⊥n ,且n // β 7.若m 是2和8的等比中项,则圆锥曲线x 2+y 2m =1的离心率为( )A.√32B.√5C.√32或√52D.√32或√58. 定义:F(x, y)=y x (x >0, y >0),已知数列{a n }满足:a n =F(n,2)F(2,n)(n ∈N ∗),若对任意正整数n ,都有a n ≥a k (k ∈N ∗)成立,则a k 的值为( ) A.12B.2C.89D.98二、填空题:本大题共6小题,每小题5分,共30分.设a ∈R ,且(a +i)2i 为正实数,则a =________.若圆C 的参数方程为{x =3cos θ+1y =3sin θ(θ为参数),则圆C 的圆心坐标为________,圆C 与直线x +y −3=0的交点个数为________.在平面直角坐标系xOy 中,将点A(√3,1)绕原点O 逆时针旋转90∘到点B ,那么点B 坐标为________,若直线OB 的倾斜角为α,则tan 2α=________.如图,直线PC 与圆O 相切于点C ,割线PAB 经过圆心O ,弦CD ⊥AB 于点E ,PC =4,PB =8,则CE =________.已知函数f(x)=|x|−sin x+1|x|+1(x ∈R )的最大值为M ,最小值为m ,则M +m =________.已知点A(a, b)与点B(1, 0)在直线3x −4y +10=0的两侧,给出下列说法: ①3a −4b +10>0;②当a >0时,a +b 有最小值,无最大值; ③√a 2+b 2>2;④当a >0且a ≠1,b >0时,ba−1的取值范围为(−∞, −52)∪(34, +∞). 其中,所有正确说法的序号是________.三、解答题:本大题共6小题,共80分.解答应写出文字说明,演算步骤或证明过程.已知函数f(x)=A sin (ωx +φ)(其中x ∈R ,A >0,ω>0,−π2<φ<π2)的部分图象如图所示.(Ⅰ)求函数f(x)的解析式;(Ⅱ)已知在函数f(x)的图象上的三点M ,N ,P 的横坐标分别为−1,1,5,求sin ∠MNP 的值.某公园设有自行车租车点,租车的收费标准是每小时2元(不足1小时的部分按1小时计算).甲、乙两人各租一辆自行车,若甲、乙不超过一小时还车的概率分别为14,12;一小时以上且不超过两小时还车的概率分别为12,14;两人租车时间都不会超过三小时. (1)求甲、乙两人所付租车费用相同的概率;(2)设甲、乙两人所付的租车费用之和为随机变量ξ,求ξ的分布列与数学期望Eξ.如图,矩形AMND 所在的平面与直角梯形MBCN 所在的平面互相垂直,MB // NC ,MN ⊥MB ,且MC ⊥CB ,BC =2,MB =4,DN =3.(1)求证:AB // 平面DNC ;(2)求二面角D −BC −N 的余弦值.已知抛物线C:x 2=4y ,M 为直线l:y =−1上任意一点,过点M 作抛物线C 的两条切线MA ,MB ,切点分别为A ,B .(Ⅰ)当M 的坐标为(0, −1)时,求过M ,A ,B 三点的圆的方程; (Ⅱ)证明:以AB 为直径的圆恒过点M .已知函数f(x)=(a +1a )ln x +1x −x(a >1).(l)试讨论f(x)在区间(0, 1)上的单调性;(2)当a ∈[3, +∞)时,曲线y =f(x)上总存在相异两点P (x 1, f(x 1)),Q (x 2, f (x 2 )),使得曲线y =f(x)在点P ,Q 处的切线互相平行,求证:x 1+x 2>65.对于数列{a n }(n =1, 2,…,m),令b k 为a 1,a 2,…,a k 中的最大值,称数列{b n }为{a n }的“创新数列”.例如数列2,1,3,7,5的创新数列为2,2,3,7,7.定义数列{C n }:c 1,c 2,c 3,…,c m 是自然数1,2,3,…,m(m >3)的一个排列.(1)当m =5时,写出创新数列为3,4,4,5,5的所有数列{C n };(2)是否存在数列{C n },使它的创新数列为等差数列?若存在,求出所有的数列{C n },若不存在,请说明理由.参考答案与试题解析2012年北京市东城区高考数学二模试卷(理科)一、本大题共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项. 1.【答案】 A【考点】命题的真假判断与应用 【解析】特称命题若判断为真,只需验证即可;全称命题若判断为真,则需进行严格证明,若判断为假,反例验证即可. 【解答】解:A 、由于x ∈R ,则x 2≥0,进而得到−x 2≤0, 则−x 2−1≤−1<0,故A 为真命题;B 、由于x 2+x +1=(x +12)2+34恒为正,则方程x 2+x =−1无实数解,故B 为假命题; C 、当x =12时,x 2−x +14=(x −12)2=0,故C 为假命题;D 、由于x 2+2x +2=(x +1)2+1恒为正,则x 2+2x +2<0无实数解,故D 为假命题. 故答案为A . 2.【答案】 B【考点】频率分布直方图 【解析】根据比例关系设出各组的频率,在频率分布表中,频数的和等于样本容量,频率的和等于1,求出前三组的频率,再频数和建立等量关系即可. 【解答】解:设第一组至第六组数据的频率分别为2x ,3x ,4x ,6x ,4x ,x , 则2x +3x +4x +6x +4x +x =1, 解得x =120,所以前三组数据的频率分别是220,320,420, 故前三组数据的频数之和等于2n 20+3n 20+4n 20=27,解得n =60. 故答案为60. 3. 【答案】 D【考点】二项式定理的应用【解析】利用二项展开式的通项公式T r+1=(−1)r ⋅C 4r⋅(2x)4−r ⋅x −r ,令x 的幂指数为0即可求得答案. 【解答】解:设(2x −1x )4的二项展开式的通项公式为T r+1,则T r+1=(−1)r ⋅C 4r⋅(2x)4−r ⋅x −r=(−1)r ⋅C 4r⋅24−r ⋅x 4−2r , 令4−2r =0,解得r =2.∴ 展开式中的常数项为T 3=(−1)2⋅C 42⋅22=24. 故选D . 4.【答案】 A【考点】由三视图求体积柱体、锥体、台体的体积计算【解析】根据三视图得几何体是底面为边长为2的正三角形,高为1的棱柱;再代入柱体的体积公式计算即可. 【解答】解:∵ 三棱柱的底面是边长为2的正三角形,高为1.∴ V =sℎ=12×2×√3×1=√3. 故选A 5.【答案】 C【考点】数量积表示两个向量的夹角 平面向量数量积的运算 【解析】由题意可得a →⋅(a →+b →)=0,即1+1×√2×cos <a →,b →>=0,由此求得cos <a →,b →>的值 即可求得<a →,b →>的值. 【解答】解:由题意可得a →⋅(a →+b →)=0, 即a →2+a →⋅b →=0,∴ 1+1×√2×cos <a →,b →>=0. 解得cos <a →,b →>=−√22.再由<a →,b →>∈[0, π], 可得<a →,b →>=3π4,故选C . 6. 【答案】 B【考点】直线与平面垂直的判定 【解析】 此题暂无解析 【解答】解:α⊥β,且m ⊂α⇒m ⊂β,或m // β,或m 与β相交,故A 不正确; m // n ,且n ⊥β⇒m ⊥β,故B 正确;α⊥β,且m // α⇒m ⊂β,或m // β,或m 与β相交,故C 不正确; 由m ⊥n ,且n // β,知m ⊥β不一定成立,故D 不正确. 故选B . 7.【答案】 D【考点】圆锥曲线的共同特征 等比数列的性质【解析】先根据等比中项的性质求得m 的值,分别看当m 大于0时,曲线为椭圆,进而根据标准方程求得a 和b ,则c 可求得,继而求得离心率.当m <0,曲线为双曲线,求得a ,b 和c ,则离心率可得.最后综合答案即可. 【解答】解:依题意可知m =±√2×8=±4, 当m =4时,曲线为椭圆, a =2,b =1,则c =√3,e =ca =√32. 当m =−4时,曲线为双曲线, a =1,b =2,c =√5则,e =√5. 故选D . 8.【答案】 C【考点】利用导数研究函数的单调性 数列递推式 【解析】根据题意可求得数列{a n }的通项公式,进而求得a n+1a n,根据2n 2−(n +1)2=(n −1)2−2,进而可知当当n ≥3时,(n −1)2−2>0,推断出当n ≥3时数列单调增,n <3时,数列单调减,进而可知n =3时a n 取到最小值求得数列的最小值,进而可知a k 的值. 【解答】解:a n =F(n,2)F(2,n)=2nn 2(n∈N∗),∴a n+1a n=2n 2(n+1)2,∵ 2n 2−(n +1)2=(n −1)2−2,当n ≥3时,(n −1)2−2>0, ∴ 当n ≥3时a n+1>a n ;当n <3时,(n −1)2−2<O ,所以当n <3时a n+1<a n . ∴ 当n =3时a n 取到最小值为f(3)=89,故答案为:89.二、填空题:本大题共6小题,每小题5分,共30分. 【答案】 −1【考点】复数代数形式的混合运算 复数的基本概念【解析】由题意知虚部等于0,实部大于0,可求a 的值. 【解答】解:(a +i)2i =(a 2−1)i +2ai 2=(a 2−1)i −2a 它是正实数,所以a =−1 故答案为:−1 【答案】 (1, 0),2 【考点】参数方程与普通方程的互化 直线与圆的位置关系【解析】先把圆的参数方程化为普通方程,由方程可得圆心坐标,利用点直线的距离公式求出圆心到直线的距离,然后与半径作比较,由其大小关系可得答案. 【解答】解:圆C 的普通方程为:(x −1)2+y 2=9, 所以圆心坐标为(1, 0),圆心到直线x +y −3=0的距离d =√2=√2,半径为3,且√2<3,所以圆与直线x +y −3=0的交点个数为2. 故答案为:2. 【答案】 (−1,√3),√3【考点】二倍角的正切公式 直线的倾斜角 【解析】可设OA →=√3+i ,OB →=OA →⋅i ,从而可求得点B 的坐标,由tan α=−√3,利用二倍角的正切可求tan 2α. 【解答】解:设OA →=√3+i ,∵ 点A(√3, 1)绕原点O 逆时针旋转90∘到点B , ∴ OB →=OA →⋅i =(√3+i)⋅i =−1+√3i , ∴ 点B 坐标为(−1, √3); ∵ 直线OB 的倾斜角为α, ∴ tan α=−√3, ∴ tan 2α=2tan α1−tan 2α=2×(−√3)1−3=√3.故答案为:(−1, √3);√3. 【答案】125【考点】与圆有关的比例线段 【解析】在圆中线段利用由切割线定理求得PA ,进而利用直角三角形PCO 中的线段,结合面积法求得CE 即可. 【解答】解:∵ PC 是圆O 的切线, ∴ 由切割线定理得:PC 2=PA ×PB ,∵ PC =4,PB =8, ∴ PA =2,∴ OA =OB =3,连接OC ,OC =3, 在直角三角形POC 中,利用面积法有, ∴ CE =OC×PC PO=125.故填:125.【答案】 2【考点】函数奇偶性的性质 函数奇偶性的判断【解析】 先把函数f(x)=|x|−sin x+1|x|+1变形为f(x)=1+−sin x|x|+1,令g(x)=−sin x|x|+1,可判断函数g(x)的奇偶性,据此找到g(x)的最大值与最小值之间的关系,在有f(x)=1+g(x),求出f(x)的最大值与最小值之和. 【解答】 解:函数f(x)=|x|−sin x+1|x|+1可变形为f(x)=1+−sin x|x|+1,令g(x)=−sin x|x|+1,则g(−x)=sin x |x|+1=−g(x),∴ g(x)为奇函数.设当x =a 时,g(x)有最大值g(a),则当x =−a 时,g(x)有最小值g(−a)=−g(a) ∵ f(x)=1+g(x),∴ 当x =a 时f(x)有最大值g(a)+1, 则当x =−a 时,f(x)有最小值−g(a)+1, 即M =g(a)+1,m =−g(a)+1, ∴ M +m =2. 故答案为:2. 【答案】 ③④ 【考点】命题的真假判断与应用 【解析】根据点A(a, b)与点B(1, 0)在直线3x −4y +10=0的两侧,我们可以画出点A(a, b)所在的平面区域,进而结合二元一次不等式的几何意义,两点之间距离公式的几何意义,及两点之间连线斜率的几何意义,逐一分析四个答案.可得结论. 【解答】解:∵ 点A(a, b)与点B(1, 0)在直线3x −4y +10=0的两侧, 故点A(a, b)在如图所示的平面区域内故3a −4b +10<0,即①错误;当a >0时,a +b >52,a +b 即无最小值,也无最大值,故②错误; 设原点到直线3x −4y +10=0的距离为d ,则d =√32+(−4)2=2,则√a 2+b 2>d =2,故③正确;当a >0且a ≠1,b >0时,b a−1表示点A(a, b)与B(1, 0)连线的斜率∵ 当a =0,b =52时,ba−1=−52,又∵ 直线3x −4y +10=0的斜率为34 故b a−1的取值范围为(−∞, −52)∪(34, +∞),故④正确;故答案为:③④三、解答题:本大题共6小题,共80分.解答应写出文字说明,演算步骤或证明过程. 【答案】(1)由图可知,A =1,最小正周期T =4×2=8. 由T=2πω=8,得ω=π4.又f(1)=sin (π4+φ)=1,且−π2<φ<π2, 所以π4+φ=π2,即φ=π4.所以f(x)=sin (π4x +π4).(2)因为f(−1)=0,f(1)=1,f(5)=−1所以M(−1, 0),N(1, 1),P(5, −1). 所以|MN|=√5,|PN|=√20,|MP|=√37. 由余弦定理得cos ∠MNP =2√5×√20=−35.因为∠MNP ∈[0, π),所以sin ∠MNP =45.【考点】由y=Asin (ωx+φ)的部分图象确定其解析式 【解析】(Ⅰ)利用最高点确定A 的值,利用周期,确定ω的值,利用最高点的坐标,确定φ的值,即可求函数f(x)的解析式;(Ⅱ)确定点M ,N ,P 的坐标,再利用余弦定理,即可求sin ∠MNP 的值. 【解答】(1)由图可知,A =1,最小正周期T =4×2=8. 由T =2πω=8,得ω=π4.又f(1)=sin (π4+φ)=1,且−π2<φ<π2, 所以π4+φ=π2,即φ=π4. 所以f(x)=sin (π4x +π4).(2)因为f(−1)=0,f(1)=1,f(5)=−1 所以M(−1, 0),N(1, 1),P(5, −1). 所以|MN|=√5,|PN|=√20,|MP|=√37. 由余弦定理得cos ∠MNP =2√5×√20=−35.因为∠MNP ∈[0, π),所以sin ∠MNP =45.【答案】 解:(1)甲、乙两人所付费用相同即为2,4,6元.… 都付2元的概率为P 1=14×12=18; 都付4元的概率为P 2=12×14=18; 都付6元的概率为P 3=14×14=116;故所付费用相同的概率为P =P 1+P 2+P 3=516.… (2)依题意,ξ的可能取值为4,6,8,10,12.… P(ξ=4)=18;P(ξ=6)=14×14+12×12=516;P(ξ=8)=14×14+12×14+12×14=516;P(ξ=10)=14×14+12×14=316; P(ξ=12)=14×14=116.故ξ的分布列为所求数学期望Eξ=4×18+6×516+8×516+10×316+12×116=152.…【考点】离散型随机变量的期望与方差 等可能事件的概率【解析】(1)甲、乙两人所付费用相同即为2,4,6元,求出相应的概率,利用互斥事件的概率公式,可求甲、乙两人所付租车费用相同的概率;(2)确定变量的取值,求出相应的概率,即可求得ξ的分布列与数学期望. 【解答】解:(1)甲、乙两人所付费用相同即为2,4,6元.… 都付2元的概率为P 1=14×12=18;都付4元的概率为P 2=12×14=18; 都付6元的概率为P 3=14×14=116;故所付费用相同的概率为P =P 1+P 2+P 3=516.… (2)依题意,ξ的可能取值为4,6,8,10,12.… P(ξ=4)=18;P(ξ=6)=14×14+12×12=516;P(ξ=8)=14×14+12×14+12×14=516;P(ξ=10)=14×14+12×14=316;P(ξ=12)=14×14=116. 故ξ的分布列为所求数学期望Eξ=4×18+6×516+8×516+10×316+12×116=152.…【答案】解:(1)∵ MB // NC ,MB ⊄平面DNC ,NC ⊂平面DNC ,∴ MB // 平面DNC .∵ 四边形AMND 为矩形,∴ MA // DN .又∵ MA ⊄平面DNC ,DN ⊂平面DNC ,∴ MA // 平面DNC . ∵ MA 、MB 是平面AMB 内的相交直线, ∴ 平面AMB // 平面DNC .又∵ AB ⊂平面AMB ,∴ AB // 平面DNC . …(2)∵ 平面AMND ⊥平面MBCN ,且平面AMND ⊥平面MBCN =MN ,DN ⊥MN , ∴ DN ⊥平面MBCN ,而MN ⊥NC ,故以点N 为坐标原点,NM 、NC 、ND 分别为x 轴、y 轴、z 轴,建立空间直角坐标系如图. 由已知得MC =2√3,∠MCN =30∘,易得MN =√3,NC =3. 则D(0, 0, 3),C(0, 3, 0),B(√3, 4, 0). ∴ DC →=(0, 3, −3),CB →=(√3, 1, 0).设平面DBC 的法向量m 1→=(x, y, z),则{m 1→⋅CB →=0˙,即{3y −3z =0√3x +y =0令x =−1,则y =z =√3,可得m 1→=(−1, √3, √3). 又∵ m 2→=(0, 0, 1)是平面NBC 的一个法向量, ∴ cos <m 1→,m 2→>=|m 1→|⋅|m 2→|˙=√217. 故所求二面角D −BC −N 的余弦值为√217.… 【考点】用空间向量求平面间的夹角 直线与平面平行的判定【解析】(1)由线面平行判定定理,可分别证出MB // 平面DNC 且MA // 平面DNC ,结合面面平行判定定理,得到平面AMB // 平面DNC ,结合AB ⊂平面AMB 可得AB // 平面DNC ;(2)根据面面垂直的性质定理,证出DN ⊥平面MBCN ,从而得到NM 、NC 、ND 两两互相垂直,因此以点N为坐标原点,建立空间直角坐标系如图.分别得到B 、C 、D 的坐标,从而得到向量DC →、CB →的坐标,利用垂直向量数量积为零建立方程组,解出平面DBC 的法向量m 1→=(−1, √3, √3),结合m 2→=(0, 0, 1)是平面NBC 的一个法向量,运用空间向量的夹角公式算出m 1→、m 2→夹角的余弦值为√217,即得二面角D −BC −N 的余弦值.【解答】解:(1)∵ MB // NC ,MB ⊄平面DNC ,NC ⊂平面DNC ,∴ MB // 平面DNC .∵ 四边形AMND 为矩形,∴ MA // DN .又∵ MA ⊄平面DNC ,DN ⊂平面DNC ,∴ MA // 平面DNC . ∵ MA 、MB 是平面AMB 内的相交直线, ∴ 平面AMB // 平面DNC .又∵ AB ⊂平面AMB ,∴ AB // 平面DNC . …(2)∵ 平面AMND ⊥平面MBCN ,且平面AMND ⊥平面MBCN =MN ,DN ⊥MN , ∴ DN ⊥平面MBCN ,而MN ⊥NC ,故以点N 为坐标原点,NM 、NC 、ND 分别为x 轴、y 轴、z 轴,建立空间直角坐标系如图. 由已知得MC =2√3,∠MCN =30∘,易得MN =√3,NC =3.则D(0, 0, 3),C(0, 3, 0),B(√3, 4, 0). ∴ DC →=(0, 3, −3),CB →=(√3, 1, 0).设平面DBC 的法向量m 1→=(x, y, z),则{m 1→⋅CB →=0˙,即{3y −3z =0√3x +y =0令x =−1,则y =z =√3,可得m 1→=(−1, √3, √3).又∵ m 2→=(0, 0, 1)是平面NBC 的一个法向量, ∴ cos <m 1→,m 2→>=|m 1→|⋅|m 2→|˙=√217. 故所求二面角D −BC −N 的余弦值为√217.… 【答案】(1)当M 的坐标为(0, −1)时,设过M 点的切线方程为y =kx −1, 由{x 2=4y y =kx −1,消y 得x 2−4kx +4=0,(1) 令△=(4k)2−4×4=0,解得:k =±1, 代入方程(1),解得A(2, 1),B(−2, 1),设圆心P 的坐标为(0, a),由|PM|=|PB|,得a +1=2,解得a =1, 故过M ,A ,B 三点的圆的方程为x 2+(y −1)2=4; (2)证明:设M(x 0, −1),由已知得y =x 24,y′=12x ,设切点分别为A(x 1, x 124),B(x 2, x 224),∴ k MA =x 12,k MB =x 22, 切线MA 的方程为y −x 124=x 12(x −x 1),即y =12x 1x −14x 12,切线MB 的方程为y −x 224=x 22(x −x 2),即y =12x 2x −14x 22,又因为切线MA 过点M(x 0, −1),所以得−1=12x 0x 1−14x 12,①又因为切线MB 也过点M(x 0, −1),所以得−1=12x 0x 2−14x 22,②所以x 1,x 2是方程−1=12x 0x −14x 2的两实根, 由韦达定理得x 1+x 2=2x 0,x 1x 2=−4, 因为MA →=(x 1−x 0, x 124+1),MB →=(x 2−x 0, x 224+1),所以MA →⋅MB →=(x 1−x 0)(x 2−x 0)+(x 124+1)(x 224+1)=x 1x 2−x 0(x 1+x 2)+x 02+x 12x 2216+14(x 12+x 22)+1=x 1x 2−x 0(x 1+x 2)+x 02+x 12x 2216+14[(x 1+x 2)2−2x 1x 2]+1,将x 1+x 2=2x 0,x 1x 2=−4代入,得MA →⋅MB →=0,则以AB 为直径的圆恒过点M . 【考点】 圆的标准方程 圆系方程【解析】(Ⅰ)当M 的坐标为(0, −1)时,设过M 切线方程为y =kx −1,与抛物线解析式联立,消去y 得关于x 的一元二次方程,根据题意得到根的判别式的值为0,求出k 的值,代入确定出A 与B 的坐标,设圆心P(0, a),由|PM|=|PB|,列出关于a 的方程,求出方程的解得到a 的值,确定出圆心坐标及半径,写出圆的标准方程即可; (Ⅱ)设M(x 0, −1),由已知抛物线解析式变形得y =x 24,求出导函数y′=12x ,设出切点A 与B 坐标分别为A(x 1, x 124),B(x 2, x 224),表示出切线MA 与切线MB 的方程,再由切线MA 与MB 过M ,将M 坐标分别代入得到两个关系式,x 1,x 2是方程−1=12x 0x −14x 2的两实根,利用韦达定理表示出两根之和与两根之积,再表示出两向量MA →与MB →,将表示出两根之和与两根之积代入计算MA →⋅MB →的值为0,即可得到以AB 为直径的圆恒过点M .【解答】(1)当M 的坐标为(0, −1)时,设过M 点的切线方程为y =kx −1, 由{x 2=4y y =kx −1,消y 得x 2−4kx +4=0,(1) 令△=(4k)2−4×4=0,解得:k =±1,代入方程(1),解得A(2, 1),B(−2, 1),设圆心P 的坐标为(0, a),由|PM|=|PB|,得a +1=2,解得a =1, 故过M ,A ,B 三点的圆的方程为x 2+(y −1)2=4; (2)证明:设M(x 0, −1),由已知得y =x 24,y′=12x , 设切点分别为A(x 1, x 124),B(x 2, x 224),∴ k MA =x 12,k MB =x 22, 切线MA 的方程为y −x 124=x 12(x −x 1),即y =12x 1x −14x 12, 切线MB 的方程为y −x 224=x 22(x −x 2),即y =12x 2x −14x 22,又因为切线MA 过点M(x 0, −1),所以得−1=12x 0x 1−14x 12,①又因为切线MB 也过点M(x 0, −1),所以得−1=12x 0x 2−14x 22,②所以x 1,x 2是方程−1=12x 0x −14x 2的两实根, 由韦达定理得x 1+x 2=2x 0,x 1x 2=−4, 因为MA →=(x 1−x 0, x 124+1),MB →=(x 2−x 0, x 224+1), 所以MA →⋅MB →=(x 1−x 0)(x 2−x 0)+(x 124+1)(x 224+1)=x 1x 2−x 0(x 1+x 2)+x 02+x 12x 2216+14(x 12+x 22)+1=x 1x 2−x 0(x 1+x 2)+x 02+x 12x 2216+14[(x 1+x 2)2−2x 1x 2]+1,将x 1+x 2=2x 0,x 1x 2=−4代入,得MA →⋅MB →=0, 则以AB 为直径的圆恒过点M . 【答案】解:(1)由已知,得x >0,f′(x)=a+1ax−1x 2−1=−x 2−(a+1a )x+1x 2=−(x−a)(x−1a)x 2.由f′(x)=0,得x 1=1a,x 2=a .因为a >1,所以0<1a<1,且a >1a.所以在区间(0, 1a )上,f′(x)<0;在区间(1a , 1)上,f′(x)>0. 故f(x)在(0, 1a )上单调递减,在(1a , 1)上单调递增.证明:(2)由题意可得,当a ∈[3, +∞)时,f′(x 1)=f′(x 2)(x 1,x 2>0,且x 1≠x 2). 即a+1ax 1−1x 12−1=a+1ax 2−1x 22−1,所以a +1a =1x 1+1x 2=x 1+x 2x 1x 2,a ∈[3, +∞).因为x 1,x 2>0,且x 1≠x 2,所以x 1x 2<(x 1+x 22)2恒成立, 所以1x1x 2>4(x1+x 2)2,又x 1+x 2>0,所以a +1a =x 1+x 2x 1x 2>4x1+x 2,整理得x 1+x 2>4a+1a,令g(a)=4a+1a,因为a ∈[3, +∞),所以a +1a 单调递增,g(a)单调递减,所以g(a)在[3, +∞)上的最大值为g(3)=65, 所以x 1+x 2>65.【考点】利用导数研究函数的单调性利用导数研究曲线上某点切线方程【解析】(1)求出f′(x),当x ∈(0, 1)时,解不等式f′(x)>0,f′(x)<0即可.(2)由题意可得,当a ∈[3, +∞)时,f′(x 1)=f′(x 2)(x 1,x 2>0,且x 1≠x 2),由此可得a +1a=x 1+x 2x 1x 2>4x 1+x2,从而x 1+x 2>4a+1a,只要求出4a+1a在[3, +∞)的最大值即可.【解答】解:(1)由已知,得x >0,f′(x)=a+1ax−1x 2−1=−x 2−(a+1a )x+1x 2=−(x−a)(x−1a)x 2.由f′(x)=0,得x 1=1a,x 2=a .因为a >1,所以0<1a<1,且a >1a.所以在区间(0, 1a )上,f′(x)<0;在区间(1a , 1)上,f′(x)>0. 故f(x)在(0, 1a )上单调递减,在(1a , 1)上单调递增.证明:(2)由题意可得,当a ∈[3, +∞)时,f′(x 1)=f′(x 2)(x 1,x 2>0,且x 1≠x 2). 即a+1ax 1−1x 12−1=a+1ax 2−1x 22−1,所以a +1a=1x 1+1x 2=x 1+x 2x 1x 2,a ∈[3, +∞).因为x 1,x 2>0,且x 1≠x 2,所以x 1x 2<(x 1+x 22)2恒成立, 所以1x1x 2>4(x1+x 2)2,又x 1+x 2>0,所以a +1a =x 1+x 2x 1x 2>4x1+x 2,整理得x 1+x 2>4a+1a,令g(a)=4a+1a,因为a ∈[3, +∞),所以a +1a单调递增,g(a)单调递减,所以g(a)在[3, +∞)上的最大值为g(3)=65, 所以x 1+x 2>65.【答案】 解:(1)由题意可得,创新数列为3,4,4,5,5的所有数列{C n }有两个,即数列3,4,1,5,2; 或数列3,4,2,5,1. …(2)存在数列{C n },使它的创新数列为等差数列. 设数列{C n }的创新数列为{e n },(n =1, 2, 3, 4…,m),因为e m 是c 1,c 2,c 3,…,c m 中的最大值,所以e m =m .由题意知,e k 为c 1,c 2,c 3,…c k 中最大值,所以,e k ≤e k+1,且e k ∈{1, 2, 3, ..., m}. 若{e n }为等差数列,设其公差为d ,则d =e k+1−e k ≥0且d ∈N .当d =0时,{e n }为常数列,又e m =m ,所以数列{e n }为m ,m ,…,m . 此时数列{C n }是首项为m 的任意一个符合条件的数列. … 当d =1时,因为e m =m ,所以数列{e n }为1,2,…,m . 此时,数列{c n }为1,2,3,…,m . …当d ≥2时,因为e m =e 1+(m −1)d ≥e 1+(m −1)2=2m −2+e 1,又m >3,e 1 为正整数,所以e m >m ,这与e m =m 矛盾,所以此时{e n }不存在,即不存在{C n }使得它的创新数列为公差d ≥2的等差数列.…综上,当数列{C n }为以m 为首项的任意一个符合条件的数列,或{C n }为数列1,2,3,…,m 时,它的创新数列为等差数列.… 【考点】等差数列的性质【解析】(1)由题意可得,创新数列为3,4,4,5,5的所有数列{C n}有两个.(2)存在数列{C n},使它的创新数列为等差数列.设数列{C n}的创新数列为{e n},若{e n}为等差数列,设其公差为d,经过检验,当d=0或1时,存在数列{C n},使它的创新数列为等差数列.【解答】解:(1)由题意可得,创新数列为3,4,4,5,5的所有数列{C n}有两个,即数列3,4,1,5,2;或数列3,4,2,5,1.…(2)存在数列{C n},使它的创新数列为等差数列.设数列{C n}的创新数列为{e n},(n=1, 2, 3, 4…,m),因为e m是c1,c2,c3,…,c m中的最大值,所以e m=m.由题意知,e k为c1,c2,c3,…c k中最大值,所以,e k≤e k+1,且e k∈{1, 2, 3, ..., m}.若{e n}为等差数列,设其公差为d,则d=e k+1−e k≥0且d∈N.当d=0时,{e n}为常数列,又e m=m,所以数列{e n}为m,m,…,m.此时数列{C n}是首项为m的任意一个符合条件的数列.…当d=1时,因为e m=m,所以数列{e n}为1,2,…,m.此时,数列{c n}为1,2,3,…,m.…当d≥2时,因为e m=e1+(m−1)d≥e1+(m−1)2=2m−2+e1,又m>3,e1为正整数,所以e m>m,这与e m=m矛盾,所以此时{e n}不存在,即不存在{C n}使得它的创新数列为公差d≥2的等差数列.…综上,当数列{C n}为以m为首项的任意一个符合条件的数列,或{C n}为数列1,2,3,…,m时,它的创新数列为等差数列.…。
