胡运权排队论习题解
胡运权运筹学第十一章习题解
11.1 某建筑工地每月需用水泥800t ，每t 定价2000元，不可缺货。
设每t 每月保管费率为0.2%，每次订购费为300元，求最佳订购批量。
解：每月需求量R=800t/月，每次订购费3003=C 元，货物单价k=2000元/t ，每t 每月的保管费%2.020001⨯=C =4元 则最佳定购量4.34648003002213*=⨯⨯==C R C Q11．2一汽车公司每年使用某种零件150000件，每件每年保管费0.2元，不允许缺货，试比较每次订购费为1000元或100元两种情况下的经济订货批量解: 类型 不允许缺货，补充时间极短根据题意知 R=150000件 1c =0.2 3c =1000或100（1） 当每次订购费为1000元时候的经济订货批量*t =R c c 132=150000*2.01000*2=151=3.65 Q *=R *t =150000*151=38729.83 (2) 当每次订购费为100元时候的经济订货批量*t =R c c 132=150000*2.0100*2=0.0816 Q *=R *t =150000*0.0816=12247.811.12某冬季商品每件进价25元，售价45元。
订购费每次20元，单位缺货费45元，单位存储费5元，期初无存货。
该商品的需求量r 的概率分布见表11-4。
解：25=K 1C =5 2C =45 203=C4.0)100(4.050205452545212====+-=+-r P C C K C该商品在冬季来临前应订购100件。
11.13某厂生产需要某种部件。
该部件外购价值有850元，订购费每次2825元。
若自产，每若选择外购策略时，若发生购物数少于实际需求量的情况，差额部分工厂将自产。
假定期初存货为零。
求工厂的订购策略。
2c =1250,1c =2825,k=850,1c =45N= (2c -k) / (2c + 1c )= (1250-850)/(1250+45)=400/1295=0.30订购90件。
清华大学《运筹学教程》胡运权主编课后习题答案
st
8x1 3x1
x2 x6
4x3 0
2 x5
10
x j 0（, j 1,,6）
基可行解
x1 x2 x3 x4 x5 x6 Z 0 3 0 0 3.5 0 3
0 0 1.5 0 8 0 3
0003500
page 10
0.7 0 0 0 2 2.2 2.2 10
5 13 April 2021
5 5 School of Management
运筹学教程
第一章习题解答
min Z 5x1 2x2 3x3 2x4
(2)
st
2x1x1 22x2x23xx33
4 x4 2 x4
7 3
x j 0, ( j 1,4)
x1 0 0 2/5
page 11 13 April 2021
基可行解
6 x2 2 x2
6 4
x1, x2 0
无穷多最优解，
x1
1, x2
1,Z 3
3是一个最优解
max Z 3x1 2x2
(2)
st.32xx11
x2 2 4x2 12
x1, x2 0
该问题无解
4
School of Management
运筹学教程
page 5 13 April 2021
a=3, j=5, k= -1.5
page 23 13 April 2021
23
School of Management
运筹学教程
第一章习题解答
1.9 若X(1)、X(2)均为某线性规划问题的
最优解，证明在这两点连线上的所有点也是
该问题的最优解。 max Z CT X
设X (1)和X (2)满足： AX b
运筹学胡运权 部分课后习题答案
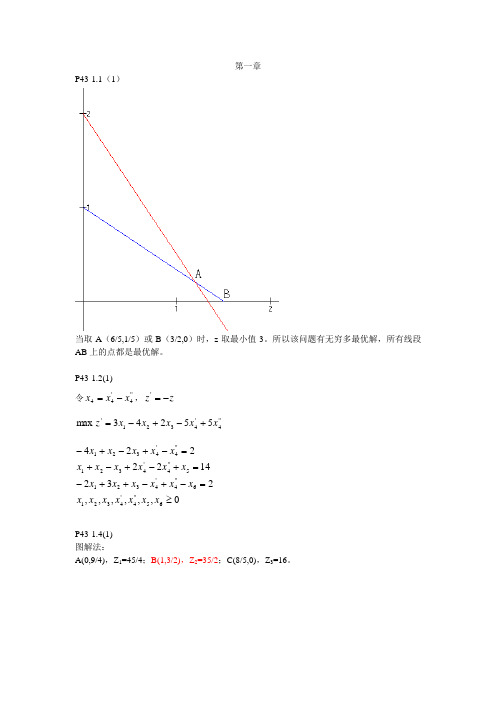
第一章P43-1.1（1）当取A （6/5,1/5）或B （3/2,0）时，z 取最小值3。
所以该问题有无穷多最优解，所有线段AB 上的点都是最优解。
P43-1.2(1)令''4'44x x x -=，z z -='''4'4321'55243max x x x x x z +-+-=,,,,,,232142222465''4'43216''4'43215''4'4321''4'4321≥=-+-++-=+-+-+=-+-+-x x x x x x x x x x x x x x x x x x x x x x x xP43-1.4(1) 图解法：A(0,9/4)，Z 1=45/4；B(1,3/2)，Z 2=35/2；C(8/5,0)，Z 3=16。
单纯形法：10 5 0 0C b X b b x1x2x3x4θ0 x39 3 4 1 0 30 x48 5 2 0 1 8/5δ10 5 0 00 x321/5 0 14/5 1 -3/5 3/210 x18/5 1 2/5 0 1/5 4δ0 1 0 -25 x23/2 0 1 5/14 -3/1410 x1 1 1 0 -1/7 2/7δ0 0 -5/14 -25/14依次相当于：原点；C；B。
P44-1.7(1)2 -1 2 0 0 0 -M -M -MC b X b b x1x2x3x4x5x6x7x8x9θ无界解。
两阶段法：阶段二：P45-1.10证明：CX (0)>=CX*，C*X*>=C*X (0) CX (0)-CX*+C*X*-C*X (0)>=0，即(C*-C)(X*-X (0))>=0。
P45-1.13设饲料i 使用x i （kg ），则543218.03.04.07.02.0m in x x x x x z ++++=s.t. 7001862354321≥++++x x x x x 305.022.05.054321≥++++x x x x x1008.022.05.054321≥++++x x x x x0,,,,54321≥x x x x x第二章P74-2.1(1)321532m ax y y y w ++=22321≤++y y y 243321≤++y y y 4334321=++y y y 无约束321,0,0y y y ≤≥P75-2.4(1),06353322232max 212121212121≥≥≤-≤+≤-≤++=y y y y y y y y y y y y w(2) (8/5,1/5)(3) 无穷多最优解。
胡运权运筹学第五版答案
胡运权运筹学第五版答案【篇一：运筹学基础及应用第四版胡运权主编课后练习答案】xt>习题一 p46 1.1 (a)412该问题有无穷多最优解，即满足4x1z?3。
6x26且0?x2?的所有?x1,x2?，此时目标函数值(b)用图解法找不到满足所有约束条件的公共范围，所以该问题无可行解。
1.2(a) 约束方程组的系数矩阵12a833106?403000200??0?1t最优解x??0,10,0,7,0,0?。
(b) 约束方程组的系数矩阵1a222314??2??最优解1.3(a)(1) 图解法11??2x??,0,,0?5?5?t。
最优解即为?3x14x295x12x28的解x31,2，最大值z352(2)单纯形法首先在各约束条件上添加松弛变量，将问题转化为标准形式 max z?10x1?5x2?0x3?0x4?3x1?4x2?x3?9s.t. ?5x12x2x48则p3,p4组成一个基。
令x1?x2?0得基可行解x??0,0,9,8?，由此列出初始单纯形表12。
??min?898,53?520，??min?2183,??142?2?新的单纯形表为1,20，表明已找到问题最优解x1?1, x2?32,x3?0 , x4?0。
最大值z*352(b) (1) 图解法6x1?2x2x1?x2?最优解即为?6x12x224x1?x2?5的解x73,22?，最大值z172(2) 单纯形法首先在各约束条件上添加松弛变量，将问题转化为标准形式 max z?2x1?x2?0x3?0x4?0x55x2?x3?15??s.t. ?6x1?2x2?x4?24xxx5125则p3，p4，p5组成一个基。
令x1?x2?0得基可行解x??0,0,15,24,5?，由此列出初始单纯形表12。
??min??,245?,??461?155,24,20，??min?3?32?2新的单纯形表为【篇二：运筹学基础及应用第四版胡运权主编课后练习答案】xt>习题一 p46 1.1 (a)41的所有?x1,x2?，此时目标函数值2该问题有无穷多最优解，即满足4x1?6x2?6且0?x2?z?3。
运筹学清华大学出版社胡运权着课后答案
�12 x1 � 3 x2 � 6 x3 � 3 x4 � 9
(1)
st
��8 ��3
x1 x1
� �
x2 x6
� 4 x3 �0
�
2 x5
� 10
�� x j � 0�, j � 1,� ,6�
min Z � 5 x1 � 2 x2 � 3 x3 � 2 x4
� x1 � 2 x2 � 3 x3 � 4 x4 � 7
运筹学教程�第二版� 习题解答
运筹学教程
1.1 用图解法求解下列线性规划问题。并指出问 题具有惟一最优解、无穷多最优解、无界解还是无可 行解。
min Z � 2 x1 � 3 x2 � 4 x1 � 6 x2 � 6
(1) st .�� 2 x1 � 2 x2 � 4 �� x1 , x2 � 0
Z
0
0.5
2
0
5
0
0
1
1
5
2/5
0
11/5
0
43/5
page 10 6 January 2011
School of Management
运筹学教程
1.4 分别用图解法和单纯形法求解下述线性规划 问题�并对照指出单纯形表中的各基可行解对应图解 法中可行域的哪一顶点。
max Z � 10 x1 � 5 x2 �3 x1 � 4 x2 � 9
max Z � x1 � x2 �6 x1 � 10 x2 � 120 (3) st.�� 5 � x1 � 10 �� 5 � x2 � 8
max Z � 3x1 � 2 x2 �2 x1 � x2 � 2
(2) st.��3x1 � 4 x2 � 12 �� x1, x2 � 0
胡运权排队论习题解
解：该系统属于 M/M/1 模型
旧装置各参数计算：
90 / h 3600 94.7
38 90 0.95
94.7
L 0.95 19 1 0.05
Lq L 19 0.95 18.05 P0 1 0.05
采用新装置各参数计算：
' 90 / h ' 3600 120
)2
[1
cN c (N
c)(1
c )cN c ]
0.42 0.60 [1 0.651 (5 1)(1 0.6) 0.651] 0!(1 0.6)
0.6962
Ls
Lq
e
0.6962
4.8 10
1.1762,
(3)系统的满意率为p5 0.04.
(4)服务台降低服务强度，原因是因为系统中没有顾客的概率比重较大.
10.8 在第10.1题中，如服务时间服从正态分布，数学期望仍然为6分钟， 方差 2 1，求店内顾客数的期望值。
8
解 ＝4人 / 小时，E(T ) 1（小时），＝ 4 ，Var[T ] 1
10
10
8
Ls
2
2Var[T ] 2(1 )
4 10
4 10
2
16
1 8
＝11.
2（1 4 ） 5
解：该系统为（M / M /1/ / ）模型， 3， 60 6. 10
(1)p0
1
1
3 6
1； 2
(2)p4
(1
)4
(1
1)( 1)4 22
1； 32
(3)1
p0
1
1 2
1； 2
(4)Ls
3 63
1(人)；
《运筹学(胡运权)》第五版课后习题答案
X33.000000 0.000000
X1,X2,X3 0.000000 0.000000
ROW SLACK OR SURPLUS DUAL PRICES
2) 0.000000 0.200000
3) 0.000000 0.600000
4) 0.0000000.000000
6) 0.0000000.008571
7) 0.000000 0.110000
8) 0.000000 -1.500000
NO. ITERATIONS= 6
计算lindo截屏
2.1a:
对偶问题为：
maxz=2y1+3y2+5y3
s.t.
y1+2y2+y3≤2
3y3+y2+4y3≤2
4y1+3y2+3y3=4
A1 1200.000000 0.000000
A2 0.000000 9.640000
A3 285.714294 0.000000
B3 10000.0000000.000000
C1 0.000000 15.900000
B1 0.000000 0.230000
A4 342.857147 0.000000
X2 1.000000 2.000000 INFINITY
X3 4.000000 1.000000 1.500000
X1,X2,X3 0.000000 0.000000 INFINITY
RIGHTHAND SIDE RANGES
ROW CURRENT ALLOWABLE ALLOWABLE
RHS INCREASE DECREASE
二三版兼用《运筹学教程》胡运权主编课后习题答案(第三章)
城市
电站
1
2
3
Ⅰ
15
18
22
Ⅱ
21
25
16
第三章习题解答
习题3.12的解答
城市 城市
电站
1-1
城市 1-2
城市2
城市 3-1
城市 3-2
产量
Ⅰ
150 15
15 250 18
22
22 400
Ⅱ
140 21
第三章习题解答
表3-35
食品厂
面粉厂
1
2
3
产量
Ⅰ
3 10
2 20
Ⅱ
4 11
8 30
Ⅲ
8 11
4 20
销量
15 25 20
第三章习题解答
习题3.10的解答
食品厂 面粉厂
Ⅰ Ⅱ Ⅲ 销量
1
3 15 4
8 15
2
10 5 11 20 11 25
3
20 2 8 4
20
4
0 10 0
0 10
产量
20 30 20
B3
B4 产量
A1 A2 A3 销量
3
7
6
45
2
4
3
22
4
3
8
56
3
3
2
2
第三章习题解答
习题3.9的解答
销地
产地
B1 B2 B3 B4 B5 产量A1源自33 7 6 24 0 5
A2
2 4 23 2 0 2
A3 销量
4 33 8 5 30 6 33223
第三章习题解答
3.10 某市有三个面粉厂，它们供给三个面食加工 厂所需的面粉。各面粉厂的产量、各面食加工厂加工 面粉的能力、各面食加工厂和各面粉厂之间的单位运 价，均表示于表3-35中。假定在第1，2和3面食加工厂 制作单位面粉食品的利润分别为12元、16元和11元， 试确定使总效益最大的面粉分配计划(假定面粉厂和面 食加工厂都属于同一个主管单位)。
胡运权习题及答案习题解答(6)
习题解答（6）1． 证明：序列7、6、5、4、3、2不可能是某个简单图的次的序列。
证明：由定理1有 q v d v v 2)(=∑∈，而在此序列中，∑∈vv v d )(27=为奇数，所以此序列不可能是某个简单图的次的序列。
2． 已知九个人921,,v v v 中1v 和两个人握过手，32,v v 各和四个人握过手，7654,,,v v v v 各 和五个人握过手，98,v v 各和六个人握过手，证明从这九个人中一定可以找出三个人互相握过手。
证明：该问题可以表述为一个9点（代表9个人）的简单图问题，不存在重复边和环，则由题意知，5)()()()(,4)()(,2)(7654321=======v d v d v d v d v d v d v d ， .6)()(98==v d v d 其中],[j i v v 表示i v 和j v 握过手。
对9v 而言，因,6)(9=v d 所以7654,,,v v v v 中至少有两点存在与9v 的连线。
设该两点为4v 和5v ，假设4v 和9v 相联的其它5点之间无边，则,358)(4=-≤v d 这与已知 5)(4=v d 相矛盾。
故假设不成立，即4v 与上述5点间必存在至少两条边，设其中一点为k v ，则k v ， 94,v v 两两相连，即存在三人互相握过手。
3．已知下图表示7个城市间抑修建一条连接各个城市的通信线路，各边的权数表示两个城市之间线路的修建费。
利用“丢边破圈法”，求连接个城市通信线路最小修建费用方案。
F 50 EB 23 C解：在上图中依次去掉GD （6），GC （52），EF （50），AF （48），BG （46）AG （45）各边后，即求得最小生成树T，如下图所示，T中各边权数之和为219。
F E39 42 40A G D37 3823B C。
胡运权《运筹学教程》习题答案(第一章)[1]
![胡运权《运筹学教程》习题答案(第一章)[1]](https://img.taocdn.com/s3/m/5266ca4b767f5acfa1c7cd73.png)
第一章习题解答1.1 用图解法求解下列线性规划问题。
并指出问题具有惟一最优解、无穷多最优解、无界解还是无可行解。
+=32min 21x x Z +=23max 21x x Z ⎪⎩⎪⎨⎧≥≥+≥+0,422664.)1(212121x x x x x x st ⎪⎩⎪⎨⎧≥≥+≤+0,124322.)2(212121x x x x x x st ⎪⎩⎪⎨⎧≤≤≤≤≤++=85105120106.max )3(212121x x x x st x x Z ⎪⎩⎪⎨⎧≥≤+−≥−+=0,23222.65max )4(21212121x x x x x x st x x Z 第一章习题解答无穷多最优解，,422664.32min )1(21212121⎪⎩⎪⎨⎧≥≥+≥++=x x x x x x st x x Z 是一个最优解3,31,121===Z x x 该问题无解⎪⎩⎪⎨⎧≥≥+≤++=0,124322.23max )2(21212121x x x x x x st x x Z 第一章习题解答85105120106.max )3(212121⎪⎩⎪⎨⎧≤≤≤≤≤++=x x x x st x x Z 唯最优解16,6,1021===Z x x 唯一最优解，该问题有无界解⎪⎩⎪⎨⎧≥≤+−≥−+=0,23222.65max )4(21212121x x x x x x st x x Z 第一章习题解答1.2 将下述线性规划问题化成标准形式。
1422245243min )1(432143214321⎪⎪⎧≤+−+−=−+−+−+−=x x x x x x x x x x x x Z .,0,,23243214321⎪⎪⎩⎨≥≥−++−无约束x x x x x x x x st ⎪⎩⎪⎨⎧≥≤≤−+−=++−+−=无约束321321321321,0,0624322min )2(x x x x x x x x x st x x x Z 第一章习题解答.2321422245243min )1(4321432143214321⎪⎪⎪⎨⎧≥−++−≤+−+−=−+−+−+−=x x x x x x x x x x x x st x x x x Z ,0,,4321⎪⎩≥无约束x x x x ⎪⎪⎩⎪⎪⎨⎧≥=−+−++−=+−+−+=−+−+−+−+−=0,,,,,232142222455243max 64241321642413215424132142413214241321x x x x x x x x x x x x x x x x x x x x x x x st x x x x x Z 第一章习题解答⎪⎪⎨⎧≥≤≤−+−=++−+−=无约束321321321321,0,0624322min)2(x x x x x x x x x st x x x Z ⎩⎪⎩⎪⎨⎧≥=++−+=−++−+−+=0,,,,6243322max 43231214323121323121323121x x x x x x x x x x x x x x st x x x x Z第一章习题解答634334max )3(3212121⎪⎪⎧=−+=++=x x x x x st x x Z 517,0,1,59,524,,1,0424321421=====⎪⎪⎩⎨=≥=++Z x x x x j x x x x j 该题是唯一最优解：）（"第一章习题解答⎪⎧≤++−≤++++=151565935121510max 321321x x x x x x x x x Z 该题无可行解。
胡运权运筹学第五版第一章习题讲解
1.3 答案：
●单纯形法：
Cj CB 0 0 基 x3 x4 Cj-Zj 0 x3
10
x1
Cj-Zj
8/5
1
0
2/5
1 1
0
0 5/14
1/5
-2 -3/14
5
x2
3/2
0
10
x1
Cj-Zj
1
1
0
0
0
-1/7
-5/14
2/7
-25/14
Return
课后题答案
z' -3x1 x 2 'x 2 ' '-2x 3 '0x 4 0x 5 - Mx6 - Mx7
台时 限制 6000 1000 0 4000 7000 4000
单位台 时费用 0.05 0.03 0.06 0.11 0.05
6 4 7 0.25 0.36 0.25 0.44 0.25 0.35
6 4 7 0.21 0.36 0.21 0.44 0.21 0.77
8
8 11
0.5 0.48
0.27 0.48
课后题答案
1.1（a）答案： 该问题有无穷多最优解。 取特殊值：(1.5,0) 计算目标函数最优值 得:min z=3。
1.1（a）
1.1（b）答案： 由图可知：该Lp问题没 有可行域，即可得出： 该问题无可行解
1.1(b)
Return
课后题答案
1.2（b）答案：
基解 基
x1 P2 P3 P4 P3 -4 2/5 -113 ) 10 x211 6000 7( x x x ) 9 x 12 x 121 122 123 221 322 10000 6( x111 x121 ) 8( x211 x221 ) 4000 s.t. 4( x112 x122 ) 11x322 7000 7( x113 x123 ) 4000 x111 , x112 , x113 , x121 , x122 , x123 , x211 , x221 , x322 0
二三版兼用运筹学教程胡运权主编课后习题答案第七章课件
假定每年只能投资一次，每次1 000万元(有多余资
金也不使用)，试给出三年末期望总资金最大的投资
策略。
投资
回收
概率
0
0.4
A
2000
0.6
1000
0.9
B
2000
0.1
第七章习题解答
解：第一年投资A的期望值为1200万元；投资B 的期望值为1100，故应该投资A，获利200万元。第 二年还应该投资A，投资A的期望值为1200万元，因 无法投资造成的损失为0.4*200=80万元，获利120万 元。第三年还应该投资A，投资A的期望值为1200万 元，因无法投资造成的损失为0.4*200=80万元，获 利120万元。这样三年都应该投资A，期望获利440万 元。
存。最需小求量费d用k 为33500。45 40 30
单位订货费用ck 850 850 775 825
单位存储费用pk 35 20
40
30
第七章习题解答
7.13 某罐头制造公司在近5周内需
要—次性地购置一批原料，估计未来5周
内价格有波动，其浮动价格及概率如表
7购-2这4所批示原．料批试价单求价格各的周数表的7学-2采4期购望策值概略率最，小使。采
40
2
12
0
18
30
25
3
23
9
0
5
10
4
34
32
4
0
8
5
45
27
11
10
0
第七章习题解答
7.5 为保证某设备正常运转，需对串联工作的三种不同 零件Al，A2，A3，分别确定备件数量。假设增加备用零件 的数量，可提高设备正常运转的可靠性，但费用要增加， 而总投资额为8千元。备用零件数与它的可靠性和费用关系 如表7-2l所示，求Al，A2，A3的备用零件数量各为多少时， 可使设备运转的可靠性最高。
胡运权运筹学第七章习题解
解：设阶段变量: k=1,2,3状态变量: 第k 个月初的库存量 决策变量: 第k 个月的生产量 状态转移方程: 阶段指标:由于在4月末, 仓库存量为0, 所以对于k=4阶段来说有两种决策：5+4=9 40x4()f x =1 41x对K=3 334()54()f x x f xK=2解得: 第一个月生产500份, 第二个月生产600份, 第三个月生产0份, 第四个月生产0份。
7.4某公司有资金4万元, 可向A, B, C三个项目投资, 已知各项目不同投资额的相应效益值如表7-20所示, 问如何分配资金可使总效益最大。
表7-20解：设阶段变量k, , 每一个项目表示一个阶段;状态变量Sk, 表示可用于第k阶段及其以后阶段的投资金额；决策变量Ｕk, 表示在第k阶段状态为Sk下决定投资的投资额；决策允许集合: 0≤Ｕk≤Sk状态转移方程: Sk+1=Sk-Ｕk;阶段指标函数: V k(SkＵk)；最优指标函数: fk(Sk)=max{ V k(SkＵk)+ fk+1(Sk+1)}终端条件: f4(x4)=0；K=4, f4(x4)=0k=3, 0≤Ｕ3≤S3k=2, 0≤Ｕ2≤S2k=1, 0≤Ｕ1≤S1所以根据以上计算, 可以得到获得总效益最大的资金分配方案为（1, 2, 1）.解: 设第k阶段的状态为Sk；第k阶段决定投入的备件为Xk;Ck(Xk)为第k阶段选择k个零件的费用；Rk(Xk)为第k个阶段选择k个零件的可靠性。
状态转移方程为: Sk+1=Sk- Ck(Xk)递退方程:114431()max{()()}()1()(1)k k K k k k K k K i i k f s R x f s f s C x S C =+=+⎧⎪=⎪⎪=⎨⎪⎪≤-⎪⎩∑所以有上可知当A 1；A 2；A 3；分别为k=1;k=2;k=3时S 1=8; S 2=5,6,7; S 3=1,2,3,4;由上表可知, 最优解的可靠性为0.042；此时X1=1；X2=1；X3=3。
胡运权运筹学第五版答案
胡运权运筹学第五版答案【篇一：运筹学基础及应用第四版胡运权主编课后练习答案】xt>习题一 p46 1.1 (a)412该问题有无穷多最优解，即满足4x1z?3。
6x26且0?x2?的所有?x1,x2?，此时目标函数值(b)用图解法找不到满足所有约束条件的公共范围，所以该问题无可行解。
1.2(a) 约束方程组的系数矩阵12a833106?403000200??0?1t最优解x??0,10,0,7,0,0?。
(b) 约束方程组的系数矩阵1a222314??2??最优解1.3(a)(1) 图解法11??2x??,0,,0?5?5?t。
最优解即为?3x14x295x12x28的解x31,2，最大值z352(2)单纯形法首先在各约束条件上添加松弛变量，将问题转化为标准形式 max z?10x1?5x2?0x3?0x4?3x1?4x2?x3?9s.t. ?5x12x2x48则p3,p4组成一个基。
令x1?x2?0得基可行解x??0,0,9,8?，由此列出初始单纯形表12。
??min?898,53?520，??min?2183,??142?2?新的单纯形表为1,20，表明已找到问题最优解x1?1, x2?32,x3?0 , x4?0。
最大值z*352(b) (1) 图解法6x1?2x2x1?x2?最优解即为?6x12x224x1?x2?5的解x73,22?，最大值z172(2) 单纯形法首先在各约束条件上添加松弛变量，将问题转化为标准形式 max z?2x1?x2?0x3?0x4?0x55x2?x3?15??s.t. ?6x1?2x2?x4?24xxx5125则p3，p4，p5组成一个基。
令x1?x2?0得基可行解x??0,0,15,24,5?，由此列出初始单纯形表12。
??min??,245?,??461?155,24,20，??min?3?32?2新的单纯形表为【篇二：运筹学基础及应用第四版胡运权主编课后练习答案】xt>习题一 p46 1.1 (a)41的所有?x1,x2?，此时目标函数值2该问题有无穷多最优解，即满足4x1?6x2?6且0?x2?z?3。
清华大学《运筹学教程》胡运权主编课后习题答案(第一章)
2)c=0
3)c>0
d<0 d=0 d>0
0
c 3 d 4
A1点 A1点 A3点
A2A3线段
3 c 5 4 d 2
c 5 d 2 c 5 d 2
c 3 d 4
A2点
A1A2线段 A1点
l.6 考虑下述线性规划问题：
max Z c1 x1 c2 x2 a11 x1 a12 x2 b1 st .a21 x1 a22 x2 b2 x1 , x2 0
-1
x2
0
x3
0
x4
-M
x5
-M
x6
CB
xB
x5
x6
x4
i
-M -M 0
3 6 4
[3] 4 1
1 3 2
0 -1 0
0 0 1
1 0 0
0 1 0 0
1 3/2 4 3 6/5 9/5
cj zj
7M-4
1 2 3 1 0 0 0
4M-1
1/3 [5/3] 5/3
5M/3+1/3
-M
0 -1 0 -M
0
0 0 1 0
0
1/3 -4/3 -1/3
-7M/3+4/3
-4 -M 0
x1
0
1 0 0
x6
x4
cj zj
cj
x6
是否基 可行解
Z
(x1,x2,x3)
(x1,x2,x4) (x1,x2,x5) (x1,x2,x6)
0
0 0 7/4
61/3
10 3 -4
-7/6
0 0 0
胡运权排队论习题解
胡运权排队论习题解10.1某修理店只有一个修理工人, 来修理的顾客到达次数服从普阿松分布,平均每小时3人,修理时间服从负指数分布,平均需10分钟, 求(1) 修理店空闲时间概率; (2) 店内有4个顾客的概率; (3) 店内至少有一个顾客的概率; (4) 在店内顾客平均数; (5) 等待服务的顾客平均数; (6) 在店内平均逗留时间; (7) 平均等待修理(服务)时间;(8) 必须在店内消耗15分钟以上的概率.04440s q s q 60M /M /1//3 6.1031(1)p 1162111(2)p (1)(1)()223211(3)1p 1223(4)L 1()631312(5)L ()632111(6)()633112(7)()636(8)1-F()W W λμρρρλμλρλμλμλρμλω∞∞====-=-==-=-=-=-====--⋅===--===--===--解：该系统为（）模型，，；；；人；人；小时；小时；1515-(6-3)--(-)6020eee .μλω⨯===11(1)(2)(3)23211(4)(5)2211(6)(7)(8)3615.15-20答：修理店空闲时间概率为；店内有三个顾客的概率为；店内至少有一个顾客的概率为；店内顾客平均数为1人；等待服务顾客平均数为人；在店内平均逗留时间分钟；平均等待修理时间为分钟；必须在店内消耗分钟以上的概率为e10.22015(1)(2)(3)(4) 1.25M /M /1.603(/20λ==设有一单人打字室，顾客的到达为普阿松流，平均到达时间间隔为分钟，打字时间服从指数分布，平均时间为分钟，求顾客来打字不必等待的概率；打字室内顾客的平均数；顾客在打字室内平均逗留时间；若顾客在打字室内的平均逗留时间超过小时，则主人将考虑增加设备及打字员，问顾客的平均到达概率为多少时，主人才会考虑这样做？解：该题属模型人小时0s s s 60)4(/).1531(1)p 11443(2)L 3()4311(3)1()431(4)1.2511.25 3.23.230.2(/).4W W μρλμλμλμλλλ===-=-====--===--=>-≥>-=-，人小时；人；小时；；，，人小时1(1)(2)3(3)41(4)0.2/.答：顾客来打字不必等待的概率为；打字室内顾客平均数为人；顾客在打字室内平均逗留时间为小时；平均到达率为人小时时，店主才会考虑增加设备及打字员 10.3 汽车按平均90辆/h 的poission 流到达高速公路上的一个收费关卡，通过关卡的平均时间为38s 。
运筹学(胡运权版)第三章运输问题课后习题答案
P66： 8.某部门有3个生产同类产品的工厂（产地），生产的产品由4个销售点出售，各工厂A 1， A 2，A 3的生产量、各销售点B 1，B 2，B 3，B 4的销售量（假定单位为t ）以及各工厂到销售点的单位运价（元/t ）示于下表中，问如何调运才能使总运费最小？解：一、该运输问题的数学模型为：可以证明：约束矩阵的秩为r (A) = 6. 从而基变量的个数为 6.34333231242322213141141312116115893102114124min x x x x x x x x x x x x x c z i j ij ij +++++++++++==∑∑==⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎨⎧==≥=++=++=++=++=+++=+++=+++4,3,2,1;3,2,1,01412148221016342414332313322212312111343332312423222114131211j i x x x x x x x x x x x x x x x x x x x x x x x x x ij 111213142122232431323334x x x x x x x x x x x x 712111111111111111111111111⨯⎛⎫ ⎪⎪⎪ ⎪⎪⎪ ⎪⎪ ⎪⎝⎭二、给出运输问题的初始可行解（初始调运方案）1. 最小元素法思想：优先满足运价（或运距）最小的供销业务。
其余（非基）变量全等于零。
此解满足所有约束条件，且基变量（非零变量）的个数为6（等于m+n-1=3+4-1=6).总运费为（目标函数值） ,1013=x ,821=x ,223=x ,1432=x ,834=x ,614=x ∑∑===3141i j ij ij x c Z 246685143228116410=⨯+⨯+⨯+⨯+⨯+⨯=2. 伏格尔（Vogel)法伏格尔法的基本思想：运输表中各行各列的最小运价与次小运价之差值（罚数）应尽可能地小。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
60 3(人 / 小时)， 60 4(人 / 小时).
20
15
(1)p0
1
1
3 4
1； 4
(2)Ls
4
3 3
3(人)；
(3)Ws
1
1 43
1(小时)；
(4)
Ws
1
1.25；
1 1.25， 3.2，3.2 3 0.2(人 / 小时). 4
答：(1)顾客来打字不必等待的概率为 1；(2)打字室内顾客平均数为3人；(3)顾客在 4
Lq ＝>5 满足这个条件。但是还有一个条件是采用新装置后要求新系统中关卡空闲时间不超
过 10％，而经计算 P0 ' 0.25 即新系统的空闲率为 25％超出了要求，所以采用新装置是不
合算的。
某车间的工具仓库只有一个管理员，平均有 4 人/h 来令工具，到达过程为 Poisson 流；领 工具的时间服从负指数分布，平均为 6min。由于场地限制，仓库内领工具的人最多不能超 过 3 人，求： （1）仓库内没有人领工具的概率；
15pn
385
v1.0 可编辑可修改
(4)服务台降低服务强度，原因是因为系统中没有顾客的概率比重较大.
当＝15，＝10时，＝1.5.
(1)有效到达率e (1 pN ) 15 (1 0.37) 9.45,
C
(1
pN
)
15 10
(1
0.37)
0.945;
服务台的服务强度为
(2)系统中平均顾客数Ls
（2）增加 1 个工人后，此系统变成 M/M/2 排队系统
c
c
6 26
0.5
1,
6 6
1,
pn
2
n2
1 ccnc
n
p0
1
p0
p1.
p0
c1 k0
1 k !
k
11
c! 1 c
c
1
0
1
1 2
1
1 0.5
1
1 1
1 2
1 0.5
1
1 3
,
p1
v1.0 可编辑可修改
胡运权排队论习题解
某修理店只有一个修理工人, 来修理的顾客到达次数服从普阿松分布,平均每小时 3 人,
修理时间服从负指数分布,平均需 10 分钟, 求
(1) 修理店空闲时间概率;
(2) 店内有 4 个顾客的概率;
(3) 店内至少有一个顾客的概率;
(4) 在店内顾客平均数;
(5) 等待服务的顾客平均数;
答：（1）仓库内没有人领工具的概率为 3 ；（2）仓库内领工具的工人的平均数为 2 人；
5
3
（3）排队等待工具的工人的平均数为 4 人；（4）工人在系统中的平均花费时间为 1 小时；
15
6
（5）工人平均排队时间为 1 小时。 15
10．6 在第题中，若顾客平均到达率增加到每小时 6 人，仍为普阿松流，服务时间不变，这 时增加了一个工人。
2
32
有一个顾客的概率为 1 ；(4)店内顾客平均数为1人；(5)等待服务顾客平均数为 1 人；
2
2
(6)在店内平均逗留时间1 分钟；(7)平均等待修理时间为 1 分钟；(8)必须在店内
3
6
消耗15分钟以上的概率为e-1250 .
10.2设有一单人打字室，顾客的到达为普阿松流，平均到达时间间隔为20分钟，
解：该系统属于 M/M/1/3 模型
4
60 10 6
4 2 10 5
（1） o=1 1 2 3 55
2
(2) L 5 2 （人） 1 3 3
5
(3) Lq L 2 2 4 （人） 3 5 15
2
(4)W L 3 1 （小时） 46
(5)W Lq 4 1 1 （小时） 15 4 15
解：因为核对申请书中的每一张表格的时间服从 k 60 的负指数分布，则依次检查 8 张表
格，即一份申请书的时间服从爱尔朗分布，所以本题可以看成是一个 M/Ek/1/∞/∞模型
且 6 ，E(Ek)=1/μ=2/15,D(Ek)=1/(kμ2)=1/45, 0.8
1) 办事员空闲的概率为 P0 1 0.2
(4)Ls
ቤተ መጻሕፍቲ ባይዱ
3 63
1(人)；
(5)Lq
1 3 2 63
1 2
(人)；
(6)Ws
1
1 63
1 (小时)； 3
1
(7)Wq
2 63
1 6
(小时)；
(8)1-F()
e-( - )
-(6-3)15
e 60
- 15
e 20 .
379
v1.0 可编辑可修改
答：(1)修理店空闲时间概率为 1 ；(2)店内有三个顾客的概率为 1 ；(3)店内至少
2)
Lq
2 2 2 （2 1- ）
（36 / 45） 0.64 2 0.2
3.6
L Lq 3.6 0.8 4.4
Wq Lq 3.6 0.6 6
10.8 在第10.1题中，如服务时间服从正态分布，数学期望仍然为6分钟， 方差 2 1，求店内顾客数的期望值。
8
解 ＝4人 / 小时，E(T ) 1（小时），＝ 4 ，Var[T ] 1
10
10
8
Ls
2
2Var[T ] 2(1 )
4 10
4 10
2
16
1 8
＝11.
2（1 4 ） 5
381
v1.0 可编辑可修改
（2）仓库内领工具的工人的平均数； （3）排队等待领工具的工人的平均数； （4）工人在系统中的平均花费时间； （5）工人平均排队时间。
解：该系统属于 M/M/1/3 模型
4 60 10
6 4 2
10 5
（1）
p0
=
1 1 4
1 2
5
1 (2 )4
5
0.6
采用新装置各参数计算：
' 90 / h ' 3600 120
30 ' 90 0.75
120 L' 0.75 3
1 1 0.75 Lq' L 3 0.75 2.25 P0 ' 1 0.25
分析：因为采用新装置后要求原系统中等待的汽车平均数超过 5 辆为合算，经计算原系统的
（1） 根据 / 的值说明增加工人的原因；
383
v1.0 可编辑可修改
（2） 增加工人后求店内空闲概率，店内有 2 人或更多顾客（即工人繁忙）的概率。
（3） 求 Ls , Lq ,Wq ,Ws .
解 （1） 6人/小时， 6人 小时，因为 c＝1， ，意味着系统的流入量等于流
出量，系统没有空闲时间。所以要增加工人。
打字室内平均逗留时间为1小时；(4)平均到达率为0.2人 / 小时时，店主才会考
虑增加设备及打字员.
汽车按平均 90 辆/h 的 poission 流到达高速公路上的一个收费关卡，通过关卡的平均时间
为 38s。由于驾驶人员反映等待时间太长，主管部门打算采用新装置，使汽车通过关卡的平
均时间减少到平均 30s。但增加新装置只有在原系统中等待的汽车平均数超过 5 辆和新系统
（4）服务台应从那些方面改进工作理由是什么
解 当＝6，＝10时,有
pn p5 0.04,
0.6
(1).有达到效率e (1 p5 ) 6(1 0.04) 5.76 服务台的服务强度
6
C
(1
pN
) 10
(1
0.04)
0.6 0.96 0.576
(2)系统中平均顾客数Ls
Lq
e
打字时间服从指数分布，平均时间为15分钟，求
(1)顾客来打字不必等待的概率；
(2)打字室内顾客的平均数；
(3)顾客在打字室内平均逗留时间；
(4)若顾客在打字室内的平均逗留时间超过1.25小时，则主人将考虑增加设备
及打字员，问顾客的平均到达概率为多少时，主人才会考虑这样做？
解：该题属M / M /1模型.
中关卡空闲时间不超过 10％时才是合算的。根据这一要求，分析新装置是否合算。
380
解：该系统属于 M/M/1 模型
v1.0 可编辑可修改
旧装置各参数计算：
90 / h 3600 94.7
38 90 0.95
94.7 L 0.95 19
1 0.05 Lq L 19 0.95 18.05 P0 1 0.05
1
1
1
p0
1
1 3
1, 3
故
pn
2
1
p0
p1
1
1 3
1 3
1. 3
（3）
pc
p2
1
2
2
p0
1 1 1 23
1, 6
Lq
c
1 c 2
pc
0.5
1 0.52
1 6
0.5 0.52
1 6
1 3
Ls
Lq
1 3
1
4 3
,
Ws
Ls
4/3 6
2 小时， 9
Wq＝
Lq
＝1/ 3＝ 1 6 18
Lq
e
,
Lq
p0
(c
c1 1)!(c
p)2
[1
Nc c
(N
c)(1
c )cN c ]
0.05
(1
1.52 1.5)2
[1
1.551
(5
1)(1
1.5)
1.551