教材第七章习题解答
高鸿业主编《西方经济学》第五版课后习题答案 带图详解 完整版第七章 习题答案 (14)
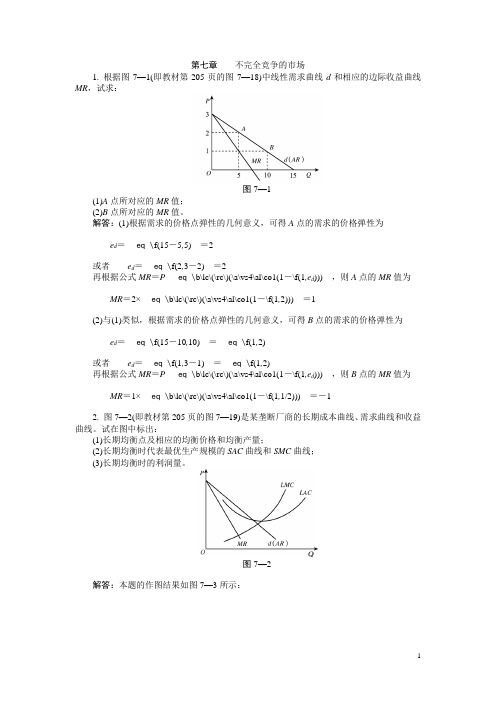
第七章不完全竞争的市场1. 根据图7—1(即教材第205页的图7—18)中线性需求曲线d和相应的边际收益曲线MR,试求:图7—1(1)A点所对应的MR值;(2)B点所对应的MR值。
解答:(1)根据需求的价格点弹性的几何意义,可得A点的需求的价格弹性为e d=eq \f(15-5,5)=2或者e d=eq \f(2,3-2)=2再根据公式MR=P eq \b\lc\(\rc\)(\a\vs4\al\co1(1-\f(1,e d))),则A点的MR值为MR=2×eq \b\lc\(\rc\)(\a\vs4\al\co1(1-\f(1,2)))=1(2)与(1)类似,根据需求的价格点弹性的几何意义,可得B点的需求的价格弹性为e d=eq \f(15-10,10)=eq \f(1,2)或者e d=eq \f(1,3-1)=eq \f(1,2)再根据公式MR=P eq \b\lc\(\rc\)(\a\vs4\al\co1(1-\f(1,e d))),则B点的MR值为MR=1×eq \b\lc\(\rc\)(\a\vs4\al\co1(1-\f(1,1/2)))=-12. 图7—2(即教材第205页的图7—19)是某垄断厂商的长期成本曲线、需求曲线和收益曲线。
试在图中标出:(1)长期均衡点及相应的均衡价格和均衡产量;(2)长期均衡时代表最优生产规模的SAC曲线和SMC曲线;(3)长期均衡时的利润量。
图7—2解答:本题的作图结果如图7—3所示:图7—3(1)长期均衡点为E点,因为在E点有MR=LMC。
由E点出发,均衡价格为P0,均衡数量为Q0。
(2)长期均衡时代表最优生产规模的SAC曲线和SMC曲线如图7—3所示。
在Q0的产量上,SAC曲线和LAC曲线相切;SMC曲线和LMC曲线相交,且同时与MR曲线相交。
(3)长期均衡时的利润量由图7—3中阴影部分的面积表示,即π=[AR(Q0)-SAC(Q0)]·Q 0。
微观经济学第七章 习题答案

MR,试求:图7—1(1)A点所对应的MR值;(2)B点所对应的MR值。
解答:(1)根据需求的价格点弹性的几何意义,可得A点的需求的价格弹性为e d =eq \f(15-5,5)=2或者e d =eq \f(2,3-2)=2再根据公式MR=P eq \b\lc\(\rc\)(\a\vs4\al\co1(1-\f(1,e d ))),则A点的MR值为MR=2×eq \b\lc\(\rc\)(\a\vs4\al\co1(1-\f(1,2)))=1(2)与(1)类似,根据需求的价格点弹性的几何意义,可得B点的需求的价格弹性为e d =eq \f(15-10,10)=eq \f(1,2)或者e d =eq \f(1,3-1)=eq \f(1,2)再根据公式MR=P eq \b\lc\(\rc\)(\a\vs4\al\co1(1-\f(1,e d ))),则B点的MR值为MR=1×eq \b\lc\(\rc\)(\a\vs4\al\co1(1-\f(1,1/2)))=-12. 图7—2(即教材第205页的图7—19)是某垄断厂商的长期成本曲线、需求曲线和收益曲线。
试在图中标出:(1)长期均衡点及相应的均衡价格和均衡产量;(2)长期均衡时代表最优生产规模的SAC曲线和SMC曲线;(3)长期均衡时的利润量。
图7—2图7—3(1)长期均衡点为E点,因为在E点有MR=LMC。
由E点出发,均衡价格为P0,均衡数量为Q0。
(2)长期均衡时代表最优生产规模的SAC曲线和SMC曲线如图7—3所示。
在Q0的产量上,SAC曲线和LAC曲线相切;SMC曲线和LMC曲线相交,且同时与MR曲线相交。
(3)长期均衡时的利润量由图7—3中阴影部分的面积表示,即π=[AR(Q0)-SAC(Q0)]·Q 0。
3. 已知某垄断厂商的短期总成本函数为STC=0.1Q3-6Q2+140Q+3 000,反需求函数为P=150-3.25Q。
高等数学第七章习题详细解答

第七章习题答案习题7.01.下列各种情形中,P 为E 的什么点?(1)如果存在点P 的某一邻域()U P ,使得()⊂c U P E (c E 为E 的余集); (2)如果对点P 的任意邻域()U P ,都有, ()(),C U P E U P E φφ≠≠; (3)如果对点P 的任意邻域()U P ,都有. 解 (1)P 为E 的外点;(2)P 为E 的边界点;(3)P 为E 的聚点。
2.判定下列平面点集的特征(说明是开集、闭集、区域、还是有界集、无界集等?)并分别求出它们的导集和边界.(1) (){},0≠x y y ;(2) (){}22,620≤+≤x y x y ; (3) (){}2,≤x y y x ;(4) ()(){}()(){}2222,11,24+-≥⋂+-≤x y x y x y x y .解 (1) 是开集,是半开半闭区域,是无界集,导集为2R ,边界集为(){},0=x y y ;(2)既不是开集也不是闭集,是半开半闭区域,是有界集,导集为(){}22,620≤+≤x y x y ,边界集为(){}2222,=6=20++,x y x y x y ;(3) 是闭集,是半开半闭区域,是无界集,导集为集合本身,边界集为(){}2,=x y y x ;是闭集,是闭区域,是有界集,导集为集合本身,边界集为()()(){}2222,11,24+-=+-=x y x y x y习题7.11. 设求1. 解 令,=-=yu x y v x,解得,11==--u uv x y v v,故()22,11⎛⎫⎛⎫=- ⎪ ⎪--⎝⎭⎝⎭u uv f u v v v ,即()()21+,1=-u v f u v v ,所以,()()21+y ,1=-x f x y y φ≠-}){()(P E P U 22,,y f x y x y x ⎛⎫-=- ⎪⎝⎭(,).f x y2.已知函数()22,cot =+-x f x y x y xy y,试求(),f tx ty .2. 解 因为()22,cot =+-y f x y x y xy x,所以,()2222,cot ,=+-t y f tx ty tx ty txty t x即()()222,cot =+-y f tx ty t x y t xy x.3.求下列各函数的定义域 (1) 25)1(=-+z ln y xy ;(2) =z ;(3) =z(4) )0;=>>u R r(5) =u3. 解 (1)(){}2,510-+>x y yxy ;(2)(){},0->x y x y ;(3)(){}2,≥x y x y ;(4)(){}22222,<++≤x y r x y z R ;(5)(){}222,≤+x y z x y4. 求下列各极限:(1) ()()233,0,31lim →-+x y x yx y ;(2)()(,1,1ln lim→+x x y y e(3)()(,0,0lim→x y(4)()(,0,0lim→x y ;(5)()()(),0,2sin lim→x y xy x ;(6)()()()()222222,0,01cos lim→-++x y x y x y xy e.4. 解 (1)()()2333,0,31101lim 0327→--==++x y x y x y ;(2)()(()1,1,1ln ln 11lim2→+++===x x y y e e e (3)()()()(,0,0,0,0limlim→→=x y x y ()(,0,01lim4→==x y (4)()(()()),0,0,0,01limlim→→=x y x y xy xy()()),0,0=lim1=2→+x y(5)()()()()()(),0,2,0,2sin sin limlim 122→→=⋅=⋅=x y x y xy xy y x xy(6)()()()()()()()()()222222222222222,0,0,0,01cos 1cos limlim→→-+-++=⋅++x y x y x y x y x y x y xy xy eex y()()()()()()()2222222022,0,0,0,01cos 10limlim=02→→-++=⋅⋅=+x y x y x y x y xy e exy5.证明下列极限不存在: (1)()(),0,0lim→-+x y x yx y ;(2)()(),0,0lim→+-x y xyxy x y .5. (1) 解 令=y kx ,有()(),0,001limlim 1→→---==+++x y x x y x kx kx y x kx k ,k 取不同值,极限不同,故()(),0,0lim→-+x y x yx y 不存在.(2) 解令=x y()()22,0,00lim lim 1→→==+-x y x xy x xy x yx ;令2=x y()()()()22,0,02,0,0022lim lim lim 0221→→→===+-++x y y y y xy y y xy x y y y y ;01≠,故()(),0,0lim→+-x y xyxy x y不存在.6.函数=y z a 为常数)在何处间断?6. 解 因为=y z 是二元初等函数,且函数只在点集(){,x y y 上无定义,故函数在点集(){,x y y 上间断.7.用 εδ- 语言证明()(,0,0lim0→=x y .7. 证明 对0∀>ε,要使220-=≤=<ε2<ε,取=2δε<δ0-<ε,所以()(,0,0lim 0→=x y习题7.21. 设()(),sin 1arctan ,π==+-xy xz f x y e y x y 试求()1,1x f 及()1,1y f1. 解()221,sin arctan 1=+++xy x x yf x y ye y xx yyπ22=sin arctan+++xy x xy ye y y x y π.()()222,sin cos 11-=++-+xy xyy x y f x y xe y e y x x yπππ 222sin cos -=+++xyxyx x xe y e y x y πππ()()1,1,1,1∴=-=-x y f e f e2.设(),ln 2⎛⎫=+ ⎪⎝⎭y f x y x x ,求()1,0'x f ,()1,0'y f .2. 解()()222122,22--==++x yx y x f x y y x x y x x()2112,22==++y x f x y yx y x x()()11,011,02∴==,x y f f . 3.求下列函数的偏导数(1) 332=++z x y xy ,(2) ()1=+xz xy , (3) ()222ln =+z y x y ,(4) ln tan=y z x, (5) ()222ln =+z x x y ;(6)=z (7) ()sec =z xy ;(8) ()1=+yz xy ;(9) ()arctan =-zy x y ;(10) .⎛⎫=⎪⎝⎭zx u y 3. 解 (1)2232,32z z x y y x x y ∂∂=+=+∂∂(2)因为 ()ln 1,x xy z e+=所以()()()()ln 1ln 11ln 111x x xy z xy xy e xy xy xy x xy xy +⎛⎫⎛⎫∂=++=+++ ⎪ ⎪∂++⎝⎭⎝⎭()()22ln 1111x x xy z x x e xy y xy xy +⎛⎫⎛⎫∂==+ ⎪ ⎪∂++⎝⎭⎝⎭(3)()2322222222,2ln z xy z y y x y x x y y x y ∂∂==++∂+∂+(4)222222sec sec 111sec ,sec tan tan tantan y yy z y y z y x x y y y y x x x y x x x x x x x x∂∂⎛⎫⎛⎫=-=-== ⎪ ⎪∂∂⎝⎭⎝⎭ (5)()32222222222ln ,z x z x y x x y x x y y x y ∂∂=++=∂+∂+(6)z z x y ∂∂====∂∂(7)()()()()sec tan ,sec tan z z y xy xy x xy xy x y ∂∂==∂∂(8)()()22ln 1111y y xy z y y e xy x xy xy +⎛⎫⎛⎫∂==+ ⎪ ⎪∂++⎝⎭⎝⎭()()()()ln 1ln 11ln 111y y xy z xy xy e xy xy xy y xy xy +⎛⎫⎛⎫∂=++=+++ ⎪ ⎪∂++⎝⎭⎝⎭ (9)()()()()()()()11222ln ,,111z z zz z z z x y z x y x y x y u u u x y z x y x y x y ------∂∂∂==-=∂∂∂+-+-+-(10)因为 ln,x z yu e=所以ln ln ln 21,,ln zzx x x z z z y y y u z x z u z x x z u x e e e x x xy y x y y y y z y y y⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎛⎫⎛⎫⎛⎫⎛⎫∂∂∂=⋅==⋅-=-= ⎪ ⎪ ⎪ ⎪∂∂∂⎝⎭⎝⎭⎝⎭⎝⎭4.设ln=z ,求证: 12∂∂+=∂∂z z xy x y . 4.证明 因为ln,z =所以z zx y∂∂====∂∂从而有12 z zx yx y∂∂+=+=+=∂∂5.求下列函数的二阶偏函数:(1)已知33sin sin=+z x y y x,求2∂∂∂zx y;(2)已知ln=xz y,求2∂∂∂zx y;(3)已知(ln=z x,求22∂∂z x和2∂∂∂z x y;(4)arctan=yzx求22222,,∂∂∂∂∂∂∂z z zx y x y和2∂∂∂zy x.5. 解(1)3323sin sin,3sin coszz x y y x x y y xx∂=+∴=+∂从而有223cos3coszx y y xx y∂=+∂∂(2)ln ln1,lnx xzz y y yx x∂⎛⎫=∴= ⎪∂⎝⎭从而有()()()ln1ln1ln11ln ln ln ln1xx xz yxy y y x yx y x y x--⎛⎫∂=+⋅=+⎪∂∂⎝⎭(3)(()1222 ln,zz x x yx-∂=∴===+∂从而有()()3322222222122zx y x x x yx--∂=-+=-+∂()()332222222122z x y y y x y x y --∂=-+=-+∂∂ (4)22221arctan,1y z y y z x xx x y y x ∂⎛⎫=∴=⋅-=- ⎪∂+⎝⎭⎛⎫+ ⎪⎝⎭ 222111z x yx x y y x ∂⎛⎫=⋅= ⎪∂+⎝⎭⎛⎫+ ⎪⎝⎭从而有()()()()2222222222222222222,x y y z xy z y x x x y x y x y x y -++∂∂-===∂∂∂+++ ()()2222222222222222,z xy z x y xy x y y y x x y x y x y ⎛⎫∂-∂+--=== ⎪∂∂∂+⎝⎭++ 6. 设()ln =z y xy ,求2∂∂∂z x y 及22∂∂zy .6. 解 因为()ln ,z y xy =所以()(),ln ln 1z y y z x y xy y xy x xy x y xy∂∂===+=+∂∂从而有22211,.z z x y x y y∂∂==∂∂∂ 习题7.31. 求下列函数的全微分.(1) 2222+=-s t u s t ;(2) ()2222+=+x y xyz x y e;(3) ()arcsin0=>xz y y;(4) ⎛⎫-+ ⎪⎝⎭=y x x y z e ;1.解 (1)()()222232322222222()()22222∂--+⋅---==∂--u s s t s t s s st s t s s s t s t()()222223232222222()()22222u t s t s t t ts t ts s t s t s t ∂--+---==∂-- ()()2322222244u u st t dz ds dt ds dt s t s t s t ∂∂-∴=+=-∂∂--(2)()()()222222222222++++∂=++⋅∂x y x y xyxyx y x y yzxe x y exxy()2222222244222222+++⎛⎫--=++⋅=+ ⎪⎝⎭x y x y x y xyxyxyx y x y xe x y e x e x y x y()()()22222222222-2+++∂=++⋅∂x y x y xy xyy x x y xzye x y eyxy()()2222222222442222+++-+⎛⎫-=+⋅=+ ⎪⎝⎭x y x y x y xyxyxyy x x y y x yeey e xy xy2244442222x y xyz z x y y x dz dx dy x edx y dy x y x y xy +⎛⎫⎛⎫∂∂--∴=+=+++ ⎪ ⎪∂∂⎝⎭⎝⎭ (3)2222211∂=⋅==∂--⎛⎫yzxyyy x y x x22⎛⎫⎛⎫∂=-=-= ⎪ ⎪∂⎝⎭⎝⎭z x x yy y z zdz dx dy x y∂∂∴=+=∂∂(4)22221y x y x x y x y z y y x e e x x y x y ⎛⎫⎛⎫-+-+ ⎪ ⎪⎝⎭⎝⎭⎛⎫∂-=-= ⎪∂⎝⎭ 22221y x y x x y x y z x x y e e y x y xy ⎛⎫⎛⎫-+-+ ⎪ ⎪⎝⎭⎝⎭⎛⎫∂-=-+= ⎪∂⎝⎭222222y x y x x y x y z z z y x x y dz dx dy e dx e dy x y y x y xy⎛⎫⎛⎫-+-+ ⎪ ⎪⎝⎭⎝⎭∂∂∂--∴=+==+∂∂∂ 2. 求函数2arctan1=+xz y 在1,1==x y 处的全微分.2.解()()()()()()()22222222222222222211111111111++∂++=⋅=⋅=∂++++++++y y z y y x xy y x y y xy()()()()()()22222222222222211222111111+∂-⋅--=⋅=⋅=∂++++++++y z x y xy xyx yy y x y y xy()()21,11125111z x ∂+∴==∂++ , ()()21,12125111∂-⋅==-∂++z y ()1,12255dz dx dy ∴=- 3. 求函数22=-xyz x y 当2,1,0.02,0.01==∆=∆=x y x y 时的全微分和全增量,并求两者之差.3.解 ()()()(),, 2.02,1.011,1z z x x y y z x y z z ∆=+∆+∆-=-()()22222.02 1.0121 2.0420.6670.667021 4.08 1.0232.02 1.01⨯⨯=-=-=-=--- ()()()2223222222222--⋅∂--===-∂---y x y xy x z x y y y x x y x y x y ()()()()22322222222--⋅-∂+==∂--x x y xy y z x xy y x y x y ()2,111413z x ∂∴=-=-∂- ,()()22,182110941z y ∂+⨯==∂- ()2,11100.020.010.070.0110.00439dz ∴=-⨯+⨯=-+=00.0040.004z dz ∴∆-=-=-.*4讨论函数()()()()(),0,0,0,,0,0⎧≠⎪=⎨⎪=⎩xy x y f x y x y 在()0,0点的连续性、可导性、可微性以及其偏导函数在()0,0的连续性.4.解()()()()()(),0,0,0,0lim,lim 00,0x y x y f x y xy f →→===(),f x y ∴在()0,0点连续 又()()()00,00,0000,0limlim 0x x x f x f f x x∆→∆→∆--===∆∆ ()()()000,0,0000,0limlim 0y y y f y f f y y∆→∆→∆--===∆∆ ()()0,00,0,00x y f f ∴==.()(()(,0,0,0,0,0,00limlim limx y x y f x yf z dzρρ→∆∆→∆∆→∆∆--∆-==()()()0,0,0x y<∆∆→∆lim0z dzρρ→∆-∴=故函数(),f x y 在()0,0点可微. 由()(),0,0x y ≠时(),=-x f x yy xy()23222sinx yy xy=-+(),=-y f x y x xy ()23222xy x xy=-+()(),0,0lim 0x y y →= ,()()()()23,0,0222lim→=+x y x yy kx xy()()()33323222=lim11→==+⋅+x kx ky kx k xk ,k 不同值不同()()()23,0,0222lim→∴+x y xy xy 不存在,故()()(),0,0lim ,xx y f x y →不存在.(),x f x y ∴在()0,0点不连续,同理可证(),y f x y 在点()0,0不连续.*5.计算()2.050.99的近似值.5.解 令00,1,2,0.01,0.05yz x x y x y ===∆=∆= 则1,ln y y z z yx x x x y-∂∂==∂∂ ()()1,21,22,0z zx y ∂∂∴==∂∂ ()()()2.0521,21,20.991120.0100.0510.02 1.02∂∂∴≈+∆+∆=+⨯+⨯=+=∂∂z zx y x y*6.设有厚度为,内高为,内半径为的无盖圆柱形容器,求容器外壳体积的近似值(设容器的壁和底的厚度相同).6.解 设容器底面积半径为r ,高为h则容器体积2V r h π=22,V Vrh r r hππ∂∂==∂∂ 22∴=+dV rhdr r dh ππ002,10,0.1,0.1r cm h cm r cm h cm ==∆=∆=()()22,102,1020.10.1400.140.1 4.4∴∆≈=⋅+⋅=⨯+⨯=V dV rh r πππππ*7. 测得直角三角形两直角边的长分别为7±0.1cm 和24±0.1cm ,试求利用上述二值来计算斜边长度时的绝对误差和相对误差.0.1cm 10cm 2cm7.解 设直角三角形的直角边长分别为,x y ,则斜边z =,zz xy∂∂==∂∂由题意007,24,0.1,0.1x y x y δδ====z ∴的绝对误差为()()7,247,247240.10.10.242525∂∂=+=⨯+⨯=∂∂z x y z z x y δδδz 的相对误差()7,240.240.009625=≈zz δ 习题7.41.设,,,求. 1.解 ()3222sin 22cos 23cos 6---∂∂=⋅+⋅=⋅-⋅=-∂∂x y x y t t du z dx z dy e t e t e t t dt x dt y dt2.设,而,,求. 2.解2123∂∂=⋅+⋅=+∂∂dz z dy z dV x dx u dx V dx2341-=x3.设,,,求,. 3.解 ()()222cos 2sin ∂∂∂∂∂=⋅+⋅=-+-∂∂∂∂∂z z u z v uv v y u uv y x u x v x()()2222222cos sin sin cos cos 2cos sin sin x y y x y y x y x y y y =-+-()23sin cos cos sin x y y y y =-()()()222sin 2cos z z u z v uv v x y u uv x y y u y v y∂∂∂∂∂=+=--+-∂∂∂∂∂ ()()()2222222cos sin sin sin cos 2cos sin cos x y y x y x y x y x y y x y =--+-()()3333cos sin 2cos sin sin cos x y y x y y y y =+-+2e x y u -=sin x t =3y t =d d u tarccos()z u v =-34u x =3v x =d d zx22z u v uv =-cos u x y =sin v x y =zx ∂∂z y∂∂4.设,而,,求,. 4.解 222ln 3∂∂∂∂∂⎛⎫=⋅+⋅=⋅+- ⎪∂∂∂∂∂⎝⎭z z u z v u y u v x u x v x v x()()()2322632ln 326ln 3x y y y y x y x y x x x x +⎛⎫=+-=+-- ⎪⎝⎭5.设求5.解 ()()1wf x xy xyz y yz x ∂'=++++∂()()()()1wf x xy xyz x xz x z f x xy xyz y∂''=+++=+++∂ ()()wf x xy xyz xy xyf x xy xyz z ∂''=++=++∂6.求下列函数的一阶偏导数(其中具有一阶连续偏导数):(1);(2);(3);(4).6.解 (1)()()222222∂''=-⋅=-∂z f x y x xf x y x()()()222222∂''=-⋅-=--∂zf x y y yf x y y(2)121110∂'''=+⋅=∂u f f f x y y12122211u x x f f f f y y z y z ⎛⎫∂⎛⎫''''=-+=-+ ⎪ ⎪∂⎝⎭⎝⎭122220∂⎛⎫'''=⋅+-=- ⎪∂⎝⎭u y y f f f z z z (3)1231231∂''''''=⋅+⋅+⋅=++∂uf f y f yz f yf yzf x123230∂'''''=⋅+⋅+⋅=+∂uf f x f xz xf xzf y2ln z u v =32u x y =+y v x =zx ∂∂z y∂∂(),w f x xy xyz =++,,.w w wx y z∂∂∂∂∂∂f 22()z f x y =-,x y u f y z ⎛⎫= ⎪⎝⎭(,,)u f x xy xyz =22(,e ,ln )xy u f x y x =-123300∂''''=⋅+⋅+⋅=∂uf f f xy xyf z (4)1231231122∂''''''=⋅+⋅⋅+⋅=++∂xy xyu f x f e y f xf ye f f x x x()12312202∂'''''=⋅-+⋅+⋅=-+∂xy xy uf y f e x f yf xe f y7.求下列函数的二阶偏导数,,(其中具有二阶连续偏导数):(1),(2). 7.解(1)22121222∂''''=⋅+⋅=+∂zf xy f y xyf y f x22121222∂''''=⋅+⋅=+∂zf x f xy x f xyf y()()222211112212222222∂'''''''''∴=+⋅+⋅+⋅+⋅∂zyf xy f xy f y y f xy f y x233341111221222422yf x y f xy f xy f y f '''''''''=++++ 23341111222244yf x y f xy f y f '''''''=+++()()2222111122212222222∂''''''''''=+⋅+⋅++⋅+⋅∂∂zxf xy f x f xy yf y f x f xy x y322223111122212222422xf x yf x y f yf x y f xy f ''''''''''=+++++ 32231111222222522xf x yf x y f yf xy f ''''''''=++++()2222211122212222222∂'''''''''=+++⋅+⋅∂zx f x x f xy xf xy f x f xy y43221112222424x f x yf xf x y f '''''''=+++(2)()()222222∂''=+⋅=+∂zf x y x xf x y x()()222222∂''=+⋅=+∂zf x y y yf x y y22zx∂∂2z x y ∂∂∂22z y ∂∂f 22(,)z f x y xy =22()z f x y =+()()()()2222222222222224∂''''''∴=+++⋅=+++∂zf x y xf x y x f x y x f x y x()()22222224∂'''=+⋅=+∂∂z xf x y y xyf x y x y()()()()2222222222222224∂''''''=+++⋅=+++∂zf x y yf x y y f x y y f x y y8.设其中F 是可微函数,证明8.解()()()cos sin sin cos cos cos sin sin ux F y x x x xF y x x∂''=+--=--∂ ()sin sin cos uF y x y y∂'=-∂ ()()cos cos cos cos sin sin cos cos sin sin cos u uy x x xF y x y yF y x x x y∂∂''∴+=--+-⎡⎤⎣⎦∂∂ ()()cos cos cos cos sin sin cos cos sin sin cos cos x y x yF y x x yF y x x y ''=--+-=.习题7.51.设,φ⎛⎫= ⎪⎝⎭x y z z 其中为可微函数,求∂∂+∂∂z z x y x y . 1.解 z是,x y函数由方程xx z y φ⎛⎫= ⎪⎝⎭确定。
水力学第七章课后习题答案

8.12梯形断面土渠,底宽b =3m ,边坡系数m =2,水深h =1.2m ,底坡i =0.0002,渠道受到中等养护,试求通过流量。
解: ()()1.23 1.22 6.48A h b hm =+=⨯+⨯=(m 2)232 1.28.367b b χ=+=+=+⨯=(m )0.7745AR χ==(m ),取0.0225n =(见教材153页表6-4)∴231 6.480.7745 3.4350.0225Q n⨯===(m 3/s )答:通过流量 3.435Q =m 3/s 。
修建混凝土砌面(较粗糙)的矩形渠道,要求通过流量Q =9.7s m /3,底坡i =0.001,试按水力最优断面设计断面尺寸。
解: 对矩形断面,水力最优断面满足2b h =。
∴22A bh h ==,24b h h χ=+=,∴2242h hR h ==∵1Q An=0.001i =,0.017n =∴23222h h ⎛⎫⋅= ⎪⎝⎭,83110.0179.7 4.14nQ h ⨯=== 1.70h =(m ), 3.40b =(m ) 答:断面尺寸为 1.70h =m , 3.40b =m 。
.14修建梯形断面渠道,要求通过流量Q =1s m /3,边坡系数m =1.0,底坡i =0.0022,粗糙系数n =0.03,试按不冲允许流速[]max v =0.8s m /,设计断面尺寸。
解: ∵ max 0.8v v ≤=,∴0.8QA≤,max 1 1.250.8Q A v ≥==(m 2) 又∵[]max 1v v n =≤,即[]2max 3120.502n v R i ≤== 0.366R =∴有 21.25hb mh +≥20.366≤即有2 1.253.42hb h b ⎫+≥⎪⎬+≥⎪⎭解得:2 1.870.6840h h -+=0.51.37h ⎧=⎨⎩, 2.012.455b ⎧=⎨-⎩∴ 2.00b =(m ),0.5h =(m )答:断面尺寸为 2.00b =m ,0.5h =m 。
高等数学(本科)第七章课后习题解答

习题7.11.在空间直角坐标系中,指出下列各点位置的特点.()0,5,0-A ;()0,3,3-B ;()3,0,6-C ;()0,0,4D ;()7,5,0-E ;()9,0,0F .【解】A 点在y 轴上;B 点在xoy 坐标面上;C 点在zox 坐标面上;D 点在x 轴上;E 点在yoz 坐标面上;F 点在z 轴上. 2.指出下列各点所在的卦限.()1,3,2-A ;()2,1,7--B ;()1,3,2---C ;()3,2,1--D .【解】A 点在第五卦限;B 点在第三卦限;C 点在第七卦限;D 点在第六卦限. 3.自点()2,3,1--M 分别作xoy 、yoz 、zox 坐标面和x 、y 、z 坐标轴的垂线,写出各垂足的坐标,并求出点M 到上述坐标面和坐标轴的距离.【解】()2,3,1--M 在xoy 坐标面上的垂足为()0,3,1-、在yoz 坐标面上的垂足为()2,3,0-、在zox 坐标面上的垂足为()2,0,1--;()2,3,1--M 在x 轴的垂足为()0,0,1-、在y 轴的垂足为()0,3,0、在z 轴的垂足为()2,0,0-;()2,3,1--M 到x 轴的距离为()132322=-+;()2,3,1--M 到y 轴的距离为()()52122=-+-;()2,3,1--M 到z 轴的距离为()103122=+-.3.已经点()2,1,3--M .求:(1)点M 关于各坐标面对称点的坐标;(2)点M 关于各坐标轴对称点的坐标;(3)点M 关于坐标原点的对称点的坐标. 【解】(1)()2,1,3--M 关于xoy 面对称点的坐标是(),2,1,3-; ()2,1,3--M 关于yoz 面对称点的坐标是(),2,1,3---;()2,1,3--M 关于zox 面对称点的坐标是(),2,1,3-.(2)()2,1,3--M 关于x 轴对称点的坐标是(),2,1,3; ()2,1,3--M 关于y 轴对称点的坐标是(),2,1,3--;()2,1,3--M 关于z 轴对称点的坐标是(),2,1,3--.(3)()2,1,3--M 关于坐标原点的对称点的坐标是(),2,1,3-. 5.求点()5,3,4-A 到坐标原点和各坐标轴的距离.【解】 ()5,3,4-A 到坐标原点距离为()25534222=+-+;()5,3,4-A 到x 轴的距离为()345322=+-;()5,3,4-A 到y 轴的距离为415422=+; ()5,3,4-A 到z 轴的距离为()53422=-+.6.在y 轴上求与点()7,2,3-A 和()7,1,3-B 等距离的点. 【解】设所求点为()0,,0y C .据题意,有 BC AC =,即()()()()=-+-+--22270230y ()()()()22270130--+-+-y解得 23=y .所以,所求之点为.0,23,0⎪⎭⎫ ⎝⎛C 7.已知三角形ABC 的顶点坐标分别为()3,2,1A 、()3,10,7B 和()1,3,1-C ,试证明 ∠BAC 为钝角. 【解】AB 边长()()()103321017222=-+-+-==AB c ;AC 边长()()()()3312311222=-+-+--=b ; BC 边长()()()()1173110371222=-+-+--=a .由余弦定理知cos ∠BAC ()010321171032222222<⨯⨯-+=-+=bc a c b ,所以,∠BAC 为钝角.8.试在xoy 面上求一点,使它到()5,1,1-A 、()4,4,3B 和()1,6,4C 各点的距离相等. 【解】设所求点为()0,,y x D .据题意,有 CD BD AD ==,即()()()()=-+--+-2225011y x ()()()222443-+-+-z y x()()()222164-+-+-=z y x解得 5,16-==y x .所以,所求之点为().0,5,16-D习题7.21.设平行四边形ABCD 的对角线向量b BD a AC ==,,试用a ,b 表示DA CD BC AB ,,,.【解】记平行四边形ABCD 的对角线的交点为O .()b a b a BD AC OD OC DC AB -=-=-=-==2121212121;同理可求出,()b a a b OC BO BC +=+=+=212121;()a b AB CD -=-=21;()b a BC DA +-=-=21.2.已知向量n m a 23-=,n m a +=.试用向量n m ,表示b a 32-. 【解】b a 32-()()n m n m n m 733232-=+--=.3.设c b a u 2-+=,c b a v +--=3.试用向量c b a ,,表示v u 32-. 【解】v u 32-()()c b a c b a c b a 71153322-+=+----+=. 4.设ABCDEF 是一个正六边形,AF b AB a ==,,试用a ,b 表示EF DE CD BC ,,,.【解】记六边形ABCDEF 的对角线的交点为O .则四边形ABOF 、CDEO 、DEFO 及ABCO 均为平行四边形.由向量加法的平行四边形法则知,b a AF AB AO BC +=+==; b AF CD ==;a BA BA AO DE -=-===;().b a BC EF +-=-=5.设向量k a j a i a a z y x ++=,,若它满足下列条件之一:(1)a 垂直于z 轴;(2)a 垂直于xoy 面;(3)a 平行于yoz 面.那么它的坐标有什么有何特征? 【解】(1)因为a 垂直于z 轴,故0.=k a ,即0=z a ;(2)因为a 垂直于xoy 面,故a 平行于z 轴,从而a ∥{}1,0,0=k ,所以,0==y x a a . (3)a 平行于yoz 面,故垂直于x 轴,从而.a 0=i ,所以,0=x a . 6.已知向量{}7,4,4-=AB ,它的终点坐标为()7,1,2-B ,求它的起点坐标. 【解】设起点()z y x A ,,,则{}z y x AB ----=7,1,2,根据已知条件,有77,41,42=--=--=-z y x ,解得 .0,3,2==-=z y x 所以,起点坐标为 ()0,3,2-A .7.已知向量{}1,1,6-=a ,{}0,2,1=b .求 (1)向量b a c 2-=; (2)向量c 的方向余弦; (3)向量c 的单位向量. 【解】(1)c {}{}{}{}{}{}1,3,401,41,260,4,21,1,60,2,121,1,6--=----=--=--=.(2()()26134222=-+-+=.故,⎭⎬⎫⎩⎨⎧--==261,263,2640c c ,所以,向量c 的方向余弦为.261cos ,263cos ,264cos -=-==γβα(3).向量c 的单位向量为⎭⎬⎫⎩⎨⎧--±261,263,264.8.试确定m 和n 的值,使向量k n j i a ++-=32和k j i m b 26+-=平行. 【解】因为a ∥b ,所以2632nm =-=-,解得 .1,4-==n m9.已知向量{}12,9,8-=b 及点()7,1,2-=A ,由点A 作向量AM 34=, 且AM 与b 的方向相同.求向量AM 的坐标表达式及点M 的坐标.【解】设()z y x M ,,,则{}7,1,2-+-=z y x AM .据题意知AM ∥b 且与b 同向,因此有λ=--=+=-1279182z y x ,① 且 0>λ. ② 由①式得 λλλ127,91,82=-++=-z y x . 又已知34=,故有 ()()()341298222=++λλλ. ③③式化简得4115628922=⇒=λλ,解得 2=λ或2-=λ(舍).所以,.17,17,18-===z y x因此AM {}24,18,16-=,()17,17,18-=M . 10.已知点()4,2,1--A 和点()z B ,2,6-9=,求z 的值. 【解】()(){}{}4,4,74,22,16+-=------=z z AB .9=,得()()9447222=++-+z ,化简得082=+z z ,解之,得 0=z 或.8-=z11.已知点()1,2,41M 和点()2,0,32M ,计算向量21M M 的模、方向余弦和方向角. 【解】{}{}1,2,112,20,4321--=---=M M ;()()2121222=+-+-=. 因为{}⎭⎬⎫⎩⎨⎧--=--==21,22,211,2,12121021M M M M .所以21M M 的方向余弦是.21cos ,22cos ,21cos =-=-=γβα 方向角为.3cos ,43,32πγπβπα===12.求与下列向量a 同方向的单位向量0a . (1){}1,4,2-=a ;(2)k j i a ++-=32.【解】(1()21142222=+-+=,所以{}⎭⎬⎫⎩⎨⎧-=-==211,214,2121,4,22110a a .(2()14132222=++-=,所以.141,143,1421410⎭⎬⎫⎩⎨⎧-==a a 习题7.31.设向量k j i a 23--=,k j i b -+=2.求:(1)b a .;(2)b a ⨯;(3)()()b a 32⨯-;(4)()b a 2⨯;(5)向量b a ,的夹角. 【解】(1)()()()3122113.=-⨯-+⨯-+⨯=b a ;(2)k j i j b a 7521++=-=⨯;(3)()()()1836.63.2-=⨯-=-=-b a b a ;(4)()()k j i b a b a 1421022++=⨯=⨯;(5)()()14213222=-+-+=()6121222=-++=,故21236143.,cos =⨯==⎪⎪⎭⎫ ⎝⎛∧b a b a ,所以向量b a ,的夹角为 .2123arccos ,=⎪⎪⎭⎫ ⎝⎛∧b a 2.设向量a ,b ,c 为单位向量,且满足0=++c b a ①.求:a c c b b a ...++. 【解】由①式得()0.=++c b a a ;()0.=++c b a b ;()0.=++c b a c .即 0..=++c a b a ; ②0..=+c b a b ; ③0..=++b c a c ; ④ 将②、③、④相加得()03...2=+++a c c b b a所以,.23...-=++a c c b b a3.已知点()2,1,1-A ,()2,6,5-B ,()1,3,1-C 求: (1)同时与AB 及AC 垂直的单位向量; (2)ABC ∆的面积. 【解】(1)AB AC ⨯{}16,12,151612153405=++=--=k j i kj .25161215222=++=. 所以,同时与AB 及AC 垂直的单位向量为 {}⎭⎬⎫⎩⎨⎧±=±=⨯±2516,2512,25116,12,15251AC AB .(2)ABC ∆的面积225==. 4.设{}2,5,3-=a ,{}4,1,2=b ,则当实数λ与μ有什么关系时,能使b a μλ+与z 轴垂直?【解】{}μλμλμλμλ42,5,23+-++=+b a .要使b a μλ+与z 轴垂直,只须b a μλ+与{}1,0,0=k 垂直,于是有()042.=+-=+μλμλk b a ,即 .2μλ=5.设质量为100kg 的物体从点()8,1,31M 沿直线移动到点()2,4,1M ,计算重力所做的功.【解】{}6,3,21--==M M s ,{}{}980,0,01008.9,0,0=⨯-=F .所以,{}{}58806,3,2.980,0,0.=---==s F W (焦耳).6.已知{}3,2,1-=a ,{}1,4,2-=b ,{}0,2,4=c ,b a ⨯是否与c 平行?【解】{}0,5,1005104221--=+--=--=⨯k j i j i b a ;因为c b a 52-=⨯,所以,b a ⨯与c 平行.7.求一个单位向量使其同时垂直向量{}0,1,1=a 和{}1,1,0=b .【解】{}1,1,111-=+-==⨯k j i j b a .()3111222=+-+=. 所以同时垂直向量a 和b 向量的单位向量为 {}1,1,131-±=⨯±b .习题7.41.求过点()1,0,3-且与平面012573=-+-z y x 平行的平面方程.【解】已经平面的法向量为{}5,7,3-=n .据题意知,所求平面的法向量可也取作n .所以据平面的点法式方程,所求平面即为 ()()()()0150733=--+---z y x . 化简得 04573=-+-z y x .2.求过点()6,9,20-M 且与连接坐标原点O 及0M 的线段0OM 垂直的平面方程. 【解】据题意知,所求平面的法向量可也取作{}6,9,20-==OM n .所以据平面的点法式方程,所求平面即为 ()()()()0669922=----+-z y x . 化简得 0121692=--+z y x .3.求过点()1,1,1-、()2,2,2--和()2,1,1-三点的平面方程. 【解】据平面的三点式方程,所求平面为()()()0121111121212111=---------------z y x . 即 ()()()0161913=++-+--z y x . 化简得 023=--z y x .4.求平面0522:=++-z y x π与坐标面xoy 、yoz 及zox 的夹角的余弦. 【解】平面π的法向量为{}1,2,2-=n ;xoy 面的法向量为{}1,0,0=k .由公式,平面π与xoy31=; 同理, 平面π与yoz32=; 平面π与zox32-=.5.求点()1,2,1平面01022:=-++z y x π的距离. 【解】12211012221222=++-⨯+⨯+=d .6.求两平行平面0:11=+++D Cz By Ax π与0:22=+++D Cz By Ax π之间的距离.【解】在1π上任取一点()1111,,z y x M ,则1M 到2π的距离d 就是所求1π与2π之间的距离.由点到平面的距离公式得 2222111CB A D Cz By Ax d +++++=. ①又11π∈M ,故有 0:11111=+++D Cz By Ax π,即1D Cz By Ax -=++. ②将②代入①,立得 22212CB A D D d ++-=.7.一平面通过()1,1,11M 和()11,02-M 两点,且垂直于平面0=++z y x .求该平面方程.【解】已知平面0=++z y x 的法向量为{}1,1,1=n ,{}2,0,121--=M M .据题意,可取所求平面的法向量为{}1,1,2211120121--=--=--=⨯k j i kj i n M M . 所以,所求平面方程为()()()011.11.2=-----z y x ,即 02=--z y x . 8.求满足下列条件的平面方程: (1)过点()2,1,3--和z 轴;(2)过点()2,0,4-及()7,1,5且平行于x 轴; (3)过点()3,5,2-,且平行于zox 面;(4)过点()1,0,1-且同时平行于向量k j i a ++=2,j i b -=. 【解】(1)根据题意,可设所求平面的一般式方程为 0:=+By Ax π. ① 又将点()2,1,3--的坐标代入①,得03=+-B A ,即 A B 3=. 因此,所求平面π为.03=+Ay Ax ②注意到0≠A (否则π的法向量为零向量),所以②两边除以A ,得到 03:=+y x π.(2)根据题意,可设所求平面的一般式方程为 0:=++D Cz By π. ①又将点()2,0,4-及()7,1,5的坐标分别代入①,得⎩⎨⎧=++=+-.07,02D C B D C ,故⎩⎨⎧-==.9,2C B C D . 因此,所求平面π为.029=++-C Cz Cy ②注意到0≠C (否则π的法向量为零向量),所以②两边除以C ,得到 029:=++-z y π.(3)根据题意,可设所求平面的一般式方程为 0:=+D By π. ① 又将点()3,5,2-的坐标代入①,得05=+-D B ,即 B D 5=. 因此,所求平面π为.05=+B By ②注意到0≠B (否则π的法向量为零向量),所以②两边除以B ,得到 05:=+y π.(4)根据题意,可设所求平面的一般式方程为0:=+++D Cz By Ax π. ① 其法向量为{}C B A n ,,=. 将点()1,0,1-的坐标代入①,得0=+-D C A . ② 又因为π同时平行于向量k j i a ++=2,j i b -=,故n 同时垂直于向量k j i a ++=2,j i b -=,于是有.02=++C B A ③ .0=-B A ④ ②、③、④联立得到A D A C AB 4,3,-=-== 因此①成为043:=--+A Az Ay Ax π . ⑤注意到0≠A (否则π的法向量为零向量),所以⑤两边除以A ,得到 043:=--+z y x π.9.平面在y 、z 轴上的截距分别为30,10,且与{}3,1,2=r 平行,求该平面方程. 【解】根据题意,可设所求平面的一般式方程为0:=+++D Cz By Ax π. ① 其法向量为{}C B A n ,,=.因为π在y 、z 轴上的截距分别为30,10,故π过点()0,30,0及(),10,0,0.将此两点坐标代入①得030=+D B . ② 及 010=+D C . ③ 又已知π与{}3,1,2=r 平行,故n 垂直于向量r ,于是有 032=++C B A . ④ ②、③、④联立得到B A BC BD 5,3,30-==-=. 因此①成为03035:=-++-B Bz By Bx π. ⑤注意到0≠B (否则π的法向量为零向量),所以⑤两边除以B ,得到 03035:=-++-z y x π. 10.指出下列各平面的特殊位置,并画出各平面. (1)013=-x ; (2)012=-+z y ; (3)02=+z x ; (4)135=-+z y x .【解】(1)因方程中z y ,前面的系数为零,故平面013=-x 平行于yoz 面; (2)因方程中x 前面的系数为零,故平面012=-+z y 平行于x 轴;(3)因方程中没有常数项,且y 前面的系数为零,故平面02=+z x 通过y 轴;012=-+z y 02=+z x ;(4)135=-+z y x 可化为113151=-++z y x ,故135=-+z y x 是在x 轴、y 轴、z 轴上的截距分别为51、31和1-的平面.习题7.51.用点向式方程及参数式方程表示直线⎩⎨⎧=++=+-.42,1:z y x z y x L【解】任取方程组的一组解⎪⎩⎪⎨⎧===.1,1,1z y x 则有,L 过点()1,,1,10M .可取直线的方向为{}3,1,232121121-=++-=-=⨯k j i j in n . 所以,所求直线L 的点向式方程为311121-=-=--z y x . 进一步,L 的参数式方程为⎪⎩⎪⎨⎧+=+=-=.31,1,21t z t y t x2.求过()1,2,31-P 、()2,0,12-P 两点的直线方程. 【解】可取直线的方向为 {}1,2,421-==P P s . 故所求直线为.112243-=+=--z y x 3.求过点()3,1,4-且平行于直线51123-==-z y x 的直线方程. 【解】根据题意知,可取所求直线的方向为{}5,1,2=s .故所求直线为.531124-=+=-z y x 4.求过()1,32-且垂直于平面0132=+++z y x 的直线方程.【解】可取直线的方向为 {}1,3,2=s . 故所求直线为.113322-=+=-z y x 5.求过点()2,1,00M 且与直线21111zy x =--=-垂直相交的直线方程.【解】 过点()2,1,0且与直线21111zy x =--=-垂直的平面π为()()()02210.1:=-+---z y x π.即 032:=-+-z y x π . ① 化直线21111zy x =--=-为参数式得 ⎪⎩⎪⎨⎧=-=+=.2,1,1t z t y t x ②将②代入①,有()()()032211=-+--+t t t . ③ 解得 21=t . 故直线21111z y x =--=-与平面π的交点为⎪⎭⎫⎝⎛1,21,231M . 因此所求直线的方向为⎭⎬⎫⎩⎨⎧--==1,21,2310M M s ∥{}2,1,3-.故所求直线为.221130-=-=--z y x 6. 过点()0,2,10-M 向平面012=+-+z y x 作垂线,求垂足坐标. 【解】 过点()0,2,10-M 且与平面012=+-+z y x 垂直的直线L 为.12211:--=-=+z y x L ① 化直线L 为参数式得⎪⎩⎪⎨⎧-=+=+-=.,22,1t z t y t x ②将②代入平面012=+-+z y x 方程中,得()()()012221=+--+++-t t t . ③解得 32-=t .故垂足坐标为⎪⎭⎫⎝⎛-32,32,351M .7.求直线⎩⎨⎧=-+-=-+-,0123,09335:1z y x z y x L 与⎩⎨⎧=-++=+-+.01383,02322:2z y x z y x L 的夹角θ.【解】1L 的方向为{}1,4,34323351-=-+=--=k j i j is ; 2L 的方向为{}10,5,101051083222-=+-==k j i j is ∥{}2,1,2-. 因为()()0211423.21=⨯-+-⨯+⨯=s s ,所以1L 与2L 垂直,从而2πθ=.8.求直线21121:+=-=-z y x L 与平面02:=+-z y x π的夹角θ. 【解】1L 的方向为{}2,1,2-=s ,平面π的法向量为{}2,1,1-=n . ()()7221112.=⨯+-⨯-+⨯=n s .()3212222=+-+=.()6211222=+-+=.故637sin ⨯==θ,所以,637arcsin⨯=θ.9.求过点()2,0,10-M 且垂直于平面032:=+-z y x π的直线方程. 【解】根据题意知,所求直线L 的方向向量即为平面π之法向量,即 {}3,12-=s .所以,由点向式方程知,所求直线为321021:+=--=-z y x L . 10.设平面π过直线130211:1--=-=-z y x L ,且平行于直线11122:2zy x L =-=+,求平面π的方程.【解】显然面π过点()3,,2,10M .可取面π的法向量为{}1,3,13120121-=+-==⨯=k j i j is s n . 所以,平面π的方程为()()()03.12.31.1=-+---z y x . 化简得023:=++-z y x π.11.求过点()1,2,10P 和直线⎩⎨⎧=--=-.032,6:z y x z x L 的平面π的方程.【解】直线L 的参数方程为⎪⎩⎪⎨⎧-=+-==.6,9,:x z x y x x L显然L 过点()6,9,01-P ,且L 的方向为{}1,11-=s . 根据题意,可取平面π的法向量为{}6,6,0660117110--=--=--=⨯=k j i j i s P P n ∥{}1,1,0. 所以,平面π的方程为()()()01.12.11.0=-+-+-z y x . 化简得03:=-+z y π.习题7.61.指出下列方程在平面解析几何与空间解析几何中分别表示何种几何图形.(1)1=-y x ;(2)x y 22=;(3)122=-y x ;(4)1222=+y x . 【解】(1)1=-y x 在平面解析几何中表示一条直线,在空间解析几何中表示一张平行于z 轴的平面;(2)x y 22=在平面解析几何中表示一条抛物线,在空间解析几何中表示一张抛物柱面;(3)122=-y x 在平面解析几何中表示一条双曲线,在空间解析几何中表示一张双曲柱面;(4)1222=+y x 在平面解析几何中表示一条椭圆曲线,在空间解析几何中表示一张椭圆柱面.2.写出下列曲线绕指定坐标轴旋转一周而得到的旋转曲面的方程. (1)zox 面上的抛物线x z 52=绕x 轴旋转一周; (2)xoy 面上的双曲线369422=-y x 绕y 轴旋转一周; (3)yoz 面上的直线0132=+-z y 绕z 轴旋转一周. 【解】(1)zox 面上的抛物线x z 52=绕x 轴旋转一周得到的曲面是 ()x zy 5222=+±,即x z y 522=+.(2)xoy 面上的双曲线369422=-y x 绕y 轴旋转一周得到的曲面是 ()36942222=-+±yz x ,即36494222=+-z y x .(3)yoz 面上的直线0132=+-z y 绕z 轴旋转一周而得到的曲面是 ()013222=+-+±z y x ,即()()222134-=+z y x .3.说明下列旋转曲面是怎样形成的.(1)1994222=++z y x ;(2)14222=+-z y x ;(3)1222=--z y x ; 【解】(1)1994222=++z y x 由曲线⎪⎩⎪⎨⎧==+,0,19422z y x 绕x 轴旋转一周而形成;或由曲线⎪⎩⎪⎨⎧==+,0,19422y z x 绕x 轴旋转一周而形成. (2)14222=+-z y x 由曲线⎪⎩⎪⎨⎧==-,0,1422z y x 绕y 轴旋转一周而形成;或由曲线⎪⎩⎪⎨⎧==-,0,1422x y z 绕y 轴旋转一周而形成. (3)1222=--z y x 由曲线⎩⎨⎧==-,0,122z y x 绕x 轴旋转一周而形成;或由曲线⎩⎨⎧==-,0,122y z x 绕x 轴旋转一周而形成. 4.指出下列各方程所表示的曲面.(1)14416916222=++z y x ;(2)144944222=+-z y x ;(3)z y x 729422=-; (4)16922=+z y ;(5)22z y x --=;(6)224y z x =+; (7)36249222=++z y x ;(8)444222=-+x y z . 【解】(1)原方程可化为()1169222=++y z x. 所以,原方程表示的是旋转椭球面.(2)原方程可化为1163838222=+-z y x . 所以,原方程表示的是双叶双曲面.(3)原方程可化为81822y x z -= 所以,原方程表示的是双曲抛物面,即马鞍面.(4)原方程可化为11691622=+z y . 所以,原方程表示的是椭圆柱面. (5)原方程可化为()22z y x +-=. 所以,原方程表示的是旋转抛物面. (6)原方程可化为4122z y x -=.所以,原方程表示的是双曲抛物面,即马鞍面. (7)原方程可化为11894222=++z y x . 所以,原方程表示的是椭球面.(8)原方程可化为1141222=-+x z y . 所以,原方程表示的是单叶双曲面.习题7.71.求球心在()3,2,1,半径为3的球面与平面5=z 的交线方程(写出一般式方程和参数式方程),并求出该曲线绕z 轴旋转一周而成的旋转曲面的方程.【解】(一)球心在()23,1,半径为3的球面方程为 ()()()9321222=-+-+-z y x .故球面与平面5=z 的交线的一般式方程为()()()⎩⎨⎧==-+-+-Γ.5,9321:222z z y x即()()⎩⎨⎧==-+-Γ.5,521:22z y x化为参数式方程为[]π2,0.5,sin 52,cos 51:∈⎪⎪⎩⎪⎪⎨⎧=+=+=Γt z t y t x .(二)利用公式()()()()()[][]()πθβαθθ2,0,,.,sin ,cos 2222∈∈⎪⎪⎩⎪⎪⎨⎧=+=+=t t z z t y t x y t y t x x . Γ绕z 轴旋转一周而成的旋转曲面的方程为 [][]()πθπθθ2,0,2,0.5,sin sin 54cos 5210,cos sin 54cos 5210∈∈⎪⎪⎩⎪⎪⎨⎧=++=++=t z t t y t t x .2.分别求出母线平行于x 轴、y 轴且通过曲线()()⎪⎩⎪⎨⎧=+-=++Γ2,01,162:222222z y x z y x 的柱面方程.【解】 (一)(1)、(2)联立消去x ,得 16322=-z y .所以,母线平行于x 轴且通过曲线Γ的柱面为16322=-z y . (二)(1)、(2)联立消去y ,得 162322=+z x .所以,母线平行于x 轴且通过曲线Γ的柱面为162322=+z x . 3.指出下列方程所表示的曲线.(1)⎩⎨⎧==++;3,25222x z y x (2)⎩⎨⎧==++;1,3694222y z y x(3)⎩⎨⎧-==+-;3,254222x z y x (4)⎩⎨⎧==+-+.4,08422y x z y【解】(1)表示平面3=x 上的圆周曲线1622=+z y ;(2)表示平面1=y 上的椭圆19323222=+zx ;(3)表示平面3-=x 上的双曲线141622=-y z ; (4)表示平面4=y 上的抛物线642-=x z .4.求()()⎪⎩⎪⎨⎧=++=++Γ2,21,:2222222Rz z y x R z y x 在三个坐标面上的投影曲线. 【解】 (一)(1)、(2)联立消去z 得 22243R y x =+. 所以,Γ在xoy 面上的投影曲线为⎪⎩⎪⎨⎧==+.0,43222z R y x (二)(1)、(2)联立消去y 得R z 21=. 所以,Γ在zox 面上的投影曲线为 .23.0,21R x y R z ≤⎪⎩⎪⎨⎧== (三)(1)、(2)联立消去x 得 R z 21=.所以,Γ在yoz 面上的投影曲线为.23.0,21R y x R z ≤⎪⎩⎪⎨⎧== 5.画出下列各曲面所围立体的图形. (1)0,22==z x y 及1224=++zy x ;(2)0,,222==+=z y x y x z 及1=x . 【解】略.6.求由球面224y x z --= ①和锥面()223y x z += ②所围成的立体在xoy 面上的投影区域.【解】联立①、②消去z 得 122=+y x 故Γ在xoy 面上的投影曲线为⎩⎨⎧==+.0,122z y x所以,球面和锥面所围成的立体在xoy 面上的投影区域为(){}1|,22≤+=y x y x D . 7.写出圆锥面22:y x z S +=的参数方程.【解】().20,0.,sin ,cos πθθθ≤≤+∞<<⎪⎩⎪⎨⎧===r r z r y r x习题7.81.设向量值函数()k t j t i t t r ++=sin cos ,求()t r t 4lim π→. 【解】()t r t 4lim π→k j i k t j t i t t t t 42222lim sin lim cos lim 444ππππ++=⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛=→→→. 2.设空间曲线C 的向量函数为(){}t t t t t r 62,34,122--+=,R t ∈.求曲线C 在与20=t 相应的点处的单位切向量.【解】因(){}64,4,2-='t t t r ,故C 相应20=t 的点处的切向量为(){}2,4,42='r .C 相应20=t 的点处的单位切向量为(){}.31,32,322,4,4612⎭⎬⎫⎩⎨⎧±=±='r 3.求曲线32,,:t z t y t x ===Γ在点)1,1,1(0M 处的切线方程和法平面方程. 【解】0M 对应参数1=t .Γ在0M 点处的切线方向为 ()()(){}|1,,='''=t t z t y t x s {}{}3,2,13,2,1|12===t t t .所以,Γ在0M 点处的切线方程为 312111-=-=-z y x . 法平面为()()()01.31.21.1=-+-+-z y x ,即 0632=-++z y x .4.在曲线32,,:t z t y t x ===Γ上求一点,使在该点处的切线平行于平面y x 2:+π4=+z .【解】平面y x 2+4=+z 的法向量为{}1,2,1=n .在Γ上任取一点()0000,,z y x M ,并设0M 对应参数0t t =.Γ在0M 点处的切线方向为()()(){}000,,t z t y t x s '''={}{}20023,2,13,2,1|0t t t t tt ===. 由题意,欲使0M 点处的切线与平面π平行,只须s 与n 垂直,为此令200341.0t t n s ++==,即0341200=++t t .解之得, 10-=t 或 310-=t .所以,所求点为()1,1,10---M 或⎪⎭⎫⎝⎛-271,91,310M .5.求曲线⎰=tu udu e x C 0cos :,t t y cos sin 2+=,t e z 31+=在0=t 处的切线方程和法平面方程.【解】参数0=t 对应曲线C 上的点()2,1,00M .C 在0M 点处的切线方向为()()(){}|,,='''=t t z t y t x s {}{}3,2,13,sin cos 2,cos |3=-==t tt e t t t e .所以,Γ在0M 点处的切线方程为 322110-=-=-z y x . 法平面为()()()02.31.20.1=-+-+-z y x ,即 0832=-++z y x .6.已知(){}t t t t r 2,1,12-+=表示空间一质点在时刻t 的位置,求质点在时刻t 的速度和加速度向量,并求质点在指定时刻1=t 的速率和运动方向.【解】(一)时刻t 的速度向量为()()()()(){}2,2,12,1,12t t t t t r t v =⎭⎬⎫⎩⎨⎧''-'+='=; 时刻t 的加速度向量为()()()()(){}{}0,2,02,2,1='''=''=t t r t a .(二)1=t 的速度为(){}2,2,11=v )32211222=++=. 1=t 的速度为(){}2,2,11=v()⎭⎬⎫⎩⎨⎧=32,32,311.复习题71.填空题(1)设b a ,为非零向量,若0.=b a ,则必有a ⊥b .(2)设b a ,为非零向量,若0=⨯b a ,则必有a ∥b .(3)若直线l 的方向向量s 与平面π的法向量n 互相平行,则直线l 与平面π必 垂直.(4)点()1,5,3P 到平面07623=+++z y x 的距离732.(5)若动()z y x M ,,到定点()5,0,0的距离等于它到x 轴的距离,则该动点的轨迹方程为25102-=-z x .(6)直线⎪⎩⎪⎨⎧+=--=+=.31,1,2t z t y t x 与平面0765=-+-z y x 的位置关系是相交但不垂直.【解】直线l 的方向向量为{}3,1,1-=s .平面的法向量为{}6,5,1-=n .因为024.≠=n s ,且s 与n s .的坐标分量不成比例, 所以直线l 与平面π相交. 2.判断题.(1)若c a b a ..=,则必有c b =.(⨯)【解】取i a =,j b =,k c =,即知上述命题是错误的 . (2)若c a b a ⨯=⨯,则必有c b =.(⨯)【解】取i a =,j b =,k c =,即知上述命题是错误的 . (3)若c a b a ..= ① 且c a b a ⨯=⨯ ② ,则必有c b =.(⨯)【解】取0=a ,j b =,k c =,即知上述命题是错误的 .【书后答案有误】. 【注意:如果假定c b a ,,均为非零向量,则上述命题是正确的,其理由如下:由①式得 ()0.=-c b a ,说明a 与c b -垂直; 由②式得 ()0=-⨯c b a ,说明a 与c b -平行.因为a 为非零向量,故c b -必为零向量,从而c b =. (4)设b a ,为非零向量,则必有a b b a ..=.(√) (5)设b a ,为非零向量,则必有a b b a ⨯=⨯..(⨯)3.已知直线⎩⎨⎧=+--=+++.03102,0123:z y x z y x l 平面024:=+-z y x π,则直线l 与平面π的位置关系为(B )A. 平行于平面π C. 在平面π上B. 垂直于平面π D. 与平面π斜交.【解】在直线l 上任取一点⎪⎭⎫⎝⎛-0,71,7100M .直线l 的方向向量为k j i j i n n s 71428123121-+-=-=⨯=∥{}1,2,4-. 平面的法向量为{}1,2,4-=n .因为s ∥n ,所以直线l 与平面π垂直.4.设c b a u 2+-=,c b a v ---=3,试用c b a ,,表示v u 32-. 【解】v u 32-()c b a 22+-=()c b a ----33c b a 775++=.5.设点C 为线段AB 上一点,且AC CB 2=,O 为AB 外一点,记OA a =,OB b =,OC c =,试用b a ,来表示c .【解】由题意知,a b OA OB AB -=-=,a b AB AC 313131-==. 所以,a b a a b OA AC AO AC c 32313131+=+⎪⎭⎫ ⎝⎛-=+=-=.6.已知k j i a +-=32,k j i b 3+-=,j i c 2-=.计算: (1)()()b c a c b a ..-; (2)()()c b b a +⨯+. 【解】(1)()()8311312.=⨯+-⨯-+⨯=b a ; ()()8302312.=⨯+-⨯-+⨯=c a .所以,()()()()k j k j b c b c b c a c b a 24838888..--=--=-=-=-.(2)k j i j ib a +--=--=⨯581132;k j i j ic a -+=--=⨯22132;k j i j ic b -+=--=⨯362111. 所以,()()c b b b c a b a c b b a ⨯+⨯+⨯+⨯=+⨯+()k j i +--=58 ()k j i -++2 ()k j i -++36 k j --=. 【或者这样做:k j i b a 443+-=+,k j i c b 332+-=+. 所以()()c b b a +⨯+.3243k j j i--=--=】 7.已知{}2,1,2=a ,{}10,1,4-=b ,a b c λ-=,且a ⊥c ,求实数λ. 【解】{}λλλλ210,1,24----=-=a b c .因为a ⊥c ,所以 ()()()λλλ210211242.0-⨯+--⨯+-⨯==c a ,即 0927=-λ .解之得 .3=λ8.设{}1,2,3-=a ,{}2,1,1-=b ,求:(1)()()b a 72⨯;(2)i a ⨯. 【解】(1) k j i j i b a 5731123--=-=⨯{}5,7,3--=. 所以,()()b a 72⨯()b a ⨯=14{}{}70,98,425,7,314--=--=.(2){}2,1,020001123--=--=-=⨯k j i kji i a .9.3=1=,6π=,计算:(1)b a +与b a -之间的夹角;(2)以b a 2+与b a 3-为邻边的平行四边形的面积.【解】232313,.cos .=⨯⨯=⎪⎪⎭⎫ ⎝⎛=∧b a b a . ①(1+()71232322=+⨯+===;-()11232322=+⨯-===; ()()().213 (2)2=-=-=-+b b a a b a b a设b a +与b a -之间的夹角为θ,则有()(72172cos =⨯==θ,所以72arccos =θ.(2+()1314234322=⨯+⨯+===;-()319236322=⨯+⨯-===; ()()().2916233.6..3.222-=⨯--=--=-+b b b a a a b a b a设b a 2+与b a 3-之间的夹角为θ,则有()(39293132932cos -=⨯-==b a b a θ,故 2613539291cos 1sin 22=⎪⎪⎭⎫⎝⎛-=-=θθ. 所以由三角形的面积公式知,以b a 2+与b a 3-为邻边的平行四边形的面积为.32526135313sin 2=⨯⨯=⎥⎦⎤⨯-+=θS10.已知点()0,0,1A 及()1,2,0B ,试在z 轴上求一点C ,使ABC ∆的面积最小. 【解】过点()0,0,1A 及()1,2,0B 直线l 的方向即为{}1,2,1-==AB s .l 的方程为 1211:zy x l ==--. 设点()z C ,0,0,则{}2,1,22101---=--=⨯z z ji s AC . 点C 距l 的距离为()()()6212222-+-+-==z z d 65245152+⎪⎭⎫ ⎝⎛-=z明显地,当51=z 时,d 取到最小值55254=. 所以,ABC ∆的面积最小值为 53055262155221=⨯⨯==∆S ABC . 所求点.51,0,0⎪⎭⎫ ⎝⎛C11.求过点()2,1,3--且与平面01235=-+-z y x 平行的平面方程. 【解】可取所求平面的法向量与已知平面相同,即为{}3,5,1-=n . 所以,所求平面方程为()()()0231.53.1=+++--z y x ,即 .0235=-+-z y x12.求过点()1,2,1且垂直于平面0=+y x 和05=+z y 的平面方程. 【解】可取所求平面的法向量为k j i j in n n 5501121+-==⨯=. 所以,所求平面方程为()()()0152.11.1=-+---z y x ,即 .045=-+-z y x 13.求满足下列条件的平面方程.(1)过点()2,1,1--M 和()1,1,3N 且垂直于平面0532:=-+-z y x π; (2)过点()3,3,2-M 且平行于xoy 面. 【解】(1)可取所求平面的法向量为k j i j is MN n 63122122--=-=⨯=∥{}2,1,4--. 所以,所求平面方程为()()()02.21.11.4=+-+--z y x ,即 .0924=---z y x(2)根据题意,可设所求平面的一般式方程为 .0=+D Cz将点()3,3,2-M 的坐标代入平面方程得.03=+D C 即 ()03≠-=C C D . 所以,所求平面为.03=-C Cz 化简得.03=-z14.求过点()3,0,2-且与直线⎩⎨⎧=+-+=-+-.01253,0742:z y x z y x l 垂直的平面方程.【解】直线l 的方向为k j i j in n s 111416532121++-=-=⨯=. 所以,所求平面方程为()()()03.110142.16=++-+--z y x ,即.065111416=+++-z y x15.求过点()1,3,20-M 和直线⎩⎨⎧=+-=--.062,0165:z y y x l 的平面方程. 【解】化直线l 的为参数式方程⎪⎩⎪⎨⎧+==+=.62,,165:y z y y y x l .因此直线l 过点()6,0,161M .可取所求平面的法向量为{}1,3,131531410--=--==⨯=k j i j is M M n . 所以,所求平面方程为 ()()()01.13.32.1=--+--z y x ,即.0103=---z y x 【书后答案有误】.16.求过点()1,1,1M 且与直线42135:-=+=-z y x l 平行的直线方程. 【解】根据题意知,可取所求直线的方向为{}4,2,3-=s .所以,所求直线为412131--=-=-z y x . 17.求过点()4,2,00M 且与两平面12:1=+z x π和23:2=-z y π都平行的直线方程.【解】根据题意知,可取所求直线的方向为{}1,3,232100121-=++-==⨯=k j i j in n s . 所以,所求直线为143220-=-=--z y x . 18.求下列旋转曲面方程.(1)⎩⎨⎧==.0,22x y z 绕y 轴旋转一周; (2)⎪⎩⎪⎨⎧==+.0,1422y z x 绕z 轴旋转一周.【解】(1)由公式,知⎩⎨⎧==.0,22x y z 绕y 轴旋转一周生成曲面 ()y z x 2222=+±,即 222z x y += ,为椭圆抛物面.(2)由公式,知⎪⎩⎪⎨⎧==+.0,1422y z x 绕z 轴旋转一周生成曲面 ()142222=++±z y x ,即 14222=++z y x ,为椭球面. 19.指出下列各方程所表示的是何种曲面.(1)11694222=++z y x ; (2)94322y x z +=; (3)64416222=-+z y x ; (4)3694222-=+-z y x .【解】(1)表示椭球面; (2)表示椭圆抛物面;(3)可化为164164222=-+z y x ,故(3)表示单叶双曲面; (4)可化为14369222-=-+z y x ,故(4)表示双叶双曲面. 20.求曲线⎪⎪⎪⎩⎪⎪⎪⎨⎧=+=+=Γ.,1,1:2t z t t y t t x ① 对应于1=t 处的切线方程. 【解】将1=t 代入① ,得切点坐标为⎪⎭⎫ ⎝⎛1,2,21. 又切向量为()|12,1,1=⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧'⎪⎭⎫ ⎝⎛+'⎪⎭⎫ ⎝⎛+=t t t t t t s ()⎭⎬⎫⎩⎨⎧-=⎭⎬⎫⎩⎨⎧-+==2,1,412,1,11|122t t t t ∥{}8,4,1-.所以,曲线Γ对应于1=t 处的切线方程为8142121-=--=-z y x .。
czez-第七章 机械能及其守恒定律-教材习题

第七章 机械能守恒定律及其守恒7.1 追寻守恒量举出生活中的一个例子,说明不同形式的机械能之间可以相互转化. 你的例子是否向我们提示,转化过程中能的总量保持不变?答:做自由落体运动的物体在下落过程中,势能不断减少,动能不断增加,在转化的过程中,动能和势能的总和不变.7.2 功1. 图7.2-8表示物体在力F 的作用下在水平面上发生了一段位移x ,分别三种情形下力F 对物体做的功. 设这三种情形下力F 和位移x 的大小都是一样的;F=10N ,x=2m. 角θ的大小如图所示.17.32J -17.32J 17.32J2. 用起重机把重量为2.0×104N 的物体匀速地提高了5m ,钢绳的拉力做了多少功?重力做了多少功?物体克服重力做了多少功?这些力做的总功是多少?拉力做功W 1=-1×105 J ,重力做功W 2=-1×105J ,物体克服重力功1×105J ,总功是0J3. 一位质量m=60kg 的滑雪运动员从高h=10m 的斜坡自由下滑. 如果运动员在下滑过程中受到的阻力F=50N ,斜坡的倾角θ=300,运动员滑至坡底的过程中,所受的几个力做的功各是多少?这些力做的总功是多少?重力做功:6.0×103J 支持力做功:0 阻力做功:-1.0×103J 总功:5.0×103J.4. 一个 重量为10N 的物体,在15N 的水平拉力作用下,一次在光滑水平面上移动0.5m ,另一次在粗糙水平面上移动相同的距离,粗糙面与物体间与物体间的动摩擦因数为0.2. 在这两种情况下,拉力做的功各是多少?拉力这两次做的功是否相同?各个力对物体做的总功是否相同?θ Fv乙θ=30° θFv甲θ=150°θ=30°vF θ 图7.2-8解:在这两种情况下,物体所受拉力相同,移动的距离也相同,所以拉力所做的功也相同,为7.5J. 拉力做的功与是否有其他力作用在物体上没有关系,与物体的运动状态也没有关系. 光滑水平面上,各个力对物体做的总功为7.5J. 粗糙水平面上,各个力对物体做的总功为6.5N.7.3 功率1. 一台电动机工作时的功率是10kw ,要用它匀速提升2.7×104kg 的货物,提升的速度将是多大?3.7×10-2 m/s2. 一台抽水机每秒能把30kg 的水抽到10m 高的水塔上,如果不计额外功的损失,这台抽水机输出的功率是多大?如果保持这一输出功率,半小时内能做多少功? 5.4×106J.3. 有一个力F,它在不断增大. 某人以此为条件,应用P=Fv 进行了如下推导. 根据P=Fv ,F 增大则P 增大;又根据F P v =,P 增大则v 增大;再根据vPF =,v 增大则F 减小. 这个人推导的结果与已知条件相矛盾. 他错在哪里?答:此人推导的前提不明确. 当F 增大,根据P =Fv 推出,P 增大的前提应是v 不变,从P v F=推出,P增大则v 增大的前提是F 不变,从P F v=推出,v 增大F 减小的前提是P 不变.4. 质量为m 的汽车在平直公路上行驶,阻力F 保持不变. 当它以速度v. 加速度a 加速前进时,发动机的实际功率正好等于额定功率,从此时开始,发动机始终在额定功率下工作. (1)汽车的加速度和速度将如何变化?说出理由. (2)如果公路足够长,汽车最后的速度是多大?解:(1)汽车的加速度减小,速度增大. 因为,此时开始发动机在额定功率下运动,即P =F 牵v . v 增大则F 牵减小,而F Fa m-=牵,所以加速度减小. (2)当加速度减小到零时,汽车做匀速直线运动,F牵=F ,所以P v F=,此为汽车在功率P 下行驶的最大速度.7.4 重力势能1. 图7.4-8中的几个斜面,它们的高度相同. 倾角不同. 让质量相同的物体沿斜面从顶端运动到底端. 试根据功的定义计算沿不同斜面运动时重力做的功,以证明这个功与斜面的倾角无关.证明:设斜面高度为h ,对应于倾角为θ1. θ2. θ3的斜面长分别为l 1. l 2. l 3.由功的公式可知,在倾角为θ1的斜面,重力与位移的夹角为(12πθ-),重力所做的功为:WG =mg l 1cos (12πθ-)=mg l 1sinθ1=mgh. 同理可证,在倾角为θ2. θ3的斜面上,重力所做的功都等于mgh ,与斜面倾角无关.2. 如图7.4-9,质量为m 的足球在地面1的位置被踢出后落到地面3的位置,在空中达到的最高点2的高度为h.(1)足球由位置1运动到位置2时,重力做了多少功?足球克服重力做了多少功?足球的重力势能增加了多少?(2)足球由位置2运动到位置3时,重力做了多少功?足球重力势能减少了多少? (3)足球由位置1运动到位置3时,重力做了多少功?足球的重力势能变化了多少?答:(1)足球由位置1运动到位置2时,重力所做的功为-mgh ,足球克服重力所做的功为mgh ,足球的重力势能增加了mgh.(2)足球由位置2运动到位置3时,重力做的功为mgh ,足球的重力势能减少了mgh. (3)足球由位置1运动到位置3时,重力做功为零,重力势能变化为零.123h图7.4-9图7.4-83. 如图7.4-10,质量m=0.5kg 的小球,从桌面以上高h 1=1.2m 的A 点下落到地面的B 点,桌面高h 2=0.8m. (1)在表格的空白外按要求填入数据.(2)如果下落时有空气阻力,表格中的数据是否应该改变?答:(1)所选择的参考平面 小球在A 点的重力势能 小球在B 点的重力势能 整个下落过程中小球重力做的功 整个下落过程中小球重力势能的变化 桌面 5.88J -3.92J 9.8J 9.8J 地面9.8J9.8J9.8J(2)如果下落过程中有空气阻力,表格中的数据不变.4. 以下说法是否正确?如果正确,说出一种可能的实际情况;如果不正确,说明这种说法为什么错.A. 物体受拉力作用向上运动,拉力做的功是1J ,但物体重力势能的增加量不是1J.B. 物体受拉力作用向上匀速运动,拉力做的功是1J ,但物体重力势能的增加量不是1J.C. 物体运动,重力做的功是-1J ,但物体重力势能的增加量不是1J.D. 没有摩擦时物体由A 沿曲线运动到B ,克服重力做的功大于1J.所选择的参考平面小球在A 点的重力势能小球在B 点的重力势能整个下落过程中小球重力做的功整个下落过程中小球重力势能的变化桌面 地面图7.4-10答:A 正确. 例如:物体在向上的拉力作用下,如果做匀加速直线运动,这时拉力的功大于重力势能的增加量. 如果物体做匀减速直线运动,这时拉力的功小于重力势能的减少量.B 错误. 物体匀速上升,拉力的大小等于重力,拉力的功一定等于重力势能的增加量.C 错误. 根据W G =E p1-E p2可知,重力做-1J 的功,物体势能的增加量为1J.D 错误. 重力做功只与起点和终点的位置有关,与路径无关,A. B 两点的位置不变,从A 点到B点的过程中,无论经过什么路径,重力的功都是相同的.7.7 动能和动能定理1. 改变汽车的质量和速度,都可能使汽车的动能发生改变. 在下列几种情形下,汽车的动能各是原来的几倍?A. 质量不变,速度增大到原来的2倍.B. 速度不变,质量增大到原来的2倍.C. 质量减半,速度增大到原来的4倍.D. 速度减半,质量增大到原来的4倍.答:a .动能是原来的4倍. b .动能是原来的2倍. c .动能是原来的8倍. d .动能不变.2. 把一辆汽车的速度从10km/h 加速到20km/h ,或者从50km/h 加速到60km/h ,哪种情况做的功比较多?通过计算说明.解:由动能定理W =E k2-E k1=22211()2m v v -可知,在题目所述的两种情况下,第二种情况增加的动能较大,需要做的功较多.速度由10km/h 加速到20km/h 的情况下:(2221v v -)=(202-102)(km/s )2=300(km/s )2 速度由50km/h 加快到60km/h 情况下:(2221v v -)=(602-502)(km/s )2=1100(km/s )2可见,后一种情况所做的功比较多.3. 质量是2g 的子弹,以300m/s 的速度射入厚度是5cm 的木板(图7.7-4),射穿后的速度是100m/s. 子弹射穿木板的过程中受到的平均阻力是多大?你对题目中所说的“平均”一词有什么认识?解:设平均阻力为f ,根据动能定理W =22211122mv mv - ,有 f scos180°=22211122mv mv -. f =1.6×103N ,子弹在木板中运动5cm 时,所受木板的阻力各处不同,题目所说的平均阻力是对这5cm 说的.4. 我们在第四章曾用牛顿运动定律解答过一个问题:民航客机机舱紧急出口的气囊是一条连接出口与地面的斜面,若斜面高3.2m ,斜面长6.5m ,质量60kg 的人沿斜面滑下时所受的阻力是240N ,求人滑至底端时的速度. 请用动能定理解答本题.42m/s≈5.66m/s5、运动员把质量是500g 的足球踢出后,某人观察它在空中的飞行情况,估计上升的最大高度是10m ,在最高点的速度为20m/s. 请你根据这个估计,计算运动员踢球时对足球做的功. 150J7.8 机械能守恒定律1. 如图7.8-6,质量为m 的小球从光滑曲面上滑下. 当它到达高度为h 1的位置A 时,速度的大小为v 1,滑到高度为h 2的位置B 时,速度的大小为v2. 在由高度h 1滑到高度h 2的过程中,重力做的功为W. (1)根据动能定理列出方程,描述小球在A. B 两点间动能的关系.(2)根据重力做功与重力势能的关系,把以上方程变形,以反映出小球运动过程中机械能是守恒的.(1)小球在从A 点下落至B 点的过程中,根据动能定理W =ΔE k , mg(h 1-h 2)=22211122mv mv -(2)由mg(h 1-h 2)=22211122mv mv -,得:mgh 1+2112mv =mgh 2+2212mv等式左边表示物体在A 点时的机械能,等式右边表示物体在B 点时的机械能,小球从A 点运动到B 点的过程中,机械能守恒.2. 神舟号载人飞船在发射至返回的过程中,以下哪些阶段中返回舱的机械能是守恒的? A. 飞船升空的阶段.B. 飞船在椭圆轨道上绕地球运行的阶段.C. 返回舱在大气层以外向着地球做无动力飞行的阶段.D. 降落伞张开后,返回舱下降的阶段.答:A .飞船升空的阶段,动力对飞船做功,飞船的机械能增加.B .飞船在椭圆轨道上绕地球运行的阶段,只有引力对飞船做功,机械能守恒.C .飞船在空中减速后,返回舱与轨道分离,然后在大气层以外向着地球做无动力飞行的过程中,只有引力做功,机械能守恒.D .进入大气层并运动一段时间后,降落伞张开,返回舱下降的过程中,空气阻力做功,机械能减少.3. 把质量为0.5kg 的石块 从10m 高处以300角斜向上方抛出(图7.8-7),初速度是v 0=5m/s. 不计空气阻力.(1)石块落地时的速度是多大?请用机械能守恒定律和动能定理分别讨论. (2)石块落地时的速度的大小与下列哪些量有关,与哪些量无关?说明理由.图7.8-6A. 石块的质量B. 石块初速度的大小C. 石块初速度的仰角D. 石块抛出时的高度解:(1)石块从抛出到落地的过程中,只有重力做功,所以机械能守恒. 设地面为零势能面,根据机械能守恒定律:2201122t mv mgh mv +=,得根据动能定理:W =E kt -E k0,即mgh = 2201122t mv mv -,v t =202v gh +v t =15m/s(2)由v t =202v gh +知,石块落地时速度大小与石块初速度大小和石块抛出时的高度有关,与石块的质量和石块初速度的仰角无关.4. 有一种地下铁道,车站的路轨建得高些,车辆进站时要上坡,出站时要下坡,如图7.8-8. 设坡高h 为2m ,进站车辆到达坡下的A 点时,速度为25.2km/h ,此时切断电动机的电源,车辆能不能“冲”到坡上?如果能够,到达坡上的速度是多大?列车能冲上站台, 3m/s7.9 实验:验证机械能守恒定律1. 把质量是0.2kg 的小球放在竖立的弹簧上,并把球往下按至A 的位置,如图7.9-3甲所示. 迅速松手后,弹簧把球弹起,球升至最高位置C (图丙),途中经过位置B 时弹簧正好于自由状态(图乙). 已知B. A 的高度差为0.1m ,C. B 的高度差为0.2m ,弹簧的质量和空气的阻力均可忽略. (1) 分别说出由状态甲至状态乙. 由状态乙至状态丙的能量转化情况. (2) 状态甲中弹簧的弹性势能是多少?状态乙中小球的动能是多少?答:(1)从状态甲至状态丙过程中,弹性势能逐渐减少,动能和重力势能逐渐增大,当弹簧对小球向上的弹力大小与小球所受重力大小相等时,小球动能最大. 之后,弹性势能和动能逐渐减小,重力势能逐渐增大,当弹簧恢复到自然长度时,弹性势能为0. 之后,重力势能仍然逐渐增大,动能逐渐减小,到达C 点时,动能减少到0,重力势能达到最大.小球从状态甲运动到状态丙的过程中,机械能守恒. 故状态甲中,弹簧的弹性势能 ()()0.2100.10.20.6p AB BC E mg h h =+=⨯⨯+= J(2)小球从状态乙到状态丙的过程中,动能逐渐减少,重力势能逐渐增大.小球从状态乙到状态丙的过程中,机械能守恒,所以小球在B 点的动能与小球在C 点的势能相等. 故小球在状态乙中的动能0.2100.20.4k BC E mgh ==⨯⨯= J2. 游乐场的过山车可以底朝上在圆轨道上运行,游客却不会掉下来(图7.9-4). 我们把这种情形抽象为图7.9-5的模型:弧形轨道的下端与竖直圆轨道相接,使小球从弧形轨道上端滚下,小球进入圆轨道下端后沿圆轨道运动. 实验发现,只要h 大于一定值,小球就可以顺利通过圆轨道的最高点. 如果已知圆轨道的半径为R ,h 至少要等于多大?不考虑摩擦等阻力.AB C甲乙 丙5R23、第五章第2节“问题与练习”第3题描述了一个实验. 实际做一做这个实验,用你当时得到的计算式计算钢球离开桌面的高度,按照机械能守恒定律计算钢球到达桌面的速度. 对比两种不同方法得到的速度值并尝试解释两者的差异.答:用平抛运动的知识测出的小球离开桌面时的速度要略大于小球从斜面上滚下的过程中用机械能守恒定律算出的速度,这是由于小球从斜面与桌面上运动时受到的摩擦阻力远大于小球做平抛运动时所受的空气阻力.7.10 能量守恒定律与能源1. 生活中的许多用品都可以看做能量转换器,它们把能量从一种形式转化为另一种形式. 请观察你家中的各种生活用品,分别指出它们工作时发生了哪些能量转化.答:家用电饭锅是把电能转化为内能;洗衣机是把电能转化为动能,等等.2. 三峡水力发电站是我国最大的水力发电站,平均水位落差约100m,水的流量约1.35×104m3/s. 船只通航需要约3500m3/s的流量,其余流量全部用来发电. 水流冲击全部用来发电. 水流冲击水轮机发电时,水流减少的机械能有20%转化为电能.(1)按照以上数据估算,三峡发电站的发电功率最大是多少?(2)根据你对家庭生活用电量的调查,如果三峡电站全部用于城市生活用电,它可以满足多少个百万人口城市的生活用电?(1)2.7×106kW (2)设三口之家每户的家庭生活用电功率为1kW,考虑到不是每家同时用1kW的电,我们平均每家同时用电0.5kW,则三峡发电站能供给=5.8×106户用电,人口数为3×5.8×106=17×106人,即可供17个百万人口城市的生活用电.3. 为了节约能源,从个人的角度讲,你能做些什么?从社会的角度讲,你能为决策者提出什么建议?。
第七章恒定磁场-习题解答

7-3 如图所示,一无限长载流绝缘直导线弯成如附图所示的
形状。求使o点的磁感应强度为零的半径a和b的比值。
解 该载流系统由三部分组成,o点的磁感
应强度为载有相同电流的无限长直导线
及两个半径分别为a和b的圆环分别在该
处激发的磁感应强度的矢量和。设磁场 方向以垂直纸面向内为正,向外为负。
方向垂直纸面向里。 (2)由磁矩定义
方向垂直纸面向里。
第七章、稳恒磁场
7-20 质谱仪的构造原理如图所示。离子源S提供质量为M、
电荷为q的离子。离子初速很小,可以看作是静止的,然后经
过电压U的加速,进入磁感应强度为B的均匀磁场,沿着半圆
周运动,最后到达记录底片P上。测得离子在P上的位置到入
口处A的距离为x。试证明该离子的质量为:M ? qB 2 x 2 。
或由磁感应线是闭合曲线,也可推知
??
Φaefd
?
? Φabcd
?
0.24Wb
? Φ ? ?B?dS ? 0
第七章、稳恒磁场
7-9 一个非均匀磁场磁感应强度的变化规律为B=ky(k为常 量),方向垂直纸面向外。磁场中有一边长为a的正方形线 框,其位置如图所示。求通过线框的磁通量。
解 在线框内坐标为y处取一长为a宽为 dy的矩形面积元dS,在dS中磁场可认 为是均匀的,则通过dS的磁通量
? I2l
? 0 I1
2πx1
I2l
? ?7.2?
F2 10?4
? B2I2l N
?
? 0 I1
2πx2
I2l
负号表示合力方向水平向左。
第七章、稳恒磁场
习题7-16 一长直导线通有电流I =20A,另一导线ab通 有电流I?=10A,两者互相垂直且共面,如图所示。求导 线ab所受的作用力和对o点的力矩。
第七章 统计热力学习题及解答

第七章 习题及解答1. 设有一个体系,由三个定位的一维简谐振子所组成,体系能量为νh 211,这三个振子在三个固定的位置上振动,试求体系全部的微观状态数.解 对振动 νυενh )21(+=,在总能量 νενh 211=时,三个一维简谐振子可能有以下四种分布方式:(1)N 0=2, N 4=1, νενh 2120⨯=, νενh 294=, 3!2!1!31==t (2)N 0=1, N 2=2, νενh 2110⨯=, νενh 2522⨯=, 3!2!1!32==t (3)N 0=1, N 1=1, N 3=1, νενh 210=, νενh 231=, νενh 273=, 6!1!1!1!33==t (4)N 1=2, N 2=1, νενh 2321⨯=, νενh 252=, 3!2!1!34==t Ω= t 1+t 2+t 3+t 4=3+3+6+3=152。
当热力学体系的熵函数S 增加0.418J ·K —1时,体系的微观状态数增加多少?用1/∆ΩΩ表示。
解 S 1=kln Ω1, S 2=kln Ω2, S 2—S 1=kln (Ω2/Ω1)ln(Ω2/Ω1)=(S 2—S 1)/k=(0。
418J·K -1)/(1.38×10—23J ·K -1)=3。
03×10221/Ω∆Ω=(Ω2—Ω1)/Ω1=(Ω2/Ω1)-1≈Ω2/Ω1= exp (3。
03×1022)3。
在海平面上大气的组成用体积百分数可表示为:N 2(g )为0.78,O 2(g)为0。
21,其他气体为0。
01。
设大气中各种气体都符合Bolzenmann 分布,假设大气柱在整个高度内的平均温度为220K 。
试求:这三类气体分别在海拔10km ,60km 和500km 处的分压.已知重力加速度为9.8m·s -2。
解 所用公式为p=p 0e —Mgh/RT ,其中M (空气) =29g·mol —1, M(N 2)=28g·mol —1, M (O 2)=32g·mol —1,M (其它)=[M(空气)—0。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第七章化学平衡习题解答1.回答下列问题(1)反应商和标准平衡常数的概念有何区别? (2)能否用r m G θ∆来判断反应的自发性?为什么? (3)计算化学反应的K θ有哪些方法?(4)影响平衡移动的因素有哪些?它们是如何影响移动方向的? (5)比较“温度与平衡常数的关系式”同“温度与反应速率常数的关系式”,有哪些相似之处?有哪些不同之处?举例说明。
(6)酸碱质子理论如何定义酸和碱?有何优越性?什么叫共轭酸碱对?(7)当往缓冲溶液中加入大量的酸和碱,或者用很大量的水稀释时,pH 是否仍保持不变?说明其原因。
(8)对于一个在标准状态下是吸热、熵减的化学反应,当温度升高时,根据勒夏特列原理判断,反应将向吸热的正方向移动;而根据公式∆r G m θ=∆r H m θ-T ∆r S m θ判断,∆r G m θ将变得更正(正值更大),即反应更不利于向正方向进行。
在这两种矛盾的判断中,哪一种是正确的?简要说明原因。
(9)对于制取水煤气的下列平衡系统:22C(s)+H O(g)CO(g)+H (g) ;r m H Θ∆。
问:① 欲使平衡向右移动,可采取哪些措施?② 欲使正反应进行得较快且较完全(平衡向右移动)的适宜条件如何?这些措施对K θ及k(正)、k(逆)的影响各如何?(10)平衡常数改变时,平衡是否必定移动?平衡移动时,平衡常数是否一定改变?【解答】(1)反应商是在一定温度下,任意给定态时,生成物的相对压力(或者相对浓度)以方程式中化学计量系数为幂的乘积除以反应物的相对压力(或相对浓度)以化学计量系数为幂的乘积。
在一定温度下,当反应达到平衡时,生成物的相对压力(或者相对浓度)以方程式中化学计量系数为幂的乘积除以反应物的相对压力(或相对浓度)以化学计量系数为幂的乘积是一个常数,称为标准平衡常数,是量纲为一的量。
标准平衡常数的数值只是温度的函数。
(2)只能用r m G θ∆判断在标准态下的反应的自发性。
任意给定态时,反应的自发进行的方向只能由r m G ∆来判断。
若r m G 0∆<,表示正反应自发进行;r m G 0∆>,表示逆反应自发进行; r m G 0∆=,表示反应处于平衡状态。
(3)根据化学平衡定律计算,即由在一定温度下,当反应达到平衡时,生成物的相对压力(或者相对浓度)以方程式中化学计量系数为幂的乘积与反应物的相对压力(或相对浓度)以化学计量系数为幂的乘积之比求得标准平衡常数;由r mG RT ln K ΘΘ∆=-,得r m G -RTK = e Θ∆Θ(4)浓度对化学平衡的影响:若提高反应物浓度(或分压)或降低生成物浓度(或分压),平衡向右移动;减少反应物的浓度(或分压)或增加生成物的浓度(或分压),平衡向左移动。
压力对化学平衡的影响:增加压力,平衡向气体分子数减少的方向移动;降低压力,平衡向气体分子数增多的方向移动。
温度对化学平衡的影响:温度升高,平衡向着吸热反应方向移动;降低温度时,平衡向着放热反应的方向移动。
(5)温度与平衡常数的关系:由r mG RT ln K ΘΘ∆=-和r mr mr mG H T S ΘΘΘ∆=∆-∆得r m r mH S ln K RT RΘΘΘ∆∆=-+;温度与反应速率常数的关系式:Ea RTk Ae-=或Ealnk ln A RT=-相似之处:平衡常数K Θ和反应速率常数k 都是温度的函数,lnK Θ和lnk 都与1T成正比; 不同之处:温度与平衡常数的关系反映了化学反应热效应对平衡常数的影响,温度与反应速率常数的关系反映了活化能对反应速率的影响。
(6)酸碱质子理论认为:凡能给出质子H +的为酸,能接受质子H +的为碱;酸碱质子理论中酸与碱不是彼此孤立的,而是统一在对质子的联系上;相差一个质子的酸碱对,称为共轭酸碱对。
(7)当往缓冲溶液中加入大量的酸和碱,或者用很大量的水稀释时,pH 要发生变化。
这是因为,缓冲溶液的缓冲能力具有一定的限度,如果外界变化超出这个限度,那么缓冲液pH 将会变化很大。
(8)第一种说法正确。
由公式r m r mH S ln K RT RΘΘΘ∆∆=-+可知,对于一个在标准状态下的吸热、熵减的化学反应,当温度升高时,化学反应标准准平衡常数K Θ增加,反应向吸热的正方向移动可降低环境的温度,勒夏特列原理只适用于已经处于平衡状态的系统;由r m r m r m G H T S ΘΘΘ∆=∆-∆可知,对于一个在标准状态下的吸热、熵减的化学反应,在标准态、任意温度下r mG 0Θ∆>,正向反应不能自发进行。
(9)①增加H 2O 浓度或减少CO 和H 2的浓度;升高温度;减小压强。
②高温低压。
升高温度,由r m r mH S ln K RT RΘΘΘ∆∆=-+可知,对于吸热反应r mH 0Θ∆>,标准平衡常K Θ增加;由Ea RTk Ae-=可知,化学反应速率常数k(正)和k (负)都增加。
降低压强,标准平衡常K Θ、化学反应速率常数k (正)和k (负)都不变,它们只是温度的函数。
(10)平衡常数改变时,平衡不一定移动。
平衡常数只与温度有关,当温度与其他量如浓度、体积、压强等一同改变时,平衡可能不移动;平衡移动时,平衡常数也不一定改变,当温度不变而由浓度、体积、压强的变化引起平衡移动时,平衡常数不变。
2.写出下列各反应的p K 、K Θ表达式 (1)222111NOCl(g)N (g)+Cl (g)+O (g)222(2)2322Al O (s)+3H (g)2Al(s)+3H O(g)(3)43NH Cl(s)HCl(g)+NH (g)(4)323222NaHCO (s)Na CO (s)+CO (g)+H O(g)【解答】 (1)222111222N Cl O P NOCl (p )(p )(p )K (p )=222111N Cl O 222NOClp p p ()()()pppK p ()p ΘΘΘΘΘ=(2)223H O P 3H (p )K (p )=,223H O 3H p ()p K p ()pΘΘΘ=(3)3P HCl NH K p p =⨯,3NH HCl p p K p pΘΘΘ=⋅ (4)22P CO H O K p p =⨯,3NH HCl p p K p p ΘΘΘ=⋅3.已知反应(1)22H (g)S(s)H S(g)+→ 3(1)K 1.010θ-=⨯ (2)22S(s)O (g)SO (g)+→ 6(2)K 5.010θ=⨯计算下列反应的K θ值2222H (g)SO (g)H S(g)O (g)+→+【解答】根据多重平衡原理,(1)-(2)得(3)3(1)106(2)K 1.110K 2.210K 5.010Θ-Θ-Θ⨯===⨯⨯ 4.将空气中的单质氮变成各种含氮的化合物的反应叫做固氮反应。
根据r m G θ∆(298.15K )及K θ。
从热力学的角度看选择哪个反应为最好?22N (g)O (g)2NO(g)+→ 2222N (g)O (g)2N O(g)+→ 223N (g)3H (g)2NH (g)+→【解答】(1) 22N (g)O (g)2NO(g)+→1f m G (kJ mol )θ-∆⋅ 0 0 86.57 1r m G 286.57173.14kJ molθ-∆=⨯=⋅,r m G 173.141000318.314298.15RTK ee4.6310Θ∆⨯--Θ-⨯===⨯(2) 2222N (g)O (g)2N O(g)+→1f m G (kJ mol )θ-∆⋅ 0 0 104.21r m G 2104.2208.4kJ molθ-∆=⨯=⋅,r m G 208.41000388.314298.15RTK ee3.0810Θ∆⨯--Θ-⨯===⨯(3) 223N (g)3H (g)2NH (g)+→1f m G (kJ mol )θ-∆⋅ 0 0 -16.5 1r m G 2(16.5)33kJ molθ-∆=⨯-=-⋅,r m G 33100058.314298.15RTK ee6.0510Θ∆-⨯--Θ⨯===⨯由上述计算可知,r m G Θ∆越正,平衡常数K θ越大,所以第三个反应平衡常数最大,进行最彻底,所以第三个反应最好。
5.已知反应2211H (g)Cl (g)HCl(g)22+→ 在298.15K 时,K θ=4.97×1016, r mH θ∆(298.15K )=-92.307 kJ·mol -1,求500K 时的K θ(500K )。
【解答】 由公式2r m 21112K H (T T )92.3071000500298.15ln 15.0331K R T T 8.314500298.15ΘΘΘ∆--⨯-=-⋅=-⋅=⨯ 已知K θ(298.15K)=4.97×1016,得K θ(500K)=1.68×10236.设汽车内燃机内温度因燃料燃烧反应达到1300℃,试估算反应2211N (g)O (g)NO(g)22+=在25℃和1300℃时的r m G θ∆和K θ的数值。
并联系反应速率简单说明在大气污染中的影响。
【解答】2211N (g)O (g)NO(g)22+= 1f m H (kJ mol )θ-∆⋅ 0 0 90.25 11m S (J mol K )θ--⋅⋅ 191.6 205.14 210.76 1r m H (298.15K)90.25kJ mol θ-∆=⋅11r m11S (298.15K)210.76205.14191.612.39J mol K 22θ--∆=-⨯-⨯=⋅⋅ r m r m r m1G (298.15K)H T S 90.251000298.1512.3986555.92J mol θΘΘ-∆=∆-∆=⨯-⨯=⋅ r m G RT86555.928.314298.1516K (298.15K)ee6.8410Θ∆-Θ-⨯-===⨯r m r m r m1G (1573.15K)H T S 90.2510001573.1512.3970758.67J mol θΘΘ-∆=∆-∆=⨯-⨯=⋅ r m G RT70758.678.3141573.153K (1573.15K)ee4.4710Θ∆-Θ-⨯-===⨯由计算结果表明,汽车内燃机内温度因燃料燃烧反应达到1300℃,2211N (g)O (g)NO(g)22+=,在标准态下正向不能自发进行,且化学反应达到平衡时,正向反应进行的程度非常低。
7.PCl 5加热分解成PCl 3和Cl 2。
将2.659gPCl 5装入体积为1.0dm 3的密闭容器中,在523K 达到平衡时系统总压力为100kPa 。
