振动与波习题课共28页文档
合集下载
振动与波习题课
b
c
O
a
.
b
c X t
a 0
b
2
3 c 2
10.如图（a）为t=0时的波形曲线,经0.5s后波形变为（b） 求（1）波动方程 Y (a) (b) u
（2）P点的振动方程
解：O处的振动方程为 0.1
yo A cos(t )
由图得A=0.1 =/2 =4m
( 2k 1) 2 2 1 1 2 ( 2k 1) 4 r1 [ ] 2 ( 2k 1) 2 ( 2k 1)
Y
u=0.08m/s P . 0.02
X yo A cos(t ) -0.04 0.04 P点的振动方程 2 1 T u 0.08 令x=0.02 u 2 2 3 4 y P 0.04 cos(4t ) T 2 x y 0.04 cos[4 ( t ) ] 0.08 2
A A A 2 A1 A2 cos( 2 1 ) A1 sin 1 A2 sin 2 tg A1 cos 1 A2 cos 2 2 1 B.同方向不同频率：拍 拍频为：
A. 同方向同频率：
2 1 2 2
C.两个相互垂直同频率的振动：椭圆 D.两个相互垂直不同频率的振动：李萨如图 5.平面简谐波波动方程：
u 0.84m / s 取 /3
故得波动方程为
17 / 3
O a b
u
X
x y 0.1cos[7 ( t ) ]( m ) 0.84 3
13.题中图a表示一水平轻绳，左端D为振动器，右端 固定于B点。t0时刻振动器激起的简谐波传到O点。其 波形如图b所示。已知OB＝2.4m，u=0.8m/s. 求：（1） 以为计时零点，写出O点的谐振动方程；（2）取O 点 为原点，写出向右传播的波动方程；（3）若B 处有 半波损失，写出反射波的波动方程（不计能量损失）。 2 D O 解：（1）由 B u 2 2 y(cm) 得 u 80 4 40 4
振动与波动习题课
A
(1) B处质元的振动动能减小 处质元的振动动能减小, 则其弹性势能必增大; 则其弹性势能必增大 错 答:质元的振动动能和弹 质元的振动动能和弹 性势能是同相位的 ,同 时增大,同时减少. 时增大,同时减少.
B
o
C
x
(2) A处质元回到平衡位置的过程中 它把自己的能量 处质元回到平衡位置的过程中,它把自己的能量 传给相邻的质元,其能量逐渐减小 其能量逐渐减小; 传给相邻的质元 其能量逐渐减小 错 在平衡位置质元的振动动能和弹性势能是最大, 答:在平衡位置质元的振动动能和弹性势能是最大,所 质元回到平衡位置的过程中能量应该逐渐增大 能量应该逐渐增大. 以A处质元回到平衡位置的过程中能量应该逐渐增大.
关于干涉条件的讨论
y1 = A1 cos( ω t + 10
y2 = A2 cos( ω t + 20
P点的合振动为 点的合振动为
2π r1
2π r2
λ
)
注意: 为正值! 注意:r1, r2为正值! P
r1
λ
)
S1 r2 S2
y = y1 + y2 = A cos( ω t + 0 )
2 1 2
波动学基础
教学要求
1 . 掌握平面简谐波波动方程的物理意义 掌握由质点 掌握平面简谐波波动方程的物理意义.掌握由质点 的谐振动方程或某时刻的简谐波波形曲线等已知条件建 立简谐波波动方程的方法. 立简谐波波动方程的方法 2 .理解波长,周期,频率,波速等概念的含意 并掌 理解波长, 理解波长 周期,频率,波速等概念的含意,并掌 握它们之间的关系. 握它们之间的关系 3 .理解波的干涉现象 掌握波的相干条件 能运用相位 理解波的干涉现象.掌握波的相干条件 理解波的干涉现象 掌握波的相干条件.能运用相位 差或波程差来确定相干波叠加后加强或减弱的条件. 差或波程差来确定相干波叠加后加强或减弱的条件 4 .理解驻波的特性及其形成条件 了解驻波与行波的 理解驻波的特性及其形成条件.了解驻波与行波的 理解驻波的特性及其形成条件 区别. 区别 5 .理解波的能量传播特征以及能流,能流密度等概念 理解波的能量传播特征以及能流, 理解波的能量传播特征以及能流 能流密度等概念. 6.掌握多普勒效应 6.掌握多普勒效应
(1) B处质元的振动动能减小 处质元的振动动能减小, 则其弹性势能必增大; 则其弹性势能必增大 错 答:质元的振动动能和弹 质元的振动动能和弹 性势能是同相位的 ,同 时增大,同时减少. 时增大,同时减少.
B
o
C
x
(2) A处质元回到平衡位置的过程中 它把自己的能量 处质元回到平衡位置的过程中,它把自己的能量 传给相邻的质元,其能量逐渐减小 其能量逐渐减小; 传给相邻的质元 其能量逐渐减小 错 在平衡位置质元的振动动能和弹性势能是最大, 答:在平衡位置质元的振动动能和弹性势能是最大,所 质元回到平衡位置的过程中能量应该逐渐增大 能量应该逐渐增大. 以A处质元回到平衡位置的过程中能量应该逐渐增大.
关于干涉条件的讨论
y1 = A1 cos( ω t + 10
y2 = A2 cos( ω t + 20
P点的合振动为 点的合振动为
2π r1
2π r2
λ
)
注意: 为正值! 注意:r1, r2为正值! P
r1
λ
)
S1 r2 S2
y = y1 + y2 = A cos( ω t + 0 )
2 1 2
波动学基础
教学要求
1 . 掌握平面简谐波波动方程的物理意义 掌握由质点 掌握平面简谐波波动方程的物理意义.掌握由质点 的谐振动方程或某时刻的简谐波波形曲线等已知条件建 立简谐波波动方程的方法. 立简谐波波动方程的方法 2 .理解波长,周期,频率,波速等概念的含意 并掌 理解波长, 理解波长 周期,频率,波速等概念的含意,并掌 握它们之间的关系. 握它们之间的关系 3 .理解波的干涉现象 掌握波的相干条件 能运用相位 理解波的干涉现象.掌握波的相干条件 理解波的干涉现象 掌握波的相干条件.能运用相位 差或波程差来确定相干波叠加后加强或减弱的条件. 差或波程差来确定相干波叠加后加强或减弱的条件 4 .理解驻波的特性及其形成条件 了解驻波与行波的 理解驻波的特性及其形成条件.了解驻波与行波的 理解驻波的特性及其形成条件 区别. 区别 5 .理解波的能量传播特征以及能流,能流密度等概念 理解波的能量传播特征以及能流, 理解波的能量传播特征以及能流 能流密度等概念. 6.掌握多普勒效应 6.掌握多普勒效应
振动和波习题课(级)
Y
能量极 小
X
能量极 大
能量极大
能量极 小
16、惠更斯原理：波阵面上的每一点，都是发射 子波的新波源，其后任意时刻，这些子波的包络 面就是新的波阵面。
17、相干条件：两波源应满足：振动方向相同，
频率相同，位相差恒定。
18、波的干涉 在P点引起的合振动的振幅为：
2 1 2 2
S2 S1
r2
p
2 ( 2 1 )＋ ( r1 r2 ) A A A 2 A1 A2 cos S1 r1 若波在两种不同介质中传播
2
y a O b u x
[A]
11.一质点同时参与了三个简谐振动，它们的振动 1 5 方程分别为 x1 A cos( t π ) x2 A cos( t π)
x3 A cos( t π ) 其合成运动的运动方程为x = ___ 0 ．
3
3
12. 一简谐波沿x轴负方向传播，波速为1 m/s，在 x轴上某质点的振动频率为1 Hz、振幅为0.01 m．t =0 时该质点恰好在正向最大位移处．若以该质点 的平衡位置为x轴的原点．求此一维简谐波的表达 式． 结 果 : y 0 . 01 cos 2π ( t x ) (SI) 13. 当机械波在媒质中传播时，一媒质质元的最大 变形量发生在 : (A) 媒质质元离开其平衡位置最大 位移处． (B) 媒质质元离开其平衡位置( 2 A / 2 )处 (A是振动振幅)． (C) 媒质质元在其平衡位置处． 1 [C] (D) 媒质质元离开其平衡位置 2 A 处.
2
2
(C)
3 x2 A cos( t π ) 2
t π ) [B] (D)x2 A cos(
能量极 小
X
能量极 大
能量极大
能量极 小
16、惠更斯原理：波阵面上的每一点，都是发射 子波的新波源，其后任意时刻，这些子波的包络 面就是新的波阵面。
17、相干条件：两波源应满足：振动方向相同，
频率相同，位相差恒定。
18、波的干涉 在P点引起的合振动的振幅为：
2 1 2 2
S2 S1
r2
p
2 ( 2 1 )＋ ( r1 r2 ) A A A 2 A1 A2 cos S1 r1 若波在两种不同介质中传播
2
y a O b u x
[A]
11.一质点同时参与了三个简谐振动，它们的振动 1 5 方程分别为 x1 A cos( t π ) x2 A cos( t π)
x3 A cos( t π ) 其合成运动的运动方程为x = ___ 0 ．
3
3
12. 一简谐波沿x轴负方向传播，波速为1 m/s，在 x轴上某质点的振动频率为1 Hz、振幅为0.01 m．t =0 时该质点恰好在正向最大位移处．若以该质点 的平衡位置为x轴的原点．求此一维简谐波的表达 式． 结 果 : y 0 . 01 cos 2π ( t x ) (SI) 13. 当机械波在媒质中传播时，一媒质质元的最大 变形量发生在 : (A) 媒质质元离开其平衡位置最大 位移处． (B) 媒质质元离开其平衡位置( 2 A / 2 )处 (A是振动振幅)． (C) 媒质质元在其平衡位置处． 1 [C] (D) 媒质质元离开其平衡位置 2 A 处.
2
2
(C)
3 x2 A cos( t π ) 2
t π ) [B] (D)x2 A cos(
振动与波习题课.
B
P x
30x
C
x
解：（1） 1 = 2 ，在BC间取一P点(如图) BP = r1 = x 由题意，应有 代入数值 CP = r2 = 30 x
4 x (30 x) (2k 1) 4k 2 2
r1 r2 ( 2 k 1) 2
x = 2k +16
k = 0, 1, 2,
（Ａ）
（B） （C） 5 （D） 0
2 4
A
a
b
o
A
2
9 8
解：由驻波位相分布特点知，同一波节两侧各点的位相相反。
所以选（Ａ）
9、当一平面简谐波通过两种均匀介质时，不会变化的物理量 是 A、波长和频率； C、波长和波速； 答案：D 10、已知一平面简谐波的表达式为y=Acos（at-bx），a、b为 正值，则 A、波的频率为a； B、波的传播速度为b/a； C、波长为π /b 答案：D D、波的周期为2π/a B、波速和频率 D、频率和周期
t x t x C y2 A cos2 0 D y2 A cos2 T T
解：反射波的传播方向与入射波方向相反，反射点为波节， 说明有半波损失。 故应选 (D)
8 某时刻驻波波形图曲线如图所示，则a,b两点位相差是
11、一周期为T的横波沿x轴正向传播，若t时刻波形曲线如图 所示，则在t+T/4时刻，x轴上1、2、3三点的振动位移分别是
A、A，0，-A； B、 -A，0，A
C、 0，A，0；
D、 0，-A，0；
12、图中为t=0时刻，以余弦函数表示的沿x轴正向传播的平面 简谐波的波动方程，则O点处质点振动的初相位为 A、 π/2 B、0 C、3 π/2 D、 π 答案:C
大学物理振动和波习题课
12、一质点作简谐振动，周期为 T。质点由平衡
位置向Ｘ轴正方向运动时，由平衡位置到二分之一 最大位移这段路程所需要的时间为（ ）。
A T 4 B T 1 C 2 T 6 D T 8
解：令简谐振动为 xA si n t
则当 xA2 时， si n t0.5
Acos2(t 1) T2
Acos2T(t 13)
.
7.图中所示为两个简谐振动的振动曲线．若以余弦函数表 示这两个振动的合成结果，则合振动的方程为
xx1x2 0.04cos(t)
x (m)
0.08
O
-0.04
1
x1 t (s)
2 x2
.
8 如果在固定端 x0处反射的反射波方程式是
y2 Aco2stx
设反射波无能量损失，则入射波的方程式是（ ） 形成的驻波的表达式是（ ）。
y1OAcos2vt y2OA cos2vt
形成的驻入 波射 为波 ：方 程 y1Acos 2 t x
y y 1 y 2 A c 2 ot s2 x A c 2 ot s2 x
得：
S
wu
1 A22u
2
3.惠更斯原理和波的叠加原理
惠更斯原理:
波阵面上每一点都可以看作是发出球面子波的 新波源，这些子波的包络面就是下一时刻的波阵面。
波的叠加原理:
当几列波在介质中某点相遇时，该质点的
振动位移等于各列波单独传播时在该点引起位 移的矢量和。
.
4.波的干涉: 相干条件： 振动方向相同
频率相同
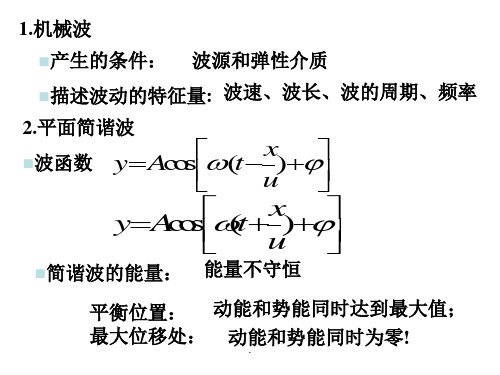
1.机械波
产生的条件： 波源和弹性介质
描述波动的特征量: 波速、波长、波的周期、频率
2.平面简谐波
波函数 yAcos(tux)
机械振动和波习题课_百度文库
2007-2008学年第二学期大学物理“振动和波”习题课1、一谐振动的余弦曲线如图,则A=ω=φ=2、一简谐振子的振动曲线如图所示,则以余弦函数表示该振动方程。
3、由曲线求振动方程。
24、一物体沿X 轴作简谐振动,振幅为0.12m ,周期为2s 。
当 t=0 时位移为0.06m ,且向X 轴正方向运动。
求:(1初相,(2在 x=-0.06m 处,且向X 轴负方向运动时,物体的速度和加速度,以及从这一位置回到平衡位置所需的时间。
5、一物体作简谐振动,其振幅为24cm ,周期为4s ,当t=0时,位移为-12cm 且向x 轴负方向运动,求1简谐振动方程; 2物体由起始位置运动到x=0处所需的最短时间。
6、一弹簧振子作简谐振动,当其偏离平衡位置的位移的大小为振幅的1/4时,其动能为振动总能量的A 1/4B 3/4C 1/16D 15/167、两个谐振动分别为cm cos(431051π+=t x ,cm cos(22106ϕ+=t x ;当ϕ2= 时,合振幅最大;当ϕ2= 时,合振幅最小,且写出它们的合振动方程。
8、沿X 轴正方向传播的平面简谐波、在 t=0 时刻的波形如图,问:(1原点O的初相及P点的初相各为多大?(2已知A及ω,写出波动方程。
9、一平面简谐波某时刻的波形如图,则OP之间的距离为多少厘米。
10、如图,某一点波源发射功率为40瓦,求球面波上单位面积通过的平均能流。
11、如图S1、S2为两平面简谐波相干波源,S2的位相比S1的位相超前π/4,λ=8m,r1=12m,r2=14m。
S1在P点引起的振幅为0.3m, S2在P点引起的振幅为0.2m,求P点的合振幅。
12、当机械波在媒质中传播时,一媒质质元的最大变形量发生在 (设振幅是A(A 媒质质元离开其平衡位置最大位移处.(B 媒质质元离开其平衡位置(2/2A 处.(C 媒质质元在其平衡位置处.(D 媒质质元离开其平衡位置A 21处.13、设沿弦线传播的一入射波的表达式为](2cos[1φλπ+-=xT t A y 波在x = L 处(B 点发生反射,反射点为固定端。
第9章 振动和波习题课
⑤相位差 ：ຫໍສະໝຸດ (2t 2 ) (1t 1 )
同相: 反相:
( 2 1 )
2k (k 0、 1、 2....)
（ 2k 1 ） (k 0、 1、 2....)
A t
M
4、旋转矢量法：
o
t0 A p x
t
x A cos(t )
4
5、简谐振动的能量：
1 2 EK kA sin 2 (t ) 简谐振动的动能： 2 1 2 1 2 2 简谐振动的势能： E p kx kA cos (t ) 2 2
简谐振动的总能量：
1 2 E Ek E p kA 2
y
B
P
C
[ B ]
x
y
o
A
y A
o
P
o x
A
P
x
A
y A y A
B
P P
o
x
o
x
20
C
D
6、一平面简谐波沿 x 轴负方向传播。已知 x = x0 处质点的
t 0 ) 。若波速为u,则此波的 振动方程为 y A cos( 波动方程为： [ A ]
A) y A cos t ( x0 x ) / u 0 B ) y A cos t ( x x0 ) / u 0 C ) y A cos t ( x0 x ) / u 0 D ) y A cos t ( x0 x ) / u 0
动力学方程： 运动学方程：
x A cos(t )
2、简谐振动的特征：
振动与波习题课
x/m
（九）波传播过程中，任一体积元的动能、 势能、总机 械能均随 t 作周期性变化，且变化是同相位的。平衡位置时， 体积元的动能、势能和总机械能均最大；位移最大时，三者 均为零。
平衡位置处 释放能量 最大位移处
Ek,Ep,E 吸收能量
0
（2）任一体积元都在不断地接收和放出能量，即不断地传 播能量。任一体积元的机械能不守恒。波动是能量传递的一 种方式。
二、基本内容
（一）简谐振动的特征
1.动力学特征 F kx
简谐振动动力学特征是物体受线性回复力作用。
简谐振动的动力学方程
d2 x 2x 0
dt2
简谐振动的特征式
2.运动学特征 x Acos(t 0 )
简谐振动的运动学方程（振动表达式或振动方程）
简谐振动的速度和加速度
v
0 )
2.时间推迟法 t x
u
y
A cos[ (t
x) u
0
]
3.波动表式的物理意义
（1）当x 一定时(x = x0)表示x0处质点的振动表式
（2）当t 一定时(t = t0)表示t0时
y/m
0.1
刻的波形曲线
o
0.05 3
（3）x、t 都变化反映了波形的传播
u 36 m/s
（2）周期 T 、频率ν和角频率ω
2π 2π
T
（3）相位 ( t 0 )和初相位 0
cos 0
x0 A
sin 0
v0
A
对给定的振动系统，频率由系统本身性质决定。
2.简谐振动的矢量图示法
M
旋转矢量表示法 3.振动曲线（x - t 图）
（九）波传播过程中，任一体积元的动能、 势能、总机 械能均随 t 作周期性变化，且变化是同相位的。平衡位置时， 体积元的动能、势能和总机械能均最大；位移最大时，三者 均为零。
平衡位置处 释放能量 最大位移处
Ek,Ep,E 吸收能量
0
（2）任一体积元都在不断地接收和放出能量，即不断地传 播能量。任一体积元的机械能不守恒。波动是能量传递的一 种方式。
二、基本内容
（一）简谐振动的特征
1.动力学特征 F kx
简谐振动动力学特征是物体受线性回复力作用。
简谐振动的动力学方程
d2 x 2x 0
dt2
简谐振动的特征式
2.运动学特征 x Acos(t 0 )
简谐振动的运动学方程（振动表达式或振动方程）
简谐振动的速度和加速度
v
0 )
2.时间推迟法 t x
u
y
A cos[ (t
x) u
0
]
3.波动表式的物理意义
（1）当x 一定时(x = x0)表示x0处质点的振动表式
（2）当t 一定时(t = t0)表示t0时
y/m
0.1
刻的波形曲线
o
0.05 3
（3）x、t 都变化反映了波形的传播
u 36 m/s
（2）周期 T 、频率ν和角频率ω
2π 2π
T
（3）相位 ( t 0 )和初相位 0
cos 0
x0 A
sin 0
v0
A
对给定的振动系统，频率由系统本身性质决定。
2.简谐振动的矢量图示法
M
旋转矢量表示法 3.振动曲线（x - t 图）