河南科技大学2003级线性代数期末考试试题
线性代数期末试题及答案
线性代数院系: 班级: 姓名: 学号:第一部分选择题(共28分)一、单项选择题（本大题共14小题，每小题2分，共28分）在每小题列出的四个选项中只有一个是符合题目要求的，请将其代码填在题后的括号内。
错选或未选均无分。
1.设行列式a aa a11122122=m，a aa a13112321=n，则行列式a a aa a a111213212223++等于（）A. m+nB. -(m+n)C. n-mD. m-n2.设矩阵A=100020003⎛⎝⎫⎭⎪⎪⎪，则A-1等于（）A.130012001⎛⎝⎫⎭⎪⎪⎪⎪⎪⎪B.100120013⎛⎝⎫⎭⎪⎪⎪⎪⎪⎪C.13000100012⎛⎝⎫⎭⎪⎪⎪⎪⎪D.120013001⎛⎝⎫⎭⎪⎪⎪⎪⎪⎪3.设矩阵A=312101214---⎛⎝⎫⎭⎪⎪⎪，A*是A的伴随矩阵，则A *中位于（1，2）的元素是（）A. –6B. 6C. 2D. –24.设A是方阵，如有矩阵关系式AB=AC，则必有（）A. A =0B. B≠C时A=0C. A≠0时B=CD. |A|≠0时B=C5.已知3×4矩阵A的行向量组线性无关，则秩（A T）等于（）A. 1B. 2C. 3D. 46.设两个向量组α1，α2，…，αs和β1，β2，…，βs均线性相关，则（）A.有不全为0的数λ1，λ2，…，λs使λ1α1+λ2α2+…+λsαs=0和λ1β1+λ2β2+…λsβs=0B.有不全为0的数λ1，λ2，…，λs使λ1（α1+β1）+λ2（α2+β2）+…+λs（αs+βs）=0C.有不全为0的数λ1，λ2，…，λs使λ1（α1-β1）+λ2（α2-β2）+…+λs（αs-βs）=0D.有不全为0的数λ1，λ2，…，λs和不全为0的数μ1，μ2，…，μs使λ1α1+λ2α2+…+λsαs=0和μ1β1+μ2β2+…+μsβs=07.设矩阵A的秩为r，则A中（）A.所有r-1阶子式都不为0B.所有r-1阶子式全为0C.至少有一个r阶子式不等于0D.所有r阶子式都不为08.设Ax=b是一非齐次线性方程组，η1，η2是其任意2个解，则下列结论错误的是（）A.η1+η2是Ax=0的一个解B.12η1+12η2是Ax=b的一个解C.η1-η2是Ax=0的一个解D.2η1-η2是Ax=b的一个解9.设n阶方阵A不可逆，则必有（）A.秩(A)<nB.秩(A)=n-1C.A=0D.方程组Ax=0只有零解10.设A是一个n(≥3)阶方阵，下列陈述中正确的是（）A.如存在数λ和向量α使Aα=λα，则α是A的属于特征值λ的特征向量B.如存在数λ和非零向量α，使(λE-A)α=0，则λ是A的特征值C.A的2个不同的特征值可以有同一个特征向量D.如λ1，λ2，λ3是A的3个互不相同的特征值，α1，α2，α3依次是A的属于λ1，λ2，λ3的特征向量，则α1，α2，α3有可能线性相关11.设λ0是矩阵A的特征方程的3重根，A的属于λ0的线性无关的特征向量的个数为k，则必有（）A. k≤3B. k<3C. k=3D. k>312.设A是正交矩阵，则下列结论错误的是（）A.|A|2必为1B.|A|必为1C.A-1=A TD.A的行（列）向量组是正交单位向量组13.设A是实对称矩阵，C是实可逆矩阵，B=C T AC.则（）A.A与B相似B. A与B不等价C. A与B有相同的特征值D. A与B合同14.下列矩阵中是正定矩阵的为（）A.2334⎛⎝⎫⎭⎪ B.3426⎛⎝⎫⎭⎪C.100023035--⎛⎝⎫⎭⎪⎪⎪D.111120102⎛⎝⎫⎭⎪⎪⎪第二部分非选择题（共72分）二、填空题（本大题共10小题，每小题2分，共20分）不写解答过程，将正确的答案写在每小题的空格内。
河南科技大学线性代数试题总汇
河南科技大学线性代数试题总汇线性代数历年试题及参考答案河南科技大学2000 年-2004 年- 1 -1999 级线性代数试题一、判断题（共24 分）1 若A，B 均为n 阶方阵，则必有（1）AB＝BA （2）|AB|＝|BA| （3）|AB|＝|A|＋|B| （4）TT（5）22BABA（6）R（AB）＝R（BA）（7）若A 2＝0，则A ＝0 （8）若ATA＝0，则A＝0 2（8 分）若 A 是mn 矩阵，且m≠n，则（1）当A 的列向量组线性无关时，A 的行向量组也线性无关（2）当RAn 时，齐次线性方程组AX＝0 只有零解（3）当RAn 时，非齐次线性方程组AX＝b，有唯一解（4）当RAm 时，非齐次线性方程组AX＝b，有无穷多解3（8 分）若A 是实对称矩阵，则（1）A 的特征值全为实数（2）A 为正定矩阵的充要条件是 A 的特征值全为正（3）若|A|＞0，则 A 为正定的（4）在二次型f＝X TAX 中，若经实满秩线性变换X＝CY，可将f 化为标准形则全为A 的特征值221nykykf Lnk,21L二、填空题（19 分）1 （4 分）设且A＋2B＝C，vxCyvuBxA43,,70则x_____, y______, u_____, v_______2 （6 分）若A 为四阶方阵，且|A|＝3，A ＊为A 的伴随矩阵，则|－2A|＝＿＿，|A －1 |＝＿＿，|A ＊|＝＿＿ 3 （3 分）方阵的特征值为＿＿，＿＿，＿＿4024 （4 分）已知四元非线性方程组的系数矩阵A 的秩为3，- 2 -是它的三个解向量，且321,，则对应齐次方程组AX＝0 的TT5,432,4,2基础解系是＿＿＿＿，AX＝b 的通解是＿＿＿5 二次型所对应的矩阵是＿＿3212321 xxxf 三、（10 分）1、计算03212 、已知A 求及1041A8四、（10 分）设，且，求B32五、（15 分）验证二次型的特征值为4，9，0，3231212321 65xxxf 求一个正交变换，将此二次型化为标准形。
线性代数期末考试试卷+答案
×××大学线性代数期末考试题、填空题（将正确答案填在题中横线上。
每小题 2分，共10分）1 -3 1P X IX 2 X 3 =02 .若齐次线性方程组 J x 1+χx 2+x 3=0只有零解，则 扎应满足X 1亠 X 2亠 X 3= 05. n 阶方阵 A 满足 A 2-3A-E = 0 ,贝U A J = _____________________ 。
、判断正误（正确的在括号内填“√”，错误的在括号内填“X” 。
每小题2分，共10分）1. 若行列式D 中每个元素都大于零，则D 0。
（）2. 零向量一定可以表示成任意一组向量的线性组合。
（）3. 向量组a 1, a 2,…,a m中，如果a 1与a m对应的分量成比例，则向量组 a 1, a 2,…，a s线性相关。
■为可逆矩阵A 的特征值，贝U A J 的特征值为’。
（）若三、单项选择题（每小题仅有一个正确答案，将正确答案题号填入括号内。
每小题1.设A 为n 阶矩阵，且A = 2 ,则I AA T =（ ）。
①2n②2n'③2n1④42. n 维向量组:∙1,:-2, , ：■ S （ 3 < S < n ）线性无关的充要条件是（）。
-0 11 0 0 0 0 04. A =0 0 0 10 1 0①：'1, ：'2 ,'：'S 中任意两个向量都线性无关②＞1,-：：S 中存在一个向量不能用其余向量线性表示③：'1, -'2 ,-■ S中任一个向量都不能用其余向量线性表示1.若0 5 -12x =0,则= —23•已知矩阵A ,B ,C = (C ij )s n ,满足AC =CB ,则A 与B 分别是 _____________ 阶矩阵。
a124 .矩阵 A= a21a 22的行向量组线性31a32丿2分，共10分）11,贝U A A =A 。
线性代数期末考试题库及答案
2、n2, 当 n 为偶数时为偶排列，当 n 为奇数时为奇排列. 4、29.
1、12.
2、 x2 y2 .
4
∑ 3、 x = 0 或 − ai . i =1
4、 λ = ±1, 2 .
三、证明题
证明提示: 由于 f(x)是关于 x 的二次多项式，在[0，1]中可导，又可计算出 f (0) = f (1) = 0 ，
3、解方程 D4( x) =
a1 a1
a1 + x
a2 a2 a2 + x a2
a3 a3 + x
a3 a3
a4 + x a4 = 0 . a4 a4
4、已知下列齐次线性方程组有非零解，求参数λ的值。
（5
− λ）x1 −6 x1
−4 x2 +(7 − λ )x2
−7 x3 +11x3
=0 =0
6 x1
（B）若 AX=0有非零解，则 AX=b有无穷多解；
（C）若 AX=b有无穷多个解，则 AX=0仅有零解；
（D）若 AX=b有无穷多个解，则 AX=0有非零解。
（7）非齐次线性方程组 AX=b中未知量个数为 n，方程个数为 m，系数矩阵 A的秩为 r，则
（）
（A）r=m时，方程组 AX=b有解； （B）r=n时，方程组 AX=b有唯一解；
《线性代数》补充练习二
一、选择题：
（1）设 n阶方阵 A的秩 r<n，则在 A的 n个行向量中（ ）
（A）必有 r个行向量线性无关； （B）任意 r个行向量均可构成极大无关组；
（C）任意 r个行向量均线性无关；（D）任一个行向量均可由其他 r个行向量线性表示
（2）若向量组α，β，γ线性无关；α，β，δ线性相关，则（ ）
线性代数期末试题及答案
第一部分选择题(共28分)一、单项选择题（本大题共14小题，每小题2分，共28分）在每小题列出的四个选项中只有一个是符合题目要求的，请将其代码填在题后的括号内。
错选或未选均无分。
1.设行列式a aa a11122122=m，a aa a13112321=n，则行列式a a aa a a111213212223++等于（）A. m+nB. -(m+n)C. n-mD. m-n2.设矩阵A=100020003⎛⎝⎫⎭⎪⎪⎪，则A-1等于（）A.130012001⎛⎝⎫⎭⎪⎪⎪⎪⎪⎪B.100120013⎛⎝⎫⎭⎪⎪⎪⎪⎪⎪C.13000100012⎛⎝⎫⎭⎪⎪⎪⎪⎪D.120013001⎛⎝⎫⎭⎪⎪⎪⎪⎪⎪3.设矩阵A=312101214---⎛⎝⎫⎭⎪⎪⎪，A*是A的伴随矩阵，则A *中位于（1，2）的元素是（）A. –6B. 6C. 2D. –24.设A是方阵，如有矩阵关系式AB=AC，则必有（）A. A =0B. B≠C时A=0C. A≠0时B=CD. |A|≠0时B=C5.已知3×4矩阵A的行向量组线性无关，则秩（A T）等于（）A. 1B. 2C. 3D. 46.设两个向量组α1，α2，…，αs和β1，β2，…，βs均线性相关，则（）A.有不全为0的数λ1，λ2，…，λs使λ1α1+λ2α2+…+λsαs=0和λ1β1+λ2β2+…λsβs=0B.有不全为0的数λ1，λ2，…，λs使λ1（α1+β1）+λ2（α2+β2）+…+λs（αs+βs）=0C.有不全为0的数λ1，λ2，…，λs使λ1（α1-β1）+λ2（α2-β2）+…+λs（αs-βs）=0D.有不全为0的数λ1，λ2，…，λs和不全为0的数μ1，μ2，…，μs使λ1α1+λ2α2+…+λsαs=0和μ1β1+μ2β2+…+μsβs=07.设矩阵A的秩为r，则A中（）A.所有r-1阶子式都不为0B.所有r-1阶子式全为0C.至少有一个r阶子式不等于0D.所有r阶子式都不为08.设Ax=b是一非齐次线性方程组，η1，η2是其任意2个解，则下列结论错误的是（）A.η1+η2是Ax=0的一个解B.12η1+12η2是Ax=b的一个解C.η1-η2是Ax=0的一个解D.2η1-η2是Ax=b的一个解9.设n阶方阵A不可逆，则必有（）A.秩(A)<nB.秩(A)=n-1C.A=0D.方程组Ax=0只有零解10.设A是一个n(≥3)阶方阵，下列陈述中正确的是（）A.如存在数λ和向量α使Aα=λα，则α是A的属于特征值λ的特征向量B.如存在数λ和非零向量α，使(λE-A)α=0，则λ是A的特征值C.A的2个不同的特征值可以有同一个特征向量D.如λ1，λ2，λ3是A的3个互不相同的特征值，α1，α2，α3依次是A的属于λ1，λ2，λ3的特征向量，则α1，α2，α3有可能线性相关11.设λ0是矩阵A的特征方程的3重根，A的属于λ0的线性无关的特征向量的个数为k，则必有（）A. k≤3B. k<3C. k=3D. k>312.设A是正交矩阵，则下列结论错误的是（）A.|A|2必为1B.|A|必为1C.A-1=A TD.A的行（列）向量组是正交单位向量组13.设A是实对称矩阵，C是实可逆矩阵，B=C T AC.则（）A.A与B相似B. A与B不等价C. A与B有相同的特征值D. A与B合同14.下列矩阵中是正定矩阵的为（）A.2334⎛⎝⎫⎭⎪ B.3426⎛⎝⎫⎭⎪C.100023035--⎛⎝⎫⎭⎪⎪⎪D.111120102⎛⎝⎫⎭⎪⎪⎪第二部分非选择题（共72分）二、填空题（本大题共10小题，每小题2分，共20分）不写解答过程，将正确的答案写在每小题的空格内。
线性代数期末考试考核试卷
4.以下哪个向量组构成一个基？
A. (1, 0, 0), (0, 1, 0), (0, 0, 0)
B. (1, 2, 3), (4, 5, 6), (7, 8, 9)
C. (1, 2, 3), (2, 4, 6), (1, 1, 1)
D. (1, 1, 0), (0, 1, 1), (1, 0, 1)
...
20.（根据实际题目内容填写答案）
二、多选题
1. BCD
2. ABCD
3. ABC
4. AB
5. ABC
...
20.（根据实际题目内容填写答案）
三、填题
1. 1
2.线性无关
3.主
...
10.（根据实际题目内容填写答案）
四、判断题
1. √
2. √
3. √
...
10. ×
五、主观题（参考）
1.向量组线性无关，可以通过计算行列式不为零来证明。一个可以由给定向量组线性表示的向量可以是它们的线性组合，例如\(a\vec{v}_1 + b\vec{v}_2 + c\vec{v}_3\)，其中\(a, b, c\)是适当的系数。
D. (1, 1), (1, -1)
（答题括号：________）
5.在求解线性方程组时，以下哪些情况下可以使用高斯消元法？
A.系数矩阵是方阵
B.系数矩阵是非奇异的
C.方程组中方程的个数等于未知数的个数
D.方程组可能有无穷多解
（答题括号：________）
（以下题目类似，省略以节约空间）
6. ...
A.若A为m×n矩阵，则A的转置为n×m矩阵
B.若A为m×n矩阵，则A的转置为m×n矩阵
线代期末试题及答案
T AB =______________.2．若三元非齐次线性方程组的系数矩阵的秩为2，123,,βββ是它的 三个解向量，且12(2,6,3),T ββ+=-23(6,8,5),T ββ+=-则该线性方 程组的通解是__________.3. 设123625t A t t ⎛⎫⎪=- ⎪ ⎪-⎝⎭的行向量线性相关，则实数t 满足的条件是 _________.4．令ii A 是三阶矩阵A 的元素ii a 的代数余子式（i =1，2，3），若A 的特征值为3，4，5，则112233A A A ++=__________.5．若101020105A c c ⎛⎫ ⎪=+ ⎪ ⎪-⎝⎭是正定矩阵，则c 的取值范围为 ___________.二． 选择题（每小题3分，共15分）1. 设A 、B 均为n 阶正交矩阵，则____________. （1）A+B 为正交矩阵 （2）A-B 为正交矩阵（3） B AB 为正交矩阵（4）k AB 为正交矩阵(k >0为实数)2．设A 为m 阶可逆矩阵，B 为n 阶可逆矩阵，则可逆分块矩阵O A D B O ⎛⎫= ⎪⎝⎭的逆矩阵是____________.（1）11A O O B --⎛⎫⎪⎝⎭ （2）11O B A O --⎛⎫⎪⎝⎭ （3） 11B O OA --⎛⎫⎪⎝⎭ （4）11O A BO --⎛⎫ ⎪⎝⎭3． 设α与β是线性无关的单位向量，则α与β的内积必 ____________.（1） >0 （2）<0 （3）>1 （4）<14.设A 为n 阶可逆矩阵，1*,,T A A A -分别是A 的转置矩阵，逆矩阵和伴随矩阵，若ξ是A 的特征向量，则下列命题中的不正确的是________.（1）ξ是T A 的特征向量 （2）2ξ是1A -的特征向量 （3）3ξ是*A 的特征向量（4） 4ξ是kA 的特征向量（k 为常数）5.设222623222,000222000A B ⎛⎫⎛⎫⎪ ⎪== ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭，则____ ____. （1）A 与B 是相似的且是合同的 （2）A 与B 是相似的但不是合同的 （3）A 与B 不是相似的但是合同的 （4）A 与B 不是相似的也不是合同的三．（15分）试求五元齐次线性方程组123451234512345330,30,0x x x x x x x x x x x x x x x ++++=⎧⎪-++-+=⎨⎪+++-=⎩的解空间V(作为5R 的子空间)的一组规范（标准）正交基。
线性代数 期末测试题及其答案
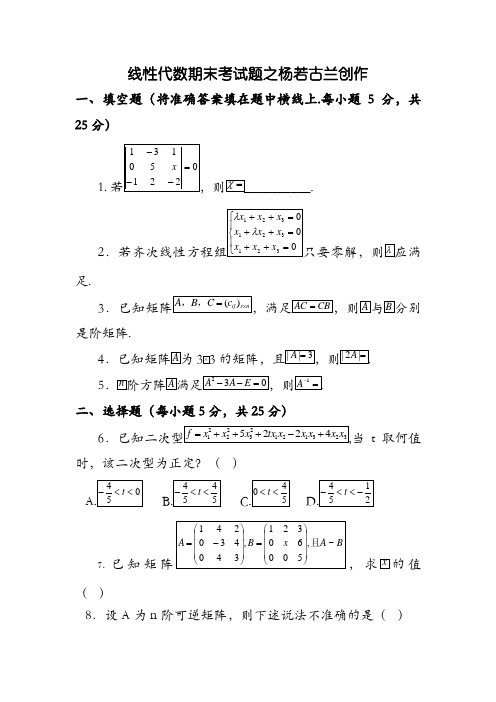
线性代数期末考试题之杨若古兰创作一、填空题（将准确答案填在题中横线上.每小题5分，共25分）1.2足.3是阶矩阵.45二、选择题（每小题5分，共25分）6当t 取何值时，该二次型为正定？（ ）7．已知矩阵，求的值（ ）8．设A 为n 阶可逆矩阵，则下述说法不准确的是（ ）A的行向量组线性相干9．过点（0，2，4行的直线方程为（）10其特征值为（）三、解答题（每小题10分，共50分）11.矩足关系式12.问取何值时，以下向量组线性相干？解和有没有量多解？当方程组有没有量多解时求其通解.14.求此向量组的秩和一个极大有关组，并将其余向量用该极大有关组线性暗示. 15.证实其中线性代数期末考试题答案一、填空题1. 5.解析:采取对角线法则,考查常识点:行列式的计算.难度系数:解析:要使该现行方程组只要零解,考查常识点:线性方程组的求解难度系数:解析;,,,阶矩阵.考查常识点:n 阶矩阵的性质难度系数: 4. 24解析:由题可知3考查常识点:矩阵的运算 难度系数: 解析:考查常识点:求解矩阵的逆矩阵 难度系数:二、选择题 6. A解析：由题可知，该二次型矩阵为，而此时，该二次型正定.考查常识点:二次型正定的判断难度系数7. C解析：由矩阵特征值性质有1-3+3=1+x+5，可解得x=-5. 考查常识点:n 阶矩阵特征值的性质 难度系数:8. D解析：由题可知，A 为n 阶可逆矩阵，则A 的行向量组线性有关.考查常识点:n 阶可逆矩阵的性质 难度系数:9. A.解析：由题可知，两平面法向量分别为，则所求直线的方向向量为考查常识点:求空间平面交线平行的直线方程 难度系数:10. C.考查常识点:求解矩阵的特征值三、解答题11.解：考查常识点:矩阵方程的运算求解难度系数:12.解：.考查常识点:向量组的线性相干性难度系数:13.解：③当时，有没有量多组解，通解为考查常识点:线性方程组的求解14.解：由题可知,且线性关系为考查常识点:向量组的秩与最大有关组难度系数:15.证实：由题可知,考查常识点:n 阶方阵的性质难度系数:。
大学线性代数期末试卷及答案
大学线性代数期末试题一、填空题（每小题2分，共10分）1. 若022150131=---x ，则=χ__________。
2．若齐次线性方程组⎪⎩⎪⎨⎧=++=++=++000321321321x x x x x x x x x λλ只有零解，则λ应满足 。
3、n 阶方阵A 满足032=--E A A ，则=-1A。
4．矩阵⎪⎪⎪⎭⎫⎝⎛=323122211211a a a a a a A 的行向量组线性 。
5．已知矩阵n s ij c C B A ⨯=)(，，，满足CB AC =，则A 与B 分别是 阶矩阵。
二、判断正误（正确的在括号内填“√”，错误的在括号内填“×”。
每小题2分，共10分）1. 若行列式D 中每个元素都大于零，则0〉D 。
（ ）2. 零向量一定可以表示成任意一组向量的线性组合。
（ ）3. 向量组m a a a ，，， 21中，如果1a 与m a 对应的分量成比例，则向量组s a a a ，，， 21线性相关。
（ ）4. ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=010*********0010A ，则A A =-1。
（ ） 5. 若λ为可逆矩阵A 的特征值，则1-A 的特征值为λ。
( ) 三、单项选择题 (每小题仅有一个正确答案。
每小题2分，共10分)1. 设A 为n 阶矩阵，且2=A ，则=TA A （ ）。
① n2② 12-n③ 12+n ④ 42. n 维向量组 s ααα，，， 21（3 ≤ s ≤ n ）线性无关的充要条件是（ ）。
① s ααα，，， 21中任意两个向量都线性无关② s ααα，，， 21中存在一个向量不能用其余向量线性表示 ③ s ααα，，， 21中任一个向量都不能用其余向量线性表示④ s ααα，，， 21中不含零向量3. 下列命题中正确的是( )。
① 任意n 个1+n 维向量线性相关 ② 任意n 个1+n 维向量线性无关 ③ 任意1+n 个n 维向量线性相关 ④ 任意1+n 个n 维向量线性无关4. 设A ，B 均为n 阶方阵，下面结论正确的是( )。
线性代数期末试题及答案
8.设A 为三阶方阵, 且3=A , 则 12-=A .一、填空题（每小题2分，共20分）1.行列式=-203297302233241.2.设014111112--=D ，则=++333231A A A .3.设 , 231102 ⎪⎪⎭⎫ ⎝⎛-=A , 102324171⎪⎪⎪⎭⎫ ⎝⎛-=B 则= )( TAB . 4.设052=-+I A A ，则=+-1)2(I A .5.已知矩阵⎪⎪⎪⎭⎫⎝⎛-=100120121A ，*A 是A 的伴随矩阵，则=-1*)(A .6.A 、A 分别为线性方程组b AX =的系数矩阵与增广矩阵，则线性方程组b AX =有解的充分必要条件是 .7.设⎪⎪⎪⎭⎫ ⎝⎛-=30511132a A ，且秩(A )=2，则=a .9.向量组1(1,2,1,1),T α=-,)0,3,0,2(2T=αT )1,4,2,1(3--=α的秩等于 . 10.设21,αα是)3(≥n n 元齐次线性方程组OAX =的基础解系，则=)(A r .二、选择题（每小题2分，共20分）1.已知101yxy x aA =，则A 中元素a 的代数余子式11A 等于（ ）.A.1- B .1 C .a - D .a2.已知4阶矩阵A 的第三列的元素依次为2,2,3,1-，它们的余子式的值分别为1,1,2,3-，则=A （ ）.A .3B .3-C .5D .5-3.B A ,均为n 阶矩阵，且2222)(BAB AB A ++=+，则必有（ ）.A.B A = B .I A = C .I B = D .BA AB =4.设A 、B 均为n 阶矩阵，满足O AB =，则必有（ ）.A.0=+B A B .））B r A r ((= C .O A =或O B = D .0=A 或0=B5.设33⨯阶矩阵),,(1γβα=A ，),,(2γβα=B ，其中γβαα,,,21均为3维列向量，若2=A ，1-=B ，则=+B A （ ）.A.4 B .4- C .2 D .16.设B AX =为n 个未知数m 个方程的线性方程组，,)(r A r =下列命题中正确的是（ ）.A .当n m =时，B AX =有唯一解 B .当n r =时，B AX =有唯一解C .当m r =时，B AX =有解D .当n r <时，B AX =有无穷多解7.若齐次线性方程组⎪⎩⎪⎨⎧=λ++=+λ+=++λ000321321321x x x x x x x x x 有非零解,则=λ（ ）.A .1或2B .1或－2C .－1或2D .－1或－28.n 阶矩阵A 的秩r n =的充分必要条件是A 中（ ）.A.所有的r 阶子式都不等于零 B .所有的1r +阶子式都不等于零 C.有一个r 阶子式不等于零 D .有一个r 阶子式不等于零, 且所有1r +阶子式都等于零9.设向量组,),,1(21T a a =α,),,1(22T b b =αT c c ),,1(23=α，则321,,ααα线性无关的充分必要条件是 （ ）.A.c b a ,,全不为0 B .c b a ,,不全为0 C .c b a ,,互不相等 D .c b a ,,不全相等10.已知21,ββ为b AX =的两个不同的解，21,αα为其齐次方程组0A X =基础解系，21,k k 为任意常数，则方程组b AX =的通解可表成（ ）.A.2)(2121211ββααα-+++k kB .2)(2121211ββααα++-+k k线性代数期末试题答案一、填空题（每小题2分，共20分）1.52.03. ⎪⎪⎪⎭⎫⎝⎛-1031314170 4. )(31I A - 5.1/211/2011/2001/2-⎛⎫⎪⎪ ⎪⎝⎭6.)()(A r A r =7.6=a8. 38 9.2 10.2-n二、选择题（每小题2分，共20分）1.B2.C3.D4.D5.A6.C7.B8.D9.C 10.B 三、（8分)解：3211324-824823592373(1)373125212412411131D -===-----18361836(1)1313241=-=-=-四、（10分）解：（1）⎪⎪⎪⎭⎫⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛-⎪⎪⎪⎭⎫ ⎝⎛-=14191269629303212114321011324TAA （2）⎪⎪⎪⎭⎫⎝⎛-----=--461351341)2(1E A (3) 由XA AX2+=，得A XE A =-)2(A E A X 1)2(--=⎪⎪⎪⎭⎫⎝⎛-----=⎪⎪⎪⎭⎫ ⎝⎛-⎪⎪⎪⎭⎫⎝⎛-----=9122692683321011324461351341五、（12分）解：将方程组的增广矩阵A 用初等行变换化为阶梯矩阵：22112411411242110228018211240134(1)(4)00(4)2k k k k k k k k k k k ⎡⎤⎢⎥----⎡⎤⎡⎤⎢⎥-⎢⎥⎢⎥⎢⎥=-→-→⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥----⎢⎥⎣⎦⎣⎦+-⎢⎥-⎣⎦A所以，⑴ 当1k≠-且4k ≠时，()()3r r ==A A ，此时线性方程组有唯一解．⑵ 当1k =-时，()2=A r ，()3=A r ，此时线性方程组无解．⑶ 当4k=时，()()2==A A r r ，此时线性方程组有无穷多组解．此时，原线性方程组化为132334x x x x =-⎧⎨=-⎩ 因此，原线性方程组的通解为13233334x x x x x x=-⎧⎪=-⎨⎪=⎩或者写为123034101x x C x -⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥==+-⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦x (C R)∈六、（10分）解：记向量组4321,,,αααα对应矩阵为A 并化为行阶梯形矩阵为12341223122324130212(,,,)12030013062300002634000A αααα--⎛⎫⎛⎫⎪ ⎪-----⎪ ⎪ ⎪ ⎪==→- ⎪ ⎪ ⎪ ⎪ ⎪ ⎪-⎝⎭⎝⎭所以向量组4321,,,αααα的秩为3且它的一个最大无关组为：123,,ααα或124,,ααα1004101020013000000A -⎛⎫⎪ ⎪- ⎪→⎪ ⎪ ⎪ ⎪⎝⎭41231432αααα=--+ 七、（12分）解：（1）.⎪⎪⎪⎪⎪⎭⎫⎝⎛--------→⎪⎪⎪⎪⎪⎭⎫⎝⎛--------=61826239131039131024511810957245113322311312A⎪⎪⎪⎪⎪⎭⎫⎝⎛----→0000000039131015801为自由未知量。
线性代数期末考试试卷及答案
一、 填空题(每空3分，共15分)1、设A 为n 阶方阵，且3A =，则|3A |= 。
2、设矩阵5678A ⎡⎤=⎢⎥⎣⎦，则A *= 。
（其中A *是A 的伴随矩阵） 3、已知n 阶矩阵A 满足2A A =，则A 的特征值为 。
4、n 阶方阵A 与对角矩阵相似的充要条件是 。
5、二次型22212312133428f x x x x x x x =-+-+的实对称矩阵为 。
二、选择题(每小题3分，共15分)1、12021k k +≠+的充要条件是（ ）（A ）1k ≠ （B ）3k ≠-（C ）1k ≠且3k ≠- （D ）1k ≠或3k ≠-2、若111221226a a a a =，则121122212020021a a a a --的值为（ ） ()A 12 ()B -12 ()C 18 ()D 03、设,A B 都是n 阶方阵，且0AB =，则下列一定成立的是（ ）()A 0A =或0B = (),B A B 都不可逆 (),C A B 中至少有一个不可逆 ()0D A B += 4、向量组()12,,,2s s ααα≥ 线性相关的充分必要条件是（ ）()A 12,,,s ααα 中含有零向量。
()B 12,,,s ααα 中有两个向量的对应分量成比例。
()C 12,,,s ααα 中每一个向量都可由其余1s -个向量线性表示。
()D 12,,,s ααα 中至少有一个向量可由其余1s -个向量线性表示。
5、当ad ≠bc 时，1a b c d -⎡⎤⎢⎥⎣⎦=（ ） （A ）d c b a -⎡⎤⎢⎥-⎣⎦（B ）1d b c a ad bc -⎡⎤⎢⎥--⎣⎦（C ）1d b c a bc ad ⎡⎤⎢⎥--⎣⎦（D ）1d c b a ad bc -⎡⎤⎢⎥--⎣⎦三、（8分）计算行列式411102*********23D -=-四、（11分）求向量组()()()()12342,1,1,1,1,1,7,10,3,1,1,2,8,5,9,11αααα==-=--=的一个最大无关组，并将其余向量用此最大无关组线性表示。
河南科技大学线性代数试题总汇【完整版】
河南科技大学线性代数试题总汇【完整版】(文档可以直接使用，也可根据实际需要修订后使用,可编辑放心下载）线性代数历年试题及参考答案河南科技大学2000年-2004年1999级线性代数试题一、 判断题：〔共24分〕1 假设A ，B 均为n 阶方阵，那么必有： （1） AB ＝BA ( ) （2） |AB|＝|BA| ( ) （3） |A+B|＝|A|＋|B| ( ) （4） ()T T TB A AB = ( )（5） ()2222B AB A B A ++=+ ( )（6） R 〔AB 〕＝R 〔BA 〕 ( ) （7） 假设 A 2＝0，那么A ＝0 ( ) （8） 假设A T A ＝0，那么A ＝0 ( ) 2〔8分〕假设A 是m ×n 矩阵，且m ≠n ，那么（1） 当A 的列向量组线性无关时，A 的行向量组也线性无关 ( ) （2） 当R(A)=n 时，齐次线性方程组AX ＝0只有零解 ( ) （3） 当R(A)=n 时，非齐次线性方程组AX ＝b ，有唯一解 ( ) （4） 当R(A)=m 时，非齐次线性方程组AX ＝b ，有无穷多解 ( ) 3〔8分〕假设A 是实对称矩阵，那么 （1） A 的特征值全为实数 ( )（2） A 为正定矩阵的充要条件是A 的特征值全为正 ( ) （3） 假设|A|＞0，那么A 为正定的 ( )（4） 在二次型f ＝X T AX 中，假设经实满秩线性变换X ＝CY ，可将f 化为标准形2222211nn y k y k y k f +++= 那么n k k k ,,,21 全为A 的特征值( ) 二、 填空题〔19分〕1 〔4分〕设⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛=v x C y v u B y x A 43,2,70且A ＋2B ＝C ，那么x=_____, y=______, u=_____, v=_______2 〔6分〕假设A 为四阶方阵，且|A|＝3，A ＊为A 的伴随矩阵，那么 |－2A|＝＿＿，|A －1|＝＿＿， |A ＊|＝＿＿3 〔3分〕方阵⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=402030201A 的特征值为＿＿，＿＿，＿＿4 〔4分〕四元非线性方程组的系数矩阵A 的秩为3，321,,ηηη是它的三个解向量，且T T )5,4,3,2(,)4,3,2,1(321=+=ηηη，那么对应齐次方程组AX ＝0的根底解系是＿＿＿＿ ，AX ＝b 的通解是＿＿＿5 二次型3231212322212222x x x x x x x x x f --+++=所对应的矩阵是＿＿三、 〔10分〕1、计算0321103221033210 2 、A =⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡--10410000340043求1-A 及8A 四、 〔10分〕设⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=311011322A ，且B A AB +=，求B五、 〔15分〕验证二次型323121232221662355x x x x x x x x x f -+-++=的特征值为4，9，0，求一个正交变换，将此二次型化为标准形。
线性代数期末附答案 (1)
《线性代数》模拟试题（一）一、单项选择题（每小题3分，共27分）1. 对于n 阶可逆矩阵A ，B ，则下列等式中（ ）不成立. (A) ()111---⋅=B A AB (B) ())/1()/1(111---⋅=B A AB (C) ()111---⋅=B AAB (D) ()AB AB /11=-2. 若A 为n 阶矩阵，且0A =3，则矩阵=--1)(A E （ ）.（A ）2A A E +- （B ）2A A E ++ （C ）2A A E -+ （D ）2A A E -- 3. 设A 是上（下）三角矩阵，那么A 可逆的充分必要条件是A 的主对角线元素为（ ）. (A) 全都非负 （B ） 不全为零 （C ）全不为零 （D ）没有限制4. 设 33)(⨯=ij a A ，⎪⎪⎪⎭⎫⎝⎛+++=133312321131131211232221a a a a aa a a a a a a B ，⎪⎪⎪⎭⎫ ⎝⎛=1000010101P ，⎪⎪⎪⎭⎫ ⎝⎛=1010100012P ，那么（ ）.（A ）B P AP =21 （B ）B P AP =12 （C ）B A P P =21 （D ）B A P P =12 5. 若向量组m ααα,,,21 线性相关，则向量组内（ ）可由向量组其余向量线性表示.（A ）至少有一个向量 （B ）没有一个向量 （C ）至多有一个向量 （D ）任何一个向量6. 若⎪⎪⎪⎭⎫⎝⎛=210253143212A ，其秩=)(A R （ ）.（A ）1 （B ）2 （C ）3 (D) 47. 若方程组b AX =中方程的个数小于未知量的个数，则有（ ）.（A ）b AX =必有无穷多解 （B ）0AX =必有非零解 （C ）0AX =仅有零解 （D ）0AX =一定无解 8. 若A 为正交阵，则下列矩阵中不是正交阵的是（ ）.（A ）1-A （B ）A 2 （C ）4A （D ）TA 9. 若满足条件（ ），则n 阶方阵A 与B 相似.（A ）B A = （B ）)()(B A R R = （C ）A 与B 有相同特征多项式 （D ）A 与B 有相同的特征值且n 个特征值各不相同 二、填空题（每空格3分，共21分）1. 若向量组321,,ααα线性无关，则向量组321211,,αααααα+++是线性 .2. 设A 为4阶方阵，且3)(=A R ，*A 是A 的伴随阵，则0=*X A 的基础解系所含的解向量的个数是 . 3. 设()2,1,11-=α，()5,,22k =α，()1,6,13-=α线性相关，则=k .4. 设⎪⎪⎪⎭⎫ ⎝⎛=300050004A ，则=--1)2(E A .5. 设三阶方阵A 有特征值4，5，6，则=A ，TA 的特征值为 ，1-A 的特征值为 .三、计算题（共42分） 1. （6分）计算行列式ba b b b b b a b b bb b a b b b b b a ----+----+2. （8分）已知矩阵⎪⎪⎪⎭⎫⎝⎛=200012021A ，求10A .3. （10分）设三阶方阵A 满足i i i αA α= )3,2,1(=i ，其中T )2,2,1(1=α，T )1,2,2(2-=α，T )2,1,2(3--=α，求A .4．（6分）在向量空间3R 中，取两组基：（I ）,110,011,101321⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛=ααα （II ）,411,222,301321⎪⎪⎪⎭⎫⎝⎛-=⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛=βββ设α在基I 下的坐标为()T3,1,1，求α在基α在基II 下的坐标.5. （12分）λ取何值时，非齐次线性方程组⎪⎩⎪⎨⎧=-+=+-=-+1610522321321321x x x x x x x x x λλ （1）有惟一解；（2）无解； （3）有无穷多解，并求其通解.四、证明题（每小题5分，共10分）1. 设A 为n 阶可逆阵，E A A =2. 证明A 的伴随阵A A =*.2. 若A ，B 都是n 阶非零矩阵，且0AB =. 证明A 和B 都是不可逆的.《线性代数》模拟试题（一）参考答案一、单项选择题（每题3分，共27分）1. B2. B3. C4. C5. A6. B7. B8. B9. D 二、填空题（每空3分，共21分）1. 无关；2. 3 ；3. 3 ；4. ⎪⎪⎪⎭⎫ ⎝⎛10000003121； 6. 120； 4，5，6； 615141,, 三、计算题（7+10+10+12=39分）1. 解：b a b b b b b a b b b b b a b b b b b a ----+----+a aa a a ab b bba 000000-+=4000000000a aa ab b b a ==. 2. 解：先求A 的特征值，λλλλ---=-20012021E A =)1)(3)(2(λλλ+--- 1,3,2321-===λλλ ，当21=λ时，由0X E A =-)2(得，A 的对应于2的特征向量是⎪⎪⎪⎭⎫ ⎝⎛=1001ξ，当32=λ时，由0X E A =-)3(得，A 的对应于3的特征向量是⎪⎪⎪⎭⎫ ⎝⎛=0112ξ，当12-=λ时，由0X E A =+)(得，A 的对应于1-的特征向量是⎪⎪⎪⎭⎫ ⎝⎛-=0113ξ，取⎪⎪⎪⎭⎫ ⎝⎛=1001η⎪⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎪⎭⎫ ⎝⎛=01121,0112132ηη.令()321,,ηηηP = ，则⎪⎪⎪⎭⎫⎝⎛-==-1321AP P AP P T，所以 T P P A 1010132⎪⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎪⎭⎫ ⎝⎛+--+=1010211021102110212000)13()13(0)13()13(.3. 解：因为)3,2,1(==i i i i αA α，所以⎪⎪⎪⎭⎫ ⎝⎛=300020001),,(),,(321321ααααααA ，因此 1321321),,(300020001),,(-⎪⎪⎪⎭⎫ ⎝⎛=ααααααA .又),,(321ααα⎪⎪⎪⎭⎫ ⎝⎛---=212122221，所以1321),,(-ααα⎪⎪⎪⎭⎫⎝⎛---=21212222191，故 =A ⎪⎪⎪⎭⎫ ⎝⎛---212122221⎪⎪⎪⎭⎫ ⎝⎛300020001⎪⎪⎪⎭⎫ ⎝⎛---21212222191⎪⎪⎪⎭⎫ ⎝⎛----=62225020731. 4．解：()()⎪⎪⎪⎭⎫ ⎝⎛--=311211112,,,,321321αααβββ,(),311,,321⎪⎪⎪⎭⎫ ⎝⎛=αααα所以 ()⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎭⎫ ⎝⎛--=-311311211112,,1321βββα ()()⎪⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎭⎫ ⎝⎛----=323532321939192939591939295321,,311,,ββββββ， α在基II 下的坐标为()T 323532,,-.5. 解：)3)(5(61011211-+=---=λλλλD ， （1）当0≠D ，即5-≠λ且3≠λ时，方程组有惟一解.（2）当5-=λ时，⎪⎪⎪⎭⎫ ⎝⎛-----==1610155122151)(βA,B −→−r ⎪⎪⎪⎭⎫ ⎝⎛---100013902151 此时3)(,2)(==B A R R ，方程组无解，（3）当3=λ时，⎪⎪⎪⎭⎫ ⎝⎛---==1610153122131)(βA,B −→−r ⎪⎪⎪⎭⎫⎝⎛--00001001717571778， 此时2)()(==B A R R ，方程组有无限多个解.，并且通解为⎪⎪⎪⎭⎫ ⎝⎛-+⎪⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎪⎭⎫ ⎝⎛10757871717321c x x x )(R c ∈. 四、证明题（5+5=10分） 1. 证：根据伴随矩阵的性质有E A AA =*又E A A =2，所以2A AA =*，再由于A 可逆，便有A A =*.2. 证：假设A 可逆，即1-A 存在，以1-Α左乘0AB =的两边得0B =，这与B 是n 阶非零矩阵矛盾；类似的，若B 可逆，即1-B 存在，以1-B 右乘0AB =的两边得0A =，这与A 是n 阶非零矩阵矛盾，因此，A 和B 都是不可逆的.。
线性代数期末考试试题
线性代数期末考试试题，（32分)填空（2分16）aaaa1、设四阶行列式的展开式中有一项,此项前面应带的符号Da，21431234ij 102为；又设三阶行列式，其第二行元素的代数余子式之和D，3453011AAA，,＝。
2122231312,,，2、当＝时，矩阵的秩＝2，此时若令矩阵＝,，A，1321ArAt，，,，,，262t,,，则的列向量组的一个极大无关组为。
A,,,,，，12343,1*1，＊AA，3、设为四阶方阵，且=2，则= ，= ,(其中，AAAA，,2为矩阵的伴随矩阵）。
AT200,，4、设，,则＝＝ ,＝。
AA，,,386，，321，，,,n5、阶矩阵为可逆矩阵的充要条件是的列向量组线性关；又为正交AAA矩阵的充要条件是的行向量组是向量组。
A1011101021100,，，，,,10,，,，,,10031,0106、＝，＝。
，,21,,,，,,00142,201，,，，,，12，，17、设二阶矩阵，矩阵，则矩阵的对角标准形A，BCAC,B，，，32,1为，= 。
BI，8、为三阶实对称矩阵，且，不可逆，＝1,则的三个特征值AAI，2AI，AAT为；以为系数矩阵的二次型的规范形AfxxxXAX,，，123为。
6 2二、(21分）计算(要求写出计算过程)（6分+7分+8分）111a111a1、计算四阶行列式： D,111aa11101101,,，，，1＊＊2、设矩阵与满足（其中为矩阵的，,,,A,，341B，212AXABX,，AA，,，,111,10,,,，伴随矩阵）,化简此矩阵方程并求矩阵. X6 3TTT3、设，,为线性方程组，，，2101，，,1110,,,,1211AXB,，,，，,,123 的三个解， rA，2，，求：此方程组的导出组的一个基础解系，使它构成一个标准正交向量组. AX,0 xxxx，，,，，223,1234,三、(13分）设线性方程组， 348xxxxt,,,，，12344484xxx,,，，,124,求:当取何值时，方程组有解；有解时求出方程组的通解. t6 4222四、(14分）设二次型 fxxxxxxxx,，,，5446，，123123231、写出此二次型的系数矩阵. A222fyyy,，，5552、正交变换下，此二次型化为标准形，求该正XTY，123 交变换. XTY,6 5101，，,五、（10分)设矩阵，，Aab,2，，,101,,a1、若能与对角形矩阵相似，则，应满足什么条件，并说明理由。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
5) 设
是一组 维向量 , 则下列正确的是 ( ).
(a) 若
不线性相关 , 就一定线性无关 ;
(b) 如果存在 个不全为零的数
使
,则
线性无关 ;
(c) 若向量组
线性相关 , 则 可由
线性表示 ;
(d) 向量组 线性表示 .
线性无关的充要条件是 不能由其余
6) 矩阵 ( ) 时可能改变其秩 .
(a) 转置 ;
是正定还是负定 : .
二 . 单项选择题（每小题 2 分 , 共 16 分） .
1) 设 是
阶方阵 , 则必有 ( ).
(a)
; (b)
;
(c)
;
(d)
.
2) 设 是 阶方阵 , 则
的必要条件是 ( ).
(a) 两行 ( 列) 元素对应成比例 ; (b) 必有一行为其余行的线性组合 ;
(c)
中有一行元素全为零 ;
七 .(15 分) 求一个正交变换
, 将二次型
形 ( 要求：写出正交变换和标准形 ).
八 .(6 分) 设 为 阶可逆矩阵 , 是 的一个特征值 , 证明
化为标准 的伴随矩
阵 的特征值之一是
.
三 .(8 分) 计算
四 .(12 分) 设
,
,
,
求矩阵 使满足
.
五 .(12 分) 设矩阵
, 求矩阵 的列向量组的一个最大无关组 , 并把不属最大无关组的列向量用最大 无关组线性表示 . 六 .(15 分). 取何值时 , 非齐次方程组
(1) 有唯一解 ; (2) 无解 ; (3) 有无穷多个解 , 并求解 .
(b)
(c) 乘以奇异矩阵 ; (d)
初等变换 ; 乘以非奇异矩阵 .
7) 设 为可逆矩阵 ,
, 则下述结论不正确的是 ( ).
个向量
(a)
; (b)
;
(c)
; (d)
.
8) 若方阵 与 相似 , 则有 ( ).
(a)
;
(b)
;
(c) 对于相同的特征值 , 矩阵 与 有相同的特征向量 ;
(d)
与 均与同一个对角矩阵相似 .
河南科技大学 2003 级线性代数期末考试试题
一．填空题（每空 2 分, 共 16 分） 1) 设 为 矩阵 , 为 矩阵 , 且
2) 设 为 3 阶方阵且
,则
.
3) 已知
,则
.
.
,
则
.
4) 设 解, 则
是方程
的解 , 若 .
也是
的
5) 三阶矩阵 的三个特征值为 1,2,3, 则
,
的特征值为 .
6) 二次型
(d) 任一行为其余行的线性组合 .
3) 设 是 阶方阵 ,
且
, 则( ).
(a)
或
; (b)
;
(c)
;
(d)
.
4) 设 为 阶可逆矩阵 , 则( ).
(a) 若
,则
;
(b) 对矩阵
施行若干次初等变换 , 当 变为 时, 相应地 变为
;(c)总可以源自过初等变换化为单位矩阵 ;(d) 以上都不对 .