2017年国考资料分析必考公式大全最新版
公务员考试必背公式大全

公务员考试必背公式大全1. 分数比例形式整除:若a∶b=m∶n(m、n互质),则a是m的倍数,b是n的倍数。
若a=m/n×b,则a=m/(m+n)×(a+b),即a+b是m+n的倍数2. 尾数法(1)选项尾数不同,且运算法则为加、减、乘、乘方运算,优先使用尾数进行判定;(2)所需计算数据多,计算复杂时考虑尾数判断快速得到答案。
常用在容斥原理中。
3. 等差数列相关公式:和=(首项+末项)×项数÷2=平均数×项数=中位数×项数;项数=(末项-首项)÷项数+1。
从1开始,连续的n个奇数相加,总和=n×n,如:1+3+5+7=4×4=16,……4. 几何边端问题相关公式:(1)单边线型植树公式(两头植树):棵树=总长÷间隔+1,总长=(棵树-1)×间隔(2)植树不移动公式:在一条路的一侧等距离栽种m棵树,然后要调整为种n棵树,则不需要移动的树木棵树为:(m-1)与(n-1)的最大公约数+1棵;(3)单边环型植树公式(环型植树):棵树=总长÷间隔,总长=棵树×间隔(4)单边楼间植树公式(两头不植):棵树=总长÷间隔-1,总长=(棵树+1)×间隔(5)方阵问题:最外层总人数=4×(N-1),相邻两层人数相差8人,n阶方阵的总人数为n²。
5-10:行程问题5. 火车过桥核心公式:路程=桥长+车长(火车过桥过的不是桥,而是桥长+车长)6. 相遇追及问题公式:相遇距离=(速度1+速度2)×相遇时间追及距离=(速度1-速度2)×追及时间7. 队伍行进问题公式:队首→队尾:队伍长度=(人速+队伍速度)×时间队尾→队首:队伍长度=(人速-队伍速度)×时间8. 流水行船问题公式:顺速=船速+水速,逆速=船速-水速9. 往返相遇问题公式:两岸型两次相遇:S=3S1-S2,(第一次相遇距离A为S1,第二次相遇距离B为S2)单岸型两次相遇:S=(3S1+S2)/2,(第一次相遇距离A为S1,第二次相遇距离A为S2);左右点出发:第N次迎面相遇,路程和=(2N-1)×全程;第N次追上相遇,路程差=(2N-1)×全程。
公务员考试行测公式大全

公务员考试行测公式大全1-100公式公式[拼音]gōngshì[释义](一)在自然科学中用数学符号表示几个量之间关系的式子。
具有普遍性,适合于同类关系的所有问题。
【例】表示矩形的面积S和它的长a、宽b之间的关系的公式为S=ab。
(二)谓通行的格式。
【例】《元典章·诏令一》:“凡有玺书颁降并用蒙古新字……所有公式文书咸遵其旧。
”(三)泛指可普遍应用于同类事物的方式方法。
代数:平方差公式:a^2-b^2=(a+b)(a-b)完全平方公式:(a±b)^2=a^2±2*a*b+b^2完全立方公式:(a±b)^3=a^3±3*a^2*b+3*a*b^2±b^3几何:面积计算圆周长: 2πr(πd) 面积: r2π勾孤定律:两直角边的平方和等于斜边的平(首项加末项)乘项数除以2m,n的最小公倍数为t,,最大公约数为l那么t*l=m*n1 过两点有且只有一条直线2 两点之间线段最短3 同角或等角的补角相等4 同角或等角的余角相等5 过一点有且只有一条直线和已知直线垂直6 直线外一点与直线上各点连接的所有线段中,垂线段最短7 平行公理经过直线外一点,有且只有一条直线与这条直线平行8 如果两条直线都和第三条直线平行,这两条直线也互相平行9 同位角相等,两直线平行10 内错角相等,两直线平行11 同旁内角互补,两直线平行12两直线平行,同位角相等13 两直线平行,内错角相等14 两直线平行,同旁内角互补15 定理三角形两边的和大于第三边16 推论三角形两边的差小于第三边17 三角形内角和定理三角形三个内角的和等于180°18 推论1 直角三角形的两个锐角互余19 推论2 三角形的一个外角等于和它不相邻的两个内角的和20 推论3 三角形的一个外角大于任何一个和它不相邻的内角21 全等三角形的对应边、对应角相等22边角边公理(SAS) 有两边和它们的夹角对应相等的两个三角形全等23 角边角公理( ASA)有两角和它们的夹边对应相等的两个三角形全等24 推论(AAS) 有两角和其中一角的对边对应相等的两个三角形全等25 边边边公理(SSS) 有三边对应相等的两个三角形全等26 斜边、直角边公理(HL) 有斜边和一条直角边对应相等的两个直角三角形全等27 定理1 在角的平分线上的点到这个角的两边的距离相等28 定理2 到一个角的两边的距离相同的点,在这个角的平分线上29 角的平分线是到角的两边距离相等的所有点的集合30 等腰三角形的性质定理等腰三角形的两个底角相等(即等边对等角)31 推论1 等腰三角形顶角的平分线平分底边并且垂直于底边32 等腰三角形的顶角平分线、底边上的中线和底边上的高互相重合33 推论3 等边三角形的各角都相等,并且每一个角都等于60°34 等腰三角形的判定定理如果一个三角形有两个角相等,那么这两个角所对的边也相等(等角对等边)35 推论1 三个角都相等的三角形是等边三角形36 推论2 有一个角等于60°的等腰三角形是等边三角形37 在直角三角形中,如果一个锐角等于30°那么它所对的直角边等于斜边的一半38 直角三角形斜边上的中线等于斜边上的一半39 定理线段垂直平分线上的点和这条线段两个端点的距离相等40 逆定理和一条线段两个端点距离相等的点,在这条线段的垂直平分线上41 线段的垂直平分线可看作和线段两端点距离相等的所有点的集合42 定理1 关于某条直线对称的两个图形是全等形43 定理2 如果两个图形关于某直线对称,那么对称轴是对应点连线的垂直平分线44定理3 两个图形关于某直线对称,如果它们的对应线段或延长线相交,那么交点在对称轴上45逆定理如果两个图形的对应点连线被同一条直线垂直平分,那么这两个图形关于这条直线对称46勾股定理直角三角形两直角边a、b的平方和、等于斜边c的平方,即a^2+b^2=c^247勾股定理的逆定理如果三角形的三边长a、b、c有关系a^2+b^2=c^2 ,那么这个三角形是直角三角形48定理四边形的内角和等于360°49四边形的外角和等于360°50多边形内角和定理n边形的内角的和等于(n-2)×180°51推论任意多边的外角和等于360°52平行四边形性质定理1 平行四边形的对角相等53平行四边形性质定理2 平行四边形的对边相等54推论夹在两条平行线间的平行线段相等55平行四边形性质定理3 平行四边形的对角线互相平分56平行四边形判定定理1 两组对角分别相等的四边形是平行四边形57平行四边形判定定理2 两组对边分别相等的四边形是平行四边形58平行四边形判定定理3 对角线互相平分的四边形是平行四边形59平行四边形判定定理4 一组对边平行相等的四边形是平行四边形60矩形性质定理1 矩形的四个角都是直角61矩形性质定理2 矩形的对角线相等62矩形判定定理1 有三个角是直角的四边形是矩形63矩形判定定理2 对角线相等的平行四边形是矩形64菱形性质定理1 菱形的四条边都相等65菱形性质定理2 菱形的对角线互相垂直,并且每一条对角线平分一组对角66菱形面积=对角线乘积的一半,即S=(a×b)÷267菱形判定定理1 四边都相等的四边形是菱形68菱形判定定理2 对角线互相垂直的平行四边形是菱形69正方形性质定理1 正方形的四个角都是直角,四条边都相等70正方形性质定理2正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角71定理1 关于中心对称的两个图形是全等的72定理2 关于中心对称的两个图形,对称点连线都经过对称中心,并且被对称中心平分73逆定理如果两个图形的对应点连线都经过某一点,并且被这一点平分,那么这两个图形关于这一点对称74等腰梯形性质定理等腰梯形在同一底上的两个角相等75等腰梯形的两条对角线相等76等腰梯形判定定理在同一底上的两个角相等的梯形是等腰梯形77对角线相等的梯形是等腰梯形78平行线等分线段定理如果一组平行线在一条直线上截得的线段相等,那么在其他直线上截得的线段也相等79 推论1 经过梯形一腰的中点与底平行的直线,必平分另一腰80 推论2 经过三角形一边的中点与另一边平行的直线,必平分第三边81 三角形中位线定理三角形的中位线平行于第三边,并且等于它的一半82 梯形中位线定理梯形的中位线平行于两底,并且等于两底和的一半L=(a+b)÷2 ,S=L×h83 (1)比例的基本性质如果a:b=c:d,那么ad=bc如果ad=bc,那么a:b=c:d wc呁/S∕ ?84 (2)合比性质如果a/b=c/d,那么(a±b)/b=(c±d)/d85 (3)等比性质如果a/b=c/d=…=m/n(b+d+…+n≠0),那么(a+c+…+m)/(b+d+…+n)=a/b86 平行线分线段成比例定理三条平行线截两条直线,所得的对应线段成比例87 推论平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例88 定理如果一条直线截三角形的两边(或两边的延长线)所得的对应线段成比例,那么这条直线平行于三角形的第三边89 平行于三角形的一边,并且和其他两边相交的直线,所截得的三角形的三边与原三角形三边对应成比例90 定理平行于三角形一边的直线和其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似91 相似三角形判定定理1 两角对应相等,两三角形相似(ASA)92 直角三角形被斜边上的高分成的两个直角三角形和原三角形相似93 判定定理2 两边对应成比例且夹角相等,两三角形相似(SAS)94 判定定理3 三边对应成比例,两三角形相似(SSS)95 定理如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例,那么这两个直角三角形相似96 性质定理1 相似三角形对应高的比,对应中线的比与对应角平分线的比都等于相似比97 性质定理2 相似三角形周长的比等于相似比98 性质定理3 相似三角形面积的比等于相似比的平方99 任意锐角的正弦值等于它的余角的余弦值,任意锐角的余弦值等于它的余角的正弦值100任意锐角的正切值等于它的余角的余切值,任意锐角的余切值等于它的余角的正切值101圆是定点的距离等于定长的点的集合102圆的内部可以看作是圆心的距离小于半径的点的集合103圆的外部可以看作是圆心的距离大于半径的点的集合104同圆或等圆的半径相等105到定点的距离等于定长的点的轨迹,是以定点为圆心,定长为半径的圆106和已知线段两个端点的距离相等的点的轨迹,是着条线段的垂直平分线107到已知角的两边距离相等的点的轨迹,是这个角的平分线108到两条平行线距离相等的点的轨迹,是和这两条平行线平行且距离相等的一条直线109定理不在同一直线上的三点确定一个圆。
公务员考试必背公式大全

公务员考试必背公式大全1. 分数比例形式整除:若a∶b=m∶n(m、n互质),则a是m的倍数,b是n的倍数。
若a=m/n×b,则a=m/(m+n)×(a+b),即a+b是m+n的倍数2. 尾数法(1)选项尾数不同,且运算法则为加、减、乘、乘方运算,优先使用尾数进行判定;(2)所需计算数据多,计算复杂时考虑尾数判断快速得到答案。
常用在容斥原理中。
3. 等差数列相关公式:和=(首项+末项)×项数÷2=平均数×项数=中位数×项数;项数=(末项-首项)÷项数+1。
从1开始,连续的n个奇数相加,总和=n×n,如:1+3+5+7=4×4=16,……4. 几何边端问题相关公式:(1)单边线型植树公式(两头植树):棵树=总长÷间隔+1,总长=(棵树-1)×间隔(2)植树不移动公式:在一条路的一侧等距离栽种m棵树,然后要调整为种n棵树,则不需要移动的树木棵树为:(m-1)与(n-1)的最大公约数+1棵;(3)单边环型植树公式(环型植树):棵树=总长÷间隔,总长=棵树×间隔(4)单边楼间植树公式(两头不植):棵树=总长÷间隔-1,总长=(棵树+1)×间隔(5)方阵问题:最外层总人数=4×(N-1),相邻两层人数相差8人,n阶方阵的总人数为n²。
5-10:行程问题5. 火车过桥核心公式:路程=桥长+车长(火车过桥过的不是桥,而是桥长+车长)6. 相遇追及问题公式:相遇距离=(速度1+速度2)×相遇时间追及距离=(速度1-速度2)×追及时间7. 队伍行进问题公式:队首→队尾:队伍长度=(人速+队伍速度)×时间队尾→队首:队伍长度=(人速-队伍速度)×时间8. 流水行船问题公式:顺速=船速+水速,逆速=船速-水速9. 往返相遇问题公式:两岸型两次相遇:S=3S1-S2,(第一次相遇距离A为S1,第二次相遇距离B为S2)单岸型两次相遇:S=(3S1+S2)/2,(第一次相遇距离A为S1,第二次相遇距离A为S2);左右点出发:第N次迎面相遇,路程和=(2N-1)×全程;第N次追上相遇,路程差=(2N-1)×全程。
2017国考资料分析
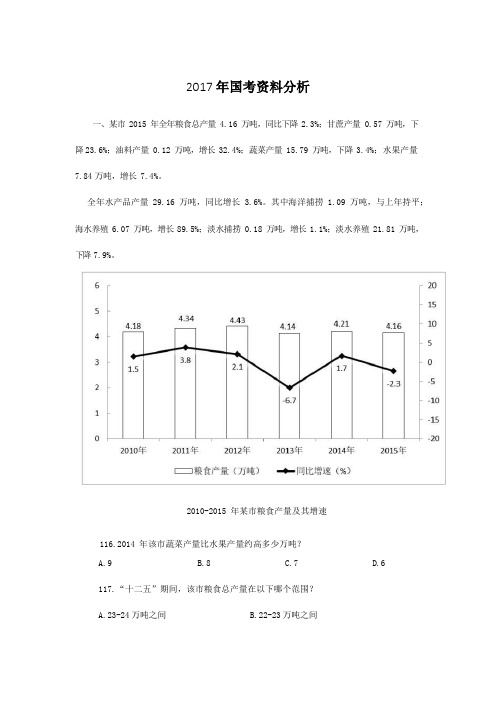
2017 年国考资料分析一、某市 2015 年全年粮食总产量 4.16 万吨,同比下降 2.3%;甘蔗产量 0.57 万吨,下降23.6%;油料产量 0.12 万吨,增长 32.4%;蔬菜产量 15.79 万吨,下降 3.4%;水果产量7.84万吨,增长 7.4%。
全年水产品产量 29.16 万吨,同比增长 3.6%。
其中海洋捕捞 1.09 万吨,与上年持平;海水养殖 6.07 万吨,增长 89.5%;淡水捕捞 0.18 万吨,增长 1.1%;淡水养殖 21.81 万吨,下降7.9%。
2010-2015 年某市粮食产量及其增速116.2014 年该市蔬菜产量比水果产量约高多少万吨?A.9B.8C.7D.6117.“十二五”期间,该市粮食总产量在以下哪个范围?A.23-24 万吨之间B.22-23 万吨之间C.21-22 万吨之间D.20-21 万吨之间118.按照 2015 年水产品产量从多到少,以下排序正确的是:A.海洋捕捞、海水养殖、淡水捕捞、淡水养殖B.淡水养殖、海水养殖、海洋捕捞、淡水捕捞C.淡水捕捞、淡水养殖、海洋捕捞、海水养殖D.淡水养殖、海洋捕捞、海水养殖、淡水捕捞119.以下哪张折线图能准确反映 2011-2015 年间,该市粮食生产同比增量的变化趋势?A.AB.BC.CD.D120.能够从上述资料中推出的是:A.2014 年油料产量超过 1000 吨B.除淡水养殖之外,其余类型的水产品 2015 年产量占水产品总产量的比重均高于上年C.4-2015 年甘蔗累计产量不到 1 万吨D.0-2015 年,粮食产量同比上升的年份多于同比下降的年份二、截至 2014 年末,我国共有博物馆 3658 个,占文物机构总数的 43.5%。
全国文物机构拥有文物藏品 4063.58 万件,比上年末增加 222.77 万件。
其中,博物馆文物藏品 2929.97万件,文物商店文物藏品 770.00 万件。
2017资料分析最新计算公式整理
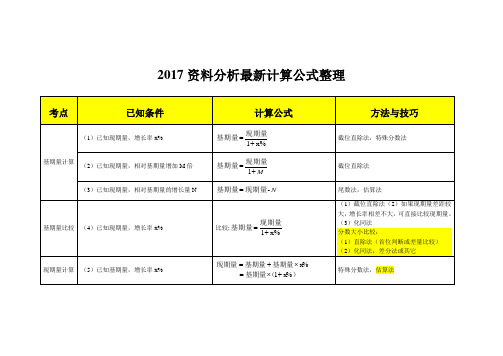
(13)已知基期量与增长量
(1)截位直除法
(2)插值法
(14)已知现期量与基期量
截位直除法
(15)如果基期量为A,经N期变为B,平均增长率为x%
代入法或公式法
(16)两期混合增长率:如果第二期与第三期增长率分别为 ,那么第三期相对第一期增长率
简单记忆口诀:连续增长,最终增长大于增长率之和;连续下降,最终下降小于增长率之和
2017
基期量计算
(1)已知现期量,增长率x%
截位直除法,特殊分数法
(2)已知现期量,相对基期量增加M倍
截位直除法
(3)已知现期量,相对基期量的增长量N
尾数法,估算法
基期量比较
(4)已知现期量,增长率x%
比较:
(1)截位直除法(2)如果现期量差距较大,增长率相差不大,可直接比较现期量。
(3)化同法
分数大小比较:
(17)合成增长率:整体分为A、B两个部分,分别增长a%与b%,整体增长率r%
(18)混合增长率:整体为A,增长率为rA,分为两个部分B和C,增长率为rB和rC
则rA介于rB和rC之间
混合增长率大小居中
增长率比较
(19)已知现期量与增长量
比较 代替增长率进行大小比较
相当于分数大小比较,同上述做法
发展速度
一般先计算 ,然后根长率a%,整体现期量B,增长率b%
一般先计算 ,然后根据a和b的大小判断大小
(26)基期比重-现期比重:某部分现期量为A增长率a%,整体现期量B,增长率b%
两期比重差值计算:
(1)先根据a与b的大小判断差值计算结果是正数还是负数;
(2)答案小于丨a-b丨
(1)直除法(首位判断或差量比较)
2017公务员考试行测常用公式集锦

公式:平均数=总数量÷总份数,或者:总份数=平均数总数量例.A,B,C,D,E五个人在一次满分为100分的考试中,得分都是大于91的互不相同的整数。
如果A,B,C的平均分为95分,B,C,D的平均分为94分,A是第一名,E是第三名得96分。
则D的得分是多少?A.96分B.98分C.97分D.99分【答案】C。
中公解析:由于几个人得分不同,所以D得分不可能为96分,排除A。
A+B+C=95 3,B+C+D=94 3,联立两式得:A-D=3,由于A≤100,故D≤97,排除B、D,选择C。
二、质合数质数:一个数如果只有1和它本身两个因数,这样的数叫做质数。
如:2、3、5、7、都是质数,质数有无限多个,最小的质数是2。
合数:一个数如果除了1和它本身还有别的因数,这样的数叫做合数。
如:4、6、15、49都是合数,合数也有无限多个,最小的合数是4。
例.一个星期天的早晨,母亲对孩子们说:“你们是否发现在你们中间,大哥的年龄等于两个弟弟年龄之和?”儿子们齐声回答说:“是的,我们的年龄和您年龄的乘积,等于您儿子人数的立方乘以1000加上您儿子人数的平方乘以10。
”从这次谈话中,你能否确定母亲在多大时,才生下第二个儿子?【答案】34。
中公解析:由题意可知,母亲有三个儿子。
母亲的年龄与三个儿子年龄的乘积等于:3 ×1000+3 ×10=27090把27090分解质因数:27090=43×7×5×3 ×2根据“大哥的年龄等于两个弟弟年龄之和”,重新组合上面的质因式得:43×14×9×5这个质因式中14就是9与5之和。
所以母亲43岁,大儿子14岁,二儿子9岁,小儿子5岁。
三、奇偶数偶数±偶数=偶数,奇数±奇数=偶数。
例.一次数学考试共有50道题,规定答对一题得2分,答错一题扣1分,未答的题不计分。
考试结束后,小明共得73分。
2017年国考资料分析必考公式大全最新版

2017年国考资料分析必考公式大全最新版2017年国考预计11月下旬笔试,想要行测拿到高分,资料分析题型必须掌握透彻,小编整理了资料分析一些常考公式,希望考生都能记熟,并运用到实际的解题过程中。
1、百分数量A占量B的百分比例:A÷B×100%。
例1:50占200的百分比是多少,50/200=25%。
2、成数几成相当于十分之几,常用于计算经济利润问题。
例2:五成,就是占5/10,即1/2。
3、折数几折相当于十分之几,例如打七折,就是售价变为原来的7/10。
例3:某商品原价为400,现打折销售,售价为100,问打了几折。
100/400=2.5,打了2.5折。
4、倍数A是B的N倍,则A=B×N。
5、增长量(增量)、减少量(减量)增长量=现在量-原有量减少量=原有量-现有量(注:大减小)增加N倍现有量=原有量×(1+N)原有量=现有量÷(1+N)例4:2010年萝卜的产量为100,2011年为110,问2011年比2010年的增长量是多少?110-100=106、增长率(增长幅度、增长速度)、减少率(减少幅度、减少速度)增长率=增长量÷原有量×100%减少率=减少量÷原有量×100%增长了x% 现有量=原有量×(1+x%) 原有量=现有量÷(1+x%)减少了y% 现有量=原有量×(1-y%) 原有量=现有量÷(1-y%)注:求“现有量”用乘法,求“原有量”用除法,增长用加法,减少用减法。
例:去年的产量为a,今年比去年增长10%,则今年产量=a×(1+10%)。
今年的产量为b,今年比去年增长10%,则去年产量=b÷(1+10%)。
去年的产量为a,今年的产量为b,则今年比去年的增长量=b-a。
今年比去年增长的百分比=(b-a)/a×100%。
今年的产量为b,只完成了(只占)计划的70%,则计划产量=b÷70%。
2017国家公务员考试-行测-2017年国考笔试备考

资料分析是行测考试的最后一个模块,一般没有公考经验的小伙伴会因为时间不够将其放弃,这实在是特别的不明智。
资料分析虽然看起来资料冗长、数据庞大、计算量大,但题目都是有章可循的,对于各个考点都有专门的公式、计算方法。
现在就国考资料分析模块中的热点题型比重比较、平均数与倍数的比较给大家做个分享,希望会对大家有帮助。
今天要跟大家分享的比重比较是要求现期比重和基期比重的比较,具体是什么样子,我们来看一道题目:【例1】2009年江苏省实现地区生产总值34061.19亿元,比上年增长12.4%,2009年江苏省规模以上工业实现增加值16727.1亿元,增长14.6%。
全年民营工业实现增加值8288.8亿元,增长18.9%,增幅同比提高4.2个百分点。
与2008年相比,2009年江苏省民营工业实现增加值在全省地区生产总值中所占比重( )。
A.无法确定B.上升了C.下降了D.不变通过读题,我们发现该题目提问中有“与2008年相比,2009年江苏省民营工业实现增加值在全省地区生产总值中所占比重×××”,有此种问法,那么就属于比重比较的问题了。
若是按部就班根据公式来做题,应将现期比重和基期比重求出来,但是这样计算量会比较大,花费的时间也很多。
针对此类题目我们有口诀:若部分的增长率大于总体,则现期的比重大于基期比重;若部分的增长率小于整体,则现期的比重小于基期比重。
知道这句口诀,我们再来做此类题目,就显得比较简单了。
例1中:江苏省民营工业作为部分其增长率为18.9%,全省地区生产总值作为整体其增长率为12.4%。
很明显部分的增长率是大于整体的增长率的,故现期比重大于基期比重,所以2009年该部分的比重较基期2008年时上升的,答案选择B选项。
大家要注意分辨此类比重比较的题目并正确运用此口诀,就可以达到快速解答出题目的目的了,那么究竟这个口诀是怎么来的,以及它还有没有其他用途呢?这就是接下来要给大家讲解的问题。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2017年国考资料分析必考公式大全最新版
2017年国考预计11月下旬笔试,想要行测拿到高分,资料分析题型必须掌握透彻,小编整理了资料分析一些常考公式,希望考生都能记熟,并运用到实际的解题过程中。
1、百分数
量A占量B的百分比例:A÷B×100%。
例1:50占200的百分比是多少,50/200=25%。
2、成数
几成相当于十分之几,常用于计算经济利润问题。
例2:五成,就是占5/10,即1/2。
3、折数
几折相当于十分之几,例如打七折,就是售价变为原来的7/10。
例3:某商品原价为400,现打折销售,售价为100,问打了几折。
100/400=2.5,打了2.5折。
4、倍数
A是B的N倍,则A=B×N。
5、增长量(增量)、减少量(减量)
增长量=现在量-原有量
减少量=原有量-现有量(注:大减小)
增加N倍现有量=原有量×(1+N)
原有量=现有量÷(1+N)
例4:2010年萝卜的产量为100,2011年为110,问2011年比2010年的增长量是多少?
110-100=10
6、增长率(增长幅度、增长速度)、减少率(减少幅度、减少速度)
增长率=增长量÷原有量×100%
减少率=减少量÷原有量×100%
增长了x% 现有量=原有量×(1+x%) 原有量=现有量÷(1+x%)
减少了y% 现有量=原有量×(1-y%) 原有量=现有量÷(1-y%)
注:求“现有量”用乘法,求“原有量”用除法,增长用加法,减少用减法。
例:去年的产量为a,今年比去年增长10%,则今年产量
=a×(1+10%)。
今年的产量为b,今年比去年增长10%,则去年产量
=b÷(1+10%)。
去年的产量为a,今年的产量为b,则今年比去年的增长量=b-a。
今年比去年增长的百分比=(b-a)/a×100%。
今年的产量为b,只完成了(只占)计划的70%,则计划产量
=b÷70%。
今年的产量为b,超额完成计划的10%,则计划产量
=b÷(1+10%)。
例5:2010年萝卜的产量为100,2011年为110,问2011年比2010年的增长率是多少?
(110-100)/100=10%
例6:2010年萝卜的产量为110,2011年为100,问2011年比2010年的减少率是多少?
(110-100)/110=1/11=9.9%
7、百分点
和百分数基本类似,但百分点不带百分号。
例7:某地去年汽车销售总额比前年增加了8%,今年汽车销售总额比去年增加了13%,则今年汽车销售总额增幅提高了多少个百分点?
13%-8%=5%,增幅提高了5%,即提高了5个百分点。
8、翻番
翻一番为原来的2倍;翻两番为原来的4倍;依此类推,翻n番为原来的2n倍。
例8:2011年的产量为100,2012年比2011年翻了3翻,那么2012年的产量是多少?
100*23=800
9、年均增长率(复合增长率)
末期值=初期值×(1+增长率)n,其中n为相差年数
例9:某公司1999年固定资产总值4亿元,固定资产年平均增长率为20%,则其2002年固定资产总值为4×(1+20%)3=6.912亿元。
10、同比、环比
同比指与去年的同一时期相比较。
这类题目的解题关键在于能否求出间隔增长率又叫隔年增长率。
下面以【例1】为例,进行公式推导。
【真题示例1】2010年上半年,全国原油产量为9848万吨,同比增长5.3%,上年同期为下降1%。
进口原油11797万吨(海关统计),增长30.2%。
原油加工量20586万吨,增长17.9%,增速同比加快16.4个百分点。
126.2010年上半年全国原油产量比2008年同期约增长了( )。
A.1.8%
B.4.2%
C.6.3%
D.9.6%
【参考答案解析】本题考查的是增长率这一知识点。
材料中要求的是2010年上半年相对于2008年上半年的增速,是一个复合增长率,我们直接套用公式。
2010年上半年相对于2008年同期的增速为5.3%+(-1%)+5%×(-1%)≈5.3%-1%=4.3%。
结合选项,选择B选项。
掌握了间隔增长率,那间隔基期量相对来说就更容易理解了,继续来看下面的题目:
【例2】2013年,全国商品房销售面积130551万平方米,比上年增长17.3%,增速比1-11月份回落3.5个百分点,比2012年提高15.5个百分点。
2011年全国商品房销售面积约为多少亿平方米?()
A.8.4
B.9.2
C.9.8
D.10.9
【参考答案解析】根据文字材料“2013年,全国商品房销售面积130551万平方米,比上年增长17.3%……比2012年提高15.5个百分点”可知,本题属于间隔基期量题目。
2012年全国商品房销售面积的同比增长率为17.3%-15.5%=1.8%;则2013年全国商品房销售面积相对于2011年的增长率,即间隔增长率为17.3%+1.8%+17.3%×1.8%≈19.4%;因此2011年全国商品房销售面积约为≈>10(亿平方米),选择D。
这类题目并不难,掌握题目特征即“间隔年份”,结合问题,灵活运用公式求解即可。
华图教育专家提醒各位考生,资料分析虽然题量大,但是却容易拿分,各位考生应该重点备考。
