知识点222 点、线、面、体(解答)
考点12 点、线、面、角

考向二 角
• 1.角平分线必须同时满足三个条件:①是从角的顶点引出的射 线;②在角的内部;③将已知角平分.
3.度、分、秒的运算方法 1°=60′,1′=60″,1°=3600″. 1周角=2平角=4直角=360°.
4.余角和补角
(1) 余角:∠1+∠2=90°⇔∠1与∠2互为余角;
(2)补角:∠1+∠2=180°⇔∠1与∠2互为补角.
(3)性质:同角(或等角)的余角相等;同角(或等角)的补角相 等.
5.方向角和方位角
向上,并且物高与影长成正比. (3)正投影:投射线与投影面垂直时的平行投影,叫做正投影.
㈡、视图 1.视图 由于可以用视线代替投影线,所以物体的正投影通常也称为物体的视图. 2.三视图 (1)主视图:从正面看得到的视图叫做主视图. (2)左视图:从左面看得到的视图叫做左视图. (3)俯视图:从上面看得到的视图叫做俯视图. 【注意】在三种视图中,主视图反映物体的长和高,左视图反映了物体的宽和高,俯视 图反映了物体的长和宽. 3.三视图的画法 (1)画三视图要注意三要素:
∠DOE=3∠COE,求∠BOE.
3.【答案】18.5 【解析】18°30′=18.5°,故答案为:18.5. 4.【解析】 ∵∠AOB=180°,∠BOC=80°, ∴∠AOC=100°, ∵OD平分∠AOC,∴∠COD=∠AOC=50°, 又∵∠DOE=3∠COE, ∴∠COE=∠COD=25°, ∴∠BOE=∠BOC-∠COE=55°.
6.点到直线的距离
人教新课标A版高中数学必修二 可编辑课件 第二章 点、直线、平面之间的位置关系 222 平面与平面平行的判定

.
2.推论:如果一个平面内有两条 相交 直线,分别平
人 教
A
行于另一个平面内的两条直线,则这两个平面平行.
版
数
用符号表示为a∥c,b∥d,a∩b=A,a⊂α,b⊂α , 学
c⊂β,d⊂β⇒α∥β
.
3.α∥β,a⊂α⇒ a∥β .
第二章 点、直线、平面之间的位置关系
人 教 A 版 数 学
第二章 点、直线、平面之间的位置关系
第二章 点、直线、平面之间的位置关系
人
2.2.2 平面与平面平行的判定
教 A 版
数
学
第二章 点、直线、平面之间的位置关系
人 教 A 版 数 学
第二章 点、直线、平面之间的位置关系
1.判定定理:如果一个平面内有两条 相交 直 线 分
别 平行 于另一个平面,那么这两个平面平行.用数学符
号表示 a∥α,b∥α,a⊂β,b⊂β,a∩b=A⇒α∥β
一、选择题
1.若两个平面内分别有一条直线,这两条直线互相平 行,则这两个平面的公共点个数
A.有限个 B.无限个
C.没有
D.没有或无限个
[答案] D
[解析] 两平面相交或平行,故选D.
(
)
人 教
A
版
数
学
第二章 点、直线、平面之间的位置关系
二、填空题
2.直线a⊂平面α,直线b⊂平面β,且α∥β,则a、b的
证明如下:在正方体ABCD-A1B1C1D1中连接PQ.
∵P,Q分别为DD1,CC1的中点,
∴PQ綊CD,CD綊AB.
人
教
∴PQ綊AB,∴四边形ABQP是平行四边形,
A 版
数
∴PA∥QB.
特殊儿童心理学各章节知识点整理复习资料

特殊儿童心理学各章节知识点整理复习资料第一章1、这门课的研究对象是什么?什么是特殊儿童?特殊儿童(Exceptional Children):儿童在身心的发展上偏离正常,即在身体、行为、语言、智力、情绪与人格等发育上与正常儿童有明显差异。
2、简述国外对特殊儿童的研究、产生和发展。
怎么产生怎么发展,什么时候产生什么时候发展。
从历史上看,人们对待残疾儿童的态度有一个从野蛮消灭到完全平等的渐渐走向文明的过程。
1)产生的原因资本主义的自由、平等、博爱等思想的产生。
医学和解剖学的发展。
哲学和普通教育学发展。
2)发展的阶段(1) 歧视阶段(1800年以前)(2)重视阶段(1800年-1900年)(3) 发展阶段(1900年至今)3、谈一谈近年对特殊儿童教育的思潮。
(全纳教育、融合教育...)4、试举出特殊儿童的常见研究方法。
第二章1、什么是神经症?包括哪些类型?有哪些共性?2、抑郁症的八个临床表现。
结合实例谈谈如何治疗抑郁症患者。
3、什么是恐惧症?其发病的原因有哪些?有哪些临床表现?4、什么是精神分裂症?有哪些临床表现?(五点,思维障碍、情感障碍、妄想、幻觉、紧张)它的发病过程是怎样的?(遇到起、发病期、发病晚期、调整期......)第三章1、学习困难儿童的定义是什么?2、谈谈对学习困难儿童教育的意义。
3、试述学习困难儿童的认知特点。
4、学习困难儿童教育方法,常见的有哪几种?5、试举出对学习困难儿童的几种教学策略。
第四章1、智力落后儿童一般可分为几个等级?其智商范围大约是多少?(中度轻度重度)2、试述智力落后儿童的形成病因。
3、我国目前对智力落后儿童常见的教育安置形式有哪几种?(三种)4、简述智力落后儿童的认知特点。
5、简述智力落后儿童的教学原则。
第五章1、什么是多动症?多动症儿童有哪些特征?2、Adhd和add有何区别?3、儿童多动症有哪些可能的病因?4、一些干预多动症的策略。
第六章1、自闭症儿童有哪些奇特表现?三联症2、自闭症儿童都是智力落后吗?(判断)不是3、有人认为自闭症儿童是因为几乎未有感受到父母的温暖导致的,你同意这一看法吗?现在主要认为生物学,从基因到孕期到神经深化,父母教养方式基本被排除。
人教版七年级上数学《点,线,面,体》课堂笔记

《点,线,面,体》课堂笔记
一、概念定义
1.点:没有大小,没有方向,是几何图形的基本元素。
2.线:由无数个点组成,有长度,可向两个方向无限延伸。
3.面:由无数条线组成,有长度和宽度,可向两个方向无限延伸。
4.体:由无数个面组成,有长度、宽度和高度,可向三个方向无限延伸。
二、关系
1.线是由无数个点组成。
2.面是由无数条线组成。
3.体是由无数个面组成。
三、特性
1.点的特性:没有长度和宽度,不可向任何方向延伸。
2.线的特性:有长度,可以向两个方向无限延伸。
3.面的特性:有长度和宽度,可以向两个方向无限延伸。
4.体的特性:有长度、宽度和高度,可以向三个方向无限延伸。
四、表示方法
1.点用大写字母表示,如A、B、C等。
2.线用小写字母表示,如a、b、c等。
线上有点,表示为a(1)、a(2)、a(3)
等。
3.面用大写字母加下标表示,如A(1)、B(2)、C(3)等。
面内有直线,表示
为A(1,2)、B(2,3)等。
4.体用大写字母加下标加括号表示,如A(1)(2)(3)、B(4)(5)(6)等。
体内
有面,表示为A(1,2,3)、B(4,5,6)等。
高中数学立体几何知识点归纳总结

高中数学立体几何学问点归纳总结一、立体几何学问点归纳第一章空间几何体(一)空间几何体的构造特征(1)多面体——由若干个平面多边形围成的几何体.围成多面体的各个多边形叫叫做多面体的面,相邻两个面的公共边叫做多面体的棱,棱与棱的公共点叫做顶点。
旋转体——把一个平面图形绕它所在平面内的一条定直线旋转形成的封闭几何体。
其中,这条定直线称为旋转体的轴。
(2)柱,锥,台,球的构造特征1.棱柱1.1棱柱——有两个面相互平行,其余各面都是四边形,并且每相邻两个四边形的公共边都相互平行,由这些面所围成的几何体叫做棱柱。
1.2相关棱柱几何体系列(棱柱、斜棱柱、直棱柱、正棱柱)的关系:①⎧⎪⎧−−−−−→⎨⎪−−−−−→⎨⎪⎪⎩⎩底面是正多形棱垂直于底面斜棱柱棱柱正棱柱直棱柱其他棱柱底面为矩形侧棱与底面边长相等1.3①侧棱都相等,侧面是平行四边形;②两个底面与平行于底面的截面是全等的多边形;③过不相邻的两条侧棱的截面是平行四边形;④直棱柱的侧棱长与高相等,侧面与对角面是矩形。
1.4长方体的性质:①长方体一条对角线长的平方等于一个顶点上三条棱的平方和;【如图】222211AC AB AD AA=++②(理解)长方体的一条对角线1AC与过顶点A的三条棱所成的角分别是αβγ,,,那么222cos cos cos1αβγ++=,222sin sin sin2αβγ++=;③(理解)长方体的一条对角线1AC 与过顶点A 的相邻三个面所成的角分别是αβγ,,,则222cos cos cos 2αβγ++=,222sin sin sin 1αβγ++=.1.5侧面绽开图:正n 棱柱的侧面绽开图是由n 个全等矩形组成的以底面周长和侧棱长为邻边的矩形.1.6面积、体积公式:2S c hS c h S S h=⋅=⋅+=⋅直棱柱侧直棱柱全底棱柱底,V (其中c 为底面周长,h为棱柱的高) 2.圆柱2.1圆柱——以矩形的一边所在的直线为旋转轴,其余各边旋转而形成的曲面所围成的几何体叫圆柱. 2.2圆柱的性质:上、下底及平行于底面的截面都是等圆;过轴的截面(轴截面)是全等的矩形. 2.3侧面绽开图:圆柱的侧面绽开图是以底面周长和母线长为邻边的矩形. 2.4面积、体积公式:S 圆柱侧=2rh π;S 圆柱全=222rh r ππ+,V 圆柱=S 底h=2r h π(其中r 为底面半径,h 为圆柱高) 3.棱锥3.1棱锥——有一个面是多边形,其余各面是有一个公共顶点的三角形,由这些面所围成的几何体叫做棱锥。
点、线、面知识点
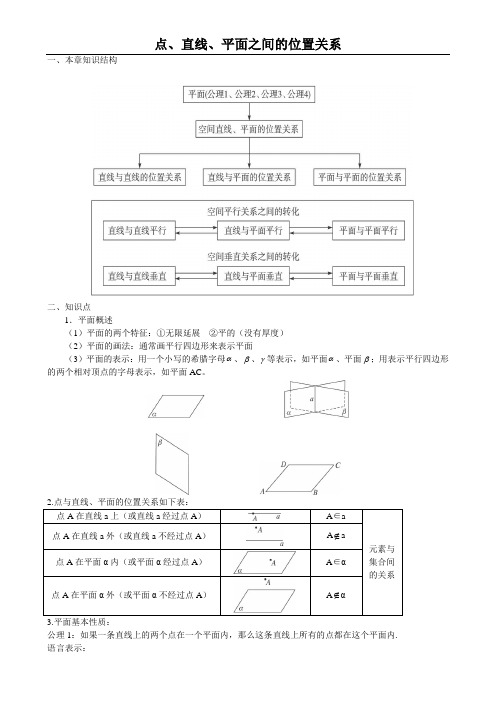
点、直线、平面之间的位置关系一、本章知识结构二、知识点1.平面概述(1)平面的两个特征:①无限延展 ②平的(没有厚度) (2)平面的画法:通常画平行四边形来表示平面(3)平面的表示:用一个小写的希腊字母α、β、γ等表示,如平面α、平面β;用表示平行四边形的两个相对顶点的字母表示,如平面AC 。
3.平面基本性质:公理1:如果一条直线上的两个点在一个平面内,那么这条直线上所有的点都在这个平面内.语言表示:若A∈a,B∈a,且A∈α,B∈α,则a⊂α.公理2:经过不在同一直线上的三点,有且只有一个平面.推论一:经过一条直线和这条直线外的一点,有且只有一个平面。
推论二:经过两条相交直线,有且只有一个平面。
推论三:经过两条平行直线,有且只有一个平面公理3:如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线.用符号语言表示为:P∈α,且P∈β⇒α∩β=l,且P∈l.4.空间的两条直线的三种位置关系:⎪⎩⎪⎨⎧⎩⎨⎧.,:;,:;,:没有公共点不同在任何一个平面内异面直线没有公共点同一平面内平行直线有且只有一个公共点同一平面内相交直线共面直线(1)异面直线的画法常用的有下列三种:(2)公理4:平行于同一条直线的两条直线互相平行。
符号表示为:a∥b,b∥c⇒a∥c.(3)等角定理:空间中如果两个角的两边分别对应平行,那么这两个角相等或互补.(4)两条异面直线所成的角:异面直线a、b,在空间中任取一点O,过点O分别引a′∥a,b′∥b,则a′,b′所成的锐角(或直角)叫做两条异面直线所成的角.两条异面直线所成角的范围是(0°,90°];_a_b_a_bαα若两条异面直线所成的角是直角,我们就说这两条异面直线互相垂直. 5.空间中直线与平面之间的3种位置关系:⎪⎩⎪⎨⎧⎩⎨⎧有无数个公共点直线在平面内没有公共点平行有且只有一个公共点相交直线在平面外:;:;:6.两个平面平行——没有公共点. 若α∩β=∅,则α∥β.两个平面相交——有一条公共直线. 若α∩β=AB,则α与β相交.图2 图37. 直线与平面平行的判定定理:平面外一条直线与此平面内的一条直线平行,那么该直线与此平面平行.符号语言为:.图形语言为:8. 直线与平面平行的性质:一条直线和一个平面平行,则过这条直线的任一平面与此平面的交线与该直线平行.符号语言为:图形语言为:9.平面与平面平行的判定定理:一个平面内有两条相交直线都平行于一个平面,则这两个平面平行。
北师大版七年级上册数学第一章丰富的图形世界知识点归纳及巩固练习
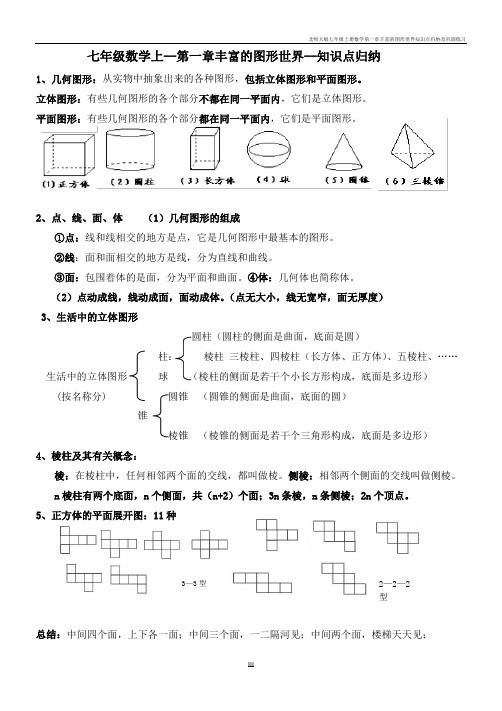
七年级数学上--第一章丰富的图形世界--知识点归纳1、几何图形:从实物中抽象出来的各种图形,包括立体图形和平面图形。
立体图形:有些几何图形的各个部分不都在同一平面内,它们是立体图形。
平面图形:有些几何图形的各个部分都在同一平面内,它们是平面图形。
2、点、线、面、体(1)几何图形的组成①点:线和线相交的地方是点,它是几何图形中最基本的图形。
②线:面和面相交的地方是线,分为直线和曲线。
③面:包围着体的是面,分为平面和曲面。
④体:几何体也简称体。
(2)点动成线,线动成面,面动成体。
(点无大小,线无宽窄,面无厚度)3、生活中的立体图形圆柱(圆柱的侧面是曲面,底面是圆)柱:棱柱三棱柱、四棱柱(长方体、正方体)、五棱柱、……生活中的立体图形球(棱柱的侧面是若干个小长方形构成,底面是多边形)(按名称分) 圆锥(圆锥的侧面是曲面,底面的圆)锥棱锥(棱锥的侧面是若干个三角形构成,底面是多边形)4、棱柱及其有关概念:棱:在棱柱中,任何相邻两个面的交线,都叫做棱。
侧棱:相邻两个侧面的交线叫做侧棱。
n棱柱有两个底面,n个侧面,共(n+2)个面;3n条棱,n条侧棱;2n个顶点。
5、正方体的平面展开图:11种3—3型2—2—2型总结:中间四个面,上下各一面;中间三个面,一二隔河见;中间两个面,楼梯天天见;中间没有面,三三连一线6、其他常见图形的平面展开图:侧面可以展开成长方形的是:圆柱和棱柱;侧面可以展开为扇形的是:圆锥7、截一个正方体:用一个平面去截一个正方体,截出的面可能是:三角形,四边形,五边形,六边形。
可能出现的:锐角三角型、等边、等腰三角形,正方形、矩形、非矩形的平行四边形、非等腰梯形、等腰梯形、五边形、六边形、正六边形不可能出现:钝角三角形、直角三角形、直角梯形、正五边形、七边形或更多边形8 、三视图:物体的三视图指主视图、俯视图、左视图。
主视图:从正面看到的图,叫做主视图。
左视图:从左面看到的图,叫做左视图。
高中文科数学立体几何知识点总结

ll//m立体几何知识点整理(文科)ml//m一.直线和平面的三种位置关系:αl1.线面平行方法二:用面面平行实现。
l//l//αl 符号表示:2.线面相交lβlαAα方法三:用平面法向量实现。
符号表示:3.线在面内nl若n 为平面的一个法向量,nl 且l,则l//。
lα α符号表示:二.平行关系:1.线线平行:l方法一:用线面平行实现。
l// ll//mm3.面面平行:方法一:用线线平行实现。
l//l' αl βm l' m'mm // l,mm ' 且相交//方法二:用面面平行实现。
l',m'且相交l//βll//m γ mmα方法二:用线面平行实现。
方法三:用线面垂直实现。
l//若l,m ,则l//m 。
m//// 方法四:用向量方法:l,m且相交βl m若向量l 和向量m 共线且l 、m 不重合,则l//m 。
α2.线面平行:方法一:用线线平行实现。
1/11WORD 格式lA αC B方法三:用向量方法:若向量l 和向量m 的数量积为0,则lm 。
三.垂直关系:三.夹角问题。
4.线面垂直:(一)异面直线所成的角:方法一:用线线垂直实现。
(1)范围:(0,90] lAC l ABAB AB AC AC,Al(2)求法: 方法一:定义法。
步骤1:平移,使它们相交,找到夹角。
P nA θOα 方法二:用面面垂直实现。
步骤2:解三角形求出角。
(常用到余弦定理)余弦定理: βlmlacmlm,lcos2 a 2 b 2abc2 θbα(计算结果可能是其补角) 5.面面垂直:方法二:向量法。
转化为向量 方法一:用线面垂直实现。
C的夹角βllθ()计算结果可能是其补角:lA BαABAC ABACcos方法二:计算所成二面角为直角。
(二)线面角6.线线垂直:(1)定义:直线l上任取一点P(交点除外),作方法一:用线面垂直实现。
m l lmlmP O于O,连结AO,则AO为斜线PA在面内的射影,PAO(图中)为直线l与面所成的角。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1、如图所示,长方形绕虚线旋转一周后,形成的图形是什么?旋转半周呢?
考点:点、线、面、体。
分析:根据线动成面的知识可得出答案,也可用纸片进行演示.
解答:解:长方形绕图示虚线旋转一周后形成的图形是圆柱,旋转半周所形成的图形也圆柱.
点评:本题考查学生灵活运用平面图形旋转形成立体图形的知识及创新能力.
2、如图,把一长方形在直线m上翻滚,请在图中作出A点所经过的路径.
考点:点、线、面、体。
分析:由题意可知,A点所经过的路径是先以长方形的长为半径,旋转90°,再以长方形的对角线为半径,旋转90°所对应的弧长.
解答:解:如图所示.
点评:本题考查了点动成线,画图时注意半径的确定.
3、如图所示,它是由什么图形旋转而成的?请你画出来.
考点:点、线、面、体。
分析:从正面看得到的平面图形是从上到下为等腰三角形,长方形,等腰三角形,那么所求的图形为原图形的一半.
解答:解:面动成体,直角三角形绕直角边旋转一周可得圆锥,长方形绕一边旋转一周可得圆柱,
那么所求的图形是直角三角形,长方形,直角三角形的组合图形.
点评:解决本题的关键是得到所求的平面图形是得到几何体的主视图的被纵向分成的一半.
4、图中的立体图形是由哪个平面图形旋转后得到?请用线连起来.
考点:点、线、面、体;认识立体图形。
分析:三角形旋转可得圆锥,长方形旋转得圆柱,半圆旋转得球,结合这些规律直接连线即可.
解答:解:如图.
点评:熟记常见平面图形旋转可得到什么立体图形是解决本题的关键.
5、用第一行的图形绕轴旋转一周,便得到第二行的几何体,用线连一连.
考点:点、线、面、体。
分析:如图本题是一个平面图形围绕一条轴旋转一周根据面动成体的原理即可解.
解答:解:图(1)旋转一周形成一个圆柱与一个圆锥的组合体,即B;图(2)旋转一周形成圆锥,即D;图(3)旋转一周形成圆柱,即A;图(4)旋转一周形成半球,即C.
(1)─B,
(2)─D,
(3)─A,
(4)─C.
点评:长方形绕它的一边旋转360度形成圆柱;直角三角形绕它的一直角边旋转360度形成圆锥;半圆绕它的直径旋转360度形成球.
6、用数学的眼光去观察问题,你会发现很多图形都能看成是动静结合,舒展自如的.下面所给的三排图形都存在着某种联系,用线将它们连起来.
考点:点、线、面、体。
分析:本题是一个平面围绕一条边为中为对称轴旋转一周根据面动成体的原理.可知形成的立体图形以及与俯视图间的关联.
解答:解:从第一行的平面图形绕某一边旋转可得到第二行的立体图形,从第二行的立体图形的上面看可得到第三行的平面图形.
(1)→(三)→(D);
(2)→(二)→(C);
(3)→(四)→(B);
(4)→(一)→(A).
点评:本题考查了平面图形和立体图形的联系,长方形绕一边旋转一周,得到的几何体是圆柱,一个三角形绕一边旋转一周,得到的几何体是圆锥.
7、如图所示,阴影部分图形绕中间的直线旋转会形成什么几何图形?
考点:点、线、面、体。
分析:根据线动成面的知识及直角三角形绕直角边旋转一周可形成圆锥、长方形绕一边旋转一周可形
成圆柱,即可得出各图形旋转后的图形.
解答:解:直角三角形绕直线1旋转一周可形成圆锥;
长方形绕直线2边旋转一周可形成圆柱;
直角梯形绕直线3旋转可形成去顶的三棱锥;
直角梯形绕直线4旋转一周可形成圆柱空心去顶三角锥.
点评:本题考查线动成面的知识,有一定难度,关键是掌握一些特殊图形旋转后的图形.。
