2010年白云区中考数学模拟试题及答案_3
2010年广东省中考数学模拟试题

2010年广东省中考数学模拟试卷数 学说明:全卷共4页,考试时间100分钟,满分120分。
请将答案写在答题纸上。
一.选择题(本题共5小题,每小题3分,共15分). 1.下列运算中,正确的是( )A .()2222b ab a b a ++=+B .532523a a a =+C .-5-2=-3D .()63262a a =2.下列的正方体表面展开图中,折成正方体后“快”与“乐”相对的是 ( )3.把不等式组⎪⎩⎪⎨⎧<+-32324x x 的解集在数轴上表示,正确的是( )4.下列图形中既是中心对称图形又是轴对称图形的是()5.如图,DE 是△ABC 的中位线,且△ADE 的周长为20,则△ABC 的周长为 ( )A .30B .40C .50D .无法计算二.填空题(本题共5小题,每小题4分,共20分).6.据有关资料表明,我国因环境污染造成的巨大经济损失,每年高达6800万元,该数据用科学记数法表示为元.7.分解因式:x x 2733-= .8.数据:1,5,9,x 的众数是5,则这组数据的中位数是 .≤0 A BCDE9.如图,在⊙O 中,C 是AB 的中点,∠AOC =40°,则∠ADB 的度数为度.10.如图,在等腰梯形ABCD 中,AD ∥BC ,∠A =120°,AD =8,BC =14,则梯形的周长为.三.解答题(本题共5小题,每小题6分,共30分). 11.计算:()20)61(130tan 32312--+----+π .12.解分式方程:11112-=-x x .13.如图,在平面直角坐标系中,已知点(42)B ,,BA x ⊥轴于A .(1)作出△OAB 绕原点逆时针方向旋转90°后的图形△O 1A 1B 1, 并写出B 1的坐标;(2)将OAB △平移得到O A B '''△,点A 的对应点是A ',点B 的对应点B '的坐标为(22)-,,在坐标系中作出O A B '''△.14.如图,已知一次函数)(01≠+=k b kx y 与反比例函数()02≠=m x my 的图象交于A 、D 两点,且与y 轴交于点C .AB 垂直于y 轴,垂足为B ,CO =BC=1,1=∆AOB S . 求两个函数的表达式.15.如图,在Rt △ABC 中,∠C =90°,∠CAB =45°,∠CAB 的平分线AD 交于BC 于D ,过点D 作DE ⊥AB 于E 。
2010年中考模拟数学卷参考答案

2010年中考模拟试卷 数学参考答案及评分标准三、解答题(本题有8小题,第17~19题每题6分,第20~21题8分,第22~23题每题10分,第24题12分,共66分) 17、(本题满分6分) 解:∵方程2233x mx x -=--无解∴方程2233x mx x -=--有增根x=3------------2分∴方程两边同乘以(x-3),得:26x m -=------------2分∴当x=3时,m =分 18、(本题满分6分)解:过C 点作BA 的延长线交于点E ,------------1分∵AB =AC =10,∠B =022.5 ∴∠EAC =045∴△EAC 为等腰直角三角形------------1分设AE =EC =X,则AB =AC =10∴x =∴111022S A B E C ∆=⋅=⨯⨯=≈35.42m ------------2分又∵53.610⨯2cm =362m >35.42m ------------1分 ∴预订草皮够用------------1分19、(本题满分6分)解:答案不唯一,酌情给分。
20、(本题满分8分)解:(1)18 0.55------------各1分(2)图略--------------共4分(虚设组不设各扣1分)(3)0.55±0.1均为正确------------2分 21、(本题满分8分) 解:(1)正确的结论:①②③------------2分(2)错误理由:当a >0时,只有1x >2x >0或2x <1x <0时,1y <2y 而2x <0<1x 时,1y >2y ------------4分 改正:当a >0时,在同一象限内,函数a y x=,y 随x 增大而减小-----2分22、(本题满分10分)解:(1)如右图------------共6分(030,045角,线段a 各1分,余酌情给分)(2)设AB =x,则R t △ABC 中,OB =x ,由题意得:6+ x ------------1分得,1)x =≈8米------------2分 答:旗杆高度约为8米。
2010年中考模拟数学试卷和答案

2010年中考模拟试卷数 学考生须知:1.本试卷分试题卷和答题卷两部分,满分120分,考试时间100分钟 .2.答题时,应该在答题卷指定位置内写明校名,姓名和准考证号 .3.所有答案都必须做在答题卷标定的位置上,请务必注意试题序号和答题序号相对应 .4.考试结束后,上交试题卷和答题卷试题卷一、仔细选一选(本题有10个小题,每小题3分,共30分)下面每小题给出的四个选项中,只有一个是正确的 .注意可以用多种不同的方法来选取正确答案 .1. 如果0=+b a ,那么a ,b 两个实数一定是( )A.都等于0B.一正一负C.互为相反数D.互为倒数2. 要了解全校学生的课外作业负担情况,你认为以下抽样方法中比较合理的是( )A.调查全体女生B.调查全体男生C.调查九年级全体学生D.调查七、八、九年级各100名学生 3. 直四棱柱,长方体和正方体之间的包含关系是( )4. 有以下三个说法:①坐标的思想是法国数学家笛卡儿首先建立的;②除了平面直角坐标系,我们也可以用方向和距离来确定物体的位置;③平面直角坐标系内的所有点都属于四个象限 .其中错误的是( )A.只有①B.只有②C.只有③D.①②③ 5. 已知点P (x ,y )在函数x xy -+=21的图象上,那么点P 应在平面直角坐标系中的( )A.第一象限B. 第二象限C. 第三象限D. 第四象限6. 在一张边长为4cm 的正方形纸上做扎针随机试验,纸上有一个半径为1cm 的圆形阴影区域,则针头扎在阴影区域内的概率为( )A.161 B.41 C.16π D.4π 7. 如果一个直角三角形的两条边长分别是6和8,另一个与它相似的直角三角形边长分别是3和4及x ,那么x 的值( ) A.只有1个 B.可以有2个 C.有2个以上,但有限 D.有无数个8. 如图,在菱形ABCD 中,∠A=110°,E ,F 分别是边AB 和BC的中点,EP ⊥CD 于点P ,则∠FPC=( ) A.35° B.45° C.50° D.55°9. 两个不相等的正数满足2=+b a ,1-=t ab ,设2)(b a S -=,则S 关于t 的函数图象是( )A.射线(不含端点)B.线段(不含端点)C.直线D.抛物线的一部分10. 某校数学课外小组,在坐标纸上为学校的一块空地设计植树方案如下:第k 棵树种植在点)(k k k y x P ,处,其中11=x ,11=y ,当k≥2时,⎪⎪⎩⎪⎪⎨⎧---+=----+=--]52[]51[])52[]51([5111k k y y k k x x k k k k ,[a ]表示非负实数a 的整数部分,例如[2.6]=2,[0.2]=0 .按此方案,第2009棵树种植点的坐标为( )A.(5,2009)B.(6,2010)C.(3,401) D (4,402)二. 认真填一填(本题有6个小题,每小题4分,共24分)要注意认真看清楚题目的条件和要填写的内容,尽量完整地填写答案 11. 如图,镜子中号码的实际号码是___________ .12. 在实数范围内因式分解44-x = _____________________ . 13. 给出一组数据:23,22,25,23,27,25,23,则这组数据的中位数是___________;方差(精确到0.1)是_______________ .14. 如果用4个相同的长为3宽为1的长方形,拼成一个大的长方形,那么这个大的长方形的周长可以是______________ .15. 已知关于x 的方程322=-+x mx 的解是正数,则m 的取值范围为______________ . 16. 如图,AB 为半圆的直径,C 是半圆弧上一点,正方形DEFG 的一边DG 在直径AB 上,另一边DE 过ΔABC 的内切圆圆心O ,且点E 在半圆弧上 .①若正方形的顶点F 也在半圆弧上,则半圆的半径与正方形边长的比是______________;②若正方形DEFG 的面积为100,且ΔABC 的内切圆半径r =4,则半圆的直径AB = __________ .三. 全面答一答(本题有8个小题,共66分)解答应写出文字说明、证明过程或推演步骤 .如果觉得有的题目有点困难,那么把自己能写出的解答写出一部分也可以 . 17. (本小题满分6分)如果a ,b ,c 是三个任意的整数,那么在2b a +,2c b +,2ac +这三个数中至少会有几个整数?请利用整数的奇偶性简单说明理由 .18. (本小题满分6分)如图,,有一个圆O 和两个正六边形1T ,2T .1T 的6个顶点都在圆周上,2T 的6条边都和圆O 相切(我们称1T ,2T 分别为圆O 的内接正六边形和外切正六边形) . (1)设1T ,2T 的边长分别为a ,b ,圆O 的半径为r ,求a r :及b r :的值; (2)求正六边形1T ,2T 的面积比21:S S 的值 .如图是一个几何体的三视图 . (1)写出这个几何体的名称;(2)根据所示数据计算这个几何体的表面积;(3)如果一只蚂蚁要从这个几何体中的点B 出发,沿表面爬到AC 的中点D ,请你求出这个线路的最短路程 .20. (本小题满分8分)如图,已知线段a .(1)只用直尺(没有刻度的尺)和圆规,求作一个直角三角形ABC ,以AB 和BC 分别为两条直角边,使AB=a ,BC=a 21(要求保留作图痕迹,不必写出作法); (2)若在(1)作出的RtΔABC 中,AB=4cm ,求AC 边上的高 .学校医务室对九年级的用眼习惯所作的调查结果如表1所示,表中空缺的部分反映在表2的扇形图和表3的条形图中.(1)请把三个表中的空缺部分补充完整;(2)请提出一个保护视力的口号(15个字以内).22. (本小题满分10分)如图,在等腰梯形ABCD中,∠C=60°,AD∥BC,且AD=DC,E、F分别在AD、DC的延长线上,且DE=CF,AF、BE交于点P .(1)求证:AF=BE;(2)请你猜测∠BPF的度数,并证明你的结论.在杭州市中学生篮球赛中,小方共打了10场球 .他在第6,7,8,9场比赛中分别得了22,15,12和19分,他的前9场比赛的平均得分y 比前5场比赛的平均得分x 要高 .如果他所参加的10场比赛的平均得分超过18分 (1)用含x 的代数式表示y ;(2)小方在前5场比赛中,总分可达到的最大值是多少? (3)小方在第10场比赛中,得分可达到的最小值是多少?24. (本小题满分12分)已知平行于x 轴的直线)0(≠=a a y 与函数x y =和函数xy 1=的图象分别交于点A 和点B ,又有定点P (2,0) . (1)若0>a ,且tan ∠POB=91,求线段AB 的长; (2)在过A ,B 两点且顶点在直线x y =上的抛物线中,已知线段AB=38,且在它的对称轴左边时,y 随着x 的增大而增大,试求出满足条件的抛物线的解析式; (3)已知经过A ,B ,P 三点的抛物线,平移后能得到259x y =的图象,求点P 到直线AB 的距离 .2010年中考模拟试卷数学参考答案一、仔细选一选(每小题3分,芬30分)二. 认真填一填(本题有6个小题,每小题4分,共24分) 11、326512.)2)(2)(2(2-++x x x 13、23;2.614、14或16或2615、46-≠->m m 或16、①5∶2 ;②21三. 全面答一答(本题有8个小题,共66分) 17、(本题6分)至少会有一个整数 .因为三个任意的整数a,b,c 中,至少会有2个数的奇偶性相同,不妨设其为a ,b , 那么2ba +就一定是整数 . 18、(本题4分)(1)连接圆心O 和T 1的6个顶点可得6个全等的正三角形 . 所以r ∶a=1∶1;连接圆心O 和T 2相邻的两个顶点,得以圆O 半径为高的正三角形, 所以r ∶b=3∶2;(2) T 1∶T 2的连长比是3∶2,所以S 1∶S 2=4:3):(2=b a .19、(本题6分)(1) 圆锥; (2) 表面积S=πππππ164122=+=+=+r rl S S 圆扇形(平方厘米)(3) 如图将圆锥侧面展开,线段BD 为所求的最短路程 . 由条件得,∠BAB ′=120°,C 为弧BB ′中点,所以BD =33 .20、(本题8分)(1)作图如右,ABC ∆即为所求的直角三角形;(2)由勾股定理得,AC =52cm , 设斜边AC 上的高为h, ABC ∆面积等于h ⨯⨯=⨯⨯52212421,所以554=h 21、(本题8分)(1)补全的三张表如下:(表一)(2)例如:“象爱护生命一样地爱护眼睛!”等 . 22、(本题10分)(1)∵BA=AD ,∠BAE=∠ADF ,AE=DF , ∴△BAE ≌△ADF ,∴BE=AF ; (2)猜想∠BPF=120° .∵由(1)知△BAE ≌△ADF ,∴∠ABE=∠DAF .∴∠BPF=∠ABE+∠BAP=∠BAE ,而AD ∥BC ,∠C=∠ABC=60°, ∴∠BPF=120° . 23、(本题10分)(1)9191215225++++=x y ;(2)由题意有x x >++++9191215225,解得x <17,所以小方在前5场比赛中总分的最大值应为17×5-1=84分;(3)又由题意,小方在这10场比赛中得分至少为18×10 + 1=181分, 设他在第10场比赛中的得分为S ,则有81+(22+15+12+19)+ S ≥181 .解得S≥29,所以小方在第10场比赛中得分的最小值应为29分 .24、(本题12分)(1)设第一象限内的点B (m,n ),则tan ∠POB 91==m n ,得m=9n ,又点B 在函数xy 1=的图象上,得m n 1=,所以m =3(-3舍去),点B 为)31,3(,而AB ∥x 轴,所以点A (31,31),所以38313=-=AB ;(2)由条件可知所求抛物线开口向下,设点A (a , a ),B (a 1,a ),则AB =a1- a =38, 所以03832=-+a a ,解得313=-=a a 或 .当a = -3时,点A (―3,―3),B (―31,―3),因为顶点在y = x 上,所以顶点为(-35,-35),所以可设二次函数为35)35(2-+=x k y ,点A 代入,解得k= -43,所以所求函数解析式为35)35(432-+-=x y .同理,当a = 31时,所求函数解析式为35)35(432+--=x y ;(3)设A (a , a ),B (a 1,a ),由条件可知抛物线的对称轴为aa x 212+= .设所求二次函数解析式为:)2)1()(2(59++--=aa x x y .点A (a , a )代入,解得31=a ,1362=a ,所以点P 到直线AB 的距离为3或136.。
2010年中考模拟卷数学参考答案

2010年中考模拟卷数学参考答案二.认真填一填(本题有6个小题,每小题4分,共24分) 11.4(x+3)(x-3) 12.10≠≥x x 且 13.15414.6)1(2+--=x y 15. ︒20 16.)12,1222(22++++n nn n n n P n 三.全面答一答(本题有8个小题,共66分) 17.(本小题满分6分) 解:11)1()1)(1(1----+⨯+=a a a a a a a 原式…………………………………………………2分 =12111--=--a a a …………………………………………………2分 当a=-2时,原式=34…………………………………………………2分18.(本题满分6分) 解:可以做2)1(-n n 条直线…………………………………………………3分 理由如下:平面上有n 个点,两点确定一条直线。
取第一个点A 有n 种取法,取第二个点B(n-1)种取法,所以一共可连成n(n-1)条直线,但AB 和BA 是同一条直线,所以应除以2,得2)1(-n n 条直线 …………………………………………………3分 19.(本题满分6分)解:过点A 作BC 的垂线段,垂足为D ,则由题可知,∠BAD=30°,∠DAC=60° ∵∠BAD=30°,△ABD 为直角三角形, ∴BD=3223663==AD …………………………………………………2分同理可得3663==AD CD …………………………………………………2分∴楼高AB=2.152388≈…………………………………………………2分 20.(本小题6分)(1)21人 …………………………………………………1分(2)众数 90 中位数80…………………………………………………2分(3)从平均数和中位数的角度来比较,一班的成绩比二班好;从平均数和众数的角度来比较,一班的成绩不如二班;从B 级以上(包括B 级)的人数的角度来比较,一班的成绩比二班好。
2010年中考模拟试卷 数学参考答案及评分标准

2010年中考模拟试卷 数学参考答案及评分标准一、选择题(每小题3分,共30分)二、填空题(每小题4分,共24分) 11. -- 2 ,例如 12.6,2.5 13.231a14. -2<a ≤ -1 15.3 16.),(24245--P ,),(2010201020P ,2512三、解答题(6+6+6+8+8+10+10+12=66分)17(本题6分)解:(1).原式233133--+=-1 ················································ (3分) (2)原式=()()21222---+a a a a ··················································································· (1分) =()()()2222-++-a a a a =()()222-+-a a a ························································································· (1分) =21+a ····················································································································· (1分) 18(本题6分)解:(1)S=πrl=50×20π=1000π ……..……………………….(2分)(2)θ=0001443605020360.=⨯=lr…………………………………………………(2分) 剪去的扇形纸片的圆心角=360°-2×144°=72°………………………………………(2分)19(本题6分)解:(1)当射线BA 绕点B 按顺时针方向旋转45度时与⊙O 相切……(1分) 理由如下:如图,设切点为F ,连OF.则OF ⊥BF ,在直角三角形OBF 中,︒=∠=∠∴==45,4,22BOF OBF OB OF ∴∠ABF=45°..(2分)(2)(2)过O 画OH ⊥MN 于H ,易知∠AOB=30°,∴OH=21OB=2 在直角三角形OMH 中,OM ︒=∠︒=∠∴=90,45,22MON MOH …………………(1分)()()422221224122-=⨯-⨯=-=∴∆ππMON MON S S S 扇形弓形∴线段MN 与⌒MN 所围成图形的面积为2π-4………………………………………………(2分) 20. (本题8分)(1)用直尺和圆规作△ABC ………………… (4分) (2)① 作ACB ∠的平分线交AB 于D ; ……………………(1分)② 过D 点作DE ⊥BC ,垂足为E .……………................(1分)(3)△ ADC ≌△ EDC ;△ ACD ∽△ ABC .(每写对一对得1分)21.(本题8分)(1)80 ,25%、40%、30%································· 4分(2)补全条形图(如右图)………2分(3)520…………………………….2分22.(本题10分)(1) 1 , 2 。
2010年中考数学模拟试卷 答卷
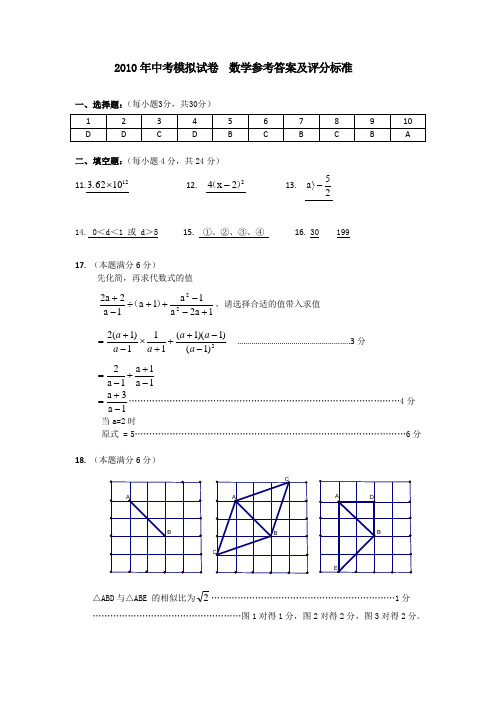
2010年中考模拟试卷 数学参考答案及评分标准一、选择题:(每小题3分,共30分)二、填空题:(每小题4分,共24分)11.12103.62⨯ 12. 22x 4)(- 13. 25a -〉14. 0<d <1 或 d >5 15. ①、②、③、④ 16. 30 19917. (本题满分6分)先化简,再求代数式的值1a 2a 1a 1a 1a 2a 222+--++÷-+)(,请选择合适的值带入求值 2)1()1)(1(111)1(2--+++⨯-+=a a aa a a ………………………………………………..3分 1a 1a 1a 2-++-=1a 3a -+=…………………………………………………………………………………4分当a=2时原式 = 5…………………………………………………………………………………6分18. (本题满分6分)△ABD 与△ABE 的相似比为2………………………………………………………1分 ……………………………………………图1对得1分,图2对得2分,图3对得2分。
19.(本题满分6分)(1)2+22+32+36+28=120,此样本抽取了120名学生才成绩……………………………2分(2)中位数落在80.5 ~90.5这个范围内.……………………………………………4分 (3)4801202836900=+⨯所以该校获得优秀成绩学生的人数约480名。
…………6分 20.(本题满分8分)(1)由△BMC 是等边三角形可知: ∠MBC=∠MCB=60°,BM=MC 又∵ED ∥BC,∴∠EMB=∠MBC;∠DMC=∠MCB ∴∠EMB =∠DMC 又 ∵点M 平分ED, ∴EM = MD则可证△EMB ≌△DMC ………2分 ∴∠EBM =∠ECM 则可得∠EBC =∠DCB∴△ABC 是等腰三角形。
(3)21. (本题满分8分)作AE ⊥y 轴于E∵42AOD S OD ==△,∴21OD.AE=4 ∴AE=4………………………………………………… 1分 ∵AB ⊥OB,且C 为OB 的中点,∴∠DOC =∠ABC =90°,OC =BC, ∠OCD =∠BCA ∴Rt △DOC ≌Rt △ABC∴AB =CD =2…………………………………………………………………………………2分 ∴A(4,2)……………………………………………………………………………………3分 将A(4,2)代入xky 1=中,得k =8∴x8y 1=……………………………………………………………………………………… 4分 将A(4,2)和D(0,-2)代入b kx y 2+=得422a b b +=⎧⎨=-⎩解之得:12a b =⎧⎨=-⎩∴22y x =-…………………………………………………………………………………6分(2)在y 轴的右侧,当21y y 〈时,0<x <2………………………………………………8分22. (本题满分10分)(1)∵半径OD = 5,则直径AB =10∴5310BD AB BD ==,则BD=6∴若设OE=x ,则BE=5-x ,由勾股定理可得:22220E -DO BE -BD =从而列方程:26-2x 5)(-=22x 5-,…………………………………………………3分,得x=524,再由垂径定理可得CD=548…………………………………………………4分 (2) ∵∠ADO:∠EDO=4:1,则可设∠ADO=4x ,∠EDO=x 又∵OA=OD,则∠OAD=∠ODA=4X由AB 垂直CD,得:4x+4x+x=90°∴x=10°……………………………………………6分 ∴∠ADE=50°,则∠AOC=100°……………………7分 (3) ∵弧AC=9251805100=⨯∏⨯∏∴2∏r =∏925,则圆锥底面圆半径为1825 (9)∴侧S =∏=∏⨯=∏1812551825rl ……………………10分23. (本题满分10分)(1)由题意设A 型货箱用了x 节,则B 型货箱用了(50-x )节,则可列不等式组: 35x +25(50-x )≥153015x+35(50-x )≥1150………………………………………………………………2分 解得:28≤x ≤30…………………………………………………………………………3分 ∵x 取整数 ∴ x = 28、29、30……………………………………………………4分 ∴ 有三种方案:当A 型货箱用了28节时,B 型货箱用了22节。
2010年中考数学模拟试题(含答案)
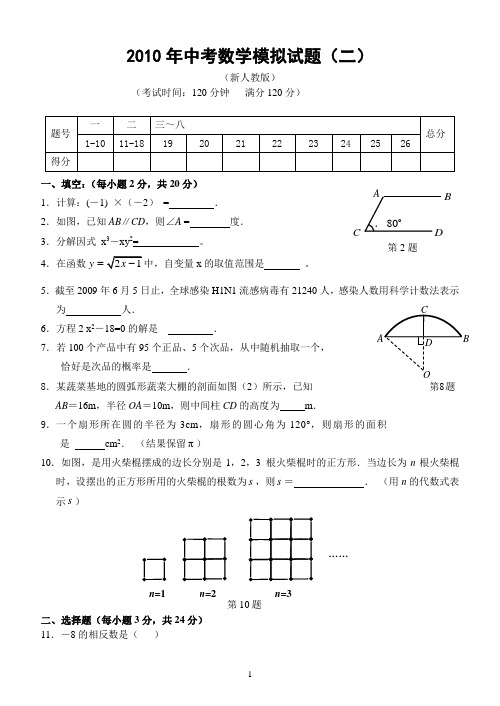
D BAOC 第8题2010年中考数学模拟试题(二)(新人教版)(考试时间:120分钟 满分120分)一、填空:(每小题2分,共20分) 1.计算:(-1) ×(-2) = . 2.如图,已知AB ∥CD ,则∠A = 度. 3.分解因式 x 3-xy 2= 。
4.在函数y =x 的取值范围是 。
5.截至2009年6月5日止,全球感染H1N1流感病毒有21240人,感染人数用科学计数法表示为 人.6.方程2 x 2-18=0的解是 .7.若100个产品中有95个正品、5个次品,从中随机抽取一个,恰好是次品的概率是 .8.某蔬菜基地的圆弧形蔬菜大棚的剖面如图(2)所示,已知 AB =16m ,半径OA =10m ,则中间柱CD 的高度为 m .9.一个扇形所在圆的半径为3cm ,扇形的圆心角为120°,则扇形的面积是 cm 2. (结果保留π)10.如图,是用火柴棍摆成的边长分别是1,2,3 根火柴棍时的正方形.当边长为n 根火柴棍时,设摆出的正方形所用的火柴棍的根数为s ,则s = . (用n 的代数式表示s )二、选择题(每小题3分,共24分)11.-8的相反数是( )CDB第2题.80A第10题 ……n =1 n =2n =3A .8B .-8C .18 D .18- 12.已知两圆的半径分别为2和3,圆心距为5,则这两圆的位置关系是( ).A.外离B. 相交C.外切D.内切13.下列四边形:①正方形、②矩形、③菱形,对角线一定相等的是( )A .①②③B .①②C .①③D .②③14.在一次射击测试中,甲、乙、丙、丁的平均环数均相同,而方差分别为8.7,9.1,6.5,7.7,则这四人中,射击成绩最稳定的是( ) A .甲B .乙C .丙D .丁15、tan 30°的值等于( )A. 21B. 22C.23 D.33 16图1中几何体的主视图是( )17.若分式 x 2-1x +1的值为零,则x 的值是( )A .1B .0C .-1D .±118.如图,抛物线y =ax 2+bx +c 的对称轴是x = 13,小亮通过观察得出了下面四条信息:①c <0,②abc <0,③a -b +c >0,④2a -3b =0. 你认为其中正确的有( )A .1个B .2个C .3个D .4 三、解答题:(共76分)19、(本题7分)计算:112sin 602-⎛⎫- ⎪⎝⎭ACBDx第18题20、(本题7分)解方程: 0)3(2)3(2=-+-x x x21.(本题8分)如图,E 是正方形ABCD 的边DC 上的一点,过A 作A F ⊥AE ,交CB 延长线于点F ,求证:△ADE ≌△ABF .22.(本题10分)已知ABC △在平面直角坐标系中的位置如图10所示. (1)分别写出图中点A C 和点的坐标;(2)画出ABC △绕点C 按顺时针方向旋转90A B C '''°后的△; (3)求点A 旋转到点A '所经过的路线长(结果保留π)._F _E _ C _ D _ B _A 第21题 第22题23、(本题10分)右边下面两图是根据某校初三(1)班同学的上学方式情况调查所制作的条形和扇形统计图,请你根据图中提供的信息,解答以下问题: (1) 求该班学生骑自行车的人数有(2)求该班学生人数 人.并将条形统计图补充完整; (3)若该校初三年有600名学生, 试估计该年级乘车上学的人数.24.(本题10分)某冰箱厂为响应国家“家电下乡”号召,计划生产A 、B 两种型号的冰箱100台.经预算,两种冰箱全部售出后,可获得利润不低于 47500元,不高于48000元,两种型号的冰箱生产成本和售价如下表:(1)冰箱厂有哪几种生产方案?(2)该冰箱厂按哪种方案生产,才能使投入成本最少?“家电下乡”后农民买家电(冰箱、彩电、洗衣机)可享受13%的政府补贴,那么在这种方案下政府需补贴给农民多少元?骑自行车20%乘车步行50%第23题25、(本题12分)如图5,在ABC △中,AB AC =,以AB 为直径的O ⊙交BC 于点M ,MN AC ⊥ 于点N .(1)求证MN 是O ⊙的切线;(2)若1202B A C A B ∠==°,,求以直径AB ,弦BC 和⌒AM 围成图形的面积(结果保留π).、第25题26.(本题12分)如图,抛物线21222y x x =-++与x 轴交于A B 、两点,与y 轴交于C 点.(1)求A B C 、、三点的坐标; (2)证明ABC △为直角三角形;(3)在抛物线上除C 点外,是否还存在另外一个点P ,使ABP △是直角三角形,若存在,请求出点P 的坐标,若不存在,请说明理由.参考答案一、1.2 2.120 3.x (x +y )(x -y )4.x≥12 5.2.124×104 6.3和-3 7.1208.4 9.3π 10.2n(n+1)二.11. A 12.C 13.B 14. C 15. D 16.D 17.A18.B19.20.X 1=3,X 2=121.证明:∵ABCD 是正方形 ∴AB AD = ︒=∠=∠=∠90DAB ABF D ∵A F ⊥AE ∴DAE EAB BAF ∠=∠-︒=∠90.在ADE ∆和ABF ∆中∵AE AD BAF DAE ABF D =∠=∠∠=∠,, ∴△ADE ≌△ABF 22.解:(1)()04A ,、()31C ,(2)图略(3)AC =⌒AA' π= 23.解:(1)8 (2)该班学生人数为40%5020=(人) 图画对(略) (3)该年级乘车上学的人数约为1806004012=⨯ 24..解:(1)设生产A 型冰箱x 台,则B 型冰箱为()100x -台,由题意得:47500(28002200)(30002600)(100x x -+-⨯-≤≤解得:37.540x ≤≤ x 是正整 ∴x 取38,39或40.(2)设投入成本为y 元,由题意有: 22002600(100)400260000y x x x =+-=-+4000-< ∴y 随x 的增大而减小∴当40x =时,y 有最小值.即生产A 型冰箱40台,B 型冰箱50台,该厂投入成本最少此时,政府需补贴给农民(280040300060)13%37960()⨯+⨯⨯=元 25.(1)证明:连接OM .∵OM OB =,∴B OMB ∠=∠,∵AB AC =,∴B C ∠=∠. ∴OMB C ∠=∠,∴OM AC ∥.又MN AC ⊥,∴OM MN ⊥,点M 在O ⊙上,∴MN 是O ⊙的切线(2)S =164π+26.解:(1)抛物线21222y x x =-++与x 轴交于A B 、两点,21202x x ∴-++=.即240x -=.解之得:12x x ==∴点A B 、的坐标为(A B ) ,将0x =代入21222y x x =-++, 得C 点的坐标为(0,2)(2)6AC BC AB ===,222AB AC BC ∴=+,则90ACB ∠=°,ABC ∴△是直角三角形.(3)将2y =代入21222y x x =-++,得212222x x -++=,120x x ∴==,P ∴点坐标为.。
2010年初中数学中考模拟试题答案
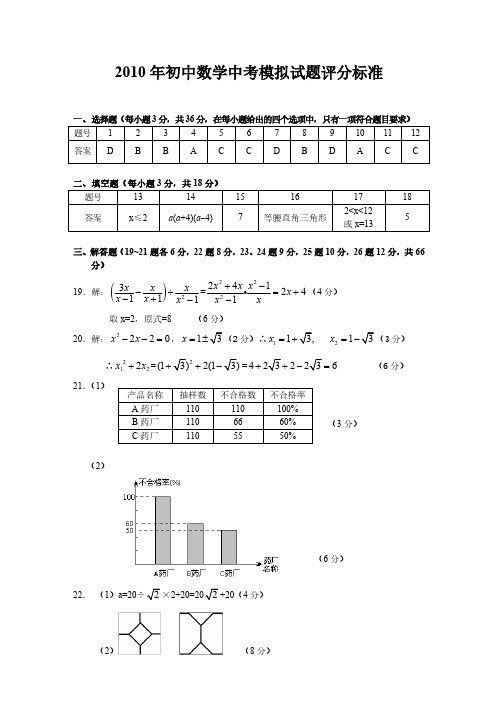
在 R t △ADE 中, EA =r, DE=6-r, AD=x,
∴ x 2 6 r 2 r 2 ,r= 1 x 2 +3,
∵ EF= EA, ∴AF=2DE,
即 y =2(6-r)=- 1 x 2 +6, (6 分) 6
D
E
C
∵AB∥CD,
∴∠AFE=∠CEF,
G
∴∠AEF=∠AFE, ∴AE=AF, ∵AE=EF,
A
B
F
( 图3 )
∴AE=AF=CE=CF, ∴△AEF 和△CEF 都是正三角形,
∴四边形 AECF 是菱形,且∠CEF=60°,
∴∠BCF=30°,
1
∴BF=
1
CF=
AF= 1 AB=2,
BC= 2 3 .(12 分)
223
②点 F 是 AB 的中点时, y =3,
图 D
E
C
H
G
A
( 图 1)
D
E
B F
C
G
A
B F
( 图2 )
1
即-
x 2 +6=3,∴ x = 3
2 .(8 分)
6
(3)(如图 3).
当x=2
3 时,
︵图 F 是AC的中点。此时,四边形 AECF 菱形.(9 分)
理由如下:
︵ ∵点 F 是AC的中点,∴∠AEF=∠CEF, AF=CF,
2.85×20+2.85×1.5×10+2.85×2×(x-30)=128.25,x=35(5 分)
∴调整后水费是:3.3×20+3.3×1.5×10+3.3×2×5=148.5(元)(6 分)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2010年白云区中考数学模拟试题及答案本试卷分选择题和非选择题两部分,共三大题25小题,满分150分.考试时间为120分钟. 注意事项:1.答卷前,考生务必在答题卡第1页上用黑色字迹的钢笔或签字笔填写自己的学校、班级、姓名、试室号、座位号、准考证号,再用2B 铅笔把准考证号对应的号码标号涂黑.2.选择题每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑;如需改动,用橡皮擦干净后,再选涂其他答案标号;不能答在试卷上.3.非选择题必须用黑色字迹的钢笔或签字笔作答,涉及作图的题目,用2B 铅笔画图.答案必须写在答题卡各题目指定区域内的相应位置上;如需要改动,先划掉原来的答案,然后再写上新的答案;改动的答案也不能超出指定的区域.不准使用铅笔、圆珠笔和涂改液.不按以上要求作答的答案无效.4.考生必须保持答题卡的整洁,考试结束后,将本试卷和答题卡一并交回.第一部分 选择题(共30分)一、选择题(本大题共10小题,每小题3分,满分30分.在每小题给出的四个选项中,只有一项是符合题目要求的) 1.下列各数中,最大的数是(*) (A)-5 (B)0 (C)1 (D)-2 2.如图1,下列关系正确的是(*)(A)∠2<∠1 (B)∠2>∠1(C)∠2≥∠1 (D)∠2=∠1 3.下列计算正确的是(*)(A)023⨯=0 (B)13-=-3 (C)623x x x ÷= (D)326()a a =(C)4 (D)16 5.方程22011x x x -=+-的解是(*) (A)x =2 (B)x =-2 (C)x =1 (D)x =-16.如图2,已知菱形ABCD的周长为12,∠A=60°,则BD的长为(*) (A)3 (B)4 (C)6 (D)87.图3所示的几何体是由三个同样大小的立方体搭成的,其俯视图为(*)8.如图4,△ABC中,∠C=90°,,则∠B的度A数为(*)(A)25° (B)30° (C)45° (D)60°9.抛物线y =x 2+4x -1的对称轴、顶点坐标分别为(*) (A)直线x =4、(4,-1) (B)直线x =2、(2,-1) (C)直线x =2、(4,-5) (D)直线x =-2、(-2,-5)10.若把点A(-5m ,2m -1)向上平移3个单位后得到的点在x 轴上,则点A在(*) (A)x 轴上 (B)第三象限 (C)y 轴上 (D)第四象限第二部分 非选择题(共120分)二、填空题(本大题共6小题,每小题3分,满分18分) 11.不等式x -2≤0的解集是 * .12.如图5,D、E分别在△ABC的边AB、AC上,且AD=12AB,AC=2EC,DE=4,则BC= * .BCDA图2图3(A) (B) (C) (D) BE CD A图5图4AB C 图11 213.一元二次方程228x x --=0的两个根x 1= * ,x 2= * ,根的判别式⊿= * . 14.如图6,E为正方形ABCD内一点,把△BEA绕着点A旋转到△DFA的位置,则∠FAE= * °. 15.计算并化简:422()x yx y xy--÷= * . y =kx(k >0)图象上16.P1(x 1,y 1),P2(x 2,y 2),P3(x 3,y 3)分别是反比例函数的三个点,且x 1<x 2<0<x 3,请用不等号表示出y 1、y 2、y 3之间的大小关系: * .三、解答题(本大题共9小题,满分102分.解答应写出文字说明、证明过程或演算步骤) 17.(本小题满分9分) 解方程组:2326x y x y -=⎧⎨+=⎩18.(本小题满分10分)已知:如图7,点E、F在BC上,BE=CF,∠A=∠D,∠B=∠C,AF与DE交于点O.(1)求证:AB=DC;(2)△OEF的形状为 * . 19.(本小题满分10分)小强对本班同学上学的交通方式进行了一次调查,他根据采集的数据,绘制了下面的统计图(图8和图9).请你根据图中提供的信息,解答下列问题: (1)本班学生共有 * 人;(2)计算本班步行上学的人数,并补全统计图8; (3)在统计图9中,“其他”学生占全班人数的百分比为 * %,求出“乘车”部分所对应的圆心角的度数.20.(本小题满分14分) 一条不经过第二象限的直线与反比例函数y =kx的图象交于点P(3,2),该直线与x 轴所夹的锐角为45°.(1)求反比例函数的解析式;(2)根据题意,在图10所给的坐标系中画出直线的图象,并求出这条直线的函数解析式; (3)在图10中画出该直线关于y 轴对称的图形. 21.(本小题满分10分)把一副抽去大小王的扑克牌洗匀后背面朝上,随机地摸出一张:(1)求摸出的牌是红桃的概率;(2)按常规,J表示数字11,Q表示数字12,K表示数字13.若甲、乙两人玩摸牌游戏,规定摸出的是奇数时,则甲获胜,而摸出偶数时,乙获18161412261084其他步行骑车乘车交通方式人数图8 其他步行乘车骑车36%图9AB CD E F O 图7 y 1x1O 图10ECD图6FDCBA 图11胜.则谁获胜的可能性大?为什么? 22.(本小题满分12分)如图11,已知,A、B、C为圆上的三点,∠ACB=90°,BD与AC的延长线交于点D,AB=10,BC=6,∠D=∠ABC. (1)求AC的长;(2)求证:BD是圆的切线; (3)求CD的长. 23.(本小题满分11分)为迎接2010年11月12日至27日在广州举行的第16届亚运会,某体育中心需要购置甲、乙两种体育器材共380件,其中乙种器材比甲种器材少60件. (1)甲、乙两种体育器材各多少件? (2)一厂家承接了这批生产任务.完成后厂家租用了A、B两种型号的货车共7辆,打算一次性将这两种器材运往体育中心.已知A型货车最多可装载甲种器材40件和乙种器材20件,B型货车最多可装载甲种器材20件和乙种器材30件,则厂家安排A、B两种货车有几种方案?请你帮助设计出来. 24.(本小题满分12分)如图12,在四边形ABCD中,AD∥BC,AE、BF分别平分∠DAB和∠ABC,交CD于点E、F,AE、BF相交于点M. (1)求证:AE⊥BF;(2)求证:点M在AB、CD边中点的连线上.25.(本小题满分14分)如图13,Rt △ABC中,∠BAC=90°,AB=AC=2,点D为BC边上的动点(D不与B、C重合),∠ADE=45°,DE交AC于点E. (1)∠BAD与∠CDE的大小关系为 * .请证明你的结论;(2)设BD=x ,AE=y ,求y 关于x 的函数关系式,并写出自变量x 的取值范围; (3)当△ADE是等腰三角形时,求AE的长;(4)是否存在x ,使△DCE的面积是△ABD面积的2倍?若存在,求出x 的值,若不存在,请说明理由.参考答案及评分建议(10一模)一、选择题二、填空题三、解答题 17.(本小题满分9分) 解法一: 2 (1)32 6 (2)x y x y -=⎧⎨+=⎩由(1)得:x =y +2 (3)………………………………………………2分 把(3)代入(2),得:3(y +2)+2y =6,……………………………4分 解得y =0,………………………………………………………………………6分C AE 图13图12M F EDC B A把y =0代入(3),得x =2,…………………………………………………7分 ∴2x y =⎧⎨=⎩…………………………………………………………………………9分解法二: 2 (1)32 6 (2)x y x y -=⎧⎨+=⎩(1)×2得:2x -2y =4 (3),………………………………………2分(3)+(2),……………………………………………………………………4分 得:5x =10,x =2,………………………………………………………6分 把x =2代入(1),解得y =0,………………………………………………7分∴20x y =⎧⎨=⎩…………………………………………………………………………9分18.(本小题满分10分) (1)证明:∵BE=CF,∴BE+EF=CF+EF,………………………………………………2分 即BF=CE.………………………………………………………………3分 在△ABF和△DCE中A DBC BF CE ∠=∠⎧⎪∠=∠⎨⎪=⎩,………………………………………………………………5分 ∴△ABF≌△DCE(AAS),………………………………………6分 ∴AB=DC;………………………………………………………………8分 (2) 等腰三角形 .…………………………………………………10分19.(本小题满分10分) 解:(1)50;………………………………………………………………2分 (2)50-12-18-6=14(人).………………………………3分 本班步行上学人数为50;…………………………………………………4分 图(略)………………………………………………………………………6分 (3)12,…………………………………………………………………7分 12÷50=24%,360°×24%=86.4°.…………………9分 ∴“乘车”部分所对应的圆心角的度数为86.4°.…………………10分20.(本小题满分14分)解:(1)∵y =kx的图象经过点P(3,2), 把x =3,y =2人代入y =kx中,…………………………………………1分∴得2=3k,即 k =6,……………………………………………………2分∴反比例函数的解析式为:y =6x;…………………………………………3分(2)如下图,过点P画与x 轴夹角为45°的直线.……………………5分 设其与x 轴的交点为B.过P点作PA⊥x 轴,垂足为A, 则PA=2,A的坐标为(3,0).………………………………………6分 在Rt △ABP中,∵∠ABP=45°, ∴∠APB=45°,∴AB=AP=2, OB=OA-AB=3-2=1, ∴点B的坐标为(1,0).…………………………………………………8分分设直线的解析式为y =k x +b ,………………………………………………9 把P(3,2)及B(1,0)的坐标代入y =k x +b , 得320k b k b +=⎧⎨+=⎩,………………………………………………………………10分解得k =1,b =-1.………………………………………………………11分 ∴这条直线的解析式为:y =x -1;………………………………………12分 (3)图略.…………………………………………………………………14分21.(本小题满分10分) 解:(1)无大小王的扑克牌,红桃、黑桃、方块、梅花的数量各为13张,摸出任意一种花色可能性相等.……………………2分 ∴P(红桃)=1352=14;…………………………………………………4分 (2)∵每一种花色的奇数为1、3、5、7、9、11、13共7个,………………………5分 偶数为2、4、6、8、10、12共6个,……………………………6分∴P(奇数)=4752⨯=713,………………………………………………7分 P(偶数)=4652⨯=613,…………………………………………………8分∵713>613,…………………………………………………………………9分 ∴甲获胜的可能性大.……………………………………………………10分22.(本小题满分12分)(1)解:∵∠ACB=90°,∴△ABC为直角三角形.……………………………………………………1分 由勾股定理,得AB2=AC2+BC2,……………………………………………………2分(2)由∠ACB=90°,可得AB是圆的直径.………………………5分 ∵∠BCD=∠ACB=90°,∴∠D+∠DBC=90°,…………………………………………………6分 又∵∠D=∠ABC,∴∠ABC+∠DBC=90°,……………………………………………7分 即∠ABD=90°,…………………………………………………………8分 ∴BD是圆的切线(过半径外端且垂直于半径的直线是圆的切线);……9分 (3)∵∠D=∠ABC,∠A为公共角,∴△ADB∽△ABC,……………………………………………………10分y 1x 1 O 图2P(3,2) AB∴AD ABAB AC=,∴AD=2ABAC=12.5,………………………………11分CD=AD-AC=12.5-8=4.5.………………………………12分[也可通过Rt△BDC∽Rt△ABC求得CD]23.(本小题满分11分)解:(1)设乙种器材有x件,………………………………………………1分则甲种器材有(60+x)件.根据题意,得:(60+x)+x=380,………………………………………………2分解得x=160,60+x=220.………………………………………3分∴甲种器材有220件,乙种器材有160件;…………………………4分[也可用二元一次方程组求解](2)设用A型货车y辆,…………………………………………………5分则B型货车(7-y)辆.根据题意,得:4020(7)2202030(7)160y yy y+-≥⎧⎨+-≥⎩,……………………………………………7分解得45yy≥⎧⎨≤⎩,∴y取4、5.……………………………………………9分∴厂家安排A、B两种货车有两种方案:①用4辆A型货车,3辆B型货车,……………………………………10分②用5辆A型货车,2辆B型货车.……………………………………11分24.(本小题满分12分)(1)证明:如下图,∵AE、BF分别平分∠DAB和∠ABC,∴∠1=∠2,∠3=∠4,………………………………………………1分∵AD∥BC,∴∠DAB+∠CBA=180°,……………………2分即(∠1+∠2)+(∠3+∠4)=180°,2∠2+2∠3=180°,∴∠2+∠3=90°,……………………………………………………3分而∠2+∠3+∠AMB=180°,∴∠AMB=90°,………………………………………………………4分即AE⊥BF;(2)设AB、CD的中点分别为G、H(如下图),…………………5分连结MG,∵M为Rt△ABM斜边AB的中点,………………………6分∴MG=AG=GB,……………………………………………………7分∴∠2=∠5,……………………………………………………………8分又∵∠1=∠2,∴∠1=∠5,∴GM∥AD.……………………9分∵已知AD∥BC,即四边形ABCD是以AD、BC为底的梯形,又G、H分别为两腰AB、DC的中点,由梯形中位线定理可知,GH∥AD,而证得GM∥AD,…………10分根据平行公理可知,过点G与AD平行的直线只有一条,……………11分∴M点在GH上,即M点在AB、CD边中点的连线上.……………12分512 3 4HGMFEDC A25.(本小题满分14分) 解:(1)相等;………………………………………………………………1分 证明如下:∵∠BAC=90°,AB=AC, ∴∠B=∠C=45°.如图1, ∵∠1+∠B+∠ADB=180°,∴∠1+∠ADB=180°-∠B=135°. 又∵∠2+∠ADE+∠ADB=180°,∴∠2+∠ADB=180°-∠ADE……………………………………2分 =180°-45°=135°, 即∠1+∠ADB=∠2+∠ADB,∴∠1=∠2;…………………………………………………………………3分(2) 由(1)知∠1=∠2,又∵∠B=∠C=45°,∴△DCE∽△ABD.………………………………………………………4分 若BD=xx , 由△DCE∽△ABD得CE CD BD AB =,即CE x =, CE=12x )x , =-122x,………………………………………………………5分y =AE=AC-CE=2-(-122x)∴y =122x+2,…………………………………………………………6分其中0<x(3) 解:∵点D不能与B点重合,∴AD=AE不能成立…………………8分 (或:∵∠ADE=45°,若AD=AE,则∠AED=ADE=45°,从而∠DAE=90°, 即B与D重合,这与已知条件矛盾).①当AE、DE为腰,即AE=DE时(如图2),∠EAD=∠EDA=45°,此时,AD平分∠BAC, ∴D为BC边的中点(“三线合一”性质),且E也为AC边的中点,∴AE=1;…………………………………………9分 ②当AD、DE为腰,即AD=DE时(如图3),由(1)△ABD∽△DCE知,此时AD与DE为对应边, ∴△ABD≌△DCE,DC=AB=2,综上所述,当△ADE是等腰三角形时,……………………………………………………AE的长为1或4-211分B C A E12图1 CADE图3(4)不存在.……………………………………………………………………12分 原因如下:∵△DCE∽△ABD,若△DCE的 面积是△ABD面积的2倍,则CDEABDS S =2, 从而CE BD122x, 解得x =0,即BD=0,就是说D点与B点重合,…………………………13分 这与已知条件矛盾,∴不存在x ,使△DCE的面积是△ABD面积的2倍.……………………14分A E 图2。
