南京工业大学物理化学课件——第一章气体的pVT性质
合集下载
大学物理化学01章气体ppt课件
第一章 气体pVT的性质
1.1 理想气体状态方程 1.2 理想气体混合物 1.3 气体的液化及临界参数 1.4 真实气体状态方程 1.5 对比状态原理及普通化压缩因子图
上一内容 下一内容 回主目录
返回
2020/6/13
1-1 理想气体状态方程
1. 理想气体状态方程
pV nRT
上一内容 下一内容 回主目录
阿马加定律
定义:V=∑V*B
理想气体混合物的总体积为各组分分体积之和。 式中V*B=nBRT/p
进一步中得:
yB= V*B /V
即理想气体混合物中某一组分B的分体积与总体 积之比等于该组分的摩尔分数yB。
上一内容 下一内容 回主目录
返回
2020/6/13
1-3气体的液化及临界参数
1 液体的. 维利方程Virial equation (纯经验方程)
pVm RT
(1 B2 Vm
B3 Vm2
)
pVm RT
(1 B2 ' p B3 ' p2
)
上一内容 下一内容 回主目录
返回
2020/6/13
其它重要方程举例
R - K equation (Redlich and Kwong)
上一内容 下一内容 回主目录
返回
2020/6/13
对应状态原理
临界压缩因子(critical compression factor )
zc
pcVm,c RTc
物质 He Ar
N2 O2 CO CO2 CH4
zc 0.299 0.291 0.289 0.294 0.288 0.274 0.289
对于大多数物质,用上式计算的zc的值约在0.26~0.29 。
1.1 理想气体状态方程 1.2 理想气体混合物 1.3 气体的液化及临界参数 1.4 真实气体状态方程 1.5 对比状态原理及普通化压缩因子图
上一内容 下一内容 回主目录
返回
2020/6/13
1-1 理想气体状态方程
1. 理想气体状态方程
pV nRT
上一内容 下一内容 回主目录
阿马加定律
定义:V=∑V*B
理想气体混合物的总体积为各组分分体积之和。 式中V*B=nBRT/p
进一步中得:
yB= V*B /V
即理想气体混合物中某一组分B的分体积与总体 积之比等于该组分的摩尔分数yB。
上一内容 下一内容 回主目录
返回
2020/6/13
1-3气体的液化及临界参数
1 液体的. 维利方程Virial equation (纯经验方程)
pVm RT
(1 B2 Vm
B3 Vm2
)
pVm RT
(1 B2 ' p B3 ' p2
)
上一内容 下一内容 回主目录
返回
2020/6/13
其它重要方程举例
R - K equation (Redlich and Kwong)
上一内容 下一内容 回主目录
返回
2020/6/13
对应状态原理
临界压缩因子(critical compression factor )
zc
pcVm,c RTc
物质 He Ar
N2 O2 CO CO2 CH4
zc 0.299 0.291 0.289 0.294 0.288 0.274 0.289
对于大多数物质,用上式计算的zc的值约在0.26~0.29 。
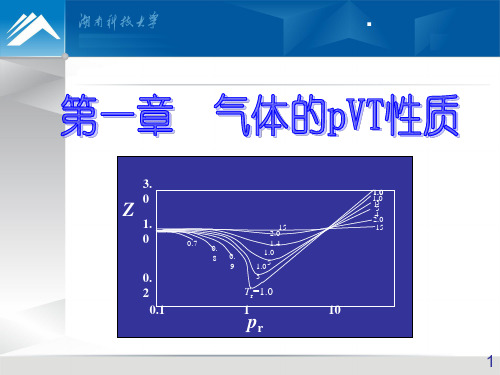
第01章 气体的pVT性质
16
.
§ 1.1 理想气体
例 1.2.1 :今有 300 K,104 . 365 kPa 的湿烃类 混合气体(含水蒸气的烃类混合气体),其中水 蒸气的分压为3.167 kPa,现欲得到除去水蒸气 的 1 kmol 干烃类混合气体,试求:(1)应从湿烃 混合气体中除去水蒸气的物质的量;(2)所需湿 烃类混合气体的初始体积。
25
.
§ 1.2 真实气体
•压力修正: 实际气体分子间有相互作用力
器 壁
内部分子
靠近器壁的分子
分子间相互作用减弱了分子对器壁的碰撞,形成内压力
p内,所以
p = p理 - p内 因为分子间引力反比于分子间距离 r 的六次方,反比于
Vm2 ,引力越大,a 越大。 p内= a / Vm2 。
p理= p + p内 = p + a / Vm2
R=pVm/T=8.3145 J·mol-1
在压力取向0的极限条件下, 任何气体的行为均服从的定量 关系,R是一个对各种气体都 适用的常数。
R[lp i0m (pV)]T/T=8.3145J·mol-1·K-1 (是一种极限结果
8
2. 理想气体模型
(1) 分子间力
.
§ 1.1 理想气体
吸引力- 分子相距较远时,有范德华引力;
排斥力- 分子相距较近时,电子云及核产生排斥力。
若用E代表分子间相互作用势能,有:
E吸引 -1/r 6 Lennard-Jones理论 E排斥 1/r 12
E 总 E 吸 引 + E 排 斥 r A 6r B 1 2 1 .1 .2
9
.
§ 1.1 理想气体
式中:A-吸引常数;B-排斥常数
26
.
.
§ 1.1 理想气体
例 1.2.1 :今有 300 K,104 . 365 kPa 的湿烃类 混合气体(含水蒸气的烃类混合气体),其中水 蒸气的分压为3.167 kPa,现欲得到除去水蒸气 的 1 kmol 干烃类混合气体,试求:(1)应从湿烃 混合气体中除去水蒸气的物质的量;(2)所需湿 烃类混合气体的初始体积。
25
.
§ 1.2 真实气体
•压力修正: 实际气体分子间有相互作用力
器 壁
内部分子
靠近器壁的分子
分子间相互作用减弱了分子对器壁的碰撞,形成内压力
p内,所以
p = p理 - p内 因为分子间引力反比于分子间距离 r 的六次方,反比于
Vm2 ,引力越大,a 越大。 p内= a / Vm2 。
p理= p + p内 = p + a / Vm2
R=pVm/T=8.3145 J·mol-1
在压力取向0的极限条件下, 任何气体的行为均服从的定量 关系,R是一个对各种气体都 适用的常数。
R[lp i0m (pV)]T/T=8.3145J·mol-1·K-1 (是一种极限结果
8
2. 理想气体模型
(1) 分子间力
.
§ 1.1 理想气体
吸引力- 分子相距较远时,有范德华引力;
排斥力- 分子相距较近时,电子云及核产生排斥力。
若用E代表分子间相互作用势能,有:
E吸引 -1/r 6 Lennard-Jones理论 E排斥 1/r 12
E 总 E 吸 引 + E 排 斥 r A 6r B 1 2 1 .1 .2
9
.
§ 1.1 理想气体
式中:A-吸引常数;B-排斥常数
26
.
南京工业大学物理化学课件——第一章气体的pVT性质

Vm3 3Vm2Vc 3VmVc2 Vm3 0
当然 和 是一码事
Vm3
(b
RTc Pc
)Vm2
a Pc
Vm
ab Pc
0
比较系数,得
3Vc
b
RTc Pc
3Vc2
a Pc
根据此式,可得特性常V数c3 PCaP、bc VC、TC与a、b之间的关系。
a 3PcVc2
Vc3
ab Pc
Vc 3b
Vc 3b
E吸引 -1/r 6 E排斥 1/r n • Lennard-Jones理论:n = 12
E
E吸引
E排斥=-
A r6
B r12
理想气体的状态方程
• 式中:A-吸引常数;B-排斥常数
• 分子间的相互作用力为: E
• •
F E r
0
•
•
•
•
r0
r
•
理想气体的状态方程
• ( 2 )理想气体模型
3
• 每一个分子的禁区是 1 ( 4 3)
3 2
23
b 4 (1 3) L
6
§1-3 实际气体的PVT性质
• 2.压力的修正
• 设分子间无引力存在时压力为Pi,有引力存在时为P, 这两者之差Pi-P=内压力,称为内压力 。内压力既正比 于(内部分子的密度),又正比于(靠近器壁的分子
密度),设两者都是ρ
第一章 气体的PVT性质
•
§1-0 物质的聚集状态
• 聚集状态
• 1.定义:物质是由大量的不断流动着的分子、原子、 离子等微观粒子聚集而成的,所以物质所表现出来的 状态 。
• 2.产生原因:分子间相互作用力
第一章 气体的PVT性质

pV ( nB ) RT
B
混合理气
m pV RT M mix
M mix : 混合物的摩尔质量
M mix yB M B
B
26
三、道尔顿分压定律与分压力 3.1 道尔顿定律 恒温、恒容条件下,理想混合气体的总压力等
于组成它的各组分在同温下单独存在于相同容
器内产生压力之和。 p pB pA pB pC
m pM V RT 3 3 20010 16.0410 3 kg m 8.315 (25 273.15) 1.294 kg m
3
17
状态变化时,计算系统各宏观性质 基本公式: 当n 一定时,
p1V1 p2V2 nR T1 T2
p1V1 p2V2 R n1T1 n2T2
36
3.2 临界参数
p*=f (T)
T ,p* ,气体液化需要加更大的压力 ;
当T=Tc 时,液相消失,加压不再可以使气体液化
临界温度Tc
:能够以加压方法使气体液化的
最高温度;
V = f(p,T)
对于数量可以变动的纯气体系统:
V=f(p,T,n)
13
2.3 理想气体状态方程
pV = nRT
n:物质的量 (mol)
T :热力学温度(K, 开尔文)
T= t + 273.15
p :压力(pa)
V:气体的体积(m3)
R:8.3145 J· mol-1 · K-1,摩尔气体常数
(1)玻义尔定律(R.Boyle,1662): pV = 常数 (n,T 一定)
在物质的量和温度恒定的条件下气体的体积 与压力成反比
9
(2)盖.吕萨克定律(J. Gay Lussac,1808): V / T = 常数 (n, p 一定)
课件:第一章 气体的pVT性质

压力分数等于该组分B的摩尔分数 此规律只近似应用于低压下的实际混合气体
上一内容 下一内容 回主目录
返回
2018/11/9
4.阿马加定律ቤተ መጻሕፍቲ ባይዱ
1) 分体积 混合气体中,组分B单独存在,并且处于与混 合气体相同的温度和压力时,所产生的体积称组
分B的分体积。
nB RT V p
B
上一内容 下一内容 回主目录
返回
2018/11/9
§1.1 理想气体的状态方程
理想气体:分子间无相互作用,分子本身无体积
× ×
× ×
可无限压缩
在任何温度、压 力下均符合理想
× × × × × × × × ×
上一内容 下一内容
气体模型,或服
从理想气体状态
方程的气体为理
想气体
回主目录
返回
2018/11/9
§1.1 理想气体的状态方程 • 理想气体的状态方程是理想气体的宏 观外在表现
pVm=RT
m pV RT M
Vm=V/n ρ=m/V
或
用于p, V, T, n, m, M, ρ的计算
上一内容 下一内容 回主目录
返回
2018/11/9
§1.1 理想气体的状态方程 例:计算25℃,101325Pa时空气的密度。
(空气的分子量为29)
解: n p 101325 3 mol m V RT 8.315 273.15 25 3 40.87 mol m n 3 3 d空气= M 40.87 29 g m 1.185 kg m V
• 理想气体的微观模型反映了理想气体
的微观内在本质
• 理想气体是真实气体在 p→ 0 情况下
上一内容 下一内容 回主目录
返回
2018/11/9
4.阿马加定律ቤተ መጻሕፍቲ ባይዱ
1) 分体积 混合气体中,组分B单独存在,并且处于与混 合气体相同的温度和压力时,所产生的体积称组
分B的分体积。
nB RT V p
B
上一内容 下一内容 回主目录
返回
2018/11/9
§1.1 理想气体的状态方程
理想气体:分子间无相互作用,分子本身无体积
× ×
× ×
可无限压缩
在任何温度、压 力下均符合理想
× × × × × × × × ×
上一内容 下一内容
气体模型,或服
从理想气体状态
方程的气体为理
想气体
回主目录
返回
2018/11/9
§1.1 理想气体的状态方程 • 理想气体的状态方程是理想气体的宏 观外在表现
pVm=RT
m pV RT M
Vm=V/n ρ=m/V
或
用于p, V, T, n, m, M, ρ的计算
上一内容 下一内容 回主目录
返回
2018/11/9
§1.1 理想气体的状态方程 例:计算25℃,101325Pa时空气的密度。
(空气的分子量为29)
解: n p 101325 3 mol m V RT 8.315 273.15 25 3 40.87 mol m n 3 3 d空气= M 40.87 29 g m 1.185 kg m V
• 理想气体的微观模型反映了理想气体
的微观内在本质
• 理想气体是真实气体在 p→ 0 情况下
物理化学_01章 气体的PVT性质

§1.2 理想气体混合物
Mixtures of ideal gases
1. 混合物的组成components of mixtures
(1) 摩尔分数 x 或 y
nB nB xB ( yB ) n总 nB
显然 xB = 1 , yB = 1
气体混合物的摩尔分数一般用 y 表示 液体混合物的摩尔分数一般用 x 表示
3. 道尔顿定律 Dalton’s Law
将A、B两种气体混和于容积为V 的容器中,总压:
nRT ( nA nB ) RT nA RT nB RT p V V V V pA pB
对于多种组分的混合气,
nRT RT p ( nA nB nC ) pB V V B
在某个较低的温度, 如270K,增大压力气体的 Vm减小。当压力加大到某 一数值时,气体开始液化。
CO2的pV图
当物质所处的温度高于临 界温度,压力大于临界压力时, 该物质处于超临界状态
一种既不同于气态,也不 同于液态和固态的新的流体态
特点 超临界流体的物性兼具液 体性质与气体性质。它基本上 仍是一种气态,但又不同于一 般气体,是一种稠密的气态。 其密度比一般气体要大两个数 量级,与液体相近。它的粘度 比液体小,扩散速度比液体快( 约两个数量级),所以有较好的 流动性和传递性能。
在压力趋于0的极限条件下, 各种气体 的行为均服从pVm=RT 的定量关系。 R 是一个对各种气体都适 用的常数——气体通用常数。
4、绝对温度与摄氏温度的关系 T/K=t/℃+273.15 5、混合理想气体的道尔顿分压定律 将A、B两种气体混和于容积为V的容器中,则总压
nRT ( nA nB ) RT n A RT nB RT p p A pB V V V V
第一章_气体的PVT性质

1.2 道尔顿定律和阿马格定律
• 理想气体混合物的总体积等于各个组分以同混 合物相同的温度和压力单独存在时的分体积之 和。
V VO2 VN 2
VO2
即理想气体的分体积等同于恒温恒压混合前的体积 ,但实际气体并不等同。
1.2 道尔顿定律和阿马格定律
例. 空气中氧气的体积分数为0.29,求101.325kPa、25℃时的1m3 空气中氧气的摩尔分数、分压力、分体积,并求若想得到1摩尔 纯氧气,至少需多少体积的空气。(将空气近似看成理想气体)
最后一式可用来计算气体的摩尔质量 M = RT(ρ/ p) p→0
§1.1 理想气体的状态方程 例:计算25℃,101325Pa时空气的密度。 (空气的分子量为29) 解:
n p 101325 3 mol m V RT 8.315 273.15 25 40.87 mol m
3
n 空气= M 40.87 29 g m 3 1.185 kg m 3 V
应用举例
例1.1· 1某空气压缩机每分钟吸入压力为101325Pa、温度为30º C
的空气41.2m3。经压缩后所排出的空气压力为192517Pa、温度
90º C,求每分钟排出的空气体积。 解:压缩机稳定操作时,每分钟吸人的空气的量与每分钟排出的 空气的量是相等的,但p、V、T均已改变,即 吸人量n1 = 排出量n2
jB = xB Vm,B / S xcVm,c
Vm,c : T, p一定时纯 c 组分的摩尔体积
2.分压力的定义与道尔顿定律
生产和科研实践中遇到的气体往往不是单一的气体,而
是由多种气体组成的气体混合物,例如空气就是。
若在一体积为V的容器中,放入n(N2)、n(O2),那
第1章气体的PVT性质

理想气体状态方程
p Pa; V m3; T K; n mol ;
R 摩尔气体常数 8.314J mol-1 K-1 理想气体状态方程也可表示为: pVm=RT pV = (m/M)RT pM= (m/V)RT=RT
理想气体状态方程也可表示为:
pVm= RT pV = (m/M)RT pM= (m/V)RT = RT
阿马加定律表明理想气体混合物的体积具有加和性,在 相同温度、压力下,混合后的总体积等于混合前各组分的体 积之和。 由二定律有:
pB VB nB yB p V n
高压下,混合前后气体体积一般将发生变化,阿马加定律 不再适用。这时需引入偏摩尔体积的概念进行计算。(见第 四章)
第三节 气体的液化和临界参数 一、理想气体 pV = nRT
理想气体混合物中某一组分B的分压 pB 等于该组分单独 存在于混合气体的T、V时产生的压力。
而理想气体混合物的总压等于各组分单独存在于混合气 体的T、V时产生的压力总和 道尔顿定律 对低压下真实气体混合物适用。在高压下,分子间的相互作
用不可忽视,且混合物不同分子间的作用与纯气体相同分子间
的作用有差别,所以某气体B的分压不再等于它单独存在时的 压力,所以分压定律不再适用
pV nRT nB RT B
及
pV = (m / Mmix) RT
式中:m 混合物的总质量; Mmix 混合物的摩尔质量; p,V 为混合物的总压与体积。
又 m = mB = nB MB = n yB MB = nMmix Mmix= m/n = yB MB 即混合物的摩尔质量又等于混合物的总质量除以混 合物的总的物质的量。 混合物的(平均)摩尔质量定义为: 混合物中各物质的摩尔 质量与其摩尔分数的乘积的和:
