曲柄滑块机构运动仿真
N2024运动仿真 曲柄滑块机构仿真

在装配环境下新建仿真部件。
方法/步骤
点击【应用模块】-【动画设计】或 者在功能区右击,弹出菜单选择【动 画设计】。
方法/步骤
左图表示了本步骤的内容,以图片内 容为准。
方法/步骤
基座添加【固定副】。
方法/步骤
添加【旋转副】,需要添加3个旋转 副。
方法/步骤
添加【滑动副】。
方法/步骤
添加【马达】,使机构运动起来。
点击【播放按钮】,开始播放仿真动画。
参考资料:典型运动机构仿真设计:基于UG NX4.0的应用实例
《典型运动机构仿真设计:基于UG NX4.0的应用实例》是2011年3月1日机械工业出版社出版的 图书,作者是张士军。
参考资料:UG NX 7.0装配与运动仿真实例教程
《UG NX 7.0装配与运动仿真实例教程》是2010年9月1日西北工业大学出版社出版的图书,作者 是曹岩。
NX1847运动仿真-曲柄滑块机构仿真
参考资料:UGNX1847从入门到精通(实战案例视频版)
《UGNX1847从入门到精通(实战案例视频版)》是化学工业出版社于2022年出版的书籍,作者 是周涛、刘浩、吕城 。
内容介绍
通过NX动画设计,制作曲柄滑块机构仿真,简单直观了解机械运动原理。
方法/步骤
谢谢观看
曲柄滑块机构运动仿真DOC

湖南农业大学工学院课程设计说明书课程名称:题目名称:班级:20 级专业班姓名:学号:指导教师:评定成绩:教师评语:指导老师签名:20 年月日曲柄滑块结构运动仿真一、概述二、各零件的创建1.曲柄·设置工作目录·创建曲轴的文档·选择好以毫米为单位点击工具栏的→→选择FRONT平面为草绘平面,RIGHT面为参考平面,进入草绘状态。
利用拉伸,选择一个拉伸面为草绘平面,以TOP面为参考平面,进入草绘状态→在第二次拉伸的中间位置创建一个平面平行于RIGHT平面为DTM1,利用镜像工具,将第二次拉伸的部分以DTM1镜像,得到利用拉伸和旋转创建出轴的其他部位如图利用创建平面工具,利用图示位置关系创建出一平面DTM2利用拉伸,以DTM2为草绘平面,创建键槽特征利用倒角选择倒角边和数据再利用倒圆角,选择倒圆角半径和需要倒圆角的边点击保存完成曲轴的创建。
2.连杆以及其他零件利用如曲轴的步骤,创建连杆和其他零件,如下只做出零件完成图连杆上部分连杆下盖活塞上盖底座三、零件的装配·设置工作目录·创建活塞的文档·选择好以毫米为单位进入装配界面后,点击装配将工作目录中的“di”文件放置到界面中,选择接下来逐一装配工作目录中其他零件,装配结果如下图点击应用程序中→机构进入运动仿真界面四、运动仿真点击右边工具栏定义伺服电动机选择如图所示轴定义如下点击确定后,进入运动分析选择分析类型点击运行后,机构将进行运动分析利用回放将运动过程制成运动图片接着利用测量进行分析五、整体爆炸视图。
基于MATLAB曲柄滑块机构运动仿真
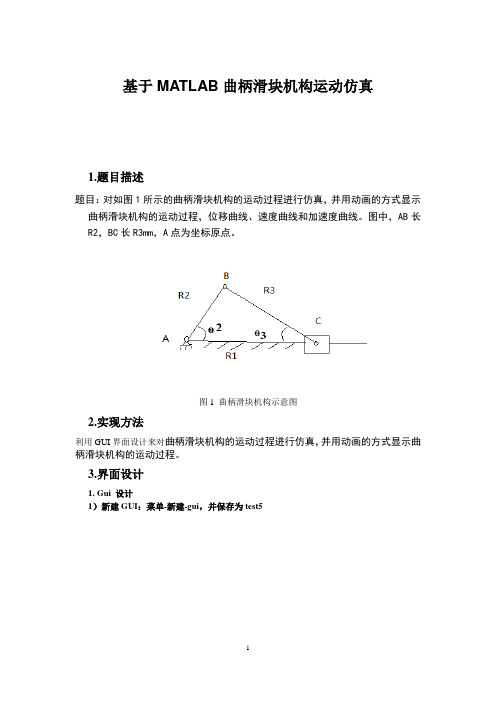
基于MATLAB曲柄滑块机构运动仿真1.题目描述题目:对如图1所示的曲柄滑块机构的运动过程进行仿真,并用动画的方式显示曲柄滑块机构的运动过程,位移曲线、速度曲线和加速度曲线。
图中,AB长R2,BC长R3mm,A点为坐标原点。
图1 曲柄滑块机构示意图2.实现方法利用GUI界面设计来对曲柄滑块机构的运动过程进行仿真,并用动画的方式显示曲柄滑块机构的运动过程。
3.界面设计1. Gui 设计1)新建GUI:菜单-新建-gui,并保存为test52)界面设计:拖拽左侧图标到绘图区,创建GUI界面拖拽左侧图标值绘图区设置如下的按钮最终的仿真界面如图所示3)代码添加:进入代码界面4.代码编程%模型求解a1=str2double(get(handles.edit1,'String'));a2=str2double(get(handles.edit2,'String'));a3=str2double(get(handles.edit3,'String'));a4=str2double(get(handles.edit4,'String'));a5=str2double(get(handles.edit5,'String'));a=a1*((1-cos(a4*a5))+0.25*(a1/a2)*(1-cos(2*a4*a5))); set(handles.edit6,'String',a);a0=(a4*a1)*(sin(a4*a5)+0.5*(a1/a2)*sin(2*a4*a5));set(handles.edit7,'String',a0);a6=(a4*a4*a1)*(cos(a4*a5)+(a1/a2)*cos(a4*a5));set(handles.edit8,'String',a6);%绘制位移、速度、加速度曲线axes(handles.axes3);r1=str2double(get(handles.edit1,'String'));r2=str2double(get(handles.edit2,'String'));omiga1=str2double(get(handles.edit4,'String'));x11=1:720;for i=1:720x1(i)=i*pi/180;%sin(x2(i)=r1/r2*sin(x1(i));x2(i)=asin(-r1/r2*sin(x1(i)));x22(i)=x2(i)*180/pi;r3(i)=r1*cos(x1(i))+r2*cos(x2(i));B=[-r1*omiga1*sin(x1(i));r1*omiga1*cos(x1(i))];A=[r2*sin(x2(i)) 1;-r2*cos(x2(i)) 0];X=inv(A)*B;omiga2(i)=X(1,1);v3(i)=X(2,1);endplot(x11/60,0.5*r1*sin(x1));xlabel('ʱ¼äÖá t/sec')ylabel('Á¬¸ËÖÊÐÄÔÚYÖáÉϵÄλÖÃ/mm')figure(2)plot(x11/60,r3);title('λÒÆÏßͼ')grid onhold off;xlabel('ʱ¼ät/sec')ylabel('»¬¿éλÒÆ r3/mm')figure(3)plot(x11/60,omiga2);title('Á¬¸Ë½ÇËÙ¶È')grid onhold off;xlabel('ʱ¼ä t/sec')ylabel('Á¬¸Ë½ÇËÙ¶È omiga2/rad/sec') figure(4)plot(x11/60,v3*pi/180);title('»¬¿éËÙ¶È')grid onhold off;xlabel('ʱ¼ä t/sec')ylabel('»¬¿éËÙ¶È v3/mm/sec')%绘制表格axes(handles.axes3);grid onaxes(handles.axes1);grid on%制作动画axes(handles.axes1);hf=figure('name','Çú±ú»¬¿é»ú¹¹'); set(hf,'color','r');hold onaxis([-6,6,-4,4]);grid onaxis('off');xa0=-5;%»îÈû×󶥵ã×ø±êxa1=-2.5;%»îÈûÓÒ¶¥µã×ø±êxb0=-2.5;%Á¬¸Ë×󶥵ã×ø±êxb1=2.2;%Á¬¸ËÓÒ¶¥µã×ø±êx3=3.5;%תÂÖ×ø±êy3=0;%תÂÖ×ø±êx4=xb1;%ÉèÖÃÁ¬¸ËÍ·µÄ³õʼλÖúá×ø±êy4=0;%ÉèÖÃÁ¬¸ËÍ·µÄ³õʼλÖÃ×Ý×ø±êx5=xa1;y5=0;x6=x3;%ÉèÖÃÁ¬Öá³õʼºá×ø±êy6=0;%ÉèÖÃÁ¬Öá³õʼ×Ý×ø±êa=0.7;b=0.7c=0.7a1=line([xa0;xa1],[0;0],'color','b','linestyle','-','linewidth',40); %ÉèÖûîÈûa3=line(x3,y3,'color',[0.5 0.60.3],'linestyle','.','markersize',300);%ÉèÖÃתÂÖa2=line([xb0;xb1],[0;0],'color','black','linewidth',10);%ÉèÖÃÁ¬¸Ëa5=line(x5,y5,'color','black','linestyle','.','markersize',40);%ÉèÖÃÁ¬¸Ë»îÈûÁ¬½ÓÍ·a4=line(x4,y4,'color','black','linestyle','.','markersize',50);%ÉèÖÃÁ¬¸ËÁ¬½ÓÍ·a6=line([xb1;x3],[0;0],'color','black','linestyle','-','linewidth',10 );a7=line(x3,0,'color','black','linestyle','.','markersize',50);%ÉèÖÃÔ˶¯ÖÐÐÄa8=line([-5.1;-0.2],[0.7;0.7],'color','y','linestyle','-','linewidth' ,5);%ÉèÖÃÆû¸×±Úa9=line([-5.1;-0.2],[-0.72;-0.72],'color','y','linestyle','-','linewi dth',5);%ÉèÖÃÆû¸×±Úa10=line([-5.1;-5.1],[-0.8;0.75],'color','y','linestyle','-','linewid th',5);%ÉèÖÃÆû¸×±Úa11=fill([-5,-5,-5,-5],[0.61,0.61,-0.61,-0.61],[a,b,c]);%ÉèÖÃÆû¸×ÆøÌålen1=4.8;%Á¬¸Ë³¤len2=2.5;%»îÈû³¤r=1.3;%Ô˶¯°ë¾¶dt=0.015*pi;t=0;while 1t=t+dt;if t>2*pit=0;endlena1=sqrt((len1)^2-(r*sin(t))^2);%Á¬¸ËÔÚÔ˶¯¹ý³ÌÖкáÖáÉϵÄÓÐЧ³¤¶Èrr1=r*cos(t);%°ë¾¶ÔÚÔ˶¯¹ý³ÌÖкáÖáÉϵÄÓÐЧ³¤¶Èxaa1=x3-sqrt(len1^2-(sin(t)*r)^2)-(r*cos(t));%»îÈûÔÚÔ˶¯¹ý³ÌÖеÄÓÒ¶¥µã×ø±êλÖÃxaa0=xaa1-2.5;%%»îÈûÔÚÔ˶¯¹ý³ÌÖеÄ×󶥵ã×ø±êλÖÃx55=x3-cos(t)*r;%Á¬¸ËÔÚÔ˶¯¹ý³ÌÖкá×ø±êλÖÃy55=y3-sin(t)*r;%Á¬¸ËÔÚÔ˶¯¹ý³ÌÖÐ×Ý×ø±êλÖÃset(a4,'xdata',x55,'ydata',y55);%ÉèÖÃÁ¬¸Ë¶¥µãÔ˶¯set(a1,'xdata',[xaa1-2.5;xaa1],'ydata',[0;0]);%ÉèÖûîÈûÔ˶¯set(a2,'xdata',[xaa1;x55],'ydata',[0;y55]);set(a5,'xdata',xaa1);%ÉèÖûîÈûÓëÁ¬¸ËÁ¬½ÓÍ·µÄÔ˶¯set(a6,'xdata',[x55;x3],'ydata',[y55;0]);set(a11,'xdata',[-5,xaa0,xaa0,-5]);%ÉèÖÃÆøÌåµÄÌî³äset(gcf,'doublebuffer','on');%Ïû³ýÕð¶¯drawnow;end5.结果(1)对它的结构参数进行设置,如下图所示。
基于某MATLAB曲柄滑块机构运动仿真报告材料

************************计算机仿真技术matlab报告************************曲柄滑块机构目录一、基于GUI的曲柄滑块机构运动仿真二、基于simulink的曲柄滑块机构运动仿真曲柄滑块机构1.题目描述题目:对如图1所示的曲柄滑块机构的运动过程进行仿真,并用动画的方式显示曲柄滑块机构的运动过程,位移曲线、速度曲线和加速度曲线。
图中,AB长R2,BC长R3mm,A点为坐标原点。
图1 曲柄滑块机构示意图2.实现方法利用GUI界面设计来对曲柄滑块机构的运动过程进行仿真,并用动画的方式显示曲柄滑块机构的运动过程。
3.界面设计1. Gui 设计1)新建GUI:菜单-新建-gui,并保存为test52)界面设计:拖拽左侧图标到绘图区,创建GUI界面拖拽左侧图标值绘图区设置如下的按钮最终的仿真界面如图所示3)代码添加:进入代码界面4.代码编程%模型求解a1=str2double(get(handles.edit1,'String'));a2=str2double(get(handles.edit2,'String'));a3=str2double(get(handles.edit3,'String'));a4=str2double(get(handles.edit4,'String'));a5=str2double(get(handles.edit5,'String'));a=a1*((1-cos(a4*a5))+0.25*(a1/a2)*(1-cos(2*a4*a5))); set(handles.edit6,'String',a);a0=(a4*a1)*(sin(a4*a5)+0.5*(a1/a2)*sin(2*a4*a5));set(handles.edit7,'String',a0);a6=(a4*a4*a1)*(cos(a4*a5)+(a1/a2)*cos(a4*a5));set(handles.edit8,'String',a6);%绘制位移、速度、加速度曲线axes(handles.axes3);r1=str2double(get(handles.edit1,'String'));r2=str2double(get(handles.edit2,'String'));omiga1=str2double(get(handles.edit4,'String'));x11=1:720;for i=1:720x1(i)=i*pi/180;%sin(x2(i)=r1/r2*sin(x1(i));x2(i)=asin(-r1/r2*sin(x1(i)));x22(i)=x2(i)*180/pi;r3(i)=r1*cos(x1(i))+r2*cos(x2(i));B=[-r1*omiga1*sin(x1(i));r1*omiga1*cos(x1(i))]; A=[r2*sin(x2(i)) 1;-r2*cos(x2(i)) 0];X=inv(A)*B;omiga2(i)=X(1,1);v3(i)=X(2,1);endplot(x11/60,0.5*r1*sin(x1));xlabel('ʱ¼äÖá t/sec')ylabel('Á¬¸ËÖÊÐÄÔÚYÖáÉϵÄλÖÃ/mm') figure(2)plot(x11/60,r3);title('λÒÆÏßͼ')grid onhold off;xlabel('ʱ¼ät/sec')ylabel('»¬¿éλÒÆ r3/mm')figure(3)plot(x11/60,omiga2);title('Á¬¸Ë½ÇËÙ¶È')grid onhold off;xlabel('ʱ¼ä t/sec')ylabel('Á¬¸Ë½ÇËÙ¶È omiga2/rad/sec') figure(4)plot(x11/60,v3*pi/180);title('»¬¿éËÙ¶È')grid onhold off;xlabel('ʱ¼ä t/sec')ylabel('»¬¿éËÙ¶È v3/mm/sec')%绘制表格axes(handles.axes3);grid onaxes(handles.axes1);grid on%制作动画axes(handles.axes1);hf=figure('name','Çú±ú»¬¿é»ú¹¹');set(hf,'color','r');hold onaxis([-6,6,-4,4]);grid onaxis('off');xa0=-5;%»îÈû×󶥵ã×ø±êxa1=-2.5;%»îÈûÓÒ¶¥µã×ø±êxb0=-2.5;%Á¬¸Ë×󶥵ã×ø±êxb1=2.2;%Á¬¸ËÓÒ¶¥µã×ø±êx3=3.5;%תÂÖ×ø±êy3=0;%תÂÖ×ø±êx4=xb1;%ÉèÖÃÁ¬¸ËÍ·µÄ³õʼλÖúá×ø±êy4=0;%ÉèÖÃÁ¬¸ËÍ·µÄ³õʼλÖÃ×Ý×ø±êx5=xa1;y5=0;x6=x3;%ÉèÖÃÁ¬Öá³õʼºá×ø±êy6=0;%ÉèÖÃÁ¬Öá³õʼ×Ý×ø±êa=0.7;b=0.7c=0.7a1=line([xa0;xa1],[0;0],'color','b','linestyle','-','linewidth',40); %ÉèÖûîÈûa3=line(x3,y3,'color',[0.5 0.6 0.3],'linestyle','.','markersize',300);%ÉèÖÃתÂÖa2=line([xb0;xb1],[0;0],'color','black','linewidth',10);%ÉèÖÃÁ¬¸Ëa5=line(x5,y5,'color','black','linestyle','.','markersize',40);%ÉèÖÃÁ¬¸Ë»îÈûÁ¬½ÓÍ·a4=line(x4,y4,'color','black','linestyle','.','markersize',50);%ÉèÖÃÁ¬¸ËÁ¬½ÓÍ·a6=line([xb1;x3],[0;0],'color','black','linestyle','-','linewidth',10);a7=line(x3,0,'color','black','linestyle','.','markersize',50);%ÉèÖÃÔ˶¯ÖÐÐÄa8=line([-5.1;-0.2],[0.7;0.7],'color','y','linestyle','-','linewidth',5);%ÉèÖÃÆû¸×±Úa9=line([-5.1;-0.2],[-0.72;-0.72],'color','y','linestyle','-','linewidth',5);%ÉèÖÃÆû¸×±Úa10=line([-5.1;-5.1],[-0.8;0.75],'color','y','linestyle','-','linewidth',5);%ÉèÖÃÆû¸×±Úa11=fill([-5,-5,-5,-5],[0.61,0.61,-0.61,-0.61],[a,b,c]);%ÉèÖÃÆû¸×ÆøÌålen1=4.8;%Á¬¸Ë³¤len2=2.5;%»îÈû³¤r=1.3;%Ô˶¯°ë¾¶dt=0.015*pi;t=0;while 1t=t+dt;if t>2*pit=0;endlena1=sqrt((len1)^2-(r*sin(t))^2);%Á¬¸ËÔÚÔ˶¯¹ý³ÌÖкáÖáÉϵÄÓÐЧ³¤¶Èrr1=r*cos(t);%°ë¾¶ÔÚÔ˶¯¹ý³ÌÖкáÖáÉϵÄÓÐЧ³¤¶È xaa1=x3-sqrt(len1^2-(sin(t)*r)^2)-(r*cos(t));%»îÈûÔÚÔ˶¯¹ý³ÌÖеÄÓÒ¶¥µã×ø±êλÖÃxaa0=xaa1-2.5;%%»îÈûÔÚÔ˶¯¹ý³ÌÖеÄ×󶥵ã×ø±êλÖà x55=x3-cos(t)*r;%Á¬¸ËÔÚÔ˶¯¹ý³ÌÖкá×ø±êλÖÃy55=y3-sin(t)*r;%Á¬¸ËÔÚÔ˶¯¹ý³ÌÖÐ×Ý×ø±êλÖÃset(a4,'xdata',x55,'ydata',y55);%ÉèÖÃÁ¬¸Ë¶¥µãÔ˶¯set(a1,'xdata',[xaa1-2.5;xaa1],'ydata',[0;0]);%ÉèÖûîÈûÔ˶¯set(a2,'xdata',[xaa1;x55],'ydata',[0;y55]);set(a5,'xdata',xaa1);%ÉèÖûîÈûÓëÁ¬¸ËÁ¬½ÓÍ·µÄÔ˶¯set(a6,'xdata',[x55;x3],'ydata',[y55;0]);set(a11,'xdata',[-5,xaa0,xaa0,-5]);%ÉèÖÃÆøÌåµÄÌî³äset(gcf,'doublebuffer','on');%Ïû³ýÕð¶¯drawnow;end5.结果(1)对它的结构参数进行设置,如下图所示点击计算按钮动画,结果如下图所示点击表格对图形进行画表格处理点击绘图,即可得到位移、速度、加速度曲线,如下图所示二、基于simulink 的曲柄滑块机构运动仿真(1)运用矢量求解法求解(2)绘制速度接线图,如下图所示:运动仿真结果如下图:(3)绘制加速度接线图,如下图所示:运行结果如图所示:。
曲柄滑块机构ProE结构分析与运动仿真

曲柄滑块机构Pro/E结构分 析与运动仿真 班级: 学号: 指导教师:
工作条件:
本机构为曲柄滑块机构的简易模拟机 构,利用杆件机构,带动滑块往返运 动。假设滑块受200N横向摩擦力,小 齿轮电机设置为常量30,要求连杆最 大承受应力4MPa。 应用:曲柄滑块机构广泛应用于往复 活塞式发动机、冲床等的主机构中。
分析结束后的云文图:可以看到有应力集中
分析结束后的云文图:可以看到有位移集中
分析结束后的云文图:可以看到有应变集中
谢谢
连杆与滑块连接处的连接位置如下图:
连杆与滑块连接处的连接速度如下图:
连杆与滑块连接处的连接加速度如下图:
第三部分、连杆静态分析
1、静态分析: 打开连杆,进入分析模块,利用上面测量 的最大应力,来定义连杆所受的力,将所 受力进行合成,定义一端力为3.8e+06 另 外一段固定。材料选择 steel
底座
先在平面做大概的图 形尺寸不定连环用6毫 米的孔再拉伸 后再镜 像再底部做垂直平面 拉伸即可
共3个销钉简单不做陈述
第二部分、动态仿真与测量
1、组装:
把上章建的基座,连杆,滑块进行组装. 各个零件组装连接如下: 1)销钉与基座采用销连接约束面与面对齐 2)销钉与连杆采用销连接约束面与面对齐 3)滑块与连杆采用销连接同时约束面与面 对齐
仿真视频如下
第一部分
曲柄滑块机构零件的建立
滑块及垫板
底板长160宽80拉伸10
滑块长40宽30拉伸 19.4圆孔直径6
连杆机构1
前臂长55中间 半径为4圆角和2圆角 上过渡和半径为8的下 过渡厚度为4 后臂长48 拉伸12 另作垂直平面做圆环 最后镜像
曲柄滑块机构的优化设计及运动仿真学位论文

曲柄滑块机构的优化设计及运动仿真学位论文曲柄滑块机构的优化设计及运动仿真目录目录...............................................................1 摘要............................................................... 第1章绪论........................................................ 选题的目的及意义............................................. 优化设计方法的概述........................................... 国内外的研究现状............................................ 主要研究内容............................................ 第2章曲柄滑块机构的受力分析......................................曲柄滑块机构的分类...........................................曲柄滑块机构的动力学特性.....................................曲柄滑块机构中运动学特性..................................... 第3章偏置式曲柄滑块机构的优化设计................................ 优化软件的介绍.............................................. MATLAB的发展历程和影响...................................MATLAB 在机构设计中的应用................................. 机构优化设计实例分析........................................ 设计目标的建立...........................................根据设计要求,确定约束条件................................利用MATLAB进行优化设计.................................... 编制优化程序.............................................. 程序运行结果及处理........................................ 对优化结果进行验证和分析................................. 第4章偏置曲柄滑块机构的运动学建模与仿真.......................... 偏置曲柄滑块机构运动特性建模................................ 仿真环境简介............................................. 机构的运动学建模........................................ 运动学仿真的实现.......................................... 函数的编制及初始参数的设定............................... 构建Simulink仿真框图.................................... 对仿真结果进行分析...................................... 总结...............................................................〔Toolboxs〕组成虽然该软件的初衷并不是为控制系统设计的,但它提供了强大的矩阵处理和绘图功能,可靠灵活且方便,非常适合现代控制理论的计算机辅助设计。
曲柄导杆滑块等机构测试仿真实验报告

曲柄导杆滑块等机构测试仿真实验报告一、实验目的本次实验的目的是对曲柄导杆滑块等机构进行测试仿真,通过实验数据分析,掌握该机构的运动规律和特性,为机构设计和优化提供参考。
二、实验原理曲柄导杆滑块等机构是一种常见的机械传动装置,其主要由曲柄、连杆、导杆和滑块等部件组成。
在运动过程中,曲柄带动连杆运动,使导杆产生往复直线运动,从而驱动滑块完成工作。
三、实验器材本次实验所使用的器材包括:计算机、SolidWorks软件、Matlab软件。
四、实验步骤1.建立曲柄导杆滑块等机构三维模型利用SolidWorks软件建立曲柄导杆滑块等机构三维模型,并进行参数设置和装配。
2.进行运动分析利用SolidWorks Motion模块对该机构进行运动分析,并得出相关数据。
3.进行力学分析利用Matlab软件对该机构进行力学分析,并得出相关数据。
4.比较分析结果将两种分析方法得到的数据进行比较和分析,掌握该机构的运动规律和特性。
五、实验结果1.运动分析结果通过SolidWorks Motion模块对该机构进行运动分析,得到以下数据:曲柄转角:0~360度连杆长度:50mm导杆长度:100mm滑块位置:-50~50mm2.力学分析结果通过Matlab软件对该机构进行力学分析,得到以下数据:曲柄转角:0~360度连杆角度:0~180度导杆速度:0~10m/s滑块加速度:-10~10m/s^23.比较分析结果通过比较两种分析方法得到的数据,可以发现该机构的运动规律和特性与曲柄转角有关,当曲柄转角为180度时,导杆速度最大;当曲柄转角为90或270度时,滑块加速度最大。
此外,连杆角度与导杆速度呈正比关系。
六、实验结论通过本次实验可以得出以下结论:1.曲柄导杆滑块等机构的运动规律和特性与曲柄转角、连杆角度等参数有关。
2.该机构在不同工况下具有不同的性能表现,需要根据具体情况进行优化设计。
3.利用SolidWorks Motion模块和Matlab软件可以对该机构进行运动分析和力学分析,为机构设计和优化提供参考。
PROE4.0曲柄滑块机构运动学仿真

曲柄滑块机构运动学仿真
1、目的
本文档旨在基于PROE4.0版本软件,设计一曲柄滑块机构,并仿真测量其关键点速度、加速度、位移等关键信息。
2、模型设计
2.1 整体尺寸介绍
模型主要包括底座、曲柄、连杆、滑块四个零部件,具体尺寸如图所示。
AB=28mm,BC=68mm,CE=435mm,AD=150mm,DF=60mm。
图1 关键位置尺寸
2.2 部件连接关系
1)底座为机架,固定连接,在PROE软件中,切记连接成“用户定义”-“缺省”
2)曲柄与底座为“铰接”。
与连杆也为“铰接”。
3)滑块与底座为“滑动杆”连接。
4)连杆一端与曲柄为“铰接”;再新建一连接关系,与滑块“铰接”。
3、运动学仿真设置
1)在装配完成后,点击“应用程序”-“机构”菜单,进入机构仿真界面。
2)添加伺服电机驱动,设置成如图界面,并在“速度”一栏,点击“速度、位置、加速度”
3)仿真。
点击仿真按钮,设置成如图所示,选择“运动学”仿真,并点击“运行”,机构开始动作。
4)回放,保存。
仿真完成后,点击回放按钮,可以回放仿真,并进行保存。
5)测量。
仿真结束后,可以测量关键信息,如关键点速度、加速度、位置等,如图所示。
在左上角可以显示相应曲线。
6)仿真结束后,保存。
下一次运行时,可以读取相关数据。
